Амплитуда скорости колебаний формула: Амплитуда скорости груза, теория и онлайн калькуляторы
alexxlab | 01.07.1984 | 0 | Разное
Гармонические колебания. | Объединение учителей Санкт-Петербурга
Основные ссылки
CSS adjustments for Marinelli theme
Объединение учителей Санкт-Петербурга
Форма поиска
Поиск
Вы здесь
Главная » Гармонические колебания.
ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ | ||
Колебания, при которых изменения физических величин происходят по закону косинуса или синуса (гармоническому закону), наз. гармоническими колебаниями. Например, в случае механических гармонических колебаний:. В этих формулах ω – частота колебания, xm – амплитуда колебания, φ0 и φ0’ – начальные фазы колебания. Приведенные формулы отличаются определением начальной фазы и при φ0’ = φ0 +π/2 полностью совпадают. |
| |
Это простейший вид периодических колебаний. Конкретный вид функции (синус или косинус) зависит от способа выведения системы из положения равновесия. Если выведение происходит толчком (сообщается кинетическая энергия), то при t=0 смещение х=0, следовательно, удобнее пользоваться функцией sin, положив φ0’=0; при отклонении от положения равновесия (сообщается потенциальная энергия) при t=0 смещение х=хm, следовательно, удобнее пользоваться функцией cos и φ0=0. |
| |
Выражение, стоящее под знаком cos или sin, наз. фазой колебания: . Фаза колебания измеряется в радианах и определяет значение смещения (колеблющейся величины) в данный момент времени. | ||
Амплитуда колебания зависит только от начального отклонения (начальной энергии, сообщенной колебательной системе). |
| |
Скорость и ускорение при гармонических колебаниях. | ||
Согласно определению скорости, скорость – это производная от координаты по времени |
| |
Таким образом, мы видим, что скорость при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания скорости опережают колебания смещения по фазе на π/2. |
| |
Величина – максимальная скорость колебательного движения (амплитуда колебаний скорости). | ||
Следовательно, для скорости при гармоническом колебании имеем: , а для случая нулевой начальной фазы (см. | ||
Согласно определению ускорения, ускорение – это производная от скорости по времени: – вторая производная от координаты по времени. Тогда: . Ускорение при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания ускорения опережают колебания скорости на π/2 и колебания смещения на π (говорят, что колебания происходят в противофазе). | ||
Величина – максимальное ускорение (амплитуда колебаний ускорения). Следовательно, для ускорения имеем: , а для случая нулевой начальной фазы: (см. график). | ||
Из анализа процесса колебательного движения, графиков и соответствующих математических выражений видно, что при прохождении колеблющимся телом положения равновесия (смещение равно нулю) ускорение равно нулю, а скорость тела максимальна (тело проходит положение равновесия по инерции), а при достижении амплитудного значения смещения – скорость равна нулю, а ускорение максимально по модулю (тело меняет направление своего движения). | ||
Сравним выражения для смещения и ускорения при гармонических колебаниях: и . |
| |
Можно записать: – т.е. вторая производная смещения прямо пропорциональна (с противоположным знаком) смещению. Такое уравнение наз. уравнением гармонического колебания. Эта зависимость выполняется для любого гармонического колебания, независимо от его природы. Поскольку мы нигде не использовали параметров конкретной колебательной системы, то от них может зависеть только циклическая частота. | ||
Часто бывает удобно записывать уравнения для колебаний в виде: , где T – период колебания. Тогда, если время выражать в долях периода подсчеты будут упрощаться. Например, если надо найти смещение через 1/8 периода, получим: . Аналогично для скорости и ускорения. | ||
Теги:
конспект
2.3.3 Колебания при наличии внешней вынуждающей периодической силы
Идеальный случай.
Пусть на шарик в пружинном маятнике действует периодическая внешняя сила
(1)
В этом случае для смещения шарика вблизи положения равновесия вместо уравнения (1) пункта 2.3.1 получаем
(2)
где .
Нетрудно проверить, что решение уравнения (1) в случае имеет вид [1-3]:
(3)
где
Первое слагаемое в (3) описывает свободные колебания, а второе – так называемые вынужденные колебания с амплитудой . Таким образом, амплитуда и начальная фаза колебаний при действии вынуждающей силы зависят не только от начальных условий, но и от параметров силы.
В предельном случае точного совпадения частот
и
система уже не может совершать периодические колебания. Зависимость координаты
от времени будет выражаться формулой
Зависимость координаты
от времени будет выражаться формулой
(4)
Такое движение можно рассматривать как колебания с линейно нарастающей со временем амплитудой. Явление раскачки колебаний под действием периодической внешней силы называется
Следует подчеркнуть, что неограниченный резонансный рост амплитуды вынужденных колебаний есть идеализация системы. Во-первых, когда амплитуда колебаний становится достаточно большой, осциллятор, как правило, перестаёт быть линейным. Во-вторых, при записи уравнения (12) не учитывались силы трения, приводящие к затуханию колебаний. Рассмотрим роль последнего фактора более подробно.
Вынужденные колебания при наличии трения.
Если на осциллятор с трением действует внешняя сила (1), то уравнение таких колебаний имеет вид
(5)
где – коэффициент затухания, определённый в пункте 2.3.2.
Общее решение (5) имеет вид [1–3]
(6)
где
– решение уравнения (5) в отсутствие внешней силы (собственные колебания осциллятора (3) – (5) пункта 2.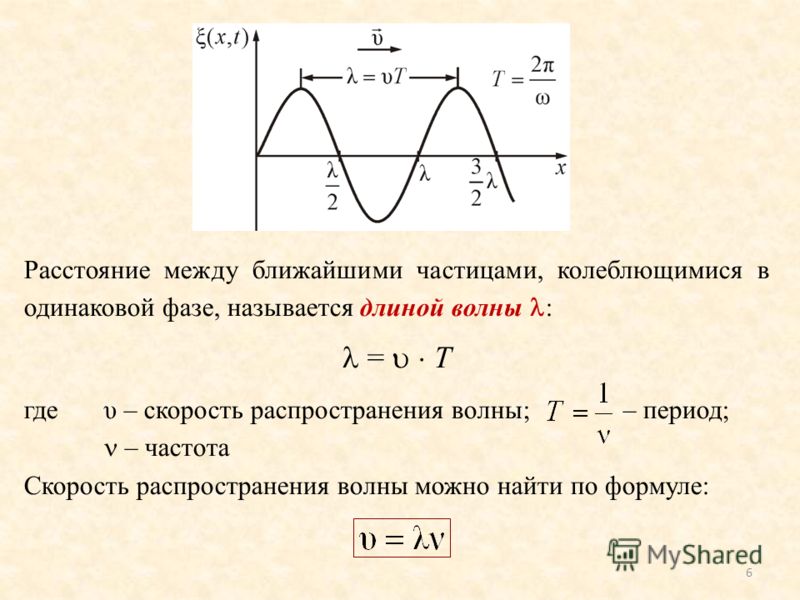 3.2.
3.2.
Благодаря трению , собственные колебания затухают: при . Поэтому через время колебательная система будет совершать только вынужденные колебания, описываемые вторым слагаемым в (6). Важно отметить, что параметры вынужденных колебаний не зависят от начальных условий. Эти колебания происходят с частотой внешней силы , характеризуются амплитудой и фазовым сдвигом
(7)
(8)
Как следствие из формулы (8), коэффициент связан с производной функции следующим образом:
(9)
Важным отличием от случая вынужденных колебаний осциллятора без трения является наличие сдвига фазы между колебаниями вынуждающей силы и колебаниями осциллятора. При точном совпадении частот, , вне зависимости от величины затухания, сдвиг фазы составляет .
Другим существенным следствием наличия затухания является качественное изменение вида резонансной кривой. На рис. 1 приведена зависимость
и
для некоторых характерных значений
.
На рис. 1 приведена зависимость
и
для некоторых характерных значений
.
Рис. 1а. Резонансные кривые (АЧХ) линейного осциллятора для различных значений коэффициента трения: , , , .
Рис. 1б. Зависимость сдвига фаз (ФЧХ) между колебаниями вынуждающей силы и осциллятора.
Максимальное значение амплитуды вынужденных колебаний (7), определяется формулой
(10)
Этому максимуму соответствует резонансная частота
(11)
при условии, что
. Если затухание мало
() то максимум резонансной кривой приблизительно совпадает с собственной частотой осциллятора
. По мере роста
этот максимум смещается в сторону меньших частот ( рис. 1а). При
максимум амплитуды вынужденных колебаний
приходится на частоту
. TПо существу это означает исчезновение резонанса. Ранее указывалось, что режим апериодического затухания свободных колебаний возникает лишь при
. Следовательно, в интервале
вынужденные колебания уже не имеют резонансного характера, а собственные движения осциллятора ещё сохраняют колебательный характер.
TПо существу это означает исчезновение резонанса. Ранее указывалось, что режим апериодического затухания свободных колебаний возникает лишь при
. Следовательно, в интервале
вынужденные колебания уже не имеют резонансного характера, а собственные движения осциллятора ещё сохраняют колебательный характер.
Как видно из формулы (7), при слабом затухании амплитуда вынужденных колебаний быстро убывает по мере удаления от резонансной частоты. В частности, она уменьшается в раза при значениях , равных
,
(12)
Величину принято называть шириной резонанса. При малых эта величина составляет . Тогда добротность, определяемая формулой (8) пункта 2.3.2, связана с шириной резонансной кривой соотношением
(13)
Таким образом, ширина резонансной кривой определяется добротностью и собственной частотой. Чем больше добротность колебательной системы, тем меньше ширина резонансного пика. Как видно из формулы (13), добротность колебательной системы можно оценить из экспериментальных АЧХ осциллятора и соответственно определить коэффициент затухания.
Как видно из формулы (13), добротность колебательной системы можно оценить из экспериментальных АЧХ осциллятора и соответственно определить коэффициент затухания.
Выводы.
- В случае действия на колебательную систему внешней вынуждающей силы, колебания системы описываются периодическим законом, причём амплитуда и начальная фаза колебаний зависят не только от начальных условий, но и от параметров силы (3).
- Если частоты и совпадают, то система совершает колебания с линейно нарастающей со временем амплитудой (4) – явление резонанса.
- В случае наличии трения и действия на колебательную систему внешней вынуждающей силы через время колебательная система будет совершать только вынужденные колебания, описываемые вторым слагаемым в (6).
- Параметры установившихся вынужденных колебаний не зависят от начальных условий. Эти колебания происходят с частотой внешней силы
, характеризуются амплитудой (7) и фазовым сдвигом (8).
 При совпадении частот,
, вне зависимости от величины затухания, сдвиг фазы составляет
.
При совпадении частот,
, вне зависимости от величины затухания, сдвиг фазы составляет
. - Ширина резонансной кривой определяется добротностью и собственной частотой колебаний (13).
Литература.
- С.Э. Хайкин. Механика. – М.: ОГИЗ, 1947. – 574 с.
- Д. В. Сивухин. Механика. – М.: Наука, 1989. – 576. с.
- Карлов Н.В., Кириченко Н.А. Колебания, волны, структуры. – М.: ФИЗМАТЛИТ, 2003. – 496 с.
Белорусский государственный университет транспорта – БелГУТ (БИИЖТ)
Регистрация на конференцию «Проблемы безопасности на транспорте»
Регистрация на конференцию «Тихомировские чтения»
Как поступить в БелГУТ:
дневное, заочное полное,
заочное сокращенное
Как получить место
в общежитии БелГУТа
Как поступить иностранному гражданину
События
Все события
| Пн | Вт | Ср | Чт | Пт | Сб | Вс |
|---|---|---|---|---|---|---|
1 Дата : 2022-09-01 | 2 | 3 | 4 | |||
5 Дата : 2022-09-05 | 6 Дата : 2022-09-06 | 7 Дата : 2022-09-07 | 8 Дата : 2022-09-08 | 9 Дата : 2022-09-09 | 10 Дата : 2022-09-10 | 11 Дата : 2022-09-11 |
12 | 13 | 14 | 15 Дата : 2022-09-15 | 16 Дата : 2022-09-16 | 17 Дата : 2022-09-17 | 18 |
19 | 20 | 21 | 22 | 23 | 24 | 25 |
26 | 27 | 28 | 29 | 30 | ||
Все анонсы
- Матч по мини-футболу между БелГУТом и ГГТУ.
 ..
.. - Велопробег «В единстве – сила»…
- Диалоговая площадка ко Дню народного единства…
- Логистика. Обучение для студентов выпускных курсов…
- ЕДИ «История белорусской государственности – основ…
- Акция «Мы едины» – поем гимн вместе…
- Набор в студию рисунка и живописи…
- Открытая лекция Быченко Олега Владимировича…
- Квиз «Гісторыя майго жыцця»…
- Набор в волонтерский сектор Студсовета…
Анонсы
Университет
Абитуриентам
Студентам
Конференции
Приглашения
Матч по мини-футболу между БелГУТом и ГГТУ…
Велопробег «В единстве – сила»…
Диалоговая площадка ко Дню народного единства…
Логистика. Обучение для студентов выпускных курсов…
Новости
Университет
Международные связи
Спорт
Воспитательная работа
Жизнь студентов
Новости подразделений
- Университет
Встреча ректора со студентами в студенческом городке. ..
..
15 сентября 2022
- Университет
Проект студента востребован в городе
14 сентября 2022
- Университет
Будущее Беларуси – в единстве
14 сентября 2022
- Университет
Видео-репортаж Дня рождения Гомеля
13 сентября 2022
- Воспитательная работа
Віктарына да Дня народнага адзінства
13 сентября 2022
- Студенческая жизнь
Интервью с участниками открытия фестиваля «Сожскi карагод» и видео-реп…
13 сентября 2022
- Спорт
Неделя спорта и здоровья
13 сентября 2022
- Университет
Опубликован сборник материалов конференции «Водоснабжение, химия и при. ..
..
12 сентября 2022
- Университет
Студент БелГУТа из Марокко рассказывает об учебе в Беларуси…
12 сентября 2022
Другие новости
- БРСМ – всегда на помощь! День города Гомеля…
- Новый номер газеты «Вести БелГУТа»
- Республиканский легкоатлетический студенческий забег…
- БелГУТ предлагает жилые помещения арендного использования…
- С Днем рождения, Гомель!
- Живой герб Гомеля на открытии «Сожскага карагода» …
- Круглый стол «Вопросы подготовки специалистов в области правовой инфор…
- Встреча первокурсников с инспектором по делам несовершеннолетних желез…
- Атрымай асалоду ад роднай мовы
- Региональный форум «Беларусь адзiная»
- Профилактика правонарушений
КУДА ПОСТУПАТЬ
Все факультеты
БелГУТ на Доске почета
Достижения университета
Предложения
Все предложения
Видеотека
Все видео
Фотогалерея
Все фото
Амплитуда вибраций с использованием скорости частицы Калькулятор
✖Скорость частицы – это скорость изменения смещения частицы. | Сантиметр / часСантиметр / минутуСантиметр / секКосмическая скорость – ПервыйКосмическая скорость – ВторойКосмическая скорость – ТретьяСкорость ЗемлиЛапка / часЛапка / минутуНога / секКилометры / часКилометры / минутуКилометры / секМорской узелУзел (Великобритания)маакМаха (стандарт СИ)Метр / часМетр / минутуМетр / секмили / часмили / минутумили / секМиллиметр / часМиллиметр / минутуМиллиметр / секМорская миля в деньМорская миля в часСкорость звука в чистой водеСкорость звука в морской воде (20 ° C и 10 метров глубиной)Двор / часДвор / минутуДвор / сек | +10% -10% | |
✖Частота – это количество раз, когда что-то происходит в определенный период.ⓘ Частота [f] | АттогерцУдары / минутаСантигерцЦикл / секДекагерцдецигерцExahertzFemtohertzфрамес 3a второйГигагерцгектогерцГерцКилогерцмегагерцмикрогерцмиллигерцнаногерцпетагерцPicohertzРеволюция / деньРеволюция / часРеволюция / минутуРеволюция / секунда ТерагерцЙоттахерцЗеттахерц | +10% -10% |
|
✖Амплитуда вибрации – это наибольшее расстояние, на которое волна, особенно звуковая или радиоволна, движется вверх и вниз. |
AU длиныствораАнгстремарпанастрономическая единицаАттометрЯчменное зерноМиллиардный светБор РадиусКабель (Международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Cubit (Великобритания)ДекаметрДециметрЗемля-Луна РасстояниеЗемли Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Положение)Световой годСсылкаДлинные CubitДлинные РидМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрНавигационный лига (INT)Навигационный лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаточкаполюскварталРидпрутРоман Actusканатныйрусский АрчинSpan (ткань)Радиус СолнцаТераметртвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр |
⎘ копия |
👎
Формула
сбросить
👍
Амплитуда вибраций с использованием скорости частицы Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Преобразование входов в базовый блок
Скорость частицы: 5 Миллиметр / сек –> 0.005 Метр / сек (Проверьте преобразование здесь)
Частота: 2 Герц –> 2 Герц Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
0.000397887357729738 метр –>0.397887357729738 Миллиметр (Проверьте преобразование здесь)
< 10+ Параметры контроля вибрации при взрывных работах. Калькуляторы
Амплитуда вибраций с использованием скорости частицы формула
Амплитуда вибрации = (Скорость частицы/(2*pi*Частота))
A = (v/(2*pi*f))
Что такое амплитуда?
Амплитуда периодической переменной является мерой ее изменения за один период. Существуют различные определения амплитуды, которые зависят от величины разницы между крайними значениями переменных. В старых текстах фаза функции периода иногда называется амплитудой.
В старых текстах фаза функции периода иногда называется амплитудой.
Что такое ускорение движения частицы?
Ускорение объекта (частицы воздуха) означает изменение его скорости с течением времени. Ускорение технически определяется как «скорость изменения скорости объекта во времени» и задается уравнением. куда. a – вектор ускорения. v – вектор скорости, выраженный в м / с.
Share
Copied!
Механические колебания | Формулы по физике
Ускорение силы упругости
Найти
Известно, что:
akxm =
Вычислить ‘a’Сила упругости
Найти
Известно, что:
Fkx =
Вычислить ‘F’Уравнение движения математического маятника
Найти
Известно, что:
agxl =
Вычислить ‘a’Уравнение свободных колебаний
Найти
Известно, что:
aωx =
Вычислить ‘a’Уравнение движения пружинного маятника
Найти
Известно, что:
ωkm =
Вычислить ‘ω’Уравнение движения математического маятника
Найти
Известно, что:
ωgl =
Вычислить ‘ω’Свободные колебания: отклонение
Найти
Известно, что:
xx_mωt =
Вычислить ‘x’Частота и период колебаний
Найти
Известно, что:
νT =
Вычислить ‘ν’Циклическая частота колебаний
Найти
Известно, что:
ωπT =
Вычислить ‘ω’Циклическая частота колебаний
Найти
Известно, что:
ωπν =
Вычислить ‘ω’Фаза гармонических колебаний
Найти
Известно, что:
φωt =
Вычислить ‘φ’Фаза гармонических колебаний
Найти
Известно, что:
φπtT =
Вычислить ‘φ’Фаза гармонических колебаний
Найти
Известно, что:
φπνt =
Вычислить ‘φ’Гармоническое колебание: отклонение
Найти
Известно, что:
xx_mωtφ =
Вычислить ‘x’Период колебания пружинного маятника
Найти
Известно, что:
Tπmk =
Вычислить ‘T’Период колебания математического маятника
Найти
Известно, что:
Tπlg =
Вычислить ‘T’Гармонические колебания: скорость тела
Найти
Известно, что:
vv_mωtπ =
Вычислить ‘v’Гармонические колебания: скорость тела
Найти
Известно, что:
vv_mωt =
Вычислить ‘v’Гармонические колебания: ускорение тела
Найти
Известно, что:
aa_mωtπ =
Вычислить ‘a’Гармонические колебания: ускорение тела
Найти
Известно, что:
aωxt =
Вычислить ‘a’Гармонические колебания: скорость тела
Найти
Известно, что:
vωxt =
Вычислить ‘v’Гармонические колебания: максимальная скорость тела
Найти
Известно, что:
v_mωx_m =
Вычислить ‘v_m’Гармонические колебания: максимальное ускорение тела
Найти
Известно, что:
a_mωv_m =
Вычислить ‘a_m’Гармонические колебания: максимальное ускорение тела
Найти
Известно, что:
a_mωx_m =
Вычислить ‘a_m’Гармонические колебания: кинетическая энергия тела
Найти
Известно, что:
E_kmv =
Вычислить ‘E_k’Гармонические колебания: потенциальная энергия тела
Найти
Известно, что:
E_pkx =
Вычислить ‘E_p’Гармонические колебания: полная энергия тела
Найти
Известно, что:
EE__kE__p =
Вычислить ‘E’Гармонические колебания: полная энергия тела
Найти
Известно, что:
Emvkx =
Вычислить ‘E’Резонанс – амплитуда колебаний
Найти
Известно, что:
xFωμ =
Вычислить ‘x’Механические колебания в физике: основные формулы и законы
Оглавление:
Механическими колебаниями называются механические движения или процессы, повторяющиеся во времени.
Если колебания происходят через равные промежутки времени, они называются периодическими.
Смещение х — это расстояние от маятника до положения равновесия. Амплитуда А — это наибольшее смещение. При гармонических колебаниях амплитуда — постоянная величина. В одном полном колебании содержится 4 амплитуды.
Период Т — время одного полного колебания. Период при гармонических колебаниях — постоянная величина.
Частота v — это число полных колебаний в единицу времени. Частота — величина, обратная периоду. Частота гармонических колебаний не изменяется в процессе колебаний.
Циклическая частота — это величина, равная числу полных колебаний, совершенных за время, равное . Циклическая частота гармонических колебаний не изменяется в процессе колебаний.
Фаза — это величина под знаком косинуса или синуса в уравнении гармонических колебаний, показывающая, какая доля периода прошла от начала колебания. Фаза гармонических колебаний в процессе колебаний изменяется.
Фаза гармонических колебаний в процессе колебаний изменяется.
Гармонические колебания — это колебания, в которых данный параметр изменяется по закону косинуса или синуса. Если момент начала отсчета времени колебаний совпадает с максимальным отклонением маятника от положения равновесия, то колебания являются косинусоидальными и их начальная фаза равна нулю. Если момент начала отсчета времени колебаний совпадает с прохождением маятником положения равновесия, то колебания являются синусоидальными и их начальная фаза тоже равна нулю.
Графики косинусоидальных гармонических колебаний смещения х, скорости v, ускорения а, силы F, потенциальной , кинетической и полной Е энергий, когда начальная фаза равна нулю, изображены на рис. 307.
Ниже приведены уравнения механических колебаний и волн.
У равнения гармонических колебаний:
Здесь х — смещение маятника (м), А — амплитуда колебаний (м), — фаза (рад), — циклическая (угловая) частота (рад/с), t — время колебаний (с), — начальная фаза (рад).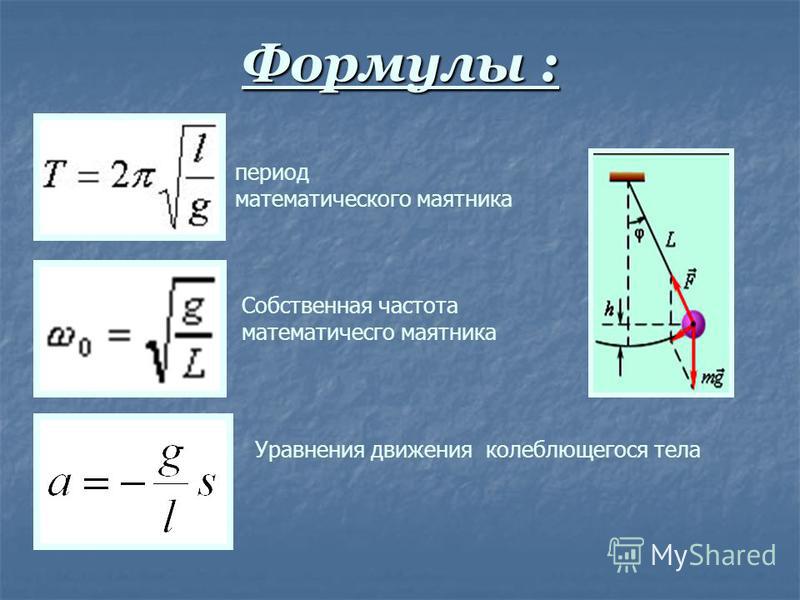
Формула фазы колебаний:
Здесь — фаза (рад), — циклическая частота (рад/с), t — время (с), — начальная фаза (рад).
Формулы циклической частоты:
Здесь —циклическая частота (рад/с), v —частота колебаний (Гц), Т — период (с), k — жесткость пружинного маятника (Н/м), m — масса маятника (кг), g — ускорение свободного падения , I — длина математического маятника (м).
Формулы периода колебаний:
Здесь Т — период (с), t — время колебаний (с), N — число колебаний за это время (безразмерное), v — частота колебаний (Гц). Остальные величины названы в предыдущей формуле.
Формулы частоты колебаний:
Здесь v — частота (Гц), N — число колебаний, Т — период (с), л = 3,14 — число «пи», t — время колебаний (с), k — жесткость пружинного маятника (Н/м), m — масса маятника (кг), g — ускорение свободного падения , I — длина математического маятника.
Формулы скорости гармонических колебаний:
Здесь v — мгновенная скорость (м/с), — первая производная смещения по времени (м/с), — циклическая частота (рад/с), А — амплитуда колебаний (м), — начальная фаза (рад), — максимальная скорость колебаний (м/с).
Формулы ускорения при гармонических колебаниях
Здесь а — мгновенное ускорение — первая производная скорости по времени , — максимальное ускорение . Остальные величины названы в предыдущей формуле.
Формулы длины волны:
Здесь — длина волны (м), v — скорость волны (м/с), Т — период (с), v — частота (Гц).
Условия максимума и минимума при интерференции волн:
Здесь — разность хода волн (м), k = 0; 1; 2; 3;… — целое число (безразмерное), — длина волны (м).
Гармонические колебанияГармонические колебания происходят под действием переменной силы, пропорциональной смещению маятника от положения равновесия и всегда направленной к положению равновесия. Поскольку в процессе колебаний эта сила изменяется, изменяется и ускорение маятника, возникающее под действием этой силы. Поэтому к колебательному движению нельзя применять формулы равномерного или равноускоренного движений, с их помощью можно определять только средние скорость и ускорение за определенный промежуток времени. Чтобы найти мгновенную скорость, надо брать первую производную смещения по времени, а чтобы найти мгновенное ускорение — первую производную скорости по времени.
Чтобы найти мгновенную скорость, надо брать первую производную смещения по времени, а чтобы найти мгновенное ускорение — первую производную скорости по времени.
Если дано уравнение гармонических колебаний с цифровыми значениями параметров и требуется из него найти какую-либо величину, то запишите рядом уравнение гармонических колебаний в общем виде и сопоставьте его с данным уравнением. Та величина, что стоит между знаком «равно» и синусом или косинусом, есть амплитуда, в каком бы виде она ни была записана. Та, что стоит между синусом или косинусом и временем t, есть циклическая частота, а та, что без t, есть начальная фаза. Например, дано уравнение:
и требуется найти амплитуду и период колебаний. Запишем это уравнение в общем виде:
Теперь раскроем скобки в данном нам уравнении и сравним его с уравнением в общем виде:
Из сравнения с предыдущим уравнением видно, что амплитуда А = 0,4 м, циклическая частота рад/с и начальная фаза . А поскольку
и частота .
Если наоборот, даны числовые значения параметров, а требуется записать уравнение колебаний, подставьте в уравнение в общем виде все числа, а время t оставьте в буквенном виде.
Например, вам даны амплитуда 5 см, период 2 с и начальная фаза 30° и требуется записать уравнение гармонических косинусоидальных колебаний. Найдите сначала циклическую частоту по формуле
Поскольку , значит, .
С учетом этого требуемое уравнение примет вид:
К свободным гармоническим колебаниям применим закон сохранения механической энергии: полная механическая энергия маятника Е в процессе гармонических колебаний сохраняется. При этом она равна его максимальной потенциальной энергии , или его максимальной кинетической энергии , или сумме мгновенных потенциальной и кинетической энергий маятника в любой промежуточной точке его траектории:
Применительно к пружинному маятнику это равенство можно записать еще и так:
а применительно к математическому:
Здесь х, v и h — мгновенные смещение, скорость и высота подъема математического маятника над положением равновесия.
Если математический маятник движется вверх с ускорением или вниз с замедлением, то период его свободных (или собственных) колебаний определяется по формуле
Если он движется вниз с ускорением или вверх с замедлением, то период его свободных колебаний определяет формула
а если он движется горизонтально с ускорением или замедлением, то его период
Если математический маятник поднят над Землей на высоту Н, сравнимую с радиусом Земли или превосходящую его, где ускорение свободного падения g меньше, чем ускорение свободного падения на Земле, то там маятник за время t отстанет от земного на время , поскольку увеличится его период колебания на величину . При этом выполняется соотношение
При этом выполняется соотношение
где Т — период на высоте Н, а — период его колебаний на Земле.
Если пружинный маятник состоит из двух последовательных пружин с жесткостями , как на рис. 308, а), то силы упругости, действующие на каждую пружину, одинаковы, а деформации пружин разные, и при этом общая амплитуда колебаний маятника равна сумме амплитуд колебаний каждой пружины:
а соотношение между амплитудами колебаний вследствие равенства сил упругости имеет вид:
Если пружины соединены параллельно, как на рис. 308, б), то амплитуды колебаний пружин будут одинаковы, а силы упругости, возникающие в пружинах при деформации, — разные, поэтому справедливым будут соотношения
Если маятник не является ни пружинным, ни математическим, то к такому — физическому — маятнику формулы периода и частоты пружинного и математического маятников неприменимы. Для решения задач на физический маятник следует пользоваться законами Ньютона, сохранения импульса и сохранения энергии. Свободные колебания реального маятника, на который действуют внешние силы сопротивления, являются затухающими. Затухающие колебания не являются ни периодическими, ни гармоническими. График затухающих колебаний изображен на рис. 309.
Свободные колебания реального маятника, на который действуют внешние силы сопротивления, являются затухающими. Затухающие колебания не являются ни периодическими, ни гармоническими. График затухающих колебаний изображен на рис. 309.
Если на реальный маятник действует периодически изменяющаяся внешняя сила, то такие колебания называются вынужденными. Вынужденные колебания, происходящие под действием гармонически изменяющейся внешней силы, тоже являются гармоническими и незатухающими. Их частота равна частоте внешней силы и называется частотой вынужденных колебаний.
Если частота собственных колебаний маятника равна частоте вынужденных колебаний, то при малом сопротивлении внешней среды наступает механический резонанс — явление резкого возрастания амплитуды колебаний, когда частота вынужденных колебаний становится равной собственной частоте маятника.
На рис. 310 изображено семейство резонансных кривых для сред с разным сопротивлением колебаниям. Чем меньше внешнее сопротивление, т. е. чем ближе реальный маятник к идеальному, тем выше и острее резонансная кривая.
е. чем ближе реальный маятник к идеальному, тем выше и острее резонансная кривая.
Механической волной называют распространение механических колебаний в упругой среде.
Механические волны бывают поперечные и продольные. Поперечной волной называют волну, в которой частицы колеблются перпендикулярно направлению распространения волны, а продольной — в которой частицы колеблются вдоль направления распространения волны.
В вакууме механические волны распространяться не могут. Поэтому, каким бы сильным ни был взрыв в космосе, на Земле его не услышат.
Вследствие отставания колебаний одних частиц среды от других в поперечных волнах возникают гребни и впадины (как в резиновом шнуре на рис. 311), а в продольных — сгущения и разрежения (как в упругой пружине на рис. 312).
Механические волны не переносят вещество среды, но переносят ее форму: гребни и впадины в поперечной волне и сгущения и разрежения в продольной.
Механические волны переносят механическую энергию, которая складывается из кинетической энергии движения частиц среды и потенциальной энергии ее упругой деформации.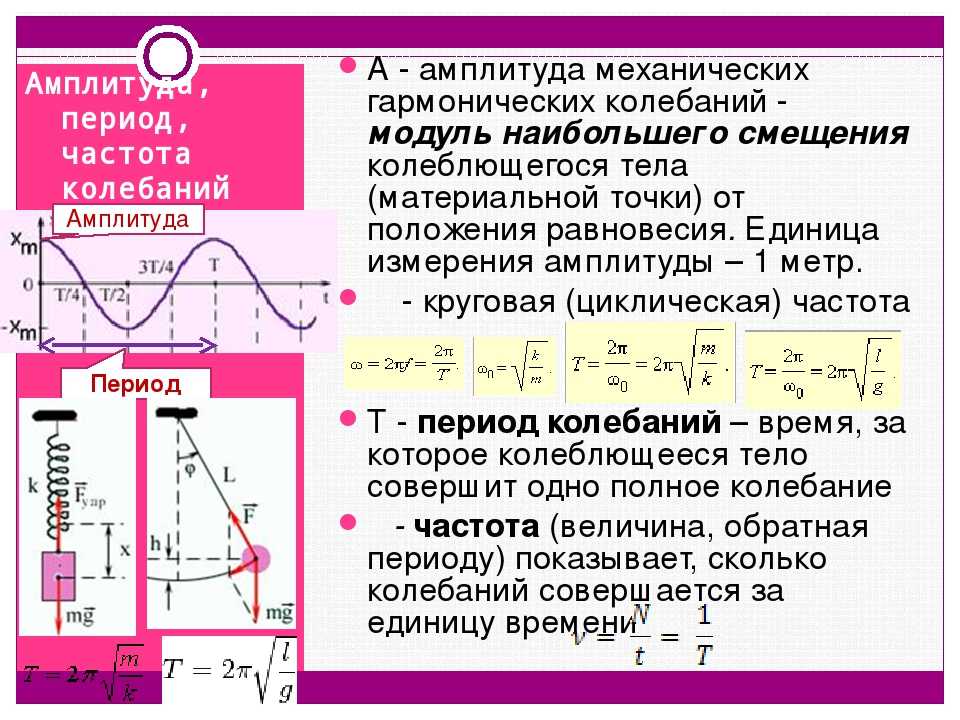
Расстояние, пройденное волной за один период колебания ее частиц, называется длиной волны.
На расстоянии длины волны располагаются соседние гребни или соседние впадины в поперечной волне, а также соседние сгущения или соседние разрежения в продольной. На расстоянии длины волны расположены частицы, колеблющиеся с разностью фаз рад.
На рис. 313 изображена графически поперечная волна и показана ее длина волны . В отличие от графика колебаний маятника здесь по оси абсцисс отложено не время колебаний t, а модуль перемещения волны S.
Скорость волны v — это скорость перемещения гребней или впадин в поперечной волне и сгущений или разрежений в продольной. Скорость волны в данной среде — постоянная величина, т.к. волны в однородной среде распространяются равномерно и прямолинейно. Скорость волны не равна скорости колебаний ее частиц, т.к. частицы волны колеблются с переменной скоростью.
Подтверждением волнового процесса в среде являются интерференция, дифракция, дисперсия и поляризация волн.
Волны, частицы которых колеблются с постоянной разностью фаз или с одинаковой частотой, называются когерентными. При наложении когерентных волн друг на друга возникает интерференция волн.
ИнтерференцияИнтерференция — это наложение волн друг на друга, в результате которого в пространстве, охваченном волной, перераспределяется волновая энергия и возникают усиления волн (максимумы) и их ослабления (минимумы). При максимуме амплитуды налагающихся волн складываются (рис. 314, а), а при минимуме — вычитаются (рис. 314, б). Если при минимуме амплитуды волн одинаковы, то волны полностью погасят друг друга.
Наилучшим условием максимума интерференции является наложение волн с одинаковой фазой или с разностью фаз, равной целому числу рад. Так будет, когда разность хода волн от их источников до места наложения М содержит четное число полуволн или целое число длин волн (рис. 315).
Наилучшим условием минимума интерференции является наложение волн в противофазе, т. е. когда разность фаз равна радиан. В этом случае разность хода волн содержит нечетное число полуволн.
е. когда разность фаз равна радиан. В этом случае разность хода волн содержит нечетное число полуволн.
Дифракция
Дифракцией волн называется загибание волн в область геометрической тени при прохождении мимо препятствия или сквозь отверстие размером порядка нескольких длин волн.
Дифракцию волн объясняет принцип Гюйгенса: каждая точка среды, до которой добежала волна, сама становится источником такой же волны.
Дисперсию и поляризацию волн мы повторим в теме «Оптика».
Продольные волны звуковой частоты называются звуковыми волнами. Звуковой частотой, т.е. частотой, при которой человеческое ухо слышит звук, является частота от 16 Гц до 20 000 Гц. Звук с частотой меньше 16 Гц называется инфразвуком, а звук с частотой выше 20 000 Гц — ультразвуком.
Высота тона звука зависит от частоты колебаний звучащего тела (вибратора). Чем больше частота колебаний, тем выше тон. Частота колебаний крыльев мухи меньше частоты колебаний крыльев комара, поэтому муха жужжит, а комар пищит.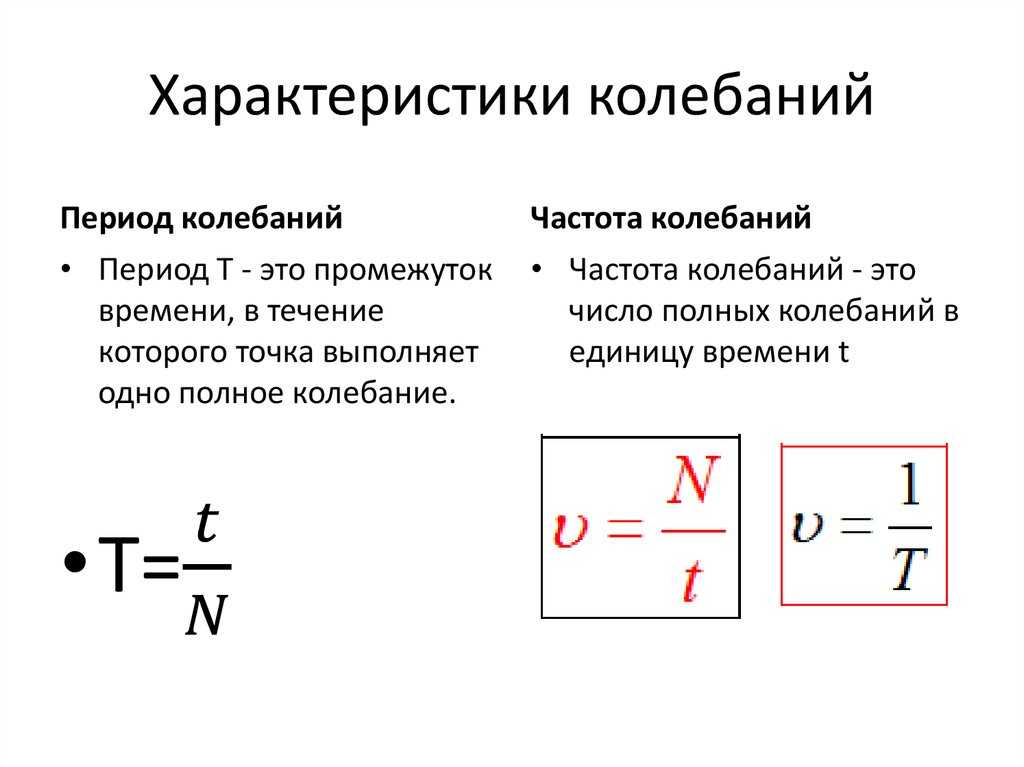
Громкость (интенсивность) звука зависит от амплитуды колебаний звучащего тела. Чем больше амплитуда колебаний, тем громче звук.
Скорость звука зависит от среды, в которой он распространяется, и от ее температуры. В более плотных и упругих средах звук распространяется быстрее. Скорость звука в воздухе составляет примерно 340 м/с. С повышением температуры скорость звука увеличивается.
Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Задачи по физике с решением
Возможно вам будут полезны эти страницы:
13.2 Свойства волны: скорость, амплитуда, частота и период
Цели обучения Волновые переменные Связь между частотой волны, периодом, длиной волны и скоростьюРешение задач о волнахПрактические задачиПроверьте свое понимание
Цели обучения
К концу этого раздела вы сможете делать следующее: период, длина волны и скорость волны
| длина волны | скорость волны |
Волновые переменные
В главе о движении в двух измерениях мы определили следующие переменные для описания гармонического движения:
- Амплитуда — максимальное смещение от положения равновесия объекта, колеблющегося вокруг такого положения равновесия
- Частота — количество событий в единицу времени
- Период — время, необходимое для совершения одного колебания
Для волн эти переменные имеют одинаковое основное значение. Однако полезно сформулировать определения более конкретным образом, применимым непосредственно к волнам:
Однако полезно сформулировать определения более конкретным образом, применимым непосредственно к волнам:
- Амплитуда — расстояние между положением покоя и максимальным смещением волны
- Частота — количество волн, проходящих через определенную точку в секунду
- Период — время, необходимое для завершения одного цикла волны
Волны характеризуют не только амплитуда, частота и период, но и их длина волны и скорость волны. Длина волны λλ — это расстояние между соседними одинаковыми частями волны, параллельными направлению распространения. Скорость волны vwvw — это скорость, с которой движется возмущение.
Советы по достижению успеха
Скорость волны иногда также называют скоростью распространения или скоростью распространения , потому что возмущение распространяется из одного места в другое.
Рассмотрим периодическую волну воды на рис. 13.7. Его длина волны — это расстояние от гребня до гребня или от впадины до впадины. Длину волны также можно рассматривать как расстояние, пройденное волной за один полный цикл или один период. Время одного полного движения вверх-вниз равно периоду простой водной волны T . На рисунке сама волна движется вправо со скоростью волны v w . Его амплитуда X — это расстояние между положением покоя и максимальным смещением — либо гребнем, либо впадиной — волны. Важно отметить, что это движение волны на самом деле является 9-м.0055 возмущение движение вправо, а не сама вода; в противном случае птица двигалась бы вправо. Вместо этого чайка качается вверх и вниз на месте, когда под ней проходят волны, преодолевая общее расстояние 2 X за один цикл. Однако, как упоминалось в текстовой статье о серфинге, настоящие океанские волны более сложны, чем этот упрощенный пример.
13.7. Его длина волны — это расстояние от гребня до гребня или от впадины до впадины. Длину волны также можно рассматривать как расстояние, пройденное волной за один полный цикл или один период. Время одного полного движения вверх-вниз равно периоду простой водной волны T . На рисунке сама волна движется вправо со скоростью волны v w . Его амплитуда X — это расстояние между положением покоя и максимальным смещением — либо гребнем, либо впадиной — волны. Важно отметить, что это движение волны на самом деле является 9-м.0055 возмущение движение вправо, а не сама вода; в противном случае птица двигалась бы вправо. Вместо этого чайка качается вверх и вниз на месте, когда под ней проходят волны, преодолевая общее расстояние 2 X за один цикл. Однако, как упоминалось в текстовой статье о серфинге, настоящие океанские волны более сложны, чем этот упрощенный пример.
Рисунок 13.7 Волна имеет длину волны λ , что является расстоянием между соседними идентичными частями волны. Возмущение поверхности вверх-вниз распространяется параллельно поверхности со скоростью v в .
Смотреть физику
Амплитуда, период, частота и длина волны периодических волн
Это видео является продолжением видео «Введение в волны» из раздела «Виды волн». В нем обсуждаются свойства периодической волны: амплитуда, период, частота, длина волны и скорость волны.
Щелкните для просмотра содержимого
Советы для достижения успеха
Гребень волны иногда также называют вершиной .
Проверка захвата
Если вы находитесь на лодке в ложбине волны в океане, и амплитуда волны составляет 1 м, какова высота волны с вашего местоположения?
- 1м
- 2 м
- 4 м
- 8м
Связь между частотой волны, периодом, длиной волны и скоростью
Поскольку частота волны — это количество волн в секунду, а период — это, по существу, количество секунд на волну, соотношение между частотой и периодом составляет
13. 1f=1Tf=1T
1f=1Tf=1T
или
13.2T=1f,T=1f,
так же, как и в случае гармонического движения объекта. Из этого соотношения видно, что более высокая частота означает более короткий период. Напомним, что единицей измерения частоты является герц (Гц), а 1 Гц — это один цикл — или одна волна — в секунду.
Скорость распространения v w — это расстояние, которое волна проходит за заданное время, которое составляет одну длину волны за время одного периода. В форме уравнения это записывается как
13.3vw=λTvw=λT
или
13.4vw=fλ.vw=fλ.
Из этого соотношения мы видим, что в среде, где v w постоянно, чем выше частота, тем меньше длина волны. См. рисунок 13.8.
Рисунок 13.8. Поскольку в данной среде они распространяются с одинаковой скоростью, низкочастотные звуки должны иметь большую длину волны, чем высокочастотные звуки. Здесь низкочастотные звуки излучаются большим динамиком, называемым низкочастотным динамиком, а высокочастотные звуки излучаются маленьким динамиком, называемым твитером.
Эти фундаментальные соотношения справедливы для всех типов волн. Например, для волн на воде v w — это скорость поверхностной волны; для звука v w — скорость звука; а для видимого света v w — это скорость света. Амплитуда X совершенно не зависит от скорости распространения v w и зависит только от количества энергии в волне.
Лаборатория Snap
Волны в чаше
В этой лаборатории вы проведете измерения, чтобы определить, как на амплитуду и период волн влияет передача энергии от пробки, брошенной в воду. Пробка изначально обладает некоторой потенциальной энергией, когда ее держат над водой — чем больше высота, тем выше потенциальная энергия. Когда пробка падает, такая потенциальная энергия преобразуется в кинетическую энергию, когда пробка падает. Когда пробка ударяется о воду, эта энергия распространяется по воде волнами.
Когда пробка ударяется о воду, эта энергия распространяется по воде волнами.
Материалы
- Большая миска или таз
- Вода
- Пробка (или мячик для пинг-понга)
- Секундомер
- Рулетка
Инструкции
Процедура
- Наполните большую миску или таз водой и подождите, пока вода не осядет, чтобы не было ряби.
- Аккуратно бросьте пробку в середину чаши.
- Оцените длину волны и период колебаний водной волны, распространяющейся от пробки. Вы можете оценить период, подсчитав количество ряби от центра к краю чаши, пока ваш партнер измеряет это время. Эта информация в сочетании с измерением чаши даст вам длину волны при использовании правильной формулы.
- Выньте пробку из миски и подождите, пока вода снова не осядет.
- Аккуратно бросьте пробку с высоты, отличной от высоты первого падения.
- Повторите шаги с 3 по 5, чтобы собрать второй и третий наборы данных, опуская пробку с разной высоты и записывая полученные длины волн и периоды.

- Интерпретируйте свои результаты.
Проверка захвата
Пробка падает в бассейн с водой, создавая волны. Зависит ли длина волны от высоты над водой, с которой брошена пробка?
- Нет, влияет только на амплитуду.
- Да, длина волны затронута.
Виртуальная физика
Волна на струне
Рисунок 13.10 Щелкните здесь для моделирования волны на струне.
В этой анимации посмотрите, как струна вибрирует в замедленном темпе, выбрав параметр «Замедленное движение». Выберите параметры «Без конца» и «Вручную» и покачивайте конец струны, чтобы создавать волны самостоятельно. Затем переключитесь на настройку Oscillate для автоматического создания волн. Отрегулируйте частоту и амплитуду колебаний, чтобы увидеть, что произойдет. Затем поэкспериментируйте с регулировкой демпфирования и натяжения.
Проверка захвата
Какая из настроек — амплитуда, частота, демпфирование или натяжение — изменяет амплитуду волны при ее распространении? Что он делает с амплитудой?
- Частота; он уменьшает амплитуду волны по мере ее распространения.

- Частота; он увеличивает амплитуду волны по мере ее распространения.
- Демпфирование; он уменьшает амплитуду волны по мере ее распространения.
- Демпфирование; он увеличивает амплитуду волны по мере ее распространения.
Решение волновых задач
Рабочий пример
Рассчитайте скорость распространения волн: чайка в океане
Рассчитайте скорость океанской волны на предыдущем рисунке, если расстояние между гребнями волн равно 10,0 м и время, за которое чайка качается вверх и вниз составляет 5,00 с.
СТРАТЕГИЯ
Заданы значения длины волны (λ=10,0 м)(λ=10,0 м) и периода (T=5,00 с)(T=5,00 с), и нас просят найти vwvw Следовательно, мы можем используйте vw=λTvw=λT, чтобы найти скорость волны.
Решение
Введите известные значения в vw=λTvw=λT
13,5vw=10,0 м5,00 с=2,00 м/с.vw=10,0 м5,00 с=2,00 м/с.
Обсуждение
Такая низкая скорость кажется приемлемой для океанской волны. Обратите внимание, что на рисунке волна движется вправо с этой скоростью, которая отличается от переменной скорости, с которой чайка качается вверх и вниз.
Обратите внимание, что на рисунке волна движется вправо с этой скоростью, которая отличается от переменной скорости, с которой чайка качается вверх и вниз.
Рабочий пример
Расчет периода и скорости волны игрушечной пружины
Женщина на рис. 13.3 каждую секунду создает две волны, встряхивая игрушечную пружину вверх и вниз. а) Каков период каждой волны? (б) Если каждая волна проходит 0,9метров после одного полного волнового цикла, какова скорость распространения волны?
СТРАТЕГИЯ ДЛЯ (A)
Чтобы найти период, мы решаем для T=1fT=1f, учитывая значение частоты (f=2s−1).(f=2s−1).
Решение для (a)
Введите известное значение в T=1fT=1f
13,6T=12 с-1=0,5 с.T=12 с-1=0,5 с.
СТРАТЕГИЯ ДЛЯ (B)
Поскольку одним из определений длины волны является расстояние, пройденное волной за один полный цикл или один период, значения длины волны (λ = 0,9м)(λ=0,9 м), а также частота. Следовательно, мы можем использовать vw=fλvw=fλ, чтобы найти скорость волны.
Решение для (b)
Введите известные значения в vw=fλvw=fλ
vw=fλ=(2 с−1)(0,9 м) = 1,8 м/с.vw=fλ=(2 с-1 )(0,9 м) = 1,8 м/с.
Обсуждение
Мы могли бы также использовать уравнение vw=λTvw=λT для определения скорости волны, поскольку мы уже знаем значение периода (T=0,5 с)(T=0,5 с) из нашего расчета в части ( а), и мы бы пришли к тому же ответу.
Практические задачи
Частота волны 10 Гц. Каков его период?
- Период волны 100 с.
- Период волны 10 с.
- Период волны 0,01 с.
- Период волны 0,1 с.
Какова скорость волны с длиной волны 2 м и частотой 5 Гц?
- 20 м/с
- 2,5 м/с
- 0,4 м/с
- 10 м/с
Проверьте свое понимание
Упражнение 7
Какова амплитуда волны?
- Четверть общей высоты волны
- Половина общей высоты волны
- Удвоенная общая высота волны
- Четырехкратная общая высота волны
Упражнение 8
Что понимают под длиной волны?
- Длина волны — это расстояние между соседними одинаковыми частями волны, параллельными направлению распространения.

- Длина волны — это расстояние между соседними одинаковыми частями волны, перпендикулярное направлению распространения.
- Длина волны — это расстояние между гребнем и прилегающей впадиной волны, параллельное направлению распространения.
- Длина волны — это расстояние между гребнем и прилегающей впадиной волны, перпендикулярное направлению распространения.
Упражнение 9
Как можно математически выразить частоту волны через период волны?
- f=1T
- ф=(1Т)2
- ф=Т
- ф=(Т)2
Упражнение 10
Когда длина волны прямо пропорциональна периоду волны?
- Когда скорость волны уменьшается вдвое
- Когда скорость волны постоянна
- Когда скорость волны удваивается
- Когда скорость волны утроится
- Печать
- Поделиться
You Should Know – Lambda Geeks
Амплитуда колебаний объясняет максимальное или наибольшее смещение колеблющегося тела. В статье исчерпывающе обсуждается, что такое амплитуда колебаний и как ее рассчитать.
В статье исчерпывающе обсуждается, что такое амплитуда колебаний и как ее рассчитать.
Амплитуда – это величина колеблющегося тела, такая как угловая частота и период времени. Величина измеряет максимальное смещение тела в обе стороны от его среднего положения. Это означает, что он показывает нам, насколько колеблющееся тело отклоняется от своего среднего положения во время колебаний.
Колебание включает движение тела вперед и назад из его положения равновесия или среднего положения . Каждое колебание имеет три основные характеристики: частоту, период времени, и амплитуда . Из них мы уже обсуждали понятия частоты и периода времени в предыдущих статьях.
Начнем обсуждение амплитуды колебаний или амплитуды колебаний на примере простого маятника . Маятник качается под углом через свое среднее положение к максимальному расстоянию от своего среднего положения. Максимальное или наибольшее расстояние колеблющегося тела от его центра или среднего положения называется его максимальное водоизмещение . Напротив, величина максимального смещения колеблющегося тела в обе стороны от среднего положения называется его амплитудой колебаний .
Напротив, величина максимального смещения колеблющегося тела в обе стороны от среднего положения называется его амплитудой колебаний .
Как рассчитать амплитуду колебаний?
На синусоидальном графике мы заметили, что амплитуда колебаний представляет собой расстояние между гребнем, впадиной и средним положением .
Таким образом, амплитуда колебаний или величина максимального смещения x задается уравнением синусоидальной волны как,
[латекс]x = Asin(\omega t+\phi )[/латекс] …………(*)
Где А — амплитуда колебаний.
[латекс]\омега[/латекс] — угловая скорость.
[латекс]\фи[/латекс] — фазовый сдвиг.
Мы обсудим, как рассчитать уравнение амплитуды колебаний (*) по синусоидальному графику в следующей части.
Поскольку каждая волна имеет амплитуду, пики на графике показывают, что амплитуда объясняет степень или уровень изменения интенсивности различных волн, таких как звуковые волны. Следовательно, это также интерпретируется как громкость звука.
Следовательно, это также интерпретируется как громкость звука.
Звуковые волны
На графике мы отметили, что разница между самым высоким пиком амплитуды или положительным значением и самым низким пиком амплитуды или отрицательным значением называется «амплитудой от пика до пика» колеблющегося тела.
Подробнее о Угловая частота Простое гармоническое движение
Как найти Колебание Амплитуда из графика?Амплитуду колебаний можно получить из графика синусоидальной функции колеблющегося тела.
Амплитуда колебаний определяется, когда мы рисуем график колебательных переменных, таких как смещение в зависимости от времени. Пики на синусоидальном графике – это амплитуда колебаний, которая описывает, на какое расстояние тело колеблется от среднего положения в любую сторону.
В любой колебательной системе величина изменения колебательной переменной тела при каждом колебании называется амплитудой колебаний . В большинстве случаев осциллирующая переменная равна смещение . Когда мы строим график синусоидальной функции с переменным смещением колебаний в качестве вертикальной оси и временем в качестве горизонтальной оси, расстояние по вертикали между средним значением и экстремумами кривой иллюстрирует амплитуду колебаний.
В большинстве случаев осциллирующая переменная равна смещение . Когда мы строим график синусоидальной функции с переменным смещением колебаний в качестве вертикальной оси и временем в качестве горизонтальной оси, расстояние по вертикали между средним значением и экстремумами кривой иллюстрирует амплитуду колебаний.
(кредит: Shutterstock)
На графике синусоидальной функции ось X рассматривается как среднее положение колебательного тела. Следовательно, каким бы ни было исходное положение тела, перемещение измеряется от его среднего положения. Поскольку график представляет собой синусоидальную функцию, что иллюстрирует периодических явлений пики на графике отображают величины колеблющегося тела, такие как период и амплитуда.
Как рассчитать амплитуду колебанийформа графика?
По пикам амплитуда колебаний рассчитывается как половина его разницы между максимальным и минимальным значениями.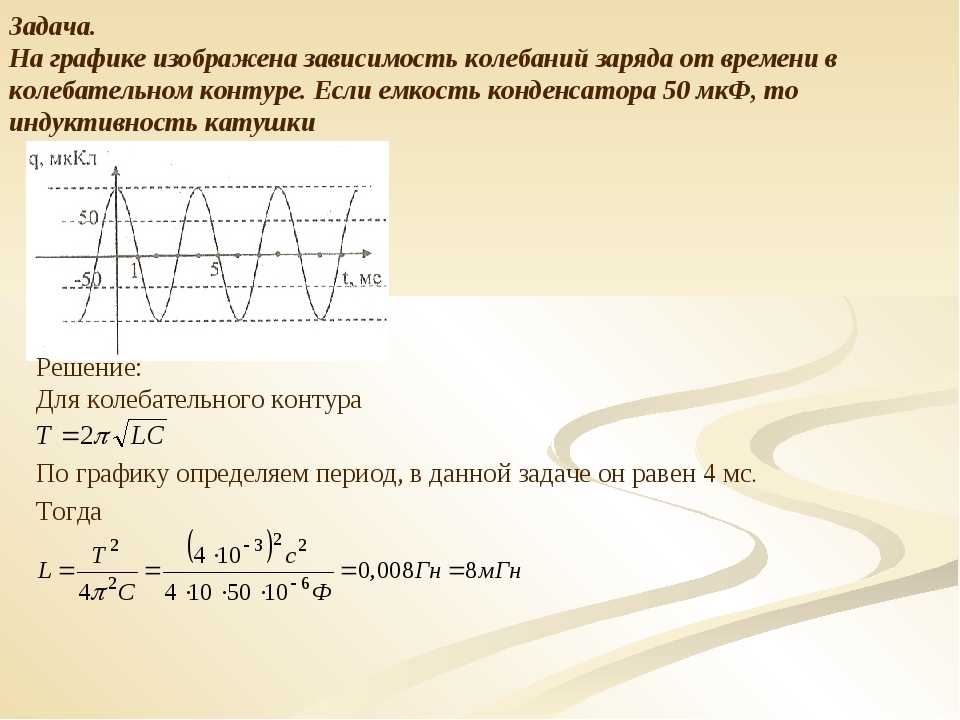
[латекс]амплитуда = \фрак{1}{2}\мид макс -мин \мид[/латекс]
Следовательно, величина амплитуды колебаний всегда положительна.
Мы также можем найти амплитуду колебаний и период времени из обобщенного уравнения синусоидального графика следующим образом:
y=A⋅sin(B(x+C))+D
где мы можем найти величины колебаний body следующим образом:
Амплитуда колебаний : A
Период времени : [latex]\frac{2\pi }{B}[/latex]
Сдвиг фазы – насколько далеко тело перемещается по горизонтали от среднее положение: C.
Вертикальное смещение – насколько далеко тело перемещается по вертикали от среднего положения: D. Как рассчитать амплитуду колебаний?
График синусоидальной функции (кредит: mathsisfun)
Подробнее о Угловое уравнение движения .
Что такое амплитуда и частота колебаний? Амплитуда и частота – это величины колебательных тел, определяющие скорость колебаний.
Тело колеблется, когда оно перемещается из своего среднего положения в самое высокое положение и возвращается в свое среднее положение. Здесь амплитуда представляет собой максимальное смещение тела от его среднего положения. В то время как частота показывает, насколько сильно тело колебалось от своего среднего положения.
Что такое амплитуда и частота колебаний?В зависимости от амплитуды и частоты колебания подразделяются на следующие три типа:
Затухающие колебания
Предположим, что тело совершает колебания с уменьшающейся амплитудой из-за наличия силы сопротивления воздуха и в один момент времени и он приходит в состояние покоя, поскольку обе величины его тела рассеялись. В этом случае это называется « затухающее колебание» .
Свободные колебания
Предположим, что тело совершает свободные колебания с постоянной амплитудой и определенной частотой из-за отсутствия силы трения. В этом случае оно называется «свободное колебание », , а его частота называется « собственная частота» колеблющегося тела.
В этом случае оно называется «свободное колебание », , а его частота называется « собственная частота» колеблющегося тела.
Вынужденное колебание
Его также называют колебанием натянутой струны или качелей. Предположим, что тело колеблется с уменьшающейся амплитудой за счет механической энергии качания и останавливается, так как обе ее величины рассеялись. В этом случае он называется «9».0381 вынужденные колебания ’.
Возьмем в качестве примера подвешенный весло, привязанный к вашей руке. Амплитуда и частота колебаний
(кредит: lumenlearning)
Случай 1:
применяемый).
Случай 2 :
Увеличивая частоту движения мяча движением руки вверх и вниз, мяч также реагирует с увеличением амплитуды. Если вы будете водить мяч с частотой, равной его собственной частоте, его амплитуда будет возрастать за одно колебание. Событие движения тела с частотой, эквивалентной собственной частоте, называется резонанс . Принимая во внимание, что тело, работающее на своей естественной или основной частоте, резонирует .
Принимая во внимание, что тело, работающее на своей естественной или основной частоте, резонирует .
Случай 3:
если еще увеличить его частоту выше собственной частоты, его амплитуда начнет уменьшаться, пока колебания почти не исчезнут. Таким образом, движение вашей руки больше не влияет на мяч.
Особое периодическое движение – College Physics: OpenStax
Глава 16 Колебательное движение и волны
Резюме
- Опишите простой гармонический осциллятор.
- Объясните связь между простым гармоническим движением и волнами.
Колебания системы, в которой результирующая сила может быть описана законом Гука, имеют особое значение, потому что они очень распространены. Они также являются простейшими колебательными системами. Простое гармоническое движение (SHM) — это название, данное колебательному движению системы, в которой результирующая сила может быть описана законом Гука, и такая система называется простой гармонический осциллятор . Если результирующая сила может быть описана законом Гука и нет демпфирования (за счет трения или других неконсервативных сил), то простой гармонический осциллятор будет колебаться с одинаковым смещением по обе стороны от положения равновесия, как показано для объекта на пружине на рисунке 1. Максимальное отклонение от равновесия называется амплитудой [латекс]\boldsymbol{X}.[/latex]Единицы измерения амплитуды и смещения одинаковы, но зависят от типа колебание. Для объекта на пружине единицами измерения амплитуды и смещения являются метры; тогда как для звуковых колебаний они имеют единицы давления (а другие типы колебаний имеют еще другие единицы). Поскольку амплитуда представляет собой максимальное смещение, она связана с энергией колебаний.
Если результирующая сила может быть описана законом Гука и нет демпфирования (за счет трения или других неконсервативных сил), то простой гармонический осциллятор будет колебаться с одинаковым смещением по обе стороны от положения равновесия, как показано для объекта на пружине на рисунке 1. Максимальное отклонение от равновесия называется амплитудой [латекс]\boldsymbol{X}.[/latex]Единицы измерения амплитуды и смещения одинаковы, но зависят от типа колебание. Для объекта на пружине единицами измерения амплитуды и смещения являются метры; тогда как для звуковых колебаний они имеют единицы давления (а другие типы колебаний имеют еще другие единицы). Поскольку амплитуда представляет собой максимальное смещение, она связана с энергией колебаний.
ЭКСПЕРИМЕНТ НА ДОМАШНЮЮ МАШИНУ: ШМ И МРАМОР
Найдите чашу или тазик, который внутри имеет форму полусферы. Поместите шарик внутрь чаши и периодически наклоняйте чашу, чтобы шарик катился от дна чаши к одинаково высоким точкам по бокам чаши. Почувствуйте силу, необходимую для поддержания этого периодического движения. Что такое возвращающая сила и какую роль играет прикладываемая вами сила в простом гармоническом движении (ГДМ) мрамора?
Почувствуйте силу, необходимую для поддержания этого периодического движения. Что такое возвращающая сила и какую роль играет прикладываемая вами сила в простом гармоническом движении (ГДМ) мрамора?
Что такого важного в простом гармоническом движении? Особенностью является то, что период[latex]\boldsymbol{T}[/latex]и частота[latex]\boldsymbol{f}[/latex]простого гармонического осциллятора не зависят от амплитуды. Струна гитары, например, будет колебаться с одной и той же частотой независимо от того, нажимаете ли вы мягко или сильно. Поскольку период постоянен, в качестве часов можно использовать простой гармонический осциллятор.
Поскольку период постоянен, в качестве часов можно использовать простой гармонический осциллятор.
На период простого гармонического осциллятора влияют два важных фактора. Период связан с тем, насколько жесткой является система. Очень жесткий объект имеет большую постоянную силы[латекс]\boldsymbol{k},[/латекс], из-за чего система имеет меньший период. Например, вы можете отрегулировать жесткость трамплина — чем он жестче, тем быстрее он вибрирует и тем короче его период. Период также зависит от массы колебательной системы. Чем массивнее система, тем больше период. Например, тяжелый человек на трамплинах подпрыгивает вверх и вниз медленнее, чем легкий.
Фактически, масса[латекс]\boldsymbol{m}[/latex]и силовая постоянная[латекс]\boldsymbol{k}[/latex]являются единственными факторами, влияющими на период и частоту простого гармонического движения. .
ПЕРИОД ПРОСТОГО ГАРМОНИЧЕСКОГО ОСЦИЛЛЯТОРА
Период простого гармонического осциллятора определяется выражением
[латекс]\boldsymbol{T=2\pi}[/latex][латекс]\boldsymbol{\sqrt{\frac{ m}{k}}}[/latex]
и, поскольку[latex]\boldsymbol{f=1/T},[/latex] частота простого гармонического осциллятора равна
[латекс]\boldsymbol{f\:=}[/latex][латекс]\boldsymbol{\frac{1}{2\pi}\sqrt{\frac{k} {m}}}. [/latex]
[/latex]
Обратите внимание, что ни [latex]\boldsymbol{T}[/latex], ни [latex]\boldsymbol{f}[/latex] не зависят от амплитуды.
ЭКСПЕРИМЕНТ ДЛЯ ДОМАШНИХ МАСС: КОЛЕБАНИЯ МАССЫ И ЛИНЕЙКИ
Найдите две одинаковые деревянные или пластмассовые линейки. Плотно прикрепите один конец каждой линейки к краю стола, чтобы длина каждой линейки, выступающей из стола, была одинаковой. На свободный конец одной линейки прикрепите тяжелый предмет, например, несколько крупных монет. Одновременно защипните концы линеек и посмотрите, какая из них претерпевает больше циклов за период времени, и измерьте период колебаний каждой из линеек.
Пример 1. Расчет частоты и периода колебаний: плохие амортизаторы в автомобиле
Если амортизаторы в автомобиле вышли из строя, то автомобиль будет колебаться по малейшему поводу, например, при проезде неровностей дороги и после остановки (см. рис. 2). Рассчитайте частоту и период этих колебаний для такого автомобиля, если масса автомобиля (включая его груз) составляет 900 кг, а силовая постоянная[латекс](\boldsymbol{k})[/латекс]системы подвески равна[латекс] \boldsymbol{6,53\times10^4\textbf{ Н/м}}. 4\textbf{Н/м}}{9{-1}=1,36\textbf{Гц}}.[/latex]
4\textbf{Н/м}}{9{-1}=1,36\textbf{Гц}}.[/latex]
[латекс]\boldsymbol{T=}[/латекс][латекс]\boldsymbol{\frac{1}{f}}[/латекс][латекс]\boldsymbol{=}[/латекс][латекс]\boldsymbol {\ frac {1} {1,356 \ textbf { Гц}}} [/ латекс] [латекс] \ жирный символ {= 0,738 \ textbf { с}}. [/ латекс]
Обсуждение
Значения [latex]\boldsymbol{T}[/latex] и [latex]\boldsymbol{f}[/latex] кажутся правильными для прыгающей машины. Вы можете наблюдать эти колебания, если сильно надавите на конец автомобиля и отпустите его.
Если бы с временной выдержкой была сделана фотография подпрыгивающей машины, когда она проезжала мимо, фара оставила бы волнообразную полосу, как показано на рис. 2. Точно так же на рис. 3 показан объект, подпрыгивающий на пружине, оставляющий волнообразный «след». его положения на движущейся полосе бумаги. Обе волны являются синусоидальными функциями. Все простые гармонические движения тесно связаны с синусоидальными и косинусоидальными волнами.
Точно так же на рис. 3 показан объект, подпрыгивающий на пружине, оставляющий волнообразный «след». его положения на движущейся полосе бумаги. Обе волны являются синусоидальными функциями. Все простые гармонические движения тесно связаны с синусоидальными и косинусоидальными волнами.
Перемещение как функция времени t при любом простом гармоническом движении, т. е. таком, при котором чистая восстанавливающая сила может быть описана законом Гука, определяется выражением
[латекс]\boldsymbol{x(t)=X\cos}[/latex][латекс]\boldsymbol{\frac{2\pi{t}}{T}},[/latex]
, где[латекс]\boldsymbol{X}[/латекс] — амплитуда.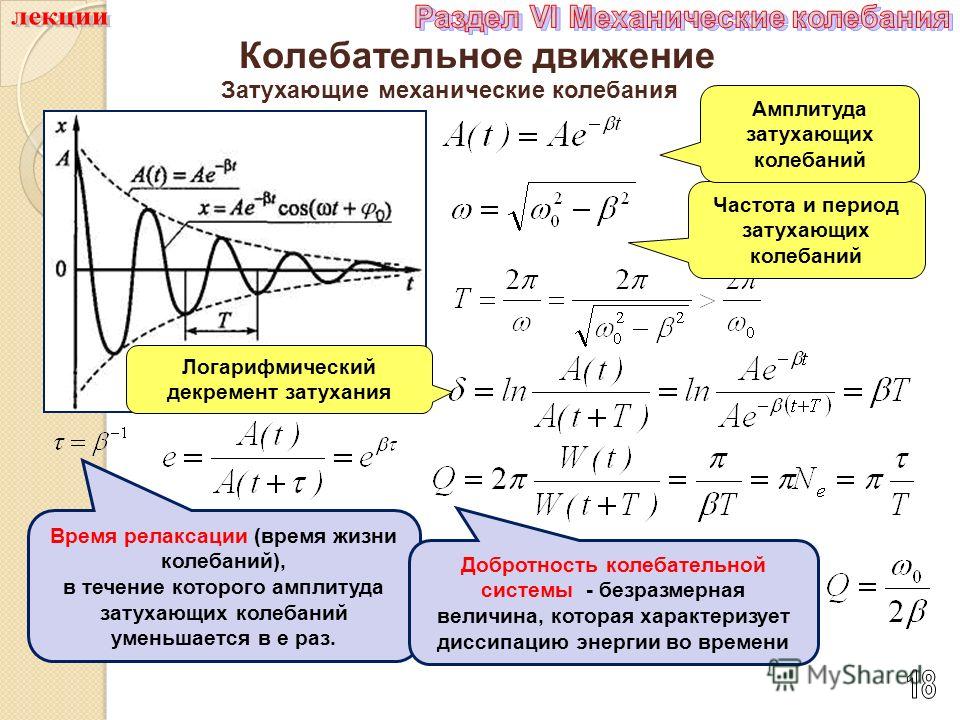 В [latex]\boldsymbol{t=0},[/latex]начальное положение равно[latex]\boldsymbol{x_0=X},[/latex]и смещение колеблется взад и вперед с периодом[latex]\boldsymbol {T}.[/latex](Когда [latex]\boldsymbol{t=T},[/latex]мы снова получаем [latex]\boldsymbol{x=X}[/latex]потому что[latex]\boldsymbol{\ cos2\pi=1}.).[/latex]Кроме того, из этого выражения для[latex]\boldsymbol{x},[/latex]скорость[latex]\boldsymbol{v}[/latex]как функция время указано:
В [latex]\boldsymbol{t=0},[/latex]начальное положение равно[latex]\boldsymbol{x_0=X},[/latex]и смещение колеблется взад и вперед с периодом[latex]\boldsymbol {T}.[/latex](Когда [latex]\boldsymbol{t=T},[/latex]мы снова получаем [latex]\boldsymbol{x=X}[/latex]потому что[latex]\boldsymbol{\ cos2\pi=1}.).[/latex]Кроме того, из этого выражения для[latex]\boldsymbol{x},[/latex]скорость[latex]\boldsymbol{v}[/latex]как функция время указано:
[латекс]\boldsymbol{v(t)=-v_{\textbf{max}}\sin}[/latex][латекс]\boldsymbol{(\frac{2\pi{t}}{T})} ,[/латекс]
, где[latex]\boldsymbol{v_{\textbf{max}}=2\pi{X/T}=X\sqrt{k/m}}.[/latex]Объект имеет нулевую скорость при максимальном смещении – для например,[латекс]\boldsymbol{v=0}[/латекс],когда[латекс]\жирныйсимвол{t=0},[/латекс]и в это время[латекс]\жирныйсимвол{х=Х}.[/латекс ]Знак минус в первом уравнении для[латекс]\boldsymbol{v(t)}[/латекс] указывает правильное направление скорости. Сразу после начала движения, например, скорость отрицательна, потому что система движется обратно к точке равновесия. Наконец, мы можем получить выражение для ускорения, используя второй закон Ньютона. [Тогда у нас есть [латекс]\boldsymbol{x(t),\:v(t),\:t,}[/latex]и [латекс]\boldsymbol{a(t)},[/latex]величины необходим для кинематики и описания простого гармонического движения.] Согласно второму закону Ньютона, ускорение равно[latex]\boldsymbol{a=F/m=kx/m}.[/latex]Итак,[latex]\boldsymbol{ a(t)}[/latex] также является функцией косинуса:
Наконец, мы можем получить выражение для ускорения, используя второй закон Ньютона. [Тогда у нас есть [латекс]\boldsymbol{x(t),\:v(t),\:t,}[/latex]и [латекс]\boldsymbol{a(t)},[/latex]величины необходим для кинематики и описания простого гармонического движения.] Согласно второму закону Ньютона, ускорение равно[latex]\boldsymbol{a=F/m=kx/m}.[/latex]Итак,[latex]\boldsymbol{ a(t)}[/latex] также является функцией косинуса:
[латекс]\boldsymbol{a(t)=-}[/латекс][латекс]\boldsymbol{\frac{kX}{m}}[/латекс][латекс]\boldsymbol{\cos}[/латекс] [латекс]\boldsymbol{\frac{2\pi{t}}{T}}.[/latex]
Следовательно, [латекс]\boldsymbol{a(t)}[/latex]прямо пропорционально [латекс]\boldsymbol{x(t)} и в обратном направлении.[/latex]
На рис. 4 показано простое гармоническое движение объекта на пружине и представлены графики [латекс]\boldsymbol{x(t),\:v(t),}[/latex]и[латекс]\boldsymbol{a( t)}[/latex]в зависимости от времени.
Рисунок 4. Графики x ( T ) , В ( T ) и A ( T ) . . . . . . . . . . . . .10388. .10388. .10388. . . . . . . ) . ) объект на пружине. Суммарная сила, действующая на объект, может быть описана законом Гука, поэтому объект совершает простое гармоническое движение. Обратите внимание, что исходное положение имеет максимальное значение вертикального смещения X ; v изначально равен нулю, а затем становится отрицательным по мере движения объекта вниз; и начальное ускорение отрицательное, возвращается к положению равновесия и становится равным нулю в этой точке.
. . . . . . . . . . . .10388. .10388. .10388. . . . . . . ) . ) объект на пружине. Суммарная сила, действующая на объект, может быть описана законом Гука, поэтому объект совершает простое гармоническое движение. Обратите внимание, что исходное положение имеет максимальное значение вертикального смещения X ; v изначально равен нулю, а затем становится отрицательным по мере движения объекта вниз; и начальное ускорение отрицательное, возвращается к положению равновесия и становится равным нулю в этой точке. Наиболее важным моментом здесь является то, что эти уравнения математически просты и справедливы для всех простых гармонических движений. Они очень полезны для визуализации волн, связанных с простым гармоническим движением, включая визуализацию того, как волны складываются друг с другом.
PHET ИССЛЕДОВАНИЯ: МАССЫ И ПРУЖИНА
Реалистичная лаборатория масс и пружин. Подвесьте грузы к пружинам и отрегулируйте жесткость пружины и демпфирование. Вы даже можете замедлить время. Перевозите лабораторию на разные планеты. Диаграмма показывает кинетическую, потенциальную и тепловую энергию для каждой пружины.
Рис. 5. Массы и пружины
- амплитуда
- максимальное смещение от положения равновесия объекта, колеблющегося вокруг положения равновесия
- простое гармоническое движение
- колебательное движение в системе, где результирующая сила может быть описана законом Гука
- простой гармонический осциллятор
- устройство, реализующее закон Гука, например груз, прикрепленный к пружине, при этом другой конец пружины соединен с жесткой опорой, например стеной
| ||||||||||||||||||
Простой калькулятор гармонического движения
Простой калькулятор гармонического движения, чтобы найти период, частоту, угловой
частота, амплитуда, смещение,
скорость и ускорение простого гармонического пружинного осциллятора в физике.
В расчетах не учитывается масса пружины. Пружина установлена горизонтально, и груз m скользит без трения по горизонтальной поверхности. Также предполагается, что Закон Гука выполняется.
| ВХОДНЫЕ ПАРАМЕТРЫ | ||
| Известные параметры | Масса [м], жесткость пружины [k] Частота [f] Период [T] Угловая частота [w] | |
| Масса [м] | гкгозлб | |
| Постоянная пружины [k] | фунт-сила/дюймН/ммфунтсила/футН/м | |
| Частота [ф] | Гц | |
| Период [Т] | с | |
| Угловая частота [w] | рад/с | |
| Функция смещения Примечание 2 | Функция синуса Функция косинуса | |
| Известные параметры | Амплитуда [A] или макс. смещениемакс. скоростьМакс. AccelerationDisplacement во время tVelocity во время tAcceleration во время t смещениемакс. скоростьМакс. AccelerationDisplacement во время tVelocity во время tAcceleration во время t | |
| Амплитуда | ммминхфт | |
| Водоизмещение в момент времени t | ||
| Максимум. Положительная скорость | мм/скм/см/см/чкм/дюйм/фут/см/ч | |
| Скорость во время t | ||
Максимум. Положительное ускорение Положительное ускорение | 92||
| Ускорение во время t | ||
| Время т | с | |
| Фазовый угол Примечание2 | рад | |
| | ||
Примечание 1: Используйте точку “. ” как десятичный разделитель.
” как десятичный разделитель.
Примечание 2. Функция косинуса (X = Acos(wt+φ)) предполагает, что колеблющийся объект выходит из состояния покоя (v = 0) при максимальном смещении (x = A) при t=0 с фазовым углом 0. Если при t=0 объект находится в положении равновесия и колебания начинаются, если дать объекту толчок к положительному x направлении, это будет синусоидальная функция (X = Asin(wt+φ)) с фазовый угол 0. См. пример простого гармонического движения для получения дополнительной информации о выборе.
| РЕЗУЛЬТАТЫ | ||
| Параметр | Значение | |
| Масса [м] | кг | |
| Постоянная пружины [k] | Н/мм | |
| Частота [f] | Гц | |
| Период [Т] | с | |
| Угловая частота [Вт] | рад/с | |
| Водоизмещение за 2 с | мм | |
| Максимальное положительное смещение | ||
| Скорость в 2с | РС | |
| Максимальная положительная скорость | 92 | |
| Максимальное положительное ускорение | ||
Калькулятор простого гармонического движения
Этот инструмент вычисляет переменные простого гармонического движения (амплитуда смещения, амплитуда скорости, амплитуда ускорения и частота) при любых двух из четырех переменных. Нажмите здесь, чтобы увидеть Как это работает и для Основные уравнения движения .
Нажмите здесь, чтобы увидеть Как это работает и для Основные уравнения движения .
Значения автоматически обновляются при вводе значения (нажмите F5 для обновления).
Динамические графики
Калькулятор простого гармонического движения – Как это работает
Расчет смещения, скорости, ускорения, частоты
и частота) при любых двух из четырех переменных.
- При изменении значений смещения, скорости или ускорения калькулятор исходит из того, что частота остается постоянной для расчета двух других неизвестных.
- При изменении значения частоты калькулятор считает ускорение постоянным и вычисляет скорость и смещение, используя это новое значение частоты.
Эти основные уравнения движения более подробно объясняются ниже в разделе «Простые гармонические уравнения движения».
Все эти значения автоматически обновляются при изменении любой переменной. Важно отметить, что они представляют амплитуда (от нуля до пика) не размах значений. Обратитесь к графикам для получения дополнительной информации о том, как эти волны движения меняются с течением времени.
Важно отметить, что они представляют амплитуда (от нуля до пика) не размах значений. Обратитесь к графикам для получения дополнительной информации о том, как эти волны движения меняются с течением времени.
Графики смещения, скорости, ускорения, частоты
На приведенном выше графике соотношения частоты, смещения, скорости и ускорения отображаются две линии, которые показывают, как скорость и частота изменяются, если ускорение (синяя линия) или смещение (оранжевая линия) остаются постоянными. Пересечение этих двух линий происходит при значениях переменных, определенных пользователем в вышеуказанных числовых полях.
Другой график отображает несколько циклов, как указано в приведенном выше диалоговом окне, для смещения, скорости и ускорения. Эти формы сигналов представляют смещение, скорость и ускорение как функцию времени при заданных или рассчитанных амплитудах и частоте. Эти основные уравнения движения объясняются более подробно ниже в разделе «Простые гармонические уравнения движения».
Псевдоним
Обратите внимание, что на простых графиках гармонического движения отображается только 100 точек данных. Это было сделано специально, чтобы проиллюстрировать важность частоты дискретизации . Например, сигналы выглядят «чистыми» при 10 или менее циклах (частота дискретизации, которая в 10 раз превышает интересующую частоту). Когда больше циклов отображается только с этими 100 точками данных, графики становятся все более неровными. То же самое происходит и при вибрационных испытаниях: если вы недостаточно быстро производите выборку, вы упустите важные характеристики своего вибрационного профиля.
По мере того, как количество циклов увеличивается до 1/2 “частоты дискретизации” (100 точек данных), в сигнале пропускается все больше и больше информации. При 1/2 «частоты дискретизации» или частоты Найквиста сигнал «складывается» сам по себе. В 99 циклов, из-за неэффективности нашей частоты дискретизации система сбора данных будет считать, что она точно измерила 1 цикл. Подробнее о частоте Найквиста и алиасинге мы расскажем в блоге.
Подробнее о частоте Найквиста и алиасинге мы расскажем в блоге.
Измерение ускорения с помощью датчиков enDAQ
Если вы заинтересованы в этом инструменте, вам, вероятно, понадобятся данные об ускорении! У нас есть продуктовая линейка датчиков и программного обеспечения под названием enDAQ. Они бывают нескольких разных диапазонов ускорения и могут использоваться для ускорения от 0,1g до 2000g и частотных диапазонов ниже 2000 Гц. Для уровней ускорения за пределами этого диапазона у нас есть блог по выбору акселерометров, в котором представлены компании-поставщики акселерометров, у которых могут быть более подходящие решения для продуктов.
Простые гармонические уравнения движения
Движение колебательной системы приводит к скорости и ускорению, которые не являются постоянными, а фактически моделируются синусоидальной волной. Синусоида, похожая на синусоиду, представляет собой гладкую повторяющуюся волну, но может иметь сдвиг по фазе, периоду или амплитуде. Важными факторами, связанными с этим колебательным движением, являются амплитуда и частота движения. Общее уравнение для движения, следующего за синусоидой, имеет вид
Важными факторами, связанными с этим колебательным движением, являются амплитуда и частота движения. Общее уравнение для движения, следующего за синусоидой, имеет вид
, где — амплитуда смещения, — частота, — время, и в данном случае это может быть смещение в момент времени. Угловая скорость может быть представлена следующим уравнением.
Тогда можно сократить до
Принимая во внимание перемещение системы, известно, что мы можем узнать больше о движении системы посредством дифференцирования. Это можно представить как
, где — скорость, а — ускорение системы, где первая производная смещения — это скорость, а вторая производная — ускорение. Это знание можно применить к нашему синусоидальному уравнению, в результате чего
будут уравнениями, связывающими скорость и ускорение со смещением. Если известны амплитуда и смещение частоты, то по ним можно определить функции скорости и ускорения.
Ту же концепцию можно использовать, если наряду с частотой известна амплитуда скорости или ускорения.



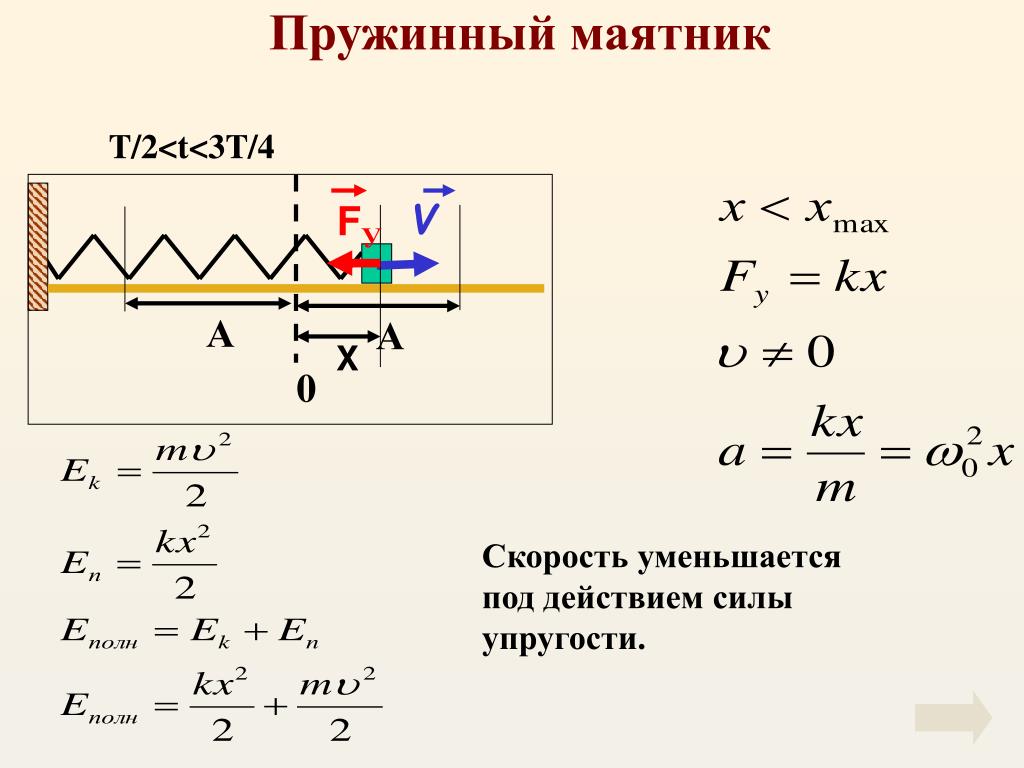 график).
график).

 При совпадении частот,
, вне зависимости от величины затухания, сдвиг фазы составляет
.
При совпадении частот,
, вне зависимости от величины затухания, сдвиг фазы составляет
. ..
.. ⓘ Скорость частицы [v]
ⓘ Скорость частицы [v] ⓘ Амплитуда вибраций с использованием скорости частицы [A]
ⓘ Амплитуда вибраций с использованием скорости частицы [A]



 движение. Если вы сместите пружину на максимальную величину x = A,
амплитуду, освободить его от покоя (ст. или = 0), фотография
и постройте положение как функцию времени, вы найдете, как показано
на рис. 3а ниже показано, что x(t) = A cos (2pt/T),
где Т — период — время одного полного колебания.
движение. Если вы сместите пружину на максимальную величину x = A,
амплитуду, освободить его от покоя (ст. или = 0), фотография
и постройте положение как функцию времени, вы найдете, как показано
на рис. 3а ниже показано, что x(t) = A cos (2pt/T),
где Т — период — время одного полного колебания. 3 выше, чтобы:
3 выше, чтобы: v = -0,1p
м/с
v = -0,1p
м/с 
 E = 1/2 кА 2 + 0 Так как
E – константа, E всегда равна 1/2 кА 2 для всех
времена и перемещения.
E = 1/2 кА 2 + 0 Так как
E – константа, E всегда равна 1/2 кА 2 для всех
времена и перемещения. Ранее мы нашли, что V max = wA
= п с -1 (0,2
м) = 0,2р м/с. v макс. 2 = 0,04p 2 м 2 /с 2 .
В положении равновесия кинетическая энергия равна
полная энергия =1/2(p 2 Н/м)(0,20 м) 2 = 1/2 mv max 2 =
Ранее мы нашли, что V max = wA
= п с -1 (0,2
м) = 0,2р м/с. v макс. 2 = 0,04p 2 м 2 /с 2 .
В положении равновесия кинетическая энергия равна
полная энергия =1/2(p 2 Н/м)(0,20 м) 2 = 1/2 mv max 2 =