Метрический конус: Конус Морзе для центрированного крепления сверл, фрез, зенковок, патронов т. п.

alexxlab | 05.06.2021 | 0 | Разное

Конус Морзе для центрированного крепления сверл, фрез, зенковок, патронов т. п.

Конус Морзе оснастка для быстрого переоснащения станка инструментом разного размера.

Чаще всего применяется для центрированного крепления режущего  инструмента: сверл, фрез, зенковок, патронов т. п.  Для этого хвостовик инструмента, изготовленный конусообразной формы, вставляется в соответствующее по диаметру и конусности отверстие на станке (шпиндель, задняя бабка),

Конус морзе для фрезерных станков.

или для уменьшения конусности — переходной конус вставляется в конус наибольшего размера.

Переходник конус Морзе

Виды конусов Морзе

Инструментальные конусы

инструментальные конусы существуют двух типов — с лапкой и без лапки.

Конусы Морзе с лапкой бывают семи размеров, обозначаемых
№ 0, 1, 2, 3, 4, 5 и 6, и метрические,
обозначаемые № 80, 100, 120, 160 и 200.

Конусы Морзе без лапки и метрические бывают тех же номеров, как и конусы с лапкой. Кроме того, существуют метрические конусы без лапки — № 4 и 6.

Наименьший конус Морзе № 0, а наибольший — № 6. Первые конусы Морзе изготовлялись в дюймовой системе, поэтому размеры их при переводе на метрические меры выражаются дробными числами.

Например, у конуса Морзе № 2 с лапкой D = 17,980 мм, d = 14,059 мм и l =  78,5 мм. Углы уклона у всех конусов различны, но колеблются в довольно узких пределах, от 1° 25′ 43″ у конуса № 1 до 1° 30′ 26″ у конуса № 5.

Неодинакова также и их конусность, которая колеблется в пределах от 0,04988 у конуса № 1 до 0,05263 у конуса № 5. Самый маленький метрический конус имеет № 4, самый большой — № 200. Номер конуса равен количеству миллиметров, содержащихся в большем диаметре данного конуса.

Например, у метрического конуса № 80 больший диаметр равен 80 мм. Углы уклона метрических конусов всех размеров и конусность их постоянны, а именно: α = 1° 25′ 56″, К = 1 : 20 = 0,05.

Конусы с конусностью 1 : 30 и 1 : 50

В инструментальном деле и в общем машиностроении приняты, конусы с конусностью 1 : 30 и 1 : 50.

Конусность 1 : 30 имеют отверстия в насадных развертках и зенкерах. Коническая форма отверстий в этих инструментах необходима для лучшего центрирования и прочности посадки их на оправках. Такую же конусность имеют и рабочие концы оправок для разверток и зенкеров. Угол уклона при конусности 1 : 30 составляет 0° 55′.

Конусность 1 : 50 имеют установочные штифты, применяемые в случае, когда необходимо, чтобы две детали машины, скрепленные болтами, не могли перемещаться одна относительно другой (например, фартук суппорта и его продольные салазки).

Установочные штифты входят в отверстия, высверленные и развернутые одновременно в обеих деталях, после их сборки. Конусность таких штифтов принята равной 1 : 50, что соответствует углу уклона α = 0° 34′.

 

---

Узнать более подробную информацию об конусах Морзе можно позвонив по тел. 8-800-100-2667

Заказать конусы Морзе можно оставив сообщение на почту: [email protected]

---

 

Неизвестный Конус Морзе… Историческая справка. – Фотографии станков

Неизвестный Конус Морзе…

 

Рабочая жизнь любого, уважающего себя, станочника, профессионала или любителя, сопровождается частым поиском, подбором, применением, заменой, а иногда и изготовлением оснастки и инструмента с необычной, для простого обывателя, хвостовой частью, сходящейся на конус. Конечно же, все (которые в курсеJ) сразу узнали КОНУС МОРЗЕ.

 

Техническая сторона вопроса.

Согласно Википедии “…Конус Морзе подразделяется на восемь размеров, от КМ0 до КМ7 (англ. MT0-MT7, нем. MK0-MK7). Конусность от 1:19,002 до 1:20,047 (угол от 1°25’43″ до 1°30’26″) в зависимости от типоразмера.

 

Стандарты на конус Морзе: ISO 296, DIN 228, Российский стандарт ГОСТ 25557-2006 (Конусы инструментальные.

Основные размеры.). В российском стандарте конус КМ7 к применению не рекомендован, вместо него применяется несовместимый метрический конус № 80. Конусы изготовленные по дюймовым и метрическим стандартам взаимозаменяемы во всем, кроме резьбы хвостовика.

 

Существует несколько исполнений хвостовика конуса: с лапкой, с резьбой, без оных. Инструмент с лапкой фиксируется в шпинделе заклиниванием этой лапки, для чего в рукаве шпинделя есть соответствующий паз. Инструмент с резьбой фиксируется в шпинделе штоком (штревелем), вворачивающимся в торец конуса. Лапка предназначена для облегчения выбивания конуса из шпинделя и предотвращения проворачивания. Резьбовые конусы гарантируют невыпадение инструмента и облегчают извлечение заклинившего конуса. Некоторые конуса снабжаются системой отверстий и канавок для подачи охлаждающей жидкости (СОЖ).

 

Метрический конус

Впоследствии понадобилось расширить диапазон размеров конусов Морзе как в большую так и в меньшую сторону.

При этом для новых типоразмеров конуса выбрали конусность ровно 1:20 (угол 1°25’56″) и назвали их метрическими конусами (англ. Metric Taper). Типоразмер метрических конусов указывается по наибольшему диаметру конуса в миллиметрах. ГОСТ 25557-2006 определяет маленькие метрические конуса № 4 и № 6 (англ. ME4, ME6) и большие метрические конуса № 80, 100, 120, 160, 200 (англ. ME80-ME200). Конструктивных различий между конусом Морзе и метрическим нет.

 

Укороченные конуса Морзе

Для многих применений длина конуса Морзе оказалась избыточной. Поэтому придумали девять размеров укороченных конусов Морзе (B7, B10, B12, B16, B18, B22, B24, B32, B45), полученные удалением более толстой части конуса. Цифра в обозначении короткого конуса — диаметр толстой части конуса в мм. Российский стандарт на укороченные конуса ГОСТ 9953-82.

B7 — укороченный до 14 мм КМ0.

B10, B12 — укороченный до 18 и 22 мм соответственно КМ1.

B16, B18 — укороченный до 29 и 37 мм соответственно КМ2.

B22, B24 — укороченный до 45 и 55 мм соответственно КМ3.

B32 — укороченный до 57 мм КМ4.

B45 — укороченный до 71 мм КМ5

… и т.д.”

Полную статью приводить не буду, а основное изложено выше.

 

Историческая сторона вопроса.

Но самое интересное (ИМХО), это сама история возникновения сверла с коническим хвостовиком, и, неразрывно связанная с этим, история человека, его придумавшего. А история эта мутная, но с белыми пятнами :).

Кто такой этот Морзе удалось найти не сразу. Русскоязычные сайты, включая Википедию дали очень скупую информацию. А ведь речь идёт о человеке, имя которого, стало именем нарицательным для многих поколений станочников и не только в бывшем СССР. Как оказалось, этот человек сначала изобрёл (и запатентовал) спиральное сверло, каким мы его знаем сейчас, в 1863 году. А уже позже разработал очень удобную и хитроумную систему крепления и одновременного центрирования режущего инструмента, собственно конус. Но, обо всём по порядку.

 

Официальная история.

Стивен А. Морзе разработал идею создания спирального сверла, состоящего из двух параллельных спиральных канавок с прямой режущей кромкой. До этого свёрла были остроконечными и были сделаны из плоского профиля методом закручивания.

 

Его оригинальный патент, № 38119, датирован 7 апреля 1863 года, и назывался он ” Improvement in drill-bits”.

 

Стивен А. Морзе начал производство сверл, в городе Ист Бриджвотер (East Bridgewater), в октябре 1861 года в небольшой мастерской, которое представляло собой 2–х этажное деревянное здание. В 1864 году он нашел заинтересованных инвесторов в Нью-Бедфорде (New Bedford), Массачусетс и создал компанию с уставным капиталом в $ 30.000. В июне того же года производство из Ист Бриджвотер переводится в Нью-Бедфорд. Компания называлась “The Morse Twist Drill & Machine Company”, другое зарегистрированное название было “Morse Twist Drill & Mfg. Co.” Использовался торговый знак “MORSE” и “M.T.D.&M.Co.” (источник).

Но из-за разногласий в методах управления компанией г-н Морзе передал бразды правления совету директоров и в 1868 году ушел из компании.

На гравюре – фабрика Морзе в Нью-Бедфорд в середине 1870-х годов.

 

В 1877 году на Centennial Exhibition (Столетняя выставка) в Филадельфии, была продемонстрировала первая экспозиция инструментов Морзе. Продукция получила международное признание за качество и продавалась в самих Соединенных Штатах, а также экспортировалась в Англию, Россию и Германию.

 

Фото продукции Морзе из музея в Нью-Бедфорде http://www.flickr.co…in/photostream/

Ссылки на статьи о фирме Морзе в The Manufacturer and Builder (Volume 0004 Issue 4, April 1872; Volume 0025 Issue 12, December 1893)

 

Во второй половине девятнадцатого века, компания стала моделью структуры, поглощающей другие предприятия, что привело к её огромному разрастанию. Компания Морзе поглотила (слилась) минимум с шестью другими, профильными компаниями:

1871 – American Standard Tool Company

Danbury, CT

1871 – Manhattan Fire Arms Company Newark, NJ

1874 – New York Tap and Die Company Bridgeport

1879 – New York Twisted Drill Company Brooklyn

1885 – Rockford Twist Drill and Patent Company Rockford, IL

1897 – T & B Tool Company Danbury, CT

Машины T & B Tool Company, используемые при изготовлении сверел с постоянным углом, были разработаны бывшим сотрудниками фирмы Морзе, которые ушли в свой собственный бизнес и создали фирму Pratt and Whitney.

Компания Морзе также приобрела патент на сверлильный патрон Beach chuck компании Meridan Tool, Meridan, штат Коннектикут, и оборудование Schofield Patent Grinding Line, помогающее обеспечить точность при заточке сверла.

 

В 1889 году уставный капитал увеличился до $ 600. 000, здания занимали общую площадь, равную одной квадратной миле. В течение первых 25 лет компания выпускала разнообразную продукцию: свёрла, инструменты, патроны, развертки, метчики, фрезы и т.д. Примечательно также, что первоначальный совет директоров был неизменным, за исключением добавления должности казначея (ссылка на источник).

 

В начале ХХ века, фирма Морзе разработала станок, используемый в производстве сверл. До начала Первой мировой войны, компания продает линию простых и универсальных шлифовальных станков. В 1923 году Van Norman Machine Company из Спрингфилда, штат Массачусетс, приобрела компанию Морзе.

Бизнес продолжает расти между войнами, и, во время Второй мировой войны, производство продукции фирмы Морзе увеличивается в 4-5 раз от довоенного уровня, внося свой вклад в военные усилия. А в 1964 году, Universal American Corp. стала компанией – правопреемницей компании Морзе.

 

 

 

Результаты собственного исследования вопроса.

 

Полное имя изобретателя – Стивен Эмброуз Морзе (Stephen Ambrose Morse), американец, по профессии – механик. Информации по годам жизни нет вообще, однако, согласно Death Certificates Index,USA, человек с такими именем и фамилией, рождённый в 1803г и умерший в 1915г (жизнь в 112 лет!), похоронен в Филадельфии, Пенсильвания. Возможно, что это “полный тёзка” нашего мистера Морзе, но это единственное совпадение, которое мне удалось найти. И ещё обнаружились несколько патентов на изобретения, принадлежащие человеку с такими же инициалами и фамилией, который проживал в Филадельфии, Пенсильвания, правда подписи на эскизах мистера Морже из Ист Бриджвотера и мистера Морзе из Филадельфии отличаются. Возможно, это ложный след, и это разные люди.

мистер Морзе из Ист Бриджвотера/Нью-Бедфорда

Мистер Морзе из Филадельфии

 

 

Однако моя математика идёт в разрез с фото (если это он), которое вывешено на страничке истории инструмента Морзе (источник).

На котором, предположительно изображён мистер Стивен Э. Морзе. На фото относительно молодой человек в возрасте 35-40 лет, а вовсе не 60 (на момент руководства компанией). И ещё один момент. В процессе поиска выяснилось, что Стивен Э. Морзе не патентовал сам конусный хвостовик и патрон к нему – самый главный патент на спиральное сверло есть, но на сам конусный хвостовик найти не удалось. Согласно официальной истории, Стивен Э. Морзе после изобретения сверла, разработал, изготовил и отправил в Бюро Стандартов в Вашингтоне, округ Колумбия, один из наборов конических хвостовиков и ответных частей к ним. Вскоре это изобретение было принято в качестве национального стандарта США. Быть может, что изобретение, которое становится Стандартом США, не подлежит патентованию, тогда понятно, почему нет патента.

 

За время правления Стивена Э. Морзе в своей компании, 1864-1868гг., нашлись ещё несколько патентов (63929, 42592), но ни один не касается конуса. Причём последний патент за № 63929, от 16.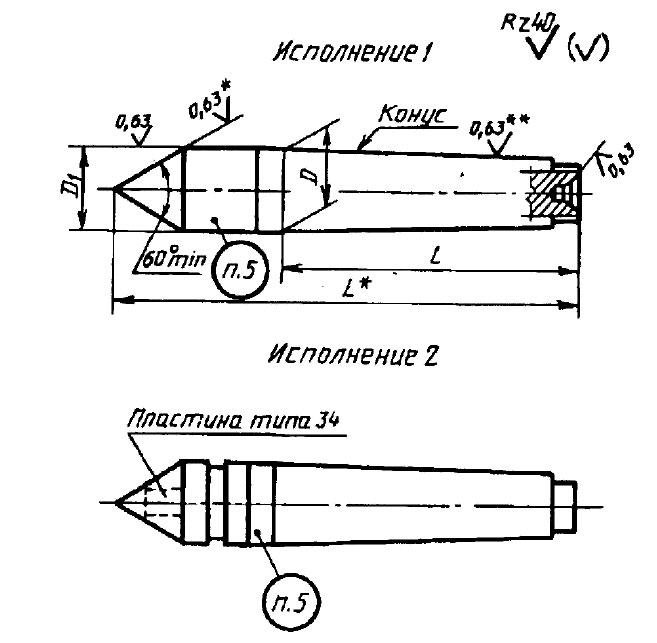 04.1867г. (за год, а может и меньше, до ухода из собственной компании) вообще странно называется ALL WHOM IT MAY CONCERN – дословно: ВСЕМ, КОГО ЭТО МОЖЕТ КАСАТЬСЯ. Патент на быстрозажимные тиски для фрезерной машины. Название патента звучит так, как-будто автор изобретения не уверен в его нужности. Очень странно…

И ещё одна деталь, после ухода из фирмы Стивена Э. Морзе в 1868 году, в названии компании постоянно присутствовала его фамилия, даже во времена перепродажи компании другим фирмам. А состав совета директоров не менялся на протяжении 25 лет. Такое впечатление, что – либо Стивен Э. Морзе – подставное лицо, как сейчас принято говорить, либо ему просто не повезло с компаньонами, которые “кинули” изобретателя, как только стали ясны перспективы производства и была определена ниша рынка, либо мистер Морзе “тёмная лошадка”, который долгое время, оставаясь в тени, управлял развитием собственной компанией с помощью совета директоров (тех самых, которые не менялись 25 лет – до дня смерти Морзе в 1889 году?!!).

Вот такая запутанная история…

Изменено 12 октября, 2012 пользователем AbraCadabra

Метрический конус – Большая Энциклопедия Нефти и Газа, статья, страница 3

Метрический конус

Cтраница 3

Недостатком конусов Морзе являются разные углы наклона у различных номеров конусов. Номер метрического конуса обозначает размер большого диаметра конического отверстия. У всех метрических конусов угол наклона делают одинаковым – в этом преимущество метрических конусов как в практическом применении, так и в изготовлении.  [31]

В корпусе коллиматора, представляющем собой метрический конус 80, находится система линз, марка с перекрестием, сетка и лампочка для освещения. Визирная труба состоит из метрического конуса, к фланцу которого прикреплен корпус трубы. В корпусе трубы смонтирован объектив, подвижная линза внутренней фокусировки и сетка.  [33]

Недостатком крутого конуса является меньшая точность центрировки по сравнению с двумя другими конусами. Однако все преимущества высокой точности центрировки метрического конуса и конуса Морзе практически используются полностью редко потому, что их внутренние конусы вследствие большой длины не всегда могут быть достаточно хорошо очищены от грязи.  [35]

Центровой оправкой называют такую, один конец которой входит в коническое гнездо шпинделя горизонтально-фрезерного станка, а другой конец поддерживается подвеской хобота. В зависимости от типа конуса гнезда шпинделя различают центровые оправки с конусом по ГОСТ 836 – 47, с конусом Морзе, с метрическим конусом и конусом Броун и Шарп. Конец центровой оправки, поддерживаемый подвеской, выполняют либо с направляющей цапфой либо без направляющей цапфы.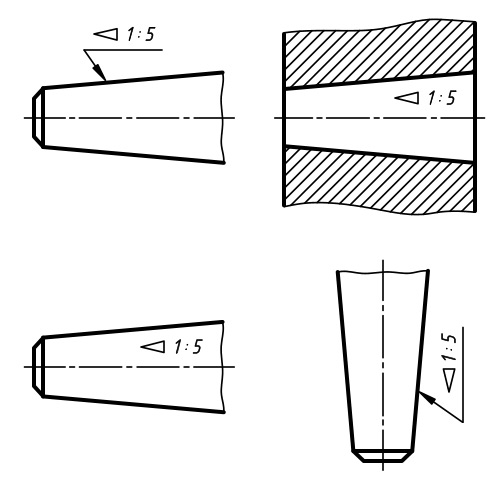 В комплект центровой оправки входят, кроме самой оправки, набор установочных колец, одна или две направляющие втулки и одна гайка. В зависимости от размеров стола станка, ширины обрабатываемой детали, ширины одной или комплекта фрез, необходимой жесткости оправки и других факторов выбирают длину оправки. Диаметр рабочей части оправки выбирают по диаметру отверстия фрезы.  [36]

Центровой оправкой называют такую оправку, один кс нец которой входит в коническое гнездо шпинделя горизонтально фрезерного станка, а другой конец поддерживается подвеской хобс та. В зависимости от типа конуса гнезда шпинделя различают, цент ровые оправки с конусом по ГОСТ 836 – 72, с конусом Морзе метрическим конусом.  [37]

Концевой оправкой называют такую, конический коне которой входит в коническое гнездо шпинделя горизонтально – ил вертикально-фрезерного станка, а на другой конец надета насадна: торцовая фреза; таким образЪм концевая оправка работает консоль но. Конический конец оправки может быть выполнен в зависимост от конструкции переднего конца шпинделя с конусом по ГОС 836 – 72, конусом Морзе и метрическим конусом. В зависимости о конструкции торцовой фрезы она может крепиться на осевой или н; торцовой шпонке.  [38]

Оправки для установки фрез разделяют на центровые и концевые. В зависимости от типа конуса гнезда шпинделя конический конец оправок может быть выполнен с конусом по ГОСТ 836 – 47, с конусом Морзе, с метрическим конусом и конусом Броун и Шарп.  [39]

Концевой оправкой называют такую, которая коническим концом входит в коническое гнездо шпинделя, горизонтально – или вертикально-фрезерного станка, а на другой конец надевают насадную торцовую фрезу; таким образом концевая оправка работает консольно. Конический конец оправки может быть выполнен в зависимости от конструкции переднего конца шпинделя с конусом по ГОСТ 836 – 47, с конусом Морзе, с метрическим конусом и с конусом Броун и Шарп. В зависимости от конструкции торцовой фрезы крепление ее может быть выполнено на осевой или на торцовой шпонке.  [40]

Уклон обозначают сочетанием острого угла ( вершина направлена в сторону уклона) с тем же отношением, в котором L означает длину, на которой разность высот или радиусов равна 1 мм. Для метрических конусов и конусов Морзе установлено пять степеней точности ЛГ4 – АТ8, которыми регламентированы отклонения угла, прямолинейности образующих и круглости конусов, а также основных размеров конусов и их лапок. Отклонения угла располагают в плюс для наружных и в минус для внутренних конусов. Для внутренних конусов степени точности АТ4 и АТ5 являются перспектив, ными. Степень точности указывают в условном обозначении конуса.  [41]

Недостатком конусов Морзе являются разные углы наклона у различных номеров конусов. Номер метрического конуса обозначает размер большого диаметра конического отверстия. У всех метрических конусов угол наклона делают одинаковым – в этом преимущество метрических конусов как в практическом применении, так и в изготовлении.  [42]

По ГОСТу 2847 – 45 дополнительно введены метрические конусы, которые не нашли такого широкого распространения в промышленности, как конусы Морзе. Обозначения их приняты по наибольшему ( расчетному) диаметру D, который имеет следующие величины: 4, 6, 80, 100, 120, 140, 160, 200 мм. Таким образом, конусы Морзе располагаются между метрическими конусами. Соответственно этому, угол конуса 2а также является переменным. Различие в конусности объясняется переводом размеров в дюймовом исчислении в размеры в миллиметровом исчислении. Вопрос об унификации конусов давно назрел, но пока не получил разрешения, несмотря на ряд предложений в этой области.  [43]

По ГОСТу 2847 – 45 дополнительно введены метрические конусы, которые не нашли такого широкого распространения в промышленности, как конусы Морзе. Обозначения их приняты по наибольшему ( расчетному) диаметру D, который имеет следующие величины: 4, 6, 80, 100, 120, 140, 160, 200 мм. Таким образом, конусы Морзе располагаются между метрическими конусами. Соответственно этому, угол конуса 2а также является переменным. Различие в конусности объясняется переводом размеров в дюймовом исчислении в размеры в миллиметровом исчислении.  [44]

Недостатком конусов Морзе являются разные углы наклона у различных номеров конусов. Номер метрического конуса обозначает размер большого диаметра конического отверстия. У всех метрических конусов угол наклона делают одинаковым – в этом преимущество метрических конусов как в практическом применении, так и в изготовлении.  [45]

Страницы:      1    2    3    4

метрический конус – это.

.. Что такое метрический конус?

метрический конус

мат. metric cone

Большой англо-русский и русско-английский словарь. 2001.

• метрический континуум
• метрический коэффициент

Смотреть что такое “метрический конус” в других словарях:

• Конус инструментальный — Содержание 1 Конус Морзе и метрический конус 1.1 Метрический конус …   Википедия

• Конус морзе — Конус инструментальный  конический хвостовик инструмента (сверло, зенкер, фреза, развёртка) и коническое отверстие соответствующего размера (гнездо) в шпинделе или задней бабке станка. Предназначено для быстрой смены инструмента с высокой… …   Википедия

• Метрический тензор — или метрика это симметричное тензорное поле ранга 2 на гладком многообразии, посредством которого задаются скалярное произведение векторов в касательном пространстве, длины кривых, углы между кривыми и т. д. В частном случае поверхности метрика… …   Википедия

• Развёртка (инструмент) — У этого термина существуют и другие значения, см. Развёртка (значения). Развёртка – режущий инструмент, который нужен для окончательной обработки отверстий после сверления, зенкерования или растачивания. Развёртыванием достигается точность до 6 9 …   Википедия

• Основной тензор — Метрический тензор или метрика это симметричный тензор ранга 2 на гладком многообразии, посредством которого задаются скалярное произведение векторов в касательном пространстве, длины кривых, углы между кривыми и т. д. В частном случае… …   Википедия

• Риманова метрика — Метрический тензор или метрика это симметричный тензор ранга 2 на гладком многообразии, посредством которого задаются скалярное произведение векторов в касательном пространстве, длины кривых, углы между кривыми и т. д. В частном случае… …   Википедия

• Фундаментальный тензор — Метрический тензор или метрика это симметричный тензор ранга 2 на гладком многообразии, посредством которого задаются скалярное произведение векторов в касательном пространстве, длины кривых, углы между кривыми и т. д. В частном случае… …   Википедия

• Тензор Риччи — Тензор Риччи, названный в честь Риччи Курбастро, задаёт один из способов измерения кривизны многообразия, то есть степени отличия геометрии многообразия от геометрии плоского евклидова пространства. Тензор Риччи, точно так же как метрический… …   Википедия

• Кривизна Риччи — В дифференциальной геометрии тензор Риччи, названный в честь Риччи Курбастро, задаёт один из способов измерения кривизны многообразия, то есть степени отличия геометрии многообразия от геометрии плоского евклидова пространства. Тензор Риччи,… …   Википедия

• Специальная теория относительности — Почтовая марка с формулой E = mc2, посвящённая Альберту Эйнштейну, одному из создателей СТО. Специальная теор …   Википедия

• ЧЁРНЫЕ ДЫРЫ — 1. Введение Ч. д. области пространства времени, обладающие горизонтом событий, т. е. области с настолько сильным гравитац. полем, что даже свет не может их покинуть. Термин Ч. д. введён в 1968 Дж. Уилером (J. A. Wheeler). Первое качественное пре …   Физическая энциклопедия

Конус инструментальный санкт-петербург конус морзе

Классический конус представляет собой наконечник строительного прибора (например, сверла) конической формы и гнездо соответствующего размера на обратной стороне станка. Подобные конусы используют для оперативной замены прибора с высокой точностью и степенью надежности. Специалисты различают несколько видов конусов, разнящихся по так называемой конусности. Поговорим о наиболее популярных из них.

Конус Морзе

Конус Морзе является самым часто встречающимся креплений приборов.

Данный вид имеет 8 основных разновидностей – маркировка от КМ0 до КМ7. Основной параметр – конусность – имеет следующие значения: от 1:19,002 до 1:20,047.

Общепринятые мировые стандарты для таких конусов – ISO 296, DIN 228. Российский аналог – ГОСТ 25557-2006 «Конус инструментальные. Основные размеры». Отечественный стандарт не рекомендует к применению конус Морзе КМ7. Рекомендуемая замена – метрический конус.

В процессе развития станкостроительной промышленности появилась необходимость в расширении размерных диапазонов привычных конусов Морзе в обоих направлениях. Именно метрические конусы стали следующей ступенью развития конусов Морзе.

Конусы Морзе и метрические являются взаимозаменяемыми практически по всем характеристикам, кроме резьбы наконечника.

Другие распространенные конусы

Конус 1:50

Такой конусностью как правило характеризуются детали, используемые при дополнительном соединении нескольких деталей, закрепленных при помощи резьбы, чтобы минимизировать их перемещение относительно друг друга. Такой конус устанавливается в специально просверленные в деталях отверстия уже после их изготовления и сборки. Угол наклона конуса составляет 0°34′.

Конус 1:30

Угол наклона такого конуса составляет 0°55′. Используется для насадных разверток и зенкеров.

Конус 1:24

Данный вид конусов изготавливается по международному стандарту, размер которого несколько меньше стандартного конуса Морзе №1.

Конус 1:20

Стандартные метрические конусы для приборов, изготавливающие по отечественному стандарту. Устанавливаются в отверстия в шпинделях на технологическом оборудовании.

Конус 1:16

Используется при изготовлении бурильных и насосных установок.

Конус 1:10

Изготавливаются по ГОСТ 5006-83 и ГОСТ 7383-72. Используются при изготовлении больших мостовых и корабельных конструкций.

Конус 1:7

Конусы такого размера являются стандартными для пробковых кранов, тяжелых станков и др.

Конус 1:5

Предназначен для оборудования концов шлифовальных шпинделей.

Конус 1:4

Широко используются для изготовления замков в нефтяной промышленности

Конус 1:1,866

Используются для скрепления деталей, расположенных в центре крупных станков.

Конус 1:0,866

Применяются в зажимной тяге

Конус 1:0,652

Используются в качестве потайных головок и заклепок

Конус 7:64

Используются для изготовления зубодолбежных приборов

Перечисленные разновидности инструментальных конусов являются наиболее распространенными, но далеко не единственными.

Конус Морзе | MoscowShpindel

Для быстрого, точного и надежного центрированного способа крепления инструмента используется хвостовик в виде конуса и коническое отверстие для него в шпинделе фрезерного станка. Чаще всего в сверлах, фрезах, зенковках и другом режущем инструменте применяется конус Морзе. Он бывает 8-ми размеров: от КМ нулевого размера до КМ седьмого размера. Этот вид хвостовика был изобретен Стивеном А. Морзе (он также первым придумал спиральное сверло). Существует еще 9 размеров укороченных конусов Морзе: В45, В32, В24, В22, В18, В16, В12, В10 и В7 (приведены в порядке убывания).

Для конуса Морзе разработаны международные стандарты: DIN 228, ISO 296. Однако существующий в России ГОСТ 25557-2006 для инструментальных конусов обнаруживает существенные различия с ними. Так, российским стандартом не рекомендовано использовать конус Морзе КМ7 – вместо него разработан метрический конус №80, который несовместим с КМ7. В остальном конусы, производимые по международным (дюймовым) и российским (метрическим) стандартам, полностью взаимозаменяемы и отличаются лишь параметрами  резьбы хвостовика.

Хвостовик инструментального конуса исполняется в нескольких вариантах: с резьбой, с лапкой или без них. Внутренняя резьба, имеющаяся в торце конуса, служит для фиксации инструмента в шпинделе с помощью специального штока – штревеля. Он не только надежно обеспечивает невыпадение инструмента, но и облегчает его извлечение при заклинивании конуса в шпинделе. Хвостовик инструмента с лапкой в шпинделе крепится за счет ее заклинивания в специальном пазу. Назначение лапки двоякое. Во-первых, она облегчает выбивание конуса из шпинделя, а во-вторых, не позволяет инструменту проворачиваться при больших нагрузках.

В некоторых конусах Морзе предусматривается целая система канавок и отверстий, через которые к режущим органам инструмента подается смазочно-охлаждающая жидкость (СОЖ).

А вот в станках с ЧПУ (в том числе и настольных) широко используется автоматическая смена инструмента. Для этих целей разработан специальный инструментальный конус, который устраняет такие недостатки конуса Морзе, как

• частое самозаклинивание хвостовика в шпинделе;
• большая длина хвостовика;
• небольшая площадь торца хвостовика и, как следствие, недостаточный осевой упор;
• множество сложностей, возникающих при автоматическом закреплении конуса инструмента в шпинделе;
• невозможность автоматической смены инструмента из-за отсутствия зацепов на хвостовике.

Китай Изготовленный на заказ мужской конический метрический конус BSP конический производитель, Поставщики – Нержавеющая сталь Мужской конический метрический конус BSP конус

Мужской Локтевой конус BSP Метрический разъем

Каталог фитингов BSP является популярным в Великобритании, Ирландии, Канаде, США и т. Д.

Все конусные фитинги BSP 60 имеют обозначение BS5200, соответствующее стандарту ISO 8434-6.

Размер таблицы размеров резьбы BSPP составляет G 1/8, G1 / 4, G1 / 2, G3 / 4, G3 / 8, G5 / 8, G1, G1-1 / 4, G1-1 / 2, G2, G2- 1/2, G3 и т. Д.

BSP – стандартная британская труба с резьбой 55 градусов.

Резьба BSPP соответствует стандартам ISO 228 и AS 1722.2.

ПБСП Нитенаправитель ко многим типам герметизации, такие как ПБСП 60 ° конуса к разъему трубки сиденье, BSPP порт с наклеенным уплотнителем, BSPP порт с ED уплотнением, G +, уплотнительное кольцо стопорного кольца G типа, G ORing регулируемого Sael типа H, G режущей поверхность печать типа B.

Адаптеры для фитингов BSPP для многих концов, такие как BSPT, ORFS, Metric ISO 6149-3, JIC-конус 74, Komatsu metric 60, NPT, SAE ORB ISO 11926-3, фитинг для сварки встык, JIC-мама 37cone, ORFS женский и др.

1BH9-OG 90 ° ELBOW BSP MALE 60 ° SEAT / МЕТРИЧЕСКИЙ MALE L-SERIES ISO 6149-3 Таблица размеров размеров следующим образом:

ПА РТ Н О.	T HR EA D		Кольцо		DIM E N S I O NS
	Е	F		F		В	S 1	S 2
1 B H9 – 02 – 10 O G	G 1/8 ” X 28	M10 X 1		O 08,1 X 1,6	20	+26,5	11	14
1 B H9 – 02 – 12 O G	G 1/8 ” X 28	M12 X 1,5		O 09,3 X 2,4	20	30,5	11	17
1 B H9 – 04 – 12 O G	G 1/4 ” X 19	M12 X 1,5		O 09,3 X 2,4	+24,5	32	14	17
1 B H9 – 04 – 14 O G	G 1/4 ” X 19	M14 X 1,5		O 11,3 X 2,4	+24,5	32,5	14	19
1 B H9 – 04 – 16 O G	G 1/4 ” X 19	M16 X 1,5		O 13,3 X 2,4	+26,5	34,8	16	22
1 B H9 – 06 – 14 O G	G 3/8 ” X 19	M14 X 1,5		O 11,3 X 2,4	+27,5	34	16	19
1 B H9 – 06 – 16 O G	G 3/8 ” X 19	M16 X 1,5		O 13,3 X 2,4	+27,5	34,8	16	22
1 B H9 – 06 – 18 O G	G 3/8 ” X 19	М18 Х 1,5		O 15,3 X 2,4	28,5	37	19	24
1 B H9 – 08 – 18 O G	G 1/2 ” X 14	М18 Х 1,5		O 15,3 X 2,4	34,5	39,5	22	24
1 B H9 – 08 – 22 O G	G 1/2 ” X 14	М22 Х 1,5		O 19,3 X 2,4	34,5	40,2	22	27
1 B H9 – 10 – 22 O G	G 5/8 ” X 14	М22 Х 1,5		O 19,3 X 2,4	35	40,2	22	27
1 B H9 – 12 – 22 O G	G 3/4 ” X 14	М22 Х 1,5		O 19,3 X 2,4	40	43,5	27	27
1 B H9 – 12 – 27 O G	G 3/4 ” X 14	M27 X 2		O 23,5 X 3,0	40	48,5	27	32
1 B H9 – 16 – 27 O G	G 1 ” X 11	M27 X 2		O 23,5 X 3,0	46	52	33	32
1 B H9 – 16 – 33 O G	G 1 ” X 11	M33 X 2		O 29,5 X 3,0	46	52,5	33	41
1 B H9 – 20 – 42 O G	G 1,1 / 4 ” X 11	M42 X 2		O 38,5 X 3,0	50,5	57,2	41	50
1 B H9 – 24 – 48 O G	G 1,1 / 2 ” X 11	M48 X 2		O 44,5 X 3,0	57,5	62,5	48	55

Hot Tags: метрический конус BSP, Китай, производители, поставщики, на заказ, латунь, Swagelok, Паркер, Штауфф, Бреннан, нержавеющая сталь

выпуклых многогранников – Геометрия метрического конуса

Допустим, что две метрики $ d $ и $ d_0 $ на множестве $ X $ связаны , если существуют положительные константы $ 0 <\ alpha \ leq \ beta $ такие, что $$ \ альфа \, \ влево (d_0 (x, y) + d_0 (y, z) - d_0 (x, z) \ right) \ leq d (x, y) + d (y, z) - d (x, z) \ leq \ beta \, \ left (d_0 (x, y) + d_0 (y, z) - d_0 (x, z) \ верно) $$ для всех $ x $, $ y $ и $ z $ в $ X $.

Простое и ключевое замечание:

Предложение. Две взаимосвязанные метрики бипшицевы и имеют точно такие же геодезические.

Под одинаковыми геодезическими я подразумеваю, что три точки $ x, y, z \ in X $ удовлетворяют $$ d (x, y) + d (y, z) – d (x, z) = 0 $$ если и только если они удовлетворяют $$ d_0 (x, y) + d_0 (y, z) – d_0 (x, z) = 0.

$

С геометрической точки зрения, две метрики связаны, если дефекты неравенства треугольника для одного из расстояний равномерно контролируются дефектами другого расстояния.

Вопрос.3 $, которые связаны с метрикой $ \ ell_ \ infty $ $ d_ \ infty (x, y) = \ max \ {| x_i – y_i | : 1 \ leq i \ leq 3 \} $?

В предыдущем вопросе МО я исследовал «связанные» нормы, которые я назвал «строго эквивалентными», и я не видел связи с работой Тони Томпсона по геометрии конусов. Это объясняется ниже.

Мотивация и объяснение названия.

Другое понимание связанных метрик можно получить, если подумать о конусе $ \ mathcal {M} (X) $ всех полуметрик (т. Е.е., $ d (x, y) $ может быть нулевым для $ x \ neq y $) на множестве $ X $.

Этот конус (как и любой другой конус) определяет частичный порядок: $ d_1 \ prevq d_2 $, если $ d_2 – d_1 $ – полуметрика. Обратите внимание, что две метрики $ d $ и $ d_0 $ связаны тогда и только тогда, когда существуют константы $ 0 <\ alpha \ leq \ beta $ такие, что $$ d \ prevq \ beta d_0 \; \ hbox {и} \; \ альфа d_0 \ prevq d. $$ Другими словами, две метрики связаны между собой тогда и только тогда, когда они находятся в одной и той же компоненте Томпсона метрического конуса $ \ mathcal {M} (X) $.п | f_i (x_i) – f_i (y_i) |, $$ где $ f_i: \ mathbb {R} \ rightarrow \ mathbb {R} $ $ (1 \ leq i \ leq n) $ – это строго возрастающие функции, насыщающие $$ 0 <\ epsilon \ leq \ frac {f_i (t) -f_i (s)} {t-s} \ leq K <\ infty $$ для некоторых положительных констант $ \ epsilon, K $ и всех действительных чисел $ t \ neq s $.

Этот результат можно обобщить на другие многогранные нормы, если они гиперметрические (они могут быть изометрически встроены в пространство $ \ ell_1 $), но $ \ ell_ \ infty $ не такой и кажется сложной задачей.п \, (\ theta_j-1) <0 $.

Я считаю, что это правильно, и несколько дней обдумывал доказательства.

Дифференциальная и риманова структура на конусе

Кажется, есть небольшая путаница.

Во-первых, есть разные понятия «конус». Стандартный относится к конусу в топологическом пространстве (см. Статью в вики) и определяется как $ CX = (X \ times [0,1]) / (X \ times \ {0 \}) $. Это, в частности, может быть применено к коллекторам. Получается топологическое пространство, которое, в общем, не является многообразием, но в некоторых частных случаях может иметь структуру гладкого многообразия (см., Например, обсуждение здесь).1 многообразий практически не существует в силу теоремы Уитни.

Что касается многообразий Сасаки, это особый тип римановых многообразий. Как объясняется в вики, упомянутой выше, один из способов определить, когда данное риманово многообразие $ X $ является Сасаки, – это использовать риманову метрику на $ X $, чтобы поместить метрику на конус, и посмотреть, делает ли полученная метрика конусом Кэлера . (В статье используется $ X \ times (0, \ infty) $, которое диффеоморфно внутренней части имеющегося у нас многообразия, так что это то же самое.) Обычно это не так (метрики Кэлера весьма специфичны), но иногда будет.

Это делается так, потому что кэлеровы многообразия более известны – они появляются как проективные или аффинные комплексные многообразия. Смысл этой конструкции в том, что многообразия Сасаки являются границами (некомпактных) кэлеровых многообразий.

Теперь, когда все это разобралось, можно спросить, как поставить риманову метрику на конус $ X \ times (0, \ infty) $. Формула есть в статье вики – она ​​называет ее «метрикой конуса».Если непонятно, что это значит, спросите – здесь в комментариях или где-нибудь еще. \ circ $ вокруг конуса, он не вернется в той же конфигурации, что и в начале.2}) $.)

Я ошибочно подумал, что если кривизна везде будет $ 0 $, этого не произойдет. Теперь я понимаю, что это верно только для односвязной гладкой области . (Острие конуса – это проблемная точка.) В противном случае доказательство того, что из нулевой кривизны $ \ следует $ плоское пространство, не работает. Моя неспособность понять это – вот почему я не более скептически относился к своей неправильной работе. Надеюсь, это интересно другим.

Общая топология

– Метрика на конусе компактного метрического пространства

Вот альтернативный подход к нахождению явной метрики на конусе $ CX $.

Сначала предположим, что $ X $ является подмножеством линейного нормированного пространства $ (E, \ lVert – \ rVert) $, а метрика $ d $ на $ X $ задается выражением $ d (x, y) = \ lVert x – y \ rVert $. Определим геометрический конус над $ X $ как подмножество $ C’X \ subset E ‘= E \ times \ mathbb R $, полученное объединением всех отрезков прямых $ L (x) = \ {((1-t ) x, t) \ mid t \ in I \} \ subset E ‘$, $ x \ in X $, соединяющий $ (x, 0) $ с $ (0,1) $. Другими словами $$ C’X = \ {(1-t) x, t) \ mid x \ in x, t \ in I \}. $$ Тогда $ C’X $ является подмножеством линейного нормированного пространства $ (E ‘, \ lVert – \ rVert’) $, где $ \ lVert (x, t) \ rVert ‘= \ lVert x \ rVert + \ lvert t \ rvert $ и, следовательно, наследует метрику $ d ‘$, заданную $ d’ ((x, t), (y, s)) = \ lVert ((x, t) – (y, s)) \ rVert ‘= \ lVert x – y \ rVert + \ lvert t – s \ rvert $.

Теперь определите $$ \ varphi: X \ times I \ to C’X, \ varphi (x, t) = ((1-t) x, t). $$ Это непрерывное отображение, такое что $ \ varphi (X \ times \ {1 \}) = \ {(0,1) \} $, следовательно, оно индуцирует непрерывное отображение $ \ phi: CX \ в C’X $, которое является очевидно, биекция. Если $ X $ компактно, то $ \ phi $ – гомеоморфизм. Следовательно, $ CX $ можно снабдить метрикой $$ D ([x, t], [(y, s]) = d ‘(\ phi ([x, t]), \ phi ([y, s])) = d’ (\ varphi (x, t), \ varphi (y, s)) \\ = \ lVert (1-t) x – (1-s) y \ rVert + \ lvert t – s \ rvert $$ что индуцирует его обычную топологию.

Пусть теперь $ (X, d) $ – метрическое пространство с ограниченной метрикой $ d $. Если $ X $ компактно, то $ d $ автоматически ограничивается. Пусть $ C_b (X) $ – векторное пространство всех непрерывных ограниченных отображений $ f: X \ to \ mathbb R $, наделенное $ \ sup $ -нормой $ \ lVert f \ rVert = \ sup_ {x \ in X} \ lvert f (x) \ rvert $. Хорошо известно, что $ (X, d) $ изометрически вкладывается в $ (C_b (X), \ lVert – \ rVert) $ через $ x \ mapsto e (x) = d (x, -): X \ to \ mathbb R $. Доказательство простое. Отождествляя $ X $ с $ e (X) \ subset C_b (X) $, наша конструкция дает геометрический конус $ C’X $ с метрикой $ d ‘$.Если $ X $ компактно, это дает следующую метрику на $ CX $:

.

$$ D ([x, t], [y, s]) = \ sup_ {z \ in X} \ lvert (1-t) d (x, z) – (1-s) d (y, z ) \ rvert + \ lvert t -s \ rvert. $$

Это, по общему признанию, менее прозрачно, чем решение Эрика Вофси.

В заключение сделаем замечание о геометрическом конусе. Если $ X $ не компактно, то $ C’X $ не гомеоморфно $ CX $. Фактически, $ CX $ не имеет счетной базы соседей на вершине, тогда как $ C’X $ является первой счетной. См. Мой ответ на эквивалентное определение $ \ text {Cone} (K) $, которое можно обобщить на данный случай.

Тем не менее, $ C’X $ имеет некоторые существенные особенности, приписываемые конусу: он стягиваем, а включение $ X \ to C’X, x \ mapsto (x, 0) $, является кофаслоением.

От объемного конуса к метрическому конусу в негладких условиях

AGS14

Амброзио Л., Джильи Н., Саваре Г.: Исчисление и тепловой поток в пространствах с метрическими измерениями и приложения к пространствам с ограничениями Риччи снизу. Inventiones Mathematicae 195 , 289–391 (2014)

MathSciNet Статья МАТЕМАТИКА Google Scholar

AGS114

Амбросио Л., Джильи Н., Саваре Г.: Метрические пространства с мерой с римановой кривизной Риччи, ограниченной снизу. Duke Mathematical Journal 163 , 1405–1490 (2014)

MathSciNet Статья МАТЕМАТИКА Google Scholar

AGS15

Амброзио Л., Джильи Н., Саваре Г.: Условие размерности кривизны Бакри-Эмери и римановы границы кривизны Риччи. Анналы вероятностей 43 , 339–404 (2015) arXiv: 1209.5786

MathSciNet Статья МАТЕМАТИКА Google Scholar

AMS14

Амбросио Л.{1,1}} \) и формулу площади для графиков. Успехи в математике 281 , 1145–1177 (2015)

MathSciNet Статья МАТЕМАТИКА Google Scholar

BS10

Бахер К., Штурм К.-Т .: Локализационные и тензорные свойства условия кривизны-размерности для метрических пространств с мерой. Журнал функционального анализа 259 , 28–56 (2010)

MathSciNet Статья МАТЕМАТИКА Google Scholar

C99

Чигер Дж.: Дифференцируемость липшицевых функций на метрических пространствах с мерой. Геометрический и функциональный анализ 9 , 428–517 (1999)

MathSciNet Статья МАТЕМАТИКА Google Scholar

CC96

Чигер Дж., Колдинг Т. Х .: Нижние границы кривизны Риччи и почти жесткости деформированных изделий. Анналы математики (2) 144 , 189–237 (1996)

MathSciNet Статья МАТЕМАТИКА Google Scholar

CC97

Чигер Дж., Колдинг Т. Х .: О структуре пространств с ограниченной снизу кривизной Риччи. I. Журнал дифференциальной геометрии 46 , 406–480 (1997)

MathSciNet МАТЕМАТИКА Google Scholar

CC00

Чигер Дж., Колдинг Т. Х .: О структуре пространств с ограниченной снизу кривизной Риччи. II. Журнал дифференциальной геометрии 54 , 13–35 (2000)

MathSciNet МАТЕМАТИКА Google Scholar

CC100

Чигер Дж., Колдинг Т. Х .: О структуре пространств с ограниченной снизу кривизной Риччи. III. Журнал дифференциальной геометрии 54 , 37–74 (2000)

MathSciNet МАТЕМАТИКА Google Scholar

EKS14

Erbar M., KuwadaK. Штурм К.-Т .: Об эквивалентности условия энтропийной кривизны-размерности и неравенства Бохнера на метрических пространствах с мерой. Inventiones mathematicae 201 , 1–79 (2014) arXiv: 1303.4382

Google Scholar

G13

N.Джильи. Теорема о расщеплении в негладком контексте, Препринт (2013). arXiv: 1302,5555.

G14

Н. Джильи. Негладкая дифференциальная геометрия – подход, разработанный для пространств с кривизной Риччи, ограниченной снизу. Принято в мемуарах Американского математического общества (2014). arXiv: 1407.0809.

G114

Джильи Н .: Обзор доказательства теоремы о расщеплении в пространствах с неотрицательной кривизной Риччи. Анализ и геометрия в метрических пространствах 2 , 169–213 (2014)

MathSciNet Статья МАТЕМАТИКА Google Scholar

G15

Н.Джильи. О дифференциальной структуре метрических пространств с мерой и приложениях. Мемуары Американского математического общества 236 (2015), vi + 91. arXiv: 1205,6622.

GH

Н. Джильи и Б. Хан. Пространства Соболева на деформированных изделиях, Препринт. arXiv: 1512.03177.

GKO13

Гигли Н., Кувада К., Охта С.-и .: Тепловые потоки в пространствах Александрова. Сообщения по чистой и прикладной математике 66 , 307–331 (2013)

MathSciNet Статья МАТЕМАТИКА Google Scholar

GM14

Джильи Н., Москони С .: Неравенство Абреша-Громолля в негладкой ситуации. Дискретные и непрерывные динамические системы 34 , 1481–1509 (2014)

MathSciNet МАТЕМАТИКА Google Scholar

GRS16

Джильи Н., Раджала Т., Штурм К.-Т .: Оптимальные отображения и возведение в степень на конечномерных пространствах с кривизной Риччи, ограниченной снизу. Журнал геометрического анализа 26 , 2914–2929 (2016)

MathSciNet Статья МАТЕМАТИКА Google Scholar

K15

Кеттерер К.: Конусы над метрическими пространствами с мерой и теорема о максимальном диаметре. Journal de Mathmatiques Pures et Appliques (9) 103 , 1228–1275 (2015)

MathSciNet Статья МАТЕМАТИКА Google Scholar

LV09

Лотт Дж., Виллани Ч .: Кривизна Риччи для пространств с метрической мерой с помощью оптимального переноса. Анналы математики (2) 169 , 903–991 (2009)

MathSciNet Статья МАТЕМАТИКА Google Scholar

O09

Охта С.-i .: Интерполяционные неравенства Финслера. Вариационное исчисление и уравнения в частных производных 36 , 211–249 (2009)

MathSciNet Статья МАТЕМАТИКА Google Scholar

R12

Rajala T .: Интерполированные меры с ограниченной плотностью в метрических пространствах, удовлетворяющих условиям размерности кривизны Штурма. Журнал функционального анализа 263 , 896–924 (2012)

MathSciNet Статья МАТЕМАТИКА Google Scholar

S14

Саваре Г.: Самоулучшение условия Бакри-Эмери и сжатие Вассерштейна теплового потока в метрических пространствах с мерой \ ({{\ rm RCD} (K, \ infty)} \). Дискретные и непрерывные динамические системы 34 , 1641–1661 (2014)

MathSciNet Статья МАТЕМАТИКА Google Scholar

S06

Штурм К.-Т .: К геометрии метрических пространств с мерой. I. Acta Mathematica 196 , 65–131 (2006)

MathSciNet Статья МАТЕМАТИКА Google Scholar

S106

Штурм К.-Т .: О геометрии метрических пространств с мерой. II. Acta Mathematica 196 , 133–177 (2006)

MathSciNet Статья МАТЕМАТИКА Google Scholar

V09

К. Виллани. Оптимальный транспорт. Старый и новый , Vol. 338 Grundlehren der Mathematischen Wissenschaften. Спрингер, Берлин (2009).

(PDF) Примеры в конических метрических пространствах: обзор

Ближневосточный журнал научных исследований 11 (12): 1636-1640, 2012

ISSN 1990-9233

© IDOSI Publications, 2012

DOI: 10.5829 / idosi.mejsr.2012.11.12.1462

Автор для переписки: Мехди Асади, Отдел математики, Зенджанское отделение, Исламский университет Азад, Зенджан, Иран

1636

Примеры в конических метрических пространствах: Обзор

1Мехди Асади Сулеймани

1 Кафедра математики, Занджанский филиал, Исламский университет Азад, Зенджан, Иран

2 Кафедра математики, Малайский филиал, Исламский университет Азад, Малайр, Иран

Аннотация: В этом обзоре мы рассматриваем множество примеров конусных метрических пространств. проверить некоторые свойства конусов

в реальных банаховых пространствах, и в дальнейшем мы представим другие примеры в метрических пространствах конусов, что

некоторые свойства некорректны в этих пространствах, но выполняются в обычном случае, например, в качестве сравнительного теста.

Тематическая классификация AMS: 47h20 • 54C60

Ключевые слова: метрическое пространство конуса • нормальный конус • ненормальный конус

ВВЕДЕНИЕ

Пусть E – реальное банахово пространство. Непустое выпуклое замкнутое подмножество

P⊆E называется конусом в E, если оно удовлетворяет:

i. P замкнуто, непусто и P ≠ {0}.

ii. Из a, b∈R, a, b≥0 и x, y∈P следует, что ax + by∈P.

iii. x∈P и – x∈P подразумевают, что x = 0.

Пространство E может быть частично упорядочено конусом

P⊆E, то есть x≤y тогда и только тогда, когда yx∈P Также мы пишем

x << y, если yx∈ int P, где int P обозначает внутренность P

Далее мы всегда предполагаем, что E – это действительное банахово пространство

, P – конус в E, а ≤ – частичный порядок

относительно P

Определение 1.1: [1] Конус P называется

1. Нормальным, если существует константа K> 0 такая, что

0≤x≤y влечет || x || ≤K || y ||.

2. Миниэдральная, если sup (x, y) существует для всех x, y∈E

3. Сильно миниэдральная, если каждое подмножество E, ограниченное сверху

, имеет супремум.

4. Непрерывно, если int P ≠ φ

5. Генерируется, если E = P-P.

6. Регулярно, если каждая возрастающая последовательность, ограниченная сверху

, сходится.То есть, если (xn)

– это последовательность, такая что

12

для некоторого y∈E, тогда существует x∈E, такая что

n

n

→ ∞

Определение 1.2: [2] Пусть X – непустое множество. Предположим

, что отображение d: X × X → E удовлетворяет

i. 0≤d (x, y) для всех x, y∈X и d (x, y) = 0 тогда и только тогда, когда

x = y.

ii. d (x, y) = d (y, x) для всех x, y∈X.

iii. d (x, y) ≤ d (x, z) + d (z, y) для всех x, y, z∈X.

Тогда d называется метрикой конуса на X, а (X, d) равно

, называемым метрическим пространством конуса.

Определение 1.3: Пусть (X, d) – метрическое пространство конуса, x∈X

и {xn} – последовательность в X. Тогда

i. {xn} называется сходящимся к x∈X всякий раз, когда для

каждого c∈E с 0 << c существует N такое, что для всех

n≥N, d (xn, x) << c, то есть n

n

→ ∞

ii.