Модуль шестерни формула: Что такое модуль шестерни? Как вычислить модуль зубчатого колеса

alexxlab | 23.12.2022 | 0 | Разное

Модуль зубьев зубчатого колеса — meig.ru

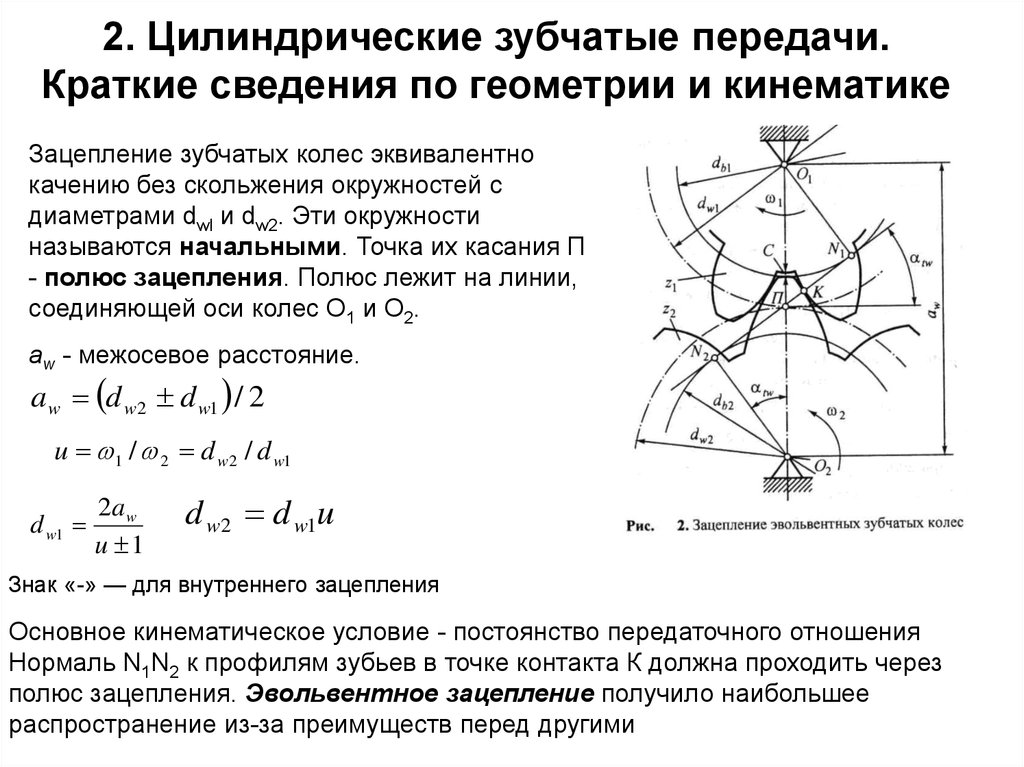
Зубчатая передача впервые была освоена человеком в глубокой древности. Имя изобретателя осталось скрыто во тьме веков. Первоначально зубчатые передачи имели по шесть зубьев — отсюда и пошло название «шестерня». За многие тысячелетия технического прогресса передача многократно усовершенствовалась, и сегодня они применяются практически в любом транспортном средстве от велосипеда до космического корабля и подводной лодки. Используются они также в любом станке и механизме, больше всего шестеренок используется в механических часах.

Зубчатое колесо

Что такое модуль зубчатого колеса

Современные шестерни далеко ушли от своих деревянных шестизубых предков, изготавливаемых механиками с помощью воображения и мерной веревочки. Конструкция передач намного усложнилась, тысячекратно возросли скорость вращения и усилия, передаваемые через такие передачи. В связи с этим усложнились и методы их конструирования. Каждую шестеренку характеризует несколько основных параметров

• диаметр;
• число зубьев;
• шаг;
• высота зубца;
• и некоторые другие.

Одним из самых универсальных характеристик является модуль зубчатого колеса. Существует для подвида — основной и торцевой.

Скачать ГОСТ 9563-60

В большинстве расчетов используется основной. Он рассчитывается применительно к делительной окружности и служит одним из важнейших параметров.

Для расчета этого параметра применяют следующие формулы:

m=t/π,

где t — шаг.

Параметры зубчатых колес

Модуль зубчатого колеса можно рассчитать и следующим образом:

m=h/2,25,

где h — высота зубца.

И, наконец,

m=De/(z+2),

где De — диаметр окружности выступов,а z — число зубьев.

Что же такое модуль шестерни?

это универсальная характеристика зубчатого колеса, связывающая воедино такие его важнейшие параметры, как шаг, высота зуба, число зубов и диаметр окружности выступов. Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач.

Формула расчета параметров прямозубой передачи

Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.

Расчет модуля зубчатого колеса

Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:

π×D=t×z,

проведя преобразование, получим:

D=(t /π)×z

Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.

t/π=m,

размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:

В=m×z;

выполнив преобразование, находим:

m=D / z.

Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса.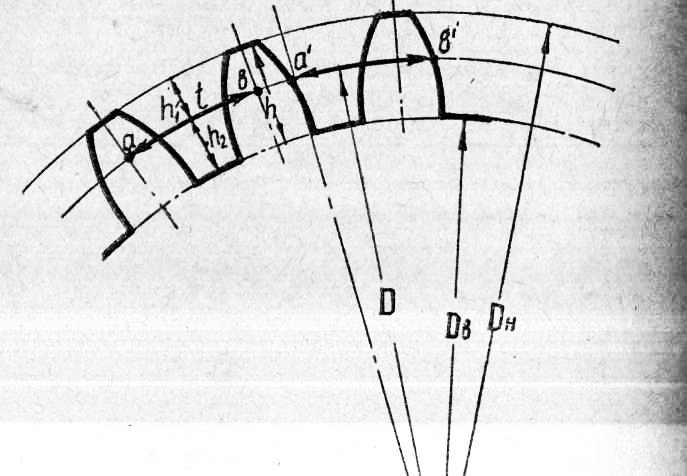 Диаметр окружности выступов D_e получается равным

De=d+2× h’,

где h’- высота головки.

Высоту головки приравнивают к m:

 h’=m.

Проведя математические преобразования с подстановкой, получим:

De=m×z+2m = m(z+2),

откуда вытекает:

m=De/(z+2).

Диаметр окружности впадин D_i соответствует D_e за вычетом двух высот основания зубца:

D_i=D-2h“,

где h“- высота ножки зубца.

Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:

h’ = 1,25m.

Устройство зубчатого колеса

Выполнив подстановку в правой части равенства, имеем:

D_i = m×z-2×1,25m = m×z-2,5m;

что соответствует формуле:

D_i = m(z-2,5m).

Полная высота:

h = h’+h“,

и если выполнить подстановку, то получим:

h = 1m+1,25m=2,25m.

Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.

Следующий важный размер, толщину зубца s принимают приблизительно равной:

• для отлитых зубцов: 1,53m:
• для выполненных путем фрезерования-1,57m, или 0,5×t

Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины s_в, получаем формулы для ширины впадины

• для отлитых зубцов: s_в=πm-1,53m=1,61m:
• для выполненных путем фрезерования- s_в= πm-1,57m = 1,57m

Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:

• усилия, прикладываемые к детали при эксплуатации;
• конфигурация деталей, взаимодействующих с ней.

Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.

Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.

Исходные данные и замеры

На практике перед инженерами часто встает задача определения модуля реально существующей шестерни для ее ремонта или замены. При этом случается и так, что конструкторской документации на эту деталь, как и на весь механизм, в который она входит, обнаружить не удается.

Самый простой метод — метод обкатки. Берут шестерню, для которой характеристики известны. Вставляют ее в зубья тестируемой детали и пробуют обкатать вокруг. Если пара вошла в зацепление — значит их шаг совпадает. Если нет — продолжают подбор. Для косозубой выбирают подходящую по шагу фрезу.

Такой эмпирический метод неплохо срабатывает для зубчатых колес малых размеров.

Для крупных, весящих десятки, а то и сотни килограмм, такой способ физически нереализуем.

Результаты расчетов

Для более крупных потребуются измерения и вычисления.

Как известно, модуль равен диаметру окружности выступов, отнесенному к числу зубов плюс два:

m=De/(z+2)

Последовательность действий следующая:

• измерить диаметр штангенциркулем;
• сосчитать зубцы;
• разделить диаметр на z+2;
• округлить результат до ближайшего целого числа.

Зубец колеса и его параметры

Данный метод подходит как для прямозубых колес, так и для косозубых.

Расчет параметров колеса и шестерни косозубой передачи

Расчетные формулы для важнейших характеристик шестерни косозубой передачи совпадают с формулами для прямозубой. Существенные различия возникают лишь при прочностных расчетах.

Быстрое моделирование шестерней по параметрам

Приветствую!

Вопрос о моделировании шестерней поднимался неоднократно, но решения либо подразумевали использование серьезных платных программ, либо были слишком упрощенными и им не хватало инженерной строгости.

В этой статье я постараюсь с одной стороны, дать сухую мэйкерскую инструкцию, как смоделировать шестерню по нескольким легко измеряемым параметрам, с другой, не обойду и теорию.

В качестве примера возьмем шестерню от дроссельной заслонки автомобиля:

Это классическая цилиндрическая прямозубая шестерня с эвольвентным зацеплением (точнее, это две таких шестерни).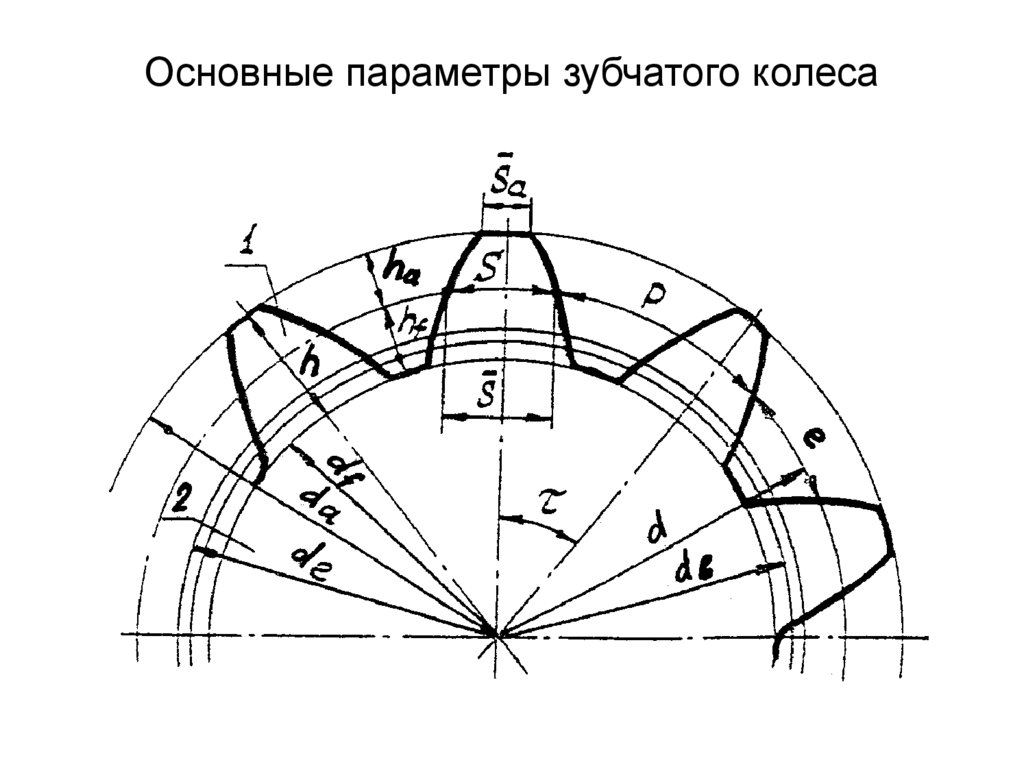

Принцип эвольвентного зацепления:

Для нас важно, что подавляющее большинство встречающихся в быту шестерней имеют именно эвольвентное зацепление.

Для изучения параметров шестерней воспользуемся программой с остроумным названием Gearotic. Мощнейшая узкоспециализированная программа для моделирования и анимирования всевозможных шестерней и передач.

Бесплатная версия не дает экспортировать сгенерированные шестерни, но нам и не надо. Непосредственно моделировать будем позже.

Итак, запускаем Gearotic

Слева в поле Gears нажимаем Circular, попадаем в редактор шестерней:

Рассмотрим предлагаемые параметры:

Первые два столбца Wheel и Pinion

Wheel – это будет наша шестерня, а Pinion – ответная часть, которая нас в данном случае не интересует.

Teeth – количество зубьев

Mods – модификаторы формы зуба. Самый простой способ понять, что они делают – поварьировать их. Не все параметры применяются автоматически. После изменения нужно нажимать кнопку ReGen. В нашем случае (как и в большинстве других) оставляем эти значения по умолчанию.

Галка Planetary – выворачивает шестерню зубьями внутрь (коронная шестерня).

Галка Rght Hnd (Right Hand) – меняет направление скоса у косозубых шестерней.

Блок Size Params

DP (Diametral Pitch) – число зубьев, деленное на диаметр делительной окружности (pitch diameter)

Неинтересный для нас параметр, т.к. измерять диаметр делительной окружности неудобно.

Module (модуль) – важнейший для нас параметр. Вычисляется по формуле M=D/(n+2), где D – внешний диаметр шестерни (легко измеряемый штангенциркулем), n – число зубьев.

Pressure Angle (угол профиля) – острый угол между касательной к профилю в данной точке и радиусом – вектором, проведенным в данную точку из центра колеса.

Существуют типичные значения этого угла: 14.5 и 20 градусов. 14.5 используется гораздо реже и в основном на очень маленьких шестернях, которые на FDM-принтере всё равно отпечатаются с большой погрешностью, так что на практике можно смело ставить 20 градусов.

Rack Fillet – сглаживание основания зуба. Оставляем 0.

Блок Tooth Form

Оставляем Involute – эвольвентное зацепление. Epicylcoidal – циклоидное зацепление, используемое в точном приборостроении, например, в часовых механизмах.

Face Width – толщина шестерни.

Блок Type

Spur – наша прямозубая шестерня.

Helical – косозубая шестерня:

Knuckle – честно говоря, не знаю, как такая по-русски называется:

Herringbone – шевронная шестерня:

Bevel – коническая шестерня:

Вернемся к нашей шестерне.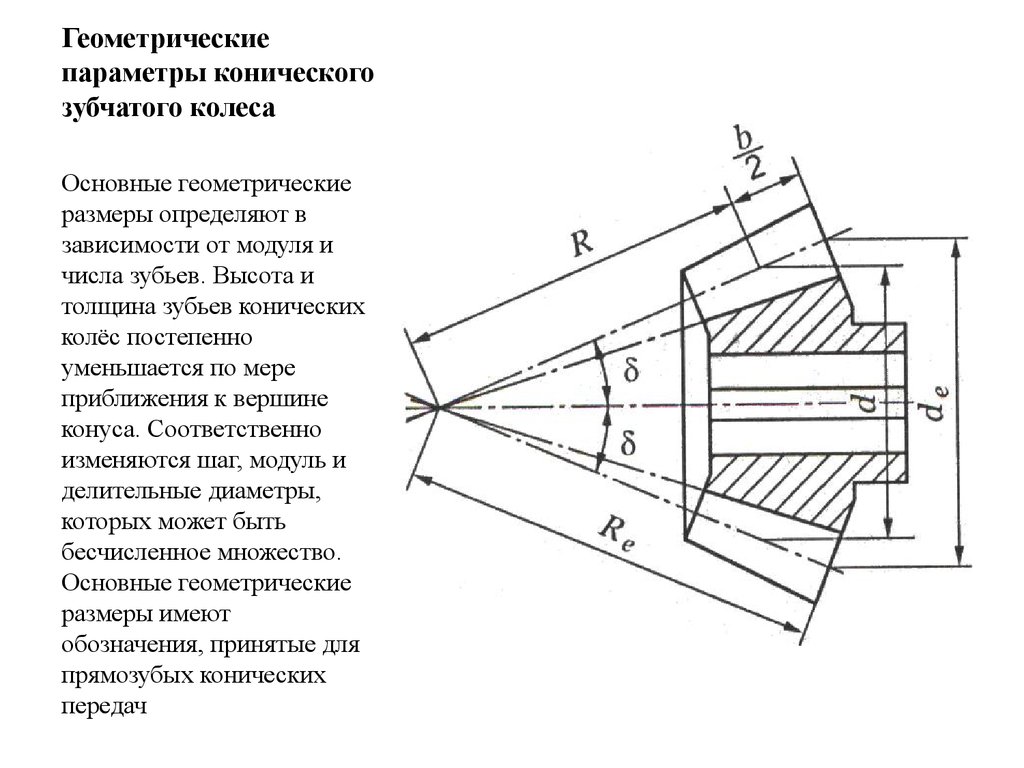

Большое колесо имеет 47 зубьев, внешний диаметр 44.6 мм, диаметр отверстия 5 мм, толщину 6 мм.

Модуль будет равен 44.6(47+2)=0.91 (округлим до второго знака).

Вносим эти данные:

Слева расположена таблица параметров. Смотрим Outside Diam (внешний диаметр) 44.59 мм. Т.е. вполне в пределах погрешности измерения штангенциркуля.

Таким образом мы получили профиль нашей шестерни, выполнив всего одно простое измерение и посчитав количество зубьев.

Укажем толщину (Face Width) и диаметр отверстия (Shaft Dia в верхней части экрана). Жмем Add Wheel to Proj для получения 3d-визуализации:

Увы, бесплатная версия не дает экспортировать результат, поэтому придется задействовать другие инструменты.

Устанавливаем FreeCAD Кто не владеет Фрикадом – не волнуйтесь, глубоких знаний не потребуется. Скачиваем плагин FCGear.

Находим папку, куда установился Фрикад. В папке Mod создаем папку gear и помещаем в нее содержимое архива.

После запуска Фрикад в выпадающем списке должен появиться пункт gear:

Выбираем его, затем Файл – Создать

Нажимаем на иконку involute gear вверху экрана, затем выделяем появившуюся шестерню в дереве слева и переходим на вкладку ‘Данные’ в самом низу:

В этой таблице параметров

teeth – количество зубьев

module – модуль

height – толщина (или высота)

alpha – угол профиля

backlash – значение угла для косозубых шестерней (мы оставляем 0)

Остальные параметры являются модификаторами и, как правило, не используются.

Вносим наши значения:

Добавим еще одну шестерню.

Укажем высоту 18 мм (общая высота нашей исходной шестерни), количество зубьев – 10, модуль 1.2083 (диаметр 14.5 мм)

Осталось сделать отверстие. Перейдем на вкладку Part и выберем Создать цилиндр. В Данных укажем радиус 2.5 мм и высоту 20 мм

Удерживая клавишу Ctrl выделим в дереве шестерни и нажмем Создать объединение нескольких фигур на панели инструментов.

Затем, опять же удерживая Ctrl, выделим сначала получившуюся единую шестерню, а затем цилиндр и нажмем Выполнить обрезку двух фигур

Далее выделяем результат, Файл – Экспортировать… сохраняем в stl. Шестерня готова.

P.S. Хотел еще немного поговорить об экзотических случаях, но статья получилась большой, так что наверное, в другой раз.

Удачи!

Что такое модуль цилиндрической шестерни? – Gzipwtf.com

Что такое модуль цилиндрического зубчатого колеса?

Также модуль определяется как деленный диаметр деленного на количество зубьев, а расстояние от делительной окружности до внешней окружности (дополнение) равно модулю в прямозубых зубчатых колесах.

Как рассчитать модуль цилиндрического зубчатого колеса?

Значение модуля определяется путем расчета сопротивления материала по отношению к передаваемой силе и передаточному числу. Две сопряженные шестерни должны иметь одинаковый модуль: m = d/z.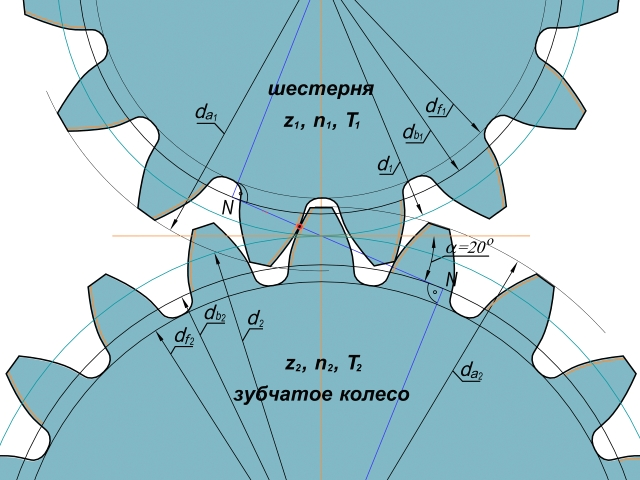 Диаметр делительной окружности (d) — диаметр окружности делительной окружности; его значение равно: d = m x z.

Как выбрать редукторный модуль?

Модуль равен удвоенному расстоянию между центрами, деленному на сумму зубьев шестерни и шестерни. Например, если расстояние между центрами равно 12 мм, шестерня имеет 50 зубьев, а шестерня имеет 10 зубьев, то удвоенное расстояние (2×12), деленное на сумму зубьев (50+10), будет 24/60. = 0,4 = модуль.

Что такое обычный модуль?

Разница между поперечным модулем и нормальным модулем определяется как разница основной формы зуба. Как показано справа, модуль опорной точки зуба, ортогональный центральной оси зубчатого колеса, называется поперечным модулем. Модуль базы зуба, ортогональный спирали резьбы, называется нормальным модулем.

Какова формула модуля?

Итого:

#	Товар	Формула
1	зубьев номер
2	модуль	м=шаг/π
3	передаточное число	i=d2/d1=z2/z1 1: ведущая шестерня и 2: ведомая шестерня
4	дополнительный коэффициент	da*=1+x x=0 для стандартных передач

Как вы рассчитываете модули?

Модуль на стандартном калькуляторе

1. Разделить a на n.
2. Вычесть целую часть полученного количества.
3. Умножьте на n, чтобы получить модуль.

Каковы недостатки цилиндрических зубчатых колес?

Недостатки

• Это тихоходные передачи.
• Они не могут передавать мощность между непараллельными осями.
• Цилиндрические шестерни производят слишком много шума при работе на высоких скоростях.
• Зубья колеса испытывают большую нагрузку.
• Их нельзя использовать для передачи энергии на большие расстояния.

Как модули влияют на шестерни?

Коэффициент контакта — это среднее число зубьев, находящихся в контакте, когда шестерни входят в зацепление и вращаются. С увеличением модуля количество зубьев будет уменьшаться, что приводит к уменьшению коэффициента контакта. Также с увеличением угла давления длина дуги контакта уменьшается, что приводит к уменьшению коэффициента контакта.

Какой нормальный модуль в редукторе?

Модуль базы зуба, ортогональный спирали резьбы, называется нормальным модулем. Характеристики каждого показаны ниже. Заменяет прямозубые шестерни с тем же модулем, числом зубьев и межосевым расстоянием.

Каковы особенности встроенных цилиндрических шестерен?

Цилиндрические зубчатые колеса со встроенными подшипниками могут использоваться для реверсивного вращения и синхронизации. Цилиндрическое зубчатое колесо – угол давления 20 градусов, модуль 0,5, 0,8, 1,0, 1,5, 2,0, 2,5, 3,0, форма B, фиксированное отверстие вала (MISUMI) Пластиковые зубчатые колеса, имеющие металлические сердечники и нейлоновые зубья MC, соединенные сплавлением друг с другом. • Конфигурация отверстия вала. : Шпоночный паз + метчик, круглое отверстие, круглое отверстие+метчик

Что такое угол давления цилиндрического зубчатого колеса?

Единицей, указывающей размеры прямозубых зубчатых колес, как указано в ISO, обычно является «модуль». В последние годы принято устанавливать угол давления 20 градусов.

Как рассчитать вершину цилиндрического зубчатого колеса и корневой зазор?

Этот расчет основан на том, что величина зазора между вершиной и корнем должна составлять 0,25 м.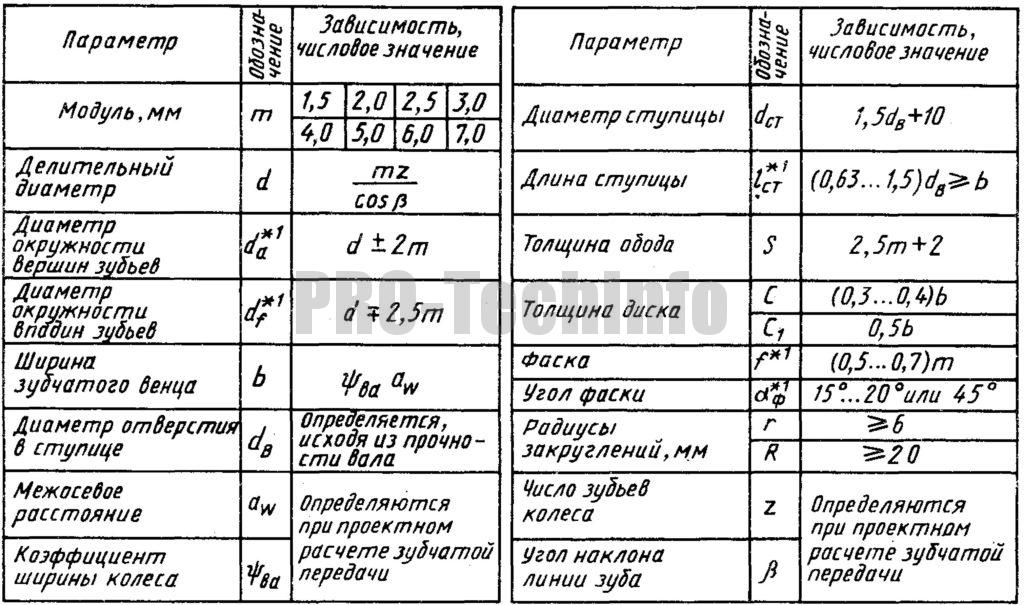

Стандартная прямозубая передача, согласно табл. 4.3, представляет собой шестерню с профильным переключением с коэффициентом переключения 0; то есть х 1 =х 2 =0. Таблица 4.4 представляет собой обратную формулу пунктов с 4 по 8 таблицы 4.3.

Что такое зубчатый модуль и что он означает?

Проще говоря, термин «модуль» шестерни относится к размеру зуба шестерни. Больший размер зуба позволяет передавать большую мощность, и, конечно, должно быть очевидно, что сопрягаемые шестерни должны иметь одинаковый модуль. Предположим, что речь идет о прямозубых зубчатых колесах. Мы хотели бы уточнить технические аспекты.

РАСЧЕТЫ ЦИЛИНДРИЧЕСКИХ ПЕРЕДАЧ – Качественные компоненты трансмиссии – Каталоги в формате PDF | Техническая документация

Добавить в избранное

{{requestButtons}}

Выдержки из каталога

3. 21 Коэффициент контакта Для обеспечения плавного непрерывного действия зубьев, когда одна пара зубьев прекращает контакт, следующая пара зубьев уже должна войти в зацепление. Желательно, чтобы было как можно больше перекрытий. Мерой этого перекрытия является коэффициент контакта. Это отношение длины линии действия к основному шагу. Рисунок 3-3 показывает геометрию. Длина действия определяется по пересечению линии действия и внешних радиусов. Для простого случая пары прямозубых зубчатых колес отношение длины действия к основному шагу определяется из: Хорошей практикой является поддержание коэффициента контакта 1,2 или выше. Ни при каких обстоятельствах это отношение не должно опускаться ниже 1,1, рассчитанного для всех допусков при наихудших значениях. Коэффициент контакта от 1 до 2 означает, что часть времени контактируют две пары зубов, а оставшееся время контактирует одна пара. Соотношение между 2 и 3 означает, что 2 или 3 пары зубов всегда находятся в контакте. Такое высокое передаточное отношение обычно не достигается с внешними цилиндрическими зубчатыми колесами, но может быть достигнуто за счет зацепления пары внутренних и внешних прямозубых колес или специально разработанных нестандартных внешних прямозубых колес. Более подробная информация о коэффициенте контакта, включая расчетные уравнения для конкретных типов зубчатых колес, представлена ​​в РАЗДЕЛЕ 11. 3.3 Эвольвентная функция На рис. 3-4 показан элемент эвольвентной кривой. Определение эвольвентной кривой – это кривая, описываемая точкой на прямой линии, которая катится без скольжения по окружности. Окружность называется базовой окружностью эвольвент. Две противоположные эвольвентные кривые, встречающиеся в вершине, образуют кривую зуба шестерни. На рис. 3-4 видно, что длина дуги базовой окружности ac равна длине прямой bc. tana = bc = rbq = q (радиан) (3-5) Oc rb q на рис. 3-4 может быть выражено как inva + a, тогда формула (3-5) примет вид: inva = tana – a (3- 6) Функция a, или inva, известна как эвольвентная функция. Эвольвентная функция очень важна в конструкции зубчатой ​​передачи. Значения эвольвентной функции можно получить из соответствующих таблиц. С центром базовой окружности 0 в начале системы координат эвольвентная кривая может быть выражена значениями x и y следующим образом: РАЗДЕЛ 4 РАСЧЕТЫ ЦИЛИНДРИЧЕСКИХ ЗУБЧАТЫХ ЗУБЧАТЫХ 4. 1 Стандартное цилиндрическое зубчатое колесо На рис. 4-1 показано зацепление стандартного цилиндрического зубчатого колеса. шестерни. Зацепление стандартных цилиндрических зубчатых колес означает, что делительные окружности двух зубчатых колес соприкасаются и вращаются друг с другом. Формулы расчета приведены в таблице 4-1. 342

Таблица 4-1 Расчет стандартных прямозубых зубчатых колес № Поз. Символ Формула Пример Шестерня 1 Модуль м 3 2 Угол давления a 20º 3 Число зубьев z1, z2* 12 24 4 Расстояние между центрами a (z1 + z2)m * 2 54.000 5 Диаметр шага D ZM 36.000 72.000 6 Диаметр основания DB D COS A 33.829 67.658 7 Приложение HA 1,00M 3.000 8 DEDENDUM HF 1,25M 3.750 9 Внешний диаметр DA D + 2M 42.000 78.000 10 Диаметр корня DF D – 2,5M 28.500 64,500 * Нижние индексы 1 и 2 у z1 и z2 обозначают шестерню и шестерню. Все расчетные значения в Таблице 4-1 основаны на заданном модуле и количестве зубьев z1 и z2. Если вместо этого модуль…

заключается в том, что стандартные шестерни с числом зубьев ниже критического значения автоматически подрезаются в процессе генерации. Условие отсутствия поднутрений в стандартной цилиндрической шестерне определяется выражением: Это указывает на то, что минимальное количество зубьев, свободных от поднутрений, уменьшается с увеличением угла зацепления. Для 14,5ø значение zc равно 32, а для 20º оно равно 18. Таким образом, нажимные зубчатые колеса 20ø с малым числом зубьев имеют то преимущество, что они намного меньше подрезают и, следовательно, являются более прочными и плавными. 4.4 Увеличенные шестерни Нежелательна подрезка зубьев шестерни…

4.6 Цилиндрическое зубчатое колесо со смещенным профилем На Рис. 4-8 показано зацепление пары зубчатых колес со смещенным профилем. Ключевыми параметрами в профильно-смещенных передачах являются рабочие (рабочие) делительные диаметры dw и рабочий (рабочий) угол давления aw. зубчатые колеса, это круги рабочего шага, которые соприкасаются и катятся друг относительно друга, что изображает действие шестерни.Стандартные круги шага больше не имеют значения, и важен угол рабочего давления. Стандартный…

Все каталоги качественных компонентов трансмиссии и технические брошюры

1. KSUW1.5-R1

   1 стр.

2. KKRCPFD10-1000J

   1 стр.

3. KSAM1.5-20045

   1 стр.

4. КШ3-20Р

   1 Стр.

5. KSS0.5-30C

   1 стр.

6. ШЕСТЕРНЯ С ДИАМЕТРИЧЕСКИМ ШАГОМ

   34 страницы

7. Q420 Каталог

   526 страниц

8. Примеры расчета прочности поверхности конического зубчатого колеса

   1 страниц

9. Определение факторов в уравнениях поверхностной прочности

   1 страниц

10. Поверхностная прочность конических зубчатых колес

    1 страниц

11. Прочность на изгиб конических зубчатых колес

    4 страницы

12. Поверхностная прочность для прямозубых и косозубых шестерен

    7 Страниц

13. Прочность на изгиб цилиндрических и косозубых шестерен

    5 страниц

14. ТОЛЩИНА ЗУБЬЯ

    16 страниц

15. ДЕТАЛИ ЭВОЛЬТНОЙ ПЕРЕДАЧИ

    1 Стр.