Прогиб балки предельный: Предельный прогиб

alexxlab | 13.03.2023 | 0 | Разное

Занятие 5. ПРЕДЕЛЬНОЕ СОСТОЯНИЕ. БАНК ПРЕДЕЛЬНЫХ ХАРАКТЕРИСТИК

П р и м е р ы 5.6-5.10 (для самостоятельного решения). Определить при внецентренном растяжении предельные продольные силы и изгибающие моменты для стержней с сечениями, представленными на рисунке 5.5.

Рис. 5.5. Поперечное сечение стержней а – кольцевое, б – коробчатое, в – двутавр № 20, г – коробчатое из швеллеров № 24, д – уголковое из уголка 100х10

Опорной базой в оценке прочности по нагрузке является все сооружение в целом. Ввиду широкого разнообразия сооружений, сечений их элементов, материалов и самих нагрузок составление банка предельных нагрузок – трудоемкая и трудно выполнимая, особенно экспериментальным путем, задача. Этот банк главным образом составляется теоретически по известным банкам предельных напряжений и усилий. Но если такой банк имеется, то оценка прочности и проектирование существенно упрощаются. Важно также то, что оценивается прочность всего сооружения.

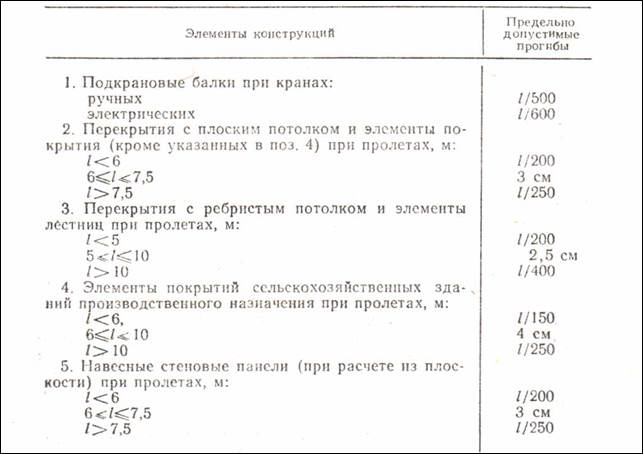
П р и м е р 5.11. Составить банк предельных нагрузок для балок пролетом 6 м, выполненных из стальных двутавров по ГОСТу 8239-72, сталь марки Ст3. Нагрузка равномерно распределена по всей длине (рис.5.6). Прогиб балки не должен превышать шести сантиметров (1/100 от пролета).

Р е ш е н и е. Рассмотрим двутавр высотой h с моментом инерции I . Так как сечение по длине стержня не меняется, наиболее опасным будет сечение с максимальным изгибающим моментом. В балке, загруженной по всему пролету распределенной нагрузкой, такой момент будет в середине пролета

M_{х при z=l/2} = ql²/ 8

где q – интенсивность нагрузки, l – пролет балки.

Максимальные нормальные напряжения возникают в крайних (верхних и нижних) волокнах сечения и равны

σ _{z max} = M_х

h/(2I_x>).

Рис. 5.6. Расчетная схема балки и эпюра изгибающих моментов к ней

Максимальный прогиб будет так же в середине пролета
y = 5 ql⁴/(384 E I_x),
где E = 200 ГПа – модуль упругости стали.

Предельный прогиб y_np = l /100. Из условия жесткости
y ≤ y_np получим 5 ql⁴/(384 E I_x) ≤ l /100

откуда предельная нагрузка по условию ограничения прогиба 1/100 пролета составит

q_np ^ж = 3,84

E I_x,/(5 l³) = 0.768 E I,_x/ l³ (5.7)

Условие прочности σ _{z max}≤ R_np, при подстановке в него напряжения, выраженного через изгибающий момент M, который в свою очередь зависит от нагрузки, преобразуется к виду

ql² h / (16I_x) ≤ R_np.

Откуда предельная нагрузка по условию прочности

q_np ⁿ ≤ 16R_npI_x / (l² h), (5.8)

где R_np = 270 МПа (см. табл. 5.1).

Из двух значений нагрузок, получаемых из условий жесткости (5.7) и прочности (5.8), выбирается меньшая.

Для получения численных значений предельной нагрузки преобразуем выражения (5.7) и (5.8), подставив в них известные величины, не зависящие от размеров двутавра. Тогда уравнение (5.7) примет вид (

E = 200 ГПа,. l = 6 м), если I_x измеряется в м⁴

q_np ^ж = 0.768EI_x/l ³ = 0.768 ·2·10¹¹I_x/6³ = 0.0711·10⁸I_х, (5.9)

или q_np ^ж = 0. 0711I_х, если I_x измеряется в см⁴, а уравнение (5.8) – вид
q_np ⁿ = 16R_npI_x / (l

2 h) = 1.2 I_х /h. (5.10)

где R_пр = 27000 кПа , I_x измеряется в см⁴, h в см

Если в полученные формулы (5.9) и (5.10) подставить момент инерции I_х в см⁴, а высоту h в см (см. ГОСТ 8239-89, помещенный в табл. 4.2), то нагрузку q_пр получим в Н/см, а чтобы перевести ее в привычную размерность кН/м необходимо ее в 10 раз уменьшить. Вычисления предельной нагрузки сведены в таблицу 5.9.

П р и м е р 5.12 (для самостоятельного решения). Построить банк данных по нагрузке (в зависимости от пролета) для черепных брусков кровли из условий прочности и жесткости.

Черепные бруски сечением 5х5 см выполнены из сосны второго сорта с расчетным сопротивлением изгибу R = 7 МПа. Допустимый прогиб 1/50 от пролета.

Приведем справочные данные¹ для вычислений. Расчетная схема черепного бруска – двухпролетная балка с шарнирными опорами по концам и в середине. На средней опоре такой балки изгибающий момент равен ql² /8, момент в середине пролета – ql² /16. Прогиб в середине пролета ql⁴ /(192EI).

¹ Справочник проектировщика. Расчетно – теоретический том, Книга 1. – М.: Стройиздат, 1976

Таблица 5.9 Предельные нагрузки для балки из двутавров по ГОСТу 8239-72 (материал – сталь Ст3)

Номер двутавра	Высота h, см	Момент инерции I х см4	qnpж, Н/см	Iх / h, см3	qnpn, Н/см	Предельная нагрузка qпр, Н/см (кН/м)
10	10	198	14. 1	19.8	23.8	14.1 (1.4)
12	12	350	24.9	29.16	35.0	24.9 (2.5)
14	14	572	40.7	40.85	49.0	40.7 (4.1)
16	16	873	62.1	54.56	65.5	62.1 (6.2)
18	18	1290	91.7	71.70	86.0	86.0 (8.6)
20	20	1840	130.8	92.0	110.4	110.4 (11.0)
22	22	2550	181. 3	115.9	139.1	139.1 (13.9)
24	24	3460	246.0	144.2	173.0	173.0 (17.3)
27	27	5010	356.3	185.6	222.7	222.7 (22.3)
30	30	7080	503.5	236.0	283.2	283.2 (28.3)
33	33	9840	699.7	298.2	357.8	357.8 (35.8)
36	36	13380	951.5	371.7	446.0	446.0 (44.6)
40	40	19062	1355. 5	476.6	571.9	571.9 (57.2)
45	45	27696	1969.5	615.5	738.6	738.6 (73.9)
50	50	39727	2825.0	794.5	953.4	953.4 (95.3)
55	55	55962	3979.5	1017.5	1221.0	1221.0 (122.1)
60	60	76806	5461.8	1280.1	1536.1	1536.1 (153.6)

Расчет стальной балки на прогиб

Теги: #ЛИРА-САПР #СТК #прогибы

При расчете стальных балок по II-й ГПС (по прогибам) необходимо создавать раскрепления для прогибов:

Информация из справки LIRA SAPR (Справка\Пояснения Сталь\Проверки прогибов):

Проверка прогиба осуществляется сопоставлением реально определенного относительного прогиба (L/f) с максимально возможным для данного конструктивного элемента прогибом.

В данной версии проверка выполняется только для балок на основании состава загружений во всех сочетаниях. Учитываются коэффициенты надежности по нагрузке (заданные при формировании РСУ в среде ПК ЛИРА-САПР) и коэффициенты сочетания.

Перемещения, вызванные загружениями с долей длительности 0, в данном расчете не используются.

Прогибы находятся для каждого сечения на основании распределения MY1, MZ1, QY1, QZ1 по длине элемента. Соответственно, увеличение количества расчетных сечений способствует более точному определению прогибов (особенно, если воздействуют сосредоточенные силовые факторы).

В режиме локального расчета элемента (см. справочную систему СТК-САПР) имеется возможность расчета прогибов по огибающим эпюрам изгибающего момента в запас. Это может потребоваться, когда редактируются расчетные сочетания усилий (или нагрузок) и теряется связь с результатами расчета на ПК ЛИРА-САПР основной схемы.

Важно: Предусмотрена возможность определять не чистые перемещения (относительно локальных осей Y и Z в недеформированной схеме), а прогиб относительно двух выбранных условно неподвижных точек – точек раскрепления (в случае консоли, например, относительно одной точки).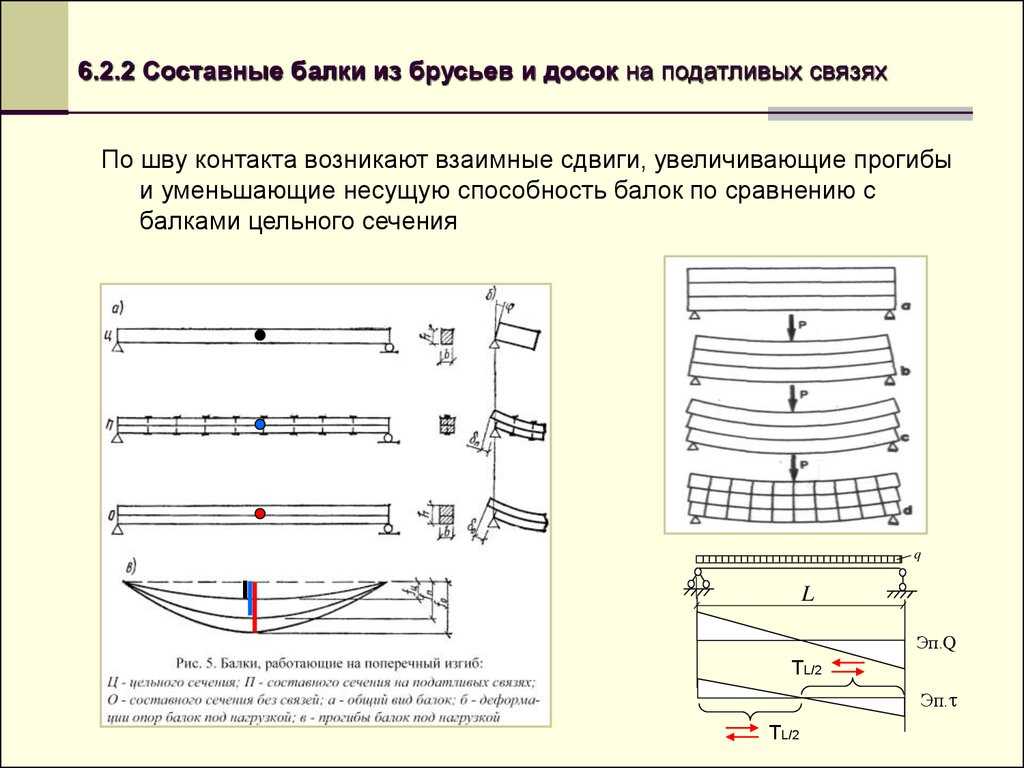

Схема к определению прогибов балки с раскреплениями и без раскреплений

На приведенном фрагменте показан механизм определения прогибов (они обозначены как di и dk) в конструктивном элементе с наложенными раскреплениями на элементы.

Если раскрепления не наложены, то прогиб принимается равным полному расстоянию до оси X.

Важно: Если балка (ригель) разбита по длине промежуточными узлами, то для нее необходимо создать конструктивный элемент и раскрепления для проверки прогибов создавать как для конструктивного элемента (т.е. для балки как единого целого). В расчете стальных конструкций коэффициент расчетной длины (и для балок, и для колонн, и для ферм) применяется к длине конечного элемента (КЭ), если не задан конструктивный элемент (КоЭ). Если задан КоЭ, то коэффициент расчетной длины применяется к полной длине КоЭ.

Пример расчета однопролетной балки

Расчётная модель рамы с цельным ригелем и разбитым на отдельные элементы

Согласно нормативной документации прогиб определяется от действия нормативных нагрузок. Поскольку в LIRA SAPR все нагрузки прикладываются к узлам и элементам их расчётными значениями, при определении прогибов программа определяет нормативное значение нагрузок путём деления их на коэффициент надёжности.

Посмотреть какие приняты коэффициенты надёжности, а также ввести их вручную, если это необходимо, можно в окне параметров расчёта.

Окно параметров расчёта, вызываемое из окна задания параметров для стальных конструкций

Подробнее о корректировке коэффициентов надёжности для расчета прогибов вручную читайте в статье “Коэффициенты к временным нагрузкам при проверке прогиба”

Мозаика результатов проверки назначенных сечений по 2 предельному состоянию

Предельно допустимый L/200=6000/200=30мм

Без задания раскреплений (по абсолютному перемещению узлов балки):
((39,8мм/ к-т надежности по нагрузке)/ 30мм))*100%=((39,8/1,1)/30)*100%=120,6%

С заданием раскреплений (по относительному перемещению узлов балки за вычетом перемещений опорных узлов):
((39,8мм-9,14)/ к-т надежности по нагрузке)/30мм))*100%=(((39,8-9,14)/1,1)/30)*100%=92,9%

Ручной ввод расчётной длины балки для расчёта прогибов

В диалоговом окне задания характеристик расчёта стальной балки присутствует группа параметров Расчёт по прогибу.

Информация из справки ЛИРА САПР:
Расчет по прогибу – данные для расчета прогиба. Длина пролета авто – вычисляется по положению раскреплений. Длина пролета точно – длина пролета при расчете приравнивается этому числу.

Рассмотрим раму из предыдущего примера, только теперь раскрепления для прогибов назначим для всех конструкций, а расчётные длины будем для первого случая задавать автоматическим способом, а для второго ручным.

Расчётная модель с информацией о назначенных расчётных длинах балок

Результаты расчётов прогибов балок

Предельно допустимый прогиб при длине 6 м L/200=6000/200=30мм

Предельно допустимый прогиб при длине 4 м L/200=4000/200=20мм

Проценты использования по предельному прогибу

Длина балки 6 м:
((39,8мм-9,14)/ к-т надежности по нагрузке)/30мм))*100%=(((39,8-9,14)/1,1)/30)*100%=92,9%

Длина балки 4 м:
((39,8мм-9,14)/ к-т надежности по нагрузке)/30мм))*100%=(((39,8-9,14)/1,1)/20)*100%=139,4%

Расчёт прогибов стрельчатой арки

Пример — рама переменного сечения (РПС) пролётом 18 м. Соединение полурам в коньке — шарнирное, опирание полурам на фундамент — шарнирное.

Расчётная модель рамы

При этом в параметрах «Дополнительные характеристики» необходимо указать вручную пролет, с которым программа будет сравнивать прогиб (автоматическое определение пролета возможно только для линейных балок, где все конечные элементы (КЭ) конструктивного элемента (КоЭ) лежат на одной оси):

Эпюра перемещений fz ригеля одной полурамы (вдоль местной оси Z1 стержня)

Мозаика перемещений узлов по Z и «Раскрепления для прогибов» (раскреплён только ригель №4)

Результаты определения прогибов в СТК-САПР:

Результаты определения прогибов ригелей №2 и №4

Предельно допустимый L/200=17664/200=88.32 мм

Без задания раскреплений (по абсолютному значению на эпюре прогибов fz):
96.7/17644=1/182 — совпадает с результатом расчёта элемента №2

С заданием раскреплений (по относительному значению на эпюре прогибов fz):
(96.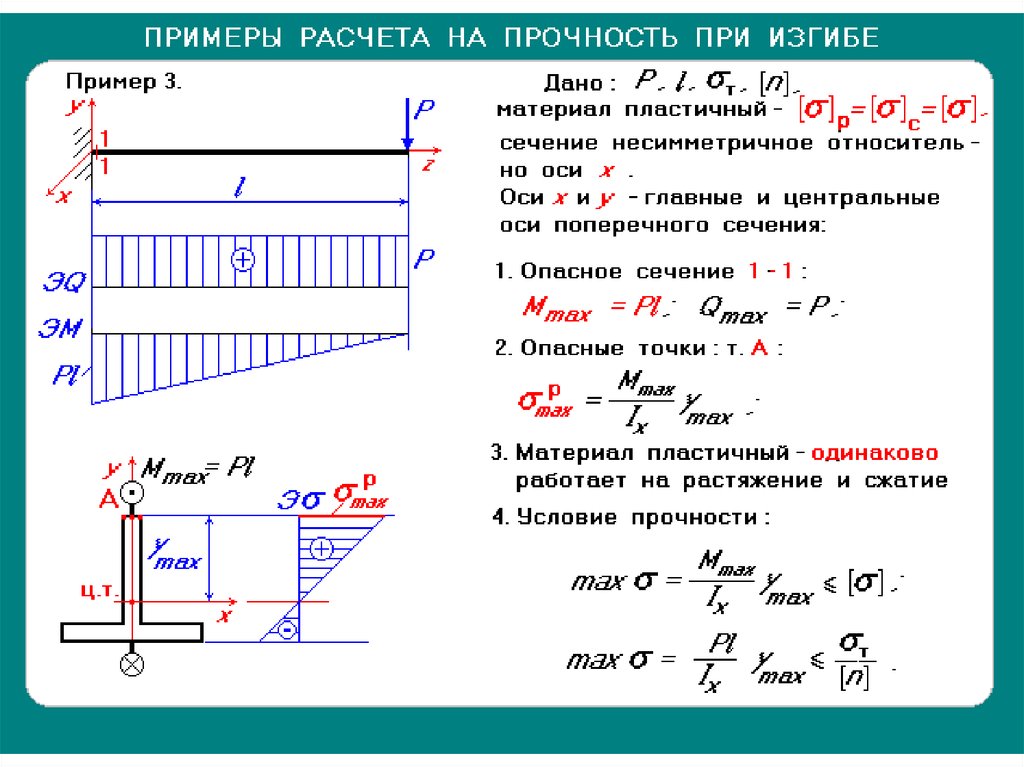 7-(-6.46))/17644=1/171 — совпадает с результатом расчёта элемента №4

Без задания раскреплений (по абсолютному значению перемещений узлов):
99.8/17644=1/177 — не совпадает ни с чем

Вывод: Расчёт на прогибы выполняется в местной системе координат стержня. Прогиб стрельчатых и цилиндрических арок, а также любых криволинейных конструкций, нужно определять по перемещениям узлов в глобальной системе координат и вручную сравнивать с предельно допустимыми значениями.

Расчёт прогибов цилиндрической арки

Пример – цилиндрическая арка пролётом 18 м, стрелой подъёма f = 9 м. Соединение всех элементов между собой — жёсткое, опирание на фундамент — шарнирное.

Нагрузки на арку приложены их расчётными значениями. Значения нагрузок для определения прогибов принимаются согласно СП 20.13330.2016 Нагрузки и воздействия, таблица Д.1 Приложения Д. В данном примере арка является конструкцией покрытия, прогиб которой должен определяться от постоянных и длительных нагрузок (п. 2 табл. Д.1). Для визуализации перемещений от нормативных значений нагрузок, необходимо создать особое РСН с нормативными длительными значениями нагрузок. Нагрузки в данном РСН нужно поделить на коэффициент надёжности, с учётом длительности. На конструкцию действуют два загружения:

Загружение 1 — постоянное, коэффициент надёжности 1.1;
Загружение 2 — кратковременное, коэффициент надёжности 1.2, доля длительности 0.35;

Вычислим коэффициенты для перехода к нормативным значениям

Загружение 1 Kn=1/1.1=0.91;
Загружение 2 Kn=1/1.2*0.35=0.292

Таблица РСН с сочетаниями расчётных и нормативных значений нагрузок с учётом длительности.

Мозаика перемещений узлов цилиндрической арки от РСН2

Предельно допустимый прогиб L/200=18000/200=90 мм

Фактический прогиб (по абсолютному значению перемещений узлов): 32.2/18000=1/559 – меньше предельно допустимого значения.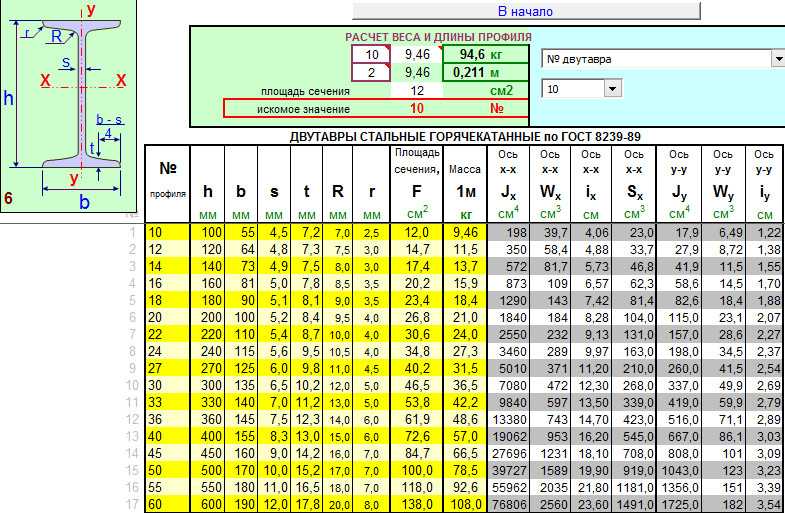

Примечание: если подобная конструкция стоит на своих опорах, то перемещения опорных точек (для получения относительных перемещений) удобно получить через «Мозаику относительных перемещений», указав реперный узел.

Мозаика перемещений узлов в глобальной СК (абсолютных)

Мозаика перемещений узлов в глобальной СК относительно реперного узла

Консольные балки – моменты и отклонения

Консольный луч – одиночная нагрузка на конце

Максимальная сила реакции

на фиксированном конце может быть выражена как:

R _A = F (1A)
R _A = F (1A)
R _A = F (1a)
R _A = F (1A)

где

R _A = сила реакции в А (Н, фунт)

F = сила однократного действия в В (Н, фунт)

Максимальный момент

0004 at the fixed end can be expressed as

M _max = M _A

          = – F L                               (1b)

where

M _A = maximum moment in A ( Нм, Нмм, фунт дюйм)

L = длина балки (м, мм, дюйм)

Максимальный прогиб

на конце консольной балки можно выразить как

δ _{B L} ³ / (3 E I) (1C)

, где

Δ _B = Максимальный отклонение в B (M, MM, In)

E = Modulus эластично 2 (Па), Н/мм ² , фунт/дюйм ² (пси))

I = момент инерции (м ⁴ , мм ⁴ , дюйм 900 0 50 , дюйм ⁴

b = длина между B и C (м, мм, дюйм)

напряжение

Напряжение в изгибающем луче может быть выражено как

σ = y m / i (1d)

, где

σ = стресс (PA (N / M ² ),

σ = стресс (N / M ² ),

σ = стресс (N / M ² ), σ = стресс (N / M ² ), Н/мм ² , psi)

y = расстояние до точки от нейтральной оси (м, мм, дюйм)

M = изгибающий момент (Нм, фунт·дюйм)

I = момент Инерция (м ⁴ , мм ⁴ , in ⁴ )

Максимальный момент в консольной балке находится в фиксированной точке, и максимальное напряжение можно рассчитать путем объединения 1b и 1d по

0 σ _{max = 12y max F L / I               (1e)}

Пример — консольная балка с одинарной нагрузкой на конце, метрические единицы

Максимальный момент на закрепленном конце стальной полочной балки UB 305 x 127 x 42 5000 мм long, with moment of inertia 8196 cm ⁴ (81960000 mm ⁴ ) , modulus of elasticity 200 GPa (200000 N/mm ² ) and with a single load 3000 N На конце можно рассчитать как

M _MAX = (3000 N) (5000 мм)

= 1,5 10 ⁷ нм

= 1,5 10 ⁴ NM

= 1,5 10 ⁴ NM

= 1,5 10 ⁴ NM

. прогиб на свободном конце можно рассчитать как

Δ _B = (3000 N) (5000 мм) ³ / (3 (2 10 ⁵ Н / мм ² ) (8,196 10 ⁷ мм ⁴ ))
мм ⁴ ))
мм ⁴ )))

    = 7,6 мм

Высота балки 300 мм и расстояние от крайней точки до нейтральной оси 150 мм . Максимальное напряжение в балке можно рассчитать как

σ _max = (150 мм) (3000 Н) (5000 мм) / ( 8,196 10 ⁷ mm ⁴ )

    = 27.4 (N/mm ² )

    = 27.4 10 ⁶ (N/m ² , Pa)

= 27,4 МПа

Максимальное напряжение намного ниже предела прочности при растяжении для большинства сталей.

Консольная балка — одиночная нагрузка

Максимальная сила реакции

на фиксированном конце может быть выражена как:

R _A = F (2A)

, где

R _A = Сила реакции в A (N, LB)

F = Сила в одиночном исполнении в B (N, LB)

Максимальный момент

на фиксированном конце может быть выражен как

M _MAX = M _A

= – F A (2B)

, где

, где . 0005

M _A = максимальный момент в A (Н·м, Н·мм, фунт·дюйм)

a = длина между A и B (м, мм, дюйм)

Максимальный прогиб

Конец консольного луча может быть выражен как

Δ _C = (F A ³ / (3 E I)) (1 + 3 B / 2 A) (2C)

, где

111 δ _C = максимальное отклонение в C (м, мм, дюйм)

E = модуль упругости (Н/м ² (Па), Н/мм ² , фунт/дюйм ² (psi))

I = момент инерции (м

9 4 , мм

⁴ , дюйм ⁴ )

b = длина между B и C (м, мм, дюйм)

Максимальный прогиб

может быть выражен как 09 09 при действии единичной силы

δ _B = F a ³ / (3 E I)                            (2d)

where

δ _B = maximum deflection in B (m, mm, in)

Maximum Stress

The maximum stress can be calculated by combining 1d and 2b to

σ _max = y _max F a / I             (2e)   

Консольная балка — Калькулятор одинарной нагрузки

Общий калькулятор — будьте последовательны и используйте метрические значения, основанные на м или миллиметрах, или британские значения, основанные на дюймах. Типичные значения по умолчанию указаны в метрических миллиметрах.

F — нагрузка (Н, фунты)

a — длина балки между A и B (м, мм, дюйм)

b — длина балки между B и C (м, мм, в)

I – Момент инерции (M ⁴ , MM ⁴ , в ⁴ )

E – Модуль эластичности (N/M ² , N/MM ^{29009 29009 29009 29009 29009 2 9 2 9 2 9 2 9 2 709 2 709 2} 709 2 709 2 709 2 70709 2 70709 2 70709 2 70709 2 70709 2 70709 2 70709 2 . , psi)

y – Расстояние от нейтральной оси (м, мм, дюйм)

Консольная балка – Равномерно распределенная нагрузка

Максимальная реакция

на фиксированном конце может быть выражена как:

R _A = Q L (3A)

, где

R _A = Реакционная сила в А. Н, фунт)

q = равномерная распределенная нагрузка (Н/м, Н/мм, фунт/дюйм)

L = длина консольной балки (м, мм, дюйм)

Максимальный момент

на фиксированном конце можно выразить как

M _A = – Q L ² /2 (3B)

Максимальный отклонение

на конце может быть выражен как

Δ _B = Q L ⁴ / (8 E. ) (3C)

, где

Δ _B = максимальное отклонение в B (M, MM, In)

Cansilever Beam – Единый нагрузочный калькулятор

Общий расчет – использование метрического показа или мм, или имперские значения, основанные на дюймах. Типичные значения по умолчанию указаны в метрических миллиметрах.

q – Равномерная нагрузка (Н/м, Н/мм, фунт/дюйм)

L – Длина балки (м, мм, дюйм)

I – Момент инерции (м ⁴ , мм ⁴ , дюйм ⁴ )

E – Модуль упругости (Па, Н/мм ² , фунт/кв. дюйм)

ym – Расстояние от оси

На консольную балку действует более одной точечной нагрузки и/или равномерной нагрузки

Если на консольную балку действует более одной точечной нагрузки и/или равномерной нагрузки – результирующий максимальный момент на закрепленном конце А и Результирующее максимальное отклонение на конце B можно рассчитать путем суммирования максимального момента в A и максимального отклонения в B для каждой точки и/или равномерной нагрузки.

Консольный луч – снижение распределенной нагрузки

Максимальная реакция

на фиксированной конце может быть выражена:

R _A = Q L / 2 (4A)

, где 9000

4

, где 9000

9004

, где 9000

, где 9000

. Где 9000

. Где 9000

. R _A = сила реакции в A (Н, фунт)

q = падающая распределенная нагрузка – максимальное значение в A – ноль в B (Н/м, фунт/фут)

Максимальный момент

в фиксированный конец может быть выражен как

M _MAX = M _A

= – Q L ² /6 (4B)

, где

M _A = максимум в атмосфере (N.M, N.M, N.M, N.M, N.M, N.M, N.M, N.M, N.M, N.M, N.M, N.M, N.M, N.M, N.M, N.M, N.M, N.M, N.M, N.M.

L = длина балки (м, мм, дюйм)

Максимальное отклонение

на конце консольной балки может быть выражено как

δ _B = L ⁴ / (30 E I)                                    (4c)

где

δ _B = максимальный прогиб в B (м, мм, дюйм)

E = модуль упругости (Н/м ^{2 Па 9), Н/м 2} , фунт/дюйм ² (psi))

I = момент инерции (м ⁴ , мм ⁴ , дюйм ⁴ )

5 90 Sketchup Extension

Прогиб свободно опертой балки: статья

– Д-р Минас Э. Лемонис, доктор философии – Обновлено: 23 июня 2020 г.

Главная > Ресурсы > Прогибы и уклоны свободно опертой балки свободно опертые балки

– Классическая теория балок

– Поиск прогибов и уклонов

– Примеры

–  Статьи по теме

Введение

Свободно опертая балка является одной из самых простых конструкций. Он имеет только две опоры, по одной на каждом конце. Штифтовая опора и роликовая опора. В этой конфигурации балке разрешено вращаться на двух концах, но любое вертикальное движение здесь запрещено. Благодаря роликовой опоре также допускается осевое расширение или сжатие, хотя свободное горизонтальное перемещение предотвращается другой опорой. Это детерминантная (также называемая критической) конструкция, означающая, что при удалении какой-либо из опор или вставке внутреннего шарнира балка больше не может нести нагрузки и становится механизмом (конструкцией, свободно перемещающейся под нагрузкой). .

Справочная таблица: максимальный прогиб свободно опертой балки

В справочных целях в следующей таблице представлены формулы предельного прогиба \delta_u свободно опертой балки при некоторых распространенных вариантах нагрузки. Во всех случаях E — модуль упругости материала, а I — момент инерции поперечного сечения вокруг упругой нейтральной оси. Также имейте в виду, что положительный знак максимального прогиба означает направление вниз.

94}{3375 E I} где C=\sqrt{15-\sqrt{120}}\left(\sqrt{15}+\sqrt{50}\right)\примерно 22,01237

Классический балочная теория

Для оценки деформации балки при поперечной нагрузке доступно несколько балочных теорий. Наиболее широко принята теория пучка Эйлера-Бернулли , также называемая классической теорией луча . Два основных предположения теории таковы:

• деформации остаются малыми
• поперечные сечения балки при деформации остаются нормальными к отклоненной оси (т.н. упругая кривая).

Второе предположение практически справедливо для балок из однородного и изотропного материала, с симметричным поперечным сечением и длиной, значительно превышающей размеры их поперечного сечения (обычно в 10 и более раз). Фактически, если балка значительно деформируется в любой другой форме, кроме симметричного изгиба, то предположение о нормальном и плоском поперечном сечении не выполняется. Примеры таких случаев включают короткие балки, балки с многослойным поперечным сечением, узкие поперечные сечения или открытые несимметричные поперечные сечения. 92} = {M(x)\over EI}

, где E — модуль упругости, а I — момент инерции поперечного сечения.

Поиск прогибов и уклонов

В зависимости от материала балка может испытывать большие прогибы без разрушения, даже оставаясь эластичной. Таким образом, он может быть застрахован от поломки, но есть и другие причины считать чрезмерные прогибы нежелательными. К ним относятся комфорт пользователей, безопасность движения (для моста), повреждение ненесущих элементов и т. д. Таким образом, определение прогибов является важным шагом в статическом анализе конструкции. 92} = {M(x)\over EI}, можно использовать как средство для нахождения прогибов и уклонов поперек балки. Если мы проинтегрируем один раз, мы найдем первую производную прогиба, которая представляет наклон балки:

\varphi(x)=\frac{d y}{d x} = {1\over EI}\int M(x)\ dx

Интегрируя еще раз найденные прогибы:

y(x) = \int \varphi(x)\ dx

Метод прямого интегрирования эффективен только для простых случаев. Другие методики расчета прогибов включают:

• Метод площади момента
• Метод сопряженных балок
• Метод Кастильяно
• Принцип виртуальной работы

Примеры

. Этот метод требует предварительного расчета диаграммы изгибающего момента. В контексте примеров это будет дано, однако, если вам нужно заняться и этой темой, пожалуйста, ознакомьтесь с нашей соответствующей статьей здесь.

Здесь повторяются этапы методики, описанные ранее в тексте.

Пример 1: прогибы свободно опертой балки с равномерно распределенной нагрузкой (udf) методом прямого интегрирования

1. Найдите прогибы свободно опертой балки с равномерно распределенной нагрузкой в ​​зависимости от расстояния x от конца A. Материал балки балки упругий с модулем упругости E, а ее поперечное сечение имеет момент инерции I, постоянный по длине L. 94\over12}+c x+k\right)

   Необходимо определить две константы. Для этого необходимо ввести граничные условия задачи. Существуют два места, где действительно известны отклонения. На двух опорах прогиб фактически равен нулю. Для опоры на конце A x=0, поэтому должно выполняться следующее условие:

   y(0)={w\over 2EI} \left( 0-0+0+k\right)=0 \Rightarrow

   k=0

   Для опоры на конце B x=L, поэтому должно выполняться следующее условие: 94\over 384EI}

   Физический смысл отрицательного знака состоит в том, что максимальное отклонение происходит в направлении вниз.

   Пример 2

   Найдите предельный прогиб свободно опертой балки при равномерной распределенной нагрузке, как показано на схеме. Его поперечное сечение может быть либо А, либо В, как показано на рисунке ниже. Оба сечения имеют одинаковые размеры, но различаются ориентацией оси изгиба (нейтральная ось показана пунктирной красной линией).