09Г2С предел текучести: Сталь 09г2с – расшифровка и характеристики

alexxlab | 18.03.2023 | 0 | Разное

09Г2С :: Металлические материалы: классификация и свойства

Сталь 09Г2С   ГОСТ 5520-79

Массовая доля элементов, %
Углерод	Кремний	Марганец	Сера	Фосфор	Хром	Никель	Молибден
			не более
Не более 0,12	0,5 – 0,8	1,3 – 1,7	0,040	0,035	–	–	–

Толщина, мм	Предел те- кучести σТ, Н/мм2 (кгс/мм2),	Временное сопротивле- ние σВ, Н/мм2 (кгс/мм2),	Относи- тельное удлине- ние δ5, %,	Ударная вязкость, KCU, Дж/см2 (кгс·м/см2), при температуре, оС					Ударная вязкость, KCU, после механического старения при +20оС, Дж/см2 (кгс·м/см2)
				+20		-40		-70
не менее
До 5	345 (35)	490 (50)	21	–	–		–		29 (3,0)
От 5 до 10	345 (35)	490 (50)		64 (6,5)	39 (4,0)		34 (3,5)
От 10 до 20 включ.	325 (33)	470 (48)		59 (6,0)	34 (3,5)		29 (3,0)
Св.20 до 32 включ.	305 (31)	460 (47)		59 (6,0)	34 (3,5)		29 (3,0)
Св.32 до 60 включ.	285 (29)	450 (46)		59 (6,0)	34 (3,5)		29 (3,0)
Св.60 до 80 включ.	275 (28)	440 (45)		59 (6,0)	34 (3,5)		29 (3,0)
Св. 80 до 160 включ.	265 (27)	430 (44)		59 (6,0)	34 (3,5)		29 (3,0)

Предел текучести σТ, Н/мм2 (кгс/мм2), при температуре оС, не менее
200	250	300	320	350	400	450
–	225 (23)	196 (20)	–	176 (18)	157 (16)	–

Физические свойства	Температура испытания, оС
	20- 100	20- 200	20- 300	20- 400	20- 500	20- 600	20- 700	20- 800	20- 900	20- 1000
Коэффициент линейного расширения   α, 10-6, 1/оС	11,4	12,2	12,6	13,2	13,8	–	–	–	–	–

Определяющие уравнения чувствительности предела текучести к скорости деформации металлов: сравнительное исследование

На этой странице

РезюмеВведениеРезультаты и обсуждениеЗаключениеСсылкиАвторское правоСтатьи по теме

Для моделирования чувствительности металлов к скорости деформации было предложено несколько основных уравнений.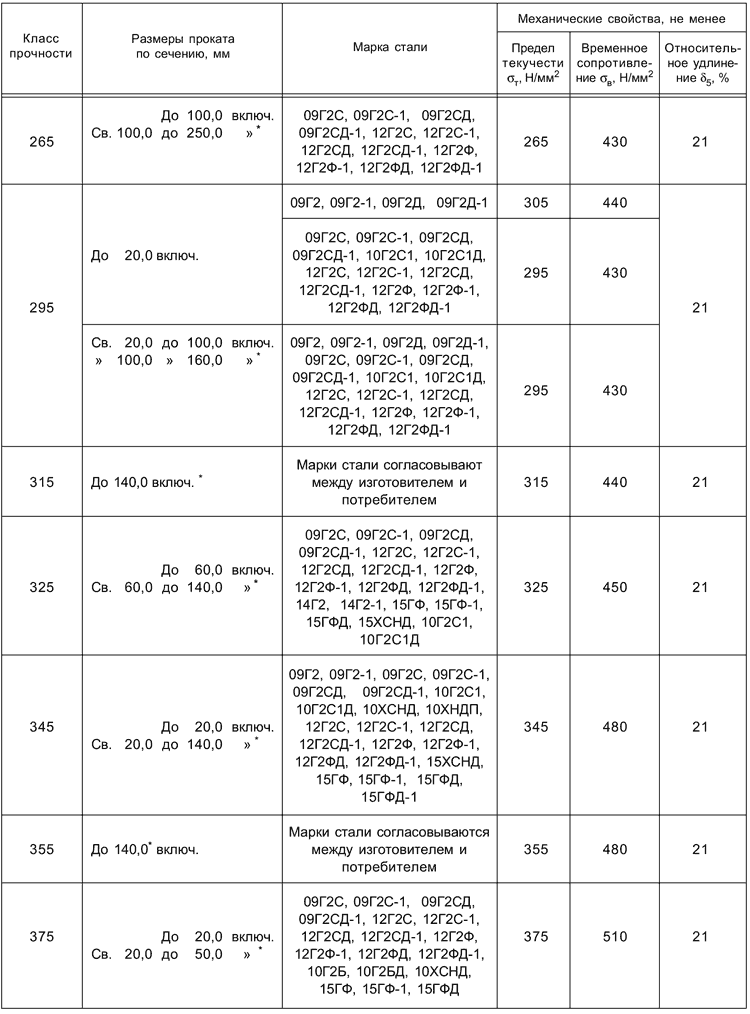 В этой статье представлено сравнение шести уравнений, опубликованных в открытой литературе. Все уравнения используются для определения предела текучести трех медных материалов и одного стального материала при двух различных температурах. Определены конкретная функция стоимости и задача оптимизации. Авторы рекомендуют использовать уравнение Каупера-Саймондса или модифицированное уравнение-Эйринга, поскольку оба они хорошо согласуются с экспериментальными данными при использовании только трех материальных констант. Затем предлагается модифицированное уравнение напряжения течения Джонсона-Кука для металлических материалов.

1. Введение

Металлические материалы широко используются в нескольких областях промышленности, например, в авиационной, военно-морской, автомобильной и военной промышленности. В этих случаях транспортные средства должны быть рассчитаны на ударные нагрузки. Таким образом, характеристика и моделирование чувствительности металлов к скорости деформации очень важны. Раздельный стержень Гопкинсона в основном используется для характеристики материалов в диапазоне высоких скоростей деформации [1, 2], в то время как стержень Гопкинсона прямого удара используется при очень высокой скорости деформации [3, 4]. В терминах определяющих уравнений закон Джонсона-Кука [5, 6] широко используется для моделирования поведения металлических материалов, включая влияние температуры или (и) скорости деформации [3, 7–9].]. Это определяющее уравнение разделяет закалку, температуру и скорость деформации. А именно, они записываются в мультипликативной форме. Влияние скорости деформации рассматривается как линейно изменяющееся относительно логарифма скорости деформации.

Несколько исследований показали, что линейное изменение предела текучести или напряжения течения в зависимости от скорости деформации справедливо только в квазистатическом и промежуточном диапазонах скоростей деформации [10–13]. Однако наблюдается резкое увеличение чувствительности к скорости деформации при высоких скоростях деформации. Это увеличение не может быть учтено классическим уравнением Джонсона-Кука. Затем были предложены некоторые модифицированные уравнения Джонсона-Кука [14]. Huh и Kang [15] предложили квадратичную зависимость чувствительности к скорости деформации. Туазон и др. В работе [16] зависимость от логарифма скорости деформации выражена в виде степенной зависимости. Couque [17] предложил модифицированное уравнение Джонсона-Кука, в котором чувствительность к скорости деформации записывается в виде четырехконстантного уравнения. Эль-Кубаа и Осман [18, 19] предложили модифицированное уравнение Эйринга для чувствительности полимеров к напряжению текучести к скорости деформации. Эта модель была успешно применена к нескольким металлическим материалам в [20].

Целью данной работы является сравнение и обсуждение указанных выше определяющих уравнений: стандартных уравнений Джонсона-Кука, Ху-Канга, Туазона и др., Кука и модифицированных уравнений-Эйринга. Также рассматривается пионерское уравнение Каупера-Саймондса [21]. С точки зрения зависимости от скорости деформации оно дает соотношение, аналогичное уравнению Зерилли-Армстронга [22].

2. Методика

2.1. Экспериментальные данные

В этой работе нас интересует оценка нескольких определяющих уравнений. Таким образом, они используются здесь для согласования чувствительности предела текучести к скорости деформации двух металлических материалов: стали и меди. Эти два материала широко охарактеризованы в литературе. В отношении предела текучести меди мы опираемся на экспериментальные данные Couque [17]. Для предела текучести стали мы будем полагаться на экспериментальные данные Clarke et al. [11].

2.2. Определяющие уравнения

Определяющие уравнения, изучаемые в этой работе, представлены в таблице 1. Здесь нас интересует только чувствительность к скорости деформации. Следует отметить, что уравнения иногда изменяют их первоначальный вид для целей идентификации.

2.3. Процедура идентификации

В этом разделе мы описываем методологию, используемую для определения материальных констант каждого из определяющих уравнений, представленных в таблице 1. На самом деле каждое определяющее уравнение зависит от набора из двух, трех или четырех материальных константы. Стандартная модель Джонсона-Кука зависит только от двух материальных констант: и . Каждое из уравнений Ху-Канга, Туазона и др., Каупера-Саймондса и модифицированного Эйринга зависит от трех материальных констант. Наконец, уравнение Кука зависит от четырех материальных констант. Основная идея этого раздела состоит в том, чтобы найти для каждого определяющего уравнения набор материальных констант, который уменьшает разницу между экспериментальными значениями пределов текучести и пределами текучести, полученными по этому уравнению.

Позвольте быть вектором, который собирает экспериментальные значения скорости деформации, которые собраны из литературы, как объяснено в Разделе 2, где обозначает скорость деформации, полученную для испытания. Точно так же пусть будет вектором, который собирает предел текучести, измеренный при скоростях деформации . Используя определяющее уравнение из Таблицы 1, можно построить вектор, который объединяет предел текучести, рассчитанный при скоростях деформации .

Чтобы получить наилучшие константы материала для каждого определяющего уравнения, нам необходимо оптимизировать функцию стоимости. Эта функция стоимости построена по разнице между экспериментальным и расчетным пределом текучести. Пусть и — евклидова норма и максимальная норма соответственно. Можно определить ошибку, используя евклидову норму.

Точнее, так же можно определить ошибку по максимальной норме. А именно, ошибка, основанная на евклидовой норме, дает измерение средней разницы между экспериментальным пределом текучести и пределом текучести, предсказанным рассматриваемым определяющим уравнением. Его можно рассматривать как измерение глобальной ошибки. Напротив, максимальная ошибка, основанная на норме, фокусируется на тестах, в которых встречается максимальная разница. Затем его можно рассматривать как измерение локальной ошибки.

В этом исследовании функция стоимости определяется как среднее между ошибкой, основанной на евклидовой норме, и максимальной ошибкой, основанной на норме: где материальные константы определяющего уравнения . Наилучшие константы материала затем получают путем минимизации функции стоимости:

3. Результаты и обсуждение

3.1. Стандартная модель Johnson-Cook

Стандартное уравнение Джонсона-Кука используется для определения предела текучести при сжатии трех медных материалов (рис. 1(a)) и стали при двух температурах (рис. 2(b)). Постоянные материала, ошибки и коэффициент корреляции рассчитаны и представлены в таблице 2. Ясно, что это уравнение не может моделировать увеличение чувствительности к скорости деформации при высоких скоростях деформации. Это наблюдается в пяти рассмотренных здесь ситуациях. Ошибка важна. Минимальная погрешность получена для стали при 273 К и равна 13,4%. Оно может увеличиваться до 48,2%, что достигается в случае меди 105.

3.2. Модель Ху-Канга

Уравнение Ху-Канга представляет собой модифицированную форму стандартной модели Джонсона-Кука с квадратичной зависимостью между пределом текучести и логарифмом скорости деформации. Подгонка этой модели к экспериментальным данным для меди и стали показана на рисунке 2. Константы материала и погрешности приведены в таблице 3. Модель приблизительно соответствует экспериментальным данным. Подгонка намного лучше со сталью, чем с медью. Погрешности составляют от 5,3 % для стали 29.3 K до 41,4% для меди 105. Он может уловить резкое увеличение деформации текучести при высокой скорости деформации. Однако он предсказывает увеличение предела текучести в диапазоне скоростей квазистатической деформации из-за квадратичной формы определяющего уравнения. Насколько известно авторам, об этом увеличении при низких скоростях деформации никогда не сообщалось в открытой литературе. Таким образом, он считается здесь нефизическим.

3.3. Туазон и др. Модель

Туазон и др. [16] модифицировали уравнение Джонсона-Кука, добавив показатель степени к логарифму скорости деформации. Точнее, выражение в стандартном уравнении Джонсона-Кука заменяется выражением . Туазон и др. Модель достаточно хорошо согласуется с экспериментальными данными стали и меди (рис. 3). Погрешность колеблется от 3,4 % (получено с медью 26) до 15,2 % (получено со сталью 29). 3) (см. табл. 4). Это уравнение может уловить увеличение чувствительности к скорости деформации при высоких скоростях деформации. Однако он предсказывает резкое падение предела текучести при низких скоростях деформации. Насколько известно авторам, об этом поведении никогда не сообщалось в литературе, и поэтому оно считается здесь нефизическим. Следовательно, мы скорее рекомендуем использовать Tuazon et al. уравнение для скоростей деформации выше, чем .

3.4. Couque Model

Couque [17] модифицировал стандартное уравнение Джонсона-Кука, добавив третий член, который записывается как степень скорости деформации, а не как логарифм скорости деформации, то есть . Это уравнение хорошо согласуется с экспериментальными данными меди и стали (рис. 4) во всем диапазоне деформаций, то есть между и . Модель хорошо описывает резкий рост предела текучести, который фиксируется при высокой скорости деформации. Ошибка невелика и колеблется от 2,8% для меди 105 до 6,2% для меди 9.(таблица 5).

3.5. Модель Cowper-Symonds

Уравнение Cowper-Symonds использует степенное уравнение скорости деформации. Он хорошо согласуется с экспериментальными данными для медных материалов и для стали при различных температурах (рис. 5). В частности, он хорошо улавливает резкое увеличение предела текучести при высоких скоростях деформации. Ошибка довольно низкая (таблица 6). Оно колеблется от 4,8% (получено для меди 105) до 7% (получено для меди 9).

3.6. Модифицированная модель Айринга

Модифицированная модель Эйринга разработана Эль-Кубаа и Отманом [18–20] на основе оригинальной работы Айринга [23], за исключением того, что они использовали активационный объем, уменьшающийся с увеличением скорости деформации. Модель хорошо работает здесь с медью и сталью в изученном диапазоне скоростей деформации (рис. 6). Это хорошо согласуется с увеличением предела текучести и повышением чувствительности предела текучести к скорости деформации, которое наблюдается при высокой скорости деформации. Ошибка невелика и колеблется от 5,8% для меди 26 до 7,8% для меди 9.(таблица 7).

3.7. Сравнение

В предыдущих разделах шесть уравнений использовались для определения предела текучести трех медных материалов и одного стального материала при двух температурах. Стандартное уравнение Джонсона-Кука дает наибольшую ошибку, так как в основном оно не может соответствовать поведению при высоких скоростях деформации. Уравнение Ху-Канга дает лишь немного лучшее соответствие. Более того, он предсказывает резкое увеличение предела текучести при квазистатических скоростях деформации, а это нефизическое поведение. Туазон и др. Модель дает приемлемую посадку в диапазоне средних и высоких скоростей деформации. Однако он предсказывает резкое снижение предела текучести при очень низких скоростях деформации, что также является нефизическим поведением. Couque, Cowper-Symonds и модифицированные уравнения-Eyring хорошо согласуются с экспериментальными данными. Модель Кука дает наименьшее значение ошибки, затем Купера-Саймондса и, наконец, модифицированное уравнение Эйринга. Однако в уравнении Кука используются четыре материальные константы, в то время как в модифицированных уравнениях Эйринга и Каупера-Саймондса используется только по три. Затем рекомендуется использовать следующее модифицированное уравнение Джонсона-Кука для моделирования металлических материалов, включая упрочнение, скорость деформации и влияние температуры: где , , , , , и – шесть констант материала, а деформация, абсолютная температура, комнатная температура, температура плавления, скорость деформации, эталонная скорость деформации и постоянная Больцмана соответственно. В этом уравнении стандартное уравнение напряжения течения Джонсона-Кука модифицируется с использованием чувствительности к скорости деформации, предсказанной для комнатной температуры модифицированным уравнением Эйринга, при сохранении исходных эффектов закалки и температуры, изначально записанных стандартным уравнением.

4. Заключение

В этой работе мы сравнили шесть определяющих уравнений, которые предсказывают чувствительность металлических материалов к скорости деформации. Они в основном используются для определения чувствительности предела текучести к скорости деформации трех медных материалов и стального сплава при двух разных температурах. Рекомендуется использовать либо уравнение Каупера-Саймондса, либо модифицированное уравнение-Эйринга, так как оба они дают точное соответствие экспериментальным данным, используя только три константы материала в каждом. Затем предлагается модифицированное уравнение Джонсона-Кука путем включения чувствительности скорости деформации, предсказанной модифицированным уравнением Эйринга, в стандартное модифицированное уравнение напряжения течения Джонсона-Кука.

Конкурирующие интересы

Авторы заявляют об отсутствии конфликта интересов в отношении публикации данной статьи.

Ссылки

1. Д. Ю. Ху, К. П. Мэн, Х. Л. Цзян, Дж. Сюй и Р. Р. Лю, «Исследование характеристического поведения стали AerMet 100 в зависимости от скорости деформации», Материалы и конструкция , том. 87, стр. 759–772, 2015.

   Посмотреть по адресу:

   Сайт издателя | Google Scholar

2. Дж. Кайберг и К. Г. Сундин, «Высокотемпературный расщепленный стержень давления Хопкинсона с ловушкой импульса для получения поведения напряжения течения и динамической рекристаллизации»,

   Штамм , об. 50, нет. 6, стр. 547–554, 2014.

   Посмотреть по адресу:

   Сайт издателя | Google Scholar

3. X. Guo, T. Heuzé, R. Othman, and G. Racineux, «Обратная идентификация при очень высокой скорости деформации конститутивной модели Джонсона-Кука на сплаве Ti-6Al-4V со специально разработанной стержневое устройство прямого действия Кольского», Штамм , вып. 50, нет. 6, стр. 527–538, 2014.

   Посмотреть по адресу:

   Сайт издателя | Академия Google

4. C. K.H. Dharan and FE Hauser, «Определение характеристик напряжение-деформация при очень высоких скоростях деформации», Experimental Mechanics , vol. 10, нет. 9, стр. 370–376, 1970.

   Посмотреть по адресу:

   Сайт издателя | Google Scholar

5. Г. Р. Джонсон и У. Х. Кук, «Характеристики разрушения трех металлов при различных деформациях, скоростях деформации, температурах и давлениях», Engineering Fracture Mechanics , vol. 21, нет. 1, стр. 31–48, 1985.

   Посмотреть по адресу:

   Сайт издателя | Google Scholar

6. Г. Р. Джонсон и У. Х. Кук, «Конструктивная модель и данные для металлов, подвергающихся большим деформациям, высокой скорости деформации и высоким температурам», в Proceedings of the 7th International Symposium on Ballistics , vol. 21, pp. 541–547, 1983.

   Просмотр по адресу:

   Google Scholar

7. О.

   Пантале и Б. Гуйе, «Влияние определяющего закона течения в МКЭ-моделировании процесса радиальной ковки», Инженерный журнал , том. 2013 г., идентификатор статьи 231847, 8 страниц, 2013 г.

   Посмотреть по адресу:

   Сайт издателя | Google Scholar

8. Y. Guo and Y. Li, «Новый подход к тестированию динамической реакции на сдвиг Ti-6Al-4V», Acta Mechanica Solida Sinica , vol. 25, нет. 3, стр. 299–311, 2012 г.

   Посмотреть по адресу:

   Сайт издателя | Google Scholar

9. Г. Люстина, М. Фагерстрем и Р. Ларссон, «Чувствительные к скорости модели непрерывного повреждения и зависимость сетки в анализе методом конечных элементов», The Scientific World Journal , vol. 2014 г., идентификатор статьи 260571, 8 страниц, 2014 г.

   Посмотреть по адресу:

   Сайт издателя | Google Scholar

10. В. Мочко, Х. А. Родригес-Мартинес, З. Л. Ковалевски, А. Русинек, «Вязкопластическая реакция на сжатие алюминиевых сплавов 6082-Т6 и 7075-Т6 в широком диапазоне скоростей деформации при комнатной температуре: эксперименты и моделирование» , Штамм , vol. 48, нет. 6, стр. 498–509, 2012.

    Посмотреть по адресу:

    Сайт издателя | Академия Google

11. К. Д. Кларк, Р. Дж. Комсток, М. С. Матая, К. Дж. Тайн и Д. К. Мэтлок, «Влияние скорости деформации на предел текучести ферритных нержавеющих сталей», Metallurgical and Materials Transactions A: Physical Metallurgy and Materials Science , vol. . 39, нет. 4, стр. 752–762, 2008 г.

    Посмотреть по адресу:

    Сайт издателя | Google Scholar

12. Ю. Ван, Д. Лин, Ю. Чжоу, Ю. Ся и К. С. Ло, «Динамические свойства сплава Ti-47Al-2Mn-2Nb при растяжении», стр. 9.0081 Журнал материаловедения , том. 34, нет. 3, стр. 509–513, 1999.

    Посмотреть по адресу:

    Сайт издателя | Google Scholar

13. T. Suo, L. Ming, F. Zhao, Y. Li, and X. Fan, «Чувствительность сверхмелкозернистой меди к температуре и скорости деформации при одноосном сжатии», International Journal of Applied Mechanics , том. 5, нет. 2, идентификатор статьи 1350016, 15 страниц, 2013 г.

    Посмотреть по адресу:

    Сайт издателя | Академия Google

14. –

    . Баландин В.В., Баландин В.В., Брагов А.М., Игумнов Л.А., Константинов А.Ю., Ломунов А.К. Высокоскоростная деформация и разрушение стали 09Г2С. . Механика твердого тела. 49, нет. 6, стр. 666–672, 2014.

    Посмотреть по адресу:

    Сайт издателя | Google Scholar

15. H. Huh и WJ Kang, «Оценка ударопрочности тонкостенных конструкций с высокопрочным стальным листом», International Journal of Vehicle Design , vol. 30, нет. 1-2, стр. 1–21, 2002.

    Посмотреть по адресу:

    Сайт издателя | Google Scholar

16. Б. Дж. Туазон, К.-О. Бэ, С.-Х. Ли и Х.-С. Шин, «Интеграция новой схемы сбора/обработки данных в испытание SHPB и характеристика динамических свойств материала высокопрочных сталей с использованием необязательной формы модели Джонсона-Кука», Journal of Mechanical Science and Technology , vol. 28, нет. 9, стр. 3561–3568, 2014.

    Посмотреть по адресу:

    Сайт издателя | Академия Google

17. H. Couque, «Использование метода прямого удара Гопкинсона, работающего под давлением, для описания термически активированных и вязких режимов металлических материалов», Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences , vol. 372, нет. 2023, идентификатор статьи 20130218, 10 страниц, 2014 г.

    Посмотреть по адресу:

    Сайт издателя | Google Scholar

18. З. Эль-Кубаа и Р. Отман, «Характеристика и моделирование чувствительности к скорости деформации предела текучести полиэфиркетона при сжатии», Материалы и конструкция , том. 66, стр. 336–345, 2015.

    Посмотреть по адресу:

    Сайт издателя | Google Scholar

19. А. А. Аль-Джуайд и Р. Отман, «Моделирование зависимости предела текучести поликарбоната от скорости деформации: оценка четырех определяющих уравнений», Journal of Engineering , vol. 2016 г., идентификатор статьи 6315421, 9 страниц, 2016 г.

    Посмотреть по адресу:

    Сайт издателя | Google Scholar

20. Р. Отман, «Модифицированное уравнение Эйринга для моделирования текучести и напряжений течения металлов при скоростях деформации в диапазоне от 10 ^-5 до 5 × 10 ⁴ с ^-1 , Достижения в области материаловедения и инженерии , том. 2015 г., идентификатор статьи 539625, 6 страниц, 2015 г.

    Посмотреть по адресу:

    Сайт издателя | Google Scholar

21. Г. Каупер и П. Саймондс, «Деформационное упрочнение и эффекты скорости деформации при ударной нагрузке консольных балок», Tech. Представитель отдела прикладной математики Брауновского университета, Провиденс, Род-Айленд, США, 1952.

    Посмотреть по адресу:

    Google Scholar

22. Ф. Дж. Зерилли и Р. В. Армстронг, «Определяющие соотношения, основанные на механике дислокаций, для расчетов динамики материалов», Journal of Applied Physics , vol. 61, нет. 5, стр. 1816–1825, 1987.

    Посмотреть по адресу:

    Сайт издателя | Google Scholar

23. Х. Айринг, «Вязкость, пластичность и диффузия как примеры абсолютных скоростей реакций», The Journal of Chemical Physics , vol.