1 ма 1 а: миллиампер [мА] в ампер [А] • Конвертер электрического тока • Электротехника • Компактный калькулятор • Онлайн-конвертеры единиц измерения
alexxlab | 12.04.2023 | 0 | Разное
Сколько миллиампер в ампере – калькулятор онлайн
В электротехнике существует множество единиц измерения, используемых при выполнении расчетов. Большие значение делятся на более мелкие, а те в свою очередь – на еще более мелкие. Поэтому, в зависимости от обстоятельств, приходится переводить одни единицы в другие. В процессе перевода нередко возникают разные вопросы, например, сколько миллиампер в ампере или ватт в киловатте и мегаватте. Что больше ампер или миллиампер?
Содержание
Ампер с точки зрения физики
В физике и электротехнике ампер является величиной, характеризующей силу тока в количественном отношении. Для ее определения используются различные способы. Среди них наибольшее распространение получил метод прямых измерений, когда используется амперметр, тестер или мультиметр. При выполнении замеров эти приборы последовательно включаются в электрическую цепь.
Другой способ считается косвенным, требующим проведения специальных расчетов. В этом случае необходимо знать напряжение, приложенное к данному участку цепи, и сопротивление этого участка. После чего, сила тока легко определяется по формуле I = U/R, а полученный результат отображается в амперах.
После чего, сила тока легко определяется по формуле I = U/R, а полученный результат отображается в амперах.
В практической деятельности амперы используются довольно редко, поскольку эта единица считается слишком большой для обычного пользования. Поэтому большинство специалистов пользуются кратными единицами – миллиамперами (10-3А) и микроамперами (10-6А), которые по-другому могут обозначаться в виде 0,001 А и 0,000001 А. Однако при выполнении расчетов необходимо вновь перевести миллиамперы в амперы и во всех формулах применять уже эти единицы. Именно на этой стадии у многих возникает вопрос, как переводить миллиамперы в амперы.
Как измерить
Для того чтобы определить силу тока на конкретном участке цепи, используются измерительные приборы, перечисленные выше. Среди них наиболее точным считается амперметр, производящий замеры только одной величины, с использованием одной шкалы. Однако более удобными считаются тестеры и мультиметры, с помощью которых осуществляется измерение не только силы тока, но и других электротехнических величин в различных диапазонах. Данные приборы обладают возможностью переключаться с одних единиц измерения на другие и точно определять, сколько миллиампер в ампере.
Данные приборы обладают возможностью переключаться с одних единиц измерения на другие и точно определять, сколько миллиампер в ампере.
В некоторых случаях измерительное устройство может показать превышение диапазона. Чтобы решить эту проблему достаточно сделать перевод миллиампер в амперы и получить требуемое значение. Несмотря на высокие погрешности измерений, мультиметры и тестеры на практике применяются намного чаще амперметров, поскольку с их помощью большинство неисправностей очень быстро обнаруживается и устраняется. Кроме того, эти приборы при выполнении измерений не требуют обязательного разрыва цепи, и сила тока может быть измерена бесконтактным способом.
Как перевести
Наиболее простым способом считается перевод единиц вручную, наглядно показывая ампер и миллиампер, разница между которыми составляет 10-3. В качестве примера можно рассмотреть участок электрической цепи с напряжением 5 вольт и сопротивлением 100 Ом. Для того чтобы определить силу тока, необходимо воспользоваться формулой и разделить значение напряжения на сопротивление I = U/R = 5/100 = 0,05 А. Полученный результат не совсем удобен использования, поэтому его рекомендуется пересчитать в кратных единицах измерения, то есть, в миллиамперах.
Полученный результат не совсем удобен использования, поэтому его рекомендуется пересчитать в кратных единицах измерения, то есть, в миллиамперах.
В этом случае 1 ампер равен 1000 миллиампер. Для пересчета 0,05 А нужно умножить на 1000 и получится 50 мА. Точно так же делается обратная процедура, когда 50 мА делится на 1000, и в итоге получаются первоначальные 0,05 А. Таким образом, решая задачу на 1 ампер сколько приходится миллиампер получается количество, равное 1000.
Для того чтобы ускорить процедуру перевода единиц, были разработаны специальные таблицы, отображающие различные типы величин. Например, если один миллиампер составляет 0,001 ампера, то в обратном порядке один ампер будет равен 1000 миллиампер. На корпусах аккумуляторов помимо силы тока, добавляется количество времени, в течение которого они смогут отдать или получить определенный заряд. На различных зарядных устройствах наносится количество ампер или миллиампер, которые дополнительно означают их мощность.
В таблице, приведенной на рисунке, исключается применение большого количества нулей. Вместо них используются специальные приставки, обозначающие какую-то часть от целых чисел. Все вместе они представляют собой единое слово, в котором присутствует не только приставка, но и сама основная единица.
Калькулятор перевода миллиамперы в амперы и обратно
| Сила тока, мА = | |
| Сила тока, А = |
| Сила тока, А = | |
| Сила тока, мА = |
1 марта – какой сегодня праздник? Праздники 1 марта 2023 года
Адрес страницы: https://www.calend.ru/holidays/3-1/
- Государственные
Россия
Украина
Беларусь
Абхазия
Австралия
Австрия
Азербайджан
Албания
Аргентина
Армения
Бельгия
Болгария
Босния
Бразилия
Великобритания
Венгрия
Вьетнам
Германия
Греция
Грузия
Дания
Египет
Зимбабве
Индия
Иордания
Ирландия
Исландия
Испания
Италия
Казахстан
Камерун
Канада
Кипр
Китай
Коми
Коста-Рика
Куба
Кыргызстан
Латвия
Ливан
Литва
Люксембург
Мадагаскар
Мексика
Молдова
Нигерия
Нидерланды
Новая Зеландия
Норвегия
Панама
Перу
Польша
Португалия
Румыния
США
Сербия
Сирия
Словения
Таджикистан
Таиланд
Тунис
Туркменистан
Турция
Узбекистан
Финляндия
Франция
Хорватия
Черногория
Чехия
Швейцария
Швеция
Эквадор
Эстония
Эфиопия
Южная Корея
Южная Осетия
Ямайка
Япония
Все государстваСвернуть - Религиозные
Православные
Католические
Лютеранские
Мусульманские
Еврейские
Буддийские
Индуизм
Бахаи
Зороастризм
Славянские
Языческие
Все религииСвернуть - По категориям
Профессиональные
Международные
ООН
Деловые
Дни воинской славы России
Армейские
Величественные
ВОВ
Водные
Гастрономические
Детские
В честь икон
Дни памяти святых
Конституционные
Культурные
Масс-медийные
Молодежные
Научно-технические
Независимые
Необычные
Природные
Медицинские
Посты
Семейные
Сетевые
Славные
Спортивные
Турниры
Учительские
Фестивали
Финансовые
Флотские
Экологические
Юридические
Языковые
Все категорииСвернуть
- Сегодня 15 февраля 2023 года, среда
День памяти о россиянах, исполнявших служебный долг за пределами Отечества
.
 ..а также еще 40 событий
..а также еще 40 событий - Завтра 16 февраля 2023 года, четверг
Всемирный день управления информацией
…а также еще 35 событий
- Послезавтра 17 февраля 2023 года, пятница
День спонтанного проявления доброты
…а также еще 47 событий
Всемирный день комплимента
Точной информации о том, кем и когда был учреждён такой интересный праздник, как Всемирный день комплимента (World Compliment Day), нет. По одной из версий, его начали праздновать в 2001 году в Нидерландах. Также нет и единого мнения о точной дате его проведения – одни предлагают отмечать этот праздник 1 марта, а другие – 21 марта.Главное, что известно, это идея учреждения праздника – спонтанн…
День джигита
День джигита – праздник, отмечаемый ежегодно в Чеченской Республике и Республике Ингушетия 1 марта.
Хотя это и неофициальный праздник, однако, ежегодно набирает популярность, благодаря верности традиционным ценностям и представлениям о мужестве, патриотизме и других качествах, которые должны быть присущи настоящему мужчине.Слово «джигит» издревле на Кавказе и в Средней Азии ассоциировалось с у…
Праздник прихода весны
1 марта в ряде стран отмечается Праздник Весны, победившей зиму. Он не имеет отношения к христианским праздникам, проходящим перед Постом в эти дни, а исходит из старинной легенды о Весне. Однажды Солнце спустилось на землю в образе прекрасной девушки. Солнцу хотелось поплясать и повеселиться. Злой Змей выкрал и закрыл его в своем дворце. Птицы перестали петь, дети забыли, что такое весель…
1 марта в США отмечается Национальный день цветных женщин (National Women of Color Day).
 Он был установлен американским Национальным институтом цветных женщин (National Institute for Women of Color, NIWC) в 1986 году. Главная задача этого института — создать содружество коренных жительниц Африки, Индии, Аляски, Азии, Испании, Латинской Америки и островов Тихого океана, решать их проблемы, пров…
Он был установлен американским Национальным институтом цветных женщин (National Institute for Women of Color, NIWC) в 1986 году. Главная задача этого института — создать содружество коренных жительниц Африки, Индии, Аляски, Азии, Испании, Латинской Америки и островов Тихого океана, решать их проблемы, пров…
А также в этот день
Здесь перечислены фестивали, памятные даты и т.п., имеющие большое значение для страны, но не являющиеся праздниками в прямом смысле этого слова.
Фестиваль сбора грейпфрутов на Кубе
Грейпфрут (Grapefruit) — вечнозеленое дерево рода цитрусовых, семейства рутовых, а также его плод, достигающий в диаметре 30-40 сантиметров. Внешне грейпфрут похож на апельсин, но мякоть его кислее и имеет привкус горечи. Несмотря на это, грейпфрут безоговорочно отнесен к диетическим плодам. Предположительно, грейпфрут является результатом природной гибридизации апельсинов и помело.
До 195…
А также в этот день 1 марта:
Именины Хроника Дни городов Все события- 26 февраля
- 27 февраля
- 28 февраля
- 1 марта
- 2 марта
- 3 марта
- 4 марта
Регистрация Вход
Регистрация Эл. почта
Логин
только латиница и символы “-“, “_”; не менее 4 символов
Пароль Еще раз
Нажимая кнопку “Зарегистрироваться”, вы подтверждаете согласие с политикой конфиденциальности сайта
Авторизация Логин
Пароль
Запомнить меня
Забыли пароль?
Калькулятор преобразованияампер в миллиампер (А в мА)
Воспользуйтесь нашим интерактивным калькулятором, чтобы легко преобразовать ампер в миллиампер (А в мА).
Калькулятор преобразования ампер в миллиампер
Ампер (А)
Ошибка: Введите допустимое количество ампер (А).
миллиампер (мА)
Формула преобразования: мА = A × 1000
Или лучше перевести миллиампер в ампер?
Ампер в Миллиампер. Таблица преобразования
Вот таблица перевода распространенных значений ампер в миллиампер.
| Amps (A) | Milliamps (mA) | ||
|---|---|---|---|
| 0.01 A | 10 mA | ||
| 0.02 A | 20 mA | ||
| 0.03 A | 30 mA | ||
| 0,04 А | 40 мА | ||
| 0,05 А | 50 мА | ||
| 0,06 А | 63 мА027 | 0.07 A | 70 mA |
| 0.08 A | 80 mA | ||
| 0.09 A | 90 mA | ||
| 0.1 A | 100 mA | ||
| 0.2 A | 200 mA | ||
| 0.25 A | 250 mA | ||
| 0.3 A | 300 mA | ||
0. 4 A 4 A | 400 mA | ||
| 0.5 A | 500 mA | ||
| 0.6 A | 600 mA | ||
| 0.7 A | 700 mA | ||
| 0.75 A | 750 mA | ||
| 0.8 A | 800 mA | ||
| 0.9 A | 900 mA | ||
| 1 A | 1000 mA | ||
| 2 A | 2000 mA | ||
| 3 A | 3000 mA | ||
| 4 A | 4000 mA | ||
| 5 A | 5000 mA |
Примечание: Нет нужных значений на этой диаграмме? Используйте наш калькулятор преобразования ампер в миллиампер в верхней части этой страницы, чтобы рассчитать их для вашего конкретного сценария.
Как преобразовать ампер в миллиампер (А в мА)
В 1 ампере 1000 миллиампер, точно так же, как в 1 метре 1000 миллиметров.
Итак, чтобы преобразовать ампер в миллиампер, просто умножьте ампер на 1000.
Формула преобразования: миллиампер = ампер × 1000
Сокращенно: мА = A × 1000
Пример
A Недавно я сделал собственное зарядное устройство для телефона на солнечных батареях и использовал USB-измеритель мощности для измерения выходной мощности. Когда я это сделал, я получил результат 0,46 ампер.
Мое зарядное устройство для телефона на солнечных батареях, сделанное своими руками, вырабатывало ток 0,46 ампер или 460 миллиампер.Вот как преобразовать это число в миллиампер:
0,46 A × 1000 = 460 мА
Итак, в этом примере мое солнечное зарядное устройство выдавало ток 460 миллиампер.
Легко!
Как преобразовать миллиампер в ампер (мА в А)
Нужно преобразовать в другую сторону?
для преобразования Milliamps в Amps, Divide Amps на 1000.
Формула преобразования: Amps = Milliamps ÷ 1000
Сокращение: A = MA ÷ 1000
Пример
Lets’s Walling У вас есть есть некоторые светодиодные строки
. Вы смотрите на этикетку на фарах и видите, что они потребляют 100 миллиампер.
Вы смотрите на этикетку на фарах и видите, что они потребляют 100 миллиампер.
Вот как преобразовать это число в ампер:
100 мА ÷ 1000 = 0,1 А
Итак, в этом примере ваш свет потребляет 0,1 ампер тока во включенном состоянии.
Что такое усилитель?
Ампер, часто сокращаемый до ампер , является базовой единицей электрического тока в системе СИ. Электрический ток – это количество заряженных частиц, протекающих через проводник.
Ампер сокращенно А . Итак, 1 ампер можно записать как 1 А.
Что такое миллиампер?
Миллиампер — часто сокращается до миллиампер — кратная ампера, эквивалентная одной тысячной ампера (10 -3 А или 0,001 А).
Миллиампер сокращенно мА . Итак, 1 миллиампер можно записать как 1 мА.
Дополнительные калькуляторы электроэнергии
- Преобразование ампер-часов в ватт-часы
- Калькулятор преобразования ватт в ампер
- Калькулятор преобразования ампер в ватт
Введение в модели временных рядов 20 ARIMA
1
Примечания по несезонным моделям ARIMA (файл в формате pdf)
Слайды по сезонным и несезонные модели ARIMA (файл в формате pdf)
Введение в
ARIMA: несезонные модели
Определение порядка различий в модели ARIMA
Определение количества терминов AR или MA в ARIMA
модель
Сезонные различия в моделях ARIMA
Сезонное случайное блуждание: ARIMA(0,0,0)x(0,1,0)
Сезонный случайный тренд: ARIMA(0,1,0)x(0,1,0)
Общие сезонные модели: ARIMA(0,1,1)x(0,1,1) и т.
 д.
д. Краткое изложение правил идентификации Модели ARIMA
Модели ARIMA с регрессорами
математическая структура моделей ARIMA (файл в формате pdf)
Введение в ARIMA: несезонные модели
ARIMA(p,d,q) уравнение прогнозирования
ARIMA(1,0,0) = авторегрессионная модель первого порядка
ARIMA(0,1,0) = случайное блуждание
ARIMA(1,1,0) = разностная авторегрессионная модель первого порядка
ARIMA(0,1,1) без константы = простое экспоненциальное сглаживание
ARIMA(0,1,1) с константой = простое экспоненциальное сглаживание
с ростом
ARIMA(0,2,1) или (0,2,2) без константы = линейная экспоненциальная
сглаживание
Реализация электронных таблиц
ARIMA(p,d,q)
уравнение прогнозирования: модели 90 279 ARIMA теоретически являются наиболее общим классом
модели для прогнозирования временных рядов, которые можно сделать
«неподвижный» путем дифференцирования (при необходимости), возможно, в сочетании
с нелинейными преобразованиями, такими как регистрация или дефлирование (при необходимости). А
случайная величина, представляющая собой временной ряд, является стационарной, если ее статистическая
все свойства постоянны во времени. Стационарный ряд не имеет тренда,
его колебания вокруг своего среднего значения имеют постоянную амплитуду, и он колеблется в
последовательная мода , т. е. ее краткосрочные случайные временные паттерны всегда выглядят
то же самое в статистическом смысле.
Последнее условие означает, что его автокорреляций (корреляции с его собственными априорными отклонениями от среднего) остаются постоянными в течение
время, или эквивалентно, что его мощность спектр остается постоянным во времени.
Случайную величину такого вида можно рассматривать (как обычно) как комбинацию
сигнала и шума, а сигнал (если он очевиден) может быть образцом
быстрый или медленный возврат к среднему, или синусоидальные колебания, или быстрое чередование в
знак, а также может иметь сезонную составляющую. Модель ARIMA можно рассматривать как
«фильтр», который пытается отделить сигнал от шума, и
Затем сигнал экстраполируется в будущее для получения прогнозов.
А
случайная величина, представляющая собой временной ряд, является стационарной, если ее статистическая
все свойства постоянны во времени. Стационарный ряд не имеет тренда,
его колебания вокруг своего среднего значения имеют постоянную амплитуду, и он колеблется в
последовательная мода , т. е. ее краткосрочные случайные временные паттерны всегда выглядят
то же самое в статистическом смысле.
Последнее условие означает, что его автокорреляций (корреляции с его собственными априорными отклонениями от среднего) остаются постоянными в течение
время, или эквивалентно, что его мощность спектр остается постоянным во времени.
Случайную величину такого вида можно рассматривать (как обычно) как комбинацию
сигнала и шума, а сигнал (если он очевиден) может быть образцом
быстрый или медленный возврат к среднему, или синусоидальные колебания, или быстрое чередование в
знак, а также может иметь сезонную составляющую. Модель ARIMA можно рассматривать как
«фильтр», который пытается отделить сигнал от шума, и
Затем сигнал экстраполируется в будущее для получения прогнозов.
АРИМА Уравнение прогнозирования для стационарного временного ряда представляет собой линейное уравнение (т. е. регрессионного типа), в котором предикторы состоят из лагов зависимых переменная и/или
Прогнозируемое значение Y = константа и/или взвешенная сумма одного или нескольких недавние значения Y и/или взвешенная сумма одного или нескольких недавних значений ошибки.
Если
предикторы состоят только из запаздывающих значений Y, это чистый авторегрессионный
(«саморегрессивная») модель, которая является лишь частным случаем
модель регрессии и которая может быть оснащена стандартной регрессией
программное обеспечение. Например,
модель авторегрессии первого порядка («AR(1)») для Y представляет собой простую
регрессионная модель, в которой независимая переменная отстает от Y только на единицу
период (LAG(Y,1) в Statgraphics или Y_LAG1 в RegressIt). Если некоторые из предикторов являются лагами
ошибки, модель ARIMA НЕ является моделью линейной регрессии, потому что
нельзя определить «ошибку последнего периода» как независимую
переменная: ошибки должны быть
рассчитывается от периода к периоду, когда модель подгоняется к данным. С технической точки зрения проблема
с использованием запаздывающих ошибок в качестве предикторов заключается в том, что предсказания модели не являются линейными функциями
коэффициенты , хотя они являются линейными функциями прошлых данных. Итак, коэффициенты в моделях ARIMA, которые
включать запаздывающие ошибки должны оцениваться нелинейно методы оптимизации («восхождение в гору»), а не просто решение
система уравнений.
Если некоторые из предикторов являются лагами
ошибки, модель ARIMA НЕ является моделью линейной регрессии, потому что
нельзя определить «ошибку последнего периода» как независимую
переменная: ошибки должны быть
рассчитывается от периода к периоду, когда модель подгоняется к данным. С технической точки зрения проблема
с использованием запаздывающих ошибок в качестве предикторов заключается в том, что предсказания модели не являются линейными функциями
коэффициенты , хотя они являются линейными функциями прошлых данных. Итак, коэффициенты в моделях ARIMA, которые
включать запаздывающие ошибки должны оцениваться нелинейно методы оптимизации («восхождение в гору»), а не просто решение
система уравнений.
аббревиатура ARIMA расшифровывается как Авторегрессивный
Интегрированная скользящая средняя . Лаги стационарного ряда в
уравнения прогнозирования называются «авторегрессивными» членами, лаги
ошибки прогноза называются терминами «скользящего среднего», а временной ряд
которое необходимо различать, чтобы сделать его стационарным, называется
«интегрированный» вариант стационарного ряда. Случайное блуждание и
модели случайного тренда, авторегрессионные модели и модели экспоненциального сглаживания
все это частные случаи моделей ARIMA.
Случайное блуждание и
модели случайного тренда, авторегрессионные модели и модели экспоненциального сглаживания
все это частные случаи моделей ARIMA.
А несезонная модель ARIMA классифицируется как модель «ARIMA (p, d, q)», где:
- p – количество членов авторегрессии,
- d — количество несезонных различий, необходимых для стационарность и
- q — количество запаздывающих ошибок прогноза в прогнозе уравнение.
Уравнение прогноза строится следующим образом. Во-первых, пусть y обозначает d th разница Y, что означает:
Если d=0: y t = Y t
Если d=1: y t = Y т – Y t-1
Если d=2: y t = (Я т – Y т-1 ) – (Y т-1 – Y т-2 ) = Y т – 2Y т-1 + Y т-2
Обратите внимание, что
вторая разница Y
(случай d=2) не отличается от 2 периодов назад. Скорее, это первая разность первой разности , которая является дискретной.
аналог второй производной, т. е. локальное ускорение ряда
а не его локальная тенденция.
Скорее, это первая разность первой разности , которая является дискретной.
аналог второй производной, т. е. локальное ускорение ряда
а не его локальная тенденция.
В пересчете у, общее уравнение прогнозирования: +…+ ϕ p y t-p – θ 1 e t-1 -…- θ q e t-q
Здесь параметры скользящего среднего (θ) определены так, что их знаки отрицательные в уравнении, следуя соглашению, введенному Боксом и Дженкинсом. Некоторые авторы и программное обеспечение (включая язык программирования R) определите их так, чтобы вместо них у них были знаки плюс. Когда реальные цифры подставляются в уравнение, нет никакой двусмысленности, но важно знать, какое соглашение, используемое вашим программным обеспечением при чтении вывода. Часто там обозначаются параметры по AR(1), AR(2), … и MA(1), MA(2), … и т.д..
Кому
определить подходящую модель ARIMA для Y, вы начинаете с определения порядка дифференцирования
(d) необходимость стационаризации ряда и удаления грубых признаков
сезонность, возможно, в сочетании с преобразованием, стабилизирующим дисперсию
таких как регистрация или дефляция.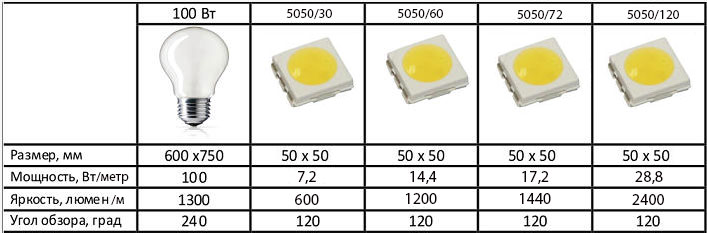 Если вы остановитесь на этом месте и предскажете, что
разностный ряд постоянен, вы просто подогнали случайное блуждание или случайное
трендовая модель. Однако
стационарные ряды могут по-прежнему иметь автокоррелированные ошибки, предполагая, что некоторые
количество терминов AR (p ≥ 1) и/или некоторое количество терминов MA (q ≥ 1)
также необходимо в уравнении прогнозирования.
Если вы остановитесь на этом месте и предскажете, что
разностный ряд постоянен, вы просто подогнали случайное блуждание или случайное
трендовая модель. Однако
стационарные ряды могут по-прежнему иметь автокоррелированные ошибки, предполагая, что некоторые
количество терминов AR (p ≥ 1) и/или некоторое количество терминов MA (q ≥ 1)
также необходимо в уравнении прогнозирования.
процесс определения значений p, d и q, которые являются лучшими для данного времени серия будет обсуждаться в последующих разделах заметок (ссылки на которые находятся в вверху этой страницы), но дается предварительный просмотр некоторых типов несезонных моделей ARIMA, которые часто встречаются. ниже.
ARIMA(1,0,0) = авторегрессия первого порядка модель: , если ряд стационарный и автокоррелированный, возможно, его можно предсказать как кратное его собственному предыдущему значению, плюс постоянный. Уравнение прогнозирования в данном случае
Ŷ т = μ + ϕ 1 Y t-1
…который представляет собой регрессию Y по
сам отстал на один период. Это «ARIMA(1,0,0)+константа»
модель. Если среднее значение Y равно нулю, постоянный член не будет включен.
Это «ARIMA(1,0,0)+константа»
модель. Если среднее значение Y равно нулю, постоянный член не будет включен.
Если коэффициент наклона ϕ 1 положителен и меньше 1 по величине (он должен быть меньше 1 по величине, если Y стационарен), модель описывает поведение с возвратом к среднему, при котором значение следующего периода должно быть предсказано как ϕ 1 раз дальше от среднего, чем значение этого периода. Если ϕ 1 отрицательное, оно предсказывает поведение с возвратом к среднему с чередованием знаков, т. е. он также предсказывает, что Y будет ниже среднего значения в следующем периоде, если оно выше среднего значения в этом периоде.
В второго порядка авторегрессионной модели (ARIMA(2,0,0)), справа также будет член Y t-2 , и поэтому
на. В зависимости от признаков и
величины коэффициентов, модель ARIMA(2,0,0) могла бы описать систему
средняя реверсия которого происходит в синусоидально
колеблется образом, подобно движению массы на пружине, которая
подвергается случайным ударам.
АРИМА(0,1,0) = случайное блуждание: Если ряд Y не является стационарным, простейшей возможной моделью для него является модель случайного блуждания, которую можно рассматривается как предельный случай модели AR (1), в которой авторегрессионный коэффициент равен 1, т. е. ряд с бесконечно медленным средним реверсия. Уравнение предсказания для этой модели можно записать как:
Ŷ t – Y t-1 = μ
или эквивалентно
Ŷ t = μ + Y t-1
…где постоянный срок — это среднее изменение от периода к периоду (т. е. долгосрочное дрейф) в Y. Эту модель можно подогнать как регрессионную модель без перехвата , в которой первое отличие Y является зависимой переменной. С тех пор включает (только) несезонную разницу и постоянный член, классифицируется как «модель ARIMA (0,1,0) с константой». Случайное блуждание- без -дрифтовая модель была бы Модель ARIMA(0,1,0) без константы
ARIMA(1,1,0)
= разностная авторегрессионная модель первого порядка: Если ошибки
модель случайного блуждания автокоррелированы,
возможно, проблему можно решить, добавив один лаг зависимой переменной к
уравнение предсказания, то есть путем регрессии 90 325 первой разности 90 326 90 325 Y 90 326 90 325 90 326 на себя, отстающую на один период. Это даст
следующее уравнение предсказания:
Это даст
следующее уравнение предсказания:
Ŷ т – Y т-1 = μ + ϕ 1 (Y t-1 – Y t-2 )
Ŷ t – Y t-1 = μ
изменить на
Ŷ t = μ + Y t-1 + ϕ 1 (Y t-1 – Y t-2 )
Это авторегрессионная модель первого порядка с одним порядком несезонного дифференцирования и постоянный член, т. е. модель ARIMA(1,1,0).
АРИМА(0,1,1)
без константы = простое экспоненциальное сглаживание: Другая стратегия
для исправления автокоррелированных ошибок в модели случайного блуждания предлагается
простая модель экспоненциального сглаживания. Напомним, что для некоторого нестационарного времени
серии (например, те, которые демонстрируют шумовые флуктуации вокруг медленно меняющейся
среднее значение), модель случайного блуждания работает не так хорошо, как скользящее среднее
прошлые ценности. Другими словами, вместо того, чтобы принимать самое последнее наблюдение за
прогноз следующего наблюдения лучше использовать средний из
несколько последних наблюдений, чтобы отфильтровать шум и точнее
оценить местное среднее значение. Простая модель экспоненциального сглаживания использует экспоненциально.
взвешенное скользящее среднее прошлых значений для достижения этого эффекта.
уравнение прогноза для простой модели экспоненциального сглаживания может быть записано
в ряде математических
эквивалентные формы, одной из которых является так называемая «коррекция ошибок»
форма, в которой предыдущий прогноз корректируется в сторону ошибки
получилось:
Простая модель экспоненциального сглаживания использует экспоненциально.
взвешенное скользящее среднее прошлых значений для достижения этого эффекта.
уравнение прогноза для простой модели экспоненциального сглаживания может быть записано
в ряде математических
эквивалентные формы, одной из которых является так называемая «коррекция ошибок»
форма, в которой предыдущий прогноз корректируется в сторону ошибки
получилось:
Ŷ t = Ŷ t-1 + αe t-1
Потому что e т-1 = Y т-1 – Ŷ т-1 по Определение, это может быть переписано как:
ŷ T = Y T-1 -(1-α) E T-1
= Y T-1 -θ 1 E-1 -θ 1 E-1 -θ 1 7. т-1
который
уравнение прогнозирования ARIMA(0,1,1) без констант с θ 1 = 1-α. Это означает, что вы можете установить простой
экспоненциальное сглаживание, указав его как модель ARIMA(0,1,1) без
постоянна, а расчетный коэффициент MA(1) соответствует 1-минус-альфа в
Формула СЭС. Напомним, что в
Модель СЕС, средний возраст данные в прогнозах на 1 период вперед равны 1/α, что означает, что они
будет иметь тенденцию отставать от тенденций или точек разворота примерно на 1/α периода. Отсюда следует, что средний возраст
данные в прогнозах на 1 период вперед модели ARIMA(0,1,1) без констант
равно 1/(1-θ 1 ).
Так, например, если θ 1 = 0,8,
средний возраст — 5 лет. Поскольку θ 1 приближается к 1,
Модель ARIMA(0,1,1) без констант становится очень долгосрочной скользящей средней,
а так как θ 1 приближается к 0 ит
становится моделью случайного блуждания без дрейфа.
Напомним, что в
Модель СЕС, средний возраст данные в прогнозах на 1 период вперед равны 1/α, что означает, что они
будет иметь тенденцию отставать от тенденций или точек разворота примерно на 1/α периода. Отсюда следует, что средний возраст
данные в прогнозах на 1 период вперед модели ARIMA(0,1,1) без констант
равно 1/(1-θ 1 ).
Так, например, если θ 1 = 0,8,
средний возраст — 5 лет. Поскольку θ 1 приближается к 1,
Модель ARIMA(0,1,1) без констант становится очень долгосрочной скользящей средней,
а так как θ 1 приближается к 0 ит
становится моделью случайного блуждания без дрейфа.
Как лучше всего исправить
автокорреляция: добавление терминов AR или добавление терминов MA? В двух предыдущих моделях, рассмотренных выше,
проблема автокоррелированных ошибок в модели случайного блуждания была исправлена в двух
различными способами: путем добавления запаздывающего
значение разностного ряда к уравнению или добавление запаздывающего значения
ошибка прогноза. Какой подход
лучший? Эмпирическое правило для этого
Ситуация, которая будет обсуждаться более подробно позже, состоит в том, что положительная автокорреляция обычно лучше
лечится добавлением члена AR к модели, а отрицательная автокорреляция обычно лучше всего лечится добавлением MA
срок. В деловое и экономическое время
ряд, отрицательный автокорреляция
часто возникает как артефакт
разность . (В общем,
разность уменьшает положительную автокорреляцию и может даже вызвать переход от
положительной к отрицательной автокорреляции.)
Так, модель ARIMA(0,1,1), в которой дифференцирование сопровождается
Термин MA используется чаще, чем модель ARIMA(1,1,0).
Какой подход
лучший? Эмпирическое правило для этого
Ситуация, которая будет обсуждаться более подробно позже, состоит в том, что положительная автокорреляция обычно лучше
лечится добавлением члена AR к модели, а отрицательная автокорреляция обычно лучше всего лечится добавлением MA
срок. В деловое и экономическое время
ряд, отрицательный автокорреляция
часто возникает как артефакт
разность . (В общем,
разность уменьшает положительную автокорреляцию и может даже вызвать переход от
положительной к отрицательной автокорреляции.)
Так, модель ARIMA(0,1,1), в которой дифференцирование сопровождается
Термин MA используется чаще, чем модель ARIMA(1,1,0).
АРИМА(0,1,1)
с константой = простое экспоненциальное сглаживание с ростом: Путем реализации
модель SES как модель ARIMA, вы действительно получаете некоторую гибкость. Первый из
всего расчетный коэффициент MA(1) может быть отрицательным : это
соответствует коэффициенту сглаживания больше 1 в модели SES, т. е.
обычно не допускается процедурой подбора модели SES. Во-вторых, у вас есть
возможность включения постоянного члена в модель ARIMA, если хотите, чтобы
оценить средний ненулевой тренд. Модель ARIMA(0,1,1) с константой имеет уравнение прогноза:
е.
обычно не допускается процедурой подбора модели SES. Во-вторых, у вас есть
возможность включения постоянного члена в модель ARIMA, если хотите, чтобы
оценить средний ненулевой тренд. Модель ARIMA(0,1,1) с константой имеет уравнение прогноза:
Ŷ t = μ + Y t-1 – θ 1 e t-1
прогнозы на один период вперед по этой модели качественно аналогичны модели SES, за исключением того, что траектория долгосрочных прогнозов обычно это наклонная линия (наклон которой равен mu), а не горизонтальная линия.
АРИМА(0,2,1)
или (0,2,2) без константы = линейное экспоненциальное сглаживание: Линейная экспоненциальная
модели сглаживания – это модели ARIMA, в которых используется два несезонные различия в сочетании с терминами MA. Второе отличие от
серия Y — это не просто
разница между Y
и сам отстал на два периода, а скорее это первая разница
первая разность — т. е. изменение-в-изменении Y в период t. Таким образом, вторая разница Y в период t равна (Y т – Y т-1 ) – (Y т-1 – Y t-2 ) = Y t – 2Y t-1 +
Y т-2 . Второе отличие дискретного
аналогична второй производной непрерывной функции: она
измеряет «ускорение» или «кривизну» в функции
в данный момент времени.
Таким образом, вторая разница Y в период t равна (Y т – Y т-1 ) – (Y т-1 – Y t-2 ) = Y t – 2Y t-1 +
Y т-2 . Второе отличие дискретного
аналогична второй производной непрерывной функции: она
измеряет «ускорение» или «кривизну» в функции
в данный момент времени.
Модель ARIMA(0,2,2) без константы предсказывает, что вторая разность ряд равен линейной функции двух последних ошибок прогноза:
× т – 2Y t -1 + Y t-2 = – θ 1 e t-1 – θ 2 e t-2
который может переставить:
ŷ T = 2 Y T -1 – Y T -2 – θ 1 E -2 – θ 1 E -2 – θ 1 E -2 – θ 1 E -2 -θ -2
где
θ 1 и θ 2 – коэффициенты MA(1) и MA(2). это вообще модель линейного экспоненциального сглаживания , по существу такая же, как
Модель Холта и модель Брауна представляют собой частный случай. Он использует экспоненциально взвешенный
скользящие средние для оценки как локальных
уровень и локальный тренд в
ряд. Долгосрочные прогнозы
этой модели сходятся к прямой линии, наклон которой зависит от среднего
Тенденция наблюдается к концу серии.
это вообще модель линейного экспоненциального сглаживания , по существу такая же, как
Модель Холта и модель Брауна представляют собой частный случай. Он использует экспоненциально взвешенный
скользящие средние для оценки как локальных
уровень и локальный тренд в
ряд. Долгосрочные прогнозы
этой модели сходятся к прямой линии, наклон которой зависит от среднего
Тенденция наблюдается к концу серии.
АРИМА(1,1,2) без константы = линейное экспоненциальное сглаживание с затухающим трендом :
Ŷ t = Y t-1 +
ϕ 1 (Y т-1 – Y т-2 ) – θ 1 e т-1 – θ 1 e 0390 3090 390 90 90 т-1
проиллюстрировано на прилагаемых слайдах
на моделях ARIMA. Это
экстраполирует локальный тренд в конце ряда, но сглаживает его в
более длительные горизонты прогнозирования, чтобы внести нотку консерватизма, практику, которая
имеет эмпирическую поддержку. См.
статью «Почему
затухающий тренд работает”
Гарднер и Маккензи и «золотое правило»
статья Армстронга и др. для деталей.
См.
статью «Почему
затухающий тренд работает”
Гарднер и Маккензи и «золотое правило»
статья Армстронга и др. для деталей.
Это в целом рекомендуется придерживаться моделей, в которых хотя бы одно из p и q отсутствует. больше 1, т. е. не пытайтесь подогнать такую модель, как ARIMA(2,1,2), так как это может привести к переоснащению и проблемам с «общим фактором», которые подробнее в примечаниях к математическому структура моделей ARIMA.
Электронная таблица
реализация: АРИМА
модели, подобные описанным выше, легко реализовать в электронной таблице.
Уравнение прогноза — это просто линейное уравнение, которое относится к прошлым значениям.
исходного временного ряда и прошлых значений ошибок. Таким образом, вы можете настроить
Электронная таблица прогнозирования ARIMA, сохраняя данные в столбце A, прогнозирование
формулу в столбце B, а ошибки (данные минус прогнозы) в столбце C.
формула прогнозирования в типичной ячейке в столбце B будет просто линейной
выражение, относящееся к значениям в предыдущих строках столбцов A и C, умноженное
соответствующими коэффициентами AR или MA, хранящимися в ячейках в другом месте на
электронная таблица.

