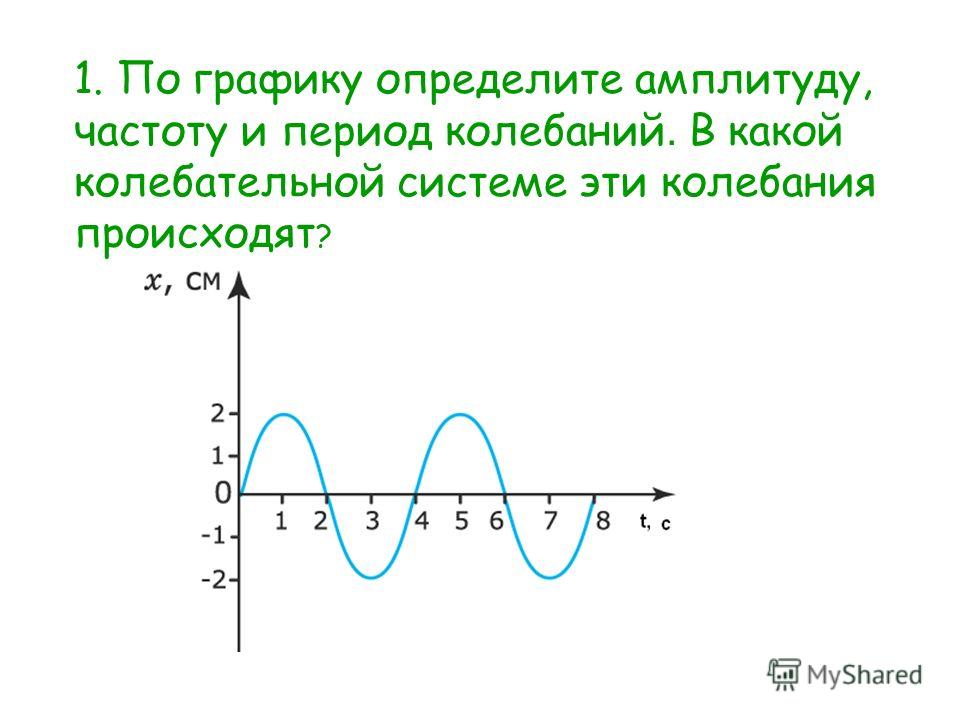
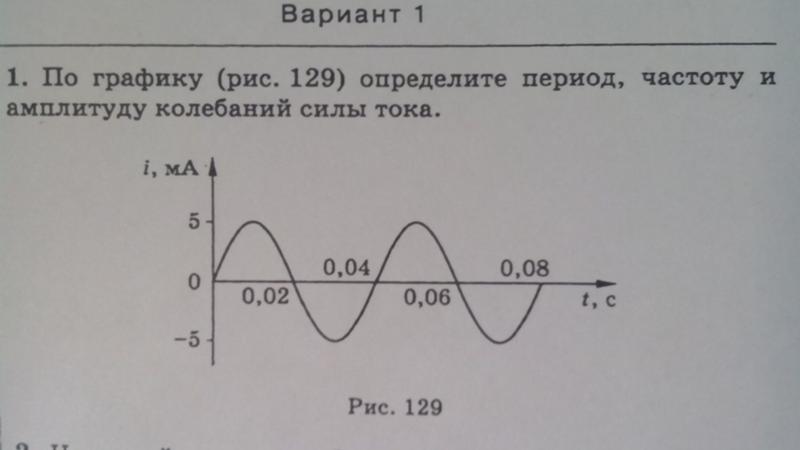
Амплитуда колебаний и период: Амплитуда, частота, период колебаний — урок. Физика, 9 класс.
alexxlab | 08.10.1985 | 0 | Разное
Гармонические колебания. Амплитуда, период и частота колебательного движения
В рамках прошлой темы говорилось о новом виде механического движения – колебательном движении.
Механическое колебательное движение —это движение, при котором состояния тела с течением времени повторяются, причем тело проходит через положение устойчивого равновесия поочередно в противоположных направлениях.
Если колебания происходят в системе только под действием внутренних сил, то такие колебания называют свободными.
Колебательной системой называют такую физическую систему, в которой при отклонении от положения равновесия возникают и существуют колебания.
Маятник – это твердое тело, совершающее под действием приложенных сил колебания около неподвижной точки или вокруг оси.
В рамках данной темы будет рассмотрен простейший вид колебательного движения — гармонические колебания.
Гармонические
колебания — это колебания, при которых смещение колеблющейся
точки от положения равновесия изменяется с течением времени по закону синуса
или косинуса.
Смещение от положения равновесия при гармонических колебаниях описывается уравнениями вида:
Эти уравнения называют кинематическим законом гармонического движения.
Покажем, что гармонические колебания действительно подчиняются закону синуса или косинуса. Для этого рассмотрим следующую установку.
Возьмем нитяной маятник, а в качестве груза к нему выберем небольшой массивный сосуд с маленьким отверстием снизу и насыплем в него песок.А под полученную систему положим длинную бумажную ленту.
Если ленту перемещать с постоянной скоростью в направлении, перпендикулярном плоскости колебаний, то на ней останется волнообразная дорожка из песка, каждая точка которой соответствует положению колеблющегося груза в тот момент, когда он проходил над ней. Из опыта видно, что след, который оставляет песок на листе бумаги, есть некая кривая.
Она называется синусоидой. Из курса математики старших классов вы узнаете о том, что аналогичные графики имеют функции типа
Значит,
графически зависимость смещения колеблющейся точки от времени изображается
синусоидой или косинусоидой.
Через точки, соответствующие положению равновесия маятника, проведена ось времени t, а перпендикулярно ей — ось смещения икс. График дает возможность приблизительно определить координату груза в любой момент времени.
Теперь разберемся с величинами, входящими в уравнение колебательного движения.
Смещение — величина, характеризующая положение колеблющейся точки в некоторый момент времени относительно положения равновесия и измеряемая расстоянием от положения равновесия до положения точки в данный момент времени.
Амплитуда колебаний — максимальное смещение тела от положения равновесия.
Циклическая, или круговая частота, показывающая, сколько колебаний совершает тело за 2p секунд.
j0 — это начальная фаза колебаний.
Фаза
колебаний — это аргумент периодической функции, который при
заданной амплитуде колебаний определяет состояние колебательной системы в любой
момент времени.
Промежуток времени, в течение которого тело совершает одно полное колебание, называется периодом колебаний.
Период колебаний обычно обозначается буквой Т и в системе СИ измеряется в секундах.
Число колебаний в единицу времени называется частотой колебаний. Обозначается частота буквой ν. За единицу частоты принято одно колебание в секунду. Эта единица названа в честь немецкого ученого Генриха Герца.
Период колебания и частота колебаний связаны следующей зависимостью:
Т.е. частота — это величина обратная периоду и равная числу полных колебаний, совершаемых за 1 секунду.
Циклическая частота также связана с периодом колебаний или частотой. Эту связь математически можно записать в следующем виде:
Таким
образом, любое колебательное движение характеризуется амплитудой, частотой
(или периодом) и фазой колебаний.
При совершении телом гармонических колебаний не только его координата, но и такие величины, как сила, ускорение, скорость, тоже изменяются по закону синуса или косинуса.
Это следует из известных вам законов и формул, в которых указанные величины попарно связаны прямо пропорциональной зависимостью, например законом Гука или вторым законом Ньютона. Из этих формул видно, что сила и ускорение достигают наибольших значений, когда колеблющееся тело находится в крайних положениях, где смещение наиболее велико, и равны нулю, когда тело проходит через положение равновесия.
Что же касается скорости, то она, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия достигает наибольшего значения.
Колебания,
практически близкие к гармоническим, совершает тяжелый шарик, подвешенный на
легкой и малорастяжимой нити, длина которой значительно больше диаметра шарика. Такую колебательную систему называют математическим маятником.
Такую колебательную систему называют математическим маятником.
Математический маятник — это материальная точка, подвешенная на невесомой нерастяжимой нити, прикрепленной к подвесу и находящейся в поле силы тяжести.
Также гармонические колебания может совершать груз подвешенный на пружине, совершающий колебания в вертикальной плоскости. Такую колебательную систему называют пружинным маятником — это система, состоящая из материальной точки массой m и пружины.
Основные выводы:
– Гармонические колебания — это колебания, при которых смещение колеблющейся точки от положения равновесия изменяется с течением времени по закону синуса или косинуса.
– Любое колебательное движение характеризуется амплитудой, частотой (или периодом) и фазой колебаний.
– Амплитуда колебаний — максимальное смещение тела от положения равновесия.
– Промежуток времени, в течение которого тело совершает одно полное колебание, называется

– Число колебаний в единицу времени называется частотой колебаний.
– Фаза колебаний — это аргумент периодической функции, который при заданной амплитуде колебаний определяет состояние колебательной системы в любой момент времени.
– Математический и пружинный маятники — это простейшие идеализированные колебательные системы, подчиняющиеся закону синуса или косинуса.
– Математический маятник — это материальная точка, подвешенная на невесомой нерастяжимой нити, прикрепленной к подвесу и находящейся в поле силы тяжести.
– Пружинный маятник — это система, состоящая из материальной точки массой m и пружины, которая совершает колебания в вертикальной плоскости.
Период, частота, амплитуда и фаза переменного тока
Период и частота переменного тока
Время, в течение которого совершается одно полное изменение ЭДС, то есть один цикл колебания или один полный оборот радиуса-вектора, называется периодом колебания переменного тока (рисунок 1).
Рисунок 1. Период и амплитуда синусоидального колебания. Период – время одного колебания; Аплитуда – его наибольшее мгновенное значение.
Период выражают в секундах и обозначают буквой Т.
Так же используются более мелкие единицы измерения периода это миллисекунда (мс)- одна тысячная секунды и микросекунда (мкс)- одна миллионная секунды.
1 мс =0,001сек =10-3сек.
1 мкс=0,001 мс = 0,000001сек =10-6сек.
1000 мкс = 1 мс.
Число полных изменений ЭДС или число оборотов радиуса-вектора, то есть иначе говоря, число полных циклов колебаний, совершаемых переменным током в течение одной секунды, называется частотой колебаний переменного тока.
Частота обозначается буквой f и выражается в периодах в секунду или в герцах.
Одна тысяча герц называется килогерцом (кГц), а миллион герц — мегагерцом (МГц). Существует так же единица гигагерц (ГГц) равная одной тысячи мегагерц.
1000 Гц = 103 Гц = 1 кГц;
1000 000 Гц = 106 Гц = 1000 кГц = 1 МГц;
1000 000 000 Гц = 109 Гц = 1000 000 кГц = 1000 МГц = 1 ГГц;
Чем быстрее происходит изменение ЭДС, то есть чем быстрее вращается радиус-вектор, тем меньше период колебания Чем быстрее вращается радиус-вектор, тем выше частота. Таким образом, частота и период переменного тока являются величинами, обратно пропорциональными друг другу. Чем больше одна из них, тем меньше другая.
Математическая связь между периодом и частотой переменного тока и напряжения выражается формулами
Например, если частота тока равна 50 Гц, то период будет равен:
Т = 1/f = 1/50 = 0,02 сек.
И наоборот, если известно, что период тока равен 0,02 сек, (T=0,02 сек.), то частота будет равна:
f = 1/T=1/0,02 = 100/2 = 50 Гц
Частота переменного тока, используемого для освещения и промышленных целей, как раз и равна 50 Гц.
Частоты от 20 до 20 000 Гц называются звуковыми частотами.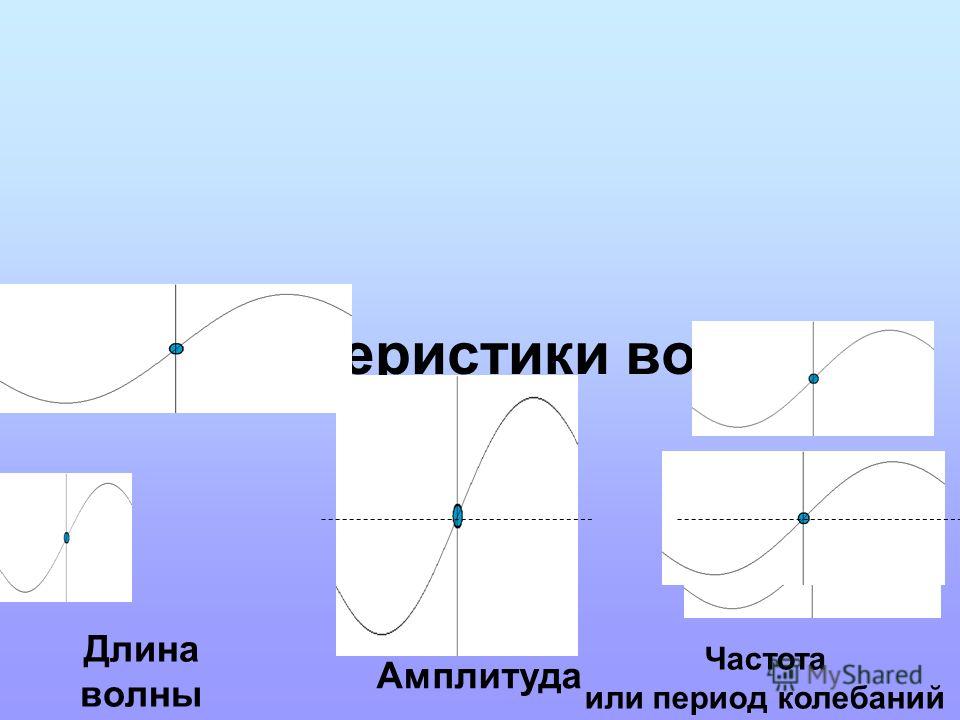 Токи в антеннах радиостанций колеблются с частотами до 1 500 000 000 Гц или, иначе говоря, до 1 500 МГц или 1,5 ГГц. Такие высокие частоты называются радиочастотами или колебаниями высокой частоты.
Токи в антеннах радиостанций колеблются с частотами до 1 500 000 000 Гц или, иначе говоря, до 1 500 МГц или 1,5 ГГц. Такие высокие частоты называются радиочастотами или колебаниями высокой частоты.
Наконец, токи в антеннах радиолокационных станций, станций спутниковой связи, других спецсистем (например ГЛАНАСС, GPS) колеблются с частотами до 40 000 МГц (40 ГГц) и выше.
Амплитуда переменного тока
Наибольшее значение, которого достигает ЭДС или сила тока за один период, называется амплитудой ЭДС или силы переменного тока. Легко заметить, что амплитуда в масштабе равна длине радиуса-вектора. Амплитуды тока, ЭДС и напряжения обозначаются соответственно буквами Im, Em и Um (рисунок 1).
Угловая (циклическая) частота переменного тока.
Скорость вращения радиуса-вектора, т. е. изменение величины угла поворота в течение одной секунды, называется угловой (циклической) частотой переменного тока и обозначается греческой буквой ? (омега). Угол поворота радиуса-вектора в любой данный момент относительно его начального положения измеряется обычно не в градусах, а в особых единицах — радианах.
Угол поворота радиуса-вектора в любой данный момент относительно его начального положения измеряется обычно не в градусах, а в особых единицах — радианах.
Радианом называется угловая величина дуги окружности, длина которой равна радиусу этой окружности (рисунок 2). Вся окружность, составляющая 360°, равна 6,28 радиан, то есть 2.
Рисунок 2. Радиан.
Тогда,
1рад = 360°/2
Следовательно, конец радиуса-вектора в течение одного периода пробегают путь, равный 6,28 радиан (2). Так как в течение одной секунды радиус-вектор совершает число оборотов, равное частоте переменного тока f, то за одну секунду его конец пробегает путь, равный 6,28 * f радиан. Это выражение, характеризующее скорость вращения радиуса-вектора, и будет угловой частотой переменного тока — ?.
Итак,
?= 6,28*f = 2f
Фаза переменного тока.
Угол поворота радиуса-вектора в любое данное мгновение относительно его начального положения называется фазой переменного тока. Фаза характеризует величину ЭДС (или тока) в данное мгновение или, как говорят, мгновенное значение ЭДС, ее направление в цепи и направление ее изменения; фаза показывает, убывает ли ЭДС или возрастает.
Фаза характеризует величину ЭДС (или тока) в данное мгновение или, как говорят, мгновенное значение ЭДС, ее направление в цепи и направление ее изменения; фаза показывает, убывает ли ЭДС или возрастает.
Рисунок 3. Фаза переменного тока.
Полный оборот радиуса-вектора равен 360°. С началом нового оборота радиуса-вектора изменение ЭДС происходит в том же порядке, что и в течение первого оборота. Следовательно, все фазы ЭДС будут повторяться в прежнем порядке. Например, фаза ЭДС при повороте радиуса-вектора на угол в 370° будет такой же, как и при повороте на 10°. В обоих этих случаях радиус-вектор занимает одинаковое положение, и, следовательно, мгновенные значения ЭДС будут в обоих этих случаях одинаковыми по фазе.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Определения по колебаниям и волнам
АВТОКОЛЕБАНИЯ – незатухающие колебания физической системы, которые поддерживаются источником энергии, находящимся в самой системе. Амплитуда и период А.К. определяются свойствами системы.
Амплитуда и период А.К. определяются свойствами системы.
АМПЛИТУДА КОЛЕБАНИЙ – наибольшее значение xm, которого достигает физическая величина х (смещение, сила тока, напряженность электрического поля и т.д.), совершающая гармонические колебания, т. е. изменяющаяся по закону x= xmсоs(ω.t+ φ), где t – время, xm, ω, φ – постоянные (при гармонических колебаниях) величины. Другими словами А. определяет “размах” колебаний. В этом смысле термин А. может применяться к негармоническим колебаниям.
БЕГУЩИЕ ВОЛНЫ – волны, переносящие энергию вдоль направления их распространения. (Ср.стоячие волны).
ВОЛНОВАЯ ПОВЕРХНОСТЬ – совокупность точек среды, в которых в данный момент времени фаза волны имеет одно и то же значение.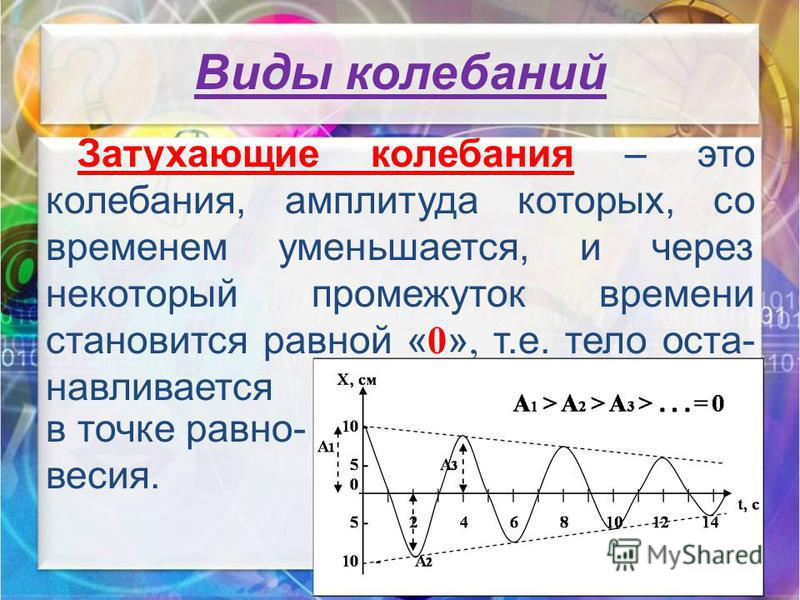
ВОЛНЫ – возмущения (изменения состояния среды или поля), распространяющиеся в пространстве с конечной скоростью. Распространение волн связано с переносом энергии без переноса вещества, при этом возможны явления отражения, преломления, дисперсии, интерференции. дифракции, поляризации, поглощения и рассеяния волн. (См. упругие волны, электромагнитные волны).
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ –колебания, возникающие в какой-либо системе под влиянием переменного внешнего воздействия. Характер их определяется как свойствами внешнего воздействия, так и свойствами самой системы. Если частота внешнего воздействия приближается к частоте собственных колебаний системы, то амплитуда В.К. резко возрастает – наступает резонанс. Ср.собственные колебания.
ВЫСОТА ЗВУКА – качество (характеристика) звука, определяемое человеком по восприятию (субъективно) и связанное с частотой звука. С ростом частоты В.з. увеличивается.
ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ – процесс периодических изменений во времени физической величины, для математического описания которого используются гармонические функции синус или косинус: или .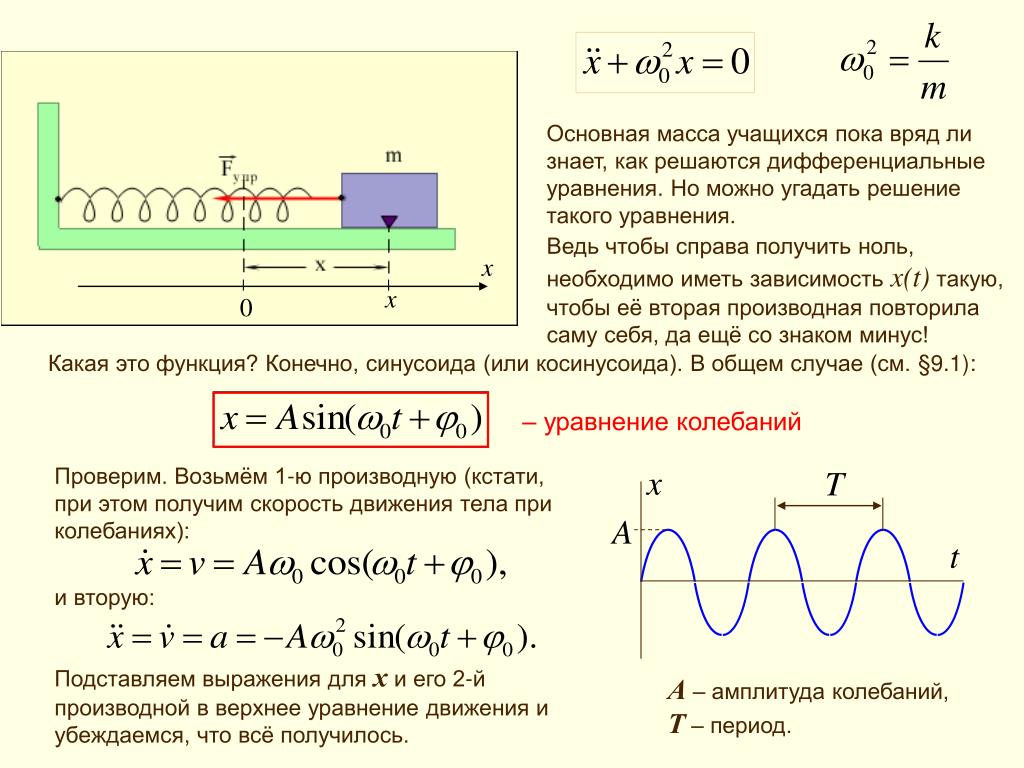 По гармоническому закону могут изменяться смещение тела от положения равновесия, величина электрического заряда, напряженность поля, сила тока и т.д. Любое сложное колебание можно представить как сумму гармонических колебаний.
По гармоническому закону могут изменяться смещение тела от положения равновесия, величина электрического заряда, напряженность поля, сила тока и т.д. Любое сложное колебание можно представить как сумму гармонических колебаний.
ГИПЕРЗВУК – упругие волны с частотой, превышающей 109 Гц. Верхний предел частоты Г. в кристаллах и жидкостях (1012-1013 Гц.), в газах (109 Гц.) соответствует частотам, при которых длина волны Г. соизмерима с межмолекулярными расстояниями, а в газах – со средней длиной свободного пробега молекул. См. такжезвук, инфразвук, ультразвук
ГРОМКОСТЬ ЗВУКА – качество (характеристика) звука, определяемая человеком по восприятию (субъективно) и связанное с амплитудой звуковых колебаний и частотой звука.
ДАВЛЕНИЕ ЗВУКА – среднее по времени избыточное давление, которое испытывает препятствие, помещенное в поле звуковой волны.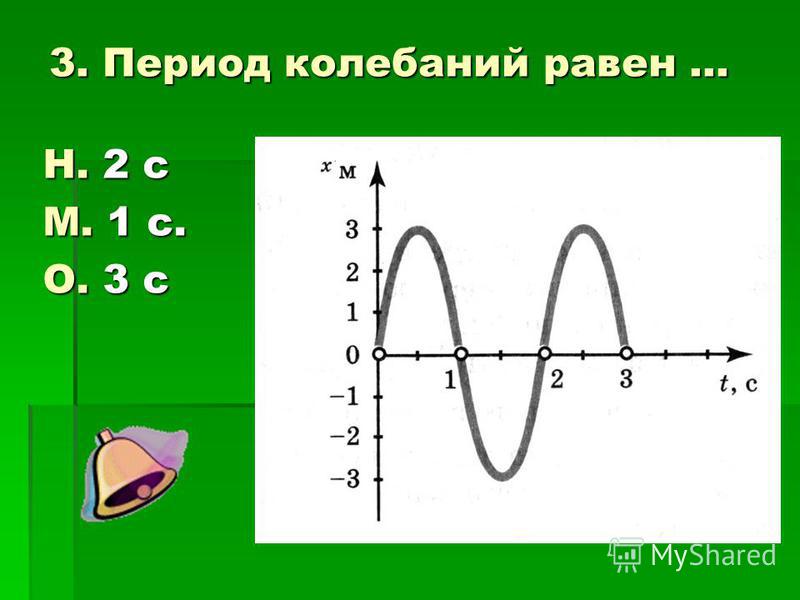 Скалярная величина, равная отношению импульса, передаваемого звуковой волной поверхности препятствия, к площади этой поверхности и времени, в течение которого происходила передача импульса. Ср. звуковое давление.
Скалярная величина, равная отношению импульса, передаваемого звуковой волной поверхности препятствия, к площади этой поверхности и времени, в течение которого происходила передача импульса. Ср. звуковое давление.
ДИСПЕРСИЯ ВОЛН – зависимость фазовой скорости гармонических (синусоидальных) волн в веществе от их частоты.
ДИФРАКЦИЯ ВОЛН – явление огибания волнами встречных препятствий. Под Д.в. понимают как нарушение прямолинейности распространения волн, так и сопутствующие ему интерференционные явления (см. интерференция волн).
ДЛИНА ВОЛНЫ – физическая величина, характеризующая синусоидальную (гармоническую) волну, равная расстоянию между двумя ближайшими точками среды, разность фаз волны в которых равна 2π. Д.в. l связана с частотой колебаний ν и фазовой скоростью ω соотношением λ=TV.
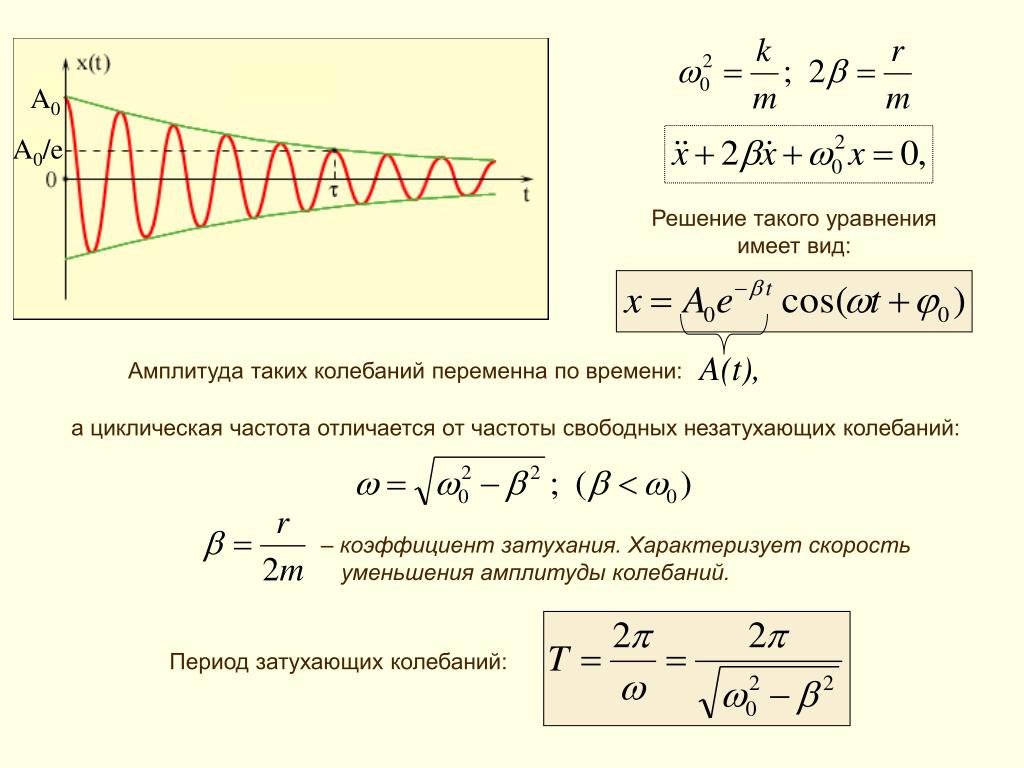
ЗАТУХАНИЕ КОЛЕБАНИЙ – постепенное ослабевание собственных колебаний, обусловленное потерями энергии колебательной системой. З.к. приводит к уменьшению амплитуды колебаний.
З.к. приводит к уменьшению амплитуды колебаний.
ЗВУК (звуковые волны) – упругие волны, распространяющиеся в твердых, жидких и газообразных средах. В зависимости от частоты колебаний З. условно подразделяется на инфразвук (частотой до 16 Гц), слышимый звук (16 Гц – 20 кГц), ультразвук (20 кГц – 1 ГГц) и гиперзвук (более 1 ГГц).
ЗВУКОВОЕ ДАВЛЕНИЕ – переменное давление, избыточное над равновесным, возникающее при прохождении звуковой волны в жидкой или газообразной среде.
ИЗЛУЧЕНИЕ – 1) И. волн и частиц – процесс испускания звуковых волн источниками звука, радиоволн – антеннами, света и рентгеновских лучей – атомами и молекулами, α-, β-частиц и γ-лучей атомными ядрами. 2) Сами эти волны и частицы как движущиеся объекты. (См. Альфа-лучи, Бета-лучи и т.д.)
ИНТЕНСИВНОСТЬ ВОЛНЫ, плотность потока излучения – физическая величина, равная при равномерном распределении энергии излучения отношению мощности волны, к площади волнового фронта. Единица в СИ – .
Единица в СИ – .
ИНТЕНСИВНОСТЬ ЗВУКА, сила звука – физическая величина, равная отношению энергии, переносимой звуковой волной через поверхность, расположенную перпендикулярно к направлению распространения волны, к площади поверхности и промежутку времени, в течение которого происходил процесс. Единица И.з. в СИ – .
ИНТЕРФЕРЕНЦИЯ ВОЛН – явление наложения двух или нескольких волн, при котором в пространстве происходит перераспределение энергии результирующей волны. Если волны когерентны, то в пространстве получается устойчивое во времени распределение амплитуд с чередующимися максимумами и минимумами (интерференционная картина). Имеет место для всех волн независимо от их природы. Ср.дифракция волн.
ИНФРАЗВУК– упругие волны с частотой менее 16 Гц, которые не воспринимаются ухом человека. Источники И.: газовые разряды в атмосфере, ветер, колебания земной коры и поверхности моря. См. звук, ультразвук, гиперзвук.
КОГЕРЕНТНОСТЬ – согласованное протекание во времени нескольких колебательных или волновых процессов. Когерентными наз. колебания с одинаковой частотой (длиной волны) и постоянной разностью фаз. К.- необходимое условие возникновения интерференции (см.интерференция волн, интерференция света).
КОЛЕБАНИЯ – движения (изменения состояния), характеризующиеся той или иной степенью повторяемости во времени. Различают К.: механические (К. маятников, струн, пластин, замкнутых объемов воздуха и т.д.), электромагнитные (К. электрического тока и напряжения в колебательном контуре или волноводе, переменный ток и т.д.) и электромеханические (К. пьезоэлектрических и магнитострикционных излучателей и т.д.). Простейшие периодические колебания – гармонические колебания.
КОЛЕБАТЕЛЬНАЯ СИСТЕМА – система тел, способная совершать свободные колебания. Признаки К.с. – наличие положения устойчивого равновесия, малое трение (электрическое сопротивление).
МАЯТНИК – твердое тело (или система тел), способное совершать колебания около неподвижной точки или оси. См. математический маятник, физический маятник.
МАЯТНИК МАТЕМАТИЧЕСКИЙ – идеализированный объект: колебательная система, состоящая изматериальной точки, подвешенная к неподвижной точке на невесомой нерастяжимой нити (или стержне) и центра тяготения (напр., Земли). М.м. совершает колебания в вертикальной плоскости. При малых колебаниях период колебаний М.м. не зависит от амплитуды и выражается формулой , где ℓ – длина нити, а g – ускорение свободного падения. Ср.маятник пружинный.
МАЯТНИК ПРУЖИННЫЙ – идеализированный объект: колебательная система, состоящая изматериальной точки, прикрепленной к концу невесомой пружины. При малых колебаниях период колебаний М.п. не зависит от амплитуды и выражается формулой , где m– масса материальной точки, k– жесткость пружины. Ср. маятник математический.
Ср. маятник математический.
МИКРОФОН – устройство для преобразования звуковых колебаний в электрические.
ОТРАЖЕНИЕ ЗВУКА – процесс возвращения звуковой волны при ее встрече с границей раздела двух сред, имеющих различную плотность и сжимаемость, обратно в первоначальную среду. Одно из проявлений о.з. – эхо.
ОТРАЖЕНИЯ ВОЛН ЗАКОН – луч падающий, луч отраженный и перпендикуляр, восставленный в точку падения луча, лежат в одной плоскости, причем угол падения равен углу преломления. Закон справедлив для зеркального отражения.
ПЕРИОД – наименьший промежуток времени, по истечении которого повторяются значения физических величин, характеризующих данный периодический процесс (напр., период колебаний).
ПОПЕРЕЧНАЯ ВОЛНА – волна, распространяющаяся в направлении, перпендикулярном к плоскости, в которой колеблются частицы среды (для упругой волны) или в которой расположены векторы электрической напряженности и магнитной индукции (для электромагнитной волны). Ср. продольная волна.
Ср. продольная волна.
РЕЗОНАНС – явление более или менее резкого возрастания амплитуды установившихся вынужденных колебаний, когда частота внешнего воздействия приближается к частоте собственных колебаний системы.
РЕЗОНАТОР – система (тело или специальное устройство), в которой может происходить резонанс. Примеры Р.: камертон, воздушная полость (акустический Р.), колебательный контур (электрический резонатор).
СВОБОДНЫЕ КОЛЕБАНИЯ (собственные колебания)
СДВИГ ФАЗ – разность фаз переменных физических величин, изменяющихся по синусоидальному закону с одинаковой частотой. Измеряется в радианах.
СКОРОСТЬ ЗВУКА – скорость распространения звуковых волн в среде. В газах с.з. меньше, чем в жидкостях, а в жидкостях меньше, чем в твердых телах. В воздухе при нормальных условиях с.з. 330 м/с, в воде – 1500 м/с, в тв. телах 2000 – 6000 м/с.
СОБСТВЕННЫЕ КОЛЕБАНИЯ, свободные колебания – колебания, возникающие в колебательной системе, которая не подвергается переменным внешним воздействиям, вследствие какого-либо начального отклонения этой системы от состояния устойчивого равновесия. В реальных макроскопических системах из-за потери энергии с.к. всегда затухают.
В реальных макроскопических системах из-за потери энергии с.к. всегда затухают.
СТОЯЧИЕ ВОЛНЫ – колебания в резонаторе (струне, мембране, камертоне и т.п.), характеризующиеся чередованием максимумов (пучностей) и минимумов (узлов) амплитуды. Возникают в результате интерференции двух бегущих волн, амплитуда которых одинакова, а направления распространения взаимно противоположны.
ТЕМБР звука – качественная субъективная оценка звука, издаваемого музыкальным инструментом, звуковоспроизводящим устройством или голосовым аппаратом людей и животных. Характеризует оттенок звучания и зависит от того, какие обертоны сопутствуют основному тону и каковы их интенсивность.
УПРУГИЕ ВОЛНЫ – механические возмущения (деформации), распространяющиеся в среде, обладающей упругостью. В жидкостях и газах могут образовываться только продольные у.в., при которых среда испытывает только деформацию сжатия (растяжения) и частицы среды колеблются вдоль направления распространения волены. В твердых телах возникают как продольные, так и поперечные у.в. При поперечных у.в. среда испытывает деформацию сдвига, и частицы среды колеблются в направлениях, перпендикулярных направлению распространения волны.
В твердых телах возникают как продольные, так и поперечные у.в. При поперечных у.в. среда испытывает деформацию сдвига, и частицы среды колеблются в направлениях, перпендикулярных направлению распространения волны.
ФАЗА КОЛЕБАНИЙ – физическая величина, применяемая для описания состояния периодического колебательного процесса в каждый момент времени: , где ω – угловая частота, φ0– значение фазы в начальный момент времени (начальная фаза). Выражается в угловых единицах (напр., радианах) или долях периода колебаний.
ФРОНТ ВОЛНЫ – см. волновая поверхность.
ЧАСТОТА КОЛЕБАНИЙ – физическая величина, равная отношению числа полных колебаний, совершаемых телом, к промежутку времени, за которое они совершены. Применяется для описания колебательного процесса. Обратно пропорциональна периоду колебаний. Единица в СИ – Герц.
ЭХО – волна, отраженная от какого-либо препятствия и принятая наблюдателем (приемником).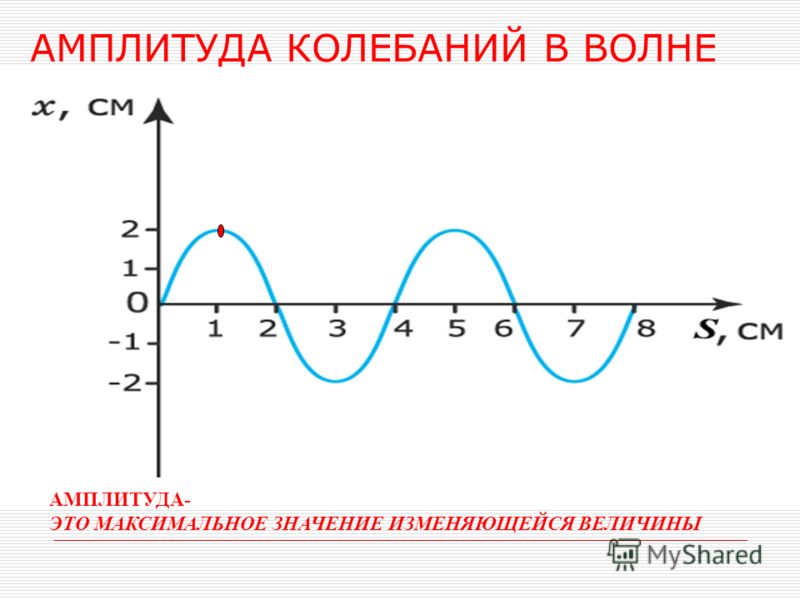 Радиоэхо используют в радиолокации, звуковое эхо – в гидролокации.
Радиоэхо используют в радиолокации, звуковое эхо – в гидролокации.
Амплитуда колебаний – определение, характеристика и формулы
Амплитуда колебаний – это максимальное значение отклонения от нулевой точки. В физике данный процесс анализируется в разных разделах.
Он изучается при механических, звуковых и электромагнитных колебаниях. В перечисленных случаях амплитуда измеряется по-разному и по своим законам.
Содержание
- Амплитуда колебаний
- Период колебаний
- Частота колебаний
- Циклическая частота
- Как определить амплитуду, период и частоту колебаний по графику
Амплитуда колебаний
Амплитудой колебания называют максимальную отдаленную точку нахождения тела от положения равновесия. В физике она обозначается буквой А и измеряется в метрах.
За амплитудой можно наблюдать на простом примере пружинного маятника.
В идеальном случае, когда игнорируется сопротивление воздушного пространства и трение пружинного устройства, устройство будет колебаться бесконечно.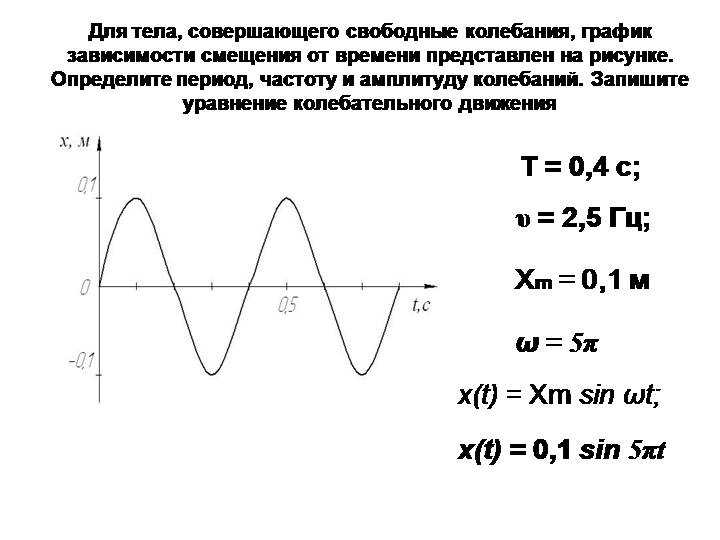 Описание движения выполняется с помощью функций cos и sin:
Описание движения выполняется с помощью функций cos и sin:
x(t) = A * cos(ωt + φ0) или x(t) = A * sin(ωt + φ0),
где
величина А – это амплитуда свободных движений груза на пружине;
(ωt + φ0) – это фаза свободных колебаний, где ω — это циклическая частота, а φ0 – это начальная фаза, когда t = 0.
В физике указанную формулу называют уравнением гармонических колебаний. Данное уравнение полностью раскрывает процесс, где маятник движется с определенной амплитудой, периодом и частотой.
Период колебаний
Результаты лабораторных опытов показывают, что циклический период движения груза на пружине напрямую зависит от массы маятника и жесткости пружины, но не зависит от амплитуды движения.
В физике период обозначают буквой Т и описывают формулами:
Исходя из формул, период колебаний – это механические движения, повторяющиеся через определенный промежуток времени. Простыми словами периодом называют одно полное движение груза.
Простыми словами периодом называют одно полное движение груза.
Частота колебаний
Под частотой колебаний следует понимать количество повторений движения маятника или прохождения волны. В разных разделах физики частота обозначается буквами ν, f или F.
Данная величина описывается выражением:
v = n/t – количество колебаний за промежуток времени,
где
n – это единица колебаний;
t – отрезок времени.
В Международной системе измерений частоту измеряют в Гц (Герцах). Она относится к точным измеряемым составляющим колебательного процесса.
Например, наукой установлена частота вращения Солнца вокруг центра Вселенной. Она равна -1035 Гц при одинаковой скорости.
Циклическая частота
В физике циклическая и круговая частота имеют одинаковое значение. Данная величина еще называется угловой частотой.
Обозначают ее буквой омега. Она равна числу собственных колебательных движений тела за 2π секунд времени:
ω = 2π/T = 2πν.
Данная величина нашла свое применение в радиотехнике и, исходя из математического расчета, имеет скалярную характеристику. Ее измерения проводят в радианах на секунду. С ее помощью значительно упрощаются расчеты процессов в радиотехнике.
Например, резонансное значение угловой частоты колебательного контура рассчитывают по формуле:
WLC = 1/LC.
Тогда как обычная циклическая резонансная частота выражается:
VLC = 1/2π*√ LC.
В электрике под угловой частотой следует понимать число полных трансформаций ЭДС или число оборотов радиуса – вектора. Здесь ее обозначают буквой f.
Как определить амплитуду, период и частоту колебаний по графику
Для определения на графике составляющих колебательного механического процесса или, например, колебания температуры, нужно разобраться в терминах этого процесса.
К ним относят:
расстояние испытываемого объекта от исходной точки – называют смещением и обозначают х;
наибольшее отклонение – амплитуда смещения А;
фаза колебания – определяет состояние колебательной системы в любой момент времени;
начальная фаза колебательного процесса – когда t = 0, то φ = φ0.
Из графика видно, что значение синуса и косинуса может меняться от -1 до +1. Значит, смещение х может быть равно –А и +А. Движение от –А до +А называют полным колебанием.
Построенный график четко показывает период и частоту колебаний. Стоить отметить, что фаза не воздействует на форму кривой, а только влияет на ее положение в заданный промежуток времени.
Предыдущая
ФизикаЭлектромагнитная индукция – причины возникновения, значение и способы применения явления
Следующая
ФизикаСила трения – виды, формула и примеры расчета
Что такое амплитуда колебаний: вы должны знать
Амплитуда колебаний объясняет максимальное или максимальное смещение колеблющегося тела.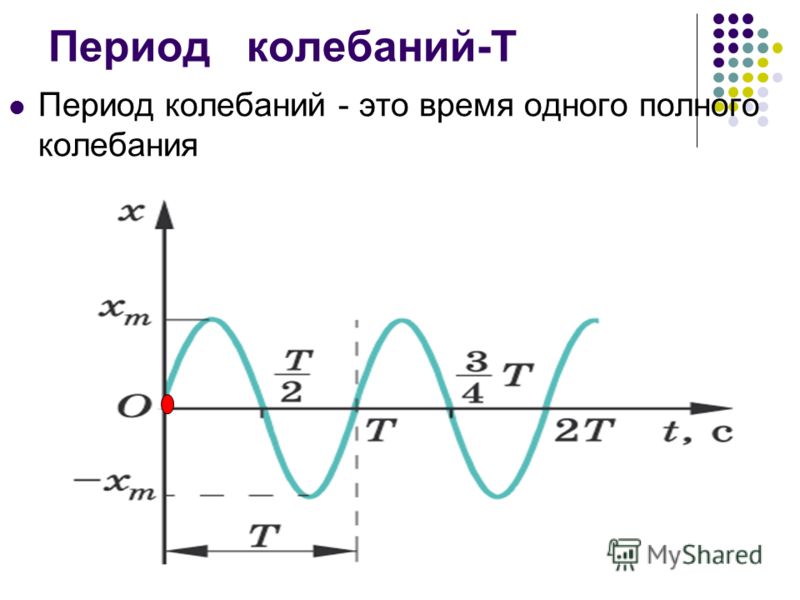 В статье подробно рассказывается о том, что такое амплитуда колебаний и как ее рассчитать.
В статье подробно рассказывается о том, что такое амплитуда колебаний и как ее рассчитать.
Амплитуда – это величина колеблющегося тела, такая как угловая частота и период времени. Величина измеряет максимальное смещение тела по обе стороны от его среднего положения. Это означает, что он показывает нам, насколько колеблющееся тело отклоняется от своего среднего положения во время колебания.
Колебание предполагает движение тела вперед и назад от его равновесного или среднего положения. Каждое колебание имеет три основные характеристики: частота, период времени, и амплитуда. Из них мы уже обсуждали концепции частоты и периода времени в предыдущие статьи.
Давайте начнем обсуждение амплитуды колебаний или амплитуды колебаний с примера простой маятник. Маятник поворачивается под углом через свое среднее положение к максимальному расстоянию от его среднего положения. Максимальное или наибольшее расстояние колеблющегося тела от его центра или среднего положения называется его.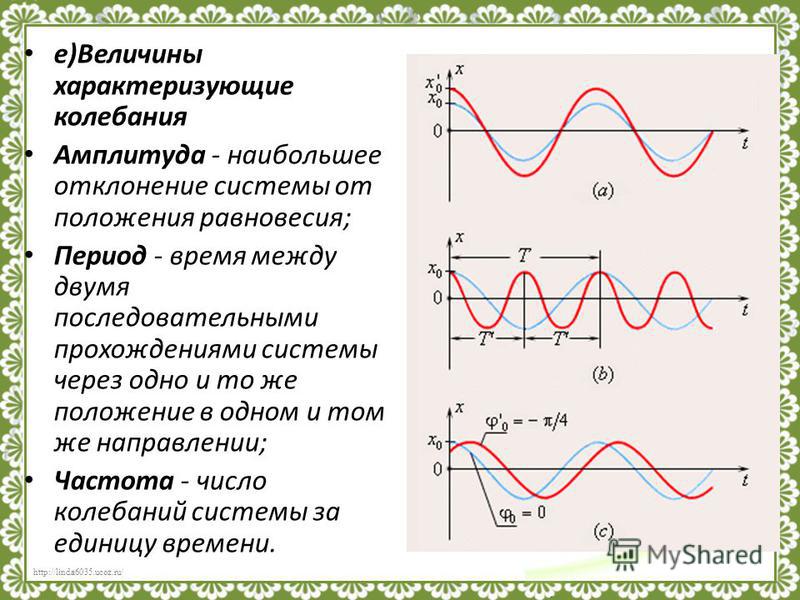 максимальное смещение. Напротив, величина максимального смещения колеблющегося тела по обе стороны от среднего положения называется его величиной. амплитуда колебаний.
максимальное смещение. Напротив, величина максимального смещения колеблющегося тела по обе стороны от среднего положения называется его величиной. амплитуда колебаний.
Как рассчитать амплитуду колебаний?
Из синусоидальный график, мы отметили, что амплитуда колебаний равна расстояние между гребнем, впадиной и средним положением.
Следовательно, амплитуда колебаний или величина максимального смещения x определяется уравнением синусоидальной волны как,
[латекс]x = Asin(\omega t+\phi )[/латекс] …………(*)
Где А – амплитуда колебаний.
[латекс]\омега[/латекс] — угловая скорость.
[латекс]\фи[/латекс] — фазовый сдвиг.
Мы обсудим, как вычислить уравнение амплитуды колебаний (*) из синусоидального графика в более поздней части.
Поскольку каждая волна имеет амплитуду, пики на графике показывают, что амплитуда объясняет степень или уровень изменения интенсивности в различных волны, такие как звук волны.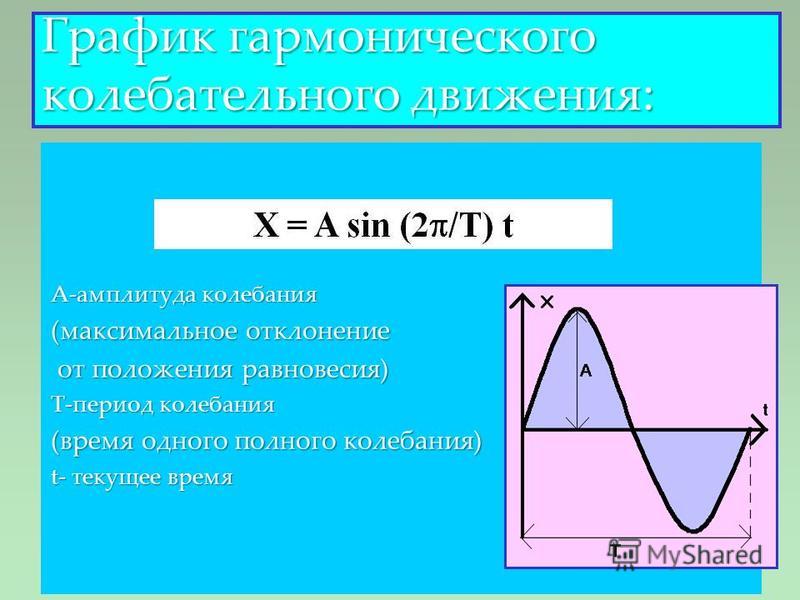 Следовательно, это также интерпретируется как громкость звука.
Следовательно, это также интерпретируется как громкость звука.
Звуковые волны
На графике мы отметили, что разница между максимальным пиком амплитуды или положительным значением и самым низким пиком амплитуды или отрицательным значением называется величиной ‘размах амплитуды’ колеблющегося тела.
Узнайте больше о Простое гармоническое движение угловой частоты
Как найти осцилляция Амплитуда из графика?Мы можем получить амплитуду колебаний из графика синусоидальной функции колеблющегося тела.
Амплитуда колебаний определяется, когда мы зарисовываем график колеблющихся переменных, таких как смещение от времени. Пики на синусоидальном графике – это амплитуда колебаний, которая описывает расстояние, на которое тело колеблется от среднего положения с каждой стороны.
В любой колебательной системе величина изменения колебательной переменной тела при каждом колебании называется амплитуда колебаний. В большинстве случаев осциллирующая переменная равна смещение. Когда мы строим график синусоидальной функции с переменным смещением колебаний в качестве вертикальной оси и временем в качестве горизонтальной оси, расстояние по вертикали между средним значением и крайними точками кривой показывает амплитуду колебаний.
В большинстве случаев осциллирующая переменная равна смещение. Когда мы строим график синусоидальной функции с переменным смещением колебаний в качестве вертикальной оси и временем в качестве горизонтальной оси, расстояние по вертикали между средним значением и крайними точками кривой показывает амплитуду колебаний.
(Кредит: Shutterstock)
На графике синусоидальной функции ось абсцисс рассматривается как среднее положение колеблющегося тела. Следовательно, каким бы ни было исходное положение тела, смещение измеряется от его среднего положения. Поскольку график является синусоидальной функцией, которая иллюстрирует периодические явленияпики на графике отображают параметры колеблющегося тела, такие как период и амплитуда.
Как рассчитать амплитуду колебанийсформировать график?
По пикам амплитуда колебаний рассчитывается как половина разницы между максимальным и минимальным значениями.
[latex]амплитуда = \frac{1}{2}\mid max -min \mid[/latex]
Следовательно, величина амплитуды колебаний всегда положительна.
Мы также можем найти амплитуду колебаний и период времени из обобщенного уравнения синусоидального графика следующим образом:
у = A⋅sin (B (x + C)) + D
где мы можем найти количество колеблющегося тела следующим образом:
Амплитуда колебаний:
Период времени: [латекс]\frac{2\pi }{B}[/латекс]
Сдвиг фазы – насколько далеко тело перемещается по горизонтали от среднего положения: C.
Вертикальный сдвиг – насколько далеко тело перемещается по вертикали от среднего положения: D.Как рассчитать амплитуду колебаний?
График функции синусоидальной волны (предоставлено: математика)
Узнайте больше о Угловое уравнение движения.
Что такое амплитуда и частота колебаний?Амплитуда и частота – это величины тел колебаний, которые определяют скорость колебаний.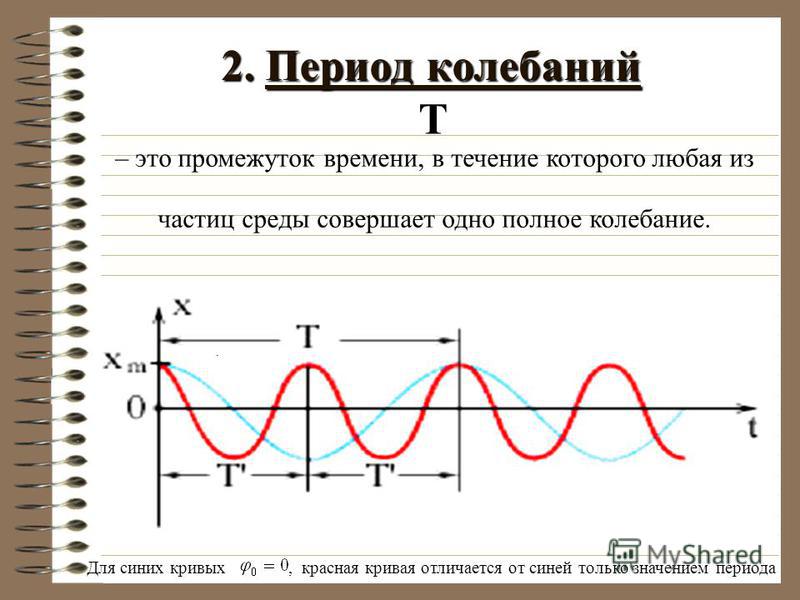
Тело колеблется, когда оно перемещается из своего среднего положения в самое верхнее и возвращается в свое среднее положение. Здесь амплитуда представляет собой максимальное смещение тела от его среднего положения. В то время как частота показывает, насколько тело колеблется от своего среднего положения.
Что такое амплитуда и частота колебаний?В зависимости от амплитуды и частоты колебания подразделяются на следующие три типа:
Затухающие колебания
Предположим, что тело колеблется с убывающей амплитудой из-за наличия сила сопротивления воздуха и в какой-то момент времени он останавливается, поскольку обе величины его тела рассеялись. В таком случае это называется «затухающие колебания ».
Свободное колебание
Предположим, тело свободно колеблется с постоянной амплитудой и определенной частотой из-за отсутствия силы трения. В этом случае это называется «свободное колебание », и его частота называется ‘собственная частота’ колеблющегося тела.
Принудительное колебание
Его еще называют колебанием натянутой струны или качанием. Предположим, что тело колеблется с уменьшающейся амплитудой из-за механической энергии качания, и оно приходит в состояние покоя, поскольку обе его величины рассеялись. В этом случае это называется ‘вынужденное колебание.
Возьмем, к примеру, подвешенный мяч для весла, который привязан к вашей руке.Амплитуда и частота колебаний
(Кредит: просвет)
Дело 1:
Если держать руку устойчиво, мяч будет подпрыгивать вверх и вниз, включая определенное количество ударов. демпфирование (То есть, сила сопротивления воздуха применяемый).
Дело 2:
Увеличивая частоту мяча, перемещая вашу руку вверх и вниз, мяч также реагирует увеличивающейся амплитудой. Если вы ведете мяч с частотой, равной его собственной частоте, его амплитуда увеличивается при каждом колебании. Событие приведения тела в движение с частотой, эквивалентной собственной частоте, называется резонанс. В то время как тело, выполняемое на своей естественной или основной частоте, считается резонировать.
В то время как тело, выполняемое на своей естественной или основной частоте, считается резонировать.
Дело 3:
если вы, кроме того, увеличиваете его частоту выше, чем его собственная частота, его амплитуда начинает уменьшаться, пока колебания почти не исчезнут. Так что движение вашей руки больше не влияет на мяч.
Величины, характеризующие колебательное движение 9 класс онлайн-подготовка на Ростелеком Лицей
Амплитуда
Обсудим количественные характеристики колебаний. Начнем с самой очевидной характеристики – амплитуды. Амплитуда обозначается большой буквой А и измеряется в метрах.
Определение
Амплитудой называют максимальное смещение от положения равновесия.
Часто амплитуду путают с размахом колебаний. Размах – это когда тело совершает колебание из одной крайней точки в другую. А амплитуда – это максимальное смещение, т. е. расстояние от точки равновесия, от линии равновесия до крайней точки, в которую оно попало.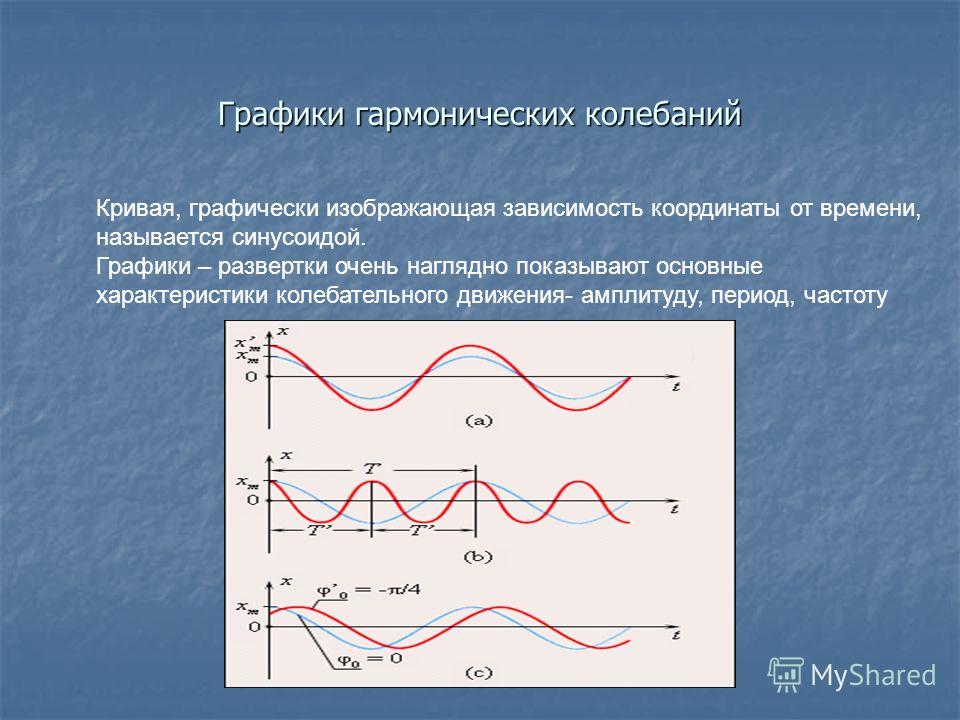 Помимо амплитуды, существует еще одна характеристика – смещение. Это текущее отклонение от положения равновесия.
Помимо амплитуды, существует еще одна характеристика – смещение. Это текущее отклонение от положения равновесия.
А – амплитуда –
х – смещение –
Рис. 1. Амплитуда
Посмотрим, как отличаются амплитуда и смещение на примере. Математический маятник находится в состоянии равновесия. Линия расположения маятника в начальный момент времени – линия равновесия. Если отвести маятник в сторону – это и будет его максимальное смещение (амплитуда). В любой другой момент времени расстояние не будет амплитудой, а будет просто смещением.
Рис. 2. Отличие амплитуды и смещения
Период
Следующая характеристика, к которой мы переходим, называется период колебаний.
Определение
Периодом колебаний называется промежуток времени, в течение которого совершается одно полное колебание.
Обратите внимание, что величина «период» обозначается большой буквой , определяется она следующим образом: , .
Рис. 3. Период
Стоит добавить, что чем больше мы берем число колебаний за большее время, тем точнее мы определим период колебаний.
Частота
Следующая величина – это частота.
Определение
Число колебаний, совершенных за единицу времени, называют частотой колебаний.
Рис. 4. Частота
Обозначается частота греческой буквой , которая читается как «ню». Частота – это отношение числа колебаний ко времени, за которое эти колебания произошли: .
Единицы измерения частоты . Эту единицу называют «герц» в честь немецкого физика Генриха Герца. Обратите внимание, что период и частота связаны через число колебаний и время, в течение которых это колебание совершается. Для каждой колебательной системы частота и период есть величины постоянные. Связь между этими величинами довольно проста: .
Кроме понятия «частота колебаний» нередко пользуются понятием «циклическая частота колебаний», то есть количество колебаний за секунд. Обозначается она буквой и измеряется в радианах за секунду .
Обозначается она буквой и измеряется в радианах за секунду .
Графики свободных незатухающих колебаний
Мы уже знаем решение главной задачи механики для свободных колебаний – закон синуса или косинуса. Также мы знаем, что графики являются мощнейшим инструментом исследования физических процессов. Поговорим о том, как будут выглядеть графики синусоиды и косинусоиды в применении к гармоническим колебаниям.
Для начала определимся с особыми точками во время колебаний. Это необходимо для того, чтобы правильно выбрать масштаб построения. Рассмотрим математический маятник. Первый вопрос, который возникает: какую функцию использовать – синус или косинус? Если колебание начинается с верхней точки – максимального отклонения, законом движения будет закон косинуса. Если же начать движение с точки равновесия – законом движения будет закон синуса.
Если законом движения будет закон косинуса, то через четверть периода маятник будет находиться в положении равновесия, еще через четверть – в крайней точке, еще через четверть – опять в положении равновесия, и еще через одну четверть вернется в начальное положение.
Если маятник колеблется по закону синуса, то через четверть периода он будет находиться в крайней точке, еще через четверть – в положении равновесия. Потом опять в крайней точке, но с другой стороны, и через еще четверть периода вернется в положение равновесия.
Итак, масштабом времени будет не произвольные значение 5 с, 10 с и т. д., а доли периода. Мы будем строить график по четвертям долей периода.
Что же сказать о координате ? Дальше, чем положение равновесия, маятник не двигается. График будет ограничен значением амплитуды.
Перейдем к построению. меняется либо по закону синуса, либо по закону косинуса. Ось ординат – , ось абсцисс – . Масштаб времени равен четвертям периода: График будет лежать в пределах от до .
Рис. 5. Графики зависимости
График для колебания по закону синуса выходит из нуля и обозначен темно-синим цветом (рис. 5). График для колебания по закону косинуса выходит из положения максимального отклонения и обозначен голубым цветом на рисунке. Графики выглядят абсолютно идентично, но сдвинуты по фазе относительно друг друга на четверть периода или радиан.
Графики выглядят абсолютно идентично, но сдвинуты по фазе относительно друг друга на четверть периода или радиан.
Аналогичный вид будут иметь графики зависимости и , ведь они тоже меняются по гармоническому закону.
Особенности колебаний математического маятника
Математический маятник – это материальная точка массой , подвешенная на длинной нерастяжимой невесомой нити длиной .
Обратите внимание на формулу периода колебаний математического маятника: , где – длина маятника, – ускорение свободного падения.
Чем больше длина маятника, тем больше период его колебаний (рис. 6). Чем длиннее нить, тем дольше маятник раскачивается.
Рис. 6. Зависимость периода колебаний от длины маятника
Чем больше ускорение свободного падения, тем меньше период колебаний (рис. 7). Чем больше ускорение свободного падения, тем сильнее небесное тело притягивает грузик и тем быстрее он стремится вернуться в положение равновесия.
Рис. 7. Зависимость периода колебаний от ускорения свободного падения
7. Зависимость периода колебаний от ускорения свободного падения
Обратите внимание, что период колебаний не зависит от массы груза и амплитуды колебаний (рис. 8).
Рис. 8. Период колебаний не зависит от амплитуды колебаний
Первым на этот факт обратил внимание Галилео Галилей. На основании этого факта предложен механизм маятниковых часов.
Следует отметить, что точность формулы максимальна лишь для малых, сравнительно небольших отклонений. Например, для отклонения погрешность формулы составляет . Для более крупных отклонений точность формулы не столь велика.
Рассмотрим качественные задачи, которые описывают математический маятник.
Задача. Как изменится ход маятниковых часов, если их: 1) перевезти из Москвы на Северный полюс; 2) перевезти из Москвы на экватор; 3) поднять высоко в гору; 4) вынести из нагретого помещения на мороз.
Для того чтобы правильно ответить на вопрос задачи, необходимо понять, что имеется в виду под «ходом маятниковых часов».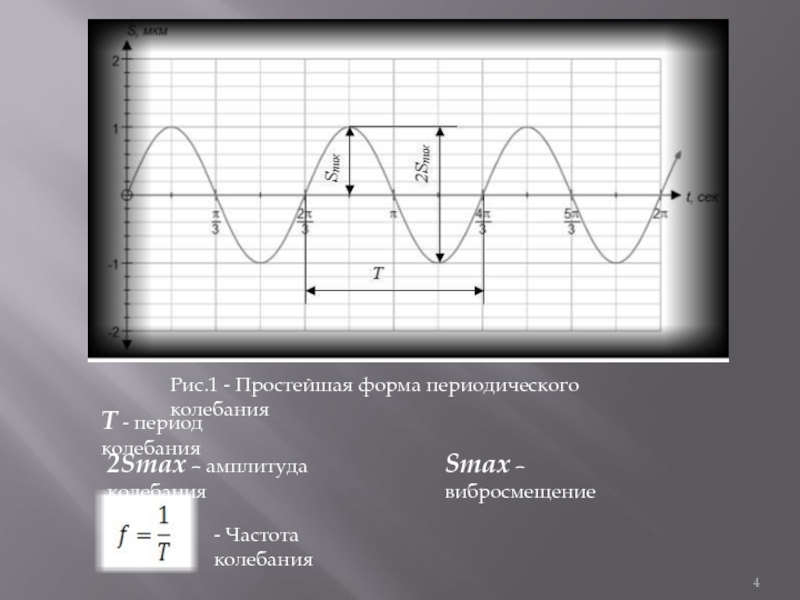 Маятниковые часы основаны на математическом маятнике. Если период колебаний часов будет меньше, чем нам нужно, часы начнут спешить. Если же период колебаний станет больше, чем необходимо, часы будут отставать. Задача сводится к ответу на вопрос: что произойдет с периодом колебаний математического маятника в результате всех перечисленных в задаче действий?
Маятниковые часы основаны на математическом маятнике. Если период колебаний часов будет меньше, чем нам нужно, часы начнут спешить. Если же период колебаний станет больше, чем необходимо, часы будут отставать. Задача сводится к ответу на вопрос: что произойдет с периодом колебаний математического маятника в результате всех перечисленных в задаче действий?
Рассмотрим первую ситуацию. Математический маятник переносится из Москвы на Северный полюс. Вспоминаем, что Земля имеет форму геоида, то есть сплюснутого у полюсов шара (рис. 9). Это значит, что на полюсе величина ускорения свободного падения несколько больше, чем в Москве. А раз ускорение свободного падения больше, то период колебаний станет несколько меньше и маятниковые часы начнут спешить. Здесь мы пренебрегаем тем, что на Северном полюсе холоднее.
Рис. 9. Ускорение свободного падения больше на полюсах Земли
Рассмотрим вторую ситуацию. Переносим часы из Москвы на экватор, предполагая, что температура не меняется. Ускорение свободного падения на экваторе несколько меньше, чем в Москве. Это значит, что период колебаний математического маятника увеличится и часы начнут отставать.
Ускорение свободного падения на экваторе несколько меньше, чем в Москве. Это значит, что период колебаний математического маятника увеличится и часы начнут отставать.
В третьем случае часы поднимают высоко в гору, тем самым увеличивая расстояние до центра Земли (рис. 10). Это значит, что ускорение свободного падения на вершине горы меньше. Период колебаний увеличивается, часы будут отставать.
Рис. 10 Ускорение свободного падения больше на вершине горы
Рассмотрим последний случай. Часы выносят из теплой комнаты на мороз. При понижении температуры линейные размеры тел уменьшаются. Это значит, что длина маятника немного сократится. Раз длина стала меньше, то период колебаний также уменьшился. Часы будут спешить.
Мы рассмотрели самые типичные ситуации, которые позволяют разобраться с тем, как работает формула периода колебаний математического маятника.
Фаза колебаний
В заключение рассмотрим еще одну характеристику колебаний – фазу. О том, что такое фаза, более подробно мы будем говорить в старших классах. Сегодня мы должны рассмотреть, с чем можно эту характеристику сравнить, сопоставить и как ее для себя определить. Удобнее всего фазу колебаний сопоставить со скоростью движения маятника.
О том, что такое фаза, более подробно мы будем говорить в старших классах. Сегодня мы должны рассмотреть, с чем можно эту характеристику сравнить, сопоставить и как ее для себя определить. Удобнее всего фазу колебаний сопоставить со скоростью движения маятника.
Рис. 11. Маятники колеблются синфазно (с одинаковыми фазами)
На рисунке 11 представлены два одинаковых маятника. Первый маятник отклонили влево на определенный угол, второй тоже отклонили влево на определенный угол, такой же, как и первый. Оба маятника будут совершать абсолютно одинаковые колебания. В этом случае можно сказать, что маятники совершают колебания с одинаковой фазой, поскольку скорости маятника имеют одно направление и равные модули.
Рис. 12. Маятники совершают колебания в противофазе
На рисунке 12 два таких же маятника, но один отклонен влево, а другой – вправо. У них тоже одинаковые по модулю скорости, но направление противоположное. В этом случае говорят, что маятники совершают колебания в противофазе.
Во всех других случаях, как правило, упоминают о разности фаз.
Рис. 13. Разница фаз
Фазу колебаний в произвольный момент времени можно рассчитать по формуле , то есть как произведение циклической частоты на время, прошедшее с начала колебаний. Измеряется фаза в радианах.
Особенности колебаний пружинного маятника
Формула колебаний пружинного маятника: . Таким образом, период колебаний пружинного маятника зависит от массы груза и жесткости пружины.
Чем больше масса груза, тем больше его инертность. То есть маятник будет медленнее разгоняться, период его колебаний будет больше (рис. 14).
Рис. 14. Зависимость периода колебаний от массы
Чем больше жесткость пружины, тем быстрее она стремится вернуться в положение равновесия. Период пружинного маятника будет меньше.
Рис. 15. Зависимость периода колебаний от жесткости пружины
Рассмотрим применение формулы на примере задачи.
Задача. На рисунке представлен график зависимости координаты от времени для пружинного маятника. Найдите массу грузика, если жесткость пружины равна .
На рисунке представлен график зависимости координаты от времени для пружинного маятника. Найдите массу грузика, если жесткость пружины равна .
Рис. 16. График зависимости координаты от времени для пружинного маятника
Решение:
Массу грузика можно определить из формулы периода колебаний пружинного маятника:
Период колебаний находим, используя график зависимости координаты от времени. Период – это время одного полного колебания. Одно полное колебание совершается за (рис. 17).
Рис. 17. Период колебаний
Если подставить теперь все необходимые значения в формулу для вычисления массы, получим:
Ответ: масса грузика составляет приблизительно 10 г.
Так же, как и в случае с математическим маятником, для пружинного маятника период колебаний не зависит от его амплитуды. Естественно, что это справедливо только для небольших отклонений от положения равновесия, когда деформация пружины является упругой. Этот факт был положен в основу устройства пружинных часов (рис. 18).
Этот факт был положен в основу устройства пружинных часов (рис. 18).
Рис. 18. Пружинные часы
Заключение
Конечно, кроме колебаний и тех характеристик, о которых мы говорили, существуют и другие не менее важные характеристики колебательного движения. Но о них мы поговорим в старшей школе.
Список литературы
- Кикоин А. К. О законе колебательного движения // Квант. – 1983. – № 9. – С. 30-31.
- Кикоин И. К., Кикоин А. К. Физика: учеб. для 9 кл. сред. шк. – М.: Просвещение, 1992. – 191 с.
- Черноуцан А. И. Гармонические колебания – обычные и удивительные // Квант. – 1991. – № 9. – С. 36-38.
- Перышкин А. В., Гутник Е. М. Физика. 9 кл.: учебник для общеобразоват. учреждений / А. В. Перышкин, Е. М. Гутник. – 14-е изд., стереотип. – М.: Дрофа, 2009. – 300 с.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «abitura.
 com» (Источник)
com» (Источник) - Интернет-портал «phys-portal.ru» (Источник)
- Интернет-портал «fizmat.by» (Источник)
Домашнее задание
- Что такое математический и пружинный маятники? Какая разница между ними?
- Что такое гармоническое колебание, период колебания?
- Груз массой 200 г колеблется на пружине с жесткостью 200 Н/м. Найдите полную механическую энергию колебаний и наибольшую скорость движения груза, если амплитуда колебаний 10 см (трением пренебречь).
Период, частота и амплитуда: определение и примеры
Чтобы понять Вселенную, вы должны понять, что все можно описать волнами, от самых сложных вещей до повседневных вещей, таких как цвет объектов, которые мы наблюдаем. Когда свет проходит через призму, он разделяется на разные компоненты, которые мы воспринимаем как цвета. Каждый из этих цветов можно идентифицировать по его уникальной частоте. Цвет может иметь разную интенсивность, так как интенсивность цвета связана с амплитудой волны. Это означает, что могут быть две волны с одинаковой частотой, но с разными амплитудами. В этой статье мы узнаем об амплитуде, частоте и периоде колебаний, а также поймем взаимосвязь между ними.
Это означает, что могут быть две волны с одинаковой частотой, но с разными амплитудами. В этой статье мы узнаем об амплитуде, частоте и периоде колебаний, а также поймем взаимосвязь между ними.
Спектр видимого света, отображающий разные цвета, можно идентифицировать по их уникальной частоте и периоду. Мы видим обратную зависимость между частотой и периодом. Чем ниже частота, тем больше период и наоборот, Wikimedia Commons, DrSciComm (CC BY-SA 3.0)
Период, частота и амплитуда: определения
Период, частота и амплитуда являются важными свойствами волн. Как мы упоминали ранее, амплитуда связана с энергией волны.
Амплитуда — максимальное отклонение от положения равновесия при колебании.
Период — время, необходимое для одного цикла колебаний. Частота определяется как величина, обратная периоду. Это относится к тому, сколько циклов он завершает за определенный промежуток времени.
Период – это время, необходимое для одного цикла колебаний.
Частота описывает, сколько циклов колебаний система совершает за определенный промежуток времени.
Например, большой период подразумевает маленькую частоту.
$$f=\frac1T$$
Где \(f\) — частота в герцах, \(\mathrm{Hz}\), а \(T\) — период в секундах, \(\матрм с\).
Период, частота и амплитуда: примеры
Чтобы визуализировать эти понятия экспериментально, представьте, что вы и ваш друг берете веревку за концы и трясете ее вверх и вниз, создавая волну, проходящую через веревку. Допустим, за одну секунду веревка совершила два оборота. Частота волны будет \(2\;\frac{\mathrm{cycles}}{\mathrm s}\). Период будет обратным частоте, поэтому период волны будет составлять полсекунды, а это означает, что для завершения одного цикла колебаний потребуется полсекунды.
Студент, наблюдающий за колеблющимся блоком, считает \(45,5\;{\textstyle\frac{\mathrm{циклы}}\мин}\). Определить его частоту и период.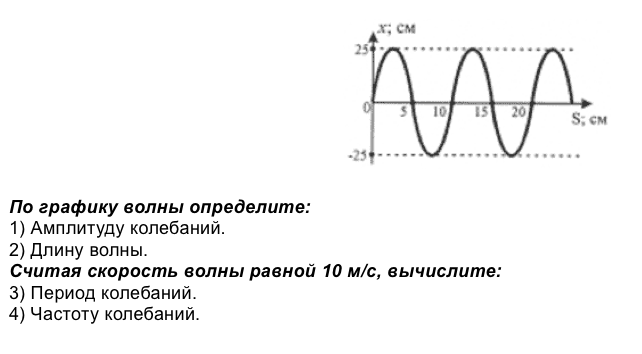
$$f=45,5\;{\textstyle\frac{\mathrm{циклы}}\мин}\times\frac1{60}{\textstyle\frac\min{\mathrm s}}=0,758\;{\ textstyle\frac{\mathrm{циклы}}{\mathrm s}}$$
$$f=0,758\;\mathrm{Hz}$$
$$T=\frac1f=\frac1{0,758\;\ mathrm{Hz}}=1.32\;\mathrm s$$
Период колебаний объекта в простом гармоническом движении связан с угловая частота движения объекта. Выражение для угловой частоты будет зависеть от типа объекта, который совершает простое гармоническое движение.
$$\omega=2\pi f$$
$$T=\frac{2\pi}\omega$$
Где \(\omega\) – угловая частота в радианах в секунду, \( \ гидроразрыва {\ mathrm {рад}} {\ mathrm s} \).
Двумя наиболее распространенными способами доказать это являются эксперименты с маятником и грузом на пружине.
Период пружины задается уравнением ниже.
$$T_s=2\pi\sqrt{\frac mk}$$
Где \(m\) – масса объекта на конце пружины в килограммах, \(\mathrm{kg}\) , а \(k\) – жесткость пружины, которая измеряет жесткость пружины в ньютонах на метр, \(\frac{\mathrm N}{\mathrm m}\).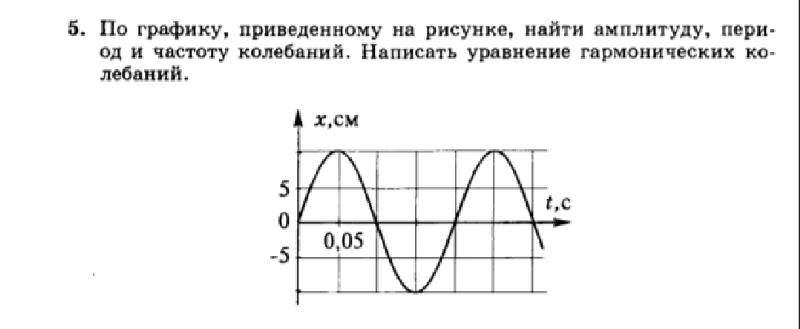 2}\).
2}\).
Связь между периодом, частотой и амплитудой
Период, частота и амплитуда взаимосвязаны в том смысле, что все они необходимы для точного описания колебательного движения системы. Как мы увидим в следующем разделе, эти величины входят в тригонометрическое уравнение, описывающее положение колеблющейся массы. Важно отметить, что на амплитуду не влияет период или частота волны.
Легко увидеть взаимосвязь между периодом, частотой и амплитудой на графике зависимости положения от времени. Чтобы найти амплитуду по графику, мы наносим положение объекта в простом гармоническом движении как функцию времени. Мы ищем пиковые значения расстояния, чтобы найти амплитуду. Чтобы найти частоту, нам сначала нужно получить период цикла. Для этого находим время, необходимое для совершения одного цикла колебаний. Это можно сделать, посмотрев на время между двумя последовательными пиками или впадинами. После того, как мы найдем период, мы возьмем его инверсию, чтобы определить частоту.
Смещение как функция времени для простого гармонического движения для иллюстрации амплитуды и периода. Расстояние от \(x=0\) до \(x=a\) — это амплитуда, а время от \(t=0\) до \(t=t\) — это период, StudySmarter Originals
Period, Частота и амплитуда тригонометрических функций
Тригонометрические функции используются для моделирования волн и колебаний. Это потому, что колебания имеют периодичность, поэтому они связаны с геометрической формой круга. Функции косинуса и синуса определяются на основе окружности, поэтому мы используем эти уравнения для нахождения амплитуды и периода тригонометрической функции.
$$y=a\;c\mathrm{os}\left(bx\right)$$
Амплитуда будет определяться величиной \(a\).
$$\mathrm{Amplitude}=\left|a\right|$$
Период определяется приведенным ниже уравнением.
$$\mathrm{Period}=\frac{2\pi}{\left|b\right|}$$
Дано выражение для положения объекта в простом гармоническом движении от времени следующим уравнением.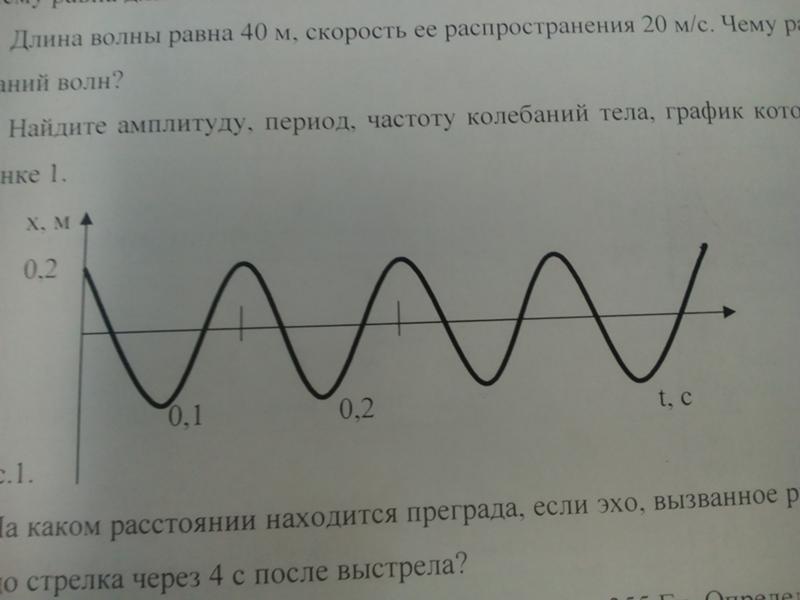
$$x=A\cos\left(\frac{2\pi t}T\right)$$
Где \(A\) – амплитуда в метрах, \(\mathrm m\) и \ (t\) – время в секундах, \(\mathrm s\).
Из этого уравнения мы можем определить амплитуду и период волны.
$$\mathrm{Amplitude}=\left|A\right|$$
$$\mathrm{Period}=\frac{2\pi}{\left|{\displaystyle\frac{2\pi} T}\right|}=T$$
Период, частота и амплитуда – ключевые выводы
- Период – это время, необходимое для одного цикла колебаний.
- Частота определяется как величина, обратная периоду. Это относится к тому, сколько циклов он выполняет за определенное время, \(f=\frac1T\).
- Период колебаний объекта в простом гармоническом движении связан с угловой частотой движения объекта, \(T=\frac{2\pi}\omega\) и \(\omega=2\pi f\) .
- Амплитуда – это максимальное отклонение от положения равновесия при колебании. Это важное свойство, связанное с энергией волны. Амплитуда не зависит от периода или частоты волны. Могут быть две волны с одинаковой частотой, но с разной амплитудой.

- Тригонометрические функции используются для моделирования волн и колебаний, поэтому мы используем эти уравнения для определения амплитуды и периода, \(y=a\cos\left(bx\right)\). Чтобы определить амплитуду, \(\mathrm{Amplitude}=\left|a\right|\). Чтобы определить период, \(\mathrm{Period}=\frac{2\pi}{\left|b\right|}\).
13.2 Свойства волн: скорость, амплитуда, частота и период — физика
Раздел Цели обучения
К концу этого раздела вы сможете делать следующее:
- Определение амплитуды, частоты, периода, длины волны и скорости волны
- Связь частоты волны, периода, длины волны и скорости
- Решение задач, связанных со свойствами волн
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим учащимся освоить следующие стандарты:
- (7) Научные понятия. Учащийся знает характеристики и поведение волн.
 Ожидается, что студент:
Ожидается, что студент:- (Б) исследовать и анализировать характеристики волн, включая скорость, частоту, амплитуду и длину волны, и рассчитывать, используя взаимосвязь между скоростью волны, частотой и длиной волны;
- (Д) исследовать поведение волн, включая отражение, преломление, дифракцию, интерференцию, резонанс и эффект Доплера.
Основные термины раздела
| длина волны | скорость волны |
Поддержка учителей
Поддержка учителей
[BL][OL][AL] Проверьте амплитуду, период и частоту для простого гармонического движения.
Волновые переменные
В главе о движении в двух измерениях мы определили следующие переменные для описания гармонического движения:
- Амплитуда — максимальное смещение от положения равновесия объекта, колеблющегося вокруг такого положения равновесия
- Частота — количество событий в единицу времени
- Период — время, необходимое для совершения одного колебания
Для волн эти переменные имеют одинаковое основное значение.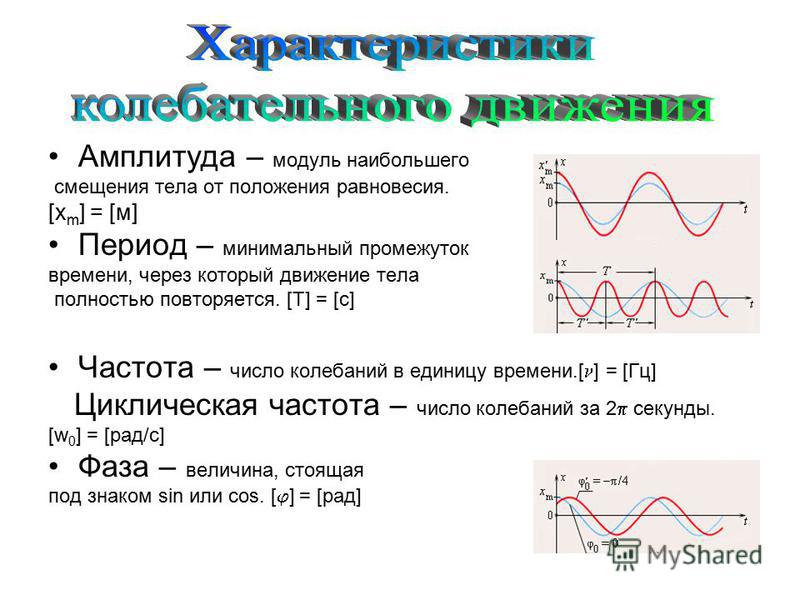 Однако полезно сформулировать определения более конкретным образом, применимым непосредственно к волнам:
Однако полезно сформулировать определения более конкретным образом, применимым непосредственно к волнам:
- Амплитуда — расстояние между положением покоя и максимальным смещением волны
- Частота — количество волн, проходящих через определенную точку в секунду
- Период — время, необходимое для завершения одного цикла волны
Волны характеризуют не только амплитуда, частота и период, но и их длина волны и скорость волны. Длина волны λλ — это расстояние между соседними одинаковыми частями волны, параллельными направлению распространения. Скорость волны vwvw — это скорость, с которой движется возмущение.
Советы для успеха
Скорость волны иногда также называют скоростью распространения или скоростью распространения , поскольку возмущение распространяется из одного места в другое.
Рассмотрим периодическую волну воды на рис. 13. 7. Его длина волны — это расстояние от гребня до гребня или от впадины до впадины. Длину волны также можно рассматривать как расстояние, пройденное волной за один полный цикл или один период. Время одного полного движения вверх-вниз равно периоду простой водной волны T . На рисунке сама волна движется вправо с волновой скоростью v w . Его амплитуда 90 212 X 90 213 — это расстояние между положением покоя и максимальным смещением — либо гребнем, либо впадиной — волны. Важно отметить, что это движение волны на самом деле является 9-м.0212 возмущение движение вправо, а не сама вода; в противном случае птица двигалась бы вправо. Вместо этого чайка качается вверх и вниз на месте, когда под ней проходят волны, преодолевая общее расстояние 2 90 212 X 90 213 за один цикл. Однако, как упоминалось в текстовой статье о серфинге, настоящие океанские волны более сложны, чем этот упрощенный пример.
7. Его длина волны — это расстояние от гребня до гребня или от впадины до впадины. Длину волны также можно рассматривать как расстояние, пройденное волной за один полный цикл или один период. Время одного полного движения вверх-вниз равно периоду простой водной волны T . На рисунке сама волна движется вправо с волновой скоростью v w . Его амплитуда 90 212 X 90 213 — это расстояние между положением покоя и максимальным смещением — либо гребнем, либо впадиной — волны. Важно отметить, что это движение волны на самом деле является 9-м.0212 возмущение движение вправо, а не сама вода; в противном случае птица двигалась бы вправо. Вместо этого чайка качается вверх и вниз на месте, когда под ней проходят волны, преодолевая общее расстояние 2 90 212 X 90 213 за один цикл. Однако, как упоминалось в текстовой статье о серфинге, настоящие океанские волны более сложны, чем этот упрощенный пример.
Рисунок
13,7
Волна имеет длину волны λ , что является расстоянием между соседними одинаковыми частями волны.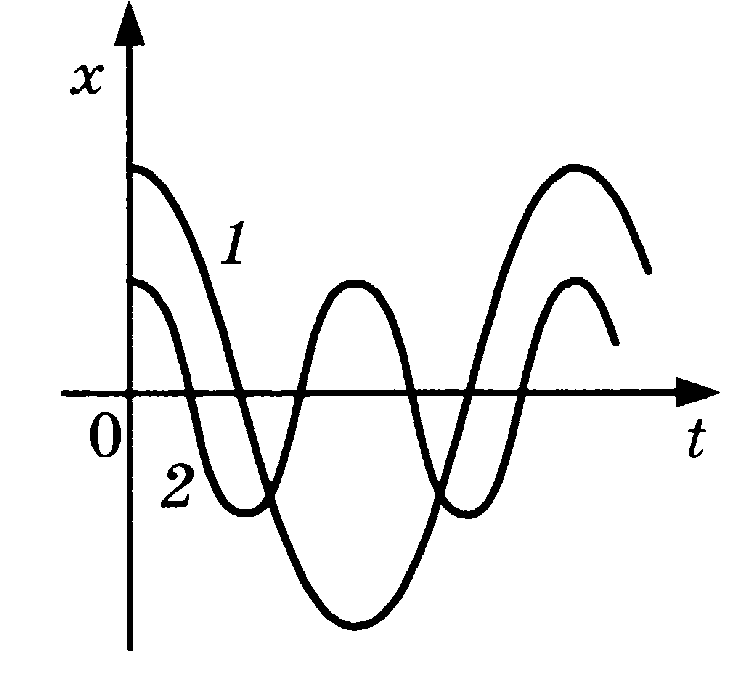 Возмущение поверхности вверх-вниз распространяется параллельно поверхности со скоростью v в .
Возмущение поверхности вверх-вниз распространяется параллельно поверхности со скоростью v в .
Смотреть физику
Амплитуда, период, частота и длина волны периодических волн
Данное видео является продолжением видео «Введение в волны» из раздела «Виды волн». В нем обсуждаются свойства периодической волны: амплитуда, период, частота, длина волны и скорость волны.
Советы для успеха
Гребень волны иногда также называют пиком .
Смотреть Физика: амплитуда, период, частота и длина волны периодических волн. В этом видео представлены несколько концепций звука; амплитуда, период, частота и длина волны периодических волн.
Нажмите, чтобы просмотреть содержимое
Если вы находитесь на лодке в ложбине волны в океане, и амплитуда волны составляет 1\,\text{м}, какова высота волны с вашего местоположения?
1\,\текст{м}
2\,\текст{м}
4\,\текст{м}
8\,\текст{м}
Взаимосвязь между частотой волны, периодом, длиной волны и скоростью
Поскольку частота волны — это количество волн в секунду, а период — это, по сути, количество секунд на волну, связь между частотой и периодом равна
f=1Tf=1T
13. 1
1
или
T=1f,T=1f,
13,2
так же, как и в случае гармонического движения объекта. Из этого соотношения видно, что более высокая частота означает более короткий период. Напомним, что единицей измерения частоты является герц (Гц), а 1 Гц — это один цикл — или одна волна — в секунду.
Скорость распространения v w — это расстояние, которое волна проходит за заданное время, которое составляет одну длину волны за время одного периода. В форме уравнения это записывается как
vw=λTvw=λT
13,3
или
vw=fλ.vw=fλ.
13,4
Из этого соотношения мы видим, что в среде, где v w постоянно, чем выше частота, тем меньше длина волны. См. рисунок 13.8.
Рисунок
13,8
Поскольку в данной среде они распространяются с одинаковой скоростью, низкочастотные звуки должны иметь большую длину волны, чем высокочастотные звуки. Здесь низкочастотные звуки излучаются большим динамиком, называемым низкочастотным динамиком, а высокочастотные звуки излучаются маленьким динамиком, называемым твитером.
Здесь низкочастотные звуки излучаются большим динамиком, называемым низкочастотным динамиком, а высокочастотные звуки излучаются маленьким динамиком, называемым твитером.
Поддержка учителей
Поддержка учителей
[BL] Для звука более высокая частота соответствует более высокому тону, а более низкая частота соответствует более низкому тону. Амплитуда соответствует громкости звука.
[BL][OL] Поскольку звук на всех частотах имеет одинаковую скорость в воздухе, изменение частоты означает изменение длины волны.
[Поддержка рисунка] Один и тот же динамик способен воспроизводить как высокочастотные, так и низкочастотные звуки. Однако высокие частоты имеют более короткую длину волны и, следовательно, лучше всего воспроизводятся динамиком с маленьким, твердым и плотным диффузором (твитер), тогда как более низкие частоты лучше всего воспроизводятся с большим и мягким диффузором (вуфер).
Эти фундаментальные соотношения справедливы для всех типов волн.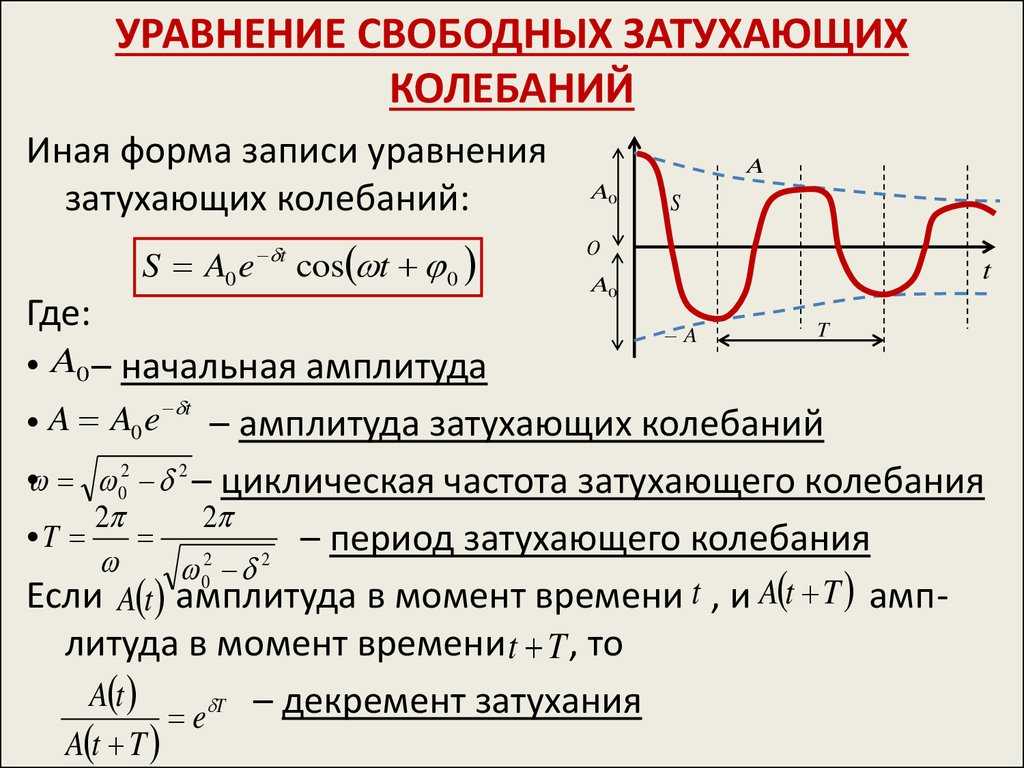 Например, для волн на воде v w — это скорость поверхностной волны; для звука v w — скорость звука; а для видимого света v w — это скорость света. Амплитуда X совершенно не зависит от скорости распространения v w и зависит только от количества энергии в волне.
Например, для волн на воде v w — это скорость поверхностной волны; для звука v w — скорость звука; а для видимого света v w — это скорость света. Амплитуда X совершенно не зависит от скорости распространения v w и зависит только от количества энергии в волне.
Снап Лаборатория
Волны в миске
В этой лаборатории вы проведете измерения, чтобы определить, как на амплитуду и период волн влияет передача энергии от пробки, брошенной в воду. Пробка изначально обладает некоторой потенциальной энергией, когда ее держат над водой — чем больше высота, тем выше потенциальная энергия. Когда пробка падает, такая потенциальная энергия преобразуется в кинетическую энергию, когда пробка падает. Когда пробка ударяется о воду, эта энергия распространяется по воде волнами.
- Большая миска или таз
- Вода
- Пробка (или мячик для пинг-понга)
- Секундомер
- Рулетка
Инструкции
Процедура
- Наполните большую миску или таз водой и подождите, пока вода не осядет, чтобы не было ряби.
- Аккуратно бросьте пробку в середину чаши.
- Оцените длину волны и период колебаний водной волны, распространяющейся от пробки. Вы можете оценить период, подсчитав количество ряби от центра к краю чаши, пока ваш партнер измеряет это время. Эта информация в сочетании с измерением чаши даст вам длину волны при использовании правильной формулы.
- Выньте пробку из чаши и подождите, пока вода снова не осядет.
- Аккуратно бросьте пробку с высоты, отличной от высоты первого падения.
- Повторите шаги с 3 по 5, чтобы собрать второй и третий наборы данных, опуская пробку с разной высоты и записывая полученные длины волн и периоды.
- Интерпретируйте результаты.

Пробка падает в бассейн с водой, создавая волны. Зависит ли длина волны от высоты над водой, с которой брошена пробка?
Нет, влияет только на амплитуду.
Да, длина волны затронута.
Поддержка учителей
Поддержка учителей
Учащиеся могут заранее измерить чашу, чтобы лучше оценить длину волны.
Виртуальная физика
Волна на струне
В этой анимации посмотрите, как струна вибрирует в замедленном темпе, выбрав параметр «Замедленное движение». Выберите параметры «Без конца» и «Вручную» и покачивайте конец струны, чтобы создавать волны самостоятельно. Затем переключитесь на настройку Oscillate для автоматического создания волн. Отрегулируйте частоту и амплитуду колебаний, чтобы увидеть, что произойдет. Затем поэкспериментируйте с регулировкой демпфирования и натяжения.
Затем переключитесь на настройку Oscillate для автоматического создания волн. Отрегулируйте частоту и амплитуду колебаний, чтобы увидеть, что произойдет. Затем поэкспериментируйте с регулировкой демпфирования и натяжения.
Проверка захвата
Какая из настроек — амплитуда, частота, затухание или натяжение — изменяет амплитуду волны при ее распространении? Что он делает с амплитудой?
- Частота; он уменьшает амплитуду волны по мере ее распространения.
- Частота; он увеличивает амплитуду волны по мере ее распространения.
- Демпфирование; он уменьшает амплитуду волны по мере ее распространения.
- Демпфирование; он увеличивает амплитуду волны по мере ее распространения.
Решение волновых задач
Рабочий пример
Рассчитайте скорость распространения волн: Чайка в океане
Рассчитайте скорость морской волны на предыдущем рисунке, если расстояние между гребнями волн равно 10,0 м, а время, за которое чайка качается вверх и вниз, составляет 5,00 с.
Стратегия
Заданы значения длины волны (λ=10,0 м)(λ=10,0 м) и периода (T=5,00 с)(T=5,00 с), и нас просят найти vwvw Следовательно, мы можем использовать vw= λTvw=λT, чтобы найти скорость волны.
Решение
Введите известные значения в vw=λTvw=λT
vw=10,0 м5,00 с=2,00 м/с.vw=10,0 м5,00 с=2,00 м/с.
13.5
Обсуждение
Такая низкая скорость кажется приемлемой для океанской волны. Обратите внимание, что на рисунке волна движется вправо с этой скоростью, которая отличается от переменной скорости, с которой чайка качается вверх и вниз.
Рабочий пример
Вычислите период и скорость волны игрушечной пружины.
Женщина на рис. 13.3 создает две волны каждую секунду, встряхивая игрушечную пружину вверх и вниз. а) Каков период каждой волны? (b) Если каждая волна проходит 0,9 метра после одного полного волнового цикла, какова скорость распространения волны?
Стратегия ЗА (А)
Чтобы найти период, мы решаем T=1fT=1f, учитывая значение частоты (f=2s−1). (f=2s−1).
(f=2s−1).
Решение для (a)
Введите известное значение в T=1fT=1f
T=12 с-1=0,5 с. T=12 с-1=0,5 с.
13,6
Стратегия ЗА (Б)
Поскольку одним из определений длины волны является расстояние, пройденное волной за один полный цикл или один период, приводятся значения длины волны (λ=0,9 м)(λ=0,9 м), а также частоты. Следовательно, мы можем использовать vw=fλvw=fλ, чтобы найти скорость волны.
Решение для (b)
Введите известные значения в vw=fλvw=fλ
vw=fλ=(2 с-1)(0,9 м) = 1,8 м/с. vw=fλ=(2 с-1)(0,9 м) = 1,8 м/с.
Обсуждение
Мы могли бы также использовать уравнение vw=λTvw=λT для определения скорости волны, поскольку мы уже знаем значение периода (T=0,5 с)(T=0,5 с) из нашего расчета в части ( а), и мы бы пришли к тому же ответу.
Практические задачи
7.
Частота волны 10 Гц. Каков его период?
Каков его период?
- Период волны 100 с.
- Период волны 10 с.
- Период волны 0,01 с.
- Период волны 0,1 с.
8.
Какова скорость волны с длиной волны 2 м и частотой 5 Гц?
- 20 м/с
- 2,5 м/с
- 0,4 м/с
- 10 м/с
Проверьте свое понимание
Поддержка учителей
Поддержка учителей
Используйте эти вопросы, чтобы оценить достижения учащихся в соответствии с целями обучения данного раздела. Если учащиеся борются с определенной целью, эти вопросы помогут определить такую цель и направить их к соответствующему содержанию.
9.
Какова амплитуда волны?
- Четверть общей высоты волны
- Половина общей высоты волны
- Удвоенная общая высота волны
- Четырехкратная общая высота волны
10.
Что понимают под длиной волны?
Длина волны — это расстояние между соседними одинаковыми частями волны, параллельными направлению распространения.
Длина волны — это расстояние между соседними одинаковыми частями волны, перпендикулярное направлению распространения.
Длина волны — это расстояние между гребнем и прилегающей впадиной волны, параллельное направлению распространения.
- 92
12.
Когда длина волны прямо пропорциональна периоду волны?
- Когда скорость волны уменьшается вдвое
- Когда скорость волны постоянна
- Когда скорость волны удваивается
- Когда скорость волны утроится
Связь амплитуды и периода – Международный бакалавриат по физике
- Поиск
- Присоединяйтесь к более чем 1,2 миллионам студентов каждый месяц
- Ускорьте свое обучение на 29%
- Неограниченный доступ всего от 6,99 фунтов стерлингов в месяц
Выдержки из этого документа…
Связь между амплитудой и периодом
Исследовательский вопрос: Как изменение амплитуды чаши влияет на период движения мяча, колеблющегося в мате?
Введение
Колебание – это движение, которое повторяется. Простое гармоническое движение — это когда объект перемещается назад и вперед в пределах стабильного положения равновесия. В идеальной ситуации, когда трение не играет никакой роли, шарик будет продолжать колебаться непрерывно. Однако в реальной жизни это невозможно, вместо этого объекты сталкиваются с демпфированием из-за трения. Любая система, в которой происходит гармоническое движение, называется осциллятором. Простыми примерами являются масса на конце вертикальной пружины, маятник или тележка, привязанная между двумя пружинами. Амплитуда колебаний – это максимальное смещение системы от положения покоя.
В идеальной ситуации, когда трение не играет никакой роли, шарик будет продолжать колебаться непрерывно. Однако в реальной жизни это невозможно, вместо этого объекты сталкиваются с демпфированием из-за трения. Любая система, в которой происходит гармоническое движение, называется осциллятором. Простыми примерами являются масса на конце вертикальной пружины, маятник или тележка, привязанная между двумя пружинами. Амплитуда колебаний – это максимальное смещение системы от положения покоя.
Гипотеза:
В этом эксперименте я буду менять положение, из которого я буду бросать мяч в чашу, таким образом амплитуда будет меняться.
На мой взгляд, чем выше амплитуда, тем дольше мяч возвращается в исходную точку выброса при максимальной амплитуде. Это приведет к длительному периоду времени. Ибо движение мяча в чаше вызывается внутренним толчком, создаваемым поверхностью чаши. Следовательно, при увеличении амплитуды период времени будет увеличиваться.
. ..читать дальше.
..читать дальше.
12:66
10:03
9:03
11:63
16,11,11 и 11
20 см
10:37
10:32
10:06
9000 2 10:3210:06
: 8112,11,10 и 11
15 см
11:10
8:91
9:10
8:56
12 000 и 8
10см
7:97
8:72
8:50
8:62
10,9,8&8
5 см
7:07
6:84
7:69
7:66
9,6,8&8
Ширина чашеобразного мата – 66 см
Время одного колебания12:66/16 | 0.79 |
10:03/11 | 0.91 |
9:03/11 | 0.82 |
11:63/11 | 1. |
Amplitude 20cm-Time for one oscillation
10:37/12 | 0.86 |
10:32/11 | 0.93 |
10.06/10 | 1.0 |
9:81/11 | 0.89 |
Amplitude 15cm-Time for one oscillation
11:10/12 | 0.92 |
8:91/9 | 0.99 |
9:10/9 | 1. |
8:56/8 | 1.07 |
Amplitude 10 cm-Time for one oscillation
7:97/10 | 0.79 |
8:72/9 | 0.96 |
8:50/8 | 1.06 |
8:62/8 | 1.07 |
…читать дальше.
Последующий эксперимент: Поскольку в этом эксперименте мы смотрели на связь между амплитудой и периодом, после этого мы можем взять на себя инициативу посмотреть и сравнить два других свойства.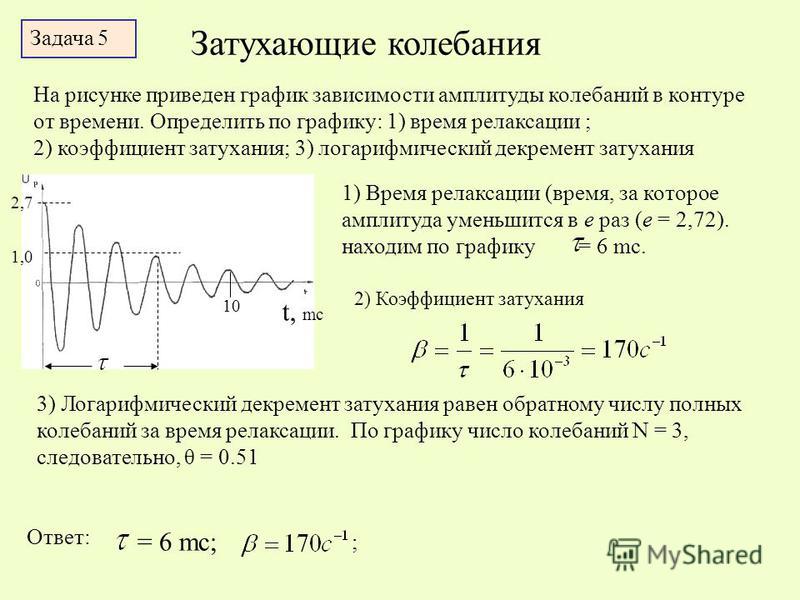 Итак, мы можем посмотреть на влияние изменения массы на период. Мы можем попробовать поместить разные грузы в маленькую цилиндрическую трубку, а затем свернуть ее. В этом случае амплитуда останется регулируемой переменной.
Итак, мы можем посмотреть на влияние изменения массы на период. Мы можем попробовать поместить разные грузы в маленькую цилиндрическую трубку, а затем свернуть ее. В этом случае амплитуда останется регулируемой переменной.
Библиография
“Гармонический осциллятор -.” Википедия, свободная энциклопедия. Веб. 11 января 2010 г.
«Колебание: определение с сайта Answers.com». Answers.com: вики-вопросы и ответы в сочетании с бесплатным онлайн-словарем, тезаурусом и энциклопедиями. Веб. 11 января 2010 г.
“Что такое амплитуда?” Университет Индианы. Веб. 11 января 2010 г.
…читать дальше.
Эта письменная работа студента — одна из многих, которые можно найти в нашем разделе физики Международного бакалавриата.
Нашли то, что искали?
Не тот? Найдите название своего сочинения.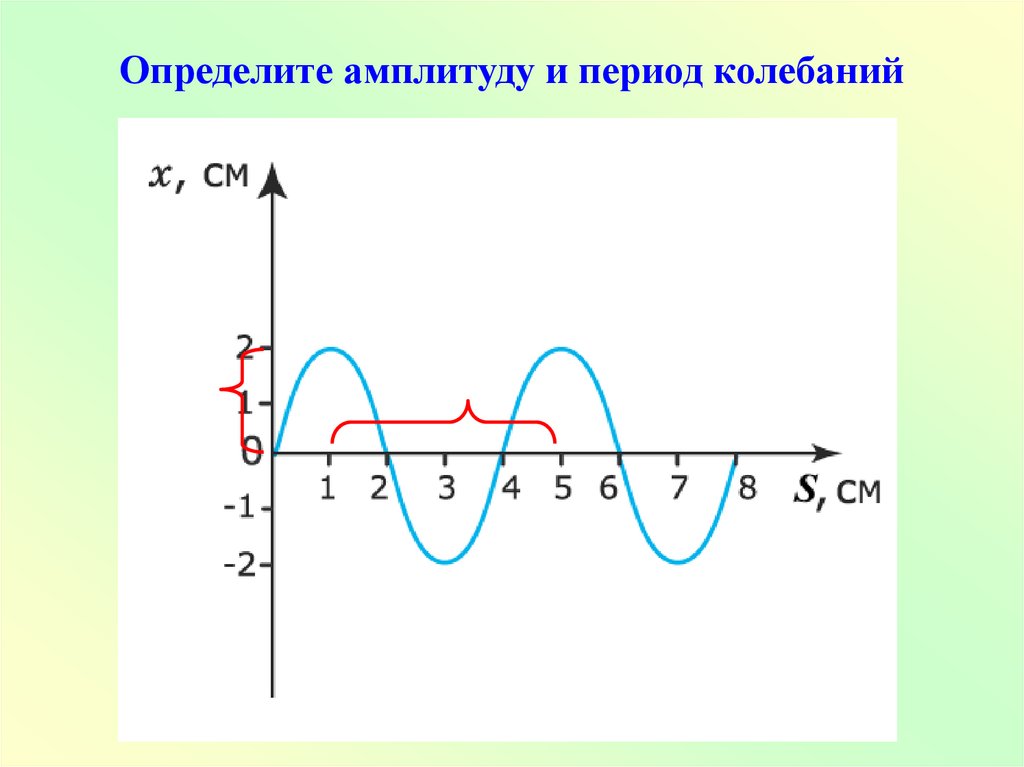 ..
..
- Присоединяйтесь к более чем 1,2 миллионам студентов каждый месяц
- Ускорьте свое обучение на 29%
- Неограниченный доступ всего от 6,99 фунтов стерлингов в месяц
Посмотреть связанные эссе
Таким образом, меняются только формулы между переменными, но общая зависимость (обратная или прямо пропорциональная) не меняется ни для каких других баров. Общее объяснение этого явления, возможно, заключается в том, что по мере того, как я увеличиваю расстояние между двумя струнами, сохраняя при этом постоянными и контролируемыми другие факторы, я увеличиваю натяжение струн.
Неопределенности: � 0,05 2,00 0,10 4,00 0,20 6,00 0,40 8,00 0,50 10,00 0,70 12,00 0,80 * Высота второго считывания, CM Неопределенности: � 0,05 Глубина, CM (D) Неопределенности: � 0,05 2,00 0,30 4,00 0,50 6,00 0,60,70 10,00 0,9 0,05 2,00 0,30 0,50 6,0 12,00 1,10 * Третье показание Высота, см Погрешности: � 0,05 Глубина, см (d)
столбцы в диапазоне от 0,02 до 0,04 кажутся реалистичными, а не слишком большими.
 Причины ошибки > Прежде всего, это человеческий фактор. Трудно точно отметить, когда 10 полных колебаний. Это, наряду со временем реакции при запуске и остановке секундомера, приводит к неточности результатов.
Причины ошибки > Прежде всего, это человеческий фактор. Трудно точно отметить, когда 10 полных колебаний. Это, наряду со временем реакции при запуске и остановке секундомера, приводит к неточности результатов.Используйте информацию из графиков, чтобы вычислить для этой волны (i) длину волны; …………………………………………. …………………………………………. …………………. (1) (ii) частота; …………………………………………. …………………………………………. …………………. (2) (iii) скорость волны. …………………………………………. …………………………………………. ………………… (1) (б) Волна движется слева направо и имеет период Т.
Это могло бы иметь эффект случайной ошибки с искажением результатов на 0,2 или 0,3 секунды. Кроме того, возможно, что при измерении длин они были измерены не совсем точно (это всегда возможно, так как это человеческий фактор)
(Silliman.
 1891) У велосипеда шины из резины, т.е. у велосипеда пневматические шины. Основной причиной сопротивления качению в пневматике является гистерезис. Гистерезис — это свойство, уникальное для всех эластичных изделий, в которых энергия теряется во время восстановления эластика после напряжения, которому он подвергается.
1891) У велосипеда шины из резины, т.е. у велосипеда пневматические шины. Основной причиной сопротивления качению в пневматике является гистерезис. Гистерезис — это свойство, уникальное для всех эластичных изделий, в которых энергия теряется во время восстановления эластика после напряжения, которому он подвергается.
Однако при использовании неопределенности для значения ускорения 1,41 м с-2 это значение может достигать примерно 1,11 м с-2. Этот результат ближе к значению, полученному на графике. Также следует отметить, что точка 0,219, 0,970 на графике находится ниже линейного тренда
.Учащиеся должны понимать, что изменение температуры планеты за определенный период времени определяется как: (интенсивность поступающего излучения – интенсивность исходящего излучения) × время/теплоемкость поверхности. Возможные модели глобального потепления: Изменение состава парниковых газов в атмосфере Увеличение солнечной вспышечной активности
- Более 160 000 штук
письменных работ студентов - Аннотировано
опытными учителями - Идеи и отзывы для
улучшения вашей работы
Амплитуда, период времени и частота вибрации
Звук – это форма энергии, создаваемая вибрирующими телами. Его распространение требует использования среды. В результате звук не может распространяться в вакууме, потому что нет материала для передачи звуковых волн. Звуковая вибрация — это возвратно-поступательное движение объекта, которое вызывает создание звука. Его часто называют колебательное движение .
Его распространение требует использования среды. В результате звук не может распространяться в вакууме, потому что нет материала для передачи звуковых волн. Звуковая вибрация — это возвратно-поступательное движение объекта, которое вызывает создание звука. Его часто называют колебательное движение .
Что такое колебания?
Колебание — это обычное ритмичное движение вперед и назад. Звук распространяется из одного места в другое в виде волн, вызванных движением объектов в среде. Волна — это явление или разрушение, при котором энергия передается от одной точки к другой без физического взаимодействия. В результате звук рассматривается как волна.
Каждая вибрация или колебание имеет три основные характеристики: Амплитуда, период времени и частота подробно обсуждаются в следующем разделе:
Амплитуда Амплитуда звуковой волны — это измерение высоты волны. Амплитуда звуковой волны называется ее громкостью или максимальным смещением вибрирующих частиц в среде от их среднего положения при воспроизведении звука. Это разница между гребнем или впадиной волны и ее средним положением.
Это разница между гребнем или впадиной волны и ее средним положением.
Амплитуда волны – это частота максимального разрушения частиц в среде по обе стороны от среднего значения.
Буква A обычно используется для его обозначения.
Единицей СИ для него является метр (м) .
Период времениПериод времени может быть описан как количество времени, которое требуется для выполнения задачи. Когда явление происходит регулярно, говорят, что оно носит периодический характер. Цикл — это количество времени, которое требуется для повторения сезонного явления. Время, которое требуется частице, чтобы завершить один цикл колебаний, является временным интервалом частицы.
Время, необходимое для совершения одного колебания в глубине среды, называется временным циклом звуковой волны.
Отношение между периодом времени (T) и частотой (f) равно
T=1 / f
Обозначается буквой T .
Единицей измерения в системе СИ является секунда (с) .
ЧастотаЧастота колебаний определяется как количество колебаний в секунду. Его единицей является герц, который обозначается символом Гц. В общем, частота волны относится к тому, как часто частицы в среде вибрируют, когда волна проходит через среду.
Частота звуковой волны определяется как количество колебаний в единицу времени.
Частота (f) = 1 / период времени (T)
Обозначается буквами f или v.
Примеры задачЗадача 1. Почему пустой сосуд издает более громкий звук, чем наполненный?
Решение:
Пустой сосуд производит более громкий звук, чем наполненный, потому что молекулы воздуха в наполненном сосуде имеют большую амплитуду и большую интенсивность, чем молекулы жидкости в наполненном сосуде.
Задача 2.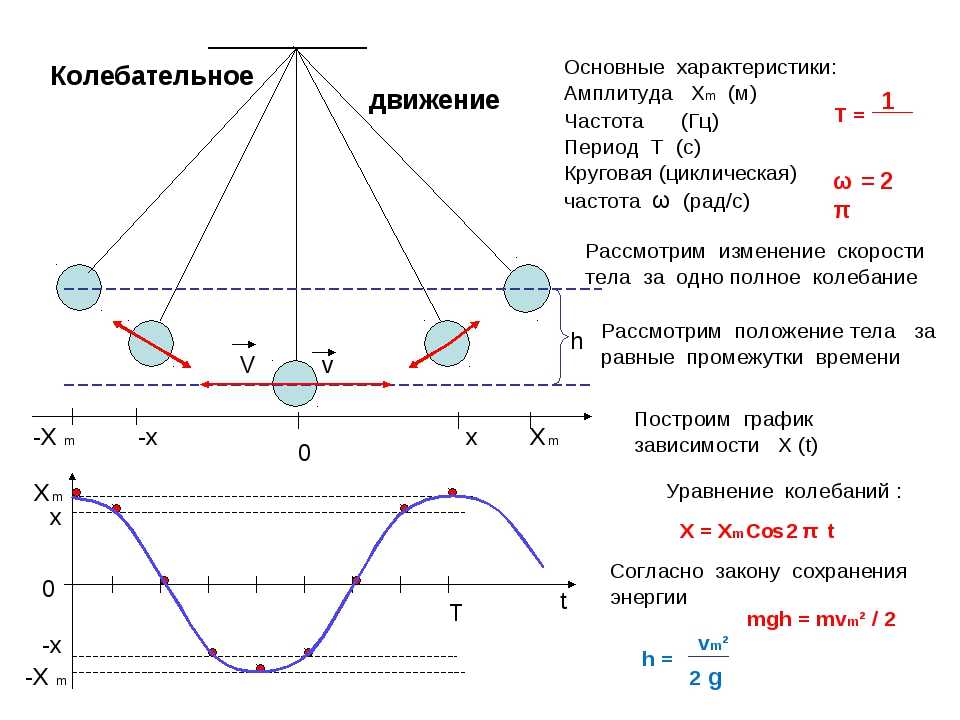 Волна какого типа является звуком?
Волна какого типа является звуком?
Решение:
Звуковые волны делятся на три категории:
1. Продольные звуковые волны: Продольная волна – это волна, в которой движение частиц среды параллельно направлению переноса энергии .
2. Механические звуковые волны: Механическая волна — это волна, которая зависит от колебаний материи, то есть передает энергию через среду для распространения
3. Звуковые волны давления: Волна давления или волна сжатия имеет регулярную структуру областей высокого и низкого давления. Поскольку звуковые волны состоят из сжатий и разрежений, их области колеблются между моделями низкого и высокого давления.
Задача 3: Человек слушает тон частотой 600 Гц, сидя на расстоянии 550 м от источника звука. Каков временной интервал между последовательными сжатиями от источника?
Решение:
Интервал времени между двумя последовательными сжатиями равен периоду волны.
Этот период времени является обратным частоте волны и определяется соотношением СОНАР.
Решение:
Преобразователь гидролокатора создает ультразвуковую волну, которая распространяется через любую среду (морскую воду). Волна, ударяясь о поверхность, отражается и обнаруживается гидролокатором. Расстояние до поверхности можно рассчитать как:
2d = v × t
, где d — расстояние, v — скорость звука, t — время.
Этот метод измерения расстояния также известен как «эхо-диапазон». Результат равен 2d, потому что волна покрывает расстояние d при выходе и снова расстояние d при возвращении после отражения.
Задача 5: Опишите, как возникают сжатия и разрежения в воздухе вблизи источника звука.
Решение:
Сжатие — это область высокого давления, где частицы находятся близко, а разрежение — это область, где частицы находятся далеко друг от друга.
Когда волна движется вперед, она сжимается из-за давления среды. Точно так же видны разрежения, когда волна движется назад. Когда волна в воздухе сталкивается со многими частицами и движется вперед и назад, возникают сжатия и разрежения.
Q4 Определите следующие термины a Амплитуда b Частота c Период времени…
Перейти к
- Объективные вопросы
- Вопросы с короткими/длинными ответами
- Иметь значение
- Физические величины и измерения
- Сила и давление
- Энергия
- Световая энергия
- Теплопередача
- Звук
- Электричество
Главная > Селина Солюшнс Класс 8 Физика > Глава 7 – Звук > Упражнение: Вопросы с короткими/длинными ответами > Вопрос 4
Вопрос 4 Краткий/Подробный ответ Вопросы
Q4) Определите следующие термины:
(a) Амплитуда
(b) Частота
(c) Период времени
Ответ:
Решение:
(a) Амплитуда.
Максимальное смещение волны по обе стороны от ее среднего положения называется Амплитудой.
(b) Частота. Число колебаний, совершаемых волной за одну секунду, называется частотой.
(c) Период времени. Время, необходимое для завершения одной вибрации, называется периодом времени, т. е. от A до B. обучающие видео с вопросами и ответами меня зовут паллаби и я математик репетитор по естествознанию на лидо давайте посмотрим на вопрос, который у нас есть здесь поэтому определим следующие термины: амплитуда частота и период времени теперь, чтобы понять это, у меня есть два картинки как вы можете видеть, давайте назовем это как картинка давайте назовем это как картинку б давайте посмотрим на картинку а Итак, как вы видите, давайте начнем с амплитуда, поэтому амплитуда максимальное смещение волны по обе стороны от его среднего положения, поэтому у нас волна который это и это музыкант линия горизонтальная линия это среднее положение сейчас, как вы можете видеть волна идет вверх и вниз прямо так максимальное водоизмещение в обе стороны, так что это максимум смещение в обе стороны так это и есть амплитуда вот как мы определяем амплитуду давайте тогда посмотрим на частоту что мы подразумеваем под частотой так что частота – это не что иное, как число вибраций производимого источником звука в одном второй Итак, давайте теперь посмотрим на картинку b так скажем отсюда до скажем, здесь была одна секунда отсюда до сюда, скажем, это один второй и когда мы видим здесь, мы можем видеть что частота количество производимые вибрации в волне номер один больше по сравнению количеству колебаний, производимых в волна номер два в течение периода времени в одну секунду, так что это одна секунда это тоже одна во-вторых, мы видим количество вибраций больше здесь по сравнению с этим давайте вернемся к определению частоты поэтому частота определяется как количество производимые вибрации по источнику звука за одну секунду частота также дается как одна за раз период период волны, поэтому единица один на второй или второй обратный, который также называется герц, поэтому единицей измерения является герц обозначается как h z теперь давайте перейдем к период времени, поэтому период времени является время взятый волной, чтобы завершить одно колебание так как вы можете видеть отсюда давайте просто посмотрим, какой период времени этой волны так что здесь это заканчивается здесь и снова вибрация будет повторяться поэтому это одна вибрация это скажем, если это одна секунда тогда это будет период времени для волны номер два давайте посмотрим на более четкая картинка на картинке а так вы все можете видеть, как период времени здесь изображено то есть это время, затраченное волной, так что это это т это т ось x равна t, поэтому это время, затрачиваемое волна чтобы завершить одну вибрацию, чтобы это было волна была в среднем положении пошла к крайности, затем в другую крайность и затем он вернулся к среднему должность так вот где период времени заканчивается так это – период времени t волны Конечно, единица измерения будет секунды, потому что это измерение времени правильно, поэтому я надеюсь, что это точка ясна, если у вас есть дальнейшие вопросы пожалуйста, оставьте свои комментарии ниже, спасибо ты”
Связанные вопросы
Q1) Как звук распространяется по воздуху?
Q2) Что такое продольная волна?
Q3) Объясните механизм образования продольной волны при колебаниях источника в воздухе.
Q5) Получите связь между периодом времени и частотой.
Q6) Назовите три характеристики музыкального звука.
Q7) Назовите приведенную ниже величину, которая определяет громкость звуковой волны: (a) Длина волны (b) F…
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Упражнения
Объективные вопросы
Короткие/длинные вопросы. Вопросы
Главы
Маттер
Физические величины и измерения
Сила и давление
Энергия
Энергия Light
Теплопередача
Sound
Electricity
Sound
Electricity
.
Курсы
Быстрые ссылки
Условия и политика
Условия и политика
2022 © Quality Tutorials Pvt Ltd Все права защищены подразумевается амплитуда, частота, период, фазовый сдвиг и вертикальный сдвиг, и как их найти из самой функции или графика.
Волны важны — они везде! В природе они встречаются в волнах на воде, цунами, землетрясениях, звуке и свете. Куда бы вы ни посмотрели, волны являются доказательством того, что мир происходит.
Мы нашли способы использования многих форм волн, включая электричество, рентгеновские лучи, микроволны, динамики и передачу информации по всему миру с ошеломляющей скоростью, и это лишь некоторые из них!
Surfer VS Sine Wave: разные волны… но математически очень похожи!В математике волны обычно изображаются в виде функции, называемой синусоидальной функцией .
В конце урока есть несколько практических вопросов, чтобы вы могли проверить свои знания.
Содержание
Из чего состоит периодическая функция
Амплитуда
Период
Частота
Фаза/Горизонтальный сдвиг
Вертикальный сдвиг
Синусоидальные функции
Нахождение амплитуды
Нахождение амплитуды
Нахождение периода
Нахождение вертикального сдвига/
Нахождение частоты
Горизонтальный сдвиг
Практические вопросы
Подведение итогов (каламбур!)Что делает периодическую функцию: амплитуда, период, фазовый сдвиг
Периодическая функция повторяется через определенное время или расстояние и, если оставить его в покое, никогда не закончится.
Измерение между повторами — это период или длина волны .
Чаще всего встречается функция синуса.
y = sin(t)
Вот как это выглядит на графике.
Эти функции имеют 5 основных атрибутов, которые также называются преобразованиями.
1. Амплитуда
Амплитуда волны – наибольшее смещение от положения покоя. Чем больше амплитуда, тем выше волна.
В звуковых волнах большая амплитуда означает более громкий звук.
В световых волнах — разновидности электромагнитного излучения — большая амплитуда означает более яркий свет.
Радио часто передается с использованием AM или передач с амплитудной модуляцией, что означает, что информация может быть получена приемником, настроенным на правильную амплитуду волн.
2. Период
Период волны – это время или расстояние между двумя колебаниями – время, за которое точка на колеблющемся объекте возвращается в исходное положение.
Его можно назвать периодом времени и он имеет символ T.
Слово период используется для волн, измеренных во времени. Если измерением является расстояние, оно называется длиной волны .
Период волны тесно связан с ее частотой.
3. Частота
Вы знаете, когда вы получаете SMS или кто-то звонит? Ваш телефон вибрирует , чтобы предупредить вас, верно? Ваш телефон делает что-то, называемое , генерирующее .
Частота колебаний показывает, сколько раз телефон «вибрирует» взад-вперед каждую секунду.
Чем выше частота, тем больше колебаний в секунду, поэтому на графике волны выглядят ближе друг к другу.
Чем выше частота, тем больше колебаний в секунду, благодаря чему волны кажутся ближе друг к другу.
Чем выше частота, тем выше тон звука. Вы можете поэкспериментировать с соотношением между высотой тона и частотой.
Частотная модуляция (FM) — это тип передачи для радио, за исключением того, что вместо изменения амплитуды для передачи информации вместо этого изменяется частота.
Однако есть и другие способы изменить поведение волны.
4. Фазовый сдвиг
Фазовый сдвиг , измеряет, насколько далеко влево или вправо, или по горизонтали , волна была сдвигом ed от нормальной функции синуса. Именно по этой причине его иногда называют горизонтальным сдвигом .
Подобно тому, как данные могут передаваться по разным каналам, изменяя частоту или амплитуду, как упоминалось для радио, иногда меняется сдвиг по горизонтали.
Это называется фазовой манипуляцией или PSK. Он используется для многих вещей, Wi-Fi и Bluetooth являются двумя наиболее широко используемыми.
5. Сдвиг по вертикали
Последняя часть головоломки, вертикальный сдвиг работает таким же образом, но измеряет, насколько вверх или вниз по оси y или по вертикали волна была смещена от нормальная синусоидальная функция.
Синусоидальные функции
Синусоидальные функции являются периодическими, но также используют тригонометрические функции, такие как синус или косинус.
Син -усоидальный.
Вы встречали одного из них ранее, грех ( т ). В данном случае t показывает время.
Вот как это снова выглядит на графике:
На этом графике показана только часть функции, примерно между -π и 6π, но, как и временная петля Доктора Стрэнджа, она на самом деле длится вечно, повторяя один и тот же шаблон. .
Вы часто будете видеть другие буквы для аргумента функции синуса вместо t . Обычно x показывает расстояние, а θ показывает углы.
В этом уроке будут использоваться только t – важно помнить, что можно использовать и другие переменные.
Как найти атрибуты синусоидальной функции
Эти атрибуты – это те, которые вы только что посмотрели:
- Амплитуда
- Период
- Частота
- Сдвиг
- Фаза/Хорзонт
.. найти, когда только одно из них отличается от стандартной синусоиды, но при объединении нескольких преобразований разных типов легко заблудиться, если не знаешь, что ищешь.В этом разделе вам будут даны инструменты, чтобы разобраться во всем этом.
Как найти амплитуду
y = A sin(B( t – φ)) + C
Амплитуда, A – это число, на которое умножается функция синуса.
Подумайте об этом так: звук будет в два раза громче, если вы удвоите его амплитуду. Умножение всей функции на 2 удваивает амплитуду.
На графике умножение всей синусоидальной функции на некоторое число А выглядит как растяжение или сжатие синусоидального графика в y -направление
Амплитуда, A, определяется путем взятия половины расстояния по вертикали между пиками и впадинами.
пиков являются наивысшими точками каждой волны, а впадин — самыми низкими точками. При написании функции для волны с использованием sin( t ) синусоидальная функция умножается на амплитуду.
Вы можете иметь отрицательное значение для A, но это не означает, что амплитуда отрицательна! Это просто означает, что график был перевернут в т -ось.
Амплитуда должна быть положительным числом, как и абсолютное значение, величина или размер этого коэффициента |A|.
Вот пример того, как найти амплитуду.
На этом графике пик находится на y = 2,5, а впадина — на y = -0,5, поэтому вертикальное расстояние между ними составляет 2,5 – (-0,5) = 3 единицы.
Амплитуда составляет половину этого расстояния, то есть 1,5 единицы.
Это означает, что уравнение для этой функции будет выглядеть так:
y = 1,5 sin(B( t – φ)) + C
Пока не беспокойтесь о значениях B, φ и C – мы доберемся до них по одному!
Как найти период
А что, если у вас нет уравнения, а есть только график?
Период волны можно определить, измерив расстояние между двумя последовательными пиками или впадинами.
Измерьте расстояние между двумя вершинами ИЛИ двумя впадинами , расположенными рядом друг с другом.
Помните, пики — это самые высокие точки функции, а впадины — самые низкие.
Если вы посмотрите на синусоидальную функцию по умолчанию (без каких-либо преобразований), вы увидите, что функция возвращается к одной и той же точке каждый раз, когда вы смотрите на 2π дальше по оси t , поэтому период базовой синусоидальной функции равен 2π.
Период T волны определяется путем измерения расстояния между двумя последовательными пиками или впадинами.
Если периодическая функция имеет период 2, то
f(t) = f( t + 2)
= f( t + 4)
= f( t + 6)Это означает, что добавление одного периода T к значению t не меняет результат.
На самом деле вы можете выбрать любую точку и измерить расстояние между ней и той же точкой на следующем фронте волны, но пики или впадины обычно проще всего использовать.
Вот пример того, как найти период.
Это та же волна, что и в предыдущем примере. Один пик приходится на t = 0 с, а следующий пик приходится на т = 2 с.
Разница между этими временами 2, поэтому период равен 2 секундам.
А что, если у вас нет графика, а есть только уравнение?
Вот где частота!
Как найти частоту
y = A sin(B( t – φ))+ C
Частоту волны f изобразить не так просто, как некоторые другие атрибуты, но его можно рассчитать по периоду времени T или наоборот, используя следующие данные:
f = 1 ⁄ T
T = 1 ⁄ fИтак, чтобы найти частоту волны, сначала найдите период, как мы показали выше, а затем возьмите его обратную величину, чтобы найти частоту.
Полезно знать, что частота означает, сколько раз волна повторяется за определенное время.
Если период времени измеряется в секундах, то частота измеряется в Герцах (Гц).
Чем больше период, тем реже будет повторяться волна, поэтому она будет иметь меньшую частоту. Чем короче период, тем выше частота.
Но мы пытаемся найти Б, а не Т или f?!
При работе с радианами вместо частоты используется угловая частота , B.
Он связан с периодом времени формулой
B = 2πf
OR
B = 2π ⁄ TВ последнем разделе мы уже нашли период, который составлял 2 секунды.
Используя формулу для угловой частоты, можно вычислить, что частота равна:
B = 2π ⁄ (2 с) = π рад/с
Теперь мы знаем амплитуду и угловую частоту, поэтому функция синуса на данный момент выглядит следующим образом:
y = 1,5 sin(π( t – φ)) + C
Когда дело доходит до записи уравнения волны как преобразования sin( t ), ввод для функции синуса умножается на угловую частоту после любого горизонтального смещения.
Как найти вертикальное смещение
y = A sin(B( t – φ)) + C
Вертикальный сдвиг — это константа C, добавляемая в конце общей синусоидальной функции.
Исходное положение функции синуса — это линия y = 0.
Когда вы вводите вертикальное смещение C, исходное положение этой функции перемещается с линии y =0 на линию y = C.
Если вертикальное смещение равно -5, то позиция покоя перемещается из строки y =0 в строку y =-5.
Функция синуса всегда симметрична относительно своего положения покоя, поэтому амплитуда поможет найти положение покоя, если у вас нет уравнения для работы.
Амплитуда составляет половин общей высоты волны от пика до впадины.
Если вы уже знаете амплитуду A, возможно, проще измерить расстояние по вертикали d от оси t до впадин, тогда вертикальное смещение равно
C = A + d
Если остальные положение выше оси t , сдвиг по вертикали положительный. Если положение покоя находится ниже оси t , сдвиг по вертикали отрицательный.
Вот пример того, как найти вертикальное смещение.
Это тот же пример, который мы использовали ранее и обнаружили, что амплитуда A = 1,5 единицы.
Расстояние по вертикали от оси t до впадин равно d=-0,5, поэтому вертикальное смещение равно
C = A + d
= 1,5 + (-0,5)
= 13 9000 нашли амплитуду, период, частоту и вертикальный сдвиг этой функции.
Это можно записать так:
y = 1,5 sin(π( t – φ)) + 1
Теперь перейдем к последней части головоломки.
Как найти фазовый сдвиг
y = A sin(B t – φ) + C
Помните из предыдущего: фазовый сдвиг волны, φ, измеряет, насколько далеко волна сместилась по горизонтали от синусоидальной волны по умолчанию.
Чтобы увидеть, насколько далеко сместилась волна, вам нужно найти время, наиболее близкое к t =0, когда волна находится в состоянии покоя и имеет положительный наклон.
Если нет смещения по вертикали, это просто, так как исходное положение – это просто t -ось, линия y =0.
Если есть некоторый сдвиг по вертикали, вам нужно сначала вычислить его — взгляните на раздел выше, чтобы найти положение покоя, используя положения пика-впадины и амплитуду — затем вы можете нарисовать линию y =С.
C — вертикальное смещение, которое вы только что вычислили.
Линия y =C — положение покоя вертикально смещенной волны.
Теперь, когда у вас есть исходное положение, давайте вернемся к фазовому сдвигу.
Используйте это руководство, чтобы выбрать правильную точку функции для измерения. Функция в этой точке должна:
- Быть одной из двух ближайших точек к оси y
- Иметь положительный наклон. Это означает, что при перемещении вдоль оси t значение y увеличивается.
Если точка, которую вы будете использовать, находится справа от оси Y, φ положительна, а если точка слева от оси Y, φ отрицательна.
Неважно, насколько близка ваша точка к t =0, но наклон должен быть положительным — функция периодическая, поэтому добавление или вычитание целых чисел, кратных периоду, к φ не меняет результирующего function — этот метод делает вещи немного проще.
Расстояние от оси y до точки, удовлетворяющей приведенным выше указаниям, представляет собой фазовый сдвиг, φ.
Вот пример того, как найти фазовый сдвиг.
Функция не симметрична относительно оси t , поэтому происходит некоторое вертикальное смещение.
Ранее мы знали, что период времени T=2 с, угловая частота B=π, вертикальное смещение C=1, а линия y =1 является положением покоя.
Посмотрим на график. Ближайшая к t =0 точка, проходящая через эту прямую с положительным наклоном, выделена и находится на t =0,25 с. Это на 0,25 секунды вправо, поэтому фазовый сдвиг равен φ=0,25 секунды!
y = 1,5 sin(π( t – 0,25)) + 1
Несмотря на то, что знак перед φ в общем уравнении отрицательный, положительное значение φ все равно вызовет сдвиг в положительном направлении.
Подумайте о преобразовании графа — смещение ввода назад заставляет график двигаться вперед.
Практические вопросы
А теперь попробуйте эти практические вопросы. Если вы сможете пройти их все, вы будете намного увереннее решать задачи о функциях периода.
Если вы не можете, оставьте комментарий о том, с чем вы боретесь, и один из нас будет рад помочь!
И помните: если вы хотите сохранить что-то свежее в своей голове, вам нужно регулярно это практиковать!
Синусоидальной волне требуется 4π секунд, чтобы завершить колебание.
а) Какова угловая частота волны?
б) Амплитуда этой волны 3 единицы, смещения по горизонтали и вертикали нет. Напишите уравнение волны.
а) Угловая частота, B равна
B = 2π ⁄ T
= 2π ⁄ 4π
= 2 рад/сB) Y = 3 SIN (2 T )
Уравнение волны дается
Y = 3 SIN ( T 93
Y = 3 SIN ( T 1393
Y = 3 SIN ( T 1393
Y = 3 SIN ( T 1313
. ) – 1
а) Какова амплитуда волны?
б) Каков период волны? (Подсказка: мы используем радианы)
c) Нарисуйте график в диапазоне -π≤t≤π.
а) 3 единицыб) 2π секунд, так как и угловая частота В=1 и период Т= 2π ⁄ B
c) Эскиз должен выглядеть так, с впадиной в точке (- π ⁄ 2 ,-4) и пиком в точке ( π ⁄ 2 ,)3 . Исходное положение и место пересечения оси y должно быть y =1.
Этот график имеет уравнение1308 t И константа фазового сдвига φ)
T=2, поэтому B= 2π ⁄ 2 = π. Кроме того, φ=1, так как положение покоя равно y=0.y = sin(π( t – φ))
= sin(π( t – 1))
= sin(π t – π)и Это означает, что P=π Q=-π.
На этом графике показана волна.а) Найдите амплитуду и вертикальное смещение.
б) Найдите частоту.
в) Найдите горизонтальное смещение.
г) Наконец, запишите уравнение волны.
а) A = 1,6 ⁄ 2 = 0,8 ед.б) Лучше всего это видно между впадинами (0,375,0) и (1,375,0). Время между ними составляет 1 секунду, но колебаний 3, поэтому T = 1 ⁄ 3 секунды.
Используйте это, чтобы найти B.
B = 2π ÷ 1 ⁄ 3
= 6πc) На линии y =0,8 имеется пересечение с положительным наклоном в точке t , а φ=0,125,125.
D) y = 0,8 SIN (6π ( T – 0,125)) + 0,8
Нарисуйте график с уравнениемy = 2 SIN ( 16 A 2222233. + 1)) – 1
В диапазоне 0≤t≤2.
5) Ваш эскиз должен выглядеть так:
Подводя итог (каламбур!)
В этой статье вы узнали не только обо всех различных атрибутах периодических и синусоидальных функций, но и о том, как их все найти!
Обобщение их всех:
- Амплитуда : «высота» волны, равная половине вертикального расстояния между пиками и впадинами.


 com» (Источник)
com» (Источник)
 Ожидается, что студент:
Ожидается, что студент:
 05
05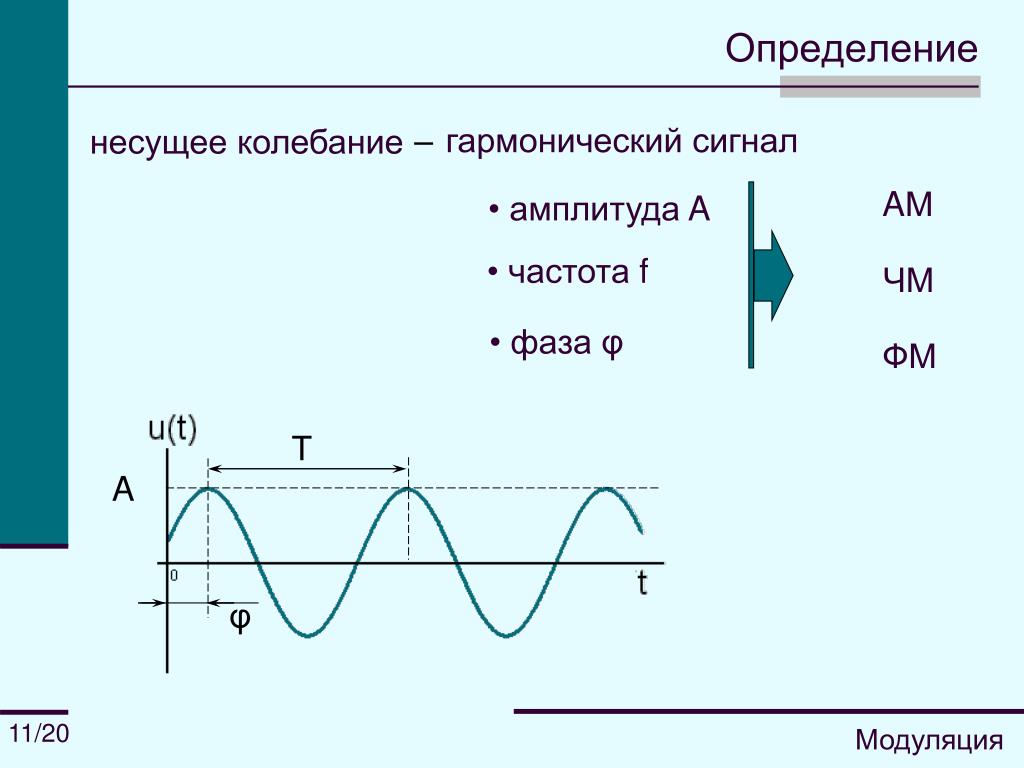 01
01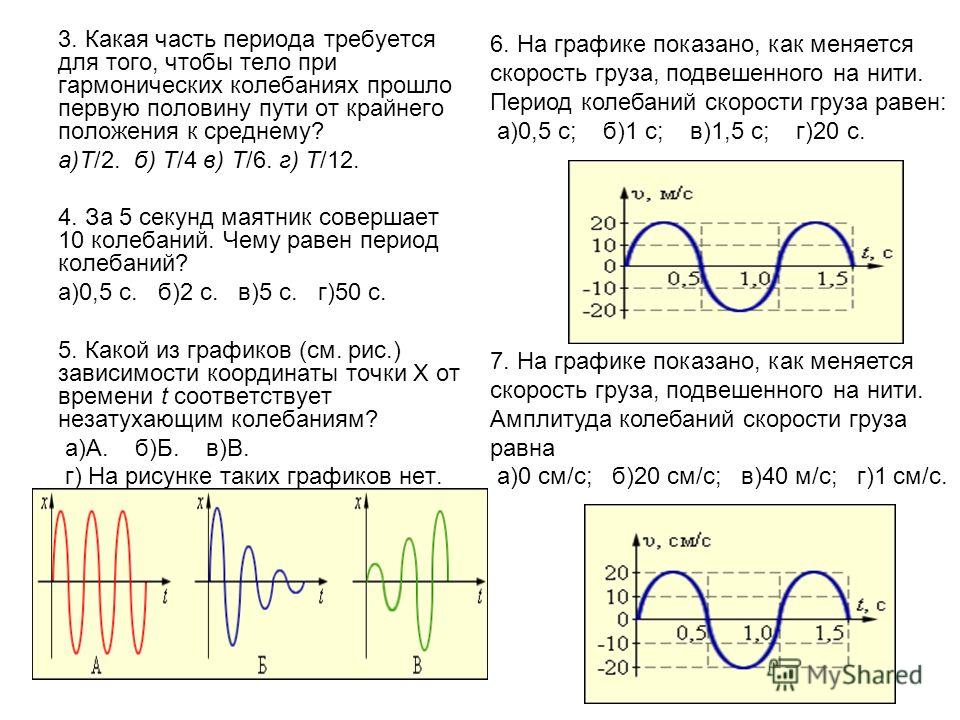 Причины ошибки > Прежде всего, это человеческий фактор. Трудно точно отметить, когда 10 полных колебаний. Это, наряду со временем реакции при запуске и остановке секундомера, приводит к неточности результатов.
Причины ошибки > Прежде всего, это человеческий фактор. Трудно точно отметить, когда 10 полных колебаний. Это, наряду со временем реакции при запуске и остановке секундомера, приводит к неточности результатов. 1891) У велосипеда шины из резины, т.е. у велосипеда пневматические шины. Основной причиной сопротивления качению в пневматике является гистерезис. Гистерезис — это свойство, уникальное для всех эластичных изделий, в которых энергия теряется во время восстановления эластика после напряжения, которому он подвергается.
1891) У велосипеда шины из резины, т.е. у велосипеда пневматические шины. Основной причиной сопротивления качению в пневматике является гистерезис. Гистерезис — это свойство, уникальное для всех эластичных изделий, в которых энергия теряется во время восстановления эластика после напряжения, которому он подвергается. Этот период времени является обратным частоте волны и определяется соотношением СОНАР.
Этот период времени является обратным частоте волны и определяется соотношением СОНАР.  Когда волна движется вперед, она сжимается из-за давления среды. Точно так же видны разрежения, когда волна движется назад. Когда волна в воздухе сталкивается со многими частицами и движется вперед и назад, возникают сжатия и разрежения.
Когда волна движется вперед, она сжимается из-за давления среды. Точно так же видны разрежения, когда волна движется назад. Когда волна в воздухе сталкивается со многими частицами и движется вперед и назад, возникают сжатия и разрежения. Максимальное смещение волны по обе стороны от ее среднего положения называется Амплитудой.
Максимальное смещение волны по обе стороны от ее среднего положения называется Амплитудой.

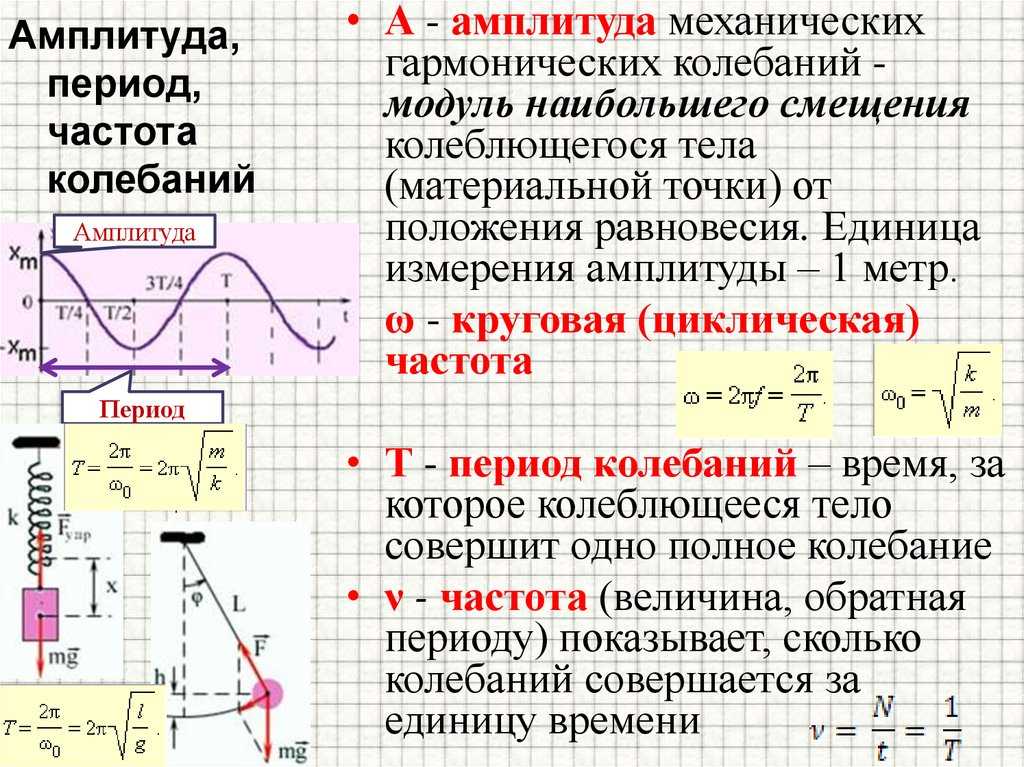 Измерение между повторами — это период или длина волны .
Измерение между повторами — это период или длина волны .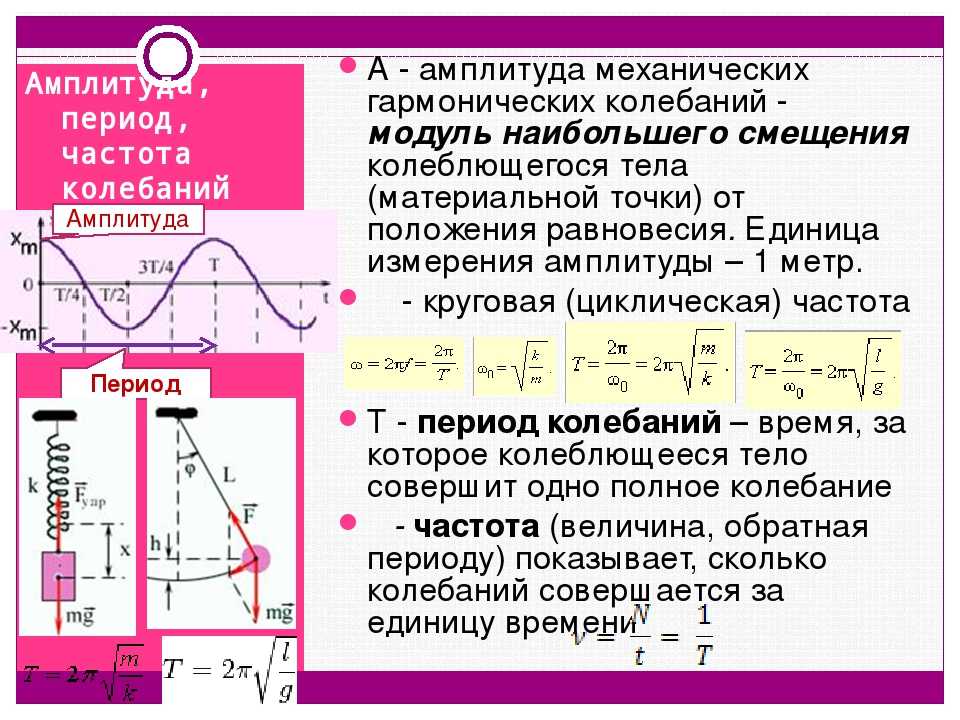 Его можно назвать периодом времени и он имеет символ T.
Его можно назвать периодом времени и он имеет символ T.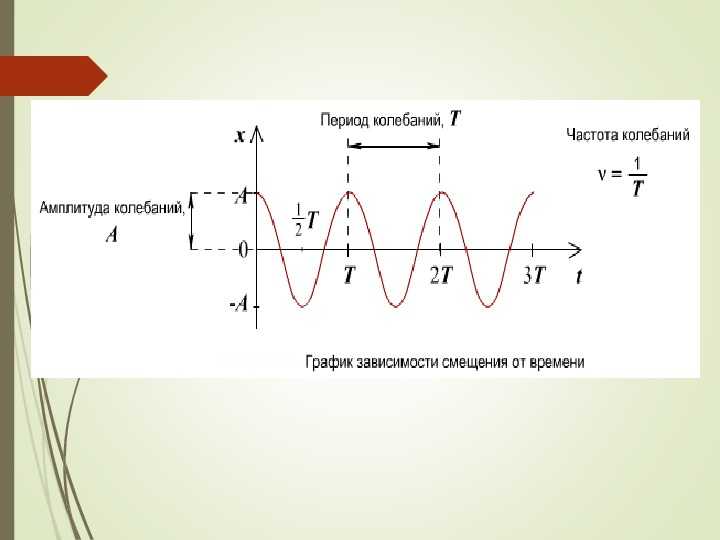
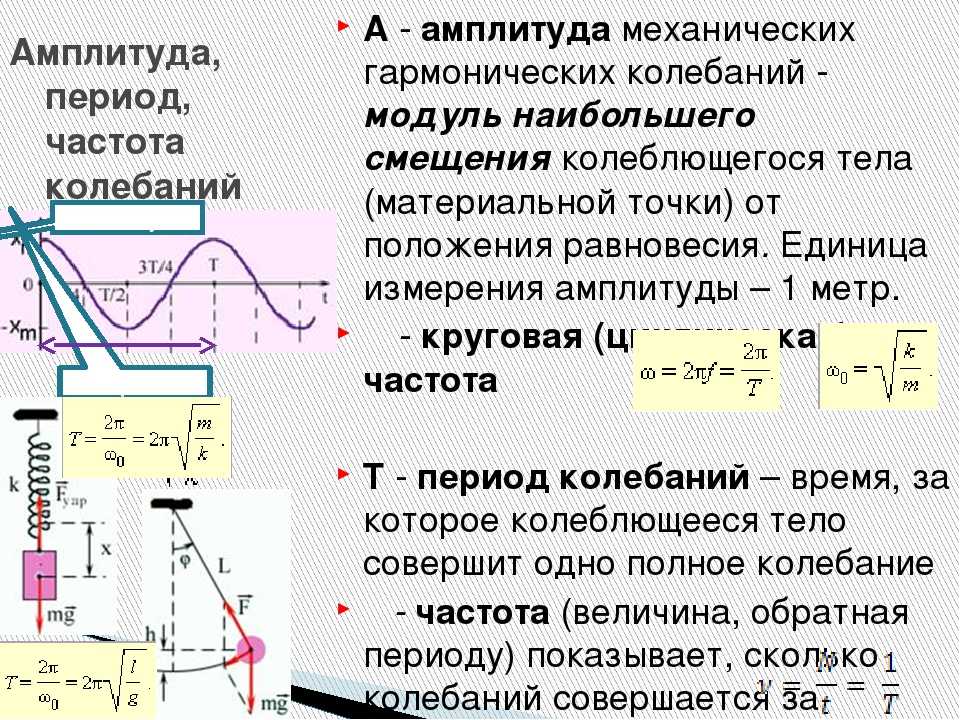 Син -усоидальный.
Син -усоидальный.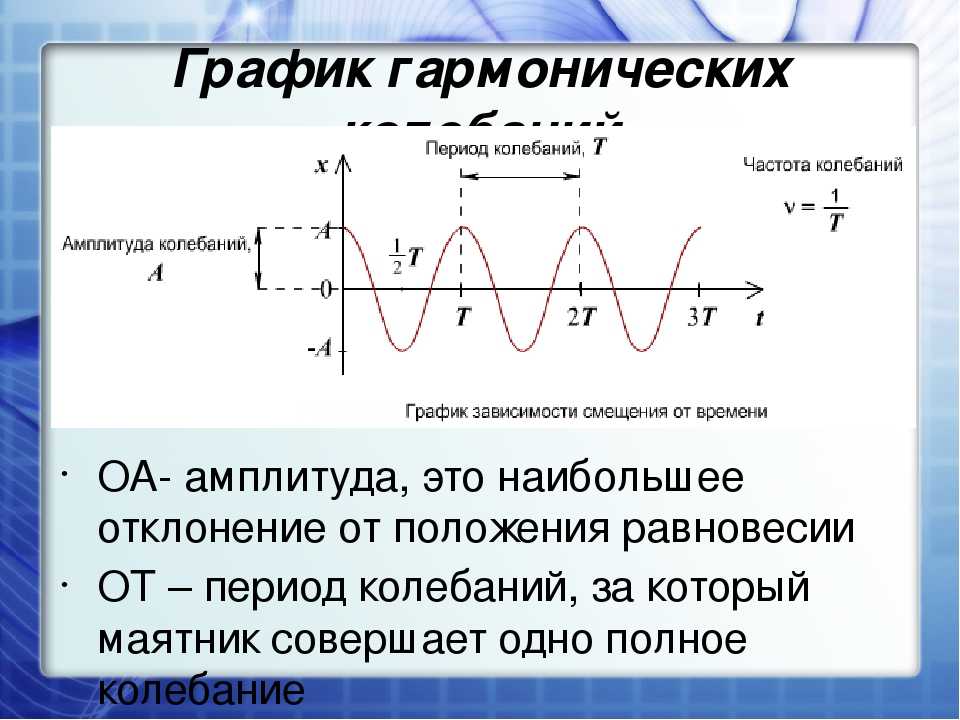
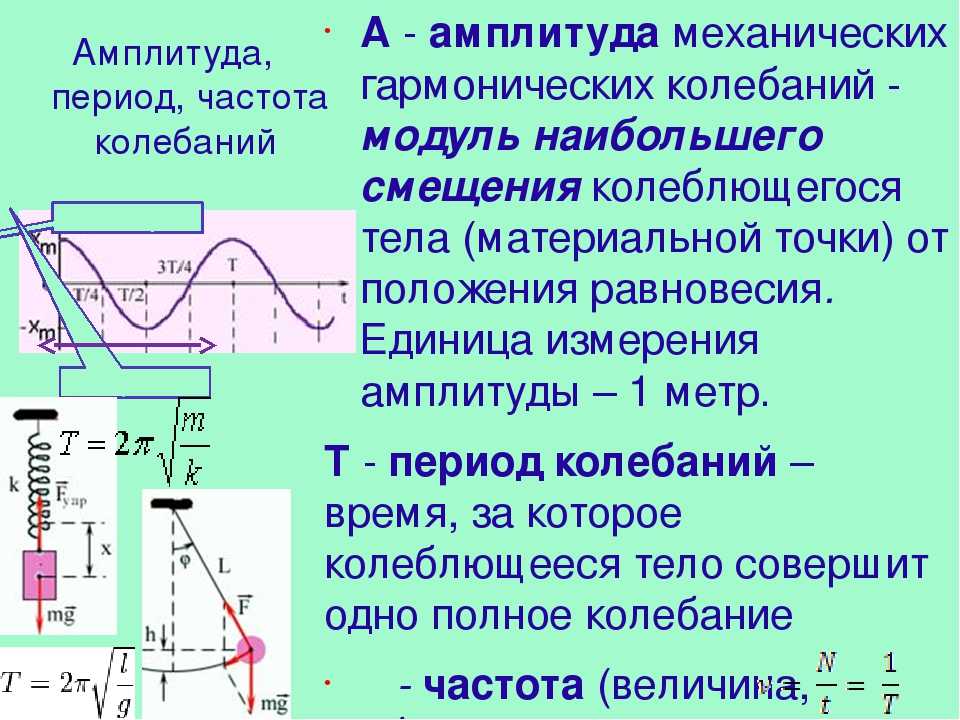
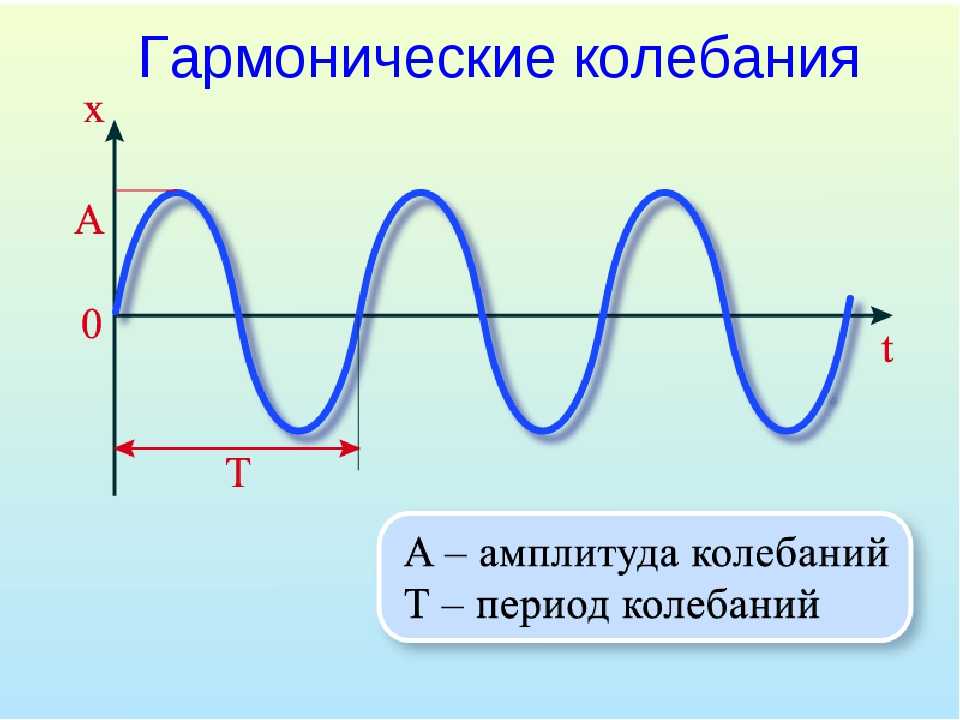
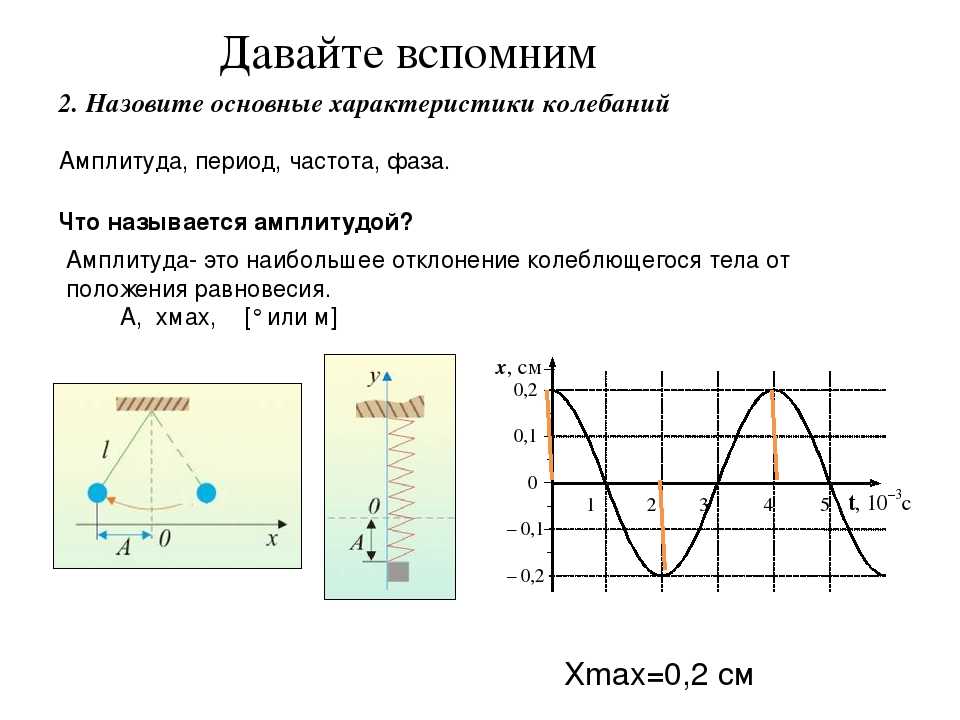 Разница между этими временами 2, поэтому период равен 2 секундам.
Разница между этими временами 2, поэтому период равен 2 секундам.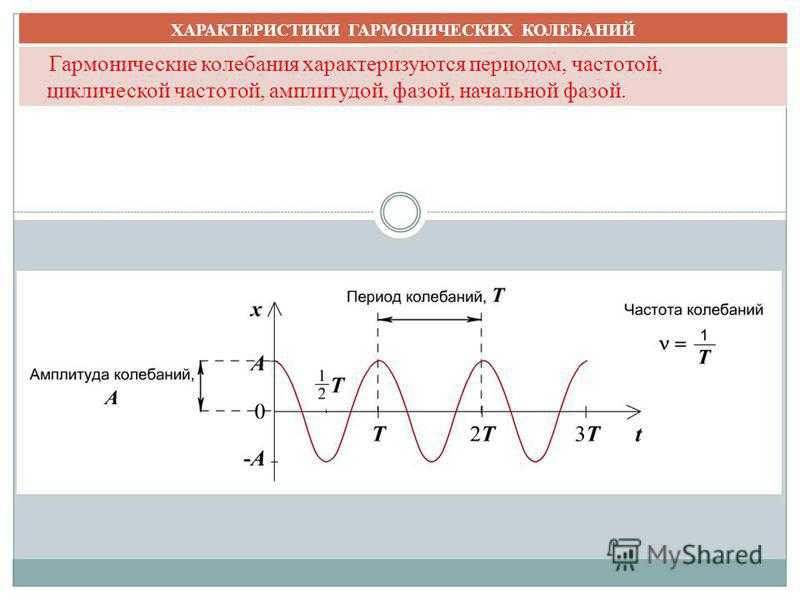 Он связан с периодом времени формулой
Он связан с периодом времени формулой
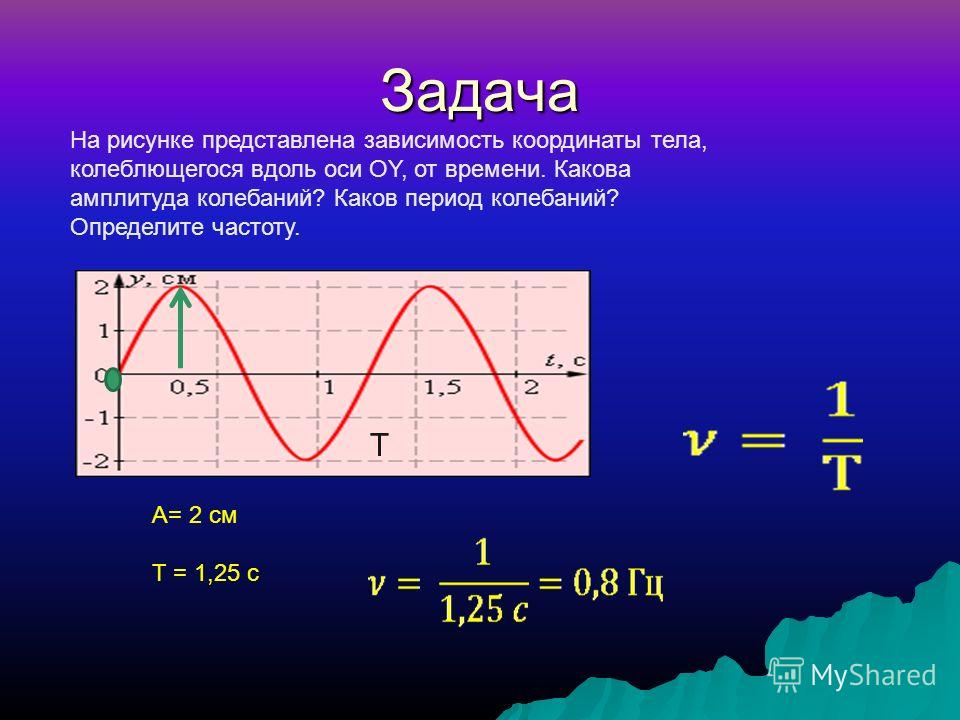 Это можно записать так:
Это можно записать так: Линия y =C — положение покоя вертикально смещенной волны.
Линия y =C — положение покоя вертикально смещенной волны.
 Если вы не можете, оставьте комментарий о том, с чем вы боретесь, и один из нас будет рад помочь!
Если вы не можете, оставьте комментарий о том, с чем вы боретесь, и один из нас будет рад помочь!