Черчение уклон – Уклон | Начертательная геометрия – nGeo.FXYZ.ru

alexxlab | 09.09.2020 | 0 | Разное

значение, формула, как определить, построение

При проведении инженерных и других расчетах, а также работе с инженерной графикой и создании чертежей приходится создавать уклон. Конусность получила весьма широкое распространение, она применяется при изготовлении самых различных деталей. Показатель конусности рассчитывается в большинстве случаев при создании деталей, которые получили широкое распространение в сфере машиностроения. Рассмотрим основные параметры, особенности начертания и многие другие моменты подробнее.

 

Значение конусности

Рассматривая конусность следует учитывать, что этот показатель напрямую связан с уклоном. Этот параметр определяет отклонение прямой лини от вертикального ил горизонтального положения. При этом конусность 1:3 или конусность 1:16 существенно отличается. Определение уклона характеризуется следующими особенностями:

1. Под уклоном подразумевается отношение противолежащего катета прямоугольного треугольника к прилежащему. Этот параметр еще называют тангенс угла.
2. Для расчета примеряется следующая формула: i=AC/AB=tga.

Стоит учитывать, что нормальные конусности несколько отличаются от рассматриваемого ранее параметра. Это связано с тем, что конусностью называется соотношение диаметра основания к высоте.

Рассчитать этот показатель можно самым различным образом, наибольшее распространение получила формула K=D/h. В некоторых случаях обозначение проводится в процентах, так как этот переменный показатель применяется для определения всех других параметров.

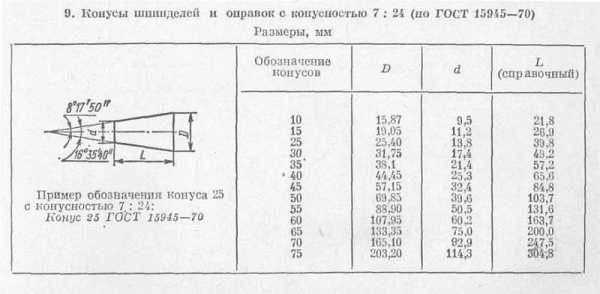
Рассматривая конусность 1:7 и другой показатель следует также учитывать особенности отображения информации на чертеже. Чаще всего подобное отображение проводится при создании технической документации в машиностроительной области.

Обозначение конусности на чертеже

При создании технической документации должны учитываться все установленные стандарты, так как в противном случае она не может быть использована в дальнейшем. Рассматривая обозначение конусности на чертежах следует уделить внимание следующим моментам:

1. Отображается диаметр большого основания. Рассматриваемая фигура образуется телом вращения, которому свойственен диаметральный показатель. В случае конуса их может быть несколько, а изменение показателя происходит плавно, не ступенчато. Как правило, у подобной фигуры есть больший диаметр, а также промежуточной в случае наличия ступени.
2. Наносится диаметр меньшего основания. Меньшее основание отвечает за образование требуемого угла.
3. Рассчитывается длина конуса. Расстояние между меньшим и большим основанием является показателем длины.
4. На основании построенного изображения определяется угол. Как правило, для этого проводятся соответствующие расчеты. В случае определения размера по нанесенному изображению при применении специального измерительного прибора существенно снижается точность. Второй метод применяется в случае создания чертежа для производства неответственных деталей.

Простейшее обозначение конусности предусматривает также отображения дополнительных размеров, к примеру, справочную. В некоторых случаях применяется знак конусности, который позволяет сразу понят о разности диаметров.

Выделяют достаточно большое количество различных стандартов, которые касаются обозначения конусности. К особенностям отнесем следующее:

1. Угол может указываться в градусах дробью или в процентах. Выбор проводится в зависимости от области применения чертежа. Примером можно назвать то, что в машиностроительной области указывается значение градуса.
2. В машиностроительной области в особую группу выделяют понятие нормальной конусности. Она варьирует в определенном диапазоне, может составлять 30, 45, 60, 75, 90, 120°. Подобные показатели свойственны большинству изделий, которые применяются при сборке различных механизмов. При этом выдержать подобные значения намного проще при применении токарного оборудования. Однако, при необходимости могут выдерживаться и неточные углы, все зависит от конкретного случая.
3. При начертании основных размеров применяется чертежный шрифт. Он характеризуется довольно большим количеством особенностей, которые должны учитываться. Для правильного отображения используется табличная информация.
4. Для начала указывается значок конусности от которого отводится стрелка и отображается величина. Особенности отображения во многом зависит от того, какой чертеж. В некоторых случаях наносится большое количество различных размеров, что существенно усложняет нанесение конусности. Именно поэтому предусмотрена возможность использования нескольких различных методов отображения подобной информации.

На чертеже рассматриваемый показатель обозначается в виде треугольника. При этом требуется цифровое значение, которое может рассчитываться при применении различных формул.

Формула для определения конусности

Провести самостоятельно расчет конусности можно при применении различных формул. Стоит учитывать, что в большинстве случаев показатель указывается в градусах, но может и в процентах – все зависит от конкретного случая. Алгоритм проведения расчетов выглядит следующим образом:

1. K=D-d/l=2tgf=2i. Данная формула характеризуется тем, что конусность характеризуется двойным уклоном. Она основана на получении значения большого и меньшего диаметра, а также расстояния между ними. Кроме этого определяется угол.
2. Tgf=D/2L. В данном случае требуется протяженность отрезка, который связывает большой и малый диаметр, а также показатель большого диаметра.
3. F=arctgf. Эта формула применяется для перевода показателя в градусы. Сегодня в большинстве случаев применяются именно градусы, так как их проще выдерживать при непосредственном проведении построений. Что касается процентов, то они зачастую указываются для возможности расчета одного из диаметров. К примеру, если соотношение составляет 20% и дан меньший диаметр, то можно быстро провести расчет большого.

Как ранее было отмечено, конусность 1:5 и другие показатели стандартизированы. Для этого применяется ГОСТ 8593-81.

На чертеже вычисления не отображаются. Как правило, для этого создается дополнительная пояснительная записка. Вычислить основные параметры довольно просто, в некоторых случаях проводится построение чертежа, после чего измеряется значение угла и другие показатели.

Скачать ГОСТ 8593-81

Угол конуса

Важным показателем при построении различных чертежей считается угол конуса. Он определяется соотношение большого диаметра к меньшему. Высчитывается этот показатель по следующим причинам:

1. На момент обработки мастер должен учитывать этот показатель, так как он позволяет получить требуемое изделие с высокой точностью размеров. В большинстве случаев обработка проводится именно при учете угла, а не показателей большого и малого диаметра.
2. Угол конуса рассчитывается на момент разработки проекта. Этот показатель наносится на чертеж или отображается в специальной таблице, которая содержит всю необходимую информацию. Оператор станка или мастер не проводит расчеты на месте производства, вся информация должна быть указана в разработанной технологической карте.
3. Проверка качества изделия зачастую проводится по малому и большему основанию, но также могут применяться инструменты, по которым определяется показатель конусности.

Как ранее было отмечено, в машиностроительной области показатель стандартизирован. В другой области значение может существенно отличаться от установленных стандартов. Некоторые изделия характеризуются ступенчатым расположение поверхностей. В этом случае провести расчеты достаточно сложно, так как есть промежуточный диаметр.

Что такое уклон?

Как ранее было отмечено, довольно важным показателем можно считать уклон. Он представлен линией, которая расположена под углом к горизонту. Если рассматривать конусность на чертеже, то она представлена сочетанием двух разнонаправленных уклонов, которые объединены между собой.

Понятие уклона получило весьма широкое распространение. В большинстве случаев для его отображения проводится построение треугольника с определенным углом.

Две вспомогательные стороны применяются для расчета угла, которые и определяет особенности наклона основной поверхности.

Как определить уклон

Для определения уклона достаточно воспользоваться всего одной формулой. Как ранее было отмечено, существенно упростить задачу можно при построении прямоугольного треугольника. Среди особенностей подобной работы отметим следующие моменты:

1. Определяется начальная и конечная точка отрезка. В случае построения сложной фигуры она определяется в зависимости от особенностей самого чертежа.
2. Проводится вертикальная линия от точки, которая находится выше. Она позволяет построить прямоугольный треугольник, который часто используется для отображения уклона.
3. Под прямым углом проводится соединение вспомогательной линии с нижней точкой.
4. Угол, который образуется между вспомогательной и основной линией в нижней точке высчитывается для определения наклона.

Формула, которая требуется для вычисления рассматриваемого показателя указывалась выше. Стоит учитывать, что полученный показатель также переводится в градусы.

Особенности построения уклона и конусности

Область черчения развивалась на протяжении достаточно длительного периода. Она уже много столетий назад применялась для передачи накопленных знаний и навыков. Сегодня изготовление всех изделия может проводится исключительно при применении чертежей. При этом ему больше всего внимания уделяется при наладке массового производства. За длительный период развития черчения были разработаны стандарты, которые позволяют существенно повысить степень читаемости всей информации. Примером можно назвать ГОСТ 8593-81. Он во многом характеризует конусность и уклон, применяемые методы для их отображения. Начертательная геометрия применяется для изучения современной науки, а также создания различной техники. Кроме этого, были разработаны самые различные таблицы соответствия, которые могут применяться при проведении непосредственных расчетов.

Различные понятия, к примеру, сопряжение, уклон и конусность отображаются определенным образом. При этом учитывается область применения разрабатываемой технической документации и многие другие моменты.

К особенностям построения угла и конусности можно отнести следующие моменты:

1. Основные линии отображаются более жирным начертанием, за исключением случая, когда на поверхности находится резьба.
2. При проведении работы могут применяться самые различные инструменты. Все зависит от того, какой метод построения применяется в конкретном случае. Примером можно назвать прямоугольный треугольник, при помощи которого выдерживается прямой угол или транспортир.
3. Отображение основных размеров проводится в зависимости от особенностей чертежа. Чаще всего указывается базовая величина, с помощью которой определяются другие. На сегодняшний день метод прямого определения размеров, когда приходится с учетом масштаба измерять линии и углы при помощи соответствующих инструментов практически не применяется. Это связано с трудностями, которые возникают на производственной линии.

В целом можно сказать, что основные стандарты учитываются специалистом при непосредственном проведении работы по построению чертежа.

Часто для отображения уклона в начертательной геометрии создаются дополнительные линии, а также обозначается угол уклона.

В проектной документации, в которой зачастую отображается конусность, при необходимости дополнительная информация выводится в отдельную таблицу.

Построение уклона и конусности

Провести построение уклона и конусности достаточно просто, только в некоторых случаях могут возникнуть серьезные проблемы. Среди основных рекомендаций отметим следующее:

1. Проще всего отображать нормальные конусности, так как их основные параметры стандартизированы.
2. В большинстве случаев вводной информацией при создании конусности становится больший и меньший диаметр, а также промежуточное значение при наличии перепада. Именно поэтому они откладываются первыми с учетом взаимного расположения, после чего проводится соединение. Линия, которая прокладывается между двумя диаметрами и определяет угол наклона.
3. С углом наклона при построении возникает все несколько иначе. Как ранее было отмечено, для отображения подобной фигуры требуется построение дополнительных линий, которые могут быть оставлены или убраны. Существенно упростить поставленную задачу можно за счет применения инструментов, которые позволяют определить угол наклона, к примеру, транспортир.

На сегодняшний день, когда компьютеры получили весьма широкое распространение, отображение чертежей также проводится при применении специальных программ. Их преимуществами можно назвать следующее:

1. Простоту работы. Программное обеспечение создается для того, чтобы существенно упростить задачу по созданию чертежа. Примером можно назвать отслеживание углов, размеров, возможность зеркального отражения и многое другое. При этом не нужно обладать большим набором различных инструментов, достаточно приобрести требуемую программу и подобрать подходящий компьютер, а также устройство для печати. За счет появления программного обеспечения подобного типа построение конусности и других поверхностей существенно упростилось. Именно поэтому на проведение построений уходит намного меньше времени нежели ранее.
2. Высокая точность построения, которая требуется в случае соблюдения масштабов. Компьютер не допускает погрешности, если вся информация вводится точно, то отклонений не будет. Этот момент наиболее актуален в случае создания проектов по изготовлению различных сложных изделий, когда отобразить все основные размеры практически невозможно.
3. Отсутствие вероятности допущения ошибки, из-за которой линии будут стерты. Гриф может растираться по поверхности, и созданный чертеж в единственном экземпляре не прослужит в течение длительного периода. В случае использования электронного варианта исполнения вся информация отображается краской, которая после полного высыхания уже больше не реагирует на воздействие окружающей среды.
4. Есть возможность провести редактирование на любом этапе проектирования. В некоторых случаях в разрабатываемый чертеж приходится время от времени вносить изменения в связи с выявленными ошибкам и многими другим причинами. В случае применения специального программного обеспечения сделать это можно практически на каждом этапе проектирования.
5. Удобство хранения проекта и его передачи. Электронный чертеж не обязательно распечатывать, его можно отправлять в электронном виде, а печать проводится только при необходимости. При этом вся информация может копироваться много раз.

Процедура построения при применении подобных программ характеризуется достаточно большим количеством особенностей, которые нужно учитывать. Основными можно назвать следующее:

1. Программа при построении наклонных линий автоматически отображает угол. Проведенные расчеты в этом случае позволяют проводить построение даже в том случае, если нет информации об большом или малом, промежуточном диаметре. Конечно, требуется информация, касающаяся расположения диаметров относительно друг друга.
2. Есть возможность использовать дополнительные инструменты, к примеру, привязку для построения нормальной конусности. За счет этого существенно прощается поставленная задача и ускоряется сама процедура. При черчении от руки приходится использовать специальные инструменты для контроля подобных параметров.
3. Длина всех линий вводится числовым методом, за счет чего достигается высокая точность. Погрешность может быть допущена исключительно при применении низкокачественного устройства для вывода графической информации.
4. Есть возможность провести замер всех показателей при применении соответствующих инструментов.
5. Для отображения стандартов используются соответствующие инструменты, которые также существенно упрощают поставленную задачу. Если программа имеет соответствующие настройки, то достаточно выбрать требуемый инструмент и указывать то, какие размеры должны быть отображены. При этом нет необходимости знания стандартов, связанных с отображением стрелок и других линий.

Есть несколько распространенных программ, которые могут применяться для построения самых различных фигур. Их применение на сегодняшний день считается стандартом. Для работы требуются определенные навыки, а также знание установленных норм по отображению различных плоскостей и размеров. Не стоит забывать о том, что рассматриваемое программное обеспечение является лишь инструментом, вся работа выполняется инженером.

Понятие конусности встречается в достаточно большом количестве различной технической литературы. Примером можно назвать машиностроительную область, в которой распространены конусные валы и другие изделия. На практике производство подобных изделий может создавать довольно большое количество проблем, так как выдерживать заданный угол не просто.

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

stankiexpert.ru

Как построить уклон на чертеже

Прямые наклонные элементы, расположенные под углом относительно базовой линии создают уклон, для отображения которого перед размерными числами наносят знак « > », причём его острый угол должен быть направлен в сторону уклона. Обозначения наносятся в непосредственной близости к наклонной линии или на полке линии-выноски.

Размерные числа уклона выражаются в отношении чисел, или в процентах.

Пример нанесения значения уклона

Уклон i отрезка ВС относительно отрезка ВА определяют отношением катетов прямоугольного треугольника ABC .

Для построения прямой ВС с заданной величиной уклона к горизонтальной прямой, например 1:4 , необходимо от точки A влево отложить отрезок AВ , равный четырем единицам длины, а вверх — отрезок АС , равный одной единице длины. Точки С и В соединяют прямой, которая дает направление искомого уклона.

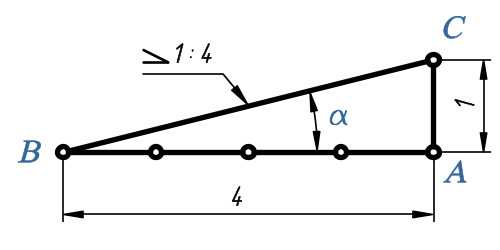
Уклон один к четырём

Если уклон задается в процентах, например, 20 % смотри на изображении ниже, то линия уклона строится так же, как гипотенуза прямоугольного треугольника. Длину одного из катетов принимают равной 100 % , а другого – 20 % . Очевидно, что уклон 20 % есть иначе уклон 1:5 .

Уклоном называют величину, характеризующую наклон одной прямой линии относительно другой прямой. Уклон численно равен тангенсу угла φ

Рис. 4.7. Построение уклона

Уклон может быть задан на чертеже либо отношением двух чисел, либо в процентах. Линию заданного уклона строят как гипотенузу прямоугольного треугольника, тангенс острого угла которого нам известен.
На рис. 4.7, а и б показаны случаи построения прямых, когда уклон их задан отношением двух чисел и в процентах. На рис. 4.7, в показаны варианты практического применения построений линий заданного уклона. Перед числовым значением уклона ставится знак уклона , острый угол которого направлен в сторону уклона.

Конусностью называется отношение диаметра основания конуса к его высоте, либо отношение разности диаметров оснований усечённого конуса к его высоте (рис.4.8). Как видно из чертежа, числовое значение конусности в два раза больше значения уклона образующей конуса к его оси. На рис. 4.8 показаны примеры построения конусности. Для обозначения конусности на чертеже применяют знак , острый угол которого направлен в сторону конусности. Значение конусности проставляется либо на полке линии выноски, либо над осевой линией.

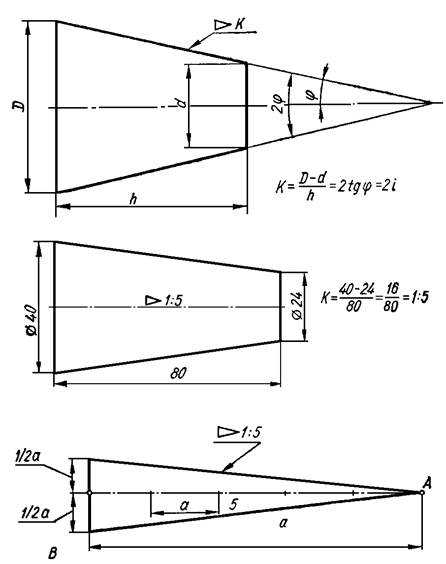
Рис.4.8. Построение конусности

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Сдача сессии и защита диплома — страшная бессонница, которая потом кажется страшным сном. 8563 — | 7055 — или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Поверхности многих деталей имеют различные уклоны. Плоские поверхности деталей, расположенные наклонно, на чертежах часто обозначаются величиной уклона. В задании «Проекционное черчение» именно так и задано ребро жесткости или тонкая стенка детали.

Уклон характеризует отклонение прямой линии или плоскости от горизонтального или вертикального направления. Для построения уклона 1:1 на сторонах прямого угла откладывают произвольные, но равные единичные отрезки. Очевидно, что уклон 1:1 соответствует углу 45º. Как видно из рис. 34,а, уклон есть отношение катетов: противолежащего к прилежащему, что может быть определено как тангенс угла наклона α прямой. Тогда, чтобы, например, построить уклон 1:7 (рис. 34,б), в направлении уклона откладывают семь отрезков, а в перпендикулярном направлении — один отрезок.

Величину наклона обозначают на чертеже в соответствии с ГОСТ 2.307-68 условным знаком с числовым значением. Уклон указывают с помощью линии-выноски, на полке которой наносят знак уклона и его величину. Расположение знака уклона должно соответствовать определенной линии: одна из прямых знака должна быть горизонтальной, а другая — наклонена примерно под углом 30º в ту же сторону, что и сама линия уклона (рис. 34,б). Вершина знака должна быть направлена в сторону уклона. Знак и размерное число располагают параллельно направлению, по отношению к которому задан уклон. На чертеже уклоны указывают либо в процентах, либо дробью в виде отношения двух чисел.

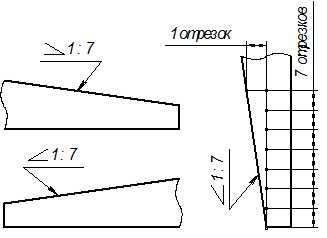(а)	(б)

Многие детали содержат коническую поверхность. На чертежах конических деталей размеры могут быть проставлены различно: диаметры большего и меньшего оснований усеченного конуса и его длина, угол конуса или величина конусности.

Конусность — это отношение диаметра основания конуса к его высоте. Для усе­ченного конуса это отношение разности диаметров двух поперечных сечений конуса к расстоянию между ними (рис. 35,а). Конусность равна удвоенному уклону образующей конуса к его оси. Так же как и уклон, она обозначается условным зна­ком, проставляемым перед её числовым обозначением. Условный знак изобража­ет­ся в виде треугольника с вершиной, направленной в сторону вершины конуса. Конус­ность (согласно ГОСТ 2.307-68) задается на чертежах отношением двух чисел (рис. 35), процентами или десятичной дробью.

Знак и цифры, указывающие величину конусности, располагают на чертежах параллельно оси конического элемента. Они могут быть расположены над осью, как на рис. 35,б, или полке, как на рис. 35,в. В последнем случае полка соединяется с обра­зующей конуса с помощью линии-выноски, заканчивающейся стрелкой. В кони­чес­ких соединениях, показанных на рис. 36, указание конусности обязательно, так как задание размеров

D, d, H из-за трудностей изготовления применяют редко. При построении очертаний конуса, задаваемого конусностью, высотой и одним из диаметров, второй диаметр вычисляют по формуле, приведенной на рис. 35,а. Конусности общего назначения стандартизованы ГОСТ 8593-81.

2. Пример выполнения РГР

На рис. 37 приведен пример варианта задания на выполнение расчетно-графической работы «Проекционное черчение», а также наглядное изображение заданной детали с вырезом.

Выполненный по этому заданию чертеж детали в трех проекциях с правильно оформленными размерами показан на рис. 38. Этот при­мер поможет студентам разобраться в их задании, начать выполнение графичес­кой работы и избежать многочисленных ошибок при ее оформлении.

Напомним, что в задании имеются только две проекции детали, поэтому и размеры распределены на двух изображениях. Однако при оформлении чертежа следует наносить размеры равномерно на всех трех проекциях.

В заключение следует отметить, что количество изображений детали (видов, разрезов, сечений) должно быть наименьшим, но обеспечивающим полное пред­став­ление о её конструкции при применении установленных всоответствующих стан­дар­тах условных обозначений, знаков и надписей.

Литература

1. Попова Г.Н., Алексеева С.Ю. Машиностроительное черчение: Справочник. -Л.: Машиностроение, Ленингр. отделение, 1986.

2. Левицкий В.С. Машиностроительное черчение. — М.: Высшая школа, 1988.

3. Гордон В.О., Семенцов-Огиевский Н.А. Курс начертательной геометрии. — М.: Наука, 1994.

4. Фролов С.А. Начертательная геометрия. — М.: Машиностроение, 1978.

Приложение. Варианты задания на расчетно-графическую работу

Варианты задания на расчетно-графическую работу по теме «Проекционное черчение» приведены в табл. П1. Правила выбора варианта задания определяются преподавателем.

Таблица П1. Варианты задания на РГР по теме «Проекционное черчение»

№ вар.	№ рис.	а	b	с	№ вар.	№ рис.	а	b	с
П1	П7
П2	П8
П3	П9
П4	П10
П5	П11
П6	П12
П7	П1
П8	П2
П9	П3
П10	П4
П11	П5
П12	П6
П1	П7
П2	П8
П3	П9
П4	П10
П5	П11
П6	П12

[1] Для вертикальных разрезов указанное требование должно выполняться также в случаях, если секущая плоскость не параллельна фронтальной или профильной плоскости проекции

[2] Условие симметричности изображений необходимо, но не достаточно для совмещения половины вида и половины разреза (подробнее см. подраздел 1.2.3).

Дата добавления: 2014-11-06 ; Просмотров: 3161 ; Нарушение авторских прав? ;

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

mytooling.ru

ПОСТРОЕНИЕ УКЛОНОВ И КОНУСНОСТИ — КиберПедия

Уклоны .Величина наклона одной прямой по отношению к другой прямой называется уклоном. Уклон выражается тангенсом угла α между этими прямыми.

Рис. 1

Уклоны обычно выражают отношением двух чисел, например 1:3, из которых числитель можно графически изобразить как один из катетов АС прямоугольного треугольника, а знаменатель — как другой катет АВ этого же треугольника .Уклон может быть выражен в процентах, например 25% .

На чертежах обозначение уклона наносят на полке линии-выноски, упирающейся в линию уклона. Полка линии-выноски параллельна линии направления, по отношению к которой задан уклон. Перед числовым значением уклона наносят знак. Вершина угла знака направлена в сторону уклона, а нижняя линия знака параллельна полке линии-выноски. (Рис.1)

Построение уклона. Дан отрезок АВ и на нем точка С. Надо провести прямую с уклоном 1:5 к линии АВ через заданную на ней точку С. От точки С откладывают пять равных отрезков произвольного размера. На перпендикуляре, проведенном из точки 5 к прямой АВ, откладывают один отрезок того же размера, получают точку D. Прямая проведенная через точки С и D будет иметь уклон 1:5 к прямой АВ.(рис.2)

 

Рис.2

 

Конусность (рис.3)

Конусностью называется отношение диаметра D основания прямого кругового конуса к его высоте Н.

Для усеченного конуса конусность выражается отношением разности диаметров D и d нормальных сечений кругового конуса к расстоянию между ними . Обозначение конусности наносится на линии-выноске со стрелкой. Перед размерным числом, характеризующим конусность, наносят знак, острый угол которого должен быть направлен в сторону вершины конуса. (рис.3 )

Рис.3

ДЕЛЕНИЕ ОКРУЖНОСТИ НА РАВНЫЕ ЧАСТИ

 

РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ РАБОТЫ.

Начертите 8 окружностей радиусом 20 мм.

1.2..I Деление на 4 равные части. (рис.4а.). Проведите в окружности 2 взаимно перпендикулярные оси. Эти оси делят окружность на 4 равные части. Соедините точки А,В,С,D) сплошной основной линией, получите вписанный квадрат.
1.2.2.Деление на 8 равных частей(рис.4б).

Разделите полученные 4 дуги пополам, проведя циркулем засечки радиусом 20-30 мм из концов этих дуг. Соединяя точки пересечения засечек с центром окружности,, вы разделите окружность на 8 равных частей. Соедините полученные 8 точек, получите вписанный восьмиугольник.
1.2.З.Деление на 3 равные части (рис.4 в).

Радиусом 20мм проведите дугу с центром в точке D. Засеките на окружности точки 1 и 2 и соедините их с точкой С.

1.2.4.Деление на 6 равных частей (рис.4 г).

Приняв за центры концы диаметра, сделайте циркулем радиусом 20мм засечки на окружности (точки 1,2,3,4). Соедините их и точки А и В , получите правильный шестиугольник.

1.2.5.Деление на 12 равных частей (рис.4 д.)

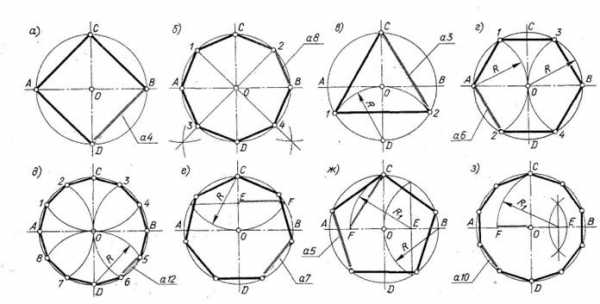Приняв за центры концы двух взаимно перпендикулярных диаметров (точки А,В,С,Д)), сделайте радиусом 20мм 8 засечек на окружности. Полученные 12 точек соедините.

Рис.4

1.2.6. Деление на 7 равных частей (рис.4 е).

Приняв за центр один из концов диаметра (точку С), проведите дугу радиусом 20 мм до пересечения с окружностью. Точки пересечения соедините отрезком прямой . Половина этого отрезка (EF) примерно равна стороне вписанного семиугольника. Радиусом FE сделайте поочередно 7 засечек на окружности, начав с точки С. Полученные 7 точек соедините.

1.2.7.Деление на 5 равных частей (рис.4 ж).

Приняв за центр один из концов диаметра (точку В), проведите дугу радиусом 20мм до пересечения с окружностью и точки пересечения соедините прямой. Приняв за центр точку пересечения прямой с :горизонтальным диаметром (точку Е), проведите дугу через точку С до пересечения с этим диаметром. Точку пересечения F соедините с точкой С. Отрезок СF будет примерно равен стороне вписанного пятиугольника ; ОF – стороне вписанного десятиугольника. Радиусом СF поочередно сделайте 5 засечек на окружности, начиная с точки С. Полученные 5 точек соедините.

1.2.8.Деление на 10 равных частей (рис.4з).

Радиусом ОF сделайте поочередно 10 засечек на окружности, полученные точки соедините.

 

 

СОПРЯЖЕНИЯ

1.3.1.Сопряжение двух прямых (рис.5.)

Даны две параллельные прямые АВ и СD (рис 5 в) , задан размер EF .Разделите отрезок EF пополам, и из точки О проведите дугу радиусом R=EF/2, соединяя точки Е и F

Рис5

1.3.2.Сопряжения углов (рис.5 а, б).

Даны две прямые , пересекающиеся под углом ( прямым, острым или тупым), и радиус сопряжения Е..

Проведите по два перпендикуляра к двум сторонам углаи отложите на них отрезки ,равные R.. Через полученные точки проведите прямые параллельно сторонам угла.. О – точка пересечения этих двух прямых -есть центр сопряжения. Из точки О опустите перпендикуляры на стороны угла. Точки пересечения перпендикуляров и сторон угла соедините дугой радиусом R с центром в точке О.

1.3.3.Сопряжение прямой сокружностью (рис.6а.) Дана прямая, окружность радиусом R и радиус сопряжения R1.. Проведите прямую, параллельную заданной , на расстоянии R1. Из центра окружности О радиусом R2= R + R1 сделайте на прямой засечку О1 . Через О и О1 проведите прямую, получите на окружности точку К. Из точки О1 проведите О1К1 перпендикулярно заданной прямой. Из центра сопряжения О1 проведите дугу радиусом R1, соединяя точки К1 и К. Это внешнее сопряжение

 

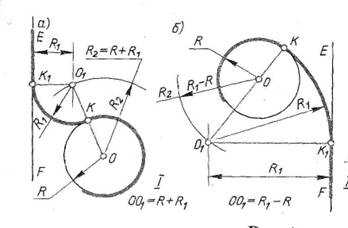Рис.6

Внутреннее сопряжение. (рис.6 б).

Дана прямая, окружность радиусом R и радиус сопряжения R1.. Проведите построение аналогично предыдущему, учитывая , что в данном случае

R2 = R-R1

 

 

1.3.4.Сопряжение двух окружностей.

Внешнее сопряжение (рис.7а).

Даны две окружности радиусом R1, и R2 и радиус сопряжения R.

Рис.7

Проведите дуги из центра О1 радиусом R.+ R 1 , из О₂ – радиусом R.+ R 2. Точка их пересечения О3 -центр сопряжения.

Внутреннее сопряжение(рис.7б)

Даны две окружности радиусом R1и R2 и радиус сопряжения R. Проведите дуги : из точки О1 радиусом R- R1, из точки О2 радиусом R-R2. Точка их пересечения О3 -центр сопряжения.

Смешанное сопряжение (рис.7 в).

Даны две окружности радиусом R1 и R2,ирадиус сопряжения R.

Проведите дуги : из центра О1 радиусом R.-R1, из центра О2 радиусом R+R2. Точка пересечения дуг О3- центр сопряжения.

 

 

cyberpedia.su

Расчет и нанесение уклона на обмерных чертежах

С необходимостью посчитать уклон постоянно сталкиваются проектировщики, строители, архитекторы, а также люди ряда других профессий, в силу того, что на земной поверхности очень трудно найти идеально ровный участок. Уклон выражается в градусах или в процентах. Обозначение в градусах показывает угол кривизны поверхности. Но уклон может быть представлен и в виде тангенса этого угла, умноженного на 100%.

Как рассчитать уклон поверхности?
Уклон – это отношение превышения (ВС) к заложению (АС) и обозначается в текстовых документах буквой i.
Например, i=1:6

Разделите противолежащий катет (вертикальное расстояние) на прилежащий (расстояние между точками). Если вам нужно получить уклон в процентах, умножьте полученное число на 100%. Чтобы получить уклон в промилле, умножьте результат деления на 1000‰.

Если вам необходимо получить уклон в градусах, воспользуйтесь тем, что полученный при делении катетов результат – тангенс угла наклона. Посчитайте его арктангенс при помощи инженерного калькулятора, в результате вы получите значение уклона в градусах.

На видах (фасадах), разрезах, сечениях и схемах перед размерным числом, определяющим величину уклона, наносят знак , острый угол которого должен быть направлен в сторону уклона.
Обозначение уклона наносят непосредственно над линией контура или на полке линии-выноски.
На планах направление уклона плоскостей указывают стрелкой, на которой, при необходимости, проставляют величину уклона (см.рис.).

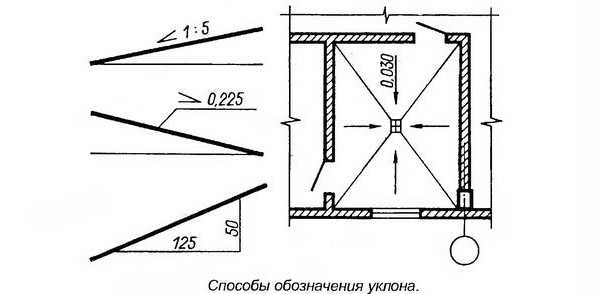
Построение и обозначение уклона. Пример изображения уклона на планах.

Величину уклона (тангенс угла наклона) указывают в виде простой или десятичной дроби с точностью до третьего знака.

Уклон (в строительстве) — показатель крутизны склона (а также ската кровли).

Укло́н (в геодезии) — показатель крутизны склона; отношение превышения местности к горизонтальному проложению, на котором оно наблюдается. Иными словами, величина уклона равна тангенсу угла между поверхностью склона и горизонталью.

Уклон поверхности равен тангенсу угла α, tgα = h/l – отношение перпендикуляра, опущенного из точки поверхности на прямую поверхность, к длине прямой поверхности от начала склона (при вершине угла α) до перпендикуляра.

Например, подъёму 12 м на 100 м перемещения по горизонтали соответствует уклон, равный 0,12 (12 % или 120 ‰).
При чтении нотации знак «%» произносится «сотых», а «‰» — «тысячных».

Источник:

книга: Единые требования по выполнению строительных чертежей.
М.: Изд-во «Архитектура-С», 2004.
Справочное пособие.
Автор: Георгиевский О.В.

Аннотация:
Справочное пособие по строительному черчению для студентов средних и высших учебных заведений. Пособие выполнено в соответствии с требованиями ГОСТов.
Настоящее справочное пособие выполнено в соответствии с требованиями ГОСТов ЕСКД (Единой системы конструкторской документации) и СПДС (Системы проектной документации для строительства).
Пособие может быть использовано при выполнении заданий по архитектурно-строительному черчению, а также при выполнении курсовых и дипломных проектов студентами всех строительных специальностей средних и высших учебных заведений.

распечатать

Вконтакте

Facebook

Twitter

Одноклассники

Google+

photogrammetria.ru

Обозначение уклона на чертежах

Прямые наклонные элементы, расположенные под углом относительно базовой линии создают уклон, для отображения которого перед размерными числами наносят знак « > », причём его острый угол должен быть направлен в сторону уклона. Обозначения наносятся в непосредственной близости к наклонной линии или на полке линии-выноски.

Размерные числа уклона выражаются в отношении чисел, или в процентах.

Пример нанесения значения уклона

Уклон i отрезка ВС относительно отрезка ВА определяют отношением катетов прямоугольного треугольника ABC.

Для построения прямой ВС с заданной величиной уклона к горизонтальной прямой, например 1:4, необходимо от точки A влево отложить отрезок AВ, равный четырем единицам длины, а вверх – отрезок АС, равный одной единице длины. Точки С и В соединяют прямой, которая дает направление искомого уклона.

Уклон один к четырём

Если уклон задается в процентах, например, 20 % смотри на изображении ниже, то линия уклона строится так же, как гипотенуза прямоугольного треугольника. Длину одного из катетов принимают равной 100 %, а другого – 20 %. Очевидно, что уклон 20 % есть иначе уклон 1:5.

Уклон двадцать процентов

 

 

 

gk-drawing.ru

Как начертить уклон 🚩 как вы относитесь к уклонистам 🚩 Наука 🚩 Другое

Вам понадобится

• – бумага;
• – чертежные принадлежности;
• – калькулятор;
• – компьютер с программой AutoCAD.

Инструкция

Проведите исходную линию. Удобнее, если она будет расположена вертикально или горизонтально, но на практике так бывает не всегда. Для того чтобы понять, как вообще считается и чертится уклон, примите эту прямую за горизонтальную. Обозначьте на ней точку А. Из точки А проведите перпендикуляр вверх.

Отложите на обеих прямых любое количество одинаковых отрезков. В данном случае не важно, какой они будут длины. Главное — чтобы они были одинаковыми по вертикальной и горизонтальной осям. Уклон обычно записывается как отношение количества таких отрезков по обеим линиям.

Обозначьте горизонтальную прямую как l, а вертикальную — как h. Тогда уклон i будет равен отношению высоты к длине. Если представить нужную вам линию уклона как гипотенузу прямоугольного треугольника, образованного горизонтальной прямой и опущенным на нее из конечной точки линии уклона перпендикуляром, то получится, что уклон равняется тангенсу угла между линией уклона и прямой l, то есть сосчитать его можно по формуле i=h/l=tgA.

Допустим, вам нужно начертить уклон, обозначенный как m:n. Отложите от точки А на прямой, которую вы обозначили как h, количество одинаковых отрезков, равное m. На прямой l отложите n таких же отрезков. Из конечных точек проведите перпендикуляры до их пересечения в некой точке, которую можно обозначить, например, как В. Соедините точки А и В. Это и будет нужный вам уклон.

В задачах очень часто требуется начертить уклон под определенным углом, но при этом соотношение не дается. В этом случае возможны варианты. Например, вы можете отложить от той же самой точки А угол к горизонтали и провести через него линию уклона. Можно и вычислить тангенс, а уже по нему строить уклон точно так же, как и в первом способе.

Компьютерные программы существенно облегчили жизнь чертежникам и проектировщикам. Если у вас установлен AutoCAD, процесс вычерчивания уклона займет совсем немного времени. Некоторые промежуточные этапы, необходимые при вычерчивании уклона на листе, при этом опускаются.

Задайте исходную линию. Сделать это можно, например, командой _xline. Введите ее в командную строку. Программа выдаст вам запрос, в ответ на который необходимо ввести координаты исходной точки.

На экране у вас появится линия, которая вращается вокруг указанной точки. Ей необходимо придать нужное положение. Если у вас уже есть линия, к которой нужно провести под углом другую, выберите опцию «Угол». В командной строке появится запрос, предлагающий ввести размер угла или базовую линию. Выберите нужное значение.

Если вы зададите размер угла, то программа предложит задать точку, через которую будет проходить прямая. При выборе базовой линии вы можете указать на чертеже линию, относительно которой будет вычерчиваться уклон.

Обратите внимание

Обозначьте уклон. Можно это сделать и словом, однако чаще применяется значок “

www.kakprosto.ru

Построение и обозначение уклонов и конусности

из “Индивидуальные задания по курсу черчения ”

Ук к)И[11 применяются ири вычерчивании многих деталей, например при выполнении чертежей профилей стальных балок и рельсов, изготавливаемых па прокатных станах (рис. 27, а, б. =), и па чертежах не-кото[)ЫХ деталей, изготовленных литьем (рис. 27, в). [c.42]
Уклон i отрезка ВС относительно отрезка ВА определяю отнсипенпем катетов прямоугольного треугольника ЛВС (рис. 28, а), т, е. [c.42]
Уклон выражают дробью или в процентах. [c.42]
При вычерчивании контура детали с уклоном 1 4 (рис. 28, в) предварительно выполняйся построение линии уклона, параллельно которой проводится контур детали. [c.42]
Если уклон задается н процентах, например 20% (рис. 28, 6, г), то линия уклона строится так же, как гипотенуза прямоугольного треугольника. Длину одного из катетов принимают равной 100%, а другого -20%. Очевидно, что уклон 20% есть уклон 1 5. [c.42]
По ГОСТ 2.307—68 перед числом, определяющим уклон, наносят условный знак, острый угол которого должен быть направлен в сторону уклона (рис. 28, в, г]. [c.42]
Па рис. 29, а, б, в показаны детали оправка, конус и сверло, которые имеют конусность. [c.42]
По ГОСТ 2.307 -68 перед числом, характеризующим конусность, необходимо наносить условный знак конусности, который имеет вид равнобедренного треугольника с вершиной, направленной в сторону вершины конуса (рис. 30, б, в). [c.43]
Обычно на чертеже конуса дается диаметр больп1его основания, так как при из-готов.лении конической детали этот диаметр измерить значительно легче. [c.43]
Нормальные конусности и углы конусов устанавливает ГОСТ 8593—81. В ГОСТ 25548- 82 приведень, соответствующие термины и определения. [c.43]
Задание 8 состоит из днух задач на построение и об )значение на чертежах уклона. На рис. 28, а, в показан пример построения уклона 1 4 относительно гори aoinajHi. Аналогично выполняется построение уклона, если он задан в процентах (см. рис. 28, О, с ). [c.43]
Выполнить изображения контуров деталей с построением уклонов, приняв для стойки уклон 1 6, а для двутавра 12%. Нанести размеры, обозначить уклон. [c.44]

Вернуться к основной статье

mash-xxl.info