Что такое период колебаний: Период колебаний – это… Что такое Период колебаний?
alexxlab | 25.07.2019 | 0 | Разное
Период колебаний – это… Что такое Период колебаний?
Период колеба́ний — наименьший промежуток времени, за который осциллятор совершает одно полное колебание (то есть возвращается в то же состояние[1], в котором он находился в первоначальный момент, выбранный произвольно).
В принципе совпадает с математическим понятием периода функции, но имея ввиду под функцией зависимость физической величины, совершающей колебания, от времени.
Это понятие в таком виде применимо как к гармоническим, так и к ангармоническим строго периодическими колебаниям (а приближенно – с тем или иным успехом – и непериодическим колебаниям, по крайней мере к близким к периодичности).
В случае, когда речь идет о колебаниях гармонического осциллятора с затуханием, под периодом понимается период его осциллирующей составляющей (игнорируя затухание), который совпадает с удвоенным временным промежутком между ближайшими прохождениями колеблющейся величины через ноль. В принципе, это определение может быть с большей или меньшей точностью и пользой распространено в некотором обобщении и на затухающие колебания с другими свойствами.
Обозначения: обычное стандартное обозначение периода колебаний: (хотя могут применяться и другие, наиболее часто это , иногда и т. д.).
Единицы измерения: секунда
Период колебаний связан соотношением взаимной обратности с частотой:
Для волновых процессов период связан кроме того очевидным образом с длиной волны
где – скорость распространения волны (точнее[2] – фазовая скорость).
В квантовой физике период колебаний прямо связан с энергией (поскольку в квантовой физике энергия объекта – например, частицы – есть частота[3] колебаний его волновой функции).
Теоретическое нахождение периода колебаний той или иной физической системы сводится, как правило, к нахождению решения динамических уравнений (уравнения), описывающего эту систему. Для категории линейных систем (а приближенно – и для линеаризуемых систем в линейном приближении, которое зачастую является очень хорошим) существуют стандартные сравнительно простые математические методы, позволяющие это сделать (если известны сами физические уравнения, описывающие систему).
Для экспериментального определения периода используются часы, секундомеры, частотомеры, стробоскопы, строботахометры, осциллографы. Также применяются биения, метод гетеродинирования в разных видах, используется принцип резонанса. Для волн можно померить период косвенно – через длину волны, для чего применяются интерферометры, дифракционные решетки итп. Иногда требуются и изощренные методы, специально разработанные для конкретного трудного случая (трудность могут представлять как само измерение времени, особенно если речь идет о предельно малых или наоборот очень больших временах, так и трудности наблюдения колеблющейся величины).
Периоды колебаний в природе
Представление о периодах колебаний различных физических процессов дает статья Частотные интервалы (учитывая то, что период в секундах есть обратная величина частоты в герцах).
Некоторое представление о величинах периодов различных физических процессов также может дать шкала частот элетромагнитных колебаний (см. Электромагнитный спектр) .
Периоды колебаний слышимого человеком звука находятся в диапазоне
- от 5·10-5с до 0,2с
(четкие границы его несколько условны).
Периоды электромагнитных колебаний, соответствующих разным цветам видимого света – в диапазоне
- от 1,1·10-15с до 2,3·10-15с.
Поскольку при экстремально больших и экстремально маленьких периодах колебаний методы измерения имеют тенденцию становятся всё более косвенными (вплоть до плавного перетекая в теоретические экстраполяции), трудно назвать четкую верхнюю и нижнюю границы для периода колебаний, измеренного непосредственно. Какую-то оценку для верхней границы может дать время существования современной науки (сотни лет), а для нижней – период колебаний волновой функции самой тяжелой из известных сейчас частиц ().
В любом случае границей снизу может служить планковское время, которое столь мало, что по современным представлениям не только вряд ли может быть вообще как-то физически измерено[4], но и вряд ли в более-менее обозримом будущем представляется возможность приблизиться к измерению величин даже на много порядков меньших. а границей сверху – время существования Вселенной – более десяти миллиардов лет.
Периоды колебаний простейших физических систем
Пружинный маятник
Период колебаний пружинного маятника может быть вычислен по следующей формуле:
,
где — масса груза, — жёсткость пружины.
Математический маятник
Период колебаний математического маятника:
где — длина подвеса (к примеру нити), — ускорение свободного падения.
Период колебаний (на Земле) математического маятника длиной 1 метр с хорошей точностью
Физический маятник
Период колебаний физического маятника:
где — момент инерции маятника относительно оси вращения, — масса маятника, — расстояние от оси вращения до центра масс.
Крутильный маятник
Период колебаний крутильного маятника:
где — момент инерции тела, а — вращательный коэффициент жёсткости маятника.
Электрический колебательный (LC) контур
Период колебаний электрического колебательного контура:
,
где — индуктивность катушки, — ёмкость конденсатора.
Эту формулу вывел в 1853 году английский физик У. Томсон.
Примечания
- ↑ Состояние механической системы характеризуется положениями и скоростями всех ее материальных точек (строже говоря – координатами и скоростями, соответствующими всем степеням свободы данной системы), для немеханической – их формальными аналогами (которые также можно назвать координатами и скоростями в смысле абстрактного описания динамической системы – в количестве, также равном количеству ее степеней свободы).
- ↑ Для монохроматических волн это уточнение самоочевидно, для близких к монохроматическим – интуитивно очевидно по аналогии со строго монохроматическими, для существенно немонохроматических – наиболее ясный случай сводится к тому, что фазовые скорости всех монохроматических компонент совпадают друг с другом, поэтому комментируемое утверждение ьакже верно.
- ↑ С точностью до единиц измерения: в традиционных (обычных) системах физических единиц частота и энергия измеряются в разных единицах (поскольку до появления квантовой теории совпадение энергии и частоты было неизвестно, и, естественно, для каждой из величин была выбрана своя независимая единица измерения), поэтому при измерении их в обычных (разных) единицах, например, джоулях и герцах требуется переводной коэффициент (так называемая константа Планка). Однако можно выбрать систему единиц измерения так, чтобы в ней константа Планка стала равной 1 и пропала из формул; в такой системе единиц энергия любой частицы просто равна частоте колебания ее волновой функции (а значит обрата периоду этого колебания).
- ↑ Имеется в виду, конечно же, невозможность экспериментального измерения времен конкретных процессов или периодов колебаний такого порядка, а не просто вычисление некоторого числа.
- ↑ Лучше, чем 0,5%, если взять метрологическое или принятое техническое значение ускорения свободного падения; И с разбросом ~0.53% для максимального и минимального значений ускорения свободного падения, наблюдаемых на земле.
Ссылки
Амплитуда, частота, период колебаний — урок. Физика, 9 класс.
Рассмотрим величины, с помощью которых можно охарактеризовать колебания.

Сравним колебания двух качелей на рисунке — пустых качелей и качелей с мальчиком. Качели с мальчиком колеблются с большим размахом, т. е. их крайние положения находятся дальше от положения равновесия, чем у пустых качелей.
Наибольшее (по модулю) отклонение колеблющегося тела от положения равновесия называется амплитудой колебаний.
Обрати внимание!
Амплитуда колебаний, как правило, обозначается буквой \(А\) и в СИ измеряется в метрах (м).
Пример:
Обрати внимание!
Амплитуду можно измерять также в единицах плоского угла, например в градусах, поскольку дуге окружности соответствует определённый центральный угол, т. е. угол с вершиной в центре окружности.
Колеблющееся тело совершает одно полное колебание, если от начала колебаний проходит путь, равный четырём амплитудам.Промежуток времени, в течение которого тело совершает одно полное колебание, называется периодом колебаний.
Обрати внимание!
Период колебаний обозначается буквой \(Т\) и в СИ измеряется в секундах (с).
Пример:
ударим по столу двумя линейками — металлической и деревянной. Линейки после этого начнут колебаться, но за один и тот же промежуток времени металлическая линейка (А) сделает больше колебаний, чем деревянная (В).
Число колебаний в единицу времени называется частотой колебаний.
Обрати внимание!
Обозначается частота греческой буквой ν («ню»). За единицу частоты принято одно колебание в секунду. Эта единица в честь немецкого учёного Генриха Герца названа герцем (Гц).
Период колебания \(Т\) и частота колебаний ν связаны следующей зависимостью:
T=1ν.
Свободные колебания в отсутствие трения и сопротивления воздуха называются собственными колебаниями, а их частота — собственной частотой колебательной системы.
Любая колебательная система имеет определённую собственную частоту, зависящую от параметров этой системы. Например, собственная частота пружинного маятника зависит от массы груза и жёсткости пружины.

Рассмотрим колебания двух одинаковых пустых качелей на рисунке выше. В один и тот же момент времени красные качели из положения равновесия начинают движение вперед, а зелёные качели из положения равновесия движутся назад. Качели колеблются с одной и той же частотой и с одинаковыми амплитудами. Однако эти колебания отличаются друг от друга: в любой момент времени скорости качелей направлены в противоположные стороны. В таком случае говорят, что колебания качелей происходят в противоположных фазах.
Красные пустые качели и качели с мальчиком тоже колеблются с одинаковыми частотами. Скорости этих качелей в любой момент времени направлены одинаково. В этом случае говорят, что качели колеблются в одинаковых фазах.
Физическая величина, называемая фазой, используется не только при сравнении колебаний двух или нескольких тел, но и для описания колебаний одного тела.
Таким образом, колебательное движение характеризуется амплитудой, частотой (или периодом) и фазой.
Источники:
Физика. 9 кл.: учебник / Перышкин А. В., Гутник Е. М. — М.: Дрофа, 2014. — 319 с.
www.ru.depositphotos.com, сайт «Фотобанк с премиум-коллекцией фотографий, векторов и видео»
www.mognovse.ru, сайт «Можно все»
Период колебаний — Википедия. Что такое Период колебаний

Период колеба́ний — наименьший промежуток времени, за который осциллятор совершает одно полное колебание (то есть возвращается в то же состояние [1], в котором он находился в первоначальный момент, выбранный произвольно).
В принципе совпадает с математическим понятием периода функции, но имея в виду под функцией зависимость физической величины, совершающей колебания, от времени.
Это понятие в таком виде применимо как к гармоническим, так и к ангармоническим строго периодическими колебаниям (а приближенно — с тем или иным успехом — и непериодическим колебаниям, по крайней мере к близким к периодичности).
В случае, когда речь идет о колебаниях гармонического осциллятора с затуханием, под периодом понимается период его осциллирующей составляющей (игнорируя затухание), который совпадает с удвоенным временным промежутком между ближайшими прохождениями колеблющейся величины через ноль. В принципе, это определение может быть с большей или меньшей точностью и пользой распространено в некотором обобщении и на затухающие колебания с другими свойствами.
Обозначения: обычное стандартное обозначение периода колебаний: T {\displaystyle T} (хотя могут применяться и другие, наиболее часто это τ {\displaystyle \tau } , иногда Θ {\displaystyle \Theta } и т. д.).
Единицы измерения: секунда и, в принципе, вообще единицы измерения времени.
Период колебаний связан соотношением взаимной обратности с частотой:
- T = 1 ν , ν = 1 T . {\displaystyle T={\frac {1}{\nu }},\ \ \ \nu ={\frac {1}{T}}.}
Для волновых процессов период связан кроме того очевидным образом с длиной волны λ {\displaystyle \lambda }
- v = λ ν , T = λ v , {\displaystyle v=\lambda \nu ,\ \ \ T={\frac {\lambda }{v}},}
где v {\displaystyle v} — скорость распространения волны (точнее[2] — фазовая скорость).
В квантовой физике период колебаний прямо связан с энергией (поскольку в квантовой физике энергия объекта — например, частицы — есть частота[3] колебаний его волновой функции).
Теоретическое нахождение периода колебаний той или иной физической системы сводится, как правило, к нахождению решения динамических уравнений (уравнения), описывающего эту систему. Для категории линейных систем (а приближенно — и для линеаризуемых систем в линейном приближении, которое зачастую является очень хорошим) существуют стандартные сравнительно простые математические методы, позволяющие это сделать (если известны сами физические уравнения, описывающие систему).
Для экспериментального определения периода используются часы, секундомеры, частотомеры, стробоскопы, строботахометры, осциллографы. Также применяются биения, метод гетеродинирования в разных видах, используется принцип резонанса. Для волн можно померить период косвенно — через длину волны, для чего применяются интерферометры, дифракционные решётки итп. Иногда требуются и изощренные методы, специально разработанные для конкретного трудного случая (трудность могут представлять как само измерение времени, особенно если речь идет о предельно малых или наоборот очень больших временах, так и трудности наблюдения колеблющейся величины).
Периоды колебаний в природе
Представление о периодах колебаний различных физических процессов дает статья Частотные интервалы (учитывая то, что период в секундах есть обратная величина частоты в герцах).
Некоторое представление о величинах периодов различных физических процессов также может дать шкала частот элетромагнитных колебаний (см. Электромагнитный спектр) .
Периоды колебаний слышимого человеком звука находятся в диапазоне
- от 5·10−5с до 0,2с
(четкие границы его несколько условны).
Периоды электромагнитных колебаний, соответствующих разным цветам видимого света — в диапазоне
- от 1,1·10−15с до 2,3·10−15с.
Поскольку при экстремально больших и экстремально маленьких периодах колебаний методы измерения имеют тенденцию становятся всё более косвенными (вплоть до плавного перетекания в теоретические экстраполяции), трудно назвать четкую верхнюю и нижнюю границы для периода колебаний, измеренного непосредственно. Какую-то оценку для верхней границы может дать время существования современной науки (сотни лет), а для нижней — период колебаний волновой функции самой тяжелой из известных сейчас частиц ().
В любом случае границей снизу может служить планковское время, которое столь мало, что по современным представлениям не только вряд ли может быть вообще как-то физически измерено[4], но и вряд ли в более-менее обозримом будущем представляется возможность приблизиться к измерению величин даже намного порядков больших, а границей сверху — время существования Вселенной — более десяти миллиардов лет.
Периоды колебаний простейших физических систем
Пружинный маятник
Период колебаний пружинного маятника может быть вычислен по следующей формуле:
T = 2 π m k {\displaystyle T=2\pi {\sqrt {\frac {m}{k}}}} ,
где m {\displaystyle m} — масса груза, k {\displaystyle k} — жёсткость пружины.
Математический маятник
Период малых колебаний математического маятника:
T = 2 π l g {\displaystyle T=2\pi {\sqrt {\frac {l}{g}}}}
где l {\displaystyle l} — длина подвеса (к примеру, нити), g {\displaystyle g} — ускорение свободного падения.
Период малых колебаний (на Земле) математического маятника длиной 1 метр с хорошей точностью[5] равен 2 секундам.
Физический маятник
Период малых колебаний физического маятника:
T = 2 π J m g l {\displaystyle T=2\pi {\sqrt {\frac {J}{mgl}}}}
где J {\displaystyle J} — момент инерции маятника относительно оси вращения, m {\displaystyle m} — масса маятника, l {\displaystyle l} — расстояние от оси вращения до центра масс.
Крутильный маятник
Период колебаний крутильного маятника:
T = 2 π I K {\displaystyle T=2\pi {\sqrt {\frac {I}{K}}}}
где I {\displaystyle I} — момент инерции маятника относительно оси кручения, а K {\displaystyle K} — вращательный коэффициент жёсткости маятника.
Электрический колебательный (LC) контур
Период колебаний электрического колебательного контура (формула Томсона):
T = 2 π L C {\displaystyle T=2\pi {\sqrt {LC}}} ,
где L {\displaystyle L} — индуктивность катушки, C {\displaystyle C} — ёмкость конденсатора.
Эту формулу вывел в 1853 году английский физик Уильям Томсон.
Примечания
- ↑ Состояние механической системы характеризуется положениями и скоростями всех её материальных точек (строже говоря — координатами и скоростями, соответствующими всем степеням свободы данной системы), для немеханической — их формальными аналогами (которые также можно назвать координатами и скоростями в смысле абстрактного описания динамической системы — в количестве, также равном количеству её степеней свободы).
- ↑ Для монохроматических волн это уточнение самоочевидно, для близких к монохроматическим — интуитивно очевидно по аналогии со строго монохроматическими, для существенно немонохроматических — наиболее ясный случай сводится к тому, что фазовые скорости всех монохроматических компонент совпадают друг с другом, поэтому комментируемое утверждение также верно.
- ↑ С точностью до единиц измерения: в традиционных (обычных) системах физических единиц частота и энергия измеряются в разных единицах (поскольку до появления квантовой теории совпадение энергии и частоты было неизвестно, и, естественно, для каждой из величин была выбрана своя независимая единица измерения), поэтому при измерении их в обычных (разных) единицах, например, джоулях и герцах требуется переводной коэффициент (так называемая константа Планка). Однако можно выбрать систему единиц измерения так, чтобы в ней константа Планка стала равной 1 и пропала из формул; в такой системе единиц энергия любой частицы просто равна частоте колебания её волновой функции (а значит обратна периоду этого колебания).
- ↑ Имеется в виду, конечно же, невозможность экспериментального измерения времен конкретных процессов или периодов колебаний такого порядка, а не просто вычисление некоторого числа.
- ↑ Лучше, чем 0,5 %, если взять метрологическое или принятое техническое значение ускорения свободного падения; И с разбросом ~0.53 % для максимального и минимального значений ускорения свободного падения, наблюдаемых на земле.
Ссылки
Период колебаний — Википедия. Что такое Период колебаний


Период колеба́ний — наименьший промежуток времени, за который осциллятор совершает одно полное колебание (то есть возвращается в то же состояние[1], в котором он находился в первоначальный момент, выбранный произвольно).
В принципе совпадает с математическим понятием периода функции, но имея в виду под функцией зависимость физической величины, совершающей колебания, от времени.
Это понятие в таком виде применимо как к гармоническим, так и к ангармоническим строго периодическими колебаниям (а приближенно — с тем или иным успехом — и непериодическим колебаниям, по крайней мере к близким к периодичности).
В случае, когда речь идет о колебаниях гармонического осциллятора с затуханием, под периодом понимается период его осциллирующей составляющей (игнорируя затухание), который совпадает с удвоенным временным промежутком между ближайшими прохождениями колеблющейся величины через ноль. В принципе, это определение может быть с большей или меньшей точностью и пользой распространено в некотором обобщении и на затухающие колебания с другими свойствами.
Обозначения: обычное стандартное обозначение периода колебаний: T {\displaystyle T} (хотя могут применяться и другие, наиболее часто это τ {\displaystyle \tau } , иногда Θ {\displaystyle \Theta } и т. д.).
Единицы измерения: секунда и, в принципе, вообще единицы измерения времени.
Период колебаний связан соотношением взаимной обратности с частотой:
- T = 1 ν , ν = 1 T . {\displaystyle T={\frac {1}{\nu }},\ \ \ \nu ={\frac {1}{T}}.}
Для волновых процессов период связан кроме того очевидным образом с длиной волны λ {\displaystyle \lambda }
- v = λ ν , T = λ v , {\displaystyle v=\lambda \nu ,\ \ \ T={\frac {\lambda }{v}},}
где v {\displaystyle v} — скорость распространения волны (точнее[2] — фазовая скорость).
В квантовой физике период колебаний прямо связан с энергией (поскольку в квантовой физике энергия объекта — например, частицы — есть частота[3] колебаний его волновой функции).
Теоретическое нахождение периода колебаний той или иной физической системы сводится, как правило, к нахождению решения динамических уравнений (уравнения), описывающего эту систему. Для категории линейных систем (а приближенно — и для линеаризуемых систем в линейном приближении, которое зачастую является очень хорошим) существуют стандартные сравнительно простые математические методы, позволяющие это сделать (если известны сами физические уравнения, описывающие систему).
Для экспериментального определения периода используются часы, секундомеры, частотомеры, стробоскопы, строботахометры, осциллографы. Также применяются биения, метод гетеродинирования в разных видах, используется принцип резонанса. Для волн можно померить период косвенно — через длину волны, для чего применяются интерферометры, дифракционные решётки итп. Иногда требуются и изощренные методы, специально разработанные для конкретного трудного случая (трудность могут представлять как само измерение времени, особенно если речь идет о предельно малых или наоборот очень больших временах, так и трудности наблюдения колеблющейся величины).
Периоды колебаний в природе
Представление о периодах колебаний различных физических процессов дает статья Частотные интервалы (учитывая то, что период в секундах есть обратная величина частоты в герцах).
Некоторое представление о величинах периодов различных физических процессов также может дать шкала частот элетромагнитных колебаний (см. Электромагнитный спектр) .
Периоды колебаний слышимого человеком звука находятся в диапазоне
- от 5·10−5с до 0,2с
(четкие границы его несколько условны).
Периоды электромагнитных колебаний, соответствующих разным цветам видимого света — в диапазоне
- от 1,1·10−15с до 2,3·10−15с.
Поскольку при экстремально больших и экстремально маленьких периодах колебаний методы измерения имеют тенденцию становятся всё более косвенными (вплоть до плавного перетекания в теоретические экстраполяции), трудно назвать четкую верхнюю и нижнюю границы для периода колебаний, измеренного непосредственно. Какую-то оценку для верхней границы может дать время существования современной науки (сотни лет), а для нижней — период колебаний волновой функции самой тяжелой из известных сейчас частиц ().
В любом случае границей снизу может служить планковское время, которое столь мало, что по современным представлениям не только вряд ли может быть вообще как-то физически измерено[4], но и вряд ли в более-менее обозримом будущем представляется возможность приблизиться к измерению величин даже намного порядков больших, а границей сверху — время существования Вселенной — более десяти миллиардов лет.
Периоды колебаний простейших физических систем
Пружинный маятник
Период колебаний пружинного маятника может быть вычислен по следующей формуле:
T = 2 π m k {\displaystyle T=2\pi {\sqrt {\frac {m}{k}}}} ,
где m {\displaystyle m} — масса груза, k {\displaystyle k} — жёсткость пружины.
Математический маятник
Период малых колебаний математического маятника:
T = 2 π l g {\displaystyle T=2\pi {\sqrt {\frac {l}{g}}}}
где l {\displaystyle l} — длина подвеса (к примеру, нити), g {\displaystyle g} — ускорение свободного падения.
Период малых колебаний (на Земле) математического маятника длиной 1 метр с хорошей точностью[5] равен 2 секундам.
Физический маятник
Период малых колебаний физического маятника:
T = 2 π J m g l {\displaystyle T=2\pi {\sqrt {\frac {J}{mgl}}}}
где J {\displaystyle J} — момент инерции маятника относительно оси вращения, m {\displaystyle m} — масса маятника, l {\displaystyle l} — расстояние от оси вращения до центра масс.
Крутильный маятник
Период колебаний крутильного маятника:
T = 2 π I K {\displaystyle T=2\pi {\sqrt {\frac {I}{K}}}}
где I {\displaystyle I} — момент инерции маятника относительно оси кручения, а K {\displaystyle K} — вращательный коэффициент жёсткости маятника.
Электрический колебательный (LC) контур
Период колебаний электрического колебательного контура (формула Томсона):
T = 2 π L C {\displaystyle T=2\pi {\sqrt {LC}}} ,
где L {\displaystyle L} — индуктивность катушки, C {\displaystyle C} — ёмкость конденсатора.
Эту формулу вывел в 1853 году английский физик Уильям Томсон.
Примечания
- ↑ Состояние механической системы характеризуется положениями и скоростями всех её материальных точек (строже говоря — координатами и скоростями, соответствующими всем степеням свободы данной системы), для немеханической — их формальными аналогами (которые также можно назвать координатами и скоростями в смысле абстрактного описания динамической системы — в количестве, также равном количеству её степеней свободы).
- ↑ Для монохроматических волн это уточнение самоочевидно, для близких к монохроматическим — интуитивно очевидно по аналогии со строго монохроматическими, для существенно немонохроматических — наиболее ясный случай сводится к тому, что фазовые скорости всех монохроматических компонент совпадают друг с другом, поэтому комментируемое утверждение также верно.
- ↑ С точностью до единиц измерения: в традиционных (обычных) системах физических единиц частота и энергия измеряются в разных единицах (поскольку до появления квантовой теории совпадение энергии и частоты было неизвестно, и, естественно, для каждой из величин была выбрана своя независимая единица измерения), поэтому при измерении их в обычных (разных) единицах, например, джоулях и герцах требуется переводной коэффициент (так называемая константа Планка). Однако можно выбрать систему единиц измерения так, чтобы в ней константа Планка стала равной 1 и пропала из формул; в такой системе единиц энергия любой частицы просто равна частоте колебания её волновой функции (а значит обратна периоду этого колебания).
- ↑ Имеется в виду, конечно же, невозможность экспериментального измерения времен конкретных процессов или периодов колебаний такого порядка, а не просто вычисление некоторого числа.
- ↑ Лучше, чем 0,5 %, если взять метрологическое или принятое техническое значение ускорения свободного падения; И с разбросом ~0.53 % для максимального и минимального значений ускорения свободного падения, наблюдаемых на земле.
Ссылки
Период колебаний
Период колебаний — минимальный промежуток времени, за который тело совершает одно полное колебание
Для нахождения периода колебаний надо время всех колебаний разделить на количество колебаний:
Период колебаний – величина, обратная частоте колебаний:
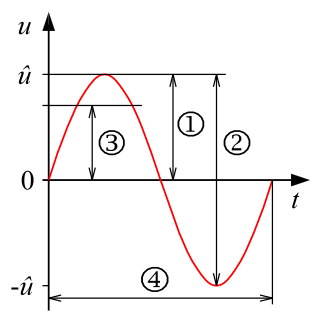
Период колебаний на графике – это расстояние между двумя точками, совершающими волебания в одинаковых фазах:
красная кривая отличается от синей только значением периода (T’ = T / 2)
Период колебаний пружинного маятника
Период колебаний математического маятника
Период колебаний физического маятника
Период колебаний крутильного маятника
Обозначения:
T — период колебаний маятника
N — количество колебаний
t — время, за которое было совершено N колебаний
m — масса груза, или масса маятника
k — жесткость пружины
L — длина подвеса
g — ускорение свободного падения
J — момент инерции маятника относительно оси вращения
l — расстояние от оси вращения до центра масс
I — момент инерции тела
K — вращательный коэффициент жёсткости маятника
Период колебания – это… Что такое Период колебания?
- Период колебания
Пери́од колеба́ний — наименьший промежуток времени, за который система совершает одно полное колебание (то есть возвращается в то же состояние, в котором она находилась в первоначальный момент, выбранный произвольно).
Периоды простейших физических систем
Период колебаний математического маятника
Период колебаний математического маятника выражается по следующей формуле:

Период колебаний физического маятника
Период колебаний физического маятника выражается по следующей формуле: где J – момент инерции маятника относительно оси вращения, m – масса маятника, l – расстояние от оси вращения до центра масс.
Период колебаний пружинного маятника
 ,
,
где m — масса груза, k — жесткость пружины.
Wikimedia Foundation. 2010.
- Период инкубации
- Период кристаллической решетки
Смотреть что такое “Период колебания” в других словарях:
ПЕРИОД КОЛЕБАНИЯ — (period of oscillation) Отрезок времени, который требуется колебательной функции, для того чтобы вернуться в любую заданную точку своего цикла. Функции y=acosx или z=bsinx имеют период колебания, равный 2π; если цикл достигает заданной точки,… … Экономический словарь
период колебания — 1. Наименьший промежуток времени, за который совершается один цикл колебания. Для периодических колебаний время, за которое совершается одно полное колебание. 2. Время, за которое совершается один полный цикл колебания. Единица измерения с [BS EN … Справочник технического переводчика
период колебания — svyravimo periodas statusas T sritis fizika atitikmenys: angl. oscillation period vok. Schwingungsperiode, f rus. период колебания, m pranc. période d’oscillation, f … Fizikos terminų žodynas
период колебания — svyravimo laikotarpis statusas T sritis Kūno kultūra ir sportas apibrėžtis Svyruojamųjų judesių apibūdinimas – trumpiausias laiko tarpas, per kurį svyruojanti sistema grįžta į pradinę padėtį. Svyravimo laikotarpio dydis yra atvirkščias svyravimo… … Sporto terminų žodynas
основной период колебания здания в интересующем горизонтальном направлении — T1 — [Англо русский словарь по проектированию строительных конструкций. МНТКС, Москва, 2011] Тематики строительные конструкции Синонимы T1 EN fundamental period of the building in the horizontal direction of interest … Справочник технического переводчика
КОЛЕБАНИЯ — движения или процессы, обладающие той или иной степенью повторяемости во времени. К. свойственны всем явлениям природы: пульсирует излучение звёзд, внутри к рых происходят циклич. яд. реакции; с высокой степенью периодичности вращаются планеты… … Физическая энциклопедия
период колебаний — период Наименьший промежуток времени, через который повторяется состояние механической системы, характеризуемое значениями обобщенных координат и их производных. [Сборник рекомендуемых терминов. Выпуск 106. Механические колебания. Академия наук… … Справочник технического переводчика
период колебаний (вибрации) — период Наименьший интервал времени, через который при периодических колебаниях (вибрации) повторяется каждое значение колеблющейся величины (характеризующей вибрацию). Пояснения Термины и определения для близких понятий, различающиеся лишь… … Справочник технического переводчика
КОЛЕБАНИЯ — КОЛЕБАНИЯ, процессы (в наиболее общем смысле), периодически меняющие свое направление со временем. Процессы эти могут быть весьма разнообразными. Если напр. подвесить на стальной спиральной пружине тяжелый шар, оттянуть его и затем предоставить… … Большая медицинская энциклопедия
ПЕРИОД КОЛЕБАНИЙ — наименьший промежуток времени, через к рый .система, совершающая колебания, снова возвращается в то же состояние, в к ром она находилась в нач. момент, выбранный произвольно. Строго говоря, понятие «П. к.» применимо лишь, когда значения к. л.… … Физическая энциклопедия
Книги
- Не сезон. Как поднять продажи в период спада, Имшинецкая Ия Анатольевна. Регулярные колебания спроса, называемые сезонностью, случаются в любом виде бизнеса. Эта книга – источник идей, которые будут зарабатывать деньги для вашей компании в период традиционного… Подробнее Купить за 661 руб
- Не сезон. Как поднять продажи в период спада, Имшинецкая Ия Анатольевна. Регулярные колебания спроса, называемые сезонностью, случаются в любом виде бизнеса. Эта книга – источник идей, которые будут зарабатывать деньги для вашей компании в период традиционного… Подробнее Купить за 560 грн (только Украина)
- Не сезон Как поднять продажи в период спада, Имшинецкая И.. “Не сезон. Как поднять продажи в период спада” . Регулярные колебания спроса, называемые сезонностью, случаются в любом виде бизнеса. Эта книга – источник идей, которые будут зарабатывать… Подробнее Купить за 460 руб
ПЕРИОД КОЛЕБАНИЙ – это… Что такое ПЕРИОД КОЛЕБАНИЙ?
- ПЕРИОД КОЛЕБАНИЙ
- ПЕРИОД КОЛЕБАНИЙ
-
наименьший промежуток времени, через к-рый .система, совершающая колебания, снова возвращается в то же состояние, в к-ром она находилась в нач. момент, выбранный произвольно. Строго говоря, понятие «П. к.» применимо лишь, когда значения к.-л. величины точно повторяются через одинаковые промежутки времени, напр. в случае гармонических колебаний. Однако понятие «П. к.» часто применяется и для приблизительно повторяющихся процессов.
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- ПЕРИОД КОЛЕБАНИЙ
-
– наименьший промежутоквремени, чер-ез к-рый система, совершающая колебания, снова возвращаетсяв то же состояние, в к-ром она находилась в нач. момент, выбранный произвольно.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
- ПЕРЕХОДНЫЕ МЕТАЛЛЫ
- ПЕРИОД ПОЛУРАСПАДА
Смотреть что такое “ПЕРИОД КОЛЕБАНИЙ” в других словарях:
период колебаний — период Наименьший промежуток времени, через который повторяется состояние механической системы, характеризуемое значениями обобщенных координат и их производных. [Сборник рекомендуемых терминов. Выпуск 106. Механические колебания. Академия наук… … Справочник технического переводчика
Период (колебаний) — ПЕРИОД колебаний, наименьший промежуток времени, через который совершающая колебания система возвращается в то же состояние, в котором она находилась в начальный момент, выбранный произвольно. Период величина, обратная частоте колебаний. Понятие… … Иллюстрированный энциклопедический словарь
ПЕРИОД КОЛЕБАНИЙ — наименьший промежуток времени, через который колеблющаяся система возвращается к исходному состоянию. Период колебаний величина, обратная частоте колебаний … Большой Энциклопедический словарь
период колебаний — период колебаний; период Наименьший промежуток времени, через который повторяется состояние механической системы, характеризуемое значениями обобщенных координат и их производных … Политехнический терминологический толковый словарь
Период колебаний — Эту статью следует викифицировать. Пожалуйста, оформите её согласно правилам оформления статей … Википедия
Период колебаний — 16. Период колебаний Наименьший интервал времени, через который при периодических колебаниях повторяется каждое значение колеблющейся величины Источник … Словарь-справочник терминов нормативно-технической документации
период колебаний — наименьший промежуток времени, через который колеблющаяся система возвращается к исходному состоянию. Период колебаний величина, обратная частоте колебаний. * * * ПЕРИОД КОЛЕБАНИЙ ПЕРИОД КОЛЕБАНИЙ, наименьший промежуток времени, через который… … Энциклопедический словарь
период колебаний — virpesių periodas statusas T sritis automatika atitikmenys: angl. oscillation period; period of oscillations; period of vibrations vok. Schwingungsdauer, m; Schwingungsperiode, f; Schwingungszeit, f rus. период колебаний, m pranc. période d… … Automatikos terminų žodynas
период колебаний — virpesių periodas statusas T sritis Standartizacija ir metrologija apibrėžtis Mažiausias laiko tarpas, po kurio pasikartoja periodiškai kintančių dydžių vertės. atitikmenys: angl. vibration period vok. Schwingungsdauer, f; Schwingungsperiode, f… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
период колебаний — virpesių periodas statusas T sritis chemija apibrėžtis Mažiausias laiko tarpas, po kurio pasikartoja periodiškai kintančių dydžių vertės. atitikmenys: angl. period of oscillation; period of vibration; vibration period rus. период колебаний … Chemijos terminų aiškinamasis žodynas
Книги
- Создание отечественной радиолокации. Научные труды, мемуары, воспоминания, Кобзарев Ю.Б.. Книга содержит научные статьи по ряду важнейших направлений радиотехники, радиолокации и радиофизики: кварцевая стабилизация частоты, теория нелинейных колебаний, теория линейных… Подробнее Купить за 2385 грн (только Украина)
- Создание отечественной радиолокации. Научные труды, мемуары, воспоминания, Кобзарев Ю.Б.. Книга содержит научные статьи по ряду важнейших направлений радиотехники, радиолокации и радиофизики: кварцевая стабилизация частоты, теория нелинейных колебаний, теория линейных… Подробнее Купить за 1844 руб
- Договор как средство обеспечения стабильности гражданского оборота, Ю. В. Рогова. В работе на научно-квалификационном уровне рассматривается договор как один из элементов механизма гражданско-правового регулирования экономических отношений. Особое внимание уделено… Подробнее Купить за 541 руб
Определение
в кембриджском словаре английского языка
КОЛЕБАНИЯ | Определение в кембриджском словаре английского языкаосцилляция существительное [C or U]
Тезаурус: синонимы и родственные слова ,Каков период колебаний массы 40 кг на пружине при постоянном k = 10 Н / м?
Наука
- Анатомия и физиология
- астрономия
- астрофизика
- Биология
- Химия
- наука о планете Земля


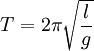
 ,
,