Центр тяжести швеллера: Геометрические характеристики плоского поперечного сечения 4 элемента (полоса, двутавр, швеллер уголок) 020

alexxlab | 30.03.2020 | 0 | Разное

Геометрические характеристики плоского поперечного сечения 4 элемента (полоса, двутавр, швеллер уголок) 020

Рис. 1

Дано схему поперечного сечения, составленную из трех элементов (рис. 1). Определить геометрические характеристики составного сечения. Площадь, центр тяжести, положение главных осей, главные моменты инерции, главные радиусы инерции, главные моменты сопротивления и построить эллипс инерции. План выполнения задачи: 1) Геометрические характеристики элементов сечения. 2) Положение центра тяжести сечения. 3) Моменты инерции относительно центральных осей. 4) Положение главных осей. 5) Определение главных моментов инерции. 6) Главные радиусы инерции. 7) Определение главных моментов сопротивления.

1) Выписываем из таблицы сортамента (ГОСТ 8240-72, ГОСТ 8239-72 и ГОСТ 8509-86) необходимые геометрические характеристики для швеллера, двутавра, уголка и вычисляем по формулам прямоугольника:

а) Полоса (прямоугольник) 300Х24

см 2, см 4, см 4,

 

б) Швеллер №20

см 2, см 4, см 4, см, см, см.

 

в) Двутавр №24

см 2, см 4, см 4, см, см.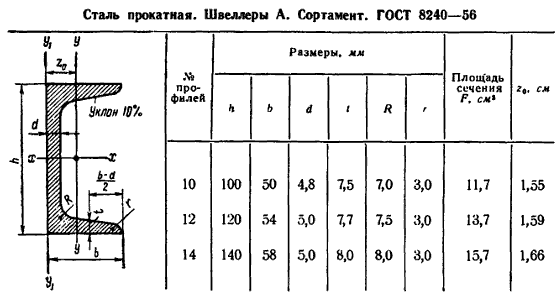

 

г) Уголок 140Х9

см 2, см 4, см 4, см 4, см, см.

 

2) Определяем положение центра тяжести сечения относительно начальных осей (осей полосы)

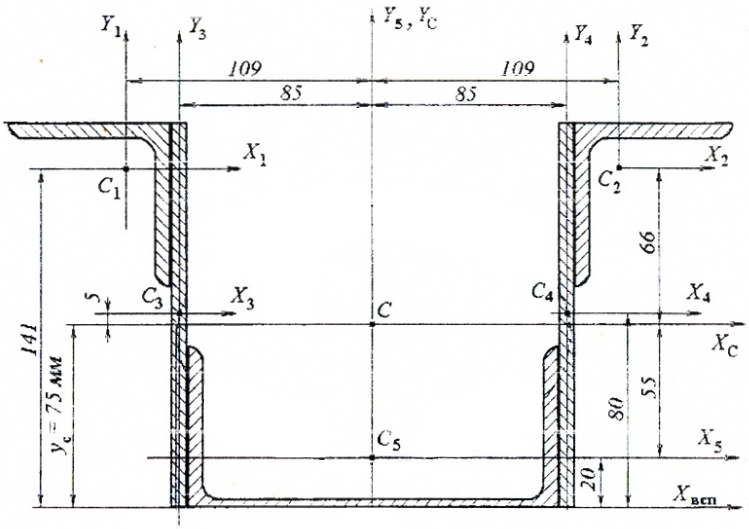
На отдельном листе бумаги в масштабе чертим схему поперечного сечения (рис. 2) и указываем положение центральных осей каждого элемента. Выполняем привязку (указываем расстояния) центров тяжести каждого элемента относительно начальных осей

Координаты центров тяжести элементов в осях

см,

см,

см,

см,

см,

см.

Рис. 2

Площадь поперечного сечения:

см ²,

Координаты центра тяжести сечения:

см,

см.

Откладываем на рисунке координаты и с учетом знаков, обозначаем положение центра тяжести (точка С) и проводим центральные оси

Контролируем достоверность определения положения центра тяжести сложного сечения. Для этого вычисляем координаты центров тяжести элементов сечения в координатных осях и (расстояния между собственными центральными осями отдельных элементов и центральными осями сечения):

см, см, см, см.

см, см, см, см.

и статические моменты площади сечения относительно центральных осей:

см ³,

погрешность:

см ³,

погрешность:

3) На основании формул параллельного перехода вычисляем моменты инерции сечения относительно центральных осей и

– осевые

см ⁴,

см ⁴,

– центробежный

см ⁴.

Понравилась статья! Поддержи проект! Ставь ЛАЙК!

Центр тяжести – методы нахождения.



Наиболее часто для нахождения центра тяжести тела или фигуры применяют следующие методы:

• метод симметрии;
• метод разбиения;
• метод отрицательных масс.

Рассмотрим приемы, применяемые в каждом из перечисленных методов.

***

Метод симметрии

Представим себе однородное тело, которое имеет плоскость симметрии. Выберем такую систему координат, чтобы оси x и z лежали в плоскости симметрии (см. рисунок 1).

В этом случае каждой элементарной частице силой тяжести G_i с абсциссой y_i = +a соответствует такая же элементарная частица с абсциссой y_i = -a, тогда:

y_C = Σ(G_ix_i)/ΣG_i = 0.

Отсюда вывод: если однородное тело имеет плоскость симметрии, то центр тяжести тела лежит в этой плоскости.

Аналогично можно доказать и следующие положения:

• Если однородное тело имеет ось симметрии, то центр тяжести тела лежит на этой оси;
• Если однородное тело имеет две оси симметрии, то центр тяжести тела находится в точке их пересечения;
• Центр тяжести однородного тела вращения лежит на оси вращения.

***

Метод разбиения

Этот метод заключается в том, что тело разбивают на наименьшее число частей, силы тяжести и положение центров тяжести которых известны, после чего применяют приведенные ранее формулы для определения общего центра тяжести тела.

Допустим, что мы разбили тело силой тяжести G на три части G’, G”, G”’, абсциссы центров тяжести этих частей x’

C, x”_C, x”’_C известны.
Формула для определения абсциссы центра тяжести всего тела:

x_C = Σ(G_ix_i)/ΣG_i.

Перепишем ее в следующем виде:

x_CΣG_i = Σ(G_ix_i)     или     Gx_C = Σ(G_ix_i).

Последнее равенство запишем для каждой из трех частей тела отдельно:

G’x’_C = Σ(G’x’_i),     G”x”_C = Σ(G”_ix”_i),     G”’x”’_C = Σ(G”’_ix”’_i).

Сложив левые и правые части этих трех равенств, получим:

G’x’_C + G”x”_C + G”’x”’_C = Σ(G’_ix’_i) + Σ(G”_{x”i) + Σ(G”’ix”’i) = Σ(Gixi).}

Но правая часть последнего равенства представляет собой произведение Gx_C, так как

Gx_C = Σ(G_ix_i),

Следовательно, x_C = (G’x’_C + G”x”_C + G”’x”’_C)/G, что и требовалось доказать.
Аналогично определяются координаты центра тяжести на координатных осях y и z:

y_C = (G’y’_C + G”y”_C + G”’y”’_C)/G,
z_C = (G’z’_C + G”z”_C + G”’z”’_C)/G.

Полученные формулы аналогичны формулам для определения координат цента тяжести, выведенные выше. Поэтому в исходные формулы можно подставлять не силы тяжести элементарных частиц G_i, а силы тяжести конечных частей; под координатами x_i, y_i, z_i понимают координаты центров тяжести частей, на которые разбито тело.

***

Метод отрицательных масс

Этот метод заключается в том, что тело, имеющее свободные полости, считают сплошным, а массу свободных полостей – отрицательной.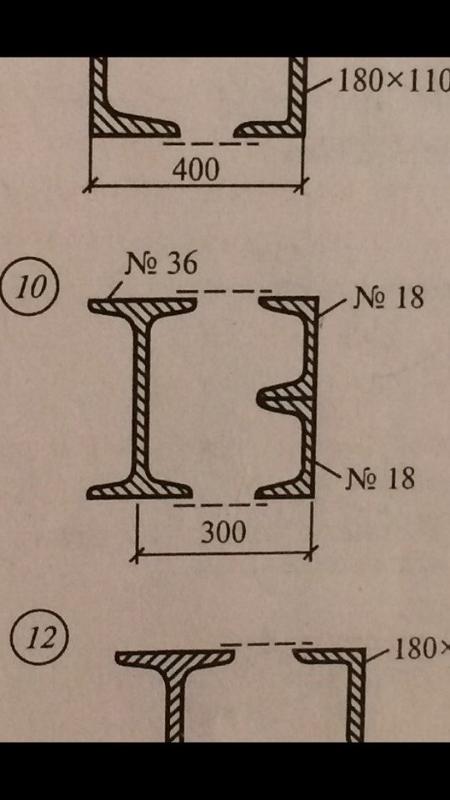 Вид формул для определения координат центра тяжести тела при этом не меняется.

Таким образом, при определении центра тяжести тела, имеющего свободные полости, следует применять метод разбиения, но считать массу полостей отрицательной.

***

Практические методы определения центра тяжести тел

На практике для определения центра тяжести плоских тел сложной формы часто применяют метод подвешивания, который заключается в том, что плоское тело подвешивают на нити за какую-нибудь точку. Прочерчивают вдоль нити линию, и тело подвешивают за другую точку, не находящуюся на полученной линии.
Затем вновь проводят линию вдоль нити.
Точка пересечения двух линий и будет являться центром тяжести плоского тела.

Еще один способ определения центра тяжести, применяемый на практике, называется метод взвешивания. Этот метод часто применяется для определения центра тяжести крупных машин и изделий – автомобилей, самолетов, колесных тракторов и т.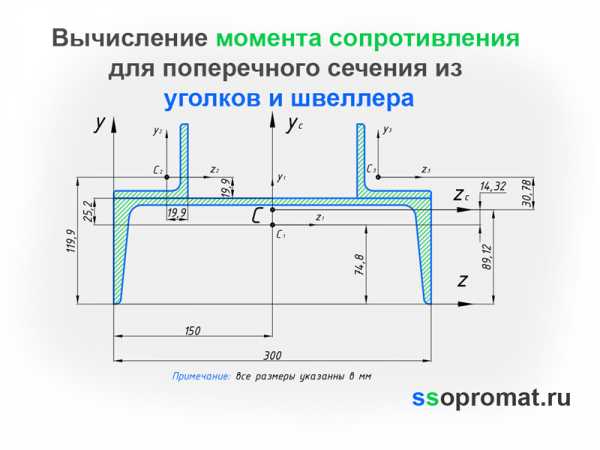 п., которые имеют сложную объемную форму и точечную опору на грунт.
Метод заключается в применении условий равновесия, исходя из того, что сумма моментов всех сил, действующих на неподвижное тело равна нулю.

Практически это осуществляется взвешиванием одной из опор машины (задние или передние колеса устанавливаются на весы), при этом показания весов, по сути, являются реакцией опоры, которая учитывается при составлении уравнения равновесия относительно второй точки опоры (находящейся вне весов).
По известной массе (соответственно – весу) тела, показанию весов в одной из точек опоры, и расстоянию между точками опоры можно определить расстояние от одной из точек опоры до плоскости, в которой расположен центр тяжести.
Чтобы найти подобным образом линию (ось), на которой расположен центр тяжести машины, необходимо произвести два взвешивания по принципу, изложенному выше для метода подвешивания (см. рис. 1а).

***



Положение центра тяжести некоторых фигур

Прямоугольник.

Так как прямоугольник имеет две оси симметрии, то центр тяжести его площади находится в точке пересечения этих осей, иначе говоря, в точке пересечения диагоналей прямоугольника.

Треугольник. Пусть дан треугольник АBD (см. рисунок 2).
Разобьем его на элементарные (бесконечно узкие) полоски, параллельные стороне AD. Центр тяжести каждой полоски будет лежать на медиане Bd (т. е. в середине каждой полоски), следовательно, на этой медиане будет лежать и центр тяжести всей площади треугольника. Разбив треугольник на элементарные полоски, параллельные стороне AB, увидим, что искомый центр тяжести лежит и на медиане aD.
Проделав аналогичное действие с треугольником относительно стороны ВD, получим тот же результат – центр тяжести находится на соответствующей медиане.
Следовательно, центр тяжести всей площади треугольника лежит на точке пересечения его медиан, поскольку эта точка является единственной общей точкой для всех трех медиан данной геометрической фигуры.

Из геометрии известно, что медианы треугольника пересекаются в одной точке и делятся в соотношении 1:2 от основания. Следовательно, центр тяжести треугольника расположен на расстоянии одной трети высоты от каждого основания.

Дуга окружности. Возьмем дугу окружности АВ радиусом R с центральным углом 2α (см. рисунок 3). Систему координат выберем так, чтобы начало координат было в центре окружности, а ось x делила дугу пополам, тогда y_C= 0 вследствие симметрии дуги относительно оси x. Определим координату центра тяжести x_C.

Разобьем дугу АВ на элементарные части l_i, одна из которых изображена на рисунке. Тогда, согласно сделанным выше выводам,

x_C =Σ(l_ix_Ci)/Σl_i.

Дугу l_i вследствие малости примем за отрезок прямой. Из подобия треугольника OD_iC_i и элементарного треугольника S (на рисунке заштрихован) получим:

L_i/Δy_i = R/x_Ci     или     l_ix_i = RΔy_i.

Тогда:

x_C =Σ(l_ix_Ci)/Σl_i = Σ(RΔy_i)/l = RΣΔy_i/l = R×AB/l,

поскольку RΣΔy_i = AB, а Σl_i = l – длина дуги АВ. Но АВ = 2R sinα, а l = 2Rα, следовательно,

x_C = (R sinα)/α.

При α = π/2 рад (полуокружность), x_C = 2R/π.

Круговой сектор. Возьмем сектор радиусом R с центральным углом 2α (см. рисунок 3а). Проведем оси координат, как показано на рисунке (ось x направлена вдоль оси симметрии сектора), тогда y_C = 0.

Определим x_C, для чего разобьем сектор на ряд элементарных секторов, каждый из которых из-за малости дуги l_i можно принять за равнобедренный треугольник с высотой R. Тогда центр тяжести каждого элементарного сектора будет находиться на дуге радиуса 2R/3 и задача определения центра тяжести сектора сводится к определению центра тяжести этой дуги.
Очевидно, что

x_C = 2 R sinα/(3α).

При α = π/2 рад (полукруг): x_C = 4R/(3π).

***

Пример решения задачи на определение центра тяжести

Задача:
Определить положение центра тяжести сечения, составленного из двутавра № 22 и швеллера № 20, как показано на рисунке 4.

Решение.
Из курса инженерной графики известно, что номер проката соответствует наибольшему габаритному размеру его сечения, выраженного в сантиметрах.

Так как сечение, составленное из двутавра и швеллера, представляет собой фигуру, симметричную относительно оси y, то центр тяжести такого сечения лежит на этой оси, т. е. x_C = 0.
По справочнику определим площади и координаты центров тяжести двутавра 1 и швеллера 2.

Для двутаврового сечения:  А₁ = 15,2 см²;     y₁ = 22/2 = 11 см.
Для швеллерного сечения:  А₂ = 12 см²;     y₂ = 22 + d – z₀ = 22 + 0,32 – 1,25 = 21,07 см,
где d – толщина стенки швеллера; z₀ – размер, определяющий положение центра тяжести швеллера.

Применим формулу для определения координаты центра тяжести всего сечения:

y_C = Σ(A_iy_i)/ΣA_i,

тогда:

y_C = (A₁y₁ +A₂y₂)/(A₁ +A₂) = (15,2×11 + 12×21,07)/(15,2 + 12) = 15,4 см.

Задача решена.

***

Кинематика точки



Главная страница

• Страничка абитуриента

Дистанционное образование

• Группа ТО-81
• Группа М-81
• Группа ТО-71
  

Специальности

• Ветеринария
• Механизация сельского хозяйства
• Коммерция
• Техническое обслуживание и ремонт автотранспорта

Учебные дисциплины

• Инженерная графика
• МДК. 01.01. «Устройство автомобилей»
•    Карта раздела
•       Общее устройство автомобиля
•       Автомобильный двигатель
•       Трансмиссия автомобиля
•       Рулевое управление
•       Тормозная система
•       Подвеска
•       Колеса
•       Кузов
•       Электрооборудование автомобиля
•       Основы теории автомобиля
•       Основы технической диагностики
• Основы гидравлики и теплотехники
• Метрология и стандартизация
• Сельскохозяйственные машины
• Основы агрономии
• Перевозка опасных грузов
• Материаловедение
• Менеджмент
• Техническая механика
• Советы дипломнику

Олимпиады и тесты

• «Инженерная графика»
• «Техническая механика»
• «Двигатель и его системы»
• «Шасси автомобиля»
• «Электрооборудование автомобиля»

Что такое центр сдвига – Расположение центра сдвига с примерами

🕑 Время чтения: 1 минута

Центр сдвига – это точка на сечении балки, в которой приложение нагрузок не вызывает ее скручивание.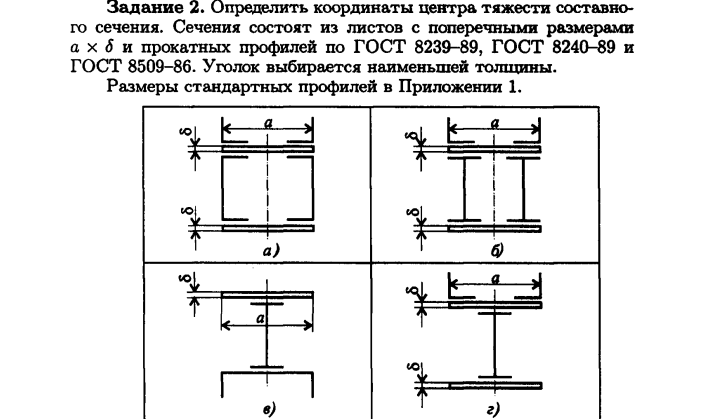 Положение центра сдвига зависит от поперечного сечения балки. Например, центр сдвига и центр тяжести совпадают в симметричном сечении, но могут не совпадать с центром тяжести в случае несимметричного сечения.

Так, в несимметричных поперечных сечениях внешние силы должны проходить через центр сдвига, а не через центр тяжести сечения, иначе создаваемый изгибающий момент будет сопровождаться скручиванием.

Как вычислить положение центра сдвига?

Рассмотрим сечение канала, как показано на рис. 1. Теперь мы найдем положение плоскости, через которую должны действовать вертикальные нагрузки, чтобы вызвать простой изгиб, с осью x в качестве нейтральной оси.

Рис. 1: Секция швеллера

Можно предположить, что вертикальная сила сдвига F в секции воспринимается только стенкой. Во фланцах будут горизонтальные напряжения сдвига, которые обозначаются как q .

Рассмотрим элемент ‘ abcd ‘, вырезанный из нижней полки двумя соседними поперечными сечениями (дельта z) друг от друга и вертикальной плоскостью, параллельной стенке, на расстоянии ‘ u ‘ (которое является переменным ) от свободного конца нижнего фланца.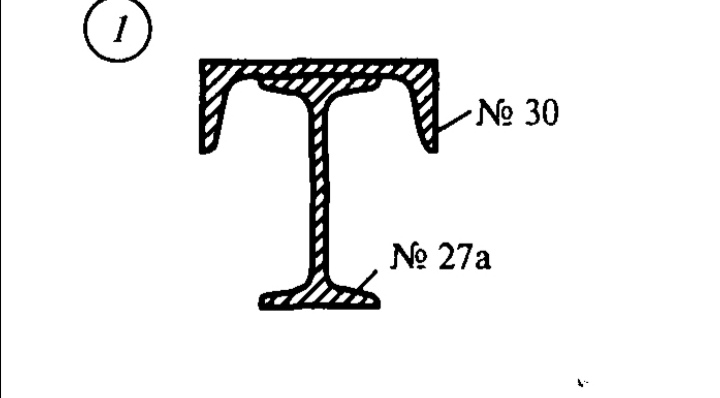

Разница в растягивающих усилиях T и T+Delta z должна быть равна поперечной силе на стороне « ad » элемента. Предполагая равномерное распределение касательного напряжения (поскольку толщина мала) по толщине, имеем:

Интегрирование выполняется по части «ab» фланца. Напряжение на единицу длины центральной линии сечения:

Отсюда видно, что q пропорционально u . Максимальное значение q :

На стыке полки и стенки распределение касательного напряжения усложняется, поэтому можно считать, что уравнение 4 справедливо при u = 0 и u = b.

Предположим, что вертикальная поперечная сила F действует через точку ‘ o ’, центр сдвига на расстоянии с от О на осевой линии стенки. Скручивания этой секции можно избежать, если:

указывает положение центра сдвига.

Примечание: Центр сдвига для площадей поперечного сечения, имеющих одну ось симметрии, всегда располагается на оси симметрии.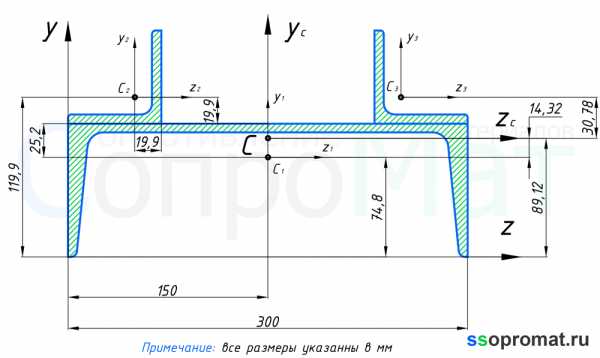 В случае двутавровой балки, симметричной как относительно оси x, так и оси y, центр сдвига совпадает с центром тяжести сечения. Точное расположение центра сдвига для несимметричных сечений сложно и может быть определено осмотром.

Пример:

Найдите центр сдвига несимметричного поперечного сечения двутавровой балки, как показано на рисунке ниже:

Здесь,

Принятие момента относительно точки D:

Подробнее: Что такое Стена сдвига? – ее типы и расположение в зданиях

Irons Creative в понижении центра тяжести

Автор   Джордж Уайт

31 января 2004 г., 12:00

ОРЛАНДО — Леса для фарватера, айроны, широкий ассортимент клиньев и, конечно же, клюшек, которые вам нужны, вы их получили, во всех мыслимых формах и размерах на выставке товаров PGA. .
 
Одним из самых уникальных является клин для песка FunJoy, созданный компанией Golf Korea Co. , Ltd. FunJoy имеет форму гребня, причем зубья гребня обращены к передней части клинка. Выстрел из бункера, как говорит Гольф Корея, похож на расчесывание волос.
 
Но, за исключением FunJoy, большинство клубных линеек выглядят довольно традиционно. Ниже приведены образцы некоторых изделий, представленных на выставке PGA Merchandise Show:
 
TOUR EDGE ‘ Это новое предложение компании – утюги JMAX. Это новый подход к относительно недавней идее объединения 3-х и 4-х айронов, «традиционно более трудных для ударов для игроков с более высоким гандикапом», в айрон-вуд. Танковый клин с 5 проходами – это традиционный железный вид. Айроны имеют полостную спинку с большими головками клюшек. А Bazooka JMAX Iron-Woods имеет деревянный корпус на протяжении всего набора, от 1 до клина.
 
MACGREGOR ‘ V-Foil M455 представляет собой крупногабаритную конструкцию, производитель переместил центр тяжести айронов ниже и глубже, чем когда-либо прежде. Это дает M455 очень большую зону поражения. Клюшки MacGregor разработаны Бобби Грейсом. Клюшка M14K, по словам МакГрегора, имеет самый высокий момент инерции, что важно для сохранения устойчивости поверхности клюшки при ударах вне центра.
 
CALLAWAY ‘ В утюгах Hawk Eye VHT используется самая передовая титановая технология Callaway. Дополнительным усовершенствованием является порт для утяжеления из вольфрама, установленный в нижней части клюшки. Это приводит к низкому центру тяжести, что облегчает движение мяча в воздухе с большим вращением, обеспечивающим остановку мяча.
 
NIKE ‘ Nike может похвастаться своими утюгами Slingshot, которые журнал Golf Digest включил в свой Hot List как ведущие или занимающие высокие места в шести из семи категорий. Утюги Slingshot были названы айронами года для гольфа. Slingshot имеет металлический стержень (Air CG) на задней части, который смещает центр тяжести ниже, чем у традиционных клюшек, у которых центр тяжести находится внутри клюшки. Эта функция запускает мяч выше и облегчает попадание в квадратную форму.
 
SRIXON ‘ Традиция кованого клинка. «Наука о цифровом воздействии», — говорится в рекламе утюгов I-302. Центр тяжести перемещается за счет расширения в задней части айрона на Tour Back Cavities. У айрона также есть увеличенная зона наилучшего восприятия, которая обеспечивает дистанционный контроль при всех промахах.
 
TOMMY ARMOR ‘ Одной из приветствуемых идей являются клюшки для игроков с высоким гандикапом, в отличие от клюшек, разработанных для игроков с гандикапом 2. С этой целью Tommy Armor выпустила серию SilverBack. Фактор играбельности Мальби — это показатель того, насколько легко бить по клюшке. SilverBack 845w и SilverBacku находятся на вершине шкалы, наряду с Callaway X-16.
 
Ссылки по теме:

Полное освещение выставки товаров PGA

Больше подобных статей

Equipment Insider

BY Golf Channel Digital —  27 января 2022 г.