Электро и теплопроводность: электро- и теплопроводность | это… Что такое электро
alexxlab | 26.01.1988 | 0 | Разное
Электро- и теплопроводность металлов и сплавов
1.1. Электро- и теплопроводность металлов и сплавов
Электропроводность металлов
Классическая электронная теория металлов представляет твердый проводник в виде системы, состоящей из узлов кристаллической ионной решетки, внутри которой находится электронный газ из коллективизированных свободных валентных электронов. К электронному газу применялись представления и законы обычных газов. Это привело к выводу законов Ома и Джоуля – Ленца, позволило описать и объяснить ранее обнаруженные экспериментальным путем основные законы электропроводности и потерь электрической энергии в металлах.
Однако исчерпывающее объяснение явлений электропроводности оказалось возможным на основе квантовой механики. В соответствии с квантово–механическими представлениями причиной наличия электрического сопротивления твердых тел является не столкновение свободных электронов с атомами решетки (как в классической теории Друде), а рассеяние их на дефектах решетки, вызывающих нарушение периодичности потенциала. Идеально правильная, бездефектная неподвижная решетка не способна рассеивать свободные носители заряда и поэтому должна обладать нулевым сопротивлением.
Идеально правильная, бездефектная неподвижная решетка не способна рассеивать свободные носители заряда и поэтому должна обладать нулевым сопротивлением.
Подвижность и длина свободного пробега электронов в твердом теле зависят от структуры материала. Чистые металлы с наиболее правильной кристаллической решеткой характеризуются наименьшими значениями удельного сопротивления r. Примеси, искажая решетку, приводят к увеличению r. С позиций квантовой механики рассеяние электронных волн происходит на дефектах кристаллической решетки, которые соизмеримы с расстоянием порядка четверти длины волны электрона; нарушения меньших размеров не вызывают заметного рассеяния волн де Бройля. В металлическом проводнике, где длина волны электрона порядка 5 Å, микродефекты создают значительное рассеяние, уменьшающее подвижность электронов и длину свободного пробега, и, следовательно, приводят к росту r.
Так как в металлах концентрация электронного газа n практически не зависит от температуры (Т), то зависимость удельного сопротивления r (и обратной величины удельной электропроводности s) от температуры полностью определяется температурной зависимостью подвижности (m) и пропорциональной ей длины свободного пробега электронов (l).
Вследствие усиления колебаний узлов кристаллической решетки с ростом температуры появляется все больше и больше препятствий на пути направленного движения свободных электронов под действием электрического поля, т.е. уменьшается среднестатистическая длина свободного пробега l, уменьшается подвижность электронов и, как следствие, уменьшается удельная проводимость металлов и возрастает удельное сопротивление (рис. 3.14).
Рис. 3.14. Зависимость удельного сопротивления металлов и сплавов от температуры: 1 – железо; 2 – электротехническая сталь с содержанием 4 % Si; 3 – сплав Fe-Ni-Cr
Удельное сопротивление сплавовКак указывалось, примеси и нарушения правильной структуры металлов ведут к увеличению их удельного сопротивления.
Значительное возрастание r наблюдается при сплавлении двух металлов в том случае, если они образуют твердый раствор, т.е. создают при отвердевании совместную кристаллизацию, и атомы одного металла входят в кристаллическую решетку другого.
Зависимость удельного сопротивления сплава двух металлов, образующих твердый раствор, от процентного содержания каждого из них представлена на рис. 3.15 (кривая а). Кривая имеет максимум, соответствующий некоторому соотношению содержания компонентов в сплаве; при уменьшении содержания каждого из них r падает, приближаясь к соответствующим значениям r чистых металлов. Обычно наблюдается определенная закономерность и в изменении ТКr (ТК – температурный коэффициент): относительно высокими значениями ТКr обладают чистые металлы, а у сплавов ТКr меньше и даже может приобретать небольшие по абсолютной величине отрицательные значения (рис. 3.15, кривая б). Это объясняется тем, что у сплавов изменение r вызывается не только изменением подвижности носителей заряда, но в некоторых случаях и возрастанием концентрации носителей при повышении температуры.
Рис. 3.15. Зависимость r (а) и ТКr (б) сплавов системы Cu-Ni от состава (в процентах по массе)
Теплопроводность
Тепло через металл передается в основном теми же свободными электронами, которые определяют и электропроводность металлов; количество их в единице объема металла весьма велико.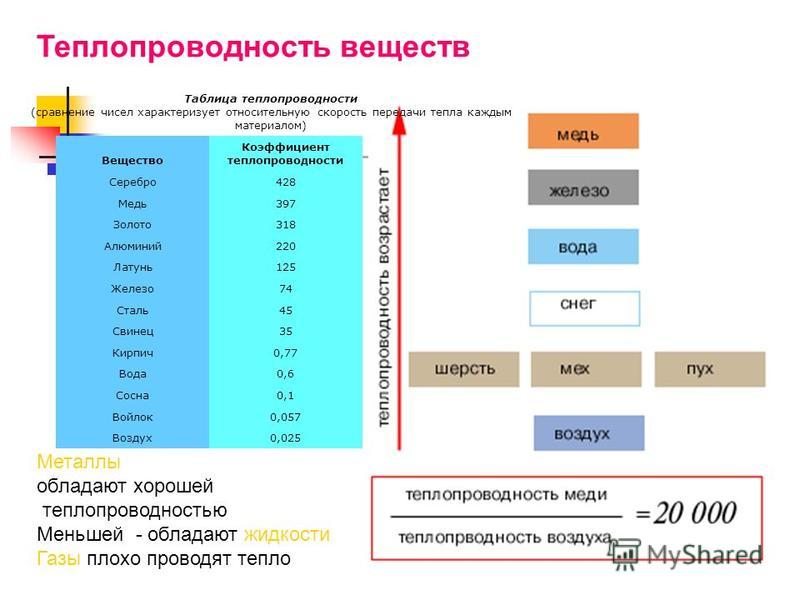 Поэтому, как правило, коэффициент теплопроводности h металлов много больше, чем у диэлектриков. Очевидно, что при прочих равных условиях чем больше удельная электрическая проводимость s металла, тем больше его коэффициент теплопроводности h. При повышении температуры, когда подвижность электронов в металле и соответственно его удельная проводимость s уменьшаются, отношение коэффициента теплопроводности металла к его удельной электрической проводимости h/s должно возрастать. Математически это выражается законом Видемана – Франца – Лорентца:
Поэтому, как правило, коэффициент теплопроводности h металлов много больше, чем у диэлектриков. Очевидно, что при прочих равных условиях чем больше удельная электрическая проводимость s металла, тем больше его коэффициент теплопроводности h. При повышении температуры, когда подвижность электронов в металле и соответственно его удельная проводимость s уменьшаются, отношение коэффициента теплопроводности металла к его удельной электрической проводимости h/s должно возрастать. Математически это выражается законом Видемана – Франца – Лорентца:
h/s = L0T, (3.1)
В лекции “13. Обзор печати” также много полезной информации.
где Т – абсолютная температура, К; L0 – число Лорентца, равное
. (3.2)
Подстановка в (3.2) значений постоянной Больцмана k = 1,38×10-23 Дж/К и заряда электрона e = -1,6×10-19 Кл дает L0 = 2,45×10-8 В2/К2.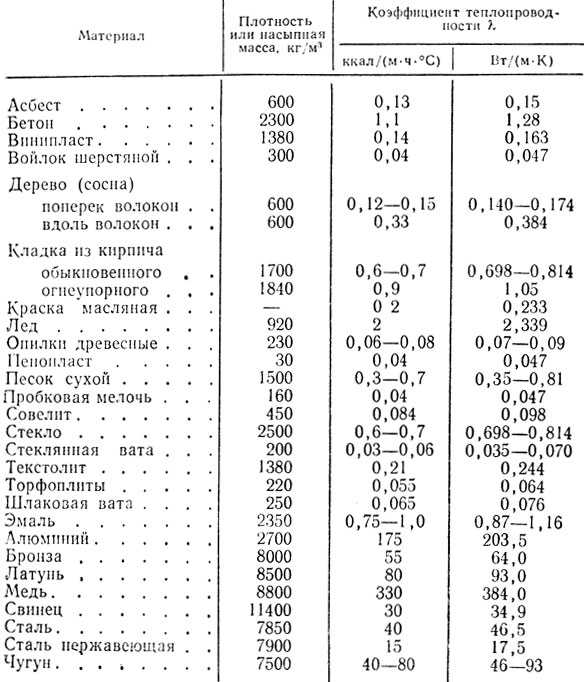
Закон Видемана – Франца – Лорентца для большинства металлов хорошо подтверждается при температурах, близких к нормальной или несколько повышенных.
Проверим справедливость этого закона для меди при нормальной температуре. Подставляя в формулу (3.1) параметры меди: s = 57×106 См/м и h= 390 Вт/(м×К), получаем (при Т = 293 К) L0 = 2,54×10-8 В2/К2, что весьма близко к теоретическому значению. При нормальной температуре для алюминия L0 = 2,1×10-8, для свинца и олова – 2,5×10-8, для железа – 2,9×10-8 В2/К2.
Однако в области низких температур коэффициент при Т в уравнении (3.1) уже не остается неизменным: так, для меди при охлаждении он проходит через минимум, а при приближении к абсолютному нулю вновь близок к теоретическому значению L0.
22 Электро- и теплопроводность металлов и сплавов » СтудИзба
Теплопроводность стали, меди, алюминия, никеля и их сплавов
Обычное железо и цветные металлы имеют разное строение молекул и атомов. Это позволяет им отличаться друг от друга не только механическими, но и свойствами теплопроводности, что, в свою очередь, влияет на применение тех или иных металлов в различных отраслях хозяйства.
Это позволяет им отличаться друг от друга не только механическими, но и свойствами теплопроводности, что, в свою очередь, влияет на применение тех или иных металлов в различных отраслях хозяйства.
Сталь имеет коэффициент теплопроводности, при температуре окружающей среды 0 град. (С), равный 63, а при увеличении градуса до 600, он снижается до 21 Вт/м*град. Алюминий, в таких же условиях, наоборот – увеличит значение от 202 до 422 Вт/м*град. Сплавы из алюминия, будут также повышать теплопроводность, по мере увеличения температуры. Только величина коэффициента будет на порядок ниже, в зависимости от количества примесей, и колебаться в пределах от 100 до 180 единиц.
Медь, при изменении температуры в тех же пределах, будет уменьшать теплопроводность от 393 до 354 Вт/м*град. При этом, медь содержащие сплавы латуни будут иметь такие же свойства, как и алюминиевые, а значение теплопроводности будет изменяться от 100 до 200 единиц, в зависимости от количества цинка и других примесей в составе сплава латуни.
Коэффициент теплопроводности чистого никеля считается низким, он будет менять свое значение от 67 до 57 Вт/м*град. Сплавы с содержанием никеля, будут также иметь коэффициент с пониженным значением, который, благодаря содержанию железа и цинка, колеблется от 20 до 50 Вт/м*град. А наличие хрома, позволит понизить теплопроводность в металлах до 12 единиц, с небольшим увеличением этой величины, при нагреве.
Статическая электропроводность и теплопроводность металлов по Друде
Обычно закон Ома для проводников записывают в виде U = IR
, где
R
— сопротивление проводника, зависящее от материала и формы проводника (в большинстве случаев и от температуры). Зависимость от формы проводника можно устранить, вводя новую величину, зависящую только от материала проводника (например, от вида металла), а именно,
удельное сопротивление
ρ, имеющее в системе СИ размерность в ом-метрах (Ом∙м).
E =ρ∙j
Это закон Ома в дифференциальном виде. В изотропном проводнике вектор плотности тока j параллелен вектору напряженности электрического поля Еи потоку заряженных частиц. В случае движения электронов электрический ток, как известно, направлен против их движения.
В изотропном проводнике вектор плотности тока j параллелен вектору напряженности электрического поля Еи потоку заряженных частиц. В случае движения электронов электрический ток, как известно, направлен против их движения.
При изучении физических процессов дифференциальный закон Ома обычно записывают в виде j= E/ ρ = σ∙E, где σ – удельная проводимость материала.
Единица, обратная ому, называется сименсом (См). Соответственно, единицей σ является сименс на метр (См/м).
В отсутствие электрического поля электроны (валентные) движутся хаотично с разными скоростями и равновероятно по направлениям. Поэтому вектор их средней тепловой скорости равен нулю. Но при наличии электрического поля появляется дополнительная составляющая скорости вдоль (но против) электрического поля. Теперь средняя скорость vср
электронов вдоль поля (иногда называемая дрейфовой) уже не равна нулю, и можно написать плотность тока в виде
j = — nevср
Эту скорость vср
можно рассчитать следующим образом. Будем предполагать, что за единицу времени электрон испытывает столкновение с ионом с вероятностью, равной 1/τ. Имеется в виду, что для электрона вероятность испытать столкновение в течение бесконечно малого промежутка времени
Будем предполагать, что за единицу времени электрон испытывает столкновение с ионом с вероятностью, равной 1/τ. Имеется в виду, что для электрона вероятность испытать столкновение в течение бесконечно малого промежутка времени
dt
равна просто
dt/τ.
Время τ называют временем релаксации или временем свободного пробега. Оно играет фундаментальную роль в теории проводимости металлов. Из этого предположения следует, что электрон, выбранный наугад в настоящий момент времени, будет двигаться
в среднем
в течение времени τ до его следующего столкновения и уже двигался
в среднем
в течение времени τ с момента его предыдущего столкновения.
Рассмотрим какой-либо электрон в нулевой момент времени. Пусть t –
время, прошедшее после его последнего столкновения. Скорость этого электрона в нулевой момент времени будет равна его скорости
vонепосредственно после столкновения плюс дополнительная скорость –eEt/m
, которую электрон приобрел после столкновения. Так как мы предполагаем, что после столкновения скорость электрона может иметь любое направление, вклад от
Так как мы предполагаем, что после столкновения скорость электрона может иметь любое направление, вклад от
voв среднюю скорость электронов равен нулю, и поэтому она равна среднему значению величины — eEt/m.
Однако среднее значение
t
равно времени релаксации τ. Поэтому имеем
vср= —eE τ/m ,
j =
Е
= σ∙E , σ =
Таким образом, мы получили линейную зависимость j от E и нашли для проводимости σ выражение, в которое входит только известные величины и время релаксации τ. Это время релаксации можно теперь определить из экспериментальных значений σ и оно оказывается при комнатных температурах порядка τ ~ 10-14 – 10-15 с.
Заметим, что в теории Друде распределение электронов по скоростям соответствует газокинетической теории в виде т. н. максвелловского распределения, т.е.
н. максвелловского распределения, т.е.
Оценки здесь средней тепловой скорости электронов дают значения порядка vTe ~
105 м/с. Эта скорость определяет среднюю длину свободного пробега электрона λ =
vTe∙
τ ~ 10-10 – 10-9 м, что сравнимо с межатомными расстояниями в металле и тем самым, казалось бы, подтверждает разумность всех предпосылок теории Друде.
Другим впечатляющим успехом модели Друде в то время, когда она была предложена, явилось объяснение эмпирического закона Видемана и Франца (1853 г.), связывающего тепловые и электрические свойства металлов. Напомним, что в соответствии с известным уравнением Фурье, плотность потока тепла jqпропорциональна градиенту температуры T,
что выражается, например, в одномерном случае в виде
jq = —
χ
∙dT/dx
где χ – коэффициент теплопроводности. Закон Видемана-Франца утверждает, что отношение коэффициентов теплопроводности и электропроводности χ/σ
для большинства металлов прямо пропорционален температуре, причем коэффициент пропорциональности
c
достаточной точностью одинаков для всех металлов, т. е.
е.
χ /σ = cT
Для объяснения этой закономерности в рамках модели Друде предполагается, что основная часть теплового потока в металле переносится электронами проводимости. Это предположение основано на том эмпирическом наблюдении, что металлы гораздо лучше проводят тепло, чем диэлектрики. Соответствующие расчеты в рамках названной модели приводят к следующему значению коэффициента c
:
с
=
близкому к экспериментальным значениям этого коэффициента.
Несмотря на эти и некоторые другие успехи, у модели Друде, однако, довольно быстро были выявлены значительные изъяны. Например, в реальности, как выяснилось, тепловые скорости электронов в металлах более чем на порядок превышают рассчитанные по теории Друде. Кроме того, теория Друде не может объяснить появления при низких температурах
длины свободного пробега электронов, в 1000 и более раз превышающую значение межатомного расстояния. Но наиболее впечатляющим недостатком модели Друде является невозможность объяснения практического отсутствия влияния электронов на теплоемкость металла. А ведь в соответствии с теорией
А ведь в соответствии с теорией
свободных и независимых
электронов каждый электрон должен был бы обладать средней энергией , что в итоге обеспечивало бы добавочный вклад не менее в молярную теплоемкость любого металла. Однако такой вклад не был обнаружен ни в одном эксперименте!!
Все указанные и многие другие недостатки модели Друде связаны с отсутствием учета квантово-механических явлений, рассмотренных далее. Справедливости ради надо указать, что во время формулирования модели Друде и проведения расчетов на ее основе развернутых квантовых представлений применительно к твердому телу еще не существовало.
Что такое теплопроводность и для чего нужна
Процесс переноса энергии атомов и молекул от горячих предметов к изделиям с холодной температурой, осуществляется при хаотическом перемещении движущихся частиц. Такой обмен тепла зависит от агрегатного состояния металла, через который проходит передача. В зависимости от химического состава материала, теплопроводность будет иметь различные характеристики. Данный процесс называют теплопроводностью, он заключается в передаче атомами и молекулами кинетической энергии, определяющей нагрев металлического изделия при взаимодействии этих частиц, или передается от более теплой части – к той, которая меньше нагрета.
Данный процесс называют теплопроводностью, он заключается в передаче атомами и молекулами кинетической энергии, определяющей нагрев металлического изделия при взаимодействии этих частиц, или передается от более теплой части – к той, которая меньше нагрета.
Способность передавать или сохранять тепловую энергию, позволяет использовать свойства металлов для достижения необходимых технических целей в работе различных узлов и агрегатов оборудования, используемого в народном хозяйстве. Примером такого применения может быть паяльник, нагревающийся в средней части и передающий тепло на край рабочего стержня, которым выполняют пайку необходимых элементов. Зная свойства теплопроводности, металлы применяют во всех отраслях промышленности, используя необходимый параметр по назначению.
Понятие термического сопротивления и коэффициента теплопроводности
Если теплопроводность характеризует способность металлов передавать температуру тел от одной поверхности к иной, то термическое сопротивление показывает обратную зависимость, т. е. возможность металлов препятствовать такой передаче, иначе выражаясь, – сопротивляться. Высоким термическим сопротивлением обладает воздух. Именно он, больше всего, препятствует передаче тепла между телами.
е. возможность металлов препятствовать такой передаче, иначе выражаясь, – сопротивляться. Высоким термическим сопротивлением обладает воздух. Именно он, больше всего, препятствует передаче тепла между телами.
Количественную характеристику изменения температуры единицы площади за единицу времени на один градус (К), называют коэффициентом теплопроводности. Международной системой единиц принято измерять этот параметр в Вт/м*град. Эта характеристика очень важна при выборе металлических изделий, которые должны передавать тепло от одного тела к другому.
Таблица 1
| Металл | Коэффициент теплопроводности металлов при температура, °С | ||||
| — 100 | 0 | 100 | 300 | 700 | |
| Алюминий | 2,45 | 2,38 | 2,30 | 2,26 | 0,9 |
| Бериллий | 4,1 | 2,3 | 1,7 | 1,25 | 0,9 |
| Ванадий | — | — | 0,31 | 0,34 | — |
| Висмут | 0,11 | 0,08 | 0,07 | 0,11 | 0,15 |
| Вольфрам | 2,05 | 1,90 | 1,65 | 1,45 | 1,2 |
| Гафний | — | — | 0,22 | 0,21 | — |
| Железо | 0,94 | 0,76 | 0,69 | 0,55 | 0,34 |
| Золото | 3,3 | 3,1 | 3,1 | — | — |
| Индий | — | 0,25 | — | — | — |
| Иридий | 1,51 | 1,48 | 1,43 | — | — |
| Кадмий | 0,96 | 0,92 | 0,90 | 0,95 | 0,44 (400°) |
| Калий | — | 0,99 | — | 0,42 | 0,34 |
| Кальций | — | 0,98 | — | — | — |
| Кобальт | — | 0,69 | — | — | — |
| Литий | — | 0,71 | 0,73 | — | — |
| Магний | 1,6 | 1,5 | 1,5 | 1,45 | — |
| Медь | 4,05 | 3,85 | 3,82 | 3,76 | 3,50 |
| Молибден | 1,4 | 1,43 | — | — | 1,04 (1000°) |
| Натрий | 1,35 | 1,35 | 0,85 | 0,76 | 0,60 |
| Никель | 0,97 | 0,91 | 0,83 | 0,64 | 0,66 |
| Ниобий | 0,49 | 0,49 | 0,51 | 0,56 | — |
| Олово | 0,74 | 0,64 | 0,60 | 0,33 | — |
| Палладий | 0,69 | 0,67 | 0,74 | — | — |
| Платина | 0,68 | 0,69 | 0,72 | 0,76 | 0,84 |
| Рений | — | 0,71 | — | — | — |
| Родий | 1,54 | 1,52 | 1,47 | — | — |
| Ртуть | 0,33 | 0,09 | 0. 1 1 | 0,115 | — |
| Свинец | 0,37 | 0,35 | 0,335 | 0,315 | 0,19 |
| Серебро | 4,22 | 4,18 | 4,17 | 3,62 | — |
| Сурьма | 0,23 | 0,18 | 0,17 | 0,17 | 0,21 |
| Таллий | 0,41 | 0,43 | 0,49 | 0,25 (400 0) | |
| Тантал | 0,54 | 0,54 | — | — | — |
| Титан | — | — | 0,16 | 0,15 | — |
| Торий | — | 0,41 | 0,39 | 0,40 | 0,45 |
| Уран | — | 0,24 | 0,26 | 0,31 | 0,40 |
| Хром | — | 0,86 | 0,85 | 0,80 | 0,63 |
| Цинк | 1,14 | 1,13 | 1,09 | 1,00 | 0,56 |
| Цирконий | — | 0,21 | 0,20 | 0,19 | — |
Теплофизические свойства, теплопроводность поваренной соли
Что такое поваренная соль? Ее характеристика и запасы представляют интерес для школьников, планирующих связать свою будущую профессию с физикой и химией. Именно это вещество называют самым распространенным в природе. Каков ее состав? Соль поваренная состоит из атомов натрия и хлора. С химической точки зрения это типичная средняя соль.
Именно это вещество называют самым распространенным в природе. Каков ее состав? Соль поваренная состоит из атомов натрия и хлора. С химической точки зрения это типичная средняя соль.
Распространенность в природе
Данный минерал в своем составе может иметь некоторые примеси. Например, соединения железа придают веществу красные оттенки. В природе галит встречается в виде прочных тонкозернистых масс, в небольших количествах поваренная соль находится в виде кубических кристаллов.
Рассматривая главные свойства поваренной соли, выделим хорошую растворимость данного соединения в воде. Именно поэтому пласты соли не выходят на поверхность, добычу осуществляют шахтным методом. Галит является основным солевым компонентом морей и океанов, кроме того, высоко содержание хлорида натрия в подземных минеральных водах и соляных озерах. Где еще можно обнаружить такой состав? Соль поваренная входит в состав осадочных пород. К примеру, такие пласты найдены в большом количестве в Канаде и Америке.
Помимо непосредственного употребления в пищу, поваренная соль является сырьем для производства соляной кислоты и иных веществ.
Варианты образования
Поваренная соль, электро и теплопроводность которой имеет высокие показатели, образуется при просачивании соленой воды через песок. После испарения воды осажденная соль накапливается в песке, постепенно образуя огромные соленосные пласты.
Растворимость галита почти не зависит от температуры, поэтому наблюдается пресыщение раствора, появляются огромные соляные залежи. Ученым удалось посчитать, что при внезапном испарении воды в морях и океанах из оставшейся соли можно было бы построить стену толщиной в 1 метр, высотой 280 метров, которая смогла бы полностью опоясать по экватору нашу планету.
Виды залежей
В зависимости от того, каковы условия залегания поваренной соли, выделяют ее разновидности:
- каменная соль, находящаяся между пластами в твердом состоянии;
- самосадочная порода, которая формируется в виде пластов на дне замкнутых бассейнов;
- вулканическая соль;
- выцветы.

Способы добычи и переработки минерала
В результате подземных разработок получают каменную соль. При выпаривании подземных вод получают выварочную соль.
Среди экзотических вариантов добычи этого полезного ископаемого отметим осаждение при низких температурах соль из подземных источников в Якутии. Самым дешевым способом переработки является использование самосадочных технологических процессов.
Теплопроводность поваренной соли зависит от ее сорта, влажности, температуры окружающей среды. Данное вещество является отличным сырьем для химической промышленности. Путем электролиза ее расплава получают газообразный хлор и металлический натрий. В случае проведения электролиза раствора одним из продуктов реакции является гидроксид натрия (щелочь).
Хлорид натрия является основным компонентом не только морской воды, но и сыворотки крови. Это вещество необходимо для дыхания и полноценного усвоения пищи. Без галита, не вырабатываемого организмом человека, не происходит процесс переноса кислорода и питательных веществ, передача импульсов, функционирование мускулов, включая и сердечную мышцу. Взрослый организм содержит около 250 граммов этого вещества, расходующегося на разнообразные физиологические процессы.
Взрослый организм содержит около 250 граммов этого вещества, расходующегося на разнообразные физиологические процессы.
Именно соль многие ученые считают натуральным антидепрессантом, повышающим настроение. В случае недостатка хлорида натрия у человека развивается депрессия, психические и нервные заболевания, проблема с пищеварительной и сердечно-сосудистой системами, анорексия, мышечные судороги. Переизбыток соли грозит повышением артериального давления, проблемами с почками. Поваренная соль может стать для организма смертельным ядом!
Физические свойства
Каковы ее теплофизические свойства? Теплопроводность поваренной соли снижается при впитывании воды. Соль не обладает запахом, температура плавления составляет 801°C. По шкале Мооса твердость галита составляет 2-2,5.
Теплопроводность поваренной соли объясняет ее основные физические свойства: плотность, точку кипения. Хлорид натрия имеет различные оттенки, связанные с примесями, входящими в состав природного минерала.
Так как между катионами натрия и анионами хлора образуется ионная кристаллическая решетка, у вещества достаточно высокий показатель температуры кипения и плавления.
Теплопроводность поваренной соли объясняется наличием в молекулах ионной кристаллической решетки. Силы притяжения частиц по разным направлениям распространяются одинаково, ионы прочно связаны между собой. При нагревании хлорида натрия до его температуры плавления происходит полное разрушение структуры кристалла, из твердого состояния образуется жидкость.
Практическое значение имеет не только теплопроводность поваренной соли, но и электрическая проводимость этого вещества.
Химические свойства
Как характеризует галит химия? Физические свойства вещества соли каковы? Это твердое вещество и проводник тока и тепла. А с какими простыми и сложными веществами он может взаимодействовать?
Путем взаимодействия хлорида натрия с концентрированной серной кислотой получают хлороводород, который применяется в химической промышленности.
Качественной реакцией на хлорид-ионы является взаимодействие с солями серебра. Продуктом взаимодействия является белый осадок хлорида серебра.
Смешивание растворов поваренной соли и сульфата меди (2) приводит к образованию комплексного соединения – тетрахлоркупрата натри, имеющего зеленую окраску.
Получение
Как можно получить хлорид натрия? Поваренная соль, теплопроводность растворов которой имеет высокие показатели, в достаточном количестве распространена в природе. Именно поэтому нет смысла в разработке промышленных и лабораторных способов получения данного соединения. Например, можно получить хлорид натрия путем синтеза простых веществ: хлора и натрия.
Области применения
В современной кулинарии и пищевой отрасли применяют хлорид натрия, который имеет чистоту не менее 97 процентов. Данное вещество выступает в качестве вкусовой добавки, а также в виде вещества, необходимого для консервирования продуктов питания. У него товарное название – поваренная соль. В зависимости от того, каково ее происхождение, выделяют морскую, каменную, фторированную, йодированную соль. В поваренной соли в незначительном количестве присутствуют соединения кальция, калия, магния, придающие ей жесткость и гигроскопичность.
В зависимости от того, каково ее происхождение, выделяют морскую, каменную, фторированную, йодированную соль. В поваренной соли в незначительном количестве присутствуют соединения кальция, калия, магния, придающие ей жесткость и гигроскопичность.
В зависимости от процентного содержания хлорида натрия, выделяют несколько сортов:
- «экстра» при содержании в количестве более 99,5%;
- первый сорт – 97,5%;
- высший – 98,2%;
- второй – 97%.
У хлорида натрия есть незначительные антисептические свойства, поэтому 10-15 процентным раствором соли можно избежать размножения разнообразных гнилостных болезней. Это свойство объясняет применение хлорида натрия в качестве консерванта.
0,9%-ный раствор хлорида натрия используют в медицине в виде дезинтоксикационного средства, которое корректирует при обезвоживании работу систем человеческого организма.
10%-ный раствор данного вещества применяют в качестве осмотического диуретика, незаменимого в случае отека головного мозга, а также при кровотечениях. Именно этим раствором обрабатывают гнойные раны, а в офтальмологии его используют как противоотечный препарат.
Именно этим раствором обрабатывают гнойные раны, а в офтальмологии его используют как противоотечный препарат.
В зимнее время смесь хлорида натрия, глины, песка (техническую соль) применяют как антифриз. Этим составом посыпают тротуары, чтобы бороться с гололедом. Безусловно, данная смесь негативно отражается на состоянии обуви, автомобильного транспорта.
Для умягчения воды применяют натрий-катионитовые фильтры. Для их регенерации применяют 6-10%-ный раствор поваренной соли.
В заключение
Поваренную соль стали использовать для консервирования рыбных и мясных продуктов примерно тысячу лет назад. Солонина запасалась, в основном, для корабельной кухни. В Голландии вели засол селедки, в Англии занимались производством бекона. В X-XII веках славяне стали применять соль для защиты продуктов от гнилостных микроорганизмов.
Помимо пищевой отрасли, хлорид натрия применяют в черной, а также цветной металлургии, при обработке металлов, в машиностроении, при выделке мехов, для производства охлаждающих растворов.
Большая часть добываемой поваренной соли поступает в химическую промышленность, где она идет на производство каустической соды (гидроксида натрия) и хлора. Среди отраслей использования этого минерала и изготовление удобрений, а также реагентов для окрашивания тканей и производства мыла.
Никто точно не может сказать, когда впервые человек стал добавлять соль в свою повседневную еду. В настоящее время трудно представить себе те далекие времена, когда поваренная соль была неизвестна человечеству.
По мере развития цивилизации изменялись и совершенствовались способы добычи хлорида натрия, изучались физические и химические свойства данного соединения. Надеемся, что статья оказалась интересной и полезной для вас!
Создан материал, который проводит электричество, но не нагревается
Новости
3 декабря 2019
—
hi-news.ru
Хорошо известно, что различного рода металлы, способные проводить электричество, в то же время довольно сильно нагреваются.
 Это обусловлено целым рядом химических и физических свойств материалов, но электро- и теплопроводность почти всегда «идут рука об руку». Однако, как мы знаем, в нашем мире нет ничего ничего не возможного. Например, как передает редакция издания Sciencealert, группа исследователей из лаборатории Университета Беркли (США) смогла создать металл, который отлично проводит электричество, но при это не нагревается.
Это обусловлено целым рядом химических и физических свойств материалов, но электро- и теплопроводность почти всегда «идут рука об руку». Однако, как мы знаем, в нашем мире нет ничего ничего не возможного. Например, как передает редакция издания Sciencealert, группа исследователей из лаборатории Университета Беркли (США) смогла создать металл, который отлично проводит электричество, но при это не нагревается.Как сообщают ученые, новый металл (а точнее соединение металла), что проводит электричество, не проводя тепла бросает вызов нашему нынешнему пониманию того, как работают проводники. Так как само его наличие противоречит тому, что называется законом Видемана-Франца. Данный физический закон утверждает, что хорошие проводники электричества также будут пропорционально хорошими проводниками тепла. Этим объясняется, например, то, что приборы, использующие для своей работы электричество, со временем нагреваются. Но команда ученых из США показала, что данное явление не наблюдается в оксиде ванадия, который обладает странной способностью «переключаться» с материала, являющегося изолятором, на проводящий металл при температуре 67 градусов Цельсия.
Это было совершенно неожиданное открытие, — сказал ведущий исследователь Джункуао Ву из отдела материаловедения Лаборатории Беркли. Это открытие имеет фундаментальное значение для понимания основного принципа работы новых проводников. Новое неожиданное свойство не только изменяет то, что мы знаем о проводниках, но и может быть невероятно полезным. Например, металл однажды может быть использован для преобразования отработанного тепла от двигателей и приборов обратно в электричество.
Так что никаких физических законов оксид ванадия не нарушает. Стоит заметить, что исследователи уже знали о нескольких других материалах, которые проводят электричество лучше, чем тепло, но они проявляют эти свойства только при температурах ниже нуля, что делает их крайне непрактичными для применения в реальной жизни. Оксид ванадия, с другой стороны, обычно является только проводником электричества при плюсовых температурах выше комнатной температуры, что означает, что он имеет быть намного более практичным.
Удивительно, но они обнаружили, что теплопроводность, которую можно было бы приписать электронам в материале, была в 10 раз меньше той величины, которая предсказывалась законом Видемана-Франца. Причина этого, по-видимому, заключается в способе перемещения электронов через материал.
Электроны двигаются синхронно друг с другом. Как жидкость, а не как отдельные частицы, что наблюдается в обычных металлах. Для электронов теплопроводность — это случайное движение. Обычные металлы переносят тепло эффективно, потому что существует много различных возможных микроскопических конфигураций поведения электронов и они могут хаотично перемещаться. А вот скоординированное движение электронов в диоксиде ванадия наносит ущерб теплопередаче, поскольку существует меньше «возможностей для движения». При этом электропроводность в данном случае не страдает.
Интересно, что когда исследователи смешали оксид ванадия с другими металлами, они смогли «настроить» количество электричества и тепла, которое он может проводить, что может быть невероятно полезно для будущих применений. Например, когда эксперты добавили металл под названием вольфрам к оксиду ванадия, они сделали его лучшим теплопроводником. Хотите узнать больше новостей из мира высоких технологий? Подписывайтесь на нас в Яндекс.Дзен.
Настраивая таким образом теплопроводность, материал может эффективно применяться для автоматического рассеивания тепла в жаркое лето, потому что он будет иметь высокую теплопроводность, но предотвращать его потерю в холодную зиму из-за низкой теплопроводности при более низких температурах.
ПоделитьсяОтправить
Твитнуть
Отправить
Научный портал “Атомная энергия 2.0“ – это открытое к сотрудничеству прогрессивное цифровое СМИ с элементами управления ядерными знаниями, семантического анализа и ценностного лидерства, ставящее своей целью решение ключевых социально-ориентированных задач фундаментальной системообразующей атомной отрасли:
– образования и общения широкой общественности и специалистов об инновационном развитии экологически устойчивых, эффективных и полезных ядерных и радиационных наук и технологий в России и мире,
– формирования популярного сообщества ученых, инноваторов, деловых, государственных, общественных и экологических лидеров, открыто поддерживающих их дальнейшее развитие и изучение,
– формирования популярного сообщества компаний и организаций, открыто обменивающихся передовым опытом, знаниями, культурой, возможностями, инновациями и инициативами,
– и поддержки и привлечения талантливой и амбициозной молодежи к реализации длительных и успешных профессиональных карьер в атомной и смежных индустриях.
Мы предлагаем Вашей организации стать одним из партнеров нашего просветительского проекта и получить уникальный пакет профессиональных коммуникационных и рекламных услуг.
Почему нужна атомная энергетика?
Анизотропия тепловых и электрофизических свойств углеродных нанотрубок и полимерных композитов с их включением – диссертация
Анизотропия тепловых и электрофизических свойств углеродных нанотрубок и полимерных композитов с их включениемдиссертация
- Научный руководитель: Чеченин Николай Гаврилович
- Автор: Воробьева Екатерина Андреевна
- Дата защиты: 21 октября 2020 года в 15:00
- Шифр диссертационного совета:
МГУ.
 01.05(закрыт)
01.05(закрыт) - Организация: МГУ имени М.В. Ломоносова
- Область знаний: Физика и математика
- Специальность: 01.04.15 – Физика и технология наноструктур, атомная и молекулярная физика
- Тип диссертации: Кандидатская
- Организация, в которой выполнялась работа: МГУ имени М.В. Ломоносова
- Оппоненты: Борисов Анатолий Михайлович, Образцова Елена Дмитриевна, Булярский Сергей Викторович
- Приоритетное направление России: Индустрия наносистем
- Критическая технология России: Технологии получения и обработки функциональных наноматериалов
- Аннотация:
Экстремально высокие функциональные характеристики углеродных нанотрубок (УНТ) определяют их широкое использование в качестве наполнителей нанокомпозитных покрытий и материалов.
 Материалы на основе полимерных матриц применяются в промышленности из-за их малого веса, низкой стоимости, простоты обработки, функциональных возможностей и химической стабильности. Однако низкие тепло- и электропроводность ограничивают их применение. В диссертации анализируется природа этих ограничений и способы их преодоления.
Объектом исследования являются многостенные УНТ, а также композиты на полимерной основе с их включением.
Предметом исследования являются условия роста и структура УНТ на различных подложках, электро- и теплопроводность массивов УНТ и композитов с их включением, анизотропия свойств проводимости.
Цель работы – исследование влияния параметров синтеза на структуру синтезируемых УНТ, модификация свойств материала путем введения УНТ в полимерную матрицу, сопоставление результатов моделирования теплопроводности материалов с включением УНТ с экспериментальными данными, выявление основных параметров, влияющих на свойства композитов.
Материалы на основе полимерных матриц применяются в промышленности из-за их малого веса, низкой стоимости, простоты обработки, функциональных возможностей и химической стабильности. Однако низкие тепло- и электропроводность ограничивают их применение. В диссертации анализируется природа этих ограничений и способы их преодоления.
Объектом исследования являются многостенные УНТ, а также композиты на полимерной основе с их включением.
Предметом исследования являются условия роста и структура УНТ на различных подложках, электро- и теплопроводность массивов УНТ и композитов с их включением, анизотропия свойств проводимости.
Цель работы – исследование влияния параметров синтеза на структуру синтезируемых УНТ, модификация свойств материала путем введения УНТ в полимерную матрицу, сопоставление результатов моделирования теплопроводности материалов с включением УНТ с экспериментальными данными, выявление основных параметров, влияющих на свойства композитов. - Добавил в систему: Власова Наталия Андреевна
- Результаты диссертации получены в рамках проектов:
- Ядерно-физические методы и физические свойства наноструктур
Прикрепленные файлы
| № | Имя | Описание | Имя файла | Размер | Добавлен |
|---|---|---|---|---|---|
1. | Отзыв официального оппонента | Otzyiv_Bulyarskogo_Vorobeva_Istina.pdf | 2,5 МБ | 6 октября 2020 | |
| 2. | Заключение диссертационного совета по диссертации | Zaklyuchenie_DS_Vorobeva.pdf | 120,2 КБ | 27 октября 2020 | |
| 3. | Сведения об официальных оппонентах, включая публикации | Svedeniya_ob_ofitsialnyih_opponentah_Vorobeva_Istina. | 475,8 КБ | 6 октября 2020 | |
| 4. | Отзыв официального оппонента | Otzyiv_Obraztsova_Vorobeva_Istina.pdf | 6,5 МБ | 12 октября 2020 | |
| 5. | Отзыв официального оппонента | Otzyiv_Borisova_Vorobeva_Istina.pdf | 1,6 МБ | 11 октября 2020 | |
6. | Решение дисс.совета о приеме/отказе к защите | Protokol_No1.pdf | 657,1 КБ | 10 сентября 2020 | |
| 7. | Полный текст диссертации | Dissertatsiya_Vorobeva.pdf | 5,9 МБ | 10 сентября 2020 | |
| 8. | Отзыв научного руководителя/консультанта | Otzyiv_nauchnogo_rukovoditelya_Vorobeva. pdf pdf | 1,9 МБ | 10 сентября 2020 | |
| 9. | Сведения о научном руководителе | Svedeniya_o_nauchnom_rukovoditele_Vorobeva.pdf | 631,0 КБ | 10 сентября 2020 | |
| 10. | Автореферат | Avtoreferat_Vorobeva.pdf | 787,2 КБ | 10 сентября 2020 |
Mеталлическая связь определяет электрические и тепловые свойства металлов, обусловливая высокие электро- и теплопроводности.

Характер металлической связи сказывается и на механических свойствах металлов.
Металлы – наиболее пластичные кристаллы, т. к. в них возможно свободное перемещение дислокаций.
Металлическая связь объясняет свойства металлов, в частности, их прочность.
Под действием деформирующей силы решетка металла может изменять свою форму, не давая трещин, в отличие от ионных кристаллов.
Высокая теплопроводность металлов объясняется тем, что если нагреть кусок металла с одной стороны, то кинетическая энергия электронов увеличится.
Это увеличение энергии распространится в “ электронном море” по всему образцу с большой скоростью.
Электропроводность металлов обусловлена валентными электронами атомов.
Эти электроны обладают подвижностью в твердом теле,
которая связана с перекрыванием атомных волновых функций и
электроны могут свободно перемещаться в идеальной решетке металлического кристалла, не испытывая столкновений с ионами в узлах.
В электрическом поле они ускоряются, переходя на более высокие энергетические уровни и поглощая при этом лишь небольшое количество энергии.
Возрастание их скорости в электрическом поле приводит к результирующему переносу заряда и возникновению электрического тока.
Высокая проводимость металлов тесно связана со структурой валентной зоны, с тем, что незанятые уровни непосредственно примыкают к занятым.
Оптические свойства металлов отличны от свойств
диэлектриков и ионных кристаллов.
Металлы непрозрачны для электромагнитных волн от самых низких частот вплоть до середины ультрафиолетовой области спектра, для больших частот металлы становятся прозрачными.
Металлы хорошо отражают излучение.
Эти два свойства непрозрачность и высокая
отражательная способность, обусловлены характерной для металлов зонной структурой.
С точки зрения механических свойств металлы характеризуются, с одной стороны, высокой упругостью и прочностью, с другой пластичностью.
Это является следствием природы металлов, обусловленной наличием свободных электронов и приводящей к ненаправленности металлических связей, а в связи с этим к сравнительной легкости диффузии ионов,
смещению дефектов (в первую очередь дислокаций) без разрушения решетки, образованной ионами.
Мерой прочности опять же может служить теплота сублимации.
Механические свойства металлов зависят как от ряда внутренних (химический состав, микроструктура), так и внешних (температура, скорость приложения силы, вид напряженного состояния) факторов.
Следует различать механические свойства отдельных
металлических монокристаллов от свойств
технических металлов со сложной поликристаллической структурой.
Металлическим кристаллам свойственна анизотропия ряда механических свойств, степень которой неодинакова для разных металлов и зависит от типа кристаллической решетки.
Для деформации кристалла характерна зависимость от кристаллографической ориентации.
Явление квантовой редукции.
В отличие от эксперимента по определению местоположения электрона, где имеет место так называемый “непрерывный” процесс измерения, рассмотрим другой процесс, называемый “мгновенным” измерением.
Последнее подразумевает, что оно производится в бесконечно малый промежуток времени, длительностью которого можно пренебречь.
С целью максимального упрощения ситуации ограничимся случаем так называемого “дихотомического измерения”, при котором осуществляется выбор между двумя альтернативными состояниями квантовой системы, (случай большего числа альтернативных состояний отличается от рассматриваемого лишь количественно, но не качественно)
Под квантовым измерением понимается процесс взаимодействия квантовой системы с другой системой, которая играет роль прибора.
Простейшим из них является дихотомическое измерение, которое позволяет различить два альтернативных состояния системы – 1 и 2.
Примерами таких состояний могут быть, например, два уровня энергии атома, или же два возможных значения проекции спина электрона.
Состояние системы до измерения носит не абсолютный, а вероятностный характер.
То есть она не находится ни в одном из состояний 1 или 2.
Такое состояние называется “смешанным”.
Математически оно записывается так: = с1 1 + с2 2, где с1 и с2 – комплексные коэффициенты.
Процесс измерения переводит систему, находящуюся в неопределенном (смешанном) состоянии в одно из состояний 1 или 2.
Согласно так называемой “копенгагенской интерпретации” квантовой механики, выбор состояния системы (квантовая редукция) происходит именно в момент наблюдения.
Постановка вопроса, в каком из двух состояний находилась система до наблюдения, не имеет смысла.
Мы не просто “не знаем”, в каком из них она была, но сам способ существования системы до редукции носит потенциальный, вероятностный характер.
В 1935 году один из отцов основателей квантовой механики Эрвин Шрёдингер рассмотрел следующий любопытный эксперимент.
В закрытый ящик помещён кот. (Лучше бы засунуть туда нашего министра, но увы.)
В ящике имеется механизм, содержащий радиоактивное ядро и колбу с ядовитым газом.
Параметры эксперимента подобраны так, что вероятность того, что ядро распадётся за 1 час, составляет 50 %.
Если ядро распадается, оно приводит механизм в действие, он разбивает колбу с газом, и кот умирает. Кота жалко, министра нет.
Кота жалко, министра нет.
Температурная зависимость электрической и тепловой проводимости одиночной серебряной нанопроволоки
Температурная зависимость электрической и тепловой проводимости одиночной серебряной нанопроволоки
Скачать PDF
Скачать PDF
- Открытый доступ
- Опубликовано:
- Zhe Cheng 1 ,
- Longju Liu 2 ,
- Shen Xu 1 ,
- Meng Lu 2 &
- …
- Xinwei Wang 1,3
Научные отчеты том 5 , Номер статьи: 10718 (2015) Процитировать эту статью
18 тыс.
 обращений
обращений155 цитирований
3 Альтметрика
Сведения о показателях
Предметы
- Машиностроение
- Нанопроволоки
Abstract
В этой работе тепловой и электрический транспорт в отдельной серебряной нанопроволоке охарактеризован до 35 K для более глубокого понимания рассеяния электронов, индуцированного сильными структурными дефектами. Результаты показывают, что при комнатной температуре удельное электрическое сопротивление увеличивается примерно в 4 раза по сравнению с объемным серебром. Температура Дебая (151 К) серебряной нанопроволоки оказалась на 36% ниже, чем температура (235 К) объемного серебра, что подтверждает сильное смягчение фононов. При комнатной температуре теплопроводность снижается на 55% по сравнению с объемным серебром. Это уменьшение увеличивается по мере снижения температуры. Для объяснения противоположных трендов теплопроводности (κ) ~ температура ( T ) серебряной нанопроволоки и объемного серебра, единое тепловое сопротивление () используется для выяснения механизма рассеяния электронов. Для серебряной нанопроволоки наблюдается большая остаточная величина Θ, в то время как для массивного серебра она практически равна нулю. Та же тенденция ~ T предполагает, что серебряная нанопроволока и объемное серебро имеют сходный механизм рассеяния фононов и электронов для теплового переноса. Из-за переноса энергии электронов через границы зерен с помощью фононов число Лоренца серебряной нанопроволоки оказывается намного больше, чем у объемного серебра, и уменьшается с понижением температуры.
При комнатной температуре теплопроводность снижается на 55% по сравнению с объемным серебром. Это уменьшение увеличивается по мере снижения температуры. Для объяснения противоположных трендов теплопроводности (κ) ~ температура ( T ) серебряной нанопроволоки и объемного серебра, единое тепловое сопротивление () используется для выяснения механизма рассеяния электронов. Для серебряной нанопроволоки наблюдается большая остаточная величина Θ, в то время как для массивного серебра она практически равна нулю. Та же тенденция ~ T предполагает, что серебряная нанопроволока и объемное серебро имеют сходный механизм рассеяния фононов и электронов для теплового переноса. Из-за переноса энергии электронов через границы зерен с помощью фононов число Лоренца серебряной нанопроволоки оказывается намного больше, чем у объемного серебра, и уменьшается с понижением температуры.
Введение
Недавно серебряная нанопроволока привлекла значительное внимание из-за ее большого потенциала для таких приложений, как гибкие сенсорные экраны, солнечные элементы и прозрачные электроды 1,2,3,4,5 . Для разработки и оптимизации этих приложений тепловые и электрические свойства отдельных серебряных нанопроводов имеют решающее значение и фундаментальны, но о них редко сообщалось. До настоящего времени электрические свойства нанопроволок, особенно инертных металлических нанопроволок и жгутов нанопроволок, измерить нетрудно 6,7,8,9 Но для характеристики тепловых свойств было сообщено лишь о нескольких экспериментальных исследованиях из-за трудностей с подвешиванием одиночной нанопроволоки, снижением контактного сопротивления и точными тепловыми измерениями. Оу и др. исследовал тепло- и электропроводность одиночной никелевой нанопроволоки в диапазоне температур от 15 K до 300 K. Его число Лоренца больше, чем значение Зоммерфельда при температуре выше 75K, и быстро уменьшается, когда температура опускается ниже 75 K9.0018 10 . Экспериментальные результаты Völklein et al. показали тепло- и электропроводность одиночной Pt-нанопроволоки от 260 K до 360 K.
Для разработки и оптимизации этих приложений тепловые и электрические свойства отдельных серебряных нанопроводов имеют решающее значение и фундаментальны, но о них редко сообщалось. До настоящего времени электрические свойства нанопроволок, особенно инертных металлических нанопроволок и жгутов нанопроволок, измерить нетрудно 6,7,8,9 Но для характеристики тепловых свойств было сообщено лишь о нескольких экспериментальных исследованиях из-за трудностей с подвешиванием одиночной нанопроволоки, снижением контактного сопротивления и точными тепловыми измерениями. Оу и др. исследовал тепло- и электропроводность одиночной никелевой нанопроволоки в диапазоне температур от 15 K до 300 K. Его число Лоренца больше, чем значение Зоммерфельда при температуре выше 75K, и быстро уменьшается, когда температура опускается ниже 75 K9.0018 10 . Экспериментальные результаты Völklein et al. показали тепло- и электропроводность одиночной Pt-нанопроволоки от 260 K до 360 K. Число Лоренца было меньше, чем значение Зоммерфельда, хотя причины в их работе 11 неясны. Стоянович и др. измерил теплопроводность массивов алюминиевых нанопроволок вместо одной нанопроволоки при комнатной температуре. Теплопроводность этих массивов нанопроволок была измерена как 105–145 Вт/К·м, когда ширина нанопроволок варьировалась от 75 нм до 150 нм. Фононный вклад в общую теплопроводность составил около 21 Вт/К·м 12 .
Число Лоренца было меньше, чем значение Зоммерфельда, хотя причины в их работе 11 неясны. Стоянович и др. измерил теплопроводность массивов алюминиевых нанопроволок вместо одной нанопроволоки при комнатной температуре. Теплопроводность этих массивов нанопроволок была измерена как 105–145 Вт/К·м, когда ширина нанопроволок варьировалась от 75 нм до 150 нм. Фононный вклад в общую теплопроводность составил около 21 Вт/К·м 12 .
Для металлических наноструктур, когда размер системы приближается или меньше средней длины свободного пробега электронов в объеме, границы зерен и поверхность становятся важными источниками рассеяния, которые ограничивают длину свободного пробега электронов и впоследствии снижают тепло- и электропроводность. Рассеянные электроны не могут пройти через границу зерна, но они могут обмениваться энергией с локальными фононами посредством электрон-фононного рассеяния. Фононы могут легче проходить через границу зерна, чем электроны. Следовательно, часть энергии рассеянных электронов передается через границу зерна через фононы, а заряд рассеянных электронов отражается обратно. Это приводит к значительному снижению электропроводности и меньшему снижению теплопроводности. Полученные числа Лоренца металлических наноструктур больше, чем значение Зоммерфельда. Большие числа Лоренца наблюдаются в большинстве экспериментальных исследований 10,13,14,15,16,17,18 . Но объемные числа Лоренца также наблюдаются экспериментально для металлических нанопленок, нанесенных на биоматериалы, такие как волокна молочая и шелк тутового шелкопряда. Это объясняется туннелированием и прыжком электронов через насыщенные молекулы и/или сопряженные молекулы в этих биоматериальных субстратах 19,20,21 . Работа Bid et al. 8 были сосредоточены на электрических свойствах массивов серебряных нанопроволок вместо одной нанопроволоки. Они измерили электрическое сопротивление массива нанопроволок, не зная площади поперечного сечения.
Следовательно, часть энергии рассеянных электронов передается через границу зерна через фононы, а заряд рассеянных электронов отражается обратно. Это приводит к значительному снижению электропроводности и меньшему снижению теплопроводности. Полученные числа Лоренца металлических наноструктур больше, чем значение Зоммерфельда. Большие числа Лоренца наблюдаются в большинстве экспериментальных исследований 10,13,14,15,16,17,18 . Но объемные числа Лоренца также наблюдаются экспериментально для металлических нанопленок, нанесенных на биоматериалы, такие как волокна молочая и шелк тутового шелкопряда. Это объясняется туннелированием и прыжком электронов через насыщенные молекулы и/или сопряженные молекулы в этих биоматериальных субстратах 19,20,21 . Работа Bid et al. 8 были сосредоточены на электрических свойствах массивов серебряных нанопроволок вместо одной нанопроволоки. Они измерили электрическое сопротивление массива нанопроволок, не зная площади поперечного сечения. Удельное электрическое сопротивление получено в предположении, что нанопроволока имеет такой же наклон электрического сопротивления в зависимости от температуры, что и объемное серебро (такая же электрон-фононная связь). Работа Койды и др. 22 , опубликованный совсем недавно, посвящен термоэлектрическим свойствам монокристаллических серебряных нанопроводов. В этой статье наша работа посвящена механизму рассеяния электронов в отдельных поликристаллических нанопроволоках Ag и его влиянию на тепловые и электрические свойства. Основным структурным рассеянием в их работе является поверхностное рассеяние, а в нашей — зернограничное рассеяние. В нашей работе введено единое тепловое сопротивление, чтобы объяснить различные тенденции температурно-зависимой теплопроводности нанопроволоки и объемного серебра. Теплопроводность в нашей работе близка к таковой в работе Койды и др. 22 Но наше удельное электрическое сопротивление намного больше, чем в работе Койды и др.
Удельное электрическое сопротивление получено в предположении, что нанопроволока имеет такой же наклон электрического сопротивления в зависимости от температуры, что и объемное серебро (такая же электрон-фононная связь). Работа Койды и др. 22 , опубликованный совсем недавно, посвящен термоэлектрическим свойствам монокристаллических серебряных нанопроводов. В этой статье наша работа посвящена механизму рассеяния электронов в отдельных поликристаллических нанопроволоках Ag и его влиянию на тепловые и электрические свойства. Основным структурным рассеянием в их работе является поверхностное рассеяние, а в нашей — зернограничное рассеяние. В нашей работе введено единое тепловое сопротивление, чтобы объяснить различные тенденции температурно-зависимой теплопроводности нанопроволоки и объемного серебра. Теплопроводность в нашей работе близка к таковой в работе Койды и др. 22 Но наше удельное электрическое сопротивление намного больше, чем в работе Койды и др. Это приводит к большому числу Лоренца в нашем образце, что можно объяснить фононным переносом электронов через границу зерна. В нашей работе также наблюдается смягчение фононов и усиление электрон-фононного взаимодействия.
Это приводит к большому числу Лоренца в нашем образце, что можно объяснить фононным переносом электронов через границу зерна. В нашей работе также наблюдается смягчение фононов и усиление электрон-фононного взаимодействия.
В этой работе одиночная серебряная нанопроволока подвешена к двум электродам, а электронно-лучевое осаждение (EBID) используется для нанесения платиновых прокладок на концы нанопроволоки для подавления электрических и тепловых контактных сопротивлений. Виды сверху и сбоку на подвешенную серебряную нанопроволоку и данные атомно-силового микроскопа (АСМ) поверхности нанопроволоки показаны на рис. 1. Рентгеновская дифракция (РД) используется для характеристики структуры серебряных нанопроволок и РД. картина показана на рис. 2. Более подробную информацию о подготовке и структуре образца можно найти в разделе методов. Тепловые и электрические свойства одиночной подвешенной серебряной нанопроволоки характеризуются стационарным электротермическим методом от комнатной температуры до 35 К. Также определяется зависящее от температуры число Лоренца. Тепловая и электрическая проводимость нанопроволоки сравнивается с их объемным аналогом, и единое тепловое сопротивление используется для выявления механизма рассеяния.
Также определяется зависящее от температуры число Лоренца. Тепловая и электрическая проводимость нанопроволоки сравнивается с их объемным аналогом, и единое тепловое сопротивление используется для выявления механизма рассеяния.
Электроды и подвешенная серебряная нанопроволока.
( a ) Схема электродов и подвешенной серебряной нанопроволоки (вид сверху). ( b ) СЭМ-изображение электродов и подвешенной серебряной нанопроволоки (вид сверху). ( c ) Схема электродов и подвешенной серебряной нанопроволоки (вид сбоку). ( d ) СЭМ-изображение электродов и подвешенной серебряной нанопроволоки (вид сбоку). ( e ) АСМ-изображение серебряных нанопроволок, диспергированных на стеклянной подложке, для измерения шероховатости. ( f ) Точно отсканированное АСМ-изображение выбранной области размером 160 × 160 нм 2 , обозначенной в ( e ) красным квадратом. Профили поперечного сечения вдоль направлений x (синий) и y (красный) показаны вверху и справа на контурной диаграмме соответственно.
Изображение в полный размер
Рис. 2Рентгенограмма серебряных нанопроволок.
По результатам РФА расстояние между плоскостями решетки для пиков (111), (220) и (311) составляет 2,3616 Å, 1,4518 Å и 1,2287 Å соответственно. Соответствующая постоянная решетки может быть рассчитана как 4,09.Å, 4,11 Å и 4,08 Å для нанопроволоки в нашей работе. Постоянная решетки объемного серебра составляет 4,09 Å. Это подтверждает ГЦК-структуру кристалла серебра.
Полноразмерное изображение
Результаты
Электропроводность
К образцу подавали набор малых электрических токов ( I ) в диапазоне от 0,1 мА до 0,5 мА. За счет джоулева нагрева температура и сопротивление образца увеличиваются. Электрическое сопротивление без джоулевого нагрева может быть получено путем линейной подгонки измеренного сопротивления к I 2 и экстраполируется до предела нулевого тока. Более подробную информацию можно найти в разделе «Методы». Зная геометрические размеры пленок, можно рассчитать удельное электрическое сопротивление. Удельное электрическое сопротивление, зависящее от температуры, показано на рис. 3 и соответствует формуле Блоха-Грюнайзена. Для сравнения, зависящее от температуры удельное электрическое сопротивление объемного серебра также показано на рис. 3 и соответствует формуле Блоха-Грюнайзена 23 . Кроме того, на рис. 3 также показано электрическое сопротивление серебряной нанопроволоки. Согласно правилу Маттиссена и теории Блоха-Грюнайзена 24 , удельное электрическое сопротивление может быть выражено как . это остаточное удельное сопротивление, возникающее в результате структурного рассеяния, такого как рассеяние на границах зерен, рассеяние на примесях и рассеяние на поверхности. Он практически не зависит от температуры, и его значение равно удельному электрическому сопротивлению, когда температура приближается к нулю. представляет собой температурно-зависимое электрическое сопротивление, индуцированное фононным рассеянием, и может быть выражено как
Зная геометрические размеры пленок, можно рассчитать удельное электрическое сопротивление. Удельное электрическое сопротивление, зависящее от температуры, показано на рис. 3 и соответствует формуле Блоха-Грюнайзена. Для сравнения, зависящее от температуры удельное электрическое сопротивление объемного серебра также показано на рис. 3 и соответствует формуле Блоха-Грюнайзена 23 . Кроме того, на рис. 3 также показано электрическое сопротивление серебряной нанопроволоки. Согласно правилу Маттиссена и теории Блоха-Грюнайзена 24 , удельное электрическое сопротивление может быть выражено как . это остаточное удельное сопротивление, возникающее в результате структурного рассеяния, такого как рассеяние на границах зерен, рассеяние на примесях и рассеяние на поверхности. Он практически не зависит от температуры, и его значение равно удельному электрическому сопротивлению, когда температура приближается к нулю. представляет собой температурно-зависимое электрическое сопротивление, индуцированное фононным рассеянием, и может быть выражено как
 0018 23 .
0018 23 .Они оснащены формулой Блоха-Грюнайзена. Электрическое сопротивление серебряной нанопроволоки, зависящее от температуры, также показано координатой справа.
Изображение полного размера
где – параметр электрон-фононного взаимодействия. температура Дебая и обычно принимает значение 5 для немагнитных металлов 8 . Посредством подгонки экспериментальных данных можно получить соответственно температуру Дебая и константу электрон-фононного взаимодействия. Температура Дебая серебряной нанопроволоки и объемного серебра составляет 151 К и 235 К, а константа электрон-фононного взаимодействия серебряной нанопроволоки и объемного серебра равна 90,90 × 10 −8 Ом·м и 5,24 × 10 −8 Ом·м. Отличные аппроксимирующие кривые показывают, что рассеяние фононов на электронах преобладает в температурно-зависимой части электрического сопротивления. Большая константа электрон-фононного взаимодействия серебряной нанопроволоки указывает на усиление электрон-фононного взаимодействия, которое также наблюдается в ультратонких медных пленках из-за шероховатости поверхности 25 . В этой работе поверхность нанопроволок сканируется с помощью атомно-силового микроскопа. Результаты показывают, что шероховатость поверхности составляет ±2 нм. Подробности о АСМ-сканировании можно найти в разделе «Методы». Эта шероховатость поверхности в сочетании с внутренними поверхностями, такими как границы зерен, отвечает за усиленную электрон-фононную связь.
В этой работе поверхность нанопроволок сканируется с помощью атомно-силового микроскопа. Результаты показывают, что шероховатость поверхности составляет ±2 нм. Подробности о АСМ-сканировании можно найти в разделе «Методы». Эта шероховатость поверхности в сочетании с внутренними поверхностями, такими как границы зерен, отвечает за усиленную электрон-фононную связь.
Из рис. 3 видно, что остаточное электрическое сопротивление объемного серебра практически равно нулю (1 × 10 −11 Ом·м), в то время как серебряная нанопроволока намного больше (3,25 × 10 −8 Ом·м). Удельное электрическое сопротивление серебряной нанопроволоки при низких температурах более чем на три порядка больше, чем у массивного серебра. Это связано с интенсивным структурным рассеянием электронов, таким как рассеяние на границах зерен и рассеяние на поверхности. Поскольку при низких температурах фононное рассеяние уменьшается, только структурное рассеяние вносит свой вклад в затруднение переноса электронов. Удельное электрическое сопротивление серебряной нанопроволоки при комнатной температуре в пять раз больше, чем у массивного серебра. Это связано с совместным действием различного структурного и фононного рассеяния. Для объемного серебра при комнатной температуре преобладает фонон-электронное рассеяние. Но для серебряной нанопроволоки как рассеяние фононов, так и структурное рассеяние вносят свой вклад в большое электрическое сопротивление.
Удельное электрическое сопротивление серебряной нанопроволоки при комнатной температуре в пять раз больше, чем у массивного серебра. Это связано с совместным действием различного структурного и фононного рассеяния. Для объемного серебра при комнатной температуре преобладает фонон-электронное рассеяние. Но для серебряной нанопроволоки как рассеяние фононов, так и структурное рассеяние вносят свой вклад в большое электрическое сопротивление.
Из рис. 3 видно, что удельное электрическое сопротивление изменяется линейно с температурой, когда температура не очень низкая. Наклон электрического сопротивления серебряной нанопроволоки в зависимости от температуры (1,68 × 10 –10 Ом м/К) намного больше, чем у объемного серебра (6,11 × 10 –11 Ом м/К). Подобное явление также наблюдается в сверхрешетках Co/Ni 26 . Кроме того, электрическое сопротивление серебряной нанопроволоки и объемного серебра хорошо согласуется с теорией Блоха-Грюнайзена. Результаты подгонки показывают, что температура Дебая серебряной нанопроволоки (151 K) намного меньше, чем у объемного серебра (235 K). Пониженная температура Дебая обусловлена смягчением поверхностных фононов. Отсутствие связей атомов на поверхностях, включая внутренние поверхности, такие как границы зерен, приводит к изменению фононных мод и частоты колебаний. Эти изменения приводят к уменьшению температуры Дебая 6,7,26,27,28 . Таким образом, усиленная электрон-фононная связь и пониженная температура Дебая приводят к большому наклону зависимости электрического сопротивления от температуры.
Пониженная температура Дебая обусловлена смягчением поверхностных фононов. Отсутствие связей атомов на поверхностях, включая внутренние поверхности, такие как границы зерен, приводит к изменению фононных мод и частоты колебаний. Эти изменения приводят к уменьшению температуры Дебая 6,7,26,27,28 . Таким образом, усиленная электрон-фононная связь и пониженная температура Дебая приводят к большому наклону зависимости электрического сопротивления от температуры.
Электропроводность серебра составляет . Здесь m и e — масса и заряд электрона; — время релаксации, n — плотность электронов. Когда температура приближается к нулю, эффект рассеяния фононов будет уменьшаться, и в переносе электронов преобладает структурное рассеяние. Остаточное сопротивление можно записать как . Электронная плотность серебра составляет 5,85 × 10 9 .0018 28 м −3 29 . Время релаксации составляет 1,87 × 10 −14 с. Скорость Ферми серебра составляет 1,39 × 10 6 м/с 29 . Таким образом, длина свободного пробега электронов, индуцированная структурным рассеянием на основе остаточного электрического сопротивления, составляет 26 нм. Длина этой характеристики близка к размеру кристалла (21 нм) в направлении (311). Направление переноса электронов в нашей работе совпадает с аксиальным направлением серебряной нанопроволоки, мы можем сделать вывод, что аксиальное направление — вдоль (311).
Таким образом, длина свободного пробега электронов, индуцированная структурным рассеянием на основе остаточного электрического сопротивления, составляет 26 нм. Длина этой характеристики близка к размеру кристалла (21 нм) в направлении (311). Направление переноса электронов в нашей работе совпадает с аксиальным направлением серебряной нанопроволоки, мы можем сделать вывод, что аксиальное направление — вдоль (311).
Теплопроводность серебряной нанопроволоки
При подаче различных электрических токов температура нанопроволоки будет изменяться из-за джоулевого нагрева. Изменение температуры вызовет изменение электрического сопротивления. После построения модели теплопередачи можно сделать вывод о теплопроводности на основе соотношения между приложенными токами и сопротивлениями. Более подробную информацию можно найти в разделе методов. Измеренная теплопроводность серебряной нанопроволоки в зависимости от температуры показана в сравнении с объемными значениями на рис. 4-9.0018 30 . Как видно из рис. 4, теплопроводность серебряной нанопроволоки при 290 K снижается на 55% от соответствующего объемного значения. Помимо фонон-электронного рассеяния, подобного рассеянию в массивном серебре, в это уменьшение также вносят вклад обширные структурные рассеяния, такие как рассеяние на границах зерен и на поверхности. Эти рассеяния ограничивают длину свободного пробега электронов и впоследствии приводят к снижению теплопроводности. Измеренная теплопроводность одиночной серебряной нанопроволоки близка к значению, указанному в [1]. 22 . При понижении температуры теплопроводность серебряной нанопроволоки ведет себя совершенно иначе, чем у объемного аналога. Теплопроводность серебряной нанопроволоки уменьшается с понижением температуры, тогда как теплопроводность объемного серебра увеличивается с понижением температуры. В частности, для массивного серебра теплопроводность увеличивается более чем в десять раз при понижении температуры до 20 К, а для серебряной нанопроволоки теплопроводность уменьшается на 79% при понижении температуры до 35 К.
Как видно из рис. 4, теплопроводность серебряной нанопроволоки при 290 K снижается на 55% от соответствующего объемного значения. Помимо фонон-электронного рассеяния, подобного рассеянию в массивном серебре, в это уменьшение также вносят вклад обширные структурные рассеяния, такие как рассеяние на границах зерен и на поверхности. Эти рассеяния ограничивают длину свободного пробега электронов и впоследствии приводят к снижению теплопроводности. Измеренная теплопроводность одиночной серебряной нанопроволоки близка к значению, указанному в [1]. 22 . При понижении температуры теплопроводность серебряной нанопроволоки ведет себя совершенно иначе, чем у объемного аналога. Теплопроводность серебряной нанопроволоки уменьшается с понижением температуры, тогда как теплопроводность объемного серебра увеличивается с понижением температуры. В частности, для массивного серебра теплопроводность увеличивается более чем в десять раз при понижении температуры до 20 К, а для серебряной нанопроволоки теплопроводность уменьшается на 79% при понижении температуры до 35 К. температур для серебряной нанопроволоки наблюдается снижение теплопроводности почти на два порядка по сравнению с объемным серебром.
температур для серебряной нанопроволоки наблюдается снижение теплопроводности почти на два порядка по сравнению с объемным серебром.
Зависящая от температуры теплопроводность серебряной нанопроволоки и объемного серебра 30 .
Линии, соединяющие экспериментальные данные, используются только для направления глаз. На вставке показана линейная зависимость между электрическим сопротивлением и квадратом электрического тока при 290 K во время измерения теплопроводности серебряной нанопроволоки. Линия примерки: R = 53,15 + 1,833 × I 2 .
Полноразмерное изображение
Для массивного серебра структурное рассеяние встречается редко, а фононное рассеяние преобладает в переносе электронов. Когда температура понижается, коротковолновые фононы вымораживаются. Число возбужденных фононов, в которых участвует фонон-электронное рассеяние, уменьшается с понижением температуры. Вот почему теплопроводность объемного серебра увеличивается с понижением температуры. Но для серебряной нанопроволоки важную роль в переносе электронов играют как структурное рассеяние, так и фононное рассеяние. Когда температура понижается, фононное рассеяние уменьшается, но структурное рассеяние все еще существует и доминирует в переносе электронов. Более того, теплоемкость электронов линейно уменьшается с температурой, когда температура не слишком высока. Вот почему теплопроводность серебряной нанопроволоки уменьшается с понижением температуры. Это явление также наблюдалось в никелевой нанопроволоке 9.0018 10 , нанопленки золота и платины 13,31,32 и сплавы 33 .
Но для серебряной нанопроволоки важную роль в переносе электронов играют как структурное рассеяние, так и фононное рассеяние. Когда температура понижается, фононное рассеяние уменьшается, но структурное рассеяние все еще существует и доминирует в переносе электронов. Более того, теплоемкость электронов линейно уменьшается с температурой, когда температура не слишком высока. Вот почему теплопроводность серебряной нанопроволоки уменьшается с понижением температуры. Это явление также наблюдалось в никелевой нанопроволоке 9.0018 10 , нанопленки золота и платины 13,31,32 и сплавы 33 .
Здесь дается объяснение аномальной зависимости теплопроводности этих наноструктур от температуры. Теплопроводность можно записать как . Здесь Кл v — объемная теплоемкость электронов; – скорость Ферми, – время релаксации. Объемная теплоемкость электронов изменяется линейно с температурой, когда температура не слишком высока (). Здесь константа (0,646 мДж/(К 2 ·моль) для серебра). Скорость Ферми серебра составляет 1,39 × 10 6 м/с, а его электронная плотность составляет 5,85 × 10 28 м −3 29 . Температура в электронной теплоемкости затмевает физику механизма рассеяния за изменением теплопроводности в зависимости от температуры. Вместо использования традиционного удельного теплового сопротивления здесь мы используем единое удельное тепловое сопротивление для объяснения теплопроводности наноструктур. Единое тепловое сопротивление связано исключительно со временем релаксации электронов, как показано ниже:
Скорость Ферми серебра составляет 1,39 × 10 6 м/с, а его электронная плотность составляет 5,85 × 10 28 м −3 29 . Температура в электронной теплоемкости затмевает физику механизма рассеяния за изменением теплопроводности в зависимости от температуры. Вместо использования традиционного удельного теплового сопротивления здесь мы используем единое удельное тепловое сопротивление для объяснения теплопроводности наноструктур. Единое тепловое сопротивление связано исключительно со временем релаксации электронов, как показано ниже:
В соответствии с правилом Маттиссена единая температуропроводность может быть разделена на две части: часть рассеяния фононов и часть структурного рассеяния, как показано ниже: унифицированное тепловое сопротивление извлекает влияние температуры на механизм рассеяния электронов. Зависимое от температуры унифицированное тепловое сопротивление серебряной нанопроволоки и объемного серебра изображено на рис. 5. Как мы видим, унифицированное тепловое сопротивление серебряной нанопроволоки () и объемного серебра () имеет одинаковую тенденцию при изменении в зависимости от температуры. . Две линии параллельны, когда температура не слишком низкая. При температуре выше 60 K крутизна изменения общего удельного теплового сопротивления серебряных нанопроволок в зависимости от температуры составляет 2,57 × 10 −3 м·K/Вт, а объемного серебра – 2,41 × 10 −3 м·K/Вт. Склоны почти одинаковые. Это связано с тем, что количество возбужденных фононов изменяется линейно с температурой, когда температура не слишком низкая. Это подтверждает, что серебряная нанопроволока и объемное серебро имеют схожий механизм фонон-электронного рассеяния (), но имеют разное структурное рассеяние (). Различные структурные рассеяния приводят к различным остаточным значениям () единого теплового сопротивления. Для объемного серебра остаточное объединенное термическое сопротивление почти равно нулю, потому что структурные дефекты в объемном серебре практически равны нулю.
Как мы видим, унифицированное тепловое сопротивление серебряной нанопроволоки () и объемного серебра () имеет одинаковую тенденцию при изменении в зависимости от температуры. . Две линии параллельны, когда температура не слишком низкая. При температуре выше 60 K крутизна изменения общего удельного теплового сопротивления серебряных нанопроволок в зависимости от температуры составляет 2,57 × 10 −3 м·K/Вт, а объемного серебра – 2,41 × 10 −3 м·K/Вт. Склоны почти одинаковые. Это связано с тем, что количество возбужденных фононов изменяется линейно с температурой, когда температура не слишком низкая. Это подтверждает, что серебряная нанопроволока и объемное серебро имеют схожий механизм фонон-электронного рассеяния (), но имеют разное структурное рассеяние (). Различные структурные рассеяния приводят к различным остаточным значениям () единого теплового сопротивления. Для объемного серебра остаточное объединенное термическое сопротивление почти равно нулю, потому что структурные дефекты в объемном серебре практически равны нулю. Для серебряной нанопроволоки остаточное единое тепловое сопротивление велико из-за рассеяния на границах зерен и поверхности, которые не зависят от температуры. Это остаточное тепловое сопротивление можно использовать для характеристики структуры серебряной нанопроволоки, поскольку фононы замораживаются, когда температура приближается к нулю. При низких температурах преобладающие структурные рассеяния не зависят от температуры. Подобно удельному электрическому сопротивлению, остаточное тепловое сопротивление слабо зависит от температуры при низких температурах. Эта тенденция подтверждается значениями объемного удельного теплового сопротивления серебра. Таким образом, мы можем оценить остаточное тепловое сопротивление, используя значение при 30 К. Согласно остаточному теплосопротивлению (0,9m·K 2 /Вт), время релаксации составляет около 2,77 × 10 −14 с, а характеристическая длина () составляет 38,5 нм. Эта характеристическая длина (длина свободного пробега электрона, ограниченная структурным дефектом) включает в себя эффект фонон-опосредованного переноса энергии электронов через границы зерен.
Для серебряной нанопроволоки остаточное единое тепловое сопротивление велико из-за рассеяния на границах зерен и поверхности, которые не зависят от температуры. Это остаточное тепловое сопротивление можно использовать для характеристики структуры серебряной нанопроволоки, поскольку фононы замораживаются, когда температура приближается к нулю. При низких температурах преобладающие структурные рассеяния не зависят от температуры. Подобно удельному электрическому сопротивлению, остаточное тепловое сопротивление слабо зависит от температуры при низких температурах. Эта тенденция подтверждается значениями объемного удельного теплового сопротивления серебра. Таким образом, мы можем оценить остаточное тепловое сопротивление, используя значение при 30 К. Согласно остаточному теплосопротивлению (0,9m·K 2 /Вт), время релаксации составляет около 2,77 × 10 −14 с, а характеристическая длина () составляет 38,5 нм. Эта характеристическая длина (длина свободного пробега электрона, ограниченная структурным дефектом) включает в себя эффект фонон-опосредованного переноса энергии электронов через границы зерен. Он больше, чем реальный структурный размер кристаллов в серебряной нанопроволоке.
Он больше, чем реальный структурный размер кристаллов в серебряной нанопроволоке.
Единое тепловое сопротивление серебряной нанопроволоки и объемного серебра, зависящее от температуры.
При температуре выше 60 K наклон кривой изменения унифицированного теплового сопротивления серебряных нанопроволок в зависимости от температуры составляет 2,57 × 10 −3 м K/Вт, а для объемного серебра – 2,41 × 10 −3 м·K /В.
Изображение в натуральную величину
Одно явление, которое следует отметить, состоит в том, что для серебряной нанопроволоки наклон изменения удельного электрического сопротивления в зависимости от температуры сильно отличается от его объемного аналога. Но наклон Θ в зависимости от температуры почти такой же, как у объемного серебра. Один и тот же механизм рассеяния фононов по-разному влияет на электрические и тепловые транспортные свойства. Для пленок Ir, нанесенных на нить из молочая, мы наблюдали, что ∂Θ/∂ T и ∂ρ e /∂ T пленки Ir показывают очень похожее отклонение от объемного Ir 19,34 . Возможными причинами очень большой разницы в тепло- и электропроводности серебряных нанопроводов являются изменение силы электрон-фононного взаимодействия, вызванное структурным беспорядком и квантовым размерным эффектом, а также изменение населенности фононов и электронной структуры, которое включает рассеяние под малыми и большими углами . 35,36 . Из-за небольшого размера нанокристаллов в серебряной нанопроволоке отношение поверхности к объему велико, и квантовый размерный эффект становится важным. Более низкая координация и неудовлетворенные связи поверхностных атомов приводят к смягчению фононов и изменению электронной структуры. Фононные моды металлических нанокристаллов дискретизируются, что приводит к изменению каналов связи электрон-фононных взаимодействий 35 . Из-за ограничения волновой функции электрона электронные состояния дискретны. Плотность состояний и плотность электронов вблизи уровня Ферми уменьшаются. Дискретность уровней энергии электрона также привела бы к изменению силы электрон-фононной связи 36 .
Возможными причинами очень большой разницы в тепло- и электропроводности серебряных нанопроводов являются изменение силы электрон-фононного взаимодействия, вызванное структурным беспорядком и квантовым размерным эффектом, а также изменение населенности фононов и электронной структуры, которое включает рассеяние под малыми и большими углами . 35,36 . Из-за небольшого размера нанокристаллов в серебряной нанопроволоке отношение поверхности к объему велико, и квантовый размерный эффект становится важным. Более низкая координация и неудовлетворенные связи поверхностных атомов приводят к смягчению фононов и изменению электронной структуры. Фононные моды металлических нанокристаллов дискретизируются, что приводит к изменению каналов связи электрон-фононных взаимодействий 35 . Из-за ограничения волновой функции электрона электронные состояния дискретны. Плотность состояний и плотность электронов вблизи уровня Ферми уменьшаются. Дискретность уровней энергии электрона также привела бы к изменению силы электрон-фононной связи 36 . Это подтверждается большой константой электрон-фононного взаимодействия, полученной с помощью подгонки Блохом-Грюнайзеном удельного электрического сопротивления серебряной нанопроволоки. Эти изменения приводят к разным откликам электрического и теплового транспорта на фононное рассеяние.
Это подтверждается большой константой электрон-фононного взаимодействия, полученной с помощью подгонки Блохом-Грюнайзеном удельного электрического сопротивления серебряной нанопроволоки. Эти изменения приводят к разным откликам электрического и теплового транспорта на фононное рассеяние.
Для чистых металлов хорошо задокументировано, что вклад решетки в общую теплопроводность незначителен 37 . Но для серебряной нанопроволоки в этой работе общая теплопроводность при низких температурах очень мала. Фононный вклад был бы значительным. Здесь мы берем случай при 36 K в качестве примера для оценки верхнего предела решеточной теплопроводности. Удельная теплоемкость серебра при 36 К составляет 64,65 Дж/(кг К), а плотность 10,49 × 10 3 кг/м 3 38 . Скорость звука (2600 м/с) используется для оценки фононной скорости серебра 39 . При низких температурах длина свободного пробега фонон-фононного рассеяния становится очень большой из-за уменьшения плотности фононов. Кроме того, N-процесс доминирует в фонон-фононном рассеянии, которое не препятствует непосредственно тепловому потоку и вносит небольшой вклад в тепловое сопротивление. Поэтому при низких температурах длина свободного пробега фононов ограничена границами зерен (21 нм). Таким образом, верхний предел теплопроводности () рассчитывается как 12,3 Вт/К·м при 36 K. Длина свободного пробега фононов должна быть меньше 21 нм, потому что другие виды рассеяния, такие как электрон-фононное рассеяние и фононное рассеяние на точечных дефектах, также будут ограничивать длина свободного пробега фононов. Реальная фононная теплопроводность должна быть меньше 12,3 Вт/К·м при 36 К. Измеренная нами теплопроводность составляет 40,46 Вт/К·м, поэтому фононный вклад в общую теплопроводность значителен, но электронная теплопроводность по-прежнему велика. доминирует при низких температурах.
Кроме того, N-процесс доминирует в фонон-фононном рассеянии, которое не препятствует непосредственно тепловому потоку и вносит небольшой вклад в тепловое сопротивление. Поэтому при низких температурах длина свободного пробега фононов ограничена границами зерен (21 нм). Таким образом, верхний предел теплопроводности () рассчитывается как 12,3 Вт/К·м при 36 K. Длина свободного пробега фононов должна быть меньше 21 нм, потому что другие виды рассеяния, такие как электрон-фононное рассеяние и фононное рассеяние на точечных дефектах, также будут ограничивать длина свободного пробега фононов. Реальная фононная теплопроводность должна быть меньше 12,3 Вт/К·м при 36 К. Измеренная нами теплопроводность составляет 40,46 Вт/К·м, поэтому фононный вклад в общую теплопроводность значителен, но электронная теплопроводность по-прежнему велика. доминирует при низких температурах.
Изменение числа Лоренца в зависимости от температуры
После того, как были получены значения удельного электрического сопротивления и теплопроводности, можно вычислить число Лоренца. Но измеренное удельное электрическое сопротивление равно Тл 0 (температура без джоулевого нагрева), а измеренная теплопроводность равна Тл ave (средняя температура при джоулевом нагреве Тл ave = ( Тл 0 + Т 1 )/2, T 1 — самая высокая температура при джоулевом нагреве). Несмотря на то, что повышение температуры в процессе измерения, а именно разница между T 0 и T 1 , очень мала (менее 5 K), мы не можем рассчитать число Лоренца напрямую. Поэтому линейная интерполяция использовалась для получения удельного электрического сопротивления при Тл а.е. . Тогда число Лоренца при Т пр. был определен как . Точно так же можно определить число Лоренца для каждого T ave , и числа Лоренца, зависящие от температуры, показаны на рис. 6.
Но измеренное удельное электрическое сопротивление равно Тл 0 (температура без джоулевого нагрева), а измеренная теплопроводность равна Тл ave (средняя температура при джоулевом нагреве Тл ave = ( Тл 0 + Т 1 )/2, T 1 — самая высокая температура при джоулевом нагреве). Несмотря на то, что повышение температуры в процессе измерения, а именно разница между T 0 и T 1 , очень мала (менее 5 K), мы не можем рассчитать число Лоренца напрямую. Поэтому линейная интерполяция использовалась для получения удельного электрического сопротивления при Тл а.е. . Тогда число Лоренца при Т пр. был определен как . Точно так же можно определить число Лоренца для каждого T ave , и числа Лоренца, зависящие от температуры, показаны на рис. 6.
На вставке показана зависящая от температуры тепловая и электрическая длина свободного пробега электронов.
Изображение в полный размер
Как видно из рис. 6, число Лоренца при 292 К (5,2 × 10 −8 Ом·Вт/К 2 ) намного больше, чем значение Зоммерфельда (2,44 × 10 −8 Ω·Вт/К 2 ). Большие числа Лоренца также наблюдаются для никелевых нанопроволок, золотых, платиновых и иридиевых нанопленок 10,13,14,15,16,17,18 . Это связано с переносом энергии электронов через границы зерен с помощью фононов. Эти наноструктуры состоят из нанокристаллов, среди которых имеется большое количество границ зерен и поверхностей. Часть электронов отразилась бы обратно при рассеянии на границах зерен. Отраженные электроны могут обмениваться энергией с локальными фононами. Фононы могут перемещаться через границы зерен легче, чем электроны. После перехода фононов через границы зерен они могут обмениваться энергией с электронами и фононами по другую сторону границ зерен. Поэтому при обратном отражении электронов заряды не переносятся через границы зерен, а часть энергии электронов переносится через границы зерен. Это приводит к значительному снижению электропроводности и меньшему снижению теплопроводности.
Это приводит к значительному снижению электропроводности и меньшему снижению теплопроводности.
Согласно рис. 6 число Лоренца серебряной нанопроволоки уменьшается с понижением температуры, особенно при низких температурах. Это связано с уменьшением числа возбужденных фононов и малоугловым рассеянием. С одной стороны, с понижением температуры число возбужденных фононов падает. Это приводит к уменьшению числа фононов, которые используются для передачи энергии электронов. Следовательно, число Лоренца при пониженной температуре станет меньше, чем при комнатной температуре. С другой стороны, при понижении температуры возбуждаются только фононы с малым волновым вектором. Волновой вектор населенности фононов постепенно поворачивается к нижнему пределу. Электрон-фононное рассеяние изменится из-за изменения волнового вектора фонона. Рассеяние электронов на фононах с большими волновыми векторами называется рассеянием на большие углы, тогда как рассеяние электронов на фононах с малыми волновыми векторами называется рассеянием на малые углы. Рассеяние под большим углом в равной степени препятствует переносу тепла и заряда, в то время как рассеяние под малым углом значительно тормозит перенос тепла и оставляет перенос заряда относительно неизменным 10,40,41 . При низких температурах число Лоренца серебряной нанопроволоки также будет уменьшаться из-за обширного малоуглового рассеяния.
Рассеяние под большим углом в равной степени препятствует переносу тепла и заряда, в то время как рассеяние под малым углом значительно тормозит перенос тепла и оставляет перенос заряда относительно неизменным 10,40,41 . При низких температурах число Лоренца серебряной нанопроволоки также будет уменьшаться из-за обширного малоуглового рассеяния.
Электрические и тепловые длины свободного пробега электронов, показанные на вставке к рис. 6, могут быть использованы для интерпретации числа Лоренца серебряной нанопроволоки. Поскольку модель свободных электронов применима к серебру, электрическая длина свободного пробега электронов рассчитывается по удельному электрическому сопротивлению0075 n электронная плотность серебра и ρ электрическое сопротивление). Кроме того, длина свободного пробега тепловых электронов рассчитывается по коэффициенту теплопроводности [ или ]. Как видно из вставки к рис. 6, как электрическая, так и тепловая длина свободного пробега электронов увеличиваются с понижением температуры. Это связано с уменьшением числа возбужденных фононов и, как следствие, уменьшением электрон-фононного рассеяния. Источники с уменьшенным рассеянием увеличивают длину свободного пробега электронов. Когда температура приближается к абсолютному нулю, все фононы вымораживаются. Фононы не будут рассеивать электроны. Единственным источником рассеяния являются структурные рассеяния, такие как дефекты границ зерен, поверхности и точечные дефекты, и эти структурные рассеяния не зависят от температуры. Таким образом, длина свободного пробега электрона при экстремально низких температурах может отражать структурную информацию о кристаллической структуре серебряной нанопроволоки. Здесь электрическая длина свободного пробега электронов при экстремально низких температурах составляет около 26 нм. Это значение согласуется с размером кристалла (21 нм) в направлении (311) согласно рентгенограмме. Для тепловой длины свободного пробега электронов ее значение больше, чем для электрической длины свободного пробега.
Это связано с уменьшением числа возбужденных фононов и, как следствие, уменьшением электрон-фононного рассеяния. Источники с уменьшенным рассеянием увеличивают длину свободного пробега электронов. Когда температура приближается к абсолютному нулю, все фононы вымораживаются. Фононы не будут рассеивать электроны. Единственным источником рассеяния являются структурные рассеяния, такие как дефекты границ зерен, поверхности и точечные дефекты, и эти структурные рассеяния не зависят от температуры. Таким образом, длина свободного пробега электрона при экстремально низких температурах может отражать структурную информацию о кристаллической структуре серебряной нанопроволоки. Здесь электрическая длина свободного пробега электронов при экстремально низких температурах составляет около 26 нм. Это значение согласуется с размером кристалла (21 нм) в направлении (311) согласно рентгенограмме. Для тепловой длины свободного пробега электронов ее значение больше, чем для электрической длины свободного пробега. Это связано с тем, что это значение включает вклад переноса энергии электронов с помощью фононов через границы зерен. Разница между электрической и тепловой длиной свободного пробега электрона приводит к большому числу Лоренца. Несмотря на то, что в этой работе мы не измеряем теплопроводность до нуля, можно предсказать, что тепловая и электрическая длины свободного пробега станут одинаковыми, когда температура приблизится к абсолютному нулю. Число Лоренца станет значением Зоммерфельда при абсолютном нуле. Анализ неопределенности этой работы можно найти в дополнительной информации. В этой работе мы изучали только одну нанопроволоку и ее структурное влияние на рассеяние электронов. Ожидается, что нанопроволоки разного диаметра могут обеспечивать различное тепловое/электрическое сопротивление. Нанопроволоки разного диаметра потенциально имеют разный размер зерен и поверхностное рассеяние. Структурные дефекты будут по-разному рассеивать электроны.
Это связано с тем, что это значение включает вклад переноса энергии электронов с помощью фононов через границы зерен. Разница между электрической и тепловой длиной свободного пробега электрона приводит к большому числу Лоренца. Несмотря на то, что в этой работе мы не измеряем теплопроводность до нуля, можно предсказать, что тепловая и электрическая длины свободного пробега станут одинаковыми, когда температура приблизится к абсолютному нулю. Число Лоренца станет значением Зоммерфельда при абсолютном нуле. Анализ неопределенности этой работы можно найти в дополнительной информации. В этой работе мы изучали только одну нанопроволоку и ее структурное влияние на рассеяние электронов. Ожидается, что нанопроволоки разного диаметра могут обеспечивать различное тепловое/электрическое сопротивление. Нанопроволоки разного диаметра потенциально имеют разный размер зерен и поверхностное рассеяние. Структурные дефекты будут по-разному рассеивать электроны.
Выводы
В этой работе были охарактеризованы тепло- и электротранспортные свойства отдельных серебряных нанопроволок вплоть до 35 К. Результаты показали, что тепло- и электропроводность были значительно снижены по сравнению с их массивными аналогами. Температура Дебая серебряной нанопроволоки (151 K) на 36 % ниже, чем у массивного серебра из-за фононного смягчения. Теплопроводность серебряной нанопроволоки уменьшалась с понижением температуры, тогда как теплопроводность массивного серебра увеличивалась. Чтобы объяснить эти различные тенденции, использовалось единое тепловое сопротивление, чтобы различать рассеяние электронов на фононах и рассеяние дефектных электронов. Большое остаточное унифицированное тепловое сопротивление (0,9m·K 2 /Вт) наблюдалось для серебряной нанопроволоки. Он количественно определяет эффект рассеяния дефектных электронов. Для объемного серебра остаточное унифицированное термическое сопротивление почти равно нулю, что отражает относительно низкий уровень дефектов внутри. Унифицированное тепловое сопротивление изменялось линейно с температурой, когда температура не была слишком низкой.
Результаты показали, что тепло- и электропроводность были значительно снижены по сравнению с их массивными аналогами. Температура Дебая серебряной нанопроволоки (151 K) на 36 % ниже, чем у массивного серебра из-за фононного смягчения. Теплопроводность серебряной нанопроволоки уменьшалась с понижением температуры, тогда как теплопроводность массивного серебра увеличивалась. Чтобы объяснить эти различные тенденции, использовалось единое тепловое сопротивление, чтобы различать рассеяние электронов на фононах и рассеяние дефектных электронов. Большое остаточное унифицированное тепловое сопротивление (0,9m·K 2 /Вт) наблюдалось для серебряной нанопроволоки. Он количественно определяет эффект рассеяния дефектных электронов. Для объемного серебра остаточное унифицированное термическое сопротивление почти равно нулю, что отражает относительно низкий уровень дефектов внутри. Унифицированное тепловое сопротивление изменялось линейно с температурой, когда температура не была слишком низкой. Это связано с тем, что число возбужденных фононов линейно уменьшалось с температурой в этом диапазоне температур. Единое тепловое сопротивление серебряной нанопроволоки и объемного серебра имело одинаковую тенденцию, предполагая, что серебряная нанопроволока и объемное серебро имеют сходное фонон-электронное рассеяние. Кроме того, благодаря фононному переносу энергии электронов через границы зерен число Лоренца серебряной нанопроволоки (5,20 × 10 -8 Ω·Вт/K 2 ) было обнаружено намного больше, чем объемный аналог (2,32 × 10 -8 Ω·Вт/K 2 ). Его значение уменьшалось с понижением температуры из-за уменьшения числа возбужденных фононов и малоуглового рассеяния.
Это связано с тем, что число возбужденных фононов линейно уменьшалось с температурой в этом диапазоне температур. Единое тепловое сопротивление серебряной нанопроволоки и объемного серебра имело одинаковую тенденцию, предполагая, что серебряная нанопроволока и объемное серебро имеют сходное фонон-электронное рассеяние. Кроме того, благодаря фононному переносу энергии электронов через границы зерен число Лоренца серебряной нанопроволоки (5,20 × 10 -8 Ω·Вт/K 2 ) было обнаружено намного больше, чем объемный аналог (2,32 × 10 -8 Ω·Вт/K 2 ). Его значение уменьшалось с понижением температуры из-за уменьшения числа возбужденных фононов и малоуглового рассеяния.
Методы
Подготовка образцов и структура
Серебряные нанопроволоки, использованные в данной работе, были приобретены у Sigma-aldrich и поставлялись в виде суспензий в изопропиловом спирте (IPA) с концентрацией 0,5%. Приобретенную дисперсию дополнительно разбавляли ИПС и капали на кусок гелевой пленки. Серебряные нанопроволоки оставались на гелевой пленке после испарения ИПС. При этом закупаемая дисперсия должна быть разбавлена до такой степени, чтобы одиночные серебряные нанопроволоки оставались на пленке геля, не контактируя с окружающими. Затем мы использовали очень простой, но эффективный способ изготовления электродов для подвешивания одиночной нанопроволоки. Прежде всего, на пластину термического оксида кремния с SiO 9 толщиной 1 мкм была нанесена пленка Au толщиной 180 нм.0265 2 слой. Пластину (Au/SiO 2 /Si) разрезали на куски и собирали в два электрода на предметном стекле. Ширина канавки регулируется, и минимальная ширина канавки для этого метода составляет 5 мкм. Если ширина меньше 5 мкм, два электрода будут склонны к электрическому соединению друг с другом. Ширина, использованная в данной работе, составляла около 25 мкм. Два конца траншеи были прикреплены к предметному стеклу эпоксидным клеем.
Серебряные нанопроволоки оставались на гелевой пленке после испарения ИПС. При этом закупаемая дисперсия должна быть разбавлена до такой степени, чтобы одиночные серебряные нанопроволоки оставались на пленке геля, не контактируя с окружающими. Затем мы использовали очень простой, но эффективный способ изготовления электродов для подвешивания одиночной нанопроволоки. Прежде всего, на пластину термического оксида кремния с SiO 9 толщиной 1 мкм была нанесена пленка Au толщиной 180 нм.0265 2 слой. Пластину (Au/SiO 2 /Si) разрезали на куски и собирали в два электрода на предметном стекле. Ширина канавки регулируется, и минимальная ширина канавки для этого метода составляет 5 мкм. Если ширина меньше 5 мкм, два электрода будут склонны к электрическому соединению друг с другом. Ширина, использованная в данной работе, составляла около 25 мкм. Два конца траншеи были прикреплены к предметному стеклу эпоксидным клеем.
Перед соединением нанопроволоки два электрода были проверены, чтобы убедиться, что они не соединяются друг с другом электрически. После этого была использована зондовая станция для манипулирования одной серебряной нанопроволокой и ее соединения с электродами. Наконец, чтобы подавить тепловое и электрическое контактное сопротивление, EBID использовали для нанесения Pt на два конца серебряной нанопроволоки. Чтобы гарантировать хороший тепловой и электрический контакт между серебряной нанопроволокой и электродами, Pt-площадки имеют большие размеры и достаточную толщину, чтобы покрыть все концы серебряной нанопроволоки. Для тепловых и электрических характеристик одиночной серебряной нанопроволоки при низких температурах использовалась криогенная система [CCS-450, JANIS], чтобы обеспечить криогенную экспериментальную среду до 10 К. Образец помещали в вакуумную камеру для подавления конвекции. теплопередача. Давление в камере ниже 0,5 мТорр. Схематическая диаграмма и СЭМ-изображение двух электродов и образца серебряной нанопроволоки (вид сверху) показаны на рис. 1 (а). Виды сбоку показаны на рис. 1(c). В соответствии с видом сверху и сбоку на серебряную нанопроволоку можно извлечь трехмерные координаты нанопроволоки, а длина подвешенной серебряной нанопроволоки рассчитывается как 27,23 мкм.
После этого была использована зондовая станция для манипулирования одной серебряной нанопроволокой и ее соединения с электродами. Наконец, чтобы подавить тепловое и электрическое контактное сопротивление, EBID использовали для нанесения Pt на два конца серебряной нанопроволоки. Чтобы гарантировать хороший тепловой и электрический контакт между серебряной нанопроволокой и электродами, Pt-площадки имеют большие размеры и достаточную толщину, чтобы покрыть все концы серебряной нанопроволоки. Для тепловых и электрических характеристик одиночной серебряной нанопроволоки при низких температурах использовалась криогенная система [CCS-450, JANIS], чтобы обеспечить криогенную экспериментальную среду до 10 К. Образец помещали в вакуумную камеру для подавления конвекции. теплопередача. Давление в камере ниже 0,5 мТорр. Схематическая диаграмма и СЭМ-изображение двух электродов и образца серебряной нанопроволоки (вид сверху) показаны на рис. 1 (а). Виды сбоку показаны на рис. 1(c). В соответствии с видом сверху и сбоку на серебряную нанопроволоку можно извлечь трехмерные координаты нанопроволоки, а длина подвешенной серебряной нанопроволоки рассчитывается как 27,23 мкм. В отличие от длины, средний диаметр нанопроволоки легко измерить с помощью СЭМ, и его значение определяется как 227 нм.
В отличие от длины, средний диаметр нанопроволоки легко измерить с помощью СЭМ, и его значение определяется как 227 нм.
Чтобы охарактеризовать структуру серебряной нанопроволоки, для сканирования образца использовали XRD. Система XRD (дифрактометр Siemens D 500) оснащена медной трубкой, которая работала при 40 кВ и 30 мА. Поскольку одна серебряная нанопроволока слишком мала по сравнению с размером пятна XRD и не может обеспечить достаточно сигналов, пять капель купленной дисперсии, содержащей большое количество серебряных нанопроволок, были нанесены на держатель образца XRD. Рентгенограмма представлена на рис. 2. Рентгенограмма показывает, что серебряная нанопроволока состоит из кристаллов. По рисунку размер кристалла можно оценить по пикам. Размер кристалла, рассчитанный по пику (111), составляет 126 нм, а размер, рассчитанный по пику (220) и пику (311), составляет 8 нм и 21 нм соответственно. Все размеры кристаллов в этих направлениях намного меньше диаметра серебряной нанопроволоки. Это доказывает, что серебряная нанопроволока является поликристаллической. Границ зерен между этими нанокристаллами в серебряных нанопроволоках много. Также разный размер кристаллитов, определяемый пиками, указывает на то, что кристаллит в нанопроволоке не является кубическим или сферическим. Вместо этого ожидается, что кристаллит будет иметь форму эллипсоида.
Это доказывает, что серебряная нанопроволока является поликристаллической. Границ зерен между этими нанокристаллами в серебряных нанопроволоках много. Также разный размер кристаллитов, определяемый пиками, указывает на то, что кристаллит в нанопроволоке не является кубическим или сферическим. Вместо этого ожидается, что кристаллит будет иметь форму эллипсоида.
Для исследования шероховатости поверхности серебряных нанопроволок использовали АСМ (MicroNano D 3000). Для подготовки образца к АСМ-сканированию на стеклянную подложку капали небольшое количество водного раствора, содержащего серебряные нанопроволоки. После испарения воды серебряные нанопроволоки были рассредоточены по подложке и готовы к сканированию. На рис. 1(e) показано АСМ-изображение серебряных нанопроволок на подложке. Затем был тщательно отсканирован тщательно выбранный участок размером 160 × 160 нм 2 , и изображение поверхности показано на рис. 1(f). Профили поперечного сечения показывают колебания шероховатости поверхности ± 2 нм.
Электрическая характеристика
Для электрической характеристики серебряной нанопроволоки был применен набор малых электрических токов в диапазоне от 0,1 мА до 0,5 мА. Источником тока является источник постоянного и переменного тока Keithley 6221. Из-за эффекта электрического нагрева электрическое сопротивление будет увеличиваться при увеличении электрического тока. Измеренное электрическое сопротивление должно изменяться пропорционально квадрату электрического тока. Линейная аппроксимация использовалась для экстраполяции электрического сопротивления без эффекта нагрева, а именно сопротивления при нулевом электрическом токе.
Тепловая характеристика
Теплопроводность нанопроволоки была охарактеризована с помощью стационарного электротермического метода. Серебряная нанопроволока была подвешена к двум электродам при характеристике. Мы можем рассматривать два электрода как два радиатора. Его температура такая же, как температура окружающей среды T 0 . Образец помещали в высоковакуумную камеру для подавления эффекта конвекции. Более того, радиационный эффект будет небольшим, поскольку нанопроволока очень короткая. Также хорошо известно, что серебро имеет очень малый коэффициент излучения (около 0,03). Поэтому влияние конвекции и излучения в данной работе пренебрежимо мало. Когда через нанопроволоку пропускают постоянный электрический ток, джоулев самонагрев в нанопроволоке вызывает повышение температуры. Управляющее уравнение стационарного теплообмена выглядит следующим образом:
Образец помещали в высоковакуумную камеру для подавления эффекта конвекции. Более того, радиационный эффект будет небольшим, поскольку нанопроволока очень короткая. Также хорошо известно, что серебро имеет очень малый коэффициент излучения (около 0,03). Поэтому влияние конвекции и излучения в данной работе пренебрежимо мало. Когда через нанопроволоку пропускают постоянный электрический ток, джоулев самонагрев в нанопроволоке вызывает повышение температуры. Управляющее уравнение стационарного теплообмена выглядит следующим образом:
Здесь – теплопроводность, – скорость тепловыделения на единицу объема. Его можно описать как . I — приложенный электрический ток; R 1 – электрическое сопротивление нанопроволоки; A c — площадь поперечного сечения нанопроволоки () и L — длина нанопроволоки. Выражение T ( x ) равно . Средняя температура по образцу
Повышение температуры . Как мы видим, повышение температуры пропорционально квадрату электрического тока. При температуре выше 35 K электрическое сопротивление серебряной нанопроволоки пропорционально ее температуре. Изменение температуры можно отслеживать по изменению электрического сопротивления:
При температуре выше 35 K электрическое сопротивление серебряной нанопроволоки пропорционально ее температуре. Изменение температуры можно отслеживать по изменению электрического сопротивления:
Из уравнения (6) видно, что оно пропорционально и наклон равен Тогда теплопроводность нанопроволоки можно определить следующим образом: пример для демонстрации процесса измерения. Сначала через образец пропускали серию электрических токов в диапазоне от 0,1 мА до 0,5 мА, и соответствующие напряжения измеряли цифровым мультиметром (Agilent 34401A). Затем мы наносим зависимость между электрическим сопротивлением и квадратом тока, как показано на вставке к рис. 4. После линейной подгонки данных наклон (1,83 Ом/мА 2 ) и точку пересечения (53,15 Ом). Точка пересечения представляет собой электрическое сопротивление ( R 0 ) при 290 К. После того, как мы измерили электрические сопротивления при разных температурах, можно определить значение (0,1165 Ом / К). Диаметр и длину серебряной нанопроволоки измеряли с помощью сканирующей электронной микроскопии (СЭМ) после завершения эксперимента. Наконец, теплопроводность серебряной нанопроволоки была определена как 191,5 Вт/К·м. Чтобы повысить точность измерений, рост электрического сопротивления, вызванный во всех экспериментах, был тщательно выбран и составлял около 1%. Все повышения температуры контролировались в пределах 5 K.
Наконец, теплопроводность серебряной нанопроволоки была определена как 191,5 Вт/К·м. Чтобы повысить точность измерений, рост электрического сопротивления, вызванный во всех экспериментах, был тщательно выбран и составлял около 1%. Все повышения температуры контролировались в пределах 5 K.
Дополнительная информация
Как цитировать эту статью : Cheng, Z. et al. Температурная зависимость электро- и теплопроводности одиночной серебряной нанопроволоки. науч. Респ. 5 , 10718; doi: 10.1038/srep10718 (2015).
Ссылки
De, S. et al. Серебряные нанопроводные сети как гибкие, прозрачные, проводящие пленки: чрезвычайно высокое соотношение постоянной и оптической проводимости. Acs Nano 3, 1767–1774 (2009 г.).
КАС Статья Google ученый
Ху, Л. Б., Ким, Х. С., Ли, Дж. Ю., Пеуманс, П. и Куи, Ю. Масштабируемое покрытие и свойства прозрачных, гибких серебряных электродов из нанопроволоки.
 Acs Nano 4, 2955–2963 (2010).
Acs Nano 4, 2955–2963 (2010).КАС Статья Google ученый
Yang, L. Q. et al. Обработанные раствором гибкие полимерные солнечные элементы с серебряными электродами из нанопроволоки. Приложение ACS Матер. Интерфейсы 3, 4075–4084 (2011).
КАС Статья Google ученый
Ю. З. Б. и др. Высокогибкие серебряные нанопроволочные электроды для полимерных светоизлучающих диодов с памятью формы. Доп. Матер. 23, 664 (2011).
КАС Статья Google ученый
Цзэн, С.Ю., Чжан, К.К., Ю, Р.М. и Лу, Ц.З. Новый прозрачный проводник: серебряная нанопроволока, скрытая на поверхности прозрачного полимера. Доп. Матер. 22, 4484–4488 (2010).
КАС Статья Google ученый
Zhang, W. et al. Анализ размерного эффекта в тонкой медной проволоке с гальваническим покрытием и реалистичная оценка для моделирования удельного сопротивления меди.
 J Appl. физ. 101, 6, 063703 (2007).
J Appl. физ. 101, 6, 063703 (2007).ОБЪЯВЛЕНИЕ Статья Google ученый
Марци, Г. Д., Якопино, Д., Куинн, А. Дж. и Редмонд, Г. Исследование собственных транспортных свойств одиночных металлических нанопроволок: формирование контакта прямой записи с использованием сфокусированного ионного пучка. J Appl. физ. 96, 3458–3462 (2004).
ОБЪЯВЛЕНИЕ Статья Google ученый
Bid, A., Bora, A. & Raychaudhuri, A.K. Температурная зависимость сопротивления металлических нанопроволок диаметром >= 15 нм: применимость теоремы Блоха-Грюнайзена. физ. Ред. В 74, 035426 (2006).
ОБЪЯВЛЕНИЕ Статья Google ученый
Карим С., Энсингер В., Корнелиус Т.В. и Нойманн Р. Исследование размерных эффектов в удельном электрическом сопротивлении одиночных электрохимически изготовленных золотых нанопроволок. Physica E 40, 3173–3178 (2008).

КАС ОБЪЯВЛЕНИЯ Статья Google ученый
Оу, М. Н. и др. Электрический и тепловой перенос в одиночной никелевой нанопроволоке. заявл. физ. лат. 92, 063101 (2008).
ОБЪЯВЛЕНИЕ Статья Google ученый
Волклейн Ф., Райт Х., Корнелиус Т.В., Раубер М. и Нойманн Р. Экспериментальное исследование теплопроводности и закона Видемана-Франца для одиночных металлических нанопроволок. Нанотехнологии 20, 325706 (2009)).
КАС Статья Google ученый
Стоянович Н., Берг Дж. М., Майтрипала Д. Х. С. и Хольц М. Прямое измерение теплопроводности алюминиевых нанопроволок. заявл. физ. лат. 95, 0 (2009).
ОБЪЯВЛЕНИЕ Статья Google ученый
Yoneoka, S. et al. Электро- и теплопроводность в наномостиках атомно-слоевого осаждения толщиной до 7 нм.
 Нано Летт. 12, 683–686 (2012).
Нано Летт. 12, 683–686 (2012).КАС ОБЪЯВЛЕНИЯ Статья Google ученый
Ма, В. Г. и Чжан, X. Изучение тепловых, электрических и термоэлектрических свойств металлических нанопленок. Междунар. J. Heat Mass Tran. 58, 639–651 (2013).
КАС Статья Google ученый
Wang, H.D., Liu, J.H., Zhang, X. & Takahashi, K. Нарушение закона Видемана-Франца в отдельных взвешенных поликристаллических нанопленках золота до 3 K. Int. J. Heat Mass Tran. 66, 585–591 (2013).
КАС Статья Google ученый
Ван, Х. Д., Лю, Дж. Х., Чжан, X., Го, З. Ю. и Такахаши, К. Экспериментальное исследование влияния рассеяния по границам зерен на перенос заряда и тепла в золотых и платиновых нанопленках. Тепломассоперенос 47, 893–898 (2011).
КАС ОБЪЯВЛЕНИЯ Статья Google ученый
Лин, Х.
 , Сюй, С., Ли, К., Донг, Х. и Ван, X. В. Тепловая и электрическая проводимость в тонких золотых пленках толщиной 6,4 нм. Наномасштаб 5, 4652–4656 (2013).
, Сюй, С., Ли, К., Донг, Х. и Ван, X. В. Тепловая и электрическая проводимость в тонких золотых пленках толщиной 6,4 нм. Наномасштаб 5, 4652–4656 (2013).КАС ОБЪЯВЛЕНИЯ Статья Google ученый
Лин, Х., Сюй, С., Ван, С. В. и Мей, Н. Тепловая и электрическая проводимость в ультратонких металлических пленках: от 7 нм до субнанометровой толщины. Смолл 9, 2585–2594 (2013).
КАС Статья Google ученый
Cheng, Z., Xu, Z., Xu, S. & Wang, X. Фононное смягчение и слабое температурно-зависимое число Лоренца для ультратонкой инфракрасной пленки на биологической основе. Препринт arXiv arXiv: 1410.1912 (2014).
Линь Х., Сюй С., Чжан Ю.-К. и Ван, X. Электронный перенос и объемное поведение закона Видемана-Франца для иридиевых пленок толщиной менее 7 нм на шелке тутового шелкопряда. Приложение ACS Матер. Интерфейсы 6, 11341–11347 (2014).

КАС Статья Google ученый
Амдурский Н. и др. Электронный транспорт через белки. Доп. Матер. 26, 7142–7161 (2014).
КАС Статья Google ученый
Койда, Д. и др. Зависящие от температуры термоэлектрические свойства отдельных серебряных нанопроволок. Препринт arXiv arXiv: 1410.1467 (2014).
Матула Р. А. Удельное электрическое сопротивление меди, золота, палладия и серебра. Дж. Физ. хим. Ссылка Данные 8, 1147–1298 (1979).
КАС ОБЪЯВЛЕНИЯ Статья Google ученый
Паттерсон Дж. и Бейли Б. Физика твердого тела: введение в теорию, 2-е изд., 247–251 (Springer 2010).
Тималсина Ю.П. и др. Влияние наноразмерной шероховатости поверхности на удельное сопротивление ультратонких эпитаксиальных пленок меди. Нанотехнологии 26, 075704 (2015).
ОБЪЯВЛЕНИЕ Статья Google ученый
Ким С.
 , Зуль Х. и Шуллер И. К. Рассеяние поверхностных фононов в электрическом удельном сопротивлении на сверхрешетках Co/Ni. физ. Преподобный Летт. 78, 322–325 (1997).
, Зуль Х. и Шуллер И. К. Рассеяние поверхностных фононов в электрическом удельном сопротивлении на сверхрешетках Co/Ni. физ. Преподобный Летт. 78, 322–325 (1997).КАС ОБЪЯВЛЕНИЯ Статья Google ученый
Кастл Г., Бойен Х.Г., Шредер А., Плеттл А. и Циманн П. Размерный эффект удельного сопротивления тонких эпитаксиальных золотых пленок. физ. Ред. В 70, 165414 (2004).
ОБЪЯВЛЕНИЕ Статья Google ученый
Ma, WG, Zhang, X. & Takahashi, K. Электрические свойства и приведенная температура Дебая поликристаллических тонких золотых пленок. Дж. Физ. Д заявл. физ. 43, 465301 (2010).
ОБЪЯВЛЕНИЕ Статья Google ученый
Киттель, С. Введение в физику твердого тела, 8-е изд., 139–146 (Wiley, 2005).
Хо, С.Ю., Пауэлл, Р.В. и Лили, П.Е. Теплопроводность элементов: всесторонний обзор.
 Дж. Физ. хим. Ссылка Данные 3, 607 (1974).
Дж. Физ. хим. Ссылка Данные 3, 607 (1974).Google ученый
Чжан, К.Г., Цао, Б.Ю., Чжан, X., Фуджи, М. и Такахаши, К. Влияние рассеяния на границах зерен на электро- и теплопроводность поликристаллических золотых нанопленок. физ. Ревизия B 74, 134109(2006).
ОБЪЯВЛЕНИЕ Статья Google ученый
Zhang, X. et al. Тепло- и электропроводность взвешенной нанопленки платины. заявл. физ. лат. 86, 171912 (2005).
ОБЪЯВЛЕНИЕ Статья Google ученый
Лу, Ю. З., Хуанг, Ю. Дж., Вэй, С. С. и Шен, Дж. Тесная корреляция между транспортными свойствами и стеклообразующей способностью системы сплавов FeCoCrMoCBY. Интерметаллиды 30, 144–147 (2012).
Артикул Google ученый
Cheng, Z., Xu, Z., Xu, S. & Wang, X. Температурно-зависимое поведение теплопроводности пленки Ir толщиной менее 5 нм: рассеяние дефектных электронов, количественно определяемое остаточным термическим сопротивлением.
 Дж. Заявл. физ. 117, 024307 (2015).
Дж. Заявл. физ. 117, 024307 (2015).ОБЪЯВЛЕНИЕ Статья Google ученый
Bayle, M. et al. Экспериментальное исследование колебательной плотности состояний и электронных возбуждений в металлических нанокристаллах. физ. Ред. Б 89, 195402 (2014).
ОБЪЯВЛЕНИЕ Статья Google ученый
Гош, С.К. Кубо щель как фактор, определяющий появление новых физико-химических характеристик мелких металлических частиц. Ассамский университет J. Sci. Тех. 7, 114–121 (2011).
Google ученый
Тритт, Т. М. в Теплопроводность: Теория, свойства и приложения, 74–79, (Kluwer Academic/Plenum, 2005).
Смит, Д. Р. и Фикетт, Ф. Р. Низкотемпературные свойства серебра. Дж. Рез. Натл. Инст. Стэн. 100, 119–171 (1995).
КАС Статья Google ученый
Самсонов Г.
 В. Справочник по физико-химическим свойствам элементов. 243 (Пленум, Нью-Йорк, 1968 г.).
В. Справочник по физико-химическим свойствам элементов. 243 (Пленум, Нью-Йорк, 1968 г.).Zhang, Y. et al. Определение отношения Видемана-Франца по коэффициенту теплопроводности Холла: приложение к Cu и YBa2Cu3O6.95. Физ. Преподобный Летт. 84, 2219–2222 (2000).
КАС ОБЪЯВЛЕНИЯ Статья Google ученый
Зиман, Дж. М. Электроны и фононы: теория явлений переноса в твердых телах. 334–420 (Кларендон Пресс, 1960).
Ссылки на скачивание
Благодарности
Поддержка этой работы со стороны Исследовательского управления армии (W911NF-12-1-0272), Управления военно-морских исследований (N000141210603) и Национального научного фонда (CBET1235852 и CMMI126439)9) с благодарностью. Х.В. благодарит за частичную поддержку программы «Тайшаньский ученый» провинции Шаньдун, Китай.
Информация о авторе
Авторы и принадлежности
Департамент машиностроения, Университет штата Айова, 2010 Black Engineering Build Электротехника и вычислительная техника, Университет штата Айова, Эймс, Айова, 50011, США
Longju Liu & Meng Lu
School of Environmental and Municipal Engineering, Qingdao Technological University, Qingdao, Shandong, 266033, P.
 R. China
R. ChinaXinwei Wang
Authors
- Zhe Cheng
View author publications
Вы также можете искать этого автора в PubMed Google Scholar
- Longju Liu
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Академия
- Shen Xu
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
- Meng Lu
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Xinwei Wang
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
Вклады
Х.В. и З.К. задумал идею. З.К. и Л.Л. проводили эксперименты. С.Х. провел АСМ исследование поверхности нанопроволоки. Z.C., X.W. и М.Л. проведена обработка и анализ данных. З.К. и X.W. написал бумагу.
Z.C., X.W. и М.Л. проведена обработка и анализ данных. З.К. и X.W. написал бумагу.
Заявление об этике
Конкурирующие интересы
Авторы не заявляют об отсутствии конкурирующих финансовых интересов.
Дополнительные электронные материалы
Дополнительная информация
Права и разрешения
Эта работа находится под лицензией Creative Commons Attribution 4.0 International License. Изображения или другие сторонние материалы в этой статье включены в лицензию Creative Commons на статью, если иное не указано в кредитной строке; если материал не включен в лицензию Creative Commons, пользователям необходимо будет получить разрешение от держателя лицензии на воспроизведение материала. Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by/4.0/
Перепечатка и разрешения
Об этой статье
Дополнительная литература
Синтез серебряных нанопроволок, анализ NaCl, CuCl2 и NaBr в виде галоидных солей с дополнительной термической, кислотной обработкой и последующей обработкой растворителем для прозрачных и гибких электродов
- Эрика Гомес Ямамото
- Марина Проенса Дантас
- Карлос Эдуардо Кава
Прикладная нанотехнология (2022)
Туннелирование электронов между колеблющимися атомами в медной нанонити
- Мохаммад Аль-Мамун
- Мариус Орловский
Научные отчеты (2021)
Повышение термоэлектромеханических свойств материала на основе BiSb с помощью нанокомпозитов SiC
- Мохамед С.
 Эль-Асфури
Эль-Асфури - Шабан М. Абду
- Ахмед Нассеф
JOM (2021)
- Мохамед С.
Электрические, тепловые и микроволновые экранирующие свойства пригодных для печати серебряных нанопроводов
- Айсвария Ремадеви
- Сабита Энн Хосе
- Кужичалил П.
 Сурендран
Сурендран
Журнал материаловедения (2021)
Ультратонкие MXene-арамидные нановолокна, защищающие от электромагнитных помех, с тактильной чувствительностью, выдерживающие суровые температуры
- Давэй Ху
- Сици Ван
- Синьи Хуан
Наноисследования (2021)
Комментарии
Отправляя комментарий, вы соглашаетесь соблюдать наши Условия и Правила сообщества. Если вы обнаружите что-то оскорбительное или не соответствующее нашим условиям или правилам, отметьте это как неприемлемое.
Если вы обнаружите что-то оскорбительное или не соответствующее нашим условиям или правилам, отметьте это как неприемлемое.
Скачать PDF
Тепло- и электропроводность алюминия. [коэффициент Зеебека; от 80 до 400/sup 0/K] (Технический отчет)
Тепло- и электропроводность алюминия. [коэффициент Зеебека; от 80 до 400/суп 0/K] (Технический отчет) | ОСТИ.GOVперейти к основному содержанию
- Полная запись
- Другие родственные исследования
- Авторов:
- Кук, Дж.
 Г.; Мур, JP; Мацумура, Т .; Ван дер Меер, член парламента
Г.; Мур, JP; Мацумура, Т .; Ван дер Меер, член парламента
- Дата публикации:
- Исследовательская организация:
- Окриджская национальная лаборатория, Теннесси (США)
- Идентификатор ОСТИ:
- 5066461
- Номер(а) отчета:
- ОРНЛ-5079
- Номер контракта Министерства энергетики:
- W-7405-ENG-26
- Тип ресурса:
- Технический отчет
- Страна публикации:
- США
- Язык:
- Английский
- Тема:
- 36 МАТЕРИАЛОВЕДЕНИЕ; АЛЮМИНИЙ; ТЕРМОЭЛЕКТРИЧЕСКИЕ СВОЙСТВА; АЛЮМИНИЕВЫЕ ОСНОВНЫЕ СПЛАВЫ; ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ; ЭФФЕКТ Зеебека; ТЕМПЕРАТУРНАЯ ЗАВИСИМОСТЬ; ТЕПЛОПРОВОДНОСТЬ; СПЛАВЫ; АЛЮМИНИЕВЫЕ СПЛАВЫ; ЭЛЕКТРИЧЕСКИЕ СВОЙСТВА; ЭЛЕМЕНТЫ; МЕТАЛЛЫ; ФИЗИЧЕСКИЕ СВОЙСТВА; ТЕРМОДИНАМИЧЕСКИЕ СВОЙСТВА; 360104* – Металлы и сплавы – Физические свойства
Форматы цитирования
- MLA
- АПА
- Чикаго
- БибТекс
Кук, Дж. Г., Мур, Дж. П., Мацумура, Т., и Ван дер Меер, член парламента . Тепловая и электрическая проводимость алюминия. [коэффициент Зеебека; от 80 до 400/суп 0/K] . США: Н. П., 1975.
Веб. дои: 10.2172/5066461.
Г., Мур, Дж. П., Мацумура, Т., и Ван дер Меер, член парламента . Тепловая и электрическая проводимость алюминия. [коэффициент Зеебека; от 80 до 400/суп 0/K] . США: Н. П., 1975.
Веб. дои: 10.2172/5066461.
Копировать в буфер обмена
Кук, Дж. Г., Мур, Дж. П., Мацумура, Т., и Ван дер Меер, член парламента Тепло- и электропроводность алюминия. [коэффициент Зеебека; от 80 до 400/суп 0/K] . Соединенные Штаты. https://doi.org/10.2172/5066461
Копировать в буфер обмена
Кук, Дж. Г., Мур, Дж. П., Мацумура, Т., и Ван дер Меер, член парламента, 1975.
«Тепло- и электропроводность алюминия. [Коэффициент Зеебека; от 80 до 400 / суп 0 / K]». Соединенные Штаты. https://doi.org/10.2172/5066461. https://www.osti.gov/servlets/purl/5066461.
Копировать в буфер обмена
@статья{osti_5066461,
title = {Тепло- и электропроводность алюминия. [коэффициент Зеебека; от 80 до 400/суп 0/K]},
[коэффициент Зеебека; от 80 до 400/суп 0/K]},
автор = {Кук, Дж. Г. и Мур, Дж. П., Мацумура, Т. и Ван дер Меер, М. П.},
abstractNote = {},
дои = {10.2172/5066461},
URL-адрес = {https://www.osti.gov/biblio/5066461},
журнал = {},
число = ,
объем = ,
место = {США},
год = {1975},
месяц = {9}
}
Копировать в буфер обмена
Посмотреть технический отчет (0,88 МБ)
https://doi.org/10.2172/5066461
Экспорт метаданных
Сохранить в моей библиотеке
Вы должны войти в систему или создать учетную запись, чтобы сохранять документы в своей библиотеке.
Аналогичных записей в сборниках OSTI.GOV:
- Аналогичные записи
Электро- и теплопроводность эпоксидно-углеродных композитов-наполнителей, обработанных каландрированием
Материалы (Базель). 2019Май; 12(9): 1522.
2019Май; 12(9): 1522.
Опубликовано в сети 9 мая 2019 г. doi: 10.3390/ma120
Информация об авторе Примечания к статье Информация об авторских правах и лицензии Отказ от ответственности расследовано. Наполнители диспергировали в жидкой матрице с помощью трехвальцового оборудования. Смесь наполнитель/матрица отливалась в форму и затем отверждалась, получая композитные образцы. В качестве наполнителей использовались многослойные углеродные нанотрубки, графеноподобные нанопластинки и графит и исследовалось их влияние на проводимость. Электрическая и теплопроводность измерялись при различных нагрузках наполнителя. Было обнаружено, что образование перколяционных путей значительно повышает электропроводность, хотя они не столь эффективны для улучшения теплопроводности. Поведение композитов, содержащих каждый отдельный наполнитель, сравнивали с поведением гибридных композитов, содержащих комбинации двух разных наполнителей. Результаты показывают, что наполнители с разным соотношением размеров проявляют синергетический эффект, приводящий к заметному улучшению электропроводности. Однако наблюдалось лишь небольшое влияние на теплопроводность.
Результаты показывают, что наполнители с разным соотношением размеров проявляют синергетический эффект, приводящий к заметному улучшению электропроводности. Однако наблюдалось лишь небольшое влияние на теплопроводность.
Ключевые слова: каландрирование, электропроводность, теплопроводность, гибридные композиты
Углеродосодержащие материалы, такие как сажа и графит, традиционно используются в качестве наполнителя для полимеров, так как они улучшают некоторые механические свойства и снижают стоимость материалов. За последние двадцать лет наноструктурированные углеродные наполнители, в частности углеродные нанотрубки (УНТ) и графен или графеноподобные нанопластинки (ЗНЧ), вызывают все больший интерес в качестве компонентов нанокомпозитов на основе полимеров. Замечательные механические, электрические и термические свойства этих видов нанонаполнителей открывают огромный потенциал для производства композитов с высокими эксплуатационными характеристиками [1,2,3].
Хотя Thostenson et al. В [4] утверждалось, что многостенные углеродные нанотрубки (МУНТ) имеют теоретический модуль упругости более 1 ТПа, прямые испытания с помощью атомно-силового микроскопа измеряли модуль упругости в диапазоне от 270 до 950 ГПа и предел прочности при растяжении в диапазоне от 11 до 63 ГПа [5, 6,7]. Измерения, проведенные на одном слое графена с использованием наконечника атомно-силового микроскопа на основе алмаза, дали результаты модуля упругости 1 ТПа и предела прочности на разрыв 130 ГПа. Эти значения, хорошо согласующиеся с теоретическим компьютерным моделированием [8,9], обусловлены прочными ковалентными связями С-С внутри графеновых слоев и, следовательно, характерны для одной графеновой пластины и одной нанотрубки. К сожалению, как модуль упругости, так и предел прочности при растяжении уменьшаются с увеличением количества слоев ЗНЧ, постепенно приближаясь к механическим характеристикам, типичным для графита.
Кроме того, электро- и теплопроводность одноуглеродных нанонаполнителей очень хорошие. На самом деле электропроводность одной МУНТ колеблется в пределах 10 5 См/м и 10 7 См/м, а 10 5 См/м — типичное значение проводимости для ВНП [3,10,11]. Значения теплопроводности 2000 Вт/(м·К) и 5000 Вт/(м·К) являются общепринятыми для МУНТ и ЗНП соответственно [10,11]. Теплопроводность этих нанонаполнителей намного лучше, чем у графита (298 Вт/(м·К)), который, наоборот, имеет аналогичную электропроводность. Кроме того, в литературе можно найти очень разные значения теплопроводности для МУНТ и ЗНЧ, поскольку на их проводимость сильно влияет наличие дефектов, производственный процесс, количество плоскостей в ЗНЧ и метод измерения [3, 12,13,14]. Например, было обнаружено, что дефекты, индуцированные облучением электронным пучком, снижают теплопроводность графена на 70 % [15]. Кроме того, как электропроводность, так и теплопроводность графеноподобных нанопластинок очень высоки в плоскости, но резко уменьшаются в направлении, перпендикулярном графеновым плоскостям, как это происходит и для графита [11].
На самом деле электропроводность одной МУНТ колеблется в пределах 10 5 См/м и 10 7 См/м, а 10 5 См/м — типичное значение проводимости для ВНП [3,10,11]. Значения теплопроводности 2000 Вт/(м·К) и 5000 Вт/(м·К) являются общепринятыми для МУНТ и ЗНП соответственно [10,11]. Теплопроводность этих нанонаполнителей намного лучше, чем у графита (298 Вт/(м·К)), который, наоборот, имеет аналогичную электропроводность. Кроме того, в литературе можно найти очень разные значения теплопроводности для МУНТ и ЗНЧ, поскольку на их проводимость сильно влияет наличие дефектов, производственный процесс, количество плоскостей в ЗНЧ и метод измерения [3, 12,13,14]. Например, было обнаружено, что дефекты, индуцированные облучением электронным пучком, снижают теплопроводность графена на 70 % [15]. Кроме того, как электропроводность, так и теплопроводность графеноподобных нанопластинок очень высоки в плоскости, но резко уменьшаются в направлении, перпендикулярном графеновым плоскостям, как это происходит и для графита [11]. Наконец, когда рассматривается сеть УНТ или ЗНЧ, сопротивление интерфейсов значительно снижает проводимость.
Наконец, когда рассматривается сеть УНТ или ЗНЧ, сопротивление интерфейсов значительно снижает проводимость.
Однородное распределение нанонаполнителей в матрице необходимо для максимального использования их потенциала, поэтому были предприняты большие усилия для улучшения процесса производства нанокомпозитов. К сожалению, эти наполнители склонны к образованию скоплений частиц или пучков нанотрубок из-за очень высоких сил притяжения Ван-дер-Ваальса. По этой причине основная проблема, с которой приходится сталкиваться при обработке нанокомпозитов, связана с отделением наночастиц/нанотрубок от их агрегатов. Несколько методов обработки были исследованы для изготовления полимерных нанокомпозитов. Например, наиболее подходящие методы для композитов с термопластичной матрицей заключаются в производстве смеси наполнителя и матрицы с последующим литьем под давлением. Смешивание расплава или компаундирование раствора (которое заключается в растворении полимера в растворителе и последующем диспергировании наполнителя в жидкости с помощью перемешивания или обработки ультразвуком) может применяться для производства смеси наполнитель/матрица [3]. ,16]. Также было разработано несколько методов диспергирования нанонаполнителей в термореактивных полимерах, которые перед отверждением находятся в жидком состоянии. Нанонаполнитель можно добавить в жидкую смолу и диспергировать путем перемешивания, высокоскоростного перемешивания, обработки ультразвуком, каландрирования или комбинации двух этих методов [3,17,18,19].,20,21]. Часто в смолу также добавляют растворитель, чтобы уменьшить вязкость и облегчить диспергирование. Использование растворителей как для термопластичных, так и для термореактивных матриц благоприятствует процессу диспергирования, но растворители необходимо испарять в конце процесса (после литья), а при испарении может происходить реагрегация нанонаполнителя.
,16]. Также было разработано несколько методов диспергирования нанонаполнителей в термореактивных полимерах, которые перед отверждением находятся в жидком состоянии. Нанонаполнитель можно добавить в жидкую смолу и диспергировать путем перемешивания, высокоскоростного перемешивания, обработки ультразвуком, каландрирования или комбинации двух этих методов [3,17,18,19].,20,21]. Часто в смолу также добавляют растворитель, чтобы уменьшить вязкость и облегчить диспергирование. Использование растворителей как для термопластичных, так и для термореактивных матриц благоприятствует процессу диспергирования, но растворители необходимо испарять в конце процесса (после литья), а при испарении может происходить реагрегация нанонаполнителя.
Смешивание, выполняемое с использованием смешивания с высоким усилием сдвига или обработки ультразвуком, часто вызывает разрушение наполнителей и, как следствие, уменьшение длины УНТ или латерального размера ЗНЧ [22].
Каланирование, выполняемое с использованием трехвалкового оборудования, представляет собой хорошо зарекомендовавший себя и щадящий процесс, основанный на принятии касательных напряжений. В соответствии с этим процессом после диспергирования нанонаполнителей в жидких матрицах (таких как эпоксидная смола или силикон), добавления отвердителя и заливки в форму материал подвергается окончательной обработке для отверждения [20, 21, 22]. ,23]. Возможного повреждения нанонаполнителя на этапе смешивания можно избежать, выбрав правильные параметры обработки, которые в то же время обеспечивают однородное распределение наполнителя внутри смолы. Углеродные нанотрубки имеют тенденцию располагаться параллельно направлению прокатки. Аналогичный эффект предпочтительной ориентации можно наблюдать и для графеноподобных пластинок, но не для каждой нагрузки ЗНЧ [21]. Кроме того, ожидается, что анизотропная проводимость материала будет результатом текстуры, вызванной каландрированием [21]. Кроме того, ЗНЧ могут отслаиваться в процессе календаря [21]. Смесь нанонаполнитель/жидкая матрица демонстрирует вязкоупругие свойства: диспергирование происходит из-за соответствующих напряжений сдвига, но когда напряжение сдвига снижается ниже порогового значения, вязкость сильно возрастает, что препятствует повторной агрегации нанотрубок или пластинок [20].
В соответствии с этим процессом после диспергирования нанонаполнителей в жидких матрицах (таких как эпоксидная смола или силикон), добавления отвердителя и заливки в форму материал подвергается окончательной обработке для отверждения [20, 21, 22]. ,23]. Возможного повреждения нанонаполнителя на этапе смешивания можно избежать, выбрав правильные параметры обработки, которые в то же время обеспечивают однородное распределение наполнителя внутри смолы. Углеродные нанотрубки имеют тенденцию располагаться параллельно направлению прокатки. Аналогичный эффект предпочтительной ориентации можно наблюдать и для графеноподобных пластинок, но не для каждой нагрузки ЗНЧ [21]. Кроме того, ожидается, что анизотропная проводимость материала будет результатом текстуры, вызванной каландрированием [21]. Кроме того, ЗНЧ могут отслаиваться в процессе календаря [21]. Смесь нанонаполнитель/жидкая матрица демонстрирует вязкоупругие свойства: диспергирование происходит из-за соответствующих напряжений сдвига, но когда напряжение сдвига снижается ниже порогового значения, вязкость сильно возрастает, что препятствует повторной агрегации нанотрубок или пластинок [20].
Общепризнано, что углеродсодержащие наполнители обеспечивают хорошую проводимость, когда их концентрация внутри полимерной матрицы превышает критическую концентрацию (называемую порогом перколяции). Достижение перколяционного порога электропроводности обязательно происходит при физическом соприкосновении нанотрубок или проводящих нанонаполнителей друг с другом, но проводимость наблюдалась и при уменьшении расстояния между нанотрубками примерно до 5 нм, поскольку действует туннельный механизм [20].
Когда наполнители выстраиваются в одном направлении, легче формируется непрерывная сеть УНТ или ВНП. Этот эффект может быть достигнут за счет приложения сдвигающих сил, а также за счет использования электрических или магнитных полей [24,25,26].
В случае ЗНЧ размер тромбоцитов также может сильно влиять на электрическую и, в основном, на теплопроводность. Композитная проводимость увеличивается с увеличением размера тромбоцитов [21]. Фактически, межфазное тепловое сопротивление играет доминирующую роль в теплопроводности, и по этой причине удобно использовать большие графеноподобные листы, чтобы ограничить влияние высокого теплового граничного сопротивления.
Согласно результатам последних исследований [2,17,27], добавление углеродных наночастиц (таких как графеновые пластинки или сажа) в композиты УНТ-полимер может обеспечить синергетический эффект, что приводит к дальнейшему улучшению механических свойств [28]. ,29], теплопроводность [30,31], электропроводность [32,33] и пьезорезистивное поведение [34]. Напротив, другие авторы не наблюдали синергетического эффекта в таких гибридных композитах [35]. Считается, что синергетический эффект на электропроводность возникает из-за комбинации двух проводящих наполнителей с различной геометрической формой и соотношением сторон, что приводит к образованию в полимере непрерывных сетчатых структур ЗНЧ-УНТ-ЗНЧ или УНТ-ЗНЧ-УНТ. 33,36]. Графен действует как «прокладка» для разделения запутанных УНТ, а УНТ перекрывают зазор между листами графена или углеродными наночастицами. Кроме того, эти сетчатые структуры могут приводить к сильному π–π-взаимодействию с бензольными кольцами и атомами кислорода, возможно присутствующими в полимерных цепях, составляющих матрицу [36]. Было высказано предположение, что как механические, так и электрические свойства существенно зависят от соотношения концентраций двух типов нанонаполнителей, но это соотношение не влияет на все эти свойства одинаково. По этой причине не существует наилучшего соотношения, которое могло бы оптимизировать как механическое, так и электрическое поведение [34,37], и гибридные нанокомпозиты должны разрабатываться для каждого конкретного применения.
Было высказано предположение, что как механические, так и электрические свойства существенно зависят от соотношения концентраций двух типов нанонаполнителей, но это соотношение не влияет на все эти свойства одинаково. По этой причине не существует наилучшего соотношения, которое могло бы оптимизировать как механическое, так и электрическое поведение [34,37], и гибридные нанокомпозиты должны разрабатываться для каждого конкретного применения.
Вышеупомянутые гибридные композиты дают возможность значительно снизить общее содержание углеродсодержащих наполнителей в проводящих полимерах и снизить стоимость материала за счет замены довольно дорогих нанотрубок более дешевыми наполнителями. Действительно, сверхвысокие объемные доли (40–50 об. %) УНТ или ЗНЧ или их комбинаций могут привести к значительному увеличению тепло- и электропроводности [17], но диспергирование такого большого количества наполнителя очень затруднено. С увеличением содержания наполнителя трудно избежать явлений агломерации и наличия дефектов (например, пористости). Такого рода дефекты микроструктуры сильно ухудшают механические свойства.
Такого рода дефекты микроструктуры сильно ухудшают механические свойства.
Настоящая работа была направлена на получение композитов с очень небольшим количеством наполнителей и хорошей электро- и теплопроводностью, полученными за счет использования синергетического эффекта наполнителя и оптимизированного пути обработки. Были исследованы комбинации УНТ с графитом и графеном. В качестве матрицы использовалась эпоксидная смола, так как этот вид материала позволяет использовать все преимущества, которые предлагает процесс каландрирования.
Нанокомпозиты обработаны с использованием в качестве матрицы эпоксидной смолы (Technovit®, Kulzer, Wehrheim, Germany), аминного отвердителя (соотношение смола:отвердитель = 2:1, плотность полимера 1,15 г/см 3 после отверждения) и различных наполнителей, обладающих следующими характеристиками в соответствии с техническими паспортами производителей:
Многостенные углеродные нанотрубки NC7000 TM (производства Nanocyl SA (Sambreville, Бельгия) с помощью химического пара процесса осаждения) со средней длиной 1,5 мкм, диаметром 9,5 нм, электропроводностью 10 6 См/м и плотностью 1,72 г/см 3 .

Графеновые нанопластинки GAbcr (приобретены у ABCR Gute Chemie, Карлсруэ, Германия) размером 15 мкм, толщиной 6–8 нм и плотностью 2 г/см 3 .
Чешуйки природного графита (приобретены у Alfa Aesar, Хаверхилл, Массачусетс, США) со средним размером от 7 до 10 мкм, степенью чистоты 99% (металлическая основа) и плотностью 2,2 г/см 3 [ 11].
Образцы по 45 г каждый были получены путем смешивания смолы с отвердителем и наполнителями с помощью трехвалковой мельницы, отливки смеси в силиконовую цилиндрическую форму и отверждения в течение 12 часов при комнатной температуре. Трехвалковый станок состоит из трех валков, вращающихся в противоположных направлениях; смесь подается между первым и вторым валками, а скребок позволяет собирать конечную смесь с третьего валка. Этот аппарат может работать в разных режимах: щелевой и контактный. В режиме зазора можно модулировать расстояние между валками, чтобы варьировать усилия сдвига. Это расстояние можно варьировать, учитывая, что зазор между первым и вторым валком (зазор 1) должен быть в три раза больше, чем зазор между вторым и третьим валком (зазор 2). Минимальный зазор между парой валков 5 мкм (при работе в зазорном режиме).
Это расстояние можно варьировать, учитывая, что зазор между первым и вторым валком (зазор 1) должен быть в три раза больше, чем зазор между вторым и третьим валком (зазор 2). Минимальный зазор между парой валков 5 мкм (при работе в зазорном режиме).
В контактном режиме валки соприкасаются друг с другом, что обеспечивает максимальное касательное напряжение в системе. Также скорость вращения валков влияет на возникающие касательные напряжения. Скорость валков связана соотношением 1:3:9, чтобы обеспечить непрерывный поток материала через аппарат. Скорость третьего валка может изменяться плавно, но максимальная скорость вращения составляет 600 об/мин в зазорном режиме и 300 об/мин в контактном режиме.
Диспергирование наполнителя в эпоксидной матрице на трехвалковой мельнице ранее исследовалось путем обработки образцов эпоксидной смолы/ГНП с 2 мас.% наполнителя и с использованием различных параметров. Смолу и наполнители сначала смешивали механическим перемешиванием, а затем обрабатывали с помощью мини-каландрирующей системы (Exakt 80E). Качество полученных образцов сравнивали посредством измерения их теплопроводности. Таким образом, были выбраны и приняты наилучшие параметры обработки для получения всех исследуемых композитов, как описано ниже. Скорость третьего валка была зафиксирована на уровне 600 об/мин. Процесс смешивания состоял из шести стадий, выполняемых с разным размером зазора между валками. Первые три этапа выполняли с использованием зазора 45 мкм между первым и вторым валком и 15 мкм между вторым и третьим валком. Следующие три этапа выполнялись с использованием зазоров 15 мкм и 5 мкм между парами валков.
Качество полученных образцов сравнивали посредством измерения их теплопроводности. Таким образом, были выбраны и приняты наилучшие параметры обработки для получения всех исследуемых композитов, как описано ниже. Скорость третьего валка была зафиксирована на уровне 600 об/мин. Процесс смешивания состоял из шести стадий, выполняемых с разным размером зазора между валками. Первые три этапа выполняли с использованием зазора 45 мкм между первым и вторым валком и 15 мкм между вторым и третьим валком. Следующие три этапа выполнялись с использованием зазоров 15 мкм и 5 мкм между парами валков.
Переработаны бинарные композиты (состоящие из матрицы и одного наполнителя) с различной концентрацией наполнителя: от 0 до 1 мас.% УНТ, от 0 до 30 мас.% ЗНЧ и от 0 до 45 мас.% графита . Также были приготовлены четыре набора тройных гибридных композитов (УНТ плюс ЗНЧ или УНТ плюс добавленный в матрицу графит). Эти гибридные композиты содержали 0,1 мас.% или 0,05 мас.% УНТ в сочетании с концентрацией ЗНЧ или графита, постепенно увеличивающейся от 0 до 5 мас. %.
%.
Стержни 20 × 10 × 2 мм 3 и диски диаметром 20 мм и толщиной 10 мм были получены из цилиндрических композитных образцов путем их вырезания алмазным диском перпендикулярно их высоте. Эти образцы использовались для измерения электропроводности и теплопроводности соответственно. Для каждого вида композита (т.е. для каждого исследованного состава) электропроводность и теплопроводность измерялись на двух или пяти образцах соответственно. Концы стержней были окрашены проводящей краской на основе серебра, а электрическое сопротивление было измерено по 2-точечному методу с использованием оборудования Agilent 34420A NanoVolt/Micro-Ohm Meter (Agilent Technologies, Санта-Клара, Калифорния, США). Измеренные данные нормировались на размер стержня (длину и толщину) с получением значений удельного сопротивления. Несколько образцов для измерения электропроводности (стержни того же размера, что и образцы, описанные выше) также были взяты в направлении, параллельном оси цилиндра. Теплопроводность исследовали при комнатной температуре с использованием анализатора тепловых констант Hot Disk (Hot disk TPS 2500, Hot Disk, Гетеборг, Швеция).
Плотность композитов измеряли методом Архимеда. Поверхности криоразрушенных композитов наблюдали с помощью сканирующей электронной микроскопии с полевой эмиссией (FE-SEM, оборудование Zeiss Merlin, Оберкохен, Германия). Во избежание заряда на образцы наносился слой хрома толщиной несколько нанометров.
3.1. Оптимизация процесса трехвалковой мельницы
Было проведено несколько проб смешивания с целью оптимизации параметров обработки и получения однородной дисперсии наполнителя в матрице с использованием минимального количества стадий. Ожидается, что однородная дисперсия наполнителя будет способствовать образованию проводящей сетки, а затем повысит как теплопроводность, так и электропроводность. Кроме того, однородная дисперсия наполнителя позволит избежать агломерации частиц наполнителя, что отрицательно сказывается на механических свойствах. В качестве показателя эффективности процесса диспергирования принимали значение теплопроводности. Каждое испытание состояло из нескольких стадий (повторных обработок смеси с помощью аппарата), выполняемых с использованием различных скоростей вращения валков и зазоров. Жесткость метода обработки постепенно повышалась за счет увеличения количества ступеней, уменьшения зазора между валками и добавления проходов в контактном режиме. Условия, принятые для этих технологических испытаний, и результирующая теплопроводность композитов с 2 мас.% НЧ показаны на рис.
Жесткость метода обработки постепенно повышалась за счет увеличения количества ступеней, уменьшения зазора между валками и добавления проходов в контактном режиме. Условия, принятые для этих технологических испытаний, и результирующая теплопроводность композитов с 2 мас.% НЧ показаны на рис.
Таблица 1
Испытания трехвалковых мельниц для обработки эпоксидных графеноподобных нанопластинок (GNP) (2 мас.%).
| Метод обработки (исследование) | Параметры обработки | Теплопроводность (W/(M · K) ± SD) | ||||
|---|---|---|---|---|---|---|
| Ноги | GAP 1 (µm) | . ) | Контактный режим | Об/мин (максимум) | ||
| A | 9 | 45 | 15 | No | 600 | 0. 349 ± 0.021 349 ± 0.021 |
| B | 3 | 45 | 15 | No | 600 | 0.375 ± 0.006 |
| 3 | 15 | 5 | No | 600 | ||
| C | 9 | 45 | 15 | No | 600 | 0. 338 ± 0.014 338 ± 0.014 |
| 9 | 15 | 5 | No | 600 | ||
| D | 3 | 45 | 15 | No | 600 | 0.365 ± 0.018 |
| 3 | 15 | 5 | No | 600 | ||
| 3 | 0 | 0 | Yes | 300 | ||
| E | 9 | 45 | 15 | No | 600 | 0. 352 ± 0.028 352 ± 0.028 |
| 9 | 15 | 5 | No | 600 | ||
| 3 | 0 | 0 | Yes | 300 | ||
| F | 9 | 45 | 15 | No | 600 | 0. 310 ± 0.034 310 ± 0.034 |
| 9 | 15 | 5 | No | 600 | ||
| 6 | 0 | 0 | Yes | 300 | ||
Открыть в отдельном окне
показывает, что наилучшая теплопроводность была достигнута при использовании условий обработки испытания «В».
Добавление дополнительных ступеней в зазорном режиме (испытание C) или как в зазорном, так и в контактном режимах (испытания D, E, F) не привело к улучшению теплопроводности, которая уменьшилась по сравнению с испытанием B. Исследование под микроскопом образцов показало, что достаточно хорошего распределения наполнителя внутри матрицы можно добиться, приняв условия опыта «Б», а увеличение количества ступеней, особенно выполняемых в контактном режиме, может привести к снижению размер тромбоцитов. Вероятно, повреждение наполнителя перевешивает улучшение однородности распределения наполнителя. Как обсуждается в следующем абзаце, процесс каландрирования также может привести к предпочтительной ориентации некоторых наполнителей, что может сделать проводимость зависящей от направления.
Исследование под микроскопом образцов показало, что достаточно хорошего распределения наполнителя внутри матрицы можно добиться, приняв условия опыта «Б», а увеличение количества ступеней, особенно выполняемых в контактном режиме, может привести к снижению размер тромбоцитов. Вероятно, повреждение наполнителя перевешивает улучшение однородности распределения наполнителя. Как обсуждается в следующем абзаце, процесс каландрирования также может привести к предпочтительной ориентации некоторых наполнителей, что может сделать проводимость зависящей от направления.
3.2. Композитная микроструктура-наполнитель Ориентация
Поверхности излома композитных образцов, полученных из стержней, используемых для измерения электрического сопротивления, а затем обработанных в направлении, перпендикулярном цилиндрическим литым образцам, изображены на . Все эти поверхности излома представляют собой поперечное сечение стержней.
Открыть в отдельном окне
Поверхность излома композита с 0,2 мас. % углеродных нанотрубок (УНТ) 50k× ( a ), 1 мас.% УНТ 25k× ( б ), 40 мас.% графита 5к× ( с ), 40 мас.% графита 25к× ( д ), 6 мас.% ВНП 25к× ( е ), 25 мас. % ВНП 10k× ( f ).
% углеродных нанотрубок (УНТ) 50k× ( a ), 1 мас.% УНТ 25k× ( б ), 40 мас.% графита 5к× ( с ), 40 мас.% графита 25к× ( д ), 6 мас.% ВНП 25к× ( е ), 25 мас. % ВНП 10k× ( f ).
На поверхностях излома композитов, содержащих 0,2 мас. % и 1 мас. % УНТ (а, б), видны несколько трубок, перпендикулярных поверхности и достаточно хорошо распределенных в матрице. Некоторые из них (обозначены красными стрелками) выступают над поверхностью и претерпели вырыв до разрушения образца. Эти изображения доказывают, что календарирование вызывает определенную степень выравнивания УНТ. Напротив, процесс трехвалковой мельницы не привел к предпочтительной ориентации чешуек графита, поскольку они кажутся беспорядочно ориентированными на поверхности излома (c, d). Вместо этого наблюдался определенный эффект ориентации для композитов, содержащих довольно низкие проценты ЗНЧ (д), в то время как эта текстура становилась менее выраженной при увеличении содержания ЗНЧ (е).
Различное влияние каландрирования на преимущественную ориентацию наполнителей с разным соотношением сторон и размером можно оценить и на поверхности излома гибридных композитов, например, композита, содержащего 0,1 мас.% УНТ и 5 мас. % графита (а). На этом изображении УНТ расположены примерно перпендикулярно поверхности (красные стрелки) и видны графитовые пластины, лежащие на поверхности (белые стрелки). Также можно наблюдать нанотрубки, соединяющие графитовые пластины (желтые стрелки).
Открыть в отдельном окне
Поверхность излома композита с 0,1% масс. УНТ плюс 5% масс. графита ( a ) и 0,1% масс. УНТ плюс 5% масс. НЧ ( b ) ).
Также в случае гибридных композитов УНТ + ЗНЧ (б) хорошо видна ориентация УНТ, при этом только одни ЗНЧ располагаются перпендикулярно поверхности излома (красная стрелка), а другие – параллельно ей (белые стрелки).
При микроскопии в образцах композита была обнаружена некоторая пористость. Плотности некоторых репрезентативных образцов суммируются и сравниваются с теоретическими, рассчитанными по правилу смешения. Из этих результатов видно, что измеренная плотность в целом была ниже ожидаемой, исходя из состава образца и плотности наполнителя и матрицы. Это отклонение от теоретической плотности прогрессивно увеличивалось с увеличением количества наполнителя, в частности, когда в качестве наполнителя использовался графит. Весьма вероятно, что увеличение концентрации наполнителя затруднило диспергирование наполнителя и способствовало агломерации частиц наполнителя, что могло привести к повышению уровня пористости и снижению как электропроводности, так и теплопроводности.
Плотности некоторых репрезентативных образцов суммируются и сравниваются с теоретическими, рассчитанными по правилу смешения. Из этих результатов видно, что измеренная плотность в целом была ниже ожидаемой, исходя из состава образца и плотности наполнителя и матрицы. Это отклонение от теоретической плотности прогрессивно увеличивалось с увеличением количества наполнителя, в частности, когда в качестве наполнителя использовался графит. Весьма вероятно, что увеличение концентрации наполнителя затруднило диспергирование наполнителя и способствовало агломерации частиц наполнителя, что могло привести к повышению уровня пористости и снижению как электропроводности, так и теплопроводности.
Таблица 2
Плотность композитов с различным содержанием наполнителя.
| Filler | Filler Concentration (wt. %) %) | Experimental Density (g/cm 3 ) | Experimental versus Theoretical Density (Ratio) |
|---|---|---|---|
| No one (net epoxy) | – | 1,1496 ± 0,0001 | >0,999 |
| МУНТ | 0,1 | 1,1496 ± 0,0005 | 41174 >0.999|
| MWCNT | 0.5 | 1. 1041 ± 0.0001 1041 ± 0.0001 | 0.959 |
| GNP | 1.0 | 1.1092 ± 0.0003 | 0.960 |
| GNP | 10.0 | 1.1482 ± 0.0001 | 0.956 |
| GNP | 25.0 | 1.1450 ± 0.0007 | 0. 890 890 |
| Graphite | 20.0 | 1.0499 ± 0.0005 | 0.896 |
| Graphite | 40.0 | 1.2026 ± 0.0009 | 0.846 |
| MWCNT + GNP | 0.1 + 2 | 1.0913 ± 0.0001 | 0.941 |
| MWCNT + GNP | 0. 1 + 5 1 + 5 | 1.1754 ± 0.0004 | 0.910 |
| MWCNT + Graphite | 0.1 + 2 | 1.0919 ± 0.0007 | 0.940 |
| MWCNT + Graphite | 0.1 + 5 | 1,1129 ± 0,0002 | 0,944 |
Открыть в отдельном окне
3.3. Электропроводность
Электропроводность двухкомпонентных и трехкомпонентных материалов показана на рис. показывает, что проводимость изменяется с концентрацией УНТ, ЗНЧ и графита; для этих трех наполнителей можно наблюдать очень разную эффективность.
показывает, что проводимость изменяется с концентрацией УНТ, ЗНЧ и графита; для этих трех наполнителей можно наблюдать очень разную эффективность.
Открыть в отдельном окне
Влияние содержания наполнителя на электропроводность композитов.
Таблица 3
Электропроводность двухкомпонентных и гибридных (трехкомпонентных) композитов на эпоксидной основе.
| Sample Composition (wt.%) | Electrical Conductivity S/m | |||
|---|---|---|---|---|
| MWCNT | GNP | Graphite | Epoxy | |
| 0 | – | – | 100 | <1 × 10 −9 |
| 0,1 | – | – | remainder | <1 × 10 −9 |
0. 2 2 | – | – | remainder | 5.18 × 10 −5 |
| 0.3 | – | – | remainder | 5.97 × 10 −4 |
| 0.4 | – | – | remainder | 5. 08 × 10 −3 08 × 10 −3 |
| 0.5 | – | – | remainder | 1.20 × 10 −2 |
| 1.0 | – | – | remainder | 1.21 × 10 −1 |
| – | From 0.5 to 5.0 | – | remainder | <1 × 10 −9 |
| – | 6. 0 0 | – | remainder | 2.44 × 10 −6 |
| – | 7.0 | – | remainder | 5.93 × 10 −6 |
| – | 9.0 | – | remainder | 6. 80 × 10 −6 80 × 10 −6 |
| – | 10.0 | – | remainder | 2.71 × 10 −6 |
| – | 15.0 | – | remainder | 9.20 × 10 −5 |
| – | 20.0 | – | remainder | 2. 14 × 10 −4 14 × 10 −4 |
| – | 25.0 | – | remainder | 1.64 × 10 −1 |
| – | 30.0 | – | remainder | 1.62 × 10 −1 |
| – | 0 | From 1. 0 to 30.0 0 to 30.0 | remainder | <1 × 10 −9 |
| – | 0 | 40.0 | remainder | 2.02 × 10 −5 |
| – | 0 | 45.0 | remainder | 1.92 × 10 −4 |
0. 1 1 | 1.0 | – | remainder | 1.20 × 10 −3 |
| 0.1 | 2.0 | – | remainder | 1.32 × 10 −3 |
| 0.1 | 5.0 | – | remainder | 5. 43 × 10 −4 43 × 10 −4 |
| 0.1 | – | 1.0 | remainder | 3.57 × 10 −5 |
| 0.1 | – | 2.0 | remainder | 1.65 × 10 −4 |
| 0.1 | – | 5. 0 0 | remainder | 1.61 × 10 −4 |
| 0.05 | 1.0 | – | remainder | 6.02 × 10 −5 |
| 0.05 | 2.0 | – | remainder | 1.25 × 10 −4 |
0. 05 05 | 5.0 | – | remainder | 3.29 × 10 −4 |
| 0.05 | – | 1.0 | remainder | <1 × 10 −9 |
| 0.05 | – | 2.0 | remainder | 3. 99 × 10 −5 99 × 10 −5 |
| 0.05 | – | 5.0 | remainder | 7.37 × 10 −5 |
Open in a separate window
Наилучшая электропроводность была достигнута при очень низкой концентрации УНТ (1 мас.%), в то время как аналогичное значение электропроводности было получено при использовании в качестве наполнителя ЗНЧ, но в гораздо более высокой концентрации (25 и 30 мас.%). Добавление графита также привело к более ограниченному увеличению проводимости при использовании большого количества этого наполнителя. Эти результаты согласуются с более высокой собственной проводимостью МУНТ (10 6 См/м) относительно ВНП (10 5 См/м [21,23]) или графита (10 5 См/м [22]). В порогах перколяции при 1,34 × 10 -1 об.% (0,2 мас.%), 9,21 об.% (15 мас.%) и 21,96 об.% (35 мас.%) можно наблюдать для МУНТ, ЗНЧ. и графита соответственно.
В порогах перколяции при 1,34 × 10 -1 об.% (0,2 мас.%), 9,21 об.% (15 мас.%) и 21,96 об.% (35 мас.%) можно наблюдать для МУНТ, ЗНЧ. и графита соответственно.
Выравнивание МУНТ в направлении измерения электропроводности, скорее всего, способствует повышению их способности повышать электропроводность. Принято считать, что при диспергировании проводящего наполнителя в диэлектрическом полимере электропроводность может быть достигнута только при достаточно высокой концентрации наполнителя для образования проводящей сети из физически связанных между собой углеродных элементов (пластин или трубок). Когда эти цепочки проводящих элементов размещены в плоскости или вдоль направления, эффект проводящих элементов максимизируется в плоскости или направлении выравнивания, но материал проявляет сильную анизотропию. С другой стороны, вероятно, лишь часть проводящих элементов принимает участие в формировании проводящих дорожек и, весьма вероятно, не все проводящие цепи проходят по всей длине композитных образцов. По этим причинам довольно сложно найти простую зависимость между концентрацией наполнителя и реальной электропроводностью. Кроме того, ожидается, что электропроводность цепочек из проводящих углеродных трубок или пластин будет ниже, чем у одиночной трубки/пластины, которую можно рассчитать или измерить. Эти характеристики нанокомпозитов затрудняют прогнозирование их электрического поведения. Было предложено несколько моделей прогнозирования, но, насколько нам известно, еще не существует общепризнанного метода. Модели, основанные на проводимости и номинальной объемной доле наполнителя в качестве исходных данных, как правило, приводят к значениям проводимости, значительно превышающим экспериментальные, если только в расчет не вводятся полуэмпирические параметры для соответствия экспериментальному поведению [38].
По этим причинам довольно сложно найти простую зависимость между концентрацией наполнителя и реальной электропроводностью. Кроме того, ожидается, что электропроводность цепочек из проводящих углеродных трубок или пластин будет ниже, чем у одиночной трубки/пластины, которую можно рассчитать или измерить. Эти характеристики нанокомпозитов затрудняют прогнозирование их электрического поведения. Было предложено несколько моделей прогнозирования, но, насколько нам известно, еще не существует общепризнанного метода. Модели, основанные на проводимости и номинальной объемной доле наполнителя в качестве исходных данных, как правило, приводят к значениям проводимости, значительно превышающим экспериментальные, если только в расчет не вводятся полуэмпирические параметры для соответствия экспериментальному поведению [38].
Предпочтительная ориентация УНТ в наших образцах, обработанных на трехвалковой мельнице, была подтверждена путем сравнения значений проводимости, измеренных в направлениях, параллельных и перпендикулярных по отношению к ориентации МУНТ. В образцах, содержащих 1 мас. % МУНТ, электропроводность, измеренная в направлении ориентации трубок, составила 1,2 × 10 –1 См/м, а в направлении (параллельно высоте цилиндрических литых образцов).
В образцах, содержащих 1 мас. % МУНТ, электропроводность, измеренная в направлении ориентации трубок, составила 1,2 × 10 –1 См/м, а в направлении (параллельно высоте цилиндрических литых образцов).
Значительная разница в электропроводности, наблюдаемая между композитами, содержащими ЗНЧ и графит, может быть объяснена тенденцией ЗНЧ ориентироваться в направлении прокатки и лежать на плоскости прокатки, в то время как графитовые пластины имеют случайную ориентацию. Фактически проводимость как ЗНЧ, так и графита значительно выше в графитовых плоскостях, чем в направлении толщины. Поэтому для получения токопроводящего материала необходимо сильно увеличить содержание графита; с другой стороны, обработка композита становится все более и более сложной с увеличением концентрации наполнителя, что приводит к увеличению пористости, что ограничивает влияние высокой концентрации наполнителя.
Электропроводность 1,2 × 10 −1 См/м, измеренная для композитов, содержащих 1 мас. % (0,67 об.%) МУНТ, согласуется с литературными данными, сообщающими о проводимости композитов эпоксид/МУНТ, обработанных тремя валками. мельнице (10 -2 См/м с использованием 1,35 мас. % МУНТ [20]) или сдвиговым перемешиванием (10 -1 См/м с использованием 1,0 мас. % МУНТ [19]). Напротив, электрическая проводимость, полученная с использованием процесса трехвалковой мельницы, была лучше, чем указанная в литературе для аналогичных композитов с гораздо более высоким содержанием МУНТ, но обработанных ультразвуком или одновременным магнитным перемешиванием и ультразвуком: 2 × 10 -2 См/м при использовании 10 об. % наполнителя [17] и 1·10 -3 См/м при использовании 2 мас. % наполнителя [18] соответственно. Тогда метод обработки, по-видимому, имеет большое значение для проводимости композитов эпоксид/МУНТ.
% (0,67 об.%) МУНТ, согласуется с литературными данными, сообщающими о проводимости композитов эпоксид/МУНТ, обработанных тремя валками. мельнице (10 -2 См/м с использованием 1,35 мас. % МУНТ [20]) или сдвиговым перемешиванием (10 -1 См/м с использованием 1,0 мас. % МУНТ [19]). Напротив, электрическая проводимость, полученная с использованием процесса трехвалковой мельницы, была лучше, чем указанная в литературе для аналогичных композитов с гораздо более высоким содержанием МУНТ, но обработанных ультразвуком или одновременным магнитным перемешиванием и ультразвуком: 2 × 10 -2 См/м при использовании 10 об. % наполнителя [17] и 1·10 -3 См/м при использовании 2 мас. % наполнителя [18] соответственно. Тогда метод обработки, по-видимому, имеет большое значение для проводимости композитов эпоксид/МУНТ.
Кроме того, литературные данные об эпоксидных нанокомпозитах GNP усиливают важность метода обработки для электропроводности. Например, Chandrasekaran et al. [39] получили проводимость 1,8 × 10 −3 См/м для композита эпоксид/ЗНЧ с 1 мас.% ЗНЧ размером 20–50 мкм, обработанного на трехвалковой мельнице, и заявили, что эта проводимость составляет три порядка. выше, чем у композита с той же концентрацией и типом ЗНЧ, но полученного с помощью обработки ультразвуком в сочетании со сдвиговым перемешиванием. Хуанг и др. [17] получили композиты эпоксид/ЗНЧ, обработанные ультразвуком, и им пришлось увеличить концентрацию ЗНЧ (5 мкм) до 15 мас.%, чтобы получить аналогичное значение проводимости около 2 × 10 −3 См/м. В настоящем исследовании при использовании трехвалковой мельницы и 25 мас. % ЗНЧ размером 15 мкм была достигнута проводимость 1,6 × 10 -1 См/м, что лучше проводимости (около 10 – 2 См/м), наблюдаемый Huang et al. для композита, обработанного ультразвуком с той же концентрацией ЗНЧ, размером 5 мкм. С другой стороны, в настоящем исследовании порог перколяции наблюдался при концентрации ЗНЧ, значительно превышающей ту, о которой сообщают Chandrasekaran et al.
[39] получили проводимость 1,8 × 10 −3 См/м для композита эпоксид/ЗНЧ с 1 мас.% ЗНЧ размером 20–50 мкм, обработанного на трехвалковой мельнице, и заявили, что эта проводимость составляет три порядка. выше, чем у композита с той же концентрацией и типом ЗНЧ, но полученного с помощью обработки ультразвуком в сочетании со сдвиговым перемешиванием. Хуанг и др. [17] получили композиты эпоксид/ЗНЧ, обработанные ультразвуком, и им пришлось увеличить концентрацию ЗНЧ (5 мкм) до 15 мас.%, чтобы получить аналогичное значение проводимости около 2 × 10 −3 См/м. В настоящем исследовании при использовании трехвалковой мельницы и 25 мас. % ЗНЧ размером 15 мкм была достигнута проводимость 1,6 × 10 -1 См/м, что лучше проводимости (около 10 – 2 См/м), наблюдаемый Huang et al. для композита, обработанного ультразвуком с той же концентрацией ЗНЧ, размером 5 мкм. С другой стороны, в настоящем исследовании порог перколяции наблюдался при концентрации ЗНЧ, значительно превышающей ту, о которой сообщают Chandrasekaran et al. [39], что можно объяснить разным видом используемых ЗНЧ (размером и возможным наличием дефектов у данного наполнителя).
[39], что можно объяснить разным видом используемых ЗНЧ (размером и возможным наличием дефектов у данного наполнителя).
Комбинация наполнителей с различным соотношением размеров (МУНТ + ЗНП и МУНТ + графит) привела к синергетическому эффекту, как показано на рис.
Открыть в отдельном окне
Синергетическое влияние комбинации наполнителей на электропроводность гибридных композитов.
показывает, что простым добавлением 1 мас. % ЗНЧ к композиту, содержащему 0,1 мас. % УНТ, можно превысить порог перколяции и получить заметные значения электропроводности (1,2 × 10 −3 См/м.) Тем не менее, графит был менее эффективен, чем ЗНЧ, поскольку добавление 1 мас. % этого наполнителя к системе эпоксид-0,1 мас. % УНТ приводило к электропроводности 3,57 × 10 только −5 См/м; дальнейшее улучшение электропроводности было достигнуто при добавлении 2 мас.% графита. Во всех случаях порог перколяции для гибридных композитов достигался при содержании УНТ вдвое меньше необходимого для порога перколяции, наблюдаемого при использовании одних УНТ, причем он достигался при содержании ЗНЧ или графита около 2–3 %. % количества этих наполнителей, необходимых для достижения порога перколяции, когда они одни. Синергетический эффект можно наблюдать и при добавлении ЗНЧ или графита в композит эпоксид/УНТ, содержащий 0,05 мас. % УНТ. В этом последнем случае хорошая проводимость достигалась при добавлении 2 мас.% ЗНЧ или графита. С другой стороны, дальнейшие добавки ЗНЧ или графита (более 1 мас. % или 2 мас. % соответственно) к композитам, содержащим 0,1 мас. % или 0,05 мас. % УНТ, не приводили к заметному увеличению электропроводности. На самом деле, например, незначительное увеличение электропроводности наблюдалось при повышении содержания НЧЗ или графита до 5 мас.%. Этот результат, по-видимому, проливает свет на основную роль УНТ и предполагает, что синергетический эффект может быть достигнут, как только будет достигнуто правильное соотношение между концентрацией УНТ и другими наполнителями. Кроме того, было обнаружено, что более удобное соотношение между УНТ и вторым наполнителем зависит от фактической концентрации УНТ.
% количества этих наполнителей, необходимых для достижения порога перколяции, когда они одни. Синергетический эффект можно наблюдать и при добавлении ЗНЧ или графита в композит эпоксид/УНТ, содержащий 0,05 мас. % УНТ. В этом последнем случае хорошая проводимость достигалась при добавлении 2 мас.% ЗНЧ или графита. С другой стороны, дальнейшие добавки ЗНЧ или графита (более 1 мас. % или 2 мас. % соответственно) к композитам, содержащим 0,1 мас. % или 0,05 мас. % УНТ, не приводили к заметному увеличению электропроводности. На самом деле, например, незначительное увеличение электропроводности наблюдалось при повышении содержания НЧЗ или графита до 5 мас.%. Этот результат, по-видимому, проливает свет на основную роль УНТ и предполагает, что синергетический эффект может быть достигнут, как только будет достигнуто правильное соотношение между концентрацией УНТ и другими наполнителями. Кроме того, было обнаружено, что более удобное соотношение между УНТ и вторым наполнителем зависит от фактической концентрации УНТ. Массовое соотношение УНТ и ЗНЧ или графита 1:10 приводило к наилучшей проводимости при содержании УНТ 0,1 мас.%, в то время как наилучшее соотношение увеличивалось до 1:40 при снижении содержания УНТ до 0,05 мас.%.
Массовое соотношение УНТ и ЗНЧ или графита 1:10 приводило к наилучшей проводимости при содержании УНТ 0,1 мас.%, в то время как наилучшее соотношение увеличивалось до 1:40 при снижении содержания УНТ до 0,05 мас.%.
Принятие трехвалковой мельницы для дисперсии наполнителя кажется более удобным, чем обработка ультразвуком или одновременное перемешивание и обработка ультразвуком также при обработке гибридных композитов эпоксидная смола-МУНТ-ЗНП. Гибридный композит с 0,1 мас. % УНТ (0,067 об. %) плюс 1 мас. % ЗНЧ (0,58 об. %) показал лучшую электропроводность (1,2 × 10 −3 См/м), чем аналогичный материал, обработанный перемешивание и обработка ультразвуком (10 -5 См/м) и содержащие 1,6 мас.% УНТ плюс 0,4 мас.% ЗНЧ [18]. Электропроводность, полученная в настоящем исследовании для этого композита, была не слишком далека от наблюдаемой для композита, обработанного ультразвуком, с гораздо более высоким содержанием наполнителя (2 × 10 -2 См/м, полученный при использовании 5 об. % УНТ плюс 5 об. % ЗНЧ) [17]. Также в случае гибридных композитов с УНТ и графита, полученных на трехвалковой мельнице, результаты соответствовали результатам, полученным для аналогичных материалов с перемешиванием сдвигом [19].
% УНТ плюс 5 об. % ЗНЧ) [17]. Также в случае гибридных композитов с УНТ и графита, полученных на трехвалковой мельнице, результаты соответствовали результатам, полученным для аналогичных материалов с перемешиванием сдвигом [19].
Было предложено и широко используется для объяснения их электрического поведения общее уравнение для прогнозирования образования проводящей сетки в гибридных композитных системах (содержащих УНТ и другой углеродный наполнитель) [2]:
VCNTsφCNts+Vcfφcf=1
(1)
В уравнении (1) VCNTs и φCNts представляют собой, соответственно, фактическую объемную долю УНТ в гибридном композите и объемную долю, необходимую для достижения порога перколяции, когда УНТ используются отдельно (не гибридные композиты). Точно так же Vcf и φcf имеют такое же значение, но относятся ко второму углеродсодержащему наполнителю. Было высказано предположение, что когда два проводящих наполнителя объединяются друг с другом с образованием проводящей сети, значение уравнения становится равным или выше единицы, как только достигается или превышается порог перколяции. В соответствии с этим уравнением два наполнителя совместно создают проводящую сеть аддитивным образом. Для исследуемых гибридных композитов мы рассчитали первый член этого уравнения для объемных долей наполнителей, необходимых для достижения порога перколяции: 6,7 × 10 -4 объемной доли (0,1 мас. %) УНТ в сочетании с 0,29 × 10 -2 объемной доли (0,5 мас. %) ЗНЧ или 0,26 × 10 -2 объемной доли (0,5 мас. %) графит соответственно. Удалось убедиться, что первый член уравнения на пороге перколяции гибридных композитов принимает значения около 0,5. В случае исследуемых композитов, содержащих только 0,05 мас. % УНТ и содержащих дополнительные нагрузки 0,6 мас. % ЗНЧ или 1,5 мас. % графита, необходимые для достижения порога перколяции, первый член уравнения стало 0,3. Тогда в этих композитах вклад двух наполнителей в достижение порога перколяции был более чем аддитивным, что наглядно демонстрирует их синергетическое взаимодействие. Этот синергетический эффект можно наблюдать при очень низкой общей загрузке наполнителей и при использовании различных соотношений УНТ/второй наполнитель.
В соответствии с этим уравнением два наполнителя совместно создают проводящую сеть аддитивным образом. Для исследуемых гибридных композитов мы рассчитали первый член этого уравнения для объемных долей наполнителей, необходимых для достижения порога перколяции: 6,7 × 10 -4 объемной доли (0,1 мас. %) УНТ в сочетании с 0,29 × 10 -2 объемной доли (0,5 мас. %) ЗНЧ или 0,26 × 10 -2 объемной доли (0,5 мас. %) графит соответственно. Удалось убедиться, что первый член уравнения на пороге перколяции гибридных композитов принимает значения около 0,5. В случае исследуемых композитов, содержащих только 0,05 мас. % УНТ и содержащих дополнительные нагрузки 0,6 мас. % ЗНЧ или 1,5 мас. % графита, необходимые для достижения порога перколяции, первый член уравнения стало 0,3. Тогда в этих композитах вклад двух наполнителей в достижение порога перколяции был более чем аддитивным, что наглядно демонстрирует их синергетическое взаимодействие. Этот синергетический эффект можно наблюдать при очень низкой общей загрузке наполнителей и при использовании различных соотношений УНТ/второй наполнитель.
3.4. Теплопроводность
Теплопроводность композитов, содержащих один наполнитель, а также теплопроводность, обнаруженная для гибридных композитов, представлена в . сравнивается влияние увеличения концентрации УНТ, ЗНЧ и графита на теплопроводность.
Открыть в отдельном окне
Влияние содержания наполнителя на теплопроводность композитов.
Таблица 4
Теплопроводность двухкомпонентных и гибридных (трехкомпонентных) композитов на эпоксидной основе.
| Sample Composition (wt.%) | Thermal Conductivity (W/(m·K) ± SD) | |||
|---|---|---|---|---|
| MWCNT | GNP | Graphite | Epoxy | |
| 0 | – | – | 100 | 0. 130 ± 0.004 130 ± 0.004 |
| 0.1 | – | – | remainder | 0.218 ± 0.002 |
| 0.2 | – | – | remainder | 0.221 ± 0.002 |
| 0.3 | – | – | remainder | 0. 227 ± 0.001 227 ± 0.001 |
| 0.4 | – | – | remainder | 0.229 ± 0.001 |
| 0.5 | – | – | remainder | 0.228 ± 0.001 |
| 1.0 | – | – | remainder | 0. 242 ± 0.001 242 ± 0.001 |
| – | 0.5 | – | remainder | 0.181 ± 0.003 |
| – | 1.0 | – | remainder | 0.325 ± 0.004 |
| – | 3.0 | – | remainder | 0392 ± 0. 006 006 |
| – | 5.0 | – | remainder | 0.472 ± 0.004 |
| – | 6.0 | – | remainder | 0.541 ± 0.004 |
| – | 10.0 | – | remainder | 0. 676 ± 0.007 676 ± 0.007 |
| – | 15.0 | – | remainder | 1.129 ± 0.010 |
| – | 20.0 | – | remainder | 1.511 ± 0.017 |
| – | 25.0 | – | remainder | 1. 960 ± 0.022 960 ± 0.022 |
| – | 30.0 | – | remainder | 1.784 ± 0.027 |
| – | – | 1.0 | remainder | 0.234 ± 0.002 |
| – | – | 2.0 | remainder | 0. 253 ± 0.001 253 ± 0.001 |
| – | – | 5.0 | remainder | 0.294 ± 0.002 |
| – | – | 10.0 | remainder | 0.365 ± 0.003 |
| – | – | 15.0 | remainder | 0. 428 ± 0.001 428 ± 0.001 |
| – | – | 20.0 | remainder | 0.552 ± 0.002 |
| – | – | 30.0 | remainder | 0.880 ± 0.008 |
| – | – | 40.0 | remainder | 0. 992 ± 0.015 992 ± 0.015 |
| – | – | 45.0 | remainder | 1.331 ± 0.001 |
| 0.1 | 1.0 | – | remainder | 0.231 ± 0.006 |
| 0.1 | 2.0 | – | remainder | 0. 314 ± 0.004 314 ± 0.004 |
| 0.1 | 5.0 | – | remainder | 0.467 ± 0.004 |
| 0.1 | – | 1.0 | remainder | 0.244 ± 0.002 |
| 0.1 | – | 2.0 | remainder | 0. 282 ± 0.002 282 ± 0.002 |
| 0.1 | – | 5.0 | remainder | 0.251 ± 0.001 |
| 0.05 | 1.0 | – | remainder | 0.280 ± 0.004 |
| 0.05 | 2.0 | – | remainder | 0. 280 ± 0.004 280 ± 0.004 |
| 0.05 | 5.0 | – | remainder | 0.475 ± 0.005 |
| 0.05 | – | 1.0 | remainder | 0.218 ± 0.002 |
| 0.05 | – | 2. 0 0 | remainder | 0.218 ± 0.002 |
| 0.05 | – | 5.0 | remainder | 0.270 ± 0.001 |
Open in a separate window
Увеличение концентрации УНТ с 0,1 мас.% до 1 мас.% привело к увеличению теплопроводности только на 11%, в то время как такое же увеличение концентрации УНТ вызвало увеличение электропроводности на восемь порядков. Поэтому УНТ по-разному влияли на электрическую и теплопроводность. Ограниченное влияние на теплопроводность при добавлении УНТ до 1 мас.% (0,67 об.%) согласуется с литературными данными, которые также показывают слабое влияние на теплопроводность пути обработки. Например, Gojny et al. [40] измерили теплопроводность 0,252 Вт/(м·К) на композите эпоксидной смолы с 0,3 об.% МУНТ, обработанном на трехвалковой мельнице, в то время как Yang et al. [30] обработали ультразвуком эпоксидную смолу-1 вес.% MWCNT, получив значение проводимости 0,211 Вт/(м·K). Представляется, что значение теплопроводности композитов, содержащих УНТ, существенно не зависит от метода обработки, вызывающего или не вызывающего выравнивание нанотрубок. На самом деле способность УНТ улучшать теплопроводность (которая потенциально очень высока из-за их собственной проводимости) сильно ограничена их огромной площадью поверхности, а затем сильным граничным рассеянием фононов, возникающим на границе раздела с матрицей. С другой стороны, межфазное сопротивление можно снизить за счет правильной функционализации УНТ [11].
Например, Gojny et al. [40] измерили теплопроводность 0,252 Вт/(м·К) на композите эпоксидной смолы с 0,3 об.% МУНТ, обработанном на трехвалковой мельнице, в то время как Yang et al. [30] обработали ультразвуком эпоксидную смолу-1 вес.% MWCNT, получив значение проводимости 0,211 Вт/(м·K). Представляется, что значение теплопроводности композитов, содержащих УНТ, существенно не зависит от метода обработки, вызывающего или не вызывающего выравнивание нанотрубок. На самом деле способность УНТ улучшать теплопроводность (которая потенциально очень высока из-за их собственной проводимости) сильно ограничена их огромной площадью поверхности, а затем сильным граничным рассеянием фононов, возникающим на границе раздела с матрицей. С другой стороны, межфазное сопротивление можно снизить за счет правильной функционализации УНТ [11].
Теплопроводность заметно увеличилась, примерно линейно, с увеличением концентрации как ЗНЧ, так и графита, но ЗНЧ позволили более быстро улучшить проводимость. Например, добавление 30 мас.% наполнителя к эпоксидной смоле привело к проводимости 1,78 Вт/(м·К) и 0,88 Вт/(м·К) при использовании ЗНЧ или графита соответственно. Аналогичные результаты должны наблюдаться при добавлении в эпоксидную матрицу одинаковых объемных долей ЗНЧ и графита, поскольку эти два наполнителя имеют очень близкие плотности. Затем проводимость улучшилась по отношению к чистой эпоксидной матрице (теплопроводность 0,13 Вт/(м·К) [28]) примерно на 1270 % или 570 % соответственно при использовании в качестве наполнителей 30 мас. % ЗНЧ или графита. Эта заметная разница ожидалась на основании очень разной теплопроводности ЗНЧ (от 400 до 5000 Вт/(м·К) [10,13]) и графита (298 Вт/(м·К) на графитовых плоскостях, но 2,2 Вт/(м·К) в направлении, перпендикулярном графитовым плоскостям [11]). Однако влияние ЗНЧ зависит и от других параметров: размера и ориентации графеновых пластин, морфологии пластин и сопротивления интерфейсов с матрицей. Положительный эффект выравнивания GNP для теплопроводных приложений был рассмотрен Zhang et al.
Например, добавление 30 мас.% наполнителя к эпоксидной смоле привело к проводимости 1,78 Вт/(м·К) и 0,88 Вт/(м·К) при использовании ЗНЧ или графита соответственно. Аналогичные результаты должны наблюдаться при добавлении в эпоксидную матрицу одинаковых объемных долей ЗНЧ и графита, поскольку эти два наполнителя имеют очень близкие плотности. Затем проводимость улучшилась по отношению к чистой эпоксидной матрице (теплопроводность 0,13 Вт/(м·К) [28]) примерно на 1270 % или 570 % соответственно при использовании в качестве наполнителей 30 мас. % ЗНЧ или графита. Эта заметная разница ожидалась на основании очень разной теплопроводности ЗНЧ (от 400 до 5000 Вт/(м·К) [10,13]) и графита (298 Вт/(м·К) на графитовых плоскостях, но 2,2 Вт/(м·К) в направлении, перпендикулярном графитовым плоскостям [11]). Однако влияние ЗНЧ зависит и от других параметров: размера и ориентации графеновых пластин, морфологии пластин и сопротивления интерфейсов с матрицей. Положительный эффект выравнивания GNP для теплопроводных приложений был рассмотрен Zhang et al. [41]. Кроме того, на собственную теплопроводность ЗНЧ большое влияние оказывает наличие дефектов [41], а также размер пластинки. Фактически, согласно Raza et al. [21] проводимость композита на основе кремния с 25 мас. % ЗНЧ снижается с 3 Вт/(м·К) до 1,18 Вт/(м·К) при использовании пластин шириной 15 мкм и 5 мкм соответственно. Шен и др. [42] экстраполировали теплопроводность встроенных графеновых пластин различной длины и обнаружили, что проводимость снижается до нескольких сотен Вт/(м·К) при размере пластин менее 100 нм. С другой стороны, необходимо учитывать, что размеры ЗНП могут быть уменьшены при обработке композита, в частности при использовании высокоскоростного смесителя, тогда как трехвалковая мельница считается более щадящим методом диспергирования [22]. Показана важность сопротивления границы раздела с матрицей, учитывая, что собственная проводимость ЗНЧ может быть даже в 16 раз больше по сравнению с графитом. Кроме того, проводимость композитов, содержащих ЗНЧ, была примерно в два раза больше, чем при добавлении графита.
[41]. Кроме того, на собственную теплопроводность ЗНЧ большое влияние оказывает наличие дефектов [41], а также размер пластинки. Фактически, согласно Raza et al. [21] проводимость композита на основе кремния с 25 мас. % ЗНЧ снижается с 3 Вт/(м·К) до 1,18 Вт/(м·К) при использовании пластин шириной 15 мкм и 5 мкм соответственно. Шен и др. [42] экстраполировали теплопроводность встроенных графеновых пластин различной длины и обнаружили, что проводимость снижается до нескольких сотен Вт/(м·К) при размере пластин менее 100 нм. С другой стороны, необходимо учитывать, что размеры ЗНП могут быть уменьшены при обработке композита, в частности при использовании высокоскоростного смесителя, тогда как трехвалковая мельница считается более щадящим методом диспергирования [22]. Показана важность сопротивления границы раздела с матрицей, учитывая, что собственная проводимость ЗНЧ может быть даже в 16 раз больше по сравнению с графитом. Кроме того, проводимость композитов, содержащих ЗНЧ, была примерно в два раза больше, чем при добавлении графита. Фактически добавление одной и той же массовой доли (или объемной доли) НЧЗ или графита приводит к очень разной степени поверхности раздела между наполнителем и матрицей. Поскольку удельная поверхность ЗНЧ намного выше, чем у графита, межфазное термическое сопротивление также должно быть намного выше при использовании ЗНЧ. Тогда более высокое межфазное термическое сопротивление ЗНЧ должно частично уравновешивать их превосходную внутреннюю теплопроводность.
Фактически добавление одной и той же массовой доли (или объемной доли) НЧЗ или графита приводит к очень разной степени поверхности раздела между наполнителем и матрицей. Поскольку удельная поверхность ЗНЧ намного выше, чем у графита, межфазное термическое сопротивление также должно быть намного выше при использовании ЗНЧ. Тогда более высокое межфазное термическое сопротивление ЗНЧ должно частично уравновешивать их превосходную внутреннюю теплопроводность.
Было выдвинуто предположение [13] об образовании проводящей сетки, когда концентрация ЗНЧ достигает порога, но показано, что теплопроводность прогрессивно увеличивается с увеличением концентрации ЗНЧ или графита, и ход этих кривых немного отличается от типичные S-образные кривые, характерные для явлений перколяции.
Было предложено несколько моделей для прогнозирования теплопроводности полимерных композитов, наполненных частицами или волокнами [16,43,44], но они не кажутся подходящими для описания поведения нанокомпозитов. Модель серии (правило смешения), которая в настоящее время применяется к композитам с непрерывными волокнами, может быть предварительно использована для композитов, содержащих выровненные УНТ выше порога просачивания. Однако эта модель сильно переоценивает составную проводимость из-за границ раздела между взаимосвязанными нанотрубками, а также из-за того, что не все нанотрубки образуют сеть. Параллельная модель, а также аналогичная модель Халпина-Цая могут быть использованы для прогнозирования проводимости композитов, содержащих нанопластинки. Однако хорошо известно, что физические свойства, рассчитанные по этим моделям, мало отличаются от свойств матрицы, особенно при содержании наполнителя менее 50 %, а добавление очень небольшого количества ЗНЧ заметно увеличивало теплопроводность. . Полутеоретическая модель Льюиса и Нильсена включает эффекты соотношения сторон и ориентации коротких волокон, поэтому она кажется адаптированной для композитов, содержащих УНТ.
Модель серии (правило смешения), которая в настоящее время применяется к композитам с непрерывными волокнами, может быть предварительно использована для композитов, содержащих выровненные УНТ выше порога просачивания. Однако эта модель сильно переоценивает составную проводимость из-за границ раздела между взаимосвязанными нанотрубками, а также из-за того, что не все нанотрубки образуют сеть. Параллельная модель, а также аналогичная модель Халпина-Цая могут быть использованы для прогнозирования проводимости композитов, содержащих нанопластинки. Однако хорошо известно, что физические свойства, рассчитанные по этим моделям, мало отличаются от свойств матрицы, особенно при содержании наполнителя менее 50 %, а добавление очень небольшого количества ЗНЧ заметно увеличивало теплопроводность. . Полутеоретическая модель Льюиса и Нильсена включает эффекты соотношения сторон и ориентации коротких волокон, поэтому она кажется адаптированной для композитов, содержащих УНТ.
Теплопроводность можно рассчитать по следующему уравнению (2):
λc=λm [1+A B Vf1−B Vf λfλm-1]; А=2 ЛД; B= λfλm−1λfλm−A; ψ=1+ (1−ΦmΦm2) Vf
(2)
где λ c , λ f , λ m – теплопроводности композита, наполнителя и матрицы; V f – объемная доля наполнителя; L и D — соответственно длина и диаметр УНТ; Φm — параметр, принятый равным 0,82 для ориентированных волокон, упакованных случайным образом.
Принимая теплопроводность МУНТ равной 1000 Вт/(м·К) (значительно ниже теоретической из-за влияния границ раздела с матрицей и возможного наличия дефектов), расчетная теплопроводность колеблется в пределах 0,157 Вт/(м·К). (м·К) и 0,396 Вт/(м·К) для композитов с концентрацией УНТ в диапазоне от 0,1 до 1 мас.%. Эти расчетные значения были аналогичны экспериментальным (тот же порядок величины), но согласно этой модели расчетная теплопроводность должна возрастать с концентрацией УНТ быстрее, чем экспериментальная. Однако следует учитывать, что увеличение пористости при загрузке наполнителя должно отрицательно сказаться на теплопроводности.
Напротив, модель Льюиса и Нильсена совершенно не пригодна для прогнозирования теплопроводности композитов с ЗНЧ, независимо от используемой для расчета теплопроводности ЗНЧ (тысяча или несколько сотен Вт/(м·К) )). Впрочем, в этом нет ничего удивительного, поскольку тромбоциты не могут влиять на проводимость так, как волокна или палочки.
В данной работе также исследовано возможное синергетическое влияние на теплопроводность наполнителей с различным соотношением сторон при добавлении возрастающего количества ЗНЧ или графита к композитам, содержащим 0,1 мас. % или 0,05 мас. % УНТ, диспергированных в эпоксидной смоле. матрица. Результаты изображены в .
% или 0,05 мас. % УНТ, диспергированных в эпоксидной смоле. матрица. Результаты изображены в .
Открыть в отдельном окне
Влияние комбинаций наполнителей на теплопроводность гибридных композитов.
При добавлении графита к композиту, содержащему 0,1 мас. % или 0,05 мас. % МУНТ, теплопроводность не увеличивалась, но эти гибридные композиты показали проводимость даже ниже, чем композиты, содержащие такую же концентрацию только графита. Наоборот, комбинация УНТ и ЗНЧ приводила к повышенной теплопроводности по сравнению с композитами, содержащими ту же концентрацию МУНТ (0,1 мас. % или 0,05 мас. %). Однако использование только ЗНЧ в качестве наполнителя (от 1 мас.% до 5 мас.%) обеспечило лучшую или аналогичную проводимость по сравнению с гибридными композитами, содержащими ту же концентрацию ЗНЧ и очень малые количества МУНТ (0,1 мас.%). или 0,05 мас.%). Таким образом, гибридные композиты не продемонстрировали улучшения теплопроводности по сравнению с композитами, содержащими только один наполнитель (а именно, ЗНЧ или графит). В настоящем исследовании не наблюдалось ни синергетического, ни аддитивного эффекта между двумя филлерами. Тем не менее, метод трехвалковой мельницы позволил производить гибридные композиты с лучшей проводимостью по сравнению с аналогичными материалами, обработанными ультразвуком. Например, гибридные композиты с 0,1 мас. % УНТ + 1 мас. % ЗНЧ или 0,1 мас. % УНТ + 5 мас. % ЗНЧ показали теплопроводность 0,23 Вт/(м·К) и 0,47 Вт/(м·К). ), соответственно, в то время как литературные отчеты для композитов, обработанных ультразвуком, показали проводимость 0,19Вт/(м·К) с 0,1 мас.% УНТ + 0,9 мас.% ЗНЧ [19] и 1,5 Вт/(м·К) с 5 об.% УНТ + 5 об.% ЗНЧ [17].
В настоящем исследовании не наблюдалось ни синергетического, ни аддитивного эффекта между двумя филлерами. Тем не менее, метод трехвалковой мельницы позволил производить гибридные композиты с лучшей проводимостью по сравнению с аналогичными материалами, обработанными ультразвуком. Например, гибридные композиты с 0,1 мас. % УНТ + 1 мас. % ЗНЧ или 0,1 мас. % УНТ + 5 мас. % ЗНЧ показали теплопроводность 0,23 Вт/(м·К) и 0,47 Вт/(м·К). ), соответственно, в то время как литературные отчеты для композитов, обработанных ультразвуком, показали проводимость 0,19Вт/(м·К) с 0,1 мас.% УНТ + 0,9 мас.% ЗНЧ [19] и 1,5 Вт/(м·К) с 5 об.% УНТ + 5 об.% ЗНЧ [17].
В литературе имеются противоречивые данные о синергетическом действии нанонаполнителей на теплопроводность. По мнению некоторых авторов, синергетический эффект между УНТ и ЗНЧ наблюдается только при суммарной концентрации наполнителей более 10 об.% [17] или при меньшей концентрации наполнителя (например, 1 мас.%) при использовании функционализированных УНТ [19]. ]. Напротив, согласно Paszkiewicz et al. [35], в широком диапазоне суммарных концентраций этих наполнителей (от 3 до 20 мас. %) синергетического эффекта не наблюдается.
]. Напротив, согласно Paszkiewicz et al. [35], в широком диапазоне суммарных концентраций этих наполнителей (от 3 до 20 мас. %) синергетического эффекта не наблюдается.
Вероятно, положительное влияние на теплопроводность, обеспечиваемое непрерывной сеткой между наполнителями с разным соотношением размеров, может быть перевесено пагубными явлениями, возникающими из-за сильного сопротивления границ раздела наполнитель/матрица и УНТ/ЗНП. Более того, пористость композита, которая, скорее всего, является следствием сложности обработки смесей наполнитель/матрица, обладающих высокой вязкостью, сильно снижает теплопроводность композитов на полимерной основе.
Метод каландрирования позволяет получать композиты с углеродсодержащим наполнителем, гомогенно диспергированным в эпоксидной матрице. Проводимость этих композитов была повышена за счет оптимизации параметров обработки.
Заметное улучшение электропроводности было достигнуто за счет образования проводящей сетки, как только загрузка наполнителя достигла порога перколяции. На механизм теплопроводности в основном не влияло образование перколяционных путей.
На механизм теплопроводности в основном не влияло образование перколяционных путей.
Углеродные нанотрубки оказались более эффективными, чем графеновые нанопластинки, для повышения электропроводности, в то время как графеновые нанопластинки показали лучшие результаты, чем углеродные нанотрубки, для улучшения теплопроводности.
Гибридные композиты, содержащие очень низкие концентрации двух наполнителей с разным соотношением размеров (в основном УНТ и ЗНЧ), показали электрическую проводимость на шесть порядков выше, чем чистая матрица. Такое поведение было связано с предпочтительной ориентацией наполнителей, вызванной каландрированием, что привело к синергетическому эффекту, способному снизить порог перколяции.
Такого синергетического эффекта для теплопроводности не наблюдалось, так как в этом случае не возникало преимущества от комбинации разных наполнителей. Термическое сопротивление границ между наполнителем и матрицей и между частицами наполнителя, а также размер частиц наполнителя определяют тепловой поток.
Концептуализация, A.C. и CB; курирование данных, Е.П. и М.П.; расследование, AC и MP; надзор, CB; написание – первоначальный вариант, КБ; написание – обзор и редактирование, CB и EP
Это исследование не получило внешнего финансирования.
Авторы заявляют об отсутствии конфликта интересов.
1. Фэн Л., Се Н., Чжун Дж. Углеродные нановолокна и их композиты: обзор синтеза, свойств и применения. Материалы. 2014;7:3919–3945. дои: 10.3390/ma7053919. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
2. Szeluga U., Kumanek B., Trzebicka B. Синергия в гибридных композитах полимер/наноуглерод. Обзор. Композиции Часть А Прил. науч. Произв. 2015;73:204–231. doi: 10.1016/j.compositesa.2015.02.021. [CrossRef] [Google Scholar]
3. Мохан В.Б., Лау К.-Т., Хуэй Д., Бхаттачарья Д. Материалы на основе графена и их композиты: обзор производства, применения и ограничений продукта. Композиции Часть Б англ. 2018;142:200–220. doi: 10.1016/j.compositesb. 2018.01.013. [Перекрестная ссылка] [Академия Google]
2018.01.013. [Перекрестная ссылка] [Академия Google]
4. Тостенсон Э.Т., Рен З., Чоу Т.-В. Достижения в области науки и техники углеродных нанотрубок и их композитов: обзор. Композиции науч. Технол. 2001; 61: 1899–1912. doi: 10.1016/S0266-3538(01)00094-X. [CrossRef] [Google Scholar]
5. Вонг Э.В., Шихан П.Е., Либер К.М. Механика нанолучей: эластичность, прочность и ударная вязкость наностержней и нанотрубок. Наука. 1997; 277:1971–1975. doi: 10.1126/science.277.5334.1971. [CrossRef] [Google Scholar]
6. Ю М.-Ф., Лурье О., Дайер М.Дж., Молони К., Келли Т.Ф., Руофф Р.С. Прочность и механизм разрушения многостенных углеродных нанотрубок при растягивающей нагрузке. Наука. 2000; 287: 637–640. doi: 10.1126/science.287.5453.637. [PubMed] [CrossRef] [Академия Google]
7. Ю М.-Ф., Файлов Б.С., Арепалли С., Руофф Р.С. Растягивающее нагружение канатов из одностенных углеродных нанотрубок и их механические свойства. физ. Преподобный Летт. 2000; 84: 5552–5555. doi: 10. 1103/PhysRevLett.84.5552. [PubMed] [CrossRef] [Google Scholar]
1103/PhysRevLett.84.5552. [PubMed] [CrossRef] [Google Scholar]
8. Bizao R.A., Botari T., Galvao DS. Материалы симпозиума Общества исследования материалов. Том 1658. Общество исследования материалов; Уоррендейл, Пенсильвания, США: 2014. Механические свойства графеновых нановигглов; стр. 14–18. [Академия Google]
9. Лю Ф., Мин П., Ли Дж. Ab initio расчет идеальной прочности и фононной нестабильности графена при растяжении. физ. Ред. Б. 2007; 76:064120. doi: 10.1103/PhysRevB.76.064120. [CrossRef] [Google Scholar]
10. Лю С., Чевали В.С., Сюй З., Хуэй Д., Ван Х. Обзор расширения характеристик эпоксидных смол с использованием углеродных наноматериалов. Композиции Часть Б англ. 2017; 136:197–214. doi: 10.1016/j.compositesb.2017.08.020. [CrossRef] [Google Scholar]
11. Имтиаз С., Сиддик М., Каусар А., Мунта С.Т., Амбрин Дж., Биби И. Обзор производства, свойств и применения углеродных нанотрубок (УНТ), армированных полимером и эпоксидные нанокомпозиты. Подбородок. Дж. Полим. науч. Часть А. 2017; 36:1–17. doi: 10.1007/s10118-018-2045-7. [Перекрестная ссылка] [Академия Google]
Дж. Полим. науч. Часть А. 2017; 36:1–17. doi: 10.1007/s10118-018-2045-7. [Перекрестная ссылка] [Академия Google]
12. Баландин А.А., Гош С., Бао В., Кализо И., Тевелдебрхан Д., Мяо Ф., Лау С.Н. Превосходная теплопроводность однослойного графена. Нано Летт. 2008; 8: 902–907. doi: 10.1021/nl0731872. [PubMed] [CrossRef] [Google Scholar]
13. Li A., Zhang C., Zhang Y.F. Теплопроводность графен-полимерных композитов: механизмы, свойства и приложения. Полимеры. 2017;9:437. [Бесплатная статья PMC] [PubMed] [Google Scholar]
14. Куманек Б., Янас Д. Теплопроводность сетей углеродных нанотрубок: обзор. Дж. Матер. науч. 2019;54:7397–7427. doi: 10.1007/s10853-019-03368-0. [CrossRef] [Google Scholar]
15. Малекпур Х., Рамнани П., Сринивасан С., Баласубраманян Г., Ника Д.Л., Мулчандани А., Лейк Р.К., Баландин А.А. Теплопроводность графена с дефектами, индуцированными облучением электронным пучком. Наномасштаб. 2016;8:14608–14616. doi: 10.1039/C6NR03470E. [PubMed] [CrossRef] [Google Scholar]
16. Yang X., Liang C., Ma T., Guo Y., Kong J., Gu J., Chen M., Zhu J. Обзор теплопроводных материалов. полимерные композиты: классификация, измерение, модель и уравнения, механизм и методы изготовления. Доп. Композиции Гибридный мат. 2018;1:207–230. doi: 10.1007/s42114-018-0031-8. [Перекрестная ссылка] [Академия Google]
Yang X., Liang C., Ma T., Guo Y., Kong J., Gu J., Chen M., Zhu J. Обзор теплопроводных материалов. полимерные композиты: классификация, измерение, модель и уравнения, механизм и методы изготовления. Доп. Композиции Гибридный мат. 2018;1:207–230. doi: 10.1007/s42114-018-0031-8. [Перекрестная ссылка] [Академия Google]
17. Huang X., Zhi C., Jiang P. На пути к эффективному синергетическому эффекту графеновых нанопластинок и углеродных нанотрубок на теплопроводность наноуглеродных эпоксидных композитов со сверхвысокой объемной долей. Дж. Физ. хим. С. 2012;116:23812–23820. doi: 10.1021/jp308556r. [CrossRef] [Google Scholar]
18. Лян Ю., Голамерза П., Сейед А., Ика М. Эпоксидные композиты с углеродными нанотрубками и графеновыми нанопластинками — диспергирование и синергетические эффекты. Углерод. 2014; 78: 268–278. doi: 10.1016/j.carbon.2014.08.065. [Перекрестная ссылка] [Академия Google]
19. Ма П.-К., Лю М.-Ю., Чжан Х., Ван С., Ван Р., Ван К., Вонг Ю.-К., Тан Б.-З. , Хонг С. .-Х., Пайк К.-В. и др. Повышенная электропроводность нанокомпозитов, содержащих гибридные наполнители из углеродных нанотрубок и технического углерода. Приложение ACS Матер. Интерфейсы. 2009; 1:1090–1096. doi: 10.1021/am
, Хонг С. .-Х., Пайк К.-В. и др. Повышенная электропроводность нанокомпозитов, содержащих гибридные наполнители из углеродных нанотрубок и технического углерода. Приложение ACS Матер. Интерфейсы. 2009; 1:1090–1096. doi: 10.1021/am
20. Chapartegui M., Markaide N., Florez S., Elizetxea C., Fernandez M., Santamaría A. Специфические реологические и электрические характеристики дисперсий углеродных нанотрубок в эпоксидной матрице. . Композиции науч. Технол. 2010;70:879–884. doi: 10.1016/j.compscitech.2010.02.008. [CrossRef] [Google Scholar]
21. Раза М.А., Вествуд А.В.К., Браун А.П., Стирлинг С. Текстура, транспорт и механические свойства композитов графитовые нанопластинки/силикон, полученные на трехвалковой мельнице. Композиции науч. Технол. 2012; 72: 467–475. doi: 10.1016/j.compscitech.2011.12.010. [CrossRef] [Google Scholar]
22. Пролонго С.Г., Хименес-Суарес А., Мориче Р., Уренья А. Обработка на месте эпоксидных композитов, армированных графеновыми нанопластинками. Композиции науч. Технол. 2013; 86: 185–191. doi: 10.1016/j.compscitech.2013.06.020. [CrossRef] [Google Scholar]
Композиции науч. Технол. 2013; 86: 185–191. doi: 10.1016/j.compscitech.2013.06.020. [CrossRef] [Google Scholar]
23. Ахмади-Могадам Б., Шарафимасулех М., Шадлоу С., Тахери Ф. Влияние функционализации графеновых нанопластинок на механический отклик графен/эпоксидных композитов. Матер. Дес. 2015;66:142–149. doi: 10.1016/j.matdes.2014.10.047. [CrossRef] [Google Scholar]
24. Du J.H., Bai J., Cheng H.M. Современное состояние и основные проблемы полимерных композитов на основе углеродных нанотрубок. Экспресс Полим. лат. 2007; 1: 253–273. doi: 10.3144/expresspolymlett.2007.39. [CrossRef] [Google Scholar]
25. Гох П.С., Исмаил А.Ф., Нг Б.К. Направленное выравнивание углеродных нанотрубок в полимерных матрицах: современные подходы и будущие достижения. Композиции Часть А Прил. науч. Произв. 2014;56:103–126. doi: 10.1016/j.compositesa.2013.10.001. [CrossRef] [Google Scholar]
26. Чой Э.С., Брукс Дж.С., Итон Д.Л., Аль-Хайк М.С., Хуссайни М.Ю., Гарместани Х., Ли Д. , Дамен К. Улучшение тепловых и электрических свойств полимерных композитов из углеродных нанотрубок обработкой магнитным полем. Дж. Заявл. физ. 2003;94:6034–6039. дои: 10.1063/1.1616638. [CrossRef] [Google Scholar]
, Дамен К. Улучшение тепловых и электрических свойств полимерных композитов из углеродных нанотрубок обработкой магнитным полем. Дж. Заявл. физ. 2003;94:6034–6039. дои: 10.1063/1.1616638. [CrossRef] [Google Scholar]
27. Zhang H., Zhang G., Tang M., Zhou L., Li J., Fan X., Shi X., Qin J. Синергетический эффект углеродных нанотрубок и графеновых нанопластин о свойствах защиты от механических, электрических и электромагнитных помех полимерных композитов и полимерных композитных пен. хим. англ. Дж. 2018; 353:381–393. doi: 10.1016/j.cej.2018.07.144. [CrossRef] [Google Scholar]
28. Чаттерджи С., Нафезарефи Ф., Тай Н.Х., Шлагенхауф Л., Нюеш Ф.А., Чу Б.Т.Т. Размер и синергетическое влияние гибридов нанонаполнителей, включая графеновые нанопластинки и углеродные нанотрубки, на механические свойства эпоксидных композитов. Углерод. 2012;50:5380–5386. doi: 10.1016/j.carbon.2012.07.021. [Перекрестная ссылка] [Академия Google]
29. Li W., Dichiara A., Bai J. Гибриды углеродных нанотрубок и графеновых нанопластинок в качестве высокоэффективных многофункциональных армирующих материалов в эпоксидных композитах. Композиции науч. Технол. 2013; 74: 221–227. doi: 10.1016/j.compscitech.2012.11.015. [CrossRef] [Google Scholar]
Композиции науч. Технол. 2013; 74: 221–227. doi: 10.1016/j.compscitech.2012.11.015. [CrossRef] [Google Scholar]
30. Ян С.Ю., Линь В.Н., Хуан Ю.Л., Тьен Х.В., Ван Дж.Ю., Ма К.К.М., Ли С.М., Ван Ю.С. Синергетические эффекты графеновых пластинок и углеродных нанотрубок на механические и термические свойства эпоксидных композитов. Углерод. 2011;49: 793–803. doi: 10.1016/j.carbon.2010.10.014. [CrossRef] [Google Scholar]
31. Yu J., Choi H.K., Kim H.S., Kim S.Y. Синергетический эффект гибридных графеновых нанопластинок и наполнителей из многостенных углеродных нанотрубок на теплопроводность полимерных композитов и теоретическое моделирование синергетического эффекта. Композиции Часть А Прил. науч. Произв. 2016;88:79–85. doi: 10.1016/j.compositesa.2016.05.022. [CrossRef] [Google Scholar]
32. Eswaraiah V., Jyothirmayee Aravind S.S., Balasubramaniam K., Ramaprabhu S. Функционализированные графеном углеродные нанотрубки для проводящих полимерных нанокомпозитов и их улучшенные чувствительные к деформации свойства. макромол. хим. физ. 2013;214:2439–2444. doi: 10.1002/macp.201300242. [CrossRef] [Google Scholar]
макромол. хим. физ. 2013;214:2439–2444. doi: 10.1002/macp.201300242. [CrossRef] [Google Scholar]
33. Пашкевич С., Шимчик А., Суй Х.М., Вагнер Х.Д., Линарес А., Эскерра Т.А., Росланец З. Синергетический эффект одностенных углеродных нанотрубок (ОУНТ) и графеновых нанопластинок ( GNP) в электропроводящих гибридных нанокомпозитах ПТТ-блок-ПТМО, полученных полимеризацией in situ. Композиции науч. Технол. 2015; 118:72–77. doi: 10.1016/j.compscitech.2015.08.011. [CrossRef] [Google Scholar]
34. Cai W., Huang Y., Wang D., Liu C., Zhang Y. Пьезорезистивное поведение нанокомпозита графеновых нанопластинок/сажи/силиконового каучука. Дж. Заявл. Полим. науч. 2014; 131:1–6. doi: 10.1002/прил.39778. [CrossRef] [Google Scholar]
35. Пашкевич С., Шимчик А., Павликовска Д., Субоч Дж., Ценкер М., Маштак Р. Электро- и теплопроводные нанокомпозиты на основе полиэтилена низкой плотности, армированные МУНТ или Гибридные нанопластинки MWCNT/графена с улучшенной термоокислительной стабильностью. Наноматериалы. 2018;8:264. doi: 10.3390/nano8040264. [Статья бесплатно PMC] [PubMed] [CrossRef] [Google Scholar]
Наноматериалы. 2018;8:264. doi: 10.3390/nano8040264. [Статья бесплатно PMC] [PubMed] [CrossRef] [Google Scholar]
36. Майти С., Хатуа Б.Б. Графеновые нанопластины и многослойные углеродные нанотрубки, встроенные в гибридные композиты из поликарбоната: высокая защита от электромагнитных помех с низким порогом перколяции. Полим. Композиции 2016;37:2058–2069. doi: 10.1002/pc.23384. [CrossRef] [Google Scholar]
37. Wegrzyn M., Galindo B., Benedito A., Gimenez E. Морфология, тепловые и электрические свойства полипропиленовых гибридных композитов, совместно наполненных многостенными углеродными нанотрубками и графеновыми нанопластинками. Дж. Заявл. Полим. науч. 2015; 132:42793–42800. doi: 10.1002/app.42793. [CrossRef] [Google Scholar]
38. Taherian R. Экспериментальная и аналитическая модель электропроводности нанокомпозитов на основе полимеров. Композиции науч. Технол. 2016; 123:17–31. doi: 10.1016/j.compscitech.2015.11.029. [CrossRef] [Google Scholar]
39. Чандрасекаран С. , Зайдель С., Шульте К. Получение и характеристика графитовых нанопластин (GNP)/эпоксидных нанокомпозитов: механические, электрические и термические свойства. Евро. Полим. Дж. 2013;49:3878–3888. doi: 10.1016/j.eurpolymj.2013.10.008. [CrossRef] [Google Scholar]
, Зайдель С., Шульте К. Получение и характеристика графитовых нанопластин (GNP)/эпоксидных нанокомпозитов: механические, электрические и термические свойства. Евро. Полим. Дж. 2013;49:3878–3888. doi: 10.1016/j.eurpolymj.2013.10.008. [CrossRef] [Google Scholar]
40. Gojny F.H., Wichmann M.H.G., Fiedler B., Kinloch I.A., Bauhofer W., Windle A.H., Schulte K. Оценка и идентификация механизмов электро- и теплопроводности в углеродных нанотрубках/эпоксидных композитах. Полимер. 2006;47:2036–2045. doi: 10.1016/j.polymer.2006.01.029. [CrossRef] [Google Scholar]
41. Zhang Z., Qu J., Feng Y., Feng W. Сборка полимерных композитов, ориентированных на графен, для теплопроводных приложений. Композиции коммун. 2018;9:33–41. doi: 10.1016/j.coco.2018.04.009. [CrossRef] [Google Scholar]
42. Shen X., Wang Z., Wu Y., Liu X., He Y.B., Kim J.K. Многослойный графен обеспечивает более высокую эффективность улучшения теплопроводности графен/эпоксидных композитов. Нано Летт. 2016;16:3585–3593. doi: 10.1021/acs.nanolett.6b00722. [PubMed] [CrossRef] [Академия Google]
doi: 10.1021/acs.nanolett.6b00722. [PubMed] [CrossRef] [Академия Google]
43. Прогельхоф Р.К. Методы прогнозирования теплопроводности композитных систем: обзор. Полим. англ. науч. 1976; 76: 615–625. doi: 10.1002/pen.760160905. [CrossRef] [Google Scholar]
44. Кумлутас Д., Тавман И.Х. Численное и экспериментальное исследование теплопроводности полимерных композитов, наполненных частицами. Дж. Термопласт. Композиции Матер. 2006; 19: 441–455. doi: 10.1177/08
706062203. [CrossRef] [Google Scholar]Теплопроводность твердых тел и металлов
Теплопроводность твердых тел
Перенос тепловой энергии в твердых телах обычно может быть обусловлен двумя эффектами:
- миграцией свободных электронов
- колебательными волнами решетки (фононами)
- 90 тепловой энергии, приводящей к теплопроводности в твердом теле, теплопроводность может быть выражена как:
k = k e + k ph
Теплопроводность металлов
Металлы являются твердыми телами и поэтому обладают кристаллической структурой, в которой ионы (ядра с окружающими их оболочками остовных электронов) занимают трансляционно эквивалентные позиции в кристаллической решетке.
 Металлы, в целом, имеют высокую электропроводность , высокую теплопроводность и высокую плотность. Соответственно перенос тепловой энергии может быть обусловлен двумя эффектами:
Металлы, в целом, имеют высокую электропроводность , высокую теплопроводность и высокую плотность. Соответственно перенос тепловой энергии может быть обусловлен двумя эффектами:- миграцией свободных электронов
- решеточные колебательные волны (фононы).
Когда электроны и фононы переносят тепловую энергию, приводящую к теплопроводности в твердом теле, теплопроводность может быть выражена как: уникальной особенностью металлов является наличие носителей заряда, а именно электронов . Электрическая и теплопроводность металлов происходит от тот факт, что их внешних электронов делокализованы . Их вклад в теплопроводность называется электронной теплопроводностью , k e . Фактически, в чистых металлах, таких как золото, серебро, медь и алюминий, тепловой ток, связанный с потоком электронов, намного превышает небольшой вклад, обусловленный потоком фононов.
 Напротив, для сплавов вкладом k ph в k уже нельзя пренебречь.
Напротив, для сплавов вкладом k ph в k уже нельзя пренебречь.Закон Видемана-Франца – число Лоренца
При заданной температуре тепло- и электропроводность металлов пропорциональны , но повышение температуры увеличивает теплопроводность при уменьшении электропроводности. Это поведение количественно выражено в законе Видемана-Франца . Этот закон гласит, что отношение электронного вклада теплопроводности ( k ) в электропроводность (σ) металла пропорционально температуре (T).
Качественно эта взаимосвязь основана на переносе тепла и электричества с участием свободных электронов в металле. Электропроводность уменьшается с увеличением скорости частиц, потому что столкновения отклоняют электроны от поступательного переноса заряда. Однако теплопроводность увеличивается со средней скоростью частиц, увеличивая прямой перенос энергии.
 Закон Видемана-Франца обычно хорошо соблюдается при высоких температурах. Однако в области низких и промежуточных температур закон нарушается из-за неупругого рассеяния носителей заряда.
Закон Видемана-Франца обычно хорошо соблюдается при высоких температурах. Однако в области низких и промежуточных температур закон нарушается из-за неупругого рассеяния носителей заряда.Следует отметить, что общая корреляция между электрической и теплопроводностью не выполняется для других материалов из-за возросшей важности переносчиков фононов для тепла в неметаллах.
Теплопроводность неметаллов
Для твердых неметаллических тел , k определяется в первую очередь k ph , которая увеличивается по мере уменьшения частоты взаимодействий между атомами и решеткой. Решеточная теплопроводность является доминирующим механизмом теплопроводности в неметаллах, если не единственным. В твердых телах атомы колеблются вокруг своих положений равновесия (кристаллическая решетка). Колебания атомов не независимы друг от друга, а довольно сильно связаны с соседними атомами. Регулярность расположения решетки существенно влияет на k ph , с кристаллическими (хорошо упорядоченными) материалами, такими как кварц , имеющими более высокую теплопроводность, чем аморфные материалы, такие как стекло, при достаточно высоких температурах k ph ∝ 1/T.

квантов колебательного поля кристалла называются « фононами ». Фонон — это коллективное возбуждение в периодическом упругом расположении атомов или молекул в конденсированных веществах, таких как твердые тела и некоторые жидкости. Фононы играют важную роль во многих физических свойствах конденсированного вещества, таких как теплопроводность и электропроводность. Фактически, для кристаллических неметаллических твердых тел, таких как алмаз k ph может быть довольно большим, превышая значения k, связанные с хорошими проводниками, такими как алюминий. В частности, алмаз обладает самой высокой твердостью и теплопроводностью (k = 1000 Вт/м·К) среди всех объемных материалов.
Теплопроводность диоксида урана
Большинство PWR используют урановое топливо , которое находится в форме диоксида урана . Диоксид урана представляет собой полупроводниковое твердое вещество черного цвета с очень низкой теплопроводностью .
 С другой стороны, диоксид урана имеет очень высокая температура плавления и имеет хорошо известное поведение . UO2 прессуется в гранулы , которые затем спекаются в твердое тело.
С другой стороны, диоксид урана имеет очень высокая температура плавления и имеет хорошо известное поведение . UO2 прессуется в гранулы , которые затем спекаются в твердое тело.Эти таблетки затем загружаются и герметизируются внутри топливного стержня (или топливной шашки), изготовленного из сплавов циркония из-за их очень низкого поперечного сечения поглощения (в отличие от нержавеющей стали). Поверхность трубы, которая покрывает таблетки, называется оболочкой твэла . Топливные стержни являются основным элементом тепловыделяющей сборки.
Теплопроводность диоксида урана очень низкая по сравнению с металлическим ураном, нитридом урана, карбидом урана и циркониевым плакирующим материалом. Теплопроводность является одним из параметров, определяющих среднюю температуру топлива . Эта низкая теплопроводность может привести к локализованному перегреву в центральной линии топлива, поэтому этого перегрева следует избегать.
 Предотвращается перегрев топлива за счет поддержания установившегося пика линейная тепловая мощность (LHR) или Коэффициент горячего канала теплового потока – F Q (z) ниже уровня, при котором происходит плавление центральной линии топлива. Расширение топливной таблетки при расплавлении центральной линии может привести к тому, что таблетка создаст нагрузку на оболочку вплоть до разрушения.
Предотвращается перегрев топлива за счет поддержания установившегося пика линейная тепловая мощность (LHR) или Коэффициент горячего канала теплового потока – F Q (z) ниже уровня, при котором происходит плавление центральной линии топлива. Расширение топливной таблетки при расплавлении центральной линии может привести к тому, что таблетка создаст нагрузку на оболочку вплоть до разрушения.Теплопроводность твердого UO 2 с плотностью 95% оценивается по следующей зависимости [Клименко; Зорин]:
, где τ = T/1000. Неопределенность этой корреляции составляет +10% в диапазоне от 298,15 до 2000 К и +20% в диапазоне от 2000 до 3120 К. А.В. Клименко и В.М. Зорин. MEI Press, 2003.
Специальная ссылка: Теплофизические свойства материалов для ядерной энергетики: Учебное пособие и сбор данных. IAEA-THPH, МАГАТЭ, Вена, 2008 г. ISBN 978–92–0–106508–7.
Теплопроводность циркония
Цирконий представляет собой блестящий серо-белый прочный переходный металл, напоминающий гафний и, в меньшей степени, титан.
 Цирконий в основном используется в качестве огнеупора и глушителя, хотя небольшие количества используются в качестве легирующего агента для повышения коррозионной стойкости. Циркониевый сплав (например, Zr + 1% Nb) широко используется в качестве оболочки топлив ядерных реакторов. Желаемыми свойствами этих сплавов являются низкое сечение захвата нейтронов и коррозионная стойкость при нормальных условиях эксплуатации. Циркониевые сплавы имеют более низкую теплопроводность (около 18 Вт/м·К), чем чистый металлический цирконий (около 22 Вт/м·К).
Цирконий в основном используется в качестве огнеупора и глушителя, хотя небольшие количества используются в качестве легирующего агента для повышения коррозионной стойкости. Циркониевый сплав (например, Zr + 1% Nb) широко используется в качестве оболочки топлив ядерных реакторов. Желаемыми свойствами этих сплавов являются низкое сечение захвата нейтронов и коррозионная стойкость при нормальных условиях эксплуатации. Циркониевые сплавы имеют более низкую теплопроводность (около 18 Вт/м·К), чем чистый металлический цирконий (около 22 Вт/м·К).Специальный справочник: Теплофизические свойства материалов для ядерной энергетики: Учебное пособие и сбор данных. IAEA-THPH, МАГАТЭ, Вена, 2008 г. ISBN 978–92–0–106508–7.
Ссылки:
Теплопередача:
- Основы тепломассообмена, 7-е издание. Теодор Л. Бергман, Эдриенн С. Лавин, Фрэнк П. Инкропера. John Wiley & Sons, Incorporated, 2011.
 ISBN: 9781118137253.
ISBN: 9781118137253. - Тепломассообмен. Юнус А. Ценгель. McGraw-Hill Education, 2011. ISBN: 9780071077866.
- Основы тепломассообмена. CP Котандараман. New Age International, 2006, ISBN: 9788122417722.
- Министерство энергетики, термодинамики, теплопередачи и потока жидкости США. Справочник по основам Министерства энергетики США, том 2 из 3, май 2016 г.
Ядерная и реакторная физика:
- Дж. Р. Ламарш, Введение в теорию ядерных реакторов, 2-е изд., Addison-Wesley, Reading, MA (1983).
- Дж. Р. Ламарш, А. Дж. Баратта, Введение в ядерную технику, 3-е изд., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
- WM Стейси, Физика ядерных реакторов, John Wiley & Sons, 2001, ISBN: 0-471-39127-1.
- Гласстоун, Сезонске. Разработка ядерных реакторов: разработка реакторных систем, Springer; 4-е издание, 1994 г., ISBN: 978-0412985317
- WSC. Уильямс. Ядерная физика и физика элементарных частиц. Кларендон Пресс; 1 издание, 1991 г.
 , ISBN: 978-0198520467
, ISBN: 978-0198520467 - Г. Р. Кипин. Физика ядерной кинетики. Паб Эддисон-Уэсли. Ко; 1-е издание, 1965 г.
- Роберт Рид Берн, Введение в работу ядерного реактора, 1988.
- Министерство энергетики, ядерной физики и теории реакторов США. Справочник по основам Министерства энергетики, том 1 и 2. Январь 1993 г.
- Пол Ройсс, Нейтронная физика. EDP Sciences, 2008. ISBN: 978-2759800414.
Advanced Reactor Physics:
- К. О. Отт, В. А. Безелла, Введение в статистику ядерных реакторов, Американское ядерное общество, исправленное издание (1989 г.), 1989 г., ISBN: 0-894-48033-2.
- К. О. Отт, Р. Дж. Нойхольд, Введение в динамику ядерных реакторов, Американское ядерное общество, 1985, ISBN: 0-894-48029-4.
- Д. Л. Хетрик, Динамика ядерных реакторов, Американское ядерное общество, 1993, ISBN: 0-894-48453-2.
- Э. Э. Льюис, В. Ф. Миллер, Вычислительные методы переноса нейтронов, Американское ядерное общество, 1993, ISBN: 0-894-48452-4.

См. выше:
Теплопроводность
сообщите об этом объявлении
Теплопроводность
В физике теплопроводность , k, — это свойство материала, указывающее на его способность проводить тепло. Он используется в основном в законе Фурье для теплопроводности.Определяется как количество теплоты, Δ Q , переданное за время Δ t через толщину L в направлении, нормальном к поверхности площадью A , из-за разности температур Δ T , в стационарных условиях и когда теплопередача зависит только от градиента температуры.
- теплопроводность = скорость теплового потока × расстояние / (площадь × разность температур)
- С другой стороны, это можно представить как поток тепла (энергия на единицу площади в единицу времени), деленный на градиент температуры (разность температур на единицу длины)
Типичные единицы измерения: СИ: Вт/(м·К) и английские единицы: БТЕ/фут/(ч·фут²·°F). Для преобразования между ними используйте соотношение 1 БТЕ·фут/(ч·фут²·°F) = 1,730735 Вт/(м·К). [Справочник инженера-химика Перри, 7-е издание, таблица 1-4]
Для преобразования между ними используйте соотношение 1 БТЕ·фут/(ч·фут²·°F) = 1,730735 Вт/(м·К). [Справочник инженера-химика Перри, 7-е издание, таблица 1-4]Дополнительные рекомендуемые знания
Содержимое
- 1 Пример
- 2 Список теплопроводностей
- 3 Измерение
- 3.1 Стандартные методы измерения
- 4 Связанные термины
- 4.1 Первое определение (общее)
- 4.2 Второе определение (здания)
- 5 Текстильная промышленность
- 6 Происхождение
- 7 См. также
- 8 ссылок
Примеры
В металлах теплопроводность примерно соответствует электропроводности в соответствии с законом Видемана-Франца, поскольку свободно движущиеся валентные электроны переносят не только электрический ток, но и тепловую энергию. Однако общая корреляция между электрической и теплопроводностью не выполняется для других материалов из-за возросшей важности переносчиков фононов для тепла в неметаллах.
 Как показано в таблице ниже, серебро с высокой электропроводностью менее теплопроводно, чем алмаз, который является электрическим изолятором.
Как показано в таблице ниже, серебро с высокой электропроводностью менее теплопроводно, чем алмаз, который является электрическим изолятором.Теплопроводность зависит от многих свойств материала, в частности от его структуры и температуры. Например, чистые кристаллические вещества демонстрируют очень разные теплопроводности вдоль разных осей кристалла из-за различий в взаимодействии фононов вдоль данной оси кристалла. Сапфир является ярким примером переменной теплопроводности в зависимости от ориентации и температуры, для которого в Справочнике CRC сообщается теплопроводность 2,6 Вт / (м·К) перпендикулярно c -ось при 373 К, но 6000 Вт/(м·К) при 36 градусах от оси c и 35 К (возможна опечатка?).
Воздух и другие газы обычно являются хорошими изоляторами при отсутствии конвекции. Следовательно, многие изоляционные материалы работают просто за счет наличия большого количества заполненных газом карманов, которые предотвращают крупномасштабную конвекцию. Их примеры включают вспененный и экструдированный полистирол (обычно называемый «пенополистирол») и аэрогель на основе диоксида кремния.
 Естественные биологические изоляторы, такие как мех и перья, достигают аналогичных эффектов, резко подавляя конвекцию воздуха или воды вблизи кожи животного.
Естественные биологические изоляторы, такие как мех и перья, достигают аналогичных эффектов, резко подавляя конвекцию воздуха или воды вблизи кожи животного.Теплопроводность играет важную роль в изоляции зданий и смежных областях. Однако материалы, используемые в таких профессиях, редко соответствуют стандартам химической чистоты. Значения k некоторых строительных материалов перечислены ниже. Их следует считать приблизительными из-за неопределенностей, связанных с определениями материалов.
Следующая таблица представляет собой небольшую выборку данных для иллюстрации теплопроводности различных типов веществ. Для получения более полных списков измеренных k -значения, см. ссылки.
Список теплопроводностей
Основная статья: Список коэффициентов теплопроводности
Это список приблизительных значений теплопроводности k для некоторых распространенных материалов. Пожалуйста, обратитесь к списку коэффициентов теплопроводности для получения более точных значений, ссылок и подробной информации.

Измерение
Для хороших проводников тепла можно использовать метод стержней Серла.[1] Для плохих проводников тепла можно использовать дисковый метод Лиза.[2] Альтернативный традиционный метод с использованием реальных термометров описан в [3]. Краткий обзор новых методов измерения теплопроводности, температуропроводности и удельной теплоемкости в рамках одного измерения доступен в [4]. Тестер теплопроводности, один из инструментов геммологии, определяет, являются ли драгоценные камни настоящими бриллиантами, используя уникально высокую теплопроводность алмаза.
Стандартные методы измерения
- Стандарт IEEE 442-1981, «Руководство IEEE по измерению удельного теплового сопротивления грунта» [5]
- Стандарт IEEE 98-2002, «Стандарт подготовки процедур испытаний для термической оценки твердых электроизоляционных материалов», ISBN 0-7381-3277-2 [6]
- Стандарт ASTM D5470-06, «Стандартный метод испытаний свойств теплопередачи теплопроводных электроизоляционных материалов» [7]
- Стандарт ASTM E1225-04, «Стандартный метод испытаний теплопроводности твердых тел с помощью метода защищенного сравнительного продольного теплового потока» [8]
- Стандарт ASTM D5930-01, «Стандартный метод испытаний на теплопроводность пластмасс с помощью метода линейного источника переходного процесса» [9]
- Стандарт ASTM D2717-95, «Стандартный метод испытаний на теплопроводность жидкостей» [10]
Связанные термины
Обратная величина теплопроводности составляет теплового сопротивления , измеренного в кельвин-метрах на ватт (К·м·Вт −1 ).

При работе с известным количеством материала можно описать его теплопроводность и обратное свойство тепловое сопротивление . К сожалению, существуют разные определения этих терминов.
Первое определение (общее)
Для общенаучного использования теплопроводность — это количество тепла, которое проходит в единицу времени через пластину из определенной площади и толщины , когда его противоположные стороны отличаются по температуре на один градус. Для пластины с теплопроводностью k , площадью A и толщиной L это значение составляет кА/л , измеренное в Вт·K −1 . Это соответствует соотношению между электропроводностью (А·м -1 · В -1 ) и электропроводностью (А·м -1 ).
Существует также показатель, известный как коэффициент теплопередачи: количество тепла, которое проходит в единицу времени через единица площади пластины определенной толщины, когда температура ее противоположных сторон отличается на один градус.
 Взаимная теплоизоляция . В итоге:
Взаимная теплоизоляция . В итоге:- Термическая проводимость = Ka / L , измеренный в W · K -1
- Термическая сопротивление = L / Ka , Searured in K w w w w w w .
- коэффициент теплопередачи = к / L , измерено в Вт·K −1 ·м −2
- теплоизоляция = л / k , измерено в K·м²·Вт
- −91
Коэффициент теплопередачи также известен как коэффициент теплопроводности
Второе определение (здания)
При работе со зданиями тепловое сопротивление или R-значение означает то, что описано выше как теплоизоляция, и теплопроводность означает обратную. Для материалов, соединенных последовательно, эти тепловые сопротивления (в отличие от проводимости) можно просто добавить, чтобы получить тепловое сопротивление в целом.

Третий термин, коэффициент теплопередачи , включает теплопроводность конструкции наряду с теплопередачей за счет конвекции и излучения. Он измеряется в тех же единицах, что и теплопроводность, и иногда известен как составная теплопроводность . Срок U-значение — еще один синоним.
Таким образом, для пластины с теплопроводностью k (значение k [1] ), площадью A и толщиной L :
- теплопроводность = к / л , измеряется в Вт·К −1 ·м −2 ;
- тепловое сопротивление ( значение R ) = л / к , измеряется в К·м²·Вт −1 ;
- коэффициент теплопередачи ( значение U ) = 1/(Σ( L / k )) + конвекция + излучение, измеренное в Вт·K −1 ·м −2 .
Текстильная промышленность
В текстиле значение tog может указываться как мера термостойкости вместо меры в единицах СИ.

Происхождение
Теплопроводность системы определяется тем, как взаимодействуют атомы, составляющие систему. Не существует простых правильных выражений для теплопроводности. Существует два различных подхода к расчету теплопроводности системы. Первый подход использует соотношения Грина-Кубо. Хотя это выражение является точным*, для расчета теплопроводности плотной жидкости или твердого тела с использованием этого соотношения требуется использование компьютерного моделирования молекулярной динамики.
- Термин “точный” применяется для обозначения разрешимости уравнений.
Второй подход основан на подходе времени релаксации. Известно, что из-за ангармонизма внутри кристаллического потенциала фононы в системе рассеиваются. Существует три основных механизма рассеяния:
- Граничное рассеяние, попадание фонона на границу системы;
- Рассеяние на дефектах масс, столкновение фонона с примесью в системе и рассеяние; 9 Определение значения k от Plastics New Zealand
- Каллистер, Уильям (2003).
 «Приложение B», Материаловедение и инженерия – Введение . John Wiley & Sons, INC, 757. ISBN 0-471-22471-5 .
«Приложение B», Материаловедение и инженерия – Введение . John Wiley & Sons, INC, 757. ISBN 0-471-22471-5 . - Халлидей, Дэвид; Резник, Роберт; и Уокер, Джерл (1997). Основы физики (5-е изд.). John Wiley and Sons, INC., NY ISBN 0-471-10558-9 .
- ТМ 5-852-6 АФР 88-19, Том 6 (издание Инженерного корпуса армии)
- Шривастава Г. П. (1990), «Физика фононов». Адам Хилгер, IOP Publishing Ltd, Бристоль.
Эта статья находится под лицензией GNU Free Documentation License. Он использует материал из статьи Википедии «Теплопроводность». Список авторов есть в Википедии. ▷ Теплопроводность с формулой и сравнением
Теплопроводность (обычно обозначается k) относится к присущей материалу способности переносить или проводить тепло. Это один из трех методов переноса тепла, два других — конвекция и излучение. Процессы переноса тепла могут быть выражены математически с использованием правильных уравнений скорости.
 Уравнение скорости этого режима теплопередачи основано на законе теплопроводности Фурье .
Уравнение скорости этого режима теплопередачи основано на законе теплопроводности Фурье .Также описывается как количество тепла, которое может быть передано в единицу времени на единицу площади через пластину единичной толщины из определенного материала, при этом поверхности пластины отличаются на одну единицу температуры.
Теплопроводность возникает из-за волнения и контакта молекул, а не из-за объемного движения самого материала. Тепло течет по температурному градиенту от области с высокой температурой и высокой молекулярной энергией к области с более низкой температурой и более низкой молекулярной энергией. Этот процесс будет повторяться до тех пор, пока не установится тепловое равновесие. Скорость передачи тепла определяется величиной температурного градиента, а также специфическими тепловыми свойствами материала.
Формула теплопроводности
Теплопроводность измеряется в Вт/м . К (Ватт на метр на градус Кельвина) и является обратной величиной удельного теплового сопротивления, которое оценивает способность объекта сопротивляться передаче тепла.
 Для получения уравнения теплопроводности можно использовать следующие формулы:1066 refers to the length or thickness of the material m,
Для получения уравнения теплопроводности можно использовать следующие формулы:1066 refers to the length or thickness of the material m, Q represents heat flow W ,
A is the surface area of material m 2 , и
T2-T1 градиент температуры K
Изменение теплопроводности
Теплопроводность материала сильно зависит от множества факторов. К ним относятся градиент температуры, характеристики материала и длина теплового канала.
Теплопроводность окружающих нас материалов сильно различается: от материалов с низкой теплопроводностью, таких как воздух (0,024 Вт/м·К при 0°C), до материалов с высокой теплопроводностью, таких как медь (385 Вт/м·К).
Теплопроводность материалов определяет, как мы их используем; например, материалы с низкой теплопроводностью отлично подходят для изоляции наших домов и предприятий, в то время как материалы с высокой теплопроводностью идеально подходят для приложений, где необходимо быстро и эффективно перемещать тепло из одной области в другую, таких как кухонная утварь и системы охлаждения в электронных устройствах.
 Мы можем получить оптимальную производительность, выбрав материалы с теплопроводностью, подходящей для конкретного применения.
Мы можем получить оптимальную производительность, выбрав материалы с теплопроводностью, подходящей для конкретного применения.Связь между температурой и теплопроводностью
Поскольку молекулярная подвижность является основой теплопроводности, температура материала оказывает существенное влияние на его теплопроводность. Поскольку молекулы движутся быстрее при более высоких температурах, тепло передается через материал с большей скоростью. Это означает, что теплопроводность одного и того же образца может резко меняться при повышении или понижении температуры.
Понимание того, как температура влияет на теплопроводность, имеет решающее значение для обеспечения того, чтобы изделия реагировали в соответствии с прогнозами при воздействии тепловых нагрузок. Это особенно важно при разработке огне- и теплозащитных материалов и работе с продуктами, выделяющими тепло, такими как электроника.
Как теплопроводность влияет на структуру?
Уровни теплопроводности сильно различаются среди материалов и сильно зависят от структуры каждого вещества.
 Это анизотропные материалы, которые имеют различные значения теплопроводности в зависимости от направления распространения тепла. Из-за того, как конструкция построена в этих условиях, тепло легче распространяется в одном направлении.
Это анизотропные материалы, которые имеют различные значения теплопроводности в зависимости от направления распространения тепла. Из-за того, как конструкция построена в этих условиях, тепло легче распространяется в одном направлении.Материалы можно разделить на три категории при обсуждении тенденций теплопроводности: газы, неметаллические твердые вещества и металлические твердые вещества. Различия в теплопередающих способностях этих трех категорий могут быть связаны с различиями в их структурах и молекулярном движении.
Поскольку молекулы в газах не так плотно упакованы, как в твердых телах, их относительная теплопроводность ниже, а теплопередача сильно зависит от свободного движения молекул и скорости молекул.
- Газы являются неэффективными теплопередатчиками. Неметаллические твердые тела, с другой стороны, имеют молекулы, которые связаны в решетчатую сеть, и поэтому теплопроводность преимущественно обусловлена вибрациями в этих решетках.
 Из-за близкого расположения этих молекул по сравнению с газами неметаллические твердые тела имеют более высокую теплопроводность из двух, но в этой категории существует широкий диапазон.
Из-за близкого расположения этих молекул по сравнению с газами неметаллические твердые тела имеют более высокую теплопроводность из двух, но в этой категории существует широкий диапазон. - Это отклонение частично связано с количеством воздуха, присутствующего в твердом ; материалы с большим количеством воздушных карманов являются отличными изоляторами, тогда как материалы с меньшим количеством воздушных карманов имеют более высокое значение теплопроводности.
- Теплопроводность металлических материалов еще раз отличается от предыдущих экземпляров. Металлы, за исключением графена, обладают самой высокой теплопроводностью среди всех веществ и уникальным сочетанием тепло- и электропроводности.
Оба этих свойства передаются одними и теми же молекулами, и закон Видемана-Франца объясняет связь между ними. Этот закон гласит, что при определенной температуре электропроводность пропорциональна теплопроводности; однако при повышении температуры теплопроводность материала увеличивается, а электропроводность уменьшается.

Как измерить и проверить теплопроводность?
Теплопроводность является важным компонентом материала, и ее взаимосвязь и понимание этого позволяют нам получить максимальную эффективность от материалов, которые мы используем во всех аспектах нашей жизни. Расчет теплопроводности и испытания являются важными компонентами этой попытки. Методы измерения теплопроводности делятся на два типа: стационарные и переходные. Это различие является отличительной чертой того, как работает каждый подход.
- Стационарные методы требуют, чтобы образец и эталонные части находились в тепловом равновесии до начала измерений.
- Переходные подходы, не требующие соблюдения этого правила, дают результаты быстрее.
Давайте обсудим некоторые применения теплопроводности в реальной жизни.
В этом исследовании изучается теплопроводность муллитовой керамики, полученной путем вспенивания и отверждения крахмалом порошка муллита, и то, как она зависит от пористости керамики.




 01.05(закрыт)
01.05(закрыт) Материалы на основе полимерных матриц применяются в промышленности из-за их малого веса, низкой стоимости, простоты обработки, функциональных возможностей и химической стабильности. Однако низкие тепло- и электропроводность ограничивают их применение. В диссертации анализируется природа этих ограничений и способы их преодоления.
Объектом исследования являются многостенные УНТ, а также композиты на полимерной основе с их включением.
Предметом исследования являются условия роста и структура УНТ на различных подложках, электро- и теплопроводность массивов УНТ и композитов с их включением, анизотропия свойств проводимости.
Цель работы – исследование влияния параметров синтеза на структуру синтезируемых УНТ, модификация свойств материала путем введения УНТ в полимерную матрицу, сопоставление результатов моделирования теплопроводности материалов с включением УНТ с экспериментальными данными, выявление основных параметров, влияющих на свойства композитов.
Материалы на основе полимерных матриц применяются в промышленности из-за их малого веса, низкой стоимости, простоты обработки, функциональных возможностей и химической стабильности. Однако низкие тепло- и электропроводность ограничивают их применение. В диссертации анализируется природа этих ограничений и способы их преодоления.
Объектом исследования являются многостенные УНТ, а также композиты на полимерной основе с их включением.
Предметом исследования являются условия роста и структура УНТ на различных подложках, электро- и теплопроводность массивов УНТ и композитов с их включением, анизотропия свойств проводимости.
Цель работы – исследование влияния параметров синтеза на структуру синтезируемых УНТ, модификация свойств материала путем введения УНТ в полимерную матрицу, сопоставление результатов моделирования теплопроводности материалов с включением УНТ с экспериментальными данными, выявление основных параметров, влияющих на свойства композитов. обращений
обращений