Элементы логика и: Элементы Логика И, Логика Т
alexxlab | 09.04.2023 | 0 | Разное
Базовые логические элементы.
В Булевой алгебре, на которой базируется вся цифровая техника, электронные элементы должны выполнять ряд определённых действий. Это так называемый логический базис. Вот три основных действия:
ИЛИ – логическое сложение (дизъюнкция) – OR;
И – логическое умножение (конъюнкция) – AND;
НЕ – логическое отрицание (инверсия) – NOT.
Примем за основу позитивную логику, где высокий уровень будет “1”, а низкий уровень примем за “0”. Чтобы можно было более наглядно рассмотреть выполнение логических операций, существуют таблицы истинности для каждой логической функции. Сразу нетрудно понять, что выполнение логических функций «и» и «или» подразумевают количество входных сигналов не менее двух, но их может быть и больше.
Логический элемент И.
На рисунке представлена таблица истинности элемента “И” с двумя входами.
| Вход X1 | Вход X2 | Выход Y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
На принципиальных схемах логический элемент “И” обозначают так.
На зарубежных схемах обозначение элемента “И” имеет другое начертание. Его кратко называют AND.
Логический элемент ИЛИ.
Элемент “ИЛИ” с двумя входами работает несколько по-другому. Достаточно логической единицы на первом входе или на втором как на выходе будет логическая единица. Две единицы так же дадут единицу на выходе.
| Вход X1 | Выход Y | |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
На схемах элемент “ИЛИ” изображают так.
На зарубежных схемах его изображают чуть по-другому и называют элементом OR.
Логический элемент НЕ.
Элемент, выполняющий функцию инверсии «НЕ» имеет один вход и один выход. Он меняет уровень сигнала на противоположный. Низкий потенциал на входе даёт высокий потенциал на выходе и наоборот.
| Вход X | Выход Y |
|---|---|
| 0 | 1 |
| 1 | 0 |
Вот таким образом его показывают на схемах.
В зарубежной документации элемент “НЕ” изображают следующим образом. Сокращённо называют его NOT.
Все эти элементы в интегральных микросхемах могут объединяться в различных сочетаниях.
Логический элемент 2И-НЕ.
Рассмотрим несколько реальных логических элементов на примере серии транзисторно-транзисторной логики (ТТЛ) К155 с малой степенью интеграции. На рисунке когда-то очень популярная микросхема К155ЛА3, которая содержит четыре независимых элемента 2И – НЕ. Кстати, с помощью её можно собрать простейший маячок на микросхеме.
Цифра всегда обозначает число входов логического элемента. В данном случае это двухвходовой элемент «И» выходной сигнал которого инвертируется. Инвертируется, это значит “0” превращается в “1”, а “1” превращается в “0”. Обратим внимание на кружочек на выходах – это символ инверсии. В той же серии существуют элементы 3И–НЕ, 4И–НЕ, что означает элементы «И» с различным числом входов (3, 4 и т.д.).
Как вы уже поняли, один элемент 2И-НЕ изображается вот так.
По сути это упрощённое изображение двух объёдинённых элементов: элемента 2И и элемента НЕ на выходе.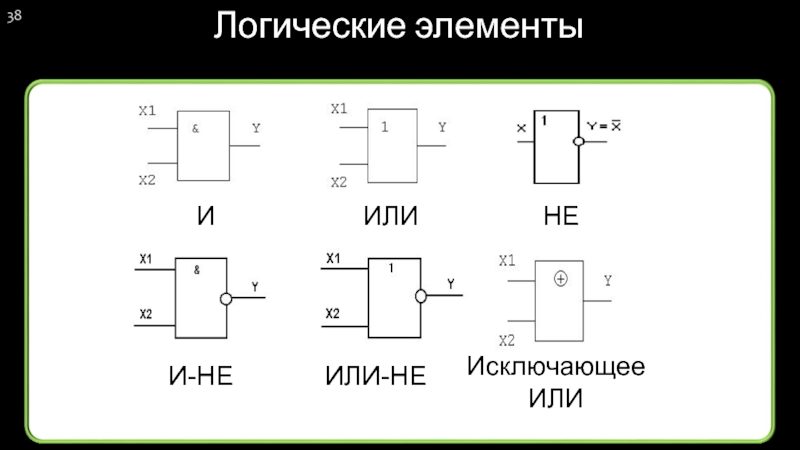
Зарубежное обозначение элемента И-НЕ (в данном случае 2И-НЕ). Называется NAND.
Таблица истинности для элемента 2И-НЕ.
| Вход X1 | Вход X2 | Выход Y |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
В таблице истинности элемента 2И – НЕ мы видим, что благодаря инвертору получается картина противоположная элементу «И».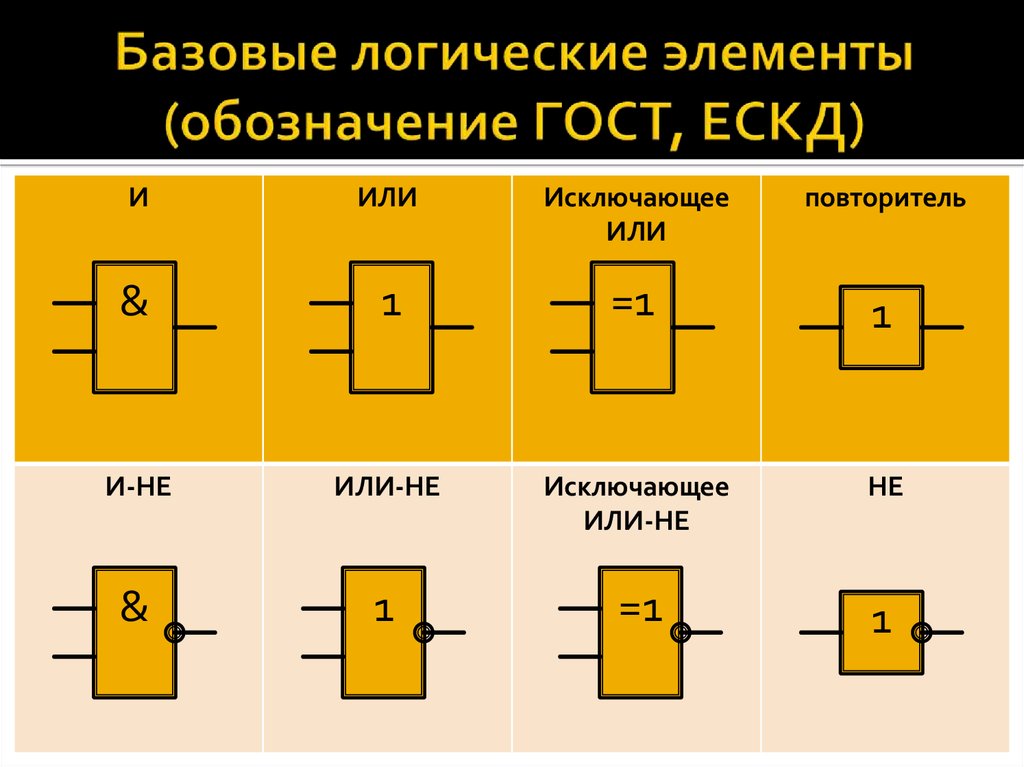 В отличие от трёх нулей и одной единицы мы имеем три единицы и ноль. Элемент «И – НЕ» часто называют элементом Шеффера.
В отличие от трёх нулей и одной единицы мы имеем три единицы и ноль. Элемент «И – НЕ» часто называют элементом Шеффера.
Логический элемент 2ИЛИ-НЕ.
Логический элемент 2ИЛИ – НЕ представлен в серии К155 микросхемой 155ЛЕ1. Она содержит в одном корпусе четыре независимых элемента. Таблица истинности так же отличается от схемы “ИЛИ” применением инвертирования выходного сигнала.
Таблица истинности для логического элемента 2ИЛИ-НЕ.
| Вход X1 | Вход X2 | Выход Y |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 0 |
Изображение на схеме.
На зарубежный лад изображается так. Называют как NOR.
Мы имеем только один высокий потенциал на выходе, обусловленный подачей на оба входа одновременно низкого потенциала. Здесь, как и на любых других принципиальных схемах, кружочек на выходе подразумевает инвертирование сигнала. Так как схемы И – НЕ и ИЛИ – НЕ встречаются очень часто, то для каждой функции имеется своё условное обозначение. Функция И – НЕ обозначается значком “&“, а функция ИЛИ – НЕ значком “1“.
Для отдельного инвертора таблица истинности уже приведена выше. Можно добавить, что количество инверторов в одном корпусе может достигать шести.
Логический элемент “исключающее ИЛИ”.
К числу базовых логических элементов принято относить элемент реализующий функцию «исключающее ИЛИ». Иначе эта функция называется «неравнозначность».
Высокий потенциал на выходе возникает только в том случае, если входные сигналы не равны. То есть на одном из входов должна быть единица, а на другом ноль. Если на выходе логического элемента имеется инвертор, то функция выполняется противоположная – «равнозначность». Высокий потенциал на выходе будет появляться при одинаковых сигналах на обоих входах.
Если на выходе логического элемента имеется инвертор, то функция выполняется противоположная – «равнозначность». Высокий потенциал на выходе будет появляться при одинаковых сигналах на обоих входах.
Таблица истинности.
| Вход X1 | Вход X2 | Выход Y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
Эти логические элементы находят своё применение в сумматорах.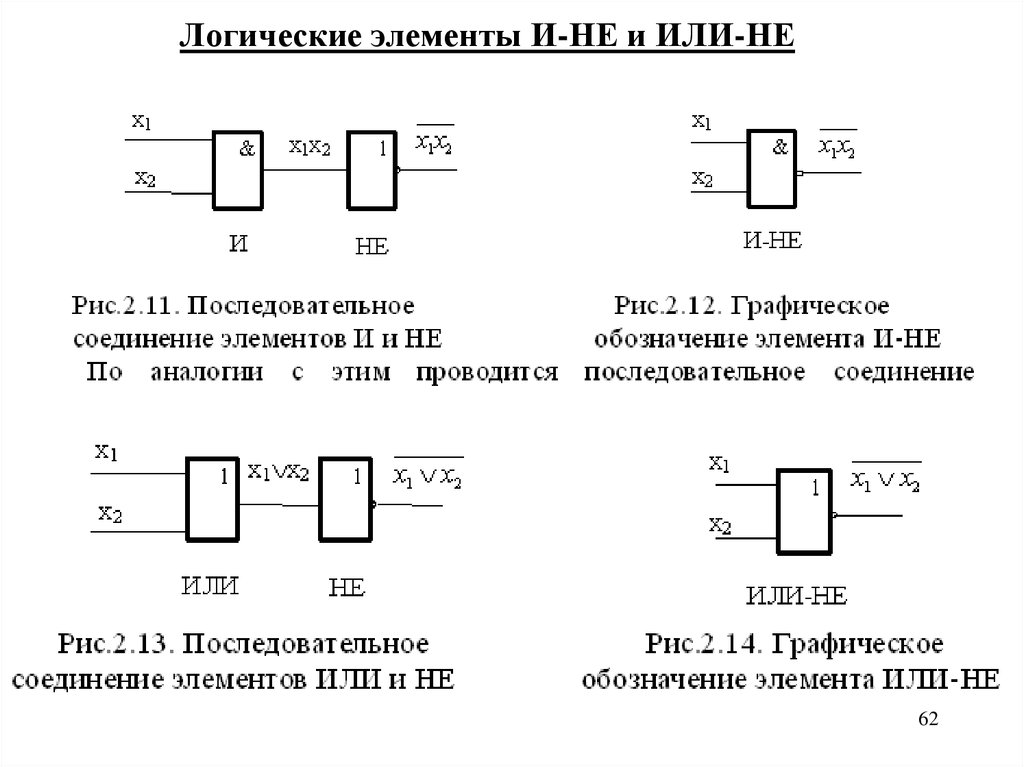 «Исключающее ИЛИ» изображается на схемах знаком равенства перед единицей “=1“.
«Исключающее ИЛИ» изображается на схемах знаком равенства перед единицей “=1“.
На зарубежный манер “исключающее ИЛИ” называют XOR и на схемах рисуют вот так.
Кроме вышеперечисленных логических элементов, которые выполняют базовые логические функции очень часто, используются элементы, объединённые в различных сочетаниях. Вот, например, К555ЛР4. Она называется очень серьёзно 2-4И-2ИЛИ-НЕ.
Её таблица истинности не приводится, так как микросхема не является базовым логическим элементом. Такие микросхемы выполняют специальные функции и бывают намного сложнее, чем приведённый пример. Так же в логический базис входят и простые элементы “И” и “ИЛИ”. Но они используются гораздо реже. Может возникнуть вопрос, почему эта логика называется транзисторно-транзисторной.
Если посмотреть в справочной литературе схему, допустим, элемента 2И – НЕ из микросхемы К155ЛА3, то там можно увидеть несколько транзисторов и резисторов.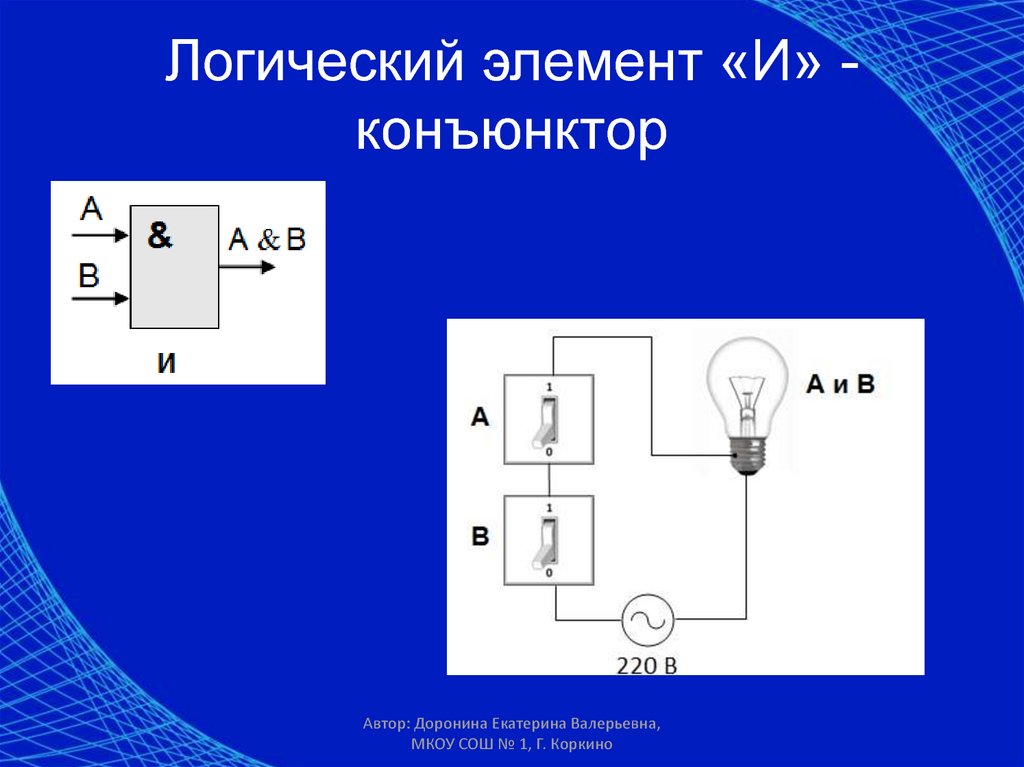 На самом деле ни резисторов, ни диодов в этих микросхемах нет. На кристалл кремния через трафарет напыляются только транзисторы, а функции резисторов и диодов выполняют эмиттерные переходы транзисторов. Кроме того в ТТЛ логике широко используются многоэмиттерные транзисторы. Например, на входе элемента 4И стоит четырёхэмиттерный транзистор.
На самом деле ни резисторов, ни диодов в этих микросхемах нет. На кристалл кремния через трафарет напыляются только транзисторы, а функции резисторов и диодов выполняют эмиттерные переходы транзисторов. Кроме того в ТТЛ логике широко используются многоэмиттерные транзисторы. Например, на входе элемента 4И стоит четырёхэмиттерный транзистор.
Главная » Цифровая электроника » Текущая страница
Также Вам будет интересно узнать:
RS-триггер.
Урок 8.3 – Логические элементы
8.3. Логические элементы
Все, абсолютно все электронные компоненты, обрабатывающие цифровые сигналы, состоят из небольшого набора одинаковых «кирпичиков». В микросхемах малой степени интеграции могут быть единицы и десятки таких элементов, а в современных процессорах их может быть очень и очень много. Они называются логические элементы. Логическим элементом называется электрическая схема, предназначенная для выполнения какой-либо логической операции с входными данными. Логический элемент — элемент, осуществляющий определенные логические зависимость между входными и выходными сигналами. Входные данные представляются здесь в виде напряжений различных уровней, и результат логической операции на выходе — также получается в виде напряжения определенного уровня. Логические элементы обычно используются для построения логических схем вычислительных машин, дискретных схем автоматического контроля и управления.
Логический элемент — элемент, осуществляющий определенные логические зависимость между входными и выходными сигналами. Входные данные представляются здесь в виде напряжений различных уровней, и результат логической операции на выходе — также получается в виде напряжения определенного уровня. Логические элементы обычно используются для построения логических схем вычислительных машин, дискретных схем автоматического контроля и управления.
Тем не менее, принцип работы цифровой логики остается неизменным – на входе логического элемента (входов может быть несколько) должен быть цифровой сигнал (сигналы, если входов несколько), который однозначно определяет сигнал на выходе логического элемента.
Конечно, логические элементы строятся, в свою очередь, из уже рассмотренных в предыдущих уроках резисторов, транзисторов и других электронных компонентов, но с точки зрения разработки цифровых схем именно логический элемент является их «элементарной» частицей.
При анализе работы логических элементов используется так называемая булева алгебра . Начала этого раздела математики было изложено в работах Джорджа Буля – английского математика и логика 19-го века, одного из основателей математической логики. Основами булевой алгебры являются высказывания, логические операции, а также функции и законы. Для понимания принципов работы логических элементов нет необходимости изучать все тонкости булевой алгебры, мы освоим ее основы в процессе обучения с помощью таблиц истинности.
Начала этого раздела математики было изложено в работах Джорджа Буля – английского математика и логика 19-го века, одного из основателей математической логики. Основами булевой алгебры являются высказывания, логические операции, а также функции и законы. Для понимания принципов работы логических элементов нет необходимости изучать все тонкости булевой алгебры, мы освоим ее основы в процессе обучения с помощью таблиц истинности.
Еще несколько замечаний. Логические элементы (как, впрочем, и другие элементы электронных схем) принято обозначать так, чтобы входы были слева, а выходы справа. Число входов может быть, вообще говоря, любым, отличным от нуля. Реальные цифровые микросхемы могут иметь до 8 входов, но мы ограничимся двумя – этого достаточно для понимания. Условные обозначения соответствуют отечественному ГОСТу, в других стандартах они могут быть иными.
Какие же бывают логические элементы?
Логические элементы имеют один или несколько входов и один или два (обычно инверсных друг другу) выхода. Значения «нулей» и «единиц» выходных сигналов логических элементов определяются логической функцией, которую выполняет элемент, и значениями «нулей» и «единиц» входных сигналов, играющих роль независимых переменных. Существуют элементарные логические функции, из которых можно составить любую сложную логическую функцию.
Значения «нулей» и «единиц» выходных сигналов логических элементов определяются логической функцией, которую выполняет элемент, и значениями «нулей» и «единиц» входных сигналов, играющих роль независимых переменных. Существуют элементарные логические функции, из которых можно составить любую сложную логическую функцию.
Элемент «И» (AND), он же конъюнктор, выполняет операцию логического умножения:
Условное обозначение – Таблица истинности
Здесь изображен логический элемент «2И» (цифра перед буквой «И» означает число входов). Знак & (амперсант) в левом верхнем углу прямоугольника указывает, что это логический элемент «И». Первые две буквы обозначения DD1.2 указывают на то, что это цифровая микросхема (Digital), цифра слева от точки указывает номер микросхемы на принципиальной схеме, а цифра справа от точки – номер логического элемента в составе данной микросхемы. Одна микросхема может содержать несколько логических элементов.
Состояние входов в таблице обозначаются «0» и «1» («ложь» и «истина»). Из таблицы видно, что выход «Y» будет иметь состояние «1» только в том случае, когда на обоих входах «Х1» и «Х2» будут «1». Это легко запомнить: умножение на «0» всегда дает «0».
Элемент «ИЛИ» (OR), он же дизъюнктор, выполняет операцию логического сложения:
Условное обозначение – Таблица истинности
Состояние «1» на выходе будет всегда, пока есть хотя бы одна «1» на входах.
Элемент «НЕ» (NOT), он же инвертор, выполняет операцию логического отрицания:
Условное обозначение – Таблица истинности
Состояние на входе обратно состоянию на входе.
Вот из этих трех элементов строятся все цифровые устройства!
Рассмотрим еще три логических элемента, которые можно получить, комбинируя уже рассмотренные. В силу исторически сложившихся схемотехнических решений эти скомбинированные схемы тоже считаются логическими элементами.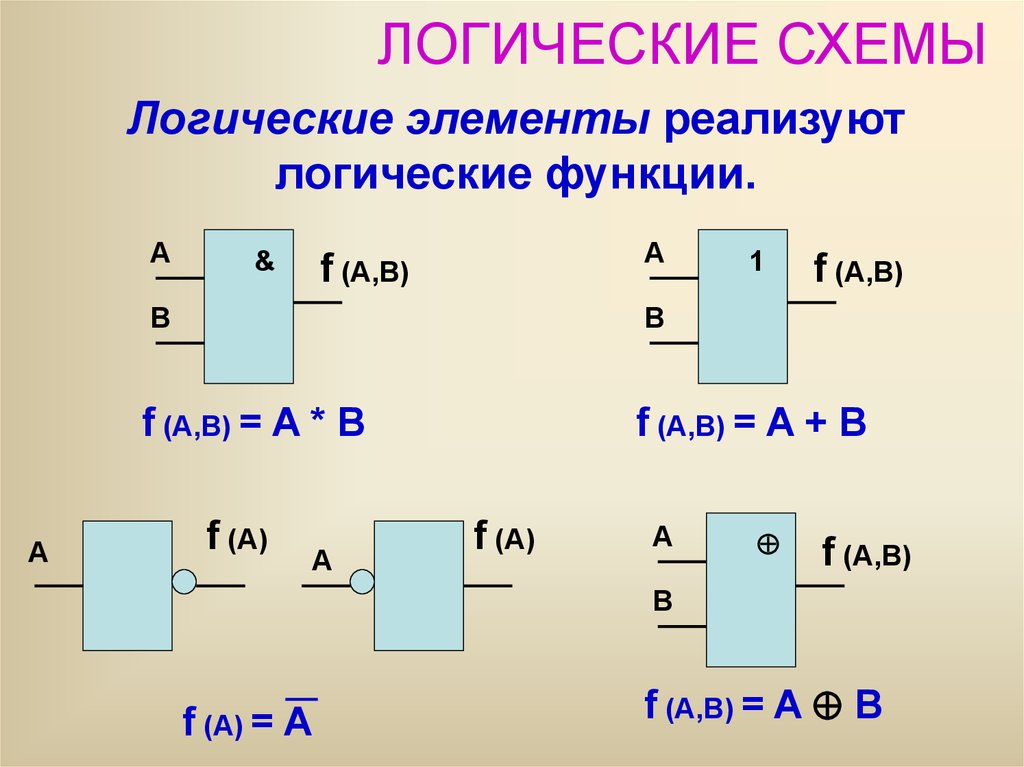
Элемент «И-НЕ» (NAND), конъюнктор с отрицанием:
Условное обозначение – Таблица истинности
Элемент И-НЕ работает точно так же как «И», только выходной сигнал противоположен. Там где у элемента «И» на выходе должен быть «0», у элемента «И-НЕ» будет единица. И наоборот.
Элемент «ИЛИ-НЕ» (NOR), дизъюнктор с отрицанием:
Условное обозначение – Таблица истинности
Элемент работает так же как и «ИЛИ», но с инверсией выхода.
Элемент «Исключающее ИЛИ» (XOR), сумматор по модулю 2:
Условное обозначение – Таблица истинности
В этом элемента «1» на выходе будет только тогда, когда на входах разные состояния.
На таких элементах строят сумматоры двоичных многоразрядных чисел. Для этого используется еще один дополнительный выход, на котором при появлении на входах двух «1» появляется сигнал переноса разряда.
Мы рассмотрели логические элементы, которые применяются в цифровой технике для построения логических схем любого уровня сложности, но рассмотренные нами элементы не могут делать одну крайне важную работу – они не умеют хранить информацию. Для хранения используется более сложный класс устройств, называемый элементами с памятью или конечными автоматами. В этот класс входят триггеры, регистры, счетчики, шифраторы (дешифраторы), мультиплексоры (демультиплексоры) и сумматоры. Некоторый из этих устройств мы рассмотрим в следующем уроке.
Элементы логики
Элементы логикина
Его Высокопреосвященство кардинал Мерсье
Третье издание
Переведено
Юэн Макферсон
Нью-Йорк
Манхэттенвилл Пресс
1912
Нихил Обстат.
РЕМИГИУС ЛАФОРТ, Д.Д.
Цензор
Подтверждение
ДЖОН КАРДИНАЛ ФАРЛИ
Архиепископ Нью-Йорка
Авторское право 1912
Манхэттенвилл Пресс
Введение
- 1.
 Определение логики
Определение логики - 2. Материалы логического порядка
- 3. Формальная причина логического порядка
- 4. Отличие психологии от логики
- 5. Конечная причина логического порядка
- 6. Отличие логики от метафизики
- 7. Логику можно рассматривать как практическую науку или как искусство.
- 8. Разделы логики
Глава I
Действующая причина логического порядка
- 9. Происхождение и характер операций мыслительной способности
- 10. Множественность операций мыслительной способности. Их фундаментальная идентичность
- 11. Абстрактный характер понятий делает возможными суждения и рассуждения
Глава II
Материя или материальная причина логического порядка
- 12. Объект и раздел главы II
Арт. I. Концепции
§ 1.
 Понятие, его предмет и свойства
Понятие, его предмет и свойства- 13. Понятие в его логическом аспекте
- 14. По какому праву логика занимается актами простого понимания?
- 15. Логические проблемы, возникающие в связи с актом простого опасения
- 16. Логические категории или затруднения
- 17. Предсказуемые
- 18. Понимание и расширение понятий
- 19. Отношения подчинения между идеями в отношении их расширения
- 20. Сравнение идей в отношении их понимания. Отношение идентичности и оппозиции
§ 2. Разделение понятий
- 21. Основные рубрики классификации понятий
- 22. Классификация идей по отношению к объекту, абстрагируемому интеллектом
- 23. Классификация идей по способу представления объекта
- 24. Классификация когниций. в отношении их происхождения или образования
Арт. II. Условия.
§ 1.
 Термин, его предмет и свойства
Термин, его предмет и свойства- 25. Объект термина
- 26. Десять частей речи
§ 2 Классификация терминов
- 27. Классификация терминов
Глава III
Формальная причина логического порядка
- 28. Предварительное примечание
Арт. I. Решение и предложение
§ 1. Понятие суждения и предложения
- 29. Решение и предложение
- 30. Функция суждений и предложений в интеллектуальной жизни
§ 2. Суждения и предложения
- 31. Общая классификация предложений
I. Классификация простых предложений
- 32. Первый отдел предложений: по существу
- 33. Два вида суждений в необходимом вопросе
- 34. Синонимические обозначения вышеперечисленных
- 35.
 Второе подразделение предложений: в отношении их формы
Второе подразделение предложений: в отношении их формы - 36. Логическое значение сказуемого простого предложения
- 37. Третье подразделение предложений: в отношении их количества
- 38. Четвертое подразделение предложений: в отношении их качества
II. Классификация сложных предложений
- 39. Классификация сложных предложений
§ 3. Отношения между предложениями
- 40. Отношения между предложениями
- 41. Эквивалентность нескольких предложений
- 42. Конвертируемость предложений
- 43. Отношения оппозиции и подчинения
- 44. Правила, касающиеся истинности или ложности противоположных утверждений
- 45. Правила, касающиеся истинности или ложности подчиненных предложений
- 46. Непосредственные выводы
Арт. II. Рассуждение
- 47. Предварительные замечания.
 Объект искусства. II
Объект искусства. II
§ 1. Рассуждение и силлогизм
- 48. Рассуждение
- 49. Силлогизм. Терминология
- 50. Природа и логическая основа силлогизма
- 51. Какого порядка необходимость принципов силлогизма?
- 52. Логические первые принципы
- 53. Фигуры и способы силлогизма
- 54. Правила силлогизма
- 55. Диапазон правил силлогизма. Логика и правда
§ 2. Силлогизмы
- 56. Предварительные замечания
I. Силлогизмы, рассматриваемые с точки зрения их формы
- 57. Деление силлогизмов по форме. .
- 58. Разновидность категорического силлогизма
- 59. Природа и правила условного силлогизма
- 60. Конъюнктив и дизъюнктивный силлогизм
- 61. Исключительный силлогизм
- 62. Дилемма
II.
 Силлогизмы, рассматриваемые по своему содержанию 90 147
Силлогизмы, рассматриваемые по своему содержанию 90 147- 63. Предварительные замечания
Различные виды демонстрации
- 64. I. Первичный отдел
- 65. Условия научной демонстрации
- 66. Доказательство фактов и демонстрация причин
- 67. II. Демонстрации априори и апостериори
- 68. III. Круговая или регрессивная демонстрация
- 69. IV. Другие случайные формы демонстрации
Возможные аргументы
- 70. Возможные аргументы
- 71. I. Аргументы по аналогии: (1) Энтимема
- 72. (2) Аналоговая индукция, или аналогия
- 73. (3) Пример
- 74. II. Аргументы от авторитета
Ошибочные и изощренные аргументы
- 75. Ложные рассуждения
- 76. Ложные рассуждения или софизмы
- 77. Собственно так называемые ложные рассуждения: I.
 Софизмы индукции
Софизмы индукции - 78. II. Софизмы дедукции
Арт. III. Научная систематизация
Предварительные замечания
- 79. Наука – это система
- 80. Научная систематизация
§ 1. Научные процессы
- 81. I. Определение. Его функция
- 82. Определения слов и вещей
- 83. Процессы определения. Синтез. Комбинированный анализ
- 84. Правила определения
- 85. II. Подразделение неотделимо от определения
- 86. Правила деления и синтеза
§ 2. Метод и методы
- 87. Метод. Разнообразие научных методов.
- 88. I. Синтетический метод
- 89. II. Метод позитивных наук. Его объект
- 90. Стадии индукционного процесса
- 91. Индуктивные методы
- 92. Объект индукции
- 93. Логические основы индукции
- 94.
 Индукция и силлогизм
Индукция и силлогизм - 95. Статистика. Их отношение к обвинению
- 96. Аналитико-синтетический метод. Заключение
- 97. Метод философии
Глава IV
Окончательная причина логического порядка
Заключение
- 98. Логика на службе науки и истины
- 99. Определение науки
<< ======= >>
элементов логики | работа Уэйтли
В истории логики: Другие логики 18-го века
…эта традиция возникла 9 Ричарда Уэйтли.0359 Elements of Logic (1826) и, следуя той же традиции, чрезвычайно популярный A System of Logic Джона Стюарта Милля (1843). Хотя в настоящее время несимволический учебник Уотли в значительной степени помещен в сноску, он переформулировал многие понятия настолько вдумчиво и ясно, что в целом (и во-первых…
Подробнее
обзор Милля
- В книге Джона Стюарта Милля: Общественная жизнь и письмо) Джона Стюарта Милля
… (1828 г.
Подробнее ) Ричарда Уэйтли Элементов логики г., он уже защищал силлогизм от шотландских философов, которые говорили о замене его предполагаемой системой индуктивной логики. Он требовал, чтобы его индуктивная логика «дополняла, а не заменяла». В течение нескольких лет он тщетно искал…
) Ричарда Уэйтли Элементов логики г., он уже защищал силлогизм от шотландских философов, которые говорили о замене его предполагаемой системой индуктивной логики. Он требовал, чтобы его индуктивная логика «дополняла, а не заменяла». В течение нескольких лет он тщетно искал…
“,”url”:”Introduction”,”wordCount”:0,”sequence”:1},”imarsData”:{“INFINITE_SCROLL”:”” ,”HAS_REVERTED_TIMELINE”:”false”},”npsAdditionalContents”:{},”templateHandler”:{“name”:”INDEX”},”paginationInfo”:{“previousPage”:null,”nextPage”:null,”totalPages “:1},”uaTemplate”:”INDEX”,”infiniteScrollList”:[{“p”:1,”t”:184321}],”familyPanel”:{“topicInfo”:{“id”:184321,” title”:”Элементы логики”,”url”:”https://www.britannica.com/topic/Elements-of-Logic”,”description”:”История логики: Другие логики 18-го века: … это традиции возникли «Элементы логики» Ричарда Уэйтли (1826 г.) и, следуя той же традиции, чрезвычайно популярная «Система логики» Джона Стюарта Милля (1843 г. ). Хотя в настоящее время несимволический учебник Уотли в значительной степени переведен в сноску, он переформулировал многие понятия настолько вдумчиво и ясно, что в целом (и во-первых…”,”type”:”TOPIC”,”titleText”:”Elements of Logic”,” metaDescription”:”Другие статьи, в которых обсуждаются элементы логики: история логики: Другие логики 18-го века: …эта традиция возникла в «Элементах логики» Ричарда Уэйтли (1826 г.) и, в той же традиции, в чрезвычайно популярной «Системе логики» Джона Стюарта Милля. Логика (1843 г.) Несмотря на то, что в настоящее время несимволический учебник Уэйтли в значительной степени отнесен к сноске, он переформулировал многие концепции настолько вдумчиво и ясно, что в целом (и во-первых…”,”identifierHtml”:”work by Whately”,”identifierText”: “работа Whately”, “topicClass”: “topic”, “topicKey”: “Elements-of-Logic”, “articleContentType”: “INDEX”, “ppTecType”: “THING”, “gaTemplate”: “INDEX”, “topicType”:”INDEX”,”relativeUrl”:”/topic/Elements-of-Logic”,”assemblyLinkPrefix”:”/media/1/184321/”},”topicLink”:{“title”:”Элементы Ло gic”,”url”:”https://www.
). Хотя в настоящее время несимволический учебник Уотли в значительной степени переведен в сноску, он переформулировал многие понятия настолько вдумчиво и ясно, что в целом (и во-первых…”,”type”:”TOPIC”,”titleText”:”Elements of Logic”,” metaDescription”:”Другие статьи, в которых обсуждаются элементы логики: история логики: Другие логики 18-го века: …эта традиция возникла в «Элементах логики» Ричарда Уэйтли (1826 г.) и, в той же традиции, в чрезвычайно популярной «Системе логики» Джона Стюарта Милля. Логика (1843 г.) Несмотря на то, что в настоящее время несимволический учебник Уэйтли в значительной степени отнесен к сноске, он переформулировал многие концепции настолько вдумчиво и ясно, что в целом (и во-первых…”,”identifierHtml”:”work by Whately”,”identifierText”: “работа Whately”, “topicClass”: “topic”, “topicKey”: “Elements-of-Logic”, “articleContentType”: “INDEX”, “ppTecType”: “THING”, “gaTemplate”: “INDEX”, “topicType”:”INDEX”,”relativeUrl”:”/topic/Elements-of-Logic”,”assemblyLinkPrefix”:”/media/1/184321/”},”topicLink”:{“title”:”Элементы Ло gic”,”url”:”https://www. britannica.com/topic/Elements-of-Logic”},”tocPanel”:{“title”:”Каталог”,”itemTitle”:”Ссылки”,” toc”:null},”groups”:[]},”byline”:null,”citationInfo”:null,”websites”:null,”freeTopicReason”:”TOPIC_IS_INDEX_PAGE”,”topicCollectionLinks”:[],”articleSchemaMarkup” :{“browserTitle”:null,”imageUrl”:null,”authors”:null,”keywords”:”Elements of Logic”,”wordcount”:0,”url”:”https://www.britannica.com /topic/Elements-of-Logic”,”creationDate”:null,”modificationDate”:null,”description”:”Другие статьи, в которых обсуждаются Elements of Logic: история логики: Другие логики 18-го века: … возникла эта традиция «Элементы логики» Ричарда Уэйтли (1826 г.) и, следуя той же традиции, чрезвычайно популярная «Система логики» Джона Стюарта Милля (1843 г.). Несмотря на то, что в настоящее время несимволический учебник Уэйтли в значительной степени отнесен к сноске, он переформулировал многие концепции настолько вдумчиво и ясно, что в целом (и сначала…”},”initialLoad”:true}
britannica.com/topic/Elements-of-Logic”},”tocPanel”:{“title”:”Каталог”,”itemTitle”:”Ссылки”,” toc”:null},”groups”:[]},”byline”:null,”citationInfo”:null,”websites”:null,”freeTopicReason”:”TOPIC_IS_INDEX_PAGE”,”topicCollectionLinks”:[],”articleSchemaMarkup” :{“browserTitle”:null,”imageUrl”:null,”authors”:null,”keywords”:”Elements of Logic”,”wordcount”:0,”url”:”https://www.britannica.com /topic/Elements-of-Logic”,”creationDate”:null,”modificationDate”:null,”description”:”Другие статьи, в которых обсуждаются Elements of Logic: история логики: Другие логики 18-го века: … возникла эта традиция «Элементы логики» Ричарда Уэйтли (1826 г.) и, следуя той же традиции, чрезвычайно популярная «Система логики» Джона Стюарта Милля (1843 г.). Несмотря на то, что в настоящее время несимволический учебник Уэйтли в значительной степени отнесен к сноске, он переформулировал многие концепции настолько вдумчиво и ясно, что в целом (и сначала…”},”initialLoad”:true}
история логики
- В истории логики: Другие логики 18-го века
…эта традиция возникла из книги Ричарда Уэйтли « Элементы логики » (1826) и, в той же традиции, из чрезвычайно популярной книги Джона Стюарта Милля « Система логики».



 Определение логики
Определение логики Второе подразделение предложений: в отношении их формы
Второе подразделение предложений: в отношении их формы Объект искусства. II
Объект искусства. II Софизмы индукции
Софизмы индукции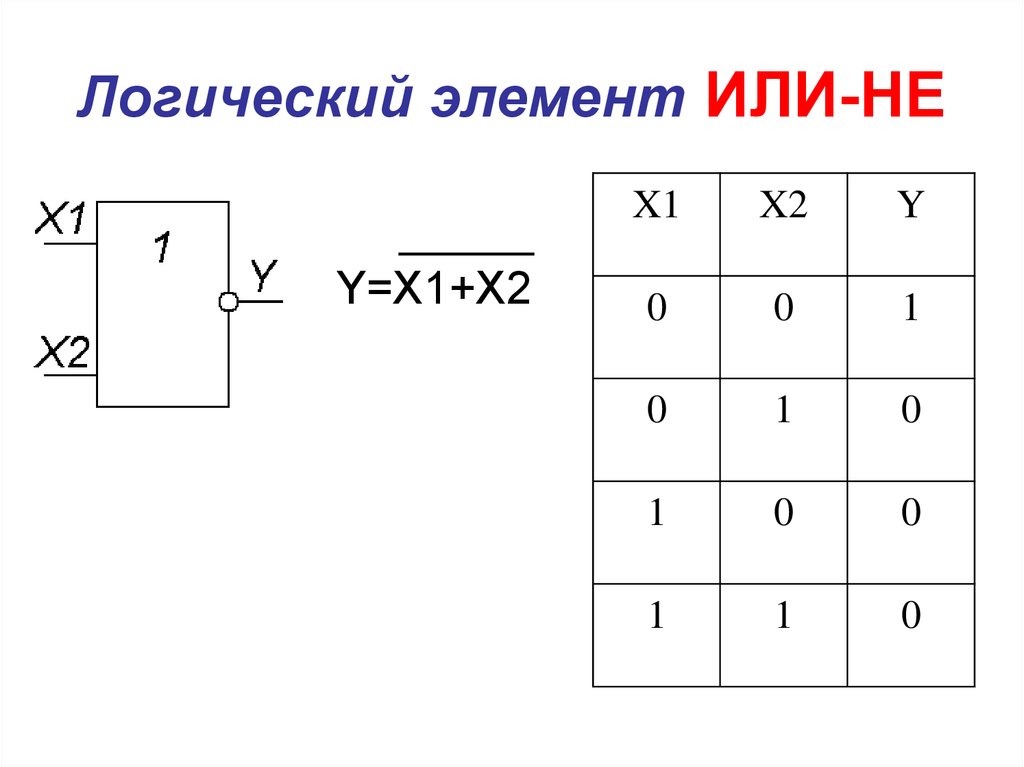 Индукция и силлогизм
Индукция и силлогизм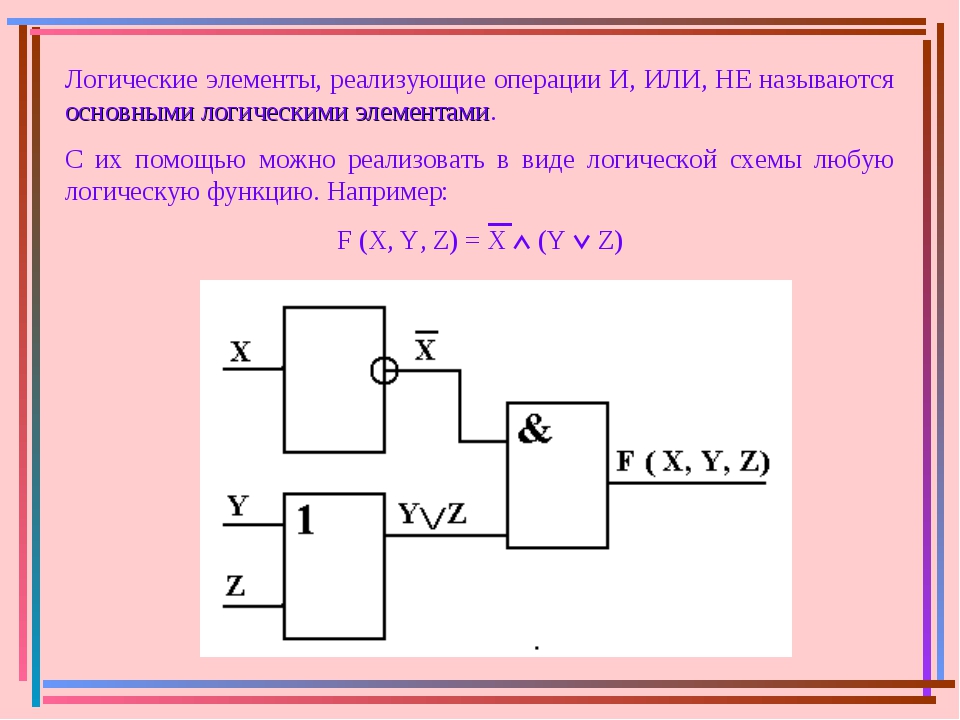 ) Ричарда Уэйтли Элементов логики г., он уже защищал силлогизм от шотландских философов, которые говорили о замене его предполагаемой системой индуктивной логики. Он требовал, чтобы его индуктивная логика «дополняла, а не заменяла». В течение нескольких лет он тщетно искал…
) Ричарда Уэйтли Элементов логики г., он уже защищал силлогизм от шотландских философов, которые говорили о замене его предполагаемой системой индуктивной логики. Он требовал, чтобы его индуктивная логика «дополняла, а не заменяла». В течение нескольких лет он тщетно искал…