Физический смысл коэффициента упругости: Лабораторная работа 116
alexxlab | 21.04.2023 | 0 | Разное
Лабораторная работа 116
Лабораторная работа № 116
Определение
коэффициента упругости
Цель работы: Экспериментальное определение коэффициента упругости стальной пружины методом колебаний.
Приборы и принадлежности: пружинный маятник, секундомер, грузы, технические весы.
Теоретическое введение
Под действием приложенных к нему сил всякое реальное тело деформируется, т.е. изменяет свои размеры и форму. Если после прекращения действия сил тело принимает первоначальные размеры и форму, деформация называется упругой. Упругие деформации наблюдаются в том случае, если сила, обусловившая деформацию, не превосходит некоторый, определенный для каждого тела, предел.
Опыт показывает, что при упругой деформации
для тела выполняется закон Гука, который гласит: упругая сила пропорциональна
абсолютному удлинению тела, т.
,
где k – коэффициент упругости тела; Dl – абсолютное удлинение.
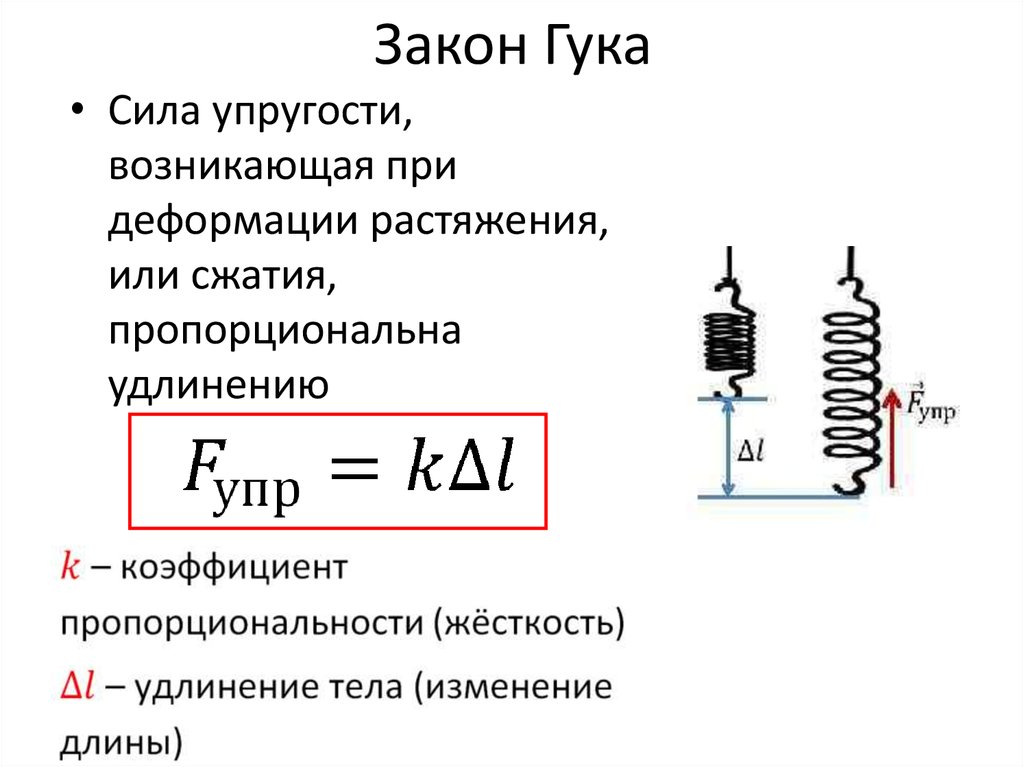
Рассмотрим пружинный маятник, представляющий собой упругую пружину с коэффициентом упругости k, на одном конце которой подвешено тело массой m, а другой конец закреплен (рис.1).
В свободном состоянии
маятника на тело массой m действуют
сила тяжести и упругая сила ,
которые равны по величине и противоположны по направлению. Поэтому тело
массой m будет находиться в
состоянии покоя (равновесия) (рис.1). Приложим к телу массой m внешнюю силу ,
которая сместит тело из положения равновесия вниз на расстояние х (рис.2), затем уберем эту силу и
предоставим маятник самому себе. Под действием упругой силы тело
возвращается в положение равновесия, по достижению его тело по инерции будет
двигаться вверх, сжимая пружину.
|
|
||
|
Рис. 1 |
Рис. |
Рис. 3 |
Найдем уравнение колебания пружинного маятника и период колебания. Для этого используем закон сохранения механической энергии. В любой момент времени полная механическая энергия пружинного маятника остается постоянной, если отсутствуют диссипативные силы и система изолирована. Тогда сумма кинетической энергии и потенциальной энергии - постоянна
где υ – скорость тела, х – смещение тела от положения равновесия, причем
.
Продифференцировав (1) по времени, получим
,
Откуда
.
Обозначив
,
получим
Соотношение (3) является дифференциальным уравнением гармонического колебания пружинного маятника, совершающегося с циклической частотой w. Циклическая частота равна числу полных колебаний, совершаемых за время 2
Решением дифференциального уравнения (3) служит уравнение гармонического колебания
где х – смещение колеблющегося тела от положения равновесия в момент времени t; А – амплитуда колебания, равная наибольшему смещению тела от положения равновесия; j0 – начальная фаза колебания.
Период колебания, равный времени, за которое совершается одно полное колебание, определяется формулой
Период колебания
пружинного маятника зависит от коэффициента упругости пружины и массы
колеблющегося тела.
Из формулы (5) коэффициент упругости пружины равен
Описание рабочей установки и метода измерений
Рабочая установка представляет собой пружинный маятник (рис.3), состоящий из груза Г, подвешенного к пружине б. Пружина крепится к перекладине, закрепленной на двух штативах а.
Если груз вывести из состояния покоя, то под действием упругой силы пружины он начнет совершать гармонические колебания. Зная массу груза m и период колебаний Т, по формуле (6) легко находится коэффициент упругости пружины k.
Правильность найденного значения коэффициента упругости k проверяется по формуле, являющейся выражением закона Гука:
где P = mg
– вес груза, под действием которого пружина удлиняется на величину Dl. Значение Dl отсчитывают по смещению миллиметровой
линейки в, укрепленной с пружиной
относительно указателя смещения g.
Значение Dl отсчитывают по смещению миллиметровой
линейки в, укрепленной с пружиной
относительно указателя смещения g.
Ход работы
1. Подобрать массу груза так, чтобы можно было легко считать число колебаний маятника. Определить массу груза m взвешиванием на технических весах.
2. Исходя из 30-50 полных колебаний, определить период колебаний груза
,
где <t> – среднее время n
полных колебаний.Время t измерить секундомером. С данным грузом время t измерить не менее 5 раз для одного и того же числа колебаний и определить среднее значение времени <t>.
3.
По формуле (6) найти значение коэффициента упругости k.
4. Грузы привести в статическое состояние, и, по смещению линейки относительно указателя, определить удлинение пружины Dl под действием веса груза.
5. По формуле (7) найти среднее значение kпров.
6. Опыт повторить при другой массе груза.
7. Вычислить абсолютную и относительную погрешности коэффициента упругости k.
8. Данные занести в таблицу.
|
№ |
т |
п |
t |
<t> |
T |
<k> |
Dl |
P |
kпров |
Е |
|
|
кг |
|
с |
с |
с |
Н/м |
м |
Н |
Н/м |
% |
|
|
|
|
|
|
|
|
|
|
|
|
Вопросы для допуска к работе
1. Какова цель работы?
Какова цель работы?
2. Запишите рабочую формулу и поясните величины, входящие в нее.
3. Опишите рабочую установку и ход эксперимента.
4. Оцените погрешность метода измерений коэффициента упругости.
Вопросы для защиты работы
1. Опишите колебания пружинного маятника.
2. Выведите дифференциальное уравнение гармонического колебания для пружинного маятника.
3. Напишите уравнение гармонического колебания пружинного маятника и поясните физический смысл всех величин.
4. Дайте определение циклической частоты и периода колебания.
5. От чего зависят циклическая частота и период колебания пружинного маятника?
6. Выведите рабочую формулу.
7. Каков физический смысл коэффициента упругости?
Каков физический смысл коэффициента упругости?
8. Какие колебания называются свободными? Вынужденными?
9. Вычислите погрешность результата эксперимента, пользуясь дифференцированным методом.
Лабораторная работа 4. Определение коэффициента упругости пружины (4 ч)
Цель – определить коэффициент упругости пружины двумя способами: 1) используя зависимость периода упругих колебаний от массы; 2) по закону Гука.
Приборы и материалы: пружина, площадка для грузов, набор грузов, секундомер, линейка.
Описание установки
Установка (рис. 4.1, 4.2) представляет собой пружину, верхний конец которой жестко соединен с кронштейном. К кронштейну прикреплена измерительная линейка. К нижнему концу пружины подвешивается площадка, на которую можно помещать различный набор грузов.
Рис. 4. 1 Рис. 4.2
1 Рис. 4.2
Задание 1. Определение коэффициента упругости пружины по закону Гука
1. Записать формулу для определения коэффициента упругости по закону Гука.
2. Продумать и записать порядок выполнения работы (рис. 4.2).
3. Составить таблицу для значений измеряемых величин и произвести необходимые измерения.
Задание 2. Определение коэффициента упругости пружины из зависимости периода упругих колебаний от массы груза
1. Навесить на пружину груз в 100 г, при этом общая масса будет равна
, (4.1)
где mnp – масса пружины,
mгр – масса груза,
тпл – масса площадки.
2.
Слегка оттянуть пружину и отпустить.
Система придет в колебательное движение.
По секундомеру определить время t,
в течение которого происходит 20–30
полных колебаний системы. Опыт повторить
не менее трех раз и найти среднее значение < t >.
Из полученных данных определить средний
период < T
> по формуле
Опыт повторить
не менее трех раз и найти среднее значение < t >.
Из полученных данных определить средний
период < T
> по формуле
. (4.2)
3. Добавляя грузы по 100 г, аналогично определить < T2 >,< T3 >.
4. Полученные данные занести в табл. 4.1.
5. Для каждого значения периода < T > определить коэффициент упругости пружины K1 , K2 , K3 из формулы
, откуда .
Найти среднее значение < K >.
6. Сравнить значения коэффициента упругости, полученные при выполнении заданий 1 и 2.
7. Сделать выводы.
Таблица 4.1
Измеряемые и расчетные величины для определения коэффициента упругости к
Номер измерений i | Масса колеблющейся системы | Число колебаний n | Время колебаний | Средний период колебаний < T > | Коэффициент упругости | ||
t | < t > | ||||||
K | < K > | ||||||
1 | |||||||
2 | |||||||
3 | |||||||
Контрольные вопросы
1. Дайте определение
гармонического колебания.
Дайте определение
гармонического колебания.
2. Дайте определение кинематических характеристик гармонического колебания: амплитуды, периода, частоты, фазы колебания.
3. Запишите уравнения смещения, скорости и ускорения при колебательном движении, их максимальные значения.
4. Получите формулу периода упругих колебаний.
5. Объясните физический смысл коэффициента упругости.
Литература [5, § 141, 142].
Лабораторная работа 5. Определение силы земного притяжения с помощью математического маятника (4 ч)
Цель – экспериментально определить модуль ускорения силы земного тяготения в данном географическом месте.
Приборы и материалы: маятник на нити изменяемой длины, шкалы с подвижным угольником и двумя барабанами, секундомер.
Самый быстрый словарь в мире | Vocabulary.com
ПЕРЕЙТИ К СОДЕРЖАНИЮ
- 05″>
коэффициент вязкости мера сопротивления потоку жидкости под действием приложенной силы
добросовестный, характеризующийся крайней осторожностью и большими усилиями
коэффициент расширения Относительное изменение длины, площади или объема на единицу изменения температуры при заданном постоянном давлении
модуль упругости (физический) отношение приложенного напряжения к изменению формы упругого тела
коэффициент самоиндукции Отношение электродвижущей силы, создаваемой в цепи за счет самоиндукции, к скорости изменения вызывающего ее тока, выраженное в генри
39″>коэффициент трения отношение веса объекта, перемещаемого по поверхности, к силе, поддерживающей контакт между объектом и поверхностью
коэффициент отражения доля лучистой энергии, которая отражается от поверхности
коэффициент корреляции Статистический показатель, показывающий, насколько близко ковариируются две переменные
коэффициент поглощения Мера скорости уменьшения интенсивности электромагнитного излучения (как света) при его прохождении через данное вещество; доля падающей лучистой энергии, поглощаемая на единицу массы или толщины поглотителя
77″>зимнее солнцестояние 22 декабря, когда солнце находится в самой южной точке
ученый-когнитивист Ученый, изучающий когнитивные процессы
Calycanthus floridus выносливый кустарник с юго-востока США, имеющий древесину с запахом гвоздики и ароматные красно-коричневые цветы
неэластичность отсутствие эластичности
коэффициент согласования коэффициент согласования (согласованности) между различными множествами ранговых порядков одного и того же множества вещей
18″>Trachinotus falcatus крупная промысловая рыба; найдено в водах Вест-Индии
концентричность качество наличия одного и того же центра
коэффициент упругости (физический) отношение приложенного напряжения к изменению формы упругого тела
коэффициент сопротивления отношение сопротивления тела, движущегося в воздухе, к произведению скорости и площади поверхности тела
коэффициент взаимной индукции мера индукции между двумя цепями
добросовестно с крайней добросовестностью
Что нужно знать о коэффициентах эластичности
Обновлено 25 августа 2022 г. Джейкоб Рид
На экзаменах по микроэкономике 2015 и 2016 годов FRQ были сосредоточены на эластичности и расчете коэффициентов эластичности. Некоторые из моих учеников чувствовали себя недостаточно подготовленными к решению этих сложных вопросов. Чтобы убедиться, что это больше не повторится, я создал приведенный ниже обзор эластичности вместе с 15 вопросами Расчеты и интерпретации коэффициента эластичности , чтобы проверить ваши навыки. Если повезет, он предоставит вам все, что вам нужно знать об эластичности, чтобы вы не были застигнуты врасплох, когда в мае начнется экзамен AP.
Основы и эластичность спроса по цене
Эластичность – это степень, в которой одно изменение вызывает другое изменение. Поскольку эластичность спроса по цене проще всего понять, мы начнем с нее. Мы знаем, что когда цены растут, объем спроса уменьшается. Эластичность говорит нам, насколько уменьшается величина спроса.
Когда большое изменение цены вызывает небольшое изменение объема спроса, кривая спроса относительно IN эластична. То есть потребители относительно IN чувствителен к изменению цены. Относительно неэластичные кривые спроса имеют тенденцию быть более вертикальными, чем горизонтальными. Если потребители требуют одинаковое количество товара независимо от цены, кривая спроса совершенно неэластична; IN потребители совершенно чувствительны к изменению цены. Совершенно неэластичные кривые спроса вертикальны.
Товары с неэластичными кривыми спроса, как правило, являются:
- Товары первой необходимости.

- Товары, у которых мало заменителей.
- Относительно недорогие товары.
Когда небольшое изменение цены вызывает большое изменение объема спроса, кривая спроса является относительно E эластичной. То есть E потребители особенно чувствительны к изменению цены. Кривые относительно эластичного спроса имеют тенденцию быть более горизонтальными, чем вертикальными. Если потребители будут требовать любое количество по одной максимальной цене, кривая спроса будет совершенно эластичной; потребители совершенно чувствительны к изменению цен. Кривые абсолютно эластичного спроса горизонтальны.
Товары, которые имеют эластичные кривые спроса, тогда будут:
- Товары, которые не являются необходимостью.
- Товары, имеющие множество заменителей.
- Относительно дорогие продукты
Существует еще один тип эластичности, и он называется единичной эластичностью. Кривая единичной эластичности спроса будет иметь рост цен, вызывающий пропорциональное уменьшение объема спроса.
Примечание. Глядя на форму кривой спроса, нельзя определить эластичность. Эластичность линейной кривой спроса уменьшается по мере увеличения количества (см. тест TR ниже)
Проверка общей выручки
Когда речь идет об эластичности спроса по цене, самым простым способом определения эластичности является проверка общей выручки (TR). Формула общего дохода: P x Q. На кривой спроса объемы падают по мере роста цен, а объемы растут по мере снижения цен. Если цена растет, а TR увеличивается (P и TR движутся в одном направлении), кривая спроса неэластична. Если цена падает, а TR уменьшается (опять же P и TR идут в одном направлении, кривая спроса также неэластична. Если цена растет, а TR падает (P и TR идут в противоположных направлениях, кривая спроса эластична. Если цена падает, а TR растет (снова PR и TR движутся в противоположных направлениях, кривая спроса также эластична. Если изменения цены не изменяют TR, кривая спроса является единично эластичной (увеличение или снижение цены сохраняет TR неизменной)9. 0003
0003
Прямолинейная кривая спроса имеет эластичный участок вверху, неэластичный участок внизу и точку единичной эластичности в середине. Если на графике есть кривая предельного дохода (вы увидите ее, узнавая о монополиях и фирмах с монополистической конкуренцией), она может помочь вам определить эластичность. Снижение цены увеличивает общий доход по мере увеличения количества, пока предельный доход больше нуля. Участок единичной эластичности кривой спроса находится там, где MR=0. Тогда снижение цены уменьшает общую выручку, поскольку предельная выручка отрицательна. В этом диапазоне кривая спроса неэластична.
Примечание. ТЕСТ ОБЩЕГО ДОХОДА ПРИМЕНЯЕТСЯ ТОЛЬКО К ЭЛАСТИЧНОСТИ СПРОСА ПО ЦЕНЕ.
Коэффициент эластичности
Другим способом определения эластичности является расчет коэффициента. Коэффициент говорит нам о пропорциях, в которых изменение цены изменяет количество. Например, коэффициент -2 говорит нам о том, что повышение цены на заданный процент вызовет вдвое большее уменьшение количества. С другой стороны, коэффициент -0,5 вызовет уменьшение объема спроса на половину (поскольку 0,5 составляет 1/2) процента повышения цены. Основная формула для расчета коэффициента – это %∆Q/%∆P (∆ означает изменение). После расчета коэффициента абсолютное значение (то есть положительное или отрицательное значение не имеет значения) можно использовать для определения эластичности. Значения эластичности следующие:
С другой стороны, коэффициент -0,5 вызовет уменьшение объема спроса на половину (поскольку 0,5 составляет 1/2) процента повышения цены. Основная формула для расчета коэффициента – это %∆Q/%∆P (∆ означает изменение). После расчета коэффициента абсолютное значение (то есть положительное или отрицательное значение не имеет значения) можно использовать для определения эластичности. Значения эластичности следующие:
- Абсолютное значение коэффициента = 0: совершенно неэластичный
- Абсолютное значение коэффициента <1 (но не ноль): относительно неэластичный
- Абсолютное значение коэффициента = 1: единичная эластичность ∞ или неопределенный): относительно эластичный
- Абсолютное значение коэффициента = ∞ или неопределенный: абсолютно эластичный.
Примечание. Это значения эластичности для всех типов эластичности.
Формулы процентного изменения коэффициента эластичности: Метод конечной точки
Метод конечной точки для расчета процентного изменения является самым простым и прямым. Кроме того, это (пока что) все, что нужно для расчета коэффициентов на опубликованных экзаменах по микроэкономике Advanced Placement Exams. Проблема с этим методом заключается в том, что он не так точен, как формула средней точки, и направление изменения может вызвать у вас проблемы.
Кроме того, это (пока что) все, что нужно для расчета коэффициентов на опубликованных экзаменах по микроэкономике Advanced Placement Exams. Проблема с этим методом заключается в том, что он не так точен, как формула средней точки, и направление изменения может вызвать у вас проблемы.
Пример: если количество увеличивается со 100 до 150, это означает увеличение на 50 %, поскольку (150 – 100)/100 x 100 = 50 %. Но если вы пойдете в обратном направлении (от 150 до 100), вы получите изменение на 33 ⅓ %. Эта разница будет означать, что вы получите 2 разных коэффициента в зависимости от того, какие числа вы используете в качестве нового и старого. Хитрость заключается в том, чтобы следовать направлению вопроса. Таким образом, если количество увеличится со 100 до 150 при снижении цены со 100 до 75 долларов, процентное изменение количества составит 50%, а процентное изменение цены составит -25%. И %∆Q/%∆P=50%/-25%=-2, поэтому эта кривая спроса эластична по цене.
Формулы процентного изменения коэффициента эластичности: Метод средней точки
Метод средней точки расчета процентного изменения устраняет проблемы направления, связанные с вычислением процентного изменения. Это связано с тем, что для расчета процентного изменения требуется средняя средняя точка между новой и старой ценой/количеством.
Недостатком этого метода является то, что экзамен AP по микроэкономике не позволяет учащимся использовать калькуляторы, а математические расчеты с помощью этого метода часто более сложны. Какой метод вы предпочитаете, действительно зависит от вас. Но выбирайте с умом.
Формула средней точки для %∆Ценовая эластичность
Как упоминалось выше, %∆Q/%∆P даст вам коэффициент ценовой эластичности. Кривые спроса имеют отрицательный коэффициент ценовой эластичности из-за обратной зависимости кривой спроса между ценой и количеством. Кривые предложения имеют положительный коэффициент ценовой эластичности из-за прямой зависимости между ценой и количеством. Эластичность спроса по цене определяется количеством заменителей, тем, насколько необходим товар и какой частью дохода потребителя требуется оплатить этот товар. Эластичность предложения по цене определяется ценами на альтернативные ресурсы, наличием ресурсов, временем, необходимым для производства продукта, и т. д.
Эластичность спроса по цене определяется количеством заменителей, тем, насколько необходим товар и какой частью дохода потребителя требуется оплатить этот товар. Эластичность предложения по цене определяется ценами на альтернативные ресурсы, наличием ресурсов, временем, необходимым для производства продукта, и т. д.
Эластичность по доходу
Эластичность по доходу показывает, насколько изменение дохода потребителя вызывает изменение величины спроса. Нормальные товары (большинство товаров попадают в эту категорию) — это товары, которые потребители покупают больше, когда их доходы растут, и меньше, когда их доходы падают. Товары низшего качества — это такие товары, как однослойная туалетная бумага, рамен высшего качества или непатентованные брендовые товары. Когда доходы потребителей растут, потребители покупают меньше этих товаров, а когда доходы падают, они покупают больше.
Одним из неценовых определяющих факторов спроса является изменение дохода. Эластичность дохода говорит нам, насколько изменение дохода изменит спрос на товар или услугу. Формула эластичности дохода: %∆Q/%∆Income. Нормальные товары имеют положительный коэффициент эластичности по доходу, поскольку увеличение доходов вызывает увеличение спроса на нормальные товары. Некачественные товары имеют отрицательный коэффициент эластичности по доходу. Это связано с тем, что рост доходов вызывает снижение спроса на товары низшего качества.
Эластичность дохода говорит нам, насколько изменение дохода изменит спрос на товар или услугу. Формула эластичности дохода: %∆Q/%∆Income. Нормальные товары имеют положительный коэффициент эластичности по доходу, поскольку увеличение доходов вызывает увеличение спроса на нормальные товары. Некачественные товары имеют отрицательный коэффициент эластичности по доходу. Это связано с тем, что рост доходов вызывает снижение спроса на товары низшего качества.
Перекрестная эластичность цен
Перекрестная эластичность цен связана с заменителями и дополнениями. Заменители — это товары, которые можно использовать вместо друг друга; как масло и маргарин, или варенье и желе. Когда цена одного увеличивается, спрос на другой также увеличивается. Дополнения — это товары, которые используются вместе; как хлеб с маслом или зубные щетки и зубная паста. Когда цена одного увеличивается, спрос на другой снижается. Перекрестная ценовая эластичность говорит нам, насколько изменение цены одного товара влияет на спрос на другой.


 2
2