Физика формула жесткость: Что такое жесткость пружины и как ее рассчитать
alexxlab | 07.04.2023 | 0 | Разное
Обозначение жесткости в физике
Сила упругости — это сила, возникающая в результате деформации тела и стремящаяся восстановить прежние размеры и форму тела. Обозначается как F у. Связь между силой упругости и упругой деформацией тела была установлена английским физиком Гуком. Челны Нальчик Находка Нижневартовск Ниж. Детские сады и ясли Школы, гимназии, лицеи Среднее профессиональное образование ссузы Высшее образование вузы Образование за рубежом Законодательство в образовании Научно-методический раздел, библиотеки Профориентация ЕГЭ, ГИА и подготовка к поступлению Олимпиады Дополнительное образование для самых маленьких Дополнительное образование для школьников Магистратура,аспирантура, доп.
Поиск данных по Вашему запросу:
Обозначение жесткости в физике
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.

По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Измерение коэффициента жесткости пружины и экспериментальная проверка закона Гука
- Сила упругости, формула
- Глоссарий. Физика
- Сила упругости обозначение в физике. Примерами пластических деформаций являются
- Буквы, используемые для обозначения величин
- Механические свойства твердых тел, сила упругости
- Коэффициент упругости
- Коэффициент жесткости пружины
- Сила упругости и закон Гука
- I.
Механика
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Физика – первый и второй законы Ньютона
Измерение коэффициента жесткости пружины и экспериментальная проверка закона Гука
Применяется в механике твердого тела в разделе упругости. Обозначается буквой k [1] , иногда D [2] или c [3].
Коэффициент упругости численно равен силе , которую надо приложить к пружине , чтобы её длина изменилась на единицу расстояния. На каждую пружину действует одна и та же сила F.
Однородный стержень постоянного сечения, упруго деформируемый вдоль оси, имеет коэффициент жёсткости. Витая цилиндрическая пружина сжатия или растяжения, намотанная из цилиндрической проволоки и упруго деформируемая вдоль оси, имеет коэффициент жёсткости. Материал из Википедии — свободной энциклопедии.
Материал из Википедии — свободной энциклопедии.
Technische Mechanik: Kinematik und Kinetik. Категории : Теория упругости Механика. Пространства имён Статья Обсуждение. Просмотры Читать Править Править код История. На других языках Добавить ссылки.
Эта страница в последний раз была отредактирована 10 апреля в Текст доступен по лицензии Creative Commons Attribution-ShareAlike ; в отдельных случаях могут действовать дополнительные условия. Подробнее см. Условия использования. Политика конфиденциальности Описание Википедии Отказ от ответственности Свяжитесь с нами Разработчики Заявление о куки Мобильная версия.
Сила упругости, формула
Сила – векторная величина. Необходимо знать точку приложения и направление каждой силы. Важно уметь определить какие именно силы действуют на тело и в каком направлении. Сила обозначается как , измеряется в Ньютонах. Для того, чтобы различать силы, их обозначают следующим образом. Ниже представлены основные силы, действующие в природе.
Формула жесткости пружины – едва ли не самый важный момент в теме об Деформация растяжения/сжатия в физике также может.
Глоссарий. Физика
Формула жесткости пружины — едва ли не самый важный момент в теме об этих упругих элементах. Ведь именно жесткость играет очень важную роль в том, благодаря чему эти комплектующие используются так широко. Сегодня без пружин не обходится практически ни одна отрасль промышленности, они используются в приборо- и станкостроении, сельском хозяйстве, производстве горно-шахтного и железнодорожного оборудования, энергетике, других отраслях. Они верой и правдой служат в самых ответственных и критических местах различных агрегатов, где требуются присущие им характеристики, в первую очередь жесткость пружины, формула которой в общем виде очень проста и знакома детям еще со школы. Любая пружина представляет собой упругое изделие, которое в процессе эксплуатации подвергается статическим, динамическим и циклическим нагрузкам. Основная особенность этой детали — она деформируется под приложенным извне усилием, а когда воздействие прекращается — восстанавливает свою первоначальную форму и геометрические размеры. В период деформации происходит накопление энергии, при восстановлении — ее передача. Именно это свойство возвращаться к исходному виду и принесло широкое распространение этим деталям: они отличные амортизаторы, элементы клапанов, предупреждающие превышение давления, комплектующие для измерительных приборов. В этих и других ситуациях, благодаря умению упруго деформироваться, они выполняют важную работу, поэтому от них требуется высокое качество и надежность. Видов этих деталей существует много, самыми распространенными являются пружины растяжения и сжатия.
В период деформации происходит накопление энергии, при восстановлении — ее передача. Именно это свойство возвращаться к исходному виду и принесло широкое распространение этим деталям: они отличные амортизаторы, элементы клапанов, предупреждающие превышение давления, комплектующие для измерительных приборов. В этих и других ситуациях, благодаря умению упруго деформироваться, они выполняют важную работу, поэтому от них требуется высокое качество и надежность. Видов этих деталей существует много, самыми распространенными являются пружины растяжения и сжатия.
Сила упругости обозначение в физике. Примерами пластических деформаций являются
При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества. Ее называют силой упругости. Простейшим видом деформации являются деформации растяжения и сжатия рис.
Главная Новости сайта Вспомни физику: 7 класс 8 класс 9 класс класс задачи кл.
Буквы, используемые для обозначения величин
Применяется в механике твердого тела в разделе упругости. Обозначается буквой k [1] , иногда D [2] или c [3]. Коэффициент упругости численно равен силе , которую надо приложить к пружине , чтобы её длина изменилась на единицу расстояния. На каждую пружину действует одна и та же сила F. Однородный стержень постоянного сечения, упруго деформируемый вдоль оси, имеет коэффициент жёсткости. Витая цилиндрическая пружина сжатия или растяжения, намотанная из цилиндрической проволоки и упруго деформируемая вдоль оси, имеет коэффициент жёсткости.
Механические свойства твердых тел, сила упругости
Формулировка этого закона выглядит следующим образом: сила упругости, которая появляется в момент деформации тела, пропорциональна удлинению тела и направлена противоположно движению частиц этого тела относительно других частиц при деформации. Сила измеряется в Ньютонах, а удлинение тела — в метрах. Для раскрытия физического смысла жесткости, нужно в формулу для закона Гука подставить единицу, в которой измеряется удлинение — 1 м, заранее получив выражение для k. Эта формула показывает, что жесткость тела численно равна силе упругости, которая возникает в теле пружине , когда оно деформируется на 1 м. Известно, что жесткость пружины зависит от ее формы, размера и материала, из которого произведено данное тело.
Эта формула показывает, что жесткость тела численно равна силе упругости, которая возникает в теле пружине , когда оно деформируется на 1 м. Известно, что жесткость пружины зависит от ее формы, размера и материала, из которого произведено данное тело.
Для раскрытия физического смысла жесткости, нужно в формулу для закона Гука подставить единицу, в которой измеряется удлинение – 1 м, заранее.
Коэффициент упругости
Обозначение жесткости в физике
Рассмотрим движение автомобиля. Например, если автомобиль за каждую четверть часа 15 мин проходит 15 км, за каждые полчаса 30 мин – 30 км, а за каждый час – 60 км, считается, что он движется равномерно. Если тело за любые равные промежутки времени проходит равные пути, его движение считается равномерным.
Коэффициент жесткости пружины
Пружины можно назвать одной из наиболее распространенных деталей, которые являются частью простых и сложных механизмов. При ее изготовлении применяется специальная проволока, накручиваемая по определенной траектории. Выделяют довольно большое количество различных параметров, характеризующих это изделие. Наиболее важным можно назвать коэффициент жесткости. Он определяет основные свойства детали, может рассчитываться и применяться в других расчетах. Рассмотрим особенности подобного параметра подробнее.
Выделяют довольно большое количество различных параметров, характеризующих это изделие. Наиболее важным можно назвать коэффициент жесткости. Он определяет основные свойства детали, может рассчитываться и применяться в других расчетах. Рассмотрим особенности подобного параметра подробнее.
Механические свойства твердых тел. Силы притяжения и отталкивания обуславливают механическую прочность твердых тел.
Сила упругости и закон Гука
Математические формулы Формулы по физике Поиск. Электростатика Постоянный ток Магнитное поле Электромагнитная индукция Механические колебания Механические волны Электромагнитные колебания Переменный ток Электромагнитные волны Фотометрия Геометрическая лучевая оптика Волновая оптика Квантовая оптика Термодинамика Пар, жидкости, твёрдое состояние Теория относительности Атом и ядро атома Кинематика Динамика Статика Законы сохранения механической энергии Давление жидкости и газа Молекулярная кинетика Тепловые явления Электрический ток в металлах. Формулы по физике Динамика Динамика. Инертность, масса, ускорение. F – сила m – масса a – ускорение. N – сила тяжести m – масса g – ускорение свободного падения.
Формулы по физике Динамика Динамика. Инертность, масса, ускорение. F – сила m – масса a – ускорение. N – сила тяжести m – масса g – ускорение свободного падения.
I. Механика
На нашем сайте собрано более бесплатных онлайн калькуляторов по математике, геометрии и физике. Не можете решить контрольную?! Мы поможем! Более 20 авторов выполнят вашу работу от руб!
Задачи на тему “Сила упругости. Закон Гука” с решениями
Можно не знать закон Ома и сидеть дома. Но если не знаешь закон Гука – лучше тоже не выходить. Особенно, если идешь на экзамен по физике.
Здесь устраняем пробелы в знаниях и разбираемся, как решать задачи на силу упругости и применение закона Гука. А за полезной рассылкой для студентов добро пожаловать на наш телеграм-канал.
Сила упругости и закон Гука: определения
Сила упругости – сила, препятствующая деформациям и стремящаяся восстановить первоначальные форму и размеры тела.
Примеры действия силы упругости:
- пружины сжимаются и разжимаются в матрасе;
- мокрое белье колышется на натянутой веревке;
- лучник натягивает тетиву, чтобы выпустить стрелу.
Простейшие деформации – деформации растяжения и сжатия.
Закон Гука:
Деформация, возникающая в упругом теле под действием внешней силы, пропорциональна величине этой силы.
Коэффициент k – жесткость материала.
Есть и другая формулировка закона Гука. Введем понятие относительной деформации «эпсилон» и напряжения материала «сигма»:
S – площадь поперечного сечения деформируемого тела. Тогда закон Гука запишется так: относительная деформация пропорциональна напряжению.
Здесь Е – модуль Юнга, зависящий от свойств материала.

Вопросы на силу упругости и закон Гука
Вопрос 1. Какие бывают деформации?
Ответ. Помимо простейших деформаций растяжения и сжатия, бывают сложные деформации кручения и изгиба. Также разделяют обратимые и необратимые деформации.
Вопрос 2. В каких случаях закон Гука справедлив для упругих стержней?
Ответ. Для упругих стержней (в отличие от эластичных тел) закон Гука можно применять при малых деформациях, когда величина эпсилон не превышает 1%. При больших деформациях возникают явления текучести и необратимого разрушения материала.
Вопрос 3. Как направлена сила упругости?
Ответ. Сила упругости направлена в сторону, противоположную направлению перемещения частиц тела при деформации.
Вопрос 4. Какую природу имеет сила упругости?
Ответ. Сила упругости, как и сила трения – электромагнитная сила. Она возникает вследствие взаимодействия между частицами деформируемого тела.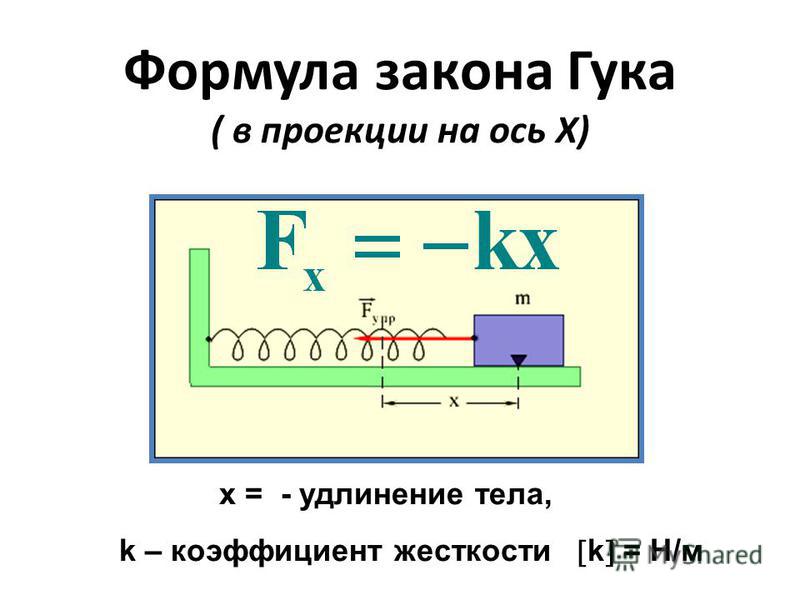 6 Н/м2.
6 Н/м2.
Решение
Запишем закон Гука:
По третьему закону Ньютона:
Ответ: 10 кН.
Задача №2. Нахождение жесткости пружины
Условие
Пружину, жесткость которой 100 Н/м, разрезали на две части. Чему равна жесткость каждой пружины?
Решение
По определению, жесткость обратно-пропорциональна длине. При одинаковой силе F неразрезанная пружина растянется на х, а разрезанная – на x1=x/2.
Ответ: 200 Н/м
При растяжении пружины в ее витках возникают сложные деформации кручения и изгиба, однако мы не учитываем их при решении задач.
Задача №3. Нахождение ускорения тела
Условие
Тело массой 2 кг тянут по гладкой горизонтальной поверхности с помощью пружины, которая при движении растянулась на 2 см. Жесткость пружины 200 Н/м. Определить ускорение, с которым движется тело. 2.
2.
Задача №4. Нахождение жесткости пружины по графику
Условие
На графике изображена зависимость модуля силы упругости от удлинения пружины. Найти жесткость пружины.
Решение
Вспоминаем, что жесткость равна отношению силы и удлинения. Представленная зависимость – линейная. В любой точке прямой отношение ординаты F и абсциссы х дает результат 10 Н/м.
Ответ: k=10 Н/м.
Задача №5. Определение энергии деформации
Условие
Для сжатия пружины на х1=2 см надо приложить силу 10 Н. Определить энергию упругой деформации пружины при сжатии на х2=4 см из недеформированного состояния.
Решение
Энергия сжатой пружины равна:
Ответ: 0,4 Дж.
Нужна помощь в решении задач? Обращайтесь за ней в профессиональный студенческий сервис.
Простое гармоническое движение
Простое гармоническое движение Частота простого гармонического движения, подобного массе на пружине, определяется массой m и жесткостью пружины, выраженной через жесткость пружины k (см. Если период T = Движение описывается
Любой из параметров в уравнении можно рассчитать, щелкнув активное слово в приведенном выше соотношении. Для любых отсутствующих данных будут введены значения по умолчанию, но эти значения можно изменить и повторить расчет.
| Индекс Концепции периодического движения | |||||||||||
|
| Индекс Концепции периодического движения | ||||||
|
Масса на пружине будет описывать синусоидальную форму в зависимости от времени, как и любой объект, вибрирующий в простом гармоническом движении. Показать преобразование энергии, связанное с этим движением | Индекс | |
|
Простое гармоническое движение массы на пружине является примером преобразования энергии между потенциальной энергией и кинетической энергией. В приведенном ниже примере предполагается, что для приведения массы в движение была совершена работа в 2 Дж.
| Индекс Концепции периодического движения | |
|
Расчет жесткости линейно-упругих конструкций.
 Часть 1
Часть 1Сегодня мы познакомимся с понятием жесткости конструкции и узнаем, как можно вычислить жесткость линейно-упругой конструкции, подвергаемой только механической нагрузке. В частности, мы рассмотрим, как его можно вычислить и интерпретировать в различных измерениях пространства моделирования (0D и 1D) и какие факторы влияют на жесткость конструкции.
Что такое структурная жесткость?
Когда внешняя сила пытается деформировать упругое тело, тело сопротивляется этой силе. Это сопротивление обозначается как жесткость . Мы часто небрежно используем этот термин как свойство материала, тогда как на самом деле это может быть свойство различных геометрических и материальных параметров. Мы рассмотрим эти случаи здесь.
Прежде чем мы углубимся, нам нужно математически определить жесткость. Предположим, что сила F 0 , действующая на тело, деформирует его на величину u 0 . Если нам потребуется небольшая сила ΔF, чтобы деформировать тело на бесконечно малую величину Δu, то отношение этих двух величин даст нам жесткость тела в рабочей точке, обозначаемую переменными состояния F 0 и и 0 .
Это определение линеаризованной жесткости , которое, как правило, может использоваться как для линейных, так и для нелинейных кривых зависимости силы от смещения. Соотношение сила-смещение и линеаризованная жесткость могут быть математически выражены с помощью следующих уравнений соответственно:
F(u)=F_0+k(F_0,u_0)(u-u_0)
k(F_0,u_0)=\lim_{\Delta u \to 0}\frac{\Delta F}{\Delta u}=\left.\frac{\partial F}{\partial u}\right|_{F=F_0,u=u_0}
Типичная кривая зависимости силы от смещения для линейной упругой конструкции.
Пример задачи
При моделировании различных типов структурных систем одной из целей анализа может быть получение эффективного значения жесткости и интерпретация его объема на основе того, как мы вычисляем его из имеющейся структурной проблемы. . Жесткость, в общем, может быть функцией свойств материала, ориентации материала, геометрических размеров, направления нагрузки, типа ограничения и выбора пространственной области, в которой применяются нагрузки и ограничения.
Для иллюстрации мы будем использовать стальную балку длиной L = 1 м, шириной b = 0,2 м и толщиной t = 0,1 м. Сторона балки, параллельная плоскости yz и расположенная в точке x = 0, жестко закреплена (т.е. нулевые перемещения в направлениях х , у и z ). На грань, параллельную плоскости yz и расположенную в точке x = L, действует равномерно распределенная сила. Все остальные грани балки не связаны и не нагружены. Следовательно, они могут свободно деформироваться.
Сплошная балка длиной L, шириной b и толщиной t, стороны которой ориентированы по направлениям x, y и z декартовой системы координат.
Мы рассчитаем жесткость этой балки как аналитически, так и с помощью COMSOL Multiphysics, сравнивая решения, полученные этими двумя методами.
Изучение пространственных измерений моделирования
Приступая к моделированию конструкции, одним из важнейших решений, которое нам необходимо сделать, является решение о том, насколько подробно мы действительно заинтересованы.
Для этого мы должны попытаться ответить на следующие вопросы — и, возможно, на несколько других, в зависимости от цели моделирования:
- Есть ли пространственная неоднородность в свойствах материала?
- Есть ли пространственная неоднородность приложенной силы?
- Изменяются ли геометрические размеры конструкции неравномерно в определенных направлениях?
- Существуют ли какие-либо плоскости симметрии, которые мы можем определить на основе симметрии в геометрии моделирования, приложенных нагрузках и ожидаемом профиле решения?
- Есть ли интересующие нас локальные эффекты, например вокруг отверстий или углов?
- Можно ли пренебречь напряжениями или деформациями в определенных направлениях?
Жесткость в 0D-моделях
Мы начнем с рассмотрения 0D-модели балки, в которой все эффекты, связанные с нагрузкой, деформацией и реакцией материала, сосредоточены в одной точке в пространстве, а вся балка моделируется как одна пружина. .
.
0D-представление балки с использованием сосредоточенной жесткости k с силой F, действующей на балку, которая вызывает смещение u. В этом случае 0D-модель также является представлением балки с одной степенью свободы (SDOF).
Предполагая, что сталь ведет себя как твердое тело Гука (т. е. напряжение линейно пропорционально деформации ниже предела текучести), мы можем записать зависимость между напряжением и деформацией, используя модуль Юнга E материала как \sigma=E \эпсилон.
Используя упрощенное определение, где напряжение равно силе на единицу площади поперечного сечения, \sigma=F/A, где A=bt, а деформация равна отношению деформации к первоначальной длине, \epsilon=u/ L, и, объединив их, мы получим F=(EA/L)u. Это дает нам линейную зависимость силы от смещения, так что жесткость не зависит от рабочей точки, а также от любых пространственных изменений силы, смещения и свойств материала.
Следовательно, мы можем выразить осевую жесткость балки для этой 0D-модели следующим уравнением: осевая жесткость балки k = 4×10 9 Н/м.
В COMSOL Multiphysics можно моделировать 0D-вариант с помощью интерфейса Global ODEs и DAE (для моделирования, зависящего от времени) или путем простой настройки Parameters или Variables в модели пространственного измерения 0D.
Скриншот таблицы параметров в программе COMSOL.
Жесткость в 1D-моделях
В действительности мы знаем, что балка закреплена на одном конце, а сила приложена к другому. Следовательно, деформация или смещение (u) неодинакова в каждом поперечном сечении по длине. Чтобы включить этот эффект, нам нужно создать как минимум 1D-модель.
Расчет осевой жесткости 92}=0
с граничными условиями на двух концах: u=0 при x=0 и E\frac{du}{dx}=\frac{F}{A} (закон Гука) при x=L.
Объединяя все это, получаем u(x)=\frac{Fx}{EA}, где x — расстояние от закрепленного конца балки, а u(x) — смещение по длине балки. Одномерная модель представляет собой бесконечное количество последовательно соединенных друг с другом пружин. Это позволяет получить более подробную информацию о пространственном изменении перемещений, напряжений и деформаций в балке. Однако это также означает, что каждая из этих пружин имеет собственную жесткость. Предполагая, что модуль Юнга и площадь поперечного сечения не изменяются по длине балки, если мы дискретизируем балку на n-количество последовательно соединенных пружин, в нашем случае жесткость каждой пружины (k i ) будет k_i=nEA/L.
Это позволяет получить более подробную информацию о пространственном изменении перемещений, напряжений и деформаций в балке. Однако это также означает, что каждая из этих пружин имеет собственную жесткость. Предполагая, что модуль Юнга и площадь поперечного сечения не изменяются по длине балки, если мы дискретизируем балку на n-количество последовательно соединенных пружин, в нашем случае жесткость каждой пружины (k i ) будет k_i=nEA/L.
Однако, если мы хотим связать 1D-модель с 0D-моделью, мы должны представить, что вся балка аппроксимируется одной пружиной. Следовательно, эквивалентная жесткость в 1D будет отношением максимального осевого смещения и осевой силы в месте приложения силы. В этом случае u будет максимальным при x = L, где его значение будет u_{max}=FL/EA. Это дает нам эквивалентную одномерную жесткость одномерной балки как:
k=\frac{EA}{L}
Это указывает на то, что для заданных параметров моделирования решение (k = 4×10 9 Н/м) 1D-модели стремится к решению 0D-модели при оценке при x = L.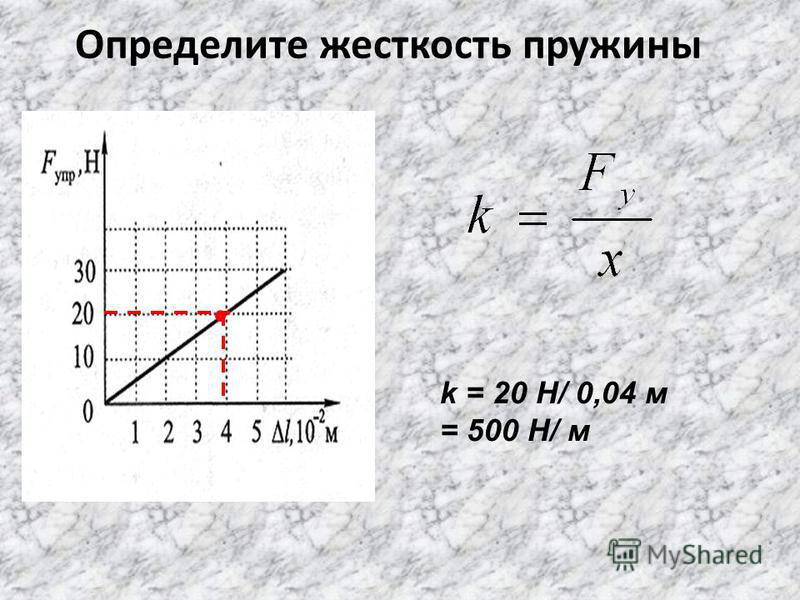
Расчет жесткости на изгиб
Дополнительным преимуществом перехода к одномерной модели является то, что теперь мы можем исследовать влияние направления нагрузки. Хотя мы ограничиваемся одномерным пространством, мы можем вычислить внеплоскостные смещения v и w, соответственно, вдоль «невидимой» y – и z – направления, когда сила действует на балку вдоль этих направлений. Обратите внимание, что на основе выбранных граничных условий (балка без зажимов) компоненты смещения v и w будут изменяться в зависимости от координаты x .
Одномерное представление балки, полученное с использованием баланса изгибающего момента в теле.
Исследование этого сценария также означало бы, что мы должны были бы ввести дополнительные условия жесткости, которые бы коррелировали изгибающую силу с смещениями вне плоскости. Это потребовало бы от нас решения следующего уравнения баланса моментов: 93}=F
В этих уравнениях мы использовали смещение (w) вдоль направления z для целей представления. Та же идея справедлива и для смещения (v) вдоль y -направления. Полагая, что деформация много меньше размеров балки, эти выражения можно физически интерпретировать следующим образом.
Та же идея справедлива и для смещения (v) вдоль y -направления. Полагая, что деформация много меньше размеров балки, эти выражения можно физически интерпретировать следующим образом.
Первая производная смещения вне плоскости по координате x представляет наклон; вторая производная представляет кривизну; а третья производная пропорциональна сдвигающей силе. В этих уравнениях член 92(3L-x)}{6EI_{yy}}
Следовательно, эквивалентная жесткость на изгиб в 1D будет отношением максимального смещения вне плоскости и изгибающей нагрузки в месте приложения силы. В этом случае как v, так и w были бы максимальными в точке x = L, когда сила приложена там вдоль направлений y – и z соответственно. Это дает нам две возможные эквивалентные одномерные изгибные жесткости одномерной балки в зависимости от направления нагрузки.
93}. Для заданных параметров моделирования k yy = 4×10 7 Н/м и k zz = 1×10 7 Н/м.
Вычисление жесткости в COMSOL Multiphysics
В COMSOL Multiphysics можно настроить одномерную модель, сначала выбрав двухмерное или трехмерное пространственное измерение, а затем используя интерфейс Ферма или Балка .
Здесь мы покажем вам, как использовать интерфейс Beam в трехмерном пространственном измерении для расчета как осевой жесткости, так и жесткости на изгиб. Одномерная структура будет смоделирована как балка Эйлера-Бернулли. Программное обеспечение COMSOL также позволяет использовать теорию балок Тимошенко, которая больше подходит для точного одномерного моделирования конструкций с низким коэффициентом удлинения.
Вот рабочий процесс для получения жесткости из 1D-модели:
Снимок 1D-модели, сделанный с использованием интерфейса Beam . Определены переменные для оценки осевой жесткости (k xx ) и жесткости на изгиб (k yy и k zz ). Оператор средней связи используется для оценки перемещений в точке x = L.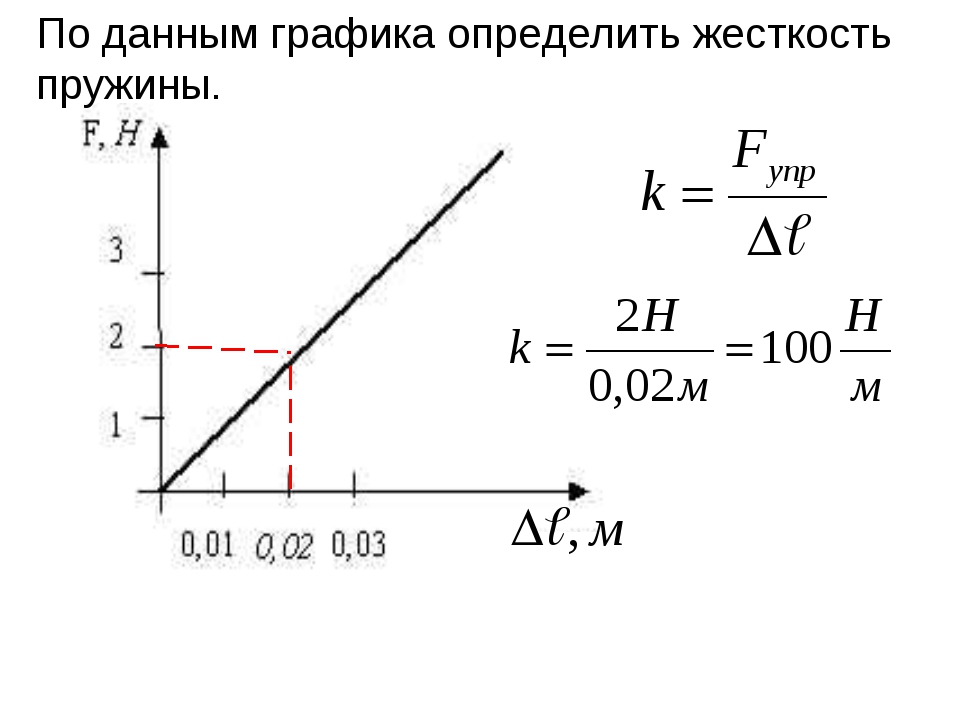 Оператор
Оператор with() используется для получения решения из различных загружений, для которых рассчитывается модель.
Моментальный снимок граничных условий, используемых в интерфейсе Beam . Ветвь точечной нагрузки назначается точке, расположенной в точке x = L.
В этой модели мы используем силу (точечную нагрузку) F 0 = 1×10 4 Н. Пока вы не включать любые нелинейные эффекты в вашу модель, вы можете использовать произвольную величину нагрузки. Если есть нелинейности, то важно использовать правильную точку линеаризации. Такие случаи будут обсуждаться в следующем блоге.
Как показано здесь, вы можете создать «переключатель», используя оператор if() и имена (например, root.group.lg1 ), связанные с группами загрузки , так что только один компонент вектор силы можно сделать отличным от нуля, когда вы решаете одну и ту же модель для нескольких загружений.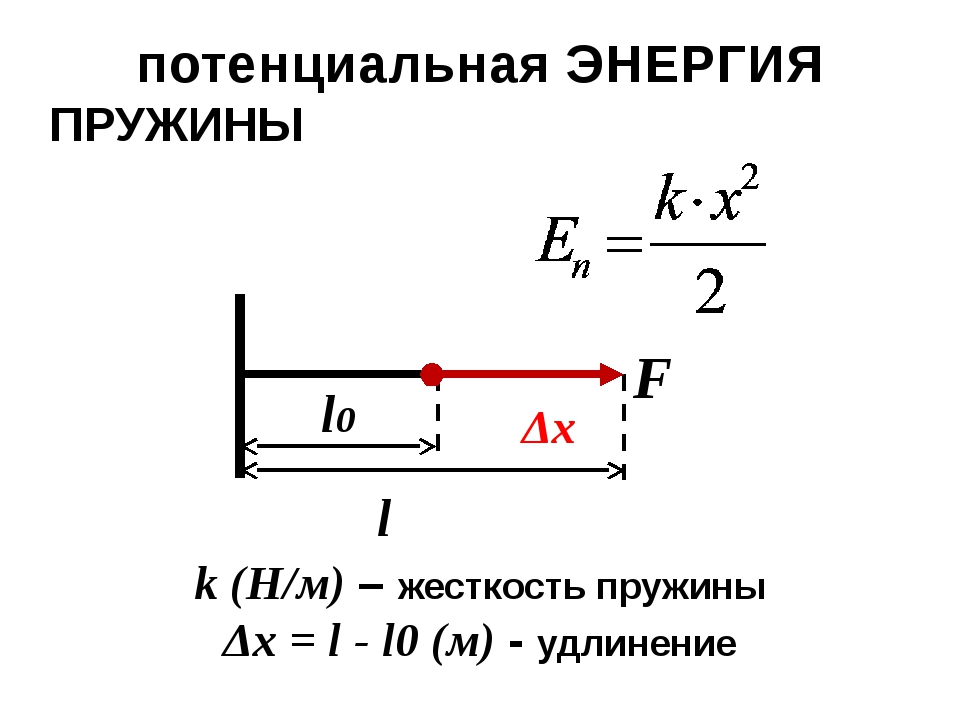
Снимок настроек исследования, показывающий, как загружения настраиваются для активации только одного компонента вектора силы за раз. Глобальная оценка используется для печати значений k xx , k yy и k zz . Программные решения COMSOL точно соответствуют аналитическим решениям.
Показанный здесь подход к оценке компонентов жесткости применим до тех пор, пока мы не ожидаем какой-либо связи между растяжением и изгибом (т. е. когда матрица жесткости является диагональной). Мы представим более общий вычислительный подход во второй части этой серии блогов.
Далее мы можем решить ту же модель, используя теорию пучка Тимошенко. Как и ожидалось, это даст точно такой же результат для осевой жесткости (k xx = 4×10 9 Н/м), но поперечная жесткость будет меньше той, что мы получили из теории Эйлера-Бернулли. Деформация сдвига, учитываемая при использовании теории балки Тимошенко, через модуль сдвига будет иметь небольшую зависимость от коэффициента Пуассона, поэтому нам также необходимо включить это в данные о материале.



 закон Гука):
закон Гука): 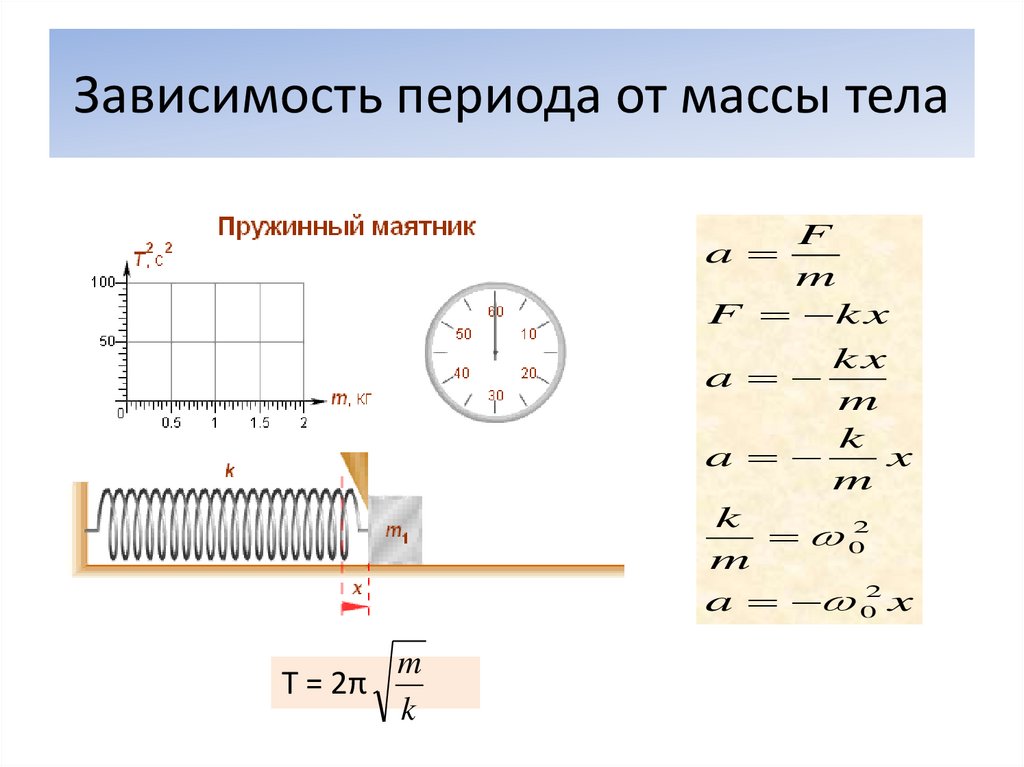
 Один из способов визуализировать этот паттерн — идти по прямой линии с постоянной скоростью, неся вибрирующую массу. Тогда масса проследит синусоидальный путь как в пространстве, так и во времени.
Один из способов визуализировать этот паттерн — идти по прямой линии с постоянной скоростью, неся вибрирующую массу. Тогда масса проследит синусоидальный путь как в пространстве, так и во времени.