Формула амплитуда колебаний скорости: Груз колеблется на нити длиной 2,5 м. Амплитуда колебаний составляет 10 см. Определите максимальную скорость…
alexxlab | 09.03.2023 | 0 | Разное
StudyPort.Ru – Механические и электромагнитные колебания
Страница 1 из 6
4. Колебания и волны
1. Гармонические колебания величины s описываются уравнением s = 0,02 cos (6πt + π/3), м. Определите: 1) амплитуду колебаний; 2) циклическую частоту; 3) частоту колебаний; 4) период колебаний.
2. Запишите уравнение гармонического колебательного движения точки, совершающей колебания с амплитудой A = 8 см, если за t = 1 мин совершается n = 120 колебаний и начальная фаза колебаний равна 45°.
3. Материальная точка совершает гармонические колебания с амплитудой A = 4 см и периодом T = 2 с. Напишите уравнение движения точки, если ее движение начинается из положения x0 = 2 см.
4. Точка совершает гармонические колебания с периодом T = 6 с и начальной фазой, равной нулю. Определите, за какое время, считая от начала движения, точка сместится от положения равновесия на половину амплитуды.
5. Напишите уравнение гармонического колебания точки, если его амплитуда A = 15 см, максимальная скорость колеблющейся точки vmax = 30 см/с, начальная фаза φ = 10°.
6. Точка совершает гармонические колебания по закону x = 3 cos (πt/2 + π/8), м. Определите: 1) период T колебаний: 2) максимальную скорость Vmax точки; 3) максимальное ускорение amax точки.
7. Точка совершает гармонические колебания с амплитудой A = 10 см и периодом T = 5 с. Определите для точки: 1) максимальную скорость; 2) максимальное ускорение.
8. Скорость материальной точки, совершающей гармонические колебания, задается уравнением v(t) = -6 sin 2 πt, м/с. Запишите зависимость смещения этой точки от времени.
9. Материальная точка совершает колебания согласно уравнению x = A sin ωt. В какой-то момент времени смещение точки x1 = 15 см. При возрастании фазы колебания в два раза смещение x2 оказалось равным 24 см. Определите амплитуду A колебания.
10. Материальная точка совершает гармонические колебания согласно уравнению x = 0,02 cos (πt + π/2), м. Определите: 1) амплитуду колебаний; 2) период колебаний; 3) начальную фазу колебаний; 4) максимальную скорость точки; 5) максимальное ускорение точки; 6) через сколько времени после начала отсчета точка будет проходить через положение равновесия.
11. Определите максимальные значения скорости и ускорения точки, совершающей гармонические колебания с амплитудой A = 3 см и периодом T = 4 с.
12. Материальная точка, совершающая гармонические колебания с частотой ν = 1 Гц, в момент времени t = 0 проходит положение, определяемое координатой х0 = 5 см, со скоростью v0 = -15 см/с. Определите амплитуду колебаний.
13. Тело массой m = 10 г совершает гармонические колебания по закону х = 0,1 cos(4πt + π/4), м. Определите максимальные значения: 1) возвращающей силы; 2) кинетической энергии.
14. Материальная точка массой m = 50 г совершает гармонические колебания согласно уравнению x = 0,1 cos 3πt/2, м. Определите: 1) возвращающую силу F для момента времени t = 0,5 с; 2) полную энергию Е точки.
15. Материальная точка массой m = 20 г совершает гармонические колебания по закону x = 0,1 cos(4πt + π/4), м. Определите полную энергию Е этой точки.
16.
Полная энергия E гармонически колеблющейся точки равна 10 мкДж, а максимальная сила Fmax, действующая на точку, равна -0,5 мН. Напишите уравнение движения этой точки, если период T колебаний равен 4 с, а начальная фаза φ = π/6.
17. Определите отношение кинетической энергии T точки, совершающей гармонические колебания, к ее потенциальной энергии П, если известна фаза колебания.
18. Определите полную энергию материальной точки массой m, колеблющейся по закону x = A cos(ω0t + φ).
19. Груз, подвешенный к спиральной пружине, колеблется по вертикали с амплитудой A = 8 см. Определите жесткость k пружины, если известно, что максимальная кинетическая энергия Tmax груза составляет 0,8 Дж.
20. Материальная точка колеблется согласно уравнению х = A cos ωt, где A = 5 см и ω = π/12 с-1. Когда возвращающая сила F в первый раз достигает значения -12 мН, потенциальная энергия П точки оказывается равной 0,15 мДж.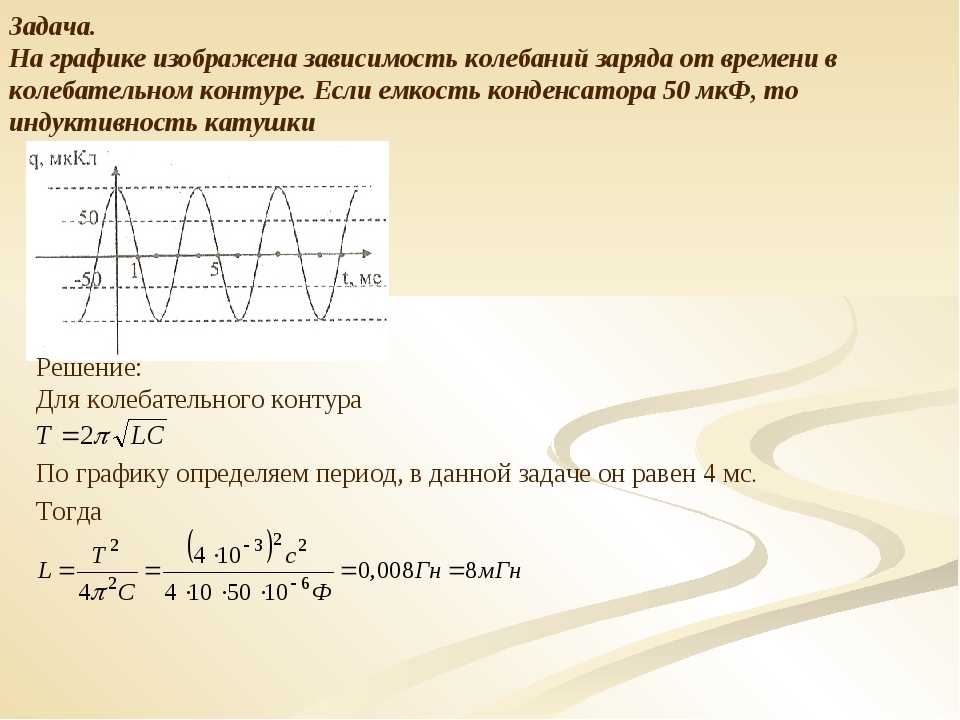
Определите: 1) этот момент времени t; 2) соответствующую этому моменту фазу ωt.
Основные формулы по физике – колебания и волны. Связь между периодом и круговой частотой
При изучении этого раздела следует иметь в виду, что колебания различной физической природы описываются с единых математических позиций. Здесь надо четко уяснить такие понятия, как гармоническое колебание, фаза, разность фаз, амплитуда, частота, период колебани.
Надо иметь в виду, что во всякой реальной колебательной системе есть сопротивления среды, т.е. колебания будут затухающими. Для характеристики затухания колебаний вводится коэффициент затухания и логарифмический декремент затухани.
Если колебания совершаются под действием внешней, периодически изменяющейся силы, то такие колебания называют вынужденными. Они будут незатухающими. Амплитуда вынужденных колебаний зависит от частоты вынуждающей силы. При приближении частоты вынужденных колебаний к частоте собственных колебаний амплитуда вынужденных колебаний резко возрастает.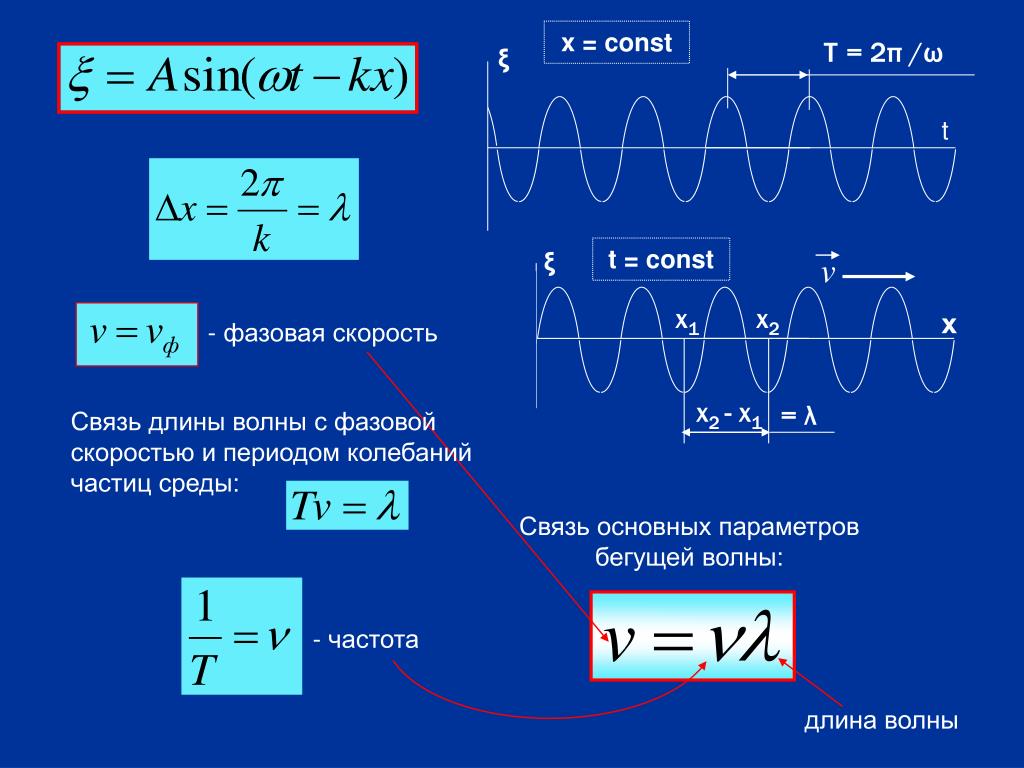
Это явление называется резонансом.
Переходя к изучению электромагнитных волн нужно четко представлять, что электромагнитная волна – это распространяющееся в пространстве электромагнитное поле. Простейшей системой, излучающей электромагнитные волны, является электрический диполь. Если диполь совершает гармонические колебания, то он излучает монохроматическую волну.
Таблица формул: колебания и волны
Физические законы, формулы, переменные | Формулы колебания и волны | ||||
Уравнение гармонических колебаний: где х – смещение (отклонение) колеблющейся величины от положения равновесия; А – амплитуда; ω – круговая (циклическая) частота; α – начальная фаза; (ωt+α) – фаза. | |||||
Связь между периодом и круговой частотой: | |||||
Частота: | |||||
Связь круговой частоты с частотой: | |||||
Периоды собственных колебаний 1) пружинного маятника: где k – жесткость пружины; 2) математического маятника: где l – длина маятника, g – ускорение свободного падения; 3) колебательного контура: где L – индуктивность контура, С – емкость конденсатора. | |||||
Частота собственных колебаний: | |||||
Сложение колебаний одинаковой частоты и направления: 1) амплитуда результирующего колебания где А 1 и А 2 – амплитуды составляющих колебаний, α 1 и α 2 – начальные фазы составляющих колебаний; 2) начальная фаза результирующего колебания | |||||
Уравнение затухающих колебаний: е = 2,71… – основание натуральных логарифмов. | |||||
Амплитуда затухающих колебаний: где А 0 – амплитуда в начальный момент времени; β – коэффициент затухания; | |||||
Коэффициент затухания: колеблющегося тела где r – коэффициент сопротивления среды, m – масса тела; колебательного контура где R – активное сопротивление, L – индуктивность контура. | |||||
Частота затухающих колебаний ω: | |||||
Период затухающих колебаний Т: | |||||
Логарифмический декремент затухания: |
(лат. amplitude — величина) — это наибольшее отклонение колеблющегося тела от положения равновесия.
Для маятника это максимальное расстояние, на которое удаляется ша-рик от своего положения равновесия (рисунок ниже). Для колебаний с малыми амплитудами за такое расстояние можно принимать как длину дуги 01 или 02, так и длины этих отрезков.
Амплитуда колебаний измеряется в единицах длины — метрах , санти-метрах и т. д. На графике колебаний амплитуда определяется как макси-мальная (по модулю) ордината синусоидальной кривой, (см. рис. ниже).
Период колебаний.
Период колебаний — это наименьший промежуток времени, через который система, соверша-ющая колебания, снова возвращается в то же состояние, в котором она находилась в начальный момент времени, выбранный произвольно.
Другими словами, период колебаний (Т ) — это время, за которое совершается одно полное ко-лебание. Например, на рисунке ниже это время, за которое грузик маятника перемещается из крайней правой точки через точку равновесия
За полный период колебаний, таким образом, тело проходит путь, равный четы-рем амплитудам. Период колебаний измеряется в единицах времени — секундах , минутах и т. д. Период колебаний может быть определен по известному графику колебаний, (см. рис. ниже).
Понятие «период колебаний», строго говоря, справедливо, лишь когда значения колеблющей-ся величины точно повторяются через определенный промежуток времени, т. е. для гармоничес-ких колебаний. Однако это понятие применяется также и для случаев приблизительно повторяю-щихся величин, например, для затухающих колебаний .
Частота колебаний.
Частота колебаний — это число колебаний, совершаемых за единицу времени, например, за 1 с .
Единица частоты в СИ названа герцем (Гц ) в честь немецкого физика Г. Герца (1857-1894). Если частота колебаний (v ) равна 1 Гц , то это значит, что за каждую секунду совершается одно колебание. Частота и период колебаний связаны соотношениями:
В теории колебаний пользуются также понятием циклической , или круговой частоты ω . Она связана с обычной частотой v и периодом колебаний Т соотношениями:
.
Циклическая частота — это число колебаний, совершаемых за 2π секунд.
Сила Кориолиса равна:
где – точечнаямасса ,-вектор угловой скорости вращающейся системы отсчёта,- вектор скорости движения точечной массы в этой системе отсчёта, квадратными скобками обозначена операциявекторного произведения .
Величина называется кориолисовым ускорением.
По физической природе
Механические
Электромагнитные (свет ,радиоволны , тепловые)
Смешанного типа – комбинации вышеперечисленных
По характеру взаимодействия с окружающей средой
Вынужденные –
колебания, протекающие в системе под
влиянием внешнего периодического
воздействия.
Примеры: листья на деревьях,
поднятие и опускание руки. При вынужденных
колебаниях может возникнуть явлениерезонанса :
резкое возрастание амплитуды колебаний
при совпадениисобственной
частоты осциллятора и частоты внешнего воздействия.
Свободные (или собственные) – это колебания в системе под действием внутренних сил, после того как система выведена из состояния равновесия (в реальных условиях свободные колебания всегдазатухающие ). Простейшими примерами свободных колебаний являются колебания груза, прикреплённого к пружине, или груза, подвешенного на нити.
Автоколебания – колебания, при которых система имеет запаспотенциальной энергии , расходующейся на совершение колебаний (пример такой системы –механические часы ). Характерным отличием автоколебаний от вынужденных колебаний является то, что их амплитуда определяется свойствами самой системы, а не начальными условиями.
Параметрические –
колебания, возникающие при изменении
какого-либо параметра колебательной
системы в результате внешнего воздействия.
Случайные – колебания, при которых внешняя или параметрическая нагрузка является случайным процессом.
Гармонические колебания
где х А ω
Обобщенное гармоническое колебание в дифференциальном виде
(Любое нетривиальное
Скорость и ускорение при гармонических колебаниях.
Согласно определению скорости, скорость – это производная от координаты по времени
Таким образом, мы видим, что скорость при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания скорости опережают колебания смещения по фазе на p/2.
Величина – максимальная скорость колебательного движения (амплитуда колебаний скорости).
Следовательно, для скорости при гармоническом колебании имеем: ,
а для случая нулевой начальной фазы (см. график).
Согласно определению ускорения, ускорение – это производная от скорости по времени:
–
вторая производная от координаты по
времени.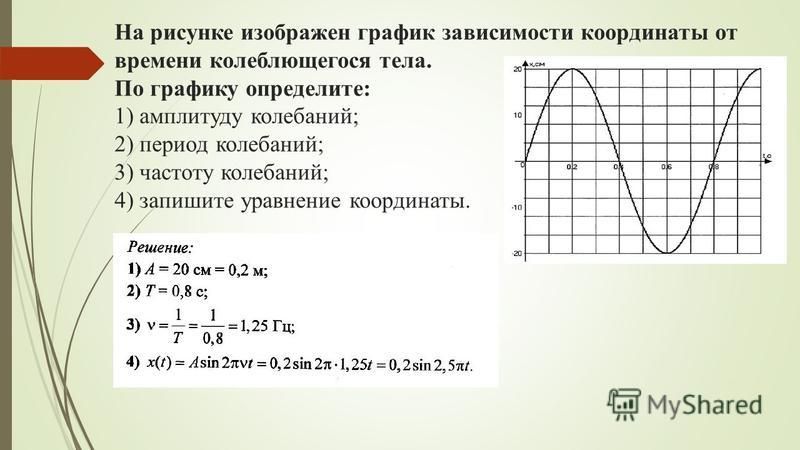
Тогда:
.
Ускорение при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания ускорения опережают колебания скорости на p/2 и колебания смещения наp(говорят, что колебания происходятв противофазе) .
Величина
Максимальное ускорение (амплитуда колебаний ускорения). Следовательно, для ускорения имеем: ,
а для случая нулевой начальной фазы: (см. график).
Из анализа процесса колебательного движения, графиков и соответствующих математических выражений видно, что при прохождении колеблющимся телом положения равновесия (смещение равно нулю) ускорение равно нулю, а скорость тела максимальна (тело проходит положение равновесия по инерции), а при достижении амплитудного значения смещения – скорость равна нулю, а ускорение максимально по модулю (тело меняет направление своего движения).
Гармонические
колебания – колебания, при которых
физическая (или любая другая) величина
изменяется с течением времени по
синусоидальному или косинусоидальному
закону.
Кинематическое уравнение
гармонических колебаний имеет вид
где х – смещение (отклонение) колеблющейся точки от положения равновесия в момент времени t;
Обобщенное гармоническое колебание в дифференциальном виде
(Любое нетривиальное решение этого дифференциального уравнения – есть гармоническое колебание с циклической частотой)
До сих пор мы рассматривали собственные колебания, т. е. колебания, происходящие в отсутствие внешних воздействий. Внешнее воздействие было нужно лишь для того, чтобы вывести систему из состояния равновесия, после чего она предоставлялась самой себе. Дифференциальное уравнение собственных колебаний вообще не содержит следов внешнего воздействия на систему: это воздействие отражается лишь в начальных условиях.
Установление колебаний. Но очень часто приходится сталкиваться с колебаниями, которые происходят при постоянно присутствующем внешнем воздействии. Особенно важен и в то же время достаточно прост для изучения случай, когда внешняя сила имеет периодический характер. Общей чертой вынужденных колебаний, происходящих под действием периодической внешней силы, является то, что спустя некоторое время после начала действия внешней силы система полностью «забывает» свое начальное состояние, колебания приобретают стационарный характер и не зависят от начальных условий. Начальные условия проявляются только в период установления колебаний, который обычно называют переходным процессом.
Синусоидальное воздействие. Рассмотрим вначале наиболее простой случай вынужденных колебаний осциллятора под действием внешней силы, изменяющейся по синусоидальному закону:
Рис. 178. Возбуждение вынужденных колебаний маятника
Такое внешнее воздействие на систему можно осуществить различными способами.
Например, можно взять маятник в виде шарика на длинном стержне и длинную пружину с малой жесткостью и прикрепить ее к стержню маятника недалеко от точки подвеса, как показано на рис. 178. Другой конец горизонтально расположенной пружины следует заставить двигаться по закону ? с помощью кривошипно-шатунного механизма, приводимого в движение электромотором. Действующая
на маятник со стороны пружины вынуждающая сила будет практически синусоидальна, если размах движения левого конца пружины В будет много больше амплитуды колебаний стержня маятника в точке закрепления пружины С.
Уравнение движения. Уравнение движения для этой и других подобных систем, в которых наряду с возвращающей силой и силой сопротивления на осциллятор действует вынуждающая внешняя сила, синусоидально изменяющаяся со временем, можно записать в виде
Здесь левая часть в соответствии со вторым законом Ньютона, является произведением массы на ускорение. Первый член в правой части представляет собой возвращающую силу, пропорциональную смещению из положения равновесия.
Для подвешенного на пружине груза это упругая сила, а во всех других случаях, когда ее физическая природа иная, эту силу называют квазиупругой. Второе слагаемое есть сила трения, пропорциональная скорости, например сила сопротивления воздуха или сила трения в оси. Амплитуду и частоту со раскачивающей систему вынуждающей силы будем считать постоянными.
Разделим обе части уравнения (2) на массу и введем обозначения
Теперь уравнение (2) принимает вид
В отсутствие вынуждающей силы правая часть уравнения (4) обращается в нуль и оно, как и следовало ожидать, сводится к уравнению собственных затухающих колебаний.
Опыт показывает, что во всех системах под действием синусоидальной внешней силы в конце концов устанавливаются колебания, которые также происходят по синусоидальному закону с частотой вынуждающей силы со и с постоянной амплитудой а, но с некоторым сдвигом по фазе относительно вынуждающей силы. Такие колебания называются установившимися вынужденными колебаниями.
Установившиеся колебания. Рассмотрим вначале именно установившиеся вынужденные колебания, причем для простоты пренебрежем трением. В этом случае в уравнении (4) не будет члена, содержащего скорость:
Попробуем искать решение соответствующее установившимся вынужденным колебаниям, в виде
Вычислим вторую производную и подставим ее вместе с в уравнение (5):
Чтобы это равенство было справедливо в любой момент времени, коэффициенты при слева и справа должны быть одинаковы. Из этого условия находим амплитуду колебаний а:
Исследуем зависимость амплитуды а от частоты вынуждающей силы. График этой зависимости показан на рис. 179. При формула (8) дает Подставив сюда значения видим, что постоянная во времени сила просто смещает осциллятор в новое положение равновесия, сдвинутое от старого на Из (6) следует, что при смещение
как, очевидно, и должно быть.
Рис. 179. График зависимости
Фазовые соотношения. По мере роста частоты вынуждающей силы от 0 до установившиеся колебания происходят в фазе с вынуждающей силой а их амплитуда постоянно увеличивается, сначала медленно, а по мере приближения со к – все быстрее и быстрее: при амплитуда колебаний неограниченно возрастает
При значениях со, превосходящих частоту собственных колебаний формула (8) дает для а отрицательное значение (рис.
179). Из формулы (6) ясно, что при колебания происходят в противофазе с вынуждающей силой: когда сила действует в одну сторону, осциллятор смещен в противоположную. При неограниченном увеличении частоты вынуждающей силы амплитуда колебаний стремится к нулю.
Амплитуду колебаний во всех случаях удобно считать положительной, чего легко добиться, вводя сдвиг фаз между вынуждающей
силой и смещением:
Здесь а по-прежнему дается формулой (8), а сдвиг фазы равен нулю при и равен при Графики зависимости от частоты вынуждающей силы показаны на рис. 180.
Рис. 180. Амплитуда и фаза вынужденных колебаний
Резонанс. Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы имеет немонотонный характер. Резкое увеличение амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к собственной частоте осциллятора называется резонансом.
Формула (8) дает выражение для амплитуды вынужденных колебаний в пренебрежении трением. Именно с этим пренебрежением связано обращение амплитуды колебаний в бесконечность при точном совпадении частот Реально амплитуда колебаний в бесконечность, конечно же, обращаться не может.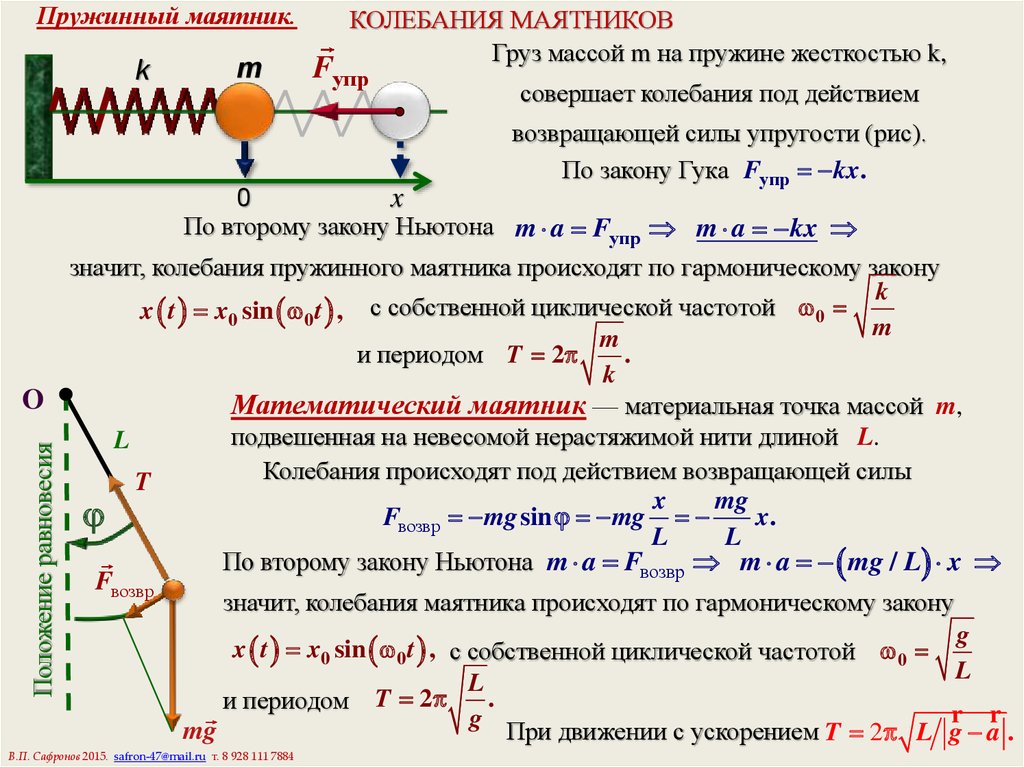
Это означает, что при описании вынужденных колебаний вблизи резонанса учет трения принципиально необходим. При учете трения амплитуда вынужденных колебаний при резонансе получается конечной. Она будет тем меньше, чем больше трение в системе. Вдали от резонанса формулой (8) можно пользоваться для нахождения амплитуды колебаний и при наличии трения, если оно не слишком сильное, т. е. Более того, эта формула, полученная без учета трения, имеет физический смысл только тогда, когда трение все же есть. Дело в том, что само понятие установившихся вынужденных колебаний применимо только к системам, в которых есть трение.
Если бы трения совсем не было, то процесс установления колебаний продолжался бы бесконечно долго. Реально это означает, что полученное без учета трения выражение (8) для амплитуды вынужденных колебаний будет правильно описывать колебания в системе только спустя достаточно большой промежуток времени после начала действия вынуждающей силы. Слова «достаточно большой промежуток времени» означают здесь, что уже закончился переходный процесс, длительность которого совпадает с характерным временем затухания собственных колебаний в системе.
При малом трении установившиеся вынужденные колебания происходят в фазе с вынуждающей силой при и в противофазе при как и в отсутствие трения. Однако вблизи резонанса фаза меняется не скачком, а непрерывно, причем при точном совпадении частот смещение отстает по фазе от вынуждающей силы на (на четверть периода). Скорость изменяется при этом в фазе с вынуждающей силой, что обеспечивает наиболее благоприятные условия для передачи энергии от источника внешней вынуждающей силы к осциллятору.
Какой физический смысл имеет каждый из членов в уравнении (4), описывающем вынужденные колебания осциллятора?
Что такое установившиеся вынужденные колебания?
При каких условиях можно использовать формулу (8) для амплитуды установившихся вынужденных колебаний, полученную без учета трения?
Что такое резонанс? Приведите известные вам примеры проявления и использования явления резонанса.
Опишите сдвиг по фазе между вынуждающей силой и смещением при разных соотношениях между частотой со в вынуждающей силы и собственной частотой осциллятора.
Чем определяется длительность процесса установления вынужденных колебаний? Дайте обоснование ответа.
Векторные диаграммы. Убедиться в справедливости приведенных выше утверждений можно, если получить решение уравнения (4), описывающее установившиеся вынужденные колебания при наличии трения. Поскольку установившиеся колебания происходят с частотой вынуждающей силы со и некоторым сдвигом по фазе то решение уравнения (4), соответствующее таким колебаниям, следует искать в виде
При этом скорость и ускорение, очевидно, тоже будут изменяться со временем по гармоническому закону:
Амплитуду а установившихся вынужденных колебаний и сдвиг фазы удобно определять с помощью векторных диаграмм. Воспользуемся тем обстоятельством, что мгновенное значение любой изменяющейся по гармоническому закону величины можно представить как проекцию вектора на некоторое заранее выбранное направление, причем сам вектор равномерно вращается в плоскости с частотой со, а его неизменная длина равна
амплитудному значению этой осциллирующей величины.
В соответствии с этим сопоставим каждому члену уравнения (4) вращающийся с угловой скоростью вектор, длина которого равна амплитудному значению этого члена.
Поскольку проекция суммы нескольких векторов равна сумме проекций этих векторов, то уравнение (4) означает, что сумма векторов, сопоставляемых членам, стоящим в левой части, равна вектору, сопоставляемому величине стоящей в правой части. Чтобы построить эти векторы, выпишем мгновенные значения всех членов левой части уравнения (4), учитывая соотношения
Из формул (13) видно, что вектор длины сопоставляемый величине опережает на угол вектор сопоставляемый величине Вектор длины сопоставляемый члену х, опережает на вектор длины т. е. эти векторы направлены в противоположные стороны.
Взаимное расположение этих векторов для произвольного момента времени показано на рис. 181. Вся система векторов вращается как целое с угловой скоростью со против часовой стрелки вокруг точки О.
Рис. 181. Векторная диаграмма вынужденных колебаний
Рис.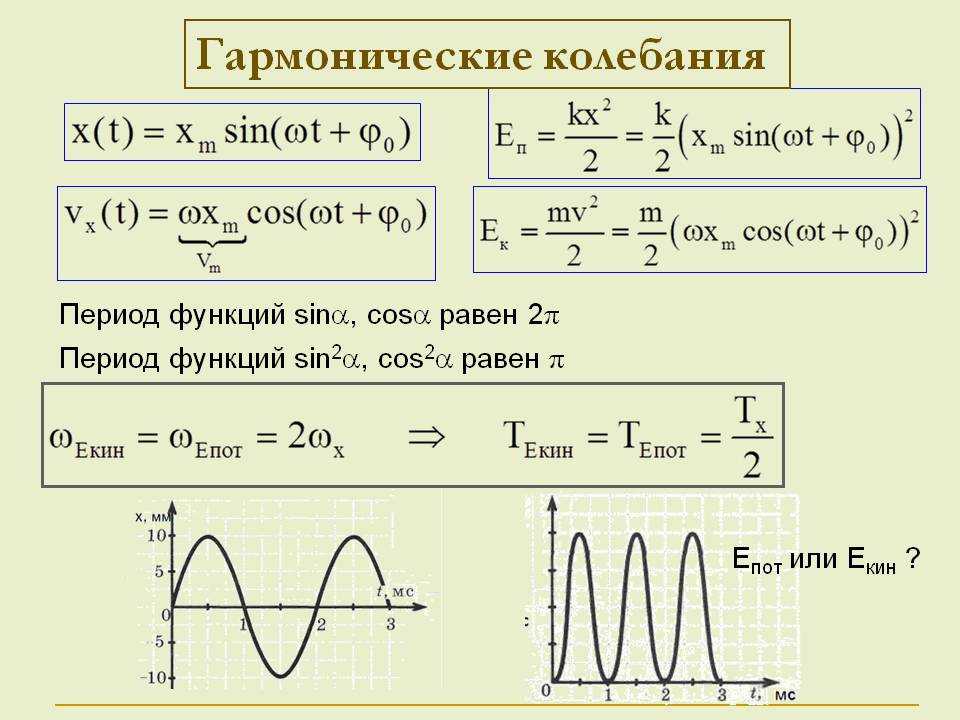
182. Вектор сопоставляемый внешней силе
Мгновенные значения всех величин получаются проецированием соответствующих векторов на заранее выбранное направление Вектор, сопоставляемый правой части уравнения (4), равен сумме векторов, изображенных на рис. 181. Это сложение показано на рис. 182. Применяя теорему Пифагора, получаем
откуда находим амплитуду установившихся вынужденных колебаний а:
Сдвиг фазы между вынуждающей силой и смещением как видно из векторной диаграммы на рис. 182, отрицателен, так как вектор длины отстает от вектора Поэтому
Итак, установившиеся вынужденные колебания происходят по гармоническому закону (10), где а и определяются формулами (14) и (15).
Рис. 183. Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы
Резонансные кривые. Амплитуда установившихся вынужденных колебаний пропорциональна амплитуде вынуждающей силы Исследуем зависимость амплитуды колебаний от частоты вынуждающей силы.
При малом затухании у эта зависимость имеет очень резкий характер. Если то при стремлении со к частоте свободных колебаний амплитуда вынужденных колебаний а стремится к бесконечности, что совпадает с полученным ранее результатом (8). При наличии затухания амплитуда колебаний в резонансе уже не обращается в бесконечность, хотя и значительно превышает амплитуду колебаний под действием внешней силы той же величины, но имеющей частоту, далекую от резонансной. Резонансные кривые при разных значениях постоянной затухания у приведены на рис. 183. Для нахождения частоты резонанса сорез, нужно найти, при каком со подкоренное выражение в формуле (14) имеет минимум. Приравнивая производную этого выражения по со нулю (или дополняя его до полного квадрата), убеждаемся, что максимум амплитуды вынужденных колебаний имеет место при
Резонансная частота оказывается меньше частоты свободных колебаний системы. При малых 7 резонансная частота практически совпадает с При стремлении частоты вынуждающей силы к бесконечности, т.
е. при амплитуда а, как видно из (14), стремится к нулю. При т. е. при действии постоянной внешней силы, амплитуда Если подставить сюда и получим Это есть статическое смещение осциллятора из положения равновесия под действием постоянной силы и смещение осциллятора происходит в противофазе с вынуждающей силой. В резонансе, как видно из (15), смещение отстает по фазе от внешней силы на Вторая из формул (13) показывает, что при этом внешняя сила изменяется в фазе со скоростью т. е. все время действует в направлении движения. Что именно так и должно быть, ясно из интуитивных соображений.
Резонанс скорости. Из формулы (13) видно, что амплитуда колебаний скорости при установившихся вынужденных колебаниях равна . С помощью (14) получаем
Рис. 184. Амплитуда скорости при установившихся вынужденных колебаниях
Зависимость амплитуды скорости от частоты внешней силы показана на рис. 184. Резонансная кривая для скорости хотя и похожа на резонансную кривую для смещения, но отличается от нее в некоторых отношениях.
Так, при т. е. при действии постоянной силы, осциллятор испытывает статическое смещение из положения равновесия и скорость его после того, как закончится переходный процесс, равна нулю. Из формулы (19) видно, что амплитуда скорости при обращается в нуль. Резонанс скорости имеет место при точном совпадении частоты внешней силы с частотой свободных колебаний
Как строятся векторные диаграммы для установившихся вынужденных колебаний при синусоидальном внешнем воздействии?
Чем определяется частота, амплитуда и фаза установившихся вынужденных гармонических колебаний?
Опишите различия резонансных кривых для амплитуды смещения и амплитуды скорости. Какими характеристиками колебательной системы определяется острота резонансных кривых?
Как связан характер резонансной кривой с параметрами системы, определяющими затухание ее собственных колебаний?
Что такое амплитуда? Амплитуда смещения частиц как рассчитать амплитуду пика звуковой волны амплитуда звукового сигнала звуковой сигнал градиент звукового давления рассчитать амплитуду в зависимости от напряжения определение скорость частиц звука термины вопрос рассчитать амплитуду максимальное смещение равновесие точное определение децибел шкала градиент давления звуковой волны RMS количество звукового поля удлинение колебания пика струны до пикового удлинения волны продольного давления длина волны период частота
Что такое амплитуда? Амплитуда смещения частиц как рассчитать амплитуду пика звуковой волны амплитуда звукового сигнала звуковой сигнал градиент звукового давления рассчитать амплитуду в зависимости от напряжения определение скорость частиц звука термины вопрос рассчитать амплитуду максимальное смещение равновесие точное определение децибел шкала градиент давления звуковой волны RMS количество звукового поля удлинение колебания пика струны до пикового удлинения продольных волн давления длина волны период частота – sengpielaudio Sengpiel Berlin| Немецкая версия |
● Что такое Амплитуда ? ●
Определение амплитуды в Условиях звука
Хороший вопрос: что понимается под амплитудой?
Какой термин обычно используется для
описать амплитуду звуковой волны?
Как рассчитать амплитуду?
В чем измеряется амплитуда?
Существует четыре термина, описывающих звуковую волну :
длина волны , период , частота 8 амплитуда
Используемый браузер не поддерживает JavaScript. 
Вы увидите программу, но функция не будет работать.
| Определение амплитуды: 1. Максимальная степень вибрации или смещения синусоидального (!) колебания, измеряемая от положение равновесия. Амплитуда – это максимальное абсолютное значение периодически изменяющегося количество. 2. Максимальное отличие переменного электрического тока или потенциала от среднего значения. Термин “амплитуда” используется для обозначения амплитуды колебаний, поэтому амплитуда синусоиды ” y = A × sin (ω×t) “, равно | A | , где | A | – абсолютное значение A . Амплитуда – переменная, характеризующая синусоидальное колебание. Она дает отклонение физическую величину от ее нейтрального положения (нулевой точки) до положительного или отрицательного значения. Амплитуда выражается физической величиной, например, напряжением, звуковым давлением и т.  д. Амплитуды выражаются либо в виде мгновенных значений, либо в основном в виде пиковых значений. Амплитуда – это отклонение или смещение волны от ее среднего значения. Со звуковыми волнами это степень смещения частиц воздуха, и эта амплитуда звука или амплитуда звука равна ощущается как громкость звука. Из «Британской энциклопедии»: Для поперечной волны, такой как волна на щипковой струне, Амплитуда измеряется максимальным смещением любой точки струны от ее положения. когда струна покоится. Амплитуда продольной волны, такой как звуковая волна, измеряется выражением максимальное смещение частицы из положения равновесия. Когда амплитуда волна неуклонно уменьшается, потому что ее энергия «теряется» (преобразуется в тепло), говорят, что демпфированный. Звуковые волны в воздухе продольные, волны давления. |
Бросьте камень в пруд
Обычно говорят об «амплитуде», как если бы была просто определенная амплитуда
как смещение или удлинение от нулевой оси (базовая линия или равновесие). Амплитуда может быть словом, которое описывает волну. Это означает, что максимальная сумма волна отличается от базовой или равновесной. Перемещение обычно используется для описывают частицы в движении, например, как далеко частица ушла от данной точки. Длина волны продольной волны относится к расстоянию между двумя последовательных сжатий или между двумя последовательными разрежениями. Определение: Амплитуда – это максимальное отклонение от равновесия. Для продольная волна, которая является волной давления, это будет максимальное увеличение (или уменьшение) давления от равновесного давления, что является причиной, когда сжатие (или разрежение) проходит точку. Амплитуда – это расстояние от положения равновесия среды до сжатия или разрежения. Пиковое значение синусоидальных сигналов переменного тока называется амплитудой, начиная с нулевая линия. Амплитуда обычно относится к скалярному или векторному размеру поля. |
Длина волны и Расстояние − Период и Время
| Амплитуда А не имеет отношения к частоте, длина волны, период времени и скорость звука.  |
| Посмотрите: «Величины звукового поля плоской волны» http://www.sengpielaudio.com/SoundfieldQuantitiesPlaneWaveAmplitude.pdf |
| Мы часто слышим вопрос: насколько велика амплитуда? В нашем случае это
“ амплитуда звука “. Обычно мы спрашиваем, как будто там просто “один” амплитуда звуковых волн в воздухе. Восприятие громкости звука – это
определяется амплитудой звуковых волн – чем выше
амплитуда, тем громче звук или шум. Какая амплитуда звука (амплитуда звука)? В приведенной выше ссылке “Величины звукового поля плоской волны” находим: амплитуду смещения частиц ξ , or displacement amplitude amplitude of sound pressure p or pressure amplitude amplitude of sound particle velocity v , or particle velocity amplitude amplitude of pressure gradient Δ p или амплитуда градиента давления.  Каждый раз, когда мы добавляем 6 дБ, фактически амплитуда сигнала удваивается. Всего этих терминов параметры звукового поля. Проблемы с количеством звуковой энергии (мощность), когда мы используем термин амплитуда. Избегайте любого применения слова «амплитуда» к уровням мощности или количества энергии. Количество звукового поля не является звуковой энергией или количество звуковой мощности. Кроме того, подумайте об амплитуде колебаний струны. Максимальная величина отклонения волны называется амплитудой. Гармоническое движение: Смещение = A × sin (2 × π × f × t ), что означает: A = частота (пиковая), t = амплитуда (пик), f = время. Скорость звуковой частицы v не следует путать со скоростью звука c или скорость звука, все измеряются в м/с: |
| Амплитуда как смещение частицы ξ = v / (2 π × f ) = p / (2 π × Z ) Pressure amplitude = Amplitude as sound pressure p = ξ × 2 π × Z = V × Z z = ρ × C Специфический акустический импеданс воздуха при 20C – Z = 413 N · S/M 9004 9.  – максимальное значение звукового давления. Поскольку звуковое давление p является периодической величиной, оно указывается как эффективное звуковое давление p RMS (среднеквадратичное значение). |
| Изменение амплитуды не связано с изменение высоты тона (частоты) и наоборот. |
| Человеческое восприятие громкости Сложение амплитуд и уровней (когерентные и некогерентные сигналы) Соотношение акустических величин Сравнительное представление размеров звукового поля Уровни и эталоны звуковых величин Добавление акустических уровней источников звука Акустические волны или звуковые волны в воздухе Расчет длины волны акустической волны Расчет скорости звука в воздухе и эффективной температуры Количество звуковых полетов на плоской волне – Амплитуды Вопросы для звуков и амплитуд – , или усиление к значению уровня (Усиление децибелы дБ) Суммарный уровень некогерентных акустических источников звука Суммарный уровень когерентных сигналов Звуковое поле Величины плоской волны |
Добавление амплитуд (и уровней)
| Амплитуды, коррелированные Сумма напряжений, когерентные (0°) 1 + 1 = 2 | Амплитуды некоррелированные Суммарная мощность, некогерентная (90°) √ (1² + 1²) = 1,414 .  .. |
| Интенсивность звука пропорциональна амплитуде (звук давление) в квадрате; I ~ p ², т.е. амплитуда (звуковое давление) пропорциональна квадратному корню из интенсивности звука; р ~ √ I . |
Что такое амплитуда?
http://www.indiana.edu/~emusic/acoustics/amplitude.htm
| http://uk.answers.yahoo.com/question/index?qid=20111025210805AAAIaFhX Вопрос из Answers.yahoo: Звук… Что такое амплитуда? Мне интересно, что создает амплитуду звука волна? Я понимаю, что в представлении поперечной волны амплитуда является максимальным значением волновая функция, но как она преобразуется в продольные волны? Это имеет смысл для меня что чем короче или дальше расстояние между воздушным карманом высокого или низкого давления, разница между звуком более высокой или более низкой частоты, но видимая как частота определяет высоту тона, а скорость звука постоянна (в зависимости от среды), что что обеспечивает более мягкий или громкий звук? Я читал, что интенсивность или энергия звука волны делают его громче или тише, но если звук распространяется с той же скоростью, что К какому свойству волны при прохождении через воздух относятся термины интенсивность или энергия? |
Ответ на ответы. yahoo: “Звук… Что такое амплитуда?” Это действительно хороший вопрос, потому что есть проблема с определением амплитуда слова. Амплитуда – величина изменения колебательной переменной при каждом колебании
внутри колебательной системы. Например, звуковые волны в воздухе — это колебания в
атмосферного давления, а их амплитуды пропорциональны изменению
давление за одно колебание. Если переменная совершает регулярные колебания и
график системы построен с осциллирующей переменной в качестве вертикальной оси и
время как горизонтальная ось, амплитуда визуально представлена вертикальной
расстояние между экстремумами кривой и равновесным значением. |
| http://answers.yahoo.com/question/index?qid=20111003100847AAP1uuF Вопрос из Answers.yahoo: Громкость звука зависит от амплитуды или частоты? Также скажите отношение между ними. |
Ответ на ответы. yahoo: Громкость зависит от звукового давления, частоты, ширины полосы и продолжительности. Громкость – это качество звука, которое в первую очередь является психологическим коррелятом физическая сила (амплитуда). Это субъективная мера, которую часто путают с объективные меры силы звука, такие как размеры звукового поля, такие как звук давление или уровень звукового давления SPL в децибелах и размеры звуковой энергии, такие как интенсивность звука или мощность звука; см.: «Громкость — Википедия»: http://en.wikipedia.org/wiki/Громкость Ура ebs PS: Не забывайте, что наши барабанные перепонки эффективно перемещаются «звуковым давлением»; см.: «Звуковое давление и звуковая мощность — следствие и причина»: http://www.sengpielaudio.com/SoundPressureAndSoundPower.pdf Мы измеряем звук с помощью измерителя SPL (SPL = уровень звукового давления). |
| Примечание.  Время, частота и фаза тесно связаны друг с другом. Высота амплитуды не влияет на эти параметры. Амплитуда А не имеет ничего общего с частотой, длиной волны, продолжительность времени и скорость звука. |
Среднеквадратичное напряжение , Пиковое напряжение и Размах напряжения
| Параметры синусоидального сигнала «117 В и 230 В среднеквадратичного переменного тока» приведены в таблице ниже. |
| Среднее напряжение | Среднеквадратичное напряжение ( В Среднеквадратичное значение ) | Пиковое напряжение ( В p ) = ( х ) | Размах напряжения ( В стр. ) |
| 0 вольт | 117 В = В Среднеквадратичное значение = ~ В | 165 вольт = √2× В среднеквадратичное значение = 0,5 × В стр. | 330 вольт = 2×√2× В среднеквадратичное значение = 2 × В p |
| 0 вольт | 230 В = В Среднеквадратичное значение = ~ В | 325 В = √2× В Среднеквадратичное значение = 0,5 × В pp | 650 вольт = 2×√2× В среднеквадратичное значение = 2 × В р |
| Значение В Среднеквадратичное значение переменного напряжения В (t) = В 0 × f(t) действующая мощность постоянного тока соответствует омическому сопротивлению средней резистивной мощности этого переменного напряжения к тому же сопротивлению. |
Коэффициент амплитуды означает отношение пикового напряжения к среднеквадратичному напряжению. Если нам нужно
для расчета аттенюатора (расчет затухания) мы вычисляем делитель напряжения . |
Преобразование напряжения
| В Среднеквадратичное значение = ~ В | В р | В стр. | |
| Среднеквадратичное значение напряжения В Среднеквадратичное значение = | — | 0,7071 × В р | 0,3535 × В стр. |
| Пиковое напряжение В p = | 1,414 × В СКЗ | — | 0,5000 × В стр. |
| Размах напряжения В pp = | 2,828 × В СКЗ | 2. 000 × В р | — |
Непонятные уравнения в книгах
| Интенсивность звука I в Вт/м 2 в плоской прогрессивной волне
задается как: или также как Но только одно уравнение может быть правильным. Иногда в этих уравнениях будет показана дополнительная информация: или также как Тилде укажет, что это среднеквадратичное значение, и крыша покажет, что это амплитудное значение, т. е. пиковое значение. Для синусоидальных сигналов пиковое значение означает амплитуда. С этими более точными данными оба уравнения верны. Вам просто нужно знать точно, применяется ли пиковое значение или среднеквадратичное значение. Интенсивность звука = звуковое давление × скорость частиц Интенсивность звука = энергия звука / (площадь × время) = мощность звука / площадь. 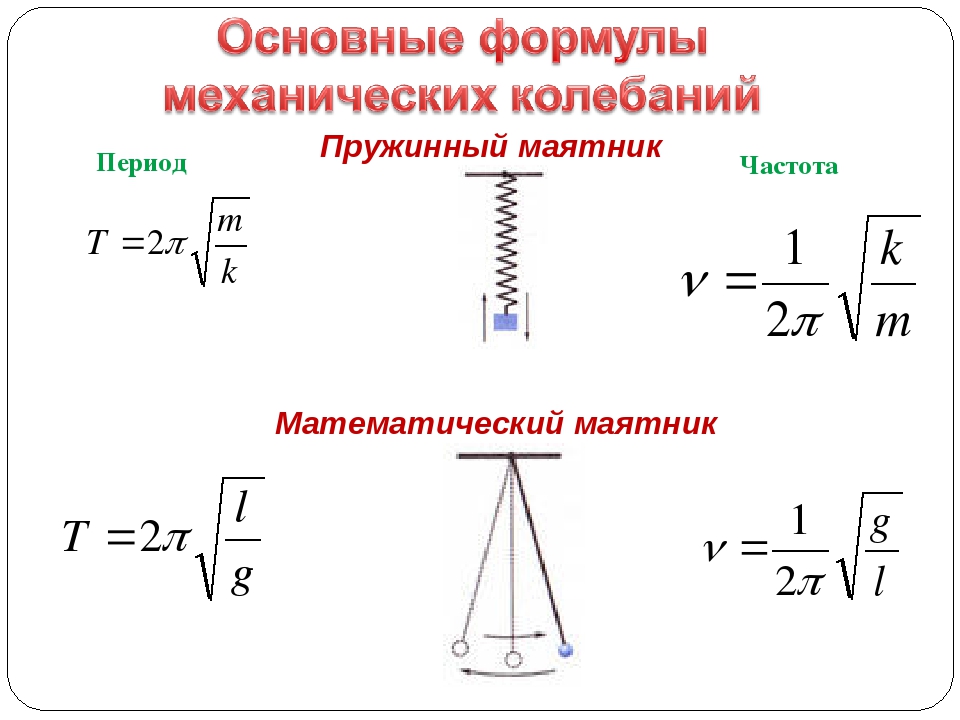 I = p × v = (F / A) × (ξ / t) = E / (A × t) = P ac / A . Звуковое давление p дюйм Па = Н/м 2 – скорость частиц v м/с − интенсивность звука I дюйм Вт/м 2 , то есть Н/м 2 · м/с Эквивалент энергии: Дж (Дж) = Н·м = Вт·с В аудиотехнике мы всегда (!) принимаем среднеквадратичное значение для величин звукового поля. (размеры), если специально не указано иное. Эталонное звуковое давление составляет p 0 = 20 мкПа = 2 × 10 −5 Па (порог слышимости), и это среднеквадратичное значение. |
Звуковые волны — это продольные волны в воздухе, которые мы воспринимаем
как вибрация: амплитуда звукового давления, интенсивность звука, звук
энергия, тональность, импульсивность, резкость, громкость, громкость,
раздражительность, шероховатость, ломкость, эхосодержание, ясность,
понятность, информативность. |
| задняя часть | Поисковая система | дом |
Лекция 15: Звуковые волны: скорость звука
Лекция 15: Звуковые волны: скорость звукаЗвук как волна давления
- Другой взгляд на звук состоит в том, чтобы рассматривать его как волну давления
- Этот вид “макроскопичен” и проще, так как давление
уже величина, усредненная по движениям атомов в некотором объеме. Так
волновые фронты – поверхности постоянного давления и т. д.
- Единицы давления: паскали Па = Н/м 2 = кг/(м с 2 )
- Стандартное атмосферное давление 101,325 кПа ~ 10 5 Па
Какие колебания давления возникают в результате колебательных перемещений атомов?
- Для простоты будем рассматривать плоские волны.
Волна смещения
определяется по формулеy(x,t) = A cos( k x x – ω t + φ 0 ) где y(x,t) — смещение x плоскости - В прошлый раз мы показали на доске, что волна смещения
вызывает локальное сжатие/разрежение объема с
- В сыпучих материалах объемное сжатие соответствует давлению
превышение атмосферного давления, Δ p = P – P а как описано объемный модуль B
- B играет роль постоянной пружины в законе Гука, но теперь для
объемные деформации (деформации). Единицами объемного модуля являются паскали, т.к.
что за давление. Пожалуйста, просмотрите главу 11.4 для обсуждения
деформации сыпучих материалов.
Обратите внимание на разницу с законом Гука. Вот это относительное изменение задействованного объема, в то время как в законе Гука мы имеем дело с абсолютное изменение длины пружины. - Если мы изменим соотношение между объемом и давлением, мы получим
Таким образом, объемный модуль описывает, как локальное давление реагирует на изменение локального плотность.
Волна смещения
определяется по формуле
- Для твердых веществ B практически постоянна и зависит от состав. Обычно он находится в диапазоне 10 11 Па .
- Для газов объемный модуль зависит от плотности и температуры газа. Так что имеет значение, как газ сжимается в волне – изотермическое ли это сжатие? адиабатическое сжатие? Типичное значение в воздухе при комнатной температуре составляет ~ 10 5 Па
Свойства волн давления
- Теперь мы готовы написать формулу для давления в плоской звуковой волне.
- Волна давления имеет ту же частоту, длину волны и скорость как волна смещения. Это описание той же звуковой волны!
- Волна давления сдвинута по фазе относительно смещения на ½&pi. Пик смещения приходится на нули изменения давления, максимальное/минимальное давление
находится при нулевом смещении.
- Амплитуда волны давления равна Δ p max = A B k . Колебания давления в воздухе, которые слышит человек, ~ 10 -4 Па что 10 -9 дробь атмосферного! Точный порог слышимости зависит от частоты и ниже на более низких частотах.
Пик смещения приходится на нули изменения давления, максимальное/минимальное давление
находится при нулевом смещении.Скорость звука
- Предполагается, что скорость звука будет определяться свойствами материала. в котором распространяется звук. Физически, по опыту с пружин, должны быть задействованы восстанавливающая сила и инерция. Размерный анализ? Имеем B ~ кг/(м с 2 ) (сила на единицу площади) плотность ρ ~ кг/м 3 (масса на единицу объема), поэтому v ~ (B/ρ) ½ ?
- Рассмотрим подробно на плате. Рассмотрим поршень, который посылает импульс
при движении в трубу с жидкостью со скоростью v y Фронт импульса движется вперед со скоростью v (скорость звука).
Шаги:
- Жидкость массы M = v t S ρ приобретает скорость v y во времени t . Это означает, что он был предметом сила F = M v y /t , полученное в результате повышения давления Δ p действующая на поверхность S . то есть Δ p = M v y /t , поэтому Δ p = v v y ρ
- С другой стороны объем жидкости V = v t S опыт сжатие на Δ V = – v y t S , следовательно Δ V / V = - v y /v
- Увеличение давления и уменьшение объема связаны модулем всестороннего сжатия v v y ρ = B v y /v , решение которого
для скорости звука v действительно дает
v = (B/ρ) ½
- Типичные значения скорости звука для металлов v ~ 2000-6000 м/с
Рассмотрим поршень, который посылает импульс
при движении в трубу с жидкостью со скоростью v y Фронт импульса движется вперед со скоростью v (скорость звука).
Шаги:Скорость звука в сплошном стержне
|
