Формула амплитуды колебаний: Амплитуда, частота, период колебаний — урок. Физика, 9 класс.
alexxlab | 26.06.2023 | 0 | Разное
Определения по колебаниям и волнам
АВТОКОЛЕБАНИЯ – незатухающие колебания физической системы, которые поддерживаются источником энергии, находящимся в самой системе. Амплитуда и период А.К. определяются свойствами системы.
АМПЛИТУДА КОЛЕБАНИЙ – наибольшее значение xm, которого достигает физическая величина х (смещение, сила тока, напряженность электрического поля и т.д.), совершающая гармонические колебания, т. е. изменяющаяся по закону x= xmсоs(ω.t+ φ), где t – время, xm, ω, φ – постоянные (при гармонических колебаниях) величины. Другими словами А. определяет “размах” колебаний. В этом смысле термин А. может применяться к негармоническим колебаниям.
БЕГУЩИЕ ВОЛНЫ – волны, переносящие энергию вдоль направления их распространения. (Ср.стоячие волны).
(Ср.стоячие волны).
ВОЛНОВАЯ ПОВЕРХНОСТЬ – совокупность точек среды, в которых в данный момент времени фаза волны имеет одно и то же значение.
ВОЛНЫ – возмущения (изменения состояния среды или поля), распространяющиеся в пространстве с конечной скоростью. Распространение волн связано с переносом энергии без переноса вещества, при этом возможны явления отражения, преломления, дисперсии, интерференции. дифракции, поляризации, поглощения и рассеяния волн. (См. упругие волны, электромагнитные волны).
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ –колебания, возникающие в какой-либо системе под влиянием переменного внешнего воздействия. Характер их определяется как свойствами внешнего воздействия, так и свойствами самой системы. Если частота внешнего воздействия приближается к частоте собственных колебаний системы, то амплитуда В.К. резко возрастает – наступает резонанс. Ср.собственные колебания.
ВЫСОТА ЗВУКА – качество (характеристика) звука, определяемое человеком по восприятию (субъективно) и связанное с частотой звука. С ростом частоты В.з. увеличивается.
С ростом частоты В.з. увеличивается.
ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ – процесс периодических изменений во времени физической величины, для математического описания которого используются гармонические функции синус или косинус: или . По гармоническому закону могут изменяться смещение тела от положения равновесия, величина электрического заряда, напряженность поля, сила тока и т.д. Любое сложное колебание можно представить как сумму гармонических колебаний.
ГИПЕРЗВУК – упругие волны с частотой, превышающей 109 Гц. Верхний предел частоты Г. в кристаллах и жидкостях (1012-1013 Гц.), в газах (109 Гц.) соответствует частотам, при которых длина волны Г. соизмерима с межмолекулярными расстояниями, а в газах – со средней длиной свободного пробега молекул. См. такжезвук, инфразвук, ультразвук
ГРОМКОСТЬ ЗВУКА – качество (характеристика) звука, определяемая человеком по восприятию (субъективно) и связанное с амплитудой звуковых колебаний и частотой звука.
ДАВЛЕНИЕ ЗВУКА – среднее по времени избыточное давление, которое испытывает препятствие, помещенное в поле звуковой волны. Скалярная величина, равная отношению импульса, передаваемого звуковой волной поверхности препятствия, к площади этой поверхности и времени, в течение которого происходила передача импульса. Ср. звуковое давление.
ДИСПЕРСИЯ ВОЛН – зависимость фазовой скорости гармонических (синусоидальных) волн в веществе от их частоты.
ДИФРАКЦИЯ ВОЛН – явление огибания волнами встречных препятствий. Под Д.в. понимают как нарушение прямолинейности распространения волн, так и сопутствующие ему интерференционные явления (см. интерференция волн).
ДЛИНА ВОЛНЫ – физическая величина, характеризующая синусоидальную (гармоническую) волну, равная расстоянию между двумя ближайшими точками среды, разность фаз волны в которых равна 2π. Д.в. l связана с частотой колебаний ν и фазовой скоростью ω соотношением λ=TV.
ЗАТУХАНИЕ КОЛЕБАНИЙ – постепенное ослабевание собственных колебаний, обусловленное потерями энергии колебательной системой. З.к. приводит к уменьшению амплитуды колебаний.
ЗВУК (звуковые волны) – упругие волны, распространяющиеся в твердых, жидких и газообразных средах. В зависимости от частоты колебаний З. условно подразделяется на инфразвук (частотой до 16 Гц), слышимый звук (16 Гц – 20 кГц), ультразвук (20 кГц – 1 ГГц) и гиперзвук (более 1 ГГц).
ЗВУКОВОЕ ДАВЛЕНИЕ – переменное давление, избыточное над равновесным, возникающее при прохождении звуковой волны в жидкой или газообразной среде.
ИЗЛУЧЕНИЕ – 1) И. волн и частиц – процесс испускания звуковых волн источниками звука, радиоволн – антеннами, света и рентгеновских лучей – атомами и молекулами, α-, β-частиц и γ-лучей атомными ядрами. 2) Сами эти волны и частицы как движущиеся объекты.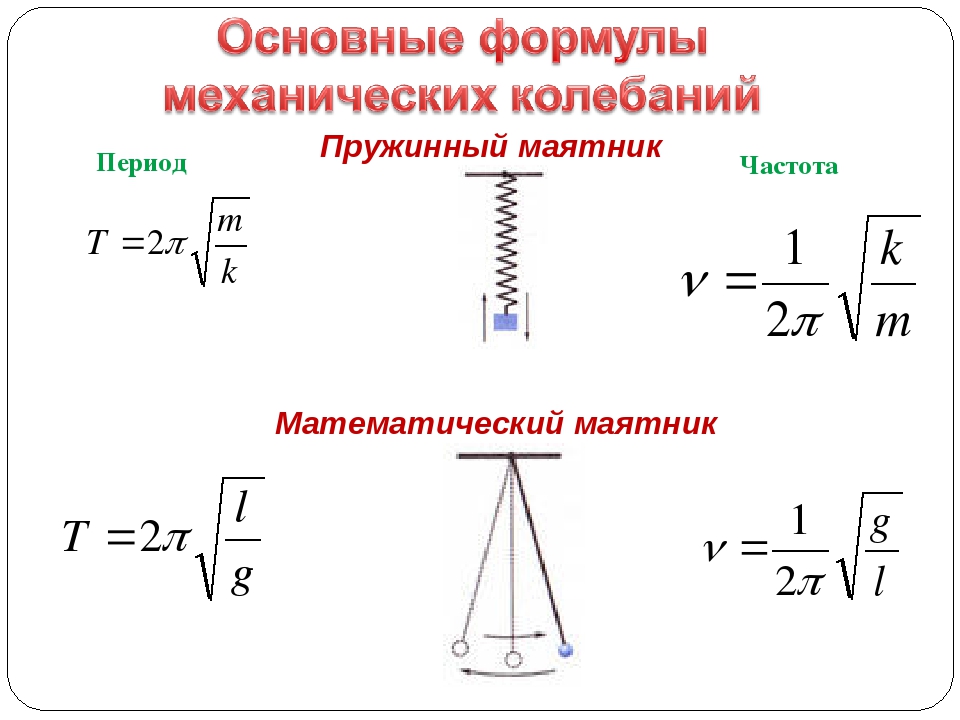 (См. Альфа-лучи, Бета-лучи и т.д.)
(См. Альфа-лучи, Бета-лучи и т.д.)
ИНТЕНСИВНОСТЬ ВОЛНЫ, плотность потока излучения – физическая величина, равная при равномерном распределении энергии излучения отношению мощности волны, к площади волнового фронта. Единица в СИ – .
ИНТЕНСИВНОСТЬ ЗВУКА, сила звука – физическая величина, равная отношению энергии, переносимой звуковой волной через поверхность, расположенную перпендикулярно к направлению распространения волны, к площади поверхности и промежутку времени, в течение которого происходил процесс. Единица И.з. в СИ – .
ИНТЕРФЕРЕНЦИЯ ВОЛН – явление наложения двух или нескольких волн, при котором в пространстве происходит перераспределение энергии результирующей волны. Если волны когерентны, то в пространстве получается устойчивое во времени распределение амплитуд с чередующимися максимумами и минимумами (интерференционная картина). Имеет место для всех волн независимо от их природы. Ср.дифракция волн.
ИНФРАЗВУК– упругие волны с частотой менее 16 Гц, которые не воспринимаются ухом человека. Источники И.: газовые разряды в атмосфере, ветер, колебания земной коры и поверхности моря. См. звук, ультразвук, гиперзвук.
КОГЕРЕНТНОСТЬ – согласованное протекание во времени нескольких колебательных или волновых процессов. Когерентными наз. колебания с одинаковой частотой (длиной волны) и постоянной разностью фаз. К.- необходимое условие возникновения интерференции (см.интерференция волн, интерференция света).
КОЛЕБАНИЯ – движения (изменения состояния), характеризующиеся той или иной степенью повторяемости во времени. Различают К.: механические (К. маятников, струн, пластин, замкнутых объемов воздуха и т.д.), электромагнитные (К. электрического тока и напряжения в колебательном контуре или волноводе, переменный ток и т.д.) и электромеханические (К. пьезоэлектрических и магнитострикционных излучателей и т.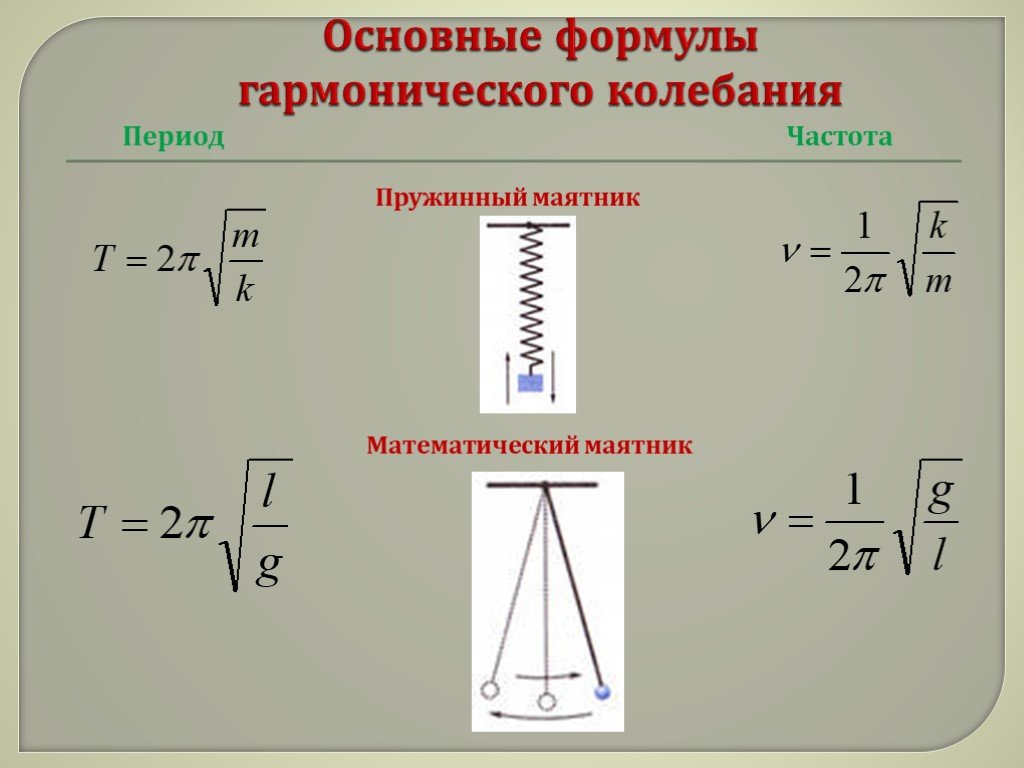 д.). Простейшие периодические колебания – гармонические колебания.
д.). Простейшие периодические колебания – гармонические колебания.
КОЛЕБАТЕЛЬНАЯ СИСТЕМА – система тел, способная совершать свободные колебания. Признаки К.с. – наличие положения устойчивого равновесия, малое трение (электрическое сопротивление).
МАЯТНИК – твердое тело (или система тел), способное совершать колебания около неподвижной точки или оси. См. математический маятник, физический маятник.
МАЯТНИК МАТЕМАТИЧЕСКИЙ – идеализированный объект: колебательная система, состоящая изматериальной точки, подвешенная к неподвижной точке на невесомой нерастяжимой нити (или стержне) и центра тяготения (напр., Земли). М.м. совершает колебания в вертикальной плоскости. При малых колебаниях период колебаний М.м. не зависит от амплитуды и выражается формулой , где ℓ – длина нити, а g – ускорение свободного падения. Ср.маятник пружинный.
МАЯТНИК ПРУЖИННЫЙ – идеализированный объект: колебательная система, состоящая изматериальной точки, прикрепленной к концу невесомой пружины. При малых колебаниях период колебаний М.п. не зависит от амплитуды и выражается формулой , где m– масса материальной точки, k– жесткость пружины. Ср. маятник математический.
МИКРОФОН – устройство для преобразования звуковых колебаний в электрические.
ОТРАЖЕНИЕ ЗВУКА – процесс возвращения звуковой волны при ее встрече с границей раздела двух сред, имеющих различную плотность и сжимаемость, обратно в первоначальную среду. Одно из проявлений о.з. – эхо.
ОТРАЖЕНИЯ ВОЛН ЗАКОН – луч падающий, луч отраженный и перпендикуляр, восставленный в точку падения луча, лежат в одной плоскости, причем угол падения равен углу преломления. Закон справедлив для зеркального отражения.
ПЕРИОД – наименьший промежуток времени, по истечении которого повторяются значения физических величин, характеризующих данный периодический процесс (напр., период колебаний).
ПОПЕРЕЧНАЯ ВОЛНА – волна, распространяющаяся в направлении, перпендикулярном к плоскости, в которой колеблются частицы среды (для упругой волны) или в которой расположены векторы электрической напряженности и магнитной индукции (для электромагнитной волны). Ср. продольная волна.
РЕЗОНАНС – явление более или менее резкого возрастания амплитуды установившихся вынужденных колебаний, когда частота внешнего воздействия приближается к частоте собственных колебаний системы.
РЕЗОНАТОР – система (тело или специальное устройство), в которой может происходить резонанс. Примеры Р.: камертон, воздушная полость (акустический Р.), колебательный контур (электрический резонатор).
СВОБОДНЫЕ КОЛЕБАНИЯ (собственные колебания)
СДВИГ ФАЗ – разность фаз переменных физических величин, изменяющихся по синусоидальному закону с одинаковой частотой.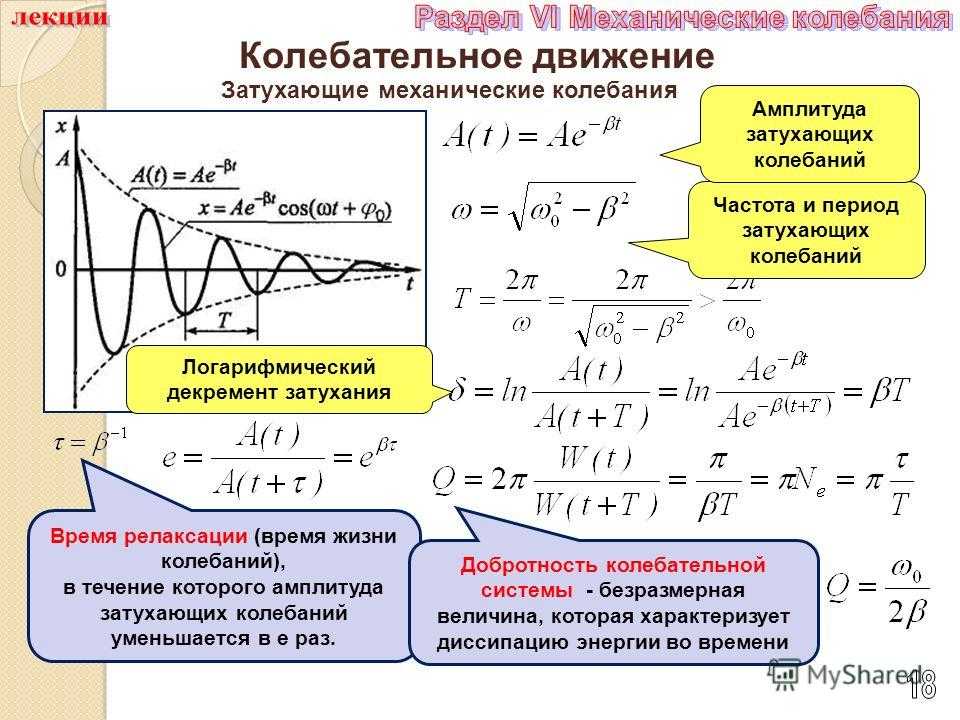 Измеряется в радианах.
Измеряется в радианах.
СКОРОСТЬ ЗВУКА – скорость распространения звуковых волн в среде. В газах с.з. меньше, чем в жидкостях, а в жидкостях меньше, чем в твердых телах. В воздухе при нормальных условиях с.з. 330 м/с, в воде – 1500 м/с, в тв. телах 2000 – 6000 м/с.
СОБСТВЕННЫЕ КОЛЕБАНИЯ, свободные колебания – колебания, возникающие в колебательной системе, которая не подвергается переменным внешним воздействиям, вследствие какого-либо начального отклонения этой системы от состояния устойчивого равновесия. В реальных макроскопических системах из-за потери энергии с.к. всегда затухают.
СТОЯЧИЕ ВОЛНЫ – колебания в резонаторе (струне, мембране, камертоне и т.п.), характеризующиеся чередованием максимумов (пучностей) и минимумов (узлов) амплитуды. Возникают в результате интерференции двух бегущих волн, амплитуда которых одинакова, а направления распространения взаимно противоположны.
ТЕМБР звука – качественная субъективная оценка звука, издаваемого музыкальным инструментом, звуковоспроизводящим устройством или голосовым аппаратом людей и животных.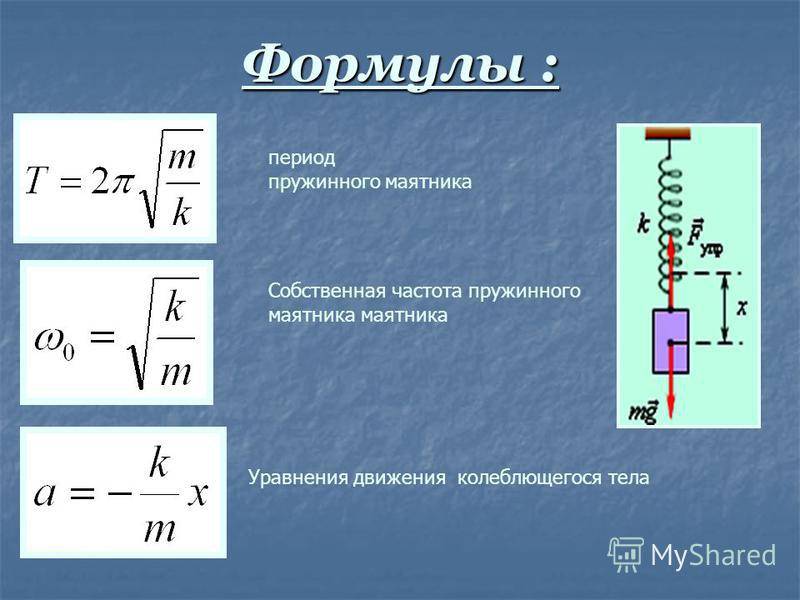 Характеризует оттенок звучания и зависит от того, какие обертоны сопутствуют основному тону и каковы их интенсивность.
Характеризует оттенок звучания и зависит от того, какие обертоны сопутствуют основному тону и каковы их интенсивность.
УПРУГИЕ ВОЛНЫ – механические возмущения (деформации), распространяющиеся в среде, обладающей упругостью. В жидкостях и газах могут образовываться только продольные у.в., при которых среда испытывает только деформацию сжатия (растяжения) и частицы среды колеблются вдоль направления распространения волены. В твердых телах возникают как продольные, так и поперечные у.в. При поперечных у.в. среда испытывает деформацию сдвига, и частицы среды колеблются в направлениях, перпендикулярных направлению распространения волны.
ФАЗА КОЛЕБАНИЙ – физическая величина, применяемая для описания состояния периодического колебательного процесса в каждый момент времени: , где ω – угловая частота, φ0– значение фазы в начальный момент времени (начальная фаза). Выражается в угловых единицах (напр. , радианах) или долях периода колебаний.
, радианах) или долях периода колебаний.
ФРОНТ ВОЛНЫ – см. волновая поверхность.
ЧАСТОТА КОЛЕБАНИЙ – физическая величина, равная отношению числа полных колебаний, совершаемых телом, к промежутку времени, за которое они совершены. Применяется для описания колебательного процесса. Обратно пропорциональна периоду колебаний. Единица в СИ – Герц.
ЭХО – волна, отраженная от какого-либо препятствия и принятая наблюдателем (приемником). Радиоэхо используют в радиолокации, звуковое эхо – в гидролокации.
2.3.3 Колебания при наличии внешней вынуждающей периодической силы
Идеальный случай.
Пусть на шарик в пружинном маятнике действует периодическая внешняя сила
(1)
В этом случае для смещения шарика вблизи положения равновесия вместо уравнения (1) пункта 2.3.1 получаем
(2)
где .
Нетрудно проверить, что решение уравнения (1) в случае имеет вид [1-3]:
(3)
где
Первое слагаемое в (3) описывает свободные колебания, а второе – так называемые вынужденные колебания с амплитудой
. Таким образом, амплитуда и начальная фаза колебаний при действии вынуждающей силы зависят не только от начальных условий, но и от параметров силы.
Таким образом, амплитуда и начальная фаза колебаний при действии вынуждающей силы зависят не только от начальных условий, но и от параметров силы.
В предельном случае точного совпадения частот и система уже не может совершать периодические колебания. Зависимость координаты от времени будет выражаться формулой
(4)
Такое движение можно рассматривать как колебания с линейно нарастающей со временем амплитудой. Явление раскачки колебаний под действием периодической внешней силы называется резонансом.
Следует подчеркнуть, что неограниченный резонансный рост амплитуды вынужденных колебаний есть идеализация системы. Во-первых, когда амплитуда колебаний становится достаточно большой, осциллятор, как правило, перестаёт быть линейным. Во-вторых, при записи уравнения (12) не учитывались силы трения, приводящие к затуханию колебаний. Рассмотрим роль последнего фактора более подробно.
Вынужденные колебания при наличии трения.
Если на осциллятор с трением действует внешняя сила (1), то уравнение таких колебаний имеет вид
(5)
где – коэффициент затухания, определённый в пункте 2.3.2.
Общее решение (5) имеет вид [1–3]
(6)
где – решение уравнения (5) в отсутствие внешней силы (собственные колебания осциллятора (3) – (5) пункта 2.3.2.
Благодаря трению , собственные колебания затухают: при . Поэтому через время колебательная система будет совершать только вынужденные колебания, описываемые вторым слагаемым в (6). Важно отметить, что параметры вынужденных колебаний не зависят от начальных условий. Эти колебания происходят с частотой внешней силы , характеризуются амплитудой и фазовым сдвигом
(7)
(8)
Как следствие из формулы (8), коэффициент связан с производной функции следующим образом:
(9)
Важным отличием от случая вынужденных колебаний осциллятора без трения является наличие сдвига фазы
между колебаниями вынуждающей силы и колебаниями осциллятора.
Другим существенным следствием наличия затухания является качественное изменение вида резонансной кривой. На рис. 1 приведена зависимость и для некоторых характерных значений .
Рис. 1а. Резонансные кривые (АЧХ) линейного осциллятора для различных значений коэффициента трения: , , , .
Рис. 1б. Зависимость сдвига фаз (ФЧХ) между колебаниями вынуждающей силы и осциллятора.
Максимальное значение амплитуды вынужденных колебаний (7), определяется формулой
(10)
Этому максимуму соответствует резонансная частота
(11)
при условии, что
. Если затухание мало
() то максимум резонансной кривой приблизительно совпадает с собственной частотой осциллятора
. По мере роста
этот максимум смещается в сторону меньших частот (рис. 1а). При
максимум амплитуды вынужденных колебаний
приходится на частоту
. TПо существу это означает исчезновение резонанса. Ранее указывалось, что режим апериодического затухания свободных колебаний возникает лишь при
. Следовательно, в интервале
вынужденные колебания уже не имеют резонансного характера, а собственные движения осциллятора ещё сохраняют колебательный характер.
По мере роста
этот максимум смещается в сторону меньших частот (рис. 1а). При
максимум амплитуды вынужденных колебаний
приходится на частоту
. TПо существу это означает исчезновение резонанса. Ранее указывалось, что режим апериодического затухания свободных колебаний возникает лишь при
. Следовательно, в интервале
вынужденные колебания уже не имеют резонансного характера, а собственные движения осциллятора ещё сохраняют колебательный характер.
Как видно из формулы (7), при слабом затухании амплитуда вынужденных колебаний быстро убывает по мере удаления от резонансной частоты. В частности, она уменьшается в раза при значениях , равных
,
(12)
Величину принято называть шириной резонанса. При малых эта величина составляет . Тогда добротность, определяемая формулой (8) пункта 2.3.2, связана с шириной резонансной кривой соотношением
(13)
Таким образом, ширина резонансной кривой определяется добротностью и собственной частотой. Чем больше добротность колебательной системы, тем меньше ширина резонансного пика. Как видно из формулы (13), добротность колебательной системы можно оценить из экспериментальных АЧХ осциллятора и соответственно определить коэффициент затухания.
Чем больше добротность колебательной системы, тем меньше ширина резонансного пика. Как видно из формулы (13), добротность колебательной системы можно оценить из экспериментальных АЧХ осциллятора и соответственно определить коэффициент затухания.
Выводы.
- В случае действия на колебательную систему внешней вынуждающей силы, колебания системы описываются периодическим законом, причём амплитуда и начальная фаза колебаний зависят не только от начальных условий, но и от параметров силы (3).
- Если частоты и совпадают, то система совершает колебания с линейно нарастающей со временем амплитудой (4) – явление резонанса.
- В случае наличии трения и действия на колебательную систему внешней вынуждающей силы через время колебательная система будет совершать только вынужденные колебания, описываемые вторым слагаемым в (6).
- Параметры установившихся вынужденных колебаний не зависят от начальных условий.
 Эти колебания происходят с частотой внешней силы
, характеризуются амплитудой (7) и фазовым сдвигом (8). При совпадении частот,
, вне зависимости от величины затухания, сдвиг фазы составляет
.
Эти колебания происходят с частотой внешней силы
, характеризуются амплитудой (7) и фазовым сдвигом (8). При совпадении частот,
, вне зависимости от величины затухания, сдвиг фазы составляет
. - Ширина резонансной кривой определяется добротностью и собственной частотой колебаний (13).
Литература.
- С.Э. Хайкин. Механика. – М.: ОГИЗ, 1947. – 574 с.
- Д. В. Сивухин. Механика. – М.: Наука, 1989. – 576. с.
- Карлов Н.В., Кириченко Н.А. Колебания, волны, структуры. – М.: ФИЗМАТЛИТ, 2003. – 496 с.
Гармоническое движение
Гармоническое движениеГоворят, что объект, движущийся вдоль оси X, демонстрирует простое гармоническое движение , если его положение как функция времени изменяется как
x(t) = x 0 + A cos(ωt + φ).
Объект колеблется вокруг положения равновесия x 0 . Если мы выбираем начало нашей системы координат так, что x 0 = 0, тогда смещение x от положения равновесия как функция времени определяется выражением
x(t) = A cos(ωt + φ).
А – амплитуда колебаний, т. е. максимальное смещение объекта из положения равновесия либо в положительное или отрицательное направление x. Простое гармоническое движение повторяется. период T — время, за которое объект совершить одно колебание и вернуться в исходное положение. угловая частота ω определяется как ω = 2π/T. Угловая частота измеряется в радианах в секунду. Обратная сторона период частота f = 1/T. частота f = 1/T = ω/2π движения дает число полных колебаний в единицу времени. Измеряется в герцах (1 Гц = 1/с).
Скорость объекта как функция времени определяется как
v(t) = -ω A sin(ωt + φ),
а ускорение дается
a(t) = -ω 2 A cos(ωt + φ) = -ω 2 x.
Величина φ называется фазовая постоянная
 Я толстый
t = 0 частица движется через положение равновесия с максимальным
скорость в отрицательном направлении x, тогда φ = π/2. Величина ωt + φ равна
называется фазой .
Я толстый
t = 0 частица движется через положение равновесия с максимальным
скорость в отрицательном направлении x, тогда φ = π/2. Величина ωt + φ равна
называется фазой .На рисунке ниже положение и скорость представлены как функция времени. для колебательного движения с периодом 5 с. Амплитуда и максимальная скорость имеют условные единицы. Положение и скорость вне фазы . Скорость равна нулю при максимальном смещении, и смещение равно нулю на максимальной скорости.
Для простого гармонического движения ускорение a = -ω 2 x равно пропорционально смещению, но в обратном направлении. Простой гармоническое движение есть ускоренное движение . Если объект демонстрирует простое гармоническое движение, на него должна действовать сила. объект. Сила
F = ма = -mω 2 х.
Он подчиняется закону Гука , F = -kx, при k = mω 2 .
Внешняя ссылка: Простой гармоническое движение (Youtube)
Сила пружины подчиняется закону Гука. Предположим, что объект
прикреплен к пружине, которая растягивается или сжимается. Тогда пружина давит
сила на объект. Эта сила пропорциональна смещению х тела.
пружинит из положения равновесия и движется в направлении, противоположном
смещение.
Предположим, что объект
прикреплен к пружине, которая растягивается или сжимается. Тогда пружина давит
сила на объект. Эта сила пропорциональна смещению х тела.
пружинит из положения равновесия и движется в направлении, противоположном
смещение.
Ф = -кх
Предположим, что пружина растянута на расстояние A от положения равновесия, а затем отпущена. Объект прикрепленный к пружине, ускоряется, возвращаясь к положению равновесия.
a = -(к/м)х
Он набирает скорость по мере продвижения к положению равновесия, потому что его
ускорение направлено в сторону его скорости. Когда он находится в равновесии
положение, ускорение равно нулю, но объект имеет
максимальная скорость. Он выходит за пределы положения равновесия и начинает замедляться.
вниз, потому что ускорение теперь в направлении, противоположном направлению
от его скорости. Пренебрегая трением, он останавливается, когда пружина
сжимается на расстояние А, а затем ускоряется обратно к равновесию
позиция. Он снова промахивается и останавливается в исходном положении, когда
пружина растягивается на расстояние A. Движение повторяется. Объект
колеблется взад и вперед. Он выполняет простое гармоническое движение. Угловой
частота движения
Он снова промахивается и останавливается в исходном положении, когда
пружина растягивается на расстояние A. Движение повторяется. Объект
колеблется взад и вперед. Он выполняет простое гармоническое движение. Угловой
частота движения
ω = √(к/м),
период
Т = 2π√(м/к),
и частота
f = (1/(2π))√(к/м).
Резюме: Если единственная сила, действующая на тело массой m, является силой закона Гука, x(t) = Acos(ωt + φ), А = амплитуда |
Проблема:
Частица совершает простые гармонические колебания, так что ее
перемещение изменяется согласно выражению x = (5 cm)cos(2t + π/6)
где x в сантиметрах, t в секундах. При t = 0 найти
При t = 0 найти
(а) смещение частицы,
(б)
его скорость и
(c) его ускорение.
(г) Найдите период и амплитуду движения.
Решение:
- Рассуждение:
Анализ простого гармонического движения.
x(t) = A cos(ωt + φ). A = амплитуда, ω = угловая частота, φ = фазовая постоянная.
v(t) = -ω A sin(ωt + φ), a(t) = -ω 2 A cos(ωt + φ) = -ω 2 x. - Детали расчета:
(a) Смещение как функция времени: x(t) = Acos(ωt + ф). Здесь ω = 2/s, φ = π/6, A = 5 см.
Перемещение при t = 0 равно x(0) = (5 см)cos(π/6) = 4,33 см.
(b) Скорость при t = 0 равна v(0) = -ω(5 см)sin(π/6) = -5 см/с.
(c) Ускорение при t = 0 равно a(0) = -ω 2 (5 см)cos(π/6) = -17,3 см/с 2 .
(d) Период движения T = 2π/ω = π с, а амплитуда равна 5 см.
Проблема:
Частица массой 20 г движется в простом гармоническом движении с частотой 3
колебаний в секунду и амплитудой 5 см.
(а) Какое общее расстояние проходит частица за один цикл
его движение?
(b) Какова его максимальная скорость? Где это происходит?
(c) Найдите максимальное ускорение частицы. Где в движении делает
происходит максимальное ускорение?
Решение:
- Рассуждение:
Проанализируйте простое гармоническое движение, x(t) = A cos(ωt + φ). - Детали расчета:
(a) Общее расстояние d, которое проходит частица за один цикл, равно от x = -A до x = +A и обратно к x = -A, поэтому d = 4A = 20 см.
(b) Максимальная скорость частицы
v макс. = ωA = 2πfA = 2π 15 см/с = 0,94 м/с.
Частица имеет максимальную скорость при прохождении через положение равновесия.
(c) Максимальное ускорение частицы равно
до макс. = ω 2 А = (2πf) 2 А = 17,8 м/с 2 .
Частица имеет максимальное ускорение в точках поворота, где имеет максимальное водоизмещение.
Предположим, что масса подвешена к вертикальной пружине с жесткостью k. В
равновесия пружина растянута на расстояние x 0 = мг/к. Если
масса смещается из положения равновесия вниз, а пружина растягивается
дополнительное расстояние x, то полная сила, действующая на массу, равна mg – k(x 0 + x) = -kx, направленный в сторону положения равновесия. Если масса
смещен вверх на расстояние x, то полная сила, действующая на массу, равна mg – k(x 0 – х) = kx, направленный к положению равновесия. Масса будет
выполнять простые гармонические движения. Угловая частота ω = SQRT(k/m) такая же
для массы, колеблющейся на пружине в вертикальном или горизонтальном положении.
Но равновесная длина пружины, вокруг которой она колеблется, различна для
вертикальное положение и горизонтальное положение.
В
равновесия пружина растянута на расстояние x 0 = мг/к. Если
масса смещается из положения равновесия вниз, а пружина растягивается
дополнительное расстояние x, то полная сила, действующая на массу, равна mg – k(x 0 + x) = -kx, направленный в сторону положения равновесия. Если масса
смещен вверх на расстояние x, то полная сила, действующая на массу, равна mg – k(x 0 – х) = kx, направленный к положению равновесия. Масса будет
выполнять простые гармонические движения. Угловая частота ω = SQRT(k/m) такая же
для массы, колеблющейся на пружине в вертикальном или горизонтальном положении.
Но равновесная длина пружины, вокруг которой она колеблется, различна для
вертикальное положение и горизонтальное положение.
Предположим, что объект, прикрепленный к пружине, совершает простое гармоническое движение. Позволять один конец пружины прикрепите к стене и дайте предмету двигаться горизонтально на столе без трения.
Какова полная энергия объекта?
Кинетическая энергия объекта
K = ½mv 2 = ½mω 2 A 2 sin 2 (ωt
+ ф).
Его потенциальная энергия является упругой потенциальной энергией. Упругий потенциал энергия, накопленная в пружине, смещенной на расстояние x от положения равновесия U = ½kx 2 . Таким образом, потенциальная энергия объекта равна
.U = ½kx 2 = ½mω 2 x 2 = ½mω 2 A 2 cos 2 (ωt + φ).
Полная механическая энергия объекта
E = K + U = ½mω 2 A 2 (sin 2 (ωt + φ) + cos 2 (ωt + φ)) = ½mω 2 A 2 .
Энергия E в системе пропорциональна квадрат амплитуды .
Е = ½ кА 2 .
Это постоянно меняющаяся смесь кинетической и потенциальной энергии.
Для любого объекта, совершающего простое гармоническое движение с угловой частотой ω,
восстанавливающая сила F = -mω 2 x подчиняется закону Гука и, следовательно, является консервативная сила .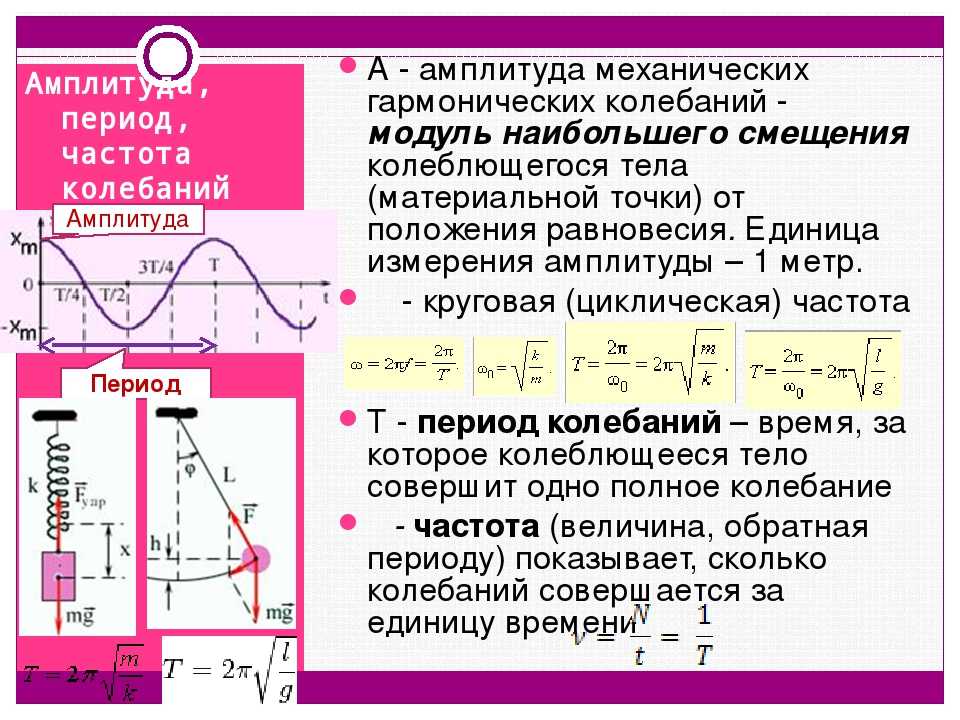 Мы можем определить потенциальную энергию U = ½mω 2 x 2 ,
а полная энергия объекта определяется выражением E = ½mω 2 А 2 . Поскольку v max = ωA,
мы также можем написать E = ½mv max 2 .
Мы можем определить потенциальную энергию U = ½mω 2 x 2 ,
а полная энергия объекта определяется выражением E = ½mω 2 А 2 . Поскольку v max = ωA,
мы также можем написать E = ½mv max 2 .
Проблема:
Частица, подвешенная на пружине, совершает колебания с угловой частотой 2
рад/с. Пружина подвешена к потолку кабины лифта и висит
неподвижно (относительно автомобиля) по мере снижения автомобиля с постоянной скоростью 1,5
РС. Затем машина внезапно останавливается. Массой пружины пренебречь.
С какой амплитудой колеблется частица?
Решение:
- Рассуждение:
При движении в лифте с постоянной скоростью общая сила, действующая на масса равна нулю. Сила, действующая на пружину, по величине равна силе силы тяжести, действующей на массу, пружина имеет равновесную длину вертикальная пружина. Когда лифт внезапно останавливается, конец пружины крепятся к потолочным упорам. Однако масса имеет импульс, p = mv,
и поэтому начинает растягивать пружину. Он движется через
положение равновесия вертикальной пружины с ее максимальной скоростью v макс. = 1,5 м/с.
Однако масса имеет импульс, p = mv,
и поэтому начинает растягивать пружину. Он движется через
положение равновесия вертикальной пружины с ее максимальной скоростью v макс. = 1,5 м/с.
Его скорость как функция времени равна v(t) = -ωAsin(ωt + φ). - Детали расчета:
Поскольку v max = ωA и ω = 2/с, амплитуда амплитуды колебания А = 0,75 м.
Проблема:
Система масса-пружина совершает колебания с амплитудой 3,5 см. Если сила
постоянная пружины 250 Н/м и масса 0,5 кг, определить
(а) механическая энергия системы,
(b) максимальная скорость массы и
в) максимальное ускорение.
Решение:
- Рассуждение:
Механическая энергия системы, совершающей простое гармоническое движение, равна E = ½kA 2 = ½mω 2 А 2 . - Детали расчета:
(а) Имеем m = 0,5 кг, A = 0,035 м, k = 250 Н/м, ω 2 = к/м = 500/с 2 , ω = 22,36/с.
Механическая энергия системы E = ½kA 2 = 0,153 Дж.
(б) Максимальная скорость массы равна v макс. = ωA = 0,78 м/с.
(c) Максимальное ускорение составляет макс. = ω 2 А = 17,5 м/с 2 .
Что такое амплитуда колебаний: вы должны знать –
Маниш Найк
Амплитуда колебаний объясняет максимальное или наибольшее смещение колеблющегося тела. В статье исчерпывающе обсуждается, что такое амплитуда колебаний и как ее рассчитать.
Амплитуда – это величина колеблющегося тела, такая как угловая частота и период времени. Величина измеряет максимальное смещение тела в обе стороны от его среднего положения. Это означает, что он показывает нам, насколько колеблющееся тело отклоняется от своего среднего положения во время колебаний.
Колебание включает движение тела вперед и назад из его положения равновесия или среднего положения . Каждое колебание имеет три основные характеристики: частоту , период времени, и амплитуда . Из них мы уже обсуждали понятия частоты и периода времени в предыдущих статьях.
Из них мы уже обсуждали понятия частоты и периода времени в предыдущих статьях.
Начнем обсуждение амплитуды колебаний или амплитуды колебаний на примере простого маятника . Маятник качается под углом через свое среднее положение к максимальному расстоянию от своего среднего положения. Максимальное или наибольшее расстояние колеблющегося тела от его центра или среднего положения называется его максимальное смещение . Напротив, величина максимального смещения колеблющегося тела в обе стороны от среднего положения называется его амплитудой колебания . Что такое амплитуда колебаний?
Как рассчитать амплитуду колебаний?
На синусоидальном графике мы заметили, что амплитуда колебаний представляет собой расстояние между гребнем, впадиной и средним положением .
Таким образом, амплитуда колебаний или величина максимального перемещения x равна x = Asin(ωt + Φ) …………(*)
Где A — амплитуда колебаний.
ω — угловая скорость.
Φ — фазовый сдвиг.
Далее мы обсудим, как рассчитать уравнение амплитуды колебаний (*) по синусоидальному графику.
Поскольку каждая волна имеет амплитуду, пики на графике показывают, что амплитуда объясняет степень или уровень изменения интенсивности различных волн, таких как звуковые волны. Следовательно, это также интерпретируется как громкость звука. Что такое амплитуда колебаний?
Звуковые волны
На графике мы отметили, что разница между наивысшим пиком амплитуды или положительным значением и наименьшим пиком амплитуды или отрицательным значением называется «размахом амплитуды» колеблющегося тела.
Подробнее о Угловая частота Простое гармоническое движение
Как найти Колебания Амплитуда из графика? Амплитуду колебаний можно получить из графика синусоидальной функции колеблющегося тела.
Амплитуда колебаний определяется, когда мы рисуем график колебательных переменных, таких как смещение в зависимости от времени. Пики на синусоидальном графике – это амплитуда колебаний, которая описывает, на какое расстояние тело колеблется от среднего положения в любую сторону.
В любой колебательной системе величина изменения колебательной переменной тела при каждом колебании называется амплитудой колебаний . В большинстве случаев осциллирующая переменная равна смещение . Когда мы строим график синусоидальной функции с переменным смещением колебаний в качестве вертикальной оси и временем в качестве горизонтальной оси, расстояние по вертикали между средним значением и экстремумами кривой иллюстрирует амплитуду колебаний. Как рассчитать амплитуду колебаний?
(кредит: Shutterstock)
На графике синусоидальной функции ось X рассматривается как среднее положение колебательного тела. Следовательно, каким бы ни было исходное положение тела, перемещение измеряется от его среднего положения. Поскольку график представляет собой синусоидальную функцию, что иллюстрирует периодических явлений пики на графике отображают величины колеблющегося тела, такие как период и амплитуда. Как рассчитать амплитуду колебаний
Поскольку график представляет собой синусоидальную функцию, что иллюстрирует периодических явлений пики на графике отображают величины колеблющегося тела, такие как период и амплитуда. Как рассчитать амплитуду колебаний
форма графика?
По пикам амплитуда колебаний рассчитывается как половина его разницы между максимальным и минимальным значениями.
амплитуда =1/2 от среднего максимума до середины минимума
Таким образом, величина амплитуды колебаний всегда положительна.
Мы также можем найти амплитуду колебаний и период времени из обобщенного уравнения синусоидального графика следующим образом:
y=A⋅sin(B(x+C))+D
где мы можем найти величины колебаний тела следующим образом:
Амплитуда колебаний : A
Период времени :2 π /B
Фазовый сдвиг – насколько далеко тело перемещается по вертикали
50005 9000 Смена – насколько далеко тело перемещается по вертикали от среднего положения: D. Как рассчитать амплитуду колебаний?
Как рассчитать амплитуду колебаний? График синусоидальной функции (кредит: mathsisfun)
Подробнее о Угловое уравнение движения .
Что такое амплитуда и частота колебаний?Амплитуда и частота – это величины колебательных тел, определяющие скорость колебаний.
Тело колеблется, когда оно перемещается из своего среднего положения в самое высокое положение и возвращается в свое среднее положение. Здесь амплитуда представляет собой максимальное смещение тела от его среднего положения. В то время как частота показывает, насколько сильно тело колебалось от своего среднего положения.
Что такое амплитуда и частота колебаний?В зависимости от амплитуды и частоты колебания подразделяются на следующие три типа:
Затухающие колебания
Предположим, что тело совершает колебания с уменьшающейся амплитудой из-за наличия силы сопротивления воздуха и в один момент времени и он приходит в состояние покоя, поскольку обе величины его тела рассеялись. В этом случае это называется «затухающее колебание » .
В этом случае это называется «затухающее колебание » .
Свободные колебания
Предположим, что тело совершает свободные колебания с постоянной амплитудой и определенной частотой из-за отсутствия силы трения. В этом случае это называется «свободное колебание », , а его частота называется « собственная частота» колеблющегося тела.
Вынужденное колебание
Его также называют колебанием натянутой струны или качелей. Предположим, что тело колеблется с уменьшающейся амплитудой за счет механической энергии качания и останавливается, так как обе ее величины рассеялись. В этом случае он называется «9».0003 вынужденные колебания ’.
Возьмем в качестве примера подвешенный весло, привязанный к вашей руке. Амплитуда и частота колебаний. применяемый).
Случай 2 :
Увеличивая частоту движения мяча движением руки вверх и вниз, мяч также реагирует с увеличением амплитуды.


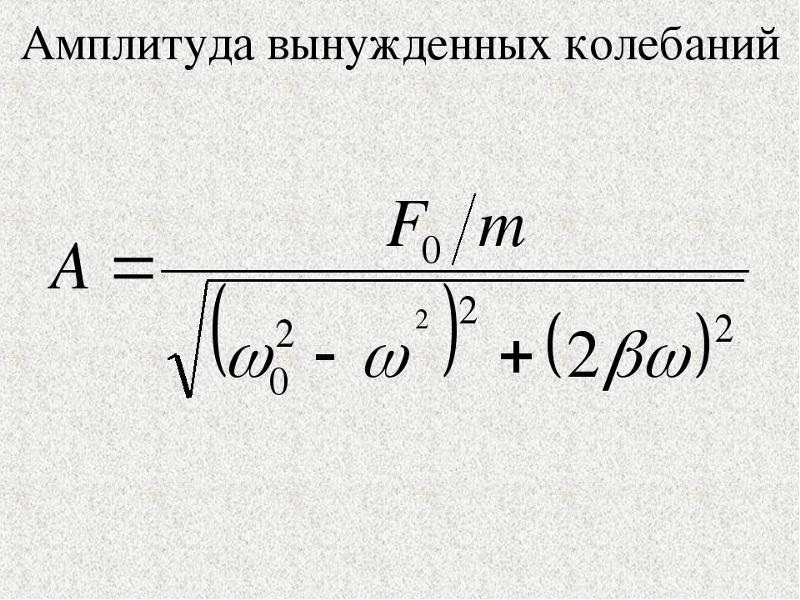 Эти колебания происходят с частотой внешней силы
, характеризуются амплитудой (7) и фазовым сдвигом (8). При совпадении частот,
, вне зависимости от величины затухания, сдвиг фазы составляет
.
Эти колебания происходят с частотой внешней силы
, характеризуются амплитудой (7) и фазовым сдвигом (8). При совпадении частот,
, вне зависимости от величины затухания, сдвиг фазы составляет
. Однако масса имеет импульс, p = mv,
и поэтому начинает растягивать пружину. Он движется через
положение равновесия вертикальной пружины с ее максимальной скоростью v макс. = 1,5 м/с.
Однако масса имеет импульс, p = mv,
и поэтому начинает растягивать пружину. Он движется через
положение равновесия вертикальной пружины с ее максимальной скоростью v макс. = 1,5 м/с. 