Формула для нахождения жесткости пружины: Что такое жесткость пружины и как ее рассчитать

alexxlab | 02.01.2023 | 0 | Разное

Содержание

Жесткость пружины: формулы и коэффициенты

Пружиной называют объект, способный с помощью деформации, вызванной внешними силами, накапливать и сохранять упругую потенциальную энергию, а после прекращения их воздействия восстанавливаться до прежнего состояния. Реально существующие пружины абсолютно точно восстановить свою прежнюю форму не в состоянии т.к. при внешнем воздействии в той или иной степени нарушается структура их материала, в результате чего возникают так называемые пластичные деформации. Чем они меньшее, тем более качественным считается изделие.

Какие бывают типы пружин

В первую очередь их принято делить на предназначенные для работы в режиме растягивания и предназначенные для работы в режиме сжатия.

Пружины растяжения при действии на них полезной нагрузки растягиваются. Они не нуждаются в жёстком захвате и, как правило, имеют нулевой шаг, т. е. витки у них прилегают вплотную друг к другу. В обычной жизни подобные изделия большинство людей может заметить, проходя через двери с механическим механизмом закрытия или при пользовании пружинными весами. В технике пружины растяжения используются для соединения элементов, положение которых меняется при их работе. В качестве примера можно привести завес рычагов.

Пружины сжатия под нагрузкой по длине уменьшаются. Для правильной работы их концы должны быть жёстко зафиксированы. Витки проволоки в свободном состоянии не касаются друг друга, т.к. им необходим некоторый промежуток, чтобы под внешней нагрузкой было куда перемещаться. В качестве примера использования таких изделий можно привести пружину в шариковой ручке или автомобильную подвеску.

В технике широкое применение находят и другие типы пружин: пружины кручения (в точных весах), плоские спиральные (как заводные в часах), плоские (в автомобильных рессорах), тарельчатые (в грузовых весах). В некотором роде пружинами можно назвать некоторые изделия из резины и из других полимерных эластичных материалов. Все они работают по одной и той же схеме – запасают кинетическую энергию в виде энергии упругости, а затем, когда нагрузка ослабнет или вовсе перестанет действовать, её возвращают.

Основные характеристики пружин

Зная материал и диаметр проволоки, форму её сечения, длину и диаметр пружины, как единого целого, можно с очень высокой достоверностью судить, насколько пружина может сопротивляться попыткам деформировать себя. Существуют также другие характеристики, от которых работоспособность пружины может зависеть очень серьёзно. К таковым относятся усталость материала проволоки, шаг витка, индекс пружины и т. д.

Материал и сила жесткости пружины

Зависимость между этими характеристиками пружин индивидуальная и вычисляется опытным путём. Чаще всего для изготовления металлических пружин используют высокоуглеродистые стали, легированные ванадием, кремнием и марганцем. Для изделий, предназначенных для длительной работы в агрессивных средах используют нержавеющую сталь, оловянносвинцовую, бериллиевую и кремнемарганцевую бронзу, различные чугуны, а также некоторые из титановых сплавов.

Небольшие пружины изготавливают из уже закалённой проволоки. Крупные изделия делают из отожжённой стали, а закалку проводят уже после формовки.

Как связана жесткость пружины с диаметром и формой сечения проволоки, из которой она сделана

Чем он меньше, тем пружина более эластична. Способность запасать энергию с уменьшением диаметра тоже становится меньше. Пружины сжатия, как правило, делают из более толстой проволоки.

Следует отметить, что не всегда сечение проволоки для пружин бывает круглым, в пружинах сжатия оно иногда бывает уплощённым. Это обеспечивает лучшую посадку одного витка на другой и делает конструкцию более устойчивой.

Длина и диаметр

Определение

Под длиной пружины понимают её длину в свободном, недеформированном состоянии.

Также следует различать длину собственно изделия и длину проволоки, из которой оно сделано. Это две совершенно разные величины. Не малое значение имеет число витков. В пружинах сжатия, чем их больше, тем выше вероятность соскальзывания изделия с опоры и, как следствие, выхода детали из строя.

О понятии жесткости. Жесткость пружины: формула

Определение

Жёсткостью пружины называют коэффициент, который связывает силу прилагаемую к ней с удлинением или сжатием.

Посмотрите на закон Гука.

Формула

Fупр = –kx

Зако́н Гу́ка — утверждение, согласно которому, деформация, возникающая в упругом теле (пружине, стержне, консоли, балке и т. д.), пропорциональна приложенной к этому телу силе.

k – это и есть жёсткость пружины.

Fупр — сила жесткости или упругости пружины.

x — расстояние, на которое изменилась длина изделия после того как та была уравновешена.

Минус в формуле свидетельствует о том, что сила F имеет по сравнению с нагрузкой противоположное направление.

Закон Гука является одним из основных законов физики.

Как найти жесткость пружины? Формулу из выше приведённого уравнения понять достаточно легко:

Коэффициент жесткости пружины можно вычислить и экспериментальным путём. Для этого нужно подвесить на вертикально закреплённую пружину груз с известной массой.

Имеем два уравнения:

Т. к. Fупр =Fтяж, получаем

Отсюда разделив обе части уравнения на x, найдём, что жёсткость равна

Массу самой пружины считаем равной нулю. Для исключения случайных ошибок проводим несколько измерений с грузами разной массы.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Как рассчитать жесткость цилиндрической пружины

В плоской пружине в момент её изгиба расстояния между молекулами, находящимися в одном месте уменьшаются, а в другом увеличиваются. Сила электромагнитных межмолекулярных связей стремится вернуть изделие в прежнее положение.

С цилиндрической пружиной всё несколько иначе. В ней энергия запасается не из-за деформации изгиба, а благодаря скручиванию проволоки вдоль своей оси навивания.

Давайте мысленно увеличим выполненное перпендикулярно её оси плоскостью сечение проволоки. Это нам позволит не учитывать спиральную форму изделия. Разобьём весь объём проволоки на очень много касающихся друг друга своими торцами цилиндров. Их диаметр совпадает с диаметром проволоки, а высота бесконечно мала. Торцам не дают разъединится действующие между ними межмолекулярные силы. Именно они препятствуют деформации.

Когда пружина растягивается или сжимается, цилиндры вынуждены вращаться друг относительно друга в противоположных направлениях вокруг общей оси. В каждом из сечений запасается некоторая энергия. Отсюда легко сделать вывод, что чем проволока длиннее, тем больше энергии такая пружина способна запасти. Увеличение проволоки по диаметру тоже способствует возрастанию её энергоёмкости.

Окончательная формула для жёсткости цилиндрической пружины такова:

Буквой R у нас обозначен радиус цилиндра пружины, n – количество витков проволоки, r—её радиус, G – коэффициент, индивидуальный для материала проволоки.

Чтобы по данной формуле сделать расчёт жёсткости, достаточно просто подставить вместо букв, обозначающих величины, их числовые значения.

Лабораторная работа 1 определение жесткости пружины. Лабораторная работа “определение жесткости пружины”

Урок 13/33

Тема. Лабораторная работа № 2 «Измерение жесткости пружины»

Цель урока: проверить справедливость закона Гука для пружины динамометра и измерить коэффициент жесткости этой пружины

Тип урока: контроля и оценивания знаний

Оборудование: штатив с муфтой и зажимом, динамометр с заклеенной шкалой, набор грузиков известной массы (по 100 г), линейка с миллиметровыми делениями

ХОД РАБОТЫ

1. Закрепите динамометр в штативе на достаточно большой высоте.

2. Подвешивая разное количество грузиков (от одного до четырех), вычислите для каждого случая соответствующее значение F = mg , а также измерьте соответствующее удлинение пружины х.

3. Результаты измерений и вычислений запишите в таблицу:

	m , кг	mg, Н

4. Начертите оси координат х и F , выберите удобный масштаб и нанесите полученные во время эксперимента точки.

6. Вычислите коэффициент жесткости по формуле k = F /x , используя результаты опыта № 4 (это обеспечивает наибольшую точность).

7. Для вычисления погрешности следует использовать опыт, который мы получили во время поведення опыта № 4, потому что ему соответствует наименьшая относительная погрешность измерений. Вычислите пределы Fmin и Fmax , в которых находится истинное значение F , считая, что Fmin = F – ΔF , F = F + ΔF . Примите ΔF = 4Δm · g , где Δm – погрешность во время изготовления грузиков (для оценки можно считать, что Δm = 0,005 кг):

где Δх = 0,5 мм.

8. Пользуясь методом оценки погрешности косвенных измерений, вычислите:

9. Вычислите среднее значение kcep и абсолютную погрешность измерения Δk по формулам:

10. Вычислите относительную погрешность измерений:

11. Заполните таблицу:

Fmin, H	Fmax, H	xmin, м	xmax, м	kmin, Н/м	kmax, Н/м	k сэр, Н/м

12.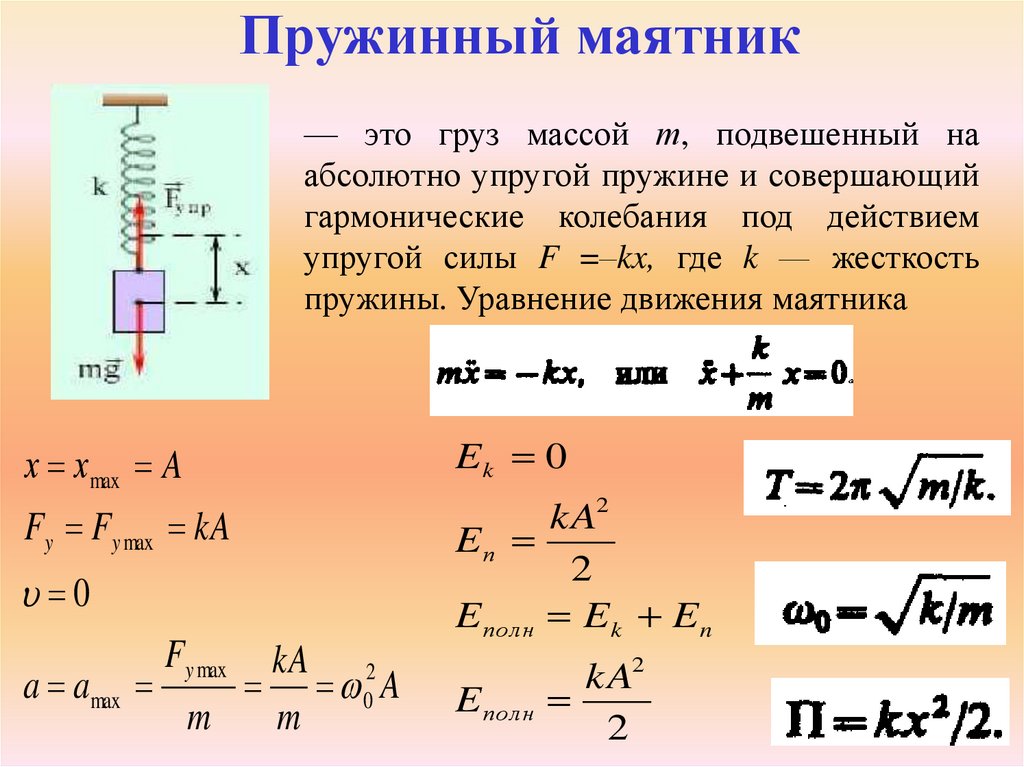 Запишите в тетради для лабораторных работ результат в виде k = kcep ± Δk , подставив в эту формулу числовые значения найденных величин.

13. Запишите в тетради для лабораторных вывод: что вы измеряли и какой получили результат.

Лабораторная работа

«Определение жесткости пружины»

Цель работы : Определение коэффициента жесткости пружины. Проверка справедливости закона Гука.Оценка погрешности измерений.

Порядок выполнения работы .

Базовый уровень

Оборудование : штатив с муфтой и лапкой, набор грузов по 100 г, пружинный динамометр, линейка.

L 0 F

L 1 в этом случае.

l = L 0 – L 1

k ср .по формуле k ср =( k 1 + k 2 + k 3 )/3

F ,Н

l ,м

k ,Н/м

k ср , Н/м

6. Начертите график зависимости l ( F ).

Продвинутый уровень

Оборудование : штатив с муфтой и лапкой, набор грузов по 100 г, пружина, линейка.

Укрепите пружину в штативе и измерьте длину пружины L 0 в отсутствие внешнего воздействия (F =0Н).

Подвесьте к пружине груз весом 1 Н и определите ее длину L 1 в этом случае.

Найдите деформацию (удлинение) пружины по формуле l = L 0 – L 1 .Результаты измерений занесите в таблицу.

Аналогично найдите удлинение пружины при подвешивании грузов весом 2 Н и 3 Н. Результаты измерений занесите в таблицу.

Вычислите среднее арифметическое значение k ср .по формуле k ср =( k 1 + k 2 + k 3 )/3

Оцените погрешность ∆ k методом средней ошибки. Для этого вычислите модуль разности │ k ср – k i │=∆ k i для каждого измерения

k = k ср ±∆ k

F ,Н

l ,м

k ,Н/м

k ср , Н/м

∆k ,Н/м

∆k ср , Н/м

Углубленный уровень

Оборудование: штатив с муфтой и лапкой, набор грузов по 100 г, пружина, линейка.

Укрепите пружину в штативе и измерьте длину пружины L 0 в отсутствие внешнего воздействия (F =0Н).

Подвесьте к пружине груз весом 1 Н и определите ее длину L 1 в этом случае.

Найдите деформацию (удлинение) пружины по формуле l = L 0 – L 1 .Результаты измерений занесите в таблицу.

Вычислите среднее арифметическое значение k ср .по формуле k ср =( k 1 + k 2 + k 3 )/3

Вычислите относительные погрешности и абсолютную погрешность измерений ∆ k по формулам

ε F =(∆ F 0 + F и ) / F max

ε l =(∆ l 0 + l и ) / l max

ε k =ε F +ε l

∆k= ε k * k ср

Полученный результат запишите в виде k = k ср±∆ k

Начертите график зависимости l ( F ).Сформулируйте геометрический смысл жесткости.

F ,Н

l ,м

k ,Н/м

k ср , Н/м

ε F

ε l

ε k

∆ k

По физике за 9 класс (И. К.Кикоин, А.К.Кикоин, 1999 год),
задача №2
к главе «ЛАБОРАТОРНЫЕ РАБОТЫ ».

Цель работы: найти жесткость пружины из измерений удлинения пружины при различных значениях силы тяжести

уравновешивающей силу упругости на основе закона Гука:

Это связано с погрешностями измерения. В этом случае график надо проводить так, чтобы примерно одинаковое число точек оказалось по разные стороны от прямой. После построения графика возьмите точку на прямой (в средней части графика), определите по нему соответствующие этой точке значения силы упругости и удлинения и вычислите жесткость k. Она и будет искомым средним значением жесткости пружины k ср.

Результат измерения обычно записывается в виде выражения k = = k cp ±Δk, где Δk – наибольшая абсолютная погрешность измерения. Из курса алгебры (VII класс) известно, что относительная погрешность (ε k) равна отношению абсолютной погрешности Δk к значению величины k:

откуда Δk – ε k k. Существует правило для расчета относительной погрешности: если определяемая в опыте величина находится в результате умножения и деления приближенных величин, входящих в расчетную формулу, то относительные погрешности складываются. В данной работе

Средства измерения: 1) набор грузов, масса каждого равна m 0 = 0,100 кг, а погрешность Δm 0 = 0,002 кг; 2) линейка с миллиметровыми делениями.

Материалы: 1) штатив с муфтами и лапкой; 2) спиральная пружина.

Порядок выполнения работы

1. Закрепите на штативе конец спиральной пружины (другой конец пружины снабжен стрелкой-указате-лем и крючком – рис. 176).

2. Рядом с пружиной или за ней установите и закрепите линейку с миллиметровыми делениями.

3. Отметьте и запишите то деление линейки, против которого приходится стрелка-указатель пружины.

4. Подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины.

5. К первому грузу добавьте второй, третий и т. д. грузы, записывая каждый раз удлинение |х| пружины. По результатам измерений заполните таблицу:

6. По результатам измерений постройте график зависимости силы упругости от удлинения и, пользуясь им, определите среднее значение жесткости пружины k cp .

7. Рассчитайте наибольшую относительную погрешность, с которой найдено значение k ср (из опыта с одним грузом). В формуле (1)

так как погрешность при измерении удлинения Δx=1 мм, то

8. Найдите

и запишите ответ в виде:

1 Принять g≈10 м/с 2 .

Закон Гука: «Сила упругости, возникающая при деформации тела, пропорциональна его удлинению и направлена противоположно направлению перемещения частиц тела при деформации».

Закон Гука

Жесткостью называют коэффициент пропорциональности между силой упругости и изменением длины пружины под действием приложенной к ней силы. Согласно третьему закону Ньютона, приложенная к пружине сила по модулю равна возникшей в ней силе упругости. Таким образом жесткость пружины можно выразить как:

где F – приложенная к пружине сила, а х – изменение длины пружины под ее действием. Средства измерения: набор грузов, масса каждого равна m 0 = (0,1±0,002) кг.

Линейка с миллиметровыми делениями (Δх = ±0,5 мм). Порядок выполнения работы описан в учебнике и комментариев не требует.

	масса, кг		удлинение \|х\|,

Лабораторная работа №

Измерение жесткости пружины

10 класс

Цель работы: найти жесткость пружины из измерений удлинения пружины при различных значениях силы тяжести , уравновешивающей силу упругости
, на основе закона Гука:
.

Приборы и материалы:

В каждом из опытов жесткость определяется при разных значениях силы упругости и удлинения, т.е. условия опыта меняются. Поэтому для нахождения среднего значения жесткости нельзя вычислить среднее арифметическое результатов измерений. Воспользуемся графическим способом нахождения среднего значения, который может быть применен в таких случаях. По результатам нескольких опытов построим график зависимости модуля силы упругости от модуля удлинения х. При построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле
. Это связано с погрешностями измерения: В этом случае график надо проводить так, чтобы примерно одинаковое число точек оказалось по разные стороны от прямой. После построения графика возьмите точку на прямой (в средней части графика), определите по нему соответствующие этой точке значения силы упругости и удлинения и вычислите жесткость k.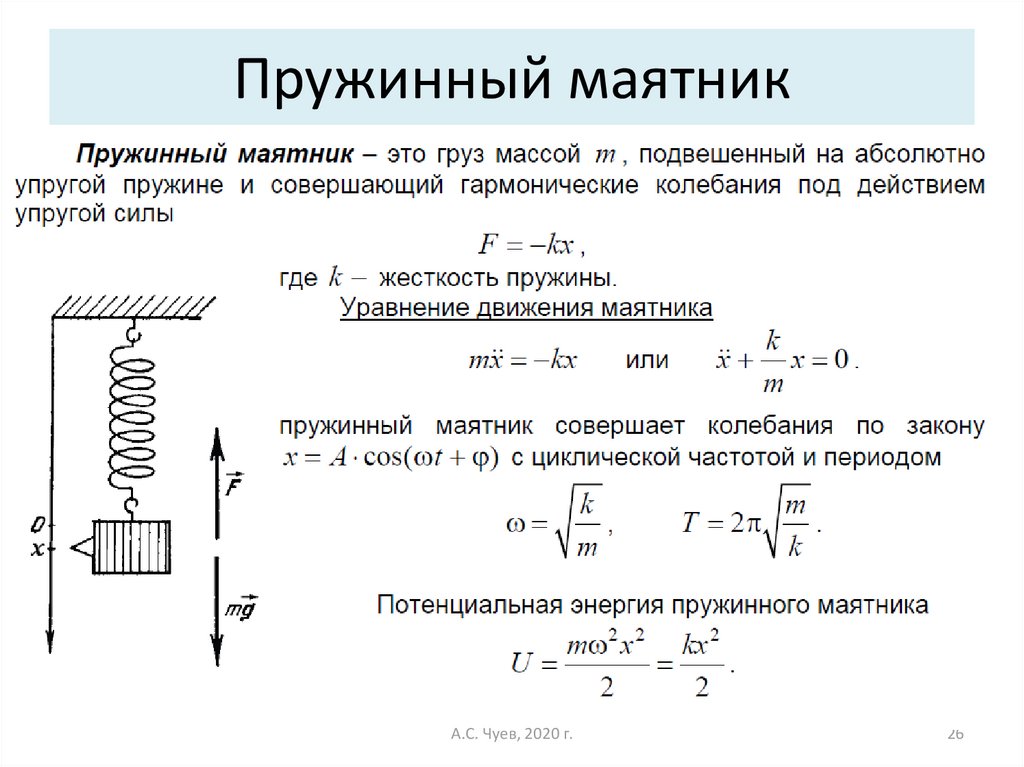 Она и будет искомым средним значением жесткости пружины .

Результат измерения обычно записывается в виде выражения
, где
– наибольшая абсолютная погрешность измерения. Известно, что относительная погрешность () разна отношению абсолютной погрешности к значению величины k:

, откуда
.

В данной работе
. Поэтому
, где
,
,

Абсолютные погрешности:

= 0,002 кг;

=1мм,

Порядок выполнения работы

Закрепите на штативе конец спиральной пружины.

Рядом с пружиной или за ней установите и закрепите линейку с миллиметровыми делениями.

Отметьте и запишите то деление линейки, против которого приходится стрелка-указатель пружины.

Подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины.

К первому грузу добавьте второй, третий и т.д. грузы, записывая каждый раз удлинение х пружины. По результатам измерений заполните таблицу:

Номер опыта

Цель работыпроверить справедливость закона Гука для
пружины динамометра и измерить коэффициент
жесткости этой пружины.
Оборудование:
штатив с муфтой и зажимом, динамометр с
заклеенной шкалой, набор грузов известной массы
(по 100 г), линейка с миллиметровыми делениями.

Подготовительные вопросы
Что такое сила упругости?
Как вычислить силу упругости,
возникающую в пружине при подвешивании
к ней груза массой m кг?
Что такое удлинение тела?
Как измерить удлинение пружины при
подвешивании к ней груза?
В чем заключается закон Гука?

Правила техники безопасности
Будьте осторожны при работе с растянутой
пружиной.
Не роняйте и не бросайте грузы.

Описание работы:
Согласно закону Гука, модуль F силы упругости и
модуль х удлинения пружины связаны
соотношением F = kx. Измерив F и х, можно найти
коэффициент жесткости k по формуле

В каждом из опытов жесткость определяется при разных значениях
силы упругости и удлинения, т. е. условия опыта меняются. Поэтому
для нахождения среднего значения жесткости нельзя вычислить
среднее арифметическое результатов измерений. Воспользуемся
графическим способом нахождения среднего значения, который
может быть применен в таких случаях. По результатам нескольких
опытов построим график зависимости модуля силы упругости Fупр от
модуля удлинения \х\. При построении графика по результатам опыта
экспериментальные точки могут не оказаться на прямой, которая
соответствует формуле Fyпp=k\x\. Это связано с погрешностями
измерений. В этом случае график надо проводить так, чтобы
примерно одинаковое число точек, оказалось, по разные стороны от
прямой. После построения графика возьмите точку на прямой (в
средней части графика) определите по нему соответствующие этой
точке значения силы упругости и удлинения, и вычислите
жесткость k. Она и будет искомым средним значением жесткости
пружины kср.

ХОД РАБОТЫ:

1. Закрепите на штативе конец спиральной пружины
(другой конец пружины снабжен стрелкой-указателем и
крючком).
2. Шкалу динамометра закройте бумагой.
3. Отметьте деление, против которого находится стрелкауказатель пружины.
4. Подвесьте к пружине груз известной массы и измерьте
вызванное им удлинение пружины. Отметьте положение
стрелки-указателя динамометра.
5. К первому грузу добавьте второй, а затем третий грузы,
отмечая каждый раз положение стрелки-указателя и
записывая каждый раз удлинение \х\ пружины. По
результатам измерений заполните таблицу

6. Начертите оси координат х и F, выберите удобный
масштаб и нанесите полученные экспериментальные
точки.
7. Оцените (качественно) справедливость закона Гука для
данной пружины: находятся ли экспериментальные точки
вблизи одной прямой, проходящей через начало
координат.
8. По результатам измерений постройте график
зависимости силы упругости от удлинения и, пользуясь
им, определите среднее значение жесткости пружины kср.
9. Рассчитайте наибольшую относительную погрешность,
с которой найдено значение kcp
10. Запишите сделанный вами вывод.

№ опыта
1
m, кг
0,1
2
0,2
3
0,3
mg, H
х, м

10.

Контрольные вопросы:
Как называется зависимость между силой
упругости и удлинением пружины?
Пружина динамометра под действием силы
4Н удлинилась на 5 мм. Определите вес
груза, под действием которого эта пружина
удлиняется на 16 мм.

Рассчитать жесткость пружины › Gutekunst Federn › Рассчитать жесткость пружины, Рассчитать жесткость пружины, Определить жесткость пружины, Festigkeitsnachweis, Закон Гука, Тело пружины, Постоянная пружины, Пружина сжатия постоянной жесткости, Жесткость пружины, Пружина сжатия жесткости пружины, Ход пружины , Коэффициент крутящего момента пружины, Момент пружины кручения

Константа пружины описывает для пружин сжатия, пружин растяжения и пружин кручения увеличение силы по отношению к ходу подвески или для пружин кручения по отношению к углу поворота. Он также называется жесткостью пружины, жесткостью пружины или жесткостью пружины и определяет жесткость пружины. С характеристикой пружины показывается ход жесткости пружины. Является ли постоянная пружины линейной, т. е. усилие пружины увеличивается равномерно с нагрузкой на пружину, тогда характеристика пружины прямолинейна (б.). Если, с другой стороны, сила пружины непропорционально или непропорционально возрастает с увеличением нагрузки, то говорят о прогрессивной (а) или дегрессивной (в) характеристике пружины. Постоянная пружины для пружин сжатия и растяжения указывается в единицах измерения ньютон/миллиметр, а для пружин кручения – как коэффициент крутящего момента пружины в ньютон-миллиметрах.

Характеристики пружины

Следовательно, к жесткости пружины с прямой характеристикой пружины относится следующее:

Пружины сжатия и растяжения

Schenkelfedern

пружины кручения:

Formula spring пружины постоянного сжатия (Н/мм) ( Formula collection пружины сжатия )

Формула пружин постоянного натяжения пружин (Н/мм) (Формула пружин растяжения)

Формула крутящего момента пружин ног (Нмм) (Формула торсионных пружин)

Объяснение формулы:
α = угол вращения (°)
d = диаметр проволоки (мм)
D = средний диаметр витка (мм)
E = модуль упругости (Н/мм²) (модуль упругости различных пружинных сталей)
F = усилие пружины (Н)
G = модуль скольжения и сдвига (Н/мм²) (G-модуль изготовлен из различных пружинных сталей)
F0 = внутреннее усилие предварительной нагрузки
M = крутящий момент (Нмм)
n = количество упругих витков (шт. )
R = жесткость пружины (Н/мм)
RM = коэффициент крутящего момента пружины (Нмм)
s = прогиб пружины (мм)

Жесткость пружины также можно определить с помощью испытания на растяжение. Пружина растягивается с силой (F) и измеряется прогиб пружины / работа пружины (s2). Это дает жесткость пружины в ньютонах на миллиметр.

Однако это испытание на растяжение следует проводить с разными усилиями, чтобы получить точный результат измерения.

Дополнительная информация

Программа расчета пружин Gutekunst WinFSB

Расчет усилия пружины

Пружинная работа

Свойства пружинной стали

Характеристика пружины

Расчет жесткости пружины

Tagged on: Рассчитать жесткость пружины Вычислить жесткость пружины Определить жесткость пружины Festigkeitsnachweis Закон Гука Тело пружины Постоянная пружины Пружина постоянного сжатия Стойкость пружины Статистика пружины сжатия Перемещение жесткости пружины Коэффициент крутящего момента пружины Момент пружины кручения

Расчет прогиба пружины | Формула закона Гука

15 февраля 2021 г.

Когда пружина отскакивает, этот отскок является результатом отклонения пружины. Отклонение пружины — это действие или движение, возникающее в результате приложения или снятия нагрузки. Это реакция на силу, когда она применяется или удаляется. Отклонение пружины также известно как ход пружины, что означает расстояние, на которое пружина перемещается между нагруженным и предварительно нагруженным положением. Ход пружины, т. е. пройденное расстояние при сжатии, растяжении или скручивании пружины, представляет собой ее отклонение.

Понимание деформации пружины необходимо при проектировании и производстве всех пружин. Отклонение происходит всякий раз, когда пружина нагружена, независимо от того, сжата ли она, растянута или радиально повернута. Расчет для оценки прогиба пружины, необходимой для приложений, основан на законе Гука, принципе физики, названном в честь британского физика 17-го века Роберта Гука, который стремился понять взаимосвязь между законами упругости, кручение и силы, которые приходят в игру, когда пружина сжимается или растягивается.

Закон Гука
Формула закона Гука выражается как Fs = kx, где F — сила пружины, равная k, постоянной пружины — сила, необходимая для растяжения или сжатия пружины, деленная на расстояние, на которое пружина становится длиннее или короче, а x — смещение пружины. Прогиб пружины для желаемого применения можно рассчитать путем деления силы пружины (Fs) на константу пружины (k) для измерения ее смещения (x). Закон Гука определил, что сила, необходимая для растяжения или сжатия пружины на некоторое расстояние, пропорциональна этому расстоянию.

Помимо вычислений, прогиб пружины для любого применения требуется для определения максимальной нагрузки, которую может выдержать пружина, поскольку он учитывает нагрузку, которую должна выдерживать пружина. Скорость отклонения пружины является еще одним расчетом при разработке нестандартных пружин, а также пружин, изготовленных для общего применения. Например, инженеры, которым требуется коэффициент отклонения 200 фунтов. на дюйм для пружины сжатия потребуется, чтобы пружина сжималась на один дюйм на каждые 200 фунтов приложенной к ней нагрузки. Формула для расчета скорости прогиба: D = L/R, т. е. нагрузка (L), деленная на скорость (R) = прогиб (D). Таким образом, скорость отклонения пружины будет определять степень отклонения пружины.

Пружины разных типов могут иметь разные характеристики прогиба пружины. Действие пружины сжатия, когда она сжимается (толкается), пружины растяжения, когда она растягивается (тянется), или пружины кручения, когда она скручивается (скручивается) при приложении или отпускании нагрузки, имеют разные характеристики отклонения пружины.

Коэффициент отклонения
Коэффициент отклонения для обычных пружин сжатия является линейным, что означает, что вес отклоняется равномерно по всей пружине, когда ее толкают. В установленном положении пружины сжатия имеют нулевую нагрузку при нулевом прогибе. Однако пружины сжатия различной формы, такие как пружины конической формы, могут иметь переменную скорость отклонения. Сила, необходимая для отклонения, возникает в разных положениях пружины по мере ее сжатия. Для приложений, требующих, например, пружин сжатия конической или бочкообразной формы, имейте в виду, что сила, необходимая для отклонения, является переменной и может изменяться.

В отличие от пружин сжатия, пружины растяжения наматываются с начальной нагрузкой или растяжением. При настройке пружины растяжения могут иметь предварительную нагрузку при нулевом отклонении. Затем скорость отклонения рассчитывается по нагрузке, необходимой для инициирования разделения витков при растяжении пружины.

Пружины кручения функционируют на радиальной оси, а не за счет сжатия или растяжения при нагрузке или разгрузке. Энергия накапливается и высвобождается в ответ на крутящий момент, вызывая угловое отклонение пружины. При приложении крутящего момента скручивающее действие уменьшает диаметр катушки и увеличивает длину корпуса. Потенциальная энергия накапливается при наматывании и высвобождается при раскручивании.

TOP HEADLINES