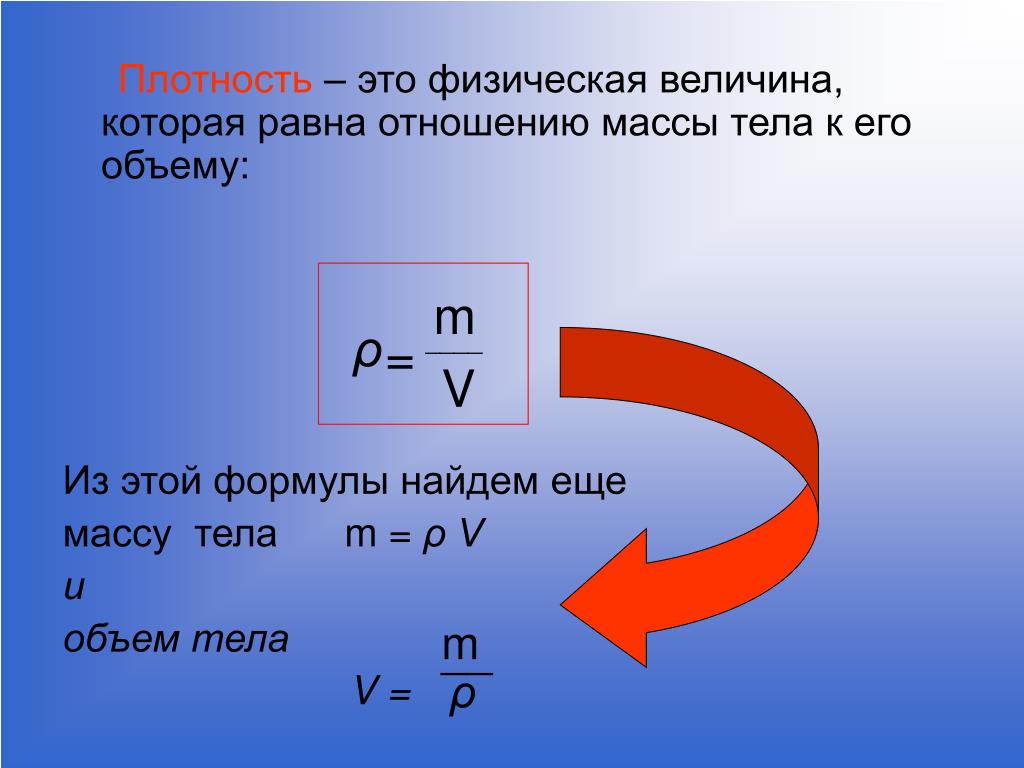
Формула для вычисления массы: Что нужно чтобы найти массу. Как найти массу вещества? Как найти массу автомобиля в физике
alexxlab | 30.11.1989 | 0 | Разное
В классической механике считают:
- масса тела не является зависимой от движения тела, от воздействия других тел, расположения тела;
- выполняется закон сохранения массы: масса замкнутой механической системы тел неизменна во времени.
Инертная масса
Свойство инертности материальной точки состоит в том, что если на точку действует внешняя сила, то у нее возникает конечное по модулю ускорение. Если внешних воздействий нет, то в инерциальной системе отсчета тело находится в состоянии покоя или движется равномерно и прямолинейно. Масса входит во второй закон Ньютона:
$$\bar{F}=m \bar{a}(2)$$
где масса определяет инертные свойства материальной точки (инертная масса).
Гравитационная масса
Масса материальной точки входит в закон всемирного тяготения, при этом она определяет гравитационные свойства данной точки.при этом она носит название гравитационной (тяжелой) массы.
Эмпирически получено, что для всех тел отношения инертных масс к гравитационным являются одинаковыми.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Какова масса 2м3 меди?
Решение. Будем считать, что медь однородна и для решения задачи используем формулу:
$$m=\rho V$$
При этом если известно вещество (медь), то можно при помощи справочника найти ее плотность. Плотность меди будем считать равной $\rho$ Cu=8900 кг/м3 . Для расчета все величины известны. Проведем вычисления:
$m=8900 \cdot 2=17800$ (кг)
Ответ. $m=8900 \cdot 2=17800$ (кг)
Читать дальше: Формула момента силы.
Масса покоя или инертная масса?
Масса покоя или инертная масса? УДК. 12:531.18+51]Масса покоя или инертная масса?
Р. И. Храпко
И. Храпко
Исключение из современных учебников физики инертной массы и замена ее массой покоя представляется ошибкой. Эта тема была поднята автором в статье [1,2]. Здесь приведены дополнительные рассуждения в подтверждение такого тезиса.
Конец 20-го века ознаменовался великой путаницей с физическим понятием “масса тела”.
1. Масса покоя
В начале века, до создания теории относительности, было все ясно. Массой тела, m, называлось количество вещества тела, и в то же время масса являлась мерой инертности тела. Инертность тела определяет его “количество движения” при заданной скорости v движения, то есть коэффициент пропорциональности в формуле
P – количество движения или, по-научному, импульс тела, а коэффициент m называется инертной массой.
Но массу как меру инертности тела можно определять и с помощью формулы
F = ma: (2)
чем больше масса, тем меньше ускорение тела при
заданной силе. Значение массы по формулам (1) и (2)
получалось одно и то же, потому что формула (2)
является следствием формулы (1), если инертная
масса не зависит от времени и скорости.
Значение массы по формулам (1) и (2)
получалось одно и то же, потому что формула (2)
является следствием формулы (1), если инертная
масса не зависит от времени и скорости.
То же значение массы можно было получить, взвесив тело, то есть измерив силу притяжения к земле или к любому другому заданному телу (масса которого обозначена M). В законе тяготения Ньютона фигурирует та же самая масса m,
, (3)
но тут она называется гравитационной (пассивной) массой. В этом выражается эквивалентность инертной и гравитационной массы. Благодаря этой эквивалентности ускорение свободного падения, как известно, не зависит от природы и массы тела:
(4)
2. Инертная масса
Однако при создании теории
относительности выяснилось, что никакое тело
нельзя разогнать до скорости света, потому что
при приближении скорости тела к скорости света
ускорение тела уменьшается до нуля, как бы ни
была велика ускоряющая сила. Другими словами,
выяснилось, что инертность тела возрастает до
бесконечности при приближении его скорости к
скорости света, хотя “количество вещества”
тела, очевидно, остается при этом неизменным.
Другими словами,
выяснилось, что инертность тела возрастает до
бесконечности при приближении его скорости к
скорости света, хотя “количество вещества”
тела, очевидно, остается при этом неизменным.
Выскажемся точнее по поводу увеличения инертности тела. Теория относительности показала, что импульс тела P при любых скоростях остается параллелен скорости
, (5)
то есть для импульса тела справедливо выражение
. (6)
В этих формулах m0 – это то значение массы
рассматриваемого тела, о котором говорилось
вначале, то есть значение, которое можно получить
после того, как тело затормозят до достаточно
малой скорости. Его называют массой покоя тела.
Поэтому формулы (1), (2), (3) следовало бы записать
так: P = m0v, F = m0a,
.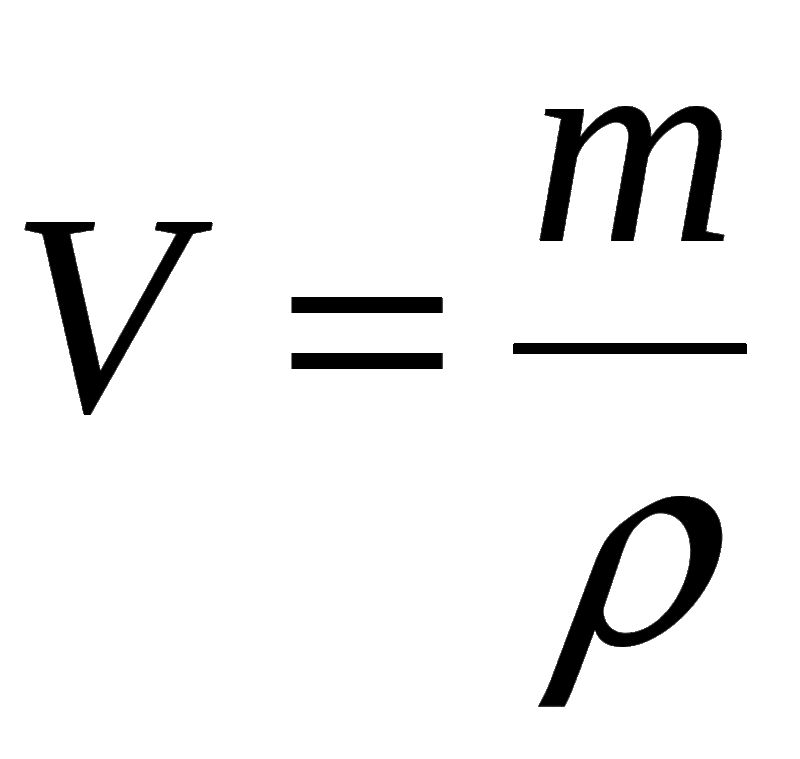 Однако для малых скоростей, как видно из формулы
(5), инертная масса равна массе покоя, m = m0, и поэтому запись (1), (2), (3) в разделе
“до теории относительности” корректна.
Однако для малых скоростей, как видно из формулы
(5), инертная масса равна массе покоя, m = m0, и поэтому запись (1), (2), (3) в разделе
“до теории относительности” корректна.
Для того, чтобы подчеркнуть, что инертная масса m зависит от скорости, ее называют иногда “релятивистской” массой: она оказывается различной с точки зрения различных наблюдателей, если эти наблюдатели движутся друг относительно друга. Однако существует выделенное значение инертной массы, именно, значение, которое наблюдает неподвижный относительно тела наблюдатель. Другими словами, масса покоя является выделенным значением инертной массы. Такое свойство инертной массы аналогично свойству времени: одни и те же часы имеют разную скорость хода с точки зрения различных наблюдателей. Однако существует собственная скорость хода часов.
При желании проверить формулу (6) вы
должны измерить скорость v тела, а потом измерить импульс тела.
Для этого следует затормозить тело некоторой
преградой, все время замеряя силу F(t), с которой при торможении тело
будет действовать на преграду, а потом
проинтегрировать.
(7)
Эта процедура, по сути, задает операционное определение инертной массы.
Заметим, что формулы (5) и (6) остаются справедливыми и для объекта, у которого нет массы покоя, m0 = 0, например, для фотона или нейтрино (если предположить, что масса покоя нейтрино равна нулю). Такие объекты обладают инертной массой и импульсом, но должны двигаться со скоростью света, их нельзя остановить, они исчезают при остановке. Тем не менее, несмотря на постоянство скорости движения, величина их инертной массы оказывается различной с точки зрения различных наблюдателей. Однако в этом случае не существует какого либо выделенного значения инертной массы. Либо, можно сказать, выделенное значение равно нулю.
Увеличение инертности тела при
больших скоростях мы объяснили уменьшением
ускорения при большой скорости. При этом мы
сослались на формулу (2). И это допустимо. Однако
именно в силу увеличения инертной массы с ростом
скорости тела формула (2) при некоторых условиях
изменяет свой вид.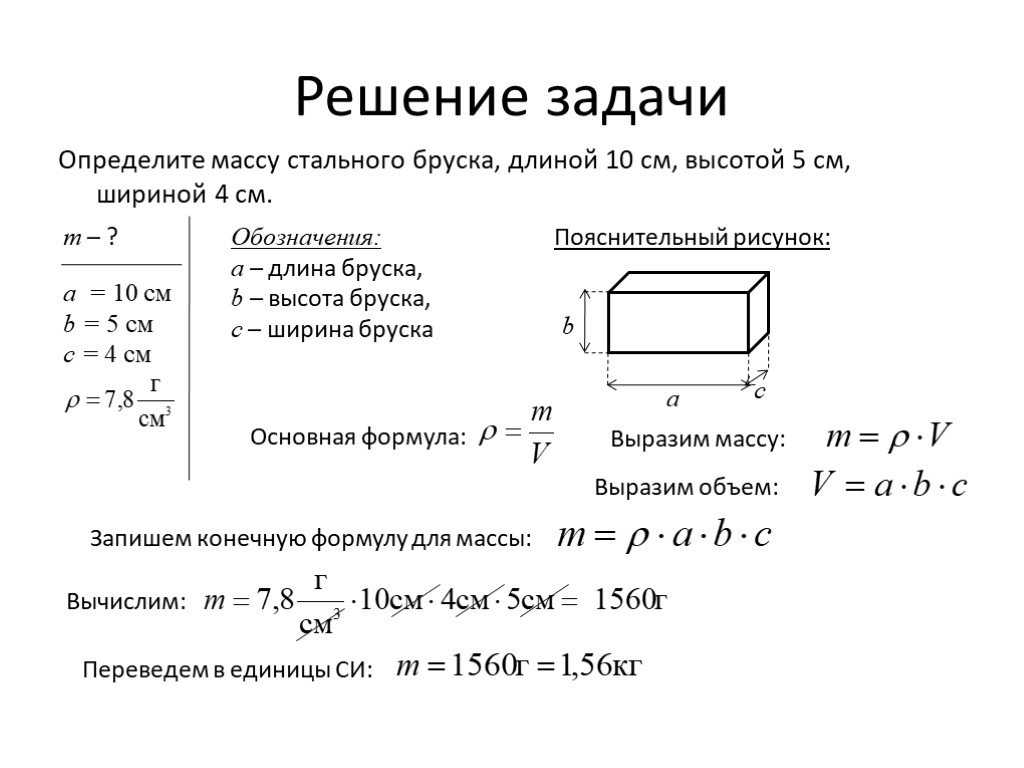
, (5)
она должна обеспечить возрастание самой массы:
. (8)
Коэффициент
называют иногда продольной массой [3] .
Если сила перпендикулярна скорости и, значит, не изменяет величину скорости и инертной массы, то формула F = ma сохраняет свой вид:
. (9)
Последнее обстоятельство позволило Р. Фейнману предложить простой способ операционного определения инертной массы, основанный на формуле (9) и справедливый для любой скорости. “Массу можно измерить так: просто привязать предмет на веревочке, крутить его с определенной скоростью и измерять ту силу, которая необходима, чтобы удержать его.” [4]
При произвольном направлении силы
относительно скорости тела коэффициент
пропорциональности в формуле (2) следует
рассматривать как некий оператор (тензор),
превращающий вектор a в вектор F: F = a. Оператор зависит от величины и
направления скорости тела и, вообще говоря,
изменяет направление вектора. Это нетрудно
принять. Ведь скорость v тела является его свойством, а сила F, действующая на тело – это внешний по
отношению к телу фактор. Понятно, что результат
воздействия силы, то есть ускорение a тела, может зависеть от соотношения
направлений векторов F и v.
Оператор зависит от величины и
направления скорости тела и, вообще говоря,
изменяет направление вектора. Это нетрудно
принять. Ведь скорость v тела является его свойством, а сила F, действующая на тело – это внешний по
отношению к телу фактор. Понятно, что результат
воздействия силы, то есть ускорение a тела, может зависеть от соотношения
направлений векторов F и v.
3. Гравитационная масса
Одновременно теория относительности показала, что не только инертность тела, но и его вес увеличивается с ростом скорости, причем по тому же закону (5) в соответствии с эквивалентностью инертной и гравитационной массы. Поэтому формула (8) для тела, падающего вниз со скоростью v, выглядит, грубо говоря, так:
= .
Точная формула для ускорения может быть получена в рамках общей теории относительности, как показано в конце статьи:
, . (10)
Эта формула является релятивистским аналогом
формулы (4).
4. Энергия
Теория относительности показала далее, что прирост инертной массы, m – m0, умноженный на квадрат скорости света, равен как раз кинетической энергии тела:
(m √ m0)c2 = Ek. (11)
Поэтому, если приписать покоящемуся телу энергию покоя E0 = m0c2, то полная энергия E = E0 + Ek тела оказывается пропорциональной инертной массе:
E = mc2 (12)
Эта знаменитая формула Эйнштейна провозглашает эквивалентность инертной массы и энергии. Два, доселе различных понятия, соединяются в одно.
Заметим, что формула (12), как и формулы (5) и (6) остается справедлива и для объекта, у которого нет массы и энергии покоя, m0 = 0.
При желании проверить формулу (11) и
одновременно убедиться в справедливости теории
относительности вы должны измерить инертную
массу и массу покоя тела как было объяснено выше,
и, кроме того, измерить кинетическую энергию
тела. Для этого следует при торможении тела
упомянутой преградой все время замерять силу, с
которой тело будет действовать на преграду в
процессе торможения в функции перемещения l преграды, F(l), а потом проинтегрировать.
Кинетическая энергия, равная, как известно, в
данном случае работе, вычисляется по формуле
Для этого следует при торможении тела
упомянутой преградой все время замерять силу, с
которой тело будет действовать на преграду в
процессе торможения в функции перемещения l преграды, F(l), а потом проинтегрировать.
Кинетическая энергия, равная, как известно, в
данном случае работе, вычисляется по формуле
.
Здесь F(l)dl – скалярное произведение силы на инфинитезимальный вектор смещения преграды. Все это рассказано в [5] .
Формула (11) связывает инертную массу, массу покоя и кинетическую энергию. Используя формулу (6) для вычисления разности m2 √ P2/c2, легко связать инертную массу, массу покоя и импульс:
. (13)
Для частиц с нулевой массой покоя получаем mc = P или E = Pc.
5. Система тел
При объединении нескольких тел в систему тел,
как известно, их импульсы и их инертные массы
складываются. Для двух тел это выглядит так:
Для двух тел это выглядит так:
P = P1 + P2, m = m1 + m2. (14)
Другими словами, импульс и инертная масса аддитивны. Не так обстоит дело с массой покоя. Из формул (13), (14) следует, что масса покоя пары тел с массами покоя m01, m02 равна не сумме m01 + m02, а сложному выражению, зависящему от импульсов P1, P2:
. (15)
Таким образом, масса покоя, вообще говоря, не аддитивна. Например, пара фотонов, не имеющих массу покоя, имеет массу покоя, если фотоны летят в разные стороны, и не имеет массу покоя, если фотоны летят в одну и ту же сторону.
Тем не менее, все три величины, P, m, m0, подчиняются
закону сохранения, то есть не изменяются со
временем для замкнутой системы.
Однако ввиду неаддитивности массы покоя, на наш взгляд, нецелесообразно рассматривать массу покоя системы тел. Имеет смысл говорить лишь о сумме масс покоя отдельных тел системы. В действительности именно так поступают на практике. Когда говорят, что при неупругих соударениях увеличивается масса покоя, имеют ввиду не массу покоя системы, которая удивительным образом сохраняется неизменной при соударениях благодаря неаддитивности, а сравнивают именно сумму масс покоя тел до столкновения и массу покоя после столкновения. Точно так же, когда говорят о дефекте массы покоя при ядерных реакциях, имеют в виду не массу покоя, определяемую формулой (15), а сумму масс покоя частей системы.
6. Сравнение масс
Теперь уместно задать вопрос. Какую из
двух масс, массу покоя или инертную массу следует
назвать простым словом масса, обозначить буквой m без индексов и тем самым признать
“главной” массой. Это – не терминологическая
проблема. Здесь имеется серьезная
психологическая подоплека.
Здесь имеется серьезная
психологическая подоплека.
Чтобы решить, какая из масс – главная, перечислим еще раз свойства обеих масс.
Масса покоя является постоянной величиной для данного тела и выражает “количество вещества тела”. Она соответствует привычному дорелятивисткому ньютоновскому представлению о массе. Но она не эквивалентна энергии, не эквивалентна гравитационной массе, она не аддитивна и поэтому не используется как характеристика системы тел или частиц. Это последнее обстоятельство вызывает путаницу (см. [1] , стр. 1365) и мешает проявлению закона сохранения массы покоя. Фотоны и частицы, движущиеся со скоростью света, не обладают массой покоя. Операционное определение массы покоя частицы предполагает торможение ее до малой скорости без использования информации о текущем состоянии частицы.
Инертная масса это – релятивистская
масса. Она принимает различное значение для
различных наблюдателей, аналогично тому, как
скорость хода часов оказывается различной
относительно различных наблюдателей. Инертная
масса эквивалентна энергии и гравитационной
массе, она аддитивна и подчиняется закону
сохранения. Инертной массой обладают частицы, не
имеющие массы покоя. Операционное определение
инертной массы основано на простой формуле P = mv.
Инертная
масса эквивалентна энергии и гравитационной
массе, она аддитивна и подчиняется закону
сохранения. Инертной массой обладают частицы, не
имеющие массы покоя. Операционное определение
инертной массы основано на простой формуле P = mv.
На наш взгляд, инертную массу следует называть массой и обозначать m, как это и делалось в настоящей статье.
7. Психологическая подоплека
К сожалению, большое количество физиков считает массу покоя главной и обозначает ее m а не m0, а инертную массу дискриминирует и оставляет без обозначения, что вносит дополнительную путаницу, поскольку из-за этого порой бывает трудно понять, о какой массе идет речь.
Эти физики соглашаются, например, с тем, что
масса газа увеличивается при нагревании, потому
что увеличивается содержащаяся в нем энергия, но
психологический барьер мешает им попросту
объяснить это увеличение ростом массы отдельных
молекул вследствие увеличения их тепловой
скорости.
Эти физики жертвуют представлением о массе как мере инертности в пользу ярлыка, прикрепляемого к каждой частице с информацией о неизменном “количестве вещества”, потому что ярлык соответствует их привычному ньютоновскому представлению о массе. Они считают, например, что излучение, которое, согласно Эйнштейну [6] , “переносит инерцию между излучающими и поглощающими телами”, не имеет массы, поскольку к излучению невозможно прикрепить ярлык.
Инертная масса отсутствует в издаваемых сейчас стандартных учебниках физики в России (И.В.Савельев) и за рубежом [7,8], а также в популярной литературе [9] . Этот факт, однако, скрыт тем обстоятельством, что сторонники массы покоя настойчиво называют массу покоя не массой покоя, а просто массой, словом, которое ассоциируется с мерой инерции.
Главная психологическая трудность заключается
в том, чтобы отождествить массу и энергию
(которая изменяется), чтобы принять эти две
сущности, как одну. Легко принять формулу E0 = m0c2 для
покоящегося тела. Труднее принять
справедливость формулы E = mc2 для любой скорости. Замечательная
формула E= mc2 представляется,
например, Л.Б. Окуню “безобразной” [10] .
Труднее принять
справедливость формулы E = mc2 для любой скорости. Замечательная
формула E= mc2 представляется,
например, Л.Б. Окуню “безобразной” [10] .
Сторонники массы покоя, видимо, не в состоянии
принять идею инертной, релятивистской массы так
же, как ранее противники теории относительности
не могли принять относительность времени. Ведь
время жизни астронавта или нестабильной частицы
изменяется так же, как изменяется их инертная
масса: . Здесь уместно процитировать М.
Планка: “Великая научная идея редко внедряется
путем постепенного убеждения и обращения своих
противников, редко бывает, что Савл становится
Павлом. В действительности дело происходит так,
что оппоненты постепенно вымирают, а растущее
поколение с самого начала осваивается с новой
идеей.” [11] К сожалению, великая идея
релятивистской массы тщательно изолируется от молодежи. На данный момент статья
[1, 2] отклонена редакциями следующих журналов:
“Известия вузов. Физика”, “Квант”, “American Journal of Physics”,
“Physics Education” (Bristol), “Physics Today”.
Физика”, “Квант”, “American Journal of Physics”,
“Physics Education” (Bristol), “Physics Today”.
8. Шварцшильдовское пространство
Мы получим здесь формулу (10), рассмотрев пространство-время Шварцшильда общей теории относительности с выражением для интервала s [12] :
.
Уравнения радиальной геодезической линии могут быть получены по общей формуле, использующей коэффициенты связности :
, (16)
. (17)
Первый интеграл уравнения (16) легко находится:
. (18)
Запишем теперь выражение для ускорения a, учитывая (18) и то, что соотношения между расстоянием l и временем , с одной стороны, и координатами r, t, с другой, даются формулами
, :
.
Выразив таким образом ускорение a через , мы можем теперь воспользоваться уравнением (17), а затем, вернувшись к l и , получить окончательно
, . (10)
(10)
Список литературы
1. Храпко Р. И. Что есть масса? // Успехи физических наук. – 2000, N12. √ с.1363-1366.
2. Храпко Р. И. Что есть масса? – http://www.mai.ru. Труды МАИ, Вып.2.
3. Фриш С. Э., Тиморева А. В. Курс общей физики. Т. 3. – М.: ГИТТЛ, 1951.- 547 с.
4. Фейнман Р. и др. Фейнмановские лекции по физике. Т. 1. – М.: Мир, 1965. √ 232 с.
5. Храпко Р. И., Спирин Г.Г., Разоренов В. М. Механика. – М.: МАИ, 1993. √ 89 с.
6. Эйнштейн А. Зависит ли инерция тела от содержащейся в нем энергии. // Принцип относительности. – ОНТИ, 1935.- с.175-178.
7. Resnick R., Halliday D., Krane K. S. Physics. V.1 – N.Y.: J. Wiley, 1992.-592p.
8. Alonso M., Finn E. J. Physics – N.Y.: Addison-Wesley, 1995.-496p.
9. Taylor E. F., Wheeler J. A. Spacetime Physics. √ San Francisco: Freeman, 1966.-
631c. Русский перевод: Тейлор Э. Ф.,
Уилер Дж. А. Физика пространства-времени. √ М.:
Мир, 1971.- 612c.
10. Окунь Л. Б. Понятие массы. // Успехи физических наук. – 1989, т. 158. – с.512-530.
11. Планк М. Происхождение научных идей и влияние их на развитие науки./ М. Планк.// Сборник статей к столетию со дня рождения Макса Планка. – М.: АНСССР, 1958.- с.52.
12. Ландау Л.Д., Лифшиц Е.М. Теория поля. – М.: Наука, 1973.- 504с.
Основные формулы для решения задач по химии
05-Авг-2012 | комментариев 450 | Лолита Окольнова
Все, все основные задачи по химии решаются с помощью
нескольких основных понятий и формул.
У всех веществ разная масса, плотность и объем. Кусочек металла одного элемента может весить во много раз больше, чем точно такого же размера кусочек другого металла.
Моль (количество моль)
обозначение: моль, международное: mol — единица измерения количества вещества. Соответствует количеству вещества, в котором содержится NA частиц (молекул, атомов, ионов). Поэтому была введена универсальная величина — количество моль. Часто встречающаяся фраза в задачах — «было получено… моль вещества»
Поэтому была введена универсальная величина — количество моль. Часто встречающаяся фраза в задачах — «было получено… моль вещества»
NA = 6,02 · 1023
NA — число Авогадро. Тоже «число по договоренности». Сколько атомов содержится в стержне кончика карандаша? Несколько миллионов. Оперировать такими величинами не удобно. Поэтому химики и физики всего мира договорились — обозначим 6,02 · 1023 частиц (атомов, молекул, ионов) как 1 моль вещества.
1 моль = 6,02 · 1023 частиц
Это была первая из основных формул для решения задач.
Молярная масса вещества
Молярная масса вещества — это масса одного моль вещества. Обозначается как M
Есть еще молекулярная масса — Mr
Находится по таблице Менделеева — это просто сумма атомных масс вещества.
Например, нам дана серная кислота — H2SO4. Давайте посчитаем молярную массу вещества: атомная масса H =1, S-32, O-16.
Mr(H2SO4)=1•2+32+16•4=98 г\моль.
Вторая необходимая формула для решения задач —
формула массы вещества:
Т.е., чтобы найти массу вещества, необходимо знать количество моль (n), а молярную массу мы находим из Периодической системы.
Закон сохранения массы — масса веществ, вступивших в химическую реакцию, всегда равна массе образовавшихся веществ.
Если мы знаем массу (массы) веществ, вступивших в реакцию, мы можем найти массу (массы) продуктов этой реакции. И наоборот.
Третья формула для решения задач по химии —
объем вещества:
Откуда взялось число 22.4? Из закона Авогадро:
в равных объёмах различных газов, взятых при одинаковых температуре и давлении, содержится одно и то же число молекул.
Согласно закону Авогадро, 1 моль идеального газа при нормальных условиях (н.у.) имеет один и тот же объём Vm = 22,413 996(39) л
Т.е., если в задаче нам даны нормальные условия, то, зная количество моль (n), мы можем найти объем вещества.
Итак, основные формулы для решения задач по химии
Число Авогадро NA
6,02 · 1023 частиц
Количество вещества n (моль)
n=m\M
n=V\22.4 (л\моль)
Масса вещества m (г)
m=n•Mr
Объем вещества V(л)
V=n•22.4 (л\моль)
или вот еще удобная табличка:
Это формулы. Часто для решения задач нужно сначала написать уравнение реакции и (обязательно!) расставить коэффициенты — их соотношение определяет соотношение молей в процессе.
В ОГЭ и ЕГЭ по химии задач , в которых нужно было бы найти только объем \ массу \ кол-во моль нет — это обычно ЧАСТЬ решения задачи. Однако, чтобы легко решать более сложные задачи, нужно тренироваться на таких вот небольших упражнениях.
Однако, чтобы легко решать более сложные задачи, нужно тренироваться на таких вот небольших упражнениях.
Находим количество вещества по массе
1 Какое количество вещества алюминия содержится в образце металла массой 10.8 г?2 Какое количество вещества содержится в оксиде серы (VI) массой 12 г?
3 Определите количество моль брома, содержащееся в массе 12.8 г.
Находим массу по количеству вещества:
4. Определите массу карбоната натрия количеством вещества 0.25 моль.
Объем по количеству вещества:
5. Какой объем будет иметь азот при н.у., если его количество вещества 1.34 моль?6. Какой объем занимают при н.у. 2 моль любого газа?
Ответы:/p>
- 0.4 моль
- 0.15 моль
- 0.08 моль
- 26.5 г
- 30 л
- 44.8 л
Категории: |
(Правила комментирования)
Что такое масса? – Определение, единицы, формула и примеры
Массу лучше всего понимать как количество материи, присутствующей в любом объекте или теле. Все, что мы видим вокруг себя, имеет массу. Например, стол, стул, ваша кровать, футбольный мяч, стакан и даже воздух имеют массу. При этом все объекты легкие или тяжелые из-за своей массы. На этом уроке мы узнаем, что такое масса, как ее вычислить, и ее примеры, открывая при этом интересные факты о ней.
Все, что мы видим вокруг себя, имеет массу. Например, стол, стул, ваша кровать, футбольный мяч, стакан и даже воздух имеют массу. При этом все объекты легкие или тяжелые из-за своей массы. На этом уроке мы узнаем, что такое масса, как ее вычислить, и ее примеры, открывая при этом интересные факты о ней.
| 1. | Что такое масса? |
| 2. | Что такое единица массы? |
| 3. | Разница между массой и весом |
| 4. | Часто задаваемые вопросы по Mass |
Что такое масса?
В физике масса — это основное свойство материи и одна из фундаментальных величин. Масса определяется как количество вещества, присутствующего в теле. Единицей массы в системе СИ является килограмм (кг). Формулу массы можно записать так:
Масса = Плотность × Объем
Примечание : Масса тела постоянна; он не меняется в любое время. Только в определенных крайних случаях, когда от тела отдается или отнимается огромное количество энергии, масса может воздействовать. Например, при ядерной реакции крошечное количество вещества превращается в огромное количество энергии, это уменьшает массу вещества.
Только в определенных крайних случаях, когда от тела отдается или отнимается огромное количество энергии, масса может воздействовать. Например, при ядерной реакции крошечное количество вещества превращается в огромное количество энергии, это уменьшает массу вещества.
Что такое единица массы?
Существуют различные единицы измерения массы, такие как килограммы, граммы, фунты, фунты и т. д., но единицей массы в системе СИ является “килограмм” или кг. Каждая единица массы может быть преобразована в другие единицы с помощью соответствующей формулы преобразования, не затрагивающей смысла и сути измеряемой величины.
Примечание. 1 кг равен 2,20462 фунта.
Разница между массой и весом
Люди часто путают массу и вес, и в конечном итоге используют эти два термина как синонимы. Однако масса и вес — это два разных термина, и важно понимать разницу между ними. Разница между массой и весом показана в приведенной ниже таблице.
| Масса | Вес | |
|---|---|---|
| Определение | Масса определяется как количество вещества в веществе | Вес определяется как количество силы, действующей на массу объекта из-за ускорения под действием силы тяжести. |
| Обозначение | Масса представлена буквой «М». | Масса представлена буквой «W». |
| Формула | •Масса тела всегда постоянна. • Один из способов расчета массы: масса = объем × плотность. | •Вес является мерой гравитационной силы, действующей на массу. • Формула веса: Вес = масса × ускорение свободного падения |
| Единица измерения | Единицей массы в СИ является “килограмм”. | Единицей веса в системе СИ является Ньютон (Н). |
| Количество Тип | •Масса является базовой величиной. • Масса имеет только величину и, следовательно, это скалярная величина | . •Вес является производной величиной. • Вес имеет как величину, так и направление (к центру тяжести) и, следовательно, является векторной величиной. |
| Измерительный прибор | Массу можно легко измерить с помощью любых обычных весов. Например, балочный баланс, рычажный баланс, панорамный баланс и т. д. | Вес можно измерить с помощью пружинных весов или по приведенной выше формуле. |
Знаете ли вы, что у нас разный вес на Земле, на Луне и в космосе? Однако наша масса везде одинакова.
Теперь давайте посмотрим на некоторые важные факты, связанные с массой:
- Масса имеет только величину, следовательно, это скалярная величина.
- Вес имеет как величину, так и направление; это векторная величина.

- Массу также можно определить как «энергию, запасенную в частицах».
- Масса представляет собой общее количество атомов или частиц, которые оно содержит.
Пример 1: Сэм на Земле весит 1000 фунтов. На какой-нибудь другой планете вес Сэма составил бы 38 % от земного. Сколько бы Сэм весил на этой планете?
Решение: Мы знаем, что вес Сэма на Земле составляет 1000 фунтов, а его вес на другой планете будет составлять 38 % от земного. Следовательно, вес Сэма на другой планете = 38 % × его вес на Земле = 0,38 × 1000 фунтов = 380 фунтовПример 2: Масса объекта составляет 6000 фунтов. Вычислите его массу в тоннах.
Решение: Мы знаем, что 1 тонна = 2000 фунтов. Таким образом, 6000 фунтов = 6000/2000=3 тонны.Пример 3: У Дамиана есть книга массой 2,2 кг. Каков вес книги на Земле?
Решение:
Масса учебника = 2,2 кг, ускорение свободного падения = 92\)
Вес учебника = 21,56 Н
Следовательно, вес учебника на Земле равен 21,56 Н.

перейти к слайду
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, зачем нужна математика, с нашими сертифицированными экспертами
Запишитесь на бесплатный пробный урок
перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы по Mass
Имеет ли воздух массу?
Да, воздух имеет массу. Например, надутый воздушный шар весит тяжелее, чем сдутый воздушный шар, что доказывает, что воздух внутри надутого воздушного шара имеет массу.
Масса и объем одинаковы?
Масса – это количество материи, из которой состоит объект. Объем — это количество свободного места, которое занимает объект. Следовательно, масса и объем не совпадают.
Плотность и масса — одно и то же?
Масса измеряет количество вещества, присутствующего в веществе. Плотность показывает количество вещества в данном пространстве для вещества. Плотность и масса могут быть такими же, как единица объема.
Плотность показывает количество вещества в данном пространстве для вещества. Плотность и масса могут быть такими же, как единица объема.
Вес и масса — одно и то же?
Нет, вес и масса не одно и то же. Вес – это сила, действующая на тело, а масса – это количество вещества в теле. Вес может изменяться в зависимости от силы, в то время как масса постоянна.
Что такое единица массы S.I?
Единицей массы в системе СИ являются килограммы (кг).
Что такое формула массы?
Формула, используемая для расчета массы объекта: Плотность × Объем.
Скачать БЕСПЛАТНЫЕ учебные материалы
Масса Рабочий лист
Что такое формула массы?
Масса — это свойство физических объектов и мера устойчивости тела к ускорению. Можно рассматривать массу объекта как меру того, сколько физического «вещества» составляет этот объект.
В отличие от относительных свойств, таких как положение, скорость или потенциальная энергия, которые всегда должны определяться по отношению к другому объекту или контрольной точке, масса является внутренним свойством, которым объект обладает независимо от его отношения к другим вещам. Массу объекта можно рассчитать несколькими способами:
Массу объекта можно рассчитать несколькими способами:
- масса=плотность×объем (m=ρV) . Плотность — это мера массы на единицу объема, поэтому массу объекта можно определить, умножив плотность на объем.
- масса=сила÷ускорение (m=F/a) . Согласно второму закону Ньютона (F=ma), ускорение тела прямо пропорционально приложенной к нему силе. Следовательно, величина ускорения, сопровождающего приложение постоянной силы, обратно пропорциональна массе.
- масса=вес÷ускорение свободного падения (м=Вт/г). Вес – это произведение ускорения массы в гравитационном поле. В зависимости от силы гравитационного ускорения вес будет разным.
Все три формулы являются способом определения массы объекта. Поскольку масса является фундаментальным свойством, она не определяется в терминах других единиц, как джоуль (Дж) Ньютона (Н). Существуют и другие способы расчета массы объекта, но эти три формулы являются наиболее распространенными.
m=ρV
m=Вт/г
m=F/a
Единицы массы
Принятая в СИ единица39 массы килограмм
0 (кг). Килограмм является единственной базовой единицей СИ с приставкой в названии (кило-). Первоначально один килограмм определялся как масса одного кубического децилитра (дл) воды при температуре ее плавления. С 1889 года килограмм был переопределен как масса Международного прототипа килограмма (IPK), физического артефакта, предназначенного для универсальной эталонной массы килограмма. Первоначально ИПК представлял собой чугунную гирю. В настоящее время принятым ИПК является цилиндр высотой 39 мм, изготовленный из специального платинового сплава.
«Слова тоже имеют подлинную субстанцию — массу, вес и удельный вес». — Тим О’Брайен
По состоянию на 2018 год килограмм является единственной единицей СИ, в которой физический объект является исходным значением. Все остальные единицы СИ были переопределены с точки зрения фундаментальных физических констант, таких как скорость света или постоянная Планка. В ноябре 2018 года Генеральная конференция мер и весов (GCPM) проголосовала за новое определение килограмма с точки зрения фундаментальных физических констант, и это изменение вступит в силу 20 мая 2019 года..
Все остальные единицы СИ были переопределены с точки зрения фундаментальных физических констант, таких как скорость света или постоянная Планка. В ноябре 2018 года Генеральная конференция мер и весов (GCPM) проголосовала за новое определение килограмма с точки зрения фундаментальных физических констант, и это изменение вступит в силу 20 мая 2019 года..
Способы вычисления массы
Из плотности и объема
Плотность объекта, иногда обозначаемая греческой буквой «ρ», является мерой массы на единицу объема. По сути, плотность говорит вам, насколько плотно упакована масса объекта. Чем плотнее объект, тем больше его масса на единицу объема.
Например, вода имеет плотность 977 кг/м 3 при стандартной температуре и давлении. То есть один кубический метр воды имеет массу 977 кг. Если мы знаем плотность и объем вещества, мы также можем вычислить массу этого вещества. Скажем, у нас есть 0,7 м 3 пробы воды. Какова масса этого образца?
Решение для массы дает нам:
m=ρV
m=(0,7 м 3 )(977 кг/м 3 ) = 683 кг
0. иметь массу 683 кг.
иметь массу 683 кг.
Некоторые объекты невероятно плотные. Нейтронная звезда, например, имеет среднюю плотность 1,1 х 10 18 кг/м 3 . Одна чайная ложка нейтронной звезды на Земле весила бы около 100 миллионов тонн.
«Масса становится неподвижной; он не может маневрировать и, следовательно, не может одерживать победы, он может только сокрушать своим весом». — Ганс фон Сект
Из «Силы и ускорения»
Свойство массы понимается также как мера сопротивления физического объекта ускорению под действием внешней силы. Это понятие массы иногда называют инерционная масса . Инерция — это тенденция движущегося тела продолжать находиться в постоянном состоянии движения, поэтому инерционная масса — это мера того, насколько сильно инерционно обладает тело и насколько трудно изменить состояние своего движения. Связь между массой, силой и ускорением выражается вторым законом Ньютона F=ma. Это математическое соотношение говорит нам о том, что перед лицом постоянной силы более массивное тело будет ускоряться медленнее. Измеряя силу, приложенную к телу, и измеряя наблюдаемое ускорение, мы можем вычислить массу тела.
Измеряя силу, приложенную к телу, и измеряя наблюдаемое ускорение, мы можем вычислить массу тела.
Например, предположим, что мы прикладываем силу 748 Н к металлическому кубу и измеряем его ускорение как 21 м/с 2 . Какова масса металлического куба? Мы можем вычислить массу, разделив величину силы на величину ускорения так:
м=F/a
м=(748 Н)/(21 м/с 2 ) ≈ 35,62 кг
Итак, мы знаем, что металлический куб должен иметь массу 35,62 кг.
От веса
Строго говоря, вес и масса — две разные вещи. В английском языке два слова «вес» и «масса» являются синонимами, однако в физических науках они имеют разные значения. Масса — это неизменное свойство, которое не меняется от места к месту. Вес является мерой силы гравитационного поля, действующего на массивное тело. Поскольку напряженность гравитационного поля может различаться, т. Е. Луна имеет более слабую напряженность гравитационного поля, чем Земля, вес объекта может различаться в разных средах.
Соотношение между массой и весом выражается формулой W = mg, где g — мера ускорения свободного падения. Точное значение g зависит от местоположения. На Земле g имеет значение приблизительно 9,81 м/с 2 , а на Луне g составляет около 1,6 м/с 2 . Выражение W=mg дает вес в ньютонах, в то время как повседневное понимание веса дается в фунтах (lbs) коэффициент преобразования из ньютонов в фунты составляет около 1 N=0,22 фунта.
Например, на поверхности Земли где г=90,81 м/с 2 , 50-килограммовый объект будет иметь вес в фунтах:
W=(50kg)(9,81м/с 2 )=490,5N
Преобразование ньютонов в фунты дает нам:
490,5 Н(0,22 фунта/1 Н)≈ 108 фунтов
И наоборот, на Луне, где g имеет значение 1,6 м/с 2 , объект массой 50 кг будет весить:
W=50(кг) (1,6 м/с 2 )(0,22 фунта/1 Н) ≈ 18 фунтов
Тот же 50-килограммовый объект весит 108 фунтов на Земле и 18 фунтов на Луне.
Точно так же, если мы знаем вес объекта, мы можем работать в обратном направлении, чтобы вычислить его массу. Скажем, объект весит 160 фунтов Земли. мы можем рассчитать массу объекта как: 2 )≈ 83,4 кг
Итак, 180-фунтовое тело на Земле имеет массу около 84,3 кг.
Массово-энергетическая эквивалентность
Очень долгое время ученые считали, что массу объекта можно считать полностью независимой от других его свойств. Однако в начале 20 века специальная теория относительности Эйнштейна показала, что масса и энергия на самом деле являются двумя разными названиями одной и той же физической величины. В частности, масса объекта и его полная энергия связаны знаменитым уравнением Эйнштейна E=mc 2 , где c — скорость света в вакууме.
E=mc 2 говорит нам, что полная энергия неподвижного тела прямо пропорциональна его массе с коэффициентом c 2 . Поскольку c = 3 000 000 м/с, c 2 является чрезвычайно большим фактором. Следовательно, даже крошечный кусочек массы содержит подавляющее количество внутренней энергии. Для сравнения, общее количество энергии от полного преобразования 1 грамма вещества в энергию примерно равно 21,5 килотоннам тротила — мощности атомной бомбы, сброшенной на Хиросиму.
Следовательно, даже крошечный кусочек массы содержит подавляющее количество внутренней энергии. Для сравнения, общее количество энергии от полного преобразования 1 грамма вещества в энергию примерно равно 21,5 килотоннам тротила — мощности атомной бомбы, сброшенной на Хиросиму.
«Любой дурак может знать. Суть в том, чтобы понять». — Альберт Эйнштейн
В некоторых физических процессах, таких как деление ядер или движение тела в интенсивном гравитационном поле, материя преобразуется в энергию и высвобождается в виде большого количества света и тепла. В частности, уравнение Эйнштейна говорит нам, как мы можем рассчитать количество энергии, высвобождаемой во время таких реакций.
Скажем, 30 кг урана (Ur) помещают в ядерный реактор. При делении примерно 0,1% этой массы полностью превращается в энергию. Сколько энергии получается?
0,1% от 30 кг это 0,3 кг. Plugging this into Einstein’s equation gives us:
E=(0.3 kg)(3,000,000) 2 =(0. 3)(8.98755179 × 10 16 )= 2.69626554 × 10 16 J
3)(8.98755179 × 10 16 )= 2.69626554 × 10 16 J
Completely converting just 0.3 кг (0,6 фунта) вещества в энерговыделение 2,69626554 × 10 16 Дж энергии. Это количество примерно равно взрыву более 6 млн тонн тротила (12 млрд фунтов), чего достаточно, чтобы полностью сровнять с землей даже самые крупные города.
Мы также можем работать в обратном направлении от некоторого количества энергии, чтобы определить количество преобразованной массы. Скажем, какая-то реакция деления высвобождает 1,6178 × 10 16 джоулей энергии. Какое количество массы перешло в энергию при этом процессе? Using our handy-dandy mass-energy equivalence formula we can determine:
1.6178 × 10 16 J =m(8.98755179 × 10 16 )
(1.6178 × 10 16 )/8.98755179 × 10 16 )=m
m ≈ 0,18 кг
Итак, около 0,18 кг массы было преобразовано в энергию.
Почему объекты имеют массу?
Только недавно ученые начали открывать ответ на вопрос, почему частицы вообще имеют массу. В 1960-х годах несколько ученых заметили некоторые проблемы с их уравнениями, описывающими поведение элементарных частиц. В частности, их уравнения предсказывали, что некоторые частицы, генерируемые во время высокоскоростных столкновений, не будут иметь массы. Однако экспериментальное наблюдение показало, что эти частицы действительно имели ненулевую массу.
В 1960-х годах несколько ученых заметили некоторые проблемы с их уравнениями, описывающими поведение элементарных частиц. В частности, их уравнения предсказывали, что некоторые частицы, генерируемые во время высокоскоростных столкновений, не будут иметь массы. Однако экспериментальное наблюдение показало, что эти частицы действительно имели ненулевую массу.
Ученые предположили, что масса бозона может генерироваться взаимодействием между этими бозонами и всепроникающим полем, называемым полем Хиггса (в честь одного из его теоретиков Питера Хиггса). Когда безмассовые бозоны движутся против этого поля, их импульс замедляется, и они теряют часть энергии. Поле Хиггса преобразует эту энергию в энергию массы, которая проявляется как свойство массы, которое мы измеряем. Было предсказано, что это взаимодействие между бозонами и полем Хиггса создаст новую частицу, крошечный бозон, названный бозоном Хиггса. Ускоритель частиц в ЦЕРНе наконец продемонстрировал существование частицы Хиггса в 2013 году, а 8 октября 2013 года Питер Хиггс и Франсуа Энглер были удостоены Нобелевской премии по физике за свою теоретическую работу над частицей.
Расчет масс-молей Учебное пособие по химии
Ключевые понятия
⚛ 1 моль чистого вещества имеет массу, равную его молекулярной массе (1) , выраженной в граммах.
· Известна как молярная масса M и выражается в г моль -1
(г/моль, грамм на моль вещества)
⚛ Соотношение между молярной массой, массой и молями можно выразить в виде математического уравнения, как показано ниже:
г моль -1 = г ÷ моль
молярная масса = масса ÷ моль
М = м ÷ п
где:
M = молярная масса чистого вещества (измеряется в г моль -1 )
m = масса чистого вещества (измеряется в граммах, г)
n = количество чистого вещества (измеряется в молях, моль)
⚛ Это математическое уравнение можно преобразовать, чтобы получить следующее:
(i) п = м ÷ М
моль = масса ÷ молярная масса
(ii) m = n × M
масса = моли × молярная масса
⚛ Для расчета молей чистого вещества: n = m ÷ M
⚛ Для расчета массы чистого вещества: m = n × M
⚛ Для расчета молярной массы чистого вещества: M = m ÷ n
Пожалуйста, не блокируйте рекламу на этом сайте.
Нет рекламы = нет денег для нас = нет бесплатных вещей для вас!
Расчет массы чистого вещества (m=nM)
1 моль чистого вещества определяется как масса в граммах, равная его относительной молекулярной массе.
Эта величина известна как молярная масса (символ М).
Итак, масса 1 моля чистого вещества = относительная молекулярная масса в граммах
А, масса 1 моля чистого вещества = молярная масса чистого вещества (г моль -1 )
Или масса 1 моля = M (г моль -1 )
В таблице ниже указана масса 1 моля ряда обычных чистых веществ:
| name | molecular formula | relative molecular mass | molar mass (g mol -1 ) | mass of 1 mole (g) | |
|---|---|---|---|---|---|
| helium gas | He | 4.003 | 4,003 г моль -1 | 4,003 г | |
| oxygen gas | O 2 | 2 × 16. 00 = 32.00 00 = 32.00 | 32.00 g mol -1 | 32.00 g | |
| carbon dioxide gas | CO 2 | 12.01 + (2 × 16,00) = 44,01 | 44,01 г моль -1 | 44,01 г | |
| H 2 O | (2 × 1,008) + 16,00 = 18,016 | 99999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999.1010101010101010 | (2 × 1,008). | 18,016 г |
Из таблицы видно, что 1 моль воды имеет массу 18,016 грамма, что не так уж и много (примерно масса воды в паре маленьких кубиков льда, которые можно приготовить в семейном морозильнике).
А что, если бы у вас было 10 молей воды? Какова будет масса 10 молей воды?
Если 1 моль воды имеет массу 18,016 г, то 10 моль воды должны иметь массу в десять раз больше:
масса 10 молей воды = 10 × масса 1 моля воды
масса 10 молей воды = 10 × 18,016 = 180,16 г (о массе воды, которую можно налить в маленький стакан)
Итак, если бы у нас было только ½ моля воды, какая масса воды была бы у нас?
Если 1 моль воды имеет массу 18,016 г, то ½ моля воды должно иметь ½ массы:
масса ½ моля воды = ½ × масса 1 моля воды
масса ½ моля воды = ½ × 18,016 = 9,008 г
В обоих приведенных выше примерах мы можем рассчитать массу воды в граммах, умножив количество молей воды на массу 1 моля воды в граммах:
масса воды = моль воды × масса 1 моля воды
, так как масса 1 моля воды в граммах известна как его молярная масса, мы можем записать:
масса воды = моли воды × молярная масса воды
В таблице ниже сравниваются массы различных количеств воды в молях:
| масса воды (г) | = | моль воды (моль) | × | mass of 1 mole of water (molar mass of water) (g mol -1 ) |
|---|---|---|---|---|
| 0 | = | 0. 00 00 | × | 18.016 |
| 9.008 | = | 0.50 | × | 18.016 |
| 18.016 | = | 1.00 | × | 18.016 |
| 27.024 | = | 1.50 | × | 18.016 |
| 180.16 | = | 10.00 | × | 18.016 |
| 270.24 | = | 15.00 | × | 18.016 |
Из данных таблицы можно обобщить и сказать, что для любого чистого вещества масса вещества в граммах равна количеству молей вещества, умноженному на массу 1 моля вещества:
масса = моли × масса 1 моля
и так как масса 1 моля вещества (в граммах) = молярная масса (в граммах на моль)
масса (г) = моли × молярная масса (г моль -1 )
м = п × М
где
m = масса чистого вещества в граммах
n = количество чистого вещества в молях
M = молярная масса чистого вещества в граммах на моль
Мы также можем нанести данные из таблицы выше на график, как показано ниже:
| масса (г) | 051015300250200150100500 |
| молей (моль) |
На приведенном выше графике показана прямая линия, проходящая через начало координат (0,0), поэтому уравнение для линии:
y = наклон × х
где:
y масса воды (г)
x моль воды (моль)
наклон (градиент) линии = вертикальный подъем ÷ горизонтальный ход
Мы можем определить наклон линии, используя 2 точки на прямой, например, (0,0) и (15,0, 270,24):
наклон = (270,24 г – 0 г) ÷ (15 моль – 0 моль) = 18,016 г моль -1
С 18,016 г моль -1 – молярная масса воды, можно сказать:
наклон = молярная масса воды (г моль -1 )
Следовательно, уравнение для этой линии:
Масса(H 2 O) = молярная масса (H 2 O) × моли (H 2 O)
В целом:
масса (г) = молярная масса (г моль -1 ) × моль (моль)
Из данных таблицы и ее графического представления можно обобщить и сказать, что для любого чистого вещества масса вещества в граммах равна количеству молей вещества, умноженному на массу 1 моля вещества:
масса = моли × масса 1 моля
и так как масса 1 моля вещества (в граммах) = молярная масса (в граммах на моль)
масса (г) = моли × молярная масса (г моль -1 )
м = п × М
Выполните следующие шаги, чтобы рассчитать массу чистого вещества, зная количество вещества в молях:
Шаг 1. Извлечь данные из вопроса:
Извлечь данные из вопроса:
масса = m = ? (единицы измерения граммы)
крота = n = запишите, что вам говорят в вопросе
молярная масса = M = запишите то, что вам сказали в вопросе (единицы измерения: г моль -1 )
(возможно, вам потребуется рассчитать это, используя молекулярную формулу чистого вещества и периодическую таблицу)
Шаг 2. Проверить соответствие единиц измерения и при необходимости преобразовать:
Количество вещества должно быть в молях (моль) !
Если количество указано в миллимолях (ммоль), разделите его на 1000, чтобы получить количество в молях (моль).
Если количество указано в микромолях (мкмоль), разделите его на 1 000 000, чтобы получить количество в молях (моль).
Если количество указано в киломолях (кмоль), умножьте его на 1000, чтобы получить количество в молях (моль).
Шаг 3. Напишите математическое уравнение (математическую формулу):
масса = моли × молярная масса
или
м = п × М
Шаг 4. Подставьте значения и решите уравнение, чтобы найти значение массы m в граммах (г).
Подставьте значения и решите уравнение, чтобы найти значение массы m в граммах (г).
↪ Наверх
Расчет молей чистого вещества (n=m/M)
В обсуждении выше мы обнаружили, что можем рассчитать массу чистого вещества, используя моли и молярную массу вещества:
масса (г) = моли (моль) × молярная масса (г моль -1 )
Как бы мы рассчитали количество молей чистого вещества, если бы знали массу этого вещества?
(a) Мы могли бы использовать некоторую алгебру: разделить обе части уравнения на молярную массу:
| масса | = | моль × | молярная масса | | | |
моль = масса ÷ молярная масса
н = м ÷ М
или
(б) Мы могли бы использовать некоторую логику:
| знаем массу в единицах | грамм (г) |
| знаем молярную массу в единицах | грамм на моль (г моль -1 ) |
| нам нужно найти моли с единицами | моль (моль) |
При рассмотрении единиц мы видим, что деление молярной массы на массу даст нам количество в единицах «моль -1 »
молярная масса/масса = г моль -1 / г = моль -1
Если мы перевернем это с ног на голову (в математических терминах, возьмем обратное), мы получим количество с единицами «моль», что и нужно:
масса/молярная масса = г / г моль -1 = моль
так
моль = масса ÷ молярная масса
н = м ÷ М
Выполните следующие шаги, чтобы рассчитать количество чистого вещества в молях, учитывая массу вещества:
Шаг 1. Извлечь данные из вопроса:
Извлечь данные из вопроса:
масса = m = запишите, что вам сказали в вопросе
моль = n = ? (единицы моль)
молярная масса = M = запишите то, что вам сказали в вопросе (единицы измерения: г моль -1 )
(возможно, вам потребуется рассчитать это, используя молекулярную формулу чистого вещества и периодическую таблицу)
Шаг 2. Проверить единицы на согласованность и при необходимости преобразовать:
Масса должна быть в граммах!
Если масса указана в миллиграммах (мг), разделите ее на 1000, чтобы получить массу в граммах (г).
Если масса указана в микрограммах (мкг), разделите ее на 1 000 000, чтобы получить массу в граммах (г).
Если масса указана в килограммах (кг), умножьте ее на 1000, чтобы получить массу в граммах (г).
Шаг 3. Напишите математическое уравнение (математическую формулу):
моль = масса ÷ молярная масса
или
н = м ÷ М
Шаг 4. Подставьте значения и решите уравнение, чтобы найти количество молей вещества (моль).
Подставьте значения и решите уравнение, чтобы найти количество молей вещества (моль).
↪ Наверх
Расчет молярной массы чистого вещества (M=m/n)
Что, если бы вы знали количество чистого вещества в молях и его массу?
Не могли бы вы вычислить его молярную массу?
Напомним, что масса = моли × молярная масса или m = n × M
(a) Мы могли бы использовать некоторую алгебру: разделить обе части уравнения на моли:
| mass | = | |
| moles | |
молярная масса = масса ÷ моль
М = м ÷ п
или (б) Мы могли бы использовать некоторую логику:
При рассмотрении единиц мы видим, что, разделив массу в граммах на количество в молях, мы получим количество с единицами грамм на моль (г моль -1 ), которые являются единицами измерения молярной массы.
Следовательно, молярная масса (г моль -1 ) = масса (г) ÷ моль (моль)
или можно написать
М = м ÷ п
Выполните следующие шаги, чтобы рассчитать молярную массу чистого вещества, зная количество вещества в молях и массу вещества:
Шаг 1. Извлечь данные из вопроса:
масса = m = запишите, что вам сказали в вопросе
крота = n = запишите, что вам говорят в вопросе
молярная масса = M = ? (единицы г моль -1 )
Шаг 2. Проверить единицы на согласованность и при необходимости преобразовать:
Масса должна быть указана в граммах (г)!
Количество, моли, должно быть указано в молях (моль)!
Шаг 3. Напишите математическое уравнение (математическую формулу):
молярная масса = масса ÷ моль
или
М = м ÷ п
Шаг 4. Подставьте значения и решите уравнение, чтобы найти молярную массу вещества в граммах на моль.
↪ Наверх
Примеры расчета массы, молей, молярной массы
В каждом из приведенных ниже рабочих примеров вам будет предложено рассчитать моль, массу или молярную массу чистого вещества.
Чтобы правильно ответить на каждый вопрос, вам необходимо:
- Шаг 1. Извлечение информации из вопроса
- Шаг 2. Проверка данных на согласованность единиц
- Шаг 3. Выберите математическое уравнение, чтобы найти неизвестное
- Шаг 4. Подставьте свои значения в уравнение и решите
Рабочий пример: масса = моли × молярная масса (m=n×M)
Вопрос: Рассчитайте массу 0,25 моль воды, H 2 O.
Решение:
Шаг 1. Извлечь данные из вопроса:
моль = n = 0,25 моль
молярная масса = M = (2 × 1,008) + 16,00 = 18,016 г моль -1
(Рассчитано с использованием периодической таблицы)
масса = м = ? г
Шаг 2. Проверить данные на непротиворечивость:
Проверить данные на непротиворечивость:
Количество воды в молях (моль)? Да.
Нам не нужно конвертировать это.
Шаг 3. Напишите математическое уравнение (математическую формулу):
масса = моли × молярная масса
или
м = п × М
Шаг 4. Подставьте значения в уравнение и найдите массу (г):
масса = m = 0,25 моль × 18,016 г моль -1 = 4,5 г
(обоснованы только 2 значащие цифры)
Рабочий пример: моли = масса &делите молярную массу (n=m/M)
Вопрос: Рассчитайте количество газообразного кислорода O 2 в молях, содержащегося в 124,5 г газообразного кислорода.
Решение:
Шаг 1. Извлечь данные из вопроса:
масса = m = 124,5 г
молярная масса = M = 2 × 16,00 = 32,00 г моль -1
(Рассчитано с использованием периодической таблицы)
моля = n = ? моль
Шаг 2. Проверить данные на непротиворечивость:
Проверить данные на непротиворечивость:
Масса газообразного кислорода указана в граммах (г)? Да.
Нам не нужно конвертировать это.
Шаг 3. Напишите математическое уравнение (математическую формулу):
моль = масса ÷ молярная масса
или
н = м ÷ М
Шаг 4. Подставьте значения в уравнение и решите, чтобы найти моли газообразного кислорода:
моль = n = 124,5 г ÷ 32,00 г моль -1 = 3,891 моль
(обоснованы 4 значащие цифры)
Рабочий пример: молярная масса = масса ÷ моль (M=m/n)
Вопрос: Рассчитайте молярную массу чистого вещества, если 1,75 моля вещества имеют массу 29,79 г.
Решение:
Шаг 1. Извлечь данные из вопроса:
масса = m = 29,79 г
моль = n = 1,75 моль
Шаг 2. Проверить данные на непротиворечивость:
Масса в граммах (г)? Да. Нам не нужно конвертировать это.
Количество вещества указано в молях (моль)? Да. Нам не нужно конвертировать это.
Шаг 3. Напишите уравнение:
молярная масса = масса ÷ моль
или
М = м ÷ н
Шаг 4. Подставьте значения в уравнение и найдите молярную массу:
молярная масса = M = 29,79 г ÷ 1,75 моль = 17,0 г моль -1
(обоснованы 3 значащие цифры)
↪ Наверх
Решение задач с использованием молей, массы и молекулярной массы
Проблема: Карбонат кальция, CaCO 3 , является важным промышленным химикатом.
У Химика Криса есть неочищенный образец карбоната кальция.
Масса нечистого образца составляет 0,1250 кг, и он состоит из 87,00% (по массе) карбоната кальция.
Прежде чем Крис сможет использовать этот карбонат кальция в химической реакции, Крису необходимо знать количество карбоната кальция в молях, присутствующее в этом образце.
Рассчитайте количество карбоната кальция в молях, присутствующее в этом нечистом образце карбоната кальция.
Решение проблемы с использованием модели StoPGoPS для решения проблемы:
| Сформулируйте вопрос. | Какой вопрос просит вас сделать? Рассчитайте количество карбоната кальция в молях n(CaCO 3 ) = моли карбоната кальция = ? моль | |
| Пауза для планирования. | Какой химический принцип вам нужно применить? Применение стехиометрии (n = m ÷ M) Какую информацию (данные) вам предоставили?
Каков ваш план решения этой проблемы? (i) Напишите математическое уравнение для расчета количества молей карбоната кальция: n(моль) = м(г) ÷ M(г моль -1 ) (ii) Рассчитайте массу карбоната кальция в образце в килограммах (кг). масса карбоната кальция (кг) = 87,00% от массы образца (кг) м (CaCO 3 ) в килограммах = ( 87,00/100 ) × м (образец) (iii) Перевести массу карбоната кальция в килограммах (кг) в массу в граммах (г) m(CaCO 3 ) в граммах = m(CaCO 3 ) в кг × 1000 г/кг (iv) Рассчитайте молярную массу карбоната кальция молярная масса = M(CaCO 3 ) = M(Ca) + M(C) + [3 × M(O)] = (v) Подставьте значения m(CaCO 3 ) в граммах и M(CaCO 3 ) в г моль -1 в математическое уравнение и найдите n (моль) n(моль) = м(г) ÷ M(г моль -1 ) | |
| Следуйте плану. | (i) Напишите математическое уравнение для расчета молей карбоната кальция: n(моль) = м(г) ÷ M(г моль -1 ) n(CaCO 3 ) = m(CaCO 3 ) ÷ M(CaCO 3 ) (ii) Рассчитайте массу карбоната кальция в образце в килограммах (кг). масса карбоната кальция (кг) = 87,00% от массы образца (кг) м (CaCO 3 ) в килограммах = ( 87,00/100 ) × м (образец) м (CaCO 3 ) в килограммах = ( 87,00/100 ) × 0,1250 кг = 0,10875 кг (iii) Перевести массу карбоната кальция в килограммах (кг) в массу в граммах (г) m(CaCO 3 ) в граммах = m(CaCO 3 ) в кг × 1000 г/кг m(CaCO 3 ) в граммах = 0,10875 кг × 1000 г/кг = 108,75 г (iv) Рассчитайте молярную массу карбоната кальция молярная масса = M(CaCO 3 ) = M(Ca) + M(C) + [3 × M(O)] М(CaCO 3 ) = 40,08 + 12,01 + [3 × 16,00] = 40,08 + 12,01 + 48,00 = 100,09 г моль -1 (v) Подставьте значения m(CaCO 3 ) в граммах и M(CaCO 3 ) в г моль -1 в математическое уравнение и найдите n (моль) n(CaCO 3 ) = m(CaCO 3 ) ÷ M(CaCO 3 ) n(CaCO 3 ) = m(CaCO 3 ) ÷ M(CaCO 3 ) = 108,75 (обоснованы 4 значащие цифры) | |
Подумайте о правдоподобии. | Вы ответили на заданный вопрос? Да, мы рассчитали количество молей карбоната кальция в образце. Разумно ли ваше решение вопроса? Давайте вернемся назад, чтобы увидеть, дадут ли рассчитанные нами моли карбоната кальция правильную массу образца. Поскольку это приблизительное значение массы образца примерно равно массе образца, указанной в вопросе, мы достаточно уверены в правильности нашего ответа. | |
Укажите решение. |