Формула конусность: Что такое конусность? Формула для расчёта конусности. Обозначение конусности на чертежах — Мегаобучалка

alexxlab | 04.04.1988 | 0 | Разное

Содержание

Подготовка школьников к ЕГЭ (Справочник по математике – Стереометрия

Справочник по математикеГеометрия (Стереометрия)Конусы
Конусы
Усеченные конусы
Объем, площади боковой и полной поверхностей конуса и усеченного конуса

Конусы

      Рассмотрим произвольную плоскость α, точку   S,   не лежащую на плоскости α,   и перпендикуляр   SO,   опущенный из точки   S   на плоскость   α   (точка   O   – основание перпендикуляра). Рассмотрим также произвольный круг с центром в точке   O,   лежащий на плоскости   α.

      Определение 1. Конусом называют фигуру, состоящую из всех отрезков, соединяющих точку   S   с точками указанного круга с центром в точке   O,   лежащего на плоскости   α   (рис. 1).

Рис.1

      Определение 2.

Точку   S   называют вершиной конуса.

Отрезок   SO   называют осью конуса.

Расстояние от точки   S   до плоскостиРасстояние от точки   S   до плоскости   α   (длину отрезка   SO)   называют высотой конуса.

Круг с центром в точке   O,   лежащий на плоскости   α,   называют основанием конуса, радиус этого круга называют радиусом основания конуса, а саму плоскость   α   называют плоскостью основания конуса.

Отрезки, соединяющие точку   S   с точками окружности называют образующими конуса.

Совокупность всех образующих конуса составляет боковую поверхность конуса (коническую поверхность).

Полная поверхность конуса состоит из основания конуса и его боковой поверхности.

      Замечание 1. Отрезок   SO   часто называют высотой конуса.

      Замечание 2. Все образующие конуса имеют одинаковую длину. У конуса с высотой   h   и радиусом основания   r   длина образующих равна

Усеченные конусы

      Рассмотрим конус с вершиной   S,   осью   SO,   радиусом основания   r   и высотой   h.   Плоскость   β,   параллельная параллельная плоскости основания конуса и расположенная на расстоянии   h1   от вершины расстоянии   h1   от вершины   S,   пересекает конус по кругу радиуса   r1   с центром в точке   O1   (рис. 2).

Рис.2

      Из подобия прямоугольных треугольников   SOA   и   SO1A1   можно выразить радиус   r1   через известные величины   r, h   и   h1:

      Таким образом, плоскость   β   делит конус на две части: конус с осью   SO1   и радиусом основания   r1,   а также вторую часть, называемую усеченным конусом (рис.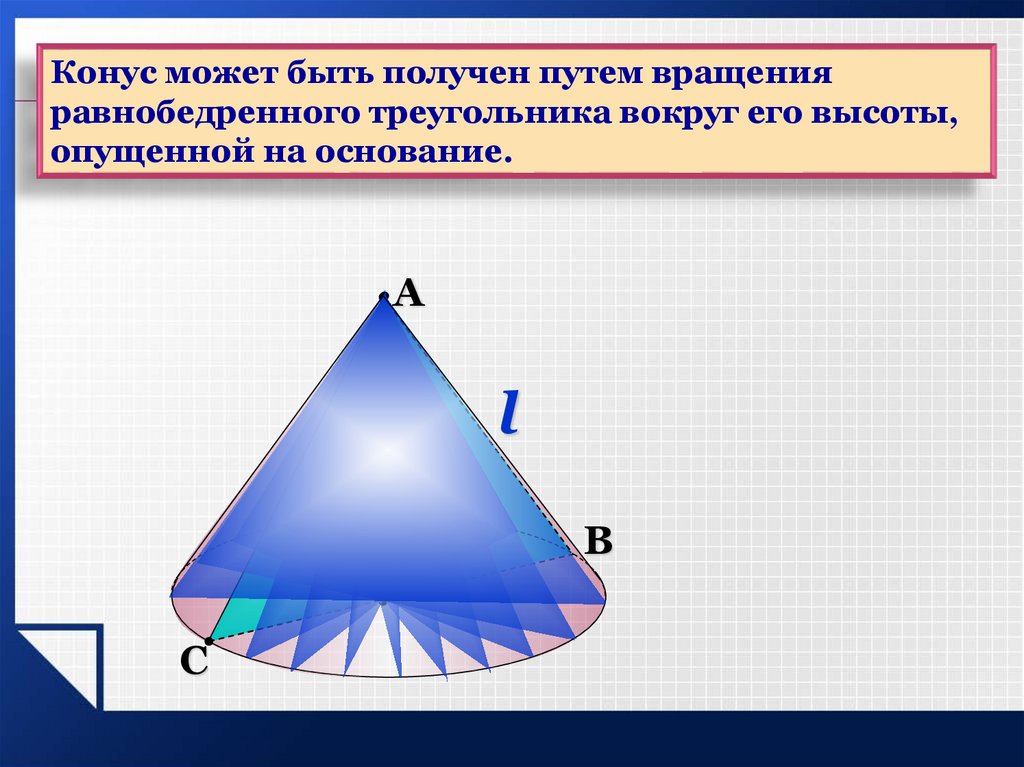 3).

Рис.3

      Усеченный конус ограничен двумя основаниями: кругом с центром в точке   O   радиуса   r   на плоскости   α   и кругом с центром в точке   O1 радиуса   r1   на плоскости   β,   а также боковой поверхностью усеченного конуса, которая представляет собой часть боковой поверхности исходного конуса, заключенную между плоскостями   α   и   β.   Полная поверхность усеченного конуса состоит из двух оснований усеченного конуса и его боковой поверхности. Часть каждой образующей исходного конуса, которая заключена между плоскостями   α   и   β,   называют образующей усеченного конуса. Например, на рисунке 3 одной из образующих усеченного конуса является отрезок   AA1.

      Высотой усеченного конуса называют расстояние между плоскостями расстояние между плоскостями оснований усеченного конуса. У усеченного конуса, изображенного на рисунке 2, высота равна   h – h1.

Объем, площади боковой и полной поверхностей конуса и усеченного конуса

      Введем следующие обозначения

Vобъем конуса (объем усеченного конуса)
Sбокплощадь боковой поверхности конуса
(площадь боковой поверхности усеченного конуса)
Sполнплощадь полной поверхности конуса
(площадь полной поверхности усеченного конуса)
Sоснплощадь основания конуса
Sверх.оснплощадь верхнего основания усеченного конуса
Sнижн.оснплощадь нижнего основания усеченного конуса

V

объем конуса (объем усеченного конуса)

Sбок

площадь боковой поверхности конуса
(площадь боковой поверхности усеченного конуса)

Sполн

площадь полной поверхности конуса
(площадь полной поверхности усеченного конуса)

Sосн

площадь основания конуса

Sверх. осн

площадь верхнего основания усеченного конуса

Sнижн.осн

площадь нижнего основания усеченного конуса

      Тогда справедливы следующие формулы для вычисления объема, площади боковой и полной поверхности конуса, а также формулы для вычисления объема, площади боковой и полной поверхности усеченного конуса.

ФигураРисунокФормулы для объема, площади боковой и полной поверхности
Конус

Sосн = πr2,

Sбок= πrl,

Sполн = πr2 + πrl,

где
r – радиус основания конуса,
l  – длина образующей конуса,
h – высота конуса.

Усеченный конус

Sбок= π (r + r1)l ,

где
h – высота усеченного конуса,
r – радиус нижнего основания усеченного конуса,
r1 – радиус верхнего основания усеченного конуса,

l – длина образующей усеченного конуса.

Конус

Формулы для объема, площади боковой и полной поверхности:

Sосн = πr2,

Sбок= πrl,

Sполн = πr2 + πrl,

где
r – радиус основания конуса,
l – длина образующей конуса,
h – высота конуса.

Усеченный конус

Формулы для объема, площади боковой и полной поверхности:

,

Sбок= π (r + r1)l ,

где
h – высота усеченного конуса,
r – радиус нижнего основания усеченного конуса,
r1 – радиус верхнего основания усеченного конуса,

l – длина образующей усеченного конуса.

      Замечание 3. Формула для вычисления объема конуса

может быть получена из формулы объема правильной n – угольной пирамиды

при помощи предельного перехода, когда число сторон правильной пирамиды n неограниченно возрастает. Однако доказательство этого факта выходит за рамки школьной программы.

      Замечание 4. Формула для вычисления объема усеченного конуса

может быть получена из формулы объема правильной усеченной n – угольной пирамиды

при помощи предельного перехода, когда число сторон правильной усеченной пирамиды n неограниченно возрастает. Однако доказательство этого факта выходит за рамки школьной программы.

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.

Конус. Формулы, признаки и свойства

Навигация по странице: Определение конуса Элементы конуса Объём конуса Площадь поверхности конуса Уравнение конуса Основные свойства кругового конуса

Определение.

Конус — это геометрическое тело, которое образовано совокупностью всех лучей, исходящих из точки и пересекающих любую плоскую поверхность. В месте пересечения образуется основание конуса.

Рис.1 Рис.2
 
 
Рис.3
Рис.4

Элементы конуса

Определение. Вершина конуса – это точка (K), из которой исходят лучи.

Определение. Основание конуса – это плоскость, образованная в результате пересечения плоской поверхности и всех лучей, исходящих из вершины конуса. У конуса могут быть такие основы, как круг, эллипс, гипербола и парабола.

Определение. Образующей конуса (L) называется любой отрезок, который соединяет вершину конуса с границей основания конуса. Образующая есть отрезок луча, выходящего из вершины конуса.

Формула. Длина образующей (L) прямого кругового конуса через радиус R и высоту H (через теорему Пифагора):

L2 = R2 + H2

Определение. Направляющая конуса – это кривая, которая описывает контур основания конуса.

Определение. Боковая поверхность конуса – это совокупность всех образующих конуса. То есть, поверхность, которая образуется движением образующей по направляющей конуса.

Определение. Поверхность конуса состоит из боковой поверхности и основания конуса.

Определение. Высота конуса (H) – это отрезок, который выходит из вершины конуса и перпендикулярный к его основанию.

Определение. Ось конуса (a) – это прямая, проходящая через вершину конуса и центр основания конуса.

Определение. Конусность (С) конуса – это отношение диаметра основания конуса к его высоте. В случае усеченного конуса – это отношение разности диаметров поперечных сечений D и d усеченного конуса к расстоянию между ними:

C = D      и      C = D – d
Hh

где C – конусность, D – диаметр основания, d – диаметр меньшего основания и h – расстояние между основаниями.

Конусность характеризует остроту конуса, то есть, угол наклона образующей к основанию конуса. Чем больше конусность, тем острее угол наклона. угол конуса α будет:

α = 2arctgR
H

где R – радиус основы, а H – высота конуса.

Определение. Осевое сечение конуса – это сечение конуса плоскостью, проходящей через ось конуса. Такое сечение образует равнобедренный треугольник, у которого стороны образованы образующими, а основание треугольника – это диаметр основания конуса.

Определение. Касательная плоскость к конусу – это плоскость, проходящая через образующую конуса и перпендикулярна к осевому сечению конуса.

Определение. Конус, что опирается на круг, эллипс, гиперболу или параболу называется соответственно круговым, эллиптическим, гиперболическим или параболическим конусом (последние два имеют бесконечный объем).

Определение. Прямой конус – это конус у которого ось перпендикулярна основе. У такого конуса ось совпадает с высотой, а все образующие равны между собой.

Формула. Объём кругового конуса:

V = 1πHR2
3
где R – радиус основы, а H – высота конуса.

Формула. Площадь боковой поверхности (Sb

) прямого конуса через радиус R и длину образующей L:

Sb = πRL

Формула.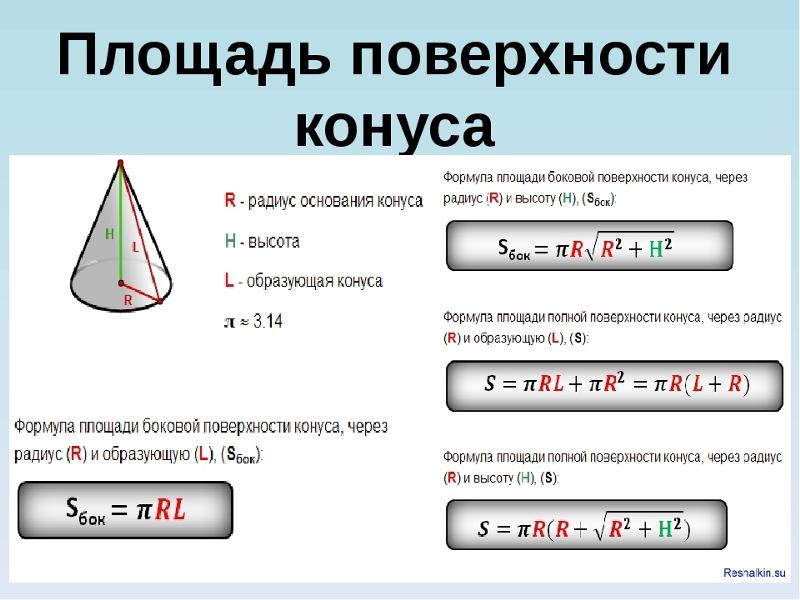 Общая площадь поверхности (Sp) прямого кругового конуса через радиус R и длину образующей L:

Sp = πRL + πR2

Определение. Косой (наклонный) конус – это конус у которого ось не перпендикулярна основе. У такого конуса ось не совпадает с высотой.

Формула. Объём любого конуса:

V = 1SH
3
где S – площадь основы, а H – высота конуса.

Определение. Усеченный конус – это часть конуса, которая находится между основанием конуса и плоскостью сечения, параллельная основе.

Формула. Объём усеченного конуса:

V = 1(S2H – S1h)
3
где S1 и S2 – площади меньшей и большей основы соответственно, а H и h – расстояние от вершины конуса до центра нижней и верхней основы соответственно.

Уравнение конуса

1. Уравнение прямого кругового конуса в декартовой системе координат с координатами (x, y, z):

x2 + y2 – z2 = 0
a2a2c2

2. Уравнение прямого эллиптического конуса в декартовой системе координат с координатами (x, y, z)

:
x2 + y2 = z2
a2b2c2

Основные свойства кругового конуса

1. Все образующие прямого кругового конуса равны между собой.

2. При вращении прямоугольного треугольника вокруг своего катета на 360 ° образуется прямой круговой конус.

3. При вращении равнобедренного треугольника вокруг своей оси на 180 ° образуется прямой круговой конус.

4. В месте пересечения конуса плоскостью, параллельной основанию конуса, образуется круг. (см. Срезанный конус)

5. Если при пересечении плоскость не параллельна основе конуса и не пересекается с основанием, то в месте пересечения образуется эллипс (рис. 3).

6. Если плоскость сечения проходит через основание, то в месте пересечения образуется парабола (рис. 4).

7. Если плоскость сечения проходит через вершину, то в месте пересечения образуется равнобедренный треугольник (см. Осевое сечение).

8. Центр тяжести любого конуса находится на одной четвертой высоты от центра основы.


Все таблицы и формулы

Что такое конусность 1 10?


Что такое конусность 1 10?

Конусность, как правило, выражается в отношении двух чисел например конусность 1:10 означает что высота полного конуса в 10 раз больше диаметра основания. Также конусность может задаваться углом вершины конуса (α). Половина угла вершины конуса называется уклоном конуса (α/2).

Как узнать конусность?

Конусностью называется отношение диаметра основания конуса к высоте. Конусность рассчитывается по формуле К=D/h, где D – диаметр основания конуса, h – высота. Если конус усеченный, то конусность рассчитывается как отношение разности диаметров усеченного конуса к его высоте.

Какой знак определяет конусность поверхности?

conus – геометрическое тело, образованное вращением прямоугольного треугольника около одного из его катетов. ». Знак конусности с размерными числами наносятся над осевой линией или на полке линии-выноски. Отношение диаметра основания конуса к его высоте называется конусностью.

Сколько градусов в конус Морзе?

Морзе приблизительно в 1864 году. Конус Морзе подразделяется на восемь размеров, от КМ0 до КМ7 (англ. Morse taper, MT0-MT7, нем. Morsekegel, MK0-MK7). Конусность от 1:19,002 до 1:20,047 (угол конуса от 2°51’26” до 3°00’52”, уклон конуса от 1°25’43” до 1°30’26”) в зависимости от типоразмера.

Как рассчитать конус Морзе?

Конусность рассчитывается по формуле К=D/h, где D – диаметр основания конуса, h – высота. Если конус усеченный, то конусность рассчитывается как отношение разности диаметров усеченного конуса к его высоте. В случае усечённого конуса, формула конусности будет иметь вид: К = (D-d)/h. Обозначение конусности на чертежах.

Как рассчитать конус формула?

Формулы для вычисления объема конуса: 1) Объем конуса равен одной трети произведения площади основания на высоту. 2) Объем конуса равен одной трети произведения числа пи (3.

Какой конус в сверлильном патроне?

Существуют различные стандарты крепления сверлильных патронов к станку: конические хвостовики, посадка на резьбу и т. п. Стоит отметить, что наивысшей точностью посадки, позволяющей минимизировать биение, отличаются сверлильные патроны с конусом Морзе (самые популярные размеры – В16 и В18).

Какой угол у конуса Морзе 2?

КонусностьУгол конусаОбозначение
1:20,020=0,049952 градуса 51 минута 41 секундаКонус Морзе 2
1:19,922=0,050202 градуса 52 минуты 32 секундыКонус Морзе 3
1:19,254=0,051942 градуса 58 минут 31 секундаКонус Морзе 4
1:19,002=0,052633 градуса 00 минут 53 секундыКонус Морзе 5

Какие бывают виды конуса?

Прямой конус – имеет симметричное основание. Ортогональная проекция вершины данной фигуры на плоскость основания совпадает с центром этого основания. Косой (наклонный) конус – ортогональная проекция вершины фигуры на ее основание не совпадает с центром этого основания.

Для чего нужен конус Морзе?

Конус инструментальный — конический хвостовик инструмента (сверло, зенкер, фреза, развёртка) и коническое отверстие соответствующего размера (гнездо) в шпинделе или задней бабке станка. Предназначено для быстрой смены инструмента с высокой точностью центрирования и надёжностью.

Где используется конус?

Знания о конусе широко применяются в жизни – в быту, на производстве, в науке. Например, в быту мы часто используем вёдра, имеющие форму усечённого конуса, служащие нам ёмкостью для различных жидкостей и сыпучих веществ. Наши растения, благоприятно развиваются в цветочных горшках.

Как называть конус?

Конус, что опирается на круг, эллипс, гиперболу или параболу называется соответственно круговым, эллиптическим, гиперболическим или параболическим конусом (последние два имеют бесконечный объем).

Как называется конус без конца?

Усеченный конус Усеченным конусом называется часть конуса, заключенная между основанием и секущей плоскостью, параллельной основанию.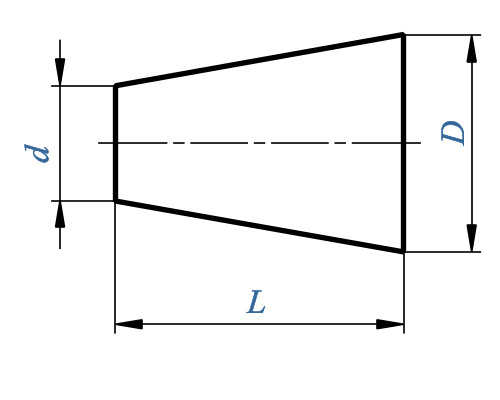 Обычно под усеченным конусом имеется ввиду часть прямого кругового конуса.

Чем отличается полный конус от усеченного?

Круговой конус — конус, основание которого является кругом. … Усечённый конус или конический слой — часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием. Равносторонний конус — конус вращения, образующая которого равна диаметру основания.

Что называется высотой усеченного конуса?

Высотой усеченного конуса называют расстояние между плоскостями расстояние между плоскостями оснований усеченного конуса.

Что такое развертка конуса?

Развертка поверхности конуса – это плоская фигура, полученная путем совмещения боковой поверхности и основания конуса с некоторой плоскостью. Варианты построения развертки: … Усеченный конус

Что такое круговой конус?

Конусом ( прямым круговым конусом ) называется тело, состоящее из круга ( основания конуса ), точки, не лежащей в плоскости этого круга ( вершины конуса ), и всех отрезков, соединяющих вершину конуса с точками основания.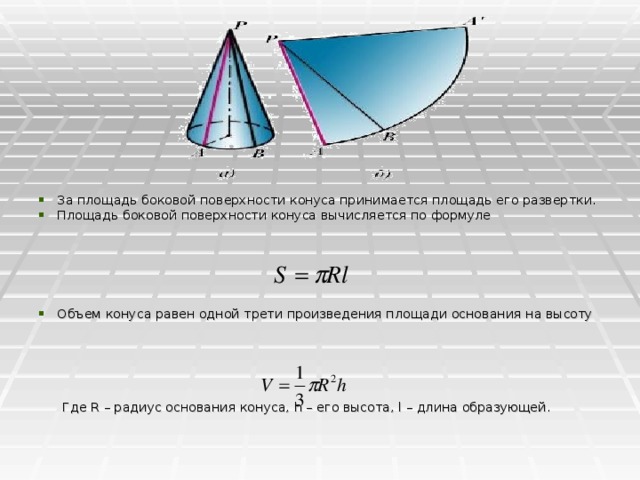 … Отрезки называют образующими конической поверхности, а кривую – направляющей.

Что называется высотой конуса?

Отрезки, соединяющие вершину конуса с точками его основания, называются образующими конуса. Высотой конуса называется перпендикуляр, опущенный из вершины конуса на плоскость его основания, а также длина этого перпендикуляра.

Сколько осевых сечений имеет конус?

Представляет из себя прямоугольник, две стороны которого – образующие цилиндра, а две другие – параллельные хорды верхнего и нижнего основания цилиндра. 9 Виды сечений конуса Осевое сечение конуса. Представляет из себя треугольник, две стороны которого – образующие конуса, а третья сторона – диаметр основания конуса.

Как получается конус?

Конус называется круговым, если в его основании лежит круг. … Прямой круговой конус образуется при вращении прямоугольного треугольника вокруг его катета. Прямой круговой конус определяется радиусом основания R и высотой H (или радиусом основания R и образующей m).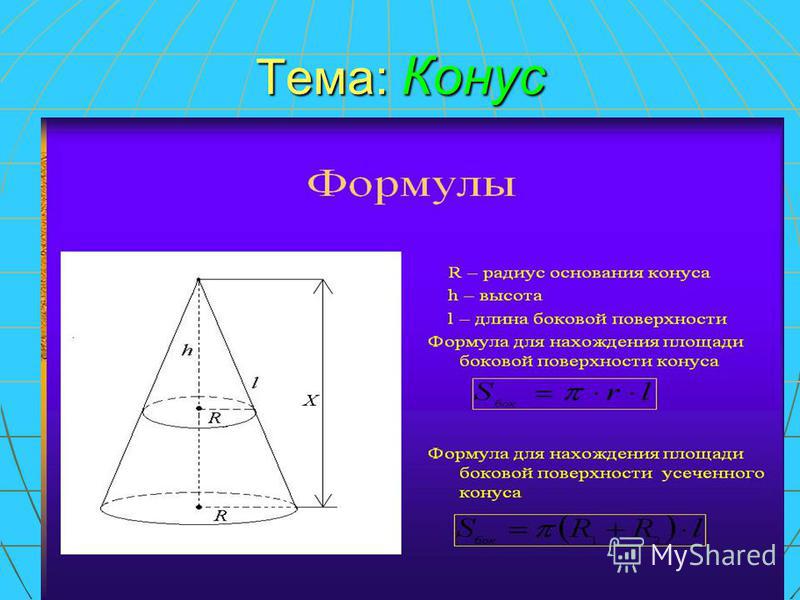

Что такое вершина конуса?

вершина конуса — Точка пересечения образующей конуса с осью. 1 вершина; 2 образующая; 3 основание; 4 коническая поверхность; 5 ось [ГОСТ (CT СЭВ 1779 79)] Тематики нормы взаимозаменяемости Обобщающие термины элементы конуса EN cone point DE Kegelspitze… …

Что такое конус нарастания?

Конус нарастания Конус нарастания, закругленно-конусовидная верхушка растущего осевого органа (стебля, корня) растения, состоящая из образовательной ткани (меристемы). … происходит рост растений.

Кто придумал конус?

Чарльз Рудбэйкер

Сколько основ имеет конус?

у конуса может быть одна из четырех основ: круг, парабола, эллипс и гипербола.

Сколько осей симметрии имеет конус?

Конус также имеет ось симметрии, причём, поскольку число поворотов конуса вокруг своей оси симметрии, приводящих к “самосовмещению” бесконечно, то говорят, что конус имеет ось симметрии типа L8.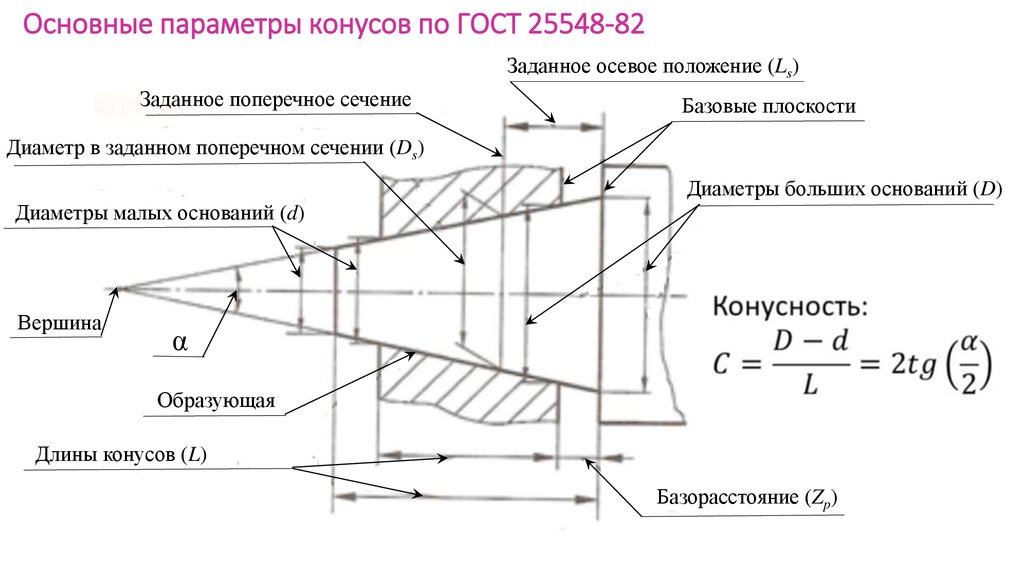

Как можно получить усеченный конус?

Усеченный конус можно получить и как тело вращения. Усеченным конусом называют тело вращения, образованное вращением прямоугольной трапеции около боковой стороны, перпендикулярной основаниям.

Как может быть вращением получен усеченный конус?

Все образующие усеченного конуса равны друг другу. Усеченный конус может быть получен вращением прямоугольной трапеции вокруг ее боковой стороны, перпендикулярной к основаниям.

Как найти площадь осевого сечения?

Формула для расчета площади основания конуса:

  1. S = π * d 2 / 4, где d – диаметр конуса. Формула для расчета площади осевого сечения конуса:
  2. S = d * h / 2, где d – диаметр конуса; h – высота конуса. …
  3. S = a * h / 2, где a – хорда основания конуса; h – высота конуса.

Что представляет собой осевое сечение усеченного конуса?

Осевым сечением усеченного конуса является равнобедренная трапеция, высота которой равна диаметру большего основания; радиусы основания равны 18 см и 10 см.

Как вычислить конусность

Главная » Статьи » Как вычислить конусность


Уклон и Конусность

Иногда, в задачах по начертательной геометрии или работах по инженерной графике, или при выполнении других чертежей, требуется построить уклон и конус. В этой статье Вы узнаете о том, что такое уклон и конусность, как их построить, как правильно обозначить на чертеже.

Что такое уклон? Как определить уклон? Как построить уклон? Обозначение уклона на чертежах по ГОСТ.

Уклон. Уклон это отклонение прямой линии от вертикального или горизонтального положения. Определение уклона. Уклон определяется как отношение противолежащего катета угла прямоугольного треугольника к прилежащему катету, то есть он выражается тангенсом угла а. Уклон можно посчитать по формуле i=AC/AB=tga.

Построение уклона. На примере (рисунок ) наглядно продемонстрировано построение уклона. Для построения уклона 1:1, например, нужно на сторонах прямого угла отложить произвольные, но равные отрезки. Такой уклон, будет соответствовать углу в 45 градусов. Для того чтобы построить уклон 1:2, нужно по горизонтали отложить отрезок равный по значению двум отрезкам отложенным по вертикали. Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а.

Обозначение уклона на чертежах. Обозначение уклонов на чертеже выполняется в соответствии с ГОСТ 2.307—68. На чертеже указывают величину уклона с помощью линии-выноски. На полке линии-выноски наносят знак и величину уклона. Знак уклона должен соответствовать уклону определяемой линии, то есть одна из прямых знака уклона должна быть горизонтальна, а другая должна быть наклонена в ту же сторону, что и определяемая линия уклона. Угол уклона линии знака примерно 30°.

Что такое конусность? Формула для расчёта конусности. Обозначение конусности на чертежах.

Конусность. Конусностью называется отношение диаметра основания конуса к высоте. Конусность рассчитывается по формуле К=D/h, где D – диаметр основания конуса, h – высота. Если конус усеченный, то конусность рассчитывается как отношение разности диаметров усеченного конуса к его высоте. В случае усечённого конуса, формула конусности будет иметь вид: К = (D-d)/h.

Обозначение конусности на чертежах. Форму и величину конуса определяют нанесением трех из перечисленных размеров: 1) диаметр большого основания D; 2) диаметр малого основания d; 3) диаметр в заданном поперечном сечении Ds , имеющем заданное осевое положение Ls; 4) длина конуса L; 5) угол конуса а; 6) конусность с . Также на чертеже допускается указывать и дополнительные размеры, как справочные.

Размеры стандартизованных конусов не нужно указывать на чертеже. Достаточно на чертеже привести условное обозначение конусности по соответствующему стандарту.

Конусность, как и уклон, может быть указана в градусах, дробью (простой, в виде отношения двух чисел или десятичной), в процентах. Например, конусность 1:5 может быть также обозначена как отношение 1:5, 11°25’16», десятичной дробью 0,2 и в процентах 20.

Для конусов, которые применяются в машиностроении, OCT/BKC 7652 устанавливает ряд нормальных конусностей. Нормальные конусности — 1:3; 1:5; 1:8; 1:10; 1:15; 1:20; 1:30; 1:50; 1:100; 1:200. Также в могут быть использованы — 30, 45, 60, 75, 90 и 120°.

chertimvam.ru

Построение уклона и конусности

Уклоном называют величину, характеризующую наклон одной прямой линии к другой прямой. Уклон выражают дробью или в процентах. Уклон / отрезка В С относительно отрезка ВЛ определяют отношением катетов прямоугольного треугольника ЛВС (рисунок 50, а), т. е. Для построения прямой ВС (рисунок 50. а) с заданной величиной уклона к горизонтальной прямой, например 1:4, необходимо от точки А влево отложить отрезок АВ, равный четырем единицам длины, а вверх отрезок АС, равный одной единице длины. Точки С и В соединяют прямой, которая даст направление искомого уклона. Уклоны применяются при вычерчивании деталей, например, стальных балок и рельсов, изготовляемых на прокатных станах, и некоторых деталей, изготовленных литьем. При вычерчивании контура детали с уклоном сначала строится линия уклона, а затем контур. Если уклон задается в процентах, например, 20 % (рисунок 50, б)> то линия уклона строится так же, как гипотенуза прямоугольного треугольника. Длину одного из катетов принимают равной 100 %, а другого — 20 %. Очевидно, что уклон 20 % есть иначе уклон 1:5. Г1о ГОСТ 2.307—68 перед размерным числом, определяющим уклон, наносят условный знак, острый угол которого должен быть направлен в сторону уклона (рисунок 50, а и б). Подробнее обозначение уклона приведено в разделе 1.7 «Нанесение размеров и предельных отклонений». Конусностью называется отношение диаметра основания конуса к его высоте (рисунок 51, а). Обозначается конусность буквой С. Если конус усеченный (рисунок 51, б) с диаметрами оснований D и d и длиной L, то конусность определяется по формуле: Например (рисунок 51, б), если известны размеры D= 30 мм, d- 20 мм и L = 70 мм, то Если известны конусность С, диаметр одного из оснований конуса d и длина конуса можно определить второй диаметр конуса.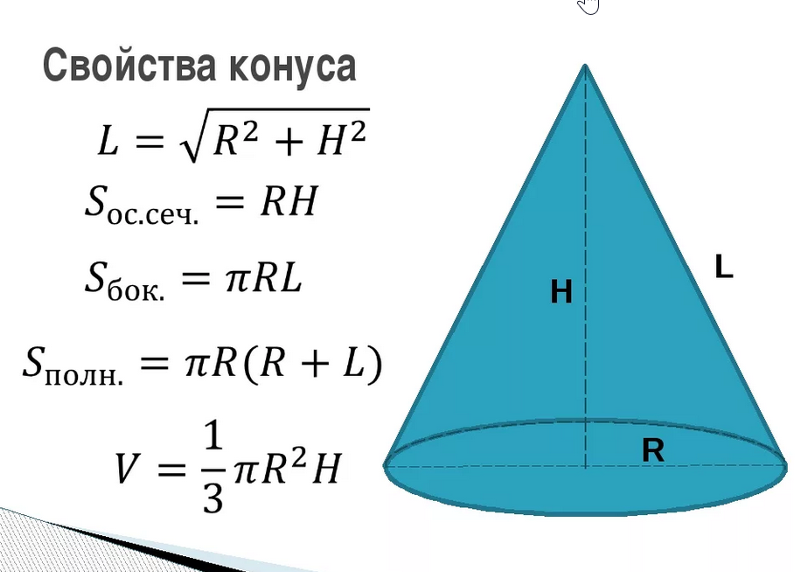 Например, С- 1:7, d- 20 мм и 1 = 70 мм; D находят по формуле (рисунок 51, б). По ГОСТ 2.307—68 перед размерным числом, характеризующим конусность, необходимо наносить условный знак конусности, который имеет вид равнобедренного треугольника с вершиной, направленной в сторону вершины конуса (рисунок 51, б). Подробнее обозначение конусности приведено в разделе 1.7 «Нанесение размеров и предельных отклонений». Вопросы для самопроверни 1. Что называется уклоном? 2. Что называется конусностью? 3. Как обозначается на чертеже конусность и уклон? 4. Как определяется конусность и уклон?

natalibrilenova.ru

ОБРАБОТКА КОНИЧЕСКИХ ПОВЕРХНОСТЕЙ

§ 1. Общие сведения 1. Область применения конусов. Наряду с цилиндрическими деталями в машиностроении получили довольно широкое распространение детали с коническими поверхностями. Примерами их могут служить конусы центров, хвостовиков сверл, зенкеров, разверток. Для крепления этих инструментов передние участки отверстий шпинделя и пиноли токарного станка имеют также коническую форму. Однако область использования конусов не ограничивается режущими инструментами. Конические поверхности имеют многие детали машин. Широкое использование конических соединений объясняется рядом их преимуществ. 1. Они обеспечивают высокую точность центрирования деталей. 2. При плотном соприкосновении пологих конусов получается неподвижное соединение. 3. Изменяя осевое положение деталей конического соединения, можно регулировать величину зазора между ними. 2. Конус и его элементы. Конус представляет собой геометрическое тело, поверхность которого получается вращением прямой линии (образующей), наклонно расположенной к оси вращения (рис. 129, а). Точка пересечения образующей с осью называется вершиной конуса. Плоскости, перпендикулярные к оси конуса, называются, основаниями. Различают полный и усеченный конусы. Первый расположен между основанием и вершиной, второй — между двумя основаниями (большим и меньшим). Конус характеризуется следующими элементами: диаметром большего основания D; диаметром меньшего основания d; длиной l; углом уклона а между образующей и осью конуса; углом конуса 2а между противоположными образующими. Кроме этого, на рабочих чертежах конических деталей часто употребляют понятия конусность и уклон. Конусностью называется отношение разности диаметров двух перечных сечений конуса к расстоянию между ними. Она опреляется по формуле

Уклоном называется отношение разности радиусов двух поперечных сечений конуса к расстоянию между ними. Его определяют по формуле

Из формул (9) и (10) видно, что уклон равен половине конусности.

Тригонометрически уклон равен тангенсу угла уклона (см. рис. 129, б, треугольник ABC), т. е.

На чертеже (рис. 130) конусность обозначают знаком

mgplm.org

Знак конусности

Конус – лат. conus – геометрическое тело, образованное вращением прямоугольного треугольника около одного из его катетов.

На чертежах с коническими поверхностями иногда указывается конусность c размерными числами в виде соотношения, перед которыми устанавливается знак в виде остроугольного треугольника « ».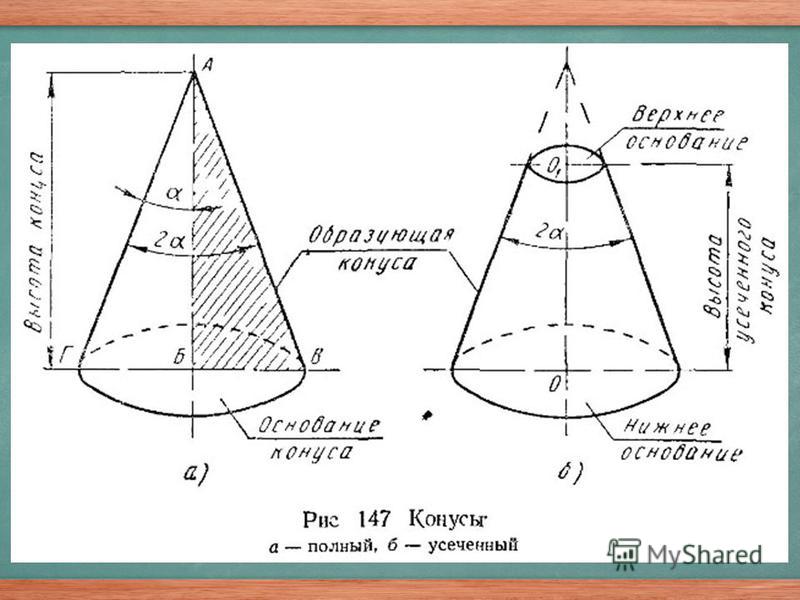 Знак конусности с размерными числами наносятся над осевой линией или на полке линии-выноски.

Обозначение конусности на чертежах

Отношение диаметра основания конуса к его высоте называется конусностью.

Конусность определяется по следующей формуле:

Определение конусности

Где:

  • С – обозначение конусности
  • D – большой диаметр
  • d – меньший диаметр
  • L – длинна

Например, если известны размеры D = 30 мм, d = 20 мм и L = 70 мм, то

Если известны конусность С, диаметр одного из оснований конуса d и длина конуса L, можно определить второй диаметр конуса. Например, С = 1:7, d = 20 мм и L = 70 мм

D находят по формуле:

D = CL + d= 1:7 × 70 + 20 = 30 мм

gk-drawing.ru

Смотрите также

  • Чем декорировать вазу
  • Душ из плитки
  • Как зашпаклевать потолок своими руками под покраску
  • Подключение алюминиевых радиаторов
  • Состав грунтовки глубокого проникновения своими руками
  • Станция насосная водяная
  • Окна на мансардном этаже
  • Горки для гостиной фото
  • Вес цементного раствора в 1 м3
  • Пробка для пола
  • Панно из крупы своими руками

 

Конусность и уклон: построение, расчет, обозначение

Общие сведения о конусах

Содержание

Обработка конических поверхностей

В машиностроении, наряду с цилиндрическими, широко применяются детали с коническими поверхностями в виде наружных конусов или в виде конических отверстий. Например, центр токарного станка имеет два наружных конуса, из которых один служит для установки и закрепления его в коническом отверстии шпинделя; наружный конус для установки и закрепления имеют также сверло, зенкер, развертка и т. д. Переходная втулка для закрепления сверл с коническим хвостовиком имеет наружный конус и коническое отверстие

1. Понятие о конусе и его элементах

Элементы конуса. Если вращать прямоугольный треугольник АБВ вокруг катета АБ (рис. 202, а), то образуется тело АВГ, называемое полным конусом. Линия АБ называется осью или высотой конуса, линия АВ — образующей конуса. Точка А является вершиной конуса.

При вращении катета БВ вокруг оси АБ образуется поверхность круга, называемая основанием конуса.

Угол ВАГ между боковыми сторонами АВ и АГ называется углом конуса и обозначается 2α. Половина этого угла, образуемая боковой стороной АГ и осью АБ, называется углом уклона конуса и обозначается α. Углы выражаются в градусах, минутах и секундах.

Если от полного конуса отрезать его верхнюю часть плоскостью, параллельной егооснованию (рис. 202, б), то получим тело, называемое усеченным конусом. Оно имеет два основания верхнее и нижнее. Расстояние OO1 по оси между основаниями называется высотой усеченного конуса. Так как в машиностроении большей частью приходится иметь дело с частями конусов, т. е. усеченными конусами, то обычно их просто называют конусами; дальше будем называть все конические поверхности конусами.

Связь между элементами конуса. На чертеже указывают обычно три основных размера конуса: больший диаметр D, меньший — d и высоту конуса l (рис. 203).

Иногда на чертеже указывается только один из диаметров конуса, например, больший D, высота конуса l и так называемая конусность. Конусностью называется отношение разности диаметров конуса к его длине. Обозначим конусность буквой K, тогда

Если конус имеет размеры: D =80 мм, d = 70 мм и l = 100 мм, то согласно формуле (10):

Это значит, что на длине 10 мм диаметр конуса уменьшается на 1 мм или на каждый миллиметр длины конуса разница между его диаметрами изменяется на

Иногда на чертеже вместо угла конуса указывается уклон конуса. Уклон конуса показывает, в какой мере отклоняется образующая конуса от его оси.
Уклон конуса определяется по формуле

где tg α — уклон конуса;
D — диаметр большого основания конуса в мм;
d — диаметр малого основания конуса в мм;
l — высота конуса в мм.

Пользуясь формулой (11), можно при помощи тригонометрических таблиц определить угол а уклона конуса.

Пример 6.

Дано D = 80 мм; d=70мм; l= 100 мм. По формуле (11) имеем

По таблице тангенсов находим величину, наиболее близкую к tg α = 0,05, т. е. tg α = 0,049, которому соответствует угол уклона конуса α = 2°50′. Следовательно, угол конуса

2α = 2·2°50′ = 5°40′.

Уклон конуса и конусность обычно выражают простой дробью, например: 1 : 10; 1 : 50, или десятичной дробью, например, 0,1; 0,05; 0,02 и т. д.

2. Способы получения конических поверхностей на токарном станке

На токарном станке обработка конических поверхностей производится одним из следующих способов:
а) поворотом верхней части суппорта;
б) поперечным смещением корпуса задней бабки;
в) с помощью конусной линейки;
г) с помощью широкого резца.

3. Обработка конических поверхностей поворотом верхней части суппорта

При изготовлении на токарном станке коротких наружных и внутренних конических поверхностей с большим углом уклона нужно повернуть верхнюю часть суппорта относительно оси станка под углом α уклона конуса (см. рис. 204). При таком способе работы подачу можно производить только от руки, вращая рукоятку ходового винта верхней части суппорта, и лишь в наиболее современных токарных станках имеется механическая подача верхней части суппорта.

Для установки верхней части суппорта 1 на требуемый угол можно использовать деления, нанесенные на фланце 2 поворотной части суппорта (рис. 204). Если угол α уклона конуса задан по чертежу, то верхнюю часть суппорта повертывают вместе с его поворотной частью на требуемое число делений, обозначающих градусы. Число делений отсчитывают относительно риски, нанесенной на нижней части суппорта.

Если на чертеже угол α не дан, а указаны больший и меньший диаметры конуса и длина его конической части, то величину угла поворота суппорта определяют по формуле (11)

Пример 7.

Даны диаметры конуса D = 80 мм, d = 66 мм, длина конуса l = 112 мм. Имеем:

По таблице тангенсов находим приближенно: а = 3°35′. Следовательно, верхнюю часть суппорта необходимо повернуть на 3°35′.

Способ обтачивания конических поверхностей поворотом верхней части суппорта имеет следующие недостатки: он допускает обычно применение только ручной подачи, что отражается на производительности труда и чистоте обработанной поверхности; позволяет обтачивать сравнительно короткие конические поверхности, ограниченные длиной хода верхней части суппорта.

4. Обработка конических поверхностей способом поперечного смещения корпуса задней бабки

Для получения конической поверхности на токарном станке необходимо при вращении заготовки вершину резца перемещать не параллельно, а под некоторым углом к оси центров. Этот угол должен равняться углу α уклона конуса. Наиболее простой способ получения угла между осью центров и направлением подачи — сместить линию центров, сдвинув задний центр в поперечном направлении. Путем смещения заднего центра в сторону резца (на себя) в результате обтачивания получают конус, у которого большее основание направлено в сторонупередней бабки; при смещении заднего центра в противоположную сторону, т. е. от резца (от себя), большее основание конуса окажется со стороны задней бабки (рис. 205).

Смещение корпуса задней бабки определяют по формуле

где S — смещение корпуса задней бабки от оси шпинделя передней бабки в мм;
D — диаметр большого основания конуса в мм;
d — диаметр малого основания конуса в мм;
L — длина всей детали или расстояние между центрами в мм;
l — длина конической части детали в мм.

Пример 8.

Определить смещение центра задней бабки для обтачивания усеченного конуса, если D = 100 мм, d = 80 мм, L = 300 мм и l = 200мм. По формуле (12) находим:

Смещение корпуса задней бабки производят, используя деления 1 (рис 206), нанесенные на торце опорной плиты, и риску 2 на торце корпуса задней бабки.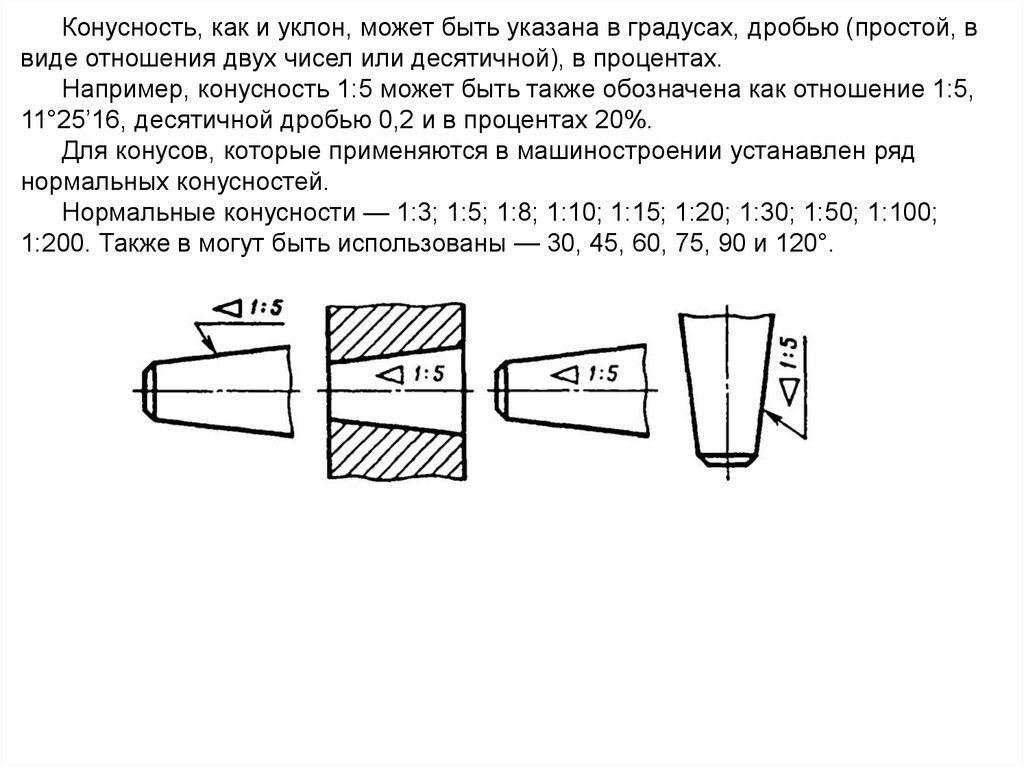

Если на торце плиты делений нет, то смещают корпус задней бабки, пользуясь измерительной линейкой, как показано на рис. 207.

Преимущество обработки конических поверхностей путем смещения корпуса задней бабки заключается в том, что этим способом можно обтачивать конусы большой длины и вести обтачивание с механической подачей.

Недостатки этого способа: невозможность растачивать конические отверстия; потеря времени на перестановку задней бабки; возможность обрабатывать лишь пологие конусы; перекос центров в центровых отверстиях, что приводит к быстрому и неравномерному износу центров и центровых отверстий и служит причиной брака при вторичной установке детали в этих же центровых отверстиях.

Неравномерного износа центровых отверстий можно избежать, если вместо обычного применять специальный шаровой центр (рис. 208). Такие центры используют преимущественно при обработке точных конусов.

5. Обработка конических поверхностей с применением конусной линейки

Для обработки конических поверхностей с углом уклона а до 10—12° современные токарные станки обычно имеют особое приспособление, называемое конусной линейкой.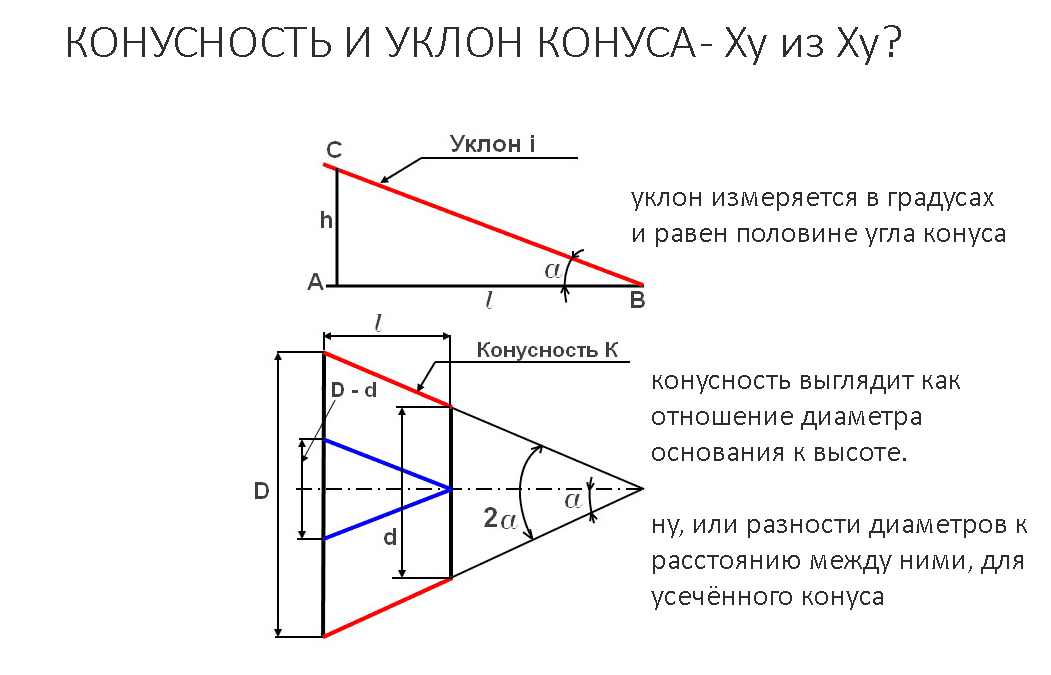 Схема обработки конуса с применением конусной линейки приводится на рис. 209.

К станине станка прикреплена плита 11, на которой установлена конусная линейка 9. Линейку можно поворачивать вокруг пальца 8 под требуемым углом а к оси обрабатываемой детали. Для закрепления линейки в требуемом положении служат два болта 4 и 10. По линейке свободно скользит ползун 7, соединяющийся с нижней поперечной частью 12 суппорта при помощи тяги 5 и зажима 6. Чтобы эта часть суппорта могла свободно скользить по направляющим, ее отсоединяют от каретки 3, вывинчивая поперечный винт или отсоединяя от суппорта его гайку.

Если сообщить каретке продольную подачу, то ползун 7, захватываемый тягой 5, начнет перемещаться вдоль линейки 9. Так как ползун скреплен с поперечными салазками суппорта, то они вместе с резцом будут перемещаться параллельно линейке 9. Благодаря этому резец будет обрабатывать коническую поверхность с углом уклона, равным углу α поворота конусной линейки.

После каждого прохода резец устанавливают на глубину резания с помощью рукоятки 1 верхней части 2 суппорта. Эта часть суппорта должна быть повернута на 90° относительно нормального положения, т. е. так, как это показано на рис. 209.

Если даны диаметры оснований конуса D и d и его длина l, то угол поворота линейки можно найти по формуле (11).

Подсчитав величину tg α, легко определить значение угла α по таблице тангенсов.
Применение конусной линейки имеет ряд преимуществ:
1) наладка линейки удобна и производится быстро;
2) при переходе к обработке конусов не требуется нарушать нормальную наладку станка, т. е. не нужно смещать корпус задней бабки; центры станка остаются в нормальном положении, т. е. на одной оси, благодаря чему центровые отверстия в детали и центры станка не срабатываются;
3) при помощи конусной линейки можно не только обтачивать наружные конические поверхности, но и растачивать конические отверстия;
4) возможна работа е продольным самоходом, что увеличивает производительность труда и улучшает качество обработки.

Недостатком конусной линейки является необходимость отсоединять салазки суппорта от винта поперечной подачи. Этот недостаток устранен в конструкции некоторых токарных станков, у которых винт не связан жестко со своим маховичком и зубчатыми колесами поперечного самохода.

6. Обработка конических поверхностей широким резцом

Обработку конических поверхностей (наружных и внутренних) с небольшой длиной конуса можно производить широким резцом с углом в плане, соответствующим углу α уклона конуса (рис. 210). Подача резца может быть продольная и поперечная.

Однако использование широкого резца на обычных станках возможно только при длине конуса, не превышающей примерно 20 мм. Применять более широкие резцы можно лишь на особо жестких станках и деталях, если это не вызывает вибрации резца и обрабатываемой детали.

7. Растачивание и развертывание конических отверстий

Обработка конических отверстий является одной из наиболее трудных токарных работ; она значительно труднее, чем обработка наружных конусов.

Обработку конических отверстий на токарных станках в большинстве случаев производят растачиванием резцом с поворотом верхней части суппорта и реже с помощью конусной линейки. Все подсчеты, связанные с поворотом верхней части суппорта или конусной линейки, выполняются так же, как при обтачивании наружных конических поверхностей.

Если отверстие должно быть в сплошном материале, то сначала сверлят цилиндрическое отверстие, которое затем растачивают резцом на конус или обрабатывают коническими зенкерами и развертками.

Чтобы ускорить растачивание или развертывание, следует предварительно просверлить отверстие сверлом, диаметр d, которого на 1—2 мм меньше диаметра малого основания конуса (рис. 211, а). После этого рассверливают отверстие одним (рис. 211, б) или двумя (рис. 211, в) сверлами для получения ступеней.

После чистового растачивания конуса его развертывают конической разверткой соответствующей конусности. Для конусов с небольшой конусностью выгоднее производить обработку конических отверстий непосредственно после сверления набором специальных разверток, как показано на рис. 212.

8. Режимы резания при обработке отверстий коническими развертками

Конические развертки работают в более тяжелых условиях, чем цилиндрические: в то время как цилиндрические развертки снимают незначительный припуск небольшими режущими кромками, конические развертки режут всей длиной их режущих кромок, расположенных на образующей конуса. Поэтому при работе коническими развертками применяют подачи и скорости резания меньше, чем при работе цилиндрическими развертками.

При обработке отверстий коническими развертками подачу производят вручную, вращая маховичок задней бабки. Необходимо следить за тем, чтобы пиноль задней бабки перемещалась равномерно.

Подачи при развертывании стали 0,1—0,2 мм/об, при развертывании чугуна 0,2—0,4 мм/об.

Скорость резания при развертывании конических отверстий развертками из быстрорежущей стали 6—10 м/мин.

Для облегчения работы конических разверток и получения чистой и гладкой поверхности следует применять охлаждение. При обработке стали и чугуна применяют эмульсию или сульфофрезол.

9. Измерение конических поверхностей

Поверхности конусов проверяют шаблонами и калибрами; измерение и одновременно проверку углов конуса производят угломерами. На рис. 213 показан способ проверки конуса с помощью шаблона.

Наружные и внутренние углы различных деталей можно измерять универсальным угломером (рис. 214). Он состоит из основания 1, На котором на дуге 130 нанесена основная шкала. С основанием 1 жестко скреплена линейка 5. По дуге основания перемещается сектор 4, несущий нониус 3. К сектору 4 посредством державки 7 может быть прикреплен угольник 2, в котором, в свою очередь, закрепляется съемная линейка 5. Угольник 2 и съемная линейка 5 имеют возможность перемещаться по грани сектора 4.

Путем различных комбинаций в установке измерительных деталей угломера можно производить измерение углов от 0 до 320°. Величина отсчета по нониусу 2′. Отсчет, полученный при измерении углов, производится по шкале и нониусу (рис. 215) следующим образом: нулевой штрих нониуса показывает число градусов, а штрих нониуса, совпадающий со штрихом шкалы основания, — число минут. На рис. 215 со штрихом шкалы основания совпадает 11-й штрих нониуса, что означает 2’Х 11 = 22′. Следовательно, угол в данном случае равен 76°22′.

На рис. 216 показаны комбинации измерительных деталей универсального угломера, позволяющие производить измерение различных углов от 0 до 320°.

Для более точной проверки конусов в серийном производстве применяют специальные калибры. На рис. 217, а показан кониче-ский калибр-втулка для проверки наружных конусов, а на рис. 217, б—конический калибр-пробка для проверки конических отверстий.

На калибрах делаются уступы 1 и 2 на торцах или наносятся риски 3, служащие для определения точности проверяемых поверхностей.

На. рис. 218 приводится пример проверки конического отверстия калибром-пробкой.

Для проверки отверстия калибр (см. рис. 218), имеющий уступ 1 на определенном расстоянии от торца 2 и две риски 3, вводят с легким нажимом в отверстие и проверяют, нет ли качания калибра в отверстии. Отсутствие качания показывает, что угол конуса правилен. Убедившись, что угол конуса правилен, приступают к проверке его размера. Для этого наблюдают, до какого места калибр войдет в проверяемую деталь. Если конец конуса детали совпадает с левым торцом уступа 1 или с одной из рисок 3 или находится между рисками, то размеры конуса правильны. Но может случиться, что калибр войдет в деталь настолько глубоко, что обе риски 3 войдут в отверстие или оба торца уступа 1 выйдут из него наружу. Это показывает, что диаметр отверстия больше заданного. Если, наоборот, обе риски окажутся вне отверстия или ни один из торцов уступа не выйдет из него, то диаметр отверстия меньше требуемого.

Для точной проверки конусности применяют следующий способ. На измеряемой поверхности детали или калибра проводят мелом или карандашом две-три линии вдоль образующей конуса, затем вставляют или надевают калибр на деталь и повертывают его на часть оборота. Если линии сотрутся неравномерно, это значит, что конус детали обработан неточно и необходимо его исправить. Стирание линий по концам калибра говорит о неправильной конусности; стирание линий в средней части калибра показывает, что конус имеет небольшую вогнутость, причиной чего обычно является неточное расположение вершины резца по высоте центров. Вместо меловых линий можно нанести на всю коническую поверхность детали или калибра тонкий слой специальной краски (синьки). Такой способ дает большую точность измерения.

10. Брак при обработке конических поверхностей и меры его предупреждения

При обработке конических поверхностей, помимо упомянутых видов брака для цилиндрических поверхностей, дополнительно возможны следующие виды брака:
1) неправильная конусность;
2) отклонения в размерах конуса;
3) отклонения в размерах диаметров оснований при правильной конусности;
4) непрямолинейность образующей конической поверхности.

1. Неправильная конусность получается главным образом вследствие неточного смещения корпуса задней бабки, неточного поворота верхней части суппорта, неправильной установки конусной линейки, неправильной заточки или установки широкого резца. Следовательно, точной установкой корпуса задней бабки, верхней части суппорта или конусной линейки перед началом обработки можно брак предупредить. Этот вид брака исправим только в том случае, если ошибка во всей длине конуса направлена в тело детали, т. е. все диаметры у втулки меньше, а у конического стержня больше требуемых.

2. Неправильный размер конуса при правильном угле его, т. е. неправильная величина диаметров по всей длине конуса, получается, если снято недостаточно или слишком много материала. Предупредить брак можно только внимательной установкой глубины резания по лимбу на чистовых проходах. Брак исправим, если снято недостаточно материала.

3. Может получиться, что при правильной конусности и точных размерах одного конца конуса диаметр второго конца неправилен. Единственной причиной является несоблюдение требуемой длины всего конического участка детали. Брак исправим, если деталь излишне длинна. Чтобы избежать этого вида брака, необходимо перед обработкой конуса тщательно проверить его длину.

4. Непрямолинейность образующей обрабатываемого конуса получается при установке резца выше (рис. 219, б) или ниже (рис. 219, в) центра (на этих рисунках для большей наглядности искажения образующей конуса показаны в сильно преувеличенном виде). Таким образом, и этот вид брака является результатом невнимательной работы токаря.

Контрольные вопросы1. Какими способами можно обработать конические поверхности на токарных станках?
2. В каких случаях рекомендуется делать поворот верхней части суппорта?
3. Как вычисляется угол поворота верхней части суппорта для обтачивания конуса?
4. Как проверяется правильность поворота верхней части суппорта?
5. Как проверить смещение корпуса задней бабки?.Как вычислить величину смещения?
6. Из каких основных элементов состоит конусная линейка? Как настроить конусную линейку на данную деталь?
7. Установите на универсальном угломере следующие углы: 50°25′; 45°50′; 75°35′.
8. Какими инструментами измеряют конические поверхности?
9. Для чего на конических калибрах сделаны уступы или риски и как ими пользоваться?
10. Перечислите виды брака при обработке конических поверхностей. Как их избежать?

Значение конусности

Рассматривая конусность следует учитывать, что этот показатель напрямую связан с уклоном. Этот параметр определяет отклонение прямой лини от вертикального ил горизонтального положения. При этом конусность 1:3 или конусность 1:16 существенно отличается. Определение уклона характеризуется следующими особенностями:

  1. Под уклоном подразумевается отношение противолежащего катета прямоугольного треугольника к прилежащему. Этот параметр еще называют тангенс угла.
  2. Для расчета примеряется следующая формула: i=AC/AB=tga.

Стоит учитывать, что нормальные конусности несколько отличаются от рассматриваемого ранее параметра. Это связано с тем, что конусностью называется соотношение диаметра основания к высоте.

Рассчитать этот показатель можно самым различным образом, наибольшее распространение получила формула K=D/h. В некоторых случаях обозначение проводится в процентах, так как этот переменный показатель применяется для определения всех других параметров.

Рассматривая конусность 1:7 и другой показатель следует также учитывать особенности отображения информации на чертеже. Чаще всего подобное отображение проводится при создании технической документации в машиностроительной области.

Обозначение конусности на чертеже

При создании технической документации должны учитываться все установленные стандарты, так как в противном случае она не может быть использована в дальнейшем. Рассматривая обозначение конусности на чертежах следует уделить внимание следующим моментам:

  1. Отображается диаметр большого основания. Рассматриваемая фигура образуется телом вращения, которому свойственен диаметральный показатель. В случае конуса их может быть несколько, а изменение показателя происходит плавно, не ступенчато. Как правило, у подобной фигуры есть больший диаметр, а также промежуточной в случае наличия ступени.
  2. Наносится диаметр меньшего основания. Меньшее основание отвечает за образование требуемого угла.
  3. Рассчитывается длина конуса. Расстояние между меньшим и большим основанием является показателем длины.
  4. На основании построенного изображения определяется угол. Как правило, для этого проводятся соответствующие расчеты. В случае определения размера по нанесенному изображению при применении специального измерительного прибора существенно снижается точность. Второй метод применяется в случае создания чертежа для производства неответственных деталей.

Простейшее обозначение конусности предусматривает также отображения дополнительных размеров, к примеру, справочную. В некоторых случаях применяется знак конусности, который позволяет сразу понят о разности диаметров.

Выделяют достаточно большое количество различных стандартов, которые касаются обозначения конусности. К особенностям отнесем следующее:

  1. Угол может указываться в градусах дробью или в процентах. Выбор проводится в зависимости от области применения чертежа. Примером можно назвать то, что в машиностроительной области указывается значение градуса.
  2. В машиностроительной области в особую группу выделяют понятие нормальной конусности. Она варьирует в определенном диапазоне, может составлять 30, 45, 60, 75, 90, 120°. Подобные показатели свойственны большинству изделий, которые применяются при сборке различных механизмов. При этом выдержать подобные значения намного проще при применении токарного оборудования. Однако, при необходимости могут выдерживаться и неточные углы, все зависит от конкретного случая.
  3. При начертании основных размеров применяется чертежный шрифт. Он характеризуется довольно большим количеством особенностей, которые должны учитываться. Для правильного отображения используется табличная информация.
  4. Для начала указывается значок конусности от которого отводится стрелка и отображается величина. Особенности отображения во многом зависит от того, какой чертеж. В некоторых случаях наносится большое количество различных размеров, что существенно усложняет нанесение конусности. Именно поэтому предусмотрена возможность использования нескольких различных методов отображения подобной информации.

На чертеже рассматриваемый показатель обозначается в виде треугольника. При этом требуется цифровое значение, которое может рассчитываться при применении различных формул.

Формула для определения конусности

Провести самостоятельно расчет конусности можно при применении различных формул. Стоит учитывать, что в большинстве случаев показатель указывается в градусах, но может и в процентах – все зависит от конкретного случая. Алгоритм проведения расчетов выглядит следующим образом:

  1. K=D-d/l=2tgf=2i. Данная формула характеризуется тем, что конусность характеризуется двойным уклоном. Она основана на получении значения большого и меньшего диаметра, а также расстояния между ними. Кроме этого определяется угол.
  2. Tgf=D/2L. В данном случае требуется протяженность отрезка, который связывает большой и малый диаметр, а также показатель большого диаметра.
  3. F=arctgf. Эта формула применяется для перевода показателя в градусы. Сегодня в большинстве случаев применяются именно градусы, так как их проще выдерживать при непосредственном проведении построений. Что касается процентов, то они зачастую указываются для возможности расчета одного из диаметров. К примеру, если соотношение составляет 20% и дан меньший диаметр, то можно быстро провести расчет большого.

Как ранее было отмечено, конусность 1:5 и другие показатели стандартизированы. Для этого применяется ГОСТ 8593-81.

На чертеже вычисления не отображаются. Как правило, для этого создается дополнительная пояснительная записка. Вычислить основные параметры довольно просто, в некоторых случаях проводится построение чертежа, после чего измеряется значение угла и другие показатели.

Скачать ГОСТ 8593-81

Угол конуса

Важным показателем при построении различных чертежей считается угол конуса. Он определяется соотношение большого диаметра к меньшему. Высчитывается этот показатель по следующим причинам:

  1. На момент обработки мастер должен учитывать этот показатель, так как он позволяет получить требуемое изделие с высокой точностью размеров. В большинстве случаев обработка проводится именно при учете угла, а не показателей большого и малого диаметра.
  2. Угол конуса рассчитывается на момент разработки проекта. Этот показатель наносится на чертеж или отображается в специальной таблице, которая содержит всю необходимую информацию. Оператор станка или мастер не проводит расчеты на месте производства, вся информация должна быть указана в разработанной технологической карте.
  3. Проверка качества изделия зачастую проводится по малому и большему основанию, но также могут применяться инструменты, по которым определяется показатель конусности.

Как ранее было отмечено, в машиностроительной области показатель стандартизирован. В другой области значение может существенно отличаться от установленных стандартов. Некоторые изделия характеризуются ступенчатым расположение поверхностей. В этом случае провести расчеты достаточно сложно, так как есть промежуточный диаметр.

Что такое уклон?

Как ранее было отмечено, довольно важным показателем можно считать уклон. Он представлен линией, которая расположена под углом к горизонту. Если рассматривать конусность на чертеже, то она представлена сочетанием двух разнонаправленных уклонов, которые объединены между собой.

Понятие уклона получило весьма широкое распространение. В большинстве случаев для его отображения проводится построение треугольника с определенным углом.

Две вспомогательные стороны применяются для расчета угла, которые и определяет особенности наклона основной поверхности.

Как определить уклон

Для определения уклона достаточно воспользоваться всего одной формулой. Как ранее было отмечено, существенно упростить задачу можно при построении прямоугольного треугольника. Среди особенностей подобной работы отметим следующие моменты:

  1. Определяется начальная и конечная точка отрезка. В случае построения сложной фигуры она определяется в зависимости от особенностей самого чертежа.
  2. Проводится вертикальная линия от точки, которая находится выше. Она позволяет построить прямоугольный треугольник, который часто используется для отображения уклона.
  3. Под прямым углом проводится соединение вспомогательной линии с нижней точкой.
  4. Угол, который образуется между вспомогательной и основной линией в нижней точке высчитывается для определения наклона.

Формула, которая требуется для вычисления рассматриваемого показателя указывалась выше. Стоит учитывать, что полученный показатель также переводится в градусы.

Как осуществлять контроль изготовления конических поверхностей

Внешние конуса измеряются с помощью универсального угломера либо специального шаблона. Калибр-втулки служат для проверки точных параметров конуса. Кроме угла конуса, они показывают и его сечения. Карандашом наносят на обработанную поверхность несколько меток. Калибр-втулку помещают сверху на контрольный конус.

Рис. 8. Калибр-втулка для проверки наружных конусов (а) и пример ее применения (б):

A, B – метки

Поворачивая инструмент в разные стороны и легко нажимая на него, добиваются, что метки на качественно обработанном конусе стираются полностью. Конец конусной детали должен быть расположен между отметками А и В.

Контроль конических отверстий осуществляют калибром-пробкой. Качество отверстия показывает плотность прилегания калибра к обработанной поверхности. Нанесением тонкого слоя красящего вещества на пробку калибра, можно определить: если краска исчезнет возле большого сечения – угол конуса занижен, если возле малого – увеличен.

Конус — свойства, виды и формулы » Kupuk.net

Из огромного перечня математических заданий часто встречаются задачи, связанные с темой «Конус». На уроках геометрии школьники должны усвоить основные понятия и названия всех элементов этой фигуры и понять, как и по каким формулам производится расчет нужных параметров. 

О данной геометрической фигуре пойдёт речь в сегодняшней статье.

Определение и элементы конуса

Под конусом понимают тело, состоящее из круга и точки, которая удалена от его поверхности на определённое расстояние. 

При этом точка соединяется с основанием посредством проведения лучей, которые называются образующими. Линия, соединяющая центр круга с удалённой точкой, является высотой данной фигуры.

Обратите внимание! Также существует такое понятие, как ось конуса. Это линия, проходящая через его центр и совпадающая с высотой. Образующие строятся относительно оси.

Хотелось бы рассмотреть ещё несколько понятий по этой теме:

1. Под конусностью понимают отношение диаметра основания фигуры и её высоты:

Важно! Конусность отвечает за угол наклона образующих. Чем больше данный параметр, тем острее угол.

2. Осевое сечение предполагает наличие плоскости, которая будет рассекать фигуру, проходя через ось:

3. Касательная— это плоскость, которая соприкасается с образующей конуса. При этом важно, чтобы она была перпендикулярна осевому сечению.

Свойства кругового конуса

Выделяют несколько особенностей, которыми обладает фигура данного типа:

  • Образующие кругового конуса равны друг другу.

  • Чтобы найти центр тяжести фигуры, нужно её высоту поделить на четыре части.

  • Место пересечения плоскости сечения и основы образует параболу. Если через вершину тела провести плоскость сечения, то получится равнобедренный треугольник.

    • Интересный факт! Если вращать прямоугольный треугольник вокруг одного из катетов, то получится конус. При этом важно, чтобы угол вращения был не менее 360 градусов.

    Общая формула объёма фигуры

    Чтобы найти объём кругового конуса, необходимо умножить число Пи на его высоту, на радиус в квадрате и всё это произведение поделить на три:

    Дополнительная информация! Чтобы узнать объём фигуры, нужно умножить площадь её основы на высоту и поделить на три:

    Объём усечённого конуса

    Это часть прямого конуса, которая находится в пространстве между основой и плоскостью, параллельной этому основанию. В общем виде выглядит следующим образом:

    Объём данного тела можно вычислить по формуле:

    Важно! S и S1 это площади соответствующих основ, которые равняются ПR2 и ПR12 При нахождении этих значений поможет онлайн калькулятор.

    Площадь поверхности фигуры

    Для вычисления данного параметра потребуется знать площадь боковой поверхности. Она равняется произведению числа π, радиуса и длины образующей.

    Чтобы рассчитать площадь всей поверхности, нужно сложить площади его основы и боковой поверхности.

    Площадь усечённого конуса

    Для нахождения данного параметра нужно воспользоваться формулами:

    • площади боковой поверхности усечённого конуса Sбок;

    • полной площади усечённой фигуры Sпол, которая равна сумме площадей двух оснований и площади боковой поверхности:

    Здесь l — длина образующей, а R и r — радиусы большего и меньшего оснований соответственно.

    Уравнение конуса

    Часто требуется при решении математических задач. Записывается в следующем виде:

    где x0, y0,z0- координаты по соответствующим осям.

    Таким образом, в данной статье были представлены основные сведения, которые могут понадобиться при решении задач на тему «Конус».

    Простая формула для расчета конусов

    синий волк
    Участник