Формула модуль зуба: Что такое модуль шестерни? Как вычислить модуль зубчатого колеса
alexxlab | 24.07.2020 | 0 | Разное
Модуль зубчатого колеса с заданным диаметром делительной окружности Калькулятор
✖Диаметр делительной окружности цилиндрического зубчатого колеса – это диаметр делительной окружности шестерни, которая касается делительной окружности зацепляющей шестерни.ⓘ Диаметр делительной окружности цилиндрического зубчатого колеса [d] | створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр | +10% -10% | |
✖Количество зубьев на прямозубой шестерне определяется как количество зубьев (которые входят в зацепление с другой совместимой зубчатой частью для передачи или преобразования крутящего момента и скорости) на рассматриваемом образце или детали. | +10% -10% |
|
✖Модуль цилиндрического зубчатого колеса – это единица размера, которая указывает, насколько большим или маленьким является зубчатое колесо.ⓘ Модуль зубчатого колеса с заданным диаметром делительной окружности [m] |
створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр |
⎘ копия |
👎
Формула
сбросить
👍
Модуль зубчатого колеса с заданным диаметром делительной окружности Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1.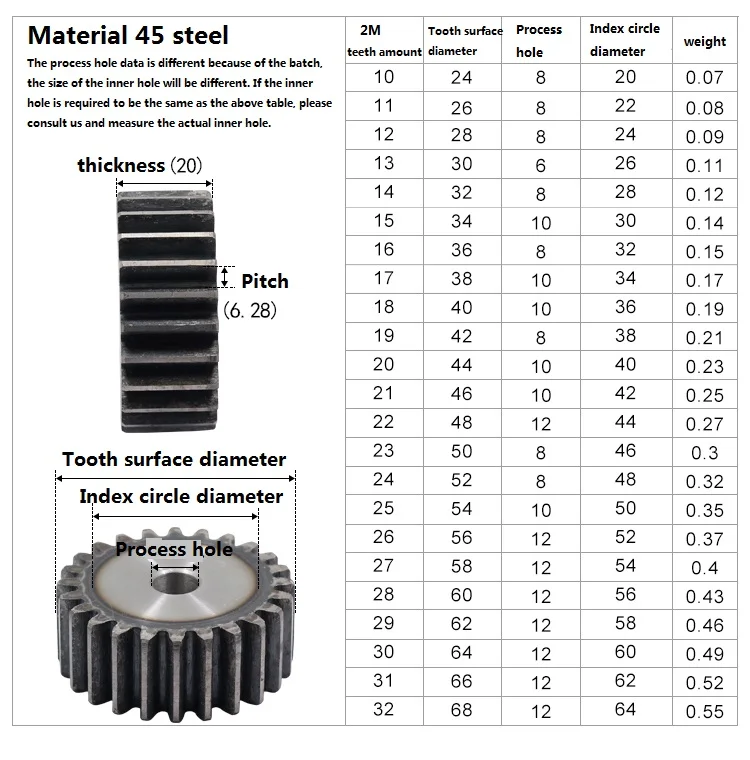
Диаметр делительной окружности цилиндрического зубчатого колеса: 118 Миллиметр –> 0.118 метр (Проверьте преобразование здесь)
Количество зубьев на цилиндрической шестерне: 30 –> Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
0.00393333333333333 метр –>3.93333333333333 Миллиметр (Проверьте преобразование здесь)
< 4 Модуль передач Калькуляторы
Модуль зубчатого колеса с заданным диаметром делительной окружности формула
Модуль цилиндрического зубчатого колеса = Диаметр делительной окружности цилиндрического зубчатого колеса/Количество зубьев на цилиндрической шестерне
m = d/z
Что такое шестеренка?
Шестерни определяются как зубчатые колеса или многолепестковые кулачки, которые передают мощность и движение от одного вала к другому посредством последовательного зацепления зубьев.
Share
Copied!
Лекции_ТММ_2018_ПТМ – Стр 4
Соотношение между диаметром начальной и основной окружности:
db = dWcos W | ( 4.2 ) |
Шагом зацепления называется расстояние между одноименными точками профилей двух соседних зубьев (см. рис. 4.3б). Шаг измеряют по дуге начальной или основной окружности. В первом случае его обозначают pW, а во втором – pb. Для косозубых и винтовых колес шаг можно измерять по торцу зуба (см. рис. 4.3в), тогда шаг называют торцевым и в индексе ставят значок “t” или по нормали к оси зуба, в этом случае его называют нормальным и в индексе ставят значок
“n”. В соответствии с выражением (4.2): |
|
pb = pWcos W | ( 4.3 ) |
Нормальный шаг: |
|
pn = ptcos | ( 4. |
где – угол наклона зубьев косозубого колеса (см. рис. 4.3в). |
|
Важнейшим параметром любого зубчатого колеса является его модуль. По | |
определению модуль зубчатого колеса это: |
|
m = pWt/ ; | ( 4.5 ) |
4 )Подчеркнем, что выражение (4.5) – это определение понятия “модуль зубчатого колеса”, а не формула для его вычисления. В дальнейшем мы узнаем, что “m” определяется по условиям прочности или точности.
Понятие модуля колеса важно в первую очередь тем, что любой размер зубчатого колеса выражают в виде некоторого безразмерного коэффициента умноженного на “m”, или комбинации коэффициентов, умноженной на “m”. Это позволяет унифицировать проектные расчеты.
31
Величины модулей зубчатых колес стандартизованы, т.е. в ГОСТах перечислены те значения “m”, которые допускается применять при проектировании.
Теперь введем еще одну характерную окружность: так называемую делительную, её диаметр:
d = mZ; | ( 4.6 ) |
где Z – количество зубьев на колесе.
В дальнейшем, когда мы будем изучать изготовление зубчатых колес методом обкатки, будет введено понятие смещения инструмента. Сейчас предварительно отметим, что при отсутствии смещения инструмента делительная и начальная окружности совпадают.
Начальная окружность делит зуб на головку и ножку. На рис. 4.3б обозначены: ha– высота головки зуба, hf– высота ножки зуба.
ha= ha* m, hf=( ha* + C*) m ( 4.7 )
где ha* – коэффициент высоты головки зуба, его значение: ha* = 1 – для нормального зуба, ha* = 0,8 – для укороченного,
C* – коэффициент радиального зазора, при изготовлении колеса без смещения инструмента его значение обычно принимают C* = 0,25.
Следующие две характерные окружности зубчатого колеса: окружность выступов – её диаметр обозначается daи окружность впадин зубьев – df (см.
рис.
4.3б): |
|
|
da = dW + 2ha; | df = dW – 2hf; | ( 4.8 ) |
Таким образом, ножка зуба больше его головки на величину радиального зазора между окружностью выступов одного колеса и окружностью впадин – другого.
4.4. Теоретический и рабочий участок линии зацепления, зоны одно- и двупарного зацепления, коэффициент перекрытия
Как уже отмечалось, при эвольвентном зацеплении не только полюс зацепления неподвижен, но неподвижна вся общая нормаль к контактирующим поверхностям. Следовательно, траектория точки контакта зубьев – это прямая, а точнее отрезок общей нормали. Таким образом, отрезок общей нормали, в пределах которого реально движется точка контакта, называется рабочим участком линии зацепления, а его предельно возможная величина – теоретическим участком линии зацепления.
На рис. 4.4а представлено построение этих отрезков.
По способу образования эвольвенты теоретический участок линии зацепления – это отрезок b1b2– тот же, что и на рис. 4.3а.
Поскольку первое касание при вхождении в контакт происходит вершиной зуба, то рабочий участок линии зацепления а1а2определяется пересечениями окружностей выступов с общей нормалью n-n.
На рис. 4.4бв показаны эпюры коэффициента удельного давления q и удельного скольжения в зависимости от положения точки контакта.
32
q | m 1 2 | ; | 1 | 1 |
| 1 | ; | 1 u | 2 | ; | |||
|
|
|
|
|
| ||||||||
|
| 2 |
| 12 | u |
|
| 2 |
| 21 | 12 |
|
|
1 |
|
| 12 |
|
|
|
|
| 1 |
| |||
где 12 – радиусы кривизны эвольвент, m – модуль зацепления, u12– передаточное число зубчатой пары.
Чтобы зацепление было плавным необходимо, чтобы до выхода из зацепления очередной пары зубьев следующая пара уже вошла в зацепление. Таким образом, в момент вхождения в зацепление очередной пары зубьев и еще некоторое время после этого в зацеплении находится две пары зубьев. Участок линии зацепления, соответствующий этому состоянию, называют зоной двупарного зацепления. Далее предыдущая пара зубьев выходит из зацепления, в зацеплении остается одна пара и вся нагрузка падает на неё. Участок линии зацепления, соответствующий этому состоянию, называют зоной однопарного зацепления. Значения удельного давления, вычисленные по формуле (4.9) соответствуют зоне однопарного зацепления, а зоне двупарного – эти величины в два раза меньше
(см. рис. 4.4б).
33
|
| a1a2 |
| a1a2 | |
|
| pbt |
| pWt cos W | |
|
|
|
| ||
И так, в зацеплении находится попеременно то одна, то две пары зубьев.
Среднее количество пар зубьев, находящихся в зацеплении называется коэффициентом перекрытия . Для прямозубой передачи его величина равна отношению
длины рабочего участка линии зацепления к шагу по основной окружности:
( 4.10 )
4.5. Методы изготовления зубчатых колес
Вообще говоря, все методы изготовления зубчатых колес можно разбить на две категории:
-метод копирования;
-метод обкатки.
4.5.1.Метод копирования
Исторически это первая категория методов, которые стали применять для изготовления “правильных” зубчатых колес, т.е. таких, зацепление которых отвечает основной теореме зацепления. Суть метода сводится к тому, что изготавливают инструмент, рабочая поверхность которого имеет форму зуба нарезаемого колеса. На рис. 4.5 дан пример, когда колесо изготавливается с помощью модульной фрезы. К методу копирования относится и штамповка колес.
К преимуществам этого метода относится возможность изготовления любого типа колес, с любым профилем зубьев.
Что и обусловило применение этого метода главным образом для изготовления колес не эвольвентным профилем зубьев.
Основным недостатком метода является его относительно высокая стоимость, т.к. для каждого типоразмера колеса требуется свой инструмент. Инструмент этот имеет весьма сложную форму рабочей поверхности. Рабочая поверхность должна иметь очень высокую твердость, следовательно, для обработки такой поверхности требуется инструмент еще более высокой твердости, и оснастка получается весьма дорогостоящей. Таким образом, применение метода копирования целесообразно для колес с не эвольвентным профилем зубьев или при массовом или крупносерийном производстве.
34
4.5.2. Метод обкатки
Этим методом можно изготовить только колеса с эвольвентным профилем зубьев. Инструментом в данном случае может являться: режущая рейка, червячная фреза или долбяк. На рис. 4.6 показана схема изготовления колеса методом обкатки режущей рейкой. Движение резанья происходит перпендикулярно плоскости рисунка.
Если инструмент и заготовка расположены друг относительно друга так, что делительная прямая режущей рейки касается делительной окружности колеса, то говорят, что колесо изготавливается без смещения инструмента (коэффициент смещения x = 0). Смещение инструмента от центра заготовки называется положительным, к центру – отрицательным. Величина смещения равна xm.
Кнедостаткам метода можно отнести то, изготовить можно только колеса
сэвольвентным профилем зубьев.
Кпреимуществам этого метода относится его относительная дешевизна. Т.к. во-первых, режущие кромки, например, режущей рейки прямолинейны и их обработка гораздо дешевле, чем для инструмента в методе копирования. А вовторых, инструмент более универсален: одной и той же рейкой можно изготавливать различные колеса с одним модулем.
4.6.Явления подреза и заострения зуба. Минимальное число зубьев на колесе
При проектировании зубчатых механизмов часто возникает задача уменьшения диаметров колес, так как при этом уменьшается металлоемкость конструкции и, следовательно, ее стоимость.
Поскольку диаметр делительной окружности колеса равен d = mZ, то уменьшить d можно либо уменьшением модуля, либо уменьшением числа зубьев.
35
Модуль колес определяется по условиям прочности и не может быть меньше, чем требуется для обеспечения контактной и изгибной прочности зубьев.
Следовательно, дальнейшее уменьшение диаметра колеса возможно только за счет уменьшения числа зубьев. Однако, как показала практика, при малом числе зубьев на колесе изготовление его методом обкатки приводит к образованию подрезанного зуба (рис. 4.7б). Это связано с тем, что эвольвента существует только снаружи от основной окружности db, а при малом числе зубьев эта окружность проходит по телу зуба, и та его часть, которая находится внутри db эвольвентой не является, а, следовательно, и не отвечает условиям основной теоремы зацепления. При достаточно большом числе зубьев основная окружность проходит ниже окружности впадин, как это показано на рис. 4.7а, или в пределах радиального зазора зацепления и тогда весь зуб или его рабочая часть имеет форму эвольвенты.
Таким образом, во избежание явления подреза зуба надо найти такое количество зубьев Zmin, начиная с которого возникает описанная выше ситуация. Рассмотрим сначала случай изготовления колеса без смещения инструмента.
На рис. 4.7в представлена расчетная схема, где режущая рейка находится в предельно допустимом положении, когда вершины ее зубьев находятся на линии bc, т.е. когда вершины зубьев рейки касаются основной окружности (см. также рис. 4.6).
По построению имеем:
ha = OW – OC = rmin – rbcos W = rmin – rmincos2 W = = rmin (1– cos2 W) = rmin sin2 W
Откуда
ha* m = (dmin/2) sin2 W ha* m = (m zmin/2) sin2 W
36
|
| 2h* |
| ||
Zmin |
|
| a |
| |
sin2 | W | ( 4. | |||
|
| ||||
Тогда |
|
|
| ||
|
|
|
| ||
11 )Для нормального зуба (ha* = 1) для колеса, изготовленного без смещения инструмента ( W = 20О) по формуле (4.11) получаем Zmin 17.
Для случая наличия смещения инструмента аналогично можно получить:
| 2(h* | x) |
| ||
Zmin | a |
|
| ( 4.12 ) | |
sin | 2 |
|
| ||
|
| W |
| ||
|
|
|
|
| |
где x – коэффициент смещения.
Формула (4.12) показывает, что введение положительного смещения позволяет уменьшить минимальное число зубьев. Однако, при увеличении положительного смещения возможно возникновение другого недопустимого явления – заострения зуба (рис. 4.7д). Зуб является заостренным, если полка на вершине зуба составляет меньше, чем (0,2…0,4)m.
4.7. Зубчатые передачи
4.7.1. Цилиндрические зубчатые передачи
При выводе формул для определения передаточных отношений будем опираться на его определение.
i | 1 |
| Vt1 / rW 1 |
| rW 2 |
| dW 2 |
| mZ 2 | ( ) | Z 2 |
| |
|
|
|
|
|
|
| |||||||
12 | 2 | Vt 2 / rW 2 |
| rW 1 |
| dW 1 |
| mZ1 |
| Z1 |
| ||
|
|
|
|
| ( 4. | ||||||||
|
| Для механизма, изображенного на рис. 4.8а: | |||||||||||
13 )где m – модуль, Z1, Z2 – числа зубьев колес.
Этому передаточному отношению приписывается знак “–” для внешнего зацепления, т.к. при этом изменяется направление вращения и знак “+” для внутреннего зацепления, т.к. при этом направление вращения не изменяется.
37
4.7.2. Пространственные зубчатые передачи
Пространственными называются зубчатые механизмы, позволяющие передавать вращение между валами, расположенными в различных плоскостях.
Кним относятся:
1.Конические зубчатые передачи.
2.Винтовые.
3.Червячные.
4.Гипоидные.
И некоторые другие.
4.7.2.1. Конические зубчатые передачи
Эти передачи позволяют передавать вращение и крутящие моменты между валами с пересекающимися осями. В общем случае угол , между осями валов может быть произвольным (рис. 4.9а). На практике чаше всего применяются механизмы с = 90O.
В этом случае передачу называют ортогональной.
В общем случае в неортогональной передаче угол, дополненный до 180O к
углу между векторами угловых скоростей 1 и 2 звеньев 1 и 2, называют межосевым углом .
|
| Связь между векторами угловых скоростей |
|
|
|
| звеньев 1 и 2: | ||||||
|
| 1 и 2 | |||||||||||
|
|
|
| 2 |
|
|
|
| ( 4.14 ) | ||||
|
|
| 1 21 | ||||||||||
где |
| 21 – угловая скорость звена 2 относительно звена 1. |
| ||||||||||
38
На рис. 4.10 представлен план угловых скоростей, соответствующий
векторному уравнению (4.14). Положение вектора |
|
| относительно векторов |
|
| ||
| 21 | 1 | |||||
и |
|
| |||||
2 определяется углами W1, W2, сумма которых равна межосевому углу : | |||||||
|
| W1 + W2 = | ( 4.15 ) | ||||
Если вектор 21 перенести в точку O пересечения осей колес, то он совпадет с мгновенной осью OP относительного движения звеньев и определит конические поверхности, называемые начальными конусами.
sin W 1 sin W 2
2 1
Углы W1 и W2 начальных конусов определяют при решении векторного уравнения по теореме синусов:
Поскольку отношение угловых скоростей по определению называется передаточным отношением, то
i 1 | sin W 2 | ( 4.16 ) | ||
12 | 2 |
| sin W 1 |
|
|
|
| ||
Для ортогональной передачи (см. рис. 4.9б) из OPA: R2 = OPsin W2
из OPB: R1 = OPsin W1
Тогда
i | sin W 2 |
| OP sin W 2 |
| R2 |
| d w2 |
| mZ 2 |
| Z 2 | ( 4. |
|
|
|
|
|
| |||||||
12 | sin W 1 |
| OP sin W 1 |
| R1 |
| d w1 |
| mZ1 |
| Z1 |
|
|
|
|
|
|
|
|
17 )Основные параметры
39
Схема конического зубчатого колеса представлена на рис. 4.11, где приняты следующие обозначения.
ДК – делительный конус, КВР – конус вершин, КВП – конус впадин,
Внешний и внутренний ДпК – внешний и внутренний дополнительные конусы.
Все параметры колеса измеряются по внешнему ДпК, что отмечается индексом “e” в обозначениях параметров.
4.7.2.2. Гиперболоидные зубчатые передачи
Геометрическое место положений мгновенных осей вращения называют аксоидом. В зубчатой передаче со скрещивающимися осями колес при постоянном передаточном отношении аксоидами относительного движения являются однополюсные гиперболоиды вращения. Поэтому зубчатые передачи со скрещивающимися осями колес называют гиперболоидными.
Винтовая передача
Эта передача состоит из двух эвольвентных цилиндрических косозубых колес (рис. 4.12), оси которых скрещиваются в общем случае под произвольным
углом . Межосевой угол
= W1 W2
где – углы наклона линий зубьев (винтовых линий) по начальным цилиндрам; знак “+” соответствует одноименному направлению винтовых линий, “–” – разноименному.
В частном случае ортогональной передачи = W1 W2 = 90O.
Как для любых косозубых колес в данном случае различают торцевой pt и нормальный pn шаг зацепления
pn = pt / cos W
На рис. 4.12б построен план скоростей для контактной точки, совпадающей с полюсом зацепления “w”.
Из pvnv1: vn = v1 cos W1 из pvnv2: vn = v2 cos W2
40
Соседние файлы в папке Лекции
- #
13.04.2019516.93 Кб39img108.jpg
- #
13.04.201915.45 Кб53Вопросы к экзамену по ТММ 2019 г.docx
- #
13.04.20191.66 Mб46Лекции_ТММ_2018_ПТМ.mht
- #
13.04.20191.49 Mб97Лекции_ТММ_2018_ПТМ.pdf
- #
13.04.2019521.77 Кб73Ответы.docx
Калькулятор размеров шестерни | Эвольвент Дизайн
Калькулятор шага зубчатого колеса: определение диаметра шага, внешнего диаметра заготовки зубчатого колеса (НД) и диаметра основания Рассчитайте основные размеры для внешнего цилиндрического зубчатого колеса. Введите количество зубьев шестерни, шаг (или модуль) и угол давления, чтобы рассчитать диаметр делителя, диаметр основания и внешний диаметр.
При этом также определяются размеры зуба: придаток, нижняя часть, рабочая глубина и общая глубина.
единицы мм (модуль) 1/дюйм (диаметральный шаг)
Тип Внешний Внутренний
Количество зубьев*
DP/модуль*Модуль в миллиметрах, DP в 1/дюйм
Угол давления*Обычные значения: 20, 14,5, 25
Количество знаков после запятой 4876543210
Коэффициент смещения производственного профиля по умолчанию равен 0. Положительные значения приводят к более толстым зубьям, как если бы ваш режущий инструмент не прорезал на полную глубину, а отрицательные значения приводят к более тонким зубьям. Ищете 3D-печать, фрезерование или лазерную резку цилиндрического зубчатого колеса? Используйте наш бесплатный генератор зубчатых колес для создания внутренних или внешних цилиндрических зубчатых колес и наборов реечных шестерен — все это с помощью готовых к загрузке файлов .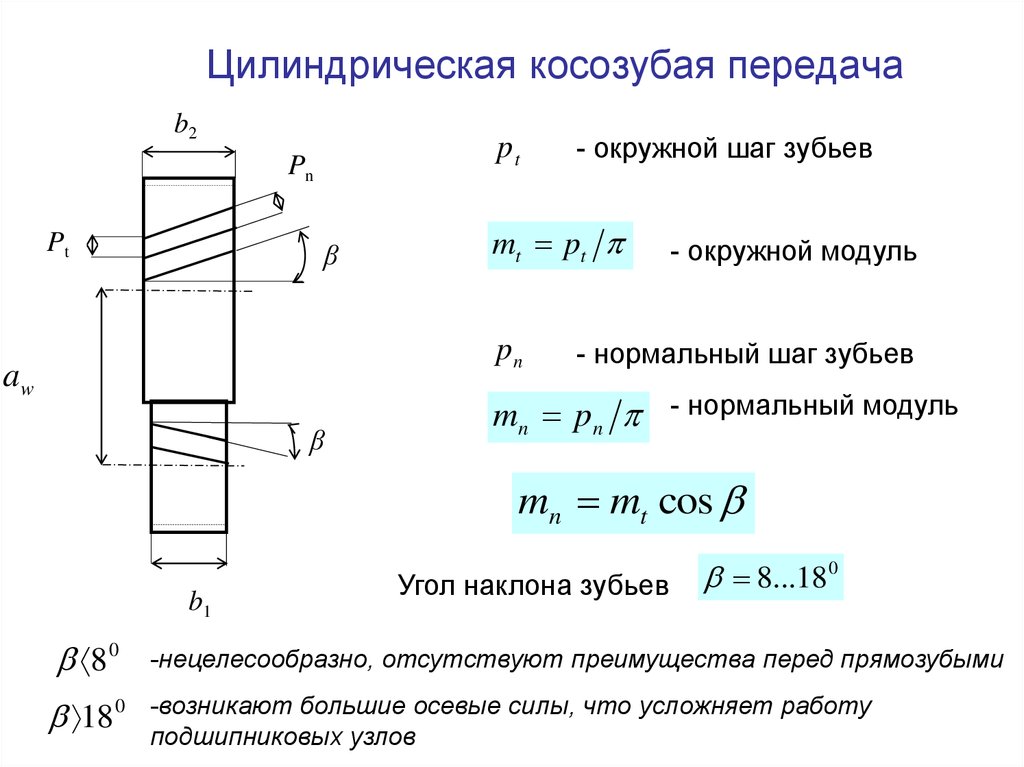
DXF или .SVG.
Найдите, сравните и купите зубчатое колесо
Режущие инструменты, необходимые для фрезерования зубчатых колес
Эвольвентные фрезы
Калькулятор заготовок шестеренМы создали этот калькулятор прямозубых зубчатых колес, чтобы убедиться, что у нас есть правильные размеры для изготовления заготовок зубчатых колес в нашем цехе. Правильная заготовка шестерни является важной частью процесса изготовления шестерни и помогает гарантировать, что ваша шестерня находится в пределах допуска
Калькулятор внешнего диаметра шестерни Вычисление наружного диаметра или наружного диаметра вашей шестерни важно для того, чтобы убедиться, что вы правильно изготовили шестерню и что она будет правильно зацепляться со своей парой. Многие процессы изготовления зубчатых колес (включая зубофрезерование, фрезерование и формообразование) зависят от точного касания детали оператором.
Во время касания оператор медленно вводит режущий инструмент в заготовку зубчатого колеса до тех пор, пока он не начнет касаться, затем набирается полная глубина относительно приземления. Если заготовка зубчатого колеса имеет неправильный размер, касание произойдет в неправильном положении, и рез будет либо слишком мелким, либо слишком глубоким
Калькулятор диаметра шага шестерниРассчитать диаметр шага шестерни можно путем деления числа зубьев шестерни на ее диаметральный шаг. Для имперских шестерен диаметральный шаг обычно представляет собой целое число в диапазоне от 3 (для очень больших шестерен) до 64 (для очень маленьких шестерен).
Как рассчитать делительный диаметр зубчатого колеса? Короче говоря, разделите количество зубьев шестерни на диаметральный шаг шестерни, чтобы вычислить ее делительный диаметр. Единицами диаметрального шага являются 1/дюйм, поэтому единицы диаметра шага будут в дюймах.
Для быстрого приближения диаметр делителя находится примерно в центре зуба шестерни. Зубчатые колеса имеют приблизительно одинаковую длину от делительного диаметра до наружного диаметра (дополнение) и от делительного диаметра до диаметра основания (дедендум).
Калькулятор модуля редуктораРасчетный модуль шестерни можно уменьшить, разделив диаметр шага шестерни на количество зубьев на шестерне. Модуль зубчатого колеса почти обратно пропорционален его диаметральному шагу, однако модуль выражается в миллиметрах, а диаметральный шаг составляет 1/дюйм.
Как рассчитать модуль зубчатого колеса?Разделите средний диаметр (в миллиметрах!) шестерни на количество ее зубьев, чтобы получить модуль шестерни. В качестве альтернативы, 25,4, деленное на диаметральный шаг шестерни, также даст вам ее модуль.
Как проверить размеры шестерни? После нарезания зубьев шестерни необходимо измерить и осмотреть шестерни, чтобы убедиться, что они идеально подходят для своего применения.
Используя Калькулятор измерения по штифтам, вы можете убедиться, что ваше снаряжение имеет правильный размер с помощью штифтов или проводов.
Калькулятор размера шестерни
› Параметры входной шестерни
› Размеры выходной шестерни
› Готов сделать заготовку для шестерни!
Используйте стрелки влево/вправо для перемещения по слайд-шоу или проведите пальцем влево/вправо, если вы используете мобильное устройство
Формула расчета стандартного модуля зубчатого колеса и числа зубьев – новости
Модуль — это число, используемое для измерения количества размеров зубьев, что является важным фактором для определения размера зуба и основных параметров изготовления зубчатого колеса. Модуль, делительная окружность, угол давления, число зубьев, шаг зубьев и т. д. являются важными параметрами, из которых состоят зубчатые колеса.
1. Стандарт серии Modulus адаптирован в соответствии с требованиями проектирования, производства и проверки.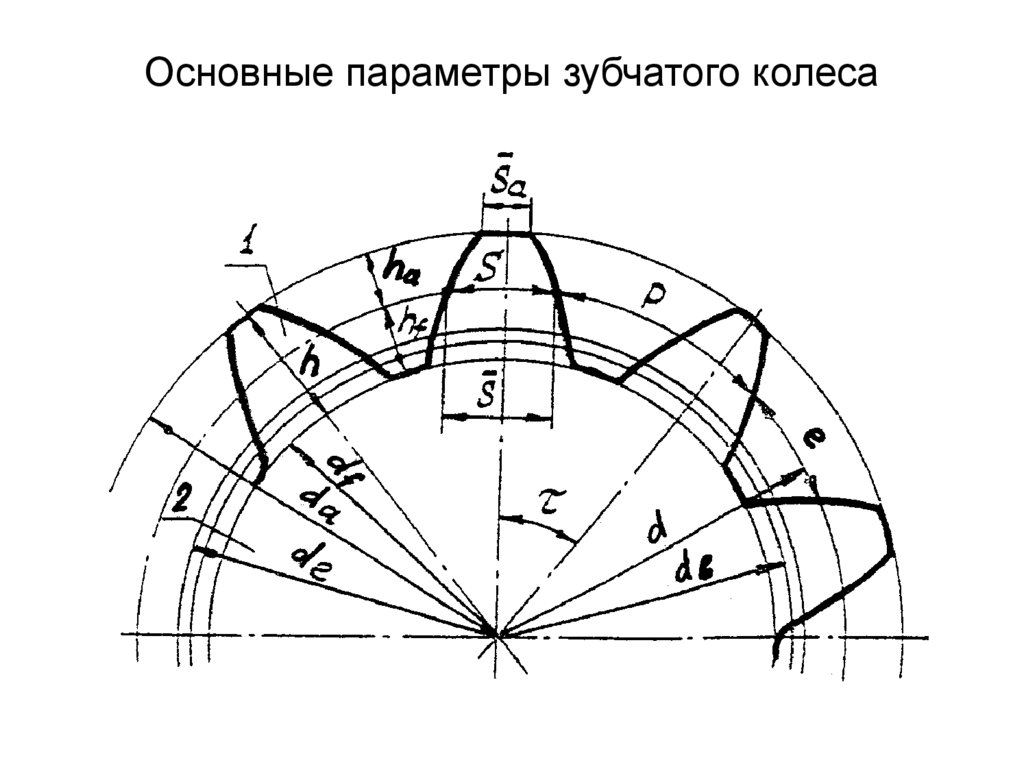
Модуль цилиндрического зубчатого колеса, косозубого зубчатого колеса и конического зубчатого колеса может относиться к стандартной таблице серии модулей.
2. Во многих нестандартных передачах используется нестандартный модуль.
3. Для шестерен с непрямыми зубьями существует разница между нормальным модулем MN, торцевым модулем MS и осевым модулем MX.
4. Для конического зубчатого колеса модуль можно разделить на большой модуль ME, средний модуль MM и малый модуль M1.
Как рассчитать модуль зубчатого колеса? Какова формула?
1. Формула расчета модуля косозубого колеса:
A. Расчет делительной окружности DO=(число зубьев Z * модуль M) / тригонометрические функции COSB
B. Расчет диаметра DK =((число зубьев z * модуль M) / тригонометрические функции COSB) + (модуль * 2)
C. Расчет периметра Z = диаметр делительной окружности DO * PI π
Примечания: расстояние до центра установки (от центральной точки до низа стойки) алгоритм: расстояние до центра установки HB = (диаметр делительной окружности DO/2) + окклюзионная средняя линия
2.
Формула расчета модуля цилиндрического зубчатого колеса
A. Диаметр делительной окружности = номер зуба Z * модуль M
B. Расчет диаметра DK = (число зубьев Z * модуль M) + (модуль M*2)
C. Расчет периметра Z = диаметр делительной окружности DO * PI * π
Примечания: расстояние до центра установки (от центральной точки до дна стойки) алгоритм: расстояние до центра установки HB = (диаметр делительной окружности DO/2) + окклюзионная срединная линия
Если число зубьев шестерни точно установлено, чем больше модуль, тем больше радиальный размер колеса; чем больше модуль, тем выше и толще зубья; Если модуль определен, то чем больше число зубцов, тем более постепенная эвольвента. Чем больше толщина окружности придатка и окружности выемки. Если число зубьев точно известно, то чем больше модуль упругости, чем больше зубья, тем выше способность сопротивляться разрушению. Конечно, чем больше заготовка зуба, тем больше размер пространства.
Итак, выбирать шестерни нужно по разным параметрам.
3. Формула расчета диаметра шестерни
Диаметр делительной окружности = (число зубьев + 2) * модуль
Диаметр делительной окружности = число зубьев * модуль
Диаметр делительной окружности = диаметр вспомогательной окружности – (4,5 * модуль)
Например, M4 32 зуба 34 * 3,5
Диаметр вспомогательной окружности = (32 + 2) * 4 = 136 мм
Диаметр делительной окружности = 32 * 4 = 128 мм
Диаметр делительной окружности = 136 – 4,5 * 4 = 118 мм
7 мм 12 Расстояние между центрами зубьев D = (диаметр делительной окружности 1 + диаметр делительной окружности 2 ) / 2 = (12 + 2) * 7 = 98 мм. Этот метод подходит для всех модульных передач.
4. Модуль выражает размер зуба шестерни
Модуль шестерни = диаметр делительной окружности / количество зубьев = внешний диаметр шестерни / (число зубьев -2).
Китайский стандартный модуль зубчатого колеса
Модуль стандартной серии (предварительный выбор): 1, 1,25, 1,5, 2, 2,5, 3, 4, 5, 6, 8, 10, 12, 14, 16, 20, 25, 32 、40、50.