Формула объема и массы: Расчет массы и объема тела по его плотности: объяснение и примеры

alexxlab | 25.06.2018 | 0 | Разное

Содержание

Расчет массы и объема тела

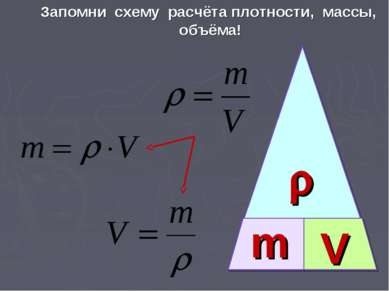
Для того чтобы определить плотность вещества, надо массу тела разделить на его объем:

(10.1)

Массу тела можно определить с помощью весов. А как найти объем тела?

Если тело имеет форму прямоугольного параллелепипеда (рис. 24), то его объем находится по формуле

V = аbс.

Если же у него какая-то другая форма, то его объем можно найти методом, который был открыт древнегреческим ученым Архимедом в III в. до н. э.

Архимед родился в Сиракузах на острове Сицилия. Его отец, астроном Фидий, был родственником Гиерона, ставшего в 270 г. до н. э. царем города, в котором они жили.

До нас дошли не все сочинения Архимеда. О многих его открытиях стало известно благодаря более поздним авторам, в сохранившихся трудах которых описываются его изобретения. Так, например, римский архитектор Витрувий (I в. до н. э.) в одном из своих сочинений рассказал следующую историю:
«Что касается Архимеда, то изо всех его многочисленных и разнообразных открытий то открытие, о котором я расскажу, представляется мне сделанным с безграничным остроумием.

Во время своего царствования в Сиракузах Гиерон после благополучного окончания всех своих мероприятий дал обет пожертвовать в какой-то храм золотую корону бессмертным богам. Он условился с мастером о большой цене за работу и дал ему нужное по весу количество золота. В назначенный день мастер принес свою работу царю, который нашел ее отлично исполненной; после взвешивания вес короны оказался соответствующим выданному весу золота.

После этого был сделан донос, что из короны была взята часть золота и вместо него примешано такое же количество серебра. Гиерон разгневался на то, что его провели, и, не находя способа уличить это воровство, попросил Архимеда хорошенько подумать об этом. Тот, погруженный в думы по этому вопросу, как-то случайно пришел в баню и там, опустившись в ванну, заметил, что из нее вытекает такое количество воды, каков объем его тела, погруженного в ванну. Выяснив себе ценность этого факта, он, не долго думая, выскочил с радостью из ванны, пошел домой голым и громким голосом сообщал всем, что он нашел то, что искал.

Он бежал и кричал одно и то же по-гречески: «Эврика, эврика! (Нашел, нашел!)».

Затем, пишет Витрувий, Архимед взял сосуд, доверху наполненный водой, и опустил в него золотой слиток, равный по весу короне. Измерив объем вытесненной воды, он снова наполнил сосуд водой и опустил в него корону. Объем воды, вытесненной короной, оказался больше объема воды, вытесненной золотым слитком. Больший объем короны означал, что в ней присутствует менее плотное, чем золото, вещество. Поэтому опыт, проделанный Архимедом, показал, что часть золота была похищена.

Итак, для определения объема тела, имеющего неправильную форму, достаточно измерить объем воды, вытесняемой данным телом. Располагая измерительным цилиндром (мензуркой), это сделать несложно.

В тех случаях, когда известны масса и плотность тела, его объем можно найти по формуле, вытекающей из формулы (10.1):

(10.2)

Отсюда видно, что для определения объема тела надо массу этого тела разделить на его плотность.

Если, наоборот, объем тела известен, то, зная, из какого вещества оно состоит, можно найти его массу:

m = ρV. (10.3)

Чтобы определить массу тела, надо плотность тела умножить на его объем.

1. Какие способы определения объема вы знаете? 2. Что вам известно об Архимеде? 3. Как можно найти массу тела по его плотности и объему?
Экспериментальное задание. Возьмите кусок мыла, имеющий форму прямоугольного параллелепипеда, на котором обозначена его масса. Проделав необходимые измерения, определите плотность мыла.

Формула массы через объем и плотность

Формула для вычисления массы через объем и плотность

Это количество можно определять по-разному. Если речь идет о числе частиц, то говорят о плотности частиц. Эту величину обозначают буквой n. В СИ она измеряется в м^-3. Если имеется ввиду масса вещества, то вводят плотность массы. Её обозначают через . В Си измеряется в кг/м³. Между и n существует связь. Так, если тело состоит из частиц одного сорта, то

= m×n,

где m – масса одной частицы.

Плотность массы можно вычислить по формуле:

= m / V.

Данное выражение можно преобразовать так, чтобы получилась формула массы через объем и плотность:

m = ×V.

Таблица 1. Плотности некоторых веществ.

Вещество	Плотность, кг/м³	Вещество	Плотность, кг/м³
Вещества атомного ядра	10¹⁷	Вода	1,00×10³
Сжатые газы в центре самых плотных звезд	10⁸	Жидкий водород	0,07×10³
Золото	1,93×10⁴	Воздух у поверхности Земли	1,2
Ртуть	1,36×10⁴	Воздух на высоте 20 км	9×10^-2
Сжатое железо в ядре Земли	1,2×10⁴	Наивысший искусственный вакуум	10^-13
Сталь	(7,6 – 7,8)×10³	Газы межзвездного пространства	10^-20
Алмаз	3,53×10³	Газы межгалактического пространства	10^-26
Алюминий	2,7 ×10³
Человеческое тело	1,07 ×10³

Независимо от степени сжатия плотности жидких и твердых тел лежат в весьма узком интервале значений (табл.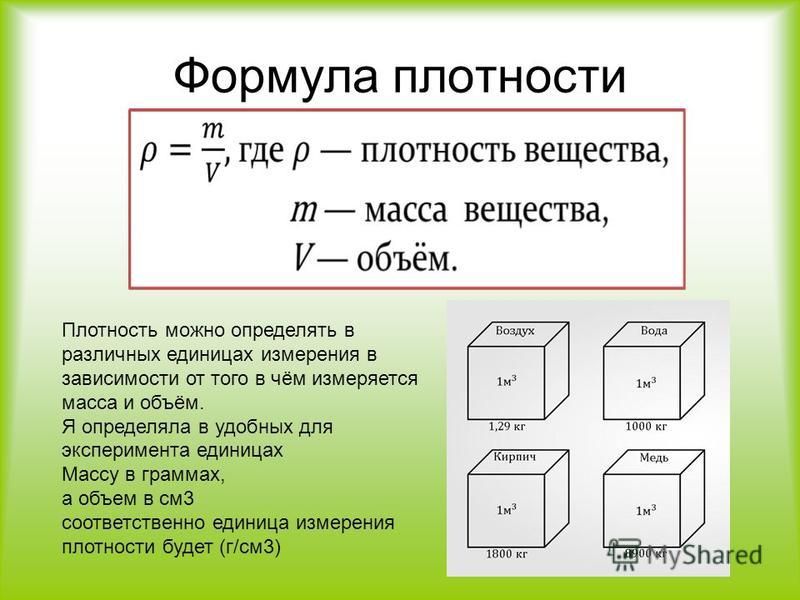 1). Плотности же газов варьируются в весьма широких пределах. Причина заключается в том, что как в твердых телах, так и в жидкостях частицы вплотную примыкают друг к другу. В этих средах расстояние между соседними частицами составляет величину порядка 1 А и сравнимо с размерами атомов и молекул. По этой причине твердые и жидкие тела обладают очень малой сжимаемостью, чем обусловлено малое различие в их плотности. В газах положение иное. Среднее расстояние между частицами значительно превышает их размеры. Например, для воздуха у поверхности Земли оно составляет 10² А. Вследствие этого газы обладают большой сжимаемостью, а их плотность может изменяться в очень широких пределах.

Примеры решения задач

Понравился сайт? Расскажи друзьям!

Формулы для вычисления массы тел различной формы

05.2013 // Владимир Трунов

Это странное название статьи объясняется только тем, что детали одной и той же формы могут быть как сплошными, так и полыми (т.е. следующая статья будет называться «Масса полой детали»).

Тут самое время вспомнить, что масса тела — это его объем , умноженный на плотность его материала (

см. таблицы плотностей):

Объем сплошной детали — это… ее объем и больше ничего.

Примечание. В приведенных ниже формулах все размеры измеряются в миллиметрах, а плотность — в граммах на кубический сантиметр.
Буквой обозначено отношение длины окружности к ее диаметру, составляющее примерно 3,14.

Рассмотрим несколько простых форм (более сложные, как вы помните, можно составить путем сложения или вычитания простых).

1. Масса параллелепипеда (бруска)

Объем параллелепипеда: , где — длина, — ширина, — высота.
Тогда масса:

2. Масса цилиндра

Объем цилиндра: , где — диаметр основания, — высота цилиндра.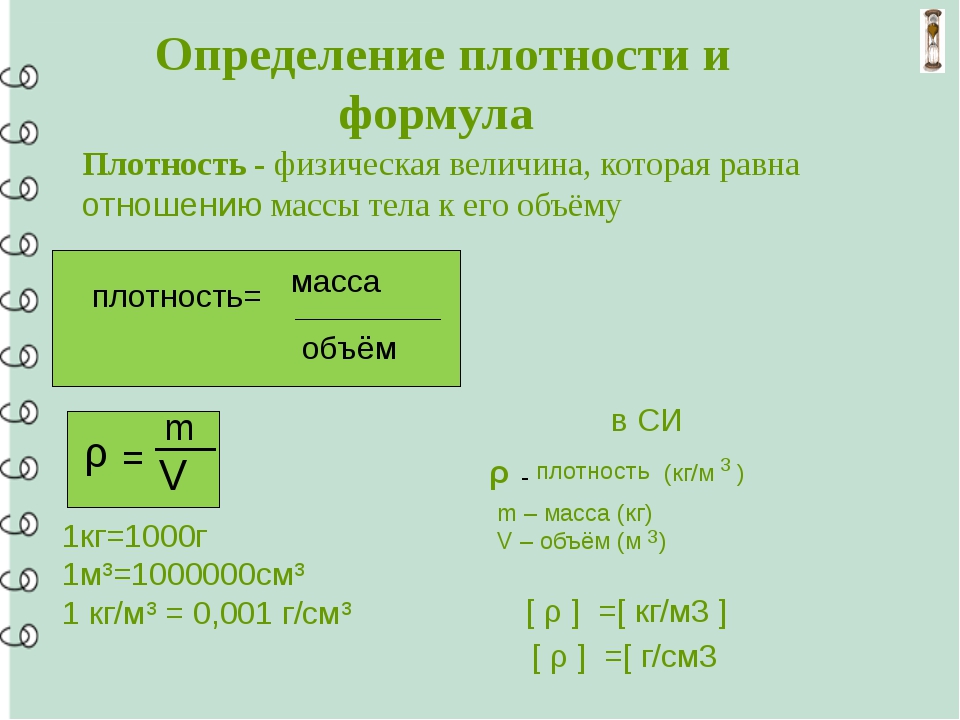
Тогда масса:

3. Масса шара

Объем шара: , где — диаметр шара.
Тогда масса:

4. Масса сегмента шара

Объем сегмента шара: , где — диаметр основания сегмента, — высота сегмента.

Тогда масса:

5. Масса конуса

Объем любого конуса: , где — площадь основания, — высота конуса.
Для круглого конуса: , где — диаметр основания, — высота конуса.
Масса круглого конуса:

6. Масса усеченного конуса

Поскольку невозможно объять необъятное, рассмотрим только круглый усеченный конус. Его объем — это разность объемов двух вложенных конусов: с основаниями и : , где , . После никому не интересных алгебраических преобразований получаем:
, где — диаметр большего основания, — диаметр меньшего основания, — высота усеченного конуса.
Отсюда масса:

7. Масса пирамиды

Объем любой пирамиды равен одной трети произведения площади ее основания на высоту (то же самое, что и для конусов (часто мы не замечаем, насколько мироздание к нам благосклонно)): , где — площадь основания, — высота пирамиды.
Для пирамиды с прямоугольным основанием: , где — ширина, — длина, — высота пирамиды.

Тогда масса пирамиды:

8. Масса усеченной пирамиды

Рассмотрим усеченную пирамиду с прямоугольным основанием. Ее объем — это разность объемов двух подобных пирамид с основаниями и : , где , .
Исчеркав половину тетрадного листа, получаем: , где , — ширина и длина большего основания, , — ширина и длина меньшего основания, — высота пирамиды.
И, оставив в покое остальную половину листа, исходя из одних соображений симметрии, мы можем написать еще одну формулу, которая отличается от предыдущей только заменой W на L и наоборот. В чем разница между длиной и шириной? Только в том, что мы их так назвали. Назовем наоборот и получим: .
Тогда масса усеченной прямоугольной пирамиды:

или

Для пирамиды с квадратным основанием (, ) формула выглядит проще:

Расчеты массы (объема, количества вещества) продукта реакции, если одно из веществ дано в виде раствора с определенной массовой долей растворенного вещества

Что такое расчеты массы (объема, количества вещества) продукта реакции, если одно из веществ дано в виде раствора с определенной массовой долей растворенного вещества

Что такое расчеты массы (объема, количества вещества) продукта реакции? Какой алгоритм поиска массы растворенного вещества, если одно из веществ дано в виде раствора с определенной массовой долей растворенного вещества.

Для расчета массы (объема, количества вещества) продукта реакции, если данные по одному из веществ представлены в виде раствора с определенной массовой долей этого растворенного вещества, следует воспользоваться нижеследующим алгоритмом:

1) Прежде всего следует найти массу растворенного вещества. Возможны две ситуации:

* В условии даны масса раствора и массовая доля растворенного вещества (концентрация). В этом случае масса растворенного вещества рассчитывается по формуле:

формула расчета массы растворенного вещества, зная массу раствора и его концентрацию

* В условии даны объем раствора вещества, плотность этого раствора и массовая доля растворенного вещества в этом растворе. В таком случае следует воспользоваться формулой для расчета массы раствора:

m(р-ра) = ρ(р-ра) ∙V(р-ра)

После чего следует рассчитать массу растворенного вещества по формуле 1.

2) Рассчитать количество вещества (моль) участника реакции, масса которого стала известна из расчетов выше. Для этого воспользоваться формулой:

n(в-ва) = m(в-ва)/M(в-ва), где М — молярная масса вещества

3) Записать уравнение реакции и убедиться в правильности расставленных коэффициентов.

4) Рассчитать количество моль интересующего участника реакции исходя из известного количества другого участника реакции, зная, что количества веществ любых двух участников реакции A и B относятся друг к другу как коэффициенты перед этими же веществами в уравнении реакции, то есть:

n(A)/n(B) = k(A)/k(B)

Если в условии требовалось рассчитать количество вещества, то действия на этом заканчиваются. Если же требуется найти его массу или объем, следует переходить к следующему пункту.

5) Зная количество вещества, определенное в п.4, мы можем рассчитать его массу по формуле:

Расчет количества продукта по данным раствора другого вещества

Также, если вещество является газообразным и речь идет о нормальных условиях (н.у.), его объем может быть рассчитан по формуле:

V(газа) = Vm ∙ n(газа) = n(газа) ∙ 22,4 л/моль

Рассмотрим пару примеров расчетных задач по этой теме.

Пример 1

Рассчитайте массу осадка, который образуется при добавлении к 147 г 20%-ного раствора серной кислоты избытка раствора нитрата бария.

Решение:

1) Рассчитаем массу чистой серной кислоты:

m(h3SO4) = w(h3SO4) ∙ m(р-ра h3SO4)/100% = 147 г ∙ 20% /100% = 29,4 г

2) Рассчитаем количество вещества (моль) серной кислоты:

n(h3SO4) = m(h3SO4) / M(h3SO4) = 29,4 г/98 г/моль = 0,3 моль.

3) Запишем уравнение взаимодействия серной кислоты с нитратом бария:

h3SO4 + Ba(NO3)2 = BaSO4↓ + 2HNO3

4) В результате расчетов стало известно количество вещества серной кислоты. Осадок представляет собой сульфат бария. Зная, что:

n(BaSO4)/n(h3SO4) = k(BaSO4)/k(h3SO4), где n — количество вещества, а k — коэффициент в уравнении реакции,

можем записать:

n(BaSO4) = n(h3SO4) ∙ k(h3SO4)/k(BaSO4) = 0,3 моль ∙ 1/1 = 0,3 моль

5) Тогда масса осадка, т.е. сульфата бария, может быть рассчитана следующим образом:

m(BaSO4) = M(BaSO4) ∙ n(BaSO4) = 233 г/моль ∙ 0,3 моль = 69,9 г

Пример 2

Какой объем газа (н.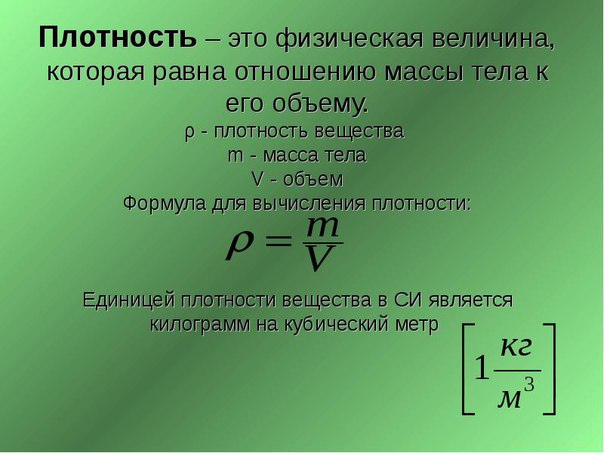 у.) выделится при растворении необходимого количества сульфида железа (II) в 20%-ном растворе соляной кислоты с плотностью 1,1 г/мл и объемом 83 мл.

Решение:

1) Рассчитаем массу раствора соляной кислоты:

m(р-ра HCl) = V(р-ра HCl) ∙ ρ(р-ра HCl) = 83 мл ∙ 1,1 г/мл = 91,3 г

Далее рассчитаем массу чистого хлороводорода, входящего в состав кислоты:

m(HCl) = m(р-ра HCl) ∙ w(HCl)/100% = 91,3 г ∙ 20%/100% = 18,26 г

2) Рассчитаем количество вещества хлороводорода:

n(HCl) = m(HCl)/M(HCl) = 18,26 г/36,5 г/моль = 0,5 моль;

3) Запишем уравнение реакции сульфида железа (II) с соляной кислотой:

FeS + 2HCl = FeCl2 + h3S↑

4) Исходя из уравнения реакции следует, что количество прореагировавшей соляной кислоты с количеством выделившегося сероводорода связано соотношением:

n(HCl)/n(h3S) = 2/1, где 2 и 1 — коэффициенты перед HCl и и h3S соответственно

Следовательно:

n(h3S) = n(HCl)/2 = 0,5/2 = 0,25 моль

5) Объем любого газа, находящегося при нормальных условиях, можно рассчитать по формуле V(газа) = Vm ∙ n(газа), тогда:

V(h3S) = Vm ∙ n(h3S) = 22,4 л/моль ∙ 0,25 моль = 5,6 л

ФИЗИКА: Задачи на плотность, массу и объем

Задачи на плотность, массу и объем с решением

Формулы, используемые в задачах по физике на плотность, массу и объем.

Название величины	Обозначение	Единицы измерения	Формула
Масса	m	кг	m = p * V
Объем	V	м³	V = m / p
Плотность	p	кг/м³	p = m / V

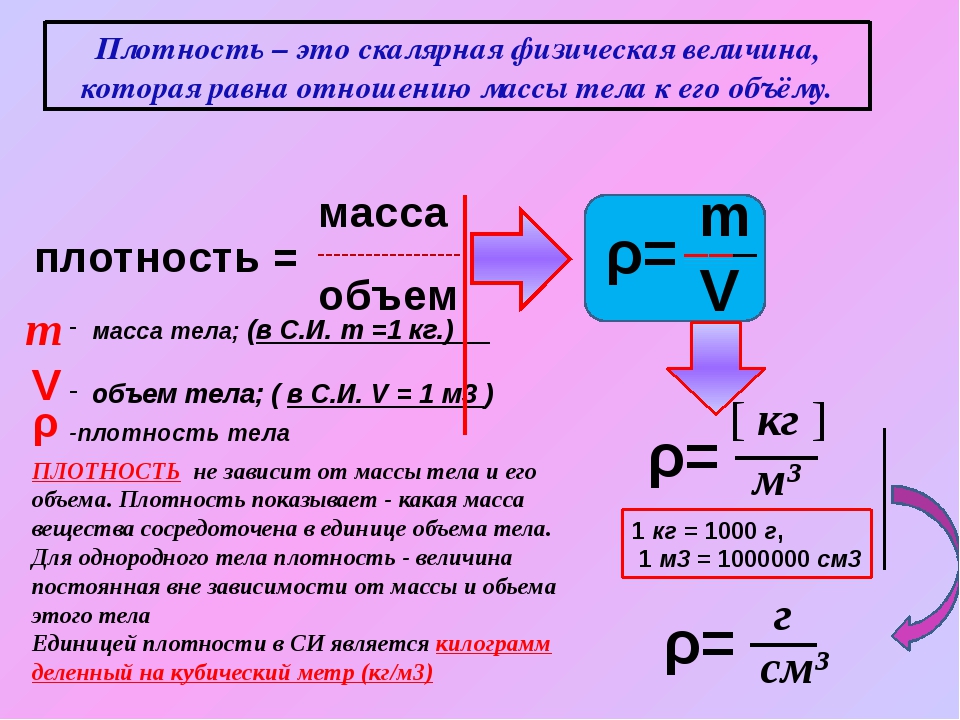
Плотность равна отношению массы тела к его объёму. Плотность обозначают греческой буквой ρ (ро).

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1. Найдите плотность молока, если 206 г молока занимают объем 200 см³?

Задача № 2. Определите объем кирпича, если его масса 5 кг?

Задача № 3. Определите массу стальной детали объёмом 120 см³

Задача № 4. Размеры двух прямоугольных плиток одинаковы. Какая из них имеет большую массу, если одна плитка чугунная, другая — стальная?

Решение: Из таблицы плотности веществ (см. в конце страницы) определим, что плотность чугуна (ρ₂ = 7000 кг/м³) меньше плотности стали (ρ₁ = 7800 кг/м³). Следовательно, в единице объема чугуна содержится меньшая масса, чем в единице объема стали, так как чем меньше плотность вещества, тем меньше его масса, если объемы тел одинаковы.

Задача № 5. Определите плотность мела, если масса его куска объемом 20 см³ равна 48 г. Выразите эту плотность в кг/м³ и в г/см³.

Ответ: Плотность мела 2,4 г/см³, или 2400 кг/м³.

Задача № 6. Какова масса дубовой балки длиной 5 м и площадью поперечного сечения 0,04 м² ?

ОТВЕТ: 160 кг.

РЕШЕНИЕ. Из формулы для плотности получаем m = p • V. С учетом того, что объем балки V = S • l , получаем: m = p • S • l.

Вычисляем: m = 800 кг/м³ • 0,04 м² • 5 м = 160 кг.

Задача № 7. Брусок, масса которого 21,6 г, имеет размеры 4 х 2,5 х 0,8 см. Определить, из какого вещества он сделан.

ОТВЕТ: Брусок сделан из алюминия.

Задача № 8 (повышенной сложности). Полый медный куб с длиной ребра а = 6 см имеет массу m = 810 г. Какова толщина стенок куба?

ОТВЕТ: 5 мм.

РЕШЕНИЕ: Объем кубика V_K= а³ = 216 см³. Объем стенок V_С можно вычислить, зная массу кубика m_К и плотность меди р: V_С = m_К / р = 91 см³. Следовательно, объем полости V_П = V_K — V_C = 125 см³. Поскольку 125 см³ = (5 см)³, полость является кубом с длиной ребра b = 5 см. Отсюда следует, что толщина стенок куба равна (а — b)/2 = (6 – 5)/2 = 0,5 см.

Задача № 9 (олимпиадный уровень). Масса пробирки с водой составляет 50 г. Масса этой же пробирки, заполненной водой, но с куском металла в ней массой 12 г составляет 60,5 г. Определите плотность металла, помещенного в пробирку.

ОТВЕТ: 8000 кг/м³

РЕШЕНИЕ: Если бы часть воды из пробирки не вылилась, то в этом случае общая масса пробирки, воды и куска металла в ней была бы равна 50 г + 12 г = 62 г. По условию задачи масса воды в пробирке с куском металла в ней равна 60,5 г. Следовательно, масса воды, вытесненной металлом, равна 1,5 г, т. е. составляет 1/8 массы куска металла. Таким образом, плотность металла в 8 раз больше плотности воды.

Задачи на плотность, массу и объем с решением. Таблица плотности веществ.

Справочный материал для «Задачи на плотность, массу и объем«

Как, зная только массу, рассчитать плотность?

Если объем тела (вещества) неизвестен или не задан явно в условиях задачи, то попытайтесь его измерить, вычислить или узнать, используя косвенные (дополнительные) данные.
Если вещество сыпучее или жидкое, то оно, как правило, находится в емкости, которая обычно имеет стандартный объем. Так, например, объем бочки обычно равен 200 литров, объем ведра – 10 литров, объем стакана – 200 миллилитров (0,2 литра), объем столовой ложки – 20 мл, объем чайной – 5 мл. Об объеме трехлитровых и литровых банок нетрудно догадаться из их названия.
Если жидкость занимает не всю емкость или емкость нестандартная, то перелейте ее в другую тару, объем которой известен.Если подходящей емкости нет, перелейте жидкость с помощью мерной кружки (банки, бутылки). В процессе вычерпывания жидкости просто посчитайте количество таких кружек и умножьте на объем мерной тары.
Если тело имеет простую форму, то вычислите его объем, используя соответствующие геометрические формулы. Так, например, если тело имеет форму прямоугольного параллелепипеда, то его объем будет равен произведению длин его ребер. То есть: Vпар. = a • b • c, где Vпар. – объем прямоугольного параллелепипеда, а a, b, c — значения его длины, ширины и высоты (толщины), соответственно.
Если тело имеет сложную геометрическую форму, то попробуйте (условно!) разбить его на несколько простых частей, найти объем каждой из них отдельно и затем сложить полученные значения.
Если тело невозможно разделить на более простые фигуры (например, статуэтку), то воспользуйтесь методикой Архимеда. Опустите тело в воду и измерьте объем вытесненной жидкости. Если тело не тонет, то «утопите» его с помощью тонкой палочки (проволоки).
Если объем вытесненной телом воды посчитать проблематично, то взвесьте вылившуюся воду, или найдите разность между начальной и оставшейся массой воды. При этом, количество килограммов воды будет равняться количеству литров, количество граммов – количеству миллилитров, а количество тонн – количеству кубометров.

Конспект урока «Задачи на плотность, массу и объем с решением».

Следующая тема: «Задачи на силу тяжести и вес тела».

Объем, масса, плотность, удельный объем. Приведение к нормальным и стандартным условиям и пересчет

Приведение к нормальным и стандартным условиям

Единицей измерения объема газа является кубический метр (м³). Измеренный объем приводится к нормальным физическим условиям.

Нормальные физические условия: давление 101 325 Па, температура 273,16 К (0 °С).

Стандартные условия: давление 101 325 Па, температура 293,16 К (+20 °С).

В настоящее время эти обозначения выходят из употребления. Поэтому в дальнейшем следует указывать те условия, к которым относятся объемы и другие параметры газа. Если эти условия не указываются, то это значит, что параметры газа даны при 0 °С (273,16 °К) и 760 мм рт. ст. (1,033 кгс/см²). Иногда объем газа (особенно в иностранной литературе и нормах) при пользовании системой СИ приводится к 288,16 °К (+15 °С) и давлению 1 бар (105 Па).

Если известен объем газа при одних условиях, то пересчитать его в объемы при других условиях можно с помощью коэффициентов, приведенных следующей таблице.

Коэффициенты для пересчета объемов газа из одних условий в другие

Температура и даление газа	0 °С и 760 мм рт. ст.	15 °С и 760 мм рт. ст.	20 °С и 760 мм рт. ст.	15 °С (288,16 °К) и 1 бар
0 °С и 760 мм рт. ст. (норм. условия)	1	1,055	1,073	1,069
15 °С и 760 мм рт. ст. (в зар. литературе)	0,948	1	1,019	1,013
20 °С и 760 мм рт. ст. (ст. условия)	0,932	0,983	1	0,966
15 °С (288,16 °К) и 1 бар (СИ)	0,936	0,987	1,003	1

Для приведения объемов газа к 0 °С (273,16 °К) и 760 мм рт. ст. (1,033 кгс/см²), а также к 20 °С (293,16 °К) и 760 мм рт. ст. (1,033 кгс/см²) могут быть применены следующие формулы:

где V_{0 °С и 760 мм рт. ст.} — объем газа при 0 °С и 760 мм рт. ст., м³;
V_{20° С и 760 мм рт. ст.} — объем газа при 20 °С и 760 мм рт. ст., м³;
V_P — объем газа в рабочих условиях, м³;
р — абсолютное давление газа в рабочих условиях, мм рт. ст.;
Т — абсолютная температура газа в рабочих условиях, °К.

Пересчет объемов газа, приведенных к 0 °С и 760 мм рт. ст., а также к 20 °С и 760 мм рт. ст., в объемы при других (рабочих) условиях можно производить по формулам:

Любой газ способен расширяться. Следовательно, знание объема, который занимает газ, недостаточно для определения его массы, так как в любом объеме, целиком заполненном газом, его масса может быть различной.

Масса — это мера вещества какого-либо тела (жидкости, газа) в состоянии покоя; скалярная величина, характеризующая инерционные и гравитационные свойства тела. Единицы массы в СИ — килограмм (кг).

Плотность, или масса единицы объема, обозначаемая буквой p, — это отношение массы тела m, кг, к его объему, V, м³:

p = m/V

или с учетом химической формулы газа:

p = M/V_М = M/22,4,

где M — молекулярная масса,
V_М — молярный объем.

Единица плотности в СИ — килограмм на кубический метр (кг/м³).

Зная состав газовой смеси и плотность ее компонентов, определяем по правилу смешения среднюю плотность смеси:

p_см = (p₁V₁ + p₂V₂ + … + p_nV_n)/100,

где p₁, p₂, …, p_n — плотность компонентов газового топлива, кг/м³;
V₁, V₂, …, V_n — содержание компонента, об. %.

Величину, обратную плотности, называют удельным, или массовым, объемом (ν) и измеряют в кубических метрах на килограмм (м³/кг).

Как правило, на практике, чтобы показать, на сколько 1 м³ газа легче или тяжелее 1 м³ воздуха, используют понятие относительная плотность d, которая представляет собой отношение плотности газа к плотности воздуха:

d = p/1,293

d = M/(22,4×1,293).

Конспект урока по теме «Плотность вещества. Косвенное измерение плотности вещества». 7 класс

Тема урока: «Плотность вещества. Косвенное измерение плотности вещества»

Цели урока.

Формирование

– представления о плотности вещества.

– знания формулы для расчета плотности вещества.

– умения анализировать связь между величинами, входящими в формулу.

– умения решать задачи с применением новых формул.

Развитие

– умения анализировать ситуацию,

– умения сравнивать результаты исследований,

– умения обобщать полученные данные,

– внимания, творческих способностей,

– умения работать в группах.

Воспитывать отношение к физике как элементу общечеловеческой культуры.

Оборудование.

Доска с мелом.
Таблички с набором магнитов для фиксирования на доске.
Презентация с заданиями на закрепление.
Набор для лабораторных исследований: весы с разновесами, три тела раной массы и одинакового объема.

Ход урока

Мотивация к учебной деятельности

«… Мир слишком удивителен, чтобы сидеть сложа руки». Ричард Бренсон, английский предприниматель и инвестор.

Учитель: Как вы понимаете эту фразу? (ответы учеников)

Эти слова известного английского предпринимателя Р.Бренсона будут эпиграфом нашего урока. Сегодня вам предстоит, используя накопленный багаж знаний, открыть для себя новые знания. Что для этого необходимо?

Ученики: Надо попробовать сделать что-то новое, и если нам не хватает нашего багажа знаний, попробовать найти пути решения получения новой информации, новых знаний, и пойти по выбранному пути.

Актуализация знаний.

Учитель: С чего начинается изучение нового материала на любом уроке?

Ученики: С повторения того, что уже знаем.

Учитель: Вспомните, что вы узнали на предыдущих уроках. Что изучает физика?

Ученики: Физика изучает наиболее общие закономерности явлений природы, свойства и строение вещества и свойства физического поля.

Учитель: Каковы основные методы исследования природы?

Ученики: Эксперимент и моделирование.

Учитель: Что представляют собой объекты исследования физики?

Ученики: Объектами исследования в физике являются явления природы, различные тела, вещество, физическое поле.

Учитель: Что такое физическая величина?

Ученики: Количественная характеристика физических явлений, свойств тел, физических полей.

Учитель: Приведите примеры физических величин.

Ученики: Масса тела, время, длина и т. д.

Учитель: Что означает «измерить величину»?

Ученики: Измерить какую-либо величину — это значит сравнить ее с однородной величиной, принятой за единицу.

Учитель: Назовите основные единицы Международной системы единиц (СИ). Приведите примеры производных единиц СИ (ученики называют).

Учитель: Назовите две важнейшие характеристики измерительного прибора.

Ученики: Цена деления и предел измерения.

Учитель: Чем отличается прямое измерение от косвенного?

Ученики: Измерение физических величин с помощью измерительных приборов — прямые измерения, косвенные измерения осуществляют при расчете физической величины по формуле через величины, значения которых измерены приборами, т. е. сделаны прямыми измерениями.

Учитель: Возьмите набор № 1 трех цилиндров. Что можно сказать о телах при их рассмотрении?

Ученики: Эти тела имеют одинаковую форму, одинаковый объем, на них написано 20 см3, но, кажется, разную массу.

Учитель: Пользуясь рычажными весами и разновесами, определите, какой из цилиндров обладает наименьшей массой, наибольшей массой. Пронумеруйте цилиндры с помощью стикера в порядке убывания их массы. (Учащиеся выполняют задание в парах).

Учитель: Я вижу, что задание выполнено. Что вы установили?

Ученики: Все три цилиндра имеют разную массу.

Учитель: Как вы думаете, почему?

Ученики: Потому что они изготовлены из разных веществ. Самый легкий цилиндр изготовлен из дерева, самый тяжелый — из одного металла, масса другого металлического цилиндра занимает промежуточное значение между массой деревянного и первого металлического цилиндра.

Учитель: Какой вывод из этого исследование мы можем сделать?

Ученики: Значит один и тот же объем разных веществ имеет разную массу.

Учитель: Действительно, это исследование показывает, что массы одинакового объема разных веществ различны. Все дело в веществе, из которого изготовлено тело. Оказывается, любое вещество характеризуется плотностью, которая показывает, чему равна масса единицы объема вещества. Как вы думаете, чему равна плотность веществ, из которых изготовлены цилиндры? Что это за вещества? Можете ли вы ответить на эти вопросы?

Ученики: Мы не знаем точно, что такое плотность и как ее найти. Не знаем, как определить вещество. Мы затрудняемся ответить на эти вопросы.

Объяснение нового материала (процесс получения новых знаний).

Учитель: Запишите тему нашего урока: «Плотность вещества. Косвенное измерение плотности вещества» (Ученики записывают тему в тетрадях, учитель на доске).

Учитель: Ребята, сформулируйте, пожалуйста, цели урока.

Ученики (с учетом корректировки учителя цели фиксируются на доске в виде табличек, прикрепленных магнитами к доске):

Учитель: Какими инструментами вы будете пользоваться для достижения этих целей?

Ученики: Нам, наверняка поможете вы, а также будем пользоваться учебником.

Учитель (объяснение учителя, запись основного материала на доске, запись опорного конспекта учениками в своих тетрадях): Как ранее было сказано,

(учитель прикрепляет табличку на доске).

В ваших исследованиях объемы цилиндров составляли 20 см3,единицей объема можно считать 1 м3 или 1 см3. Что удобнее найти в вашем случае?

Ученики: Массу 1 см3 вещества, из которого изготовлены цилиндры.

Учитель: Почему?

Ученики: Мы знаем массу цилиндров объемом 20 см3, можно найти и массу 1 см3 вещества цилиндра.

Учитель: Как же это сделать?

Ученики: Надо массу цилиндра разделить на его объем, в нашем случае на 20 см3

Учитель: Действительно, что бы найти плотность вещества надо массу тела из этого вещества разделить на объем тела (прикрепляет очередную табличку к доске):

Учитель: В физике пользуются формулами, где физические величины вместо слов записывают буквами. Вы уже знаете, как обозначается масса и объем. А как же обозначается плотность? Плотность обозначается греческой буквой ρ (читается «ро»).

Попробуйте записать формулу для расчета плотности. Кто-нибудь готов проговорить ее вслух?

Ученики: Формула такова: ρ=m/V.

Учитель: Действительно, формула для расчета плотности тела:

Учитель: Теперь вернемся к массе наших цилиндров. Чему она равна?

Ученики: 156 г, 54 г и 14 г соответственно.

Учитель: Ребята, единицей плотности вещества в СИ является. 1кг/м3. На практике используются другие единицы плотности: 1 г/см3 и 1т/м3. В вашем случае при нахождении плотности у нас получается, что она будет выражена в г/см3. Как же оформить решение трех задач: задач по нахождению плотности цилиндров? Оказывается, это надо делать следующим образом. Слева в тетрадях, а мне на доске, надо записать номер задания, а затем записать слово «Дано:», под ним исходные данные: в вашем случае это результаты прямых измерений массы и объема тела. А потом уже обозначение той величины, которую надо найти. Справа пишется формула, по которой рассчитывается неизвестная величина, на следующей строке непосредственные расчеты. А затем ответ. Получается так.

Можно оформить решение трех задач в одном примере:

Учитель: Вы нашли плотность трех веществ. Как это было сделано: прямым или косвенным измерением?

Ученики: Косвенным измерением, мы рассчитали плотность по формуле, а массу и объем нашли непосредственно измерением.

Учитель: Да, действительно при похожих ситуациях на практике массу измеряют на весах, для измерения объема тела можно также прибегнуть к формулам, если это правильная геометрическая фигура (куб, прямоугольный параллелепипед), или же найти объем с помощью мензурки — измерительного цилиндра.

Учитель: Как же определить, из какого вещества изготовлены цилиндры по найденной плотности?

Ученики: Затрудняемся ответить.

Учитель: Существуют справочные таблицы, где указаны плотности веществ. В нашем учебнике такая таблица находится на стр.21–22. В ней приведены плотности некоторых веществ. Обратите внимание, что там выражена плотность веществ в кг/ м3. Как же связаны между собой разные единицы плотности? Для этого надо вспомнить связь между различными единицами массы: 1 т, 1 кг и 1 г.

Ученики: 1 т = 1000 кг, а 1 кг =1000 г.

Учитель: На самом деле, плотность вещества, выраженная в единицах СИ, т. е. выраженная в кг/м3 будет отличаться в 1000 раз от плотности того же вещества, выраженной в г/см3. Например, в столбце твердые вещества первым идет золото. Его плотность равна 19 300 кг/ м3. Это означает, что 1 м3 золота будет иметь массу 19300 кг.

С другой стороны, плотность золота равна 19,3 г/ см3. Это означает, что 1 см3 золота будет иметь массу 19,3 г (фиксирует равенство на доске).

Вы рассчитали плотности трех веществ. Определите по таблице, что это за вещества?

Ученики: Первый цилиндр железный, второй — алюминиевый, третий изготовлен из дуба.

Учитель: Что означает, что плотность каждого вещества равна определенному значению?

Ученики: Например, плотность железа равна 7,8 г/см3. Это означает, что 1 см3 железа имеет массу 7,8 г, а соответственно алюминия — 2, 7 г, дуба 0,7 г.

Учитель: Вспомните, какой из цилиндров самый тяжелый?

Ученики: Из железа.

Учитель: Что можно сказать о его плотности по отношению к плотностям других цилиндров?

Ученики: Она самая большая.

Учитель: Какой вывод можно сделать о связи массы тел с их плотностью при одинаковом объеме?

Ученики: Если тела имеют одинаковый объем, то чем больше масса тела, тем больше плотность вещества этого тела, или чем больше плотность вещества тела, тем больше будет масса этого тела.

Учитель: Как же из формулы для определения плотности найти массу тела?

Ученики: Чтобы найти массу тела, нужно плотность вещества тела умножить на объем этого тела, т. е. m= ρ*V.

Учитель: Действительно (закрепляет формулу на доске):

Учитель: А как их формулы для нахождения плотности найти объем?

Ученики: Чтобы найти объем тела, нужно массу тела разделить на плотность вещества этого тела, т. е. V = m/ ρ.

Учитель: Да, на самом деле

Учитель: Что можно сказать о телах одинаковой массы изготовленных из разных веществ?

Ученики: Из этой формулы видно, что если масса тел одинакова, то тело с большей плотностью вещества будет иметь меньший объем, а тело с меньшей плотностью вещества будет иметь больший объем.

Первичное закрепление нового материала.

Учитель: Итак, вы познакомились с формулой для нахождения плотности вещества. Вы также узнали, как найти массу вещества и объем вещества по его плотности. Перед вами задания, которые вам предстоит выполнить:

Задание 1 (выполняется фронтально). Определите объем твердого тела, если шкала мензурки проградуирована в см3.

Задание 2 (выполняется в парах).

Определите плотность вещества, из которого изготовлено тело.

Задание 3 (выполняется самостоятельно). Каков объем медного цилиндра массой 89 г.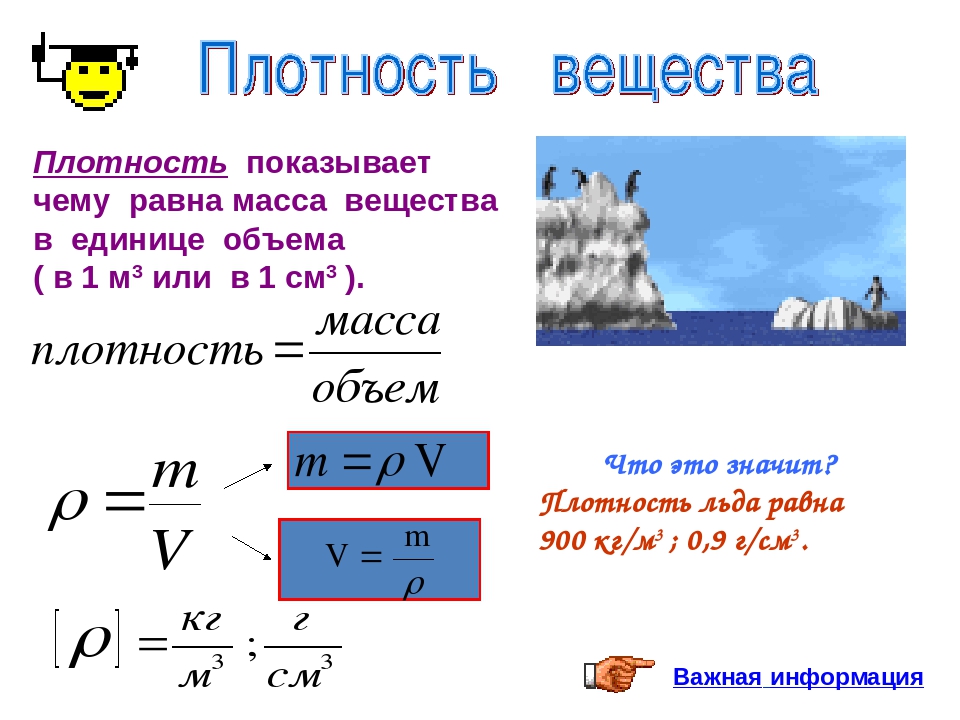

Задание 4 (выполняется самостоятельно).

Войдет ли 4 кг меда в банку вместимостью 3 л?

(Подсказка: 3л = 3 дм3 = 0,003 м3)

(В ходе работы на уроке, в том числе и при решении задач можно выставлять хорошие отметки по желанию учащихся).

Учитель (после выполнения заданий 2–4 выводит решение задачи, по которому ученики себя проверяют). Ребята, у кого задания вызвали трудности при выполнении? Почему они у вас возникли? Что надо делать, что ошибок не было? Где могут пригодиться полученные знания? (получает ответы на вопросы).

5. Рефлексия учебной деятельности.

Учитель: Что нового вы узнали на уроке? Достигли ли мы поставленных целей? Какие личные качества вам помогли при достижении цели? (слушает ответы учеников).

Учитель: Оцените свою работу на уроке: поставьте свои руки локтями на парту, а ладонями изобразите чаши весов. В левой чаше-ладони представьте весь объем знаний и умений по сегодняшней теме, а в правой — полученный и усвоенный вами объем знаний и умений по этой теме. Покажите, в каком положении оказались ваши чаши-ладони. Проанализируйте это положение, а выводы мы сделаем вместе (анализ ситуации) и поставим новые цели.

(Учитель задает дифференцированное домашнее задание)

Учитель: Спасибо! До свидания.

Литература:

Хижнякова Л. С., «Физика, 7 класс», М.:Вентана-Граф, 2014.
http://koledj.ru/docs/index-6336.html

Основные термины (генерируются автоматически): учитель, ученик, плотность вещества, масса, вещество, масса тела, объем, плотность, тело, формула.

Расчет массы и тела

Для того чтобы определить плотность вещества, надо массу тела разделить на его объем:

(10,1)

Массу тела можно определить с помощью весов. А как найти объем тела?

Если тело имеет форму прямоугольного параллелепипеда (рис. 24), то его объем находится по формуле

В = аbс.

До нас дошли не все сочинения Архимеда. О многих его открытиях стало известно благодаря более поздним авторам, в сохранившихся трудах описываются его изобретения. Так, например, римский архитектор Витрувий (I в. До н. Э.) В одном из своих сочинений рассказал историю:
«Что касается Архимеда, то изо всех его военных и разнообразных открытий то открытие, о котором я расскажу, представ мне сделанным с безграничным остроумием.Во время своего царствования в Сиракузах Гиерон после благополучного окончания всех мероприятий дал обет пожертвовать в какой-то храм золотую корону бессмертным богам. Он условился с мастером о большой цене за работу и дал ему нужное по весу количество золота. В назначенный день мастер принес свою работу царю, который нашел ее отлично исполненной; после взвешивания вес короны оказался соответствующим выданному весу золота.

После этого был сделан донос, что из короны была взята часть золота и вместо него такое же количество серебра.Гиерон разгневался на то, что его провели, и, не находя способ уличить это воровство, попросил Архимеда хорошенько подумать об этом. Тот, погруженный в думы по этому вопросу, как-то случайно пришел в ванну и там, опустился в ванну, заметил, что из нее вытекает такое количество воды, каков объем его тела, погруженного в ванну. Выяснив себе ценность этого факта, он, не долго думая, выскочил с радостью из ванны, пошел домой голым и громким голосом сообщал всем, что он нашел то, что искал. Он бежал и кричал одно и то же по-гречески: «Эврика, эврика! (Нашел, нашел!) ».

Затем, пишет Витрувий, Архимед взял сосуд, доверху наполненный водой, и опустил в него золотой слиток, равный по весу короне. Измерив объем вытесненной воды, он снова наполнил сосуд водой и опустил в него корону. Объем воды, вытесненной короной, превышение объема воды, вытесненной золотым слитком. Больший объем короны означал, что в ней присутствует менее плотное, чем золото, вещество. Поэтому опыт, проделанный Архимедом, показал, что часть золота была похищена.

Итак, для определения объема имеющего неправильную форму, достаточно измерить объем воды, вытесняемой данным телом.Располагая измерительным цилиндром (мензуркой), это сделать несложно.

(10,2)

Отсюда видно, что для определения объема этой массы тела разделить на его плотность надо .

Если, наоборот, объем тела известен, то, зная, из какого вещества оно состоит, можно найти его массу:

м = ρV. (10.3)

Чтобы определить массу тела, надо плотность тела умножить на его объем.

1. Какие способы определения вы знаете? 2. Что вам об известно Архимеде? 3. Как можно найти массу тела по его плотности и объему?
Экспериментальное задание. Возьмите кусок мыла, имеющий форму прямоугольного параллелепипеда, на обозначенном его массу. Проделав измерения, определите плотность мыла.

Формула массы через объем и плотность

Формула для вычисления массы через объем и плотность

Это количество можно определять по-разному.Если речь идет о частицах, то речь идет о частицах плотности. Эту обозначают буквой n . В СИ она измеряется в м ^-3. Если имеется ввиду масса вещества, то вводят плотность массы. Её обозначают через. В Си измеряется в кг / м ³. Между и n существует связь. Так, если состоит из частиц одного сорта, то

= м × n ,

где м – масса одной частицы.

Плотность массы можно вычислить по формуле:

= м / В.

Настоящее выражение можно преобразовать так, чтобы получилась формула массы через объем и плотность:

м = × В.

Таблица 1. Плотности некоторых веществ.

Вещество	Плотность, кг / м ³	Вещество	Плотность, кг / м ³
Вещества атомного ядра	10 ¹⁷	Вода	1,00 × 10 ³
Сжатые газы в центре самых плотных звезд	10 ⁸	Жидкий водород	0,07 × 10 ³
Золото	1,93 × 10 ⁴	Воздух у поверхности Земли	1,2
Ртуть	1,36 × 10 ⁴	Воздух на высоте 20 км	9 × 10 ^-2
Сжатое железо в ядре Земли	1,2 × 10 ⁴	Наивысший искусственный вакуум	10 ^-13
Сталь	(7,6 – 7,8) × 10 ³	Газы межзвездного пространства	10 ^-20
Алмаз	3,53 × 10 ³	Газы межгалактического пространства	10 ^-26
Алюминий	2,7 × 10 ³
Человеческое тело	1,07 × 10 ³

от степени сжатия жидких и Независимых тел лежат в весьма интервале значений (табл. 1). Плотности же газов различных в весьма широких пределах. Причина заключается в том, что как в твердых телах, так и в жидкостях частицы частицы друг друга примыкают к другу. В этих средах расстояние между соседними частями составляет порядок 1 А и сравнимо с размерами атомов и молекул. По этой причине твердые и жидкие тела обладают очень малой сжимаемостью, чем обусловлено малое различие в их плотности. В газах рейтинге. Среднее расстояние между частицами большими их размерами.Например, для воздуха у поверхности Земли оно составляет 10 ² А. Вследствие этого газы обладают большой сжимаемостью, а их плотность может изменяться в очень широких пределах.

Примеры решения задач

Понравился сайт? Расскажи друзьям!

Формулы для вычислений массы тел различной формы

05.2013 // Владимир Трунов

Тут самое время вспомнить, что масса тела – это его объем, умноженный на его плотность материала ( см. Таблицы плотностей ):

Объем сплошной детали – это… ее объем и больше ничего.

Примечание .В приведенных ниже формулах все размеры измеряются в миллиметрах, а плотность – в граммах на кубический сантиметр.
Буквой обозначено отношение окружности к ее диаметру, составляющее примерно 3,14 .

Рассмотрим несколько простых форм (более сложный, как вы помните, можно составить путем сложения или вычитания простых).

1. Масса параллелепипеда (бруска)

Объем параллелепипеда:, где – длина, – ширина, – высота.
Тогда масса:

2. Масса цилиндра

Объем цилиндра:, где – диаметр основания, – высота цилиндра.
Тогда масса:

3. Масса шара

Объем шара:, где – диаметр шара.
Тогда масса:

4. Масса сегмента шара

Объем сегмента:, где – диаметр основания сегмента, – высота сегмента.
Тогда масса:

5. Масса конуса

Объем любого конуса:, где – площадь основания, – высота конуса.
Для круглого конуса:, где – диаметр основания, – высота конуса.
Масса круглого конуса:

6. Масса усеченного конуса

Невозможно объять необъятное, рассмотрим круглый усеченный конус. Его объем – это разность объема двух вложенных конусов: с основания и:, где,. После никому не интересных алгебраических преобразований получаем:
, где – диаметр большего основания, – диаметр меньшего основания, – высота усеченного конуса.
Отсюда масса:

7. Масса пирамиды

Объем любоймиды равенства одной трети произведения площади ее основания на высоту (то же самое, что и для конусов, насколько мироздание к нам благосклонно)):, где – площадь основания, – высота пирамиды.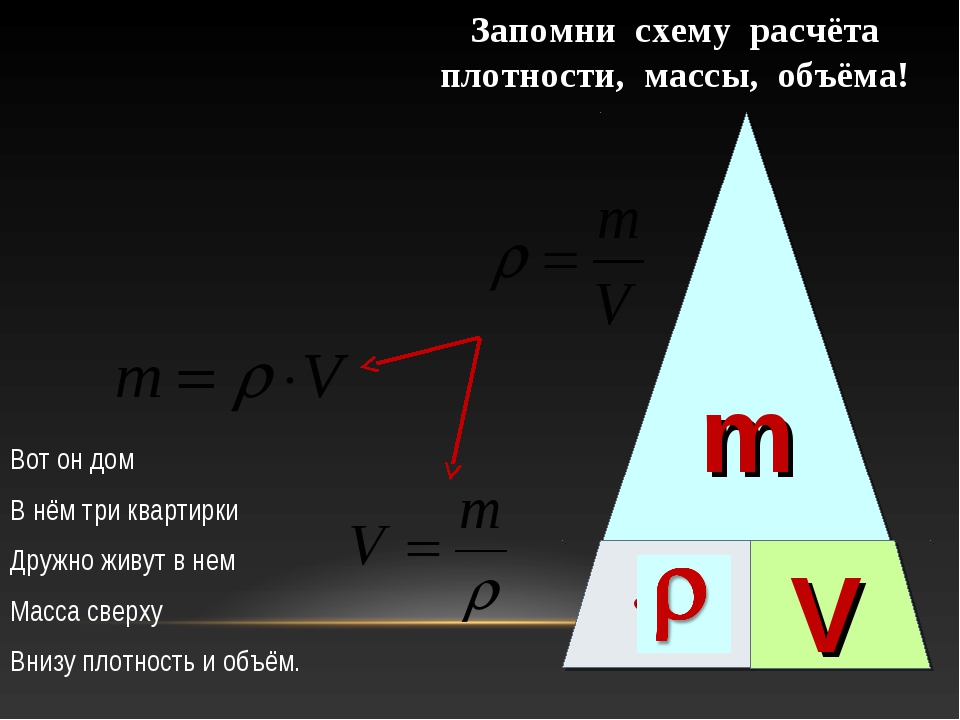
Для пирамиды с прямоугольным основанием:, где – ширина, – длина, – высота пирамиды.
Тогда масса пирамиды:

8. Масса усеченной пирамиды

Рассмотрим усеченную пирамиду с прямоугольным основанием. Ее объем – это разность размеров двух подобных пирамид с основания и:, где,.
Исчеркав половину тетрадного листа, получаем:, где, – ширина и длина большего основания,, – ширина и длина меньшего основания, – высота пирамиды.
И, оставив в покое остальную половину листа, исходя из одних соображений, мы можем написать еще одну формулу, которая отличается от предыдущей только заменой W на L и наоборот.В чем разница между длиной и шириной? Только в том, что мы их так назвали. Назовем наоборот и получим:.
Тогда масса усеченной прямоугольной пирамиды:

или

Для пирамиды с квадратным основанием (,) формула выглядит проще:

Расчет массы и тела по его плотности

Методическая разработка урока физики для 7 класса по теме “Расчет массы и объема тела по его плотности.

Класс: 7

Цели урока: повторить тему «Плотность тела», научиться определять объем тела и его по средней плотности, научиться решать задачи с применением этой формулы.

Задачи урока: использовать полученные знания в новой ситуации; больше интерес к предмету путём выполнения разных заданий: практических и теоретических.

Дидактические материалы и оборудование к уроку: презентация, плакаты «Международная система единиц», «Приставки для образования кратных и дольных единиц», индивидуальные карточки с проверочными заданиями; весы с разновесами, мензурка, линейка, мыло, картофелина, камень.

План урока

И.Организационный момент

II. Актуализация знаний

1. Фронтальный опрос по теоретическому материалу

2. Заполнить таблицу (устно)

в		т		ρ	В
	кг		м

3. Назовите число, составленное вами из номеров верных формул.

v = S / t ;
v = St ;
S = vt ;
ρ = мв ;
ρ = м / V ;
м = ρ / V .

3. Выразите в СИ.

4,8 т; 502 г; 175 г; 35 см; 2341 мм; 584 л; 3846 см ³; 0,00567 г / см ³

III Проверка д / з

Проверочная работа по теме «Масса.Плотность »

Вариант 1

1) При нагревании тело расширяется. При этом плотность вещества, из которого оно сделано,…

а) не меняется б) увеличивается в) уменьшается г) увеличивается, потом уменьшается

2) Из некоторого вещества изготовили массой 42 г в форме параллелепипеда. Параллелепипед имеет следующие размеры: высота 1 см, ширина 2 см, длина 3 см. Определите его плотность.

3) После того как на одну чашу весов поместили тело другого – набор гирь (20 г, 500 мг, 200 мг, 100 мг, 10 мг, 20 мг, 20 мг и 50 мг), весы пришли в равновесие. Чему равна масса тела?

Вариант 2

1) При охлаждении тело сжимается. При этом плотность вещества, из которого оно сделано,…

а) не меняется б) увеличивается в) уменьшается г) увеличивается, потом уменьшается

2) Канистра имеет размеры: высота 3 дм, ширина 1 дм, длина 5 дм.Масса пустая канистры 1 кг, заполненной – 13 кг. Чему плотность жидкости.

3) После того как на одну чашу весов поместили тело, другого – набор гирь (50 г, 500 мг, 200 мг, 100 мг, 10 мг, 10 мг, 20 мг и 50 мг), весы пришли в равновесие. Чему равна масса тела?

IV. Решение практических задач

1) Перед вами лежит кусочек камня. Какие измерения и расчеты необходимы для выполнения его плотности? С помощью какого прибора удобно измерить объем тела неправильной формы? Оформите задачу с решением.

2) Теперь вы видите кусок мыла. Какие измерения и расчеты необходимы для определения плотности этого тела? С помощью какого прибора удобно измерить объем мыла? Оформите задачу с решением.

Постановка проблемы

3) Недавно в одном из телепередач был показан сюжет о крестьянском хозяйстве, в котором вырастили замечательную картошку. Из всех городов закупают картофель, но только картофелины берут определенного объема. Примерно вот такую картофелину я вам принесла на урок.Давайте определим ее объем. Вот только в мензурку, да и в отливной стакан она не войдет. Ваши предложения?

Это и есть тема нашего урока: Расчет объема и массы по его плотности.

Оформите эту задачу в тетрадях: Как найти объем тела, если известна масса тела и его плотность?

Рассмотрим примеры решения задач.

1) Перед вами в мензурке находятся вода, молоко и подсолнечное масло. Необходимо рассчитать этих жидкостей, зная их плотность.

2) Рядом с мензурками находятся пластмассовый и стальной шарики, электронные весы. По таблице из учебника проверьте плотность этих веществ. Рассчитайте объемы шариков.

V. Самостоятельное решение расчетных задач

Масса чугунного шара 800 г, его объем 125 см ³. Сплошной этот шар или полый?
Чему масса железного листа длиной 1 м, шириной 80 см, толщиной 1 мм?
Дубовый брусок имеет массу 800 г.Определите его объем, если плотность дуба 800 кг / м ³.

VI. Рефлексия (подведение итогов урока, оценки)

Что ж, наше занятие подходит к завершению. Вы должны использовать их в повседневной жизни. А теперь рубрика обратной связи. На экране вы видите высказывания. Выберите любое и закончите его (устно).

Предлагаются варианты ответов: Сегодня я узнал… Было интересно… Было трудно… Я понял, что… Я научился… Меня удивило…

VII.Д / з

1) § 23 – учить

2) Придумать 3 интересные задачи на расчет плотности, массы или объема тел, применяемых в быту (оформить на А4 с решением и иллюстрациями, принести эти тела в класс для решения некоторых задач)

Объем, масса, плотность, удельный объем. Приведение к нормальным и стандартным условиям и пересчет

Приведение к нормальным и стандартным условиям

Единицей измерения объема газа является кубическим метр (м³).Измеренный объем к нормальным физическим условиям.

Нормальные физические условия: давление 101 325 Па, температура 273,16 К (0 ° С).

Стандартные условия: давление 101 325 Па, температура 293,16 К (+20 ° С).

В настоящее время эти обозначения выходят из употребления. Поэтому в дальнейшем следует указывать те условия, к которым относится к этому объемы и другие параметры газа. Если эти условия не указываются, то это значит, что параметры газа даны при 0 ° С (273,16 ° К) и 760 мм рт.ст. (1,033 кгс / см²). Иногда объем газа (особенно в иностранной литературе и нормах) при пользовании системой СИ работает к 288,16 ° К (+15 ° С) и давлению 1 бар (105 Па).

Если указан объем газа при одних условиях, то пересчитать его объемы при других условиях можно с помощью коэффициентов, приведенных в следующей таблице.

Коэффициенты для пересчета системы газа из одних условий в другие

Температура и даление газа	0 ° С и 760 мм рт.ст.	15 ° С и 760 мм рт. ст.	20 ° С и 760 мм рт. ст.	15 ° С (288,16 ° К) и 1 бар
0 ° С и 760 мм рт. ст. (норм. условия)	1	1,055	1 073	1 069
15 ° С и 760 мм рт. ст. (в зар. литературе)	0,948	1	1,019	1 013
20 ° С и 760 мм рт.ст. (ст. условия)	0,932	0,983	1	0,966
15 ° С (288,16 ° К) и 1 бар (СИ)	0,936	0,987	1 003	1

Для приведения газа к 0 ° С (273,16 ° К) и 760 мм рт. ст. (1,033 кгс / см²), а также до 20 ° С (293,16 ° К) и 760 мм рт. ст. (1,033 кгс / см²) могут быть применены следующие формулы:

где V _{0 ° С и 760 мм рт.ст.} – объем газа при 0 ° С и 760 мм рт. ст., м³;
V _{20 ° С и 760 мм рт. ст.} – объем газа при 20 ° С и 760 мм рт. ст., м³;
V _P – объем газа в рабочих условиях, м³;
р – абсолютное давление газа в рабочих условиях, мм рт. ст .;
Т – абсолютная температура газа в рабочих условиях, ° К.

Пересчет объема газа, приведенных к 0 ° С и 760 мм рт. ст., а также к 20 ° С и 760 мм рт. ст., в объемы при других (рабочих) условиях можно печатать по формулам:

Любой газ способен расширяться.Следовательно, знание размера, занимает газ, недостаточно для определения его массы, так как в любом объеме, целиком заполненным газом, его масса может быть определенным.

Масса – это мера вещества какого-либо тела (жидкости, газа) в состоянии покоя; скалярная величина, характеризующая инерционные и гравитационные свойства тела. Единицы массы в СИ – килограмм (кг).

Плотность, или масса единицы, обозначаемая буквой p, – это отношение массы тела m, кг, к его объему, V, м³:

p = м / V

или с химической формулы газа:

p = M / V _M = M / 22,4,

где M – молекулярная масса,
V _M – молярный объем.

Единица плотности в СИ – килограмм на кубический метр (кг / м³).

p _см = ( p ₁ V ₁ + p ₂ V ₂ +… + p _n V _n ) / 100,

где p ₁ , p ₂ ,…, p _n – плотность компонентов газового топлива, кг / м³;
V ₁ , V ₂ ,…, V _n – содержание компонента, об. %.

Величину, обратную плотность, называют удельным, или массовым, объемом (ν) и измеряют в кубических метрах на килограмм (м³ / кг).

Как правило на практике, чтобы показать, сколько 1 м³ газа или тяжелее 1 м³ воздуха, используют понятие относительная плотность d , которая представляет собой отношение плотности газа к плотности воздуха:

d = p / 1,293

d = M / (22,4 × 1293).

02-в. Плотность вещества

§ 02-в. Плотность вещества

Для знакомства с новой физической величиной – плотностью вещества отправимся в литейный цех, взяв с собой весы завода и линейку. Выберем несколько разных по размерам чугунных и алюминиевых слитков прямоугольной формы (см. Рисунок). Используя весы, измерим массы слитков, используя линейку и формулу V = l · b · h , найдём объёмы.

По результатам наших измерений м и V заполним следующую таблицу:

Табл. 2.8. Результаты эксперимента с чугунными и алюминиевыми брусками.

	Чугунные слитки				Алюминиевые слитки
Масса, кг	8,5	45	18	29	6,2	18	9,7	4,5
Объём, дм ³	1,3	6,5	2,6	3,9	2,3	6,5	3,6	1,8
Поделив массу на объёмы, получим:
их частное	≈ 7	≈ 7	≈ 7	≈ 7	≈ 3	≈ 3	≈ 3	≈ 3

Заметим: при делении массы каждого слитка на его объём получаются одинаковые значения частного для всех чугунных слитков (≈ 7 кг / дм³) и для всех алюминиевых (≈ 3 кг / дм³).Другими словами, независимо от определенных значений массы и объёма их постоянно частное для одного и того же вещества.

Эта закономерность послужила причиной введения в физику новой величины – плотности вещества (см. Далее формулу). Основная единица плотности – 1 кг / м³ (читается: килограмм на кубический метр).

Итак, физическая величина, равная масса вещества к его объёму, называется плотностью вещества . Это – определение плотности. Его можно записать в виде формулы:

Формула для вычислений плотности: «ро равно эм разделить на вэ».

	ρ =	. м .			ρ – плотность вещества, кг / м³ м – масса вещества, кг V – объём вещества, м³
		V

Из математики вы знаете, что значение всякой дроби показывает количество единиц, стоящей в числителе, приходящееся на одну единицу величины, стоящей в знаменателе. Плотность вещества – тоже значение дроби. Поэтому числовое значение плотности вещества массы этого вещества объёма. В этом состоит физический смысл числового значения плотности.

Например, плотность чугуна составляет 7 кг / дм³. Это значит, что 1 дм³ чугуна будет иметь массу 7 кг. Соответственно, 1 м³ чугуна будет иметь массу в 1000 раз больше – 7000 кг. Плотность пресной воды 1 кг / л. Следовательно, масса 1 л воды 1 кг, а 1 м³ – 1000 кг.Аналогично и для других веществ: верна пропорция .

Вспомним, что формулы можно преобразовывать по правилам математики. Поэтому формулу плотности можно записать в других формах:

	m = ρ · V	и	V =	. м .
				ρ

При пользовании этим формулами нужно следить, чтобы все величины были выражены в согласующихся друг с другомах, больших килограммах и кубических единиц.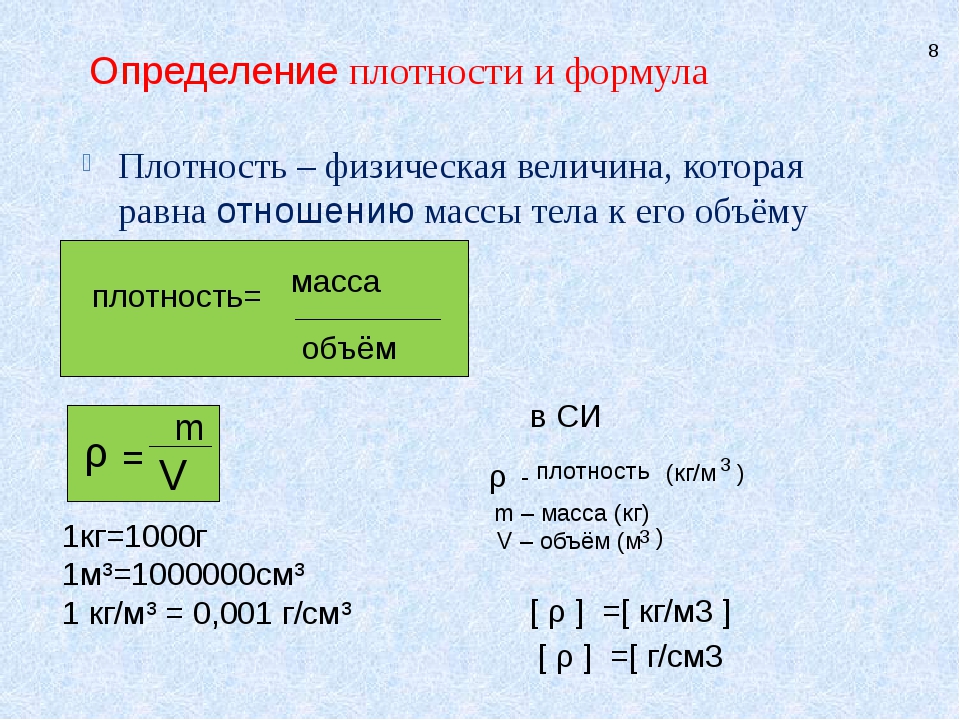 Эти стандартные рекомендованы, что они часто используются в соответствующих таблицах плотности, таких, которые помещены в следующем параграфе.

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

4) Рассчитать количество моль интересующего участника из известного количества другого вещества, зная, что количества веществ любых двух реакций A и B отношения друг к другу как коэффициенты перед этими же веществами в уравнении реакции, то есть: