Формула периода для пружинного маятника: Формула периода колебаний пружинного маятника в физике

alexxlab | 14.06.2023 | 0 | Разное

Содержание

Формула периода колебаний пружинного маятника в физике

Формула периода колебаний пружинного маятника в физике Определение

Период – это минимальное время, за которое совершается одно полное колебательное движение.

Обозначают период буквой $T$.

\[T=\frac{\Delta t}{N}\left(1\right),\]

где $\Delta t$ – время колебаний; $N$ – число полных колебаний.

Уравнение колебаний пружинного маятника

Рассмотрим простейшую колебательную систему, в которой можно реализовать механические колебания. Это груз массы $m$, подвешенный на пружине, коэффициент упругости которой равен $k\ $(рис.1). Рассмотри вертикальное движение груза, которое обусловлено действием силы тяжести и силы упругости пружины. В состоянии равновесия такой системы, сила упругости равна по величине силе тяжести. Колебания пружинного маятника возникают, когда систему выводят из состояния равновесия, например, слегка дополнительно растянув пружину, после этого маятник предоставляют самому себе. 2_0=\frac{k}{m}$ – циклическая частота колебаний пружинного маятника. Решением уравнения (7) (это проверяется непосредственной подстановкой) является функция:

\[x=A{\cos \left({\omega }_0t+\varphi \right)=A{\sin \left({\omega }_0t+{\varphi }_1\right)\ }\ }\left(8\right),\]

где ${\omega }_0=\sqrt{\frac{k}{m}}>0$- циклическая частота колебаний маятника, $A$ – амплитуда колебаний; ${(\omega }_0t+\varphi )$ – фаза колебаний; $\varphi $ и ${\varphi }_1$ – начальные фазы колебаний.

Формулы периода колебаний пружинного маятника

Мы получили, что колебания пружинного маятника описывается функцией косинус или синус. Это периодические функции, значит, смещение $x$ будет принимать равные значения через определенные одинаковые промежутки времени, которые называют периодом колебаний. Обозначают период буквой T.

Еще одной величиной, характеризующей колебания является величина обратная периоду колебаний, ее называют частотой ($\nu $):

\[T=\frac{1}{\nu }\left(9\right).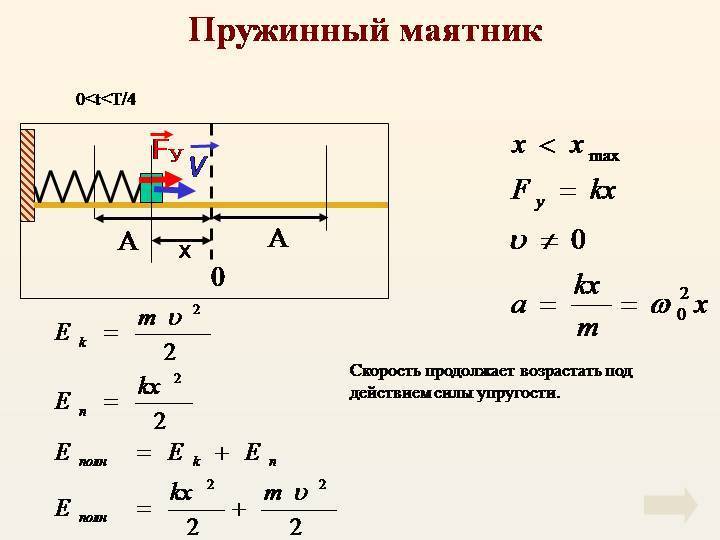

Период связан с циклической частотой колебаний как:

\[T=\frac{2\pi }{{\omega }_0}\left(10\right).\]

Выше мы получали для пружинного маятника ${\omega }_0=\sqrt{\frac{k}{m}}$, следовательно, период колебаний пружинного маятника равен:

\[T=2\pi \sqrt{\frac{m}{k}}\ \left(11\right).\]

Формула периода колебаний пружинного маятника (11) показывает, что $T$ зависит от массы груза, прикрепленного к пружине и коэффициента упругости пружины, но не зависит от амплитуды колебаний (A). Данное свойство колебаний называют изохронностью. Изохронность выполняется до тех пор, пока справедлив закон Гука. При больших растяжениях пружины закон Гука нарушается, появляется зависимость колебаний от амплитуды. Подчеркнем, что формула (11) для вычисления периода колебаний пружинного маятника справедлива при малых колебаниях.

Примеры задач на период колебаний

Пример 1

Задание. Пружинный маятник совершил 50 полных колебаний за время равное 10 с .

Каков период колебаний маятника? Чему равна частота этих колебаний?

Решение. Так как период – это минимальное время необходимое маятнику для совершения одного полного колебания, то найдем его как:

\[T=\frac{\Delta t}{N}\left(1.1\right).\]

Вычислим период:

\[T=\frac{10}{50}=0,2\ \left(с\right).\]

Частота – величина обратная периоду, следовательно:

\[\nu =\frac{1}{T}\left(1.2\right).\]

Вычислим частоту колебаний:

\[\nu =\frac{1}{0,2}=5\ \left(Гц\right).\]

Ответ. $1)\ T=0,2$ с; 2) 5Гц

Пример 2

Задание.Две пружины, имеющие коэффициенты упругости $k_1$ и $k_2$ соединены параллельно (рис.2), к системе присоединен груз массы $M$. Каков период колебаний полученного пружинного маятника, если массами пружин можно пренебречь, сила упругости, действующая на груз, подчиняется закону Гука?

Решение. Воспользуемся формулой для вычисления периода колебаний пружинного маятника:

\[T=2\pi \sqrt{\frac{M}{k}}\ \left(2.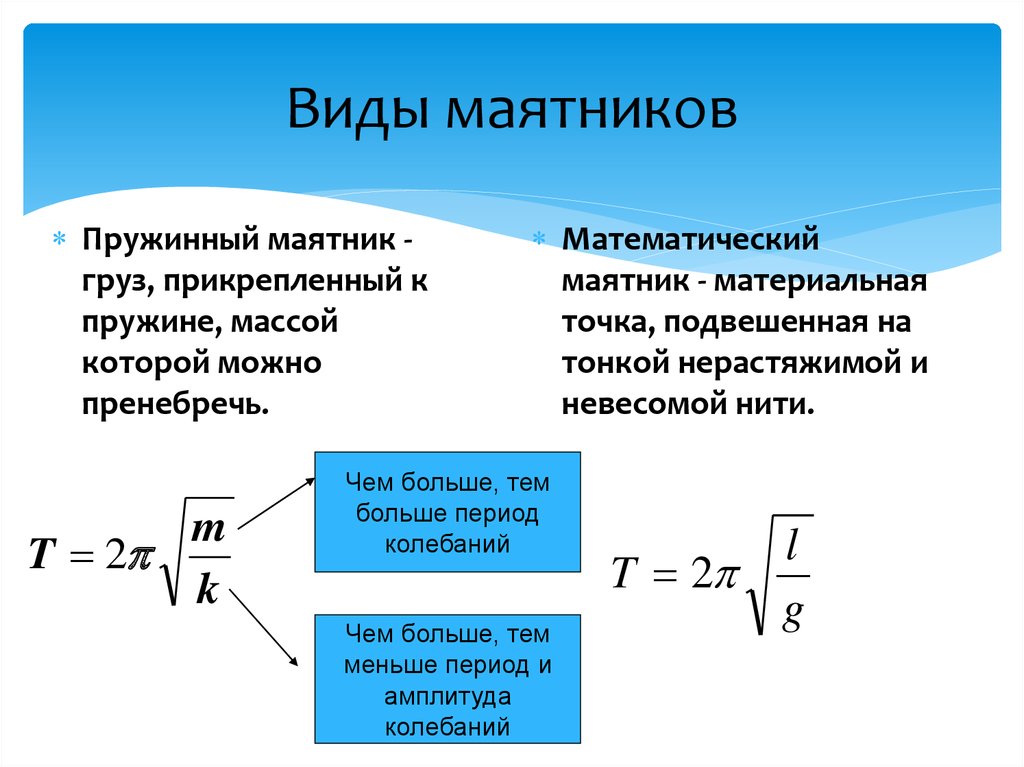

1\right).\]

При параллельном соединении пружин результирующая жесткость системы находится как:

\[k=k_1{+k}_2\left(2.2\right).\]

Это означают, что вместо $k$ в формулу для вычисления периода пружинного маятника подставим правую часть выражения (2.2), имеем:

\[T=2\pi \sqrt{\frac{M}{k_1{+k}_2}}.\]

Ответ. $T=2\pi \sqrt{\frac{M}{k_1{+k}_2}}$

Читать дальше: формула плеча силы.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

PhysBook:Электронный учебник физики — PhysBook

Содержание

1 Учебники
2 Механика
- 2.1 Кинематика
- 2. 2 Динамика
- 2.3 Законы сохранения
- 2.4 Статика
- 2.5 Механические колебания и волны
3 Термодинамика и МКТ
- 3.1 МКТ
- 3.2 Термодинамика
4 Электродинамика
- 4.1 Электростатика
- 4. 2 Электрический ток
- 4.3 Магнетизм
- 4.4 Электромагнитные колебания и волны
5 Оптика. СТО
- 5.1 Геометрическая оптика
- 5.2 Волновая оптика
- 5.3 Фотометрия
- 5.4 Квантовая оптика
- 5.5 Излучение и спектры
- 5. 6 СТО
6 Атомная и ядерная
- 6.1 Атомная физика. Квантовая теория
- 6.2 Ядерная физика
7 Общие темы
8 Новые страницы

Здесь размещена информация по школьной физике:

материалы из учебников, лекций, рефератов, журналов;
разработки уроков, тем;
flash-анимации, фотографии, рисунки различных физических процессов;
ссылки на другие сайты

и многое другое.

Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.

Учебники

Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –

Механика

Кинематика

Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве

Динамика

Законы Ньютона – Силы в механике – Движение под действием нескольких сил

Законы сохранения

Закон сохранения импульса – Закон сохранения энергии

Статика

Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика

Механические колебания и волны

Механические колебания – Механические волны

Термодинамика и МКТ

МКТ

Основы МКТ – Газовые законы – МКТ идеального газа

Термодинамика

Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение

Электродинамика

Электростатика

Электрическое поле и его параметры – Электроемкость

Электрический ток

Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках

Магнетизм

Магнитное поле – Электромагнитная индукция

Электромагнитные колебания и волны

Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны

Оптика.

СТО

Геометрическая оптика

Прямолинейное распространение света. Отражение света – Преломление света – Линзы

Волновая оптика

Свет как электромагнитная волна – Интерференция света – Дифракция света

Фотометрия

Квантовая оптика

Излучение и спектры

СТО

Атомная и ядерная

Атомная физика. Квантовая теория

Строение атома – Квантовая теория – Излучение атома

Ядерная физика

Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы

Общие темы

Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ – Репетитор по физике

Новые страницы

Запрос не дал результатов.

Ньютоновская механика – Период пружинного маятника

спросил 1 год, 2 месяца назад

Изменено 3 месяца назад

Просмотрено 461 раз

$\begingroup$

Если в автомобиле, движущемся по круговой траектории (равномерно со скоростью $v$), подвешен пружинный маятник, то почему его период времени не зависит от $g$ и ускорения автомобиля, хотя и гравитация, и псевдосила создают крутящий момент согласно угловой смещение массы?

ньютоновская механика
системы отсчета
пружина
осцилляторы

$\endgroup$

$\begingroup$

посмотрите на этот пример

масса m прикреплена с помощью пружины (коэффициент пружины k) к потолку

уравнение движения

$$m\,\ddot z+k\,(z-l)=-m\ ,г$$ где $~k\,l~$ — усилие предварительного натяга пружины.

для статического равновесия $~-k\,l=-m\,g\quad\Rightarrow l=\frac{m\,g}{k}~$

получаем

$$m\,\ ddot z+k\,(z-\frac{m\,g}{k})=-m\,g\quad\стрелка вправо\\ м\,\дточка z+k\,z=0\\ \ddotz+\frac km\,z=0$$ период $~T=2\,\pi\sqrt{\frac{m}{k}}~$ не зависит от g

$\endgroup$

$\begingroup$

Если вы определяете «пружинный маятник» как массу, подпрыгивающую на пружине и одновременно раскачивающуюся вбок, то результирующее (сложное) движение будет зависеть от силы любой реальной или псевдогравитации.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания и подтверждаете, что прочитали и поняли нашу политику конфиденциальности и кодекс поведения.

Период маятника: значение, формула и частота

Когда что-то свободно свисает с потолка, и вы толкаете его, оно начинает раскачиваться взад и вперед. Но как быстро он будет качаться и почему? Это то, на что мы действительно можем ответить, и есть довольно простая формула, чтобы понять это. Эти вопросы связаны со свойством, называемым периодом маятника.

Значение периода маятника

Чтобы понять, что такое период маятника, нам нужно знать значение двух вещей: периода и маятника.

Маятник представляет собой систему, состоящую из объекта определенной массы, подвешенного на стержне или шнуре к неподвижной оси. Висячий объект называется боб .

Маятник будет качаться вперед и назад, и максимальное значение, которое принимает угол θ шнура с вертикалью, называется амплитудой . Эта ситуация на самом деле довольно сложная, и в этой статье мы будем говорить только о простой версии маятника.

Простой маятник представляет собой маятник, в котором стержень или шнур не имеют массы, а ось не имеет трения.

На рисунке ниже изображен простой маятник.

Рисунок 1: Простой маятник.

В этой статье всякий раз, когда мы говорим о маятнике, мы имеем в виду простой маятник с небольшой амплитудой. Теперь, когда мы понимаем, что мы подразумеваем под маятником, нам нужна еще одна информация, а именно, что мы подразумеваем под периодом.

период маятника – это продолжительность одного полного колебания боба.

Например, продолжительность времени между двумя последовательными ситуациями, в которых груз маятника находится полностью вправо, составляет один период маятника.

Влияние длины на период маятника

Длина шнура маятника влияет на период маятника, которому он принадлежит.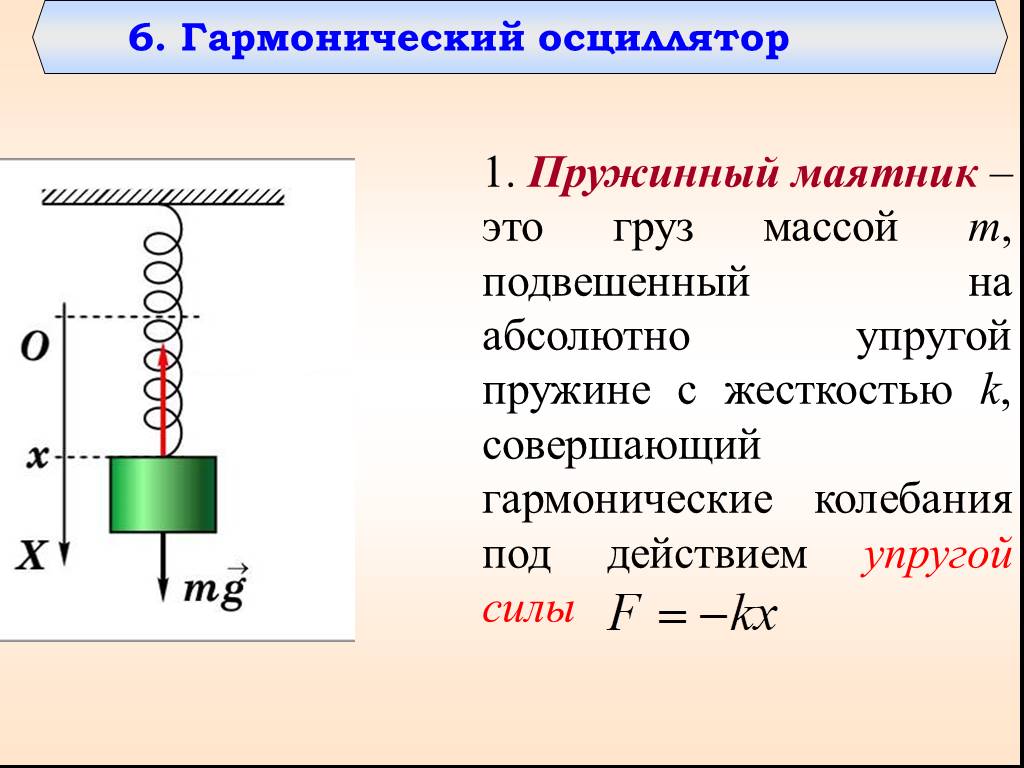 Это утверждение довольно убедительно, если мы просто посмотрим на несколько повседневных примеров.

Некоторые елочные игрушки являются довольно хорошими примерами маятника. Эти маленькие украшения имеют небольшую длину шнура в пару сантиметров и небольшие периоды менее полсекунды (быстро раскачиваются).

Качели для детской площадки являются примером маятника с длиной шнура в несколько метров. Период этих колебаний часто превышает 3 секунды.

Набор свингов, из которых левый будет иметь более короткий период, чем правый.

Таким образом, чем длиннее шнур, тем больше период маятника.

Другие факторы, влияющие на период маятника

Есть два других фактора, влияющих на период маятника: ускорение свободного падения и амплитуда маятника. Поскольку мы говорим только о маятниках с малыми амплитудами, единственный другой фактор, который мы должны учитывать, — это гравитационное ускорение. С очень малым гравитационным ускорением мы можем представить, как вещи разыгрываются в замедленном темпе. Таким образом, мы ожидаем, что чем больше ускорение свободного падения, тем быстрее качается маятник и тем меньше период маятника.

Но подождите, почему масса шарика не влияет на период маятника? Это очень похоже на то, что масса объекта не влияет на скорость его падения: если масса удваивается, сила тяжести, действующая на него, тоже удваивается, но ускорение остается прежним: То же самое испытывает груз нашего маятника: сила, действующая на груз 1, который в два раза массивнее, чем на груз 2, в два раза больше, но и сам груз в два раза тяжелее, чем груз 2. Таким образом, груз 1 в два раза так же трудно переместить, как и боб 2, и поэтому ускорение обоих бобов будет одинаковым (опять же на). Следовательно, период маятника не зависит от массы груза.

Вы можете экспериментально проверить это, подойдя к качелям на детской площадке и измерив период качания, когда на них кто-то находится и когда на них никого нет. Два измеренных периода окажутся одинаковыми: масса шарика не влияет на период колебания.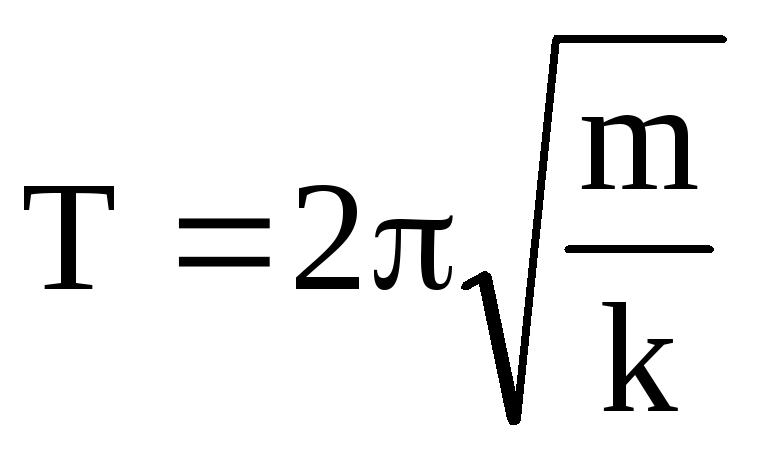

Формула периода времени для маятника

Если длина шнура маятника и g ускорение свободного падения, формула для периода T маятника:

Мы видим, что были правы в своих предсказаниях. Большая длина шнура маятника и меньшее гравитационное ускорение вызывают больший период маятника, а масса груза вообще не влияет на период маятника.

Это хорошее короткое упражнение, чтобы проверить правильность единиц измерения в этом уравнении.

Схема простого маятника малой амплитуды с указанием соответствующих величин.

Немного посчитав, мы можем вывести формулу для периода маятника. Нам нужно измерять углы в радианах, чтобы для малых углов мы имели примерно sin( θ ) = θ . Единственные результирующие силы, действующие на груз массой м , — это горизонтальные силы, а единственная горизонтальная сила, которую мы можем найти, — это горизонтальная часть натяжения шнура.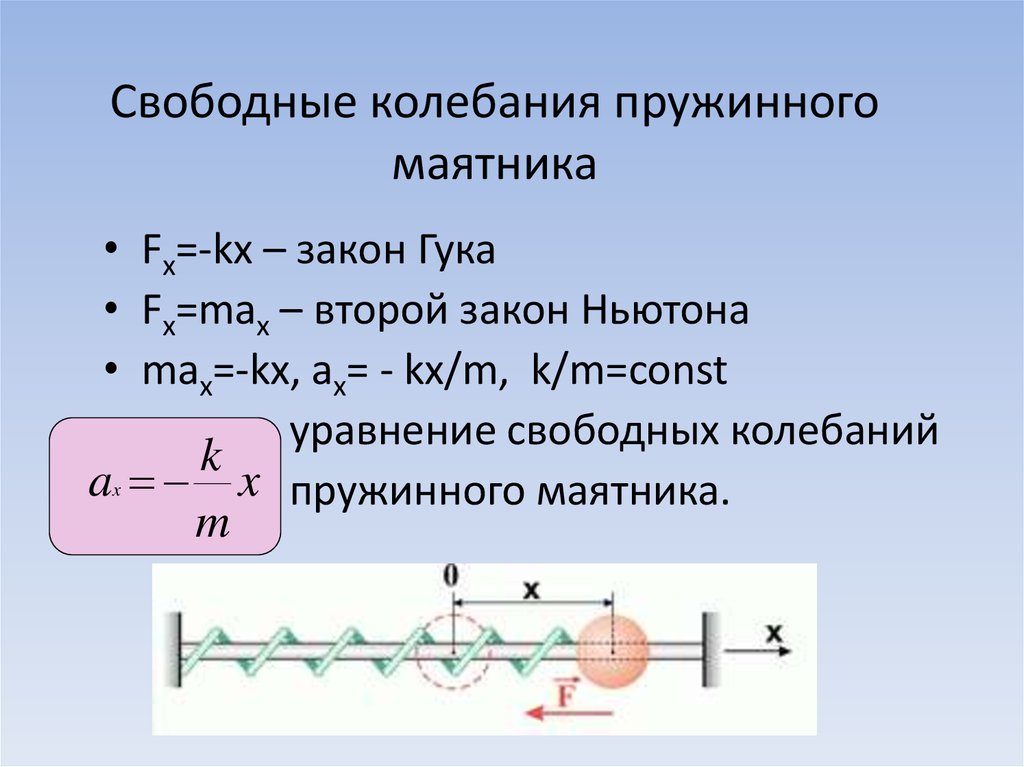

Общее натяжение шнура примерно равно вертикальной составляющей натяжения, поскольку амплитуда маятника мала. Эта вертикальная составляющая равна направленной вниз силе на груз (поскольку на груз нет результирующей вертикальной силы), что составляет его вес мг .

Тогда горизонтальная часть напряжения равна – мг sin( θ ) (со знаком минус, потому что ускорение направлено в сторону, противоположную его положению, которое мы принимаем за положительное). Это примерно – мг θ из-за малой амплитуды маятника. Итак, ускорение боба равно.

Ускорение также измеряется как вторая производная по времени от горизонтального положения, что приблизительно. But постоянна, так что уравнение теперь, где мы должны решить для угла θ как функция времени t . Решение этого уравнения (как вы можете проверить) таково, где A — амплитуда маятника. Мы видим, что θ равно A в каждую единицу времени, поэтому период маятника определяется выражением.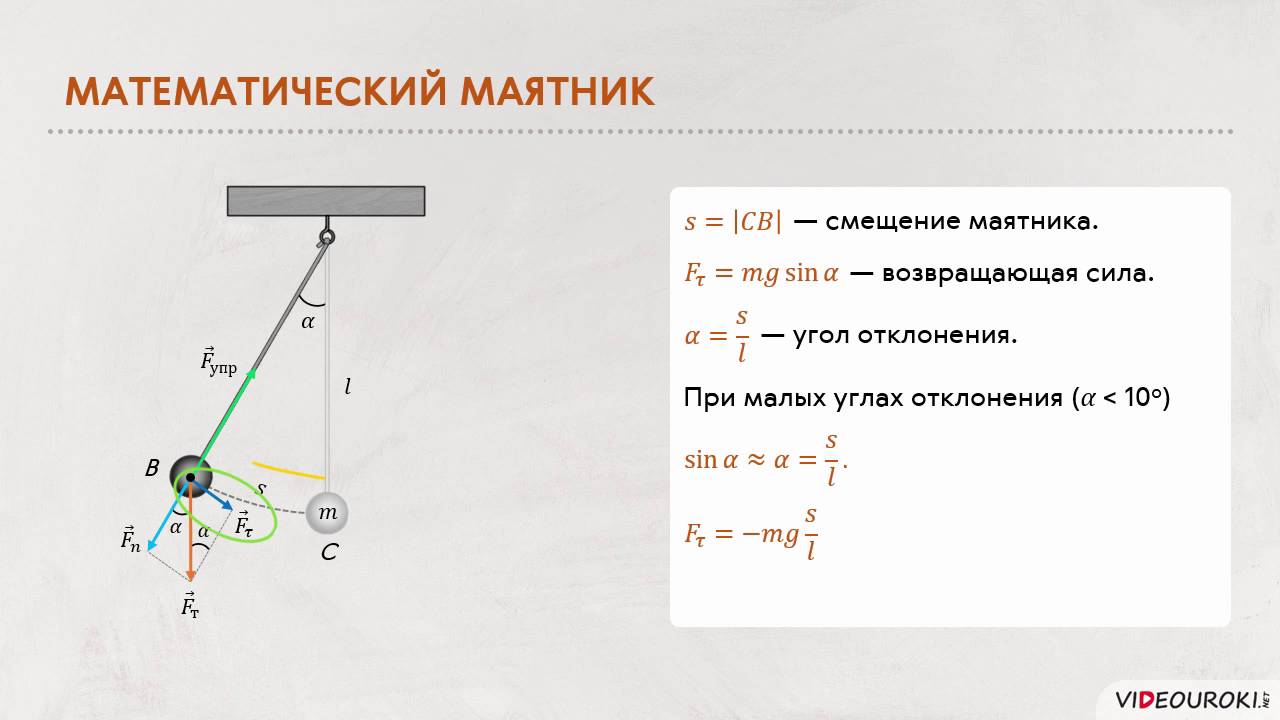 Этот вывод ясно показывает, откуда берутся все факторы, влияющие на период маятника.

Делаем вывод, что на Земле единственным фактором, влияющим на период маятника, является длина шнура маятника.

Вычисление периода маятника

Предположим, мы можем рассматривать детские качели как простой маятник. Каков период качелей, седло которых расположено на 4 м ниже оси вращения, если мы позволим им раскачиваться только плавно, т. е. с небольшой амплитудой?

Мы знаем, что г = 10 м/с ² и т.д. Тогда период T этого маятника вычисляется как:

Это действительно то, что мы знаем из собственного опыта.

Предположим, мы можем рассматривать сережку как простой маятник. Если кто-то идет, он лишь немного толкает сережку, вызывая небольшую амплитуду. Каков срок службы такой серьги, если длина шнура 1 см?

Период этого маятника рассчитывается следующим образом:

Это также то, что мы знаем из опыта: маленький маятник качается очень быстро.

Частота маятника

Частота (часто обозначаемая как f ) системы всегда обратна периоду этой системы.

Следовательно, частота маятника определяется как:

Помните, что стандартной единицей измерения частоты является герц (Гц), который является обратным значением секунды.

Период маятника – основные выводы

Маятник представляет собой систему, состоящую из объекта определенной массы, подвешенного на стержне или шнуре к неподвижной оси. Висячий объект называется бобом. Максимальный угол шнура с вертикалью называется амплитудой.
Простой маятник — это маятник, в котором стержень или шнур не имеют массы, а ось не имеет трения.
Период маятника – это продолжительность одного полного колебания груза.