Формула площадь двутавра: Площадь поперечного сечения двутавра: параметры расчета

alexxlab | 26.05.2023 | 0 | Разное

Калькулятор приведенной толщины металла | ЛЕНПОЖЗАЩИТА

Калькулятор приведенной толщины металла | ЛЕНПОЖЗАЩИТА

Размер шрифта

Цвет фона и шрифта

Изображения

Озвучивание текста

Обычная версия сайта

Приведённая толщина металла (ПТМ) – это важнейший параметр, на основе которого рассчитывается огнезащита несущих металлических конструкций, определенный в ГОСТ Р 53295-2009, как отношение площади поперечного сечения профиля (S) к периметру его обогреваемой поверхности сечения (P), по формуле: ПТМ=S/P. Таким образом, приведенная толщина металла не равна толщине металла.

Калькулятор ПТМ позволяет быстро произвести онлайн расчет приведенной толщины металла (ПТМ) для огнезащиты и дальнейшего расчёта необходимой толщины выбранного огнезащитного покрытия, с учётом обогреваемой поверхности, основных строительных профилей: двутавра, швеллера, уголка, профиля, трубы по размерам и листа по толщине.

Как пользоваться калькулятором?

1. Вначале выберите интересующий вас профиль и стандартный тип металла.

2. В левой таблице выберите:

• сортамент для двутавров и швеллеров;
• высоту, ширину и толщину для уголков и профилей;
• или введите свои значения для сварных двутавров, трубы или листа;

3. В правой таблице выберите обогреваемый периметр, стандартно выбраны все стороны и выделены синим цветом (для того чтобы исключить сторону, нажмите на неё на схематичном рисунке металла).

4. Готово! Вычисления отображаются моментально, на основе выбранных параметров, справа от изображения металла: приведенная толщина металла, обогреваемый периметр, площадь поверхности на один погонный метр и на одну тонну профиля.

• Тип Б – Нормальные двутавры
• Тип Ш – Широкополочные двутавры
• Тип К – Колонные двутавры
• Тип С – Свайные двутавры
• Тип ДБ – Дополнительные балочные двутавры
• Тип ДК – Дополнительные колонные двутавры

Двутавр СТО АСЧМ 20-93 ГОСТ Р 57837-2017 ГОСТ 26020-83 ГОСТ 8239-89 ГОСТ 19425-74 DIN 1025 по размерам Швеллер ГОСТ 8240-97 DIN 1026 Уголок ГОСТ 8509-93, 8510-86 DIN EN 10056-1-1998 Профиль ГОСТ 30245-2003 DIN EN 10210-2-2006 DIN EN 10219-2-2006 Труба по размерам Лист ГОСТ 19904, 19903 ммкгРассчитать

Нажмите на поверхность для исключения
из обогреваемого периметра

Профиль не выбран

Приведенная толщина металла:	мм
Обогреваемый периметр:	мм
Площадь поверхности / 1м:	м2
Площадь поверхности / 1т:	м2

Корзина

Очистить корзину

Построение эпюры касательных напряжений для двутавра

Пример решения задачи на построение эпюры касательных напряжений τ для двутаврового сечения стальной балки.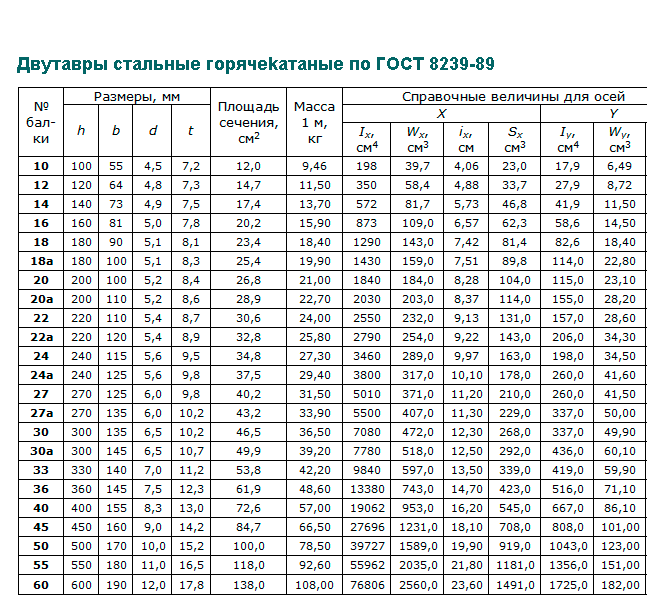

Предыдущий пункт решения:
Построение эпюры нормальных напряжений.

Задача
Построить эпюру касательных напряжений для двутавра при следующих данных:

• Величина поперечной силы в сечении балки — 58,3 кН
• Двутавровое сечение — №24а

Другие примеры решений >
Помощь с решением задач >

Пример решения

Расчет касательных напряжений в сечении балки ведется по формуле Журавского

Двутавровое сечение по высоте имеет 5 характерных точек: крайние, среднюю и точки, на уровне которых стенка двутавра соединяется с полками.

Обозначим их цифрами и проведем из них горизонтальные линии.

Другие видео

Начнем с крайних точек.

Статический момент в формуле Журавского одним из множителей включает в себя площадь сечения расположенную за рассматриваемой точкой.

Выше точки 1 и ниже точки 5 площадь сечения равна нулю, поэтому касательных напряжений там нет.

Максимальные напряжения следует ожидать в точке 3, потому что относительно нее будет самый большой статический момент. Его принимаем из сортамента.

Чтобы найти напряжения в точках 2 и 4 надо сначала рассчитать статический момент полки двутавра.

Для этого временно заменим её прямоугольником со сторонами b и t, центр тяжести которого, очевидно будет на расстоянии t/2 от точки 1.

Это сильно упрощает расчеты без особого ущерба для правильности вычислений.

Статический момент полки определяется произведением её площади на расстояние от оси x до её центра тяжести.

В этих точках сечение резко меняет свою ширину, поэтому получится скачок напряжений, и нам потребуется найти их величину в стенке и полке.

Другие видео

Начнем с полки, то есть сразу выше точки 2. Для этого в знаменатель формулы Журавского подставляем ширину полки b.

При расчете напряжения под точкой 2 подставляем толщину стенки d.

По полученным значениям строим эпюру касательных напряжений

Другие примеры решения задач >

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.

Если стоимость устроит вы сможете оформить заказ.

---

НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ

На нашем сайте можно бесплатно скачать:

– Рамки A4 для учебных работ
– Миллиметровки разного цвета
– Шрифты чертежные ГОСТ
– Листы в клетку и в линейку

Сохранить или поделиться с друзьями

---

Помощь с решением

---

Поиск формул и решений задач

Калькулятор площади поперечного сечения

Создано Rahul Dhari

Отзыв Стивена Вудинга

Последнее обновление: 11 февраля 2023 г.

Содержание:

• Что такое поперечное сечение и как рассчитать площадь поперечного сечения?
• Как найти площадь поперечного сечения?
• Пример: Использование калькулятора площади поперечного сечения.
• Применение форм поперечного сечения
• Часто задаваемые вопросы

Калькулятор площади поперечного сечения определяет площадь для различных типов балок. Брус – очень важный элемент в строительстве. Несущие элементы мостов, крыш и полов в зданиях доступны в различных поперечных сечениях. Читайте дальше, чтобы понять, как рассчитать площадь поперечного сечения 9Профиль 0021 I , профиль T , балка C , балка L , круглый стержень, труба и балки с прямоугольным и треугольным поперечным сечением.

Что такое поперечное сечение и как рассчитать площадь поперечного сечения?

Поперечное сечение определяется как общая область, полученная в результате пересечения плоскости с трехмерным объектом. Например, рассмотрим длинную круглую трубу, вырезанную (пересеченную) плоскостью. Вы увидите пару концентрических кругов. Концентрические окружности – это поперечное сечение трубы. Аналогично балки — L , I , C и T — названы по форме поперечного сечения.

Разрез трубы

Чтобы рассчитать площадь поперечного сечения, вам нужно рассматривать их как основные формы. Например, трубка представляет собой концентрический круг.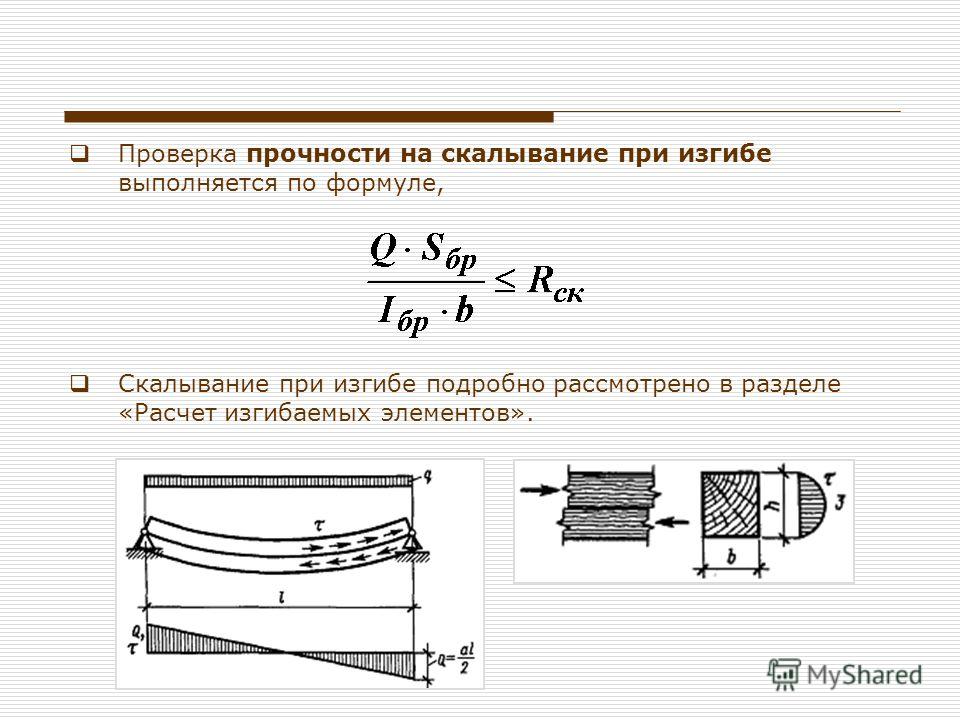 2)/4AC​=π×(D2−d2)/4 92)/4AC​=π×(D2−(D−2t)2)/4

Аналогично, площадь поперечного сечения для всех других форм, имеющих ширину W , высоту H и толщину t₁ и t₂ приведены в таблице ниже.

Различные перекрестные сечения191 W₁ + H – t) × t

Раздел	Область
Полово прямоугольник	(h w) – (w -2t₁).
Rectangle	W × H
I	2 × W × t₁ + (H – 2 × t₁) × t₂
C	2 × W × T₁ + (H – 2 × T₁) × T₂
T	W × T₁ + (H – T₁) × T₂
L
L 9499191
L 99919191919191991
Равнобедренный треугольник	0. 5 × B × H
Equilateral Triangle	0.4330 × L²
Circle	0.25 × π × D²
Tube	0,25 × π × (D² – (D – 2 × t)²)

Как найти площадь поперечного сечения?

Выполните следующие действия, чтобы найти площадь поперечного сечения.

• Шаг 1: Выберите форма поперечного сечения из списка, скажем, Полый прямоугольник . Теперь будет видна иллюстрация поперечного сечения и связанных с ним полей.
• Шаг 2: Введите ширину полого прямоугольника, W .
• Шаг 3: Заполните высоту поперечного сечения, H .
• Шаг 4: Вставьте толщину
  полого прямоугольника, t .
• Шаг 5: Калькулятор вернет площадь поперечного сечения .

Пример: Использование калькулятора площади поперечного сечения.

Найдите площадь поперечного сечения трубы, имеющей внешний диаметр 10 мм и толщину 1 мм .

• Шаг 1: Выберите из списка форму поперечного сечения , т. е. Труба .

• Шаг 2: Введите наружный диаметр трубы, D = 10 мм .

92AC​=π×(102−(10−2×1)2)/4=28,274 мм2

Применение форм поперечного сечения

Знаете ли вы?

• Балка I или H широко используется на железнодорожных путях.
• Балки T используются в ранних мостах и ​​используются для усиления конструкций, чтобы выдерживать большие нагрузки на перекрытия мостов и опор. См. наш калькулятор нагрузки на балку , чтобы узнать больше!

FAQ

Как рассчитать площадь поперечного сечения трубы?

Для расчета поперечного сечения трубы:

1. Вычесть квадратов внутреннего диаметра из наружного диаметра.
2. Умножьте число на π.
3. Разделите произведение на 4.

Как рассчитать площадь двутавра?

Площадь I сечения общей шириной W , высотой H и толщиной t можно рассчитать как:

Площадь = 2 × W × t + (H - 2 × t) × t

Как рассчитать площадь таврового сечения?

Площадь таврового сечения общей шириной W , высотой H и толщиной t можно рассчитать как:

Площадь = W × t + (H - 2 × t) × t

Каково поперечное сечение куба?

Поперечное сечение куба равно квадрату . Точно так же для прямоугольного параллелепипеда это либо квадрат, либо прямоугольник.

Rahul Dhari

Cross Section

Ширина (W)

Высота (H)

Толщина (T)

Область (A)

Проверьте 23 аналогичные калькуляторы с 2 -й геометрией 📏

Область прямоугольной ящики из Сумма. … 20 more форма, которая используется для прогнозирования прогиба, изгиба и напряжения в балках.

Area Moment of Inertia – Imperial units

• inches ⁴

Area Moment of Inertia – Metric units

• mm ⁴
• cm ⁴
• M ⁴

Преобразование между единицами

• 1 CM ⁴ = 10 ^-8 M ⁴ = 10 ^-8 M ⁴ = 10 ^-8 M ⁴ = 10 ^-8 M ⁴ = 10 ^-8 M ⁴ .0381
• 1 in ⁴ = 4.16×10 ⁵ mm ⁴ = 41.6 cm ⁴

Example – Convert between Area Moment of Inertia Units

9240 cm ⁴ can be converted to mm ⁴ by multiplying with 10 ⁴

(9240 cm ⁴ ) 10 ⁴ = 9. 24 10 ⁷ mm ⁴

Площадь момента инерции (момент инерции для области или второй момент площади)

для изгиба вокруг оси x может быть выражен как

I _x = y ² DA (1) DA (1) DA (1)

where

I _x = Area Moment of Inertia related to the x axis ( m ⁴ , mm ⁴ , inches ⁴ )

y = перпендикулярное расстояние от оси x до элемента DA (м, мм, дюймов )

DA = область элементала ( M

DA = область элемента ( M ^{2 DA = элементная область ( M 2 DA = элементная область ( M 2 DA = Элементная область ( M 2}

DA = элементная область ( M ²

DA. , дюймов ² )

Момент инерции для изгиба вокруг y -оси может быть выражен как

I _y 303030303030303030303030303 гг. 0371

where

I _y = Area Moment of Inertia related to the y axis ( m ⁴ , mm ⁴ , inches ⁴ )

x = перпендикулярное расстояние от оси y до элемента dA (м, мм, дюймов ) Разделы II

Solid Square Cross Section

The Area Moment of Inertia for a solid square section can be calculated as

I _x  = a ⁴  / 12                        (2)

where

a = сторона (мм, м, в …)

I _Y = ⁴ /12 (2B)

Сплошная сета

/12 (2B)

Сплошная сечение

Сплошная секция

.0442

The Area Moment of Ineria for a rectangular section can be calculated as

I _x = b h ³ / 12                          (3)

where

b = width

h = высота

I _Y = B ³ H/ 12 (3B)

Сплошной поперечный сечение

0002 The Area Moment of Inertia for a solid cylindrical section can be calculated as

I _x = π r ⁴ / 4

    = π d ⁴ / 64                            (4)

where

r = radius

d = diameter

 

I _y  = π r ⁴  / 4

    = π d ⁴  / 64                             (4b)

Полый цилиндрический поперечный сечение

Момент инерции площади для пологой цилиндрической секции может быть рассчитана как

I _x = D _O ^{4 = D _O 4 – D _O 4 – D _O 4 – D _. – D _O 4 = π} 0 – D _O 4 . ) / 64 (5)

, где

D _O = цилиндр.0370

I _Y = π (D _O ⁴ – D _I ⁴ ) / 64 (5B)

. Инерция для квадратного сечения может быть рассчитана как

I _x = I _y = a ⁴ / 12                   (6)

Моменты на любой прямоугольной линии, проходящей через центр площади сечения0442

Прямоугольное сечение и площадь момента на линии, проходящей через центр тяжести, можно рассчитать как

I _x = (b h / 12) (h ² cos ² a + b 2038 2 A) (7)

Симметричная форма

Площадь момента инерции для симметричной формы секции может быть рассчитана как

I x = (A 3 /12) + (B / 12) + (B / 12) + (B / 12) + (B / 12) + (B / 12) + (B / 12) + (B / 12) + (B / 12) + (B / 12) + (B / 12) + (B / 12) + (B / 12) + (B / 12) + (B / 12) + (B / 12) + (B / 12) + (B / 12) + (B / 12) + (B / 12) + (B / 12) + (B / 12) + (B / 12) + (B / 12) + (B / 12) + (B / 12) + (B / 12) + (B / 12) + (B / 12).