Формула предел прочности при растяжении – Предел прочности при растяжении определяют по формуле

alexxlab | 02.07.2020 | 0 | Разное

Предел прочности при растяжении определяют по формуле

Предел прочности при растяжении определяют по формуле:

σ_р = P/F₀ Па,

где P_{– наибольшая нагрузка, при которой произошел разрыв образца, Н;}

F₀ – площадь поперечного сечения образца до испытания, м².

Величину относительного удлинения образца при разрыве в процентах к первоначальной длине образца определяют следующим образом

ε = ∆l/l₀·100%,

где ε – удлинение образца, %; ∆l – приращение длины; l₀ – первоначальная длина.

2. Определение прочности при сжатии.

Прочность при сжатии (разрушающее напряжение при сжатии) характеризуется напряжением при сжатии, соответствующем нагрузке , вызывающей разрушение образца. Метод заключается в следующем. Образец в форме прямоугольной призмы, прямого цилиндра или прямой трубки стандартных размеров помещается между двумя плитами, которые сближаются с постоянной скоростью. В момент разрушения фиксируется нагрузка, при которой это разрушение произошло.

Разрушающее напряжение при сжатии рассчитывают по формуле:

σ_сж = P/F₀ Па,

где P_{– наибольшая нагрузка, при которой произошло разрушение образца, Н;}

F₀ – площадь поперечного сечения образца до испытания, м².

3. Испытание на ударный изгиб

(определение удельной ударной вязкости)

Удельная ударная вязкость определяется работой удара, необходимой для разрушения стандартного образца, свободно лежащего на двух опорах, при испытании его на изгиб ударной нагрузкой. Испытание проводится на маятниковом копре. Образец в форме бруска размером 10х15х120 мм. устанавливается на двух опорах копра так, чтобы удар пришелся по его широкой стороне. Маятник поднимается до верхнего исходного положения, в котором он фиксируется соответствующей защелкой. Стрелка устанавливается в начальное (нулевое) по-ложение. Маятник освобождается, и, свободно падая, ударяет по образцу, разрушая его. Работа А_н , затраченная на разрушение образца, определяется по формуле

А_н = Рl (cosβ – cosα), Дж,

где Р– вес маятника, Н ; l – длина маятника, т.е. расстояние от его оси до центра тяжести, м; α и β- углы подъема маятника соответственно до и после излома образца в градусах.

Ударная вязкость а_н определяется по формуле:

а_н = А_н / F Дж/м² ,

где А_н – работа, поглощенная образцом при его изломе; F – площадь поперечного сечения образца, м².

Чтобы не вычислять величину А_н по формуле, пользуются специальной таблицей (Приложение 7), в которой для каждого угла α и β указана величина работы А_н.

4. Определение прочности при статическом изгибе

Прочность при изгибе (разрушающее напряжение при изгибе) характеризуется изгибающим напряжением, возникающим в момент разрушения образца. При испытании на изгиб образцы из полимерных материалов в форме брусков размером 10х15х120 мм своей широкой стороной свободно устанавливают на опоры гидравлического пресса.. Середина образца должна совпадать с осью наконечника, передающего нагрузку. Образец подвергают действию разрушающей силы, создаваемой плунжером насоса. Скорость приложения нагрузки к образцу должна находится в пределах 20 – 60 мм/мин. Испытание проводят на ручном прессе.

Предел прочности при статическом изгибе определяется по формуле

σ_и = 3Рl/2вh² Па,

где Р – величина разрушающей силы, Н; l – расстояние между опорами, м; в –ширина образца, м; h – толщина образца, м.

Величина разрушающей силы определяется по формуле:

Р = f_пл ·( Р_м − Р₁ ) Н,

где f_пл – площадь плунжера ручного пресса, м²; Р_м – показание манометра при разрушении образца, Па; Р₁ – показание манометра при холостом ходе, Па.

4. Определение твердости материалов.

Твердость (поверхностная прочность) характеризуется способностью материала сопротивляться внедрению инородного тела. Твердость оценивают как отношение силы, под действием которой внедряется инородное тело, к размеру отпечатка, образовавшегося при его внедрении. Существует несколько методов определения твердости, которые различаются по значениям нагрузок, глубины внедрения, времени приложения нагрузки и по форме инородного тела, внедряемого в образец.

Наиболее распространенным методом определения твердости полимерных материалов является метод Бринелля. Он заключается во вдавливании в материал стального шарика под заданной нагрузкой и измерении глубины его вдавливания в поверхность образца через определенное время действия нагрузки, приложенной после предварительного нагружения.

Твердость по Бринеллю НВ (МПа) определяют по формуле:

где Р – нагрузка при испытании, Н; D – диаметр шарика, мм; d – диаметр лунки, мм.

Таблица 1. Общие сведения и применение полимерных диэлектриков

Наименование диэлектрика	Общие сведения и применение
Полиэтилен высокого, среднего и низкого давления (ПЭВД, ПЭСД, ПЭНД)	Непрозрачный термопластичный материал. Изготовление каркасов, панелей, гибкой изоляции.
Поливинилхлоридный пластикат (ПВХ)	Гибкий материал. Изоляция и защитные оболочки кабелей, проводов; шланги и трубки.
Винипласт (ПВХ жесткий)	Термопластичный негорючий материал. Применяется для дугогашения, изготовления пленок, листов, трубок, стержней и уголков.
Полиметилметакрилат (ПММА)	Прозрачный дугогасящий материал. Изготовление оснований, панелей, трубок, шкал, камер.
Полистирол	Прозрачный термопластичный материал. Изготовление катушек, лаков, пленок, нитей.

Таблица 2. Физико-механические свойства полимеров

Показатели	ПЭВД	ПЭНД	ПЭСД	ПП	ПВХ	ПММА	Поли-стирол
Прочность при растяжении σр ,МПа	17-10	45-18	40-18	30-40	40-60	60-90	35-50
Прочность при изгибе σизг ,МПа	20-17	40-20	40-25	90-120	80-120	80-120	80-100
Ударная вязкость ан, КДж/м2	Не лом.	2-150	7-120	100-110	2-10	8-20	1,5-20
Твердость по Бринеллю, НВ, МПа	17-25	49-60	60-68	60-65	130-160	170-240	140-200

СОДЕРЖАНИЕ ОТЧЕТА ПО РАБОТЕ

Отчет по работе должен содержать следующие разделы.

1. Цель работы.

2. Теоретические положения.

Раздел должен содержать основные определения (полимеры полимериза-ционные, поликонденсационные, термопласты, реактопласты, пластмассы, полимеры линейные, разветвленные, сетчатые и др.). Свойства полимеров, их применение в электротехнике, особенности механических свойств полимеров.

3. Практическая часть.

Раздел должен содержать описания методик испытаний полимерных материалов на растяжение, сжатие, статический изгиб, ударную вязкость, твердость, а также результаты испытаний с соответствующими расчетами.

Контрольные вопросы к работе № 8.

1. Чем отличаются термопласты от реактопластов?

2. Как можно повысить прочность полимерных материалов?

3. В чем заключается главная особенность строения полимеров?

4. На какие группы делят полимеры по форме макромолекул?

5. В чем особенность сетчатых полимеров?

6. В чем особенность механических свойств полимеров?

7. В каких физических состояниях могут находиться полимеры?

8. Чем обусловлена гибкость полимеров?

9. Как ведет себя линейный аморфный полимер ниже температуры хрупкости?

Библиографический список к работе №8

1. Энциклопедия полимеров. В 3-х томах. – М.: Советская энциклопедия, 1972. – Т.1. – 1224 с.; Т.2. – 1032 с.; Т.3. – 1150 с.

2. Кацнельсон М.Ю., Балаев Г.А. Полимерные материалы: Справочник. – Л.: Химия, 1982. – 317 с.

3. Ярославский Н.Е. Полимерные материалы в энергетике. – М.: Энергия, 1981. – 216 с.

4. Самоходский А.И., Кунявский М.Н. Лабораторные работы по металловедению и термической обработке металлов. – М.: Машиностроение, 1981. – 75 – 79 с.

ЛАБОРАТОРНАЯ РАБОТА № 9

ПРИГОТОВЛЕНИЕ ЭЛЕКТРОЛИТОВ ДЛЯ АККУМУЛЯТОРОВ И ОПРЕДЕЛЕНИЕ ПЛОТНОСТИ ЭЛЕКТРОЛИТОВ

Общие сведения

Для кислотных (свинцовых) аккумуляторов в качестве электролита применяют безводную (аккумуляторную) серную кислоту, растворенную в дистиллированной воде. Исправная работа аккумулятора во многом зависит от чистоты электролита, поэтому составные части электролита – кислота и вода – не должны содержать вредных примесей.

Плотность электролита сравнивают с плотностью дистиллированной воды, которая равна 1. Тогда плотность безводной серной кислоты равна 1,84 Г/см³. плотность электролита для различных типов аккумуляторов устанавливает завод–изготовитель.

С изменением температуры электролита меняется его плотность. За номинальную температуру электролита принята температура 15˚C. При температуре выше 15˚C вводят поправку +0,0007, при температуре ниже 15˚C вводят поправку -0,0007. Чем меньше плотность электролита, тем меньше внутреннее сопротивление аккумулятора, тем более долговечны его пластины. Но зато, чем больше масса аккумулятора и его габариты, тем больше подвержен электролит замерзанию. По значению плотности электролита судят о процессе зарядки аккумулятора и ее окончания, поэтому плотность необходимо измерять.

Для приготовления электролита определенной плотности можно пользоваться данными, приведенными в табл.1.

Рассмотрим несколько примеров составления электролита.

Пример1. Имеется раствор серной кислоты плотностью 1,41. Какое количество такого раствора и дистиллированной воды необходимо для приготовления 5л электролита плотностью 1,22.

По табл.1 находим, что 1л электролита плотностью 1,22 содержит 364 г безводной кислоты. 5л электролита должны содержать 364 х 5 = 1820 г = 1,82 кг кислоты. По той же таблице находим, что 1л раствора плотностью 1,41 содержит 721 г безводной кислоты. Следовательно, для получения 1,82 кг кислоты надо взять 1,82 : 0,721 = 2,5 л раствора плотностью 1,41. для получения 5л электролита плотностью 1,22 следует взять 2,5 л раствора серной кислоты плотностью 1,41, а остальные 2,5 л – дистиллированной воды.

Пример 2. Определить, сколько надо взять безводной серной кислоты плотностью 1,84 для приготовления 10 л электролита плотностью 1,274.

По табл. 1 находим, что 1 л электролита плотностью 1,724 содержит 461 г безводной кислоты. 10 л такого электролита должны содержать 461 х 10 = 4610 г = 4,61 кг кислоты. 1 л безводной кислоты весит 1,84 кг, поэтому для получения 4,61 кг необходимо взять 4,61 : 1,84 = 2,5 л кислоты.

Для получения 10 л электролита плотностью 1,274 следует взять 2,5 л чистой безводной кислоты, а остальные 7,5 л – дистиллированной воды.

Таблица 1

Содержание безводной серной кислоты плотностью 1,84 г/см³

в электролите

плотность электролита, г/см3	количество безводной серной кислоты на 1 л раствора при 15˚C	плотность электролита, г/см3	количество безводной серной кислоты на 1 л раствора при 15˚C	плотность электролита, г/см3	количество безводной серной кислоты на 1 л раствора при 15˚C
1 1,007 1,014 1,022 1,029 1,037 1,045 1,052 1,060 1,067 1,075 1,083 1,091 1,100 1,108 1,116 1,125 1,134 1,143 1,152 1,161 1,171 1,180	0 12 23 34 46 58 71 81 93 105 117 130 145 158 172 186 199 214 229 244 259 275 292	1,190 1,200 1,210 1,220 1,231 1,241 1,252 1,263 1,274 1,285 1,297 1,308 1,320 1,332 1,345 1,357 1,370 1,383 1,397 1,410 1,424 1,438 1,453	310 328 346 361 382 401 421 441 461 483 504 527 548 572 596 619 643 669 697 721 748 776 805	1,468 1,483 1,498 1,515 1,530 1,547 1,563 1,580 1,597 1,615 1,635 1,652 1,671 1,693 1,710 1,732 1,753 1,775 1,790 1,820 1,839	834 863 894 926 958 900 1022 1054 1091 1128 1168 1200 1249 1293 1340 1386 1442 1491 1539 1636 1839

ЦЕЛЬ РАБОТЫ

Получить практические навыки по приготовлению электролита. Освоить приемы определения плотности электролитов.

Приборы и оборудование

Для определения плотности электролита требуется ареометр, который состоит из стеклянной запаянной полой трубки и бумажной шкалы с делениями. Нижняя часть ареометра представляет собой трубку большего диаметра, на дне которой находится балласт – определенное количество ртути или дроби. Кроме того, нужно иметь стеклянную или фарфоровую посуду, мерный стакан и стеклянные или эбонитовые палочки.

Порядок выполнения работы

1. Залить в приготовленную посуду дистиллированную воду. Количество воды и кислоты брать в соответствии с табл. 1.

2. Вливать осторожно тонкой струей кислоту из мерного стакана в дистиллированную воду, помешивая раствор стеклянной или эбонитовой палочкой.

3. После остывания раствора измерить плотность электролита ареометром и сравнивать его с данными, приведенными в табл.1.

4. Результаты измерения и вычислений записать в табл. 2.

Таблица 2

№ п/п	Температура воздуха, ˚C	Электролит
		Наименование	Содержание кислоты,%	Расчетное значение плотности, г/см3	Плотность, измеренная ареометром г/см3,

refdb.ru

2.4. Расчеты на прочность при растяжении

2.4. РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ РАСТЯЖЕНИИ Основной задачей расчета конструкции на растяжение является обеспечение ее прочности в условиях эксплуатации. Условие прочности – оценка прочности элемента конструкции, сводящаяся к сравнению расчетных напряжений с допускаемыми: σ≤рσ[р ]; σ с ≤[ с],σ (2.9) где σр и σс – наибольшие расчетные растягивающие и сжимающие напряжения; [σр] и [σс] – допускаемые напряжения при растяжении и сжатии. Допускаемое напряжение – наибольшее напряжение, которое можно допустить в элементе конструкции при условии его безопасной, долговечной и надежной работы: Здесь σпред – предельное напряжение (состояние), при котором конструкция перестает удовлетворять эксплуатационным требованиям; им мо- гут быть предел текучести, предел прочности, предел выносливости, пре- дел ползучести и др. Для конструкций из пластичных материалов при определении допускаемых напряжений используют предел текучести σт (рис. 2.4, а). Это связано с тем, что в случае его превышения деформации резко возрастают при незначительном увеличении нагрузки и конструкция перестает удовлетворять условиям эксплуатации. Допускаемое напряжение в этом случае определяют как Для хрупких материалов (чугун, бетон, керамика) где σвр и σвс – пределы прочности при растяжении и сжатии (рис. 2.4, б). Здесь [n] – нормативный коэффициент запаса прочности. В зависимости от той предельной характеристики, с которой сравнивают расчетное напряжение σ, различают [nт] – нормативный коэффициент запаса прочности по отношению к пределу текучести σт и [nв] – нормативный коэффициент запаса прочности по отношению к пределу прочности σв. Запас прочности – отношение предельно допустимой теоретической нагрузки к той нагрузке, при которой возможна безопасная работа конструкции с учетом случайных перегрузок, непредвиденных дефектов и недостоверности исходных данных для теоретических расчетов. Нормативные коэффициенты запаса прочности зависят: − от класса конструкции (капитальная, временная), − намечаемого срока эксплуатации, − условий эксплуатации (радиация, коррозия, загнивание), − вида нагружения (статическое, циклическое, ударные нагрузки) − неточности задания величины внешних нагрузок, − неточности расчетных схем и приближенности методов расчета − и других факторов. Нормативный коэффициент запаса прочности не может быть единым на все случаи жизни. В каждой отрасли машиностроения сложились свои подходы, методы проектирования и приемы технологии. В изделиях общего машиностроения принимают [nт] = 1,3 – 2,2; [nв] = 3 – 5. Вероятность выхода из строя приближенно можно оценить с помощью коэффициента запаса в условии прочности: n = 1 соответствует вероятности невыхода из строя 50 %; n = 1,2 соответствует вероятности невыхода из строя 90 %; n = 1,5 соответствует вероятности невыхода из строя 99 %; n = 2 соответствует вероятности невыхода из строя 99,9 %. Для неответственных деталей n = 2 много. Для ответственных – мало. Так для каната подъемного лифта это означает на 1000 подъемов одно падение. При расчете конструкций на прочность встречаются три вида задач, которые вытекают из условия прочности а) поверочный расчет (проверка прочности). Известны усилие N и площадь A. Вычисляют σ = N/A и, сравнивая его с предельным σт или σв (для пластичного и хрупкого материалов соответственно), находят фактический коэффициент запаса прочности который затем сопоставляют с нормативным [n]; б) проектный расчет (подбор сечения). Известны внутреннее усилие N и допускаемое напряжение [σ]. Определяют требуемую площадь поперечного сечения стержня в) определение грузоподъемности (несущей способности). Известны площадь А и допускаемое напряжение [σ]. Вычисляют внутреннее усилие N≤N[ ] = ⋅[σ]A, (2.15) а затем в соответствие со схемой нагружения – величину внешней нагрузки F ≤ [F].

dx-dy.ru

при растяжении, кручении и изгибе.

Эта статья будет посвящена расчетам на прочность, которые выполняются в сопромате и не только. Расчеты на прочность бывают двух видов: проверочные и проектировочные (проектные).

Проверочные расчеты на прочность – это такие расчеты, в ходе которых проверятся прочность элемента заданной формы и размеров, под некоторой нагрузкой.

В ходе проектировочных расчетов на прочность определяются какие-то размеры элемента из условия прочности. Причем, очевидно, что для разных видов деформаций эти условия прочности различны. Также к проектным расчетам можно отнести расчеты на грузоподъемность, когда вычисляется максимальная нагрузка, которую может выдерживать конструкция, не разрушаясь.  Рассмотрим более подробно, как проводится прочностные расчеты для разных случаев.

Расчеты на прочность при растяжении (сжатии)

Начнем, пожалуй, с самого простого вида деформации растяжения (сжатия). Напряжение при центральном растяжении (сжатии) можно получить, разделив продольную силу на площадь поперечного сечения, а условие прочности выглядит вот так:

где сигма в квадратных скобках – это допустимое напряжение. Которое можно получить, разделив предельное напряжения на коэффициент запаса прочности:

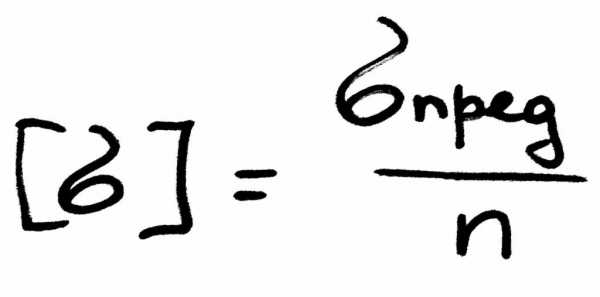
Причем, за предельное напряжение для разных материалов принимают разное значение. Для пластичных материалов, например, для малоуглеродистой стали (Ст2, Ст3) принимают предел текучести, а для хрупких (бетон, чугун) берут в качестве предельного напряжения – предел прочности (временное сопротивление). Эти характеристики получают при испытании образцов на растяжение или сжатие на специальных машинах, которые фиксируют характеристики в виде диаграммы.

Коэффициент запаса прочности выбирается конструктором исходя из своего личного опыта, назначения проектируемой детали и сферы применения. Обычно, он варьируется от 2 до 6.

В случае если необходимо подобрать размеры сечения, площадь выражают таким образом:

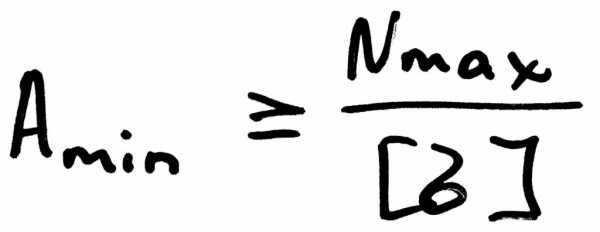
Таким образом, минимальная площадь поперечного сечения при центральном растяжении (сжатии) будет равна отношению продольно силы к допустимому напряжению.

Расчеты на прочность при кручении

При кручении расчеты на прочность в принципе схожи с теми, что проводятся при растяжении. Только здесь вместо нормальных напряжений появляются касательные напряжения.

На кручение работают, чаще всего, детали, которые называются валами. Их назначение заключается в передаче крутящего момента от одного элемента к другому. При этом вал по всей длине имеет круглое поперечное сечение. Условие прочности для круглого поперечного сечения можно записать  так:

где Ip — полярный момент сопротивления, ρ — радиус круга. Причем по этой формуле можно определить касательное напряжение в любой точке сечения, варьируя значение ρ. Касательные напряжения распределены неравномерно по сечению, их максимальное значение находится в наиболее удаленных точках сечения:

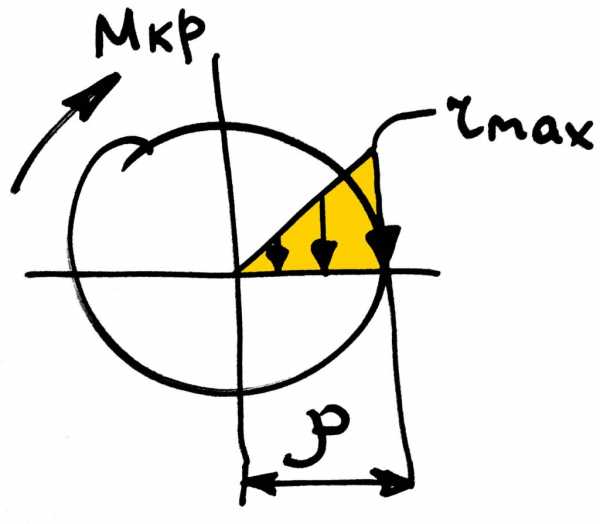
Условие прочности, можно записать несколько проще, используя такую геометрическую характеристику как момент сопротивления:

То бишь максимальные касательные напряжения равны отношению крутящего момента к полярному моменту сопротивления и должны быть меньше либо равны допустимому напряжению. Геометрические характеристики для круга, упомянутые выше можно найти вот так:

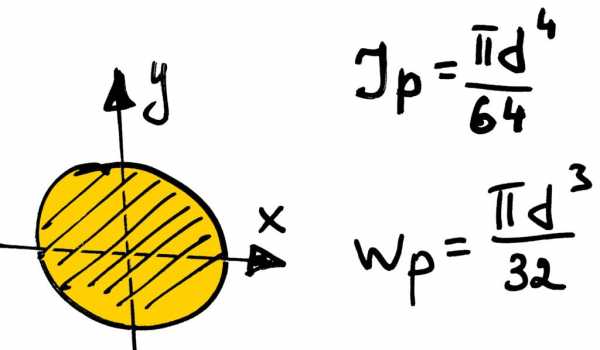
Иногда в задачах встречаются и прямоугольные сечения, для которых момент сопротивления определяется несколько сложнее, но об этом я расскажу в другой статье.

Расчеты на прочность при изгибе

ssopromat.ru

4.4.3 Метод определения предела прочности при одноосном растяжении

Определение предела прочности при растяжении осуществляется косвенным методом. Сущность метода заключается в определении максимальной разрушающей силы, приложенной перпендикулярно к оси образца породы цилиндрической формы, в результате чего в образце возникают растягивающие напряжения, приводящие к его разрушению в плоскости предельного сечения.

Образец цилиндрической формы, диаметром 40…50 мм устанавливают так, что ось его параллельна плоскостям пресса (рисунок 4.29) и прикладывают силу Р. После разрушения образца измеряют размеры поверхности разрушения в двух направлениях: вдоль образующей h и диаметра d.

Предел прочности при растяжении определяется по формуле

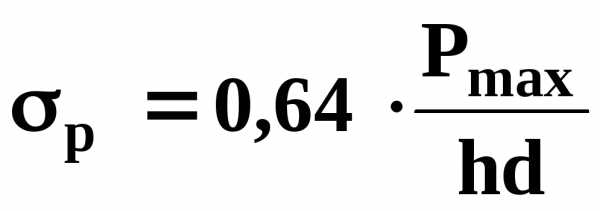, (4.45)

где d – диаметр образца, м;

h – высота образца, м;

P_max– разрушающая сила, Н.

Рисунок 4.29 – Испытание на растяжение: 1 – образец; 2 – плиты пресса; 3 – проекция плоскости разрушения

Результаты испытания применяются при построении паспорта прочности.

4.4.4 Метод определения предела прочности при срезе

Сущность метода заключается в определении максимального разрушающего касательного напряжения при действии на образец пород срезающих и нормальных сжимающих нагрузок в матрицах испытательного устройства.

Заготовки для образцов получают выбуриванием из проб керна диаметром 44 мм или обтачиванием на токарном станке до нужного диаметра. Образцы должны быть с явно выраженной слоистостью или упорядоченной трещиноватостью. Высота образца равна диаметру. Торцевые и боковые поверхности тщательно шлифуются специальным порошком.

Образец 1 помещается в специальное устройство, состоящее из трех пар сменных матриц 2 с углом наклона α = 30⁰; 45 и 60⁰, пара бронзовых разрезных цилиндрических обойм – вкладышей 3 с внутренним диаметром 44 мм, две плиты 4 и ролики 5 (рисунок 4.30).

Боковую поверхность образца оборачивают медной фольгой, устанавливают образец во вкладыши, устанавливают верхнюю матрицу, затем роликовую опору, располагая оси роликов параллельно срезающей кромке матриц. Устанавливают устройство между плитами пресса и нагружают силой до разрушения образца.

Нормальное давление на плоскость среза

, (4.46)

где Р_max– вертикальная разрушающая нагрузка, Н;

α – угол между плоскостью среза и направлением действия силы;

d – диаметр образца, м;

h – высота образца, м.

Р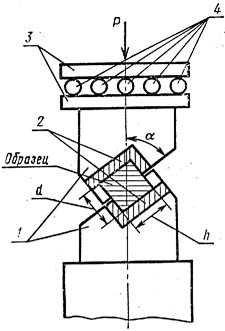исунок 4.30 – Приспособление для испытания на срез

Предел прочности при срезе, соответствующий определенному нормальному давлению

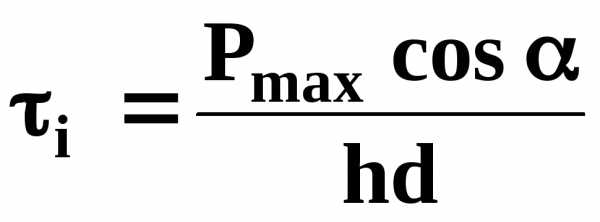(4.47)

По результатам строят предельную кривую прочности горных пород при срезе в зависимости от нормального давления, действующего на плоскость среза, в координатах σ и τ (рисунок 4.31). По оси абсцисс откладывают для каждого из углов наклона матриц α значения нормальных давлений, а по оси ординат соответствующие им значения пределов прочности породы при срезе. Кривая представлена на рисунке, где τ_о– предел прочности при чистом сдвиге.

Рисунок 4.31 – Предельная кривая прочности горных пород при срезе

4.4.5 Метод определения предела прочности при изгибе

Образцы получают из проб керна, диаметром 90…100 мм. От полученных заготовок отрезают с помощью камнерезной машины диски толщиною 10 ± 1 мм.

Образец 1 устанавливают на опорное кольцо 2, а сверху ставят на него кольцевой пуансон 3 (рисунок 4.32), прикладывают силу и определяют разрушающую нагрузку.

Предел прочности при изгибе определяют по формуле

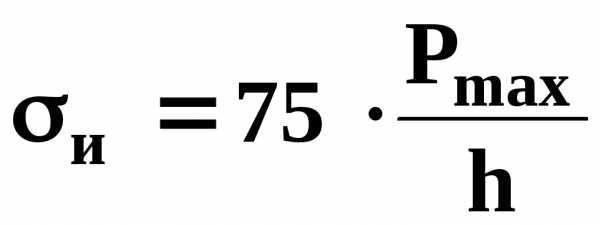, Па, (4.48)

где Р_max– максимальная разрушающая сила, Н;

h – толщина образца, м.

Р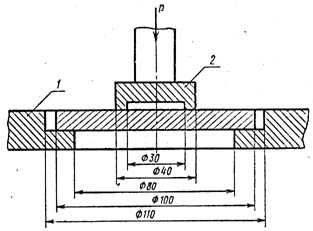исунок 4.32 – Схема установки для испытания на изгиб

studfiles.net

Условие прочности при растяжении-сжатии

При продольном осевом нагружении (растяжении-сжатии) в поперечных сечениях бруса имеют место только нормальные напряжения σ. Поэтому для обеспечения прочности стержней и стержневых систем достаточно выполнение условия:

Здесь
σ_max – максимальные расчетные нормальные напряжения в стержне,
N – внутренние продольные силы (принимаются с построенных эпюр),
А – соответствующая площадь поперечного сечения бруса,
[σ] – допустимые напряжения (расчетное сопротивление) для материала стержня, определяемое как:

n – коэффициент запаса прочности, устанавливаемый нормативными документами.

Данное условие означает что для того чтобы стержень при растяжении-сжатии оставался прочным, напряжения σ в его сечениях не должны превышать допустимых значений [σ].

В случаях, когда для материала стержней допустимые напряжения на растяжение [σ]_р и на сжатие [σ]_сж отличаются, при сравнении необходимо учитывать знак напряжений σ, который зависит только от знака соответствующих внутренних сил N.

Так, положительные значения напряжений σ сравниваются с [σ]_р, отрицательные напряжения по модулю не должны превышать значения [σ]_сж.

Три задачи расчета на прочность

Данное условие прочности позволяет решать три основных задачи сопротивления материалов и технической механики:

Проверка на прочность.

В случае, когда известны внешние нагрузки, а также размеры и материал стержня можно выполнить проверку его прочности. Для этого по каждому участку рассчитывается величина нормальных напряжений σ, после чего максимальная из них сравнивается с заданным допустимым значением [σ].

Ответ в данной задаче дается в виде заключения:

• если σ_max ≤ [σ] стержень прочный,
• если σ_max > [σ] стержень непрочный.

Подбор размеров сечения (проектировочный расчет)

Эта задача является основной в технической механике. Здесь, по известным схеме нагружения и материалу стержня определяется минимально необходимая площадь поперечного сечения A обеспечивающая его прочность.

Для этого условие прочности записывается относительно искомой величины.

Полученные размеры в случае необходимости можно только увеличивать. Уменьшение размеров приведет к превышению напряжениями допустимых значений.

Определение грузоподъемности стержня.

Данная формула позволяет по известным размерам и материалу рассчитать величину допустимой внутренней силы, которую может выдержать стержень, оставаясь прочным.

В данном случае условие прочности записано относительно внутренней силы N.

Напряжения при растяжении-сжатии >
Расчеты на прочность при растяжении-сжатии >

isopromat.ru

2.3 Расчеты на прочность и жесткость при растяжении (сжатии)

Одна из основных задач сопротивления материалов – подобрать размеры деталей, обеспечивающие прочность и жесткость этих деталей, подверженных тому или иному силовому, температурному или другому воздействию. Указанные размеры можно определить из расчета на прочность или жесткость. Рассмотрим условия прочности и жесткости для случаев простого растяжения (сжатия). Опасность наступления разрушения характеризуется величинами наибольших нормальных и касательных напря­жений, возникающих при нагружении в опасных (т. е. наиболее напряжен­ных) точках сечения. Очевидно, что реальные материалы не могут выдерживать сколь угодно большие напряжения. Поэтому величины наибольших напряжений из условия надежности работы детали необходимо ограничивать некоторыми допустимыми значениями, такими, чтобы деталь испытывала только упругие деформации. Их называют допускаемыми напряжениями. При растяжении и сжатии допускаемые напряжения обозначают [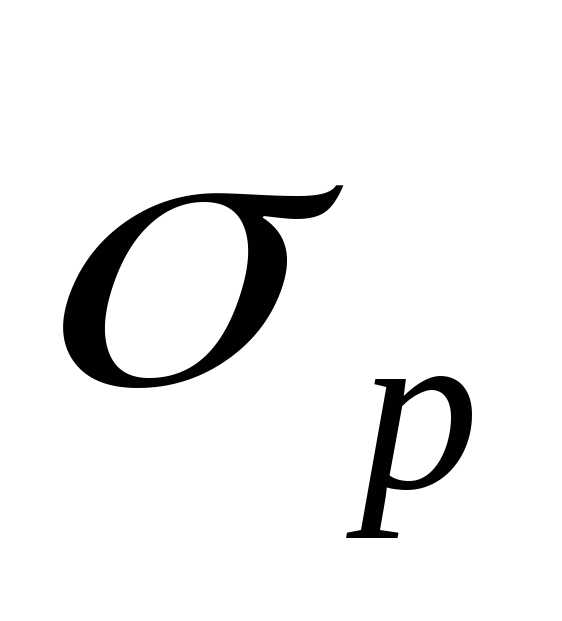], [] 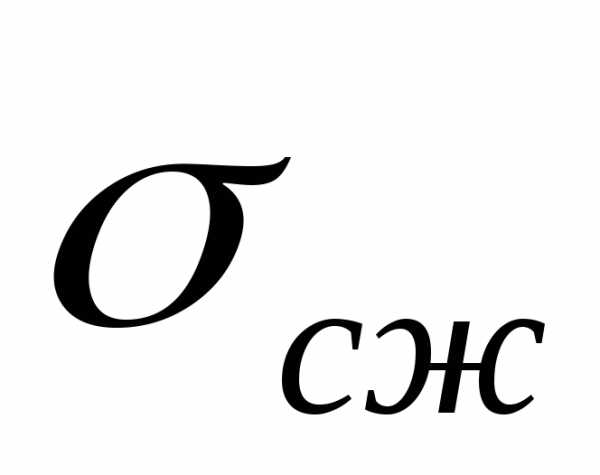соответственно.

Если из расчета известны максимальные и минимальные (по алгебраической величине) напряжения, возникающие в опасном сечении детали, то условия прочности могут быть записаны следующим образом:

; .

Если материал одинаково сопротивляется растяжению и сжатию, что характерно для пластичных материалов (более строго для материалов в пластичном состоянии), а значит

,

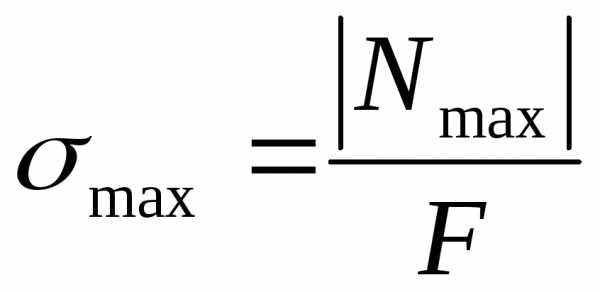(2.15)

и условие прочности при растяжении (сжатии) запишем в виде:

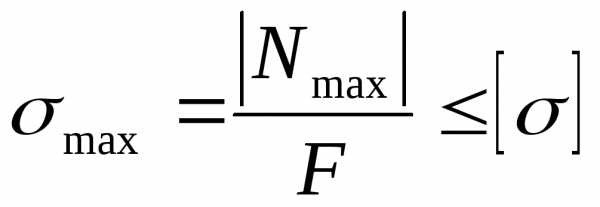. (2.16)

В некоторых случаях для обеспечения нормальной работы машин и сооружений размеры их деталей нужно выбирать так, чтобы обеспечивалось условие жесткости, то есть ограничить предельные деформации (перемещения) элементов конструкции.

Условие жесткости, ограничивающее изменение длины элемента, имеет следующий общий вид: ,

где – изменение размеров детали;

[]- допускаемая величина этого изменения.

Учитывая, что при растяжении (сжатии) абсолютное удлинение в общем виде определяется как алгебраическая сумма величин по участкам

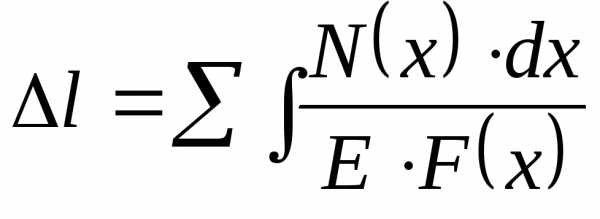, (2.17)

условие жесткости при растяжении (сжатии) запишем следующим образом:

. (2.18)

3 Механические свойства материалов

3.1 Методика проведения испытаний

При проектировании конструкций, машин и механизмов инженеру необходимо знать значения величин, характеризующих прочностные и деформационные свойства материалов. Их можно получить путем механических испытаний, проводимых в лабораториях на соответствующих испытательных машинах. Таких испытаний проводится много и самых различных, например испытания на твердость, сопротивляемость ударным и переменным нагрузкам, противодействие высоким температурам и т.д. Нами будут рассмотрены испытания на растяжение, они позволяют получить наибольшую информацию о механических свойствах материалов. Испытания проводятся в соответствии с ГОСТ 1497-89.

При испытаниях на растяжение применяют цилиндрические или плоские образцы. Образцы имеют рабочую часть с начальной длиной 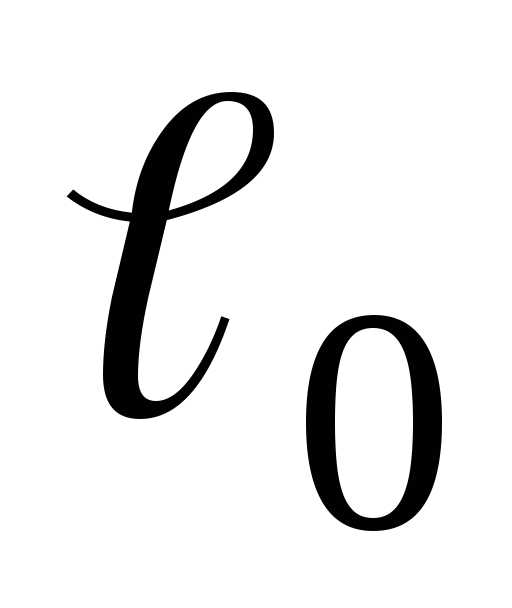, на которой определяется удлинение, и головки с переходным участком, форма и размеры которых зависят от способов их крепления в захватах машины (рис. 3.1). Различают длинные образцы с отношениеми короткие -. Размеры образцов делают стандартными для того, чтобы результаты испытаний, полученные в разных лабораториях, были сравнимы.

Испытания проводят на разрывных или универсальных машинах. В зависимости от метода приложения нагрузки машины бывают с механическим или гидравлическим приводом. Все машины снабжены устройством для автоматической записи в определенном масштабе диаграммы растяжения, т.е. графика зависимости между растягивающей силой P и удлинением рабочей части образца .

studfiles.net

Расчеты на прочность при растяжении и сжатии — Мегаобучалка

 

Расчеты на прочность ведутся по условиям прочности — нера­венствам, выполнение которых гарантирует прочность детали при данных условиях.

Для обеспечения прочности расчетное напряжение не должно превышать допускаемого напряжения:

Расчетное напряжение а зависит от нагрузки и размеров попе­речного сечения, допускаемое только от материала детали и усло­вий работы.

Существуют три вида расчета на прочность.

1. Проектировочный расчет — задана расчетная схема и на­грузки; материал или размеры детали подбираются:

– определение размеров поперечного сечения:

– подбор материала

по величине σ_пред можно подобрать марку материала.

 

2. Проверочный расчет — известны нагрузки, материал, раз­меры детали; необходимо проверить, обеспечена ли прочность.

Проверяется неравенство

3. Определение нагрузочной способности (максимальной нагрузки):

Примеры решения задач

Прямой брус растянут силой 150 кН (рис. 22.6), материал — сталь σ_т = 570 МПа, σ_в = 720 МПа, запас прочности [s] = 1,5. Определить размеры поперечного сечения бруса.

Решение

1. Условие прочности:

2. Потребная площадь поперечного сече­ния определяется соотношением

3. Допускаемое напряжение для материала рассчитывается из заданных механических характеристик. Наличие предела текучести означает, что материал — пластичный.

4. Определяем величину потребной площади поперечного сече­ния бруса и подбираем размеры для двух случаев.

Сечение — круг, определяем диаметр.

 

Полученную величину округляем в большую сторону d = 25 мм, А = 4,91 см².

Сечение — равнополочный уголок № 5 по ГОСТ 8509-86.

Ближайшая площадь поперечного сечения уголка — А = 4,29 см² (d = 5 мм). 4,91 > 4,29 (Приложение 1).

Контрольные вопросы и задания

1. Какое явление называют текучестью?

2. Что такое «шейка», в какой точке диаграммы растяжения она образуется?

3. Почему полученные при испытаниях механические характе­ристики носят условный характер?

4. Перечислите характеристики прочности.

5. Перечислите характеристики пластичности.

6. В чем разница между диаграммой растяжения, вычерченной автоматически, и приведенной диаграммой растяжения?

7. Какая из механических характеристик выбирается в качестве предельного напряжения для пластичных и хрупких материалов?

8. В чем различие между предельным и допускаемым напряже­ниями?

9. Запишите условие прочности при растяжении и сжатии. Отли­чаются ли условия прочности при расчете на растяжение и расчете на сжатие?

10.

Ответьте на вопросы тестового задания.

Темы 2.2. Растяжение и сжатие

megaobuchalka.ru