Формула предел прочности при сжатии: Прочность при сжатии — Материалы и свойства
alexxlab | 18.05.2023 | 0 | Разное
Прочность при сжатии — Материалы и свойства
Главная » Материалы и свойства
Автор Admin На чтение 3 мин. Просмотров 152 Опубликовано
Прочность при сжатии – важное механическое свойство. Характеризуется пределом прочности породы при сжатии в сухом состоянии. Действующий стандарт на блоки подразделяет породы по Этому показателю на три класса: прочные (свыше 80 МПа), средней прочности (40—80 МПа), и низкопрочные (5—40 МПа).
Рис. 16. Схема гидравлического пресса для испытаний образцов на сжатие
Стандарт на камни бортовые (ГОСТ 6666—81) допускает изготовление этой продукции из горных пород с пределом прочности при сжатии не ниже, МПа: для изверженных пород – 90, метаморфических и осадочных – 60. Стандарт на камни брусчатые (ГОСТ 23668—79) допускает изготовление их из изверженных пород с пределом прочности не ниже 100 МПа.
1 – станина; 2 – гидроцилиндр; 3 – поршень, 4 – нижняя плита; 5 – испытываемый образец камня; в – верхняя плита; 7 – установочный винт; 8 – манометры; 9 – насос
Определение предела прочности горных пород при сжатии производят на пяти образцах кубической формы с ребром 40—50 мм или цилиндрах диаметром и высотой 40 – 50 мм. Каждый образец перед испытанием очищают щеткой от рыхлых частиц, пыли и высушивают до постоянной массы. Затем тщательно обрабатывают на шлифовальном станке грани образцов, к которым будет приложена нагрузка, для обеспечения их параллельности. После этого образцы измеряют штангенциркулем, устанавливают в центре опорной плиты пресса (рис. 16), имеющей разметку для центровки образцов, и прижимают верхней плитой пресса, которая должна плотно прилегать по всей поверхности верхней грани образцов.
Нагрузку на образец при испытании увеличивают непрерывно и постоянно со скоростью, обеспечивающей его разрушение через 20—60 с после начала испытаний.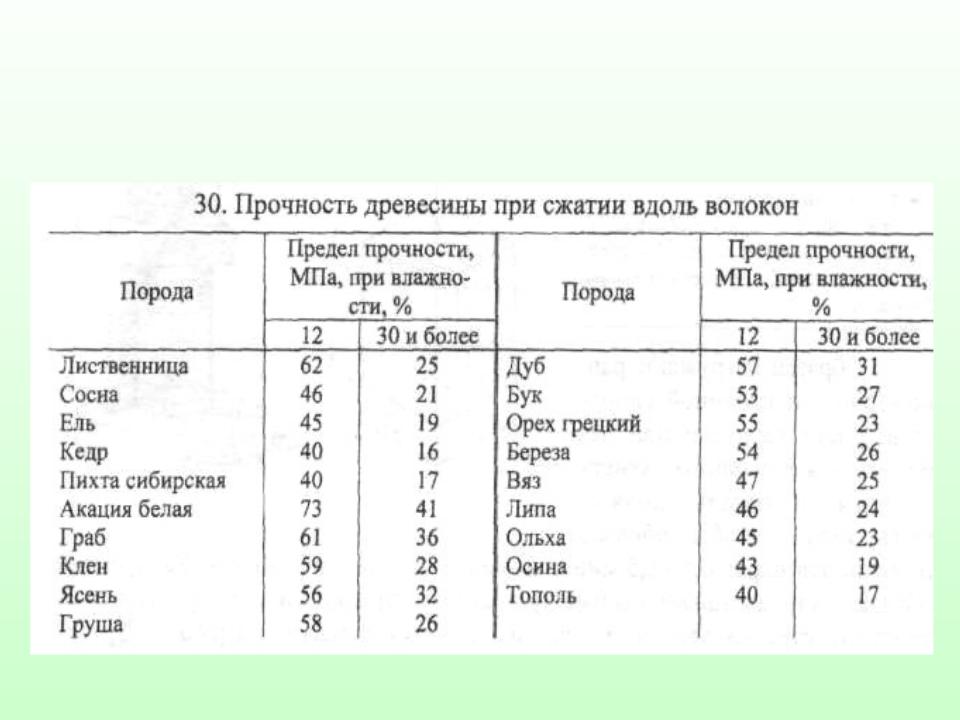 Величина разрушающей нагрузки должна составлять не менее 10 % от предельно развиваемого прессом усилия. Момент разрушения образца устанавливают по началу обратного движения указательной стрелки силоизмерителя при работающем нагружающем устройстве.
Величина разрушающей нагрузки должна составлять не менее 10 % от предельно развиваемого прессом усилия. Момент разрушения образца устанавливают по началу обратного движения указательной стрелки силоизмерителя при работающем нагружающем устройстве.
Предельную (разрушающую) нагрузку определяют по положению -фиксирующей стрелки пресса. Если она отсутствует, надо внимательно следить за указательной стрелкой. За предельную нагрузку принимают наибольшее число делений, достигнутое движущейся стрелкой. При испытаниях образцов низкопрочных пород разрушение более продолжительно и нередко наблюдается плавный сброс нагрузки; в этом случае за предельную нагрузку принимают наибольшее число делений по шкале, которое было достигнуто указательной стрелкой.
Для вычисления предела прочности при сжатии определяют разрушающее усилие непосредственно по силоизмерителю или по тарировочным таблицам, прилагаемым прессу. При использовании манометров разрушающее усилие может быть определено как произведение площади поршня пресса на максимальное давление масла в прессе в момент разрушения образца (по показанию манометра).
Предел прочности образца при сжатии Rсж, МПа, вычисляют с точностью до I МПа по формуле
Rсж = P(10*F),
где P – разрушающее усилие пресса, Н; F – площадь поперечного сечения образца, м2.
Предел прочности породы при сжатии вычисляют как среднее арифметическое результатов испытаний пяти образцов. Значения этого показателя для большинства видов облицовочного камня, используемого в строительстве, даны в приложении.
Кроме предела прочности горных пород при сжатии в сухом состоянии, в процессе проведения испытания обычно определяют также и значение этого показателя у пород в водонасыщенном состоянии, что необходимо для оценки размягчения породы. Эти испытания проводятся аналогично вышеописанным (испытания сухих образцов) с той лишь разницей, что перед раздавливанием на прессе образцы выдерживаются в сосуде с водой комнатной температуры в течение 48 ч.
ОглавлениеПРЕДИСЛОВИЕГЛАВА 1. ВВЕДЕНИЕ 1. Сопротивление материалов — наука о прочности и надежности конструкций 2. Модели прочностной надежности Модели прочностной надежности. Конструкционные материалы. Три уровня моделей материала. Модели материала в общей модели прочностной надежности.  Модели формы. Модели нагружения. Модели разрушения. ГЛАВА 2. НАПРЯЖЕНИЯ 3. Нормальные и касательные напряжения Нормальные и касательные напряжения. 4. Напряженное состояние в точке Свойства парности касательных напряжений. 5. Плоское напряженное состояние Главные площадки при плоском напряженном состоянии. Главные напряжения при плоском напряженном состоянии. Наибольшие касательные напряжения. 6. Объемное напряженное состояние Напряжения в произвольной косой площадке. Главные площадки и главные напряжения при объемном напряженном состоянии. Инварианты напряженного состояния в точке. Понятие о тензоре напряженного состояния. 7. Дифференциальные уравнения равновесия элемента тела и краевые условия Дифференциальные уравнения равновесия элемента тела. Краевые условия для напряжений. Действие сосредоточенных сил. Принцип Сен-Венана для краевых условий. ГЛАВА 3. ДЕФОРМАЦИИ Определение линейной деформации.  Определение угловой деформации. 9. Связь перемещений и деформаций Формулы Коши для линейных деформаций. 10. Линейная деформация в произвольном направлении. Главные деформации, тензор деформаций Главные направления и главные деформации. 11. Уравнения совместности деформаций ГЛАВА 4. МЕХАНИЧЕСКИЕ СВОЙСТВА КОНСТРУКЦИОННЫХ МАТЕРИАЛОВ 12. Диаграммы деформирования, пределы текучести и прочности Упругость, модуль упругости, пластичность, закон разгрузки и закон упрочнения. Пределы текучести и прочности при сжатии. Определение предела прочности материала с помощью испытания твердости. 13. Деформации и характеристики пластичности Дополнительные характеристики хрупкости и пластичности материала. 14. Истинные диаграммы деформирования и их схематизация Особенности кривых деформирования 15. Ползучесть и длительная прочность Кривые ползучести. Пределы ползучести. Влияние ползучести на напряженное состояние в элементах конструкций. 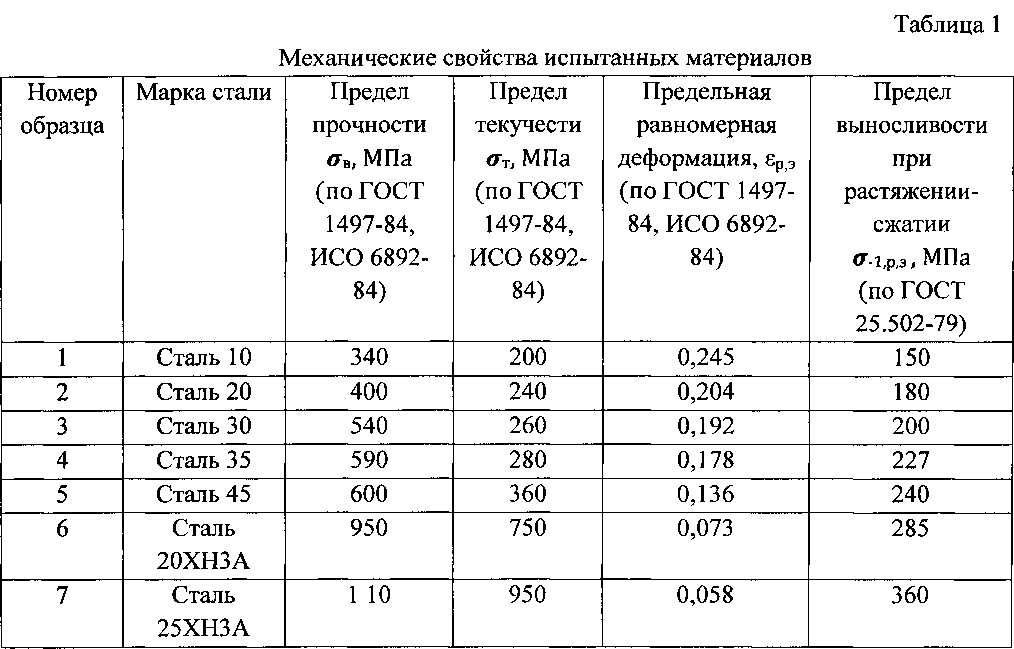 Длительная прочность, предел длительной прочности. Зависимость пределов длительной прочности от времени нагружения. Рассеяние долговечности при испытаниях длительной прочности. Зависимость пределов длительной прочности от температуры. Длительная пластичность и особенности разрушения при длительной прочности. 16. Усталость материалов и элементов конструкций Циклы переменных напряжений. Испытания на усталость. Влияние числа циклов нагружения на усталостную прочность, кривые выносливости, пределы выносливости. Уравнение кривых выносливости. Влияние постоянных напряжений на усталостную прочность. Влияние поверхностного слоя. Влияние абсолютных размеров деталей. Рассеяние усталостной долговечности. 17. Малоцикловая усталость Изотропное и анизотропное упрочнения при пластических деформациях. Явление малоцикловой усталости. ГЛАВА 5. МОДЕЛИ УПРУГОСТИ, ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ Связь деформаций сдвига и касательных напряжений.  Связь модуля сдвига с модулем упругости и коэффициентом Пуассона. Температурная деформация. Общая форма закона упругости. Другие формы закона упругости. Матричная запись закона упругости. Модель упругости для анизотропного тела. 19. Модели пластичности Уравнения пластичности в векторной форме. Интенсивность напряжений и деформаций. Интенсивность упругих и пластических деформаций. Обобщенная кривая деформирования. Еще одна форма уравнений Генки — Ильюшина. Коэффициент Пуассона при упругопластических деформациях. Метод переменных параметров упругости. Ограничения при использовании модели пластичности на основе деформационной теории. 20. Модели ползучести и вязкоупругости Модели ползучести, основанные на теории старения. Изохронные кривые ползучести. Модели ползучести, основанные на теории течения и теории упрочнения. Установившаяся ползучесть. Модели вязкоупругости. ГЛАВА 6. РАСТЯЖЕНИЕ И СЖАТИЕ СТЕРЖНЕЙ 21.  Растяжение и сжатие стержней сосредоточенными и распределенными силами Растяжение и сжатие стержней сосредоточенными и распределенными силамиПриближенные модели растяжения и сжатия стержней. Растяжение стержня с учетом действия собственного веса. Растяжение стержня в поле центробежных сил. Приближенная модель прочностной надежности лопатки газовой турбины. Связь запаса прочности по напряжениям и запаса прочности по долговечности. Прочностная модель болтового соединения. Модель прочностной надежности болта при действии переменных нагрузок. Приближенные модели термоциклической прочности элемента конструкции. Учет ползучести материала при определении температурных напряжений. 23. Стержневые системы (фермы) Статически определимые фермы. Общие замечания о статически определимых фермах и сопоставление со статически неопределимыми. 24. Статически неопределимые стержневые системы Работа статически неопределимой системы после возникновения пластических деформаций.  Модель надежности по несущей способности. Сопоставление двух моделей надежности. Расчет в упругопластической стадии методом переменных параметров упругости. 25. Гибкие нити Гибкая нить под действием распределенной нагрузки. Нить при малых провисаниях. ГЛАВА 7. КРУЧЕНИЕ СТЕРЖНЕЙ 26. Кручение круглых валов Кручение полого вала. Кручение вала в упругопластической стадии. Кручение вала в стадии установившейся ползучести. Модели прочностной надежности вала при кручении. 27. Общая задача кручения стержней и концентрация напряжений Математическая постановка задачи. Функция кручения. Функция напряжения. Примеры точных решений. Стержень эллиптического сечения. Стержень прямоугольного сечения. Концентрация напряжений при кручении. 28. Кручение тонкостенных стержней Кручение стержня замкнутого профиля. Кручение тонкостенных стержней открытых профилей. Пологие профили. Кручение прокатных балок. Кручение тонкостенных стержней открытого профиля с переменными параметрами упругости. 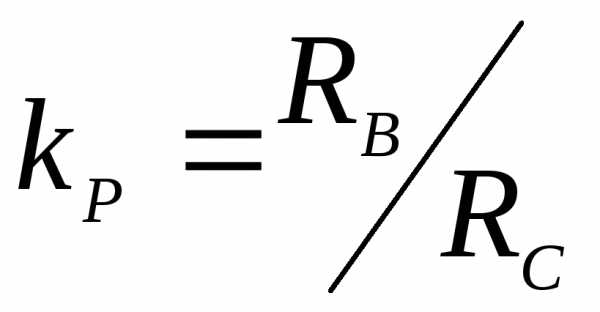 ГЛАВА 8. ИЗГИБ СТЕРЖНЕЙ 29. Гипотеза плоских сечений и нормальные напряжения изгиба Распределение нормальных напряжений изгиба. Система уравнений для определения нормальных напряжений изгиба и растяжения стержня и ее упрощение. Напряжения растяжения и изгиба в стержне от действия внешних сил. Температурные напряжения. Обоснование гипотезы плоских сечений. 30. Упруго-геометрические характеристики сечения стержня при изгибе. Главные оси, главные моменты инерции Геометрические характеристики сечения стержня. Главные моменты инерции сечения. Упруго-геометрические характеристики сечения стержня. 31. Условия равновесия элемента стержня и касательные напряжения изгиба Скачки перерезывающей силы и изгибающего момента. Условие равновесия элемента стержня при наличии распределенных изгибающих моментов. Распределение касательных напряжений в стержне постоянного сечения. Распределение касательных напряжений в стержнях переменного сечения. 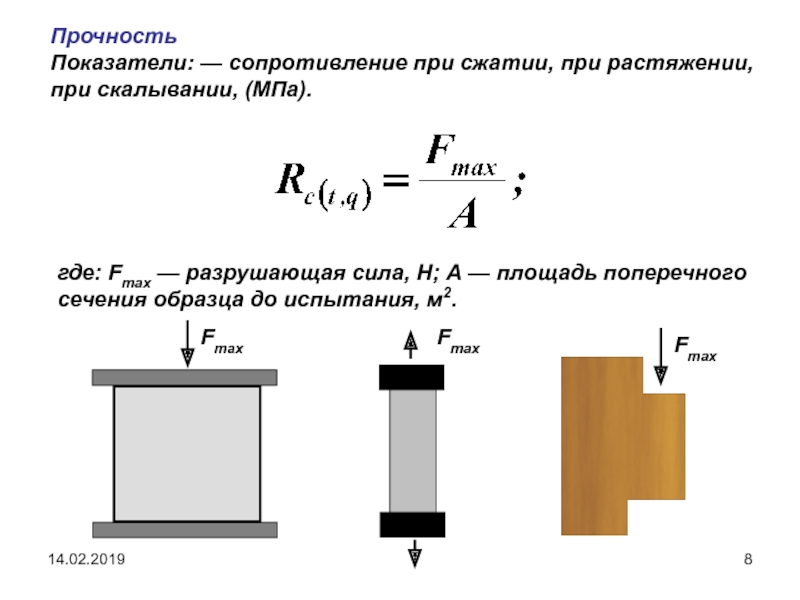 Касательные напряжения изгиба в тонкостенных стержнях. 32. Изгиб и растяжение стержней с учетом деформации пластичности и ползучести Изгиб стержней при пластичности без упрочнения. Предельный изгибающий момент. Остаточные напряжения. Общий случай расчета стержня в упругопластнческой стадии. Метод переменных параметров упругости. Стержни из нелинейного или разномодульного материала. Касательные напряжения при изгибе стержней в упругопластической стадии. Расчет стержней в упругопластической области с учетом нормальных и касательных напряжений изгиба. Учет деформации ползучести при изгибе стержня. Общий случай расчета стержней на изгиб при учете ползучести материала. 33. Прочностные модели надежности при изгибе Прочностная модель надежности при статической нагрузке по напряжениям. Прочностная модель надежности при переменной нагрузке. Детерминированная и статистическая модели усталостней прочности лопатки компрессора или турбины, вероятность разрушения.  Прочностная модель надежности валов. 34. Прогибы стержней Геометрическая картина изгибной деформации. Уравнение упругой линии стержня. Уравнение упругой линии при изгибе стержней постоянного сечения. Основная форма дифференциального уравнения плоского изгиба стержня. Дифференциальное уравнение плоского изгиба в матричной форме. Нормальные фундаментальные функции дифференциального уравнения изгиба и начальные параметры. Статически неопределимые задачи изгиба стержней. Учет деформации сдвига при изгибе стержня. Уравнение упругой линии стержня при изгибе в двух главных плоскостях. ГЛАВА 9. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ, ВАРИАЦИОННЫЕ МЕТОДЫ РАСЧЕТА КОНСТРУКЦИЙ, ОБЩИЕ СВОЙСТВА УПРУГИХ СИСТЕМ 35. Потенциальная энергия деформации Удельная потенциальная энергия деформации. Потенциальная энергия деформации стержней при растяжении и изгибе. Потенциальная энергия деформации, связанная с касательными напряжениями изгиба. 36. Вариационные методы Условия экстремума функционала, уравнение Эйлера — Пуассона, метод Рэлея — Ритца.  Применение начала возможных перемещений, вариационное уравнение Лагранжа. Вариационное уравнение изгиба стержня. Применение метода Рэлея — Ритца к задаче изгиба стержня. Применение начала возможных перемещений для определения прогибов стержней. Интеграл Мора. Общий случай определения прогибов с помощью интеграла Мора. Вычисление интеграла Мора по правилу Верещагина. 37. Вариационные методы и общие свойства упругих систем Вариационное уравнение метода вариации напряжений. Следствия вариационного уравнения. Теорема Кастильяно. Общие свойства упругих систем. ГЛАВА 10. СЛОЖНЫЕ МОДЕЛИ СТЕРЖНЕЙ 38. Тонкостенные стержни Чистое кручение тонкостенных стержней открытого профиля. Стесненное кручение тонкостенных стержней. Основные гипотезы. Нормальные напряжения стесненного кручения. Касательные напряжения стесненного кручения. Решение уравнения стесненного кручения тонкостенных стержней и краевые условия. Изгиб и кручение тонкостенных стержней.  Нормальные напряжения. Нормальные напряжения.Касательные напряжения изгиба. Центр жесткости сечения. Уравнения изгибно-крутильных деформаций тонкостенного стержня. Определение секториальных упруго-геометрических характеристик сечения и координат центра жесткости. Общие свойства расположения центра жесткости. Расчет секториальных характеристик сечений. 39. Полупространственные модели стержня Напряжения в плоскости поперечного сечения. Расчет стержней по полупространствениой теории. ГЛАВА 11. КОЛЬЦА 40. Изгиб колец 41. Осесимметричная деформация колец ГЛАВА 12. ДИНАМИКА И УСТОЙЧИВОСТЬ СТЕРЖНЕЙ 42. Изгибные и продольные колебания стержней Собственные колебания груза. Вынужденные колебания груза. Собственные колебания стержня с несколькими сосредоточенными массами. Дифференциальное уравнение изгибных колебаний стержней. Изгибные колебания стержней постоянного сечения. Изгибные колебания балки переменного сечения. Решение с помощью интегральных уравнений.  Применение вариационного метода для определения частот и форм изгибных колебаний стержня. Динамическая модель лопатки осевого компрессора при изгибных колебаниях. Продольные колебания стержня. 43. Критические частоты вращения и крутильные колебания валов Учет начального эксцентриситета центра тяжести диска. Учет упругости опор. Силы, действующие на вращающийся диск при прогибах вала. Критическая частота вращения вала с дисками. Критическая частота вращения вала переменного сечения с непрерывно распределенными массами. Крутильные колебания валов. 44. Устойчивость стержней Критическая нагрузка для стержня с шарнирно закрепленными концами. Формула Эйлера. Общее дифференциальное уравнение устойчивости стержня и краевые условия. Решение дифференциального уравнения устойчивости для стержня постоянного сечения. Влияние условий закрепления концов стержня на величину критической силы. Приведенная длина стержня. Обобщенная формула Эйлера.  Интегральное уравнение устойчивости стержня. Устойчивость стержней при упругопластических деформациях. Модуль Кармана. Устойчивость стержней в условиях продолжающегося нагружения в пластической области. Практические расчеты на устойчивость. ГЛАВА 13. МОДЕЛИ РАЗРУШЕНИЯ 45. Модели статического и длительного разрушения Модели статического разрушения пластичных материалов. Критерий максимальных касательных напряжений. Предельные поверхности по критериям интенсивности напряжений и максимальных касательных напряжений. Модель статического разрушения пластичных материалов, дополненная условием отрыва. Модели статического разрушения хрупких материалов. Более общие модели статического разрушения. Предельная поверхность в пространстве главных напряжений по критерию Мора. Предельная поверхность в пространстве главных напряжений по критерию Писаренко — Лебедева. Модели длительного разрушения. Прочность при наличии трещин. Линейная механика разрушения.  Критическая длина трещины. Формула Гриффитса. 46. Модели усталостного и малоциклового разрушения Модели усталостного разрушения при многоосном (многокомпонентном) напряженном состоянии. Модели усталостного разрушения при стационарном нагружении с учетом числа циклов нагружений. Модели малоциклового разрушения при одноосном и сложном напряженных состояниях. ГЛАВА 14. ЦИЛИНДРЫ И ДИСКИ 47. Прочностные модели толстостенных труб и цилиндров. Напряжения и деформации Уравнения равновесия элемента цилиндра. Толстостенная труба под действием внутреннего и внешдего давлений. Действие осевого усилия. Прочностная модель цилиндрической части сосуда высокого давления. Прочностная модель прессового соединения. Температурные напряжения и, напряжения от центробежных сил. Цилиндр с переменными параметрами упругости. 48. Прочностные модели дисков Дифференциальное уравнение для диска постоянной толшины с постоянными параметрами упругости. Распределение напряжений в диске постоянной толщины.  Напряжения в диске переменной толщины с переменными параметрами упругости. Модели общей статической и длительной прочности диска. Эквивалентный запас по разрушающей частоте вращения. ГЛАВА 15. БАЛКИ НА УПРУГОМ ОСНОВАНИИ, КРИВОЛИНЕЙНЫЕ СТЕРЖНИ И ПРУЖИНЫ 49. Изгиб балок на упругом основании Уравнения изгиба для балки постоянного сечения на упругом основании. Структура решения. Метод начальных параметров и решение уравнения изгиба балки на упругом основании в матричной форме. 50. Криволинейные стержни и пружины Модели прочностной надежности пружин. Модель прочностной надежности пружин при ударном нагружении. Стержни большой кривизны. Нормальные напряжения. Определение приведенного центра тяжести сечения криволинейного стержня. Примеры. Касательные напряжения при изгибе криволинейного стержня. Перемещения на изгибе криволинейного стержня. ГЛАВА 16. ПЛАСТИНКИ И ОБОЛОЧКИ 51. Пластинки Деформация круглых пластинок. Круглая пластинка постоянной толщины с постоянными параметрами упругости.  Напряжения изгиба в круглой пластинке. Изгиб прямоугольных пластинок. Деформации. Определение прогибов и напряжений в пластинке вариационным методом. 52. Цилиндрические оболочки Краевой эффект и безмоментное напряженное состояние в длинных цилиндрических оболочках. 53. Приближенные методы расчета прочности и устойчивости рболочек вращения при осесимметричном нагружении Безмоментное напряженное состояние и условие равновесия элемента оболочки. Общее условие равновесия произвольной части оболочки. Приближенная модель прочности оболочки вращения при осесимметричном нагружении. Приближенные модели устойчивости оболочки. ГЛАВА 17. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ 54. Введение в метод конечных элементов 55. Основные уравнения метода конечных элементов Вариационное уравнение метода конечных элементов. |
Как рассчитать прочность на сжатие
Обновлено 26 ноября 2018 г.
Автор Lisa Maloney
Прочность на сжатие — это эффективный способ измерения нагрузки, которую может выдержать поверхность или материал. Испытание на прочность такого рода выполняется путем приложения силы вниз к верхней части объекта в сочетании с равной и противоположной силой, приложенной вверх к нижней части. Другими словами, вы сжимаете его, а затем используете простую математическую формулу, чтобы определить сжимающую нагрузку, которая потребовалась до того, как материал разрушился.
Испытание на прочность такого рода выполняется путем приложения силы вниз к верхней части объекта в сочетании с равной и противоположной силой, приложенной вверх к нижней части. Другими словами, вы сжимаете его, а затем используете простую математическую формулу, чтобы определить сжимающую нагрузку, которая потребовалась до того, как материал разрушился.
TL;DR (слишком длинно, не читал)
Формула напряжения сжатия:
CS = F ÷ A, где CS — прочность на сжатие, F — сила или нагрузка в точке разрушение и A — начальная площадь поверхности поперечного сечения.
Рекомендации по испытанию на сжимающую нагрузку
Испытание на прочность при сжатии требует точных измерений, поэтому процесс «сдавливания» при испытании на сжатие должен проводиться в тщательно контролируемых условиях, включая равные и противоположные силы, приложенные для сжатия материала от как сверху, так и снизу.
Из-за этого, а также из-за того, что испытание проводится до момента разрушения или остаточной деформации, вы не стали бы испытывать реальную конструкцию на месте; вместо этого вы испытаете кубический или цилиндрический образец. Форма куба или цилиндра гарантирует, что у вас будут плоские параллельные поверхности в верхней и нижней части образца, и обе грани должны быть поперечными, то есть взятыми под прямым углом к вертикальной оси образца.
Точки данных в формуле напряжения сжатия
После того, как вы поместите свой образец в соответствующий аппарат для вашего научного процесса «раздавливания», вам нужно будет принять к сведению две точки данных. Первый — это площадь поперечного сечения образца, который вы пересекаете, или, другими словами, площадь поверхности только одной из его граней.
Еще одна точка данных, которую вам необходимо измерить, — это сила, приложенная к вашему образцу в момент его разрушения. Вы будете прилагать усилие медленно до отказа, который обычно определяется как необратимая деформация. Другими словами, деформация, которая не вернется к своей первоначальной форме после устранения сжимающей силы. Часто «постоянная деформация» происходит при разрушении объекта.
Вы будете прилагать усилие медленно до отказа, который обычно определяется как необратимая деформация. Другими словами, деформация, которая не вернется к своей первоначальной форме после устранения сжимающей силы. Часто «постоянная деформация» происходит при разрушении объекта.
Если вы используете общепринятые единицы измерения США, измерьте силу в фунтах и площадь в квадратных дюймах, чтобы результат был в стандартных единицах psi или фунтах на квадратный дюйм.
Расчет прочности на сжатие
Когда у вас есть эти точки данных – независимо от того, измерили ли вы их самостоятельно в лаборатории или получили в словесной задаче – вы можете рассчитать прочность вашего объекта на сжатие. Формула:
CS = F ÷ A, где CS — прочность на сжатие, F — сила или нагрузка в точке разрушения, а A — начальная площадь поверхности поперечного сечения.
Пример: Вас попросили рассчитать прочность бетонного цилиндра на сжатие. Каждая сторона поперечного сечения цилиндра имеет ширину 6 дюймов, и цилиндр вышел из строя при усилии в 71 000 фунтов. Какова прочность на сжатие этого образца бетона?
Вы можете подставить измерение силы, 71 000 фунтов, в свое уравнение для Ф . Но не торопитесь и подставьте 6 дюймов для площади поперечного сечения, A . Вам дан диаметр поверхности цилиндра, но вам нужна площадь поверхности этой поверхности.
Чтобы рассчитать площадь поверхности, помните, что площадь круга равна πr 2 , где r — радиус круга, равный 1/2 диаметра круга. Таким образом, при диаметре 6 дюймов радиус вашего круга равен 3 дюймам, а его площадь равна π(3) 9.0061 2 = 28,26 в 2 .
Теперь, когда у вас есть эта информация, ваше уравнение выглядит следующим образом:
CS = 71 000 фунтов ÷ 28,26 дюйма 2 = 2512 фунтов на квадратный дюйм
Таким образом, прочность на сжатие вашего образца составляет 2512 фунтов на квадратный дюйм. Между прочим, это соответствует стандартной прочности бетона на сжатие 2500 фунтов на квадратный дюйм для жилых помещений; бетон для коммерческих конструкций может иметь прочность на сжатие 4000 фунтов на квадратный дюйм или более.
Между прочим, это соответствует стандартной прочности бетона на сжатие 2500 фунтов на квадратный дюйм для жилых помещений; бетон для коммерческих конструкций может иметь прочность на сжатие 4000 фунтов на квадратный дюйм или более.
Что такое сила сжатия? – МТ Коупленд
Фундаментальная концепция, которую инженеры, архитекторы и строители должны тщательно понять, прежде чем приступать к работе над любой структурой — от домов на одну семью до массивных мостов и небоскребов — это идея сжатия и растяжения. Сила растяжения — это сила, которая растягивает материалы, а сила сжатия сжимает элементы. Каждый материал способен выдерживать определенное сжатие и определенное растяжение.
Чтобы показать разницу между сжатием и растяжением, инструкторы по инженерному делу часто демонстрируют материал, например, веревку, которая может выдерживать большое натяжение или тянуть до того, как разрушится, но практически не имеет прочности на сжатие, поскольку, если вы надавите на нее с противоположные стороны, он просто согнется.
В этой статье
- 1 Что такое сила сжатия?
- 2 4 силы, действующие на все конструкции
- 3 Как действует сжимающая сила в здании?
- 4 Измерение прочности материалов на сжатие
- 5 Какие материалы имеют самую высокую прочность на сжатие?
Что такое сила сжатия?
Прочность материала на сжатие — это его способность противостоять внешним силам, воздействующим на него. Когда колонна поддерживает нагрузку сверху, она испытывает сжимающее напряжение. На молекулярном уровне следствием этой силы является то, что атомы и молекулы частиц в материале укорачиваются.
Сжатие является фактором во всех зданиях, поскольку нагрузки и усилия в конечном итоге должны быть направлены на землю. Этот принцип также действует в строительстве, когда такие материалы, как гравий, необходимо прессовать, чтобы они стали стабильными и уплотнены. Испытательные лаборатории определяют степень уплотнения материала под зданием; строительные нормы обычно требуют, чтобы материал под плитами, асфальтом или другими поверхностями фундамента имел коэффициент уплотнения 95 процентов.
4 силы, действующие на все конструкции
Сжатие и растяжение — две из четырех основных сил, действующих друг на друга внутри конструкции. Два других – кручение и сдвиг.
- Сжатие: Частицы материала прижимаются друг к другу, заставляя их укорачиваться или сжиматься. В здании сжатие обычно происходит сверху.
- Растяжение: Противоположное сжатию, при котором тянущая сила удлиняет материал. Если балка сжимается сверху, она будет растягиваться снизу.
- Скручивание: Конструктивный элемент подвергается крутящему моменту или скручивающей силе.
- Сдвиг: Противодействующие структурные силы вызывают проскальзывание на плоскости. Другими словами, сила сдвига, которая заставляет слои скользить друг относительно друга в противоположных направлениях. Здания нуждаются в несущих стенах, чтобы выдерживать боковые или сдвигающие силы.
Узнайте больше о том, как силы и напряжения воздействуют на конструкции и материалы, в классе MT Copeland по древесным материалам, который преподает мастер-строитель Джордан Смит.
Как действует сила сжатия в здании?
Один из способов взглянуть на сжатие — это действие и противодействие. На элементы конструкции действуют внутренние и внешние силы. Внешняя сила называется конструкционной нагрузкой, а внутренняя сила — напряжением, где нагрузка — это действие (нагрузка на колонну), а напряжение — сила реакции. Когда инженеры проектируют конструкции, они должны учитывать все силы, которые могут воздействовать на них с течением времени.
В реальных условиях эти силы будут включать 3 типа нагрузок: временная нагрузка (люди или материалы, которые будут храниться в здании), статическая нагрузка (вес самой конструкции) и нагрузка окружающей среды (элементарные факторы). как снеговая нагрузка, ветровая нагрузка и землетрясение). Строительные нормы обычно устанавливают параметры для этих расчетных нагрузок.
как снеговая нагрузка, ветровая нагрузка и землетрясение). Строительные нормы обычно устанавливают параметры для этих расчетных нагрузок.
Подумайте о том, как строились здания с течением времени: греческие и римские храмы и готические соборы — это здания, построенные с использованием силы сжатия. Кирпичная или каменная арка использует равномерное сжатие, которое направлено вниз и поглощается конструкцией, созданной для поддержки бокового давления, например каменными опорами. Известный пример такого использования сжатия можно увидеть в соборе Нотр-Дам в Париже, где контрфорс направляет силу сжатия с крыши и стен на фундамент.
Измерение прочности материалов на сжатие
По определению, прочность материала на сжатие представляет собой значение напряжения одноосного сжатия (имеется в виду максимальное напряжение сжатия, которого достигает материал до полного разрушения). Проще говоря, к материалу (обычно цилиндрическому, поэтому он называется «одноосным») прикладывается сжимающая нагрузка, которая укорачивается и расширяется до тех пор, пока не разрушится. Это наносится на кривую напряжения-деформации.
Это наносится на кривую напряжения-деформации.
Формула для расчета прочности на сжатие: F = P/A, где:
- F=Прочность на сжатие (МПа)
- P=Максимальная нагрузка (или нагрузка до разрушения) на материал (Н)
- A=Поперечное сечение площади материала, выдерживающего нагрузку (мм2)
Чтобы дать некоторое представление о том, как эти числа используются в здании, стандартные здания требуют, чтобы бетон соответствовал прочности на сжатие от 10 МПа до 60 МПа (от 1450 до 8700 фунтов на квадратный дюйм). Бетон сверхвысокой прочности, полученный с помощью специальных смесей, может соответствовать требованиям по прочности 500 МПа (72 519фунтов на квадратный дюйм).
Инженеры измеряют прочность дерева на сжатие, нагружая деревянный брусок параллельно волокнам до тех пор, пока он не выйдет из строя (сломается). Они измеряют это в psi (фунтах на квадратный дюйм).
Прочность на сжатие пластичного (металлического) материала можно измерить с помощью универсальной испытательной машины, в которой материал помещается между двумя пластинами и подвергается сжатию до тех пор, пока не будет достигнута определенная нагрузка или материал не разрушится.
Какие материалы имеют самую высокую прочность на сжатие?
Одним из наиболее важных технических свойств бетона является его высокая прочность на сжатие. Однако по сравнению со сталью он имеет слабую прочность на растяжение. Сталь может иметь как высокую прочность на сжатие, так и высокую прочность на растяжение, и может выдерживать те же сжимающие усилия, что и бетон или кирпичная кладка, но без объема. Инженеры часто ссылаются на группы «хрупких» и «пластичных» материалов по прочности на сжатие: группа хрупких включает камень, песчаник и цемент, а группа пластичных включает сталь и другие металлы.
Вот некоторые значения средней прочности на сжатие обычных строительных материалов в psi (фунтах на квадратный дюйм):
- Сталь A36 (обычная конструкционная сталь): 22 000
- Гранит: 19 000
- Твёрдый кирпич: 12 000
- , Hickory
- Limestone: 9,000
- Standard concrete: 1450-8700
- Maple, hard: 7,830
- Walnut: 7,580
- Douglas fir: 7,230
- Ash: 7,410
- Ponderosa pine: 5,320
- Легкие кирпичи: 1 000
Поняв, как взаимодействуют сжатие и растяжение — и как прочность на сжатие некоторых материалов может работать в контексте других сил в конструкции — вы поймете важность строительных норм и правил при установке нормы безопасности строительства.


 А., Мавлютов Р. Р. Сопротивление материалов: Учебное пособие.— М.: Наука. Гл. ред. физ.-мат. лит., 1986.— 560 с.
А., Мавлютов Р. Р. Сопротивление материалов: Учебное пособие.— М.: Наука. Гл. ред. физ.-мат. лит., 1986.— 560 с.