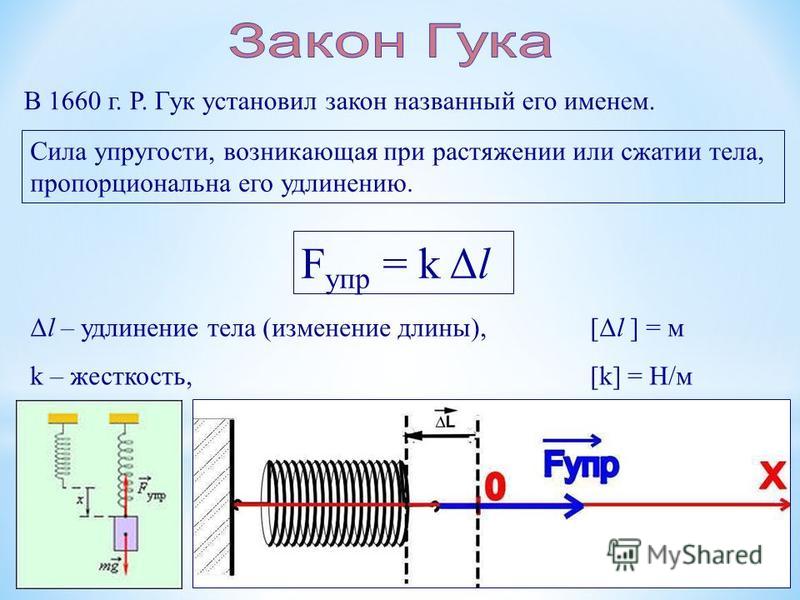
Формула сила сжатия пружины: 7<> Для сжатия пружины приложена сила 100Н.Какая работа совершена,если пружина сжалась на 4см?

alexxlab | 21.04.2023 | 0 | Разное

Физика. 8 класс

Физика. 8 класс

Кикоин И.К., Кикоин А.К. Физика. 8 класс. Учебное пособие. — 4-е изд., перераб. — М.: Просвещение, 1973. — 256 с. Советская фундаментальная наука, и физика в частности, была одной из сильнейших в мире. А по каким учебникам учились в школе и готовились к экзаменам будущие лучшие в мире ученые? Вашему вниманию предлагается учебник по физике для советских восьмиклассников. Охватывает разделы “Кинематика”, “Динамика, “Равновесие тел” и “Законы сохранения в механике”. Оглавление Глава 1. Общие сведения о движении § 1. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ. МАТЕРИАЛЬНАЯ ТОЧКА § 2. ПОЛОЖЕНИЕ ТОЧКИ (ТЕЛА) В ПРОСТРАНСТВЕ § 3. ПЕРЕМЕЩЕНИЕ § 4. ПОНЯТИЕ О ВЕКТОРАХ. ВЕКТОР ПЕРЕМЕЩЕНИЯ. КООРДИНАТЫ ТЕЛА § 5. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: СЛОЖЕНИЕ ВЕКТОРОВ § 6. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: ВЫЧИТАНИЕ ВЕКТОРОВ § 7. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: УМНОЖЕНИЕ ВЕКТОРА НА СКАЛЯР § 8. ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ § 9. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДВИЖЕНИЯ § 10. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ § 11. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ (ПРОДОЛЖЕНИЕ) § 12. ЕДИНИЦЫ ИЗМЕРЕНИЙ ДЛИНЫ И ВРЕМЕНИ Глава 2. Прямолинейное неравномерное движение § 13. СРЕДНЯЯ СКОРОСТЬ § 14. МГНОВЕННАЯ СКОРОСТЬ § 15. УСКОРЕНИЕ. РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ § 16. НАПРАВЛЕНИЕ УСКОРЕНИЯ § 17. ПЕРЕМЕЩЕНИЕ ПРИ РАВНОУСКОРЕННОМ ДВИЖЕНИИ § 18. СРЕДНЯЯ СКОРОСТЬ ПРИ ПРЯМОЛИНЕЙНОМ РАВНОУСКОРЕННОМ ДВИЖЕНИИ. СВЯЗЬ МЕЖДУ ПЕРЕМЕЩЕНИЕМ И СКОРОСТЬЮ § 19. ИЗМЕРЕНИЕ УСКОРЕНИЯ § 20. СВОБОДНОЕ ПАДЕНИЕ ТЕЛ § 21. ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО ВЕРТИКАЛЬНО ВВЕРХ Глава 3. Криволинейное движение § 22. ПЕРЕМЕЩЕНИЕ И СКОРОСТЬ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ § 23. УСКОРЕНИЕ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ § 24. ДВИЖЕНИЕ ПО ОКРУЖНОСТИ. УГОЛ ПОВОРОТА И УГЛОВАЯ СКОРОСТЬ § 25. УСКОРЕНИЕ ПРИ РАВНОМЕРНОМ ДВИЖЕНИИ ТЕЛА ПО ОКРУЖНОСТИ § 26. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА § 27. ОБ ОТНОСИТЕЛЬНОСТИ ДВИЖЕНИЯ ТЕЛА ПРИ ВРАЩЕНИИ СИСТЕМЫ ОТСЧЕТА Динамика Глава 4. Законы движения § 28. ТЕЛА И ИХ ОКРУЖЕНИЕ. ПЕРВЫЙ ЗАКОН НЬЮТОНА § 29. ПОЧЕМУ ВОЗНИКАЮТ УСКОРЕНИЯ § 30. ВЗАИМОДЕЙСТВИЕ TEЛ. УСКОРЕНИЯ ТЕЛ ПРИ ИХ ВЗАИМОДЕЙСТВИИ § 31. ИНЕРТНОСТЬ ТЕЛ § 32. МАССА ТЕЛ § 33. МАССА ЛУНЫ § 34. СИЛА § 35. ВТОРОЙ ЗАКОН НЬЮТОНА § 36. ВТОРОЙ ЗАКОН НЬЮТОНА (продолжение) § 37. ИЗМЕРЕНИЕ СИЛ. ДИНАМОМЕТР § 38. ТРЕТИЙ ЗАКОН НЬЮТОНА § 39. ЗНАЧЕНИЕ ЗАКОНОВ НЬЮТОНА Глава 5. Силы природы § 40. ЭЛЕКТРОМАГНИТНЫЕ СИЛЫ § 41. СИЛА УПРУГОСТИ § 42. СИЛА ВСЕМИРНОГО ТЯГОТЕНИЯ § 43. ПОСТОЯННАЯ ВСЕМИРНОГО ТЯГОТЕНИЯ § 44. СИЛА ТЯЖЕСТИ § 45. ВЕС ТЕЛ § 46. ИЗМЕРЕНИЕ МАССЫ ТЕЛ ВЗВЕШИВАНИЕМ § 47. МАССА ЗЕМЛИ § 48. СИЛА ТРЕНИЯ. ТРЕНИЕ ПОКОЯ § 49. СИЛА ТРЕНИЯ СКОЛЬЖЕНИЯ § 50. СИЛА СОПРОТИВЛЕНИЯ, ВОЗНИКАЮЩАЯ ПРИ ДВИЖЕНИИ ТЕЛА В ЖИДКОСТИ ИЛИ В ГАЗЕ Глава 6. Применение законов движения § 51. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ УПРУГОСТИ § 52. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: НАЧАЛЬНАЯ СКОРОСТЬ ТЕЛА РАВНА НУЛЮ ИЛИ ПАРАЛЛЕЛЬНА СИЛЕ ТЯЖЕСТИ § 53. ВЕС ТЕЛА, ДВИЖУЩЕГОСЯ С УСКОРЕНИЕМ § 54. НЕВЕСОМОСТЬ § 55. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ПОД УГЛОМ К ГОРИЗОНТУ § 56. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ГОРИЗОНТАЛЬНО § 57. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ПЕРВАЯ КОСМИЧЕСКАЯ СКОРОСТЬ § 58. ДВИЖЕНИЕ ПЛАНЕТ § 59. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ ТРЕНИЯ § 60. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ НЕСКОЛЬКИХ СИЛ § 61. ПАДЕНИЕ ТЕЛА В ГАЗЕ ИЛИ В ЖИДКОСТИ § 62. НАКЛОН ТЕЛ ПРИ ДВИЖЕНИИ НА ПОВОРОТАХ § 63. ПРИ КАКИХ УСЛОВИЯХ ТЕЛА ДВИЖУТСЯ ПОСТУПАТЕЛЬНО? ЦЕНТР МАСС И ЦЕНТР ТЯЖЕСТИ § 64. ВСЕГДА ЛИ ВЕРНЫ ЗАКОНЫ МЕХАНИКИ НЬЮТОНА Равновесие тел Глава 7. Элементы статики § 65. РАВНОВЕСИЕ ТЕЛ ПРИ ОТСУТСТВИИ ВРАЩЕНИЯ § 66. РАВНОВЕСИЕ ТЕЛА С ЗАКРЕПЛЕННОЙ ОСЬЮ. МОМЕНТ СИЛЫ § 67. ПРАВИЛО МОМЕНТОВ § 68. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ ТЕЛ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ § 69. РАВНОВЕСИЕ ТЕЛ НА ОПОРАХ Законы сохранения в механике Глава 8. Закон сохранения импульса § 70. СИЛА И ИМПУЛЬС § 71. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА § 72. РЕАКТИВНОЕ ДВИЖЕНИЕ Глава 9. Механическая работа и мощность § 74. ПОЧЕМУ РАБОТА ОПРЕДЕЛЯЕТСЯ КАК ПРОИЗВЕДЕНИЕ § 75. БОЛЕЕ ОБЩЕЕ ОПРЕДЕЛЕНИЕ РАБОТЫ § 76. РАБОТА, СОВЕРШАЕМАЯ СИЛАМИ, РАВНОДЕЙСТВУЮЩАЯ КОТОРЫХ НЕ РАВНА НУЛЮ. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ § 77. РАБОТА СИЛЫ ТЯЖЕСТИ § 78. РАБОТА СИЛЫ УПРУГОСТИ § 79. РАБОТА СИЛЫ ТРЕНИЯ § 80. МОЩНОСТЬ Глава 10. Закон сохранения энергии § 82. РАБОТА ТЕЛА И ИЗМЕНЕНИЕ ЕГО СОСТОЯНИЯ. ПОНЯТИЕ ОБ ЭНЕРГИИ § 83. ПОТЕНЦИАЛЬНАЯ И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ § 84. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ УПРУГО ДЕФОРМИРОВАННОГО ТЕЛА § 85. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ТЕЛА, НАХОДЯЩЕГОСЯ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ § 36. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ § 87. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ § 88. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ И СИЛА ТРЕНИЯ § 89. ПРЕВРАЩЕНИЕ ЭНЕРГИИ И ИСПОЛЬЗОВАНИЕ МАШИН § 90. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ § 91. СТОЛКНОВЕНИЕ ТЕЛ § 92. ДВИЖЕНИЕ ЖИДКОСТИ ПО ТРУБАМ. ЗАКОН БЕРНУЛЛИ § 93. О ЗНАЧЕНИИ ЗАКОНОВ СОХРАНЕНИЯ Заключение Лабораторные работы 1. Определение ускорения тела при равноускоренном движении 2. Определение коэффициента трения скольжения 3. Изучение движения тела по параболе 4. Выяснение условия равновесия рычага 5. Определение центра тяжести плоской пластины Ответы к упражнениям

Сила упругости. Деформация: ее величина и типы. Закон Гука

 

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: силы в механике, сила упругости, закон Гука.

Как мы знаем, в правой части второго закона Ньютона стоит равнодействующая (то есть векторная сумма) всех сил, приложенных к телу. Теперь нам предстоит изучить силы взаимодействия тел в механике. Их три вида: сила упругости, гравитационная сила и сила трения. Начинаем с силы упругости.

 

Деформация.

 

Силы упругости возникают при деформациях тел. Деформация – это изменение формы и размеров тела. К деформациям относятся растяжение, сжатие, кручение, сдвиг и изгиб.
Деформации бывают упругими и пластическими. Упругая деформация полностью исчезает после прекращения действия вызывающих её внешних сил, так что тело полностью восстанавливает форму и размеры. Пластическая деформация сохраняется (быть может, частично) после снятия внешней нагрузки, и тело уже не возвращается к прежним размерам и форме.

Частицы тела (молекулы или атомы) взаимодействуют друг с другом силами притяжения и отталкивания, имеющими электромагнитное происхождение (это силы, действующие между ядрами и электронами соседних атомов). Силы взаимодействия зависят о расстояний между частицами. Если деформации нет, то силы притяжения компенсируются силами отталкивания. При деформации изменяются расстояния между частицами, и баланс сил взаимодействия нарушается.

Например, при растяжении стержня расстояния между его частицами увеличиваются, и начинают преобладать силы притяжения. Наоборот, при сжатии стержня расстояния между частицами уменьшаются, и начинают преобладать силы отталкивания. В любом случае возникает сила, которая направлена в сторону, противоположную деформации, и стремится восстановить первоначальную конфигурацию тела.

Сила упругости – это сила, возникающая при упругой деформации тела и направленная в сторону, противоположную смещению частиц тела в процессе деформации. Сила упругости:

1. действует между соседними слоями деформированного тела и приложена к каждому слою;
2. действует со стороны деформированного тела на соприкасающееся с ним тело, вызывающее деформацию, и приложена в месте контакта данных тел перпендикулярно их поверхностям (типичный пример – сила реакции опоры).

Силы, возникающие при пластических деформациях, не относятся к силам упругости. Эти силы зависят не от величины деформации, а от скорости её возникновения. Изучение таких сил
выходит далеко за рамки школьной программы.

В школьной физике рассматриваются растяжения нитей и тросов, а также растяжения и сжатия пружин и стержней. Во всех этих случаях силы упругости направлены вдоль осей данных тел.

 

Закон Гука.

 

Деформация называется малой, если изменение размеров тела много меньше его первоначальных размеров. При малых деформациях зависимость силы упругости от величины деформации оказывается линейной.

Закон Гука. Абсолютная величина силы упругости прямо пропорциональна величине деформации. В частности, для пружины, сжатой или растянутой на величину , сила упругости даётся формулой:

(1)

где – коэффициент жёсткости пружины.

Коэффициент жёсткости зависит не только от материала пружины, но также от её формы и размеров.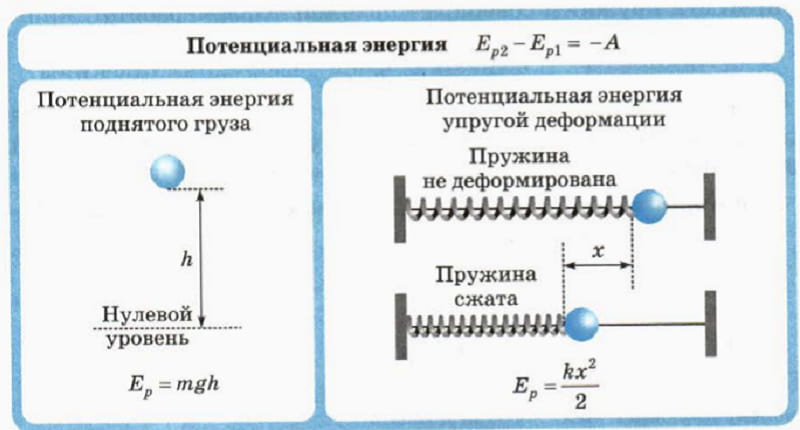

Из формулы (1) следует, что график зависимости силы упругости от (малой) деформации является прямой линией (рис. 1 ):

Рис. 1. Закон Гука

 

Коэффициент жёсткости – о угловой коэффициент в уравнении прямой . Поэтому справедливо равенство:

,

где – угол наклона данной прямой к оси абсцисс. Это равенство удобно использовать при экспериментальном нахождении величины .

Подчеркнём ещё раз, что закон Гука о линейной зависимости силы упругости от величины деформации справедлив лишь при малых деформациях тела. Когда деформации перестают быть малыми, эта зависимость перестаёт быть линейной и приобретает более сложный вид. Соответственно, прямая линия на рис. 1 – это лишь небольшой начальный участок криволинейного графика, описывающего зависимость от при всех значениях деформации .

 

Модуль Юнга.

 

В частном случае малых деформаций

стержней имеется более детальная формула, уточняющая общий вид ( 1 ) закона Гука.

Именно, если стержень длиной и площадью поперечного сечения растянуть или сжать
на величину , то для силы упругости справедлива формула:

.

Здесь – модуль Юнга материала стержня. Этот коэффициент уже не зависит от геометрических размеров стержня. Модули Юнга различных веществ приведены в справочных таблицах.

 

Спасибо за то, что пользуйтесь нашими материалами. Информация на странице «Сила упругости.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена: 09.03.2023

Сила пружины: определение, формула и примеры

В физике сила отвечает за изменение состояния движения объекта. От компьютеров до автомобилей машины выполняют несколько функций, и некоторые из них требуют от них последовательного перемещения частей вперед и назад. Одна часть, которая используется во многих различных машинах, — это простая деталь, которую мы сегодня знаем как пружину. Если вы хотите узнать больше о пружинах, не ищите дальше. Давайте приступим к делу и изучим физику!

Пружинные силы: определение, формула и примеры

Пружина имеет незначительную массу и при растяжении или сжатии создает силу, пропорциональную смещению от ее расслабленной длины. Когда вы берете предмет, прикрепленный к пружине, тянете его на расстояние от положения равновесия и отпускаете, восстанавливающая сила возвращает предмет обратно в равновесие. Для системы пружина-масса на горизонтальном столе единственной силой , действующей на массу в направлении смещения, является восстанавливающая сила, действующая со стороны пружины . Используя Второй закон Ньютона, , мы можем составить уравнение движения объекта. Направление возвращающей силы всегда будет против и антипараллельно смещению объекта. Возвращающая сила, действующая на систему пружина-масса, зависит от жесткости пружины и смещения объекта от положения равновесия.

Рис. 1 – Представление системы пружины-массы, где масса колеблется вокруг положения равновесия.

92})\), \(k\) — жесткость пружины, которая измеряет жесткость пружины в ньютонах на метр \((\frac{\mathrm N}{\mathrm m})\), и \(x\ ) — смещение в метрах \((\mathrm m)\).

Это соотношение также известно как закон Гука, и его можно доказать, установив пружинную систему с подвешенными массами. Каждый раз, когда вы добавляете массу, вы измеряете удлинение пружины. Если процедуру повторить, то будет видно, что растяжение пружины пропорционально возвращающей силе, в данном случае весу подвешенных масс. 92=\frac km$$

$$\omega=\sqrt{\frac km}$$

Пружина \(12\;\mathrm{cm}\) имеет жесткость \(400\;{ \textstyle\frac{\mathrm N}{\mathrm m}}\). Какая сила требуется, чтобы растянуть пружину до длины \(14\;\mathrm{см}\)?

Смещение имеет величину

$$x=14\;\mathrm{см}\;-\;12\;\mathrm{см}=2\;\mathrm{см}=0,02\;\mathrm m$$

Сила пружины имеет величину

8\;\mathrm N$$

Говорят, что система пружины-массы находится в равновесии, если на объект не действует результирующая сила. Это может произойти, когда величина и направление сил, действующих на объект, идеально сбалансированы или просто потому, что на объект не действуют никакие силы. Не все силы пытаются вернуть объект обратно в равновесие, но силы, которые делают это, называются восстанавливающими силами, и сила пружины является одной из них.

Возвращающая сила — это сила, действующая против смещения, чтобы попытаться вернуть систему в равновесие. Этот тип силы отвечает за генерацию колебаний и необходим для того, чтобы объект находился в простом гармоническом движении. Кроме того, восстанавливающая сила вызывает изменение ускорения объекта при простом гармоническом движении. По мере увеличения смещения запасенная упругая энергия увеличивается, а восстанавливающая сила увеличивается.

На диаграмме ниже мы видим полный цикл, который начинается, когда масса высвобождается из точки \(\text{A}\). Пружинные силы заставляют массу проходить через положение равновесия до \(\text{-A}\), чтобы снова пройти через положение равновесия и достичь точки \(\text{A}\) для завершения целый цикл.

Рис. 2 – Полный цикл колебаний системы пружина-масса.

Комбинация пружин

Набор пружин может действовать как одна пружина с эквивалентной жесткостью пружины, которую мы будем называть \(k_{\text{eq}}\). Пружины могут быть расположены последовательно или параллельно. Выражения для \(k_{\text{eq}}\) будут различаться в зависимости от типа аранжировки. В последовательном соединении обратная величина эквивалентной жесткости пружины будет равна сумме обратных величин отдельных жесткостей пружины. Важно отметить, что при последовательном соединении эквивалентная жесткость пружины будет меньше наименьшей жесткости отдельной пружины в наборе.

$$\frac1{k_{eq\;series}}=\sum_n\frac1{k_n}$$

Рис. 3 – Две последовательно соединенные пружины.

Набор из 2 последовательно соединенных пружин имеет константы пружин \(1{\textstyle\frac{\mathrm N}{\mathrm m}}\) и \(2{\textstyle\frac{\mathrm N}{\ матрм м}}\). Каково значение эквивалентной жесткости пружины?

$$\frac1{k_{eq\;ряд}}=\frac1{1\frac{\mathrm N}{\mathrm m}}+\frac1{2\frac{\mathrm N}{\mathrm m} }$$

$$\frac1{k_{eq\;series}}=\frac32{\textstyle\frac{\mathrm m}{\mathrm N}}$$

$$k_{eq\;series}=\frac23{\textstyle\frac{\mathrm N}{\mathrm m}}$$

Параллельно эквивалентная жесткость пружины будет равна сумме индивидуальных константы пружины.

$$k_{eq\;parallel}=\sum_nk_n$$

Рис. 4 – Две параллельные пружины.

Набор из 2 параллельных пружин имеет константы пружин \(1{\textstyle\frac{\mathrm N}{\mathrm m}}\) и \(2{\textstyle\frac{\mathrm N}{\ матрм м}}\). Каково значение эквивалентной жесткости пружины?

$$k_{eq\;parallel}=1\;{\textstyle\frac{\mathrm N}{\mathrm m}}+\;2{\textstyle\frac{\mathrm N}{\mathrm m} }=3\;{\textstyle\frac{\mathrm N}{\mathrm m}}$$

График силы и смещения

Мы можем построить график силы пружины как функцию положения и определить площадь под кривой. Выполнение этого расчета даст нам работу, совершаемую над системой силой пружины, и разность потенциальной энергии, запасенной в пружине из-за ее смещения. Поскольку в этом случае работа силы пружины зависит только от начального и конечного положений, а не от пути между ними, мы можем вывести изменение потенциальной энергии из этой силы. Эти виды сил называются 92.\end{array}$$

Рис. 5 – График зависимости силы от смещения, жесткость пружины представляет собой наклон, а потенциальная энергия представляет собой площадь под кривой.

Усилие пружины. Ключевые выводы

• Пружина имеет незначительную массу и при растяжении или сжатии создает силу, пропорциональную смещению от ее длины в расслабленном состоянии. Когда вы берете предмет, прикрепленный к пружине, тянете его на расстояние от положения равновесия и отпускаете, восстанавливающая сила возвращает предмет обратно в равновесие. 92}\).
• Направление возвращающей силы всегда будет противоположным и антипараллельным перемещению объекта.
• Набор пружин может действовать как одна пружина с эквивалентной пружинной константой, которую мы назовем \(k_eq\).
• В серии обратная величина эквивалентной жесткости пружины будет равна сумме обратных величин отдельных жесткостей пружины, \(\frac1{k_{eq\;series}}=\sum_n\frac1{k_n}\) .
• Параллельно эквивалентная жесткость пружины будет равна сумме индивидуальных пружинных констант \(k_{eq\;parallel}=\sum_nk_n\).

---

Каталожные номера

1. Рис. 1 — Представление системы пружина-масса, где масса колеблется вокруг положения равновесия, StudySmarter Originals
2. Рис. 2 — Полный цикл колебаний системы пружина-масса, StudySmarter Originals
3. Рис. 3 — Две последовательно соединенные пружины, StudySmarter Originals
4. Рис. 4 — Две пружины параллельно, StudySmarter Originals
5. Рис. 5 — График зависимости силы от смещения, константа пружины — это наклон, а потенциальная энергия — это площадь ниже кривая, StudySmarter Originals

Формула силы пружины – GeeksforGeeks

Пружина — это инструмент, который прикладывает равную и противоположную силу к телу, сжимая или растягивая его. Такое поведение демонстрирует пружина из-за ее незначительной инерции. Он демонстрирует гармоническое простое движение, так что его сила пружины (или восстанавливающая сила) пропорциональна смещению. Единицей измерения усилия пружины является Ньютон (Н). Он обозначается символом F, а его размерная сила определяется как [M ¹ L ¹ T ^-2 ]. Его значение равно произведению жесткости пружины на смещение.

Формула

F = – K (x – x _O )

, где,

F – это сила,

x _O – равное положение,

x _O – равное место,

x _O . – смещение пружины от положения равновесия.

Знак минус указывает на то, что сила пружины является восстанавливающей силой, так что она действует в противоположном направлении.

Примеры задач

Задача 1. Вычислить жесткость пружины длиной 10 см, нагруженной 2 кг и растянутой на 20 см.

Решение:

Имеем,

м = 2

х = 20

х _о = 10

900 сила пружины.

F = ma

= 2 (20 – 10)

= 2 (10)

= 20 Н

Используя формулу для жесткости пружины, получаем,

k = – F/(x – x _o )

= – 20/(20 – 10)

= – 20/10

= -2 Н/м

Задача 2. упругая постоянная для пружины длиной 5 см, она нагружена 3 кг и растянута на 10 см.

Рассчитаем силу пружины.

F = мА

= 3 (10 – 5)

= 3 (5)

= 15 Н

Используя формулу для жесткости пружины, получаем

= – 15/5

= -3 Н/м

Задача 3. Рассчитайте жесткость пружины длиной 7 см, нагруженной 2,5 кг и растянутой на 15 см.

Решение:

Имеем,

m = 2,5

x = 15

x _o = 7

Рассчитайте усилие пружины.

F = ma

= 2,5 (15 – 7)

= 2,5 (8)

= 20 Н )

= – 20/(15 – 7)

= – 20/8

= -2,5 Н/м

Задача 4. Рассчитать усилие пружины длиной 2 см при ее растяжении на 5 см. Значение жесткости пружины составляет 6 Н/м.

Решение:

Имеем,

k = 6

x = 5

x _o = 2

F x 0 x 9002 = 9000 _o )

= – 6 (5 – 2)

= -6 (3)

= -18 Н

Задача 5. Рассчитать усилие пружины длиной 4 см при ее растяжении на 12 см. Значение жесткости пружины составляет 2 Н/м.

Решение:

Имеем,

k = 2

x = 12

x _o = 4

Используя формулу для силы пружины получаем,

18 x 9 o

F = – 9 k

= – 2 (12 – 4)

= -2 (8)

= -16 Н

Задача 6.