Формула уклон: Калькулятор уклонов – посчитать онлайн

alexxlab | 23.02.2023 | 0 | Разное

Введение в уклон: определение, формула и типы

Содержание страницы

Форма пересечения наклона линии

Пожалуйста, включите JavaScript

Распространять любовь

В алгебре наклон широко используется для измерения уравнения прямой линии и различных алгебраических выражений. Наклон очень важен для решения методов уравнения прямой. Этими методами являются форма пересечения наклона, форма точки-наклона и форма пересечения двух точек.

В этом посте мы узнаем об определении, формуле и типах наклона, а также на множестве примеров.

Какой наклон?

В алгебре наклон используется для измерения крутизны линии. Наклон каждой линии остается одинаковым в каждой точке линии. используя координаты точек линии, наклон также может описывать направление линии.

Наклон обычно представляет собой долю изменения точек координаты y за счет изменения точек координаты x. Изменение координат x линии называется пробегом. В то время как изменение координаты y линии известно как подъем.

Таким образом, дробный результат подъема и бега известен как наклон. Обозначается строчной буквой «м». Математически это можно записать так:

Наклон = m = изменение координаты y / изменение координаты x

Наклон = м = подъем / бег

Уклон = m = Δy/Δx 

Уклон = м = у₂ – у₁ / Икс₂ – Икс₁

• В приведенном выше уравнении у₁ и у₂ координаты y линии.
• x₁ & Икс₂ координаты x линии.
• м – уклон линии.

Виды наклона линии

В алгебре есть четыре основных виды склона линии, часто используемой для представления уклона.

1. Положительный наклон линии
2. Отрицательный наклон линии
3. Нулевой наклон линии
4. Неопределенный наклон линии

Давайте кратко обсудим эти типы наклона.

Положительный наклон линии

Когда объект или человек следует по крутому пути вверх слева направо, говорят, что это положительный наклон линии. в этом типе наклона значения положительны. Ниже приведен решенный пример этого типа наклона.

Пример

Найдите наклон линии, используя координаты x и y линии, (12, 2) и (15, 4).

Решения

Шаг 1: Определить точки линии.

Объявления

ПРОДОЛЖИТЕ ЧИТАТЬ НИЖЕ

x₁ = 12, х₂ = 15, у₁ = 2, у₂ = 4

Шаг 2: Возьмите общую формулу наклона прямой.

Наклон линии = m = Δy/Δx 

Шаг 3: Подставьте заданные точки прямой в формулу.

Наклон линии = m = Δy/Δx = (y₂ – у₁) / (Икс₂ – Икс

1)

Наклон линии = m = (4 – 2) / (15 – 12)

Наклон линии = m = 2/3

Наклон линии = m = 0.6667

Отрицательный наклон линии

Когда объект или человек следует по крутому пути, чтобы спуститься слева направо, говорят, что это отрицательный наклон линии. В этом типе наклона значения отрицательные. Ниже приведен решенный пример этого типа наклона.

Пример

Найдите наклон линии, используя координаты x и y линии, (52, 32) и (26, 19).

Решения

Шаг 1: Определить точки линии.

x₁ = 52, х₂ = 26, у₁ = -4, у₂ = 9

Объявления

ПРОДОЛЖИТЕ ЧИТАТЬ НИЖЕ

Шаг 2: Возьмите общую формулу наклона прямой.

Наклон линии = m = Δy/Δx 

Шаг 3: Подставьте заданные точки прямой в формулу.

Наклон линии = m = Δy/Δx = (y₂ – у₁) / (Икс₂ – Икс₁)

Наклон линии = m = (26 – 52) / (9 – (-4))

Наклон линии = m = (26 – 52) / (9 + 4)

Наклон линии = m = -26/13

Наклон линии = m = -2

Вы также можете использовать калькулятор уклона найти наклон линии, используя точки линии. выполните следующие шаги, чтобы использовать этот инструмент.

Шаг 1: Введите заданные точки линии.

Шаг 2: Хит вычислять кнопку.

Шаг 3: Результат отобразится под кнопкой расчета. Нажимать показать шаги для просмотра решения с шагами.

Нулевой наклон линии

Когда объект или человек следует прямому пути, не поднимаясь и не опускаясь слева направо, говорят, что это нулевой наклон линии. В этом типе наклона значения равны 0. Другими словами, этот тип наклона имеет дело с координатами x наклона.

Таким образом, он также известен как наклон горизонтальной линии. Ниже приведен решенный пример этого типа наклона.

Пример

Найдите наклон линии, используя координаты x и y линии, (-32, 12) и (17, 12).

Решения

Шаг 1: Определить точки линии.

x₁ = -32, х₂ = 17, у₁ = 12, у₂ = 12

Шаг 2: Возьмите общую формулу наклона прямой.

Наклон линии = m = Δy/Δx 

Шаг 3: Подставьте заданные точки прямой в формулу.

Наклон линии = m = Δy/Δx = y₂ – у₁ / Икс₂ – Икс₁

Наклон линии = m = (12 – 12) / (17 – (-32))

Наклон линии = m = (12 – 12) / (17 + 32)

Наклон линии = m = 0/49

Наклон линии = m = 0

Неопределенный наклон линии

Когда объект или человек следует вертикальному пути вверх или вниз, не двигаясь слева направо, говорят, что это неопределенный наклон линии. В этом типе наклона значения находятся на бесконечности. Другими словами, этот тип наклона имеет дело с координатами y наклона.

Так, это также известно как наклон вертикальной линии. Ниже приведен решенный пример этого типа наклона.

Пример

Найдите наклон линии, используя координаты x и y линии, (-22, -32) и (-22, 2).

Решения

Шаг 1: Определить точки линии.

x₁ = -22, х₂ = -22, у₁ = -32, у₂ = 2

Шаг 2: Возьмите общую формулу наклона прямой.

Наклон линии = m = Δy/Δx 

Шаг 3: Подставьте заданные точки прямой в формулу.

Наклон линии = m = Δy/Δx = (y₂ – у₁) / (Икс₂ – Икс₁)

Наклон линии = m = (2 – (-32)) / (-22 – (-22))

Наклон линии = m = (2 + 32) / (-22 + 22)

Наклон линии = m = 34/0

Наклон линии = m = не определено

Заключение

В этом посте мы узнали об определении, формуле и видах уклона с примерами. Теперь вы можете легко решить любую проблему, связанную с наклоном линии, просто изучив основы этого поста.

Распространять любовь

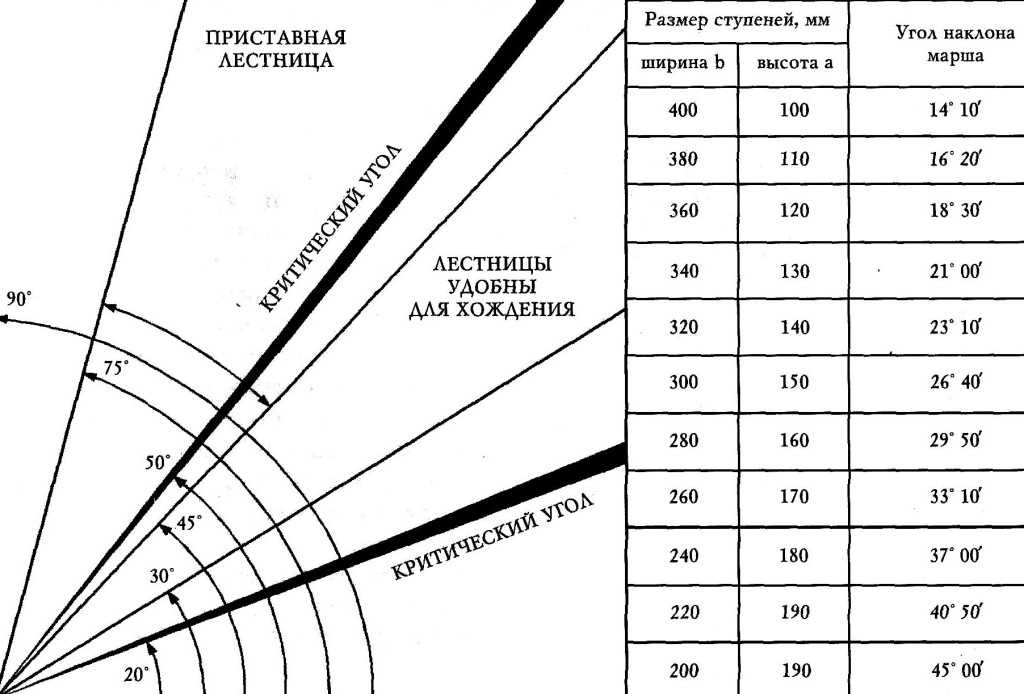
Расчёт уклона железнодорожного пути

Очень часто у специалистов, работников промышленных предприятий, складов, погрузочно-выгрузочных площадок на территориях которых есть железнодорожные пути необщего пользования возникает необходимость посчитать уклон железнодорожного пути самостоятельно. Чаще всего эти специалисты не имеют железнодорожного образования и не каждый день сталкиваются с подобными расчётами.

На этой странице предоставлена уникальная возможность посчитать любой уклон, будь то фактический или спрямлённый (он же приведённый) уклон железнодорожного пути. Для расчёта нужно знать отметки уровня головки рельса вначале и в конце расчетного участка, и длину между этими отметками.

Под калькулятором есть пример, и подробное описание действий при расчёте уклона железнодорожного пути

Ниже рассмотрен пример расчета приведённого уклона железнодорожного пути.

Смотрим рисунок 1. Это продольный профиль участка железнодорожного пути.

• Первая строка «отметки головки рельса» — это отметки, которые измерены геодезическим прибором, типа нивелир. В нашем случае отсчеты (замеры) произведены каждые 25 метров.
• Вторая строка — это «фактический уклон» и длина. В этой строке посчитаны уклоны между ближайшими отсчётами, а также указано расстояние между отсчетами «длина»
• Третья строка — это строка с указанием границ приведенного участка, его спрямлённый уклон.

Посчитан он так. Разница высот, поделённая на расстояние между этими высотами. Конкретно на нашем примере; берем из первой отметки (в нашем случае 103,57) вычитаем вторую (103,51), получаем разницу высот которая равна 6 сантиметров, или 0,06 метров. Далее делим 0,06 м, на расстояние между отметками (в нашем примере это 100 метров) получаем значение уклона 0,06/100=0,0006. Так как железнодорожные уклоны считается в промилле (в тысячных) Полученное значение уклона умножаем на 1000.

Теперь сам калькулятор: вводим первое значение в метрах, затем второе значение в метрах и расстояние между этими значениями. Нажимаем кнопку рассчитать, получаем результат.

Со знаком минус отображается спуск, то есть второе значение ниже первого, а положительное значение результата говорит о том что второе значение выше чем первое, а значит подъём.

Опубликовано 1 год назад. Просмотров с момента размещения на сайте 12554

Рубрика записи: Интересные факты
Самые уникальные железнодорожные сооружения со всего мира

За 3 года с момета публикации, статью прочитали 7019 раз(а)
У записи 4 комментария

Рубрика записи: Важно знать
Использование полосы отвода

За 6 лет с момета публикации, статью прочитали 7778 раз(а)
У записи 1 комментарий

Рубрика записи: Важно знать

Сопроводительная документация при перевозке опасных грузов по железной дороге

За 1 неделя с момета публикации, статью прочитали 128 раз(а)
У записи пока нет комментариев

Формула уклона

— что такое формула уклона? Уравнение, примеры

Формула уклона используется для расчета наклона или крутизны линии. Он находит применение при определении наклона любой линии путем нахождения отношения изменения по оси у к изменению по оси х. Наклон линии определяется как изменение координаты «у» по отношению к изменению координаты «х» этой линии.

Что такое формула уклона?

Формула наклона относится к формуле, используемой для расчета крутизны линии и определения ее наклона. Для вычисления наклона линий можно использовать координаты x и y точек, лежащих на линии. Другими словами, это отношение изменения по оси у к изменению по оси х.

Формула наклона

Формула для расчета наклона приведена как,

M = (Y ₂ – Y ₁ )/(x ₂ – x ₁ ) = Δy/δx

где m — наклон линии, x ₁ , x ₂ — координаты по оси x, а y ₁ , y ₂ — координаты по оси y.

Вывод формулы наклона

Координаты x и y линии используются для расчета наклона линии. Чистое изменение координаты y равно Δy, а чистое изменение координаты x равно Δx. Таким образом, изменение координаты y по отношению к изменению координаты x можно записать как

м = Δy/Δx

где

• м — уклон
• Δy — изменение координаты y
• Δx — изменение координаты x

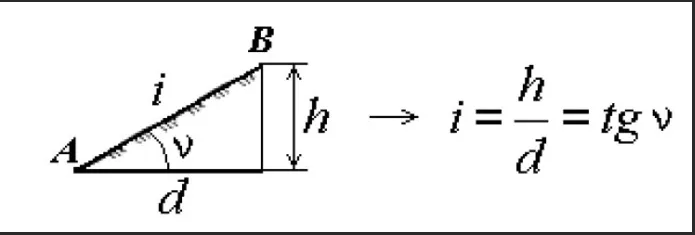
Мы знаем, что тангенс θ также является наклоном линии, где θ — это угол, образуемый линией с положительным направлением оси x.

И, tanθ = высота/основание

Так как высота/основание между любыми двумя заданными точками = (y

2 – y ₁ )/(x ₂ – x ₁ )

Таким образом, уравнение наклона имеет вид m = tanθ = Δy/Δx

Из графика видно: у ₁ )

Δx = (х ₂ – х ₁ )

Таким образом, формула наклона задается как: Уклон = m = (y ₂ – y ₁ )/(x ₂ – x ₁ )

Уравнение наклона

сечения, формула наклона может быть использована для определения наклона любой линии. Таким образом, уравнение, которое можно использовать для определения этого наклона, можно записать в виде 9.0099 m = подъем/спуск = tanθ = Δy/Δx = (y ₂ – y ₁ )/(x ₂ – x ₁ )

где

• м4 – уклон
• Δy — изменение координаты y
• Δx — изменение координаты x
• θ — угол, образуемый линией с положительной осью x

Кроме того, уравнение наклона любой линии с использованием уравнения линии может быть задано как
у = mx + b

где,

• м – уклон линии
• b – точка пересечения по оси y линии
.

Рассмотрим применение формулы наклона в следующих решенных примерах.

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Запись на бесплатный пробный урок

Примеры использования формулы наклона

Пример 1: Найдите наклон линии с координатами (2,9) и (4,1)?

Решение:

Найти: Наклон прямой с координатами (2,9) и (4,1)

Дано, (x ₁ , y ₁ ) = (2, 9) и (x ₂ , y ₂ ) = (4, 1)

Формула наклона:

м = (1 − 9)/(4 − 2)

м = -8/2 = -4

Ответ: Наклон данной прямой = -4

Пример 2: Определите значение b, если наклон прямой, проходящей через точки (b, 7) и (8, -5), равен 6

Решение:

Найти: значение b

Дано, Наклон = m = 6, Точки: (x ₁ , y ₁ ) = (b, 7) и (x ₂ , у ₂ ) = (8, -5)
Мы знаем, что Уклон (м) = (y ₂ – y ₁ )/(x ₂ – x ₁ )
6 = (-5-7)/(8-б)
6 = (-12)/(8-б)
-2= (8-б)
-2-8 = -б,
b = 10
Ответ: Значение b = 10.

Пример 3: Если угол, образуемый линией с положительной осью y, равен 30°, то каково значение наклона линии ?

Решение:

Найти: наклон прямой

Дано: Угол, образуемый линией с положительной осью ординат = 30°

Мы знаем, что если линия образует угол 30° с положительной оси y, то он составляет угол 120° от положительной оси x. Следовательно, значение наклона линии равно tg120° = -√3

Ответ: Значение наклона линии = -√3

Часто задаваемые вопросы о формуле наклона

Что такое формула наклона в геометрии?

В геометрии формула наклона определяется как формула для вычисления наклона любой линии путем нахождения отношения изменения по оси Y к изменению по оси X.

Что означает m в формуле уклона?

В формуле уклона m обозначает уклон, который рассчитывается как m = (y ₂ – y ₁ )/(x ₂ – x ₁ ) = Δy/Δx

Для чего используется формула наклона?

Формула наклона используется для расчета крутизны линии, а координаты линий x и y используются для того же. Мы знаем, что наклон линии является одной из наиболее важных характеристик линии, поскольку он помогает измерить скорость изменения.

Как рассчитать уклон, используя формулу уклона?

Наклон линии можно рассчитать по следующим формулам:

Когда заданы координаты:

• Шаг 1: Найдите координаты линии.
• Шаг 2: Подставьте их значения в формулу (m) = (y ₂ – y ₁ )/(x ₂ – x ₁ )

Если задан угол:

• Шаг 1: Определите угол, образуемый с осью.
• Шаг 2: Подставьте значение в формулу, m = tanθ

Что такое уравнение наклона линии?

Уравнение наклона любой линии можно рассчитать по следующей формуле:

м = подъем/пробег = tanθ = Δy/Δx = (y ₂ – y ₁ )/(x ₂ – x ₁ )

где,

• м – уклон
• Δy — изменение координаты y
• Δx — изменение координаты x
• θ — угол, образуемый линией с положительной осью x

Уравнение наклона с использованием уравнения прямой задается как y = mx + b, здесь m — это наклон, а b — точка пересечения с осью y.

Склонный калькулятор

, созданный Mateusz Muda и Julia żuławińska

, рассмотренные Bogna Szyk и Jack Bowater

Последнее обновление: Dec 21, 2022

Соглашение:

• Как найти Slope
• . связанные темы
• Часто задаваемые вопросы

Калькулятор уклона определяет уклон или градиент между двумя точками в декартовой системе координат. Наклон — это в основном величина наклона линии, которая может иметь положительное, отрицательное, нулевое или неопределенное значение. Прежде чем пользоваться калькулятором, наверное, стоит научиться находить уклон по формуле уклона. Чтобы найти уравнение прямой для любых двух точек, через которые проходит эта линия, используйте наш калькулятор формы пересечения наклона.

Как найти уклон

1. Определите координаты (x1,y1)(x_1, y_1)(x1​,y1​) и (x2,y2)(x_2, y_2)(x2​,y2​). Мы будем использовать формулу для расчета наклона линии, проходящей через точки (3,8)(3, 8)(3,8) и (−2,10)(-2, 10)(−2,10) .
2. Введите значения в формулу. Это дает нам (10-8)/(-2-3)(10-8)/(-2-3)(10-8)/(-2-3).
3. Вычтите значения в скобках, чтобы получить 2/(-5)2/(-5)2/(-5).
4. Упростите дробь, чтобы получить наклон −2/5–2/5–2/5.
5. Проверьте результат с помощью калькулятора уклона.

Чтобы найти наклон линии, нам нужны две координаты на линии. Достаточно любых двух координат. В основном мы измеряем величину изменения координаты y, часто известную как рост , деленную на изменение координаты x, известную как run . Вычисления по нахождению наклона просты и включают в себя не что иное, как базовое вычитание и деление.

🙋 Чтобы найти градиент нелинейных функций, вы можете использовать калькулятор средней скорости изменения.

Формула наклона. наклон линии легко вычисляется вручную с использованием небольших целых чисел координат. Формула становится все более полезной по мере того, как координаты принимают большие значения или десятичные значения.

Стоит отметить, что любая горизонтальная линия имеет нулевой градиент, потому что горизонтальная линия имеет те же координаты y. Это приведет к нулю в числителе формулы наклона. С другой стороны, вертикальная линия будет иметь неопределенный наклон, поскольку координаты x всегда будут одинаковыми. Это приведет к ошибке деления на ноль при использовании формулы.

Точно так же, как наклон можно вычислить, используя конечные точки сегмента, можно вычислить и среднюю точку. Середина — важное понятие в геометрии, особенно при вписании многоугольника внутрь другого многоугольника, когда его вершины касаются середины сторон большего многоугольника. Это можно получить с помощью калькулятора средней точки или просто взяв среднее значение каждой координаты x и среднее значение координаты y, чтобы сформировать новую координату.

Наклон линий важен для определения того, является ли треугольник прямоугольным. Если любые две стороны треугольника имеют наклоны, которые умножаются на -1, то треугольник является прямоугольным. Вычисления для этого можно выполнить вручную или с помощью калькулятора прямоугольного треугольника. Вы также можете использовать калькулятор расстояний, чтобы вычислить, какая сторона треугольника является самой длинной, что поможет определить, какие стороны должны образовывать прямой угол, если треугольник прямоугольный.

Знак перед градиентом, предоставленным калькулятором наклона, указывает, является ли линия возрастающей, убывающей, постоянной или неопределенной. Если график линии перемещается из нижнего левого угла в верхний правый, он увеличивается и, следовательно, является положительным. Если он уменьшается при движении из левого верхнего угла в правый нижний, то градиент отрицательный.

Часто задаваемые вопросы

Как найти наклон по уравнению?

Метод для определения наклона по уравнению зависит от формы уравнения перед вами. Если форма уравнения y = mx + c, то наклон (или градиент) просто m . Если уравнение не в этой форме, попробуйте изменить уравнение. Чтобы найти градиент других полиномов, вам нужно будет продифференцировать функцию по x .

Как рассчитать уклон холма?

1. Используйте карту, чтобы определить расстояние между вершиной и основанием холма по прямой.
2. Использование той же карты или GPS, найти высоту между вершиной и подошвой холма . Убедитесь, что точки, от которых вы измеряете, такие же, как в шаге 1.
3. Преобразуйте оба измерения в одни и те же единицы.
4. Разделите разницу высот на расстояние между двумя точками.
5. Это число представляет собой уклон холма, если он увеличивается линейно. Если это не так, повторите шаги, но там, где есть заметное изменение наклона.

Как рассчитать длину склона?

1. Измерьте разницу между верхней и нижней частью уклона относительно осей x и y.
2. Если вы можете измерить только изменение по оси x, умножьте это значение на градиент, чтобы найти изменение по оси y.
3. Убедитесь, что единицы измерения для обоих значений одинаковы.
4. Используйте теорему Пифагора, чтобы найти длину склона . Возведите в квадрат как изменение x, так и изменение y.
5. Сложите два значения вместе.
6. Найдите квадратный корень из суммы.
7. Это новое значение представляет собой длину склона.

Что такое наклон 1 из 20?

Уклон 1/20 — это уклон, который увеличивается на 1 единицу за каждые 20 единиц, пройденных по горизонтали . Так, например, пандус длиной 200 футов и высотой 10 футов будет иметь уклон 1/20. Наклон 1/20 эквивалентен градиенту 1/20 (как ни странно) и образует угол 2,86° между собой и осью x.

Как найти наклон кривой?

Поскольку наклон кривой меняется в каждой точке, вы можете найти наклон кривой, продифференцировав уравнение по x и в полученном уравнении подставив x вместо точки, в которой вы хотите найти градиент.

Скорость изменения равна наклону?

Скорость изменения графика также является его наклоном , который также совпадает с градиентом. Скорость изменения можно найти, разделив изменение в направлении y (по вертикали) на изменение в направлении по оси x (горизонтально), если, конечно, оба числа выражены в одних и тех же единицах. Скорость изменения особенно полезна, если вы хотите предсказать будущее предыдущего значения чего-либо , так как при изменении переменной x будет присутствовать соответствующее значение y (и наоборот).

Где вы используете уклон в повседневной жизни?

Уклоны (или уклоны) имеют множество применений в повседневной жизни . Есть несколько очевидных физических примеров – у каждого холма есть склон, и чем круче холм, тем больше его уклон . Это может быть полезно, если вы смотрите на карту и хотите найти лучший холм для спуска на велосипеде. Вы тоже, наверное, спите под скатом, крыша . Наклон крыши будет меняться в зависимости от стиля и места вашего проживания. Но, что более важно, если вы когда-нибудь захотите узнать, как что-то меняется со временем, вы в конечном итоге построите график с наклоном .

Что такое уклон 10%?

Уклон 10 % — это наклон, который увеличивается на 1 единицу за каждые 10 единиц, пройденных по горизонтали (10 %). Например, крыша с уклоном 10% и шириной 20 м будет иметь высоту 2 м. Это то же самое, что и градиент 1/10 , а между линией и осью x формируется угол 5,71°.

Как найти площадь под уклоном?

Чтобы найти площадь под уклоном, необходимо проинтегрировать уравнение и вычесть нижнюю границу площади из верхней границы. Для линейных уравнений:

1. Запишите уравнение в виде y = mx + c .
2. Напишите новую строку, в которой вы добавляете 1 к порядку x (например, x становится x ² , х ^2,5 становится х ^3,5 ).