Формула w кинетическая энергия: Кинетическая энергия — урок. Физика, 9 класс.
alexxlab | 26.07.1985 | 0 | Разное
Кинетической энергией системы называется скалярная величина w, равная арифметической сумме кинетических энергий всех точек системы
, где Vi-скорость i-й материальной точки массой mi
Найдем формулы для вычисления кинетической энергии тела в разных случаях движения.
1. Поступательное движение. В этом случае все точки тела движутся с одинаковыми скоростями, равными скорости движения центра масс. То есть, для любой точки Vi=VC
или
Таким образом, кинетическая энергия тела при поступательном движении равна половине произведения массы тела на квадрат скорости центра масс. От направления движения значение Wне зависит.
2. Вращательное
движение. Если
тело вращается вокруг какой-нибудь
оси Оz (см.
рис.1), то скорость любой его точки где –
расстояние точки от оси вращения, а –
угловая скорость тела. Подставляя это
значение и вынося общие множители за
скобку, получим:
Подставляя это
значение и вынося общие множители за
скобку, получим:
Величина, стоящая в скобке, представляет собою момент инерции тела относительно оси z. Таким образом, окончательно найдем:
т.е. кинетическая энергия тела при вращательном движении равна половине произведения момента инерции тела относительно оси вращения на квадрат его угловой скорости. От направления вращения значение W не зависит.
изменение (приращение) кинетической энергии материальной точки равно работе всех сил, приложенных к этой точке:
Потенциальная энергия (определение, единицы измерения). Консервативная система, потенциальные силы.
Потенц.энергия-механическая
энергия системы тел, определяемая их
взаимным расположением и характером
сил взаимодействия между ними. Это
энергия взаимодействия тела с Землей.
Консервативная система –механическая система, при движении которой сумма ее кинетической и потенциальной энергии остается величиной постоянной, т.е. имеет место закон сохранения механической энергии.
Кинетическая энергия может переходить в потенциальную и обратно в равных количествах Сохранение механической энергии является следствием однородности времени.
Однородность времени означает, что одинаковые физические эксперименты, поставленные в различные моменты времени, дают одинаковые результаты
Потенциальная сила — сила, работа которой при перемещении тела зависит только от начального и конечного положений тела в пространстве. Для непотенциальной силы работа зависит от траектории движения тела между начальным и конечным положениями тела
Закон сохранения полной механической энергии системы материальных точек
Механической
энергией или полной механической
энергией называется энергия механического
движения и взаимодействия. Механическая
энергия равна сумме кинетической и
потенциальной энергии.
Механическая
энергия равна сумме кинетической и
потенциальной энергии.
Если в системе действуют лишь консервативные силы, то полная механическая энергия такой системы остается постоянной. W = const.
+
Вынужденные колебания. Каноническое уравнение вынужденных колебаний.
Вынужденные колебания, колебания, возникающие в какой-либо системе под действием переменной внешней силы.
Fo/m – отношение амплитудного значения внешней вынуждающей силы
Момент силы (определение, единицы измерения), плечо силы (определение, единицы измерения).
Плечо силы – это перпендикуляр, проведённый из точки опоры на линию действия силы.
Моментом
силы относительно неподвижной точки О
называется физическая величина М,
определяемая векторным произведением
радиус-вектора r,
проведенного из точки О в точку А
приложения силы, на силы F.
Каноническое уравнение гармонических колебаний.
X’’+w2x=0 , где w– частота гармонических колебаний.
Пример: движение математического маятника. –решение кан.ур.
Момент импульса вращающегося тела (определение, единицы измерения). Закон сохранения момента импульса.
Моментом импульса вращающегося тела называют физическую величину, равную произведению момента инерции тела I на угловую скорость ω его вращения. Момент импульса обозначается буквой L:
|
Поскольку уравнение вращательного движения можно представить в виде:
Окончательно
будем иметь: Это
уравнение, полученное здесь для случая,
когда I = const,
справедливо и в общем случае, когда
момент инерции тела изменяется в процессе
движения.
Если суммарный момент M внешних сил, действующих на тело, равен нулю, то момент импульса L = Iω относительно данной оси сохраняется:
ΔL = 0, если M = 0. |
Следовательно,
|
Это и есть закон сохранения момента импульса
Семинар 1*
ВведениеФундаментальные частицы и фундаментальные взаимодействия В физике микромира все частицы делятся на два класса: фермионы и бозоны. Фермионы – частицы с полуцелыми значениями спина,
бозоны – частицы с целыми значениями спина. Фундаментальными называют частицы, которые по современным представлениям не имеют внутренней структуры. В природе существует 12 фундаментальных фермионов (со спином 1/2 в единицах ) приведены в табл.1. Последний столбец табл.1 – электрические заряды фундаментальных фермионов в единицах величины заряда электрона e.
12 фундаментальным фермионам соответствуют 12
антифермионов.
Квантами сильного взаимодействия являются нейтральные безмассовые глюоны.
Фундаментальные фермионы, между которыми реализуется сильное взаимодействие –
кварки – характеризуются квантовым числом “цвет”, которое может принимать 3
значения. Глюоны имеют 8 разновидностей “цветных” зарядов. Длины волн и энергии частиц Объекты, которые изучает физика ядра и частиц («субатомная
физика») имеют гораздо меньшие характерные размеры, чем атомы и молекулы. (Этот
факт также является следствием того, что структура объектов субатомной физики
определена сильными взаимодействиями)
где p – импульс частицы, h – константа Планка.
Единицы субатомной физики Энергия – 1 МэВ =1 МэВ = 106 эВ = 10-3 ГэВ = 1.6.10-13 Дж. Важные формулы релятивистской физики
Здесь Т- кинетическая энергия частицы с массой покоя m и модулем импульса р.
В субатомной физике, особенно в физике высоких энергий, в настоящее время все более широко используется система единиц (система Хевисайда), в которой ћ = 1 и с = 1. В этой системе формулы релятивистской физики имеют более простую и удобную форму:
В системе ћ
= с = 1 энергия, импульс и масса измеряются в одних и тех же энергетических
единицах – МэВ (MeV) или ГэВ (GeV). Значительное упрощение в решении задач может
быть достигнуто за счет использования константы конверсии ћc ≈ 200 МэВ·Фм.
Длина волны электрона равна Отсюда T2 + 2T.mc2 = (2π)2(200 МэВ)2. Поскольку энергия покоя электрона составляет всего около 0.5 МэВ, второй член в предыдущем выражении меньше первого на три порядка, отсюда кинетическая энергия электрона с длиной волны де-Бройля в 1 Фм составляет T 1260 МэВ = 1.26 ГэВ.
Для электрона Для протона Длина волны протона с той же кинетической энергией, что и у электрона, почти
в 5 раз меньше!
Приведенная длина волны частицы выражается как: откуда Поскольку энергия покоя электрона mc2 всего 0.511 МэВ, то при высоких энергиях (E > 500 МэВ) его полная и кинетическая энергии практически совпадают (их разность при условиях задачи меньше 0.1%.) Поэтому окончательный ответ имеет вид: E ≈ T ≈ 20 ГэВ. Энергии электронов 20 ГэВ и выше достижимы в настоящее время на ряде электронных ускорителей высоких энергий. Например, на ускорителе LEP в Европейском центре ядерных исследований (CERN) энергии электронов и позитронов, движущихся навстречу друг другу на встречных пучках, составляли около 100 Гэв. (В настоящее время в туннеле ускорителя LEP сооружается новый ускоритель LHC). Задание 1
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Как найти кинетическую энергию вращательного движения. Теорема об изменении кинетической энергии. Силы внутреннего трения
Механической энергией называют способность тела или системы тел совершать работу . Различают два вида механической энергии: кинетическая и потенциальная энергии.
Кинетическая энергия поступательного движения
Кинетической называетсяэнергия, обусловленная движением тела. Она измеряется работой, которую совершает равнодействующая сила, чтобы разогнать тело из состояния покоя до данной скорости.
Пусть тело массой m начинает двигаться под действием
равнодействующей силы. Тогда элементарная работаdA равнаdA = F · dl · cos.
В данном случае направление силы и
перемещения совпадают. Поэтому= 0,cos = 1
иdl = · dt ,
где – скорость, с которой движется тело в
данный момент времени. Эта сила сообщает
телу ускорение
Тогда элементарная работаdA равнаdA = F · dl · cos.
В данном случае направление силы и
перемещения совпадают. Поэтому= 0,cos = 1
иdl = · dt ,
где – скорость, с которой движется тело в
данный момент времени. Эта сила сообщает
телу ускорение
По второму закону НьютонаF = ma =
Поэтому
и полная работаА на путиl равна:
Согласно определению, W k = A , поэтому
(6)
Из формулы (6) следует, что значение кинетической энергии зависит от выбора системы отсчёта, поскольку скорости тел в различных системах отсчёта различны.
Кинетическая энергия вращательного движения
Пусть тело с моментом инерции I z вращается относительно осиz с некоторой угловой скоростью. Тогда из формулы (6), пользуясь аналогией между поступательным и вращательным движениями, получаем:
(7)
Теорема о кинетической энергии
Пусть тело массой т движется поступательно. Под действием
различных сил, приложенных к нему,
скорость тела изменяется от
до
Под действием
различных сил, приложенных к нему,
скорость тела изменяется от
до
Тогда работаА этих сил равна
(8)
где W k 1 иW k 2 -кинетическая энергия тела в начальном и конечном состоянии. Соотношение (8) называетсятеоремой о кинетической энергии. Его формулировка:работа всех сил, действующих на тело, равна изменению его кинетической энергии. Если тело одновременно участвует в поступательном и вращательном движениях, например, катится, то его кинетическая энергия равна сумме кинетической энергии при этих движениях.
Консервативные и неконсервативные силы
Если на тело в каждой
точке пространства действует какая-нибудь
сила, то совокупность этих сил называют силовым
полем или полем .
Существует два вида полей –
потенциальные и непотенциальные (или
вихревые). В потенциальных полях на
тела, помещённые в них, действуют силы,
зависящие только от координат тел. Эти
силы получили название консервативных или потенциальных . Они обладают замечательным свойством: работа
консервативных сил не зависит от пути
переноса тела и определяется только
его начальным и конечным положением .
Отсюда следует, что при движении тела
по замкнутому пути (рис. 1) работа не
совершается. Действительно, работа A на всём пути равна сумме работы A 1B2 ,
совершаемой на пути 1B2 ,
и работы A 2C1
на пути 2C1 ,
т.е. А = A 1B2
+ A 2C1 .
Но работа A 2C1 =
–A 1C2 ,
так как движение происходит в
противоположном направлении и A 1B2 = A 1C2 .
Тогда А = A 1B2
– A 1C2
= 0, что и
требовалось доказать. Равенство нулю
работы по замкнутому пути можно записать
в виде
Они обладают замечательным свойством: работа
консервативных сил не зависит от пути
переноса тела и определяется только
его начальным и конечным положением .
Отсюда следует, что при движении тела
по замкнутому пути (рис. 1) работа не
совершается. Действительно, работа A на всём пути равна сумме работы A 1B2 ,
совершаемой на пути 1B2 ,
и работы A 2C1
на пути 2C1 ,
т.е. А = A 1B2
+ A 2C1 .
Но работа A 2C1 =
–A 1C2 ,
так как движение происходит в
противоположном направлении и A 1B2 = A 1C2 .
Тогда А = A 1B2
– A 1C2
= 0, что и
требовалось доказать. Равенство нулю
работы по замкнутому пути можно записать
в виде
(9)
Значок ” ” на интеграле означает, что интегрирование производится по замкнутой кривой длиною l . Равенство (9) является математическим определением консервативных сил.
В макромире имеется всего лишь три
вида потенциальных силгравитационная, упругая и электростатическая
силы. К неконсервативным силам относятся
силы трения, называемыедиссипативными .
В этом случае направления силыивсегда противоположны. Поэтому работа
этих сил по любому пути отрицательная,
вследствие чего тело непрерывно теряет
кинетическую энергию.
К неконсервативным силам относятся
силы трения, называемыедиссипативными .
В этом случае направления силыивсегда противоположны. Поэтому работа
этих сил по любому пути отрицательная,
вследствие чего тело непрерывно теряет
кинетическую энергию.
Основные динамические характеристики вращательного движения – момент импульса относительно оси вращения z:
и кинетическая энергия
В общем случае, энергия при вращении с угловой скоростью находится по формуле:
, где – тензор инерции .В термодинамике
Точно по тем же самым рассуждениям, как и в случае поступательного движения, равнораспределение подразумевает, что при тепловом равновесии средняя вращательная энергия каждой частицы одноатомного газа: (3/2)k B T . Аналогично, теорема о равнораспределении позволяет вычислить среднеквадратичную угловую скорость молекул.
См. также
Wikimedia Foundation . 2010 .
Смотреть что такое “Энергия вращательного движения” в других словарях:
У этого термина существуют и другие значения, см. Энергия (значения). Энергия, Размерность … Википедия
Энергия (значения). Энергия, Размерность … Википедия
ДВИЖЕНИЯ – ДВИЖЕНИЯ. Содержание: Геометрия Д………………..452 Кинематика Д……………….456 Динамика Д………………..461 Двигательные механизмы…………465 Методы изучения Д. человека………471 Патология Д. человека…………. 474… … Большая медицинская энциклопедия
Кинетическая энергия энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения. Более строго, кинетическая энергия есть разность между полной… … Википедия
Тепловое движение α пептида. Сложное дрожащее движение атомов, составляющих пептид, случайно, и энергия отдельного атома флуктуирует в широких пределах, но с помощью закона равнораспределения вычисляют как среднюю кинетическую энергию каждого… … Википедия
Тепловое движение α пептида. Сложное дрожащее движение атомов, составляющих пептид, случайно, и энергия отдельного атома флуктуирует в широких пределах, но с помощью закона равнораспределения вычисляют как среднюю кинетическую энергию каждого… … Википедия
– (франц. marées, нем. Gezeiten, англ. tides) периодические колебания уровня воды вследствие притяжения Луны и Солнца. Общие сведения. П. всего заметнее по берегам океанов. Тотчас после малой воды наибольшего отлива, уровень океана начинает… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
marées, нем. Gezeiten, англ. tides) периодические колебания уровня воды вследствие притяжения Луны и Солнца. Общие сведения. П. всего заметнее по берегам океанов. Тотчас после малой воды наибольшего отлива, уровень океана начинает… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Рефрижераторное судно Ivory Tirupati начальная остойчивость отрицательна Остойчивость способность … Википедия
Рефрижераторное судно Ivory Tirupati начальная остойчивость отрицательна Остойчивость способность плавучего средства противостоять внешним силам, вызывающим его крен или дифферент и возвращаться в состояние равновесия по окончании возмущающего… … Википедия
Просмотр: эта статья прочитана 49298 раз
Pdf Выберите язык… Русский Украинский Английский
Краткий обзор
Полностью материал скачивается выше, предварительно выбрав язык
Два случая преобразования механического движения материальной точки или системы точек:
- механическое движение переносится с одной механической системы на другую в качестве механического движения;
- механическое движение превращается в другую форму движения материи (в форму потенциальной энергии, теплоту, электричество и т.
 д.).
д.).
Когда рассматривается преобразование механического движения без перехода его в другую форму движения, мерой механического движения является вектор количества движения материальной точки или механической системы. Мерой действия силы в этом случае является вектор импульса силы.
Когда механическое движение превращается в другую форму движения материи, в качестве меры механического движения выступает кинетическая энергия материальной точки или механической системы. Мерой действия силы при превращении механического движения в другую форму движения является работа силы
Кинетическая энергия
Кинетическая энергия это способность тела преодолевать препятствование во время движения.
Кинетическая энергия материальной точки
Кинетической энергией материальной точки называется скалярная величина, которая равняется половине произведения массы точки на квадрат ее скорости.
Кинетическая энергия:
- характеризует и поступательное, и вращательное движения;
- не зависит от направления движения точек системы и не характеризует изменение этих направлений;
- характеризует действие и внутренних, и внешних сил.

Кинетическая энергия механической системы
Кинетическая энергия системы равняется сумме кинетических энергий тел системы. Кинетическая энергия зависит от вида движения тел системы.
Определение кинетической энергии твердого тела при разных видах движения движениях.
Кинетическая энергия поступательного движения
При поступательном движении кинетическая энергия тела равна Т =m V 2 /2.
Мерой инертности тела при поступательном движении является масса.
Кинетическая энергия вращательного движения тела
При вращательном движении тела кинетическая энергия равняется половине произведения момента инерции тела относительно оси вращения и квадрата его угловой скорости.
Мерой инертности тела при вращательном движении является момент инерции.
Кинетическая энергия тела не зависит от направления вращения тела.
Кинетическая энергия плоскопаралельного движения тела
При плоскопаралельном движении тела кинетическая энергия равна
Работа силы
Работа силы характеризует действие силы на тело при некотором перемещении и определяет изменение модуля скорости подвижной точки.
Элементарная работа силы
Элементарная работа силы определяется как скалярная величина, равная произведению проекции силы на касательную к траектории, направленную в направлении движения точки, и бесконечно малого перемещения точки, направленного вдоль этой касательной.
Работа силы на конечном перемещении
Работа силы на конечном перемещении равна сумме ее работ на элементарных участках.
Работа силы на конечном перемещении М 1 М 0 равняется интегралу вдоль этого перемещения от элементарной работы.
Работа силы на перемещении М 1 М 2 изображается площадью фигуры, ограниченной осью абсцисс, кривой и ординатами, соответствующими точкам М 1 и М 0 .
Единица измерения работы силы и кинетической энергии в системе СИ 1 (Дж).
Теоремы о работе силы
Теорема 1 . Работа равнодействующей силы на некотором перемещении равна алгебраической сумме работ составляющих сил на том же перемещении.
Теорема 2. Работа постоянной силы на результирующем перемещении равна алгебраической сумме работ этой силы на составляющих перемещениях.
Работа постоянной силы на результирующем перемещении равна алгебраической сумме работ этой силы на составляющих перемещениях.
Мощность
Мощность – это величина, которая определяет работу силы за единицу времени.
Единицей измерения мощности есть 1Вт = 1 Дж/с.
Случаи определения работы сил
Работа внутренних сил
Сумма работ внутренних сил твердого тела на любом его перемещении равна нулю.
Работа силы тяжести
Работа силы упругости
Работа силы трения
Работа сил, приложенных к вращающемуся телу
Элементарная работа сил, приложенных к твердому телу, вращающемуся вокруг неподвижной оси, равна произведению главного момента внешних сил относительно оси вращения на приращение угла поворота.
Сопротивление качению
В зоне контакта неподвижого цилиндра и плоскости возникает местная деформация контактного сжатия, напряжение распределяются по эллиптическому закону и линия действия равнодействующей N этих напряжений совпадает с линией действия силы нагрузки на цилиндр Q. При перекатывании цилиндра распределение нагрузки становится несимметричным с максимумом, смещенным в сторону движения. Равнодействующая N смещается на величину k – плечо силы трения качения, которая еще назвается коэффициентом трения качения и имеет размерность длины (см)
При перекатывании цилиндра распределение нагрузки становится несимметричным с максимумом, смещенным в сторону движения. Равнодействующая N смещается на величину k – плечо силы трения качения, которая еще назвается коэффициентом трения качения и имеет размерность длины (см)
Теорема об изменении кинетической энергии материальной точки
Изменение кинетической энергии материальной точки на некотором ее перемещении равняется алгебраической сумме робот всех действующих на точку сил на том же перемещении.
Теорема об изменении кинетической энергии механической системы
Изменение кинетической энергии механической системы на некотором перемещении равняется алгебраической сумме робот внутренних и внешних сил, действующих на материальные точки системы на том же перемещении.
Теорема об изменении кинетической энергии твердого тела
Изменение кинетической энергии твердого тела (неизменной системы) на некотором перемещении равняется сумме робот внешних сил, действующих на точки системы на том же перемещении.
КПД
Силы, действующие в механизмах
Силы и пары сил (моменты), которые приложены к механизму или машине, можно разделить на группы:
1.Движущие силы и моменты, совершающие положительную работу (приложенные к ведущим звеньям, например, давление газа на поршень в ДВС).
2. Силы и моменты сопротивления, совершающие отрицательную работу:
- полезного сопротивления (совершают требуемую от машины работу и приложены к ведомым звеньям, например сопротивление поднимаемого машиной груза),
- силы сопротивления (например, силы трения, сопротивление воздуха и т.п.).
3. Силы тяжести и силы упругости пружин (как положительная, так и отрицательная работа, при этом работа за полный цикл равна нулю).
4. Силы и моменты, приложенные к корпусу или стойке извне (реакция фундамента и т.п.), которые не совершают работу.
5. Силы взаимодействия между звеньями, действующие в кинематических парах.
6. Силы инерции звеньев, обусловленные массой и движением звеньев с ускорением, могут осуществлять положительную, отрицательную работу и не совершать работы.
Работа сил в механизмах
При установившемся режиме работы машины ее кинетическая энергия не изменяется и сумма работ приложенных к ней движущих сил и сил сопротивления равна нулю.
Работа, затрачиваемая на приведение машины в движение, расходуется на преодоление полезных и вредных сопротивлений.
КПД механизмов
Механический коэффициент полезного действия при установившемся движении равен отношению полезной работы машины к работе, затраченной на приведение машины в движение:
Элементы машины могут соединяться последовательно, параллельно и смешанно.
КПД при последовательном соединении
При последовательном соединении механизмов общий КПД меньше с наименьшего КПД отдельного механизма.
КПД при параллельном соединении
При параллельном соединении механизмов общий КПД больше наименьшего и меньше наибольшего КПД отдельного механизма.
Формат: pdf
Язык: русский, украинский
Пример расчета прямозубой цилиндрической передачи
Пример расчета прямозубой цилиндрической передачи. Выполнен выбор материала, расчет допускаемых напряжений, расчет на контактную и изгибную прочность.
Выполнен выбор материала, расчет допускаемых напряжений, расчет на контактную и изгибную прочность.
Пример решения задачи на изгиб балки
В примере построены эпюры поперечных сил и изгибающих моментов, найдено опасное сечение и подобран двутавр. В задаче проанализировано построение эпюр с помощью дифференциальных зависимостей, провелен сравнительный анализ различных поперечных сечений балки.
Пример решения задачи на кручение вала
Задача состоит в проверке прочности стального вала при заданном диаметре, материале и допускаемых напряжениях. В ходе решения строятся эпюры крутящих моментов, касательных напряжений и углов закручивания. Собственный вес вала не учитывается
Пример решения задачи на растяжение-сжатие стержня
Задача состоит в проверке прочности стального стержня при заданных допускаемых напряжениях. В ходе решения строятся эпюры продольных сил, нормальных напряжений и перемещений. Собственный вес стержня не учитывается
Применение теоремы о сохранении кинетической энергии
Пример решения задачи на применение теоремы о сохранение кинетической энергии механической системы
Определим
кинетическую энергию твёрдого тела,
вращающегося вокруг неподвижной оси. Разобьем это тело на n
материальных точек. Каждая точка движется
с линейной скоростью υ i =ωr i ,
тогда кинетическая энергия точки
Разобьем это тело на n
материальных точек. Каждая точка движется
с линейной скоростью υ i =ωr i ,
тогда кинетическая энергия точки
или
Полная кинетическая энергия вращающегося твердого тела равна сумме кинетических энергий всех его материальных точек:
(3.22)
(J – момент инерции тела относительно оси вращения)
Если траектории всех точек лежат в параллельных плоскостях (как у цилиндра, скатывающегося с наклонной плоскости, каждая точка перемещается в своей плоскости рис), это плоское движение . В соответствии с принципом Эйлера плоское движение всегда можно бесчисленным количеством способов разложить на поступательное и вращательное движение. Если шарик падает или скользит вдоль наклонной плоскости, он двигается только поступательно; когда же шарик катится – он ещё и вращается.
Если тело совершает поступательное и вращательное движения одновременно, то его полная кинетическая энергия равна
(3.23)
Из
сопоставления формул кинетической
энергии для поступательного и
вращательного движений видно, что мерой
инертности при вращательном движении
служит момент инерции тела.
§ 3.6 Работа внешних сил при вращении твёрдого тела
При вращении твёрдого тела его потенциальная энергия не изменяется, поэтому элементарная работа внешних сил равна приращению кинетической энергии тела:
dA
= dE
или
Учитывая, что Jβ = M, ωdr = dφ, имеем α тела на конечный угол φ равна
(3.25)
При вращении твёрдого тела вокруг неподвижной оси работа внешних сил определяется действием момента этих сил относительно данной оси. Если момент сил относительно оси равен нулю, то эти силы работы не производят.
Примеры решения задач
Пример 2.1. Маховик массой m =5кг и радиусом r = 0,2 м вращается вокруг горизонтальной оси с частотой ν 0 =720 мин -1 и при торможении останавливается за t =20 с. Найти тормозящий момент и число оборотов до остановки.
Для определения тормозящего момента применим основное уравнение динамики вращательного движения
где
I=mr 2 –
момент инерции диска; Δω
=ω
– ω 0 ,
причём ω
=0 конечная угловая скорость, ω 0 =2πν 0
– начальная. М –тормозящий момент сил,
действующих на диск.
М –тормозящий момент сил,
действующих на диск.
Зная все величины, можно определить тормозящий момент
Mr 2 2πν 0 = МΔt (1)
(2)
Из кинематики вращательного движения угол поворота за время вращения диска до остановки может быть определён по формуле
(3)
где β–угловое ускорение.
По условию задачи: ω =ω 0 – βΔt, так как ω=0, ω 0 = βΔt
Тогда выражение (2) может быть записано в виде:
Пример 2.2. Два маховика в виде дисков одинаковых радиусов и масс были раскручены до скорости вращения n = 480 об/мин и предоставили самим себе. Под действием сил трения валов о подшипники первый остановился через t =80 с, а второй сделал N = 240 оборотов до остановки. У какого и маховика момент сил трения валов о подшипники был больше и во сколько раз.
Момент сил терния М 1 первого маховика найдём, воспользовавшись основным уравнением динамики вращательного движения
M 1 Δt = Iω 2 – Iω 1
где Δt – время действия момента сил трения, I=mr 2 – момент инерции маховика, ω 1 = 2πν и ω 2 = 0– начальная и конечная угловые скорости маховиков
Тогда
Момент сил трения М 2 второго маховика выразим через связь между работой А сил трения и изменением его кинетической энергии ΔE к:
где Δφ = 2πN
– угол поворота, N
-число оборотов маховика.
Тогда, откуда
Отношение будет равно
Момент сил трения второго маховика в 1.33 раза больше.
Пример 2.3. Масса однородного сплошного диска m, массы грузов m 1 и m 2 (рис.15). Скольжения и трения нити в оси цилиндра нет. Найти ускорение грузов и отношение натяжений нити в процессе движения.
Проскальзывания нити нет, поэтому, когда m 1 и m 2 будут совершать поступательное движение, цилиндр будет совершать вращение относительно оси, проходящей через точку О. Положим для определённости, что m 2 > m 1 .
Тогда груз m 2 опускается и цилиндр вращается по часовой стрелке. Запишем уравнения движения тел, входящих в систему
Первые два
уравнения записаны для тел с массами
m 1
и m 2
, совершающих поступательное движение,
а третье уравнение – для вращающегося
цилиндра. В третьем уравнении слева
стоит суммарный момент сил, действующих
на цилиндр (момент силы T 1
взят
со знаком минус, так как сила T 1
стремится
повернуть цилиндр против часовой
стрелки). Справа I – момент инерции
цилиндра относительно оси О, который
равен
Справа I – момент инерции
цилиндра относительно оси О, который
равен
где R – радиус цилиндра; β – угловое ускорение цилиндра.
Так как
проскальзывания нити нет, то
. С учётом выражений для I и β получим:
Складывая уравнения системы, приходим к уравнению
Отсюда находим ускорение a грузов
Из полученного уравнения видно, что натяжения нитей будут одинаковы, т.е. =1, если масса цилиндра будет гораздо меньше массы грузов.
Пример
2.4. Полый
шар массой m = 0,5 кг имеет внешний радиус
R = 0,08м и внутренний r = 0,06м. Шар вращается
вокруг оси, проходящей через его центр.
В определённый момент на шар начинает
действовать сила, в результате чего
угол поворота шара изменяется по закону
.
Определить момент приложенной силы.
Решаем задачу,
используя основное уравнение динамики
вращательного движения
.
Основная трудность – определить момент
инерции полого шара, а угловое ускорение
β находим как
. Момент инерции I полого шара равен
разности моментов инерции шара радиуса
R и шара радиуса r:
Момент инерции I полого шара равен
разности моментов инерции шара радиуса
R и шара радиуса r:
где ρ – плотность материала шара. Находим плотность, зная массу полого шара
Отсюда определим плотность материала шара
Для момента силы M получаем следующее выражение:
Пример 2.5. Тонкий стержень массой 300г и длиной 50см вращается с угловой скоростью 10с -1 в горизонтальной плоскости вокруг вертикальной оси, проходящей через середину стержня. Найдите угловую скорость, если в процессе вращения в той же плоскости стержень переместится так, что ось вращения пройдёт через конец стержня.
Используем закон сохранения момента импульса
(1)
(J i -момент инерции стержня относительно оси вращения).
Для изолированной системы тел векторная сумма моментов импульса остаётся постоянной. Вследствие того, что распределение массы стержня относительно оси вращения изменяется момент инерции стержня также изменяется в соответствии с (1):
J 0 ω 1
=
J 2 ω 2 .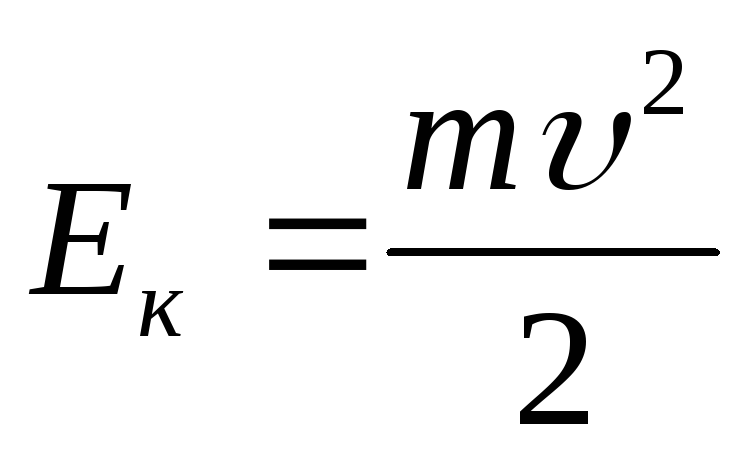 (2)
(2)
Известно, что момент инерции стержня относительно оси, проходящей через центр масс и перпендикулярной стержню, равен
J 0 = mℓ 2 /12. (3)
По теореме Штейнера
J =J 0 +mа 2
(J-момент инерции стержня относительно произвольной оси вращения; J 0 – момент инерции относительно параллельной оси, проходящей через центр масс; а – расстояние от центра масс до выбранной оси вращения).
Найдём момент инерции относительно оси, проходящей через его конец и перпендикулярной стержню:
J 2 =J 0 +mа 2 , J 2 = mℓ 2 /12 +m(ℓ/2) 2 = mℓ 2 /3. (4)
Подставим формулы (3) и (4) в (2):
mℓ 2 ω 1 /12 = mℓ 2 ω 2 /3
ω 2 = ω 1 /4 ω 2 =10с-1/4=2,5с -1
Пример
2.6 .
Человек массой m =60кг,
стоящий на краю платформы массой М=120кг,
вращающейся по инерции вокруг неподвижной
вертикальной оси с частотой ν 1 =12мин -1 ,
переходит к её центру. Считая платформу
круглым однородным диском, а человека
– точечной массой, определите, с какой
частотой ν 2 будет
тогда вращаться платформа.
Дано: m=60кг, М=120кг, ν 1 =12мин -1 = 0,2с -1 .
Найти: ν 1
Решение: Согласно условию задачи, платформа с человеком вращается по инерции, т.е. результирующий момент всех сил, приложенных к вращающейся системе, равен нулю. Поэтому для системы «платформа-человек» выполняется закон сохранения момента импульса
I 1 ω 1 = I 2 ω 2
где
–
момент инерции системы, когда человек
стоит на краю платформы (учли, что момент
инерции платформы, равен(R
– радиус п
латформы),
момент инерции человека на краю платформы
равенmR 2).
– момент инерции системы, когда человек стоит в центре платформы (учли, что момент человека, стоящего в центре платформы, равен нулю). Угловая скорость ω 1 = 2π ν 1 и ω 1 = 2π ν 2 .
Подставив записанные выражения в формулу (1), получаем
откуда искомая частота вращения
Ответ : ν 2 =24мин -1 .
1. Рассмотрим вращение тела вокруг неподвижной оси Z. Разобьем все тело на множество элементарных масс m i . Линейная скорость элементарной массы m i – v i = w·R i , где R i – расстояние массы m i от оси вращения. Следовательно, кинетическая энергия i -ой элементарной массы будет равна . Полная кинетическая энергия тела: , здесь – момент инерции тела относительно оси вращения.
Линейная скорость элементарной массы m i – v i = w·R i , где R i – расстояние массы m i от оси вращения. Следовательно, кинетическая энергия i -ой элементарной массы будет равна . Полная кинетическая энергия тела: , здесь – момент инерции тела относительно оси вращения.
Таким образом, кинетическая энергия тела, вращающегося относительно неподвижной оси равна:
2. Пусть теперь тело вращается относительно некоторой оси, а сама ось перемещается поступательно, оставаясь параллельной самой себе.
НАПРИМЕР: Катящийся без скольжения шар совершает вращательное движение, а центр тяжести его, через который проходит ось вращения (точка «О») перемещается поступательно (рис.4.17).
Скорость i -той элементарной массы тела равна , где – скорость некоторой точки «О» тела; – радиус-вектор, определяющий положение элементарной массы по отношению к точке «О».
Кинетическая энергия элементарной массы равна:
ЗАМЕЧАНИЕ: векторное произведение совпадает по направлению с вектором и имеет модуль, равный (рис. 4.18).
4.18).
Учтя это замечание, можно записать, что , где – расстояние массы от оси вращения. Во втором слагаемом сделаем циклическую перестановку сомножителей, после этого получим
Чтобы получить полную кинетическую энергию тела, просуммируем это выражение по всем элементарным массам, вынося постоянные множители за знак суммы. Получим
Сумма элементарных масс есть масса тела «m». Выражение равно произведению массы тела на радиус-вектор центра инерции тела (по определению центра инерции). Наконец, – момент инерции тела относительно оси, проходящей через точку «О». Поэтому можно записать
.
Если в качестве точки «O» взять центр инерции тела «С», радиус-вектор будет равен нулю и второе слагаемое исчезнет. Тогда, обозначив через – скорость центра инерции, а через – момент инерции тела относительно оси, проходящей через точку «С», получим:
(4.6)
Таким образом, кинетическая энергия тела при плоском движении слагается из энергии поступательного движения со скоростью, равной скорости центра инерции, и энергии вращения вокруг оси, проходящей через центр инерции тела.
Работа внешних сил при вращательном движении твердого тела.
Найдем работу, которую совершают силы при вращении тела вокруг неподвижной оси Z.
Пусть на массу действуют внутренняя сила и внешняя сила (результирующая сила лежит в плоскости, перпендикулярной оси вращения) (рис. 4.19). Эти силы совершают за время dt работу:
Осуществив в смешанных произведениях векторов циклическую перестановку сомножителей, находим:
где , – соответственно, моменты внутренней и внешней сил относительно точки «О».
Просуммировав по всем элементарным массам, получим элементарную работу, совершаемую над телом за время dt :
Сумма моментов внутренних сил равна нулю. Тогда, обозначив суммарный момент внешних сил через , придем к выражению:
.
Известно, что скалярным произведением двух векторов называется скаляр, равный произведению модуля одного из перемножаемых векторов на проекцию второго на направление первого, учтя, что , (направления оси Z и совпадают), получим
,
но w·dt =d j, т. е. угол, на который поворачивается тело за время dt . Поэтому
е. угол, на который поворачивается тело за время dt . Поэтому
.
Знак работы зависит от знака M z , т.е. от знака проекции вектора на направление вектора .
Итак, при вращении тела внутренние силы работы не совершают, а работа внешних сил определяется формулой .
Работа за конечный промежуток времени находится путем интегрирования
.
Если проекция результирующего момента внешних сил на направление остается постоянной, то ее можно вынести за знак интеграла:
, т.е. .
Т.е. работа внешней силы при вращательном движении тела равна произведению проекции момента внешней силы на направление и угол поворота.
С другой стороны работа внешней силы, действующей на тело идет на приращение кинетической энергии тела (или равна изменению кинетической энергии вращающегося тела). Покажем это:
;
Следовательно,
. (4.7)
Самостоятельно:
Упругие силы;
Закон Гука.
| ЛЕКЦИЯ 7 |
Гидродинамика
Линии и трубки тока.
Гидродинамика изучает движение жидкостей, однако ее законы примени- мы и к движению газов. При стационарном течении жидкости скорость ее частиц в каждой точке пространства есть величина, независимая от времени и являющаяся функцией координат. При стационарном течении траектории частиц жидкости образуют линию тока. Совокупность линий тока образует трубку тока (рис. 5.1). Будем считать жидкость несжимаемой, тогда объем жидкости, протекающей через сечения S 1 и S 2 , будет одинаков. За секунду через эти сечения пройдет объем жидкости, равный
, (5.1)
где и – скорости жидкости в сечениях S 1 и S 2 , а вектора и определяются как и , где и – нормали к сечениям S 1 и S 2 . Уравнение (5.1) называют уравнением неразрывности струи. Из него следует, что скорость жидкости обратно пропорциональна сечению трубки тока.
Уравнение Бернулли.
Будем рассматривать идеальную несжимаемую жидкость, в которой внутреннее трение (вязкость) отсутствует. Выделим в стационарно текущей жидкости тонкую трубку тока (рис. 5.2) с сечениями S 1 и S 2 , перпендикулярными к линиям тока. В сечении 1 за малое время t частицы сместятся на расстояние l 1 , а в сечении 2 – на расстояние l 2 . Через оба сечения за время t пройдут одинаковые малые объемы жидкости V = V 1 = V 2 и перенесут массу жидкости m=rV , где r – плотность жидкости. В целом изменение механической энергии всей жидкости в трубке тока между сечениями S 1 и S 2 , произошедшее за время t , можно заменить изменением энергии объема V , произошедшим при его перемещении от сечения 1 до сечения 2 . При таком движении изменится кинетическая и потенциальная энергия этого объема, и полное изменение его энергии
Выделим в стационарно текущей жидкости тонкую трубку тока (рис. 5.2) с сечениями S 1 и S 2 , перпендикулярными к линиям тока. В сечении 1 за малое время t частицы сместятся на расстояние l 1 , а в сечении 2 – на расстояние l 2 . Через оба сечения за время t пройдут одинаковые малые объемы жидкости V = V 1 = V 2 и перенесут массу жидкости m=rV , где r – плотность жидкости. В целом изменение механической энергии всей жидкости в трубке тока между сечениями S 1 и S 2 , произошедшее за время t , можно заменить изменением энергии объема V , произошедшим при его перемещении от сечения 1 до сечения 2 . При таком движении изменится кинетическая и потенциальная энергия этого объема, и полное изменение его энергии
, (5.2)
где v 1 и v 2 – скорости частичек жидкости в сечениях S 1 и S 2 соответственно; g – ускорение земного притяжения; h 1 и h 2 – высоты центра сечений.
В идеальной жидкости потери на трение отсутствуют, поэтому приращение энергии DE должно быть равно работе, совершаемой силами давления над выделенным объемом. При отсутствии сил трения эта работа:
Приравнивая правые части равенств (5.2) и (5.3) и перенося члены с одинаковыми индексами в одну часть равенства, получим
. (5.4)
Сечения трубки S 1 и S 2 были взяты произвольно, поэтому можно утверждать, что в любом сечении трубки тока справедливо выражение
. (5.5)
Уравнение (5.5) называется уравнением Бернулли. Для горизонтальной линии тока h = const , и равенство (5.4) приобретает вид
r /2 + p 1 = r· /2 + p 2 , (5.6)
т.е. давление оказывается меньшим в тех точках, где скорость больше.
Силы внутреннего трения.
Реальной жидкости присуща вязкость, которая проявляется в том, что любое движение жидкости и газа самопроизвольно прекращается при отсутствии причин, вызвавших его. Рассмотрим опыт, в котором слой жидкости расположен над неподвижной поверхностью, а сверху его перемещается со скоростью , плавающая на ней пластина с поверхностью S (рис. 5.3). Опыт показывает, что для перемещения пластины с постоянной скоростью необходимо действовать на нее с силой . Так как пластина не получает ускорения, значит, действие этой силы уравновешивается другой, равной ей по величине и противоположно направленной силой, которая является силой трения . Ньютон показал, что сила трения
Рассмотрим опыт, в котором слой жидкости расположен над неподвижной поверхностью, а сверху его перемещается со скоростью , плавающая на ней пластина с поверхностью S (рис. 5.3). Опыт показывает, что для перемещения пластины с постоянной скоростью необходимо действовать на нее с силой . Так как пластина не получает ускорения, значит, действие этой силы уравновешивается другой, равной ей по величине и противоположно направленной силой, которая является силой трения . Ньютон показал, что сила трения
, (5.7)
где d – толщина слоя жидкости, h – коэффициент вязкости или коэффициент трения жидкости, знак минус учитывает различное направление векторов F тр и v o . Если исследовать скорость частиц жидкости в разных местах слоя, то оказывается, что она изменяется по линейному закону (рис. 5.3):
v(z) = = (v 0 /d)·z.
Дифференцируя это равенство, получим dv/dz = v 0 /d . С учетом этого
формула (5.7) примет видF тр =– h(dv/dz)S , (5. 8)
8)
где h – коэффициент динамической вязкости . Величина dv/dz называется градиентом скорости. Она показывает, как быстро изменяется скорость в направлении оси z . При dv/dz = const градиент скорости численно равен изменению скорости v при изменении z на единицу. Положим численно в формуле (5.8) dv/dz = -1 и S = 1, получим h = F . Отсюда следует физический смысл h : коэффициент вязкости численно равен силе, которая действует на слой жидкости единичной площади при градиенте скорости, равном единице. Единица вязкости в СИ называется паскаль-секундой (обозначается Па с). В системе СГС единицей вязкости является 1 пуаз (П), причем 1 Па с = 10П.
материалы для подготовки к ЕГЭ по Физике
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: работа силы, мощность, кинетическая энергия, потенциальная энергия, закон сохранения механической энергии.
Мы приступаем к изучению энергии – фундаментального физического понятия. Но предварительно нужно разобраться с другой физической величиной – работой силы.
Работа.
Пусть на тело действует постоянная сила и тело, двигаясь прямолинейно по горизонтальной поерхности, совершило перемещение . Сила не обязательно является непосредственной причиной перемещения (так, сила тяжести не является непосредственной причиной перемещения шкафа, который передвигают по комнате).
Предположим сначала, что векторы силы и перемещения сонаправлены (рис. 1; остальные силы, действующие на тело, не указаны)
| Рис. 1.A=Fs |
В этом простейшем случае работа определяется как произведение модуля силы на модуль перемещения:
. (1)
Единицей измерения работы служит джоуль (Дж): Дж=Н м. Таким образом, если под действием силы 1 Н тело перемещается на 1 м, то сила совершает работу 1 Дж.
Таким образом, если под действием силы 1 Н тело перемещается на 1 м, то сила совершает работу 1 Дж.
Работа силы, перпендикулярной перемещению, по определению считается равной нулю. Так, в данном случае сила тяжести и сила реакции опоры не совершают работы.
Пусть теперь вектор силы образует с вектором перемещения острый угол (рис. 2).
| Рис. 2. A=Fs cos |
Разложим силу на две составляющие: (параллельную перемещению) и (перпендикулярную перемещению). Работу совершает только . Поэтому для работы силы получаем:
. Итак,
. (2)
Если вектор силы образует с вектором перемещения тупой угол , то работа по-прежнему определяется формулой (2). В этом случае работа оказывается отрицательной.
Например, работа силы трения скольжения, действующей на тело в рассмотренных ситуациях, будет отрицательной, так как сила трения направлена противоположно перемещению. В этом случае имеем:
В этом случае имеем:
, и для работы силы трения получаем:
,
где – масса тела, – коэффициент трения между телом и опорой.
Соотношение (2) означает, что работа является скалярным произведением векторов силы и перемещения:
.
Это позволяет вычислять работу через координаты данных векторов:
.
Пусть на тело действуют несколько сил и – равнодействующая этих сил. Для работы силы имеем:
,
или
,
где – работы сил . Итак, работа равнодействующей приложенных к телу сил равна сумме работ каждой силы в отдельности.
Мощность.
Часто имеет значение быстрота, с которой совершается работа. Скажем, на практике важно знать, какую работу сможет выполнить данное устройство за фиксированное время.
Мощность – это величина, характеризующая скорость совершения работы. Мощность есть отношение работы ко времени , за которое эта работа совершена:
.
Мощность измеряется в ваттах (Вт). 1 Вт = 1 Дж/с, то есть 1 Вт – это такая мощность, при которой работа в 1 Дж совершается за 1 с.
Предположим, что силы, действующие на тело, уравновешены, и тело движется равномерно и прямолинейно со скоростью . В этом случае существует полезная формула для мощности, развиваемой одной из действующих сил .
За время тело совершит перемещение . Работа силы будет равна:
.
Отсюда получаем мощность:
,
или
,
где -угол между векторами силы и скорости.
Наиболее часто эта формула используется в ситуации, когда – сила “тяги” двигателя автомобиля (которая на самом деле есть сила трения ведущих колёс о дорогу). В этом случае , и мы получаем просто:
.
Механическая энергия.
Энергия является мерой движения и взаимодействия любых объектов в природе. Имеются различные формы энергии: механическая, тепловая, электромагнитная, ядерная. . .
. .
Опыт показывает, что энергия не появляется ниоткуда и не исчезает бесследно, она лишь переходит из одной формы в другую. Это самая общая формулировка закона сохранения энергии.
Каждый вид энергии представляет собой некоторое математическое выражение. Закон сохранения энергии означает, что в каждом явлении природы определённая сумма таких выражений остаётся постоянной с течением времени.
Измеряется энергия в джоулях, как и работа.
Механическая энергия является мерой движения и взаимодействия механических объектов (материальных точек, твёрдых тел).
Мерой движения тела является кинетическая энергия. Она зависит от скорости тела. Мерой взаимодействия тел является потенциальная энергия. Она зависит от взаимного расположения тел.
Механическая энергия системы тел равна сумме кинетической энергии тел и потенциальной энергии их взаимодействия друг с другом.
Кинетическая энергия.
Кинетической энергией тела (принимаемого за материальную точку) называется величина
,
где – масса тела, – его скорость.
Кинетической энергией системы из тел называется сумма кинетических энергий каждого тела:
.
Если тело движется под действием силы , то кинетическая энергия тела, вообще говоря, меняется со временем. Оказывается, именение кинетической энергии тела за некоторый промежуток времени равно работе силы . Покажем это для случая прямолинейного равноускоренного движения.
Пусть – начальная скорость, – конечная скорость тела. Выберем ось вдоль траектории тела (и, соответственно, вдоль вектора силы ). Для работы силы получаем:
.
(мы воспользовались формулой для , выведенной в статье “Равноускоренное движение”). Заметим теперь, что в данном случае проекция скорости отличается от модуля скорости разве что знаком; поэтому и . В результате имеем:
,
что и требовалось.
На самом деле соотношение справедливо и в самом общем случае криволинейного движения под действием переменной силы.
Теорема о кинетической энергии. Изменение кинетической энергии тела равно работе, совершённой приложенными к телу внешними силами за рассматриваемый промежуток времени.
Если работа внешних сил положительна, то кинетическая энергия увеличивается (, тело разгоняется).
Если работа внешних сил отрицательна, то кинетическая энергия уменьшается (, тело замедляет движение). Пример – торможение под действием силы трения, работа которой отрицательна.
Если же работа внешних сил равна нулю, то кинетическая энергия тела за это время не меняется. Нетривиальный пример – равномерное движение по окружности, совершаемое грузом на нити в горизонтальной плоскости. Сила тяжести, сила реакции опоры и сила натяжения нити всегда перпендикулярны скорости, и работа каждой из этих сил равна нулю в течение любого промежутка времени. Соответственно, кинетическая энергия груза (а значит, и его скорость) остаётся постоянной в процессе движения.
Задача. Автомобиль едет по горизонтальной дороге со скоростью и начинает резко тормозить. Найти путь , пройденный автомобилем до полной остановки, если коэффициент трения шин о дорогу равен .
Решение. Начальная кинетическая энергия автомобиля , конечная кинетическая энергия . Изменение кинетической энергии .
Начальная кинетическая энергия автомобиля , конечная кинетическая энергия . Изменение кинетической энергии .
На автомобиль действуют сила тяжести , реакция опоры и сила трения . Сила тяжести и реакция опоры, будучи перпендикулярны перемещению автомобиля, работы не совершают. Работа силы трения:
.
Из теоремы о кинетической энергии теперь получаем:
.
Потенциальная энергия тела вблизи поверхности Земли.
Рассмотрим тело массы , находящееся на некоторой высоте над поверхностью Земли. Высоту считаем много меньше земного радиуса. Изменением силы тяжести в процессе перемещения тела пренебрегаем.
Если тело находится на высоте , то потенциальная энергия тела по определению равна:
где – ускорение свободного падения вблизи поверхности Земли.
Высоту не обязательно отсчитывать от поверхности Земли. Как мы увидим ниже (формулы (3), (4)), физическим смыслом обладает не сама по себе потенциальная энергия, но её изменение. А изменение потенциальной энергии не зависит от уровня отсчёта. Выбор нулевого уровня потенциальной энергии в конкретной задаче диктуется исключительно соображениями удобства.
А изменение потенциальной энергии не зависит от уровня отсчёта. Выбор нулевого уровня потенциальной энергии в конкретной задаче диктуется исключительно соображениями удобства.
Найдём работу, совершаемую силой тяжести при перемещении тела. Предположим, что тело перемещается по прямой из точки , находящейся на высоте , в точку , находящуюся на высоте (рис. 3).
| Рис. 3.A=mg(h2-h3)[/math] |
Угол между силой тяжести и перемещением тела обозначим . Для работы силы тяжести получим:
.
Но, как видно из рис. 3, . Поэтому
,
или
. (3)
Учитывая, что , имеем также:
. (4)
Можно доказать, что формулы (3) и (4) справедливы для любой траектории, по которой тело перемещается из точки в точку , а не только для прямолинейного отрезка.
Работа силы тяжести не зависит от формы траектории, по которой перемещается тело, и равна разности значений потенциальной энергии в начальной и конечной точках траектории. Иными словами, работа силы тяжести всегда равна изменению потенциальной энергии с противоположным знаком. В частности, работа силы тяжести по любому замкнутому пути равна нулю.
Иными словами, работа силы тяжести всегда равна изменению потенциальной энергии с противоположным знаком. В частности, работа силы тяжести по любому замкнутому пути равна нулю.
Сила называется консервативной, если при перемещении тела работа этой силы не зависит от формы траектории, а определяется только начальным и конечным положением тела. Сила тяжести, таким образом, является консервативной. Работа консервативной силы по любому замкнутому пути равна нулю. Только в случае консервативной силы возможно ввести такую величину, как потенциальная энергия.
Потенциальна яэнергия деформированной пружины.
Рассмотрим пружину жёсткости . Начальная деформация пружины равна . Предположим,
что пружина деформируется до некоторой конечной величины деформации . Чему равна при этом работа силы упругости пружины?
В данном случае силу на перемещение не умножишь, так как сила упругости меняется в процессе деформации пружины. Для нахождения работы переменной силы требуется интегрирование. Мы не будем приводить здесь вывод, а сразу выпишем конечный результат.
Для нахождения работы переменной силы требуется интегрирование. Мы не будем приводить здесь вывод, а сразу выпишем конечный результат.
Оказывается, сила упругости пружины также является консервативной. Её работа зависит лишь от величин и и определяется формулой:
.
Величина
называется потенциальной энергией деформированной пружины (x – величина деформации).
Следовательно,
,
что полностью аналогично формулам (3) и (4).
Закон сохранения механической энергии.
Консервативные силы называются так потому, что сохраняют механическую энергию замкнутой системы тел.
Механическая энергия тела равна сумме его кинетической и потенциальной энергий:
.
Механическая энергия системы тел равна сумме их кинетических энергий и потенциальной энергии их взаимодействия друг с другом.
Предположим, что тело совершает движение под действием силы тяжести и/или силы упругости пружины. Будем считать, что трения нет. Пусть в начальном положении кинетическая и потенциальная энергии тела равны и , в конечном положении – и . Работу внешних сил при перемещении тела из начального положения в конечное обозначим .
Будем считать, что трения нет. Пусть в начальном положении кинетическая и потенциальная энергии тела равны и , в конечном положении – и . Работу внешних сил при перемещении тела из начального положения в конечное обозначим .
По теореме о кинетической энергии
.
Но работа консервативных сил равна разности потенциальных энергий:
.
Отсюда получаем:
,
или
.
Левая и правая части данного равенства представляют собой механическую энергию тела в начальном и конечном положении:
.
Следовательно, при движении тела в поле силы тяжести и/или на пружине механическая энергия тела остаётся неизменной при отсутствии трения. Справедливо и более общее утверждение.
Закон сохранения механической энергии. Если в замкнутой системе действуют только консервативные силы, то механическая энергия системы сохраняется.
При этих условиях могут происходить лишь превращения энергии: из кинетической в потенциальную и наоборот. Общий запас механической энергии системы остаётся постоянным.
Общий запас механической энергии системы остаётся постоянным.
Закон изменения механической энергии.
Если между телами замкнутой системы имеются силы сопротивления (сухое или вязкое трение), то механическая энергия системы будет уменьшаться. Так, автомобиль останавливается в результате торможения, колебания маятника постепенно затухают и т. д. Силы трения неконсервативны: работа силы трения очевидным образом зависит от пути, по которому перемещается тело между данными точками. В частности, работа силы трения по замкнутому пути не равна нулю.
Снова рассмотрим движение тела в поле силы тяжести и/или на пружине. Вдобавок на тело действует сила трения, которая за рассматриваемый промежуток времени совершает отрицательную работу . Работу консервативных сил (тяжести и упругости) по-прежнему обозначаем .
Изменение кинетической энергии тела равно работе всех внешних сил:
.
Но , следовательно
.
Отсюда
,
или
.
В левой части стоит величина – изменение механической энергии тела:
.
Итак,при движении тела в поле силы тяжести и/или на пружине изменение механической энергии тела равно работе силы трения. Так как работа силы трения отрицательна,изменение механической энергии также отрицательно: механическая энергия убывает.
Справедливо и более общее утверждение.
Закон изменения механической энергии. Изменение механической энергии замкнутой системы равно работе сил трения, действующих внутри системы.
Ясно, что закон сохранения механической энергии является частным случаем данного утверждения.
Конечно, убыль механической энергии не противоречит общефизическому закону сохранения энергии. В данном случае механическая энергия превращается в энергию теплового движения частиц вещества и их потенциальную энергию взаимодействия друг с другом, т. е. переходит во внутреннюю энергию тел системы.
PhysBook:Электронный учебник физики — PhysBook
Содержание
- 1 Учебники
- 2 Механика
- 2.
 1 Кинематика
1 Кинематика - 2.2 Динамика
- 2.3 Законы сохранения
- 2.4 Статика
- 2.5 Механические колебания и волны
- 2.
- 3 Термодинамика и МКТ
- 3.1 МКТ
- 3.2 Термодинамика
- 4 Электродинамика
- 4.1 Электростатика
- 4.2 Электрический ток
- 4.
 3 Магнетизм
3 Магнетизм - 4.4 Электромагнитные колебания и волны
- 5 Оптика. СТО
- 5.1 Геометрическая оптика
- 5.2 Волновая оптика
- 5.3 Фотометрия
- 5.4 Квантовая оптика
- 5.5 Излучение и спектры
- 5.6 СТО
- 6 Атомная и ядерная
- 6.1 Атомная физика.
 Квантовая теория
Квантовая теория - 6.2 Ядерная физика
- 6.1 Атомная физика.
- 7 Общие темы
- 8 Новые страницы
Здесь размещена информация по школьной физике:
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- flash-анимации, фотографии, рисунки различных физических процессов;
- ссылки на другие сайты
и многое другое.
Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.
Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
 СТО
СТОГеометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ – Репетитор по физике
Новые страницы
Запрос не дал результатов.
Глава 8. Выполняем работу – FIZI4KA
Физика с формулами ›
В этой главе…
- Приглядываемся к работе силы
- Изучаем отрицательную работу
- Оцениваем кинетическую энергию
- Приобретаем потенциальную энергию
- Постигаем консервативные и неконсервативные силы
- Вычисляем механическую энергию и мощность
С работой в обыденном смысле мы сталкиваемся всякий раз, например, когда приходится решать задачи по физике. Нужно брать книги, калькулятор, бумагу с ручкой, а потом потеть и корпеть над задачей. После получения решения мы выполнили вполне определенную работу, но… совсем не в том смысле, в котором термин “работа” определяется в физике.
Нужно брать книги, калькулятор, бумагу с ручкой, а потом потеть и корпеть над задачей. После получения решения мы выполнили вполне определенную работу, но… совсем не в том смысле, в котором термин “работа” определяется в физике.
В физике работой называется произведение прилагаемой силы и перемещения, выполняемого этой силой. Помимо понятия “работа” в этой главе рассматриваются связанные с ней понятия потенциальной и кинетической энергии, консервативной и неконсервативной силы, а также механической энергии и мощности. Пора приступать к… работе!
Содержание
- Работа: не совсем то, о чем вы подумали
- Работаем в разных системах единиц измерения
- Толкаем груз
- Тянем груз под углом
- Выполняем отрицательную работу
- Получаем компенсацию в виде кинетической энергии
- Запоминаем формулу кинетической энергии
- Используем соотношение для кинетической энергии
- Вычисляем кинетическую энергию объекта по результирующей силе
- Сохраняем энергию: потенциальная энергия
- Работа против силы тяжести
- Преобразуем потенциальную энергию в кинетическую
- Выбираем путь: консервативные и неконсервативные силы
- Как ни крути, а энергия сохраняется
- Определяем конечную скорость с помощью закона сохранения энергии
- Определяем максимальную высоту подъема с помощью закона сохранения энергии
- Мощность: ускоряем темп работы
- Единицы измерения мощности
- Вычисляем мощность другими способами
Работа: не совсем то, о чем вы подумали
Итак, работа \( W \) — это произведение прилагаемой силы \( \mathbf{F} \) и перемещения \( \mathbf{s} \), выполняемого этой силой. Точнее говоря речь идет о проекции прилагаемой силы на направление перемещения, т.е. \( W=Fs\cos\theta \), где \( \theta \) — угол между векторами силы \( \mathbf{F} \) и перемещения \( \mathbf{s} \). С точки зрения физика, работа равна произведению компоненты силы в направлении перемещения и величины перемещения.
Точнее говоря речь идет о проекции прилагаемой силы на направление перемещения, т.е. \( W=Fs\cos\theta \), где \( \theta \) — угол между векторами силы \( \mathbf{F} \) и перемещения \( \mathbf{s} \). С точки зрения физика, работа равна произведению компоненты силы в направлении перемещения и величины перемещения.
Прежде чем переходить к подробному рассмотрению особенностей работы, познакомимся с единицами измерения работы в разных системах единиц измерения.
Работаем в разных системах единиц измерения
Работа является скалярной, а не векторной величиной, т.е. она имеет величину, но не имеет направления (подробнее скаляры и векторы рассматриваются в главе 4). Согласно формуле \( W=Fs\cos\theta \), работа измеряется в единицах “Н·м” в системе СИ или в единицах “г·см2/с2” — в системе СГС. Но с такими единицами не очень удобно работать, и физики для измерения работы используют специальную единицу измерения — джоуль (или сокращенно Дж) в системе СИ. Иначе говоря, в системе СИ 1 Дж = 1 Н · 1 м.
Иначе говоря, в системе СИ 1 Дж = 1 Н · 1 м.
В системе СГС работа измеряется в единицах “г·см2/с2”. Вместо нее для удобства физики также используют специальную единицу измерения — эрг (неплохое название для единицы работы, поскольку очень похоже на энергичное междометие, произнесенное во время подъема тяжелого груза). Иначе говоря, 1 эрг = 1 дин · 1 см. В системе фут-фунт-секунда работа измеряется в единицах “фунт-фут”. (Эти системы единиц подробно описываются в главе 2 .)
Толкаем груз
Не такая уж и легкая работа — держать тяжелый груз, например большие гантели, на вытянутых вверх руках. Однако с точки зрения физики, несмотря на приложенную силу, здесь нет никакого перемещения, а значит, нет и работы. Хотя с точки зрения биологии здесь выполняется огромная работа, но с точки зрения физики работы нет, если нет перемещения. Даже с точки зрения химии наше тело поставляет огромное количество энергии нашим мышцам для удержания груза. Но, несмотря на очевидную физическую усталость, работа с точки зрения физики не выполняется.
Для работы необходимо движение. Представьте, что вы нашли огромный слиток золота и толкаете его домой, как показано на рис. 8.1. Какую работу придется при этом выполнить? Во-первых, нужно определить силу, которую нужно приложить к слитку.
Пусть коэффициент трения скольжения, \( \mu_c \) (подробнее об этом см. главу 6), между поверхностями слитка и дороги равен 0,25, а слиток имеет массу 1000 кг. Итак, какую силу нужно приложить к слитку, чтобы поддерживать его движение вопреки силе трения скольжения \( F_{трение} \)? Начнем поиск ответа на этот вопрос со следующей формулы, известной нам из главы 6:
где \( F_н \) — это нормальная сила.
Предполагая, что поверхность дороги абсолютно плоская, получим, что нормальная сила \( F_н \) равна произведению массы слитка \( m \) на ускорение свободного падения \( g \) под действием силы гравитационного притяжения (силы тяжести) между слитком и Землей:
Подставляя численные значения, получим:
Итак, для преодоления силы кинетического трения нужно приложить силу 2450 Н. Допустим, что длина пути до вашего дома равна 3 км. Какую работу придется проделать, чтобы дотолкать этот слиток золота домой? Поскольку угол \( \theta \) между направлением прилагаемой силы \( \mathbf{F} \) и перемещением \( \mathbf{s} \), выполняемым под действием этой силы, равен нулю, то формула работы \( W=Fs\cos\theta \) упрощается, поскольку \( \cos\theta \) = 1. Подставляя численные значения, получим:
Допустим, что длина пути до вашего дома равна 3 км. Какую работу придется проделать, чтобы дотолкать этот слиток золота домой? Поскольку угол \( \theta \) между направлением прилагаемой силы \( \mathbf{F} \) и перемещением \( \mathbf{s} \), выполняемым под действием этой силы, равен нулю, то формула работы \( W=Fs\cos\theta \) упрощается, поскольку \( \cos\theta \) = 1. Подставляя численные значения, получим:
Итак, потребуется выполнить работу, равную 7,35·106 Дж, чтобы дотолкать этот слиток золота домой. Насколько это много? Чтобы поднять груз массой 1 кг на высоту 1 м, требуется выполнить работу около 9,8 Дж. Теперь понятно: чтобы дотолкать слиток золота домой, потребуется выполнить приблизительно в 750 тыс. раз большую работу.
Работу измеряют также в калориях (или сокращенно кал), причем 1 кал = 4,186 Дж. Эту единицу измерения используют также для измерения энергии, и ее часто можно встретить на упаковках продуктов питания. Так вот, чтобы дотолкать слиток золота домой, вам потребуется потратить 1,755·106 калорий, или 1755 Ккал (т.е. килокалорий, где 1 килокалория = 1 Ккал). Забегая вперед, скажем, что в электротехнике для измерения работы и энергии используется единица “киловатт·час” (кВт·ч), которая равна 3,6·106 Дж. Итак, для выполнения этой работы потребуется около 2 кВт·ч. (Более подробно эти и другие единицы измерения описываются в конце этой главы и в главе 13.)
Так вот, чтобы дотолкать слиток золота домой, вам потребуется потратить 1,755·106 калорий, или 1755 Ккал (т.е. килокалорий, где 1 килокалория = 1 Ккал). Забегая вперед, скажем, что в электротехнике для измерения работы и энергии используется единица “киловатт·час” (кВт·ч), которая равна 3,6·106 Дж. Итак, для выполнения этой работы потребуется около 2 кВт·ч. (Более подробно эти и другие единицы измерения описываются в конце этой главы и в главе 13.)
Тянем груз под углом
А может, попробовать не толкать, а тянуть слиток золота с помощью веревки, как показано на рис. 8.2?
Поскольку веревка направлена под углом \( \theta \) к направлению перемещения, то нам для вычисления работы придется использовать формулу:
где \( F_{натяжение} \) — это сила натяжения веревки.
Допустим, что нить привязана к центру слитка. Поскольку вертикальная компонента силы натяжения веревки \( F_{натяжение}\sin\theta \) направлена вверх, то она частично компенсирует нормальную силу. В конечном итоге вертикальная компонента силы натяжения веревки \( F_{натяжение}\sin\theta \) уменьшает силу трения:
В конечном итоге вертикальная компонента силы натяжения веревки \( F_{натяжение}\sin\theta \) уменьшает силу трения:
Для перемещения слитка в данном случае горизонтальная компонента силы натяжения \( F_{натяжение}\cos\theta \) должна компенсировать силу трения:
Из двух последних соотношений получаем, что:
и необходимая сила натяжения веревки равна:
В предыдущем примере (где прилагаемая сила не имела наклона) прилагаемая сила компенсировала силу трения \( F_{натяжение(прежнее)}=\mu_cmg \) и была равна 2450 Н.
Следовательно, теперь необходимая сила натяжения веревки равна:
(Обратите внимание на следующие интересные особенности использования веревки, которую тянут под углом к горизонтали. Во-первых, при наклоне 10° потребуется приложить меньшую силу, чем при толкании слитка без наклона. Во-вторых, минимальное значение силы натяжения веревки достигается при максимальном значении знаменателя \( \mu_c\sin\theta+\cos\theta \), когда \( \mu_c=tg\,\theta \), т. е. для \( \mu_c \) = 0,25 при угле \( \theta \) ≈ 14°, а сама минимальная сила натяжения веревки равна 2376 Н. — Примеч. ред.)
е. для \( \mu_c \) = 0,25 при угле \( \theta \) ≈ 14°, а сама минимальная сила натяжения веревки равна 2376 Н. — Примеч. ред.)
Выполняем отрицательную работу
Представьте себе, что вы купили огромный телевизор массой 100 кг, вам нужно поднять его с пола и занести его наверх по ступенькам, поднимая приблизительно на высоту около 0,5 м. Какую работу нужно выполнить, если предполагается, что ее придется выполнять для преодоления силы тяжести \( F=mg \), где \( m \) — это масса телевизора, a \( g \) — ускорение свободного падения?
В таком случае работа равна:
Допустим, что груз оказался слишком тяжелым (не удивительно, ведь телевизор весит 100 кг!) и его пришлось опустить снова на пол. Какую работу нужно выполнить, чтобы опустить телевизор? Верите или нет, но эта работа будет отрицательной! Действительно, теперь вектор силы направлен противоположно вектору перемещения, т.е. угол между этими векторами \( \theta \) = 180°, a \( \cos \)180° = -1.
Поэтому в этом случае работа равна:
Общая работа \( W=W_1+W_2=0 \). Нулевая работа? Да, с точки зрения физики общая работа в этом случае равна нулю.
Если компонента вектора силы направлена в том же направлении, что и компонента вектора перемещения, то работа будет положительной. А если они направлены в противоположные стороны, то работа будет отрицательной.
Получаем компенсацию в виде кинетической энергии
Если сила, приложенная к объекту, больше силы сопротивления, например силы трения или силы тяжести, то результирующая сила приводит объект в движение. Соответствующая работа этой силы приводит к увеличению скорости объекта, т.е. увеличению его энергии движения или, иначе говоря — кинетической энергии. Здесь кинетической энергией называется способность объекта совершать некую работу за счет энергии его движения.
Представьте себе мячик для игры в гольф, который движется по окружности, как показано на рис. 8. 3. Причем в самой нижней точке траектории скорость мячика максимальна, а в самой верхней точке — минимальна, например равна нулю. С точки зрения физики в самой нижней точке траектории мячик имеет бОльшую кинетическую энергию, чем в самой верхней точке, где она равна нулю. Куда пропадает и откуда снова берется кинетическая энергия при периодическом вращательном движении по этой траектории?
3. Причем в самой нижней точке траектории скорость мячика максимальна, а в самой верхней точке — минимальна, например равна нулю. С точки зрения физики в самой нижней точке траектории мячик имеет бОльшую кинетическую энергию, чем в самой верхней точке, где она равна нулю. Куда пропадает и откуда снова берется кинетическая энергия при периодическом вращательном движении по этой траектории?
На самом деле энергия никуда не пропадает и ниоткуда не берется. Она просто переходит из одной формы в другую. В самой высокой точке энергия переходит из кинетической формы в потенциальную, а в самой нижней — наоборот, из потенциальной формы в кинетическую. Потенциальной энергией называется способность объекта совершить работу при изменении его координат под действием силы, т.е. в данном случае при перемещении вниз под действием силы тяжести. (Более подробно потенциальная энергия описывается далее в этой главе.)
Допустим, что в самой нижней точке траектории мячик имеет кинетическую энергию 20 Дж. В самой верхней точке кинетическая энергия равна 0 Дж. В таких случаях говорят, что 20 Дж кинетической энергии преобразуется в 20 Дж потенциальной энергии. А в самой нижней точке наоборот: 20 Дж потенциальной энергии преобразуется в 20 Дж кинетической энергии. Такое взаимное превращение энергии из одной формы в другую без потерь называется законом сохранения энергии. (Более подробно он описывается далее.)
В самой верхней точке кинетическая энергия равна 0 Дж. В таких случаях говорят, что 20 Дж кинетической энергии преобразуется в 20 Дж потенциальной энергии. А в самой нижней точке наоборот: 20 Дж потенциальной энергии преобразуется в 20 Дж кинетической энергии. Такое взаимное превращение энергии из одной формы в другую без потерь называется законом сохранения энергии. (Более подробно он описывается далее.)
А что происходит с кинетической энергией при наличии силы трения, как в предыдущем примере со слитком на горизонтальной плоскости? Если на движущийся слиток не действует никакая движущая сила, то его скорость постепенно уменьшается. Дело в том, что его кинетическая энергия рассеивается на нагрев соприкасающихся поверхностей объекта и плоскости.
Итак, после предварительного знакомства с превращениями энергии попробуем подсчитать ее величину.
Запоминаем формулу кинетической энергии
Работа по ускорению объекта тратится на увеличение его скорости или, как говорят физики, на увеличение кинетической энергии:
Кинетическую энергию \( K \) можно легко вычислить, зная массу \( m \) и скорость \( v \) объекта.
Как получить связь между кинетической энергией и работой? Как известно, связь между силой и ускорением имеет вид:
Работа силы при перемещении объекта равна:
Предположим, что сила прилагается в том же направлении, в котором происходит перемещение объекта (\( \cos\theta \) = 1), то есть:
Из главы 3 нам известно следующее соотношение между начальной \( v_1 \) и конечной \( v_2 \) скоростями объекта, перемещающегося с ускорением \( a \) на расстояние \( s \):
Иначе говоря, получаем:
Подставляя это соотношение для ускорения в формулу для работы, получим:
Используем соотношение для кинетической энергии
Попробуем определить кинетическую энергию пули с массой 10 г, которая вылетает из ствола пистолета со скоростью 600 м/с. Зная формулу кинетической энергии, подставим в нее численные значения (не забудьте преобразовать 10 грамм в 0,01 килограмма) и получим:
Маленькая пуля массой всего 10 г обладает очень большой энергией 1800 Дж.
Выражение для кинетической энергии можно применять для вычисления скорости, приобретенной объектом после выполнения некоторой работы по его ускорению. Предположим, что вы находитесь в космическом корабле на околоземной орбите и должны запустить искусственный спутник. Нужно открыть створки грузового отсека вашего космического корабля, выгрузить спутник массой 1000 кг и выполнить работу, прилагая силу 2000 Н на расстоянии 1 м. Какую скорость приобретет спутник в результате этой работы?
Как известно, работа определяется следующей формулой:
Поскольку сила прилагается в том же направлении, в котором происходит перемещение спутника (\( \cos\theta \) = 1), то:
Подставляя численные значения, получим:
Эта работа приводит к разгону спутника, т.е. работа преобразуется в кинетическую энергию спутника:
Отсюда легко можно определить искомую скорость спутника:
Такой будет скорость спутника относительно космического корабля.
Учтите, что работа может иметь и отрицательный знак, если, например, нужно затормозить движущийся спутник. Действительно, для этого придется приложить силу, направленную против перемещения. В этом случае приращение кинетической энергии спутника также будет иметь отрицательную величину.
В этом примере мы учли только одну силу, а в реальном мире на любой объект действует сразу несколько сил.
Вычисляем кинетическую энергию объекта по результирующей силе
Допустим, что вам нужно найти общую работу всех сил, приложенных к объекту, и определить полученную кинетическую энергию объекта. В примере из главы 6 со слитком на наклонной плоскости на слиток в направлении, перпендикулярном к наклонной плоскости, действуют нормальная сила и компонента силы тяжести. Обе эти силы компенсируют друг друга в этом направлении. Слиток не перемещается в направлении, перпендикулярном к наклонной плоскости. Это значит, что эти две силы не выполняют работу и не придают слитку кинетическую энергию.
На рис. 8.4 показан уже знакомый нам пример с холодильником на наклонной плоскости. Допустим, что холодильник нужно спустить по наклонной плоскости, удерживая его с помощью каната с силой натяжения \( F_н \). Попробуем с помощью формул работы результирующей силы и кинетической энергии определить скорость холодильника в самом конце наклонной плоскости.
Какова результирующая сила, которая действует на холодильник? Из главы 6 мы уже знаем, что компонента силы тяжести вдоль наклонной плоскости равна:
где \( m \) — это масса холодильника, a \( g \) — ускорение свободного падения. Нормальная сила (см. главу 6) равна:
А сила трения скольжения (см. главу 6) равна:
где \( \mu_c \) — коэффициент трения скольжения. Результирующая сила \( F_{рез} \) направлена вдоль наклонной поверхности и равна:
Большая часть пути пройдена! Если угол наклона плоскости \( \theta \) = 30°, а коэффициент трения скольжения \( \mu_c \) = 0,15, то, подставляя численные значения, получим:
Итак, результирующая сила, которая действует на холодильник, равна 363 Н. Она действует на всем протяжении наклонной плоскости, т.е. 3 м, и совершаемая ею работу равна:
Она действует на всем протяжении наклонной плоскости, т.е. 3 м, и совершаемая ею работу равна:
Если вся эта работа тратится на ускорение холодильника, то она преобразуется в кинетическую энергию, то есть:
Отсюда легко найти финальную скорость холодильника:
Итак, в конце наклонной плоскости холодильник будет иметь скорость 4,67 м/с.
Сохраняем энергию: потенциальная энергия
Объекты могут обладать не только энергией движения, т.е. кинетической энергией, но и энергией положения, т.е. потенциальной энергией. Эта энергия имеет такое название потому, что может быть преобразована (т.е. имеет потенциал преобразования) в кинетическую или другую энергию.
Представьте себе, что вы катаете с горки маленького ребенка. Для подъема на горку вам придется совершить определенную работу. Чем выше стартовая позиция малыша, тем большую скорость он приобретает в конце горки. Выше, еще выше, еще выше… Обычно на каком-то из этих этапов эксперименты решительно прекращается взволнованной мамой малыша.
Что же происходило на горке (до появления мамы)? Откуда возникла кинетическая скорость малыша? Она произошла от работы против силы тяжести, которую вы совершили по подъему малыша на горку. Действительно, малыш, сидя в стартовой позиции в верхней части горки, обладает нулевой скоростью и нулевой кинетической энергией. Выполнив работу против силы тяжести по подъему малыша наверх, вы тем самым увеличили его (и свою) потенциальную энергию. И только после спуска вниз под действием силы тяжести малыш приобретает кинетическую энергию в результате преобразования этой потенциальной энергии.
Работа против силы тяжести
Какую работу нужно выполнить против силы тяжести? Допустим, что вам нужно переместить тяжелое ядро с пола на верхнюю полку на высоту \( h \). Необходимая для этого работа \( W \) силы \( \mathbf{F} \) при перемещении на расстояние \( \mathbf{s} \) при угле между их векторами \( \theta \) выражается формулой:
В данном случае сила тяжести \( \mathbf{F = mg} \), а угол \( \theta \) между векторами \( \mathbf{F} \) и \( \mathbf{s} \) можно выразить с помощью разности высот \( h=s\cos\theta \) между полом и верхней полкой.
Таким образом, работа против силы тяжести по перемещению тяжелого ядра с пола на верхнюю полку на высоту \( h \) равна:
Если ядро упадет с верхней полки на пол, то какую скорость оно разовьет, т.е. какую кинетическую энергию приобретет ядро? Запомните: оно приобретет кинетическую энергию, равную разнице потенциальных энергий, т.е. \( mgh \). Это значит, что затраченная работа на подъем ядра преобразуется в кинетическую энергию в точке соприкосновения ядра с полом.
Вообще говоря, объект с массой \( m \) вблизи поверхности Земли, где ускорение свободного падения \( g \) постоянно, при перемещении вверх на высоту \( h \) приобретает потенциальную энергию \( U \), равную \( mgh \). Если вы перемещаете объект вертикально против силы тяжести с высоты \( h_0 \) на высоту \( h_1 \) то изменение его потенциальной энергии равно:
Работа по преодолению силы тяжести тратится на увеличение потенциальной энергии объекта.
Преобразуем потенциальную энергию в кинетическую
Объект может характеризоваться разными видами потенциальной энергии в зависимости от типа сил, которые действуют на него. Действительно, работа может выполняться не только против силы тяжести, но, например, и против силы упругости пружины. Однако в задачах по физике источником потенциальной энергии чаще всего является сила тяжести. В этом случае на поверхности Земли потенциальную энергию принято считать равной нулю, а этот уровень потенциальной энергии называют нулевым. Тогда говорят, что на высоте \( h \) объект с массой \( m \) обладает потенциальной энергией \( mgh \).
Допустим, что ядро с массой 40 кг падает с высоты 3 м на пол. Какую скорость оно приобретет при касании с полом? В данном случае его потенциальная энергия \( U \), равная
преобразуется в кинетическую \( K \), т.е.:
Поэтому, используя сведения из предыдущего раздела, можно вычислить финальную скорость в момент касания пола:
Подставляя численные значения, получим:
Падающее на пол ядро с массой 40 кг и скоростью 7,67 м/с — это впечатляющее зрелище, но не совсем приятное, если на пути ядра находится ваша нога. Учтите это и постарайтесь не допустить нежелательной встречи.
Учтите это и постарайтесь не допустить нежелательной встречи.
Выбираем путь: консервативные и неконсервативные силы
Если работа силы при перемещении объекта определяется только начальной и конечной координатами объекта и не зависит от траектории перемещения, то такая сила называется консервативной. Примером консервативной силы является сила гравитационного притяжения. А сила трения не является такой, поскольку совершаемая ею работа зависит от траектории перемещения. Сила трения является неконсервативной.
Допустим, что две группы друзей решили покорить небольшую гору высотой \( h_1 \) стартуя с места на высоте \( h_0 \). Одна группа пошла коротким и крутым путем, а другая — длинным, но более пологим и живописным. Обе группы встретились наверху и решили сравнить увеличение потенциальной энергии \( \Delta{U} \). “Наша потенциальная энергия увеличилась на \( mg(h_1-h_0) \)”, — сказали одни. “Наша потенциальная энергия тоже увеличилась на \( mg(h_1-h_0) \)”, — ответили другие.
Действительно, согласно рассуждениям в прежнем разделе, изменение потенциальной энергии выражается следующей формулой:
Это уравнение фактически означает, что независимо от выбранного пути на вершину горы, на увеличение потенциальной энергии путников влияет только разница между высотой исходной точки \( h_0 \) и высотой вершины \( h_1 \). Именно потому, что работа против силы гравитационного притяжения не зависит от выбранного пути, эта сила является консервативной силой.
А вот еще один пример проявления консервативности силы тяжести. Предположим, что вы отдыхаете в отеле в одной из горных деревушек в Альпах и решили прогуляться на машине по долине, а затем по близлежащим перевалам и горным вершинам. За день вы множество раз совершали спуск и подъем, а к вечеру вернулись к исходному месту — к своему отелю. Чему в итоге равно изменение вашей потенциальной энергии? Иначе говоря, каков результат всей дневной работы против силы тяжести? Ответ прост: поскольку сила тяжести является консервативной и вы вернулись в исходную точку, то изменение потенциальной энергии равно 0. Результирующая работа против силы тяжести равна 0.
Результирующая работа против силы тяжести равна 0.
Конечно, на всем пути со стороны дороги на автомобиль действовала нормальная сила, но она всегда направлена перпендикулярно дороге и перемещению, а потому не совершает работы.
С консервативными силами удобно работать, поскольку они не допускают “утечки” энергии вдоль замкнутого пути перемещения, когда конечная точка перемещения совпадает с исходной (работа консервативных сил по замкнутому пути равна нулю). Однако все гораздо сложнее с такими силами, как сила трения скольжения или сила сопротивления воздуха. Если тянуть тяжелый груз по шершавой поверхности, то работа против сил трения будет очень сильно зависеть от выбранного пути и не будет равной нулю для замкнутого пути. В этом случае мы имеем дело с неконсервативной силой, работа против которой зависит от выбранного пути.
Рассмотрим подробнее силу трения, как типичный пример неконсервативной силы. При совершении работы против силы трения происходит “утечка” механической энергии объекта, которая объединяет кинетическую и потенциальную энергии. При совершении работы при перемещении объекта с трением часть работы рассеивается в виде тепла. Забегая вперед, следует сказать, что закон сохранения полной энергии при этом не нарушается, если учесть преобразование части работы в тепловую энергию.
При совершении работы при перемещении объекта с трением часть работы рассеивается в виде тепла. Забегая вперед, следует сказать, что закон сохранения полной энергии при этом не нарушается, если учесть преобразование части работы в тепловую энергию.
Как ни крути, а энергия сохраняется
Механической энергией называется сумма потенциальной и кинетической энергии объекта. Благодаря закону сохранения этой полной механической энергии, процедура решения задач по физике существенно упрощается. Рассмотрим поподробнее этот закон.
Пусть тележка на аттракционе “Американские горки” в разных точках 1 и 2 на разных высотах \( h_1 \) и \( h_2 \) имеет разные скорости \( v_1 \) и \( v_2 \). Полная механическая энергия тележки \( E_1 \) в точке 1 равна:
а полная механическая энергия тележки \( E_2 \) в точке 2 равна:
Чему равна разница между величинами \( E_1 \) и \( E_2 \). При наличии неконсервативных сил эта разница должна быть равна работе \( W_{неконс} \) этих сил
С другой стороны, если неконсервативные силы отсутствуют, т. е. \( W_{неконс} \) = 0, то:
е. \( W_{неконс} \) = 0, то:
или:
или:
Именно эти равенства представляют собой закон сохранения механической энергии. Если работа неконсервативных сил равна нулю, то полная механическая энергия сохраняется. (Закон сохранения механической энергии гласит, что при наличии консервативных сил полная энергия остается неизменной, а могут происходить только превращения потенциальной энергии в кинетическую и обратно. — Примеч. ред.)
Иногда удобно сократить массу \( m \) в следующей формулировке закона сохранения энергии:
и использовать более простую формулировку:
Определяем конечную скорость с помощью закона сохранения энергии
Совсем непросто проводить физические эксперименты на аттракционе “Американские горки”. Но ведь кто-то должен их делать! Представьте себе, что вы находитесь в тележке, которая практически без трения скользит по рельсам вниз с высоты \( h_1 \) = 400 м. Предположим, что где-то на полпути вниз выходит из строя спидометр и уже нельзя определить скорость тележки по приборам. Как вычислить скорость \( v_2 \) в самой нижней точке спуска \( h_2 \)? Нет проблем. Все, что нам нужно, это закон сохранения энергии. Согласно этому закону, полная механическая энергия объекта должна сохраняться, если равна нулю работа всех неконсервативных сил. Из предыдущего раздела нам уже знакома следующая сокращенная формулировка закона сохранения энергии:
Предположим, что где-то на полпути вниз выходит из строя спидометр и уже нельзя определить скорость тележки по приборам. Как вычислить скорость \( v_2 \) в самой нижней точке спуска \( h_2 \)? Нет проблем. Все, что нам нужно, это закон сохранения энергии. Согласно этому закону, полная механическая энергия объекта должна сохраняться, если равна нулю работа всех неконсервативных сил. Из предыдущего раздела нам уже знакома следующая сокращенная формулировка закона сохранения энергии:
Для простоты предположим, что начальная скорость \( v_1 \) = 0, а высота самой нижней точки спуска \( h_2 \) = 0. Тогда предыдущее уравнение существенно упрощается:
Откуда очень легко получить формулу для конечной скорости:
Подставляя численные значения, получим:
Итак, скорость тележки в самой нижней точке спуска на аттракционе “Американские горки” будет равна 89 м/с или около 320 км/ч. Довольно быстро: дух перехватит даже у самых отчаянных смельчаков!
Определяем максимальную высоту подъема с помощью закона сохранения энергии
Помимо определения конечной скорости, с помощью закона сохранения энергии можно также определить максимальную высоту подъема. Предположим, что Тарзан находится у кишащей крокодилами реки и хочет с помощью гибкой лианы перепрыгнуть с низкого берега на другой более высокий берег, высота которого на 9 м больше. Пусть максимальная скорость \( v_1 \), с которой он может разогнаться на низком берегу (т.е. в самой нижней точке траектории), равна 13 м/с. Достаточно ли этой скорости, чтобы запрыгнуть на противоположный высокий берег? Попробуем применить известную нам сокращенную формулировку закона сохранения энергии:
Предположим, что Тарзан находится у кишащей крокодилами реки и хочет с помощью гибкой лианы перепрыгнуть с низкого берега на другой более высокий берег, высота которого на 9 м больше. Пусть максимальная скорость \( v_1 \), с которой он может разогнаться на низком берегу (т.е. в самой нижней точке траектории), равна 13 м/с. Достаточно ли этой скорости, чтобы запрыгнуть на противоположный высокий берег? Попробуем применить известную нам сокращенную формулировку закона сохранения энергии:
Предположим, что высота начального положения \( h_1 \) = 0. Чтобы определить максимально возможную высоту конечного положения на другом высоком берегу, следует предположить, что конечная скорость \( v_2 \) = 0. При таких условиях прежняя формула существенно упрощается:
Отсюда очень легко получить формулу для высоты конечного положения \( h_2 \) на другом берегу:
Подставляя численные значения, получим:
Итак, Тарзану не хватит 40 см, чтобы с максимальной скоростью разгона 13 м/с запрыгнуть на другой берег с помощью лианы.
Мощность: ускоряем темп работы
Иногда нужно знать не только объем работы, но и темп, с которым она выполняется. Скорость выполнения работы за единицу времени называется мощностью. Она выражается следующей простой формулой:
где \( W \) — это работа, выполненная за время \( t \).
В качестве примера рассмотрим два гоночных катера, способных развивать скорость до 200 км/ч. Какой из них обладает более мощным мотором? Конечно тот, который быстрее разгоняется до максимальной скорости, т.е. быстрее проделывает одинаковую работу по ускорению катера.
Если с течением времени скорость выполнения работы меняется, то в таких случаях часто используют понятие средней мощности, т.е. отношения всей выполненной работы \( W \) за все время \( t \):
Усредненные величины в физике принято обозначать знаком подчеркивания над соответствующей величиной. Прежде, чем приступать к применению понятии мощности, следует познакомиться с единицами измерения мощности.
Единицы измерения мощности
Поскольку мощность— это работа за единицу времени, то единицей измерения мощности является Дж/с, т.е. единица работы (джоуль), деленная на единицу времени (секунда), или ватт (Вт).
Обратите внимание, что поскольку работа и время являются скалярными величинами (подробнее о скалярах рассказывается в главе 4), то и мощность является скалярной величиной. Кроме ватта, для измерения мощности по историческим причинам часто используется единица “лошадиная сила” (л.с.), которая приблизительно равна 745,7 Вт. (Физики очень редко пользуются этой единицей из-за ее неоднозначного определения. Например, в метрической системе единиц измерения она равна 735,49875 Вт и получила название “метрической” лошадиной силы, а в английской системе единиц измерения — 745,6998 Вт и более известна под названием “механической” лошадиной силы. Кроме того, существуют “электрическая” (746 Вт) и даже “бойлерная” (9810 Вт) лошадиные силы. Однако, несмотря на эти различия, по историческим причинам единица “лошадиная сила” получила широкое распространение, особенно в автомобильной промышленности. — Примеч. ред.)
— Примеч. ред.)
Предположим, что среднестатистическая лошадь массой \( m_л \) = 500 кг способна разогнать себя и санки массой \( m_с \) = 500 кг от скорости \( v_1 \) = 1 м/с до скорости \( v_2 \) = 2 м/с за время \( t \) = 2 с. Какой мощностью обладает эта лошадь? Берем формулу работы:
и, подставляя в нее эти значения, получим:
А теперь, зная работу, вычислим мощность лошади:
Совсем неплохо для среднестатистической лошади иметь мощность чуть больше 1 л.с.!
Вычисляем мощность другими способами
Поскольку работа равна произведению силы и времени, то формулу для мощности можно записать следующим образом:
Однако скорость \( v = s/t \), и потому:
Интересный результат, не так ли? Оказывается, что мощность равна произведению скорости и силы. Аналогичную формулу можно использовать и для вычисления средней мощности \( \overline{P} \) , если прикладываемая сила \( F \) постоянна:
Глава 9. Двигаем объекты: количество движения и импульс →
Двигаем объекты: количество движения и импульс →
← Глава 7. Движемся по орбитам
Кинетическая энергия: определение, формула и примеры
Что общего между автомобилем, едущим по шоссе, падающей на землю книгой и ракетой, улетающей в космос? Это все движущиеся объекты, и поэтому все они обладают кинетической энергией. Любой движущийся объект обладает кинетической энергией, а это значит, что этот объект может совершать работу над другим объектом. Пассажир, едущий в автомобиле, едущем по шоссе, движется вместе с автомобилем, потому что движущийся автомобиль воздействует на пассажира силой, приводя в движение и пассажира. В этой статье мы дадим определение кинетической энергии и обсудим взаимосвязь между кинетической энергией и работой. Мы разработаем формулу, описывающую кинетическую энергию, и поговорим о различиях между кинетической энергией и потенциальной энергией. Мы также упомянем типы кинетической энергии и рассмотрим некоторые примеры.
Определение кинетической энергии
Использование второго закона Ньютона с векторами силы и ускорения для описания движения объекта иногда может быть затруднено. Векторы могут усложнить уравнения, поскольку мы должны учитывать как их величину, так и направление. Для физических задач, которые трудно решить с помощью векторов силы и ускорения, гораздо проще использовать энергию. Кинетическая энергия — это способность движущегося объекта совершать работу. Существуют различные типы кинетической энергии, такие как тепловая и электрическая кинетическая энергия, но в этой статье мы сосредоточимся на механической кинетической энергии. Единицей кинетической энергии в системе СИ является джоуль, который обозначается аббревиатурой . Джоуль – это ньютон-метр, или. Кинетическая энергия является скалярной величиной, поэтому с ней проще работать, чем с вектором. Поступательная кинетическая энергия объекта зависит от массы и скорости объекта и определяется следующей формулой: 92 $$
Векторы могут усложнить уравнения, поскольку мы должны учитывать как их величину, так и направление. Для физических задач, которые трудно решить с помощью векторов силы и ускорения, гораздо проще использовать энергию. Кинетическая энергия — это способность движущегося объекта совершать работу. Существуют различные типы кинетической энергии, такие как тепловая и электрическая кинетическая энергия, но в этой статье мы сосредоточимся на механической кинетической энергии. Единицей кинетической энергии в системе СИ является джоуль, который обозначается аббревиатурой . Джоуль – это ньютон-метр, или. Кинетическая энергия является скалярной величиной, поэтому с ней проще работать, чем с вектором. Поступательная кинетическая энергия объекта зависит от массы и скорости объекта и определяется следующей формулой: 92 $$
Более подробно мы обсудим, как мы пришли к этому уравнению, в следующем разделе. Из уравнения мы видим, что кинетическая энергия объекта может быть только положительной величиной или равна нулю, если объект не движется. Это не зависит от направления движения.
Это не зависит от направления движения.
Кинетическая энергия : способность движущегося объекта совершать работу.
Давайте быстро рассмотрим, что такое работа, чтобы лучше понять кинетическую энергию. В этой статье мы сосредоточимся только на постоянных силах, действующих на объекты; мы рассмотрим различные силы в другой статье. работа , совершенная над объектом, представляет собой скалярное произведение вектора силы, действующей на объект, и вектора перемещения.
Работа : скалярное произведение вектора силы, действующей на объект, и вектора смещения.
Мы можем найти работу над объектом, взяв скалярное произведение силы и перемещения:
$$ W = \vec{F} \cdot \vec{d} $$
Если мы просто возьмем компонент вектора силы, который параллелен вектору смещения, мы можем записать нашу формулу следующим образом:
$$ W = Fd \cos{\theta}$$
В приведенном выше уравнении \(F\) — величина вектора силы, \(d\) — величина вектора смещения, а \ (\theta\) – угол между векторами. Обратите внимание, что работа, как и кинетическая энергия, является скалярной величиной.
Обратите внимание, что работа, как и кинетическая энергия, является скалярной величиной.
Теперь, когда мы рассмотрели, что такое работа, мы можем обсудить, как кинетическая энергия связана с работой. Как было сказано выше, кинетическая энергия — это способность движущегося объекта совершать работу. Величина изменения кинетической энергии тела равна полной работе, совершенной над телом: 92\), как работу, совершаемую для приведения объекта из состояния покоя в его текущую скорость.
Только составляющая силы, параллельная вектору смещения, изменяет кинетическую энергию. Если у объекта есть составляющая силы, перпендикулярная вектору смещения, эта составляющая силы может изменить направление движения, не совершая над объектом работы. Например, объект, совершающий равномерное круговое движение, имеет постоянную кинетическую энергию, а центростремительная сила, перпендикулярная направлению движения, удерживает объект в равномерном круговом движении. 9{\circ}\) относительно горизонтали. Как изменится кинетическая энергия бруска? Примите величину силы от толчка равной \(50\,\mathrm{N}\), а величину силы трения равной \(25\,\mathrm{N}\).
Как изменится кинетическая энергия бруска? Примите величину силы от толчка равной \(50\,\mathrm{N}\), а величину силы трения равной \(25\,\mathrm{N}\).
Блок, толкаемый по поверхности, StudySmarter Originals
Изменение кинетической энергии равно чистой работе, проделанной над объектом, поэтому мы можем использовать силы, чтобы найти чистую работу. Нормальная сила и сила тяжести перпендикулярны вектору смещения, поэтому работа этих сил равна нулю. Работа, совершаемая силой трения, совершается в направлении, противоположном направлению вектора смещения, и, следовательно, отрицательна. 9{\circ}) \\ &= 410\,\mathrm{J} \end{aligned}$$
Таким образом, изменение кинетической энергии:
$$ \begin{aligned} \Delta K &= W_{ net} \\ &= W_g + W_n + W_f + W_p \\ &= 0\,\mathrm{J} + 0\,\mathrm{J} – 250\,\mathrm{J} + 410\,\mathrm{ J} \\ &= 160\,\mathrm{J} \end{aligned}$$
Разработка формулы для кинетической энергии
Как мы пришли к формуле, связывающей кинетическую энергию с работой? Рассмотрим объект, к которому приложена постоянная сила, движущийся горизонтально. Затем мы можем использовать формулу постоянного ускорения и найти ускорение: 92 $$
Затем мы можем использовать формулу постоянного ускорения и найти ускорение: 92 $$
Теперь мы можем определить работу, проделанную над объектом, а также конечную и начальную кинетическую энергию:
$$W = K_2 – K_1$$
Это уравнение показывает нам, как работа, проделанная над объектом, равна изменение кинетической энергии, которое он испытывает.
До сих пор мы обсуждали соотношение между кинетической энергией и работой только при приложении к объекту постоянной силы. Мы обсудим их взаимосвязь, когда будет разная сила, в следующей статье. 92$$
В этом уравнении \(I\) — момент инерции твердого тела, а \(\vec{\omega}\) — его угловая скорость. Изменение кинетической энергии вращения представляет собой работу, совершаемую над объектом, и определяется путем умножения углового смещения \(\Delta \theta\) и чистого крутящего момента \(\tau\):
$$ \ begin{aligned} W &= \Delta K \\ &= \tau \Delta \theta \end{aligned}$$
Более подробно о вращательных системах мы поговорим в разделе, посвященном вращательному движению.
Кинетическая энергия и потенциальная энергия
Мы обсудили, что кинетическая энергия зависит только от массы объекта и его скорости. Потенциальная энергия – это энергия, связанная с положением системы и ее внутренней конфигурацией. Полную механическую энергию системы можно найти, взяв сумму кинетической и потенциальной энергий. Если на систему действуют только консервативные силы, то полная механическая энергия сохраняется.
Быстрый пример: мяч в свободном падении с определенной высоты \(h\). Мы пренебрежем сопротивлением воздуха и примем гравитацию как единственную силу, действующую на мяч. На высоте \(h\) шар обладает гравитационной потенциальной энергией. Когда мяч падает, гравитационная потенциальная энергия уменьшается до тех пор, пока мяч не упадет на землю, после чего она теперь равна нулю. Кинетическая энергия мяча увеличивается по мере его падения, потому что увеличивается его скорость. Полная механическая энергия системы остается неизменной в любой точке.
Полная механическая энергия мяча в свободном падении, StudySmarter Originals
Более подробно мы обсудим потенциальную энергию и различные виды потенциальной энергии в статьях учебного комплекта «Потенциальная энергия и сохранение энергии».
Примеры кинетической энергии
Рассмотрим \(1000,0\,\mathrm{кг}\) автомобиль, движущийся со скоростью \(15,0\,\frac{\mathrm{m}}{\mathrm{s}}\ ). Какая работа требуется, чтобы автомобиль разогнался до \(40\,\frac{\mathrm{m}}{\mathrm{s}}\)? 92\).

Калькулятор кинетической энергии – найдите (KE) с формулой и уравнением
Онлайн-калькулятор кинетической энергии поможет вам рассчитать кинетическую энергию, которой обладает движение или движение любого объекта. Кроме того, этот калькулятор KE использует простое уравнение кинетической энергии для расчета как линейной, так и вращательной кинетической энергии (KE) тела.
Теперь приготовьтесь узнать, как рассчитать кинетическую энергию (КЭ) с помощью калькулятора и шаг за шагом, формулу кинетической энергии и ее вывод, единицы кинетической энергии, изучить работу и кинетическую энергию, а также некоторую информацию, связанную с КЭ.
Итак, прежде всего, вам следует изучить основное определение физики кинетической энергии.
Что такое кинетическая энергия (КЭ)? Согласно определению физики, энергия, которой обладает благодаря движению или перемещению любого объекта, является кинетической энергией. Если объект покоится и мы приложим к нему силу, толкая его, он начнет двигаться. Это движение принесет кинетическую энергию. Следовательно, его можно определить как работу, необходимую для перемещения тела данной массы из состояния покоя до заданной скорости. Теперь, чтобы привести тело в состояние покоя из движения, снова потребуется некоторая работа. В заключение можно сказать, что КЭ является свойством движущихся объектов и зависит от движения и массы конкретного объекта.
Это движение принесет кинетическую энергию. Следовательно, его можно определить как работу, необходимую для перемещения тела данной массы из состояния покоя до заданной скорости. Теперь, чтобы привести тело в состояние покоя из движения, снова потребуется некоторая работа. В заключение можно сказать, что КЭ является свойством движущихся объектов и зависит от движения и массы конкретного объекта.
Возьмем пример. Если поставить двигатель на грузовик и машину, то скорость не будет одинаковой из-за разной массы машины и грузовика. Вычисление кинетической энергии может показаться сложным, но вы можете легко найти его с помощью калькулятора KE.
Кроме того, вы можете использовать этот онлайн-калькулятор скорости физики, который позволяет вам рассчитать скорость/скорость движущегося объекта.
Что такое формула кинетической энергии?Формула кинетической энергии описывает связь между массой объекта и его скоростью. Уравнение кинетической энергии:
КЭ = 0,5 * м * v² или К. Э. = ½ * m * v²
Э. = ½ * m * v²
где:
- м подавляет массу любого объекта
- v представляет скорость объекта.
С помощью этой формулы можно оценить, сколько энергии потребуется для перемещения объекта определенной массы. Такое же количество энергии потребуется для замедления или остановки объекта, но имейте в виду, что скорость квадратична. Это означает, что даже незначительное увеличение скорости может привести к относительно большому количеству изменений в КЕ. Кроме того, вы можете попробовать этот калькулятор формулы кинетической энергии, который использует формулу KE для расчета кинетической энергии любого движущегося объекта.
Вывод формулы кинетической энергииДавайте рассмотрим пример объекта «m», который находится в состоянии покоя на столе. Сила «F» будет приложена, чтобы переместить его на расстояние «S».
- Проделанная работа=F x S
- Ш=Ш x Ш
Работа, выполненная над объектом, приводит к изменению скорости от u до V. Кроме того, нужно принять «a» за ускорение.
Кроме того, нужно принять «a» за ускорение.
Согласно третьему уравнению движения:
- V²-u²=2as
- с=V²-u²/2a
Теперь применим Второй закон Ньютона:
- F=ma
Объедините уравнения:
- Вт=ma*(V²-u²/2a) \= (1/2) m(V²-u²)
Как объект в состоянии покоя, u=0
- Вт= (1/2) мВ²
Точно так же кинетическая энергия объекта, движущегося с определенной скоростью, эквивалентна работе, совершаемой над объектом. Эта работа предназначена для определения получения этой скорости из состояния покоя.
Следовательно, уравнение кинетической энергии можно записать в виде:
- KE =1/2 мВ²
Пример:
Предположим, что:
- масса «m» и m = 10 кг
- скорость равна «v» и v = 10 км/ч.
Теперь уравнение кинетической энергии: Ek = 1/2 mv2
Поставьте значения:
- KE = 1/2 (10 кг) (10 км/ч)
- КЭ = 50 Дж
- Кинетическая энергия = 50 Дж.

Стандартной единицей кинетической энергии является джоуль (Дж), британской единицей кинетической энергии (кЭ) является фут-фунт (фут⋅фунт-сила). Если вы используете калькулятор кинетической энергии; вы можете выбрать единицу по вашему выбору в соответствии с текущими условиями, нажав на единицы, и значение будет немедленно преобразовано. Некоторые из наиболее распространенных единиц кинетической энергии упомянуты ниже:
- Джоуль (Дж), эквивалентный кг * м² / с² – единица СИ,
- Фунт-фунт (ft•lb) – имперская единица,
- Электронвольт (эВ),
- калорий (кал),
- Ватт-час (Втч).
Их можно легко преобразовать друг в друга с помощью следующих соотношений:
1 Дж = 0,7376 фут•фунт = 6,242•10¹⁸ эВ = 0,239 кал = 2,778•10⁻⁴Втч.
О Калькуляторе кинетической энергии: Онлайн-калькулятор кинетической энергии поможет вам оценить энергию, которую тело приобретает при любом движении. Вы можете использовать этот калькулятор КЭ для определения кинетической энергии (КЭ) человека, транспортного средства (грузовика, мотоцикла, грузовика, поезда и т. д.), самолета, футбольного мяча и даже падающих предметов, которые врезаются в землю. Также этот инструмент можно рассматривать для расчета энергии разного рода снарядов. Искатель KE использовал стандартную формулу кинетической энергии для определения KE твердого объекта. Если объект движется прямолинейно, то его линейную кинетическую энергию можно рассчитать, введя значения массы и скорости в этот калькулятор. Для кругового движения объекта для расчета его вращательного КЭ необходимы значения момента инерции и угловой скорости. Он обеспечивает выходную мощность в джоулях (Дж, кДж, МДж), ватт-часах (Втч, кВтч), калориях (Кал, кКал) и футо-фунтах (фут-фунт). Этот 100% бесплатный калькулятор поддерживает как метрические, так и имперские единицы измерения кинетической энергии.
Вы можете использовать этот калькулятор КЭ для определения кинетической энергии (КЭ) человека, транспортного средства (грузовика, мотоцикла, грузовика, поезда и т. д.), самолета, футбольного мяча и даже падающих предметов, которые врезаются в землю. Также этот инструмент можно рассматривать для расчета энергии разного рода снарядов. Искатель KE использовал стандартную формулу кинетической энергии для определения KE твердого объекта. Если объект движется прямолинейно, то его линейную кинетическую энергию можно рассчитать, введя значения массы и скорости в этот калькулятор. Для кругового движения объекта для расчета его вращательного КЭ необходимы значения момента инерции и угловой скорости. Он обеспечивает выходную мощность в джоулях (Дж, кДж, МДж), ватт-часах (Втч, кВтч), калориях (Кал, кКал) и футо-фунтах (фут-фунт). Этот 100% бесплатный калькулятор поддерживает как метрические, так и имперские единицы измерения кинетической энергии.
Этот калькулятор KE предназначен для поиска пропущенных значений в уравнении кинетической энергии, когда известны две переменные или значения:
KE=1/2*mv2
Введите любые два значения, т. и скорость для расчета кинетической энергии. Нажмите на кнопку Рассчитать. Кроме того, чтобы упростить концепцию, взгляните на следующую процедуру калькулятора:
и скорость для расчета кинетической энергии. Нажмите на кнопку Рассчитать. Кроме того, чтобы упростить концепцию, взгляните на следующую процедуру калькулятора:
Выберите опцию «линейная» в раскрывающемся меню калькулятора ке. Это следует из следующего уравнения:
Линейный KE: = 1/2 (M * (V * V))
Ввод
- Прежде всего, введите значение массы
- Далее введите значение скорости
- Нажмите кнопку расчета
Вывод
- Самым первым выводом будет значение KE в джоулях
- Масса будет доставлена так же, как и ввод со стандартной единицей измерения, которая составляет кг .
- Скорость будет передаваться так же, как ввод со стандартной единицей измерения, м/с
- Чтобы сделать другой расчет, просто нажмите кнопку пересчета
Если у вас есть значение КЕ и скорости, то массу можно рассчитать следующим образом: , введите значение КЕ
Вывод
- Самым первым выводом будет значение KE в джоулях, такое же, как и ввод.

- Масса будет поставляться в качестве второго вывода со стандартной единицей измерения, равной кг .
- Скорость будет передаваться так же, как ввод со стандартной единицей измерения, м/с
- Чтобы сделать другой расчет, просто нажмите кнопку пересчета
Если у вас есть значение KE и массы, то скорость может быть рассчитана с помощью этого инструмента следующим образом:
Вывод
- Самым первым выводом будет значение KE в джоулях, такое же, как и ввод.
- Масса будет доставлена так же, как и ввод со стандартной единицей измерения, которая составляет кг .
- Скорость будет передана в качестве последнего вывода со стандартной единицей, которая м/с
- Чтобы сделать другой расчет, просто нажмите кнопку пересчета
В раскрывающемся меню выберите «вращательный». Этот калькулятор формулы кинетической энергии следует следующей формуле вращательного KE:
Этот калькулятор формулы кинетической энергии следует следующей формуле вращательного KE:
KE(вращательный)=1/2Iω2
Ввод
- Сначала нужно ввести значение момента инерции
- Теперь введите значение угловой скорости
- Нажмите кнопку расчета
Выход
- Вы получите значение вращательного KE в джоулях в качестве стандартной единицы.
- Момент инерции будет поставляться таким же, как ввод в кг.м², как стандартная единица.
- Значение угловой скорости будет передано так же, как введенное значение в рад/с в качестве стандартной единицы.
- Чтобы произвести еще один расчет, просто нажмите кнопку пересчета.
Если у вас есть значения вращательного KE и угловой скорости, момент инерции можно рассчитать следующим образом:
Выход
- Вы получите значение вращательного КЕ, такое же, как и на входе в джоулях.

- В качестве необходимой мощности вы получите значение момента инерции в кг.м².
- Вы получите такое же значение угловой скорости, как и введенное значение в рад/с.
- Чтобы произвести еще один расчет, просто нажмите кнопку пересчета.
Если известны значения вращательного КЭ и момента инерции, то угловую скорость можно узнать следующим образом:0132
Выход
- У вас будет значение KE, такое же, как и на входе в джоулях.
- Вы получите момент инерции такой же, как ввод в кг.м².
- В качестве желаемого результата вы получите значение угловой скорости в рад/с.
- Чтобы сделать другой расчет, нажмите кнопку пересчета
Кинетическая энергия — это энергия объекта, присутствующая в результате движения. Любое изменение скорости объекта приведет к изменению кинетической энергии. Вычитание КЕ движущегося объекта до приложения силы или работы из КЕ после приложения силы или работы может дать значение изменения КЕ. его легко рассчитать по формуле:
Любое изменение скорости объекта приведет к изменению кинетической энергии. Вычитание КЕ движущегося объекта до приложения силы или работы из КЕ после приложения силы или работы может дать значение изменения КЕ. его легко рассчитать по формуле:
- Формула изменения кинетической энергии: W = KEf – Kei.
Где
- W = выполненная работа.
- KEf = кинетическая энергия после выполненной работы.
- Kei = кинетическая энергия до совершения работы.
формула кинетической энергии (KE = 0,5 x mv2) может помочь нам рассчитать значение KE, выполнив следующие простые шаги:
- предположим, что масса объекта 55 кг, а скорость 3,87 м/с
- введите значения в уравнение кинетической энергии: (KE = 0,5 x mv2) = 0,5*55*3,872 = 411,675 Дж.
KE = 411,675 Дж. - Вычисления вручную могут вызывать затруднения. Чтобы избежать неудовлетворительных расчетов, лучше всего использовать калькулятор кинетической энергии для расчета кинетической энергии объекта.

Между этими двумя типами энергии существует следующее основное различие:
КЭ = Кинетическая энергия: движения объекта называется КЭ.- Это форма энергии, которая присутствует благодаря положению объекта.
- Невозможно передать.
- Не имеет отношения к окружению объекта.
- Его формула: PE = mgh.
Работа и кинетическая энергия строго связаны. Это означает, что увеличение или уменьшение объема работы вызовет изменение КЭ. Эту связь можно объяснить с помощью теоремы о работе и энергии. В нем говорится, что работа всех внешних сил преобразуется в изменение кинетической энергии:
W = ΔKE = KE₂ – KE₁
- Сеть «W» – это работа, совершаемая внешней силой над объектом.
 2,
2,- где кинетическая энергия в джоулях,
- масса в килограммах,
- и скорость в метрах в секунду м с⁻¹.
Рассмотрим движущийся объект, введите значения в уравнение. У вас будет значение KE в джоулях, так как это стандартная единица для представления энергии.
От чего зависит кинетическая энергия?КЭ зависит от двух переменных:
- масса (м) объекта
- скорость (v) объекта.
- Следующее уравнение используется для представления кинетической энергии (KE) объекта: KE = 1/2MV2
Если скорость любого объекта утроится, то кинетическая энергия будет в девять раз больше, чем начальная кинетическая энергия.
Какая связь между кинетической энергией и скоростью?Можно предположить, что скорость и скорость — это одно и то же. Итак, кинетическая энергия объекта связана с квадратом его скорости (скорости).
Приведите примеры кинетической энергии? Другими словами, при двойном увеличении скорости кинетическая энергия увеличится в четыре раза.
Другими словами, при двойном увеличении скорости кинетическая энергия увеличится в четыре раза.- Движущийся автомобиль. Движущиеся автомобили обладают кинетической энергией из-за своего движения.
- Пуля из ружья имеет очень большую кинетическую энергию, поэтому легко может попасть в любой предмет.
- Летающий самолет обладает большим количеством КЭ. Активируется
- Ходьба и бег.
- Процесс циклирования
- Мяч для крикета на игровой площадке.
Кинетическая энергия идеального газа может быть рассчитана простым умножением формулы для средней линейной кинетической энергии на общее количество молекул, присутствующих в пробе газа.
От каких трех вещей зависит потенциальная энергия?Энергия PE зависит от следующих трех факторов:
- Общая масса объекта.

- высота от земли,
- сила тяжести.
Согласно определению кинетической энергии, ею обладает тело из-за его движения. Поэтому у каждой движущейся вещи в доме есть КЕ:
- Запуск вентилятора на потолке,
- проточная вода из-под крана,
- дети бегают по комнате
- Кинетическая энергия – это жизненная сила массы или движущегося объекта.
- КЭ будет увеличиваться со скоростью движения объекта.
- Любой объект, находящийся в состоянии движения, обладает кинетической энергией.

- Любой движущийся объект, обладающий энергией благодаря своему движению.
Этот калькулятор кинетической энергии является эффективным инструментом, который предлагает помощь в расчете энергии KE каждого движущегося объекта. Его рабочий процесс основан на стандартной формуле кинетической энергии, которая применяется к каждому объекту в вертикальном или горизонтальном движении.
Ссылки:Из Википедии, свободной энциклопедии – В физике кинетическая энергия (КЭ) – История и этимология –Обзор – Ньютоновская кинетическая энергия – Вращающиеся тела – единицы кинетической энергии – Кинетическая энергия систем – Кинетическая энергия в квантовой механике
Из источника Wikihow – Недавно обновлено – В соавторстве с wikiHow Staff – Как рассчитать кинетическую энергию
Источник toppr – формула кинетической энергии – уравнение кинетической энергии – что такое кинетическая энергия – Решенные примеры по формуле кинетической энергии
Из источника hanacademy – Узнайте, что означает кинетическая энергия и как она связана с работой – как рассчитать кинетическую энергию – работа и кинетическая энергия (КЭ)
7.
 2 Кинетическая энергия и теорема о работе-энергии – Биомеханика движения человека
2 Кинетическая энергия и теорема о работе-энергии – Биомеханика движения человекаРезюме
- Объясните работу как передачу энергии, а чистую работу как работу чистой силы.
- Объясните и примените теорему о работе и энергии.
Что происходит с работой, выполненной в системе? Энергия передается в систему, но в какой форме? Остается ли он в системе или движется дальше? Ответы зависят от ситуации. Например, если газонокосилку в главе 7.1 на рис. 1(а) толкнуть достаточно сильно, чтобы поддерживать постоянную скорость, то энергия, вкладываемая в косилку человеком, непрерывно удаляется за счет трения и в конечном итоге оставляет систему в нерабочем состоянии. форма передачи тепла. Напротив, работа, проделанная с портфелем лицом, несущем его по лестнице в главе 7.1, рис. 1(d), сохраняется в системе портфель-Земля и может быть восстановлена в любое время, как показано в главе 7.1, рис. 1(e). На самом деле строительство пирамид в Древнем Египте является примером накопления энергии в системе путем совершения работы над системой.
 Часть энергии, сообщаемой каменным блокам при их подъеме во время строительства пирамид, остается в системе камень-Земля и может совершать работу.
Часть энергии, сообщаемой каменным блокам при их подъеме во время строительства пирамид, остается в системе камень-Земля и может совершать работу.В этом разделе мы начинаем изучение различных видов работы и форм энергии. Мы обнаружим, что некоторые виды работы оставляют энергию системы постоянной, например, тогда как другие каким-то образом изменяют систему, например, заставляя ее двигаться. Мы также разработаем определения важных форм энергии, таких как энергия движения.
Изучая законы Ньютона, мы знаем, что результирующая сила вызывает ускорение. В этом разделе мы увидим, что работа, совершаемая результирующей силой, дает системе энергию движения, и в процессе мы также найдем выражение для энергии движения.
Давайте начнем с рассмотрения общей или чистой работы, выполненной в системе. Чистая работа определяется как сумма работы, выполненной всеми внешними силами, то есть чистая работа — это работа, выполненная чистой внешней силой F чистая .
 В форме уравнения это W нетто = F нетто d cos θ , где θ
В форме уравнения это W нетто = F нетто d cos θ , где θ7
8 вектор силы и угол смещения.
На рис. 1(а) показан график зависимости силы от смещения для составляющей силы в направлении смещения, то есть график F cos θ против d . В этом случае F cos θ является константой. Вы можете видеть, что площадь под графиком равна Fd cos θ или проделанной работе. На рис. 1(b) показан более общий процесс, когда сила изменяется. Площадь под кривой разделена на полосы, каждая из которых имеет среднюю силу ( F cos θ ) i (ср.) . The work done is ( F cos θ ) i (ave) d i for each strip, and the total work done is the sum of the W i . Таким образом, общая проделанная работа представляет собой общую площадь под кривой, полезное свойство, к которому мы обратимся позже.
Таким образом, общая проделанная работа представляет собой общую площадь под кривой, полезное свойство, к которому мы обратимся позже.
Сетевую работу будет проще исследовать, если мы рассмотрим одномерную ситуацию, когда сила используется для ускорения объекта в направлении, параллельном его начальной скорости. Такая ситуация возникает для упаковки на роликовой ленточной конвейерной системе, показанной на Рисунке 2 9.0007 .
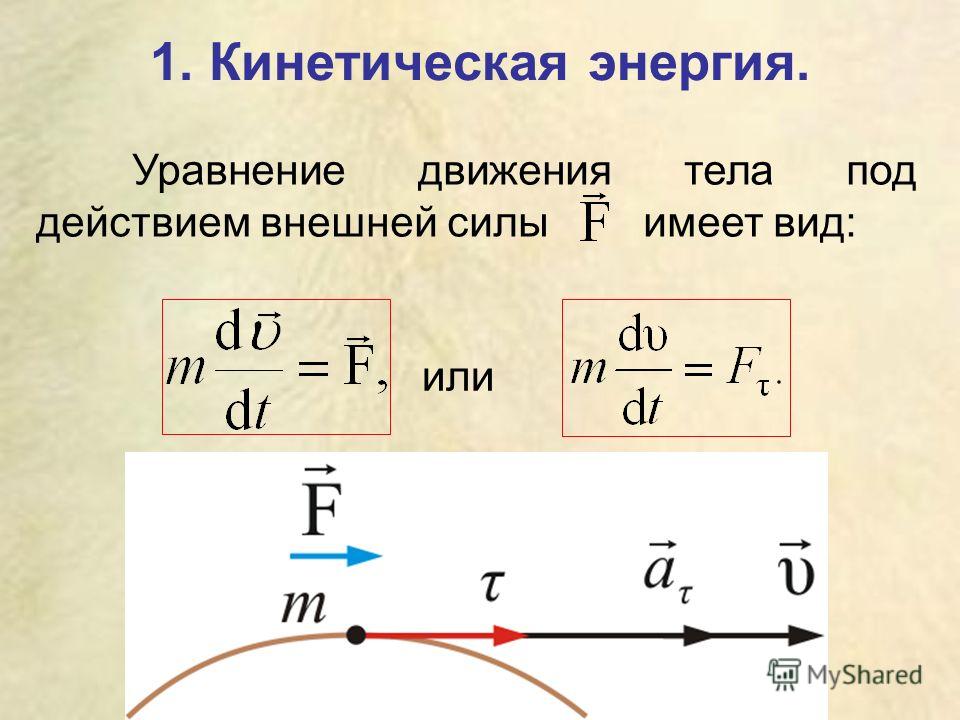 Пакет на роликовой ленте перемещается горизонтально на расстояние d .
Пакет на роликовой ленте перемещается горизонтально на расстояние d .Сила тяжести и нормальная сила, действующие на упаковку, перпендикулярны перемещению и не совершают работы. Кроме того, они также равны по величине и противоположны по направлению, поэтому они сокращаются при расчете результирующей силы. Чистая сила возникает исключительно из горизонтальной приложенной силы Fapp и горизонтальной силы трения f . Таким образом, как и ожидалось, результирующая сила параллельна смещению, так что θ = 0° и cos θ = 1 , а чистая работа определяется как
[латекс]\boldsymbol{W_{\textbf{net}}=F_{\textbf{net}}d}.[/latex]
Эффект чистой силы F net заключается в ускорении пакета с v 0 до v . Кинетическая энергия пакета увеличивается, что указывает на то, что чистая работа, выполненная системой, положительна. (См. пример 1.) Применяя второй закон Ньютона и занимаясь алгеброй, мы можем прийти к интересному выводу. Замена F net = ma из второго закона Ньютона дает
(См. пример 1.) Применяя второй закон Ньютона и занимаясь алгеброй, мы можем прийти к интересному выводу. Замена F net = ma из второго закона Ньютона дает
[латекс]\boldsymbol{W_{\textbf{net}}=безумие}.[/латекс]
Чтобы получить зависимость между чистой работой и скоростью, сообщаемой системе действующей на нее чистой силой, возьмем d = x – x 0 и воспользуемся уравнением, изученным в главе 2.5 Движение. Уравнения для постоянного ускорения в одном измерении для изменения скорости на расстоянии 92},[/латекс]
— это энергия, связанная с поступательным движением. Кинетическая энергия — это форма энергии, связанная с движением частицы, отдельного тела или системы объектов, движущихся вместе.
Мы знаем, что требуется энергия, чтобы разогнать объект, такой как автомобиль или пакет на рис. 2, до скорости, но может показаться немного удивительным, что кинетическая энергия пропорциональна квадрату скорости. Эта пропорциональность означает, например, что автомобиль, движущийся со скоростью 100 км/ч, имеет в четыре раза больше кинетической энергии, чем на скорости 50 км/ч, что помогает объяснить, почему столкновения на высокой скорости настолько разрушительны. Теперь мы рассмотрим ряд примеров, иллюстрирующих различные аспекты работы и энергии. 92=3.75\textbf{ J}}.[/latex]
Эта пропорциональность означает, например, что автомобиль, движущийся со скоростью 100 км/ч, имеет в четыре раза больше кинетической энергии, чем на скорости 50 км/ч, что помогает объяснить, почему столкновения на высокой скорости настолько разрушительны. Теперь мы рассмотрим ряд примеров, иллюстрирующих различные аспекты работы и энергии. 92=3.75\textbf{ J}}.[/latex]
Обсуждение
Обратите внимание, что единицей кинетической энергии является джоуль, такая же, как единица работы, как упоминалось при первом определении работы. Интересно и то, что, хотя это достаточно массивный пакет, его кинетическая энергия невелика при такой относительно небольшой скорости. Этот факт согласуется с наблюдением, что люди могут перемещать такие пакеты, не утомляя себя.
Пример 2. Определение работы по ускорению пакета
Предположим, что вы толкаете груз массой 30,0 кг, показанный на рис. 2, с постоянной силой 120 Н на расстояние 0,800 м, а сила противодействующего трения в среднем составляет 5,00 Н.
(a) Рассчитайте чистую работу, выполненную на посылка. (б) Решите ту же задачу, что и в части (а), на этот раз найдя работу, совершаемую каждой силой, которая вносит вклад в результирующую силу.
Стратегия и концепция для (a)
Это задача о движении в одном измерении, потому что направленная вниз сила (от веса упаковки) и нормальная сила имеют одинаковую величину и противоположное направление, так что они компенсируются в расчет чистой силы, в то время как приложенная сила, трение и смещение горизонтальны. (См. рис. 2.) Как и ожидалось, чистая работа равна чистой силе, умноженной на расстояние.
Решение для (a)
Чистая сила равна силе толкания за вычетом силы трения, или F нетто = 120 Н – 5,00 Н = 115 Н . Таким образом, чистая работа равна
[латекс]\begin{array}{lcl} \boldsymbol{W_{\textbf{net}}} & \boldsymbol{=} & \boldsymbol{F_{\textbf{net}}d= (115\textbf{N})(0,800\textbf{m})} \\ {} & \boldsymbol{=} & \boldsymbol{92. 0\textbf{N}\cdotp\textbf{m}=92.0\textbf{ J .}} \end{array}[/latex]
0\textbf{N}\cdotp\textbf{m}=92.0\textbf{ J .}} \end{array}[/latex]
Обсуждение для (a)
Это значение представляет собой чистую работу, выполненную над пакетом. На самом деле человек выполняет больше работы, потому что трение препятствует движению. Трение совершает отрицательную работу и удаляет часть затрачиваемой человеком энергии и преобразует ее в тепловую энергию. Чистая работа равна сумме работы, выполненной каждой отдельной силой.
Стратегия и концепция для (b)
Силы, действующие на упаковку, включают силу тяжести, нормальную силу, силу трения и приложенную силу. Нормальная сила и сила тяжести перпендикулярны перемещению и, следовательно, не совершают работы. 9{\circ}=-F _{\textbf{fr}}d} \\ {} & \boldsymbol{=} & \boldsymbol{(-5,00\textbf{N})(0,800\textbf{m})} \\ {} & \boldsymbol{=} & \boldsymbol{-4.00\textbf{ J.}} \end{array}[/latex]
Таким образом, количество работы, выполненной силой тяжести, нормальной силой, приложенной силой , и по трению равны соответственно
[латекс]\begin{array}{lcl} \boldsymbol{W_{\textbf{gr}}} & \boldsymbol{=} & \boldsymbol{0,} \\ \boldsymbol {W_{\textbf{N}}} & \boldsymbol{=} & \boldsymbol{0,} \\ \boldsymbol{W_{\textbf{приложение}}} & \boldsymbol{=} & \boldsymbol{96. 0\textbf{J,}} \\ \boldsymbol{W_{\textbf{fr}}} & \boldsymbol{=} & \boldsymbol{-4.00\textbf{J.}} \end{array}[/latex]
0\textbf{J,}} \\ \boldsymbol{W_{\textbf{fr}}} & \boldsymbol{=} & \boldsymbol{-4.00\textbf{J.}} \end{array}[/latex]
Общая проделанная работа как сумма работы, проделанной каждой силой, тогда видится как
[латекс]\boldsymbol{W _{\textbf{total}}=W_{\textbf{gr}}+W_{\ textbf{N}}+W_{\textbf{приложение}}+W_{\textbf{fr}}=92.0\textbf{J.}}[/latex]
Обсуждение для (b)
Расчетная сумма работа Вт всего , так как сумма работы каждой силы согласуется, как и ожидалось, с работой W net сделано чистой силой. Работа, совершаемая совокупностью сил, действующих на объект, может быть рассчитана любым подходом.
Пример 3: Определение скорости по работе и энергии
Найдите скорость пакета на рис. 2 в конце толчка, используя понятия работы и энергии.
Стратегия
Здесь можно использовать теорему о работе-энергии, поскольку мы только что вычислили чистую работу, Вт 92}{30. 0\textbf{ кг}}}} \\ {} & \boldsymbol{=} & \boldsymbol{2.53\textbf{ м/с.}} \end{array}[/latex]
0\textbf{ кг}}}} \\ {} & \boldsymbol{=} & \boldsymbol{2.53\textbf{ м/с.}} \end{array}[/latex]
Обсуждение
Используя работу и энергию, мы не только приходим к ответу, но и видим, что конечная кинетическая энергия является суммой начальной кинетической энергии и чистой работы, выполненной на упаковке. Это означает, что работа действительно добавляет энергии упаковке.
Пример 4. Работа и энергия также могут показать расстояние
Как далеко уйдет пакет на рис. 2 после толчка, если предположить, что трение остается постоянным? Используйте соображения работы и энергии.
Стратегия
Мы знаем, что как только человек перестанет толкать, трение остановит упаковку. С точки зрения энергии трение совершает отрицательную работу до тех пор, пока оно не уберет всю кинетическую энергию упаковки. Работа, совершаемая трением, равна произведению силы трения на пройденное расстояние, умноженному на косинус угла между силой трения и перемещением; следовательно, это дает нам способ найти расстояние, пройденное после того, как человек перестанет толкать.
Решение
Нормальная сила и сила тяжести компенсируются при расчете результирующей силы. Тогда сила горизонтального трения является чистой силой и действует противоположно смещению, поэтому θ = 180° . Чтобы уменьшить кинетическую энергию пакета до нуля, работа Вт fr трения должна быть минус кинетическая энергия, с которой пакет стартовал, плюс то, что пакет накопил за счет толкания. Таким образом W fr 9{\prime}=19,2\textbf{ м.}}[/latex]
Обсуждение
Это разумное расстояние для того, чтобы пакет мог двигаться по инерции на конвейерной системе с относительно низким трением. Обратите внимание, что работа, совершаемая трением, отрицательна (сила действует в направлении, противоположном движению), поэтому она удаляет кинетическую энергию.
Некоторые примеры в этом разделе могут быть решены без учета энергии, но за счет упущения понимания того, что делают работа и энергия в этой ситуации. В целом решения, связанные с энергией, обычно короче и проще, чем решения, использующие только кинематику и динамику. 92}[/latex] для поступательного (т.е. невращательного) движения объекта массой m движущегося со скоростью v
В целом решения, связанные с энергией, обычно короче и проще, чем решения, использующие только кинематику и динамику. 92}[/latex] для поступательного (т.е. невращательного) движения объекта массой m движущегося со скоростью v
Работа, энергия и мощность
Определения
Работа может быть определена как передача энергии. В физике мы говорим, что работа совершается над объектом, когда вы передаете этому объекту энергию. Если один объект передает (отдает) энергию второму объекту, то первый объект совершает работу над вторым объектом.
Работа — это приложение силы на расстоянии. Поднять вес с земли и поставить его на полку — хороший пример работы. Сила равна весу объекта, а расстояние равно высоте полки (W= Fxd).
Принцип работы-энергии — Изменение кинетической энергии объекта равно чистой работе, выполненной над объектом. 2.
2.
Типы энергии
Существуют два типа энергии во многих формах:
Кинетическая энергия = энергия движения
Потенциальная энергия = накопленная энергия
Формы энергии
Соль Сол -излучение -бало – Инфракрасное тепло, радиоволны, гамма-лучи, микроволны, ультрафиолетовый свет
Атомная/ядерная энергия – энергия, выделяющаяся в ядерных реакциях. Когда нейтрон расщепляет ядро атома на более мелкие части, это называется делением. Когда два ядра соединяются вместе при температуре в миллионы градусов, это называется слиянием 9.0003
Электрическая энергия — Производство или использование электроэнергии в течение определенного периода времени, выраженное в киловатт-часах (кВтч), мегаватт-часах (НМ) или гигаватт-часах (ГВтч).
Химическая энергия — Химическая энергия является формой потенциальной энергии, связанной с разрывом и образованием химических связей. Он хранится в продуктах питания, топливе и батареях и высвобождается в виде других форм энергии во время химических реакций.
Механическая энергия. Энергия движущихся частей машины. Также относится к движениям человека
Тепловая энергия — форма энергии, которая передается за счет разницы температур
Что такое мощность
Мощность – это работа, совершаемая в единицу времени. Другими словами, мощность — это мера того, насколько быстро можно выполнить работу. Единицей мощности является ватт = 1 джоуль/1 секунду.
Одной из общепринятых единиц измерения энергии является киловатт-час (кВтч). Если мы используем один кВт мощности, одного кВтч энергии хватит на один час.
Расчет работы, энергии и мощности
WORK = W=Fd
Поскольку энергия – это способность выполнять работу, мы измеряем энергию и работу в одних и тех же единицах (Н*м или джоули).
МОЩНОСТЬ (P) – это скорость выработки (или поглощения) энергии с течением времени: P = E/t
Единицей измерения мощности в СИ является ватт, представляющий выработку или поглощение энергии со скоростью 1 Дж/сек. . Единицей измерения мощности в английской системе является лошадиная сила, которая эквивалентна 735,7 Вт.
. Единицей измерения мощности в английской системе является лошадиная сила, которая эквивалентна 735,7 Вт.
См. также: Работа, энергия и мощность — Как понять и рассчитать счет за электроэнергию.
Попробуйте это упражнение!
1) Сила в 20 ньютонов толкает объект на 5 метров в направлении действия силы. Сколько работы сделано?
Пожалуйста, введите свой ответ в отведенное место:
джоули
2) Если вы выполняете работу 100 Дж за одну секунду (используя 100 Дж энергии). Сколько энергии используется?
ватт
3) 1 лошадиная сила равна скольким ваттам?
ватт
Вопросы с несколькими вариантами ответов
1. Пример кинетической энергии:
а) движущийся автомобиль
б) растянутая резинка, только что выпущенная
в) заряженная частица в электрическом поле
г) все вышеперечисленное
2. Пример потенциальной энергии:
Пример потенциальной энергии:
а) движущийся автомобиль
б) аккумулятор
в) книга на столе
г) как б, так и в
3. Что не является примером солнечной радиации
а) микроволновые печи
б) магнетизм
в) гамма-лучи
г) видимый свет
4. Примером системы, обладающей как кинетической, так и потенциальной энергией, может быть:
а) книга на столе
б) кусок сахара
в) объект в свободном падении
г) эластичная резинка
5. Какое из следующих утверждений неверно верно
а) энергия – это способность совершать работу
б) Работа может быть выражена как Сила x Расстояние
в) мощность – это количество работы, совершаемой в единицу времени
г) единицей мощности является джоуль
ньютоновская механика – Как была найдена формула кинетической энергии и кто ее нашел?
Второй закон Ньютона
Как вы, наверное, знаете, Ньютон считал, что энергия линейно пропорциональна скорости: то, что сегодня называется , энергия . Первоначальная формулировка второго закона гласит: «Mutationem motus Proportionalem esse vi motrici impressae » = «любое изменение движения (скорости) пропорционально движущая сила впечатленная”.
Первоначальная формулировка второго закона гласит: «Mutationem motus Proportionalem esse vi motrici impressae » = «любое изменение движения (скорости) пропорционально движущая сила впечатленная”.
Этот закон, который в настоящее время ошибочно интерпретируется как: $F = ma$ (здесь нет ссылки на массу) просто утверждает: $$[\Delta/\delta v]( v_1-v_0) \propto Vis_m$$ и в современных терминах иногда ( незаконно ) также интерпретируется как импульс, вроде: $$\Delta v \propto J [/m] \rightarrow \Delta p = J$$. Но масса вообще не упоминается во втором законе (как видно из исходного текста), а только во втором определении .0757 , где мы можем увидеть определение импульса как « мера [количества] движения»
Quantitas motus est mensura ejusdem ( motus ) orta ex velocitate et quantite materiæ conjunctim = ‘количество движения’ (современное ‘ импульс ‘) есть мера того же ( движения ), возникшая совместно посредством скорости и ‘количества материи’ (общая масса)
и, кроме того, «движущая сила» ( vis motrix ) употребляется, как и всеми другими учеными того времени, применительно к еще неизвестной кинетической «сила », заставляющая тела двигаться, которую Галилей назвал « impeto », а Лейбниц « движущая сила ». Толкование этой формулы как определения силы в современном обиходе есть ex post facto историческая манипуляция, совершенная помимо воли автора: он знал об этой интерпретации, предложенной Германом, и отказался принять ее в окончательной редакции
Толкование этой формулы как определения силы в современном обиходе есть ex post facto историческая манипуляция, совершенная помимо воли автора: он знал об этой интерпретации, предложенной Германом, и отказался принять ее в окончательной редакции
Исторические факты
Это был Готфрид Лейбниц , уже в 1686 году (за год до публикации Principia ), который первым подтвердил, что кинетическая энергия пропорциональна квадрату скорости или что скорость пропорциональна квадратному корню из энергии: $$ v \propto \sqrt{V_{viva}}$$. Несколько лет спустя он назвал это vis viva = ‘a- живое/живое ‘ сила в отличие от vis mortua = ‘ мертвых ‘ сила: Декартов импульс ([масса/вес =] размер * скорость: $m *|v|$). Это сопровождалось первой формулировкой принципа 92$
сохранялось до тех пор, пока массы не взаимодействовали. Этот принцип представляет собой точную формулировку приблизительного сохранения кинетической энергии в ситуациях, когда отсутствует трение или при упругих столкновениях. Многие физики того времени считали, что закон сохранения импульса, сохраняющийся даже в системах с трением , определяемый импульсом:
$\,\!\sum_{i} m_i v_i$
– сохраняющаяся кинетическая энергия.
Многие физики того времени считали, что закон сохранения импульса, сохраняющийся даже в системах с трением , определяемый импульсом:
$\,\!\sum_{i} m_i v_i$
– сохраняющаяся кинетическая энергия.
Понятие ФЭ роли не играло, его еще не было, как и понятия механическая энергия, на которую вы ссылаетесь (E = U + V), но Лейбниц в этой первой статье использует термин potentia motrix/ viva [движущая сила] для обозначения как энергии , которую тело приобретает, падая с высота и сила , необходимая для подъема на одну и ту же высоту (масса/вес * пространство: $F*s$), которые считаются равными. Некоторые ученые ошибочно видят здесь первое определение PE, но это просто одна из аксиом Галилея.
Принцип, на который вы ссылаетесь: $E_{mech} [KE + PE] = k$ в астродинамике называется vis viva уравнение в его честь. Лейбниц заявил о сохранении KE per se помимо сохранения всех (видов) энергии во всей вселенной. Мы должны подчеркнуть этот удивительный гениальный ход.
Его теория была резко отвергнута ньютонианцами и декартианцами, потому что она казалась противоположной, несовместимой с сохранением импульса . У Ньютона не было различия (, как показано выше, ) между скоростью, движением, импульсом и энергией, но quantitas motus ( импульс ) была преобладающей концепцией, и было доказано, что она сохраняется во всех ситуациях, поэтому Лейбниц vis viva считался угрозой для всей системы. Только позже было признано, что и энергия, и импульс, будучи разными сущностями, могут сохраняться (Бошковичем, а затем (1748 г.) Даламбером).
Мы можем поблагодарить Эмили дю Шатле за современное понимание кинетической энергии – user121330
Есть нет формулы энергии ..в открытии сохранения энергии Джоулей и… – Бен Кроуэлл
Это упуская из виду исторические факты (Джоуль не интересовался КЭ) : вскоре после смерти Лейбница квадратичное соотношение было подтверждено независимыми экспериментами итальянца Полени в 1719 году и голландца Гравезанда в 1722 году, которые бросали мячи с разной высоты. на мягкую глину и обнаружил, что шарики с удвоенной скоростью производят вмятины в четыре раза глубже. Последний сообщил M.me du Châtelet его результатов, и она обнародовала их . Два столетия спустя, после того как Джоуль показал, что механическая работа может быть преобразована в теплоту, Гельмгольц предположил, что потерянная энергия при неупругих столкновениях могла быть преобразована в теплоту.
на мягкую глину и обнаружил, что шарики с удвоенной скоростью производят вмятины в четыре раза глубже. Последний сообщил M.me du Châtelet его результатов, и она обнародовала их . Два столетия спустя, после того как Джоуль показал, что механическая работа может быть преобразована в теплоту, Гельмгольц предположил, что потерянная энергия при неупругих столкновениях могла быть преобразована в теплоту.
Считается, что Томас Юнг был первым, кто заменил термины « vis viva/ potentia motrix » на « энергия » в 1807 году (от греческого слова: ἐνέργεια energeia , которое было ствол ergon = работа, следовательно: energeia [= состояние-бытия-на-работе]). Позже (1824-1829) Кориолис ввел действующую формулу и термины ‘работа’ и ‘ semi-vis viva ‘; эта концепция и последующая теория сохранения энергии были в конечном итоге формализованы лордом Кельвином, Рэнкином и др. в области термодинамики. 2$, любой коэффициент (0,2, 0,5, 2..) мог быть добавлен как нерелевантный и произвольный выбор который зависел только от выбора единиц .
2$, любой коэффициент (0,2, 0,5, 2..) мог быть добавлен как нерелевантный и произвольный выбор который зависел только от выбора единиц .
Единственным доступным (и точно измеримым ) источником КЭ в то время была гравитация, и уравнения Галилея были слишком сильным искушением, поскольку они также включали квадратичное отношение [0,5]: казалось гениальным сделать так, чтобы энергия единичной массы при унитарном (равномерном) ускорении совпадала с пространством. Таким образом, энергия была просто интегрированием [m] $g$ в пространстве.
Выводы
Привязывать энергию к гравитации, то есть к ускорению и в частности к постоянному ускорению не было мудрой идеей, было грубой ошибкой связывать, заключать ньютоновскую механику в пролив ситуаций, когда КЭ связана с скоростью и когда происходит просто передача энергии: понятие импульса было просто 0756 ad hoc неуклюжая попытка справиться с этим.

Связывание работы-энергии с пространством, а не с простой передачей энергии было безумным решением, имевшим иррациональные, катастрофические практические последствия. Но последствия были еще более разрушительными на концептуальном, теоретическом уровне, потому что объяснение и отождествление КЭ с ускорением создавало иллюзию понимания вопроса о движении-КЭ и предотвращало дальнейшие предположения.
92$ сопротивляясь сирене гравитации, предложил правильный путь интеграции и установил универсальный принцип «сохранения энергии» как преобладающий/независимый от «сохранения импульса» (выходящий за пределы принципа Гюйгенса ‘ консервация КЕ’ ).
Он участвовал в страстных спорах до самой своей смерти, но противостоял и подавлял тупых/невежественных ньютоновских современников. Он был уязвим, поскольку не мог объяснить потерю энергии при неупругих столкновениях. Он проиграл, и ньютоновское интегрирование на пространстве дало: $\frac{1}{2}$ mv 2 что не формула , а просто одна из возможных формул KE: ньютоновская формула. Если бы он выиграл, то вместо джоулей мы бы теперь использовали « лейбница » (= 1/2 Дж) и получили бы другое, возможно, более глубокое понимание законов движения и мира.
Если бы он выиграл, то вместо джоулей мы бы теперь использовали « лейбница » (= 1/2 Дж) и получили бы другое, возможно, более глубокое понимание законов движения и мира.
- Историю , как известно, пишут победители.
Дополнительную информацию о работе можно найти здесь
7.2 Кинетическая энергия и теорема о работе-энергии – Колледж физики 2e
Цели обучения
К концу этого раздела вы сможете:
- Объясните работу как передачу энергии, а чистую работу как работу чистой силы.
- Объясните и примените теорему о работе и энергии.
Работа Передача энергии
Что происходит с работой, выполненной в системе? Энергия передается в систему, но в какой форме? Остается ли он в системе или движется дальше? Ответы зависят от ситуации. Например, если газонокосилку на рис. 7.2(а) толкнуть достаточно сильно, чтобы она продолжала двигаться с постоянной скоростью, то энергия, вкладываемая в косилку человеком, непрерывно удаляется за счет трения и, в конце концов, покидает систему в форме передачи тепла. Напротив, работа, проделанная с портфелем лицом, несущем его по лестнице на рис. 7.2(d), сохраняется в системе «портфель-Земля» и может быть восстановлена в любое время, как показано на рис. 7.2(e). На самом деле строительство пирамид в Древнем Египте является примером накопления энергии в системе путем совершения работы над системой. Часть энергии, сообщаемой каменным блокам при их подъеме во время строительства пирамид, остается в системе камень-Земля и может совершать работу.
Напротив, работа, проделанная с портфелем лицом, несущем его по лестнице на рис. 7.2(d), сохраняется в системе «портфель-Земля» и может быть восстановлена в любое время, как показано на рис. 7.2(e). На самом деле строительство пирамид в Древнем Египте является примером накопления энергии в системе путем совершения работы над системой. Часть энергии, сообщаемой каменным блокам при их подъеме во время строительства пирамид, остается в системе камень-Земля и может совершать работу.
В этом разделе мы начинаем изучение различных видов работы и форм энергии. Мы обнаружим, что некоторые виды работы оставляют энергию системы постоянной, например, тогда как другие каким-то образом изменяют систему, например, заставляя ее двигаться. Мы также разработаем определения важных форм энергии, таких как энергия движения.
Чистая работа и теорема о работе-энергии
Мы знаем из изучения законов Ньютона в книге «Динамика: сила» и «Законы движения Ньютона», что результирующая сила вызывает ускорение. В этом разделе мы увидим, что работа, совершаемая результирующей силой, дает системе энергию движения, и в процессе мы также найдем выражение для энергии движения.
В этом разделе мы увидим, что работа, совершаемая результирующей силой, дает системе энергию движения, и в процессе мы также найдем выражение для энергии движения.
Начнем с рассмотрения общей или чистой работы, выполненной системой. Чистая работа определяется как сумма работы над объектом. Чистая работа может быть записана в терминах чистой силы, действующей на объект. ФнетФнет. В форме уравнения это Wnet=FnetdcosθWnet=Fnetdcosθ, где θθ — угол между вектором силы и вектором смещения.
На рис. 7.3(а) показан график зависимости силы от смещения для составляющей силы в направлении смещения, то есть график зависимости FcosθFcosθ от dd. В этом случае FcosθFcosθ постоянна. Вы можете видеть, что площадь под графиком равна FdcosθFdcosθ, или проделанной работе. На рис. 7.3(b) показан более общий процесс, когда сила изменяется. Площадь под кривой разделена на полосы, каждая из которых имеет среднюю силу (Fcosθ)i(ave)(Fcosθ)i(ave). Проделанная работа равна (Fcosθ)i(ave)di(Fcosθ)i(ave)di для каждой полосы, а общая проделанная работа равна сумме WiWi. Таким образом, общая проделанная работа представляет собой общую площадь под кривой, полезное свойство, к которому мы обратимся позже.
Таким образом, общая проделанная работа представляет собой общую площадь под кривой, полезное свойство, к которому мы обратимся позже.
Рисунок 7.3 (а) График зависимости FcosθFcosθ от dd, когда FcosθFcosθ постоянна. Площадь под кривой представляет собой работу силы. (b) График зависимости FcosθFcosθ от dd, при котором сила изменяется. Работа, выполненная для каждого интервала, равна площади каждой полосы; таким образом, общая площадь под кривой равна общей проделанной работе.
Работу сети будет проще исследовать, если мы рассмотрим одномерную ситуацию, когда сила используется для ускорения объекта в направлении, параллельном его начальной скорости. Такая ситуация возникает для упаковки на роликовой конвейерной системе, показанной на рис. 7.4.
Рисунок 7.4 Пакет на роликовой ленте толкают горизонтально на расстояние dd.
Сила тяжести и нормальная сила, действующие на упаковку, перпендикулярны смещению и не совершают работы. Кроме того, они также равны по величине и противоположны по направлению, поэтому они сокращаются при расчете результирующей силы. Чистая сила возникает исключительно из горизонтальной приложенной силы FappFapp и горизонтальной силы трения ff. Таким образом, как и ожидалось, результирующая сила параллельна смещению, так что θ=0ºθ=0º и cosθ=1cosθ=1, а результирующая работа определяется выражением
Чистая сила возникает исключительно из горизонтальной приложенной силы FappFapp и горизонтальной силы трения ff. Таким образом, как и ожидалось, результирующая сила параллельна смещению, так что θ=0ºθ=0º и cosθ=1cosθ=1, а результирующая работа определяется выражением
Wnet=Fnetd.Wnet=Fnetd.
7.7
Эффект чистой силы FnetFnet заключается в ускорении пакета с v0v0 до vv. Кинетическая энергия пакета увеличивается, что указывает на то, что чистая работа, выполненная системой, положительна. (См. пример 7.2.) Применяя второй закон Ньютона и занимаясь алгеброй, мы можем прийти к интересному выводу. Замена Fnet=maFnet=ma из второго закона Ньютона дает
Wnet=mad.Wnet=mad.
7,8
Чтобы получить соотношение между чистой работой и скоростью, придаваемой системе действующей на нее чистой силой, мы берем d=x−x0d=x−x0 и используем уравнение, изученное в разделе «Уравнения движения для постоянного ускорения в одном измерении» для изменение скорости на пути dd, если ускорение имеет постоянное значение
аа; а именно,
v2=v02+2adv2=v02+2ad (обратите внимание, что
aa появляется в выражении для сети). Решение для ускорения дает
а=v2-v022da=v2-v022d. Когда
aa подставляется в предыдущее выражение для
WnetWnet получаем
Решение для ускорения дает
а=v2-v022da=v2-v022d. Когда
aa подставляется в предыдущее выражение для
WnetWnet получаем
Wnet=mv2-v022dd.Wnet=mv2-v022dd.
7,9
dd отменяется, и мы переставляем это, чтобы получить
Wnet=12mv2−12mv0 2.Wnet=12mv2−12mv0 2.
7,10
Это выражение называется теоремой работы-энергии, и оно фактически применяется вообще (даже для сил, меняющихся по направлению и величине), хотя мы вывели его для частного случая постоянной силы, параллельной перемещению. Из теоремы следует, что чистая работа над системой равна изменению величины 12mv212mv2. Эта величина является нашим первым примером формы энергии.
Теорема о работе-энергии
Чистая работа системы равна изменению количества 12mv212mv2.
Wnet=12mv2−12mv0 2Wnet=12mv2−12mv0 2
7,11
Величина 12mv212mv2 в теореме о работе-энергии определяется как поступательная кинетическая энергия (КЭ) массы mm, движущейся со скоростью vv. ( поступательная кинетическая энергия отличается от вращательной кинетической энергии, которая рассматривается позже.) В форме уравнения поступательная кинетическая энергия
( поступательная кинетическая энергия отличается от вращательной кинетической энергии, которая рассматривается позже.) В форме уравнения поступательная кинетическая энергия
KE=12mv2,KE=12mv2,
7.12
— энергия, связанная с поступательным движением. Кинетическая энергия — это форма энергии, связанная с движением частицы, отдельного тела или системы объектов, движущихся вместе.
Мы знаем, что требуется энергия, чтобы разогнать объект, такой как автомобиль или пакет на рис. 7.4, до скорости, но может показаться немного удивительным, что кинетическая энергия пропорциональна квадрату скорости. Эта пропорциональность означает, например, что автомобиль, движущийся со скоростью 100 км/ч, имеет в четыре раза больше кинетической энергии, чем на скорости 50 км/ч, что помогает объяснить, почему столкновения на высокой скорости настолько разрушительны. Теперь мы рассмотрим ряд примеров, иллюстрирующих различные аспекты работы и энергии.
Пример 7.2
Расчет кинетической энергии упаковки
Предположим, что упаковка массой 30,0 кг на роликовом ленточном конвейере на рис. 7.4 движется со скоростью 0,500 м/с. Какова его кинетическая энергия?
Стратегия
Поскольку масса mm и скорость vv заданы, кинетическая энергия может быть рассчитана по ее определению, данному в уравнении KE=12mv2KE=12mv2.
Решение
Кинетическая энергия определяется выражением
KE=12mv2.KE=12mv2.
7.13
Ввод известных значений дает
KE=0,5(30,0 кг)(0,500 м/с)2, KE=0,5(30,0 кг)(0,500 м/с)2,
7,14
3203 что дает
23 KE=3,75 кг⋅м2/с2=3,75 Дж.KE=3,75 кг⋅м2/с2=3,75 Дж.
7,15
Обсуждение
Обратите внимание, что единицей кинетической энергии является джоуль, как и единица работы. , как упоминалось, когда работа была впервые определена. Интересно и то, что, хотя это достаточно массивный пакет, его кинетическая энергия невелика при такой относительно небольшой скорости. Этот факт согласуется с наблюдением, что люди могут перемещать такие пакеты, не утомляя себя.
Интересно и то, что, хотя это достаточно массивный пакет, его кинетическая энергия невелика при такой относительно небольшой скорости. Этот факт согласуется с наблюдением, что люди могут перемещать такие пакеты, не утомляя себя.
Пример 7.3
Определение работы по ускорению пакета
Предположим, что вы толкаете пакет массой 30,0 кг, показанный на рис. 7.4, с постоянной силой 120 Н на расстояние 0,800 м, а сила противодействующего трения в среднем составляет 5,00 Н.
а) Рассчитайте чистую работу, совершенную над пакетом. (б) Решите ту же задачу, что и в части (а), на этот раз найдя работу, совершаемую каждой силой, которая вносит вклад в результирующую силу.
Стратегия и концепция (а)
Это задача о движении в одном измерении, потому что направленная вниз сила (от веса упаковки) и нормальная сила имеют одинаковую величину и противоположное направление, так что они сокращаются при расчете чистой силы, в то время как приложенная сила, трение , и смещения все горизонтальны. (См. рис. 7.4.) Как и ожидалось, чистая работа равна чистой силе, умноженной на расстояние.
(См. рис. 7.4.) Как и ожидалось, чистая работа равна чистой силе, умноженной на расстояние.
Решение для (a)
Чистая сила равна толкающей силе минус трение, или Fnet = 120 Н – 5,00 Н = 115 NFnet = 120 Н – 5,00 Н = 115 Н. Таким образом, чистая работа равна
Wnet=Fnetd=115 N0,800 м=92,0 Н⋅м=92,0 Дж.Wnet=Fnetd=115 N0,800 м=92,0 Н⋅м=92,0 Дж
7,16
Обсуждение для (a)
Это значение представляет собой чистую работу, выполненную над пакетом. На самом деле человек выполняет больше работы, потому что трение препятствует движению. Трение совершает отрицательную работу и удаляет часть затрачиваемой человеком энергии и преобразует ее в тепловую энергию. Чистая работа равна сумме работы, выполненной каждой отдельной силой.
Стратегия и концепция (b)
Силы, действующие на упаковку, включают силу тяжести, нормальную силу, силу трения и приложенную силу. Нормальная сила и сила тяжести перпендикулярны перемещению и, следовательно, не совершают работы.
Нормальная сила и сила тяжести перпендикулярны перемещению и, следовательно, не совершают работы.
Решение для (b)
Приложенная сила работает.
Wapp=Fappdcos0º=Fappd=120 Н0,800 м= 96,0 JWapp=Fappdcos0º=Fappd=120 Н0,800 м= 96,0 Дж 180º, а работа трения равна
Wfr=Ffrdcos180°=-Ffrd=-5,00 N0,800 м=-4,00 J.Wfr=Ffrdcos180°=-Ffrd=-5,00 N0,800 м=-4,00 Дж.
7,18
силы тяжести, нормальной силой, приложенной силой и трением равны соответственно
Wgr=0,WN=0,Wapp=96,0 Дж,Wfr=-4,00 Дж.Wgr=0,WN=0,Wapp= 96,0 Дж,Wfr=-4,00 Дж.
7,19
Общая работа, выполненная как сумма работы, выполненной каждой силой, будет равна
Wtotal=Wgr+WN+Wapp+Wfr=92,0 Дж.Wtotal= Wgr+WN+Wapp+Wfr=92,0 Дж.
7,20
Обсуждение для (b)
Рассчитанная общая работа WtotalWtotal как сумма работы каждой силы согласуется, как и ожидалось, с работой WnetWnet, выполненной результирующей силой. Работа, совершаемая совокупностью сил, действующих на объект, может быть рассчитана любым подходом.
Работа, совершаемая совокупностью сил, действующих на объект, может быть рассчитана любым подходом.
Пример 7.4
Определение скорости по работе и энергии
Найдите скорость пакета на рис. 7.4 в конце толчка, используя понятия работы и энергии.
Стратегия
Здесь можно использовать теорему о работе-энергии, потому что мы только что вычислили чистую работу, WnetWnet, и начальную кинетическую энергию, 12мв0212мв02. Эти вычисления позволяют нам найти конечную кинетическую энергию 12mv212mv2 и, следовательно, конечную скорость vv.
Решение
Теорема о работе-энергии в виде уравнения:
Wnet=12mv2−12mv02.Wnet=12mv2−12mv02.
7.21
Решение для 12mv212mv2 дает
12mv2=Wnet+12mv02.12mv2=Wnet+12mv02.
7,22
Таким образом,
12mv2=92,0 Дж+3,75 Дж=95,75 Дж. 12mv2=92,0 Дж+3,75 Дж=95,75 Дж. v=2(95,75 Дж)m=191,5 кг⋅м2/с230,0 кг=2,53 м/с.v=2(95,75 Дж)m=191,5 кг⋅м2/с230,0 кг=2,53 м/с.
12mv2=92,0 Дж+3,75 Дж=95,75 Дж. v=2(95,75 Дж)m=191,5 кг⋅м2/с230,0 кг=2,53 м/с.v=2(95,75 Дж)m=191,5 кг⋅м2/с230,0 кг=2,53 м/с.
7.24
Обсуждение
Используя работу и энергию, мы не только приходим к ответу, но и видим, что конечная кинетическая энергия является суммой начальной кинетической энергии и чистой работы, выполненной на упаковке. Это означает, что работа действительно добавляет энергии упаковке.
Пример 7,5
Работа и энергия также могут показать расстояние
Как далеко уйдет пакет на рис. 7.4 после толчка, если предположить, что трение остается постоянным? Используйте соображения работы и энергии.
Стратегия
Мы знаем, что как только человек перестанет толкать, трение остановит упаковку. С точки зрения энергии трение совершает отрицательную работу до тех пор, пока оно не уберет всю кинетическую энергию упаковки. Работа, совершаемая трением, равна произведению силы трения на пройденное расстояние, умноженному на косинус угла между силой трения и перемещением; следовательно, это дает нам способ найти расстояние, пройденное после того, как человек перестанет толкать.
Решение
Нормальная сила и сила тяжести сокращаются при вычислении результирующей силы. Тогда сила горизонтального трения является чистой силой, и она действует противоположно смещению, поэтому θ=180ºθ=180º. Чтобы уменьшить кинетическую энергию пакета до нуля, работа трения WfrWfr должна быть равна минус кинетическая энергия, с которой пакет стартовал, плюс то, что пакет накопил за счет толкания. Таким образом, Wfr=-95,75 JWfr=-95,75 Дж. Кроме того, Wfr=fd’cosθ= -fd’Wfr=fd’cosθ= -fd’, где d’d’ — расстояние, необходимое для остановки. Таким образом,
d′=−Wfrf=−−95,75 J5,00 N,d′=−Wfrf=−−95,75 J5,00 N,
7,25
и т. д.
d′=19,2 м.d′=19,2 м.
7.26
Обсуждение
Это разумное расстояние для того, чтобы упаковка могла двигаться по инерции на конвейерной системе с относительно низким трением. Обратите внимание, что работа, совершаемая трением, отрицательна (сила действует в направлении, противоположном движению), поэтому она удаляет кинетическую энергию.




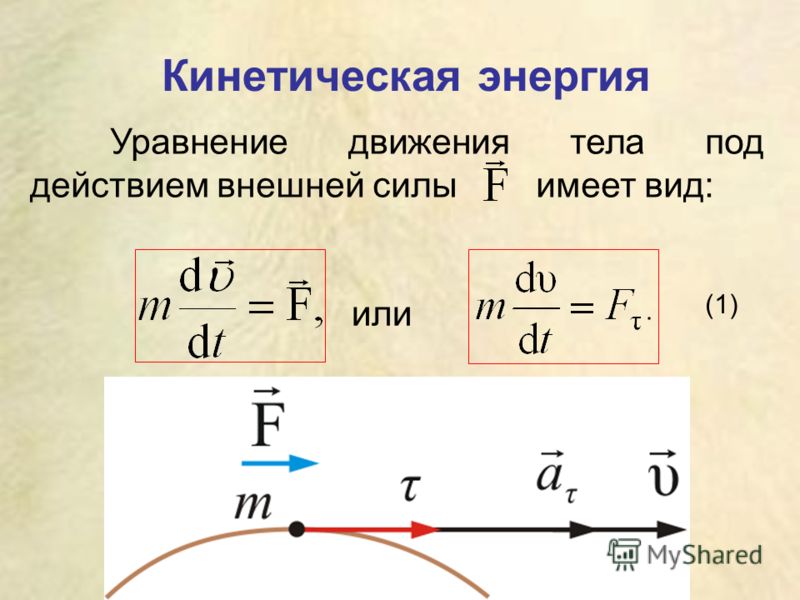
 γ-кванты имеют
нулевую массу покоя. В электромагнитных взаимодействиях участвуют
фундаментальные частицы, занимающие последние три строки в таблице 1, т.е.
заряженные лептоны и кварки. Поскольку кварки в свободном состоянии не
наблюдаются, а входят в состав адронов, т.е. барионов и мезонов, все адроны,
наряду с сильными взаимодействиями, участвуют и в электромагнитных
взаимодействиях.
γ-кванты имеют
нулевую массу покоя. В электромагнитных взаимодействиях участвуют
фундаментальные частицы, занимающие последние три строки в таблице 1, т.е.
заряженные лептоны и кварки. Поскольку кварки в свободном состоянии не
наблюдаются, а входят в состав адронов, т.е. барионов и мезонов, все адроны,
наряду с сильными взаимодействиями, участвуют и в электромагнитных
взаимодействиях. Спины всех фундаментальных бозонов равны 1.
Спины всех фундаментальных бозонов равны 1. Вторую
строку занимают электрон, мюон и таон – заряженные бесструктурные частицы,
участвующие как в слабом, так и электромагнитном взаимодействиях.
Вторую
строку занимают электрон, мюон и таон – заряженные бесструктурные частицы,
участвующие как в слабом, так и электромагнитном взаимодействиях.




 Рассчитать полную энергию электрона.
Рассчитать полную энергию электрона.
 д.).
д.).
 1 Кинематика
1 Кинематика 3 Магнетизм
3 Магнетизм Квантовая теория
Квантовая теория



 2,
2, Другими словами, при двойном увеличении скорости кинетическая энергия увеличится в четыре раза.
Другими словами, при двойном увеличении скорости кинетическая энергия увеличится в четыре раза.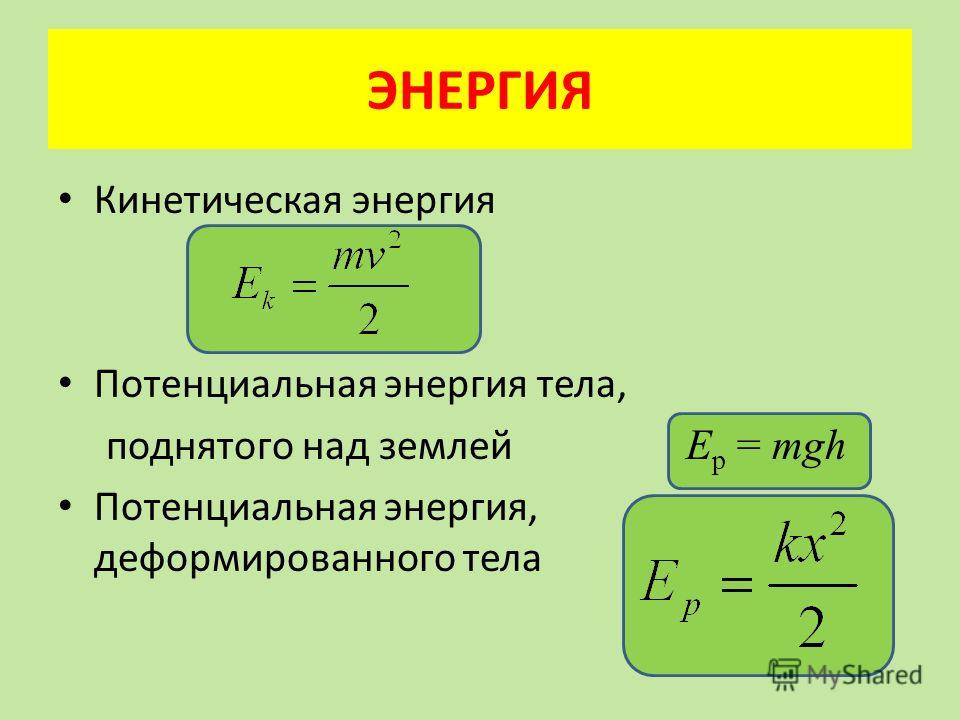

 2 Кинетическая энергия и теорема о работе-энергии – Биомеханика движения человека
2 Кинетическая энергия и теорема о работе-энергии – Биомеханика движения человека Часть энергии, сообщаемой каменным блокам при их подъеме во время строительства пирамид, остается в системе камень-Земля и может совершать работу.
Часть энергии, сообщаемой каменным блокам при их подъеме во время строительства пирамид, остается в системе камень-Земля и может совершать работу. В форме уравнения это W нетто = F нетто d cos θ , где θ
В форме уравнения это W нетто = F нетто d cos θ , где θ