Характеристика зубчатого колеса: Характеристика зубчатых колес
alexxlab | 27.09.1987 | 0 | Разное
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
⇐ ПредыдущаяСтр 41 из 47Следующая ⇒ В современных машинах широко применяют зубчатые передачи. Различают силовые зубчатые передачи, предназначенные для передачи крутящего момента с изменением частоты вращения валов, и кинематические передачи, служащие для передачи вращательного движения между валами при относительно небольших крутящих моментах. Зубчатые передачи, используемые в различных механизмах и ма-шинах, делят на цилиндрические, конические, червячные, смешан-ные и гиперболоидные (винтовые и гипоидные). Наибольшее распространение получили цилиндрические, кони-ческие и червячные передачи (рис. 1.91).
Рис. 1.91. Виды зубчатых передач: а — цилиндрическая; б— коническая; в —червячная; 1 — шестерня; 2— зубчатое колесо; 3— червяк; 4— червячное колесо
Ниже рассмотрены способы формообразования зубьев цилиндрических зубчатых колес. Обработка конических зубчатых колес, червяков и червячных ко-лес излагается, например, в работах [15, 29]. Цилиндрические зубчатые колеса изготовляют с прямыми и ко-сыми зубьями, реже — с шевронными. Стандарт устанавливает 12 степеней точности цилиндрических зубчатых колес (в порядке убы-вания точности): 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12. Для 1, 2-й степеней допуски стандартом не предусматриваются. Для каждой степени точности предусматривают следующие нормы: — кинематической точности колеса, определяющие полную по-грешность угла поворота зубчатых колес за один оборот; — плавности работы колес, определяющие составляющую пол-ной погрешности угла поворота зубчатого колеса, многократно по-вторяющейся за оборот колеса; — контакта зубьев, определяющие отклонение относительных размеров пятна контакта сопряженных зубьев в передаче. Независимо от степени точности колес установлены нормы боко-вого зазора (виды сопряжении зубчатых колес). Существуют шесть видов сопряжении зубчатых колес в передаче, которые в порядке убывания гарантированного бокового зазора обозначаются буквами А, В, С, D, Е, Н, и восемь видов допуска (Tjn) на боковой зазор: х, у, z, a, b, с, d, h. В соответствии со стандартом, точность зубчатых колес может быть определена как комплексными, так и дифференцированными показателями. По технологическому признаку зубчатые колеса делятся на: — цилиндрические и конические без ступицы и со ступицей, с гладким или шлицевым отверстием; — многовенцовые блочные с гладким или шлицевым отверстием; — цилиндрические, конические и червячные типа фланца; — цилиндрические и конические с хвостовиком; — валы-шестерни. У цилиндрических колес зубья выполняют прямыми, спиральными или шевронными. Обработка зубчатых колес разделяется на два этапа: обработку до нарезания зубьев и обработку зубчатого венца. Задачи первого этапа соответствуют в основном аналогичным задачам, решаемым при обработке деталей классов: диски (зубчатое колесо плоское без ступицы), втулки (со ступицей) или валов (вал-шестерня). Операции второго этапа обычно сочетают с отделочными операциями обработки
Рис.
корпуса колеса. На построение технологического процесса обработки зубчатых колес влияют следующие факторы: форма зубчатого колеса; форма и расположение зубчатого венца и количество венцов; степень точности колеса; методы контроля зубчатых колес; материал колеса; наличие и вид термообработки; габаритные размеры; объем выпуска. На рис. 1.92 показаны типовые требования к точности полуфаб-риката для нарезания зубьев в зависимости от вышеперечисленных факторов. 1. Точность размера окружности выступа (d) зависит от метода контроля толщины зуба: когда d является измерительной базой, то Δd = 0,5 Tн, когда d не является измерительной базой, диаметр d мо-жет изготавливаться по IT12, где Тн— допуск на смещение исходного контура. 2. Радиальное биение поверхности вершин зубьев относительно оси отверстия (измерительной базы) не более 0,25 Тн, когда d используется для контроля толщины зуба, например, при контроле смещения исходного контура.
6. Отверстие изготавливается по H6 для зубчатых колес 5-й степени точности и по H7 для зубчатых колес 6,7,8-й степени точности. Наибольшее влияние на протяженность технологического мар-шрута оказывает степень точности колеса. При изготовлении высо-коточных колес (6, 5 и выше степеней точности) механическая обработка должна чередоваться с операциями термической обработки для снятия внутренних напряжений, а количество отделочных операций технологических баз и зубчатого венца значительно возрастает. Технологические задачи Точность размеров. Самым точным элементом зубчатого колеса является отверстие, которое выполняется обычно по 7-му квалитету, если нет особых требований. Точность формы. В большинстве случаев особых требований к точности формы поверхностей не предъявляется. Точность взаимного расположения. Требования к точности взаим-ного расположения представлены на рис. 1.92. Твердость рабочих поверхностей. Твердость незакаливаемых поверхностей обычно находится в пределах НВ 180…270. Для рассматриваемого зубчатого колеса (см. рис. 1.98): — посадочное отверстие выполняется по 7-му квалитету; — точность формы не задается; — точность взаимного расположения ограничена величинами торцового и радиального биений относительно оси отверстия не бо-лее 0,016 и 0,025 мм, а также отклонением от симметричности шпо-ночного паза относительно оси отверстия не более 0,02 мм; — шероховатость поверхности зубчатого венца Ra = 0,63 мкм, отверстия и торцов 1,25 мкм. Зубчатый венец закаливается ТВЧ до HRСЭ45…50 на глубину 1…2 мм.
⇐ Предыдущая36373839404142434445Следующая ⇒ Читайте также: Где возникла философия и почему? Относительная высота сжатой зоны бетона Сущность проекции Гаусса-Крюгера и использование ее в геодезии Тарифы на перевозку пассажиров |
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 918; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
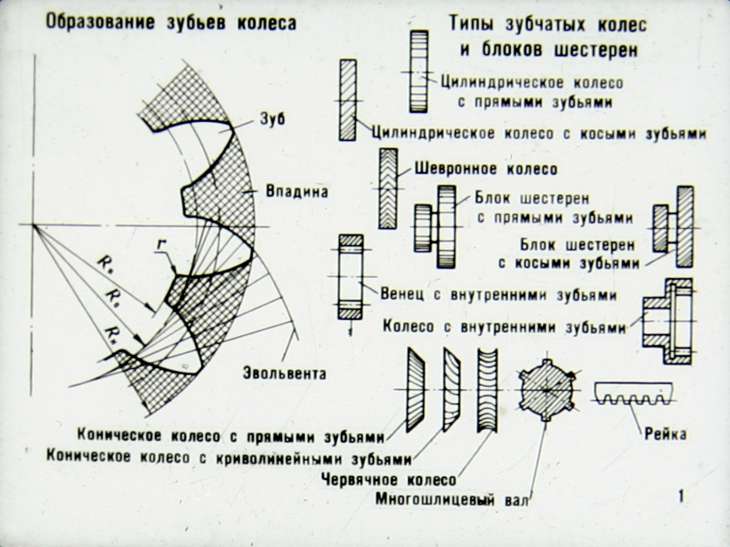
16.1. Виды зубчатых колес, их назначение и характеристики
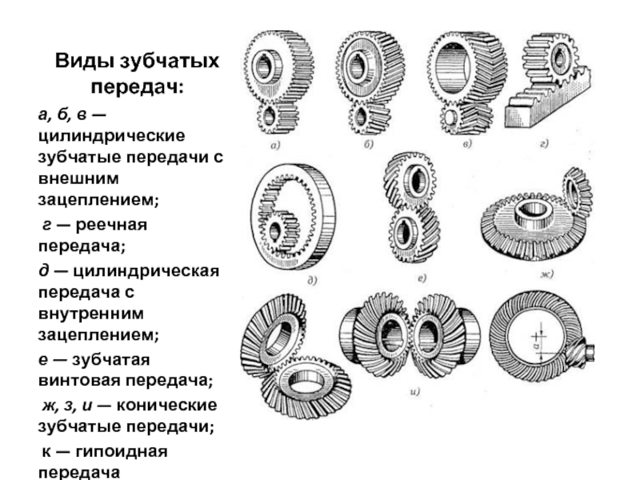
В передачах современных машин широко используются зубчатые колёса, разнообраз-ные по форме, размерам и профилям (рис. 16.1). Наиболее распространены цилиндрические зубчатые колёса с прямыми (рис. 16.1а) и косыми (рис. 16.1б) зубьями. Соединение двух косых зубьев с противоположными углами наклона на ободе цилиндрического колеса представляет собой зубчатую передачу с шевронными (ёлочными) зубьями.
Рис. 16.1. Типы зубчатых передач
На рис. 16.1в представлена коническая передача с пересекающимися осями, причём угол встречи осей может быть любым. Конические колёса могут иметь прямые, косые и криволинейные зубья.
На рис. 16.1г
представлена зубчатая передача со
скрещивающимися осями, состоящая из
двух зубчатых колёс с
16.1г
представлена зубчатая передача со
скрещивающимися осями, состоящая из
двух зубчатых колёс с
На рис. 16.1е изображена реечная передача, одним элементом которой является зубчатое колесо с прямым или косым зубом, а другим – зубчатая рейка, которую можно представить как зубчатое колесо с бесконечно большим чи-слом зубьев. Реечная пара передаёт движение как от зубчатого колеса к рейке,
так и наоборот.
На рис. 16.1ж
представлена схема волновой
передачи,
основанной на передаче движения за счёт
бегущей волновой деформации одного из
зубчатых ко-лёс. Эта передача состоит
из водила 3 с двумя роликами, свободно
вращающимися на осях, закреплённых в
водиле, неподвижного жесткого зубчатого
колеса 1 с внутренними зубьями и вращающего
гибкого колеса 2 с наружными зубьями. Жёсткое зубчатое колесо соединяется с
корпусом передачи. Гибкое зубчатое
колесо изготавливают либо в виде стакана
с тонкой легко деформирующейся стенкой,
либо в виде свободно деформирующегося
кольца.
Жёсткое зубчатое колесо соединяется с
корпусом передачи. Гибкое зубчатое
колесо изготавливают либо в виде стакана
с тонкой легко деформирующейся стенкой,
либо в виде свободно деформирующегося
кольца.
В современных механизмах применяют зубчатые колёса с профилем зуба, очерченным эвольвентной кривой. В ряде случаев используются передачи с зацеплением Новикова, основным отличием которых является выпуклый и вогнутый круговые профили зубьев.
Действующими ГОСТами установлено 12 степеней точности цилиндрических зубчатых колёс и передач, с обозначением степеней в порядке убывания точности. За основу принята 7-я степень точности, соответствующая 7-му квалитету. Для каждой степени точности установлены нормы: кинематическая точность колеса; плавность работы колеса; контакта зубьев; бокового зазора.
Показатели кинематической точности представлены на рис. 16.2.
Нормы кинематической
точности определяют значение наибольшей
погрешности угла поворота зубчатого
колеса за оборот при зацеплении с точным
колесом. Эта погрешность возникает при
нарезании зубчатых колёс вследствие
погрешностей взаимного расположения
заготовки обрабатываемого колеса и
режущего инструмента, а также вследствие
кинематической погрешности зуборезного
станка. Показателем кинематической
точности является предельная
кинематическая погрешность (рис. 16.2а).
Эта погрешность возникает при
нарезании зубчатых колёс вследствие
погрешностей взаимного расположения
заготовки обрабатываемого колеса и
режущего инструмента, а также вследствие
кинематической погрешности зуборезного
станка. Показателем кинематической
точности является предельная
кинематическая погрешность (рис. 16.2а).
Кинематическую погрешность можно оценить предельной накопленной погрешностью окружного шага , являющейся наибольшей погрешностью во взаимном расположении двух любых одноименных профилей зубьев по одной окружности колеса (рис. 16.2б).
Показателем кинематической погрешности, обозначаемым называемым колебанием длины общей нормали, т.е. размер между наибоьшей и наименьшей длинами общей нормали в одном и том же колеса (рис. 16.2в).
Норма плавности
работы зубчатого колеса определяет
составляющую
полной погрешности углов поворота
зубчатого колеса, многократно повторяющуюся
за оборот колеса (рис. 16.2г). Показателем
плавности работы колёс является циклическая
погрешность , которая представляет собой среднее
значение размаха колебаний кинематической
погрешности зубчатого колеса по всем
циклам за оборот колеса. Плавность
работы зубчатого зацепления влияет на
бесшумность и долговечность передач
(рис. 16.2д).
Плавность
работы зубчатого зацепления влияет на
бесшумность и долговечность передач
(рис. 16.2д).
Погрешность профиля характеризует расстояние расстояние по нормали между двумя теоретическими профилями зуба колеса, ограничивающими действительный профиль в пределах его рабочего участка (рис. 16.2е).
Рис. 16.2. Показатели кинематической точности зубчатой передачи
Нормы контакта зубьев определяют точность выполнения сопряжённых зубьев в передаче. Пятном контакт называется часть боковой поверхности зуба колеса, на которой располагаются следы прилегания его к зубьям парного колеса после вращения передачи при лёгком торможении (рис.16.2ж). Норма точности определяется относительными размерами пятна контакта (в процентах):
1) по длине зуба – отношением расстояния между крайними точками следов прилегания за вычетом разрывов с, превосходящих размер модуля, к полной длине В зуба (см. рис. 16.2ж):
2) по высоте зуба – отношение средней высоты пятна прилегания по всей длине зуба к рабочей высоте зуба:
Пример норм
размеров пятна контакта приведен в
табл. 16.1.
16.1.
Боковым зазором называется зазор между зубьями сопряжённых колёс в передаче , обеспечивающий свободный поворот одного из колёс при неподвиж-ном втором колесе. Боковой зазор определяется в сечении, перпендикулярном направлению зубьев, в плоскости, касательной к основным цилиндрам.
Гарантированный боковой зазор обозначается .
Для зубчатых колёс в передаче установлены шесть видов сопряжений: А, В, С, D, E, H и восемь видов допуска на боковой зазор, обозначенных в порядке
Таблица 16.1
Виды зубчатых колес, их назначение и характеристики — Студопедия
Поделись
В передачах современных машин широко используются зубчатые колёса, разнообраз-ные по форме, размерам и профилям (рис. 16.1). Наиболее распространены цилиндрические зубчатые колёса с прямыми (рис. 16.1а) и косыми (рис. 16.1б) зубьями. Соединение двух косых зубьев с противоположными углами наклона на ободе цилиндрического колеса представляет собой зубчатую передачу с шевронными (ёлочными) зубьями.
Рис. 16.1. Типы зубчатых передач
На рис. 16.1в представлена коническая передача с пересекающимися осями, причём угол встречи осей может быть любым. Конические колёса могут иметь прямые, косые и криволинейные зубья.
На рис. 16.1г представлена зубчатая передача со скрещивающимися осями, состоящая из двух зубчатых колёс с винтовыми зубьями. На рис. 16.1д пре-дставлена ещё одна схема передачи со скрещивающимися осями – червячная передача, отличающаяся от перечисленных выше тем, что один элемент передачи представляет собой винт (червяк), а другой – зубчатое колесо с фасонным зубом, сцепляющимся с витками винта.
На рис. 16.1е изображена реечная передача, одним элементом которой является зубчатое колесо с прямым или косым зубом, а другим – зубчатая рейка, которую можно представить как зубчатое колесо с бесконечно большим чи-слом зубьев. Реечная пара передаёт движение как от зубчатого колеса к рейке,
так и наоборот.
На рис. 16.1ж представлена схема волновой передачи, основанной на передаче движения за счёт бегущей волновой деформации одного из зубчатых ко-лёс. Эта передача состоит из водила 3 с двумя роликами, свободно вращающимися на осях, закреплённых в водиле, неподвижного жесткого зубчатого колеса 1 с внутренними зубьями и вращающего гибкого колеса 2 с наружными зубьями. Жёсткое зубчатое колесо соединяется с корпусом передачи. Гибкое зубчатое колесо изготавливают либо в виде стакана с тонкой легко деформирующейся стенкой, либо в виде свободно деформирующегося кольца.
16.1ж представлена схема волновой передачи, основанной на передаче движения за счёт бегущей волновой деформации одного из зубчатых ко-лёс. Эта передача состоит из водила 3 с двумя роликами, свободно вращающимися на осях, закреплённых в водиле, неподвижного жесткого зубчатого колеса 1 с внутренними зубьями и вращающего гибкого колеса 2 с наружными зубьями. Жёсткое зубчатое колесо соединяется с корпусом передачи. Гибкое зубчатое колесо изготавливают либо в виде стакана с тонкой легко деформирующейся стенкой, либо в виде свободно деформирующегося кольца.
В современных механизмах применяют зубчатые колёса с профилем зуба, очерченным эвольвентной кривой. В ряде случаев используются передачи с зацеплением Новикова, основным отличием которых является выпуклый и вогнутый круговые профили зубьев.
Действующими ГОСТами установлено 12 степеней точности цилиндрических зубчатых колёс и передач, с обозначением степеней в порядке убывания точности. За основу принята 7-я степень точности, соответствующая 7-му квалитету. Для каждой степени точности установлены нормы: кинематическая точность колеса; плавность работы колеса; контакта зубьев; бокового зазора.
Для каждой степени точности установлены нормы: кинематическая точность колеса; плавность работы колеса; контакта зубьев; бокового зазора.
Показатели кинематической точности представлены на рис. 16.2.
Нормы кинематической точности определяют значение наибольшей погрешности угла поворота зубчатого колеса за оборот при зацеплении с точным колесом. Эта погрешность возникает при нарезании зубчатых колёс вследствие погрешностей взаимного расположения заготовки обрабатываемого колеса и режущего инструмента, а также вследствие кинематической погрешности зуборезного станка. Показателем кинематической точности является предельная кинематическая погрешность (рис. 16.2а).
Кинематическую погрешность можно оценить предельной накопленной погрешностью окружного шага , являющейся наибольшей погрешностью во взаимном расположении двух любых одноименных профилей зубьев по одной окружности колеса (рис. 16.2б).
Показателем кинематической погрешности, обозначаемым называемым колебанием длины общей нормали, т. е. размер между наибоьшей и наименьшей длинами общей нормали в одном и том же колеса (рис. 16.2в).
е. размер между наибоьшей и наименьшей длинами общей нормали в одном и том же колеса (рис. 16.2в).
Норма плавности работы зубчатого колеса определяет составляющую полной погрешности углов поворота зубчатого колеса, многократно повторяющуюся за оборот колеса (рис. 16.2г). Показателем плавности работы колёс является циклическая погрешность , которая представляет собой среднее значение размаха колебаний кинематической погрешности зубчатого колеса по всем циклам за оборот колеса. Плавность работы зубчатого зацепления влияет на бесшумность и долговечность передач (рис. 16.2д).
Погрешность профиля характеризует расстояние расстояние по нормали между двумя теоретическими профилями зуба колеса, ограничивающими действительный профиль в пределах его рабочего участка (рис. 16.2е).
Рис. 16.2. Показатели кинематической точности зубчатой передачи
Нормы контакта зубьев определяют точность выполнения сопряжённых зубьев в передаче. Пятном контакт называется часть боковой поверхности зуба колеса, на которой располагаются следы прилегания его к зубьям парного колеса после вращения передачи при лёгком торможении (рис. 16.2ж). Норма точности определяется относительными размерами пятна контакта (в процентах):
16.2ж). Норма точности определяется относительными размерами пятна контакта (в процентах):
1) по длине зуба – отношением расстояния между крайними точками следов прилегания за вычетом разрывов с, превосходящих размер модуля, к полной длине В зуба (см. рис. 16.2ж):
2) по высоте зуба – отношение средней высоты пятна прилегания по всей длине зуба к рабочей высоте зуба:
Пример норм размеров пятна контакта приведен в табл. 16.1.
Боковым зазором называется зазор между зубьями сопряжённых колёс в передаче , обеспечивающий свободный поворот одного из колёс при неподвиж-ном втором колесе. Боковой зазор определяется в сечении, перпендикулярном направлению зубьев, в плоскости, касательной к основным цилиндрам.
Гарантированный боковой зазор обозначается .
Для зубчатых колёс в передаче установлены шесть видов сопряжений: А, В, С, D, E, H и восемь видов допуска на боковой зазор, обозначенных в порядке
Таблица 16.1
Нормы размера пятна контакта (%%) для цилиндрических колёс
| Способ | Степень точности | ||||||
| измерения | |||||||
| По высоте | |||||||
| По длине |
его возрастания буквами: h, d, c, b, a, z, y, x.
Для конических колёс и червячных пар установлены особые нормы точности.
Что такое модуль зубчатого колеса? Как вычислить модуль зубчатого колеса
Содержание
- История
- Модуль зубьев зубчатого колеса
- Что такое модуль зубчатого колеса
- Чему равен модуль зубчатого колеса?
- Для чего нужен модуль зубчатого колеса?
- Как определить параметры шестерни?
- Как найти модуль шестерни?
- Как найти делительный диаметр шестерни?
- Как найти модуль зуба?
- Какие бывают модули зубчатых колес?
- Цилиндрические зубчатые колёса
- Продольная линия зуба
- Прямозубые колёса
- Косозубые колёса
- Шевронные колеса
- Колёса с круговыми зубьями
- Винтовые шестерни
- Секторные колёса
- Зубчатые колёса с внешним и внутренним зацеплением
- Звездочка
- Реечная передача (кремальера)
- Коронные колёса
- Конические зубчатые колёса
- Зубчатые передачи
- Типы зубчатых передач
- Эвольвентное зацепление
- Форма зубьев
- Коррегирование зубчатого зацепления
- Зубчатые передачи с точно заданным межосевым расстоянием
- Зубчатые передачи с изменяемым межосевым расстоянием
- Расчетные формулы для зубчатых передач
- Основные параметры зубчатых цилиндрических передач
- Межосевые расстояния
- Межосевые расстояния для двухступенчатых несоосных редукторов общего назначения
- Коэффициент запаса прочности при работе зуба двумя сторонами
- Межосевые расстояния для трехступенчатых несоосных редукторов общего назначения
- Номинальные передаточные числа
- Почему шестерни часто выполняют заодно с валом?
История
Сама по себе идея механической передачи восходит к идее колеса.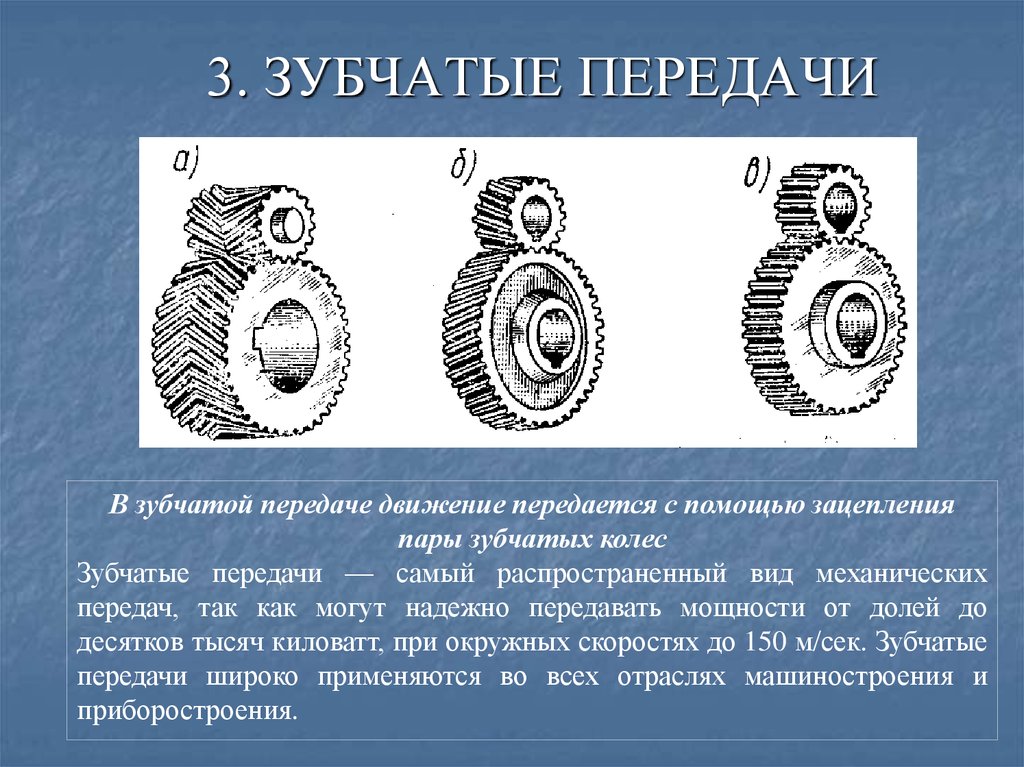 Применяя систему из двух колёс разного диаметра, можно не только передавать, но и преобразовывать движение. Если ведомым будет большее колесо, то на выходе мы потеряем в скорости, но зато крутящий момент этой передачи увеличится. Эта передача удобна там, где требуется «усилить движение», например, при подъеме тяжестей. Но сцепление между передаточными колесами с гладким ободом недостаточно жесткое, колёса проскальзывают. Поэтому вместо гладких колес начали использовать зубчатые.
Применяя систему из двух колёс разного диаметра, можно не только передавать, но и преобразовывать движение. Если ведомым будет большее колесо, то на выходе мы потеряем в скорости, но зато крутящий момент этой передачи увеличится. Эта передача удобна там, где требуется «усилить движение», например, при подъеме тяжестей. Но сцепление между передаточными колесами с гладким ободом недостаточно жесткое, колёса проскальзывают. Поэтому вместо гладких колес начали использовать зубчатые.
В Древнем Египте для орошения земель уже использовались приводимые в действие быками устройства, состоявшие из деревянной зубчатой передачи и колеса с большим числом ковшей.
Вместо зубьев первоначально использовали деревянные цилиндрические или прямоугольные пальцы, которые устанавливали по краю деревянных ободьев.
Изготовленный в I веке до н.э. Антикитерский механизм состоял из десятков металлических зубчатых колес [4] .
Модуль зубьев зубчатого колеса
Зубчатая передача впервые была освоена человеком в глубокой древности. Имя изобретателя осталось скрыто во тьме веков. Первоначально зубчатые передачи имели по шесть зубьев — отсюда и пошло название «шестерня». За многие тысячелетия технического прогресса передача многократно усовершенствовалась, и сегодня они применяются практически в любом транспортном средстве от велосипеда до космического корабля и подводной лодки. Используются они также в любом станке и механизме, больше всего шестеренок используется в механических часах.
Имя изобретателя осталось скрыто во тьме веков. Первоначально зубчатые передачи имели по шесть зубьев — отсюда и пошло название «шестерня». За многие тысячелетия технического прогресса передача многократно усовершенствовалась, и сегодня они применяются практически в любом транспортном средстве от велосипеда до космического корабля и подводной лодки. Используются они также в любом станке и механизме, больше всего шестеренок используется в механических часах.
Что такое модуль зубчатого колеса
Современные шестерни далеко ушли от своих деревянных шестизубых предков, изготавливаемых механиками с помощью воображения и мерной веревочки. Конструкция передач намного усложнилась, тысячекратно возросли скорость вращения и усилия, передаваемые через такие передачи. В связи с этим усложнились и методы их конструирования. Каждую шестеренку характеризует несколько основных параметров
- диаметр;
- число зубьев;
- шаг;
- высота зубца;
- и некоторые другие.

Одним из самых универсальных характеристик является модуль зубчатого колеса. Существует для подвида — основной и торцевой.
В большинстве расчетов используется основной. Он рассчитывается применительно к делительной окружности и служит одним из важнейших параметров.
Для расчета этого параметра применяют следующие формулы:
Параметры зубчатых колес
Модуль зубчатого колеса можно рассчитать и следующим образом:
где h — высота зубца.
где De — диаметр окружности выступов,а z — число зубьев.
Чему равен модуль зубчатого колеса?
Модуль зубчатого колеса Модуль зубчатого колеса, геометрический параметр зубчатых колёс. Для прямозубых цилиндрических зубчатых колёс модуль m равен отношению диаметра делительной окружности dд к числу зубьев z или отношению шага t по делительной окружности к числу: m = dд/z = ts/p.
Для чего нужен модуль зубчатого колеса?
Что же такое модуль шестерни? это универсальная характеристика зубчатого колеса, связывающая воедино такие его важнейшие параметры, как шаг, высота зуба, число зубов и диаметр окружности выступов. Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач.
Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач.
Как определить параметры шестерни?
Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр. Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.
Как найти модуль шестерни?
Как определить модуль косозубой шестерни.
Измеряем диаметр:
- Диаметр окружности выступов (De) равен 28,6 мм.
- Считаем количество зубьев. Z=25.
- Делительный диаметр (De) делим на количество зубьев 25 +2. Равно 28,6 разделить на 27=1,05925925925926.
- Округляем до ближнего модуля. Получается модуль 1.
Как найти делительный диаметр шестерни?
Диаметр делительной окружности d является одним из основных параметров, по которому производят расчет зубчатого колеса: d = m × z, где z – число зубьев; m – модуль.
Как найти модуль зуба?
Модуль = De/Z+2. То есть диаметр окружности выступов разделить на количество зубьев плюс 2. Измеряем диаметр: Диаметр окружности выступов (De) равен 28,6 мм.
Какие бывают модули зубчатых колес?
Модуль — это линейная величина, в π раз меньшая шага зубьев p (окружного pt, осевого рx, нормального рn и других шагов) эвольвентного зубчатого колеса m = р/π. Соответственно различают модули: окружной mt, осевой mx, нормальный mn и др.
Цилиндрические зубчатые колёса
Параметры зубчатого колесаПрофиль зубьев колёс как правило имеет эвольвентную боковую форму. Однако существуют передачи с круговой формой профиля зубьев (передача Новикова с одной и двумя линиями зацепления) и с циклоидальной. Кроме того, в храповых механизмах применяются зубчатые колёса с несимметричным профилем зуба.
Параметры эвольвентного зубчатого колеса:
- m — модуль колеса. Модулем зацепления называется линейная величина в π раз меньшая окружного шага P или отношение шага по любой концентрической окружности зубчатого колеса к π, то есть модуль — число миллиметров диаметра делительной окружности приходящееся на один зуб.
 Тёмное и светлое колёсо имеют одинаковый модуль. Самый главный параметр, стандартизирован, определяется из прочностного расчёта зубчатых передач. Чем больше нагружена передача, тем выше значение модуля. Через него выражаются все остальные параметры. Модуль измеряется в миллиметрах, вычисляется по формуле:
Тёмное и светлое колёсо имеют одинаковый модуль. Самый главный параметр, стандартизирован, определяется из прочностного расчёта зубчатых передач. Чем больше нагружена передача, тем выше значение модуля. Через него выражаются все остальные параметры. Модуль измеряется в миллиметрах, вычисляется по формуле:
- z — число зубьев колеса
- p — шаг зубьев (отмечен сиреневым цветом)
- d — диаметр делительной окружности (отмечена жёлтым цветом)
- da — диаметр окружности вершин тёмного колеса (отмечена красным цветом)
- db — диаметр основной окружности — эвольвенты (отмечена зелёным цветом)
- df — диаметр окружности впадин тёмного колеса (отмечена синим цветом)
- haP+hfP — высота зуба тёмного колеса, x+haP+hfP — высота зуба светлого колеса
Для целей стандартизации, удобства изготовления и замены зубчатых колёс в машиностроении приняты определённые значения модуля зубчатого колеса m, представляющие собой ряд из чисел на выбор: 0,05; 0,06; 0,08; 0,1; 0,12; 0,15; 0,2; 0,25; 0,3; 0,4; 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 25; 32; 40; 50; 60; 80; 100.
Зубчатые колеса могут быть изготовлены с различным смещением режущей рейки: без смещения (нулевое зубчатое колесо или «с нулевыми зубцами»), с положительным смещением (смещение в сторону увеличения материала), с отрицательным смещением (смещение в сторону уменьшения материала).
Высота головки зуба — haP и высота ножки зуба — hfP — в случае нулевого зубчатого колеса соотносятся с модулем m следующим образом: haP = m; hfP = 1,25 m, то есть:
Отсюда получаем, что высота зуба h (на рисунке не обозначена):
Вообще из рисунка ясно, что диаметр окружности вершин da больше диаметра окружности впадин df на двойную высоту зуба h. Исходя из всего этого, если требуется практически определить модуль m зубчатого колеса, не имея нужных данных для вычислений (кроме числа зубьев z), то необходимо точно измерить его наружный диаметр da и результат разделить на число зубьев z плюс 2:
Продольная линия зуба
Цилиндрические зубчатые колеса классифицируются в зависимости от формы продольной линии зуба на:
ПРЯМОЗУБЫЕ | КОСОЗУБЫЕ | ШЕВРОННЫЕ | ЗУБЬЯ НОВИКОВА |
Прямозубые колёса
Зубья расположены в радиальных плоскостях, а линия контакта зубьев обеих шестерён параллельна оси вращения. При этом оси обеих шестерён также должны располагаться строго параллельно. Прямозубые колеса имеют наименьшую стоимость, их работа имеет наивысший КПД, но, в то же время, предельный передаваемый крутящий момент таких колес ниже, чем косозубых и шевронных.
При этом оси обеих шестерён также должны располагаться строго параллельно. Прямозубые колеса имеют наименьшую стоимость, их работа имеет наивысший КПД, но, в то же время, предельный передаваемый крутящий момент таких колес ниже, чем косозубых и шевронных.
Косозубые колёса
Зубья располагаются под углом к оси вращения, а по форме образуют часть винтовой линии. Зацепление таких колёс происходит плавнее, чем у прямозубых, и с меньшим шумом. Также увеличена площадь контакта, что при тех же размерах с прямозубыми позволяет передавать больший крутящий момент. При работе косозубой пары зацепления возникает механическая осевая сила, направленная вдоль оси вращения каждого колеса и стремящаяся раздвинуть оба колеса в противоположные стороны от плоскости контакта, что обязательно требует применения упорных подшипников. Увеличенная площадь трения зубьев косозубого зацепления вызывает дополнительные потери мощности на нагрев. В целом, косозубые колёса применяются в механизмах, требующих передачи большого крутящего момента на высоких скоростях, либо имеющих жёсткие ограничения по шумности.
Шевронные колеса
Изобретение шевронного профиля зуба часто приписывают Андре Ситроену, однако на самом деле он лишь выкупил патент на более совершенную схему, которую придумал польский механик-самоучка [6] . Зубья таких колёс изготавливаются в виде буквы «V» (либо они получаются стыковкой двух косозубых колёс со встречным расположением зубьев). Шевронные колёса решают проблему осевой силы. Осевые силы обеих половин такого колеса взаимно компенсируются, поэтому отпадает необходимость в установке валов на упорные подшипники. При этом передача является самоустанавливающейся в осевом направлении, по причине чего в редукторах с шевронными колесами один из валов устанавливают на плавающих опорах (как правило — на подшипниках с короткими цилиндрическими роликами).
Колёса с круговыми зубьями
Передача на основе колёс с круговыми зубьями (Передача Новикова) имеет ещё более высокие ходовые качества, чем косозубые — высокую нагрузочную способность зацепления, высокую плавность и бесшумность работы.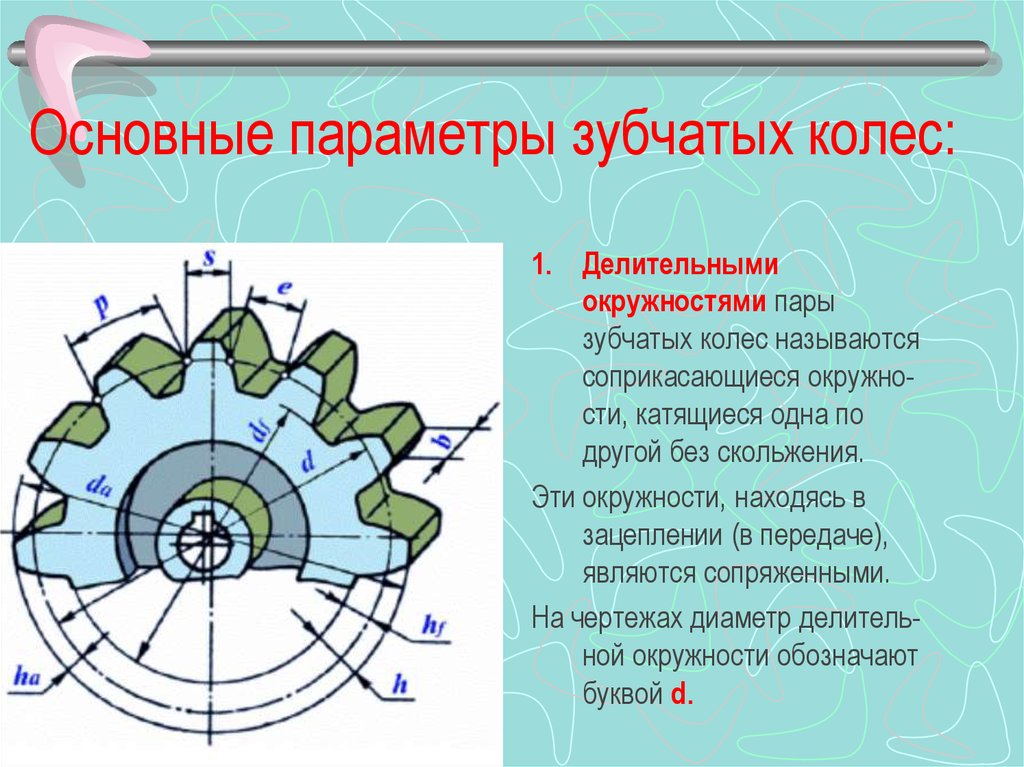 Однако они ограничены в применении сниженными, при тех же условиях, КПД и ресурсом работы, такие колёса заметно сложнее в производстве. Линия зубьев у них представляет собой окружность радиуса, подбираемого под определённые требования. Контакт поверхностей зубьев происходит в одной точке на линии зацепления, расположенной параллельно осям колёс.
Однако они ограничены в применении сниженными, при тех же условиях, КПД и ресурсом работы, такие колёса заметно сложнее в производстве. Линия зубьев у них представляет собой окружность радиуса, подбираемого под определённые требования. Контакт поверхностей зубьев происходит в одной точке на линии зацепления, расположенной параллельно осям колёс.
Винтовые шестерни
Шестерни имеют форму цилиндра с расположенными на нем зубьями по винтовой линии. Эти шестеренки используются на непересекающихся валах, которые располагаются перпендикулярно друг друга, угол между ними 90°.
Секторные колёса
Секторное колесо представляет собой часть обычного цилиндрического колеса с зубьями любого типа. Такие колёса применяются в тех случаях, когда не требуется вращение звена на полный оборот, и поэтому можно сэкономить на его габаритах.
Зубчатые колёса с внешним и внутренним зацеплением
Пара зубчатых колёс с ВНЕШНИМ зацеплением.  Передаточное число — 3 (42/14). Вращение колёс происходит противонаправлено. | Пара зубчатых колёс с ВНУТРЕННИМ зацеплением. Передаточное число — 3 (42/14). Вращение колёс происходит сонаправленно. |
Звездочка
Шестерня-звезда – это основная деталь цепной передачи, которая используется совместно с гибким элементом – цепью для передачи механической энергии.
Реечная передача (кремальера)
Реечная передача (кремальера)Реечная передача (кремальера) применяется в тех случаях, когда необходимо преобразовать вращательное движение в поступательное и обратно. Состоит из обычной прямозубой шестерни и зубчатой планки (рейки). Работа такого механизма показана на рисунке.
Зубчатая рейка представляет собой часть колеса с бесконечным радиусом делительной окружности. Поэтому делительная окружность, а также окружности вершин и впадин превращаются в параллельные прямые линии. Эвольвентный профиль рейки также принимает прямолинейное очертание. Такое свойство эвольвенты оказалось наиболее ценным при изготовлении зубчатых колёс.
Такое свойство эвольвенты оказалось наиболее ценным при изготовлении зубчатых колёс.
Также реечная передача применяется в зубчатой железной дороге.
Цевочная передачаКоронная шестерняКоронные колёса
Коронное колесо — особый вид колёс, зубья которых располагаются на боковой поверхности. Такое колесо, как правило, стыкуется с обычным прямозубым, либо с барабаном из стержней (цевочное колесо), как в башенных часах. Передачи с цевочным колесом — одни из самых ранних и просты в изготовлении, но характеризуются очень большими потерями на трение.
Конические зубчатые колёса
Главная передача в заднеприводном автомобилеВо многих машинах осуществление требуемых движений механизма связано с необходимостью передать вращение с одного вала на другой при условии, что оси этих валов пересекаются. В таких случаях применяют коническую зубчатую передачу. Различают виды конических колёс, отличающихся по форме линий зубьев: с прямыми, тангенциальными, круговыми и криволинейными зубьями. Конические колёса с круговым зубом, например, применяются в автомобильных главных передачах коробки передач.
Конические колёса с круговым зубом, например, применяются в автомобильных главных передачах коробки передач.
Зубчатые передачи
Зубчатые передачи — это механизм или часть механизма механической передачи, в состав которого входят зубчатые колёса. Зубчатые передачи служат для того, чтобы непрерывно передавать силу и крутящий момент двух валов, расположение которых определяет тип имеющейся зубчатой передачи. Вот о том, что представляют зубчатые передачи, мы и поговорим в этой статье.
Типы зубчатых передач
Эвольвентное зацепление
Все прямозубые цилиндрические передачи с одинаковым модулем зацепления могут изготавливаться на одном оборудовании, независимо от количества зубьев и размеров головки.
Модули зацепления цилиндрических и конических зубчатых колес стандартизированы по DIN 780; модули зацепления червячных передач по DIN 780; модули шлицевых соединений по DIN 5480; модули зубчатого зацепления нормального профиля для шестерен со спиральными зубьями по DIN 780.
Форма зубьев
Для прямозубых цилиндрических передач форма зубьев определяется DIN 867, DIN 58400; конических передач — DIN 3971; червячных передач — DIN 3975; шлицевых соединений — DIN 5480 (см. рис. «Прямые и косые зубья (наружное зацепление)» ).
Форма зубьев гипоидных передач регламентируется стандартом DIN 867. В дополнение к стандартным углам зацепления (20° для зубчатых передач и 30° для шлицевых соединений) применяются также и углы зацепления 12°, 14°30 15°, 17°30′| 22°30′ и 25°.
Коррегирование зубчатого зацепления
Коррегирование зубчатого зацепления (изменение высоты головки зуба (см. рис. «Коррегирование зубчатого зацепления прямозубой цилиндрической передачи (циклоидное зацепление)» ) применяется для предотвращения подрезания у шестерен с малым количеством зубьев. Оно позволяет увеличить прочность ножки зуба и точно обеспечить межосевое расстояние.
Зубчатые передачи с точно заданным межосевым расстоянием
У зубчатых пар с точно заданным межосевым расстоянием изменение высоты головки зуба для шестерни и зубчатого колеса производится на одинаковую величину, но в противоположных направлениях, что позволяет сохранить межосевое расстояние неизменным.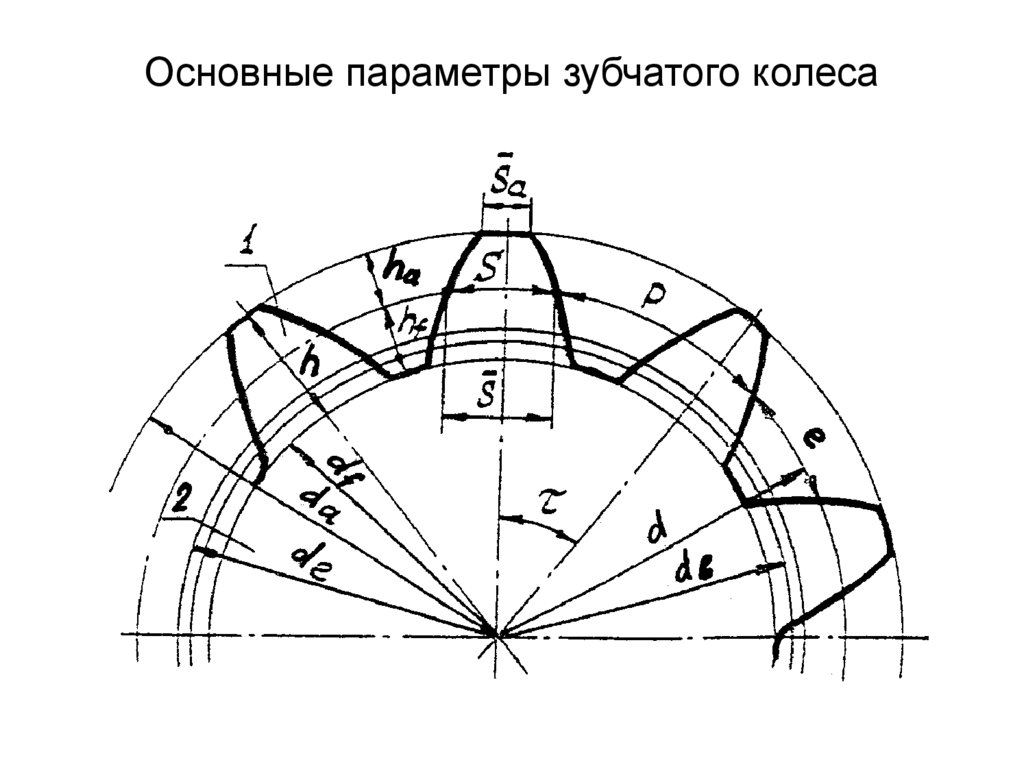 Такое решение применяется в гипоидных и косозубых передачах.
Такое решение применяется в гипоидных и косозубых передачах.
Зубчатые передачи с изменяемым межосевым расстоянием
Изменение высоты головки зуба для шестерни и зубчатого колеса производится независимо друг от друга, поэтому межосевое расстояние передачи может изменяться. Допускаемые отклонения линейных размеров зубчатых передач регламентированы. Для прямозубых цилиндрических передач — DIN 3960, DIN 58405; для конических передач — DIN 3971; червячных передач — DIN 3975.
Подставляя jη = 0 в приведенные ниже формулы, рассчитывают параметры зацепления без зазора между зубьями. Для определения зазора между зубьями допускаемые отклонения толщины зубьев и зоны их зацепления принимают в соответствии со стандартами DIN 3967 и DIN 58405 в зависимости от требуемой степени точности зубчатой передачи.
Следует отметить, что не обязательно стремиться к нулевому зазору между зубьями. Для компенсации имеющихся отклонений размеров зубьев и сборки шестерен достаточно иметь минимальный зазор, который, кроме того, предотвращает возможность заклинивания зубчатых колес.
Допускаемые отклонения других расчетных параметров (зазор между ножками двух смежных зубьев, межцентровое расстояние) приведены в стандартах DIN 3963, DIN 58405, DIN 3962 Т2, DIN 3967, DIN 3964.
Расчетные формулы для зубчатых передач
Основные параметры зубчатых цилиндрических передач
Стандарт распространяется на цилиндрические передачи внешнего зацепления для редукторов и ускорителей, в том числе и комбинированных (коническо-цилиндрических, цилиндро-червячных и др.), выполняемых в виде самостоятельных агрегатов. Стандарт не распространяется на передачи редукторов специального назначения и специальной конструкции Для встроенных передач стандарт является рекомендуемым
Межосевые расстояния
| 1 ряд | 40 | 50 | 63 | 80 | 100 | 125 | — | 160 | — | 200 | — | 250 | — | 315 | — | 400 |
| 2 ряд | — | — | — | — | — | — | 140 | — | 180 | — | 225 | — | 280 | — | 355 | — |
| 1 ряд | — | 500 | — | 630 | — | 800 | — | 1000 | — | 1250 | — | 1600 | — | 2000 | — | 2500 |
| 2 ряд | 450 | — | 560 | — | 710 | — | 900 | — | 1120 | — | 1400 | — | 1800 | — | 2240 | — |
1-й ряд следует предпочитать 2-му
Межосевые расстояния для двухступенчатых несоосных редукторов общего назначения
| Быстроходная ступень | 40 | 50 | 63 | 80 | 100 | 125 | 140 | 160 | 180 | 200 | 225 | 250 | 280 | 315 |
| Тихоходная ступень | 63 | 80 | 100 | 125 | 160 | 200 | 225 | 250 | 280 | 315 | 355 | 400 | 450 | 500 |
| Быстроходная ступень | 355 | 400 | 450 | 500 | 560 | 630 | 710 | 800 | 900 | 1000 | 1120 | 1250 | 1400 | 1600 |
| Тихоходная ступень | 560 | 630 | 710 | 800 | 900 | 1000 | 1120 | 1250 | 1400 | 1600 | 1800 | 2000 | 2240 | 2500 |
Коэффициент запаса прочности при работе зуба двумя сторонами
Например: зубья реверсивных передач или зубья сателлитов в планетарных передачах
| Материал колес и термо- обработка | Отливки стальные и чугунные без термо- обработки | Отливки стальные и чугунные с термо- обработкой | Поковки стальные нормали- зованные или улучшенные | Поковки и отливки стальные с поверх- ностной закалкой (сердцевина вязкая) | Стальные, нормали- зованные или улучшенные, а также с поверх- ностной закалкой | Стальные с объемной закалкой | Стальные, подверг- нутые цементации, азоти- рованию, циани- рованию и др. | Чугунные и пласт- массовые колеса |
| Коэфф. | 1,9 | 1,7 | 1,5 | 2,2 | 1,4 — 1,6 | 1,8 | 1,2 | 1 — 1,2 |
Межосевые расстояния для трехступенчатых несоосных редукторов общего назначения
| Быстроходная ступень | 40 | 50 | 63 | 80 | 100 | 125 | 140 | 160 | 180 | 200 |
| Промежуточная ступень | 63 | 80 | 100 | 125 | 160 | 200 | 225 | 250 | 280 | 315 |
| Тихоходная ступень | 100 | 125 | 160 | 200 | 250 | 315 | 355 | 400 | 450 | 500 |
| Быстроходная ступень | 225 | 250 | 280 | 315 | 355 | 400 | 450 | 500 | 560 | 630 |
| Промежуточная ступень | 355 | 400 | 450 | 500 | 560 | 630 | 710 | 800 | 900 | 1000 |
| Тихоходная ступень | 560 | 630 | 710 | 800 | 900 | 1000 | 1120 | 1250 | 1400 | 1600 |
Номинальные передаточные числа
| 1 ряд | 1,0 | — | 1,25 | — | 1,6 | — | 2,0 | — | 2,5 | — | 3,15 | |
| 2 ряд | — | 1,12 | — | 1,4 | — | 1,8 | — | 2,24 | — | 2,8 | — | |
| 1 ряд | — | 4,0 | — | 5,0 | — | 6,3 | — | 8,0 | — | 10 | — | 12,5 |
| 2 ряд | 3,55 | — | 4,5 | — | 5,6 | — | 7,1 | — | 9,0 | — | 11,2 | — |
1-й ряд следует предпочитать 2-му Фактические значения передаточных чисел не должны отличаться от номинальных более чем на 2,5% при номинальном меньше 4,5 и на 4% при номинальном больше 4,5
Коэффициент ширины зубчатых колес (отношение ширины зубчатого колеса к межосевому расстоянию) должен соответствовать: 0,100; 0,125; 0,160; 0,200; 0,315; 0,400; 0,500; 0,630; 0,800; 1,0; 1,25
Численные значения ширины зубчатых колес округляются до ближайшего числа из ряда Ra20 по ГОСТу 6636.
При различной ширине сопряженных зубчатых колес значение коэффициента ширины зубчатых колес относится к более узкому из них.
Почему шестерни часто выполняют заодно с валом?
Несмотря на это, в редукторах шестерню часто выполняют заодно с валом и даже при толщине, значительно превышающей указанные нормы. Это объясняется большей жесткостью и прочностью, а также технологичностью вала-шестерни, что в конечном итоге оправдывает ее стоимость.
Источники
- https://ru.wikipedia.org/wiki/%D0%97%D1%83%D0%B1%D1%87%D0%B0%D1%82%D0%BE%D0%B5_%D0%BA%D0%BE%D0%BB%D0%B5%D1%81%D0%BE
- https://doctordent.su/pulpit/kak-opredelit-modul-zuba-shesterni-po-diametru.html
- https://novoe-info.ru/chto-takoe-modul-zubchatogo-kolesa/
- https://novoe-info.ru/kak-nayti-modul-zubchatogo-kolesa/
- https://morflot.su/kak-vychislit-modul-zubchatogo-kolesa/
- https://wiki2.org/ru/%D0%97%D1%83%D0%B1%D1%87%D0%B0%D1%82%D0%BE%D0%B5_%D0%BA%D0%BE%D0%BB%D0%B5%D1%81%D0%BE
- https://nzmetallspb.
 ru/prochee/modul-zubev-zubchatogo-kolesa-raschet-standartnye-opredelenie.html
ru/prochee/modul-zubev-zubchatogo-kolesa-raschet-standartnye-opredelenie.html - https://armatool.ru/modul-zubev-zubcatogo-kolesa-rascet-standartnye-opredelenie/
Определение геометрических параметров зучатых КОЛЕС
1.1. ЦЕЛЬ И СОДЕРЖАНИЕ РАБОТЫ:
С помощью измерительного инструмента экспериментально определить основные геометрические характеристики зубчатого колеса: модуль, шаг зацепления, высотные и шаговые параметры зубьев и проверить их соответствие стандартным значениям.
1.2. ОБОРУДОВАНИЕ И ПРИБОРЫ:
1. Зубчатые колеса с разными числами зубьев;
2. Штангенциркуль с ценой деления 0,1 мм;
3. Измерительная линейка с ценой деления 1 мм;
4. Калькулятор.
1.3. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Одной из важных характеристик зубчатых колес является модуль зацепления m, через который принято выражать основные геометрические параметры зубчатой передачи.
Модуль имеет размерность в мм и определяется из условия прочности зубьев на действие контактных напряжений.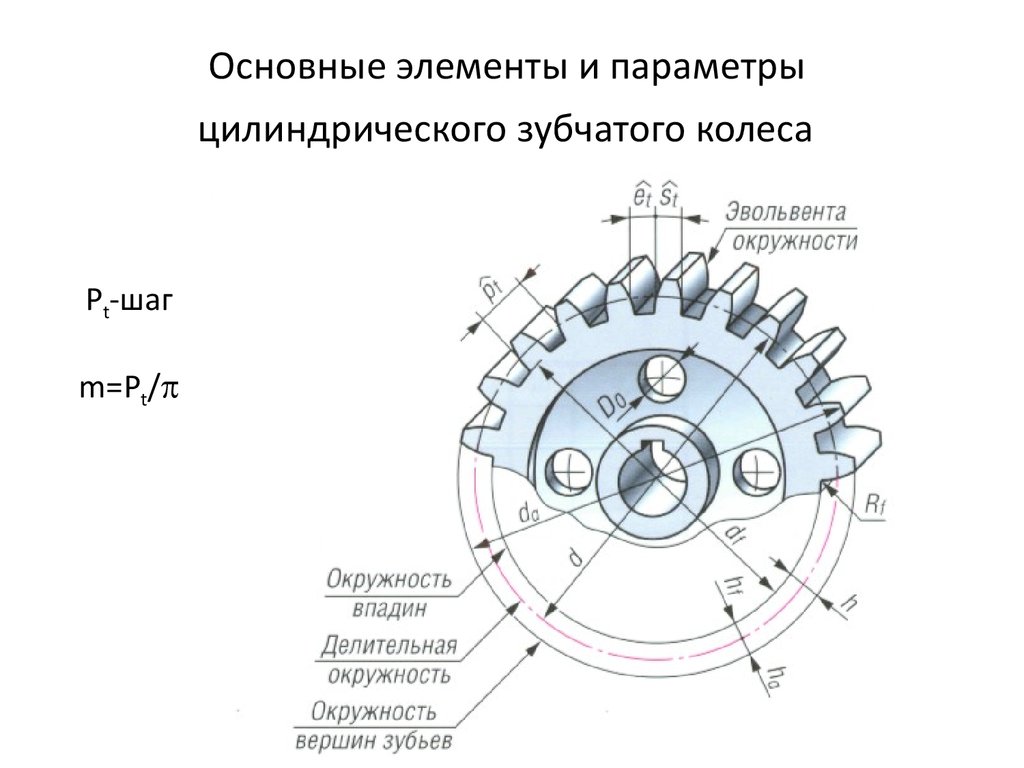 Численные значения модуля стандартизованы и выбираются по рекомендациям ГОСТ 9563 – 60 из следующего ряда:
Численные значения модуля стандартизованы и выбираются по рекомендациям ГОСТ 9563 – 60 из следующего ряда:
1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20; 25; 32.
Модулем зацепления называют часть делительного диаметра d, приходящей на один зуб:
m = d / z. (1.1)
Здесь z – число зубьев колеса, экспериментально определяется методом подсчета. Для удобства подсчета z начало отсчета удобно отметить на колесе с помощью мела. Для исключения возможных ошибок, подсчет числа зубьев рекомендуется производить не менее двух раз, один раз по часовой стрелке и второй
– против часовой стрелки.
Делительный диаметр – это диаметр d (рис.1.1) воображаемой окружности w – w, проходящей в средней части зуба, на которой ширина зуба st равна ширине впадины et.
Рис. 1.1. Геометрические элементы зубчатого колеса
При выполнении условия st = et образуется плотное (теоретическое) зацепление зубчатых колес, без образования бокового зазора между зубьями. На практике ширину впадины et выполняют несколько большей, чем ширину зуба st (в пределах
0,5…1 процентов), для образования бокового зазора между зубьями, с целью компенсации возможных погрешностей изготовления и сборки зубчатой передачи.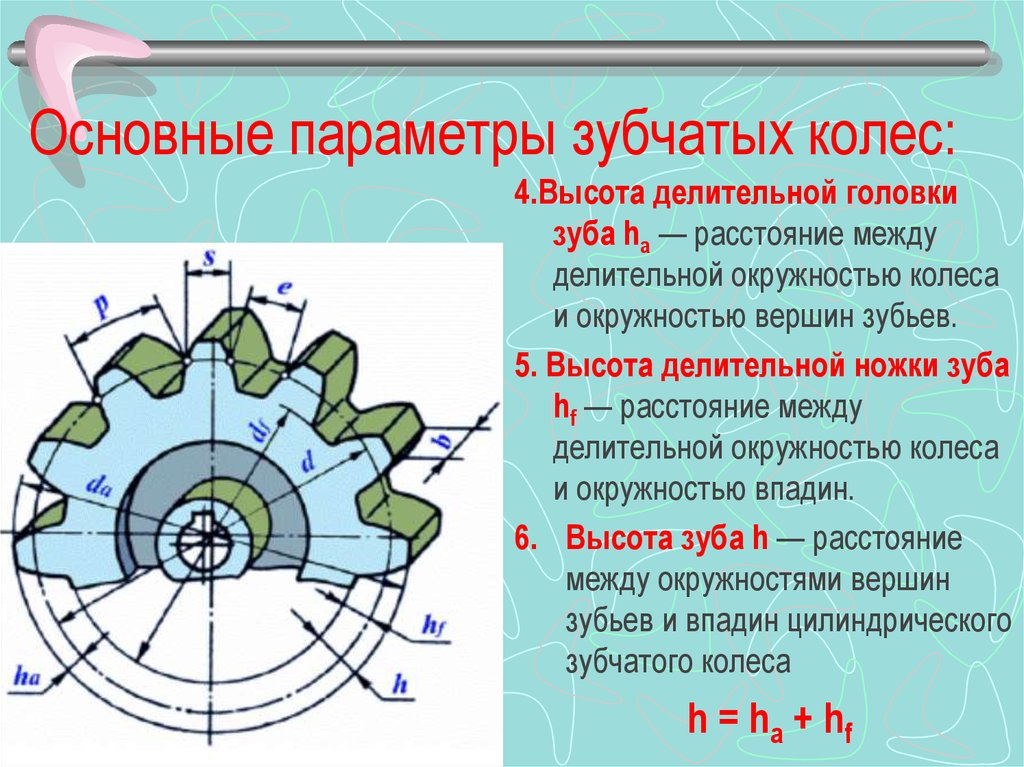
Делительный диаметр d делит зуб по высоте на две неравные части в следующих соотношениях:
– головка зуба высотой | ha = m; | (1.2) |
– ножка зуба высотой | hf = 1,25m. | (1.3) |
Полная высота нормального зуба составит:
h = ha + hf = m + 1,25m = 2,25m. (1.4) Разные высоты ножки и головки зубьев обеспечивают образование радиального зазора с между окружностями вершин и впадин зацепляющихся колес. Величину радиального зазора c
можно определить как разность высот ножки и головки зуба:
с = ∆h = hf – ha = 1,25m – m = 0,25m. (1.5)
Наличие гарантированного радиального зазора c исключает возможность заклинивания и поломки вращающихся колес в результате касания вершин зубьев одного колеса z1 с впадинами зубьев другого колеса z2, из-за возможных неточностей изготовления и сборки зубчатой передачи.
Для уменьшения габаритов и массы колес стандартом предусмотрено использование укороченных зубьев со следующими размерами: h′a = 0,8 m; h′f = m; h′ = 1,8 m; радиальный зазор при этом также уменьшается и составит: с′ = ∆h′ = h′f – h′a= m – 0,8m = 0,2m. Следует отметить, что отношение высоты головки ha к высоте ножки hf как для нормальных, так и укороченных зубьев выполняется одинаковым и составляет 1 : 1,25.
Следует отметить, что отношение высоты головки ha к высоте ножки hf как для нормальных, так и укороченных зубьев выполняется одинаковым и составляет 1 : 1,25.
Окружность вершин (выступов) – максимальная окружность a – a с диаметром da, проведенная по вершинам зубьев. Диаметр окружности вершин можно измерить с помощью штангенциркуля или линейки. С целью снижения случайных ошибок измерения, замеры диаметра da рекомендуется проводить для трех положений измерительного инструмента, приняв в качестве расчетного среднеарифметическое значение
da =
da1 + da 2 + da 3 , мм. (1.6)
3
Окружность впадин – минимальная окружность (f – f) с диаметром df, проведенная по впадинам зубьев. Диаметр df на колесе можно измерить с помощью линейки или штангенциркуля, также в трех положениях, используя в расчетах среднеарифметическое значение
d f =
d f 1 + d f 2 + d f 3 , мм. (1.7)
3
Для построения эвольвентного профиля зубьев используется основная окружность (b – b), диаметр db которой определяется по уравнению
d b = d cosα = mz cosα . (1.8)
(1.8)
Здесь α – угол зацепления, по стандарту принимается равным 20º, соответственно, в практических расчетах можно принять: cos 20º = 0,94; tg 20º = 0,364; sin 20º = 0,342.
Основная окружность b – b находится во всех случаях внутри делительной окружности w – w. Она может совпадать с окружностью впадин f – f при числе зубьев z ≈ 42 в колесах с внешними зубьями. Для колес с внутренними зубьями основная окружность b – b совпадает с окружностью выступов a – a при числе зубьев z ≈ 33.
Шаг зацепления pt – расстояние между одинаковыми элементами соседних зубьев, измеренное по делительной окружности w – w. Шаг (иногда его называют торцевым) связан с модулем зацепления по уравнению:
pt = π m. (1.9)
Для случая плотного зацепления (без бокового зазора), ширина зуба st и ширина впадины et выполняются одинаковыми, равными половине шага, т. е.:
s = e =
pt =
πm. (1.10)
t t 2 2
Непосредственное измерение шага зацепления pt с целью определение через него модуля m на колесе по уравнениям (1. 9) или (1.10) не представляется возможным, поскольку геометрическое положение делительной окружности w – w в измеряемом колесе явно не определено. На практике величину модуля находят через основной шаг pb, который, в отличие от торцевого шага зацепления pt, поддается точному экспериментальному измерению с помощью измерительного инструмента, независимо от того, нормальную или укороченную высоту имеют зубья исследуемого колеса.
9) или (1.10) не представляется возможным, поскольку геометрическое положение делительной окружности w – w в измеряемом колесе явно не определено. На практике величину модуля находят через основной шаг pb, который, в отличие от торцевого шага зацепления pt, поддается точному экспериментальному измерению с помощью измерительного инструмента, независимо от того, нормальную или укороченную высоту имеют зубья исследуемого колеса.
Основной шаг pb – это расстояние между одинаковыми элементами соседних зубьев, измеренное по основной окружности b – b. Как следует из рис. 1.1, основной шаг pb и шаг зацепления pt связаны соотношением:
pb = pt · сos α = π m · сosα . (1.11)
Отсюда получим расчетное уравнение для определения искомого модуля m:
m = pb
π cosα
. (1.12)
На практике величину основного шага pb можно определить по результатам двух замеров на колесе с помощью измерительного инструмента – штангенциркуля (рис. 1.2).
Сначала внутренними губами штангенциркуля охватывают n зубьев колеса и определяют размер l1, затем – размер l2, охватив на один зуб больше. Для точного охвата эвольвентных участков профилей, число зубьев n необходимо принять в зависимости от числа зубьев z измеряемого колеса по табл. 1.1. Например, для колеса с z = 32 следует принять n = 4.
Для точного охвата эвольвентных участков профилей, число зубьев n необходимо принять в зависимости от числа зубьев z измеряемого колеса по табл. 1.1. Например, для колеса с z = 32 следует принять n = 4.
Таблица 1.1.
Число охватываемых зубьев n для определения основного шага pb зубчатого колеса z
z | 12-18 | 19-27 | 28-36 | 37-45 | 46-54 | 55-63 | 64-72 | 73-81 |
n | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Рис. 1.2. Схема измерения основного шага pb на колесе
Замеры длин l1 и l2 следует проводить не менее трех раз, в разных местах колеса, по которым вычисляются их среднеарифметические значения и основной шаг в виде:
pb = l2 – l1 . (1. 13)
13)
Далее по полученному значению pb по уравнению (1.12)
находят искомый модуль m исследуемого колеса.
Полученное значение модуля следует сравнить со стандартным значением и сделать заключение об их соответствии (или несоответствии), с указанием возможных причин отклонения.
Модуль зацепления колеса может быть определен по результатам измерения диаметров окружностей вершин da и впадин df, а также по вычисленной через них высоте зуба h. Однако при этом должно быть известно, нормальную или укороченную высоту имеют зубья исследуемого колеса.
В случае изготовления колеса с нормальной высотой зубьев, диаметр окружности вершин (рис.1.1) получается прибавлением к делительной окружности d двух высот головок ha зубьев:
da = d + 2 ha = m z + 2 · m = m (z + 2). (1.14) Диаметр окружности впадин df, наоборот, получается вычитанием из делительной окружности d двух высот ножек hf
зубьев:
df = d – 2 hf = m z – 2 ·1,25m = m (z – 2,5).
(1.15)
Высота зуба h может быть представлена через разность диаметров da и df в виде:
h = 0,5(df – da) = 0,5(m (z + 2) – m (z – 2,5)) = 2,25 m. (1.16)
(1.16)
Отсюда для определения величины модуля m исследуемого колеса по измеренным значениям диаметров da, df и высоты h зуба, имеющего нормальную высоту, можно рекомендовать следующие расчетные уравнения:
В случае изготовления колес с укороченными зубьями, расчетные уравнения для определения модуля будут иметь вид соответственно:
1.4. ПРАКТИЧЕСКАЯ ЧАСТЬ
Задание № 1.4.1. Определение модуля через основной шаг
1. Получите у преподавателя зубчатое колесо для проведения необходимых измерений.
2. Подсчитайте число зубьев колеса z (для достоверности полученных данных подсчет проводите не менее двух раз: по часовой и против часовой стрелки). Окончательный результат занесите в таблицу П1.1.
3. По табл. 1.1 определите число охватываемых зубьев n. С помощью штангенциркуля проводите не менее трех измерений размеров l1i и l2i, по их средним значениям l1 и l2 определите основной шаг зацепления: pb = l2 – l1. Результаты замеров и расчетов занесите в таблицу П1. 1.
1.
4. По уравнению (1.12) рассчитайте модуль зацепления m. Полученный результат сравните с ближайшим стандартным значением модуля mТ по ГОСТ 9563 – 60.
5. Рассчитайте величину относительного отклонения полученного модуля от стандартного значения. (Допускаемая погрешность в инженерных расчетах ± 5 %). Сделайте заключение о соответствии (или несоответствии) с пояснением возможных причин отклонения полученного модуля от стандартного.
6. Заполните таблицу П1.1.
10
Сводная таблица для определения модуля через основной шаг
Параметры | Число зубьев колеса | Колво зубьев по таб.1.1 | Расстояние l1, мм | Расстояние l2, мм | Основной шаг | Модуль | Отклонение от стандарта | |||||||
Измеренные расстояния l1i | Ср еднее | Измеренные расстояния l2i | Ср еднее | Расчетный | Стандартный | |||||||||
Обозначения | z | n | l11 | l12 | l13 | l1 | l21 | l22 | l23 | l2 | pb | m | mТ | % |
Результаты |
Задание № 1. 4.2. Определение (проверка) модуля через диаметральные размеры колеса
4.2. Определение (проверка) модуля через диаметральные размеры колеса
1. С помощью штангенциркуля (или линейки) определите диаметр окружности вершин dai и диаметр окружности впадин dfi. Для исключения случайных ошибок опытов замеры проводите не менее трех раз на различных участках окружности вершин колеса. Определите среднеарифметические значения измеренных диаметров da и df. Результаты замеров и вычислений занесите в таблицу П1.2.
2. По средним значениям диаметров определите измеренную высоту зуба по уравнению hиз = (da – df)/2.
3. По полученным значениям средних диаметров da, df и
высоту hиз зуба, используя уравнения (1.17), (1.18) и (1.19) рассчитайте опытные значения модуля m1 , m2 , m3. По ГОСТ 9563 –
60 подберите ближайшие значения стандартизованных модулей
m1Т, m2Т, m3Т и рассчитайте величину их отклонений (в %). Результаты занесите в таблицу П1.2.
11
Сводная таблица для расчета модуля через диаметраль
|
ные размеры колеса
hиз
m m m
4. Используя полученный в таблице П1.1 стандартный модуль mТ, по уравнениям (1.14), (1.15) и (1.16) определите теоретические значения диаметров окружности вершин daТ, впадин dfТ и высоту зуба hТ, а также величину их отклонения (в %) от измеренных значений диаметров. Результаты расчетов занесите в таблицу П1.2. Обоснуйте возможные причины отклонения геометрических размеров исследованного колеса от теоретических.
Отчет по лабораторной работе должен содержать название, цель работы, заполненные таблицы П1. 1 или П1.2 с результатами замеров и проведенных вычислений (в зависимости от предложенного преподавателем задания), выводы с необходимыми пояснениями.
1 или П1.2 с результатами замеров и проведенных вычислений (в зависимости от предложенного преподавателем задания), выводы с необходимыми пояснениями.
1.5. ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Дайте определение модулю зацепления. Объясните его физический смысл.
2. С какой целью высоту ножки зуба выполняют большей,
чем высоту головки?
3. Наиболее близко от делительной окружности расположена: А – окружность вершин; В – окружность впадин; С – основная окружность.
4. На какой из перечисленных окружностей определяется шаг зацепления pt: А – на делительной; В – на основной; С – на окружности вершин; D – на окружности впадин.
5. Выберите правильное соотношение между торцевым pt
и основным шагом pb зацепления:
А) pt = pb ; В) pt < pb ; С) pt > pb.
6. Какой из вариантов соотношения ширины зуба st и ширины впадины et позволяет компенсировать ошибки изготовления и сборки зубчатой передачи: А) st = et; В) st < et; С) st > et.
7. Укажите, какие из перечисленных диаметров зубчатого
колеса можно непосредственно измерить на колесе с помощью измерительного инструмента: А – делительной окружности; В – основной окружности; С – окружности вершин; D – окружности впадин.
8. Выведите уравнения для определения диаметров вершин da и впадин df для колеса с укороченными зубьями. Определите величину отношения высоты головки к высоте ножки для укороченных зубьев и сравните его с аналогичным отношением для нормальных зубьев.
(Материал взят из книги Исследование геометрических и кинематических параметров зубчатых передач — М. А. Закиров)
Зубчатые колеса, шестерни. Виды шестерен. Цилиндрические и конические шестерни. Расчет шестерни. Модуль шестерни.
Цилиндрические шестерни
Поперечный профиль зуба
Обычно шестерни имеют профиль зубьев с эвольвентной боковой формой. Так как эвольвентное зацепление имеет ряд преимуществ перед остальными: форма этих зубьев соответствует условиям их прочности, зубья легко изготовить и обработать, шестерни не чувствительны к точности установки. Тем не менее, существуют зубчатые передачи с циклоидальной формой профиля зубьев, а так же с шестернями с круговой формой профиля зубьев, например – передача Новикова. Помимо этого, применяется несимметричный профиль зуба, например в храповых механизмах.
Помимо этого, применяется несимметричный профиль зуба, например в храповых механизмах.
Параметры эвольвентной шестерни:
Модуль шестерни (m) – это основной параметр, который определяется из прочностного расчёта зубчатых передач. Чем сильнее нагрузка на передачу, тем больше значение модуля, единица измерения модуля – миллиметры.
Расчет модуля шестерни:
d — диаметр делительной окружности
z — число зубьев шестерни
p — шаг зубьев
da — диаметр окружности вершин темной шестерни
db — диаметр основной окружности – эвольвенты
df — диаметр окружности впадин темной шестерни
haP+hfP — высота зуба темной шестерни, x+haP+hfP — высота зуба светлой шестерни
В машиностроении приняты стандартные значения модуля зубчатого колеса для удобства изготовления и замены зубчатых колёс, представляющие собой числа от 1 до 50.
Высота головки зуба – haP и высота ножки зуба – hfP в случае, так называемого, «нулевого» зубчатого колеса соотносятся с модулем m следующим образом: haP = m; hfP = 1,2 m, то есть:
Отсюда получаем, что высота зуба h = 2,2m
Так же можно практически вычислить модуль шестерни, при этом, не имея всех данных для определения модуля, по следующей формуле:
Продольная линия зуба
Прямозубые шестерни
Прямозубые шестерни – самый применяемый тип зубчатых колёс. Зубья расположены в радиальных плоскостях, линия контакта зубьев пары зубчатых колес параллельна оси вращения, как и оси обеих зубчатых колес (шестеренок) располагаются строго параллельно.
Косозубые шестерни
Косозубые шестерни – это модернизированная версия прямозубых шестерен. Зубья, в таком случае, расположены под углом к оси вращения. Зацепление зубьев этих шестерен происходит тише и плавнее, чем у прямозубых. Они применяются либо в малошумных механизмах, либо в тех которые требуют передачи большого крутящего момента на больших скоростях. К недостаткам этого типа шестерен можно отнести: увеличенную площадь соприкосновения зубьев, что вызывает значительное трение и нагрев деталей, а вследствие: потеря мощности и дополнительное использование смазочных материалов; так же механическая сила, направленная вдоль оси шестеренки, вынуждает применять упорные подшипники для установки вала.
Они применяются либо в малошумных механизмах, либо в тех которые требуют передачи большого крутящего момента на больших скоростях. К недостаткам этого типа шестерен можно отнести: увеличенную площадь соприкосновения зубьев, что вызывает значительное трение и нагрев деталей, а вследствие: потеря мощности и дополнительное использование смазочных материалов; так же механическая сила, направленная вдоль оси шестеренки, вынуждает применять упорные подшипники для установки вала.
Шевронные колёса
Шевронные шестерни решают проблему механической осевой силы, которая возникает в случае применения косозубых колес, так как зубья шевронных (елочных) колёс изготавливаются в виде буквы «V» (или же они образовываются стыковкой двух косозубых колёс со встречным расположением зубьев). Осевые механические силы обеих половин шевронной шестерни взаимно компенсируются, поэтому нет нет необходимости использования упорных подшипников для установки валов. Шевронная передача является самоустанавливающейся в осевом направлении, в следствии чего, в редукторах с шевронными колесами один из валов устанавливают на подшипниках с короткими цилиндрическими роликами – плавающих опорах.
Шестерни с внутренним зацеплением
Шестерни такого типа имеют зубья, нарезанные с внутренней стороны. При их использовании происходит одностороннее вращение ведущей и ведомой шестерен. В данной зубчатой передаче меньше затрат на трение, а значит выше КПД. Применяются зубчатые колеса с внутренним зацеплением в ограниченных по габаритам механизмах, в планетарных передачах, в шестеренных насосах, в приводе башни танка.
Винтовые шестерни
Шестерни имеют форму цилиндра с расположенными на нем зубьями по винтовой линии. Эти шестеренки используются на непересекающихся валах, которые располагаются перпендикулярно друг друга, угол между ними 90°.
Секторные шестерни
Секторная шестерня – это часть (сектор) шестерни любого типа, она позволяет сэкономить в габаритах полноценной шестерни, так как применяется в передачах, где не требуется вращение этого зубчатого колеса (шестеренки) на полный оборот.
Шестерни с круговыми зубьями
Шестерни этого типа имеют линию зубьев в виде окружности радиуса, за счет этого контакт в передаче происходит в одной точке на линии зацепления, которая располагается параллельно осям шестерен. Передачи с круговыми зубьями «Передача Новикова» имеет лучшие ходовые качества, чем косозубые – высокую плавность хода и бесшумность, высокую нагрузочную способность зацепления, но при одинаковых условиях их ресурс работы и КПД ниже, к прочему изготовление этих шестерен значительно сложнее. Поэтому применение таких шестеренок ограниченно.
Передачи с круговыми зубьями «Передача Новикова» имеет лучшие ходовые качества, чем косозубые – высокую плавность хода и бесшумность, высокую нагрузочную способность зацепления, но при одинаковых условиях их ресурс работы и КПД ниже, к прочему изготовление этих шестерен значительно сложнее. Поэтому применение таких шестеренок ограниченно.
Конические шестерни
Конические шестерни имеют различные виды, отличаются они по форме линий зубьев, с прямыми, с криволинейными, с тангенциальными, с круговыми зубьями. Применяются конические зубчатые передачи в машинах для движения механизма, где требуется передать вращение с одного вала на другой, оси которых пересекаются. Например, в автомобильных дифференциалах, для передачи момента от двигателя к колесам.
Зубчатая рейка
Зубчатая рейка является частью зубчатого колеса с бесконечным радиусом делительной окружности. Вследствие этого ее окружности представляют собой прямые параллельные линии. Эвольвентный профиль зубчатой рейки тоже имеет прямолинейное очертание. Это свойство эвольвенты является наиболее важным при изготовлении зубчатых колёс. Передачу с применением зубчатой планки (рейки) называют – реечная передача (кремальера), она используется для преобразования вращательного движения в поступательное и наоборот. Состоит передача из зубчатой рейки и прямозубого зубчатого колеса (шестеренки). Применяется такая передача в зубчатой железной дороге.
Это свойство эвольвенты является наиболее важным при изготовлении зубчатых колёс. Передачу с применением зубчатой планки (рейки) называют – реечная передача (кремальера), она используется для преобразования вращательного движения в поступательное и наоборот. Состоит передача из зубчатой рейки и прямозубого зубчатого колеса (шестеренки). Применяется такая передача в зубчатой железной дороге.
Звездочка
Шестерня-звезда – это основная деталь цепной передачи, которая используется совместно с гибким элементом – цепью для передачи механической энергии.
Коронная шестерня
Коронная шестерня – это особый тип шестерен, их зубья находятся на боковой поверхности. Такая шестерня работает, как правило, в паре с прямозубой или с барабаном (цевочное колесо), состоящим из стержней. Такая передача используется в башенных часах.
Характеристики конструкции зубчатых колес
Всего существует восемь общих зубчатых колес, различающихся по конструкции. Каждое снаряжение предназначено для конкретных сценариев и ситуаций, в зависимости от того, где оно будет вписываться в сборку продукта. Чтобы получить внутреннюю информацию о различных функциях и характеристиках конструкций зубчатых колес для каждого типа зубчатых колес, продолжайте читать ниже.
Чтобы получить внутреннюю информацию о различных функциях и характеристиках конструкций зубчатых колес для каждого типа зубчатых колес, продолжайте читать ниже.
В дополнение к характеристикам и особенностям шестерни, обсуждаемым ниже, каждое объяснение также дает представление о различных областях ее применения. Надеюсь, эта информация поможет вам определить, какое оборудование вам нужно и когда, в зависимости от проекта или продукта, над которым вы работаете.
Цилиндрическое зубчатое колесо
В целом, это очень простое в изготовлении зубчатое колесо, и оно используется чаще всего. Эта передача передает мощность и движение назад и вперед между вращающимися двумя параллельными валами. Если смотреть на фактическую конструкцию, зубья прямые и параллельны оси вала. В этом конкретном типе зубчатой передачи осевая сила отсутствует. Важно отметить, что эта передача часто используется в составе трансмиссий.
Косозубая шестерня
При сравнении косозубой шестерни с цилиндрической шестерней, описанной выше, косозубая шестерня значительно прочнее. Он не только обладает высокой прочностью, но и чрезвычайно эффективен в снижении шума, который он издает, когда он включен, а также в снижении общей вибрации. Важно отметить, что зубья этой шестерни закручены наискось к оси шестерни. Эта шестерня используется не только в качестве компонента трансмиссии, но и в автомобилях и редукторах.
Он не только обладает высокой прочностью, но и чрезвычайно эффективен в снижении шума, который он издает, когда он включен, а также в снижении общей вибрации. Важно отметить, что зубья этой шестерни закручены наискось к оси шестерни. Эта шестерня используется не только в качестве компонента трансмиссии, но и в автомобилях и редукторах.
Винтовая шестерня
Эта винтовая шестерня передает мощность с одного вала на другой. Он непараллелен и не пересекается. В целом, эту конкретную передачу можно использовать как для уменьшения, так и для увеличения скорости. Не используйте эту конкретную передачу для передачи высокой мощности. Однако его следует использовать для любого автомата, требующего замысловатого движения.
Внутреннее зубчатое колесо
Важно отметить, что это конкретное зубчатое колесо всегда входит в зацепление или идет с внешним зубчатым колесом. Без двух таких механизмов они не будут работать должным образом или даже не будут работать вообще. Эта конкретная шестерня представляет собой кольцевую шестерню, имеющую зубья на внутренней поверхности обода, и когда она входит в зацепление с внешними шестернями, она вращается в противоположных направлениях. Если посмотреть на применение этой конкретной передачи, она часто используется для сцепления.
Если посмотреть на применение этой конкретной передачи, она часто используется для сцепления.
Зубчатая рейка
Эта конкретная шестерня немного отличается от остальных. По сути, он спроектирован так, что рейка представляет собой стержень, а на этом стержне есть зубья с одной стороны, которые входят в зацепление с шестерней. Эти стойки собраны так, что они могут быть настолько длинными или короткими, насколько это необходимо. Зубчатая рейка часто используется для системы передачи или станков. Он также используется для таких продуктов, как печатный станок и роботы.
Коническая шестерня
Существует два типа конических шестерен. Первая из них представляет собой прямозубую коническую шестерню, а вторая называется спирально-конической шестерней. В обеих конструкциях зубья нарезаны по делительному конусу. Вот некоторые характеристики обоих типов конических зубчатых колес:
- Прямая коническая шестерня — эта конкретная шестерня проста в изготовлении и используется во множестве различных областей применения.
 Прямая коническая шестерня имеет прямые зубья и сходится в месте пересечения осей вала. Станки и печатные станки являются двумя наиболее распространенными сферами применения этого конкретного механизма.
Прямая коническая шестерня имеет прямые зубья и сходится в месте пересечения осей вала. Станки и печатные станки являются двумя наиболее распространенными сферами применения этого конкретного механизма. - Спиральное коническое зубчатое колесо — важно отметить, что это зубчатое колесо намного сложнее и сложнее в изготовлении, чем прямое коническое зубчатое колесо. Эта шестерня имеет изогнутые косые зубья. Он разработан таким образом, потому что он обеспечивает постепенное зацепление и большую контактную поверхность, особенно по сравнению с прямым коническим зубчатым колесом. В целом конструкция этой шестерни обеспечивает более высокую прочность и долговечность, чем прямозубая коническая шестерня. Это также позволяет повысить передаточное отношение и повысить эффективность передачи. Эта передача используется для автомобилей, тракторов, транспортных средств и подходит для привода с большой нагрузкой, а также в сценариях с высокой скоростью.
Угловая шестерня
Обратите внимание, что это другой тип конической шестерни. Это особая и уникальная коническая шестерня. Он сконструирован таким образом, что вал пересекается под углом 90 градусов, а передаточное число составляет 1:1. Эта шестерня используется для изменения направления вала шестерни, не позволяя шестерне изменять скорость. Хотя это не наиболее часто используемая коническая шестерня, она используется для конкретных и уникальных проектов и продуктов.
Это особая и уникальная коническая шестерня. Он сконструирован таким образом, что вал пересекается под углом 90 градусов, а передаточное число составляет 1:1. Эта шестерня используется для изменения направления вала шестерни, не позволяя шестерне изменять скорость. Хотя это не наиболее часто используемая коническая шестерня, она используется для конкретных и уникальных проектов и продуктов.
Червячная передача
Червячная передача — это передача, которая используется для передачи движения между двумя 9 валами.0 градусов друг от друга в одной плоскости. Эта особая конструкция обеспечивает большие передаточные числа, а также бесшумную и плавную работу во время работы. Общие области применения этой конкретной конструкции редуктора включают редукторы скорости, станки, делительные устройства, цепные блоки, портативные генераторы и многое другое.
Все эти шестерни, описанные выше, имеют разные компоненты и аспекты, которые отличают их друг от друга. Хотя многие из них имеют сходство, именно их различия позволяют им идеально подходить для конкретных задач в рамках нескольких различных типов продуктов. Надеемся, что представленная выше информация о характеристиках конструкции зубчатых колес помогла вам получить четкое или, по крайней мере, базовое представление о различных типах зубчатых колес.
Надеемся, что представленная выше информация о характеристиках конструкции зубчатых колес помогла вам получить четкое или, по крайней мере, базовое представление о различных типах зубчатых колес.
Если вы случайно ищете производителя индивидуального снаряжения, который может не только помочь вам найти именно тот тип снаряжения, который вам нужен, но и помочь вам создать это снаряжение, то вы попали в нужное место. Здесь, в Blaz-Man Gear Inc. — группе Power Transmission, мы можем помочь создать механизм для любой цели или проекта. Все, что вам нужно сделать, это позвонить или посетить наш веб-сайт сегодня, чтобы поговорить с нашими специалистами обо всех наших индивидуальных услугах.
Какие существуют типы шестерен
Шестерни — один из самых распространенных, полезных и разнообразных инструментов в машинах. Проще говоря, шестерни используются для передачи движения между отдельными компонентами. В зависимости от уникальных характеристик шестерни будут создаваться различные виды движения и крутящего момента. Шестерни зацепляются друг с другом благодаря тщательно изготовленным зубьям. Чаще всего шестерни крепятся к валу.
Шестерни зацепляются друг с другом благодаря тщательно изготовленным зубьям. Чаще всего шестерни крепятся к валу.
Поскольку шестерни являются строительными блоками движения и крутящего момента, были созданы десятки их разновидностей с уникальными преимуществами. Например, шестерни, созданные для трансмиссий, могут быть не оптимизированы для другого механизма.
Какое оборудование вам нужно для вашего проекта? Если вы не уверены, этот блог — отличное место для начала! В приведенном ниже содержании мы обсудим три характеристики, которые отличают шестерни, а затем углубимся в список типов шестерен.
Характеристики зубчатых колес
Прежде чем углубляться в разновидности зубчатых колес, важно выделить несколько важных характеристик, определяющих каждое зубчатое колесо.
Зубчатые формы
Форма зубчатых колес на первый взгляд кажется довольно очевидной. Большинство шестерен круглые, верно? Хотя это правда, шестерни могут быть самых разных форм, в том числе эллиптических и треугольных. Различные формы предназначены для уникальных целей. Например, круглые шестерни обеспечивают одинаковые передаточные числа — передаточные числа на выходе и на входе одинаковы. Если для вашего проекта требуется постоянный крутящий момент, лучшим вариантом будет круглая шестерня.
Различные формы предназначены для уникальных целей. Например, круглые шестерни обеспечивают одинаковые передаточные числа — передаточные числа на выходе и на входе одинаковы. Если для вашего проекта требуется постоянный крутящий момент, лучшим вариантом будет круглая шестерня.
С другой стороны, шестерни уникальной формы создают переменное отношение крутящего момента. В одном отраслевом ресурсе говорится: «Переменная скорость и крутящий момент позволяют некруглым зубчатым колесам выполнять специальные или неравномерные требования к движению, такие как попеременное увеличение и уменьшение выходной скорости, многоскоростное и реверсивное движение».
Форма радикально влияет на функциональность снаряжения.
Зубья шестерни
Во время использования зубья шестерни блокируются. Зубья шестерни спроектированы и изготовлены с уникальными характеристиками.
Например, некоторые шестерни имеют зубья, встроенные в корпус шестерни, а другие имеют встроенные зубья, которые при необходимости можно заменить. Кроме того, зубья шестерни могут быть добавлены внутри или снаружи корпуса шестерни. Это называется «внутренним» или «внешним» расположением зубов. Хотя одно не лучше другого, внутреннее или внешнее расположение зубьев будет влиять на движение шестерни. Наконец, профиль зубьев — или форма зубьев — будет влиять и влиять на рабочие характеристики шестерни, такие как скорость и трение. Эвольвента, трохоид и циклоида – три наиболее распространенных профиля зуба.
Кроме того, зубья шестерни могут быть добавлены внутри или снаружи корпуса шестерни. Это называется «внутренним» или «внешним» расположением зубов. Хотя одно не лучше другого, внутреннее или внешнее расположение зубьев будет влиять на движение шестерни. Наконец, профиль зубьев — или форма зубьев — будет влиять и влиять на рабочие характеристики шестерни, такие как скорость и трение. Эвольвента, трохоид и циклоида – три наиболее распространенных профиля зуба.
Помимо дизайна, можно приобрести шестерни с различным количеством зубьев и углами зубьев. Возможности настройки зубьев шестерни обширны.
Конфигурации зубчатых колес
Существует три конфигурации осей зубчатых колес: параллельная, пересекающаяся и непараллельная/непересекающаяся.
Шестерни с параллельными осями располагались параллельно друг другу, один вал вращался в направлении, противоположном другому. Шестерни с пересекающимися осями пересекаются на одном плане. Непараллельные/непересекающиеся зубчатые колеса , такие как винтовые зубчатые колеса, имеют оси, пересекающиеся в разных плоскостях. Эта конфигурация не так эффективна и быстра, как две другие.
Непараллельные/непересекающиеся зубчатые колеса , такие как винтовые зубчатые колеса, имеют оси, пересекающиеся в разных плоскостях. Эта конфигурация не так эффективна и быстра, как две другие.
Различные типы зубчатых колес
Следующий список будет рассмотрен с использованием терминологии характеристик зубчатых колес, рассмотренной выше.
Цилиндрическое зубчатое колесо
Цилиндрическое зубчатое колесо часто работает на параллельных валах. Кроме того, эта шестерня работает с одной линией контакта между зубьями, что означает, что только один зуб находится в контакте с другим в любой момент времени. Одиночный контакт делает цилиндрические шестерни более шумными, чем их аналогичные аналоги, такие как косозубая шестерня. Несмотря на это, цилиндрические зубчатые колеса являются наиболее распространенным типом зубчатых колес из-за их простоты и точности.
Косозубая шестерня
Косозубая шестерня сконструирована аналогично цилиндрическим шестерням и может использоваться для привода параллельных осей или непараллельных/непересекающихся валов. Кроме того, винтовые зубья ориентированы под углом, в результате чего несколько зубьев в любой момент времени контактируют друг с другом. Это обеспечивает более тихую и плавную работу.
Кроме того, винтовые зубья ориентированы под углом, в результате чего несколько зубьев в любой момент времени контактируют друг с другом. Это обеспечивает более тихую и плавную работу.
Коническое зубчатое колесо
Коническое зубчатое колесо работает на пересекающихся осях, особенно под углом 90 градусов. Как и косозубые шестерни, зубья конических шестерен расположены под углом, в результате чего несколько зубьев находятся в контакте одновременно. Все конические шестерни имеют коническую форму, но можно приобрести множество различных конических шестерен, в том числе: спиральные конические шестерни, прямые конические шестерни и конические шестерни с короной.
Винтовые шестерни
Винтовые шестерни напоминают конические шестерни. Однако винтовые передачи работают с углом закручивания 45 градусов на непараллельных/непересекающихся валах. Хотя винтовые передачи важны для определенных обстоятельств, они не обладают большой грузоподъемностью.
Червячная передача
Червячная передача встречается парами, часто состоящими из винтовой шестерни и круглой шестерни. Червячные передачи работают плавно и бесшумно и создают большое трение. Наконец, они используются исключительно для конфигураций с непараллельными/непересекающимися осями и идеально подходят для приложений с высокими ударными нагрузками.
Червячные передачи работают плавно и бесшумно и создают большое трение. Наконец, они используются исключительно для конфигураций с непараллельными/непересекающимися осями и идеально подходят для приложений с высокими ударными нагрузками.
Реечная передача
Реечная передача также встречается парами, состоящими из цилиндрической шестерни и зубчатой рейки. Они используются для конфигураций с параллельными осями. Из-за своей конструкции зубчатые рейки и шестерни создают высокое трение и напряжение.
Гипоидная передача
Визуально гипоидные передачи напоминают конические шестерни. В отличие от конических передач, они работают на непересекающихся валах.
Illinois Pulley & Gear: производители шкивов
Компания Illinois Pulley & Gear производит широкий ассортимент высококачественных шкивов ГРМ. Наш ассортимент изготавливается на заказ, в соответствии с точными спецификациями заказчика. Выберите материал, профиль зуба и количество зубьев, и мы изготовим заготовку.
Если вы не уверены в том, какое именно снаряжение вам нужно, мы будем рады ответить на ваши вопросы и направить вас в правильном направлении. Не стесняйтесь связаться с нашей командой экспертов по телефону 847-407-9595 или через нашу контактную форму онлайн.
Нелинейная динамическая характеристика зубчатой передачи с эксцентриситетом | Extrica
Лю Дж., Чжоу С., Ван С., «Нелинейная динамическая характеристика зубчатой передачи с эксцентриситетом», Journal of Vibroengineering , Vol. 17, № 5, стр. 2187–219.8 августа 2015 г.
- Рис
TY – ЖУР УР – https://www.extrica.com/article/15788 TI – Нелинейная динамическая характеристика зубчатой передачи с эксцентриситетом T2 – Журнал вибротехники AU – Лю, Цзе AU – Чжоу, Шихуа AU – Ван, Шицзе ПГ – 2015 ДА – 15.08.2015 ПБ – JVE International Ltd. СП – 2187-2198 ВЛ – 17 ИС – 5 СН – 1392-8716 СН – 2538-8460 ЭР –
Содержание Загрузить PDFБлагодарностиСсылки
Процитировать эту статью
Просмотров 222
Чтение 101
Загрузки 1234
22 октября 2022 г. в
Дубай, Объединенные Арабские Эмираты
в
Дубай, Объединенные Арабские Эмираты
18 ноября 2022 г. в Решица, Румыния
12-13 декабря 2022 г. в Удайпур, Индия
www.jveconferences.com
Аннотация.
В этой статье было изучено динамическое поведение системы цилиндрических зубчатых колес с внешним и внутренним динамическим стимулом. Дифференциальные уравнения вибрации цилиндрической зубчатой передачи были выражены в эквивалентных дискретных моделях массовых, демпфирующих и пружинных элементов с использованием уравнения Лагранжа, учитывающего влияние поперечно-крутильной вибрационной связи на динамику зубчатых колес, которое решалось методом Ньюмарка. Исследование проводилось с системой с несколькими степенями свободы для модели цилиндрического зубчатого колеса, которая учитывала силу тяжести, эксцентриситет зубчатого колеса, люфт, динамическую ошибку передачи и внешнее динамическое воздействие. Были проанализированы боковые и крутильные характеристики зубчатой передачи по изменению значения скорости вращения, люфта и эксцентриситета. В ходе исследования было показано, что скачкообразный скачок возникал при более низком значении люфта с увеличением скорости вращения, амплитуды частоты также увеличивались, а области непрерывной частоты становились более извилистыми, когда разница в скорости вращения была больше. Более того, сложные комбинационные частотные составляющие подчинялись правилу сначала возрастания, а затем убывания с разным люфтом и эксцентриситетом. Исследование может способствовать дальнейшему пониманию динамических характеристик такой системы зубчатый ротор-подшипник.
Более того, сложные комбинационные частотные составляющие подчинялись правилу сначала возрастания, а затем убывания с разным люфтом и эксцентриситетом. Исследование может способствовать дальнейшему пониманию динамических характеристик такой системы зубчатый ротор-подшипник.
Ключевые слова: редукторная система , связанные поперечно-крутильные колебания, эксцентриситет, нелинейная динамика.
1. Введение
Хорошо известно, что система зубчатой передачи является эффективной системой передачи мощности почти во всех машинах, которая имеет преимущества широкого диапазона мощности, высокого отношения крутящего момента к массе, высокой надежности и стационарности, высокой эффективности передачи, и точное передаточное отношение. Поэтому при производстве промышленных вращающихся машин системы зубчатых передач широко используются в различных приложениях, таких как ветряные турбины, корабли, автомобили и самолеты, и считаются одним из наиболее важных механических компонентов. Однако сложная конструкция и рабочее состояние зубчатой передачи в большей степени вызывают вибрацию и шум. Таким образом, это оказывает большое влияние на точность работы, надежность, вибрационный шум, динамические характеристики и производительность всей машины. Динамический анализ системы зубчатой передачи имеет важное значение при анализе шумовых и вибрационных характеристик. Из-за зацепления прямозубых зубчатых колес система зубчатых колес имеет другие характеристики вибрации по сравнению с упрощенной системой ротора. Одной из основных особенностей зубчатой модели является наличие связанных боковых крутильных колебаний между ведущей и ведомой шестернями. Если не учитывать связанную вибрацию, которая не только может снизить точность расчета, но и может привести к потере некоторых важных характеристик в системе передач (крутильное возбуждение возбуждает боковую реакцию, связанная вибрация вызывает новую частотную составляющую). Поэтому важно создать точную математическую модель динамических характеристик зубчатой передачи.
Однако сложная конструкция и рабочее состояние зубчатой передачи в большей степени вызывают вибрацию и шум. Таким образом, это оказывает большое влияние на точность работы, надежность, вибрационный шум, динамические характеристики и производительность всей машины. Динамический анализ системы зубчатой передачи имеет важное значение при анализе шумовых и вибрационных характеристик. Из-за зацепления прямозубых зубчатых колес система зубчатых колес имеет другие характеристики вибрации по сравнению с упрощенной системой ротора. Одной из основных особенностей зубчатой модели является наличие связанных боковых крутильных колебаний между ведущей и ведомой шестернями. Если не учитывать связанную вибрацию, которая не только может снизить точность расчета, но и может привести к потере некоторых важных характеристик в системе передач (крутильное возбуждение возбуждает боковую реакцию, связанная вибрация вызывает новую частотную составляющую). Поэтому важно создать точную математическую модель динамических характеристик зубчатой передачи.
В последние годы многие исследователи показали, что типичные динамические модели могут быть использованы для тщательного анализа динамического поведения зубчатой передачи, в которой были достигнуты некоторые замечательные достижения. Для проверки и пересмотра теоретической модели было выполнено множество экспериментальных и имитационных работ с использованием различных форм испытательных стендов и методов [1-4]. Озгувен [5] всесторонне рассмотрел математические модели и динамические явления динамики зубчатых колес, где основное внимание уделялось линейному случаю. Чен [6] разработал нелинейную динамическую модель системы пар цилиндрических зубчатых колес с учетом изменяющихся во времени жесткости зацепления и люфта, которая была решена с помощью численного метода. Статистические свойства виброперемещения и динамической силы зацепления зубчатого колеса были получены путем статистического анализа результатов моделирования. Ма [7-9] установили общую динамическую модель винтовой зубчатой пары с полной степенью свободы с учетом статической погрешности передачи и геометрических эксцентриситетов, и система была смоделирована с использованием метода конечных элементов. Хан [10, 11] исследовал динамическое поведение зубчатой роторной системы при периодических во времени движениях основания и использовал численный метод для получения поперечной и крутильной реакции зубчатой системы с ошибкой передачи, неуравновешенными массовыми возбуждениями и трещинами корня зуба. А. Кахарман и Р. Сингх [12] изучали нелинейные динамические характеристики цилиндрических зубчатых передач методом гармонического баланса. Для дальнейшего изучения нелинейных характеристик системы зубчатых передач А. Кахарман [13] вывел нелинейные динамические уравнения системы цилиндрических зубчатых колес, влияния различных параметров были изучены с помощью метода гармонического баланса и Рунге-Кутта. В связи с влиянием изменяющейся во времени жесткости зацепления А. Кахарман [14] последовательно проанализировал влияние зубчатой системы ротор-подшипник на зазор шестерни и изменяющуюся во времени жесткость зацепления, а детальный анализ перенес на зубчатую систему . Ву [15] проанализировал чисто вращательную модель составной планетарной зубчатой передачи Равиньо.
Хан [10, 11] исследовал динамическое поведение зубчатой роторной системы при периодических во времени движениях основания и использовал численный метод для получения поперечной и крутильной реакции зубчатой системы с ошибкой передачи, неуравновешенными массовыми возбуждениями и трещинами корня зуба. А. Кахарман и Р. Сингх [12] изучали нелинейные динамические характеристики цилиндрических зубчатых передач методом гармонического баланса. Для дальнейшего изучения нелинейных характеристик системы зубчатых передач А. Кахарман [13] вывел нелинейные динамические уравнения системы цилиндрических зубчатых колес, влияния различных параметров были изучены с помощью метода гармонического баланса и Рунге-Кутта. В связи с влиянием изменяющейся во времени жесткости зацепления А. Кахарман [14] последовательно проанализировал влияние зубчатой системы ротор-подшипник на зазор шестерни и изменяющуюся во времени жесткость зацепления, а детальный анализ перенес на зубчатую систему . Ву [15] проанализировал чисто вращательную модель составной планетарной зубчатой передачи Равиньо. Влияние люфта зубчатого колеса, изменяющейся во времени жесткости сетки и синтетической ошибки сетки было проанализировано путем изменения значения параметров, а степень нелинейности системы была увеличена за счет связи колебаний жесткости, ошибки сетки и люфта. Raghothama [16] исследовал периодические движения нелинейной зубчатой системы ротор-подшипник методом инкрементного гармонического баланса и использовал метод продолжения длины дуги для отслеживания бифуркационных диаграмм. Следует отметить из предшествующей литературы, что в опубликованной литературе появилось мало аналитических решений нелинейной системы зубчатых колес со скоростью вращения, эксцентриситетом зубчатого колеса и амплитудой возбуждения. Таким образом, относительно точная динамическая модель с сопряженной поперечно-крутильной вибрацией для прогнозирования вибрационных реакций необходима для оценки шума и поведения зубчатых передач, а также для определения и реализации возможных решений любой проблемы.
Влияние люфта зубчатого колеса, изменяющейся во времени жесткости сетки и синтетической ошибки сетки было проанализировано путем изменения значения параметров, а степень нелинейности системы была увеличена за счет связи колебаний жесткости, ошибки сетки и люфта. Raghothama [16] исследовал периодические движения нелинейной зубчатой системы ротор-подшипник методом инкрементного гармонического баланса и использовал метод продолжения длины дуги для отслеживания бифуркационных диаграмм. Следует отметить из предшествующей литературы, что в опубликованной литературе появилось мало аналитических решений нелинейной системы зубчатых колес со скоростью вращения, эксцентриситетом зубчатого колеса и амплитудой возбуждения. Таким образом, относительно точная динамическая модель с сопряженной поперечно-крутильной вибрацией для прогнозирования вибрационных реакций необходима для оценки шума и поведения зубчатых передач, а также для определения и реализации возможных решений любой проблемы.
Хотя в литературе было разработано много моделей цилиндрических зубчатых колес, очень немногие учитывали эксцентриситет, гравитацию и другие нелинейные факторы установленных моделей. Поэтому для точного аналитического моделирования, которое может указать отношения зацепления и подробные нелинейные характеристики, необходимо тщательное исследование при моделировании нелинейного динамического поведения зубчатой передачи. Обнаружено, что в нескольких источниках изучается влияние изменения скорости вращения, изменения эксцентриситета и изменения люфта на зубчатую передачу. В этой статье, учитывая сложную нелинейную характеристику, была предложена аналитическая модель методом сосредоточенных параметров, которая может быть использована для систематического изучения вибрационных характеристик зубчатой передачи. И настоящая работа исследовала сложное, нелинейное динамическое поведение системы, обсуждая влияние на характеристики вибрации с различными параметрами.
Поэтому для точного аналитического моделирования, которое может указать отношения зацепления и подробные нелинейные характеристики, необходимо тщательное исследование при моделировании нелинейного динамического поведения зубчатой передачи. Обнаружено, что в нескольких источниках изучается влияние изменения скорости вращения, изменения эксцентриситета и изменения люфта на зубчатую передачу. В этой статье, учитывая сложную нелинейную характеристику, была предложена аналитическая модель методом сосредоточенных параметров, которая может быть использована для систематического изучения вибрационных характеристик зубчатой передачи. И настоящая работа исследовала сложное, нелинейное динамическое поведение системы, обсуждая влияние на характеристики вибрации с различными параметрами.
2. Нелинейная модель цилиндрической зубчатой передачи
Динамическая модель цилиндрической зубчатой передачи, исследуемая в настоящем исследовании, представлена на рис. 1. Модель состоит из двух шестерен на двух валах, соединенных с нагрузкой и первичный двигатель. Связанная боковая и торсионная модель с 4 степенями свободы представляет собой сильно нелинейную систему, и валы и подшипники учитываются как соответствующие жесткость и демпфирование. Кроме того, взаимосвязь зацепления между ведущей и ведомой шестернями представлена с помощью набора жесткости сетки и постоянного зацепления демпфирующих элементов, действующих в направлении линии действия зацепления шестерни.
Связанная боковая и торсионная модель с 4 степенями свободы представляет собой сильно нелинейную систему, и валы и подшипники учитываются как соответствующие жесткость и демпфирование. Кроме того, взаимосвязь зацепления между ведущей и ведомой шестернями представлена с помощью набора жесткости сетки и постоянного зацепления демпфирующих элементов, действующих в направлении линии действия зацепления шестерни.
Согласно предыдущим геометрическим соотношениям, как показано на рис. 1, угловые перемещения φi(t) ведущей и ведомой шестерен могут быть выражены следующими уравнениями:
(1)
φ1t=ω1t+θ1t, φ2t=ω2t+θ2t,
, где ω1 и ω2 – составляющие постоянной угловой скорости ведущей и ведомой шестерен.
Соотношения между G1, G2 и O1, O2 выражаются следующим образом:
(2)
yg1=y1+ρ1sin-φ1, yg2=y2-ρ2sinφ2.
Чтобы обеспечить контакт поверхности зубьев при зацеплении, предполагается, что относительная деформация зубчатой пары полностью изменяется на упругую деформацию на поверхности зубьев вместе с направлением зацепления. Зацепляющаяся зубчатая пара связана через пружину и демпфирование. Следовательно, комплексная деформация между ведущей и ведомой шестернями вдоль направления линии зацепления выражается как:
Зацепляющаяся зубчатая пара связана через пружину и демпфирование. Следовательно, комплексная деформация между ведущей и ведомой шестернями вдоль направления линии зацепления выражается как:
(3)
δ=yg1-yg2+φ1rb1-φ2rb2-et.
Расчет и моделирование силы зацепления зубчатых колес на основе теории вязкоупругости. Таким образом, сила может быть описана как:
(4)
Fm=cmδ˙+kmfδ,
где km и cm представляют среднюю жесткость сетки и демпфирование; rb1 и rb2 — радиусы оснований косозубых колес; f(δ) — функция люфта. e(t) указывает на общие ошибки передачи.
В данной статье момент внешнего/внутреннего возбуждения Ti(t) (i=d, l) можно записать:
2.1. Вывод дифференциальных уравнений вибрации
Предполагается, что жесткость зацепления системы цилиндрических зубчатых колес является усредненной и не учитывает люфт в зацеплении, трение в зацеплении и изменение положения в зацеплении. Сила зацепления F в направлении напорной линии действует на центр ширины зуба. Дифференциальные уравнения вибрации системы цилиндрических зубчатых колес, показанные на рис. 1, могут быть получены через четыре обобщенные координаты y1, θ1, y2 и θ2. Динамическая модель цилиндрической зубчатой передачи может быть записана как:0234 = M1ρ1φ˙12sinφ1-M1ρ1θ¨12COSφ1-CMΔ˙2+CME˙t-M1G,
Сила зацепления F в направлении напорной линии действует на центр ширины зуба. Дифференциальные уравнения вибрации системы цилиндрических зубчатых колес, показанные на рис. 1, могут быть получены через четыре обобщенные координаты y1, θ1, y2 и θ2. Динамическая модель цилиндрической зубчатой передачи может быть записана как:0234 = M1ρ1φ˙12sinφ1-M1ρ1θ¨12COSφ1-CMΔ˙2+CME˙t-M1G,
J1θ¨1+Cmrb1y˙1+CT1+CMRB12d124111111111111111111111112411111111111111124111241241112411124111111111111111111111111111111111111111111111111111111111112411. m1ρ12θ¨1cos2φ1+m1ρ1y¨1cosθ1-cmrb1Δ˙2
-fmρ1cosφ1+cmrb1e˙t+td,
m2y¨2-cmy˙1-cmrb1θd1+cm+cs2y˙2+cmrb2du -m2ρ2θ¨22cosφ2+cmδ˙2-cme˙t-m2g,
J2θ¨2-cmrb2y˙1-cmrb1rb2θ˙1+cmrb2y˙2+ct2+cmrb22θ˙2+kt2θ2
=m2ρ22φ˙22sinφ2cosφ2-m2ρ22θ¨2cos2φ2+m2ρ2y ¨2cosθ2-cmrb2δ˙2
-Fmρ2cosφ2-cmrb2e˙t-Td,
где ksi и kti (i= 1, 2) — эквивалентная боковая жесткость и жесткость на кручение вала и подшипника соответственно; csi и cti (i= 1, 2) — эквивалентные боковые и крутильные демпфирования вала и подшипника.
3. Динамические характеристики зубчатой передачи с постоянной скоростью
Из предыдущих выводов и результатов видно, что зубчатая передача представляет собой сложную систему с сильной нелинейностью, отклонением во времени, опорным подшипником и сложной работой. Окружающая среда. Поэтому необходимо дать подробный анализ системы. Динамическое поведение системы исследуется методом Ньюмарка. Исходя из этого, параметры геометрии системы передачи, проанализированные в этой статье, приведены в таблице 1. В этом разделе выполняется серия численных симуляций. Цель состоит в том, чтобы изучить влияние люфта b и эксцентриситета ρ на динамическую реакцию.
Fig. 1. Dynamic model of coupled lateral-torsional vibration spur gear system
Table 1. Main parameters for the spur gear system
Case study | Driving/driven gear | Тематическое исследование | Вождение/приводная передача | ||||
Число зубов Z1/Z2 | 20 | Messhing KM | 1 Meshing KMSINGSHINCY 9000 2 | MSISHINCSING | . 0003 0003 | 5.0×10 8 N/m | |
Mass | 5 kg | Meshing damping cm | 1.2×10 3 N/(m/s) | ||||
Moment of inertia J1/J2 | 0.8 kg.m 2 | Error mean em | 2.0×10 -5 m | ||||
Radius rb1 /rb2 | 0.1 m | Error fluctuation er | 3.0×10 -5 m | ||||
Torsional stiffness kt1/kt2 | 1.0×10 7 N.m/rad | Torque mean Tdm/Tlm | 300 N/m | ||||
Torsional damping ct1/ct2 | 4.0×10 2 N/(rad/s) | Torque fluctuation Tdr /Тлр | 700 N/m | ||||
Backlash b | 3. | Module m | 8 mm | ||||
Eccentricity ρ | 2,0 × 10 -5 M | Ускорение гравитации G | 9,8 мс 2 |




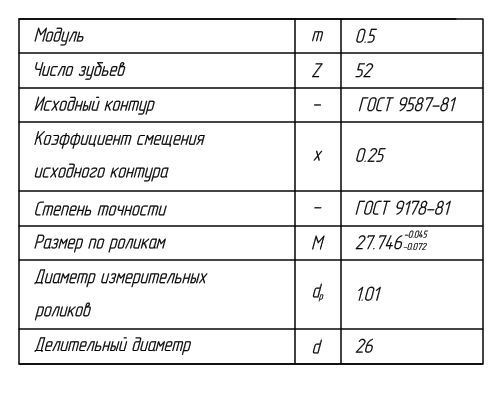 1.92. Зубчатое колесо с типовыми требованиями к точности его изготовления
1.92. Зубчатое колесо с типовыми требованиями к точности его изготовления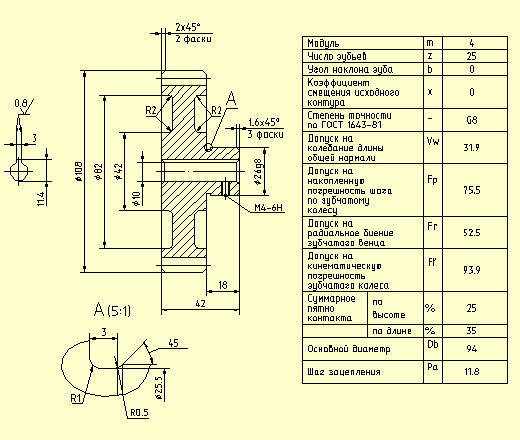
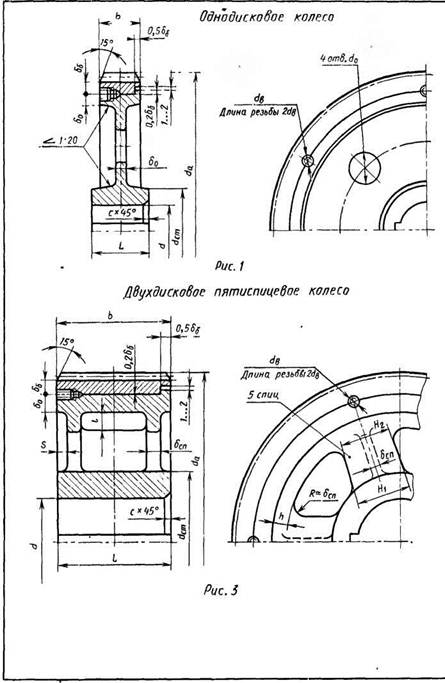 В результате термической обра-ботки поверхностная твердость зубьев цементируемых зубчатых колес должна быть в пределах HС Э45…6О при глубине слоя цементации 1…2 мм. При цианировании твердость HRСЭ42…53, глубина слоя должна быть в пределах 0,5…0,8 мм.
В результате термической обра-ботки поверхностная твердость зубьев цементируемых зубчатых колес должна быть в пределах HС Э45…6О при глубине слоя цементации 1…2 мм. При цианировании твердость HRСЭ42…53, глубина слоя должна быть в пределах 0,5…0,8 мм. su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь – 161.97.168.212 (0.005 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь – 161.97.168.212 (0.005 с.)