Износ оборудования формула: Коэффициент износа основных средств – формула расчета

alexxlab | 19.02.2023 | 0 | Разное

Формула коэффициента износа основных средств

Онлайн калькуляторы

На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник

Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение

Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!

Главная Справочник Формулы по экономике Формула коэффициента износа основных средств

Понятие коэффициента износа основных средств

В процессе учета состояния основных фондов (средств) используют различные методики начисления амортизации, для каждого из методов нужно применять специальный промежуточный коэффициент износа.

С течением времени все основные средства подвергаются износу, даже если они не эксплуатируются, а просто хранятся в бездействии. В процессе износа происходит уменьшение остаточной стоимости основного средства.

Амортизация является процессом уменьшения стоимости, когда происходит ее переносна выпущенную продукцию. Амортизация может происходить в разных темпах, зависящих от амортизационной группы, а также от периода для расчета.

Формула коэффициента износа основных средств

Формула коэффициента износа основных средств вычисляется отношением суммы амортизационных отчисленийк первоначальной стоимости основного средства.  Коэффициент износа определяется в процентном соотношении, для чего результат формулы коэффициента износа основных средств умножают на 100 %.

Общая формула коэффициента износа основных средств выглядит таким образом:

Киз. = А/ПС * 100%

Здесь К из. – коэффициент износа основного средства,

А – сумма амортизационных отчислений,

ПС – первоначальная (полная) стоимость.

Вся информация, необходимая для расчета по формуле, берется из бухгалтерской отчетности компании. В случае, если проводилась модернизация (улучшение) объекта основных средств (то есть его стоимость увеличилась), в формулу подставляется окончательный показатель, с учетом осуществленных мер.

Значение коэффициента износа

Формула коэффициента износа основных средств используется в аналитическом учете, при этом она не всегда отражает действительное состояние определенного фонда. Актив, который фактически не изношен окончательно, может обладать нулевой остаточной стоимостью.

Причиной условности коэффициента износа является его зависимость от используемого способа определения амортизационных отчислений, поэтому он характеризует лишьстепень амортизированности основных фондов, а не степень их износа.

При оценке значения коэффициента износа, проводят его сравнение с определенными данными по предприятиям аналогичной отрасли или конкурентов.

Формула коэффициента износа основных средств может вычисляться по отношению к следующим показателям:

• физическая амортизация основных фондов;
• моральное устаревание инструмента, оборудования;
• соотношение остаточной стоимости средств и их рыночных цен и др.

Норматив показателя износа

Коэффициент износа основных средств не имеет определенного норматива, утвержденного нормативными актами или законодательством. Данный показатель чаще всего рассчитывается в аналитических целях. При этом его значение все же должно определяться на каждом предприятии, и быть зафиксировано в учетных документах.

Фиксация в учетных документах позволяет определить граничное значение износа, при достижении которого степень износа можно считать достаточно большой для осуществления определенных мер (ремонт, замена основного средства).

Большая часть компаний придерживается значения коэффициента износа 50 %, что означает состояние основного средства в пределах установленных норм. Если показатель в 50 % будет превышен, это говорит о том, что необходимо принимать меры, связанные с данным объектом основного средства.

Если показатель износанаходится в пределах нормы, но приближается к 50%, необходима  дополнительная оценка состояния по каждой группе илипо всем единицам в отдельности.

Примеры решения задач

Понравился сайт? Расскажи друзьям!

Расчет коэффициента физического износа основных средств

Физический износ основных средств рассчитывается различными способами в зависимости от их типа. При этом следует отличать физический износ от морального. Подробнее об этом читайте в статье.

 

 

Физический и моральный износ основных средств

С течением времени в процессе эксплуатации основные средства (далее — ОС) изнашиваются и теряют свою стоимость. Эта потеря функционала (ухудшение физических, механических и иных свойств) у ОС, выражающаяся в снижении их стоимости, и является износом.

Износ ОС высчитывается за календарный год в целом, независимо от того, когда они были приобретены, в соответствии с существующими нормами. Когда размер износа приблизится к 100% первоначальной стоимости ОС, они считаются обесцененными и могут быть списаны. При этом начисленный стопроцентный износ по годным для эксплуатации ОС не является основанием для их списания (ликвидации).

Различают моральный и физический износ. Первый не связан с техсостоянием ОС напрямую, а зависит от появления на рынке моделей с лучшими конкурентными преимуществами. В результате появления более дешевых или технически развитых аналогов стоимость ОС снижается до момента окончания срока их службы.

Физический износ в отличие от морального указывает на то, что эксплуатируемые ОС обветшали, а их составляющие элементы износились (или как-то по-другому проявились признаки ухудшения первоначальных характеристик таких фондов).

Износ основных средств: формула

Для расчета физического износа (ФИ) используется 2 способа:

1. По объему изготовленной продукции путем сопоставления фактического и нормативного сроков службы — этот способ применим лишь в отношении техники, у которой определена производительность:

ФИ = (Фсс × ОПф) / (Нсс × ПМ),

где:

Фсс — фактический срок службы, измеряемый в годах;

ОПф — фактический объем производства продукции в год, в натуральных показателях;

Нсс — нормативный срок службы, в годах;

ПМ — установленная мощность оборудования по выпуску продукции в год, в натуральных показателях.

2. По сроку фактической службы — формула является универсальной и может применяться для различных типов ОС:

ФИ = Фсс / Нсс.

Для расчета морального износа (МИ) используется общая формула, но определение восстановительной стоимости устаревших ОС различно. Выбор одной из них обусловлен причинами возникновения старения ОС до окончания срока их службы.

Рассмотрим эти ситуации:

1. В случае появления более дешевых аналогов:

МИ = (ПСос — ВСос) / ПСос,

где:

ПСос — первоначальная стоимость ОС;

ВСос — восстановительная стоимость ОС (по балансу).

2. Если моральный износ связан с появлением более эффективных и производительных ОС, то восстановительная стоимость устаревшего оборудования (ВСус) будет определяться по формуле:

ВСус = (ВСса × ПМус) / ПМса,

где:

ВСса — восстановительная стоимость современного аналога;

ПМус — производственная мощность современного оборудования, в натуральных показателях;

ПМса — производственная мощность современного аналога.

Также советуем вам изучить аспекты расчета амортизации — об этом подробнее вы узнаете из статьи «Какой выбрать метод начисления амортизации в налоговом учете?».

Итоги

ОС, потерявшие свою стоимость вследствие износа, могут считаться устаревшими или изношенными. В отношении изношенных ОС (потерявших свои первоначальные качественные характеристики) принято говорить о физическом износе. Устаревшие (потерявшие в цене) из-за выпуска на рынок более дешевых и/или модернизированных и технически эффективных ОС подвержены моральному износу.

При расчете физического износа следует ориентироваться на срок службы и производительность ОС, при расчете морального износа важна восстановительная стоимость ОС.

О том, как управлять ОС на предприятии, вы узнаете из статьи «Правила управления внеоборотными активами предприятия».

Лаборатория трибологии Университета Лихай:

Износ материалов

Износ — это сложный процесс, происходящий при скольжении двух поверхностей друг относительно друга, что приводит к постепенному удалению одного или обоих материалов. Простой факт износа заключается в том, что он кажется неизбежным, изменяя работу механических и биологических систем и в конечном итоге приводя к отказу системы. Износ материалов становится все более важным и может иметь такое же функциональное и экономическое значение, как трение. Например, во многих промышленных приложениях компоненты изнашиваются и должны быть заменены. Эти замены могут быть дорогостоящими из-за дорогих компонентов, рабочей силы и времени простоя оборудования во время замены детали.

Исследования износа представляют как фундаментальный, так и прикладной интерес. Одно замечательное наблюдение состоит в том, что износ может различаться более чем на восемь порядков в зависимости от системы материалов. Он может варьироваться на несколько порядков для одного и того же материала просто за счет изменения окружающей среды или идентичности контрматериала, по которому материал скользит.

Инженеров-механиков обучают проектировать с учетом структурных, тепловых и даже экологических критериев отказа, поэтому неудивительно, что многие системы в достаточной степени разработаны в этих областях. Отсутствие знаний о правильном выборе материалов и проектировании трибологических компонентов в сочетании с неудовлетворительной доступностью материалов с низким износом в конечном итоге приводит к износу, вызывающему окончание срока службы и часто к катастрофическим отказам многих систем.

На самом деле, перефразируя моего консультанта, износ настолько часто является окончанием срока службы конструкции или продукта, что термин «износ» является синонимом приемлемого окончания срока службы продукта. Нынешняя глобальная тенденция к эффективности, устойчивости и стремлению к тому, чтобы конструкции были быстрее и прочнее, дольше и работали в экстремальных условиях, подтолкнула фундаментальную потребность в разработке материалов, особенно в области трибологии, что привело к возникновению подполя трибологии материалов. .

Принятая метрика для сообщения об износе материала была разработана намного позже, чем для коэффициента трения. Арчард и Холм предположили, что общий объем материала, удаляемого при скольжении (объем износа), V, пропорционален реальной площади контакта, умноженной на расстояние скольжения на безразмерную константу пропорциональности, известную как коэффициент износа, K [1].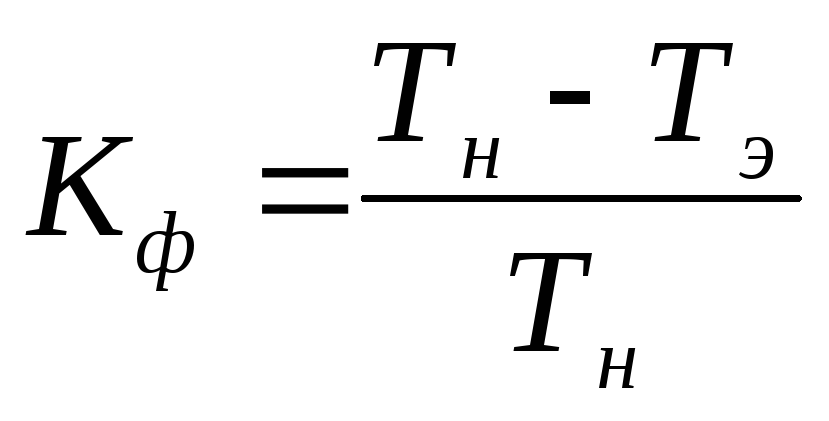

-3]. Этот коэффициент износа может быть свойством набора материалов, условий скольжения, топографии поверхности и окружающей среды, среди прочего. Коэффициентом износа можно управлять для расчета часто более удобной и физически более прямой удельной скорости износа [4] (также известной как размерная скорость износа [5]), k, обычно измеряемой в единицах мм3/Нм. Удельная скорость износа — это просто объем износа, деленный на произведение нормальной нагрузки и пути скольжения d, как показано на рисунке:

Существует множество методов измерения потери объема, используемых для расчета степени износа. Эти измерения могут быть выполнены непосредственно, или объемные потери могут быть получены на основании:

• размерных изменений материала, включая изменения высоты
• топографические измерения износа, выполненные профилометром, например:
• оптические измерения (микроскоп, РЭМ и т. д.)
• интерферометрическое измерение (интерферометр)
• щуп для профилометрии
• атомно-силовая микроскопия
• прерванные измерения массы
• предполагаемые измерения, основанные на прохождении покрытия путем наблюдения за повышенным коэффициентом трения

Используя плотность материала, можно рассчитать потерю объема по изменению массы. Скорость износа легко рассчитать по:

Schmitz et al. , Колберт и др. и Burris and Sawyer предоставляют современный анализ неопределенности для нескольких методов, используемых в этом исследовании для определения степени износа [6-8].

1. Archard, J.F., Контакт и трение плоских поверхностей. Journal of Applied Physics, 1953. 24 (8): с. 981-988.
2. Арчард Дж. Ф., Одиночные контакты и множественные встречи. Journal of Applied Physics, 1961.

32 (8): с. 1420-и.
3. Холм, Р. и Э. Холм, Справочник по электрическим контактам . 1958, Берлин: Springer.
4. Stachowiak, G.W. и А.В. Бэтчелор, Инженерная трибология . 2005, Оксфорд: Эльзевир.
5. Уильямс, Дж.А., Инженерная трибология . 1994, Оксфорд: Oxford University Press, Inc.
6. Schmitz, T.L., et al., Сложность измерения низкого трения: анализ неопределенностей для измерений коэффициента трения. Journal of Tribology-Transactions of the Asme, 2005. 127 (3): с. 673-678.
7. Беррис Д.Л. и WG Sawyer, Неопределенности измерения скорости износа. Tribology Letters, 2009. 36 (1): с. 81-87.
8. Колберт, Р.С. и WG Sawyer, Термическая зависимость износа покрытий из дисульфида молибдена. Wear, 2010.

269 (11-12): с. 719-723.

Доступные исследовательские должности бакалавриата

Возможность получить практический исследовательский опыт.

Сейчас принимаются заявки.

В Лаборатории трибологии студенты будут проводить экспериментальные исследования, посвященные межфазным взаимодействиям конденсированных сред. Это включает в себя изучение основных причин трения, износа, поверхностной деформации и адгезии на сложных поверхностях и материалах, от клеток до нанокомпозитов, в средах от космоса до километров под водой.

Активные исследования включают в себя анализ материалов, недавно возвращенных с международной космической станции, оценку износа окаменелостей зубов динозавров, разработку и патентование полимерных нанокомпозитов со сверхнизким износом, изучение и проектирование биосовместимых и биологически вдохновленных полимерных и гидрогелевых материалов, а также сотрудничество на международном уровне. по физике взаимодействия мягких веществ. Это исследование в области трибологии находится на стыке машиностроения, материаловедения и физики поверхности.

Наномеханические и трибологические свойства динозавров-гадрозаврид

Проф. Грег Сойер, Грег Эриксон и Брэндон Крик измерили наномеханические и трибологические свойства окаменелостей зубов гадрозаврид (утконосых динозавров) из Американского музея естественной истории. Используя специальные инструменты, мы измерили твердость тканей и скорость износа, которые сохранились в зубе возрастом 65 миллионов лет. Эти свойства сохраняются в окаменелых зубах, потому что содержание минералов апатита является основным фактором, определяющим твердость зубной ткани. Измеренные скорости износа тканей использовались для моделирования формирования жевательных поверхностей зубов гадрозаврид с использованием трехмерного моделирования износа. В результате моделирования профиль поверхности почти идентичен естественному износу зубной батареи гадрозаврид. Модель показала, как каждая ткань (с разной скоростью износа) способствовала формированию сложных функций нарезки и измельчения у этих рептилий за десятки миллионов лет до того, как млекопитающие развили аналогичную жевательную способность. Эта способность измерять свойства, связанные с износом, сохранившиеся в окаменелостях, открывает новый путь для изучения биомеханики на протяжении всей эволюции. См. Журнальные статьи:
Наука, 5 октября 2012 г., стр. 98-101.

Эксперименты, возвращенные с Международной космической станции

Космические трибометры и образцы, возвращенные для анализа

Материалы по экспериментам на Международной космической станции (MISSE) Космические трибометры были первыми активными трибометрами, непосредственно подвергавшимися воздействию окружающей среды на низкой околоземной орбите

Трибология Лаборатория в Университете Лихай находится в стадии строительства

Лаборатория на май 2013 г.

Лаборатория по состоянию на 3 июля 2013 г.

Основная лаборатория находится в лаборатории Lehigh’s Packard.

Другие новости

«Космическая трибология с Брэндоном Криком» Общество трибологов и инженеров-смазочников Подкаст Compass, ведущий Кара Лемар.

Расчет степени износа мелющих тел в шаровой мельнице

Содержание

• Данные по заряду шаров
• Прогноз износа шаров шаровой мельницы
• Резюме формул износа шаров
• Практическое применение теории0018

В предыдущем обсуждении был установлен факт, что работа, совершаемая мячом, когда он ударяется в конце своей параболической траектории, пропорциональна его весу и скорости; тогда, поскольку скорость можно считать постоянной для всех шаров в мельнице, работа, совершаемая шаром, пропорциональна его весу. Поскольку количество измельченной руды изменяется в зависимости от проделанной над ней работы, кажется разумным, что количество стали, изношенной шарами, изменяется в зависимости от проделанной над ними работы; другими словами, износ шарика пропорционален проделанной работе. Но было показано, что проделанная работа пропорциональна весу мяча; следовательно, износ пропорционален весу шарика, или

R = KW………………………………………..(23)

где R – скорость износа любого шарика массой W; К — постоянная величина, зависящая от условий работы мельницы и сопротивления материала, из которого изготовлены шары. Чтобы установить точность этого уравнения, необходимы некоторые преобразования.

После непрерывной и стабильной работы шаровой мельницы, скажем, в течение года, в течение которого через равные промежутки времени добавлялись шары только одного диаметра, можно предположить, что загрузка шаров достигла постоянного рабочего состояния . В этом постоянном состоянии в заряде изо дня в день не меняется ни вес заряда, ни средний диаметр составляющих его шариков. Любой конкретный шар входит в мельницу с максимальным диаметром D и постепенно изнашивается до полного износа; однако остаточный заряд шаров всегда остается одним и тем же.

Предположим, что эти шары, составляющие остаточный заряд, выложены в линию, начиная с самого большого и заканчивая самым маленьким. Предположим, что вдоль этой линии размечены интервалы так, что все шары диаметром от Dm до D1 находятся в первом интервале, от D1 до D2 — во втором интервале, от D2 до D3 — в третьем интервале и т. д. Пусть N1, N2, N3 и т. д. обозначают количество шаров в каждом интервале, а D’1, D’2, D’3 и т. д. обозначают средние диаметры шаров в соответствующих интервалах.

В постоянном состоянии количество шаров в каждом из этих интервалов не меняется, и при добавлении в первый интервал нового шара диаметром Dm во второй интервал переходит шар диаметром D1, и так далее вниз линии до тех пор, пока в последнем интервале один шар не будет полностью изношен. Затем с течением времени каждый добавленный шарик диаметра Dm постепенно проходит вдоль линии до тех пор, пока его диаметр не станет равным D1 при переходе из первого интервала во второй. Если за время T добавить Nw шаров диаметром Dm, то Nw шаров перейдут из каждого отрезка в следующий за ним отрезок. Время T, необходимое для того, чтобы любой мяч прошел через любой интервал, может быть выражено формулой

T = N’t/Nw

или время, необходимое для того, чтобы любой шар уменьшил свой диаметр с Da до Db, равно общему количеству шаров в интервале, деленному на количество шаров, добавленных в интервалы, или прохождение с интервала за это время.

Если, как предполагалось ранее, износ зависит от веса шарика, то R = KW = Kπ/6SD³, где S — вес материала, из которого изготовлены шарики, а D — диаметр шарика. обсуждаемый.

Эта формула показывает скорость износа в любой момент времени. Поскольку скорость всегда равна дифференциалу пространства по времени, то R = dw/dt, где dw — вес материала, изнашиваемого за очень небольшой интервал времени dt.

Эта формула дает общее количество шаров диаметром от Da до Db.

Скорость износа равна степени износа, деленной на требуемое время; но величина износа в любом интервале составляет 1/6πS (Da³ – Db³).

Общий вес шаров в любом интервале равен количеству шаров в интервале, умноженному на средний вес этих шаров,

Но сумма весов шаров в каждом отрезке есть вес всего заряда шара, или

– вес шаров за один интервал. Процент, масса шаров в интервале определяется по формуле средний вес шаров диаметром от Da до Db равен общему весу шаров, деленному на общее количество шаров, или

. шары в мельнице. Если шары удаляются из мельницы, когда они достигают определенного минимального диаметра D0, формула (31) принимает вид

% W’t = Da³ – Db³/Dm³ – Do³………………………………(34)

где Da и Db – верхний и нижний пределы диаметра для любого заданного интервала, Dm — диаметр шаров, загружаемых в мельницу, а Do — диаметр, ниже которого шары извлекаются из мельницы.

Следует, однако, помнить, что эти формулы (31) и (34) справедливы только при условии, что шарики изнашиваются со скоростью, пропорциональной их весу. Казалось бы, если бы процентное содержание массы, рассчитанное по формулам (31) и (34), достаточно близко согласовывалось бы с фактическими результатами, полученными путем тщательного просеивания шаровой загрузки после того, как мельница работала, то в течение достаточного периода времени, чтобы загрузка стабилизировалась. , и если бы это согласие могло быть обеспечено в ряде случаев при различных условиях, это было бы убедительным доказательством того, что износ мяча изменяется в зависимости от веса мяча.

Данные об ударах мячом

В стремлении следовать этому плану была предпринята попытка получить надежные данные, показывающие экранный анализ зарядов мяча, которые постоянно использовались в течение длительного периода. Кажется, трудно получить достоверную информацию по этому вопросу, но следующие результаты, кажется, указывают на истинность этого закона износа шариков.

Экранный анализ заряда мяча 8-фут. на 22 дюйма. (2,4 м на 55,8 см) Коническая мельница Hardinge показана в таблице 19.был изготовлен на заводе

Miami Copper Co. после того, как мельница проработала год с шаровой нагрузкой 14 800 фунтов (6713 кг), которая поддерживалась за счет добавления 400 фунтов (181 кг .) из 2-в. (50,8-мм.) стальных шариков ежедневно.

В этой таблице фактический процент веса, полученный при взвешивании мячей, сравнивается с теоретическим процентом веса, рассчитанным по формуле (30). Два столбца рисунков почти идентичны, тем самым показывая точность формулы и истинность закона износа шариков.

На заводе Golden Cycle Mining and Reduction Co. было проведено испытание на сухое дробление на 6 футов 2 дюйма на 6 футов. (1,85 х 1,8 м.) Мельница шаровая Комитер. Мельница проработала 694 часа, за это время было изготовлено 4825 фунтов (2188 кг) 5½-дюйм. Добавлены шарики диаметром 139,7 мм. Первоначальная загрузка шаров в мельнице составляла 6614 фунтов (3000 кг), а нагрузка в конце 694-часовой работы. составлял 6338 фунтов (2874,8 кг). За это время из мельницы было выброшено 590 фунтов (267,6 кг) шаров диаметром менее 3 дюймов (76,2 мм). Анализ грохота шарового заряда в конце операции показан в таблице 20.

Незначительную неравномерность в этих результатах можно объяснить тем фактом, что однажды во время испытания, примерно через 400 часов, двадцать два 5½-дюйм. шары были добавлены в одно время. Это может объяснить неровности примерно на 5 дюймов. размер.

По данным двух проведенных испытаний соответствие между фактическим процентом, весом и вычисленным процентом, весом настолько близко, насколько можно было ожидать. Один был на конической мельнице мокрого дробления, а другой на цилиндрической мельнице сухого дробления, и по имеющимся данным закон износа шаров кажется доказанным. Однако, когда будет собрано больше данных, может сложиться так, что износ будет пропорционален не кубу диаметра, а несколько большей или меньшей мощности.

Шаровая мельница Прогноз износа шаров

1. В любой мельнице скорость уменьшения веса любого шара прямо пропорциональна его весу.
2. В любой мельнице скорость уменьшения диаметра шара прямо пропорциональна его диаметру.
3. В любой мельнице скорость уменьшения поверхности любого шара пропорциональна его поверхности.
4. Поскольку скорость, с которой шар теряет вес, изменяется в зависимости от работы, совершаемой над ним в мельнице, отсюда следует, что работа, совершаемая при износе (или дроблении) шара, изменяется в зависимости от веса шара. Видно, что это закон Кика.
5. Тогда оказывается, что закон Кика верен для износа шаров во вращающейся мельнице.
6. Естественная тенденция заключается в том, что маленькие шарики накапливаются в шихте мельницы.
   
7. Поскольку эти маленькие шары очень мало дробят и исключают из мельницы руду и более крупные шары, если они накапливаются слишком долго, это приведет к заметному снижению эффективности дробления.
8. Поскольку большой шар с такой же вероятностью ударит по маленьким кускам руды, а маленький шар с такой же вероятностью поразит большие куски руды, как и наоборот, кажется, что все шары должны быть такого размера, чтобы их можно было раздавить. любая из частиц руды.
9. Это означает, что шарики должны быть максимально одного размера.
10. Так как сферы одинакового размера обеспечивают наибольшее пространство между зернами, шихта мельницы, состоящая из шаров одинакового размера, обеспечивает более свободную миграцию частиц руды, чем шихта, содержащая шары разных размеров.

Резюме формул износа шаров

Nw = количество шаров, добавленных за время T для компенсации износа шаров.
Nt = общее количество шаров в мельнице.
N’t = общее количество мячей в любом интервале.
N1, N2, N3 и т. д. = количество мячей в первом, втором, третьем и т. д. интервалах.
D = диаметр любого рассматриваемого шара.
Dm = диаметр шариков, добавленный для компенсации износа.
D’a = средний диаметр шаров в любом интервале.
Da = диаметр в начале интервала.
Db = диаметр в конце интервала.
D1, D2, D3 и т. д. = диаметр шаров в конце первого, второго, третьего и т. д. интервалов.
Вт = общий вес шаров в мельнице,
W’t = общий вес шаров в любом интервале.
w = вес любого мяча.
R = степень износа шарика.
Rt = потеря массы мельничной шихты за время T. Она равна π/6Dm³ SNw.
T = время, необходимое любому мячу для прохождения любого интервала.
S = вес материала, из которого изготовлены мячи.

Практическое применение теоретических выводов

Наконец возникает вопрос, как можно улучшить практику тонкого дробления путем применения любого из изложенных принципов. Считается, что главная польза для оператора мельницы будет заключаться в том, что он может лучше знать, что именно происходит внутри шаровой мельницы в различных условиях. Он должен иметь мысленную картину действия заряда и лучше знать, как исправить возникшие затруднения. Он также должен иметь лучшее представление о том, как действовать, чтобы получить желаемый результат.

Хотя математически, как было показано, можно рассчитать правильную скорость мельницы для любого определенного объема загрузки, размер используемых шаров должен определяться экспериментально. Размер шаров является наиболее важным фактором при дроблении, и в каждом отдельном случае требуются шары разного размера. Твердая или мягкая руда, крупная или мелкая, не влияет на правильную скорость мельницы или объем загрузки; они почти полностью зависят от размера и, возможно, в некоторой степени от характеристик мельницы. Но правильный размер шаров можно определить только при тщательном изучении существующих условий. Здесь следует прибегнуть к экспериментальным данным, и в качестве хорошего средства для определения точного размера шаров, которые следует использовать, рекомендуется следующий метод.

Загрузить мельницу большими шарами, скажем, диаметром 5 дюймов. (127 мм.) диаметр. Меньший размер может быть лучше, но следует использовать мячи, которые, как известно, слишком велики. Амперметр или ваттметр должен быть подключен к цепи приводного двигателя, чтобы оператор мог поддерживать постоянную нагрузку шариков, наблюдая за мощностью, требуемой мельницей. Для поддержания этой постоянной загрузки шаров следует добавлять только шары того же диаметра, что и те, которые уже находятся в мельнице. То есть, если тест запустить со всеми 5-в. шарики, в конце 24 час. все эти шары будут, скажем, 4¾ дюйма; шаровая нагрузка затем должна быть восстановлена ​​до ее первоначального веса путем добавления только 4¾-дюймовых шаров. Таким образом, каждый раз, когда добавляются шары, необходимо использовать другой размер.

Таким образом, мельница будет постоянно заполняться шарами приблизительно одинакового диаметра. Затем, сохраняя записи о каждом дневном пробеге, оператор сможет определить, какой именно размер дал наилучшие результаты в текущих условиях. Затем заряд шаров должен состоять из шаров такого размера, который является практичным и экономичным.

Существует два метода определения надлежащего размера шариков, которые следует добавлять в конце каждых 24 часов. Один из методов состоит в том, чтобы взять пробу заряда шара и измерить шары. В некоторых типах мельниц через разгрузочную цапфу можно ввести пробоотборник. Если это невозможно, размер шаров можно рассчитать, но через определенные промежутки времени следует получать образцы для проверки расчетов. Метод расчета размера мяча исходит непосредственно из формулы износа мяча и выглядит следующим образом:

Сначала определите износ шарика за предыдущие 24 часа. Это можно сделать путем грубой калибровки измерителя мощности в цепи двигателя, чтобы любое определенное уменьшение мощности указывало на заданное уменьшение веса заряда. Это износ мяча в фунтах в день.

Тогда в формуле износа шариков (25) T = 6,9/K Log10 Da/Db; но из (29) K = Rt/Wt. Тогда T = 6,9Wt/Rt Log10 Da/Db T — 1 день, Wt — первоначальный вес заряда шара, Rt — износ мяча за один день. Тогда Log10 Da/Db = Rt/6,9Wt все известны, и нужно решить только Db, диаметр добавляемых шаров. Если добавить только Rt фунтов этих шаров, то любая ошибка в вычислении Rt не будет накапливаться, а будет исправлена ​​на следующий день.

Описанный выше метод определения надлежащего размера шаров, конечно же, потребует тщательного внимания со стороны кого-либо, не являющегося обычным персоналом мельницы. Это также требует большого ассортимента шаров различного диаметра. В качестве компенсации за труды и расходы, необходимые для надлежащего проведения этого эксперимента, оператор имеет хороший шанс значительно увеличить производительность шаровой мельницы.

После определения надлежащего размера шаров загрузку следует поддерживать таким образом, чтобы она состояла из шаров как можно большего и меньшего размера, чем шар среднего диаметра. То, насколько точно можно поддерживать надлежащий заряд шара, зависит от оборудования и экономических условий на заводе. Удаление маленьких шариков, составляющее основную трудность, не так серьезно, как может показаться сначала; надлежащее оборудование делает это простым и недорогим. Следует надеяться, что изготовителям шаровых мельниц удастся создать мельницу, которая будет автоматически отбрасывать шары любого желаемого диаметра сразу же после их формирования.

Другим вопросом, требующим изучения, является емкость классификатора. Как уже отмечалось, большие циркуляционные нагрузки кажутся необходимыми для наибольшей эффективности. Классификация дешева по сравнению с тонким дроблением, и производительность классификации, превышающая производительность шаровой мельницы, очень желательна.

Выражается благодарность за разрешение на публикацию данных менеджерам этого Синдиката Месаби и союзникам, под чьим руководством выполнялась эта работа; Б. Б. Готтсбергеру, генеральному директору Майами Коппер Ко.