Как на чертежах обозначается диаметр: Знак диаметра, Номер в Юникоде: U+2300,в Разделе: Разнообразные технические символы 📖 узнать значение и ✂ скопировать символ (◕‿◕) SYMBL
alexxlab | 24.06.2023 | 0 | Разное
Диаметры и радиусы на чертеже – обозначение по ГОСТ, как начертить / отметить / показать знаки
Радиус – это отрезок, который соединяет центр окружности с любой точкой, которая лежит на этой окружности. Диаметр равен двум радиусам.
На чертежах радиусы используются для обозначения внутренних и наружных скруглений, криволинейных элементов.
Нанесение размеров согласно ГОСТу
Любой чертеж строится согласно определенным размерам, с учетом принятого масштаба, а также в процессе оформления все имеющие значения размеры выносятся с точностью до миллиметра. По типу все размеры делятся на линейные и угловые. К первым относятся размеры прямонаправленных участков, а ко вторым – размеры, измеряемые в градусах, секундах и минутах. Радиусы и диаметры также относятся к размерам, которые указываются на чертежах. Поэтому их оформление должно соответствовать требованиям ГОСТа.
До 2012 года на территории Российской Федерации действовал ГОСТ 2 307.608 «Нанесение размеров и предельных отклонений», который был заменен на ГОСТ 2. 307.2011. Оба документа имеют схожую структуру, но последняя версия стандарта учитывает изменения, которые произошли с начала цифровизации. Среди определений можно встретить «электронную модель изделия» и «электронный макет». Оба документа определяют правила нанесения размеров и максимальные допуски отклонений.
307.2011. Оба документа имеют схожую структуру, но последняя версия стандарта учитывает изменения, которые произошли с начала цифровизации. Среди определений можно встретить «электронную модель изделия» и «электронный макет». Оба документа определяют правила нанесения размеров и максимальные допуски отклонений.
Оба ГОСТ требуют минимального, но достаточного количества размеров. Например, один из размеров замкнутой цепочке наносится справочно, отмечается с помощью знака *.
Рисунок 1. ГОСТ 2.307.2011
Радиусы и диаметры на чертеже по ГОСТу
Традиционно, в пояснительных записках и на чертежах используется условное обозначение радиуса латинской буквой R. После этого символа идет размерное число.
Отрезок начинается от центра окружности, на конце отрезка рисуется стрелка, направленная к самой окружности.
Бывают случаи, когда значение радиуса велико и поэтому линию приближают к дуге и показывают с изломом под 90 градусов.
Также зачастую исполнителю нет необходимости показывать центр окружности, особенно если размер очень большой и составляет несколько метров, поэтому сам отрезок не доводят до центра.
Рисунок 2. Радиусы и диаметры на чертеже по ГОСТу
Как начертить радиус на чертеже
Чтобы начертить радиус на листе необходимо воспользоваться таким инструментом как циркуль. С помощью линейки циркулем отмеряют радиус, размер которого известен заранее. Устанавливают острие циркуля в центр будущей окружности и проводят сектор, часть дуги или окружность целиком в зависимости от условий задачи. Обратным действием можно найти радиус, зная где находится центр окружности. Определить диаметр можно, зная радиус круга, для этого нужно его значение увеличить в два раза. Также, зная длину контура окружности, можно вычислить радиус или диаметр через число Пи.
При построении радиуса на компьютере воспользуемся соответствующим инструментом на панели, обычно можно начертить окружность по заданному центру и значению, начертить сектор или дугу ограничив ее на плоскости. Вводя нужные значения и указав точку на плоскости, программа сама построит окружность по радиусу. Чтобы соединить отрезки с помощью радиуса используется инструмент «Сопряжение». Необходимо выбрать отрезки, а программа сама подберет нужный радиус. Эта функция очень удобна, когда необходимо соединить два элемента, располагающихся под углом, к примеру стены дома на плане или полку и стенку двутавра на чертеже.
Чтобы соединить отрезки с помощью радиуса используется инструмент «Сопряжение». Необходимо выбрать отрезки, а программа сама подберет нужный радиус. Эта функция очень удобна, когда необходимо соединить два элемента, располагающихся под углом, к примеру стены дома на плане или полку и стенку двутавра на чертеже.
Радиусы можно начертить в любой программе векторной графики, начиная от Корел Дро, заканчивая Автокадом, Ревитом, Компасом и Архикадом. Линейный размер наносится после того, как сам элемент вычерчен, через инструмент «Размеры», расположенный в основном меню. Через свойства можно изменить высоту текста, тип оформления концов отрезков, толщину и прочее.
Рисунок 3. Как начертить радиус на чертеже
Как показать несколько радиусов на чертеже
Если из одного центра проводятся несколько радиусов, то согласно принятой практике для простоты прочтения чертежа их не располагают на одной прямой, между ними должен быть угол.
Если необходимо показать несколько линий радиуса, то до центра доводят только крайние радиусы, а остальные остаются укороченными.
В ситуациях, когда применяется большое количество одинаковых радиусов скругления, наносить размеры и показывать условные обозначения не обязательно. В примечаниях указывают всю необходимую информацию, к примеру, что «радиусы скругления составляют 10 мм» или «неуказанные радиусы 7 мм».
Рисунок 4. Несколько радиусов на чертеже
Как показать радиус отверстия
На машиностроительных, строительных, сборочных чертежах зачастую приходиться изображать отверстия, к примеру, отверстия трубопроводов, имеющих внутреннюю резьбу или же болты, которые имеют наружную резьбу. В этом случае также используется радиус, который позволяет определить точный размер элемента. Малый размер может не позволить уместить всю информацию внутри изображения, поэтому все указания и полки размещают снаружи.
На одном листе показывают вид на разные плоскости проекции, на плане трубы показывается ось, на виде справа или слева, отверстие и его радиус или диаметр.
Рисунок 5. Изображение радиуса отверстия на чертеже
Изображение радиуса отверстия на чертеже
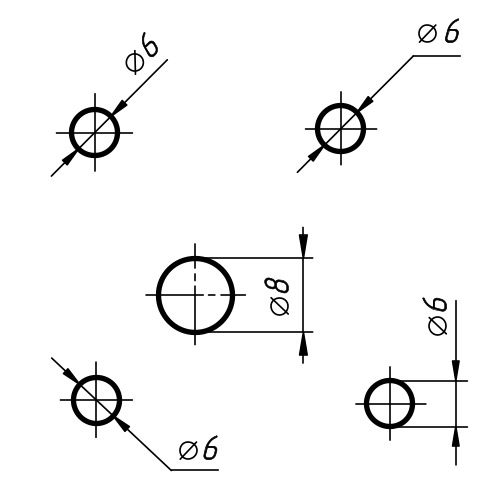
Как показать диаметр на чертеже
Диаметр на чертеже обозначается с помощью символа перечеркнутого круга, после которого следует размерное число. Если диаметр элемента меньше 12 мм, то размерное число и стрелка располагаются снаружи. Если размер элемента от 12 до 40 мм, то стрелки, располагают внутри элемента (проходят через центр окружности), а размерные числа выносят наружу. Для диаметра более 40 мм и размерные числа, и стрелки располагают внутри. Чтобы обозначит сферы перед перечёркнутой окружностью наносят еще один круг.
Рисунок 6. Как отметить диаметр на чертеже
Ответы на вопросы
В каком случае допускается не показывать радиус?
Радиус не показывают, если размер скругления в масштабе чертежа равен или менее 1 мм.
Рисунок 7. Пример обозначения радиусов на чертеже
Как можно упростить обозначение одинаковых радиусов?
Зачастую детали выполняются симметричными, и их скругления имеют одинаковые значения. В этом случае обозначается стрелка для каждого скругления, но все они имеют общую полку, на которой выполняется простановка размерного числа.
В этом случае обозначается стрелка для каждого скругления, но все они имеют общую полку, на которой выполняется простановка размерного числа.
Рисунок 8. Одинаковые радиусы
Нужно ли писать единицу измерения после обозначения радиуса?
Радиус, так же, как и ширина, толщина, длина или высота изделия относится к линейным размерам. Согласно требованиям ГОСТа, по умолчанию их наносят в миллиметрах. Соответственно других единицы измерения указывают, если размер определяется в метрах, сантиметрах, дециметрах, футах или иных единицах.
Рисунок 9. Единицы измерения радиуса
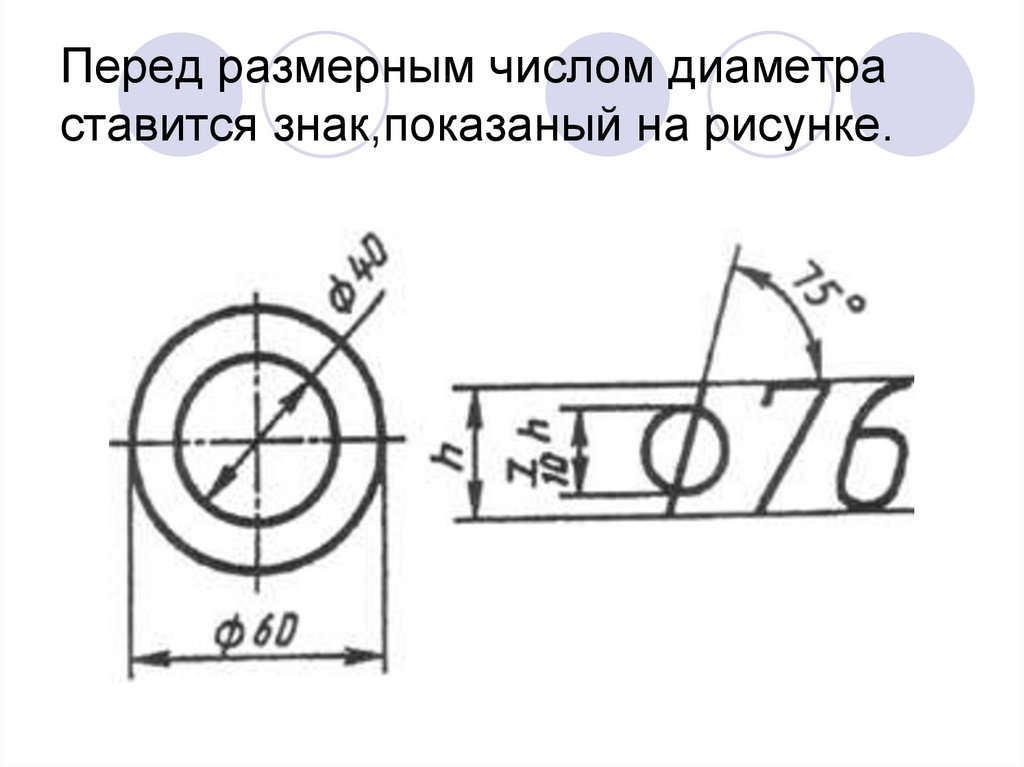
⇐ Предыдущая234567891011Следующая ⇒ На чертежах используются следующие знаки: Ø- диаметр, R – радиус, – квадрат, – уклон, – конусность. Относительные размеры знаков по отношению к цифрам показаны на рис. Диаметр. Цилиндрические поверхности обозначаются на чертежах знаком Ø, который представляет собой окружность, пересеченную прямой линией. Высота и наклон прямой линии одинаковы с высотой и наклоном цифр размерного числа, а диаметр окружности равен 5/7 высоты цифр. Наносится знак диаметра над размерной линией перед размерным числом (рис. 46, 47). Радиус. Перед размерным числом, определяющим радиус, обязательно пишется прописная латинская буква R (например, R25). Высота этой буквы и высота размерного числа должны быть одинаковыми. На Рис. 50 Рис. 51 Радиусы скругления, размер которых в масштабе чертежа 1мм и менее, на чертеже не изображают и размеры их наносят, как показано на рис. 52,а. Способ нанесения размерных чисел при различных положениях размерных линий (стрелок) на чертеже определяется наибольшим удобством чтения. а) б) Рис. 52 При проведении нескольких размерных линий радиусов из одного центра они не должны располагаться на одной прямой (рис. 53). В случае если необходимо указать центр дуги большого радиуса, допускается приближать его, выполняя размерную линию с изломом под углом 90 0 (рис. 54). При необходимости положение центра дуги задается пересечением центровых или выносных линий (рис. 55). Рис. 53 Рис. 54 Рис. 55 Квадрат. Перед размерным числом, определяющим ширину квадрата, ставят знак □, высота которого равна высоте размерных чисел. Этот знак наносят, как правило, на том изображении, на котором квадрат не проецируется в натуральном виде (рис. 56, а). Плоская грань поверхности отмечается на чертеже диагоналями, проведенными тонкими линиями. а) б) в) Рис. 56 Конусность. Перед размерным числом, определяющим конусность, ставят знак, который представляет собой равнобедренный треугольник, острый угол которого направлен в сторону вершины конуса (рис. 57).
Рис. 57 Уклон. Перед размерным числом, определяющим уклон прямой, изображающей плоскость по отношению к какому-либо направлению, принятому за основное, наносят знак,вершина которого должна быть направлена в сторону уклона (ската) (рис. 58). Рис. 58 Рис. 59 Сфера. Перед размерными числами диаметра или радиуса сферы наносятся знаки Ø или R без дополнительного знака сферы (рис. ⇐ Предыдущая234567891011Следующая ⇒
|
Принципы определения размеров | Технический проект
Алфавит линий
Какой главный образ мы используем во всех наших проектах, проектах, чертежах?Это строка !
В практике графической коммуникации существует целый набор различных линий, которые используются для рисования.
Алфавит линий представляет собой набор стандартных типов линий, установленных Американским национальным институтом стандартов (ANSI) для технического черчения. Алфавит линий и приблизительные размеры, используемые для создания различных типов линий, обозначаются как 9.0005 стилей линий при использовании с САПР.
Стандартные типы линий, используемые в технических чертежах:
Осевые линии используются:
- для представления симметрии,
- для представления путей движения,
- для обозначения центров окружностей и осей симметричных деталей, таких как цилиндры и болты.

Линии разрыва используются , чтобы показать, где объект разрывается, чтобы сэкономить место на чертеже или показать внутренние элементы.
Разрывные линии бывают двух видов:
- толстая линия от руки и
- длинная тонкая линия с зигзагами.
Размерные и выносные линии используются для обозначения размеров элементов на чертеже.
Линии сечения (штриховка) используются в разрезах для представления поверхностей объекта, разрезаемых секущей плоскостью.
Фантомные линии
Линии стежка – для обозначения процесса шитья или сшивания.
Видимые линии используются для представления объектов, которые можно увидеть в текущем виде.
Скрытые линии , как вы уже знаете, используются для представления объектов, которые не видны в текущем виде.
Линии секущих плоскостей используются на чертежах в разрезе, чтобы показать расположение секущих плоскостей.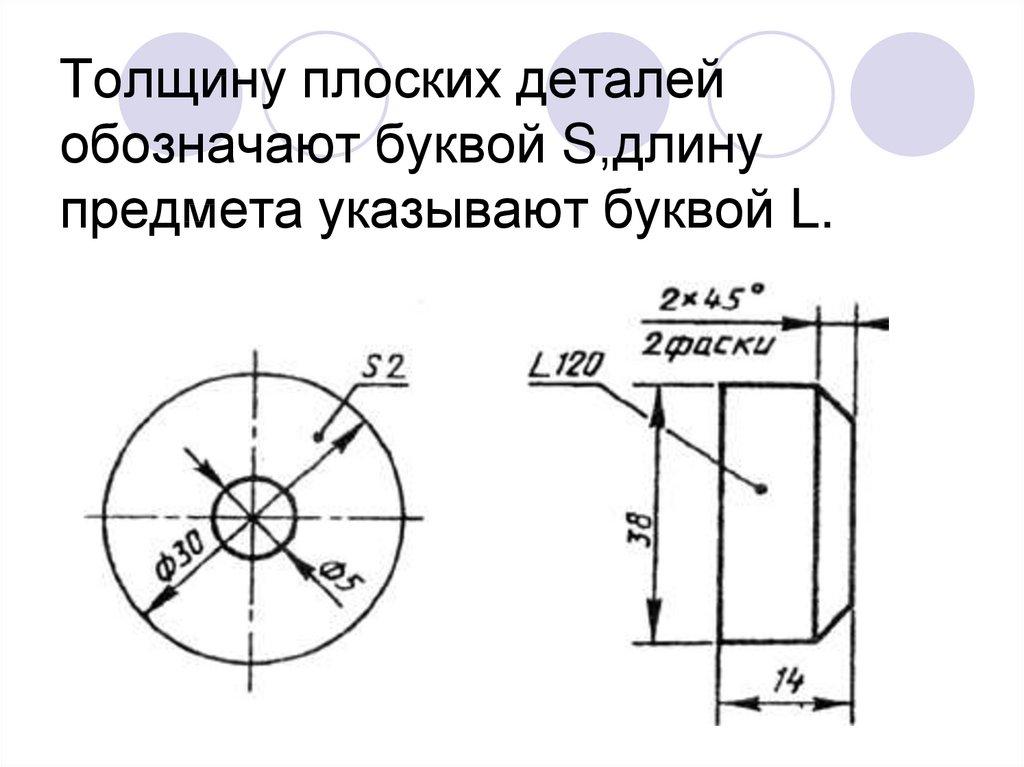
В некоторых случаях также используются строки:
Цепные линии – для обозначения дополнительной обработки поверхности.
Линии симметрии – как оси симметрии конкретного вида.
При подготовке чертежей необходимо соблюдать правила, установленные для линейной техники .
Каждая линия должна иметь одну из двух толщин, толстую или тонкую, и соотношение толщин должно быть не менее 2:1. Во многих учебниках (особенно американских авторов) вы встретите толщину линий: 0,3 мм и 0,6 мм . В общих случаях это достаточно хорошо для практической работы.
Алфавит линий определяет толщину каждой линии и не может быть произвольно изменен.
В случаях, когда , отличные от показанных типов линий , используются для специальных чертежей (например, электрических чертежей, схем трубопроводов или строительных чертежей), принятые условные обозначения должны быть четко указаны путем ссылки на конкретные стандарты или примечаниями к чертежам .
Для всех видов одной детали или сборки в одном масштабе толщина линий должна быть одинаковой. Средние и очень толстые линии следует использовать только в особых случаях.
Минимальное расстояние между параллельными линиями никогда не должно быть меньше двойной толщины самой толстой линии. Рекомендуется, чтобы эти зазоры были 0,7 мм или больше.
На видах с торца круглых элементов точка пересечения двух осевых линий должна быть показана двумя пересекающимися короткими штрихами, за исключением очень маленьких кружков, как показано:
Линии разрыва используются для сокращения вида длинных однородных или конических секций или когда необходим только частичный вид, и используются как на чертежах деталей, так и на сборочных чертежах.
Тонкая линия с зигзагами от руки рекомендуется для длинных разрывов и может использоваться для сплошных деталей или для сборок, содержащих открытое пространство.
Толстые линии от руки используются для коротких разрывов
и зубчатые линии для деревянных деталей.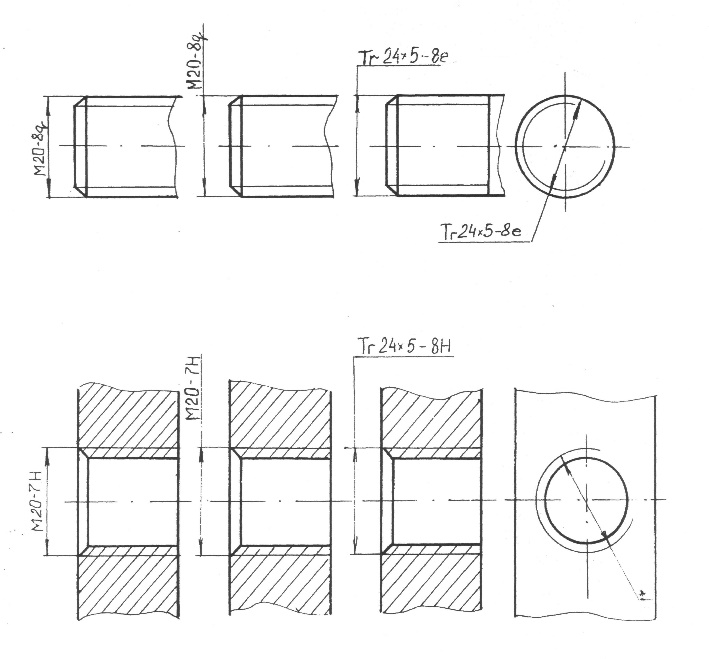
Специальные толстые линии разрыва, показанные для цилиндрических и трубчатых деталей, полезны, когда не показан вид с торца, но в других случаях достаточно толстой линии разрыва от руки.
Обратите внимание, что все эти разрывные линии были предназначены для подготовки чертежей по старинке с использованием чертежной доски. Иногда инженеры и дизайнеры до сих пор работают над чертежами карандашами и линейками. Однако современное программное обеспечение 3D CAD, которое преобладает в наши дни, может предложить другие типы линий для линий разрыва на компьютерных чертежах.
Практика нанесения размеров
После определения формы детали с помощью орфографического чертежа (т. е. в проекциях) добавляется информация о размерах в виде размеров .
Элементы размеров
Нанесение размеров на чертеж также определяет допуск (или точность), необходимый для каждого размера.
- Размер — числовое значение, определяющее размер, форму, местоположение, текстуру поверхности или геометрическую характеристику элемента.

- Базовый размер — числовое значение, определяющее теоретически точный размер, положение или ориентацию относительно системы координат. Основные размеры заключены в прямоугольную рамку и не имеют допусков.
- Справочный размер — числовое значение, заключенное в круглые скобки, предназначено только для информации.
- Размерная линия — тонкая сплошная линия, показывающая протяженность и направление размера.
- Стрелки — символы на концах размерных линий, показывающие пределы размерных линий, выноски и линии секущей плоскости.
- Выносная линия — тонкая сплошная линия, перпендикулярная размерной линии, указывающая, какой элемент связан с размером.
- Видимый зазор — между углами элемента и концом выносной линии должен быть видимый зазор 1 мм.
- Линия выноски — тонкая сплошная линия со стрелкой, проведенной под углом и указывающая элемент, с которым связан размер или примечание.

- Пределы размера — максимально допустимый размер и минимально допустимый размер объекта.
- Плюс и минус измерение — допустимое положительное и отрицательное отклонение от указанного измерения.
- Символ диаметра — символ, указывающий, что размер показывает диаметр окружности. Используемый символ — греческая буква фи Ø.
- Символ радиуса — символ, указывающий, что размер показывает радиус окружности. Используемый символ радиуса — заглавная буква R.
- Допуск — величина, на которую может отличаться конкретный размер.
Основные концепции и принципы
- Единица измерения для определения размеров должна соответствовать политике пользователя. На чертеже для использования в американской промышленности для производства все размеры указаны в дюймов , если не указано иное.
- В большинстве стран за пределами США, включая Канаду, используется метрическая система измерения или международная система единиц (СИ), основанная на метре.

Общепринятой метрической единицей измерения на технических чертежах является миллиметров , сокращенно мм .
Иногда вам придется размещать размеры в двух единицах измерения одновременно!
Размеры должны быть размещены в наиболее наглядном представлении объекта.
Если вид переполнен разными размерами, можно создать два и более отдельных чертежа с одним и тем же видом.
Размещение размерного текста
Текст размеров может быть размещен по-разному:
- размер внутри выносные линии, со стрелками внутри или снаружи; и
- размер снаружи выносные линии, со стрелками снова внутри или снаружи.
В условиях ограниченного пространства выносные линии могут быть проведены под углом:
Выносные линии не должны пересекать размерные линии и, по возможности, не должны пересекаться с другими выносными линиями. Когда выносные линии пересекают линии объекта или другие выносные линии, они не должны прерываться.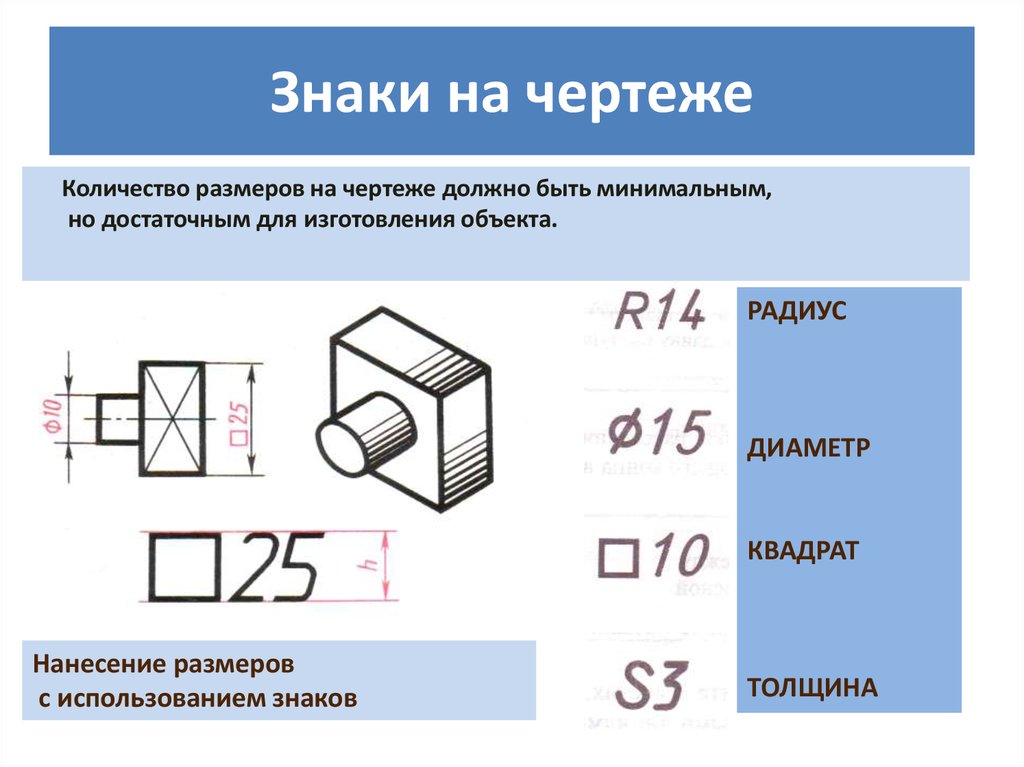 Когда выносные линии пересекаются или находятся близко к наконечникам стрелок, они должны быть разорваны для наконечника стрелки.
Когда выносные линии пересекаются или находятся близко к наконечникам стрелок, они должны быть разорваны для наконечника стрелки.
Простановка размеров без стрелок
Чтобы избежать большого количества размеров, отходящих от детали, можно использовать простановку размеров без стрелок.
- «нулевые» линии представляют вертикальную и горизонтальную исходные линии,
- каждый из размеров, показанных без стрелок, указывает расстояние от нулевой линии.
- Никогда не должно быть более одной нулевой линии в каждом направлении.
- Простановка размеров без стрелок используется для локационных размеров ряда элементов, таких как отверстия и прорези.
Все размеры и текст примечаний должны быть ориентированы так, чтобы их можно было читать снизу чертежа. Это называется однонаправленным определением размеров .
Метод выравнивания (когда текст размещается параллельно размерной линии) можно увидеть на старых чертежах или архитектурных чертежах, но он не одобрен текущим стандартом ANSI.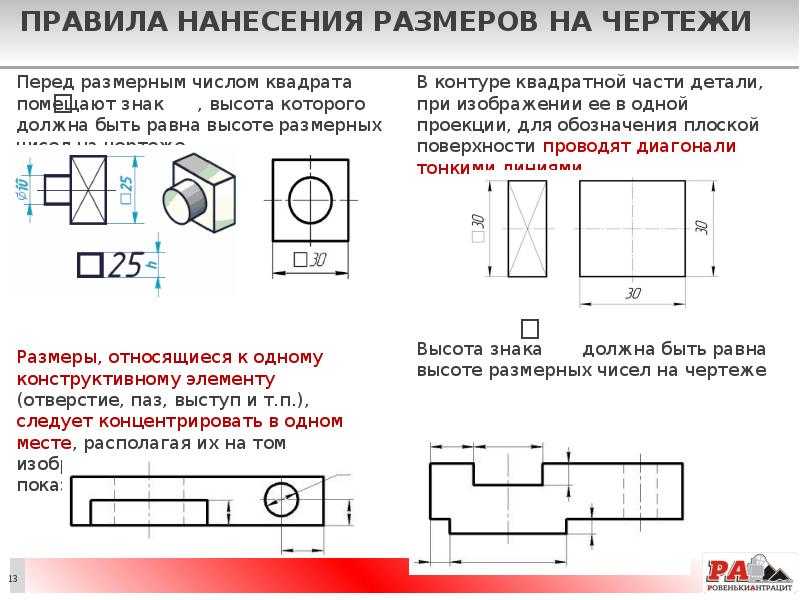
Групповые размеры
В стандартной практике размеры группируются на чертеже для единообразия внешнего вида.
Избегайте использования линий объекта в качестве выносных линий для размера.
Размеры должны быть вынесены за пределы вида, где это целесообразно.
Размеры могут располагаться последовательно и параллельно.
- Когда ряд размеров применяется по принципу “точка-точка”, это называется цепочка размеров .
Первый размер в ряду должен быть привязан к базовой линии.
Недостаток этой системы: это может привести к нежелательному накоплению допусков между отдельными элементами.
- Когда несколько размеров начинаются с общей точки отсчета или линии, метод называется измерением общей точки или параллельным измерением .
Базовая линия может быть продолжением контура исходной точки, базовой линией или системной линией.
Базовая поверхность — это внешняя поверхность детали, которая должна быть обработана в первую очередь.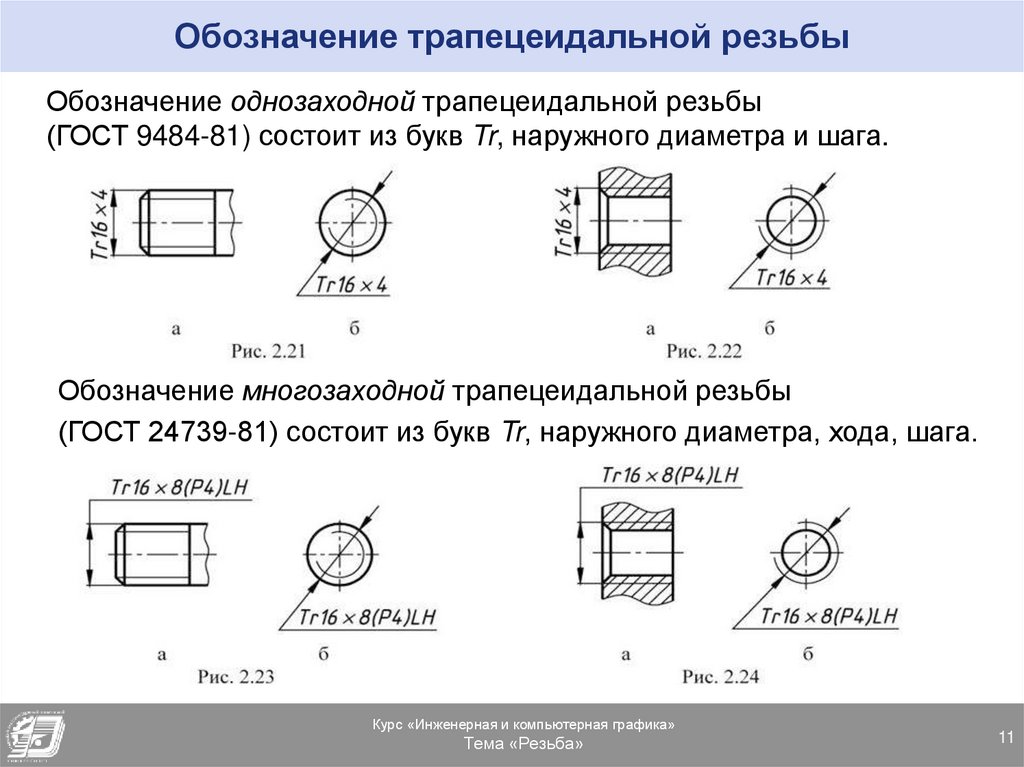
Размеры могут располагаться параллельно или последовательно, но во всех случаях они должны относиться к базовой (базовой) поверхности.
Смещение размеров
Общей практикой является размещение размерного текста на нескольких параллельных измерениях.
Размер размерный
Размеры можно классифицировать по видам размеров:
- Горизонтальный — расстояние слева направо относительно листа чертежа. Здесь ширина является единственным размером по горизонтали.
- По вертикали — расстояние вверх и вниз относительно чертежного листа. Здесь высота и глубина оба являются вертикальными размерами, даже если они находятся в двух разных направлениях на детали.
- Диаметр — полное расстояние по окружности, измеренное через центр.
- Радиус —расстояние от центра дуги до любой точки дуги. Радиус обычно используется для дуг меньше половины окружности.
Размеры расположения и ориентации
Размеры можно классифицировать по типу расположения или ориентации:
- Положение по горизонтали — определяет положение объекта в горизонтальном направлении относительно основания;
- Положение по вертикали – определяет положение элемента по вертикали относительно основания e ;
- Угол – дает угол между горизонтальной плоскостью и наклонной поверхностью.

Угловые единицы
- Угловые размеры отображаются либо в десятичных градусах, либо в градусах, минутах и секундах.
- Если указаны только минуты и секунды, количеству минут или секунд предшествует 0 0 .
Также хорошо иметь изометрический вид детали на ее чертеже. Не обязательно, но предпочтительнее для сложных деталей.
На изометрическом виде не должны отображаться никакие размеры. Масштаб должен быть указан, если он отличается от общего.
Детальное определение размеров (Как определить размеры различных элементов)
- Отверстия обычно имеют размеры на виде, который лучше всего описывает форму отверстия. Диаметры должны быть обозначены символом диаметра перед числовым значением. Если размеры отверстий указаны с помощью линии выноски, эта линия должна быть радиальной.
A радиальная линия e — линия, проходящая через центр окружности или дуги, если ее продолжить.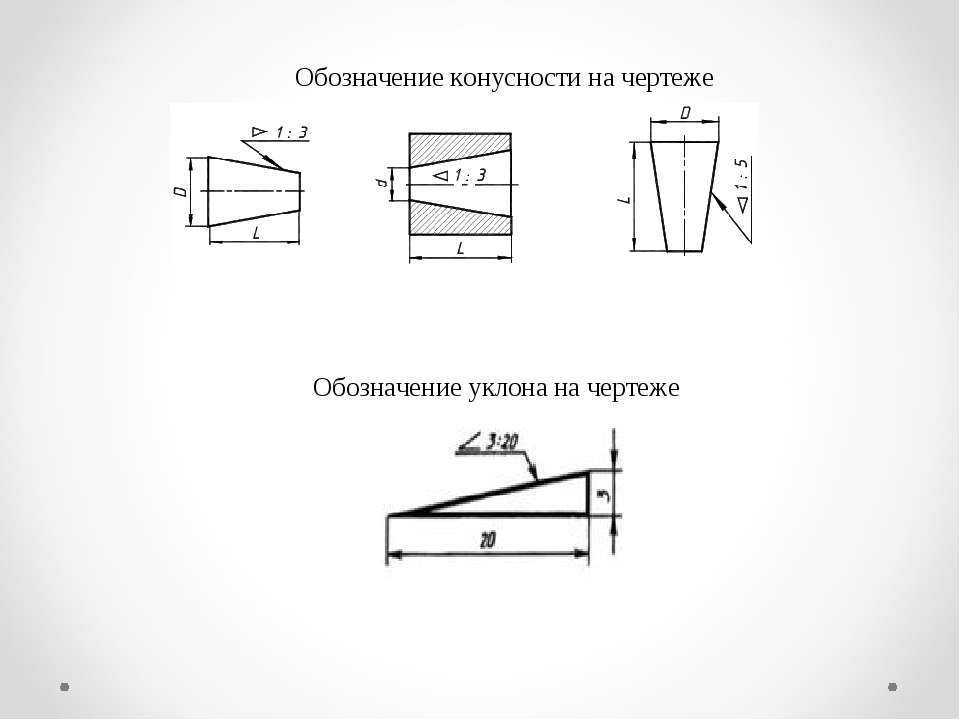
- Символы могут использоваться для прицельной поверхности , цековки и потайных отверстий . Эти символы всегда предшествуют символу диаметра.
Символ глубины может использоваться для обозначения глубины отверстия. Символ глубины ставится перед числовым значением.
- Если указана глубина глухого отверстия , это относится к глубине полного диаметра отверстия.
- Фаски измеряются либо углом и линейным размером, либо двумя линейными размерами.
Фаски 45 0 могут быть указаны в примечании.
- Отверстия с прорезями могут иметь любой из нескольких размеров в зависимости от того, какой из них наиболее подходит для применения.
- Можно указать уклон линии или плоской поверхности:
( a ) по углу; ( b ) как отношение в сочетании с символом наклона; ( c ) размерами, показывающими разность высот двух точек от базовой линии и расстояние между ними; ( д ) по символу уклона, длине базовой линии и высоте уклона.
- Определение размеров хорд, дуг и углов
- Шпоночные гнезда и шпоночные канавки , которые являются крепежными устройствами, имеют особые размеры, поскольку они создают некоторые необычные проблемы.
Высота самого шпоночного гнезда не измеряется, потому что после того, как верхняя часть вала срезана, не остается ничего, что можно было бы измерить.
Также размеры односторонние :
- для шпонки, размер минимальный;
- для шпоночного паза, размер максимальный.
Это необходимо для обеспечения помех после того, как ключ будет вставлен между частями.
Размеры повторяющихся элементов
- Повторяющиеся элементы и размеры могут быть указаны с помощью « X » в сочетании с цифрой для обозначения « количество раз » или « мест » они обязательны. Между « X » и размером объекта оставлено полное пространство.

« X » иногда используется для обозначения « BY » между размерами координат, указанными в форме примечания. В этом случае между « X » и размерами остается пробел.
Чтобы избежать повторения одного и того же размера или длинных линий выноски, мы можем использовать справочные письма в сочетании с пояснительной таблицей или примечание .
- Обозначение отверстий одинакового размера
- Размеры шестерен
Шестерня представляет собой зубчатое механическое устройство, используемое для передачи мощности и движения между частями машины. Обычно вал используется как для подачи, так и для приема мощности от шестерен.
Когда две шестерни разных размеров входят в зацепление, большая из них называется 9-й.0005 шестерня и меньшая шестерня .
Обычно чертежи зубчатых колес содержат таблицу данных, называемых режимами резания, для изготовления.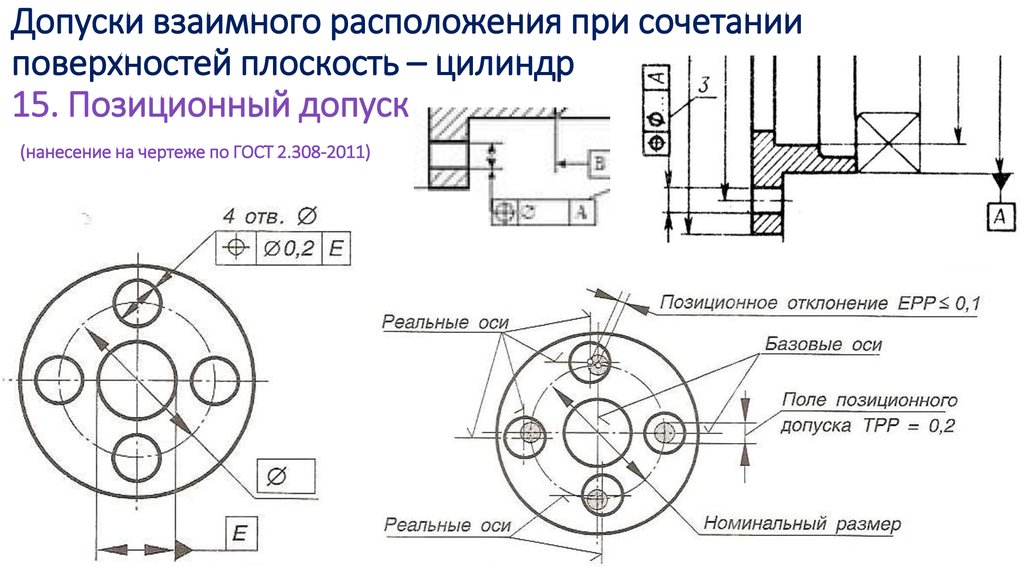 Детальный чертеж шестерни также будет включать другие размеры, не указанные в таблице (диаметр основания, диаметр отверстия, размеры шпоночной канавки).
Детальный чертеж шестерни также будет включать другие размеры, не указанные в таблице (диаметр основания, диаметр отверстия, размеры шпоночной канавки).
В качестве альтернативы, шестерни и шлицы могут быть показаны сплошной линией, представляющей основной контур детали, и более светлой линией, представляющей основание зубьев.
Линию основного тона можно добавить, используя стандартную центральную линию. Это то же соглашение, что и для винтовой резьбы.
Диаметр круга – определение, формула, примеры
В круге диаметр – это линия, проходящая через центр и пересекающаяся с окружностью на противоположных концах. Он в два раза больше радиуса окружности. Другими словами, диаметр окружности — это линия, проходящая через центр и делящая окружность на две равные части. Давайте узнаем больше об определении диаметра и свойствах в этой статье.
| 1. | Каков диаметр круга? |
2. | Диаметр окружности Формула |
| 3. | Как найти диаметр круга? |
| 4. | Диаметр против радиуса |
| 5. | Часто задаваемые вопросы по диаметру |
Каков диаметр круга?
Диаметром окружности называется любой отрезок прямой линии, проходящий через центр окружности и концы которого лежат на окружности окружности. Диаметр также известен как самая длинная хорда окружности.
Определение диаметра
Диаметр определяется как удвоенная длина радиуса окружности. Радиус измеряется от центра круга до одной конечной точки на границе круга, тогда как расстояние диаметра измеряется от одного конца круга до точки на другом конце круга, проходящей через центр. Обозначается буквой D. На окружности окружности бесконечное число точек, это означает, что окружность имеет бесконечное число диаметров, и каждый диаметр окружности имеет одинаковую длину.
Символ диаметра
Ø — это символ, который используется в технике для обозначения диаметра. Этот символ обычно используется в технических спецификациях и чертежах. Ø25 мм означает, что диаметр круга составляет 25 мм.
Диаметр окружности Формула
Все мы знаем, что диаметр является частью круга. Давайте разберемся с некоторыми терминами, прежде чем мы узнаем формулу диаметра круга.
- Радиус (r) — это длина отрезка от центра окружности до конечной точки окружности.
- Окружность (C) относится к замкнутой границе круга. Он также известен как периметр круга.
- Площадь круга — это общее пространство внутри границы круга. Он рассчитывается по формуле πr 2 , где r — радиус.
Мы можем вывести формулу диаметра из длины окружности, площади и радиуса круга.
Диаметр окружности с использованием длины окружности
Мы можем легко вывести формулу диаметра из длины окружности. Формула длины окружности: C = πd; здесь, C = окружность, d = диаметр окружности, π = 22/7 или 3,142 прибл. Формула диаметра с использованием окружности:
Формула длины окружности: C = πd; здесь, C = окружность, d = диаметр окружности, π = 22/7 или 3,142 прибл. Формула диаметра с использованием окружности:
Диаметр = Окружность ÷ π.
Диаметр круга с использованием радиуса
Радиус — это длина отрезка от центра круга до конечной точки на круге, а диаметр равен удвоенной длине радиуса круга. Используя это определение, формула для диаметра равна D = Радиус × 2 .
Формула диаметра, использующая площадь круга
Мы можем вывести формулу диаметра круга, используя формулу площади круга, то есть площадь (A) = π(радиус) 2 . Подставляя значение радиуса в качестве D/2, мы получаем A/π = (D/2) 2 .
⇒ D/2 = √(A/π)
⇒ D = 2 × √(A/π)
Следовательно, формула диаметра круга с использованием площади: D = 2√Площадь/π .
Как найти диаметр круга?
Диаметр круга можно рассчитать, если известны радиус, длина окружности или площадь.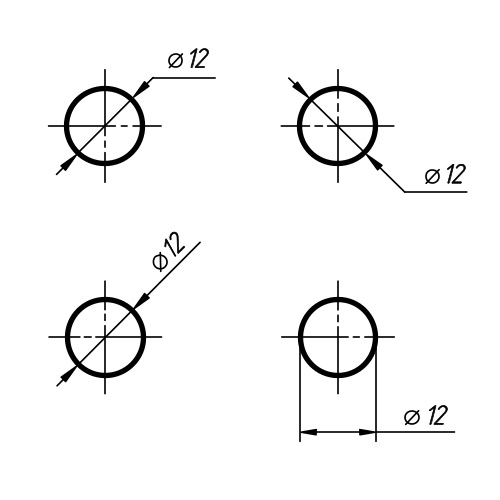 Выполните шаги, указанные ниже, чтобы найти диаметр круга:
Выполните шаги, указанные ниже, чтобы найти диаметр круга:
- Шаг 1: Первый шаг — определить, что дано в вопросе: радиус, площадь или окружность.
- Шаг 2: Примените соответствующую формулу из трех приведенных выше формул.
- Шаг 3: Упростите и получите ответ.
Давайте попробуем использовать формулы, упомянутые выше в практической иллюстрации, чтобы найти диаметр. Обратите внимание на приведенный ниже пример.
Пример: Джек нарисовал круг радиусом 3 единицы. Каков диаметр круга?
Решение:
Дано: Радиус окружности = 3 единицы.
Диаметр круга = 2 × радиус
= 2 × 3 = 6 единиц
Следовательно, диаметр круга равен 6 единицам.
Диаметр против радиуса
Как мы уже говорили, длина диаметра в два раза больше радиуса. Есть некоторые сходства и различия между диаметром и радиусом, которые мы собираемся изучить в этом разделе. Прежде чем перейти к разнице между диаметром и радиусом, сначала поговорим об их сходстве. И диаметр, и радиус являются частями круга, которые определяют различные свойства, такие как размер круга, длина окружности и площадь круга. Они разделяют отношения в форме уравнения. и.в. Диаметр = 2 × Радиус.
Прежде чем перейти к разнице между диаметром и радиусом, сначала поговорим об их сходстве. И диаметр, и радиус являются частями круга, которые определяют различные свойства, такие как размер круга, длина окружности и площадь круга. Они разделяют отношения в форме уравнения. и.в. Диаметр = 2 × Радиус.
Посмотрите на приведенную ниже таблицу, чтобы понять диаметр и радиус.
| Диаметр | Радиус |
|---|---|
| Диаметр круга в два раза больше его радиуса. | Это половина длины от диаметра. |
| Для любой окружности длина диаметра больше длины радиуса. | Длина радиуса меньше диаметра. |
| Начинается от границы круга и заканчивается на самой границе. | Он начинается от центра и касается окружности в точке. |
☛ Похожие темы
Проверьте эти интересные статьи, связанные с диаметром круга.
- Хорды и диаметры
- Формула диаметра сферы с использованием объема
- Окружность к диаметру
Примеры диаметров
Пример 1: Радиус круга равен 15 единицам. Вычислите его диаметр.
Решение:
Дано, радиус = 15 единиц
Мы это знаем,
Диаметр = 2 × радиус
= 2 × 15
Следовательно, диаметр = 30 единиц.Пример 2: Можете ли вы определить значение радиуса, если диаметр окружности равен 36 единицам?
Решение:
Дано: Диаметр = 36 единиц
Мы знаем, что диаметр в два раза больше радиуса. Это означает, что радиус равен половине значения диаметра.
Диаметр = 2 × радиус
Р = Д ÷ 2
Радиус = 36 ÷ 2 = 18 единиц
Следовательно, радиус = 18 единиц.Пример 3: Диаметр круглого бассейна составляет 7 футов. Какова окружность бассейна? Выразите ответ через число π.

Решение:
Дано: Диаметр = 7 футов
Мы знаем, что длина окружности = π × d
. Таким образом, длина окружности бассейна = π × 7
. Следовательно, окружность бассейна = 7π футов.
перейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика — это жизненный навык. Помогите своему ребенку усовершенствовать это с помощью реального приложения с Cuemath.
Записаться на бесплатный пробный урок
Практические вопросы по Diameter
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о Diameter
Что такое диаметр?
Диаметр – это прямая линия, проходящая через центр окружности и делящая окружность на две части/полуокружности. Это самая длинная хорда окружности, которая пересекает окружность на противоположных концах.
Какой символ используется для обозначения диаметра?
В технике для обозначения диаметра используется символ ⌀. Его часто называют «фи». Этот символ фи используется для описания диаметра круглого сечения. Например, «⌀20» означает, что диаметр круга составляет 20 единиц измерения.
Его часто называют «фи». Этот символ фи используется для описания диаметра круглого сечения. Например, «⌀20» означает, что диаметр круга составляет 20 единиц измерения.
Что такое радиус и диаметр?
Радиус и диаметр круга являются двумя важными частями круга, которые взаимозависимы друг от друга. Радиус круга — это отрезок, который начинается от центра круга и заканчивается на окружности круга. Это половина длины диаметра круга, т. Е. Радиус = диаметр / 2. Диаметр окружности — это отрезок, проходящий через центр окружности и имеющий две точки на окружности. Это в два раза больше длины радиуса окружности, т. е. диаметр = 2 × радиус.
Как рассчитать диаметр?
Диаметр круга можно рассчитать по заданным параметрам. Если заданы такие параметры, как радиус, окружность или площадь, мы можем напрямую использовать следующие формулы.
- Диаметр = Окружность ÷ π (если длина окружности дана)
- Диаметр = 2 × радиус (если указан радиус)
- Диаметр = 2√[Площадь/π] (если дана площадь)
Пример диаметра?
Если вы посмотрите на колесо цикла, шипы, идущие от одного конца к другому через центр, являются примером диаметра.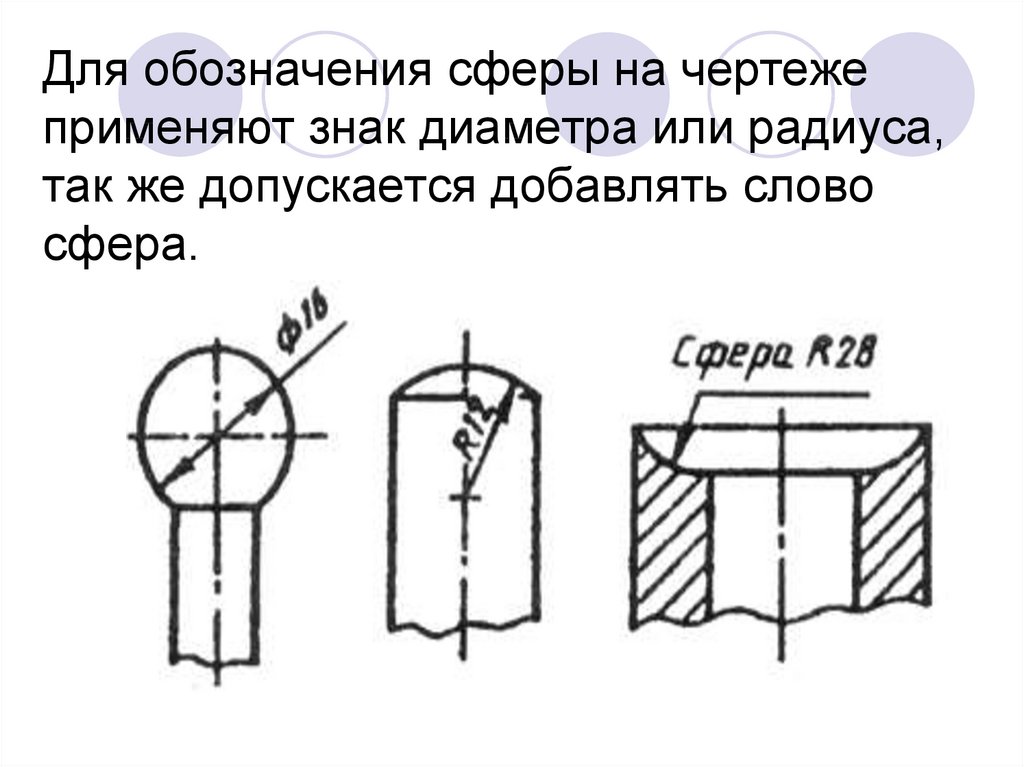 Мы можем связать это с диаметром круга, поскольку диаметр — это отрезок, который начинается с одного конца круга и заканчивается на другом конце круга, проходящем через центр.
Мы можем связать это с диаметром круга, поскольку диаметр — это отрезок, который начинается с одного конца круга и заканчивается на другом конце круга, проходящем через центр.
Как найти диаметр по окружности?
Если длина окружности известна, то мы можем легко найти значение диаметра, подставив значения в формулу: Диаметр = C ÷ π; где «C» — длина окружности, а значение π равно примерно 22/7 или 3,14.
Как найти площадь круга по диаметру?
Площадь круга рассчитывается по формуле: πr 2 . Если задан диаметр, мы можем найти радиус, разделив значение диаметра на 2. Получив радиус, мы можем подставить его значение в формулу: πr 2 , чтобы получить площадь круга, или напрямую применить формулу площади. с диаметром, A = π(d/2) 2 = πd 2 /4 кв.
Для чего нужен калькулятор отношения диаметра к окружности?
Калькулятор отношения диаметра к окружности — это онлайн-инструмент, используемый для определения значения длины окружности.


 18.
18. Размеры одинаковых радиусов допускается указывать на общей полке, как показано на рис. 52,б.
Размеры одинаковых радиусов допускается указывать на общей полке, как показано на рис. 52,б. На изображении квадрата, спроецированного в натуральном виде, предпочтительно указывать размеры двух его сторон (рис. 56, б). Допускается также нанесение размера квадрата, как показано на рис. 56, в.
На изображении квадрата, спроецированного в натуральном виде, предпочтительно указывать размеры двух его сторон (рис. 56, б). Допускается также нанесение размера квадрата, как показано на рис. 56, в.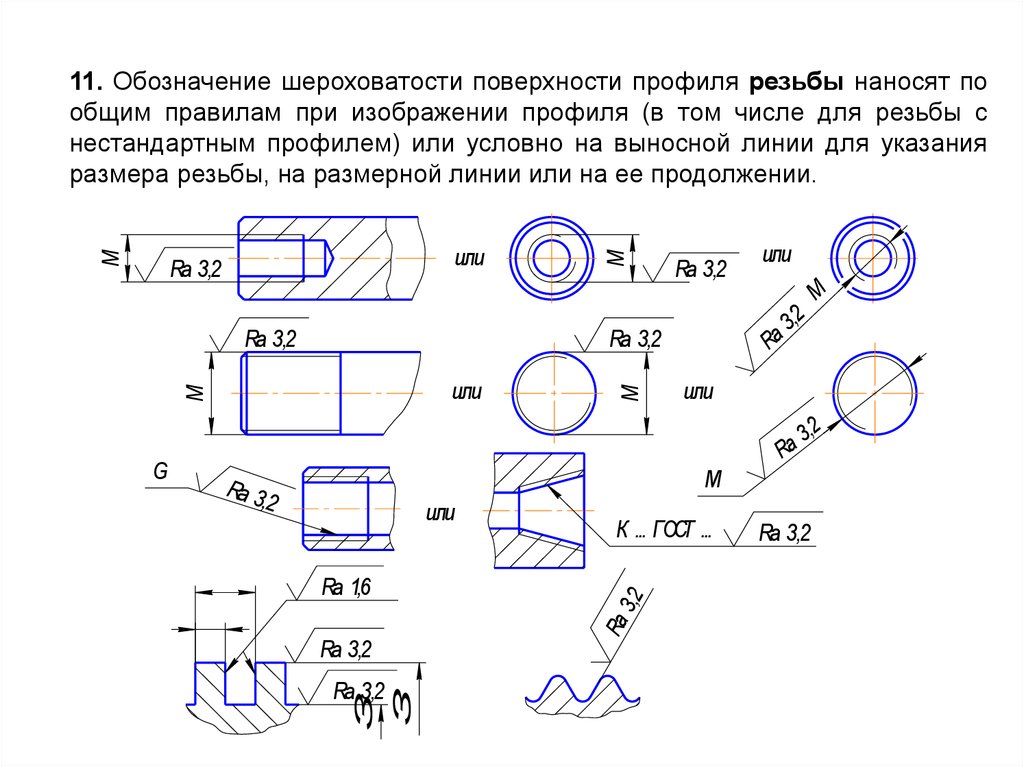 59). Знак сферы О, представляющий собой окружность с диаметром, равным высоте размерных чисел, наносится перед размерным числом в том случае, если начертеже трудно отличить сферу от других поверхностей.
59). Знак сферы О, представляющий собой окружность с диаметром, равным высоте размерных чисел, наносится перед размерным числом в том случае, если начертеже трудно отличить сферу от других поверхностей.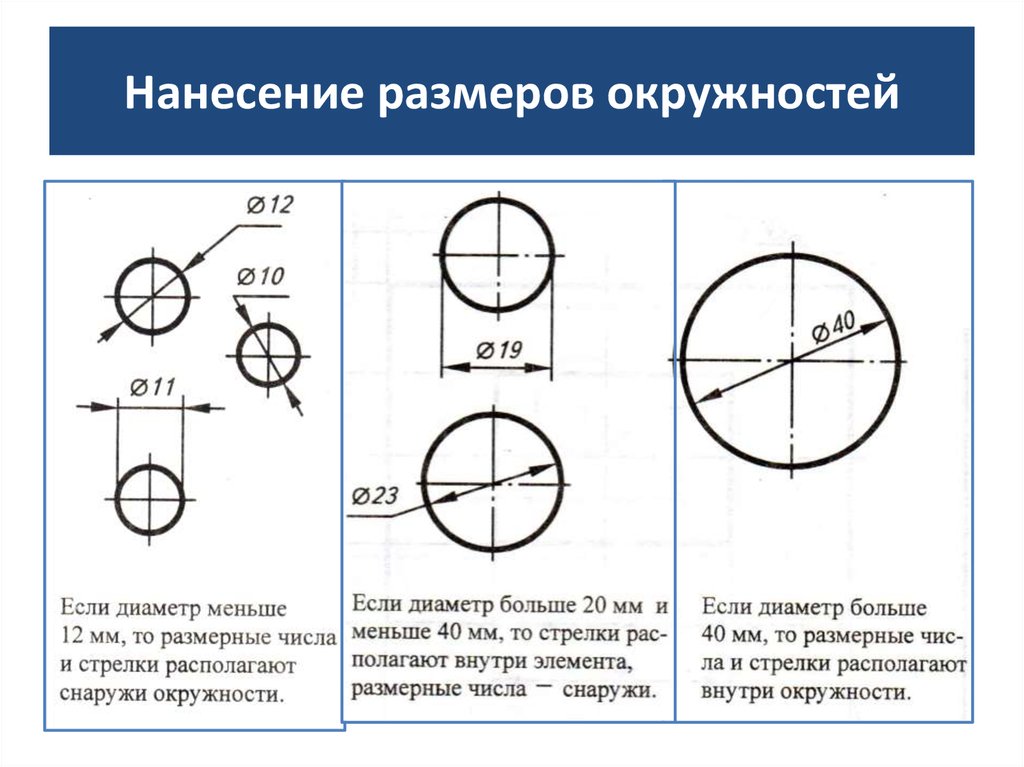

 info – Студопедия – 2014-2023 год
. (0.023 сек.) русская версия | украинская версия
info – Студопедия – 2014-2023 год
. (0.023 сек.) русская версия | украинская версия