Как найти период пружинного маятника: Найти период колебания пружинного маятника жёсткостью 250н/м ,массой 100грамм.

alexxlab | 18.12.2022 | 0 | Разное

2_0=\frac{k}{m}$ – циклическая частота колебаний пружинного маятника. Решением уравнения (1) является функция:

\[x=A{\cos \left({\omega }_0t+\varphi \right)=B{\sin \left({\omega }_0t+{\varphi }_1\right)\ }\ }\left(2\right),\]

где ${\omega }_0=\sqrt{\frac{k}{m}}>0$- циклическая частота колебаний маятника, $A$ и $B$ – амплитуда колебаний; ${(\omega }_0t+\varphi )$ – фаза колебаний; $\varphi $ и ${\varphi }_1$ – начальные фазы колебаний.

Частота и период колебаний пружинного маятника

Косинус (синус) – периодическая функция, смещение $x$ будет принимать одинаковые значения через определенные одинаковые промежутки времени, которые называют периодом колебаний. Обозначают период буквой T.

Еще одной величиной, характеризующей колебания является величина обратная периоду колебаний, ее называют частотой ($\nu $):

\[T=\frac{1}{\nu }\left(3\right).\]

Период связан с циклической частотой колебаний как:

\[T=\frac{2\pi }{{\omega }_0}\left(4\right). \]

Зная, что для пружинного маятника ${\omega }_0=\sqrt{\frac{k}{m}}$, период колебаний его определим как:

\[T=2\pi \sqrt{\frac{m}{k}}\ \left(5\right).\]

Из выражения (5) мы видим, что период колебаний пружинного маятника зависит от массы груза, находящегося на пружине и коэффициента упругости пружины, но не зависит от амплитуды колебаний (A). Такое свойство колебаний называют изохронностью. Изохронность выполняется до тех пор, пока справедлив закон Гука. При больших растяжениях пружины закон Гука нарушается, при этом возникает зависимость колебаний от амплитуды. Отметим, что формула (5) для вычисления периода колебаний пружинного маятника справедлива при малых колебаниях.

Единицей измерения периода являются единицы времени, в Международной системе единиц это секунды:

\[\left[T\right]=с.\]

Примеры задач на период колебания пружинного маятника

Пример 1

Задание.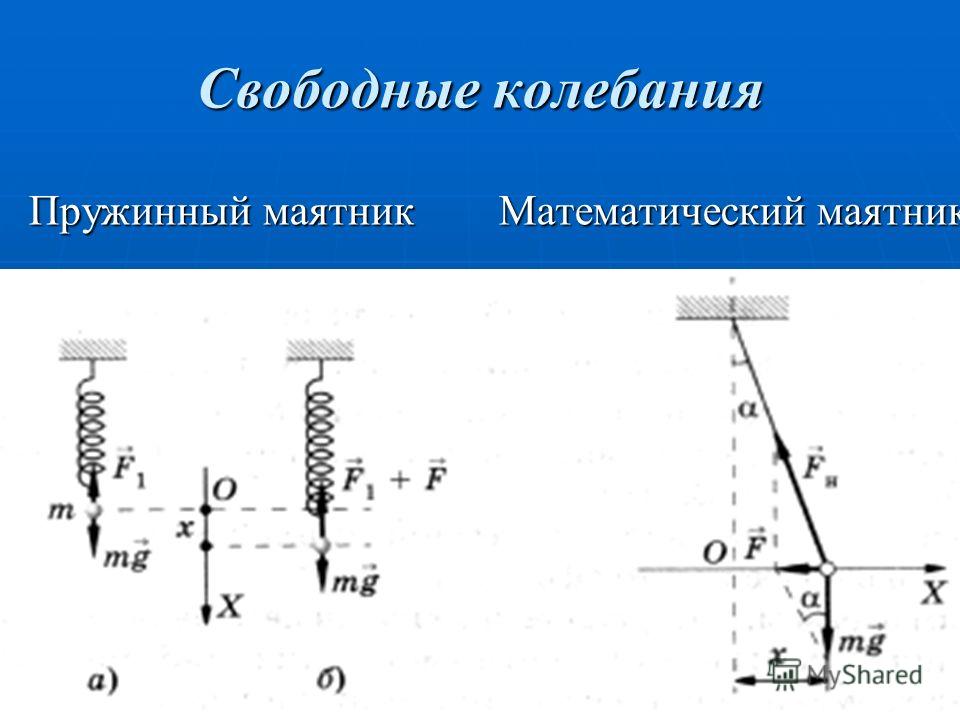 К упругой пружине прикрепили небольшой груз, при этом пружина растянулась на $\Delta x$=0,09 м. Каким будет период колебаний данного пружинного маятника, если его вывести из равновесия?

Решение. Сделаем рисунок.

Рассмотрим состояние равновесия пружинного маятника. Груз прикрепили, после этого пружина растянулась на величину $\Delta x$, маятник находится в состоянии равновесия. На груз действуют две силы: сила тяжести и сила упругости. Запишем второй закон Ньютона для состояния равновесия груза:

\[m\overline{g}+{\overline{F}}_u=0\ \left(1.1\right).\]

Запишем проекцию уравнения (1.1) на ось Y:

\[mg=F_u\left(1.2\right).\]

Так как груз по условию задачи небольшой, пружина растянулась не сильно, следовательно выполняется закон Гука, величину силы упругости найдем как:

\[F_u=k\Delta x\ \left(1.3\right).\]

Используя выражения (1.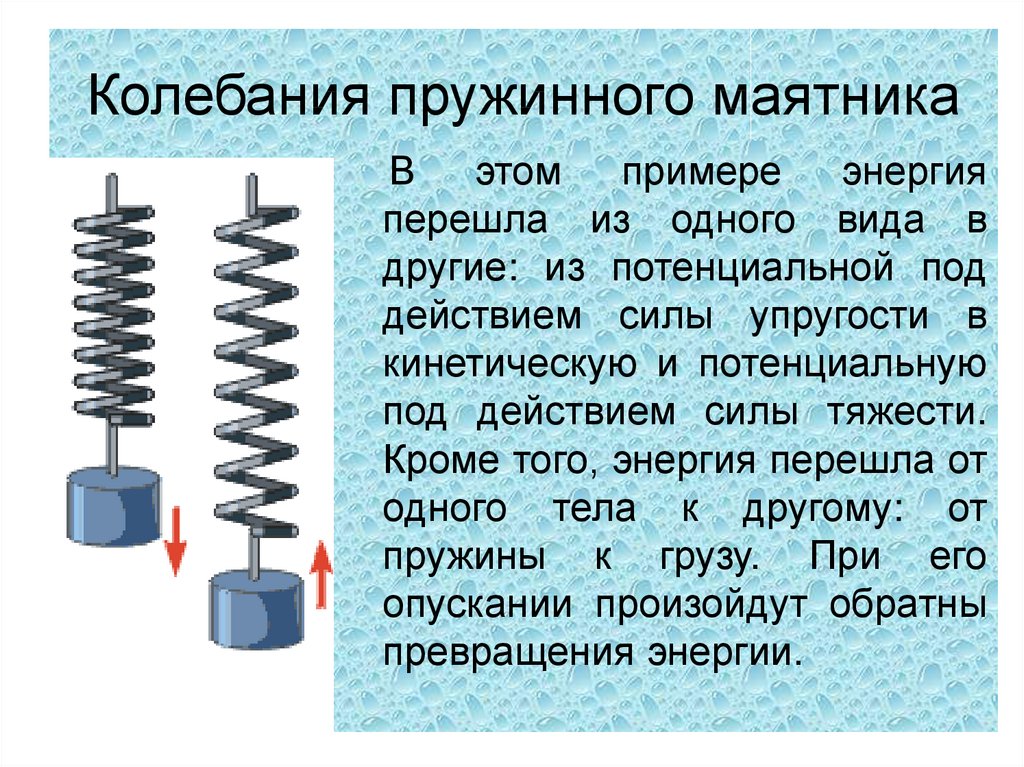 2}$:

\[T=2\pi \sqrt{\frac{0,09\ \ }{9,8}\ \approx 0,6\ (с)}\]

Ответ. $T$=0,6 с

   

Пример 2

Задание. Две пружины с жесткостями $k_1$ и $k_2$ соединены последовательно (рис.2), к концу второй пружины присоединен груз массы $m$, Каков период колебаний данного пружинного маятника, если массами пружин можно пренебречь, сила упругости, действующая на груз, подчиняется закону Гука.

Решение.Период колебаний пружинного маятника равен:

\[T=2\pi \sqrt{\frac{m}{k}}\ \left(2.1\right).\]

Если две пружины соединены последовательно, то их результирующая жесткость ($k$) находится как:

\[\frac{1}{k}=\frac{1}{k_1}+\frac{1}{k_2}\to k=\frac{k_1k_2}{k_1{+k}_2}\left(2.2\right).\]

Вместо $k$ в формулу для вычисления периода пружинного маятника подставим правую часть выражения (2. 2), имеем:

\[T=2\pi \sqrt{\frac{m(k_1{+k}_2)}{k_1k_2}}.\]

Ответ. $T=2\pi \sqrt{\frac{m(k_1{+k}_2)}{k_1k_2}}$

   

Читать дальше: плечо силы.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Период пружинного маятника, теория и онлайн калькуляторы

Период пружинного маятника, теория и онлайн калькуляторы

Определение и основные понятия пружинного маятника

Одной из самых простых систем, в которой можно возбудить механические колебания является система, состоящая из пружины, с коэффициентом упругости $k$, на которой подвешен груз с массой $m$. Пусть система расположена вертикально. На груз действуют сила упругости и сила тяжести, если систему вывести из состояния равновесия и предоставить самой себе, то груз будет совершать колебания.

2_0=\frac{k}{m}$ – циклическая частота колебаний. Решение уравнения (1) – это функция вида:

\[x=A{\cos \left({\omega }_0t+\varphi \right)\ }\left(2\right),\]

где ${\omega }_0=\sqrt{\frac{k}{m}}>0$- циклическая частота колебаний маятника, $A$ – амплитуда колебаний; ${(\omega }_0t+\varphi )$ – фаза колебаний; $\varphi $ – начальная фаза колебаний.

Период колебаний пружинного маятника

Косинус является периодической функцией, следовательно, смещение $x$ будет принимать одинаковые значения через определенные одинаковые промежутки времени, которые называются периодом колебаний. Его обозначают буквой.

Другая величина, характеризующая колебания, это величина обратная периоду колебаний, называемая частотой ($\nu $):

\[T=\frac{1}{\nu }\left(3\right).\]

Период связан с циклической частотой колебаний как:

\[T=\frac{2\pi }{{\omega }_0}\left(4\right). \]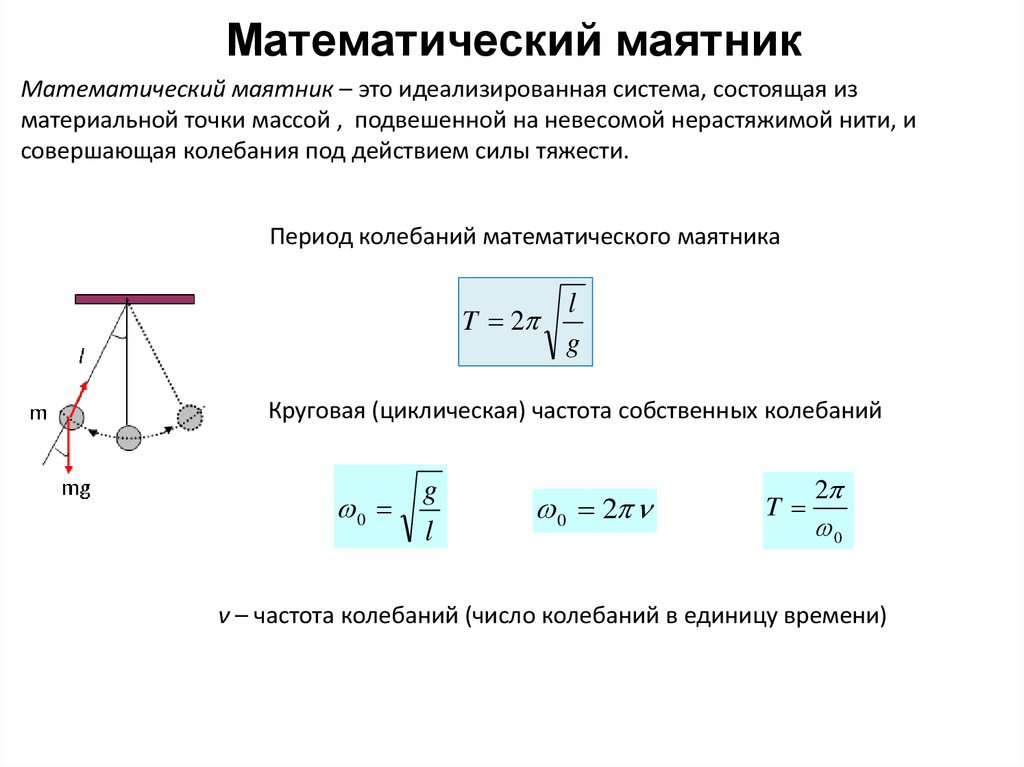

Для пружинного маятника ${\omega }_0=\sqrt{\frac{k}{m}}$, следовательно, период колебаний пружинного маятника равен:

\[T=2\pi \sqrt{\frac{m}{k}}\ \left(5\right).\]

Формула (5), говорит о том, что период колебаний пружинного маятника пропорционален квадратному корню от массы груза, подвешенного к пружине, обратно пропорционален квадратному корню от коэффициента упругости пружины, и не зависит от амплитуды колебаний (A). Это свойство колебаний называется изохронностью. Изохронность реализуется до тех пор, пока справедлив закон Гука. При больших растяжениях пружины закон Гука нарушается, и появляется зависимость периода колебаний от амплитуды. Следует сказать, что выражение (5) для вычисления периода колебаний пружинного маятника справедливо при малых колебаниях.

Единица измерения периода это единицы времени, в Международной системе единиц это секунды:

\[\left[T\right]=с.\]

Примеры задач на колебания пружинного маятника

Пример 1

Задание: Пружинный маятник совершает гармонические колебания. 2}\approx 9,9\ (\frac{Н}{м}).\]

Ответ: $k\approx 9,9\frac{Н}{м}$

   

Читать дальше: плавание тел.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

ньютоновская механика – Пружинный маятник – почему можно использовать это уравнение?

спросил 6 лет, 6 месяцев назад

Изменено 6 лет, 6 месяцев назад

Просмотрено 2к раз

$\begingroup$

Известно, что при описании пружинного маятника мы обязаны пользоваться формулой $T = 2\pi \sqrt{m/k}$, однако можно пойти дальше и положить
$\omega = \frac{2\pi}{T}$
Я размышляю, почему эта замена законна, ведь в этом маятнике нет углового движения!

• ньютоновская механика
• гармонический осциллятор
• частота
• пружина

$\endgroup$

2

$\begingroup$

В этом уравнении $\omega$ относится не к скорости углового движения, а к частоте колебаний, измеренной в угловых единицах (обычно в радианах/сек, но может быть и в градусах/сек). Частота обычно измеряется в циклах в секунду (Герцах), но иногда ее удобнее измерять в угловых единицах, когда ее называют угловой частотой.

Угол, который здесь измеряется, является фазовым углом, который описывает, как далеко за цикл прошло колебание, как если бы колебание двигалось по кругу с постоянной угловой скоростью $\omega$.

Вы можете быть сбиты с толку, потому что не видите никакого углового движения в «пружинном» маятнике. Но это еще более запутанно, когда имеешь дело со «струнным» маятником, потому что здесь смещение измеряется углом $\theta$, но этот угол не совпадает с фазовым углом (который обычно называют $\phi$, т.е. греческое фи для фазы). Угловая скорость равна $\large{\frac{d\theta}{dt}}$, что обычно называют $\omega$, но это $\omega=\large{\frac{d\theta}{dt}} $ не совпадает с угловой частотой $\omega=\large{\frac{d\phi}{dt}=\frac{2\pi}{T}}$. Угловая скорость во время колебаний изменяется от $0$ в крайних точках до максимальной при прохождении через вертикаль.

Но угловая частота при колебании не меняется, она является постоянной величиной для идеальных струнных или пружинных маятников, зависящей от $\large{\frac Lg}$ или $\large{\frac km}$.

$\endgroup$

$\begingroup$

Представьте себе точку $P$, движущуюся по окружности радиуса $R$ с угловой скоростью $\omega$.

Проекция $P$ на ось $y$:

$$y=R\sin \theta=R\sin \omega t$$

Точка $P’$ находится в простых гармонических колебаниях (ШО).

Для системы пружинных масс так получилось, что:

$$x=A\sin \omega t$$ куда: $$\omega=\sqrt{\frac{k}{m}}$$

Итак, хотя в пружинной массе SHO нет углового движения, по аналогии с SHO точки $P’$ мы все же называем его угловой скоростью.

$\endgroup$

$\begingroup$

Уравнение для периода $T$ получено путем использования второго закона Ньютона $F=ma$ для получения уравнения движения системы пружина-масса

$$-kx =ma \Rightarrow a=-\frac k m$ $

, где $x$ — смещение от фиксированной точки, а $a$ — ускорение. 92 x$, где $\omega$ — константа простого гармонического движения.

Можно показать, что для простого гармонического движения $ T = \frac{2 \pi}{\omega}$, что дает $T=2\pi \sqrt{\frac{m}{k}}$.

Возможным уравнением для смещения массы как функции времени $t$ является $x= \sin \omega t$.

Так как углы обычно измеряются в радианах, а время в секундах, единицей постоянной $\omega$ является радиан в секунду.

Таким образом, в этом случае движение массы является линейным, и причина, по которой появляется единица измерения угла, радиан, заключается в том, что функция синуса является частью уравнения для смещения.

Ваша путаница, вероятно, связана с тем, что вы встретили тот же символ $\omega$, что и угловая скорость, которая также имеет единицу радиан в секунду и то же уравнение $T=\frac{2\pi}{\omega }$ при круговом движении.

$\endgroup$

Период SHM — Физика для старших классов

Все ресурсы по физике для старших классов

6 Диагностических тестов 233 практических теста Вопрос дня Карточки Учитесь по концепции

Справка по физике для старших классов » Движение и механика » Гармоничное движение » Период SHM

Пружина имеет жесткость .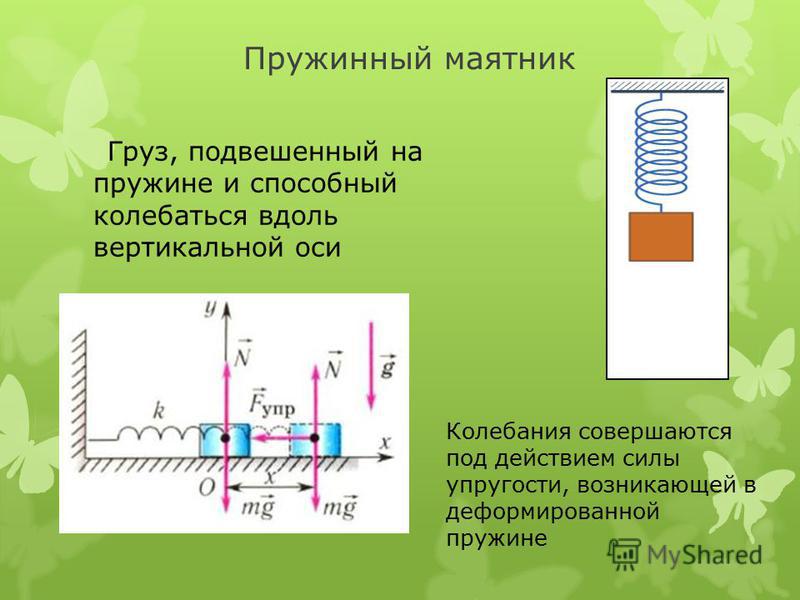 Если для растяжения пружины используется сила , то каково полное перемещение пружины?

 

Возможные ответы:

Правильный ответ:

Объяснение:

Для этой задачи используйте закон Гука:

 

В этой формуле – постоянная пружины, – сжатие пружины, – необходимое усилие. Нам дана постоянная пружины и сила, что позволяет нам найти смещение.

Подставьте полученные значения и решите.

 

Обратите внимание, что и сила, и смещение положительны, поскольку сила растяжения будет тянуть в положительном направлении. Если бы пружина была сжата, изменение расстояния было бы отрицательным.

 

Сообщить об ошибке

Пружина прикреплена к массе, свободно колеблющейся в простом гармоническом движении.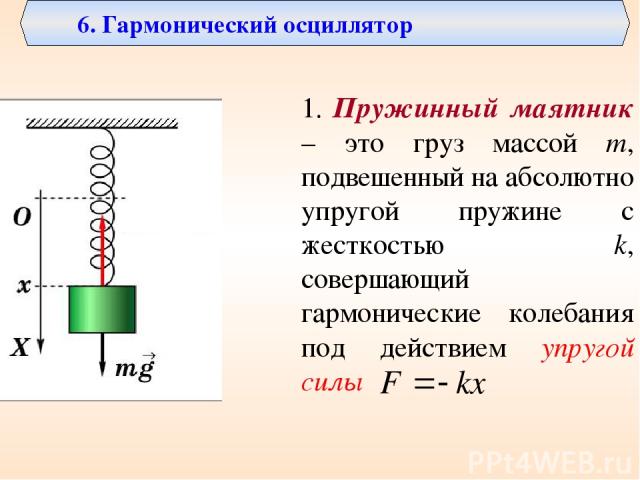 Какое изменение можно сделать, чтобы увеличить период колебаний?

Возможные ответы:

Удлинить пружину

Использовать пружину с большей жесткостью

Увеличить массу на конце пружины

Переместить пружину на планету с меньшим ускорением свободного падения

Уменьшение массы в конце пружины

 

Правильный ответ:

Увеличить массу на конце пружины

Объяснение:

Уравнение для периода пружины в простом гармоническом движении:

 

В этой формуле m — это масса, а k — постоянная пружины. Единственные две вещи, которые мы можем настроить, которые могут изменить период, — это масса и постоянная пружины. Длина пружины и ускорение свободного падения значения не имеют.

 

Если мы увеличим массу, мы получим больший числитель, что, в свою очередь, даст нам больший период. Если мы уменьшим массу, мы получим меньший числитель, что даст нам меньший период. Если мы используем более высокую жесткость пружины, мы получаем больший знаменатель, что также дает нам меньший период.

 

Сообщить об ошибке

Мужчина качает ведро вперед-назад на конце веревки, создавая маятник. Какой фактор можно использовать для увеличения периода маятника?

Возможные ответы:

Перемещение маятника на нижнюю высоту

Снимите воду из ведра

Используйте более сильную веревку

Увеличьте длину веревки

Добавить воду в бакте Ответ:

Увеличить длину веревки

Объяснение:

Уравнение для периода маятника:

 

Обратите внимание, что материал маятника и масса на конце вообще не входят в уравнение. Единственное, что может повлиять на период, — это длина маятника и ускорение свободного падения.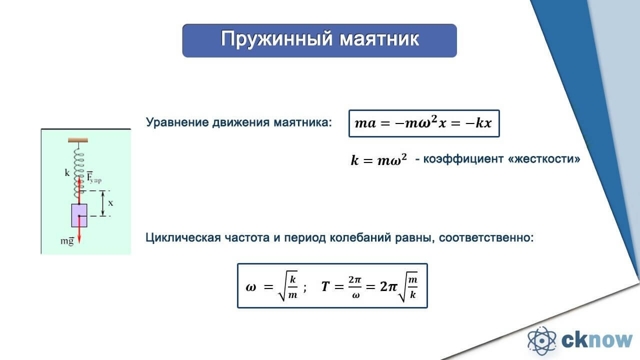

 

Хотя изменение высоты маятника изменит период, он сделает это лишь незначительно, если только вы не поднимете его на несколько миль над земной корой. Кроме того, уменьшение высоты маятника увеличит силу гравитации, что приведет к уменьшению периода. Лучший ответ — увеличить длину веревки. Это увеличит период маятника.

 

Сообщить об ошибке

Длина маятника ваших напольных часов составляет . Если часы отстают на полминуты в день, как отрегулировать длину маятника?

Возможные ответы:

Мы должны сократить маятник на

. Правильный ответ:

Мы должны удлинить маятник на

Объяснение:

Мы также можем рассчитать общее количество секунд в сутках.

 

В сутках есть секунды.

Поэтому мы хотим, чтобы наши часы качались определенное количество раз с периодом от  до .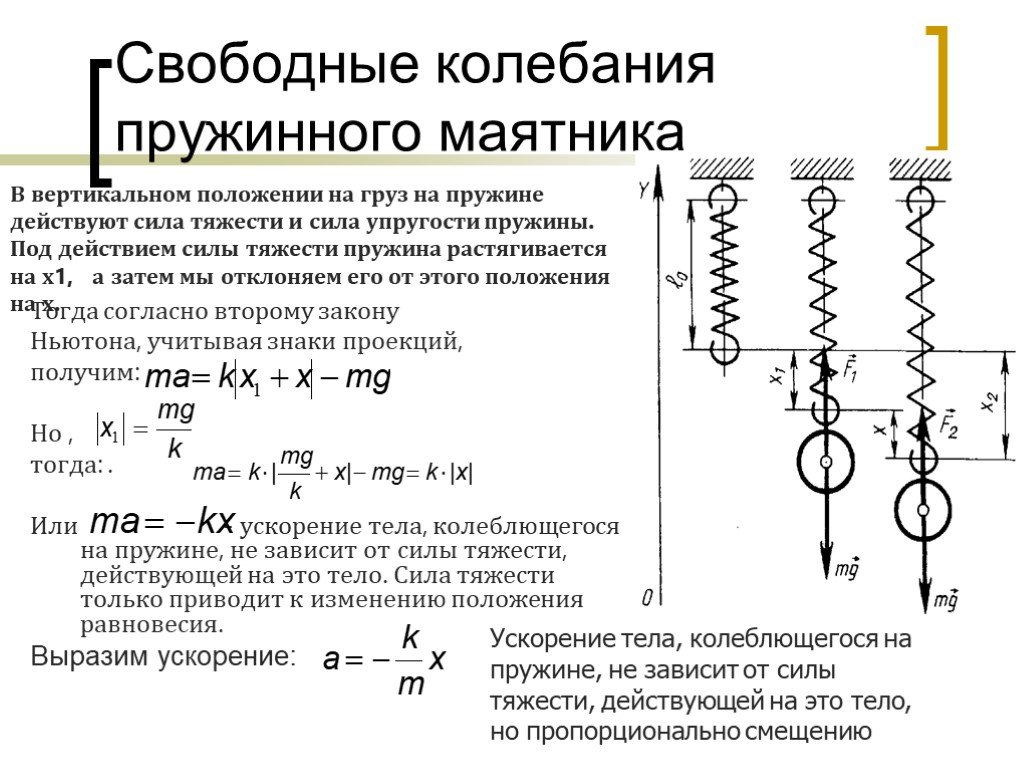

 

Мы знаем, что наши текущие часы имеют определенное количество колебаний с периодом, равным

Таким образом, мы имеем

Мы можем рассчитать текущий период маятника, используя уравнение

2 9 можно установить отношение каждого из этих двух периодов, чтобы определить недостающую длину.

Обратите внимание, что 2, pi и g находятся как в числителе, так и в знаменателе и поэтому выпадают из задачи.

Теперь мы можем найти недостающую деталь.

Возведите в квадрат обе стороны, чтобы избавиться от квадратного корня.

Мы должны удлинить маятник на

Сообщить об ошибке

На конце пружины находится груз. Он имеет начальную скорость и может свободно колебаться. Если масса имеет начальную скорость , каков будет период?

 

Возможные ответы:

Период будет равен 14.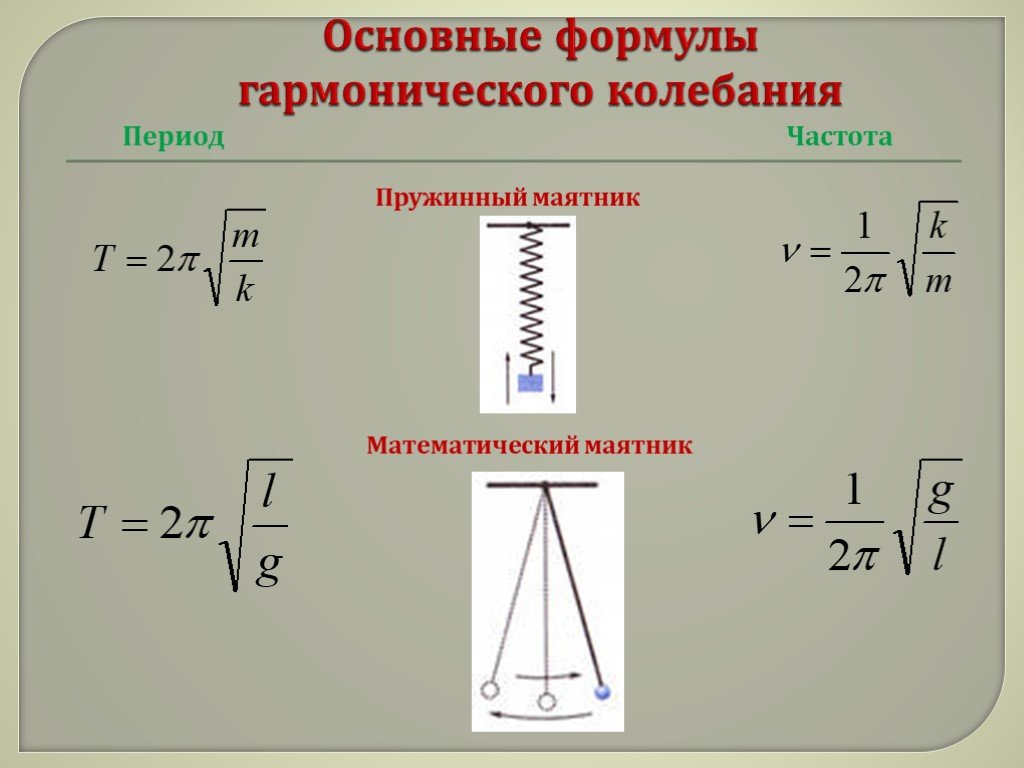

Период увеличился бы в 4 раза.

Период останется прежним.

Период будет вдвое больше.

Период будет вдвое короче.

Правильный ответ:

Период останется прежним.

Пояснение:

Когда речь идет о периоде пружины, скорость объекта не имеет значения.

 

Уравнение

 

Сообщить об ошибке

К пружине прикреплен груз, который совершает колебания с периодом . Какова частота?

Возможные ответы:

Правильный ответ:

Пояснение:

Масса не влияет на соотношение между частотой и периодом. Это отношение задается уравнением:

При заданном периоде частота будет равна его обратной величине.

Сообщить об ошибке

Период маятника на Земле составляет . Каков его период на Марсе, где ускорение свободного падения примерно такое же, как на Земле?

Возможные ответы:

Правильный ответ:

Пояснение:

Для начала мы хотим определить исходную длину маятника.

Уравнение для определения периода маятника:

Мы можем изменить это уравнение, чтобы найти длину ().

Теперь мы можем найти длину, зная, что период маятника равен 2 секундам.

Теперь мы можем использовать то же уравнение и вместо этого подставить значение ускорения под действием силы тяжести на Марсе.

Сообщить об ошибке

Какой длины должен быть простой маятник, чтобы он совершал ровно одно колебание в секунду? (То есть одно полное колебание заняло бы 2 секунды. )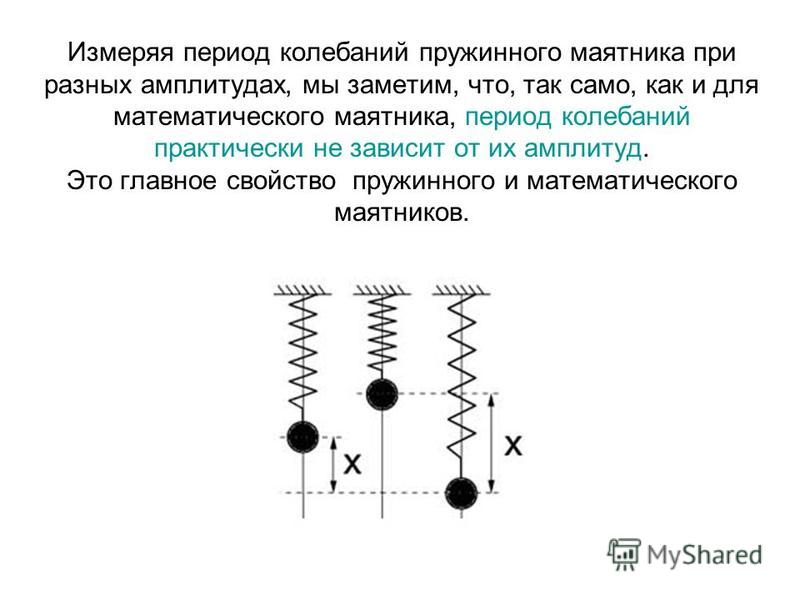

Возможные ответы:

Правильный ответ:

Объяснение:

Уравнение для определения периода маятника:

Мы можем изменить это уравнение, чтобы найти длину ().

Теперь мы можем найти длину, зная, что период маятника равен 2 секундам.

Сообщить об ошибке

Если частица совершает движение простой гармоники с амплитудой . Какое общее расстояние он проходит за один период?

Возможные ответы:

Правильный ответ:

Объяснение:

Период – это время, за которое совершается одно колебание. В этом случае полное колебание будет уносить объект от центра (амплитуда), возвращаться к центру, перемещаться ниже точки равновесия и затем возвращаться к центру.