Как определить флюс: Как понять, что назревает флюс зуба?
alexxlab | 21.02.2023 | 0 | Разное
Флюс, причины и симптомы | Cтоматология Люксар
Флюс (медицинское название — периостит) представляет собой воспаление надкостницы, привести к которой может невнимательное отношение к состоянию своих зубов, либо нежелание посещать стоматолога.
В 85% случаев флюс поражает поверхность челюстей, обращенных к губам. В остальных 15% — нёбо.
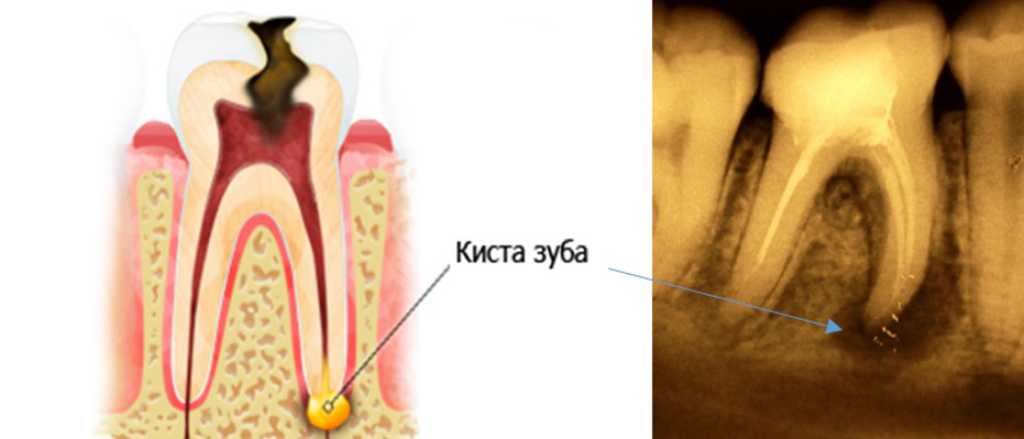
Формирование флюса начинается с воспаления, вызванного инфекцией, в области корня зуба. Образующийся гной, проходит через надкостницу и мягкую ткань десны, образуя шишку.
Опасность флюса заключается в разрыве мешочка с гноем и разнесением его с током крови по всему организму. Это в свою очередь вызывает абсцесс или флегмону, вызывающих у больного смертельный исход.
Срочная помощь стоматолога потребуется при наблюдении у больного следующих симптомов:
- сильная боль в области больного зуба, отражающаяся в области шеи и головы
- боль в зубе при жевании
- припухлость щеки, губы, носа, нижнего века на стороне больного зуба
- высокая температура
Гнойник может прорваться сам, но при этом не происходит снятия воспаления десны и надкостницы.
Причинами флюса могут быть травма зуба или слизистой оболочки рта, запущенный кариес, занесение инфекции в десну вместе с уколом, воспаление десневого кармана, отсутствие гигиены полости рта.
Диагностику данного заболевания проводит стоматолог при визуальном осмотре и при помощи рентгена.
Существует две стадии развития флюса:
- ранняя
- гнойная или острая
Первая стадия характеризуется воспалительным процессом внутри зуба, без образования характерной шишки. При осмотре корня зуба стоматолог решает вопрос об его удалении или сохранении. В обоих случаях назначаются противовоспалительные и обезболивающие препараты.
При отсутствии своевременного медицинского лечения первая форма переходит во вторую. Лечение зуба здесь возможно только хирургическим путем. Десну и при необходимости надкостницу, сделав обезболивание, надрезают. После выхода гноя наружу воспаленную зону обрабатывают антисептиками и укладывают в рану дренаж. Он позволяет десне не заживать до тех пор, пока не выйдет весь гной. После выхода гноя дренаж удаляется, десна при необходимости зашивается.
Он позволяет десне не заживать до тех пор, пока не выйдет весь гной. После выхода гноя дренаж удаляется, десна при необходимости зашивается.
Лечение флюса народными средствами не принесет положительных результатов. Скорее всего можно получить обратный эффект.
Для облегчения болевых симптомов нельзя греть флюс, принимать антибиотики, обезболивающие препараты. Соответствующее лечение может назначить только врач. В случае отсутствия облегчения состояния больного через 10 часов после оперативного вмешательства нужно срочно обратиться к стоматологу.
Вам может быть интересно:
Категория: Лечение десен
Теги: Пульпит
Цены Запись на прием Читать отзывы
Флюс (периостит): причины, симптомы, профилактика заболевания ротовой полости
Оглавление
Что такое флюс?
Итак, начнем с того, что такое периостит — это воспаление надкостницы, в случае с челюстью такое воспаление называют флюсом, то есть это опухание десны, которое сопровождается сильнейшими болями.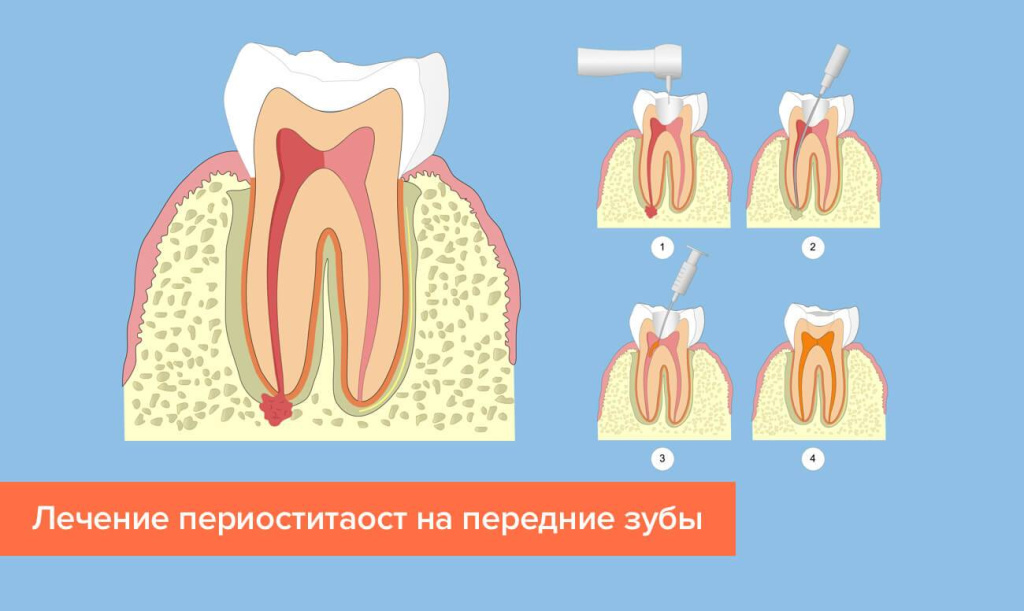
Флюс на десне. Причины
Причинами периостита могут служить как занесение инфекции или воспалительные процессы в зубах, так и открытые ранки мягкой ткани десны. Кроме этого спровоцировать развитие флюса могут:
- Запущенный кариес;
- Гайморит, ангина;
- Патологический рост зубов либо их продолжительное прорезывание;
- Общее переохлаждение организма;
- Постоянные стрессы и нервные срывы.
Обращаем внимание, что зависимо от причины появления флегмоны, принято выделять четыре формы периостита:
- Воспалительная. В большинстве случаев причиной периостита являются осложнения после неудачного терапевтического лечения зубов. Либо же в данной ситуации флюс развивается из-за пренебрежительного отношения к устранению имеющихся стоматологических проблем (кариес, пародонтит и т.д.).
- Специфическая. В этом случае развитие флюса является результатом системы патологий, которые имеются в организме пациента.
- Травматическая.
 Причинами периостита являются повреждения зубов либо десён, вызванные механическим и другими типами воздействий.
Причинами периостита являются повреждения зубов либо десён, вызванные механическим и другими типами воздействий. - Токсическая. При этой форме флюс развивается ввиду инфекционных поражений, которые могут проявляться в виде стоматита, ангины и других заболеваний.
При этом в любом из рассмотренных случаев проявлением клинической картины периостита выступает развитие воспаления, а также ускоренное заражение мягких тканей болезнетворными микроорганизмами.
Флюс — симптомы и как определить заболевание?
Своевременное определение симптоматики и обращение к стоматологу нередко позволяет предупредить переход флюса в стадию, когда происходит формирование гноя и без оперативного хирургического вмешательства уже не обойтись. В первую очередь стоит заметить, что наиболее характерными проявлениями флюса являются стремительно увеличивающая припухлость и отёчность щеки, челюсти или губы. Кроме этого наиболее распространенными симптомами периостита являются:
- Боль при переживании пищи, которая имеет тенденцию к усилению;
- Припухлости, а также покраснения, которые можно увидеть рядом с поврежденным зубом;
- Высокая температура;
- Пульсирующие болевые ощущения, которые распространяются на висок и ухо;
- Увеличение лимфатических узлов.

Кроме этого флюс зуба проявляется общей слабостью организма и ухудшением самочувствия пациента.
Важно отметить, что проявление симптомов периостита происходит одинаково у всех людей независимо от возраста, пола и других отличительных признаков. При этом согласно статистике флюс является преимущественно заболеванием взрослых людей, но и детский периостит тоже встречается. Подобная ситуация обусловлена в первую очередь тем, что ввиду возраста старшие пациенты имеют достаточно большое количество проблем с зубами, которые выступают катализатором развития периостита.
Появился флюс — что делать?
Лечить периостит можно двумя методами:
- Консервативный, когда ещё нет прямой угрозы заражения других тканей или осложнения заболевания. В данном случае чаще всего проценту прописываются лекарственные препараты, которые снимают имеющийся отёк и воспаление. Кроме этого антибиотики позволяют избавиться от болезнетворных организмов, спровоцировавших развитие флюса.
 Дополнительно в такой ситуации рекомендуется прием витаминов, таблеток и препаратов общего действия, которые предоставляют возможность укрепить иммунитет.
Дополнительно в такой ситуации рекомендуется прием витаминов, таблеток и препаратов общего действия, которые предоставляют возможность укрепить иммунитет. - Оперативный, когда уже начался воспалительный процесс и остановить его невозможно без вмешательства хирургии. Если же периостит начался из-за больного зуба, то приходится удалять зуб и, при необходимости, ставить дренаж, чтобы дать гною вытекать. Дополнительно после проведения оперативного вмешательства чаще всего пациенту назначается комплексный приём антибиотиков и иммуномодуляторов. Это позволяет полностью избавиться от инфекции и успешно укрепить иммунитет.
Если флюс уже перешел в сложную форму развития, то нередко для лечения дополнительно используется лазерная терапия, а также ионофорез.
Обратиться к врачу — лучшее решение!
Если же Вы заметили у себя хотя бы один из признаков развивающегося периостита, то немедленно надо обратиться к врачу за помощью. Помните про опасность флюса для всей полости рта. Не старайтесь вылечиться сами, без специалиста, так как это может вызвать сильное ухудшение и размножение микробов.
Не старайтесь вылечиться сами, без специалиста, так как это может вызвать сильное ухудшение и размножение микробов.
В стоматологической клинике, как правило, лечат периостит хирургическим путем. Сначала производится разрез десны, а затем при необходимости, вводится дренаж, чтобы обеспечить быстрый и лучший отток гноя. Если же периостит начался из-за больного зуба, то вместе с разрезом производят удаление зуба.
Наш подход
Клиника COMPLEX DENT максимально ответственно и внимательно подходит к лечению флюса у каждого пациента. На основании проведенной диагностики выбираем наиболее оптимальные и эффективные способы устранения периостита. Делаем всё возможное, чтобы не просто избавить Вас от флюса, но и сохранить поврежденный зуб. Успешно беремся за лечение даже самых сложных и запущенных периоститов. Не боимся трудностей, даём рекомендации по профилактике болезней и помогаем навсегда сохранить идеальную улыбку!
Flux – Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 573
- Ларри Грин
- Общественный колледж Лейк-Тахо
Вспомните, что единичный вектор нормали к поверхности может быть задан как
\[ \textbf{n} = \dfrac{\textbf{r}_u \times \textbf{r}_v}{\left| \textbf{r}_u \times \textbf{r}_v \right| }\номер\]
Существует другой выбор вектора нормали к поверхности, а именно вектор в противоположном направлении, \(-\textbf{n}\).
К этому моменту вы могли заметить сходство между формулами для единичного вектора нормали и поверхностного интеграла. Эта идея приводит нас к определению Интеграл потока. Рассмотрим жидкость, текущую через поверхность \(S\). Поток жидкости через \(S\) измеряет количество жидкости, проходящей через поверхность в единицу времени. Если поток жидкости представить векторным полем \(F\), то для небольшого участка площадью \(\Delta S\) поверхности поток будет равен
\[\Delta \text{Flux} = F \cdot n\, \Delta S \nonumber \]
Сложив все это вместе и взяв предел, мы получим
Определение: Интеграл потока
Пусть \(F\) — дифференцируемое векторное поле на поверхности \(S\), ориентированной единичным вектором нормали \(n\). Интеграл потока \(F\) через \(n\) определяется как
\[ \iint_{S} (F \cdot n) d\sigma . \номер\]
Обратите внимание, что метод выбора значения \(d\sigma\) для потока идентичен тому, как это делается для интегралов, описанных выше. Также обратите внимание, что знаменатель \(n\) и формула для \(dS\) включают \( |\textbf{r}_u \times \textbf{r}_v|\). Отменяя, получаем
Также обратите внимание, что знаменатель \(n\) и формула для \(dS\) включают \( |\textbf{r}_u \times \textbf{r}_v|\). Отменяя, получаем
\[ \textbf{n}\, dS = \textbf{r}_u \times \textbf{r}_v dv\, du\nonumber \]
для поверхности, заданной функцией \(z = g(x,y)\), мы получаем красивую формулу
\[ \textbf{n}\, dS = -g_x(x,y) \hat{\textbf{i}} – g_y(x,y)\hat{\textbf{j}} + \hat{\textbf {k}} \text{(ориентировано вверх)}\nonumber \]
или
\[ \textbf{n}\, dS = g_x(x,y) \hat{\textbf{i}} + g_y(x,y)\hat{\textbf{j}} – \hat{\textbf{ k}} \text{(ориентировано вниз)}\nonumber \]
9{2}}} = \ frac {2y \ hat {\ textbf {i}} + 2z \ hat {\ textbf {k}}} {2 \ sqrt {1}} = y \ hat {\ textbf {j}} + z\hat{\textbf{k}} \nonumber \] Далее вычисляем значение для \(d\sigma = \frac{\nabla g}{| \nabla g \cdot p|} dA \) . Обратите внимание на сходство со значением \(n\). Все, что нам нужно сделать, это найти значение \(p\). Поскольку область тени нашего цилиндра находится в плоскости xy, вектор нормали к этой области направлен в направлении \(k\). Таким образом,
Таким образом,
\[ d\sigma = \frac{\nabla g}{| \nabla g \cdot k|} dA = \frac{2}{2z} dA = \frac{1}{z} dA \nonumber \] 9{1} -2 dy \\ &= 0 \end{align*}\nonumber \]
Общий поток через поверхность равен 0,
Пример \(\PageIndex{3}\)
Найдите поток
\[ \textbf{F}(x,y,z) = x\hat{\textbf{i}} + 2y\hat{\ textbf{j}} + z\hat{\textbf{k}}\nonumber \]
по части поверхности
\[ z = x + y2 \nonumber \]
с направленной вверх нормалью, лежащей внутри поле
\( 0 \le x \le 3 \) и \( 2 \le y \le 5\)
Решение 92\,dy\,dx = -351\номер\]
- Майкл Ри (UCD)
- Ларри Грин (Общественный колледж Лейк-Тахо)
Эта страница под названием Flux распространяется по незаявленной лицензии и была создана, изменена и/или курирована Ларри Грином.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Ларри Грин
- Показать страницу TOC
- нет
- Теги
- флюс
Векторное исчисление: понимание потока – BetterExplained
Если вы интуитивно понимаете потоки, вам не нужно запоминать формулы. Осмелюсь сказать, формулы становятся «очевидными». Однако потребовалось немало усилий, чтобы по-настоящему понять, что:
Осмелюсь сказать, формулы становятся «очевидными». Однако потребовалось немало усилий, чтобы по-настоящему понять, что:
- Поток — это количество «чего-то» (электрического поля, бананов, чего угодно), проходящего через поверхность.
- Общий поток зависит от силы поля, размера поверхности, через которую оно проходит, и их ориентации.
Ваша математическая жизнь с векторным исчислением станет намного лучше, как только вы поймете потоки. А кто этого не хочет?
Физическая интуиция
Думайте о потоке как о сумме чего-то , пересекающего поверхность. Это «что-то» может быть водой, ветром, электрическим полем, бананами, чем угодно, что только можно себе представить. В учебниках по математике будут использоваться абстрактные понятия, такие как электрические поля, которые довольно сложно визуализировать. Я нахожу бананы более запоминающимися, поэтому мы будем использовать их.
Для измерения потока (например, бананов), проходящего через поверхность, нам необходимо знать
- Поверхность, которую вы рассматриваете (форма, размер и ориентация)
- Источник потока (сила поля, и каким образом оно выплевывает
банановпотока)
Сила поля важна — вы бы предпочли, чтобы горстка банкнот по 5 или 20 долларов «потекла» на ваш банковский счет? Вы бы предпочли, чтобы к вам прилетел большой или маленький банан? Нет необходимости отвечать на этот вопрос.
Фоновые идеи
Имейте в виду несколько идей при рассмотрении потока:
Векторное поле: это источник потока: объект, стреляющий бананами или проявляющий некоторую силу (например, гравитацию или электромагнетизм). Поток не обязательно должен быть физическим объектом — вы можете измерить «силу притяжения», создаваемую полем.
Поверхность: это граница, через которую проходит или на которую воздействует поток. Граница может быть сферой, плоскостью, даже верхом ведра. Обратите внимание, что граница может и не существовать — верхняя часть ведра очерчивает круг, но на самом деле дыры там нет. Мы рассматриваем поток, проходящий через область, которую определяет круг.
Время: Мы измеряем поток в один момент времени. Остановите время и спросите: «Прямо сейчас, в этот момент, сколько вещества проходит через мою поверхность?». Если ваше поле не меняется со временем, то все в порядке. Если ваше поле

Измерение: Поток является общим, а не «на единицу площади» или «на единицу объема». Поток — это общая сила, которую вы чувствуете, общее количество бананов, пролетающих над вашей поверхностью. Думайте о потоке как о весе. (Есть отдельная идея «плотности потока» (поток/объем), называемая дивергенцией, но это отдельная статья.)
Факторы потока
Источник потока оказывает огромное влияние на общий поток. Удвоение источника (удвоение «бананности» каждого банана) удвоит поток, проходящий через поверхность.
Общий поток также зависит от ориентации поля и поверхности. Когда наша поверхность полностью обращена к полю, она улавливает максимальный поток, как парус, обращенный прямо против ветра. Когда поверхность отклоняется от поля, поток уменьшается по мере того, как все меньше и меньше потока пересекает поверхность.
В итоге мы получаем нулевой поток, когда источник и граница параллельны — поток проходит через границу, но не пересекает ее. Это все равно, что держать боком ведро под водопадом. Вы не поймаете много воды (игнорируя брызги) и можете получить несколько забавных взглядов.
Это все равно, что держать боком ведро под водопадом. Вы не поймаете много воды (игнорируя брызги) и можете получить несколько забавных взглядов.
Общий поток также зависит от размера нашей поверхности. На одном и том же поле больший ковш улавливает больше потока, чем меньший. Когда мы определяем наш общий поток, нам нужно увидеть, сколько поля проходит через всю нашу поверхность.
Пока все просто, верно? Если забудете, просто подумайте о захвате воды из водопада. Какие вопросы? Сила водопада, размер ведра и ориентация ведра.
Положительный и отрицательный поток
И последняя деталь — нам нужно выбрать положительное и отрицательное направление потока. Это решение произвольное, но по соглашению (то есть ваш учитель математики накажет вас, если вы не согласны), положительных потоков покидают замкнутую поверхность , а отрицательных потоков входят в замкнутую поверхность .
Думайте о флюсе как о шланге, разбрызгивающем воду. Положительный поток означает, что поток выходит из шланга; шланг является источником флюса. Отрицательный поток подобен воде, попадающей в раковину; это поглотитель потока. Итак, положительный поток = уход, отрицательный = вход. Понятно? (Кстати, для описания полей иногда используются термины «источник» и «приемник»).
Положительный поток означает, что поток выходит из шланга; шланг является источником флюса. Отрицательный поток подобен воде, попадающей в раковину; это поглотитель потока. Итак, положительный поток = уход, отрицательный = вход. Понятно? (Кстати, для описания полей иногда используются термины «источник» и «приемник»).
Краткий обзор
Быстрая проверка: Поток зависит от
- Размер поверхности
- Величина исходного поля
- Угол между ними
Пожарный шланг, стреляющий в крошечное ведро (маленькая поверхность, большая магнитуда), может иметь такой же поток, как и садовый шланг, направленный в большое ведро (большая поверхность, малая магнитуда). И если вы забыли, поток напоминает нам держать ведро так, чтобы оно было обращено к источнику. Это должно быть очевидно — но разве вы не хотите, чтобы идеи (особенно математические!) были очевидны?
Математическая интуиция
Теперь, когда у нас есть физическая интуиция, давайте попробуем вывести математику. В большинстве случаев источник потока будет описываться как векторное поле: для заданной точки (x, y, z) существует формула, задающая вектор потока в этой точке.
В большинстве случаев источник потока будет описываться как векторное поле: для заданной точки (x, y, z) существует формула, задающая вектор потока в этой точке.
Мы хотим знать, какая часть этого векторного поля действует/проходит через нашу поверхность, принимая во внимание величину, ориентацию и размер. По нашей интуиции это должно выглядеть примерно так:
Общий поток = напряженность поля * размер поверхности * ориентация поверхности
Однако эта формула работает, только если векторное поле одинаково во всех точках. Обычно это не так, поэтому примем стандартный математический подход к решению задач:
- Разделим поверхность на части
- Найти поток на каждой детали
- Сложите малые единицы потока, чтобы получить общий поток (интегрируйте).
Давайте рискнем и назовем крошечный кусочек поверхности dS. Общий поток:
Общий поток = (напряженность поля * dS * ориентация) для каждого dS.
или
Общий поток = интеграл (напряженность поля * ориентация * dS)
Пока есть смысл? Теперь нам нужно выяснить, насколько на самом деле важна ориентация. Как мы уже говорили, если поле и поверхность параллельны, то поток равен нулю. Если они перпендикулярны, поток полный.
(На этой диаграмме поток параллелен верхней поверхности, и с этого направления ничего не поступает. Математически мы представляем поверхности их нормальный вектор , который торчит из поверхности. Не позволяйте этой бухгалтерской детали нарушить вашу визуализацию.)
Если есть угол, то он является промежуточным фактором:
Сколько именно? Ну, это работа для скалярного произведения, которое представляет собой проекцию поля на поверхность. Скалярное произведение дает нам число (от 0 до 1), которое говорит нам, какой процент поля проходит через поверхность. Итак, уравнение принимает вид:
Общий поток = интеграл (векторная напряженность поля, точка dS)
И, наконец, преобразуем в запутанное уравнение, которое вы увидите в учебнике, где F — наше поле, S — единица площади, а n — вектор нормали к поверхности:
Время для последней детали — как найти вектор нормали для нашей поверхности?
Хороший вопрос. Для такой поверхности, как плоскость, вектор нормали одинаков во всех направлениях. Для сферы вектор нормали находится в том же направлении, что и $\vec{r}$, ваше положение на сфере: вершина сферы имеет вектор нормали, выходящий из вершины; снизу один выходит снизу и т.д.
Для такой поверхности, как плоскость, вектор нормали одинаков во всех направлениях. Для сферы вектор нормали находится в том же направлении, что и $\vec{r}$, ваше положение на сфере: вершина сферы имеет вектор нормали, выходящий из вершины; снизу один выходит снизу и т.д.
Более сложные формы могут иметь вектор нормали, который сильно варьируется. В этом случае попытайтесь разбить форму на более мелкие области (такие как сферы, цилиндры и плоскости) и найти поток в каждой части. Затем сложите потоки в каждой области, чтобы получить общий поток (с учетом положительных и отрицательных потоков).
Если форма более сложная, вам может понадобиться компьютерная модель или более сложные теоремы; но по крайней мере вы знаете, что происходит за кулисами.
Примеры флюса
Давайте проведем несколько мысленных экспериментов, чтобы понять потоки. Представьте себе трубку, через которую проходит вода. Держим трубку под водопадом, ждем несколько секунд, потом спрашиваем, что такое поток. Мне нужен числовой ответ – каков поток?
Мне нужен числовой ответ – каков поток?
Вы можете подумать, что нам нужно знать скорость водопада, размер трубы, ориентацию и т. д. Но это не так.
Помните наше соглашение об ориентации потока: положительное значение означает, что поток уходит, отрицательное значение означает, что поток входит. В этом примере вода падает вниз или входит в трубу. Это означает, что верхняя поверхность имеет отрицательный поток (похоже, она откачивает воду).
Однако что происходит на дне коробки? Вода прошла через верх и теперь покидает дно, что является положительным потоком:
Ах, эта красивая диаграмма показывает, что происходит. В верхней части коробки/трубки написано, что вода поступает, а в нижней — что вода уходит. Если предположить, что одинаковое количество воды уходит и поступает (скорость падения воды постоянна), чистый поток будет равен нулю. Думайте об этом как X + (-X) = 0.
Что, если бы мы увеличили расход воды? Уменьшился? Что случилось бы?
Мой (возможно, неверный) ответ: Если мы увеличим скорость, это означает, что на короткое время войдет больше воды, чем выйдет. У нас будет мгновенный всплеск отрицательного потока (трубка будет выглядеть как раковина), пока скорости не выровняются. Наоборот, если бы мы уменьшили расход воды — у нас был бы короткий всплеск положительного потока (больше воды ушло, чем поступило), пока скорость не выровнялась.
У нас будет мгновенный всплеск отрицательного потока (трубка будет выглядеть как раковина), пока скорости не выровняются. Наоборот, если бы мы уменьшили расход воды — у нас был бы короткий всплеск положительного потока (больше воды ушло, чем поступило), пока скорость не выровнялась.
Несмотря на то, что суммарный поток равен нулю, это отличается от прохождения через каждую поверхность нулевого потока. Если вы находитесь в пустом поле, никакая форма не будет генерировать никакого потока. Но если вы находитесь в поле, где поток отменяется, изменение вашей формы или ориентации может привести к ненулевому потоку. Признайте разницу между нулевым потоком, потому что поле равно нулю, и отсутствием всего потока.
Еще один момент: рассматриваемая нами «трубка» — это область, которую мы определяем, а не физическая трубка. Измерение потока — это рисование воображаемых границ, не имеющих физической формы. Итак, когда мы определяем область «ковша», она не будет «заполняться» потоком. Поток — это то, что проходит через стенки ведра в определенный момент времени. Понятно, что если мы поместим физическое ведро, оно наполнится, но это не то, что мы измеряем. Мы видим, сколько потока войдет в область, которую мы определяем, со всех сторон (не только через отверстие). Понятно?
Поток — это то, что проходит через стенки ведра в определенный момент времени. Понятно, что если мы поместим физическое ведро, оно наполнится, но это не то, что мы измеряем. Мы видим, сколько потока войдет в область, которую мы определяем, со всех сторон (не только через отверстие). Понятно?
И еще один момент. На самом деле мы не говорили о единицах потока. В чем он измеряется? Насколько я понимаю, единицы могут быть любыми — это зависит от единицы вашего векторного поля. Таким образом, ваше векторное поле может представлять бананы, и в этом случае вы получите общее количество бананов, пересекающих поверхность. Или ваше поле может представлять количество бананов в секунду, и в этом случае вы получите количество бананов в секунду, пересекающих вашу поверхность. Единицы потока зависят от единиц вашего векторного поля.
Flux относительно прост для понимания и очень полезен в векторном исчислении и физике. Пытаться понять поток, глядя на беспорядок интегралов, — не лучший путь. Сначала получите интуитивное понимание, и детали будут иметь больше смысла.
Сначала получите интуитивное понимание, и детали будут иметь больше смысла.
Insights
Вот несколько идей, которые пришли ко мне после изучения потока:
Вы можете взять производную по времени от потока. Если векторное поле (F) изменяется со временем (t), вы можете использовать dF/dt, чтобы увидеть, как изменяется общий поток во времени. Несмотря на то, что поток берется в единицу времени, вы можете измерить поток в два последовательных момента, чтобы увидеть, как быстро он меняется.
Вы можете интегрировать поток, что означает определение того, сколько потока прошло за определенное время. Если поле F постоянно во времени, вы можете умножить поток в один момент на продолжительность. Но если F меняется со временем, то нужно измерять в каждый момент и интегрировать. Каждый расчет потока выполняется в определенный момент времени, затем они суммируются. Опять же, это стандартная техника исчисления.
В нашем примере с водопадом мы рассмотрели единственный момент времени, когда вода текла какое-то время.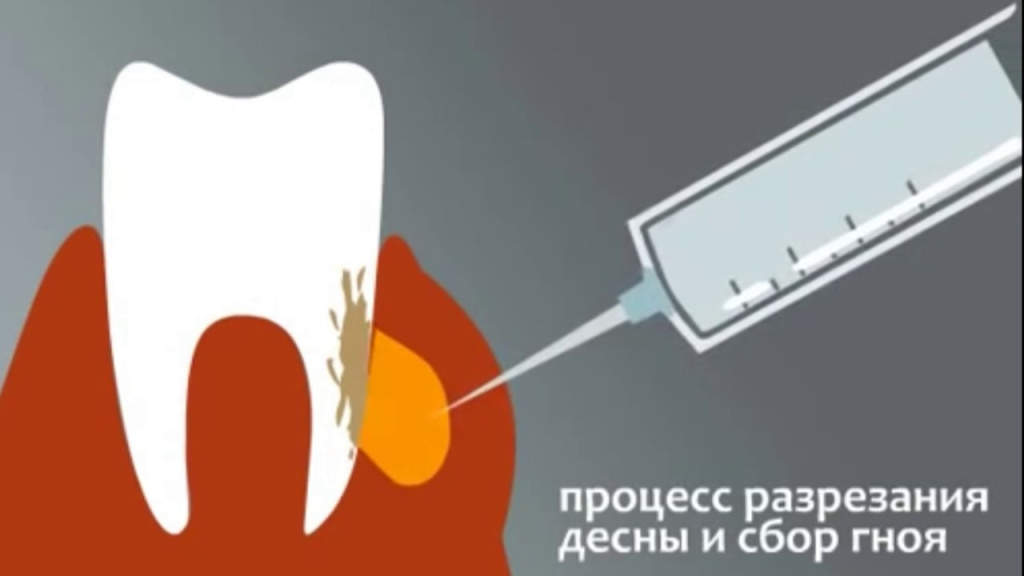


 Причинами периостита являются повреждения зубов либо десён, вызванные механическим и другими типами воздействий.
Причинами периостита являются повреждения зубов либо десён, вызванные механическим и другими типами воздействий.
 Дополнительно в такой ситуации рекомендуется прием витаминов, таблеток и препаратов общего действия, которые предоставляют возможность укрепить иммунитет.
Дополнительно в такой ситуации рекомендуется прием витаминов, таблеток и препаратов общего действия, которые предоставляют возможность укрепить иммунитет.