Как померить радиус скругления: Как измерить радиус штангенциркулем
alexxlab | 18.01.1990 | 0 | Разное
Как измерить радиус штангенциркулем
Как правильно пользоваться штангенциркулем
Штангенциркуль – высокоточный инструмент, используемый для измерения наружных и внутренних линейных размеров, глубин отверстий и пазов, разметки. Свое название этот универсальный прибор получил от линейки-штанги, которая служит основой его конструкции.
Определение показаний по нониусу
Для определения показаний штангенциркуля необходимо сложить значения его основной и вспомогательной шкалы.
- Количество целых миллиметров отсчитывается по шкале штанги слева направо. Указателем служит нулевой штрих нониуса.
- Для отсчета долей миллиметра необходимо найти тот штрих нониуса, который наиболее точно совпадает с одним из штрихов основной шкалы. После этого нужно умножить порядковый номер найденного штриха нониуса (не считая нулевого) на цену деления его шкалы.
Результат измерения равен сумме двух величин: числа целых миллиметров и долей мм. Если нулевой штрих нониуса точно совпал с одним из штрихов основной шкалы, полученный размер выражается целым числом.
На рисунке выше представлены показания штангенциркуля ШЦ-1. В первом случае они составляют: 3 + 0,3 = 3,3 мм, а во втором — 36 + 0,8 = 36,8 мм.
Нониус с ценой деления 0,05 мм
Шкала прибора с ценой деления 0,05 мм представлена ниже. Для примера приведены два различных показания. Первое составляет 6 мм + 0,45 мм = 6,45 мм, второе — 1 мм + 0,65 мм = 1,65 мм.
Аналогично первому примеру необходимо найти штрихи нониуса и штанги, которые точно совпадают друг с другом. На рисунке они выделены зеленым и черным цветом соответственно.
Устройство механического штангенциркуля
Устройство двустороннего штангенциркуля с глубиномером представлено на рисунке. Пределы измерений этого инструмента составляют 0—150 мм. С его помощью можно измерять как наружные, так и внутренние размеры, глубину отверстий с точностью до 0,05 мм.
Основные элементы
- Штанга.
- Рамка.
- Губки для наружных измерений.
- Губки для внутренних измерений.

- Линейка глубиномера.
- Стопорный винт для фиксации рамки.
- Шкала нониуса. Служит для отсчета долей миллиметров.
- Шкала штанги.
Губки для внутренних измерений 4 имеют ножевидную форму. Благодаря этому размер отверстия определяется по шкале без дополнительных вычислений. Если губки штангенциркуля ступенчатые, как в устройстве ШЦ-2, то при измерении пазов и отверстий к полученным показаниям необходимо прибавлять их суммарную толщину.
Величина отсчета по нониусу у различных моделей инструмента может отличаться. Так, например, у ШЦ-1 она составляет 0,1 мм, у ШЦ-II 0,05 или 0,1 мм, а точность приборов с величиной отсчета по нониусу 0,02 мм приближается к точности микрометров. Конструктивные отличия в устройстве штангенциркулей могут быть выражены в форме подвижной рамки, пределах измерений, например: 0–125 мм, 0–500 мм, 500–1600 мм, 800–2000 мм и т.д. Точность измерений зависит от различных факторов: величины отсчета по нониусу, навыков работы, исправного состояния инструмента.
Порядок проведения измерений, проверка исправности
Перед работой проверяют техническое состояние штангенциркуля и при необходимости настраивают его. Если прибор имеет перекошенные губки, пользоваться им нельзя. Не допускаются также забоины, коррозия и царапины на рабочих поверхностях. Необходимо, чтобы торцы штанги и линейки-глубиномера при совмещенных губках совпадали. Шкала инструмента должна быть чистой, хорошо читаемой.
- Губки штангенциркуля плотно с небольшим усилием, без зазоров и перекосов прижимают к детали.
- Определяя величину наружного диаметра цилиндра (вала, болта и т. д.), следят за тем, чтобы плоскость рамки была перпендикулярна его оси.
- При измерении цилиндрических отверстий губки штангенциркуля располагают в диаметрально противоположных точках, которые можно найти, ориентируясь по максимальным показаниям шкалы. При этом плоскость рамки должна проходить через ось отверстия, т.е. не допускается измерение по хорде или под углом к оси.

- Чтобы измерить глубину отверстия, штангу устанавливают у его края перпендикулярно поверхности детали. Линейку глубиномера выдвигают до упора в дно при помощи подвижной рамки.
- Полученный размер фиксируют стопорным винтом и определяют показания.
Работая со штангенциркулем, следят за плавностью хода рамки. Она должна плотно, без покачивания сидеть на штанге, при этом передвигаться без рывков умеренным усилием, которое регулируется стопорным винтом. Необходимо, чтобы при совмещенных губках нулевой штрих нониуса совпадал с нулевым штрихом штанги. В противном случае требуется переустановка нониуса, для чего ослабляют его винты крепления к рамке, совмещают штрихи и вновь закрепляют винты.
Источник: tehnouzel.ru
Примеры измерений штангенциркулем
Штангенциркуль – удобный и простой в обращении измерительный инструмент. Грамотное его применение позволяет выполнять замеры линейных величин в различных ситуациях, и для разнообразных объектов, начиная от протектора шин, и заканчивая пластиковыми гибкими трубками.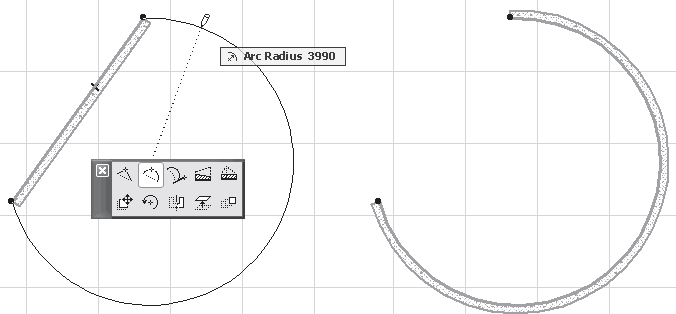 Как измерять штангенциркулем – примеры и последовательность – эти вопросы рассматриваются далее.
Как измерять штангенциркулем – примеры и последовательность – эти вопросы рассматриваются далее.
Замеры при конструировании и изготовлении резьбовых соединений
Соединение типа «болт-гайка» — одно из наиболее распространённых в механике. При разработке и изготовлении конструкций задача – как измерить болт штангенциркулем – часто представляет трудности.
Перед работами стоит вспомнить, что главными размерами болта /гайки являются длина изделия и диаметр резьбы. Стандартный болт любого исполнения в проведении таких измерений не нуждается. Иное дело, когда болт изготовлен в кустарных условиях, либо требуется замерить крепёжную деталь без демонтажа соединения. Здесь возможны следующие ситуации:
- Между головкой и противоположным торцом стержня имеется плоскость или деталь/плита, размеры которой не позволяют ввести измерительные губки штангенциркуля. В этом случае, используя основную измерительную шкалу и глубиномер (иногда именуемый «колумбиком»), определяют последовательно высоту головки, толщину шайбы (если есть), толщину промежуточного элемента и высоту выступающей с противоположной стороны соединения части детали.
 Полученный результат складывают, а затем по таблицам соответствия длин стержня и размеров «под ключ», которыми обладает болт, устанавливают типоразмер крепёжной детали.
Полученный результат складывают, а затем по таблицам соответствия длин стержня и размеров «под ключ», которыми обладает болт, устанавливают типоразмер крепёжной детали.Измерение внутренний резьбы и оттиск ниток резьбы
Измерение шага резьбы
Замеры размеров рисунка на протекторах
Как измерить протектор шин, если необходимо оценить степень износа? Поможет глубиномер, которым выполняются измерения по всей образующей протектора шины. Следует учесть, что износ практически всегда неравномерен, и количество замеров должно быть не менее 3…5, причём на равномерно принятых для оценки участках протектора шины. Перед измерениями покрышку следует тщательно очистить от грязи, пыли и фрагментов мелких камней, застрявших внутри.
Измерение протектора шин цифровым глубомером
Иногда требуется решить задачу – как измерить протектор шин штангенциркулем, чтобы определить степень равномерности износа. Этим устанавливается износ шин протектора не только по глубине, но и по радиусу перехода от окружности выступов к окружности впадин. Поступают так. Измеряют глубину рисунка на новом протекторе шины, а затем — линейный размер визуально изменённой зоны на эксплуатировавшейся детали. Разница определит степень износа и поможет принять верное решение о замене колеса.
Поступают так. Измеряют глубину рисунка на новом протекторе шины, а затем — линейный размер визуально изменённой зоны на эксплуатировавшейся детали. Разница определит степень износа и поможет принять верное решение о замене колеса.
Все измерения производят глубиномером, который должен быть установлен строго перпендикулярно образующей протектора шины.
Измерение износ протектора колумбиком
Измерения диаметров
Как измерить диаметр штангенциркулем? Различают детали с постоянным и переменным по длине сечением. К последним относятся, в частности, арматурные стержни. Как измерить диаметр арматуры штангенциркулем? Всё зависит от арматурного профиля, который может быть:
Измерение внутреннего диаметра штангенциркулем
Проще всего замерять такие параметры арматуры во втором случае. Вначале внешними измерительными губками определяют высоту выступов профиля, а затем глубиномером – размер по впадине. Замеры необходимо производить в двух взаимно перпендикулярных направлениях, поскольку арматура, да ещё производимая не на специализированных предприятиях, часто имеет овальность сечения.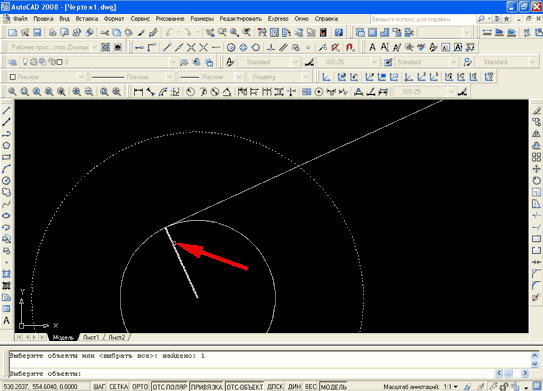 После этого по таблицам стандартных арматурных профилей отыскивают максимально подходящее значение (особой точности здесь не требуется). Как измерить диаметр арматуры штангенциркулем, если она имеет другой тип профиля? Здесь вместо диаметра выступов определяют диаметр выступающей части серповидных насечек, а далее поступают так же, как и предыдущем случае.
После этого по таблицам стандартных арматурных профилей отыскивают максимально подходящее значение (особой точности здесь не требуется). Как измерить диаметр арматуры штангенциркулем, если она имеет другой тип профиля? Здесь вместо диаметра выступов определяют диаметр выступающей части серповидных насечек, а далее поступают так же, как и предыдущем случае.
Измерение наружного диаметра трубы
При измерении внутренних габаритов труб используют внутреннюю измерительную шкалу инструмента. Как измерить штангенциркулем толщину трубы, особенно, если зазор невелик? Достаточно вычислить разницу между внешним и внутренним диаметрами и разделить результат на два.
Измерения линейных размеров
Как измерить линейные размеры с помощью штангенциркуля? Всё зависит от материала детали/заготовки. Для жёстких элементов изделие плотно прижимается к какой-нибудь опорной плите, после чего внешними измерительными губками инструмента производят измерение.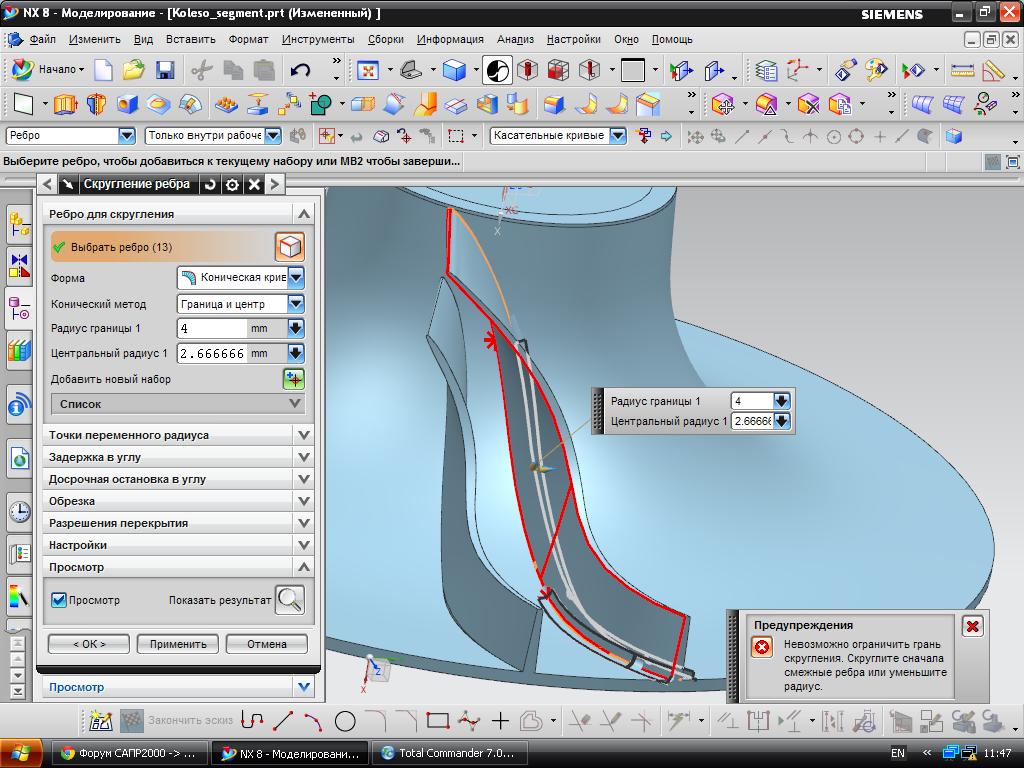 Предварительно следует установить пригодность имеющегося типа штангенциркуля работе. Например, основная измерительная шкала на штанге должна быть длиннее детали на менее, чем на 25…30 мм (с учётом собственной ширины губок). При использовании глубиномера эта величина ещё меньше, поскольку в расчёт следует принимать и длину рамки (для наиболее часто встречающихся инструментов 0-150 мм и точностью от 0,05 до 0,1 мм этот параметр принимается не менее 50 мм).
Предварительно следует установить пригодность имеющегося типа штангенциркуля работе. Например, основная измерительная шкала на штанге должна быть длиннее детали на менее, чем на 25…30 мм (с учётом собственной ширины губок). При использовании глубиномера эта величина ещё меньше, поскольку в расчёт следует принимать и длину рамки (для наиболее часто встречающихся инструментов 0-150 мм и точностью от 0,05 до 0,1 мм этот параметр принимается не менее 50 мм).
Как измерить штангенциркулем сечение провода? Неметаллические изделия гибки, а потому существенно искажают результат, полученный обычным способом. Поэтому в кембрик следует ввести жёсткую стальную деталь (винт, гвоздь, кусок прутка), после чего внешними губками определить диаметр сечения провода. Аналогично поступают, если требуется узнать внутренний размер провода.
Измерение диаметра провода
Вопрос – как измерить цепь штангенциркулем – часто задают велосипедисты, поскольку износ цепи, определяемый как расстояние между её смежными звеньями, позволяет принять решение о замене изделия. Наружное губки устанавливают на расстояние 119 мм и вводят в звено, после чего растягивают их в стороны, пока дальнейшее увеличение размера окажется невозможным (для облегчения работ цепь можно предварительно нагрузить растягивающим усилием). Отклонение от первоначального размера покажет фактический износ, который далее необходимо сравнить с максимально допустимым.
Наружное губки устанавливают на расстояние 119 мм и вводят в звено, после чего растягивают их в стороны, пока дальнейшее увеличение размера окажется невозможным (для облегчения работ цепь можно предварительно нагрузить растягивающим усилием). Отклонение от первоначального размера покажет фактический износ, который далее необходимо сравнить с максимально допустимым.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Источник: stankiexpert.ru
Как пользоваться штангенциркулем
Штангенциркулем можно измерять как наружные и внутренние размеры, так и глубину. Ко всему прочему штангенциркуль очень точный измерительный прибор и им можно измерить даже десятые (а порой и сотые) миллиметра.
Постоянные посетители моего канала наверно заметили, что я очень часто использую при измерении штангенциркуль, это не прихоть или понт, это реально очень удобный для измерений инструмент. Рулетка и линейка это конечно круто, но такой точности мы на них однозначно не получим. Давайте сначала представим себе, что из себя представляет этот самый штангенциркуль и как называются его части.
Давайте сначала представим себе, что из себя представляет этот самый штангенциркуль и как называются его части.
Теперь когда я буду говорить о какой то части это замечательного измерительного прибора, вы хотя бы будете знать о чем идет речь.
Начнем с простого, давайте измерим наружный размер какой нить деревяшки. Для этого просто нужно сомкнуть губки для наружных измерений на брусочке
Линейка на подвижной раме называется НОНИУС, теперь смотрим рядом с какой цифрой на шкале встал ноль нониуса.
Ширина нашего брусочка почти 38 мм. В конце я объясню как мерять десятые миллиметра штангенциркулем, пока же общие данные.
Теперь давайте измерим внутренний размер квадрат трубы. Для этого нужно сомкнуть губки для внутренних измерений внутри квадрат трубы.
И снова смотри с какой цифрой на шкале встал ноль нониуса.
Линейкой глубиномера удобно измерять отверстия, что бы знать на какую глубину уже просверлили. Я буду мерять высоту этого квадрата, что бы было видно как работает глубиномер. Ставим штангу на деталь и опускаем подвижную рамку до упора вниз.
Ставим штангу на деталь и опускаем подвижную рамку до упора вниз.
Опять смотри с какой цифрой на шкале встал ноль нониуса.
Ну а теперь давайте научимся измерять десятые (или сотые, смотря какой штангенциркуль).
Внимание на фото
Если вы были внимательны, то заметили, что на нониусе есть своя шкала — это и есть десятые и соты. Сначала обратим внимание на право, там написан чем равен один шаг, на этом штангенциркуле он равен 0,05 мм. Целое число миллиметров у нас равно 30, его мы видим слева где ноль нониуса. Теперь смотрим где сошлись палочки на шкале и нониусе, видим что между 5 и 6. Цифра 5 равна пяти десятым миллиметра, а следующий шаг равен 0,05 итого у нас вышло 0,55, плюсуем к этому целое значение 30 и получаем точно значение до сотых 30,55 миллиметра.
Источник: zen.yandex.ru
Штангенциркуль: измеряем правильно
При выполнении любых столярных или слесарных работ нужно знать, как измерять штангенциркулем, а также уметь им пользоваться. Этот распространенный универсальный метрический инструмент применяется для снятия внутренних и внешних линейных размеров с детали. Штангенциркуль позволяет произвести измерение диаметров (внутренних и внешних) и глубину отверстия.
Этот распространенный универсальный метрический инструмент применяется для снятия внутренних и внешних линейных размеров с детали. Штангенциркуль позволяет произвести измерение диаметров (внутренних и внешних) и глубину отверстия.
Конструктивные элементы приборов
Штангенциркуль устроен просто, работать им легко и удобно. Любая его модификация состоит из следующих конструктивных элементов:
- Измерительная линейка (штанга) – главная часть прибора, на верхней поверхности которого нанесена шкала разметки с градацией в 1 мм. Стандартная линейка имеет длину 150 мм. Этот показатель определяет максимально доступную величину измерения. Выпускаются приборы, имеющие более длинную штангу, для замеров больших деталей.
- Измерительная рамка – подвижный элемент прибора, перемещающийся по линейке. Внутри рамки размещена плоская пружина, которая плотно прижимает ее к штанге. На рамке имеется дополнительная измерительная шкала (нониус), по которой отсчитываются десятые или сотые доли миллиметра при совмещении с одним из штрихов основной шкалы.

- Неподвижные губки. Один элемент жестко прикреплен к штанге, другой закреплен на рамке и перемещаются вместе с ней. Рабочая поверхность внутри. Используются для наружных замеров.
- Подвижные губки. Рабочие элементы располагаются по тому же принципу, что большие неподвижные губки, но размещены по другую сторону линейки. Рабочая поверхность обращена наружу. Дополнительные губки применяются для внутренних замеров.
- Линейка глубиномера – выдвигающаяся планка, жестко соединенная с двигающейся рамкой.
Разновидности и маркировка
По конструкции и своему назначению штангенциркули бывают следующих видов:
- ШЦ-1. Рабочие губки размещены с 2 сторон. Применяется для проведения наружных и внутренних измерений. Оснащены стержнем для измерения уступов и глубин. Удобны для разметочных работ.
- ШЦ-2. Губки для внутренних и наружных замеров совмещены и имеют одинаковый размер.
 При этом плоские рабочие поверхности располагаются внутри, а цилиндрические повернуты наружу. С противоположной стороны от штанги находятся разметочные остро заточенные кромки. Дополнительно прибор оснащен рамкой микрометрической подачи, с помощью которой можно производить более точные измерения.
При этом плоские рабочие поверхности располагаются внутри, а цилиндрические повернуты наружу. С противоположной стороны от штанги находятся разметочные остро заточенные кромки. Дополнительно прибор оснащен рамкой микрометрической подачи, с помощью которой можно производить более точные измерения. - ШЦ-3. Одностороннее размещение измерительных губок. Специфика этих моделей в том, что они предназначены для больших замеров.
Штангенциркули делятся по способу снятия результата замеров:
- Нониусные (ШЦ). Механический инструмент, в котором целые миллиметры отмечаются на основной шкале, а доли миллиметра отсчитываются с помощью нониусной шкалы.
- Циферблатные (ШЦК). Используется механический принцип замера. На подвижной рамке размещен циферблат, который соединяется со штангой с помощью зубчатой передачи. Миллиметры определяются по основной разметке, а доли по круговой шкале.
- Цифровые (ШЦЦ). На измерительной рамке размещен цифровой дисплей, который показывает результаты измерения.
 Электронный модуль имеет ряд удобных настроек.
Электронный модуль имеет ряд удобных настроек.
Тип индикатора определяет, с какой точностью штангенциркуль снимает показания. Нониусные приборы считаются менее точными, но в использовании они просты и надежны. Циферблатный инструмент точнее и удобнее, но зубчатая рейка может загрязняться от деталей. Цифровой штангенциркуль позволяет производить замеры с высокой точностью, но зависит от температурных перепадов.
Правила эксплуатации штангенциркуля
Прежде чем приступать к замерам, нужно проверить инструмент. Для этого губки ШЦ сводят вместе и смотрят на просвет, нет ли между ними зазора. Нужно проверить и совпадение шкал на нуле. Прибор должен быть чистым, особенно подвижные части. Результат замера будет более точным, т. к. ржавчина и грязь сильно увеличивают погрешность измерения.
С помощью ШЦ можно определить размеры внешнего и внутреннего диаметра, толщину поверхности и глубину выемки или уступа. Во время проведения работ нужно знать, в каком положении должны находиться губки штангенциркуля при измерении и как правильно снять показания.
Как правильно измерять штангенциркулем наружные поверхности
Для снятия наружных размеров (толщины) нужно развести губки штангенциркуля, поместить между ними измеряемый предмет, затем сдвинуть губки и слегка сжать. Измерительные кромки должны располагаться параллельно поверхности заготовки. Деление на основной шкале штангенциркуля, совместившееся с нулевой риской дополнительной шкалы, будет обозначать целые миллиметры. Риска, которая на нониусе совпадет с риской на штанге, определяет десятые доли миллиметра.
Аналогичным образом измеряется внешний диаметр трубы, при этом губки должны касаться диаметрально противоположных точек на наружном диаметре изделия. Таким же образом измеряются и другие детали, имеющие круглое сечение: кабель, размер болта и пр.
Как измерить штангенциркулем внутренний диаметр детали
Для замера внутреннего диаметра требуется сдвинуть штанги губки в нулевое положение и ввести в отверстие параллельно измеряемой плоскости. Затем их нужно развести до упора, при этом стараясь добиться максимального значения показаний. Этим же способом штангенциркулем проверяют расстояние между параллельными плоскостями, только стараются получить минимальные показания шкалы. Диаметр отверстия от сверла небольшого диаметра замерить не удастся, все определяется толщиной губок.
Затем их нужно развести до упора, при этом стараясь добиться максимального значения показаний. Этим же способом штангенциркулем проверяют расстояние между параллельными плоскостями, только стараются получить минимальные показания шкалы. Диаметр отверстия от сверла небольшого диаметра замерить не удастся, все определяется толщиной губок.
Определение глубины
Воспользовавшись выдвижной линейкой глубиномера штангенциркуля можно замерить глубину отверстия или высоту уступа. Для этого выдвигают глубиномер и опускают его в отверстие до соприкосновения с дном. Он должен располагаться параллельно поверхностям объекта. Затем торец штанги прибора двигают обратно на измерительную планку до упора в верхний край измеряемой детали.
Замер резьбовых соединений
Штангенциркулем можно осуществлять замеры резьбовых соединений. Диаметры резьбы могут быть измерены по выступам. Болт зажимается между губок вертикально, затем снимаются показания.
Для того чтобы замерить штангелем шаг резьбы, нужно произвести замер внешнего диаметра и высоту стержня и подсчитать количество витков резьбы. Шаг резьбы получится в результате деления длины стержня на число витков. Используя функцию микроподачи (если она есть), можно замерить шаг измерительными губками штангенциркуля. Для этого они размещаются на одинаковых склонах.
Шаг резьбы получится в результате деления длины стержня на число витков. Используя функцию микроподачи (если она есть), можно замерить шаг измерительными губками штангенциркуля. Для этого они размещаются на одинаковых склонах.
Как правильно хранить инструмент
Штангенциркуль считается высокоточным метрическим инструментом, поэтому обращаться с ним нужно бережно. Хранить его необходимо в пластиковом или деревянном футляре. Допускается и мягкий чехол, но следует избегать случайных деформаций. Держать прибор нужно в сухом месте, где исключены случайные падения тяжелых предметов, а также загрязнение пылью, грязью, опилками прочим мусором. При соблюдении этих условий инструмент будет вам исправно служить многие годы.
Источник: instrumentyvdom.ru
Как измерить радиус штангенциркулем
Измерение штангенциркулем
При разметке и обработке деталей широко используется контрольно-измерительный инструмент. С простейшим из них — измерительной линейкой вы уже знакомы. Она позволяет определить размеры деталей с точностью до 1 мм. Для измерения с большей точностью (до 0,1 мм) применяют штангенциркуль. Это универсальный измерительный инструмент. С его помощью можно измерять наружные и внутренние размеры деталей и глубину отверстия.
С простейшим из них — измерительной линейкой вы уже знакомы. Она позволяет определить размеры деталей с точностью до 1 мм. Для измерения с большей точностью (до 0,1 мм) применяют штангенциркуль. Это универсальный измерительный инструмент. С его помощью можно измерять наружные и внутренние размеры деталей и глубину отверстия.
В немецком языке штангенциркулем (Stangenzirkel) называется циркуль для начертания окружностей и дуг больших радиусов. По-немецки штангенциркуль называется Messschieber или Schieblehre — соответственно, «раздвижной измеритель» или «раздвижная линейка».
Разновидность штангенциркуля, оснащённая глубиномером на профессиональном сленге называется «Колумбус» или «Колумбик». Это название произошло от «Columbus» — производителя измерительного инструмента, такой штангенциркуль массово поставлялся в СССР под этой маркой.
В авиационной промышленности такие штангенциркули назывались «Маузер», по причине того что штангенциркули повышенного качества поставлялись в СССР фирмой «Маузер»
Штангенциркули бывают разных видов, они отличаются пределами и точностью измерения. На рисунке справа показан штангенциркуль ШЦ-1. Он состоит из штанги с неподвижными губками 1 и 2, по которой перемещается рамка 4 с подвижными губками 3 и 8. Рамку можно закреплять в нужном положении стопорным винтом. На штанге 5 нанесены деления, которые образуют миллиметровую шкалу. Цена ее деления—1 мм. Длина миллиметровой шкалы — 150 мм.
На подвижных губках нанесена вспомогательная шкала, называемая нониусом (рис. слева). Она разделена на 10 равных частей, а вся длина нониусной шкалы составляет 19 мм. Значит, длина каждой части равна 1,9 мм. Эта величина является ценой деления нониуса.
Она разделена на 10 равных частей, а вся длина нониусной шкалы составляет 19 мм. Значит, длина каждой части равна 1,9 мм. Эта величина является ценой деления нониуса.
При измерении штангенциркулем целое число миллиметров отсчитывают по миллиметровой шкале до нулевого штриха нониуса, а десятые доли миллиметра — по шкале нониуса начиная от нулевой отметки до той риски, которая совпадает с какой-либо риской миллиметровой шкалы (рис. справа). На рисунке показаны положение шкал штангенциркуля при отсчёте размеров: а – 0,5 мм; б – 6,9 мм; в – 34,3 мм.
Перед началом измерений штангенциркулем надо осмотреть его и проверить на точность. Для этого надо совместить губки инструмента. При этом нулевые риски обеих шкал должны совпасть. Одновременно должен совместиться десятый штрих нониуса с девятнадцатым штрихом миллиметровой шкалы.
Штангенциркуль ШЦ-II (см. рис. слева) можно применять не только для измерения, но и для разметки. С его помощью наносят прямые риски от строго прямолинейных базовых кромок или поверхностей заготовок, делают засечки, проводят окружности.
С его помощью наносят прямые риски от строго прямолинейных базовых кромок или поверхностей заготовок, делают засечки, проводят окружности.
Штангенциркуль является дорогостоящим и точным инструментом, поэтому бережное обращение с ним должно быть основным правилом работы. Перед началом работы штангенциркуль протирают чистой мягкой тканью, удалив смазку и пыль (особенно тщательно очищают измерительные поверхности). Нельзя очищать инструмент шлифовальной шкуркой или ножом. Измерять можно только чистые и сухие плоскости деталей, без задиров, заусенцев, стружки и царапин. Инструмент нельзя класть на нагревательные приборы и держать на солнце. Измерение следует выполнять чистыми и сухими руками.
Измеряя деталь, нельзя допускать перекоса губок штангенциркуля. Положение их обязательно фиксируется стопорным винтом.
Читая показания штангенциркуля, надо держать его прямо перед глазами.
Губки штангенциркуля имеют острые концы, поэтому при пользовании им соблюдайте осторожность.
Штангенциркуль должен лежать на рабочем месте так, чтобы им было удобно пользоваться. На него не должны попадать стружки, опилки.
После работы штангенциркуль надо протереть чистой ветошью.
Ниже вы можете проверить свои умения пользования штангенциркулем.
1.Выбираете заготовку
2.Находите на шкалах штангенциркуля(справа) размер.
3.Вписываете в прямоугольник внизу полученное значение и получаете оценку вашего ответа
ШЦК — (штангенциркуль с круговой шкалой). В выемке штанги размещена рейка, с которой сцеплена шестерёнка головки, поэтому показания штангенциркуля, отвечающие положению губок, читают по шкале штанги и круговой шкале головки по положению стрелки. Это значительно проще, быстрее, чем чтение отсчёта по нониусу.
ШЦЦ — с цифровой индикацией (электронный) может измерять с точностью до сотых долей миллиметра.
Источник: technologys.info
Радиусы скруглений. Размеры и предельные отклонения
Источник: ОСТ 92-0093-69Рис 1. Размеры и предельные отклонения радиусов скруглений и фасок для сопряжений типа “вал – отверстие”
Таблица 1. Рекомендуемый подбор сопряжений радиуса с радиусом и радиуса с фаской, мм
|
Диаметр вала d |
Радиус вогнутой поверхности |
Радиус выпуклой поверхности и фаска |
||
|
r |
Предельное отклонение |
r1=C |
Предельное отклонение |
|
|
|
0,05 |
-0,03 |
0,1 |
0,05 |
|
От 0,5 до 1 |
0,1 |
-0,05 |
0,2 |
0,1 |
|
Св. |
0,2 |
-0,1 |
0,3 |
0,2 |
|
3 – 6 |
0,3 |
-0,2 |
0,5 |
0,3 |
|
6 – 10 |
0,5 |
-0,3 |
0,8 |
|
|
10 – 14 |
0,8 |
1,0 |
||
|
14 – 18 |
1,0 |
1,6 |
0,5 |
|
|
18 – 30 |
1,6 |
-0,5 |
2,0 |
|
|
30 – 50 |
2,0 |
2,5 |
||
|
50 – 80 |
2,5 |
3,0 |
||
|
80 – 120 |
3,0 |
4,0 |
1,0 |
|
|
120 – 180 |
4,0 |
-1,0 |
5,0 |
|
|
180 – 220 |
5,0 |
6,0 |
||
|
220 – 260 |
6,0 |
8,0 |
2,0 |
|
|
260 – 360 |
8,0 |
-2,0 |
10,0 |
|
|
360 – 500 |
10,0 |
12,0 |
||
Таблица 2.
 Размеры и предельные отклонения радиусов скруглений или фасок для сопрягаемых поверхностей валов и втулок, мм
Размеры и предельные отклонения радиусов скруглений или фасок для сопрягаемых поверхностей валов и втулок, мм
|
Номинальный диаметр |
r или С |
Предельное отклонение |
Номинальный диаметр |
r или С |
Предельное отклонение |
|
До 0,5 |
0,05 |
± 0,03 |
Св. |
2,0 |
± 0,5 |
|
От 0,5 до 1 |
0,1 |
± 0,05 |
50 – 80 |
2,5 |
|
|
Св. 1 – 3 |
0,2 |
± 0,1 |
80 – 120 |
3,0 |
|
|
3 – 6 |
0,3 |
± 0,2 |
120 – 180 |
4,0 |
± 1 |
|
6 – 10 |
0,5 |
± 0,3 |
180 – 260 |
5,0 |
|
|
10 – 18 |
1,0 |
± 0,5 |
260 – 360 |
6,0 |
|
|
18 – 30 |
1,6 |
При применении радиусов скруглений или фасок размером св. 6 до 10 мм предельное отклонение ±1,5 мм; св. 10 до 20 – ±2 мм; св. 20 до 32 – ±2,5 мм и свыше 32 – ±3 мм.
6 до 10 мм предельное отклонение ±1,5 мм; св. 10 до 20 – ±2 мм; св. 20 до 32 – ±2,5 мм и свыше 32 – ±3 мм.
Таб 3. и Рис.2 Размеры и предельные отклонения радиусов скруглений валов и корпусов, сопрягаемых с шарико- и роликоподшипниками, мм
|
Радиус подшипника |
r |
0,2 |
0,3 |
0,4 |
0,5 |
0,8 |
1,0 |
1,2 |
1,5 |
2,0 |
2,5 |
|
Радиус вала или корпуса |
r1 |
0,1 |
0,2 |
0,3 |
0,5 |
0,6 |
0,8 |
1,0 |
1,6 |
||
|
Пред. |
-0,05 |
-0,1 |
-0,2 |
-0,3 |
-0,5 |
||||||
|
Радиус подшипника |
r |
3,0 |
3,5 |
4,0 |
5,0 |
6,0 |
8,0 |
10 |
12 |
15 |
18 |
|
Радиус вала или корпуса |
r1 |
2,0 |
2,5 |
3,0 |
4,0 |
5,0 |
6 |
8 |
10 |
12 |
|
|
Пред. |
-0,5 |
-1,0 |
-2,0 |
||||||||
Рис 3. и Таб 4. Размеры фасок и радиусов и предельные отклонения на механически обрабатываемые плоские детали
|
С=r |
0,2 |
0,5 |
0,8 |
1,0 |
1,6 |
2,0 |
2,5 |
3,0 |
4,0 |
5,0 |
6,0 |
8,0 |
|
Предельное отклонение |
± 0,1 |
± 0,2 |
± 0,5 |
± 1,0 |
± 2,0 |
|||||||
Рис.
 4 и Таб. 5. Размеры и предельные отклонения фасок на валах под запрессовку
4 и Таб. 5. Размеры и предельные отклонения фасок на валах под запрессовку
|
d1 |
0,6 |
0,8 |
1 |
1,2 |
1,6 |
2,0 |
2,5 |
3 |
4 |
5 |
6 |
8 |
10 |
|
c1 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
1,0 |
1,2 |
1,6 |
||
|
предельное отклонение |
± 0,05 |
± 0,1 |
± 0,2 |
± 0,4 |
|||||||||
|
d1 |
от 10 до 20 |
от 20 до 30 |
от 30 до 50 |
свыше 50 |
|
c1 |
2 |
3 |
4 |
5 |
|
предельное отклонение |
± 0,4 |
± 0,6 |
||
Таб.
 6
6
|
с1 |
0,1 |
от 0,2 до 0,3 |
от 0,4 до 1,0 |
свыше 1 |
|
r |
0,1 |
0,2 |
0,3 |
0,8 |
|
предельное отклонение |
± 0,05 |
± 0,1 |
± 0,1 |
± 0,5 |
Рис.
 5 и Таб.7. Размеры и предельные отклонения фасок на втулках под запрессовку
5 и Таб.7. Размеры и предельные отклонения фасок на втулках под запрессовку
|
S |
от 1 до 1,5 |
от 1,5 до 2 |
от 2 до 3 |
от 3 до 4 |
от 4 до 5 |
от 5 до 8 |
свыше 8 |
|
C2 |
0,3 |
0,5 |
0,8 |
1,0 |
2,0 |
3,0 |
4,0 |
|
предельное отклонение |
± 0,1 |
± 0,2 |
± 0,4 |
± 06 |
|||
|
C3 |
0,4 |
0,5 |
0,5 |
0,5 |
1,0 |
1,0 |
1,6 |
|
предельное отклонение |
± 0,2 |
± 0,4 |
|||||
Примечание: величину радиуса скругления и предельные отклонения на него выбирать по таблице 5.
Размеры радиусов и фасок сопрягаемых поверхностей типа “вал – отверстие”, валов и корпусов с шарико- и роликоподшипниками, а также валов и втулок под запрессовки, должны быть указаны в чертежах с числовыми значениями предельных отклонений.
Размеры радиусов скруглений и фасок несопрягаемых поверхностей валов и втулок и размеры фасок и радиусов на плоских деталях должны быть указаны в чертежах. Предельные отклонения этих размеров на изображении не наносятся, а в технических требованиях чертежа пишется: “Неуказанные предельные отклонения размеров радиусов и фасок по ОСТ 92-0093-69”.
Предельные отклонения на угловые размеры фасок ± 3°.
К оглавлению
Радиус закругления. Скругление с переменным радиусом
Радиус закругления
Стоя близ одного из таких закруглений, могли бы вы определить величину его радиуса? Это не так легко, как найти радиус дуги, начерченной на бумаге. На чертеже дело просто: вы проводите две произвольные хорды и из середин их восставляете перпендикуляры: в точке их пересечения лежит, как из-вестно, центр дуги; расстояние его от какой-либо точки кривой и есть искомая длина радиуса.
Но сделать подобное же построе-ние на местности было бы, конечно, очень неудобно: ведь центр закруг-ления лежит в расстоянии 1-2 км от дороги, зачастую в недоступном ме-сте. Можно было бы выполнить по-строение на плане, но снять закругле-ния на план – тоже нелегкая работа.
Все эти затруднения устраняются, если прибегнуть не к построению, а вычислению радиуса. Для этого можно воспользоваться следующим приемом. Дополним (рис. 84) мысленно дугу АВ закругления до окружности. Соединив произвольные точки С и D дуги закругления, измеряем хорду CD , а также «стрелку» EF (т, е, высоту сегмента CED ). По этим двум данным уже нетрудно вычислить искомую длину радиуса. Рас-сматривая прямые CD и диаметр круга как пересекающиеся хорды, обозначим длину хорды через а , длину стрелки через h , радиус через R ; имеем:
и искомый радиус 1)
Например, при стрелке в 0,5 м и хорде 48 м искомый радиус
Это вычисление можно упростить, если считать 2 R -h равным 2 R – вольность позволительная, так как h весьма мало по сравнению с R (ведь R – сотни метров, а h – единицы их). Тогда получается весьма удобная для вычислений приближен-ная формула
Тогда получается весьма удобная для вычислений приближен-ная формула
Применив ее в сейчас рассмотренном случае, мы получили бы ту же величину
R = 580.
Вычислив длину радиуса закругления и зная, кроме того, что центр закругления находится на перпендикуляре к середине хорды, вы можете приблизительно наметить и то место, где должен лежать центр кривой части дороги.
Если на дороге уложены рельсы, то нахождение радиуса закругления упрощается. В самом деле, натянув веревку по касательной к внутреннему рельсу, мы получаем хорду дуги наружного рельса, стрелка которой h (рис. 85) равна ширине колеи-1,52 м. Радиус закругления в таком случае (если a -длина хорды) равен приближенно
При а=120м радиус закругления равен 1200 м 2).
1) То же могло быть получено и иным путем – из прямоугольного треугольника COF , где OC = R , CF =а/2 , OF = R – h ,
По теореме Пифагора
2 ) На практике способ этот представляет то неудобство, что ввиду большого радиуса закругления веревка для хорды требуется очень длинная.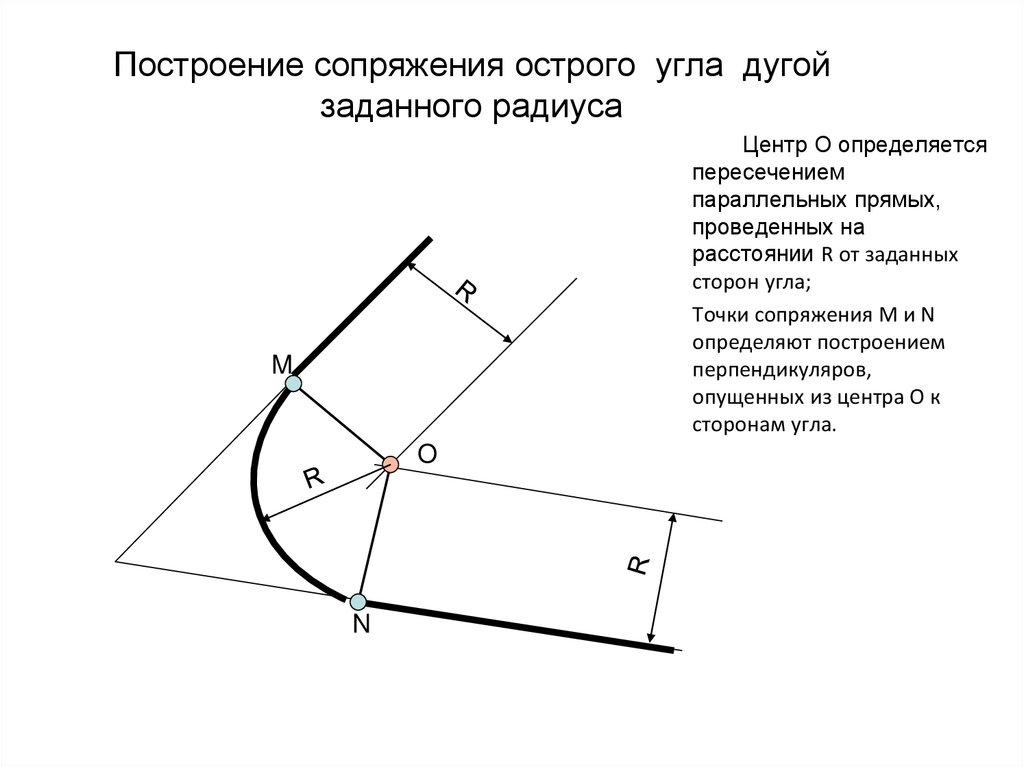
Рис. 85. К вычислению радиуса железнодорожного закругления
0,5; 0,8; 1; 1,2; 1,5; 1,8; 2; 2,2; 2,5; 2,8; 3; 3,5; 4; 4,5; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15; 16; 17; 18; 19; 20; 21;22; 23; 24; 25; 26; 28; 30; 32; 34; 35; 36; 38; 40; 42; 44; 45; 46; 48; 50; 52; 55; 58; 60; 62; 65; 68; 70; 72; 75; 78; 80; 82; 85; 88; 90; 92; 95; 98; 100; 105; 110; 115; 120; 125; 130; 135; 140; 145; 150; 155; 160; 165; 170; 175; 180; 185; 190; 200; 210; 220; 230; 240; 250; 260; 270; 280; 290; 300; 310; 320; 330; 340; 350; 360; 370; 380; 390; 400; 410; 420; 430; 440; 450; 460; 470; 480; 500.
При нанесении размера радиуса перед размерным числом помещают прописную букву высотой, равной высоте размерного числа.
Если надо указать размеры, определяющие положение центра дуги окружности, то размерную линию радиуса окружности проводят между дугой или её продолжением и центром. Последний в этом
случае изображают пересечением () | выносных (рис. | ||||
R 1 ) или центровых линий (рис. 4.22).Размерная линия радиуса | |||||
имеет только одну стрелку. | При нанесении размеров | ||||
положения вершины скругленного | |||||
угла или центра дуги скругления | |||||
выносные линии | проводят от | ||||
точек пересечения | сторон угла | ||||
от центра | дуги скругления | ||||
При проведении нескольких радиусов из | |||||
одного центра их размерные линии не должны | |||||
располагаться на одной прямой (рис. | |||||
При большой величине радиуса центр дуги окружности допускается приближать к дуге, а размерную линию проводить с изломом под углом 90О (рис. 4.23).
Если не требуется указывать | ||||
размеры, определяющие | положение | |||
центра дуги окружности , то размер- | ||||
ную линию допускается не доводить | ||||
до центра и смещать относительно | ||||
его (рис. 4.24). | ||||
совпадении | ||||
нескольких | радиусов их | размерные | ||
линии допускается не доводить до | ||||
центра, кроме крайних (рис. | ||||
Размеры радиусов | наружных | |||
скруглений наносят, как показано на | ||||
рис. 4.26а, а внутренних скруглений – | ||||
на рис. 4.26б. Следует избегать сов- | ||||
падения направления размерной линии радиуса с направлением штриховки. И в этом случае способ нанесения размерных чисел при различных положениях размерных линий определяется наибольшим удобством чтения чертежа.
Радиусы скруглений , раз- | |
мер которых в масштабе чертежа | |
1мм и менее, на чертеже не | |
изображают, нанося только | |
размер дуги с её внешней | |
стороны (рис. | |
Размеры одинаковых | |
радиусов допускается указывать | |
на общей полке (рис. 4.27б). | |
Ниже приводятся нормальные радиусы скруглений по ГОСТ
10948-64*: 0,2; 0,3; 0,4; 0,5; 0,6; 0,8; 1; 1,2; 1,6; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20; 25; 32; 40; 50; 60; 80; 100; 125; 160; 200; 250.
Если радиусы скруглений, сгибов и т.п. на всем чертеже одинаковы или какой-то радиус является преобладающим, то вместо нанесения размеров этих радиусов на изображении рекомендуется в технических требованиях делать запись типа: “Радиусы скруглений 4 мм ”, “Внутренние радиусы сгибов 10 мм ”, “Неуказанные радиусы 8 мм ” и т.п.
Если дуга окружности на чертеже больше 180 О , то принанесении её размера указывают диаметр окружности, а для дуги
окружности, не превышающей 180
О
,указывают её радиус
. | ||||||
Размер окружности, даже преры- | ||||||
вающейся, но имеющей противолежащие | ||||||
точки на диаметре, всегда следует | ||||||
задавать диаметром (рис. 4.28). | ||||||
Допускается не наносить на чертеже | ||||||
радиуса дуги | окружности | |||||
сопрягающихся параллельных линий (рис. | ||||||
4.29). Тем самым на чертеже контура | ||||||
призматической шпонки с закругленными | ||||||
торцами и паза под такую шпонку | ||||||
допускается наносить | только два | |||||
размера: длину и ширину
. | ||||||
4.6 .Нанесение длины дуги окружности | ||||||
При нанесении размера | ||||||
дуги окружности | ||||||
размерную | линию проводят | |||||
концентрично дуге, выносные | ||||||
линии – параллельно биссект- | ||||||
рисе угла, а над размерным | ||||||
(рис. 4.30а). | ||||||
охватывает | ||||||
большой угол, то выносные линии должны выходить за 7min
пределы размерных на 1. до ближайшей размерной должно быть не менее 10 мм, а между параллельными размерными линиями – не менее 7 мм ; шахматный порядок нанесения размерных чисел при наличии нескольких концентричных размерных дуг. Правила нанесения размерных чисел угловых размеров иллюстрирует рис. 4.33. Размерные числа, расположенные выше горизонтальной линии , помещают над размерными линиями со стороны их выпуклос- ти, а расположенные ниже горизонтальной линии – со стороны вогнутости размерных линий. В заштрихо- ванной зоне размерные числа указывают на горизонтально нанесенных полках линий-выносок. | ||||||
Многие моделируемые детали имеют скругления, поэтому при построении тел требуется выполнять операцию скругления ребер тела. Рассмотрим построение поверхности, которая в дальнейшем будет использоваться для скругления ребер тел. Пока будем строить поверхности скругления, не связывая их с телами.
Пусть имеются две пересекающиеся поверхности, описываемые радиус-векторами . Вблизи линии пересечения пространство делится поверхностями на четыре сектора.
Вблизи линии пересечения пространство делится поверхностями на четыре сектора.
Сектор 1: перпендикуляры, восстановленные от поверхностей к точкам первого сектора, имеют направление, совпадающее с нормалями обеих поверхностей.
Сектор 2: перпендикуляр, восстановленный от первой поверхности к точкам второго сектора, совпадает по направлению с нормалью первой поверхности, а перпендикуляр, восстановленный от второй поверхности к точкам второго сектора, противоположен по направлению нормали второй поверхности.
Сектор 3: перпендикуляры, восстановленные от поверхностей к точкам третьего сектора, противоположны по направлению нормалям обеих поверхностей.
Сектор 4: перпендикуляр, восстановленный от первой поверхности к точкам четвертого сектора, противоположен по направлению нормали первой поверхности, а перпендикуляр, восстановленный от второй поверхности к точкам четвертого сектора, совпадает по направлению с нормалью ко второй поверхности.
Построим поверхность скругления, представляющую собой след от качения сферы радиуса , касающейся одновременно двух поверхностей.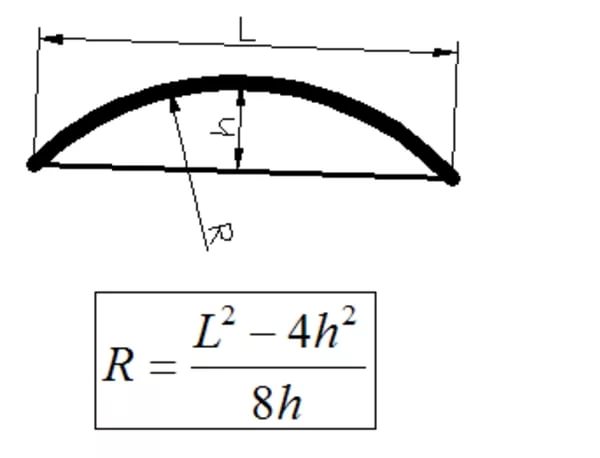
Рис. 4.10.1. Скругление плоских граней
Сфера будет двигаться около линии пересечения поверхностей в одном из четырех упомянутых секторов. На рис. 4.10.1 показано сечение поверхностей и сферы.
Частные случаи.
Если скругляемыми поверхностями являются плоскости, то угол а между поверхностями остается постоянным при движении вдоль линии их пересечения. Пусть радиус скругления остается постоянным и равным р. В этом случае линии перехода с поверхности скругления на сопрягаемые плоскости можно получить как эквидистантные линии к линии пересечения.
Имея согласованные по параметру линии перехода и линию пересечения плоскостей 1 (i), поверхность скругления можно представить в виде (3.10.3)
Линии перехода построим в виде линий на поверхностях. Каждая из них представляет собой двухмерную линию и поверхность (в данном случае – плоскость). Двухмерные линии могут быть получены как эквидистантные линии к линии пересечения плоскостей , отстоящие от нее на расстоянии .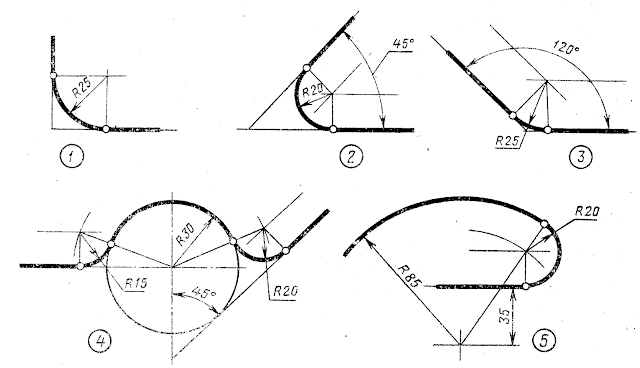 Знак d зависит от ориентации линии пересечения и от сектора, в котором строится поверхность скругления. Область определения параметра t поверхности скругления зависит от дальнейшего ее использования. Полученная поверхность скругления по форме совпадает с частью цилиндрической поверхности. Как правило, в рассмотренном случае строится именно часть цилиндрической поверхности. Аналогичным образом в качестве поверхности скругления между цилиндрической поверхностью и ортогональной ее оси плоскостью может быть использована часть поверхности тора.
Знак d зависит от ориентации линии пересечения и от сектора, в котором строится поверхность скругления. Область определения параметра t поверхности скругления зависит от дальнейшего ее использования. Полученная поверхность скругления по форме совпадает с частью цилиндрической поверхности. Как правило, в рассмотренном случае строится именно часть цилиндрической поверхности. Аналогичным образом в качестве поверхности скругления между цилиндрической поверхностью и ортогональной ее оси плоскостью может быть использована часть поверхности тора.
Общий случай.
Рассмотрим построение поверхности скругления в общем случае. Построим точки касания катящейся сферы радиуса с поверхностями. Продолжение нормалей к поверхностям в точках касания пересекутся в центре катящейся сферы. Обозначим нормали (1.7.18) поверхностей через , а проекции на эти нормали векторов из точек касания до центра сферы – через соответственно. Величины по модулю равны радиусу сферы , но имеют знак, характеризующий упомянутый сектор.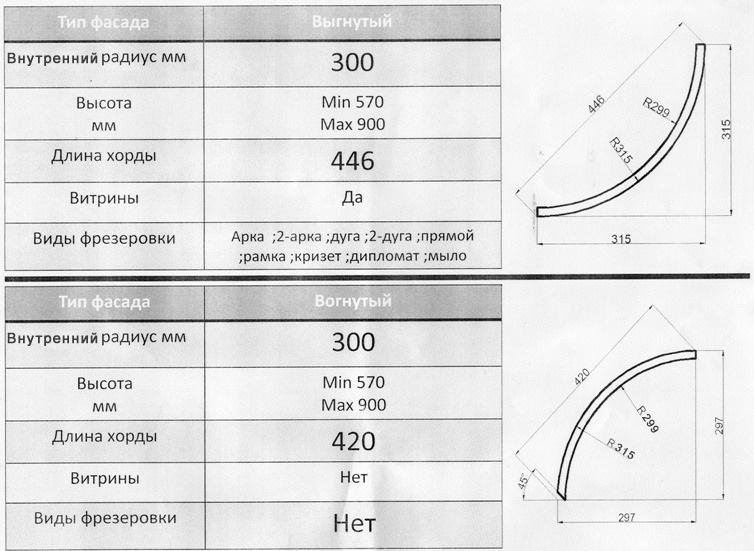 Параметры точек касания сферы связаны уравнением
Параметры точек касания сферы связаны уравнением
Это векторное уравнение содержит три скалярных уравнения для компонент нормалей поверхностей и четыре искомых параметра , v, а, b. Построение поверхности скругления по уравнению (4.10.1) сходно с задачей построения линии пересечения поверхностей. В обоих случаях результатом решения являются две двухмерные линии на соответствующих поверхностях.
Переменный радиус скругления.
Пусть требуется построить поверхность скругления переменного радиуса. Для этого нам потребуется кривая пересечения поверхностей. Величины радиуса скругления будем считать функциями длины дуги s линии пересечения скругляемых поверхностей. В данном случае катящаяся сфера будет иметь переменный радиус. Кроме того, положение центра катящейся сферы связано с точкой на линии пересечения. Расположим центр катящейся сферы в нормальной плоскости кривой пересечения. Нормальная плоскость ортогональна касательному вектору кривой. Вместо векторного уравнения (4. 10.1) параметры точек касания сферы свяжем уравнениями
10.1) параметры точек касания сферы свяжем уравнениями
Эти уравнения содержат четыре скалярных уравнения относительно четырех искомых параметров . Параметр s линии пересечения является известной величиной. По текущему параметру s мы вычислим радиусы точку и касательный вектор кривой в ней Решив систему уравнений (4.10.2) и (4.10.3), получим параметры , касания катящейся сферы и поверхностей.
Система уравнений (4.10.2), (4.10.3) может быть использована вместо системы уравнений (4.10.1) для построения поверхности скругления постоянного радиуса. В этом случае необязательно в качестве параметра кривой пересечения использовать длину ее дуги.
Результатом решения системы уравнений (4.10.1) или системы уравнений (4.10.2) и (4.10.3) являются две двухмерные линии на поверхностях
на соответствующих поверхностях. В общем случае линии могут быть получены как сплайны, проходящие через заданные точки. Пространственные линии, построенные по этим линиям на поверхностях, обозначим соответственно через
(4. 10.5)
10.5)
Они определяют края поверхности скругления, полученной качением сферы одновременно по двум поверхностям.
По двум кривым на поверхностях (4.10.5) и (4.10.6), являющимися следами касания катящейся сферы, построим поверхность скругления. Первый параметр поверхности скругления совместим с параметром t граничных кривых (4.10.5) и (4.10.6). При движении вдоль второго параметра поверхности скругления при фиксированном первом параметре должна быть описана дуга окружности. Построим эту дугу окружности в виде рациональной кривой Безье (2.6.16). Для этого при каждом значении параметра кривых на поверхности нужно знать радиус-вектор средней точки и ее вес. Вес средней точки рациональной кривой Безье (2.6.16) равен косинусу половины угла между векторами .
где вес w(t) и радиус-вектор определяются равенствами (4.10.7) и (4.10.8), а через z обозначен второй параметр поверхности. Рассмотренная поверхность скругления не имеет четких границ в направлении первого параметра. Эти границы будут определены при дальнейшем использовании поверхности для скругления ребер тел. На рис. 4.10.2 приведен пример поверхности скругления. В зависимости от замкнутости скругляемых поверхностей и линий (4.10.5) и (4.10.6) поверхность скругления может быть замкнутой или незамкнутой.
На рис. 4.10.2 приведен пример поверхности скругления. В зависимости от замкнутости скругляемых поверхностей и линий (4.10.5) и (4.10.6) поверхность скругления может быть замкнутой или незамкнутой.
При решении системы уравнений (4.10.1) и (4.10.2) требуется вычислять производные нормалей поверхностей по параметрам. Эти производные дают формулы Вейнгартена (1.7.26).
Рис. 4.10.2. Поверхность скругления
Радиус-вектор точки поверхности за ее пределами может быть вычислен по одной из формул (3.14.8)-(3.14.10) в зависимости от замкнутости поверхности. Эти же формулы позволяют определить нормали поверхности и их производные за пределами поверхности.
Радиусы закруглений и фаски. Размеры
действующий
Настоящий стандарт распространяется на размеры радиусов и фасок для деталей, изготовленных из металла и пластмасс.
Стандарт не распространяется на размеры радиусов закруглений (сгиба) гнутых деталей, фасок на резьбах, радиусов проточек для выхода резьбообразующего инструмента, фасок и радиусов закруглений шарико- и роликоподшипников и на их сопряжения с валами и корпусами на технологические межоперационные радиусы
Текст ГОСТ 10948-64
С поправками и изменениями:
Изменение №1 к ГОСТ 10948-64 от 01.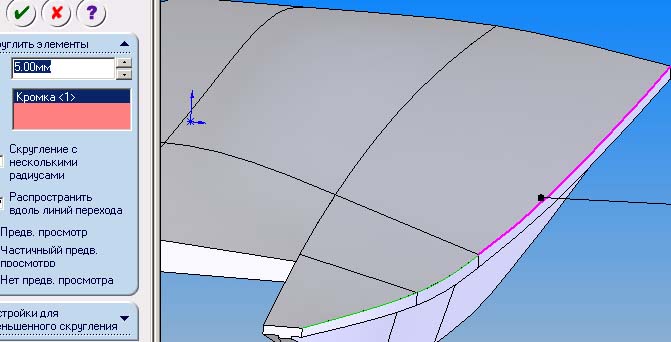 07.1982 (текст интегрирован в текст или описание стандарта)
07.1982 (текст интегрирован в текст или описание стандарта)
Другие ГОСТы
ГОСТ 22580-84 Радиостанции с угловой модуляцией морской подвижной службы. Типы, основные параметры, технические требования и методы измерений
ГОСТ 12252-86 Радиостанции с угловой модуляцией сухопутной подвижной службы. Типы, основные параметры, технические требования и методы измерений
ГОСТ 16019-78 Радиостанции сухопутной подвижной службы. Требования по устойчивости к механическим и климатическим воздействиям и методы испытаний
ГОСТ Р 57298-2016 Радиофармацевтические лекарственные препараты. Общие требования к организации изготовления радиофармацевтических препаратов в медицинских организациях
ГОСТ Р 57496-2017 Радиофармацевтические препараты. Общее руководство по организации производства
ГОСТ Р 50888-96 Радиоэкологический паспорт специализированного предприятия по обращению с радиоактивными отходами. Основные положения
ГОСТ 26080-84 Радиоэлектронная аппаратура и изделия электронной техники. Общие требования к защите от воздействия плесневых грибов
Общие требования к защите от воздействия плесневых грибов
ГОСТ 11183-71 Развертки конические с цилиндрическим хвостовиком под метрические конусы. Конусность 1:20. Конструкция и размеры
ГОСТ 11182-71 Развертки конические с цилиндрическим хвостовиком под конусы Морзе. Конструкция и размеры
ГОСТ 10080-71 Развертки конические с коническим хвостовиком под метрические конусы. Конусность 1:20. Конструкция и размеры
ГОСТ 10079-71 Развертки конические с коническим хвостовиком под конусы Морзе. Конструкция и размеры
Создает скругление со значениями переменного радиуса. Используйте контрольные точки для более простого определения скругления.
| Пример точек управления для переменных радиусов | |
| Без точек управления | |
| Точки управления для переменных радиусов | С точками управления |
Скруглить элементы
Некоторые поля, которые предусматривают ввод цифровых значений, позволяют создавать уравнение посредством ввода знака равно (=) и выбора глобальных переменных, функций и свойств файла в раскрывающемся списке. См. раздел Ввод уравнений напрямую .
См. раздел Ввод уравнений напрямую .
| В графической области выберите объекты, которые необходимо скруглить. | ||
| Распространить вдоль линий перехода | Скругление распространяется на все грани, расположенные касательно к выбранной грани. Пример: Распространить вдоль линий перехода | |
| Полный предв. просмотр | Отображает предварительный вид скругления всех кромок. | |
| Частичный предв. просмотр | Отображает предварительный вид скругления только одной кромки. Нажмите клавишу A для последовательного предварительного просмотра каждого скругления. | |
Нет предв. просмотра просмотра | Уменьшает время перестроения моделей со сложными поверхностями. |
Настройки перемен. радиуса
| Радиус | Устанавливает радиус скругления. | |
| Присоединенные радиусы | Список вершин кромок, выбранных в разделе Скруглить элементы , для параметра Кромки, грани, элементы и петли , а также список управляющих точек, выбранных в графической области. | |
| Настроить неуказанные | Применение текущего радиуса ко всем элементам, для которых не назначены радиусы в разделе Присоединенные радиусы . | |
| Настроить все | Применение текущего радиуса
ко всем элементам в разделе Присоединенные радиусы
. | |
| Количество экземпляров | Задает число управляющих точек на кромках. | |
| Плавный переход | Создает скругление, плавно изменяющееся от одного радиуса к другому при согласовании кромки скругления со смежной гранью. | |
| Линейный переход | Создание скругления, линейно изменяющегося от одного радиуса к другому, без согласования касательности кромки со смежным скруглением. |
Параметры для уменьшенного скругления
При использовании этих параметров можно создавать плавный переход между смежными поверхностями, включая кромку детали, в скругляемом угле. Можно выбрать вершину и радиус, а затем назначить одинаковые расстояния уменьшенного скругления для каждой кромки. Уменьшенное расстояние – это точка вдоль каждой кромки, в которой начинается скругление на три грани, которые сходятся в одной вершине. Пример: Предварительный просмотр уменьшенного скругления
Пример: Предварительный просмотр уменьшенного скругления
Прежде чем задать Параметры для уменьшенного скругления , в разделе Скруглить элементы выполните следующие действия.
| Расстояние | Устанавливает уменьшенное расстояние скругления, измеряемого от вершины. | |
| Уменьшенные скругления | Выберите одну или несколько вершин в графической области. Кромки уменьшенных скруглений соединяются в выбранных вершинах. | |
| Расстояние | Список номеров кромок с соответствующими значениями уменьшенного расстояния . Чтобы применить различные уменьшенные расстояния к кромкам, выберите кромку в поле Уменьшения . Затем задайте расстояние и нажмите клавишу Enter . | |
| Настроить неуказанные | Применение текущего расстояния
ко всем кромкам, для которых не назначены расстояния в разделе Расстояние
. | |
| Настроить все | Применение текущего расстояния ко всем кромкам в разделе Расстояние . |
Параметры скругления
| Выбрать сквозь грани | Дает возможность выбирать кромки сквозь грани, которые эти кромки скрывают. |
| Тип перекрытия | Управляет поведением скруглений на отдельных замкнутых кромках (например, окружностях, сплайнах, эллипсах) при соединении с кромками. Пример: Тип перекрытия . Выберите один из указанных ниже параметров: |
Радиус круга – формула, определение
Радиус определяется как отрезок, соединяющий центр с границей круга или сферы. Длина радиуса остается неизменной от центра до любой точки на окружности круга или сферы. Это половина длины диаметра. Давайте узнаем больше о радиусе в этой статье.
Давайте узнаем больше о радиусе в этой статье.
| 1. | Что такое радиус? |
| 2. | Формулы радиуса |
| 3. | Радиус окружности |
| 4. | Как найти радиус окружности? |
| 5. | Уравнение радиуса окружности |
| 6. | Радиус сферы |
| 7. | Часто задаваемые вопросы о Radius |
Что такое радиус?
В геометрии радиус определяется как отрезок, соединяющий центр круга или сферы с его окружностью или границей. Это важная часть кругов и сфер, которая обычно обозначается аббревиатурой «r». Множественное число радиуса — « радиусов », которое используется, когда мы говорим о более чем одном радиусе одновременно. Наибольший отрезок в окружности или сфере, соединяющий любые точки, лежащие на противоположной стороне от центра, является диаметром, а длина радиуса составляет половину длины диаметра. Его можно выразить как d/2, где d — диаметр круга или сферы. Посмотрите на изображение круга, приведенное ниже, показывающее соотношение между радиусом и диаметром.
Его можно выразить как d/2, где d — диаметр круга или сферы. Посмотрите на изображение круга, приведенное ниже, показывающее соотношение между радиусом и диаметром.
Теперь давайте изучим формулы радиуса, которые помогут вам вычислить его длину с учетом данной информации.
Формулы радиуса
Радиус круга и сферы можно рассчитать с помощью определенных формул, которые вы изучите в этом разделе. Здесь мы поговорим о формулах радиуса для окружности. Формула радиуса сферы обсуждается в разделе ниже.
Формула радиуса от диаметра: Диаметр представляет собой прямую линию, проходящую через центр и соединяющую точку на одном конце с точкой на другом конце окружности. Диаметр в два раза больше длины радиуса. Математически это записывается как диаметр = 2 × радиус. Это также самая длинная хорда окружности. Когда диаметр круга дан, тогда формула радиуса выражается как:
Радиус = Диаметр/2 или D/2 единиц
Формула радиуса из окружности: Периметр круга называется его окружностью. Это граница круга и может быть выражена формулой: C = 2πr единиц. Здесь C — длина окружности, r — радиус окружности, а π — константа, равная 3,14159.. Радиус равен отношению длины окружности к 2π. Формула радиуса с использованием длины окружности выражается следующим образом:
Это граница круга и может быть выражена формулой: C = 2πr единиц. Здесь C — длина окружности, r — радиус окружности, а π — константа, равная 3,14159.. Радиус равен отношению длины окружности к 2π. Формула радиуса с использованием длины окружности выражается следующим образом:
Радиус = Окружность/2π или C/2π единиц
Формула радиуса с площадью: Площадь круга – это пространство, занимаемое кругом. Связь между радиусом и площадью определяется формулой Площадь круга = πr 2 квадратных единиц. Здесь r — радиус, а π — константа, равная 3,14159. Формула радиуса с использованием площади круга выражается как:
Радиус = √(Площадь/π) единиц
Радиус окружности
Радиус — одна из важных частей окружности. Это расстояние от центра круга до любой точки на его границе. Другими словами, когда мы соединяем центр круга с любой точкой его окружности с помощью прямой линии, этот отрезок линии является радиусом этого круга. Круг может иметь более одного радиуса, потому что на его окружности бесконечное число точек. Это означает, что круг имеет бесконечное число радиусов и все радиусы круга равноудалены от центра круга. Размер круга меняется при изменении длины радиуса.
Круг может иметь более одного радиуса, потому что на его окружности бесконечное число точек. Это означает, что круг имеет бесконечное число радиусов и все радиусы круга равноудалены от центра круга. Размер круга меняется при изменении длины радиуса.
На приведенном ниже рисунке точки A, B, M, N, P, Q, X и Y лежат на границе окружности. Заметим, что эти точки равноудалены от центра O. Итак, все отрезки OA, OB, OM, ON, OY, OX, OP и OQ называются радиусами окружности. Обратите внимание, что OA = OB = OM = ON = OP = OQ = OX = OY.
Как найти радиус окружности?
Радиус круга можно найти с помощью трех основных формул радиуса, т.е. когда известны диаметр, площадь или длина окружности. Воспользуемся этими формулами, чтобы найти радиус окружности.
- Когда диаметр известен, формула Радиус = Диаметр/2.
- Если длина окружности известна, формула Радиус = Длина окружности/2π.
- Когда площадь известна, формула для радиуса: Радиус = ⎷(Площадь круга/π).

Например, если диаметр равен 24 единицам, то радиус равен 24/2 = 12 единицам. Если длина окружности равна 44 единицам, то ее радиус можно рассчитать как 44/2π. Отсюда следует, что (44×7)/(2×22) = 7 единиц. И, если площадь круга равна 616 квадратных единиц, то радиус равен ⎷(616×7)/22 = ⎷28×7 = ⎷196 = 14 единиц.
Уравнение радиуса окружности
Радиус уравнения окружности на декартовой плоскости с центром (h, k) определяется как (x − h) 2 + (y − k) 2 = r 2 . Здесь (x, y) — точки на окружности окружности, находящиеся на расстоянии «r» (радиус) от центра (h, k). Когда центр окружности находится в начале координат (0,0), уравнение окружности сводится к x 2 + y 2 = r 2 . Обратите внимание на схему окружности на декартовой плоскости, показанную ниже. Здесь координаты центра равны (0, b), а радиус окружности представлен буквой «r», соединяющей центр с точкой (x, y) на окружности. Итак, нам просто нужно подставить эти значения в приведенное выше уравнение, чтобы получить радиус уравнения окружности. Уравнение для нахождения радиуса этой окружности:0085 2 .
Итак, нам просто нужно подставить эти значения в приведенное выше уравнение, чтобы получить радиус уравнения окружности. Уравнение для нахождения радиуса этой окружности:0085 2 .
Радиус сферы
Сфера — трехмерная объемная фигура. Радиус сферы — это отрезок от центра до любой точки на границе сферы. Это определяющий фактор при рисовании сферы, так как ее размер зависит от ее радиуса. Как и в случае с кругом, внутри сферы могут быть нарисованы бесконечные радиусы, и все эти радиусы будут равны по длине. Чтобы вычислить объем и площадь поверхности сферы, нам нужно знать ее радиус. И мы можем легко вычислить радиус сферы по формулам ее объема и площади поверхности.
Радиус сферы от объема = 3 ⎷(3V)/4π единиц, где V представляет объем, а значение π приблизительно равно 3,14.
Радиус сферы с использованием площади поверхности = ⎷(A/4π) единиц, где A представляет собой площадь поверхности.
Воспользуйтесь нашим бесплатным онлайн-калькулятором радиуса сферы, чтобы рассчитать радиус с заданным объемом, площадью поверхности или диаметром сферы.
☛ Статьи по теме
Проверьте эти интересные статьи, связанные с радиусом и его формулами.
- Формула радиуса кривизны
- Сегмент круга
- Сектор круга
Часто задаваемые вопросы о радиусе окружности
Что такое радиус круга в геометрии?
Радиус окружности — это длина отрезка от центра до точки на окружности окружности. Обычно обозначается аббревиатурой «р». В круге может быть бесконечное количество радиусов, и длина всех этих радиусов будет одинаковой. Это половина диаметра круга.
Как диаметр связан с радиусом окружности?
Диаметр круга в два раза больше радиуса, или радиус равен половине диаметра. Связь между радиусом и диаметром можно выразить формулой: Диаметр = 2 × радиус. Используйте бесплатный онлайн-калькулятор радиуса, чтобы рассчитать радиус с заданным диаметром.
Как найти радиус окружности с помощью длины окружности?
Длина окружности и радиус связаны друг с другом, и их отношение можно выразить как Длина окружности = 2πR, где R — радиус. Итак, когда длина окружности известна, формула, используемая для расчета радиуса круга, выглядит следующим образом: Радиус = Окружность / 2π.
Итак, когда длина окружности известна, формула, используемая для расчета радиуса круга, выглядит следующим образом: Радиус = Окружность / 2π.
Что такое радиус кривой?
Радиус кривой или дуги — это радиус окружности, частью которой они являются. Когда длина хорды, определяющей основание (W), и высота, измеренная в середине основания дуги (H), даны, формула для нахождения радиуса: Радиус = (H / 2) + (W 2 / 8Н).
Что такое формула радиуса?
Радиус круга можно рассчитать с помощью различных формул. Соблюдайте следующие формулы для расчета радиуса:
- Когда диаметр известен, формула Радиус = Диаметр / 2.
- Когда длина окружности известна, формула для радиуса равна Окружность / 2π.
- Если площадь известна, формула Радиус = ⎷(Площадь круга / π).
Как рассчитать радиус окружности с помощью калькулятора?
Длина радиуса равна половине длины диаметра, который можно рассчитать с помощью онлайн-калькулятора Cuemath, просто введя любое заданное значение среди диаметра, окружности или площади круга.
Как найти радиус круга с площадью?
Если известна площадь круга, то формула для нахождения радиуса дается как Радиус = ⎷(A/π) единиц, где A – заданная площадь.
калькулятор окружности
, созданный Bogna Szyk и Mateusz Muga
, рассмотрено Jack Bowater
Последнее обновление: 11 марта 2022 г.
Содержание:- Определение окружности
- Формула для окружности
- Как найти окружность круга
- Отношение длины окружности к диаметру
- Часто задаваемые вопросы
Если вам нужно решить некоторые геометрические задачи, этот калькулятор длины окружности — то, что вам нужно. Это инструмент, специально созданный для определения диаметра, длины окружности и площади любого круга. Читайте дальше, чтобы узнать:
- Что такое определение окружности
- Как найти длину окружности
- Как преобразовать длину окружности в диаметр
Как и в случае со всеми нашими инструментами, калькулятор длины окружности работает во всех направлениях – он также является калькулятором длины окружности в диаметр и может использоваться для преобразования длины окружности в радиус, длины окружности в площадь, радиуса в длину окружности, радиуса в диаметр (да!), радиус в площадь, диаметр в окружность, диаметр в радиус (да, опять же с ракетостроением), диаметр в площадь, площадь в окружность, площадь в диаметр или площадь в радиус.
Если вы хотите нарисовать круг на декартовой плоскости, вам может пригодиться это уравнение калькулятора окружности.
Определение длины окружности
Длина окружности — это линейное расстояние от края окружности. Это то же самое, что и периметр геометрической фигуры, но термин «периметр» используется исключительно для многоугольников.
Окружность часто неправильно пишется как окружность .
Формула для длины окружности
Следующее уравнение описывает соотношение между длиной окружности и радиусом R круга:
C = 2πR
Где π — константа, приблизительно равная 3,14159265…
| 💡 Точное значение числа π найти невозможно. Это иррациональное число, поэтому мы обычно используем приблизительные значения, такие как 3,14 или 22/7. Если вам интересна эта тема, взгляните на первый миллион цифр числа π! |
Такая же простая формула определяет отношение площади круга к его радиусу:
A = π * R²
Как найти длину окружности
- Определить радиус окружности.
 Предположим, что она равна 14 см.
Предположим, что она равна 14 см. - Подставьте это значение в формулу длины окружности:
C = 2 * π * R = 2 * π * 14 = 87,9646 см. - Вы также можете использовать его, чтобы найти площадь круга:
A = π * R² = π * 14² = 615,752 см². - Наконец, вы можете найти диаметр – он просто удваивает радиус:
Д = 2 * Р = 2 * 14 = 28 см. - Используйте наш калькулятор длины окружности, чтобы найти радиус, когда у вас есть только длина окружности или площадь круга.
Если вы хотите рассчитать свойства трехмерного твердого тела, такого как сфера, цилиндр или конус, лучше всего использовать наш калькулятор объема.
Окружность к диаметру
Вы, наверное, заметили, что, поскольку диаметр в два раза больше радиуса, отношение длины окружности к диаметру равно π:
C/D = 2πR / 2R = π
Эта пропорция (длина окружности к диаметру) является определением константы числа пи. Он используется во многих областях, таких как физика и математика. Например, вы можете найти его в калькуляторе центробежной силы.
Он используется во многих областях, таких как физика и математика. Например, вы можете найти его в калькуляторе центробежной силы.
🔎 Если вас интересует взаимосвязь между окружностью и другими переменными, вы можете взглянуть на наши калькуляторы окружности к диаметру и окружности и площади круга .
FAQ
Как найти длину окружности?
Чтобы вычислить длину окружности, вам нужен радиус окружности :
- Умножьте радиус на 2, чтобы получить диаметр.
- Умножьте результат на π или 3,14 для оценки.
- Вот и все; вы нашли окружность круга .
Или вы можете использовать диаметр круга :
- Умножьте диаметр на π, или 3,14.
- Результатом является длина окружности .
Какова длина окружности?
Длина окружности равна линейному расстоянию от края окружности . Он эквивалентен периметру геометрической формы, хотя этот термин периметр используется только для многоугольников.
Он эквивалентен периметру геометрической формы, хотя этот термин периметр используется только для многоугольников.
Кто первым вычислил окружность Земли?
Первым человеком, вычислившим окружность Земли, был Эратосфен, греческий математик , в 240 г. до н.э. Он обнаружил, что объекты в городе в северном тропике не отбрасывают тень в полдень в день летнего солнцестояния, а находятся в более северном месте. Зная это и расстояние между точками, ему удалось вычислить окружность Земли.
Как найти диаметр по окружности?
Если вы хотите найти диаметр окружности , выполните следующие действия:
- Разделите длину окружности на π или 3,14 для оценки.
- Вот и все; у вас есть диаметр круга .
Как найти площадь круга по длине окружности?
Чтобы найти площадь круга по окружности , выполните следующие действия:
- Разделите длину окружности на π.

- Разделите результат на 2, чтобы получить радиус круга .
- Умножьте на радиус, чтобы получить его квадрат.
- Умножьте квадрат на π или 3,14 для оценки.
- Вы нашли площадь круга из длины окружности .
Как найти радиус окружности?
Чтобы найти радиус окружности , вы должны сделать следующее:
- Разделите длину окружности на π или 3,14 для оценки. В результате получится диаметр круга.
- Разделить диаметр на 2.
- Ну вот, вы нашли радиус окружности .
Как измерить окружность?
- Вычислите длину окружности как 2 ⨉ радиус ⨉ π .
- Вычислить длину окружности как диаметр ⨉ π .
- Оберните нить вокруг предмета и измерьте его длину.

- Используйте Калькулятор окружности Omni .
Какова формула длины окружности?
Формула для длины окружности , если задан радиус окружности, выглядит следующим образом:
- 2 ⨉ радиус ⨉ π
Или, если дана длина окружности:
- Окружность ⨉ π
Вы можете оценить π как 3,14.
Какова длина окружности радиусом 1 метр?
Чтобы рассчитать длину окружности с радиусом 1 метр , просто выполните следующие действия:
- Умножьте радиус на 2, чтобы получить диаметр 2 метра.
- Умножьте результат на π или 3,14 для оценки.
- Вот и все; длина окружности радиусом 1 метр равна 6,28 метра .
Как найти длину окружности цилиндра?
Чтобы найти длину окружности цилиндра , вы должны знать, что поперечное сечение цилиндра представляет собой круг. Если вы знаете радиус цилиндра:
Если вы знаете радиус цилиндра:
- Умножьте радиус на 2, чтобы получить диаметр.
- Умножьте результат на π или 3,14 для оценки.
- Вот и все; вы нашли окружность цилиндра .
Или вы можете использовать диаметр цилиндра :
- Умножьте диаметр на π, или 3,14.
- Результатом является длина окружности цилиндра .
Как найти площадь круга с длиной окружности 1 метр?
Если вы хотите найти площадь круга с длиной окружности 1 метр , сделайте следующее:
- Разделите длину окружности на π. Это диаметр круга , в данном случае 31,8 сантиметра.
- Разделите на 2. Этот результат равен радиусу окружности 15,9 см.
- Умножьте радиуса на себя, получив квадрат, в нашем случае 256 см².

- Умножить на π или 3,14 для оценки.
- Вот и все; круг с окружностью 1 метр имеет площадь 795,78 см² .
Как найти радиус окружности с длиной окружности 10 сантиметров?
Чтобы найти радиус окружности с длиной окружности 10 сантиметров , вы должны сделать следующее:
- Разделите длину окружности на π или 3,14 для оценки. В результате получается диаметр круга 3,18 сантиметра.
- Разделить диаметр на 2.
- И вот, радиус круга с окружностью 10 сантиметров равен 1,59 сантиметра .
Какова единица длины окружности?
Поскольку длина окружности представляет собой линейное расстояние от края окружности, она описывает длину. Таким образом, наиболее распространенными единицами длины окружности являются миллиметры, сантиметры, метры для метрической системы и дюймы, футы и ярды для имперской системы9. 0070 .
0070 .
Богна Шик и Матеуш Муха
Радиус (r)
Диаметр
Окружность (c)
Проверить 8 подобных калькуляторов окружностей … еще 5
Измерение радиуса Земли в 240 г. до н.э. – e=mc2andallthat
Мозг шире неба,
Эмили Дикинсон, «Мозг»
Для того, чтобы поставить их рядом,
Один другой будет включать
С легкостью, и ты рядом.
Большинство преподавателей естествознания считают, что «Космос» является одной из самых увлекательных тем для многих студентов: чувство чуда, возникающее по мере того, как наша родная планета теряется в пустых просторах Солнечная система, которая затем теряется в бескрайних звездных просторах галактики Млечный Путь, доставляет удовольствие.
Но ученики часто задают вопрос: как нам знает все это? Откуда мы знаем, что расстояние до ближайшей к Солнцу звезды равно 4 световым годам? Или как узнать расстояние до Солнца? Или Луна?
Со смущением признаюсь, что я обычно отвечал небрежным и невольно-пренебрежительным «Ну что ж, ученые их измерили!», что (хотя и верно) должно было звучать скорее как исповедание веры, чем как трезвый рассказ о эмпирический факт. Что, если честно, так оно и было; просто потому, что я еще не пытался выяснить, как эти измерения были сделаны впервые.
Что, если честно, так оно и было; просто потому, что я еще не пытался выяснить, как эти измерения были сделаны впервые.
Технологические ресурсы, доступные нашим предкам, кажутся нам примитивными и рудиментарными, но в сочетании с глубоким колодцем человеческой изобретательности, который, как мне нравится, является отличительной чертой нашего вида, он оказался не просто «лучшим в мире», а « побеждающий вселенную».
Надеюсь, вам понравится эта обзорная экскурсия по этому малопосещаемому уголку научной глубинки, и вы захотите поделиться этими историями со своими учениками. Хорошо знать, что мозг действительно «шире неба».
Я представил это в стиле и формате, подходящем для обмена и обсуждения со студентами KS3/KS4 (11-16 лет).
Бешеные псы и Эратосфен выходят в полуденное Солнце…
Начнем с самого начала: первое достоверное измерение размеров Земли было сделано в 240 г. до н.э., а началось все (по крайней мере, в этом пересказе) с тот факт, что Эратосфен любил общаться с туристами. («Err-at-oss-THen-ees» с «TH» произносится как «термометр» — никогда не забывайте, что ученики всех возрастов часто приветствуют помощь в обучении произношению незнакомых слов)
(«Err-at-oss-THen-ees» с «TH» произносится как «термометр» — никогда не забывайте, что ученики всех возрастов часто приветствуют помощь в обучении произношению незнакомых слов)
Александрия (на территории современного Египта) была процветающим городом и притягивала туристов. Эратосфен взял за правило разговаривать с как можно большим количеством посетителей. Их истории, взятые с долей скептицизма, были бесценным источником информации о мире в целом. Эратосфен был главным библиотекарем Александрийской библиотеки, считавшейся в то время одним из семи чудес света, и считал своим долгом собрать, каталогизировать и классифицировать как можно больше информации.
Один посетитель, присутствовавший в Александрии в самый длинный день в году (21 июня по нашему календарю), мимоходом упомянул Эратосфену что-то такое, что Библиотекарю было трудно забыть: «Знаете, — сказал посетитель, — в полдень в этот день в моем родном городе теней нет .’
Как же так? задумался Эратосфен. Объяснение было только одно: в тот день в Сиене (родном городе туриста, ныне известном как Асуан) Солнце было прямо над головой.
Объяснение было только одно: в тот день в Сиене (родном городе туриста, ныне известном как Асуан) Солнце было прямо над головой.
То же самое не было в Александрии. В полдень появилась небольшая, но заметная тень. Эратосфен измерил угол тени в полдень самого длинного дня. Было семь градусов.
Никаких теней в Сиене, но в то же самое время тень в 7 градусов в Александрии. Объяснение опять-таки было только одно: Александрия была «наклонена» на 7 градусов по отношению к Сиене.
Семь степеней разделения
Сферичность Земли была признана астрономами ок. 500 г. до н.э., так что эта разница не была неожиданностью для Эратосфена, но он понял, что, поскольку он сравнивал длину теней в двух местах на поверхности Земли одновременно, то 7 o не было просто углом тени. : 7 o — угол, образуемый в центре Земли радиальными линиями, проведенными из обоих мест.
Эратосфен заплатил человеку, чтобы тот прошел расстояние между Александрией и Сиеной. (Это была не такая странная просьба, как кажется нам: в древнем мире были профессионалы, называемые бематистами, которых обучали измерять расстояния, считая шаги.)
(Это была не такая странная просьба, как кажется нам: в древнем мире были профессионалы, называемые бематистами, которых обучали измерять расстояния, считая шаги.)
Бематисту понадобился почти месяц, чтобы пройти это расстояние, и по нашим измерениям оно составило 5000 стадий или 780 км.
Затем Эратосфен использовал метод простого соотношения для расчета окружности Земли, C :
Тогда:
Современное значение радиуса Земли составляет 6371 км.
Если и но…
До сих пор ведутся споры относительно фактической длины одного греческого стадиона, но измерения Эратосфена, как правило, согласуются в пределах 1-2% от современного значения.
К сожалению, ни один из экземпляров книги, в которой Эратосфен объяснял свой метод под названием «Об измерении земли », не сохранился с древних времен, поэтому представленная здесь версия является упрощенной версией, изложенной Клеомедом в более поздней книге. За дальнейшими подробностями читатели могут обратиться к превосходной статье в Википедии об Эратосфене.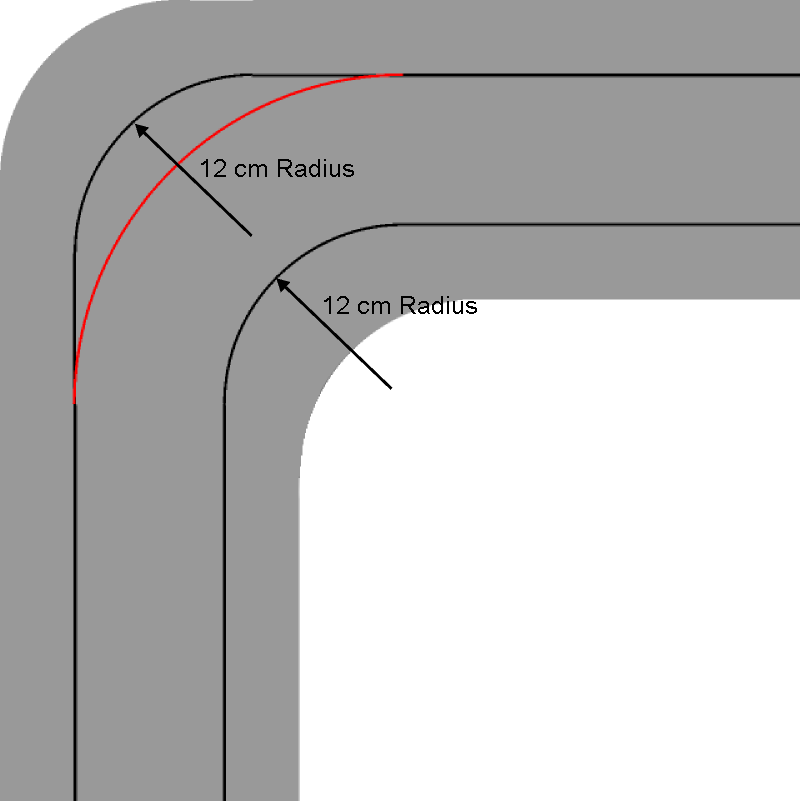





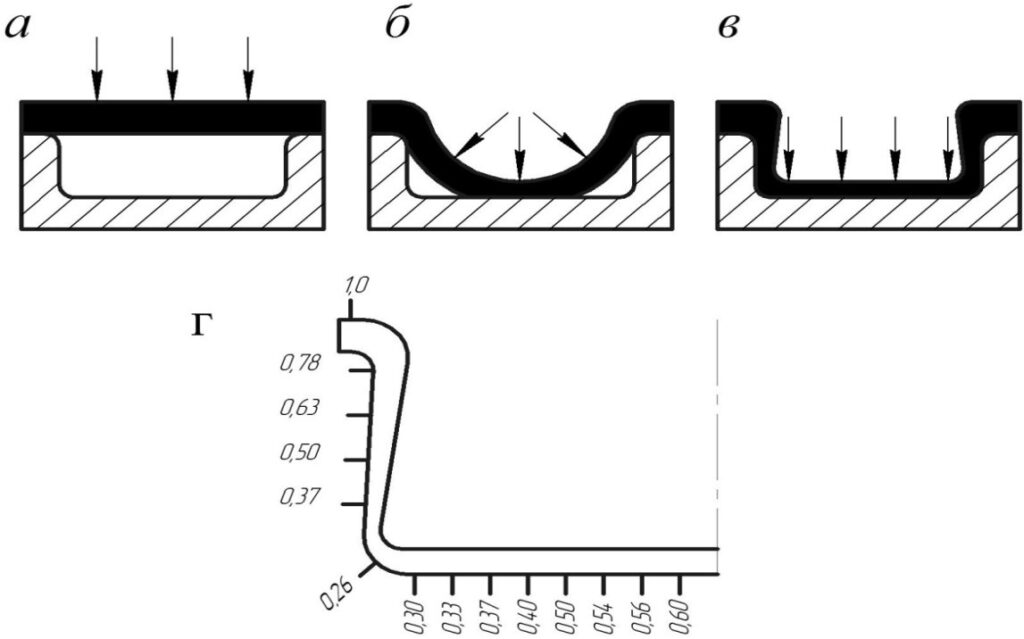 При этом плоские рабочие поверхности располагаются внутри, а цилиндрические повернуты наружу. С противоположной стороны от штанги находятся разметочные остро заточенные кромки. Дополнительно прибор оснащен рамкой микрометрической подачи, с помощью которой можно производить более точные измерения.
При этом плоские рабочие поверхности располагаются внутри, а цилиндрические повернуты наружу. С противоположной стороны от штанги находятся разметочные остро заточенные кромки. Дополнительно прибор оснащен рамкой микрометрической подачи, с помощью которой можно производить более точные измерения. Электронный модуль имеет ряд удобных настроек.
Электронный модуль имеет ряд удобных настроек. 1 – 3
1 – 3 30 до 50
30 до 50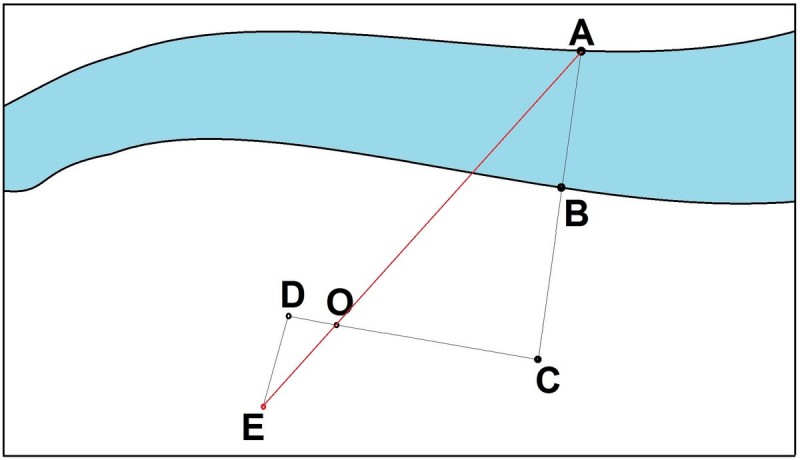 откл.
откл.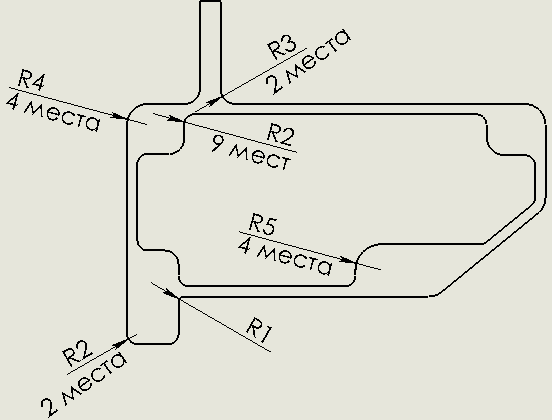 откл.
откл. 4.21, размер
4.21, размер 4.22).
4.22). 4.25).
4.25).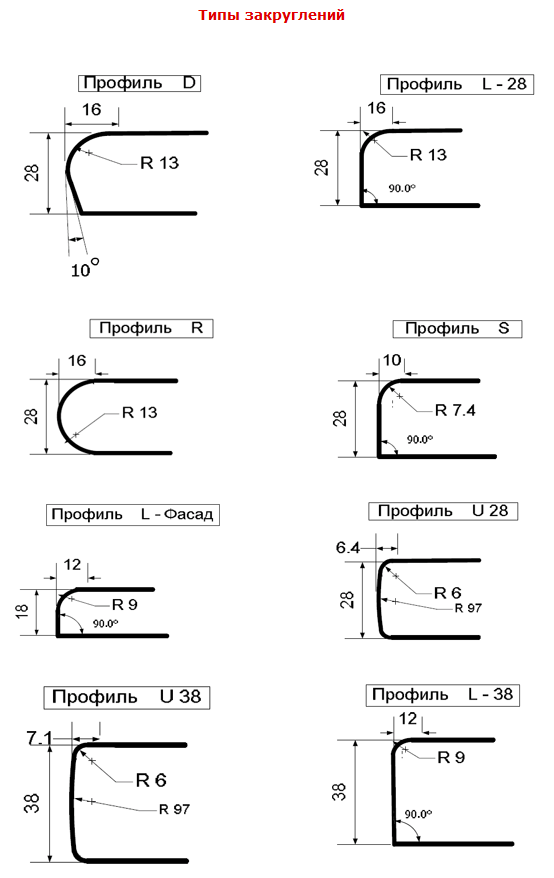 27а).
27а).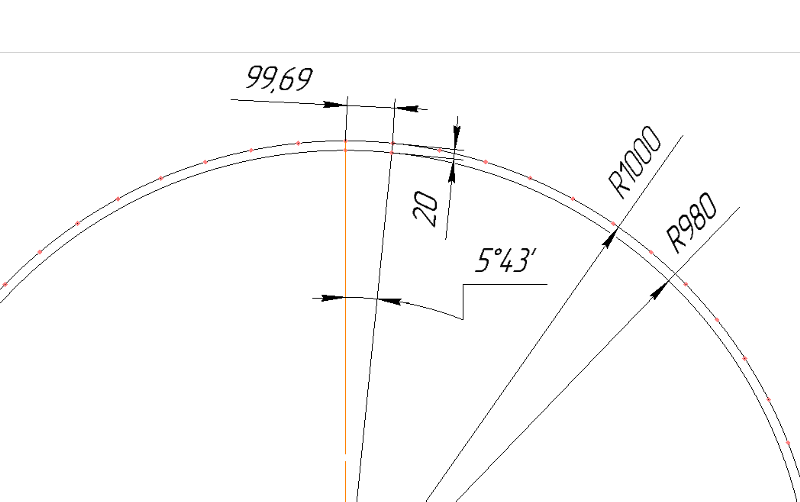
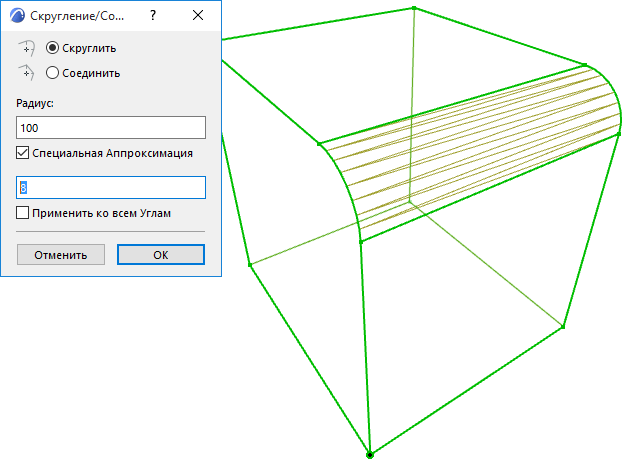
 ..5 мм;
расстояние от контурной линии
..5 мм;
расстояние от контурной линии
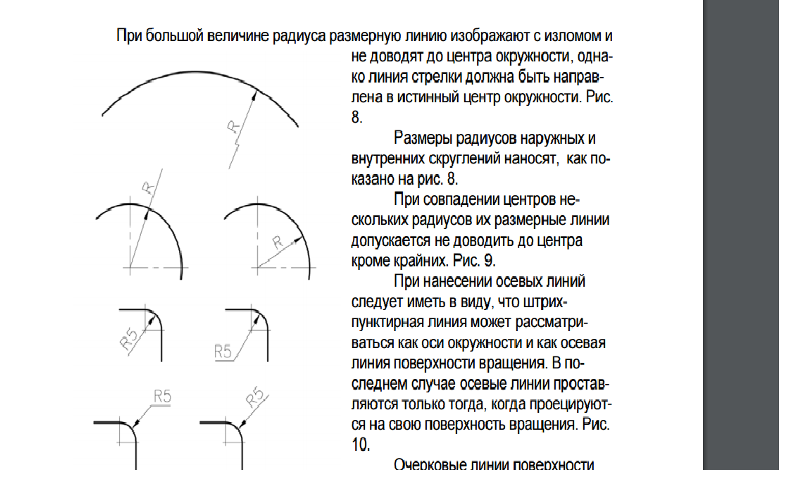 Предположим, что она равна 14 см.
Предположим, что она равна 14 см.

