Как померить радиус скругления – Простая формула для определения радиуса дуги
alexxlab | 20.09.2019 | 0 | Разное
определить радиус скругления углов на psd-макете – Zencoder
При создании макетов в Photoshop дизайнеры очень любят использовать скругление углов для самых различных блоков.
Причем, они любили это делать всегда, с самых незапамятных времен. Спору нет, блоки с такими углами смотрятся гораздо приятнее, что положительным образом сказывается на самом дизайне сайта.
Но вот верстальщику в данной ситуации не совсем легко. Как передать в коде такое скругление углов? Раньше, до появления CSS3, выходили из положения трудоемким и кропотливым способом – вырезали из изображения скругленные углы и всталяли их в код к качестве фоновых изображений.
Но вот появился CSS3 и дело значительно облегчилось, так как в этой спецификации есть свойство, специально созданное для отрисовки круглых углов у блоков. Оно называется .
На момент своего появления поддержка браузерами осуществлялась с помощью браузерных префиксов, таких как , , и так далее. Но на сегодняшний день, насколько я знаю, от использования подобных префиксов можно уже отказаться.
Но речь в данной статье не об этом. Точнее, не о том, как создать скругленный угол в CSS3. А о том, как померить этот угол на psd-макете. Допустим, у нас есть присланный дизайнером макет сайта:
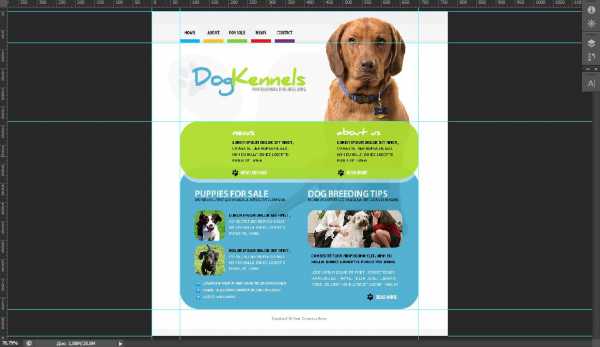
Видно, что художник постарался от души – скруглений хоть отбавляй. Ну, ничего сложного для верстальщика здесь нет. Блоки со скругленными углами – достаточно узнать радиус скругления этих углов, которые нарисовал дизайнер, и прописать для них свойство , к примеру.
А вот как его узнать? Не звонить же дизайнеру с вопросом – какой радиус ты заложил в макете?
Скажу, что сразу ответ на этот вопрос я не получил. По привычке отправился на форум forum.htmlbook.ru, но конкретного ничего не вынес оттуда. После поисков в Инете все-же решение было найдено. И оно оказалось очень простым.
Давайте масштабируем макет так, чтобы был хорошо виден скругленный угол блока. Видим на нем, как прямая линия блока плавно переходит в скругление, которое после своего завершения опять превращается в прямую. Для нас интересны здесь две точки – там, где скругление начинается, и там, где оно заканчивается. Назовем их касательными точками:
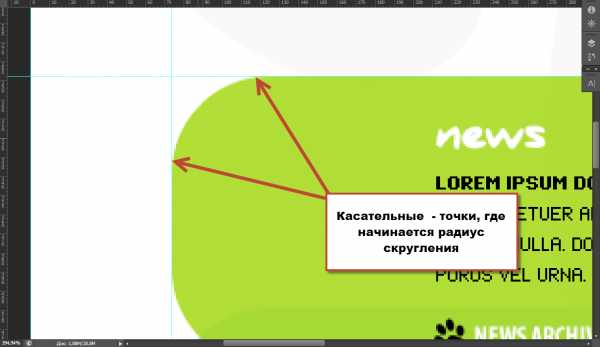
Проведем в качестве вспомогательных линий две направляющие – вертикальную и горизонтальную. На рисунке они отображены тонкими синими линиями. Нам они будут необходимы для того, чтобы получить точку их пересечения. Затем выберем в панели инструментов Photoshop прямоугольное выделение (Rectangular Marqee).
И построим квадрат (зажав клавишу Shift) так, чтобы его левый верхний угол совпал с точкой пересечения направляющих. Протянем его мышкой так, чтобы стороны расширяющегося квадрата совпали с касательными точками, о которых говорилось ранее. Как только линии квадрата и касательные точки совпадут, отпускаем мышь – построение закончено.
Можно выполнить построение другим способом. Начать выделение из одной точки (касательной) и закончить в другой, то есть, как бы по диагонали. Результат будет тот же самый, но не нужно создавать направляющие:
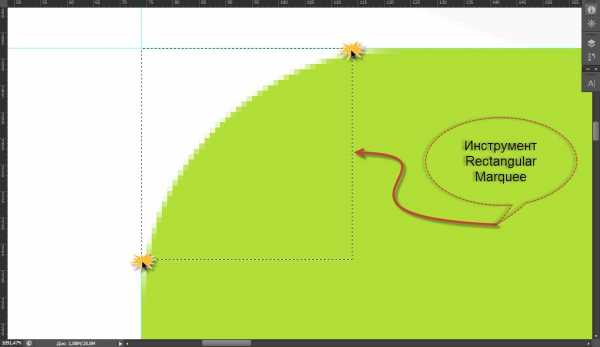
Теперь откроем панель “Инфо”, и взглянем на размеры построенного квадрата. Длины сторон и будут радиусом скругления для данного блока на макете:
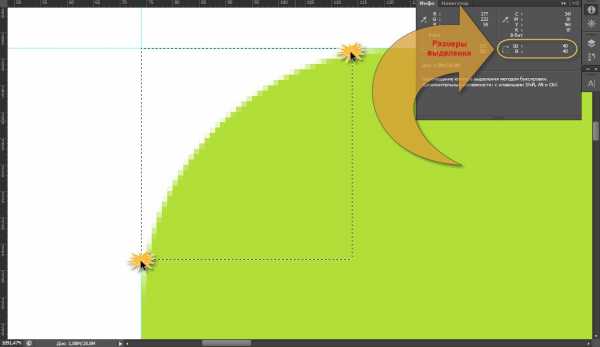
Не верите? Это точно – любая из сторон построенного квадрата будет радиусом данного скругления! Чтобы еще немного разъяснить, я нарисовал в AutoCAD круг с радиусом , а затем построил квадрат с длинной стороны так, чтобы вписать его правый верхний угол в центр созданного круга. На рисунке хорошо видно, что любая из его сторон является радиусом круга, в который он вписан:
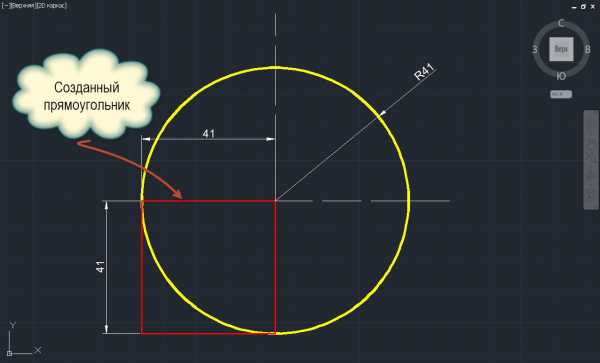
При построении квадрата выделения на psd-макете бывает, что невозможно точно попасть так, чтобы стороны квадрата совпали с направляющими guideline. Для себя нашел такой выход. Ну, не попал, так не попал.
Строю квадрат дальше. Когда он построен и мышь отпущена, я просто перемещаю выделение в нужное место с помощью клавиш-стрелок на клавиатуре. А дальше – все как и прежде. Смотрю на панель “Инфо” и получаю точный радиус скругления:
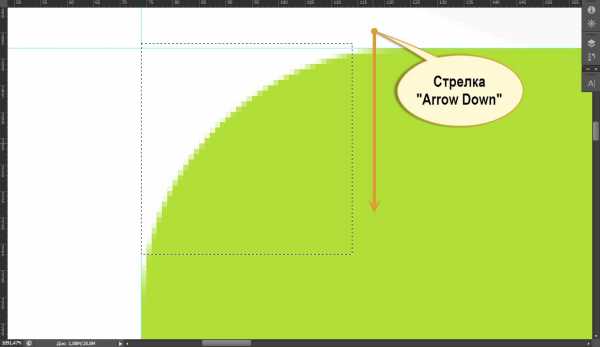
Как видно, все оказалось очень просто. Теперь, зная точное значение радиуса скругления, можно создать шаблон сайта, максимально соответсвующий psd-макету.
P.S.
На рисунке с изображением круга и квадрата, созданных в AutoCAD, имеется неточность. В выноске указано, что построен прямоугольник, хотя на самом деле это конечно же квадрат.
Почему на psd-макете радиус скругления равен
На этом все.
photoshop
gearmobile.github.io
Радиусы скруглений. Размеры и предельные отклонения
Источник: ОСТ 92-0093-69
Рис 1. Размеры и предельные отклонения радиусов скруглений и фасок для сопряжений типа “вал – отверстие”
Таблица 1. Рекомендуемый подбор сопряжений радиуса с радиусом и радиуса с фаской, мм
|
Диаметр вала d |
Радиус вогнутой поверхности |
Радиус выпуклой поверхности и фаска |
||
|
r |
Предельное отклонение |
r1=C |
Предельное отклонение |
|
|
До 0,5 |
0,05 |
-0,03 |
0,1 |
0,05 |
|
От 0,5 до 1 |
0,1 |
-0,05 |
0,2 |
0,1 |
|
Св.1 – 3 |
0,2 |
-0,1 |
0,3 |
0,2 |
|
3 – 6 |
0,3 |
-0,2 |
0,5 |
0,3 |
|
6 – 10 |
0,5 |
-0,3 |
0,8 |
|
|
10 – 14 |
0,8 |
1,0 |
||
|
14 – 18 |
1,0 |
1,6 |
0,5 |
|
|
18 – 30 |
1,6 |
-0,5 |
2,0 |
|
|
30 – 50 |
2,0 |
2,5 |
||
|
50 – 80 |
2,5 |
3,0 |
||
|
80 – 120 |
3,0 |
4,0 |
1,0 |
|
|
120 – 180 |
4,0 |
-1,0 |
5,0 |
|
|
180 – 220 |
5,0 |
6,0 |
||
|
220 – 260 |
6,0 |
8,0 |
2,0 |
|
|
260 – 360 |
8,0 |
-2,0 |
10,0 |
|
|
|
10,0 |
12,0 |
||
Таблица 2. Размеры и предельные отклонения радиусов скруглений или фасок для сопрягаемых поверхностей валов и втулок, мм
|
Номинальный диаметр |
r или С |
Предельное отклонение |
Номинальный диаметр |
r или С |
Предельное отклонение |
|
До 0,5 |
0,05 |
± 0,03 |
Св. 30 до 50 |
2,0 |
± 0,5 |
|
От 0,5 до 1 |
0,1 |
± 0,05 |
50 – 80 |
2,5 |
|
|
Св. 1 – 3 |
0,2 |
± 0,1 |
80 – 120 |
3,0 |
|
|
3 – 6 |
0,3 |
± 0,2 |
120 – 180 |
4,0 |
± 1 |
|
6 – 10 |
0,5 |
± 0,3 |
180 – 260 |
5,0 |
|
|
10 – 18 |
1,0 |
± 0,5 |
260 – 360 |
6,0 |
|
|
18 – 30 |
1,6 |
При применении радиусов скруглений или фасок размером св. 6 до 10 мм предельное отклонение ±1,5 мм; св. 10 до 20 – ±2 мм; св. 20 до 32 – ±2,5 мм и свыше 32 – ±3 мм.
Таб 3. и Рис.2 Размеры и предельные отклонения радиусов скруглений валов и корпусов, сопрягаемых с шарико- и роликоподшипниками, мм

|
Радиус подшипника |
r |
0,2 |
0,3 |
0,4 |
0,5 |
0,8 |
1,0 |
1,2 |
1,5 |
2,0 |
2,5 |
|
Радиус вала или корпуса |
r1 |
0,1 |
0,2 |
0,3 |
0,5 |
0,6 |
0,8 |
1,0 |
1,6 |
||
|
Пред. откл. |
-0,05 |
-0,1 |
-0,2 |
-0,3 |
-0,5 |
||||||
|
Радиус подшипника |
r |
3,0 |
3,5 |
4,0 |
5,0 |
6,0 |
8,0 |
10 |
12 |
15 |
18 |
|
Радиус вала или корпуса |
r1 |
2,0 |
2,5 |
3,0 |
4,0 |
5,0 |
6 |
8 |
10 |
12 |
|
|
Пред. откл. |
-0,5 |
-1,0 |
-2,0 |
||||||||
Рис 3. и Таб 4. Размеры фасок и радиусов и предельные отклонения на механически обрабатываемые плоские детали
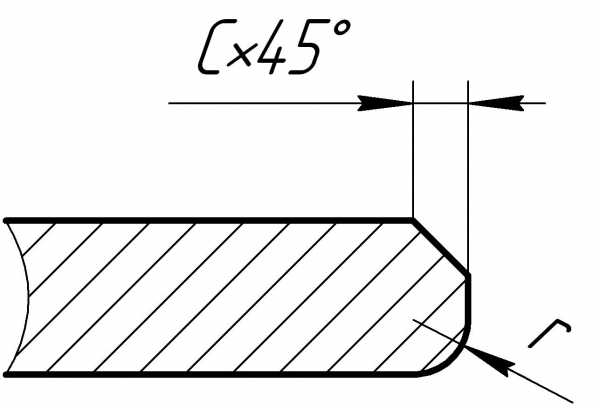
|
С=r |
0,2 |
0,5 |
0,8 |
1,0 |
1,6 |
2,0 |
2,5 |
3,0 |
4,0 |
5,0 |
6,0 |
8,0 |
|
Предельное отклонение |
± 0,1 |
± 0,2 |
± 0,5 |
± 1,0 |
± 2,0 |
|||||||
Рис. 4 и Таб. 5. Размеры и предельные отклонения фасок на валах под запрессовку
|
d1 |
0,6 |
0,8 |
1 |
1,2 |
1,6 |
2,0 |
2,5 |
3 |
4 |
5 |
6 |
8 |
10 |
|
c1 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
1,0 |
1,2 |
1,6 |
||
|
предельное отклонение |
± 0,05 |
± 0,1 |
± 0,2 |
± 0,4 |
|||||||||
|
d1 |
от 10 до 20 |
от 20 до 30 |
от 30 до 50 |
свыше 50 |
|
c1 |
2 |
3 |
4 |
5 |
|
предельное отклонение |
± 0,4 |
± 0,6 |
||
Таб. 6
|
с1 |
0,1 |
от 0,2 до 0,3 |
от 0,4 до 1,0 |
свыше 1 |
|
r |
0,1 |
0,2 |
0,3 |
0,8 |
|
предельное отклонение |
± 0,05 |
± 0,1 |
± 0,1 |
± 0,5 |
Рис. 5 и Таб.7. Размеры и предельные отклонения фасок на втулках под запрессовку
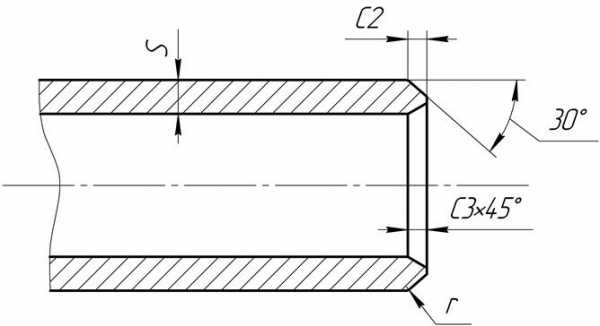
|
S |
от 1 до 1,5 |
от 1,5 до 2 |
от 2 до 3 |
от 3 до 4 |
от 4 до 5 |
от 5 до 8 |
свыше 8 |
|
C2 |
0,3 |
0,5 |
0,8 |
1,0 |
2,0 |
3,0 |
4,0 |
|
предельное отклонение |
± 0,1 |
± 0,2 |
± 0,4 |
± 06 |
|||
|
C3 |
0,4 |
0,5 |
0,5 |
0,5 |
1,0 |
1,0 |
1,6 |
|
предельное отклонение |
± 0,2 |
± 0,4 |
|||||
Примечание: величину радиуса скругления и предельные отклонения на него выбирать по таблице 5.
Размеры радиусов и фасок сопрягаемых поверхностей типа “вал – отверстие”, валов и корпусов с шарико- и роликоподшипниками, а также валов и втулок под запрессовки, должны быть указаны в чертежах с числовыми значениями предельных отклонений.
Размеры радиусов скруглений и фасок несопрягаемых поверхностей валов и втулок и размеры фасок и радиусов на плоских деталях должны быть указаны в чертежах. Предельные отклонения этих размеров на изображении не наносятся, а в технических требованиях чертежа пишется: “Неуказанные предельные отклонения размеров радиусов и фасок по ОСТ 92-0093-69”.
Предельные отклонения на угловые размеры фасок ± 3°.
К оглавлению
glavconstructor.ru
Обмер деталей – Технические чертежи
Обмер деталей
Категория:
Технические чертежи
Обмер деталей
Для обмера деталей применяется различный мерительный инструмент: металлическая линейка, складной метр, кронциркуль и нутромер, угольник, штангенциркуль, резьбомер, радиусомер и другие.
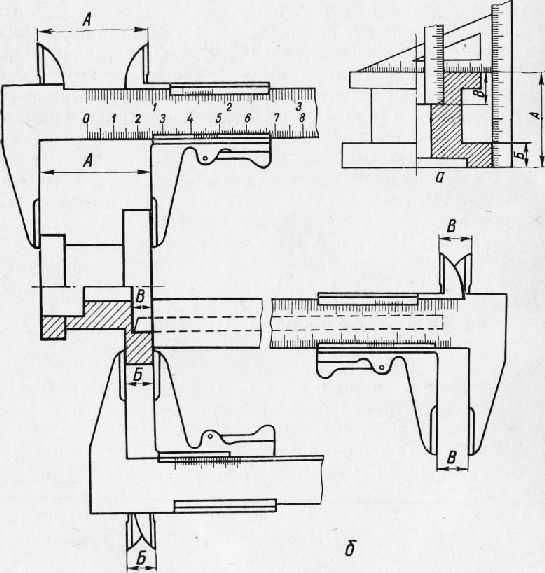
Рис. 1. Измерение прямолинейных частей детали.
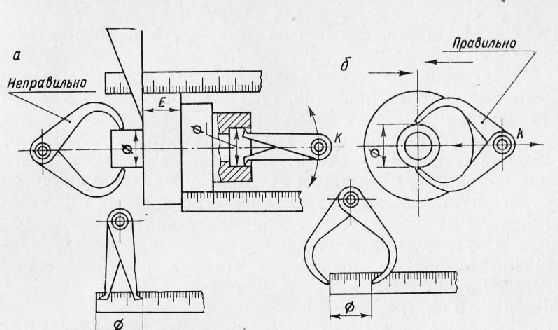
Рис. 2. Измерение диаметров с помощью кронциркуля и нутромера: а — наружного; б — внутреннего.
Измерение прямолинейных частей детали. Прямолинейные части детали можно измерить металлической линейкой или штангенциркулем. На рис. 147, а показано измерение высоты детали А, толщины фланца Б, глубины проточки Б с помощью металлической линейки и угольника, а на рис. 147, б — измерение этих же частей детали с помощью штангенциркуля.
Измерение наружных и внутренних диаметров производится кронциркулем или штангенциркулем. На рис. 148, б показан правильный прием измерения. Ножки кронциркуля следует раздвинуть несколько больше измеряемого диаметра. Взяв кронциркуль двумя пальцами за шарнир К, надо слегка постукивать нижней ножкой по детали и тем самым уменьшать раствор ножек до тех пор, пока при измерении диаметра не будет ощущаться легкое трение ножек о деталь. Направление движения кронциркуля показано на рисунке стрелками. Если пользоваться кронциркулем, как показано слева на рис. 2, а, расстояние между ножками кронциркуля может оказаться меньшим, чем действительный диаметр детали.
внутренние диаметры можно замерить нутромером или штангенциркулем (рис. 2, б). Ножки нутромера следует раздвинуть несколько больше измеряемого диаметра и под углом вставить в измеряемое отверстие. Взяв нутромер за шарнир К двумя пальцами, надо слегка покачивать его в направлении, показанном стрелками, до тех пор, пока не будет ощущаться легкое трение ножек нутромера о поверхность детали. Полученные при измерении кронциркулем или нутромером размеры накладываются на линейку. Наружные диаметры точно обработанных цилиндрических деталей можно измерять микрометром или предельными скобами, а внутренние — пробками.
Измерение расстояний между центрами отверстий. Допустим, что диаметры отверстий d, между которыми нужно измерить расстояние, равны. При помощи нутромера или линейки измеряем расстояние между соответствующими образующими правого и левого отверстия (расстояние Г), которое и будет равно межцентровому расстоянию А (А =Г).
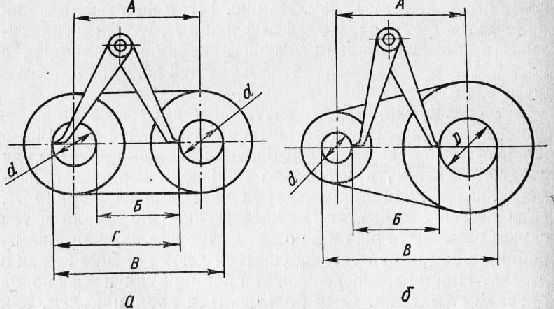
Рис. 3. Измерение расстояний между центрами отверстий.
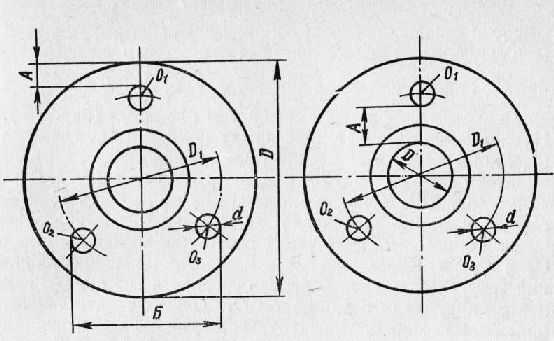
Рис. 4. Измерение расстояний между центрами отверстий на фланце: а — по наружному диаметру; б — по внутреннему диаметру.
Если расстояние Г измерить невозможно, следует измерить расстояние Б между ближайшими образующими отверстий и к нему прибавить диаметр d (А = Б + d) или измерить расстояние В между левой и правой образующими и из него вычесть диаметр d (А = В — d). Таким же путем измеряют расстояние между центрами отверстий на фланце, если они расположены по окружности или в углах квадрата и если их четное число.
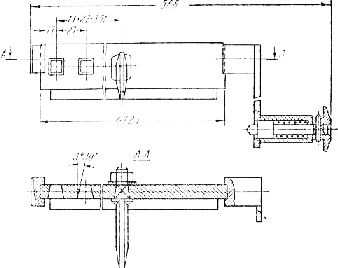
Рис. 5. Измерение труднодоступных мест детали.
Измерение труднодоступных мест детали. Если в детали невозможно измерить непосредственно мерительным инструментом ширину или глубину проточки, то пользуются оттисками, полученными на бумаге или пластилине.
На проточку накладывают полоску бумаги, каким-либо предметом прижимают ее к проточке, затем полученный оттиск замеряют линейкой (рис. 152). Или в проточку вдавливают кусок пластилина и по полученному оттиску определяют требуемый размер.
Измерение радиусов закруглений. Радиусы закруглений измеряют набором радиусомеров. При отсутствии ради-усомеров радиусы можно определить по оттискам на бумаге. Для этого необходимо кусочек бумаги наложить на измеряемый участок и нажать твердым предметом или постучать по бумаге, прижатой к кромке детали. Затем полученный на бумаге оттиск надо замерить циркулем путем подбора радиуса. Такое измерение закруглений не дает большой точности, но погрешность в 1—2 мм для литых деталей допустима.
Радиусы литейных закруглений углов до 5 мм на эскизах обычно не указываются, а оговариваются надписью на поле чертежа.
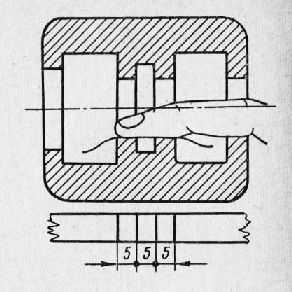
Рис. 6. Измерение крепежной резьбы.
Измерение крепежной резьбы. Измерение резьбы сводится к определению шага резьбы и диаметра, на котором (для стержня) или в котором (для отверстия) выполнена резьба.
Шаг резьбы измеряется резьбомером путем наложения пластинок (подбором по шагу) на резьбовой участок детали (рис. 6, а). При отсутствии резьбомера шаг резьбы можно определить оттиском резьбы на листе бумаги. Если лист плотно прижать к резьбе, то на бумаге останутся риски выступов резьбы (рис. 6, б, в). Измерив линейкой длину участка с рисками и разделив полученное число на количество рисок без одной, получим шаг резьбы.
Допустим, что на бумаге получено 11 рисок (рис. 6) выступов резьбы. Длина участка с рисками 15 мм. Разделив это число на 10 рисок, т. е. на число рисок без одной, получим шаг резьбы— 1,5 мм (рис. 6, г).
Диаметр резьбового участка на стержне измеряется штангенциркулем или кронциркулем, а в отверстии — штангенциркулем или нутромером.
Следует иметь в виду, что диаметр резьбового участка на стержне будет несколько меньше номинального за счет среза выступов и впадин треугольного профиля резьбы.
А диаметр резьбового отверстия составит приблизительно 0,85 от номинального диаметра резьбы.
Измерив диаметр и шаг, по таблицам стандартных резьб устанавливают условное обозначение данной резьбы.
Реклама:
Читать далее:
Понятие о поверхностях и базах
Статьи по теме:
pereosnastka.ru
Принцип действия и примеры радиусомеров
О чем эта статья
Для измерения радиуса вогнутых и выпуклых цилиндрических поверхностей (например, закруглений на деталях или дугообразных поверхностей изделий) используют радиусомер. Наибольшее распространение данный измерительный инструмент нашёл в машиностроении.
Выделяют три вида радиусомеров
- шаблонные
- индикаторные
- оптоэлектронные.
Шаблонный радиусомер

Шаблонный измерительный прибор представляет собой набор изготовленных из высококачественной легированной стали пластинок. Они делятся на две группы – на одном конце радиусомера закреплены шаблоны для измерения впадин, с другого – выступов.
В зависимости от типа шаблонного радиусомера (всего их три), пластинки имеют закругления определённого радиуса. Прибором типа 1 измеряются закругления от 1 до 6 мм, типа 2 – от 8 до 25 мм, типа 3 – от 7 до 25 мм. Диапазон измеряемой кривизны указывается на колодке прибора, величина радиуса шаблона обозначается непосредственно на пластинке.
Измерение кривизны шаблонным радиусомером сводится к подбору пластинки, соответствующей закруглению.
Индикаторный радиусомер
Радиусомер индикаторного типа состоит из двух элементов: непосредственно измерительного устройства и индикатора – стрелочного или цифрового (электронного), на котором отображается результат измерения.
Приборы индикаторного типа используют для определения радиусов кривизны цилиндрических поверхностей. Сферические индикаторные радиусомеры позволяют измерить диаметр и радиус сферических изделий.
Измерения производятся способом трёх- или четырёхточечного (для сферических радиусомеров) контакта. Подвидом индикаторного является сферический радиусомер.
Радиусомеры серии 589 и 590
Радиусомеры серии 589, изготавливаемые Южно-Уральским опытно-механическим заводом, используются для измерения радиуса поверхностей цилиндрических деталей и изделий. Диапазон измерения – 100-1000 мм. Модель 589-121 снабжена стрелочным индикатором в противоударном исполнении, модель 250 поставляется с электронным индикатором. Цена деления прибора – 0,001 мм.
Сферические радиусомеры 590 серии также изготавливаются с индикаторами электронного и стрелочного типа. В зависимости от исполнения, диапазон измерений составляет 325-1250 или 15-100 мм, цена деления – 0,001 или 0,01 мм соответственно.
Оптоэлектронный радиусомер
Оптоэлектронный радиусомер применяют для замера геометрических параметров отверстий. Прибор может использоваться в двух режимах –
- измерения линейных геометрических размеров
- измерения радиусов.
Измерительное устройство радиусомера представляет собой массив считывающих фотоэлементов и преобразователь сигнала.
Радиусомер оптоэлектронный LVS-24

Данный прибор предназначен для сверхточного измерения радиусов и других геометрических параметров входных кромок стандартных диафрагм. Радиусомер LVS-24 работает совместно с компьютером: в комплект поставки прибора входит необходимое программное обеспечение.
Диапазон измерений прибора 15-200 мкм, значение допустимой абсолютной погрешности составляет 10 мкм, дискретность отсчёта – 1 мкм.
Опубликована 24-02-13.
Если вам понравилась статья нажмите на одну из кнопок ниже
www.devicesearch.ru.com
Онлайн калькулятор: Сегмент круга
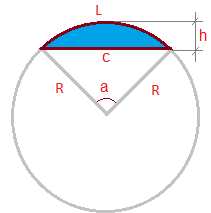 Сегмент круга
Сегмент кругаКруговой сегмент — часть круга ограниченная дугой и секущей (хордой).
На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота
Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:
Формулы вычисления параметров сегмента
Площадь сегмента:
[1]
Длина дуги:
Длина хорды:
Высота сегмента:
Сегмент
Угол в градусах, образуемый радиусами сектора
Точность вычисленияЗнаков после запятой: 2
save Сохранить share Поделиться extension Виджет
Однако, как справедливо заметил наш пользователь:«на практике часто случается, что как радиус дуги, так и угол неизвестны» (см. длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор:
Параметры сегмента по хорде и высоте
Точность вычисленияЗнаков после запятой: 2
Угол (градусы)
save Сохранить share Поделиться extension Виджет
Калькулятор вычисляет радиус круга по длине хорды и высоте сегмента по следующей формуле:
Далее, зная радиус и длину хорды, легко найти угол сегмента по формуле:
Остальные параметры сегмента вычисляются аналогично первому калькулятору, по формулам, приведенным в начале статьи.
Следующий калькулятор вычисляет площадь сегмента по высоте и радиусу:
Площадь сегмента круга по радиусу и высоте
Точность вычисленияЗнаков после запятой: 2
Угол (градусы)
planetcalc.ru
Как определить радиус дуги или сегмента круга и найти центр
Первый метод определения радиуса дуги или сегмента круга
Изначально это выглядит так:
Рисунок 463.1. а) имеющаяся дуга, б) определение длины хорды сегмента и высоты.
Таким образом, когда имеется дуга, мы можем соединить ее концы и получим хорду длиной L. Посредине хорды мы можем провести линию, перпендикулярную хорде и таким образом получим высоту сегмента H. Теперь, зная длину хорды и высоту сегмента, мы можем сначала определить центральный угол α, т.е. угол между радиусами, проведенными из начала и конца сегмента (на рисунке 463.1 не показаны), а затем и радиус окружности.
Решение подобной задачи достаточно подробно рассматривалось в статье “Расчет арочной перемычки”, поэтому здесь лишь приведу основные формулы:
tg(a/4) = 2Н/L (278.1.2)
тогда
а/4 = arctg(2H/L)
R = H/(1 – cos(a/2)) (278.1.3)
Как видим, с точки зрения математики никаких проблем с определением радиуса окружности нет. Данный метод позволяет определить значение радиуса дуги с любой возможной точностью. Это главное достоинство данного метода.
А теперь поговорим о недостатках.
Проблема данного метода даже не в том, что требуется помнить формулы из школьного курса геометрии, успешно забытые много лет назад – для того, чтобы напомнить формулы – есть интернет. А вот калькулятор с функцией arctg, arcsin и проч. есть далеко не у каждого пользователя. И хотя эту проблему также успешно позволяет решить интернет, но при этом не следует забывать, что мы решаем достаточно прикладную задачу. Т.е. далеко не всегда нужно определить радиус окружности с точностью до 0.0001 мм, точность 1 мм может быть вполне приемлема.
Кроме того, для того, чтобы найти центр окружности, нужно продлить высоту сегмента и отложить на этой прямой расстояние, равное радиусу. Так как на практике мы имеем дело с не идеальными измерительными приборами, к этому следует прибавить возможную погрешность при разметке, то получается, что чем меньше высота сегмента по отношению к длине хорды, тем больше может набежать погрешность при определении центра дуги.
Опять же не следует забывать о том, что мы рассматриваем не идеальный случай, т.е. это мы так сходу назвали кривую дугой. В действительности это может быть кривая, описываемая достаточно сложной математической зависимостью. А потому найденный таким образом радиус и центр окружности могут и не совпадать с фактическим центром.
В связи с этим я хочу предложить еще один способ определения радиуса окружности, которым сам часто пользуюсь, потому что этим способом определить радиус окружности намного быстрее и проще, хотя точность при этом значительно меньше.
Второй метод определения радиуса дуги (метод последовательных приближений)
Итак продолжим рассмотрение имеющейся ситуации.
Так как нам все равно необходимо найти центр окружности, то для начала мы из точек, соответствующих началу и концу дуги, проведем как минимум две дуги произвольного радиуса. Через пересечение этих дуг будет проходить прямая, на которой и находится центр искомой окружности.
Теперь нужно соединить пересечение дуг с серединой хорды. Впрочем, если мы из указанных точек проведем не по одной дуге, а по две, то данная прямая будет проходить через пересечение этих дуг и тогда искать середину хорды вовсе не обязательно.
Ну а дальше все просто: измеряем расстояние от пересечения дуг до начала (или конца) рассматриваемой дуги, а затем расстояние от пересечения дуг до точки, соответствующей высоте сегмента.
Если расстояние от пересечения дуг до начала или конца рассматриваемой дуги больше, чем расстояние от пересечения дуг до точки, соответствующей высоте сегмента, то значит центр рассматриваемой дуги находится ниже на прямой, проведенной через пересечение дуг и середину хорды. Если меньше – то искомый центр дуги выше на прямой.
Исходя из этого на прямой принимается следующая точка, предположительно соответствующая центру дуги, и от нее производятся те же измерения. Затем принимается следующая точка и измерения повторяются. С каждой новой точкой разница измерений будет все меньше.
Вот собственно и все. Не смотря на столь пространное и мудреное описание, для определения радиуса дуги таким способом с точностью до 1 мм достаточно 1-2 минут.
Теоретически это выглядит примерно так:
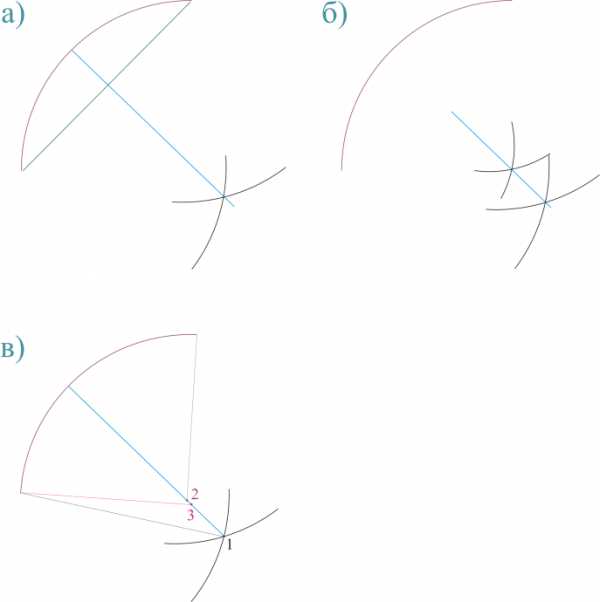
Рисунок 463.2. Определение центра дуги методом последовательных приближений.
А на практике примерно так:

Фотография 463.1. Разметка заготовки сложной формы с разными радиусами.
Тут только добавлю, что иногда приходится находить и чертить несколько радиусов, потому на фотографии так много всего и намешано.
doctorlom.com
Уклоны, радиусы закруглений, кюветы, придорожная полоса
Уклоны
Дороги, проходящие по пересеченной местности, практически повторяют ее профиль, где подъемы чередуются со спусками. Уклоны (подъемы), идущие вдоль осевой линии проезжей части дороги, именуются продольными.
Для обеспечения отекания воды с проезжей части ее обустраивают таким образом, чтобы края проезжей части располагались ниже ее середины (двускатный профиль). Образующиеся при этом уклоны именуются поперечными.
На некоторых участках закруглений дороги ее проезжая часть может быть с равномерным понижением от внешней стороны закругления к внутренней (вираж, односкатный профиль).
Поперечные уклоны измеряются в направлении, перпендикулярном к осевой линии дороги.
Определить угол продольного уклона дороги можно следующим способом:
- на середине проезжей части дороги закрепляется конец рулетки с отметкой «ноль» (прижать камнем, колесом ТС и др.)
- рулетка разматывается, и с помощью наблюдателя полотну рулетки придается горизонтальное положение
- измеряется расстояние от поверхности проезжей части до полотна рулетки (а), против одного из ее делений 3, 5 или 10м (б)
Рис. Угол продольного уклона дороги
Результаты измерений фиксируются схематически и вносятся в протокол. Следует также измерить длину уклона и указать ее в протоколе.
Пример записи в протоколе осмотра:
Нулевая отметка рулетки закреплялась на середине проезжей части (понятой удерживал рукой). После придания полотну рулетки горизонтального положения расстояние от полотна рулетки на отметке 3 м до проезжей части составило 20 см. Длина уклона 280 м. Уклон по всей длине одинаков.
Измерения для определения величины поперечного уклона или виража проезжей части производятся аналогичным образом в направлении, перпендикулярном оси дороги.
Радиусы закруглений
В случае, когда ДТП совершено на участке закругления дороги, величина радиуса закругления определяется по результатам следующих измерений:
- в наиболее выраженной части закругления на линии, определяющей данное закругление (осевая линия, кромка проезжей части), делаются две отметки, которые должны находиться в границах закругления. Расстояние между отметками выбираются произвольно, но не менее 15-20 м
- между отметками растягивается шпагат либо полотно рулетки, имеющей достаточную длину.
Измеряется расстояние от середины растянутого между отметками шпагата до линии:
Рис. Расстояние от середины растянутого между отметками шпагата до линии
Пример записи в протоколе осмотра:
На кромке проезжей части посередине закругления были отмечены точки А и Б, расстояние между которыми составило 24 м. Расстояние от точки А до дорожного знака составило 172 м. От середины линии, соединяющей точки А и Б, расстояние до кромки проезжей части равнялось 60 см.
В случаях, когда при ДТП транспортное средство сходит с дороги, оно может оставлять следы на проезжей части, на обочине, на откосах дорожного полотна и кювета, на придорожной полосе и т.д. На схему при этом следует нанести поперечный разрез дорожного полотна в месте с наиболее отчетливым отпечатком пути перемещения ТС, с указанием расположения, вида и характера следов.
Рис. Поперечный разрез дорожного полотна в месте с наиболее отчетливым отпечатком пути перемещения ТС: а — кромка проезжей части; б — бровка дорожного полотна; а-б — обочина шириной 1,8 м; б-в — откос дорожного полотна шириной 1,6 м; в — дно кювета; в-г — откос кювета шириной 1,5 м; б-а — ширина кювета 2,8 м; з — внешняя бровка кювета ниже поверхности обочины (линии горизонта) на 0,4 м; б-линия горизонта к дороге. От точки з прилегающая к дороге луговина на длине 5 м понижается на 0,6 м.
Если ТС на пути своего перемещения контактировало, например, с деревьями либо с другими препятствиями, расположение этих препятствий и следы, имеющиеся на них, следует измерить и описать в протоколе.
Для производства измерений уклонов, радиусов закруглений и иных элементов дороги целесообразно привлечь в качестве специалиста сотрудника инженерно-технической службы ДЭУ, ДСР либо других дорожных организаций.
ustroistvo-avtomobilya.ru


