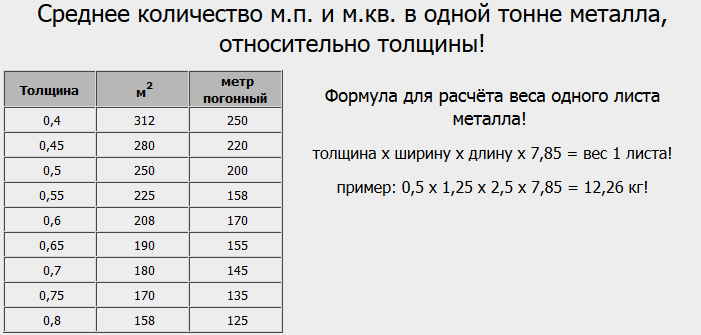
Как рассчитать массу круга из стали: Калькулятор веса стального круга

alexxlab | 02.03.2022 | 0 | Разное

Калькулятор веса металлопроката » Металлургпром

Универсальный калькулятор веса металлов, сплавов и стали позволяет быстро и точно рассчитать вес металлопроката в зависимости от материала. Вы можете подсчитать теоретический вес стали, чугуна, алюминия, латуни, бронзы, меди, а также их сплавов.

Калькулятор рассчитает вес круглой и профильной трубы, уголка, листа, ленты, круга, проволоки, швеллера, балки и шестигранника.

Сервис работает в онлайн-режиме и абсолютно бесплатен для использования. Для расчета веса стали для конкретного проката, или веса цветного металла, необходимо:

  1. выбрать необходимый металлопрокат
  2. ввести размеры проката, вес которого нужно подсчитать
  3. выбрать материал и марку стали.

После этого автоматически будет показан расчетный вес проката с вашими параметрами. 

Необходимо понимать, что вес является теоретическим, фактические данные должны быть указаны в сертификате производителя.

Тип прокатаРазмерыМеталлы и сплавы

Листовая сталь

Лист

Шина

Лента (полоса)

Плита

Сортовая сталь

Круг

Шестигранник

Квадрат

Труба

Проволока

Уголок

Длина (мм)

Ширина (мм)

Толщина (мм)

Длина (мм)

Ширина (мм)

Толщина (мм)

Длина (мм)

Ширина (мм)

Толщина (мм)

Длина (мм)

Ширина (мм)

Толщина (мм)

Длина (мм)

Диаметр (мм)

Длина (мм)

Сечение (мм)

Длина (мм)

Сечение (мм)

Длина (мм)

Толщина стенки (мм)


Диаметр (мм)

Длина (мм)

Диаметр (мм)

Длина (мм)

Толщина стенки (мм)

Высота полки1 (мм)

Высота полки2 (мм)

-Выберите-СтальНержавеющие сталиАлюминийМедьЛатуньБронзаОловоСвинецЦинкНикелевые сплавыМедно-никелевые сплавыНихром

Ст. 3

09Г2С

Ст.45

10ХСНД

Ст.40Х

А5

АД0

АМг6

АМг5

АМг3

АМг2

АД31

АД1

АМц

1915

Д16

Д1

М1, М2, М3

ЛС59-1

Л63

Л68

БрАМц9-2

БрАЖН10-4-4

БрКМц3-1

БрКН1-3

БрБ2

БрАЖ9-4

БрОЦС5-5-5

БрОЦ4-3

БрАЖМц10-3-1,5

БрОФ6,5-0,15

БрОФ7-0,2

БрОФ4-0,25

С0, С1, С2

Ц0, Ц1

НМц2,5

НМц5

НК0,2

Алюмель НМцАК2-2-1

Монель НМЖМц28-2,5-1,5

Хромель Т НХ9,5

МНЖ5-1

Манганин МНМц3-12

Мельхиор МН19

Копель МНМц43-0,5

Константан МНМц40-1,5

Куниаль А МНА6-1,5

Куниаль Б МНА6-1,5

Нейзильбер МНЦ15-20

Х15Н60

Х20Н80

08Х17Т

08Х13

12Х13

12Х17

15Х25Т

04Х18Н10Т

08Х18Н10

08Х18Н10Т

08Х18Н12Т

08Х17Н15М3Т

12Х18Н10Т

12Х18Н12Т

08Х20Н14С2

10Х17Н13М2Т

08Х18Н12Б

10Х23Н18

12Х18Н9

08Х22Н6Т

05ХН28МДТ

Теоретическая масса*: 0 кг.

* Теоретическая масса является справочной величиной

15.6: Расчет центров масс и моментов инерции

  1. Последнее обновление
  2. Сохранить как PDF
  • Идентификатор страницы
    2614
    • Гилберт Стрэнг и Эдвин «Джед» Герман
    • ОпенСтакс
    Цели обучения
    • Использование двойных интегралов для определения центра масс двумерного объекта.
    • Используйте двойные интегралы, чтобы найти момент инерции двумерного объекта.
    • Используйте тройные интегралы для определения центра масс трехмерного объекта.

    Мы уже обсудили несколько применений кратных интегралов, таких как нахождение площадей, объемов и среднего значения функции в ограниченной области. В этом разделе мы разрабатываем вычислительные методы для нахождения центра масс и моментов инерции нескольких типов физических объектов, используя двойные интегралы для пластины (плоской пластины) и тройные интегралы для трехмерного объекта с переменной плотностью. Плотность обычно считается постоянным числом, когда пластинка или объект однородны; то есть объект имеет однородную плотность.

    Центр масс в двух измерениях

    Центр масс также известен как центр тяжести, если объект находится в однородном гравитационном поле. Если объект имеет однородную плотность, центр масс является геометрическим центром объекта, который называется центроидом. На рисунке \(\PageIndex{1}\) показана точка \(P\) как центр масс пластинки. Пластинка идеально сбалансирована относительно своего центра масс.

    Рисунок \(\PageIndex{1}\): Пластинка идеально сбалансирована на шпинделе, если центр масс пластинки находится на шпинделе.

    Чтобы найти координаты центра масс \(P(\bar{x},\bar{y})\) пластинки, нужно найти момент \(M_x\) пластинки относительно \( x\)-ось и момент \(M_y\) относительно \(y\)-оси. Нам также нужно найти массу \(m\) пластинки. Тогда

    \[\bar{x} = \dfrac{M_y}{m} \nonumber \]

    и

    \[\bar{y} = \dfrac{M_x}{m}. \nonumber \]

    Обратитесь к разделу “Моменты и центры масс” за определениями и методами одинарного интегрирования для нахождения центра масс одномерного объекта (например, тонкого стержня). Мы собираемся использовать аналогичную идею здесь, за исключением того, что объект представляет собой двумерную пластинку, и мы используем двойной интеграл.

    Если мы допускаем постоянную функцию плотности, то \(\bar{x} = \dfrac{M_y}{m}\) и \(\bar{y} = \dfrac{M_x}{m}\) дают центроид пластинки.

    Предположим, что пластинка занимает область \(R\) в \(xy\)-плоскости, и пусть \(\rho (x,y)\) – ее плотность (в единицах массы на единицу площади) в любой точка \((х,у)\). Следовательно,

    \[\rho(x,y) = \lim_{\Delta A \rightarrow 0} \dfrac{\Delta m}{\Delta A} \nonumber \]

    , где \(\Delta m\) и \(\Delta A\) – масса и площадь маленького прямоугольника, содержащего точку \((x,y)\), и предел берется, когда размеры прямоугольника идут к \(0\) (см. следующий рисунок). 9{x=3} = \dfrac{27}{8}. \nonumber \]

    Расчет прост и дает ответ \(m = \dfrac{27}{8} \, кг\).

    Упражнение \(\PageIndex{1}\)

    Рассмотрим ту же область \(R\), что и в предыдущем примере, и используем функцию плотности \(\rho (x,y) = \sqrt{xy}\ ). Найдите общую массу.

    Ответить

    \(\dfrac{9\pi}{8} \, кг\)

    Теперь, когда мы установили выражение для массы, у нас есть инструменты, необходимые для вычисления моментов и центров масс. Момент \(M_z\) относительно оси \(x\) для \(R\) является пределом сумм моментов областей \(R_{ij}\) относительно оси \(x\) . Отсюда 92 y \, dy \, dx = \dfrac{81}{20}, \nonumber \]

    Расчет довольно прост.

    Упражнение \(\PageIndex{2}\)

    Рассмотрим ту же пластинку \(R\), что и выше, и используем функцию плотности \(\rho (x,y) = \sqrt{xy}\). Найдите моменты \(M_x\) и \(M_y\).

    Ответить

    \(M_x = \dfrac{81\pi}{64}\) и \(M_y = \dfrac{81\pi}{64}\)

    Наконец, мы готовы переформулировать выражения для центра масс в виде интегралов. Обозначим x -координата центра масс через \(\bar{x}\) и y -координата через \(\bar{y}\). В частности,

    \[\bar{x} = \dfrac{M_y}{m} = \dfrac{\iint_R x\rho (x,y) \,dA}{\iint_R \rho (x,y)\, dA} \nonumber \]

    и

    \[\bar{y} = \dfrac{M_x}{m} = \dfrac{\iint_R y\rho (x,y) \,dA}{\iint_R \rho (x,y)\,dA} \nonumber \]

    Пример \(\PageIndex{3}\): центр масс

    Снова рассмотрим ту же треугольную область \(R\) с вершинами \((0,0 ), \, (0,3), \, (3,0)\) и с функцией плотности \(\rho (x,y) = xy\). Найдите центр масс.

    Решение

    Используя разработанные нами формулы, имеем

    \[\bar{x} = \dfrac{M_y}{m} = \dfrac{\iint_R x\rho (x,y) \,dA }{\iint_R \rho (x,y)\,dA} = \dfrac{81/20}{27/8} = \dfrac{6}{5}, \nonumber \]

    \[\bar{y } = \dfrac{M_x}{m} = \dfrac{\iint_R y\rho (x,y) \,dA}{\iint_R \rho (x,y)\,dA} = \dfrac{81/20} {27/8} = \dfrac{6}{5}. \nonumber \]

    Следовательно, центром масс является точка \(\left(\dfrac{6}{5},\dfrac{6}{5}\right). \)

    Анализ

    Если мы выберем плотность \(\rho(x,y)\) вместо того, чтобы она была равномерной по всей области (т. е. постоянной), такой как значение 1 (подойдет любая константа), то мы можем вычислить центроид,

    \[x_c = \dfrac{M_y}{m} = \dfrac{\iint_R x \, dA}{\iint_R \,dA} = \dfrac{9/2}{9/2} = 1 , \nonumber \]

    \[y_c = \dfrac{M_x}{m} = \dfrac{\iint_R y \, dA}{\iint_R \,dA} = \dfrac{9/2}{9/2} = 1. \nonumber \]

    Обратите внимание, что центр масс \(\left(\dfrac{6}{5},\dfrac{6}{5}\right)\) не совпадает с центром тяжести \((1,1)\) треугольной области. Это связано с переменной плотностью \(R\). Если плотность постоянна, то мы просто используем \(\rho(x,y) = c\) (константа). Это значение исключается из формул, поэтому при постоянной плотности центр масс совпадает с центром тяжести пластинки.

    Упражнение \(\PageIndex{3}\)

    Снова используйте ту же область \(R\), что и выше, и функцию плотности \(\rho (x,y) = \sqrt{xy}\). 2\) в интервале \(0 \leq x \leq 2\) (см. следующий рисунок). 92} х(х + у) \,dy \, dx = \dfrac{176}{15}. \nonumber \]

    Наконец, оцените центр масс,

    \[\bar{x} = \dfrac{M_y}{m} = \dfrac{\iint_R x \rho (x,y) \,dA} {\iint_R \rho (x,y)\,dA} = \dfrac{176/15}{36/5} = \dfrac{44}{27}, \nonumber \]

    \[\bar{y} = \dfrac{M_x}{m} = \dfrac{\iint_R y \rho (x,y) \,dA}{\iint_R \rho (x,y)\,dA} = \dfrac{80/7}{ 36/5} = \dfrac{100}{63}. \nonumber \]

    Следовательно, центр масс равен \((\bar{x},\bar{y}) = \left(\dfrac{44}{27}, \dfrac{100}{63} \right )\). 92 + 1)\справа). \nonumber \]

    Упражнение \(\PageIndex{5}\)

    Вычислить центр тяжести области между кривыми \(y = x\) и \(y = \sqrt{x}\) с равномерной плотностью интервал \(0 \leq x \leq 1\).

    Ответить

    \(x_c = \dfrac{M_y}{m} = \dfrac{1/15}{1/6} = \dfrac{2}{5}\) и \( y_c = \dfrac{M_x}{m} = \dfrac{1/12}{1/6} = \dfrac{1}{2}\)

    Моменты инерции

    Для ясного понимания того, как вычислять моменты инерции с помощью двойных интегралов, нам нужно вернуться к общему определению в разделе \(6. *) \Delta A\). Момент инерции связан с вращением массы; в частности, он измеряет тенденцию массы сопротивляться изменению вращательного движения вокруг оси. 92\), где \(r\) — расстояние частицы от оси, также известное как радиус вращения .

    Следовательно, радиусы вращения относительно оси \(x\), оси \(y\) и начала координат равны

    \[R_x = \sqrt{\dfrac{I_x}{m}}, \, R_y = \sqrt{\dfrac{I_y}{m}}, \, и \, R_0 = \sqrt{\dfrac{I_0}{m}}, \nonumber \]

    соответственно. В каждом случае радиус вращения говорит нам, как далеко (перпендикулярное расстояние) от оси вращения может быть сосредоточена вся масса объекта. Моменты объекта полезны для получения информации о балансе и крутящем моменте объекта относительно оси, но радиусы вращения используются для описания распределения массы вокруг его центральной оси. Есть много приложений в технике и физике. Иногда необходимо найти радиус вращения, как в следующем примере.

    Пример \(\PageIndex{7}\): нахождение радиуса вращения треугольной пластинки

    Рассмотрим ту же треугольную пластинку \(R\) с вершинами \((0,0), \, (2,2 )\) и \((2,0)\) и с плотностью \(\rho(x,y) = xy\), как в предыдущих примерах. Найдите радиусы вращения относительно оси \(x\), оси \(y\) и начала координат.

    Решение

    Если мы вычислим массу этой области, то найдем, что \(m = 2\). Мы нашли моменты инерции этой пластинки в примере \(\PageIndex{4}\). Из этих данных радиусы вращения относительно оси \(x\), оси \(y\) и начала координат равны соответственно

    \[\begin{align} R_x = \sqrt{\dfrac{I_x}{m}} = \sqrt{\dfrac{8/3}{2}} = \sqrt{\dfrac{8}}{6} } = \dfrac{2\sqrt{3}}{3},\\R_y = \sqrt{\dfrac{I_y}{m}} = \sqrt{\dfrac{16/3}{2}} = \sqrt {\ dfrac {8} {3}} = \ dfrac {2 \ sqrt {6}} {3}, \\ R_0 = \ sqrt {\ dfrac {I_0} {m}} = \ sqrt {\ dfrac {8} {2}} = \sqrt{4} = 2.\end{align} \nonumber \]

    Упражнение \(\PageIndex{7}\)

    Используйте тот же регион \(R\) из примера \(\ PageIndex{7}\) и функцию плотности \(\rho (x,y) = \sqrt{xy}\). Найдите радиусы вращения относительно оси \(x\), оси \(y\) и начала координат. 92з\). Найдите центр масс.

    Подсказка

    Убедитесь, что \(M_{xy} = \dfrac{27}{35}, \, M_{xz} = \dfrac{243}{140},\) и \(M_{yz} = \dfrac{81} {35}\). Затем используйте \(m\) из предыдущего контрольного вопроса.

    Ответить

    \(\left(\dfrac{3}{2}, \dfrac{9}{8}, \dfrac{1}{2}\right)\)

    Завершим этот раздел примером нахождения моментов инерции \(I_x, \, I_y\) и \(I_z\). 92 yz\) (см. рисунок \(\PageIndex{7}\)). Найти моменты инерции тетраэдра \(Q\) относительно плоскостей \(yz\), \(xz\) и \(xy\)-плоскостей.

    Решение

    Опять же, мы можем почти сразу написать пределы интегрирования и, следовательно, мы можем быстро перейти к оценке моментов инерции. Используя приведенную выше формулу, моменты инерции тетраэдра \(Q\) относительно плоскости \(yz\), плоскости \(xz\) и плоскости \(xy\) равны

    92з\). Найдите моменты инерции относительно трех координатных плоскостей.

    Ответить

    Моменты инерции тетраэдра \(Q\) относительно плоскости \(yz\), плоскости \(xz\) и плоскости \(xy\) равны \(99/35, \, 36/7\) и \(243/35\) соответственно.

    Ключевые понятия

    Нахождение массы, центра масс, моментов и моментов инерции в двойных интегралах:

    • Для пластины \(R\) с функцией плотности \(\rho (x,y)\) в любой точке \((x,y)\) плоскости масса равна \[m = \iint_R \rho (x,y) \,dA. \номер\] 92) \rho(x,y) \,dA. \номер\]

    Нахождение массы, центра масс, моментов и моментов инерции в тройных интегралах:

    • Для твердого тела \(Q\) с функцией плотности \(\rho(x,y,z)\) при любая точка \((x,y,z)\) в пространстве имеет массу \[m = \iiint_Q \rho (x,y,z) \,dV. \номер\]
    • Моменты относительно плоскости \(xy\), плоскости \(xz\) и плоскости \(yz\) равны \[M_{xy} = \iiint_Q z\rho (x,y,z )\,dV, \, M_{xz} = \iiint_Q y\rho (x,y,z)\,dV, \, M_{yz} = \iiint_Q x\rho (x,y,z)\,dV \номер\] 9*) \,\Delta A = \iint_R x\rho(x,y)\,dA \nonumber \]
    • Центр масс пластинки \[\bar{x} = \dfrac{M_y}{m} = \dfrac{\iint_R x\rho (x,y) \,dA}{\iint_R \rho (x ,y) \,dA} \, и \, \bar{y} = \dfrac{M_x}{m} = \dfrac{\iint_R y\rho (x,y) \,dA}{\iint_R \rho ( x,y) \,dA} \номер\]

    Глоссарий

    радиус вращения
    расстояние от центра масс объекта до его оси вращения

    Эта страница под названием 15. 6: Вычисление центров масс и моментов инерции распространяется в соответствии с лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Гилбертом Стрэнгом и Эдвином «Джедом» Германом (OpenStax) через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

    1. Наверх
      • Была ли эта статья полезной?
      1. Тип изделия
        Раздел или Страница
        Автор
        ОпенСтакс
        Лицензия
        CC BY-NC-SA
        Версия лицензии
        4,0
        Программа OER или Publisher
        ОпенСтакс
        Показать страницу TOC
        нет
      2. Теги
        1. автор @ Эдвин «Джед» Герман
        2. автор@Гилберт Странг
        3. центр тяжести
        4. центр масс
        5. Моменты инерции
        6. радиус вращения
        7. источник@https://openstax. org/details/books/calculus-volume-1

      Химия 110 – Дополнения к эксперименту 2

      Химия 110 – Дополнения к эксперименту 2

      Эксперимент 2

      Измерения и графики

      В первый день этой лабораторной работы вы измерите диаметр комплекта из стальных шариков (подшипников) и набора деревянных шариков. Цель этой части эксперимента заключается в том, чтобы получить математическую соотношение между вашим измеренным диаметром (или производным радиусом) и массой твердой сферы. После того, как вы определите диаметр конкретного мяч, вы должны также измерить соответствующую массу этого мяча (вы должны сохраните массу и диаметр каждого шара вместе для последующих вычислений). Эти коррелированные значения будут отображены на графике в течение второго дня этого лаборатории с помощью компьютера и программного обеспечения LabWorks. Из этих компьютерных графики, вы сможете определить правильную математическую зависимость между длиной (диаметром) и массой (объемом). Масса и объем прямо связаны, исходя из определения плотности (D=m/V).

      После того, как вы получили правильное математическое соотношение и уравнение описывая эту зависимость, вы будете измерять диаметр и массу другого стальной шар (это будет большой стальной шар, с помощью описанной процедуры ниже как Результат обучения ). Затем вы будете использовать математическое уравнение полученный выше, и рассчитайте его массу, исходя из измеренного диаметра. После того, как вы определите массу на основе математической зависимости (используя уравнение для прямой линии), вы проведете анализ процентной ошибки фактической измеренной массы к этой математически рассчитанной массе.

      Во второй части этого эксперимента вы будете использовать несколько различных измерительных контейнеры для измерения 40 мл воды. Для этой части эксперимента вы будете использовать химический стакан на 100 мл (или 150 мл), градуированный цилиндр на 100 мл, Мерный цилиндр на 50 мл и мерный цилиндр на 10 мл. От них измерений, вы определите, какое измерительное устройство дает вам больше всего точные результаты. Вы определите анализ ошибок для этой части эксперимента.

      День 1: Измерение массы и диаметра мячей и измерение объема воды

      Диаметр и масса стальных и деревянных шариков

      Достаньте из тележки набор стальных шаров. С помощью штангенциркуля (т. объяснение по его использованию будет дано вашим инструктором) для измерения диаметра каждого шара в наборе. После того, как вы определили диаметр для каждого шаров в наборе, вы должны получить их массы и записать эти данные в тетради (помните, что вы должен соотносить массу и радиус за каждый шар). И вы, и ваш партнер определите самостоятельно значения для этой части эксперимента.

      Дополнительно, в зависимости от рекомендаций инструктора: Приобретите набор деревянных шариков и, как и прежде, измерить диаметр и массу (оба ученика собирают и записать независимые данные измерений). Легче всего взвесить мяч поместив каждый шар на предварительно обнуленные весы с помощью крышки контейнера положить вверх дном на чашу весов, чтобы шарики не катались.

      Не будет никаких расчетов или манипуляций с вашими данными во время первый день. Все компьютерные анализы будут выполняться на втором день лаборатории.

      Измерения 40 мл воды

      Эта часть эксперимента преследует двоякую цель: (1) определить, какие измерительное устройство дает вам самое точное измерение 40 мл воды, и (2) выполнение анализа процентной ошибки ваших измерений на основе теоретическое количество воды, которое вы должны получить (теоретически у вас должно быть 40,00 мл воды, и, используя плотность при той температуре, которую вы использовали, вы можете определите теоретическую массу воды, которая у вас должна быть) при каждом измерении. Обязательно измерьте температуру воды, которую вы используете, так как плотность воды зависит от температуры. Плотность воды, на температуру, которую вы измеряли, можно получить из справочника CRC (ваш инструктор покажет вам, как читать эту таблицу). Использовать Д.И. вода по всем параметрам.

      Чтобы начать эту часть эксперимента, возьмите чистую и сухую пробу объемом 100 или 150 мл. химический стакан из ящика и определите его массу. Вы будете использовать этот стакан для всех четырех измерений объема, но он должен быть только абсолютно сухим для первого измерения.

      1. Используя промывочную бутыль, добавьте достаточное количество D.I. воды в предварительно взвешенный стакан туда, где, по вашему мнению, должен быть объем 40 мл, исходя из калибровки стакана шкала. После добавления воды поставьте этот стакан на весы и определил его общую массу ( убедитесь, что баланс обнулился! ). Эта общая масса включает массу стакана (которую вы только что определили), и массу воды, которую вы только что добавили (предположительно 40 мл). Вычесть масса стакана из этой суммы, и вы получите массу воды добавлен.
      2. Во второй части этого эксперимента вылейте всю воду из стакан на первом этапе. Неважно, останется ли немного остаточной воды, так как вы должны повторно взвесить стакан, прежде чем добавлять воду. Любая остаточная вода просто становится частью массы стакана и не будет мешать или изменять ваши другие измерения. Теперь, используя мерный цилиндр на 100 мл, добавьте достаточное количество воды, чтобы получить объем 40 мл. Свалка содержимое этого мерного цилиндра в химический стакан (который вы только что взвешивается пустым и может содержать некоторое количество остаточной воды). Место этот химический стакан с недавно отмеренными 40 мл воды на предварительно обнуленных весах и запишите новую массу. Масса воды, добавленной из 100-мл цилиндра будет равна общей массе минус масса стакана (содержащего некоторое остаточное вода; , а не масса абсолютно сухого стакана). Запишите это масса воды.
      3. Следуйте процедуре, описанной во второй части, но теперь вы будете использовать 50 мл мерный цилиндр. Добавьте достаточное количество воды, чтобы оно равнялось 40 мл (используя калибровочные метки на цилиндре). Дамп содержимого этого градуированного цилиндр в тот же стакан, который использовался ранее (который вы только что повторно взвесили пустой, после сброса воды, добавленной на втором этапе, и который может содержать немного остаточной воды). Поместите этот стакан с только что отмеренными 40 мл воды на предварительно обнуленные весы и записывают его массу. Масса воды, добавленной с помощью цилиндра на 50 мл, будет равна общей массе минус масса стакана (с небольшим количеством остаточной воды). Запишите эту массу воды.
      4. Следуйте процедуре, описанной в шагах два и три, чтобы измерить 40 мл воды с помощью мерного цилиндра на 10 мл. Поскольку вы не можете измерить 40 мл воды за одно измерение, вам нужно будет заполнить 10-мл градуированную цилиндр до отметки 10 мл, слейте эту воду в пустой (и предварительно взвешенный химический стакан для этой части эксперимента) и повторите эти 10-мл измерения три дополнительных раза. Общий объем воды, который вы должны были добавить в стакан будет равно 40 мл. Поместите стакан с этим 40 мл воды, полученной с помощью мерного цилиндра на 10 мл, на предварительно обнуленную взвесьте и запишите его массу. Масса воды, добавленная с использованием 10-мл цилиндра (в четырех сложениях) будет равна полной массе минус масса стакан (содержащий немного остаточной воды). Запишите эту массу воды.

      Это единственные измерения, которые необходимо выполнить в течение первого дня. лаборатории.

      День 2: Определение соотношения между массой и диаметром и вычисление процентной погрешности измерений воды.

      Анализ диаметра и массы

      Вы будете следовать пошаговым процедурам, изложенным в опубликованном экспериментальные протоколы для компьютерного анализа измерений, которые вы изготовлены на наборе стальных шариков и деревянных шариков. На самом деле нет изменение этого объяснения, так как использование компьютера и LabWorks очень хорошо описано.

      В основном ученые и математики манипулируют данными для получения графиков. Обычно, если вы можете построить прямую линию из ваших экспериментальных данных, вы можете сделать выводы о математических отношениях между двумя переменными. Например, площадь круга имеет формулу πr 2 , где r — радиус (диаметр/2). Если вы начертите площадь (ось Y) в стихах радиус (ось x) вы видите параболу или параболическую кривую, так как площадь увеличивается на квадрат радиуса, как показано ниже в таблице. Однако, если вы возвели значения радиуса в квадрат и нанесли их на график относительно площади, вы бы теперь увидеть прямую, линейную корреляцию. Это соотношение означает, что площадь есть функция квадрата радиуса, что соответствует формуле для круг, в который входит квадрат радиуса ( πr 2 ).

      радиус (см)

      Площадь (см 2 )

      радиус в квадрате (см 2 )

      2,00

      12. 57

      4.00

      4.00

      50.27

      16.00

      6.00

      113.1

      36.00

      8.00

      201.1

      64.00

      10.00

      314.2

      100,0

      Вы можете видеть, что связь между радиусом и площадью не просто линейная. отношения (например, для показанных значений радиус увеличивается на коэффициент в 5 раз, а площадь увеличивается в 25 раз). Фактические отношения оказывается квадратным отношением между радиусом и площадью, и легко наблюдается путем построения графика зависимости площади от квадрата радиуса, как показано на Таблица. Для вашего эксперимента вы нанесете измеренный диаметр соответствует соответствующей массе этого шара. Если ваш рассчитанный «лучший линия подходит” не соответствует вашим точкам данных, то вы должны построить массу стихов квадрат диаметра и, при необходимости, куб диаметра. Одно из этих трех математических соотношений должно соответствовать вашим данным. Лучший. В своей тетради объясните, почему отношения, которые вы выбрали (прямые линейная зависимость, квадратичная зависимость или кубическая зависимость) – это скорее всего правильно, исходя из других математических рассуждений.

      После того, как вы нанесете свои данные и получите приемлемый график, распечатайте единственную копию (сделайте дополнительные ксерокопии для партнеров лаборатории). Прежде чем распечатать свой скопируйте, обязательно добавьте свои имена в графу. (Вы будете оценены от того, насколько точно вы следуете этим инструкциям.)

      Результат обучения: После того, как вы определили лучший математический отношения, чтобы соответствовать вашим измерениям, вы будете использовать полученную формулу для прямолинейного графика для расчета экспериментальной массы для большого стальной шар. Получите один из больших стальных шаров от инструктора. С помощью штангенциркуля измерьте его диаметр. Используйте этот диаметр как переменная в уравнении для прямой линии, которую вы только что определили. Это расчетная (экстраполированная) масса. Сравните это рассчитанное массы к его фактической массе (с использованием весов) с использованием формулы процентной ошибки показано ниже:

      Эта процентная ошибка отражает, насколько близка ваша измеренная масса (от весов) к расчетной массе (с использованием математического уравнения). Процент ошибка (%error) рассчитывается по следующей формуле ( ответ – это абсолютное значение, всегда положительное )

      Процентная ошибка в измерениях воды

      Основываясь на теоретической плотности воды (из справочника CRC), получите экспериментальный объем воды в ваших измерениях (вы измерили массу, поэтому разделите ваши значения массы на плотность). Используя приведенный ниже пример, установите составьте таблицу, чтобы определить объем воды, фактически присутствующий в каждом из ваших образцы. Затем рассчитайте процентную ошибку (формула, показанная выше) для ваши измерения. Например, чистая вода при 20 или C имеет плотность 0,9982063 г/мл.

      В таблице ниже приведен пример, составленный вашим инструктором. Это не обязательно представляет ваши собственные данные.

      Пример измеренных значений воды и вычислений %Error

      Мерный сосуд

      Масса воды

      Объем воды

      Теоретический объем воды

      % Ошибка

      Стакан на 150 мл

      36,558 г

      36,622 мл

      40,00 мл

      8,445%

      Цилиндр 100 мл

      40,125 г

      40,195 мл

      40,00 мл

      0,4875%

      Цилиндр 50 мл

      39,581 г

      39,650 мл

      40,00 мл

      0,8750

      Цилиндр 10 мл

      33,256 г

      33,314 мл

      40,00 мл

      16,72%

      Плотность чистой воды при различных температурах 1

      Температура ( o С)

      Плотность (г/мл)

      Температура ( o С)

      Плотность (г/мл)

      Температура ( o С)

      Плотность (г/мл)

      12,0

      0,99950

      17,0

      0,99877

      22,0

      0,99777

      13. 0

      0,99938

      18.0

      0,99860

      23.0

      0,99754

      14,0

      0,99924

      19.0

      0,99841

      24.0

      0,99730

      15,0

      0,99910

      20,0

      0,99820

      25,0

      0,99704

      16.

      Добавить комментарий

      Ваш адрес email не будет опубликован. Обязательные поля помечены *