Как рассчитать угол конуса: Как рассчитать угол наклона конуса?
alexxlab | 25.07.1986 | 0 | Разное
Формула расчета угла конуса
Формулы для вычисления элементов конуса
| Элементы конуса | Расчетные формулы | Элементы конуса | Расчетные формулы |
| K | K = (D-d)/ l K = 2tga | D | D = K× l + d D = 2× l×tga + d |
| a | tga = (D-d)/ 2l tga = K / 2 | d | d = D — 2× l×tga d = D — K× l |
Угол a вычисляют по тригонометрической функции тангенса.
Нормальные конические поверхности должны быть изготовлены по стандартным размерам, некоторые из которых указаны в табл.4.
Кроме этих поверхностей, различают также конусы Морзе и метрические конусы. Наружные конусы Морзе выполняют на хвостовой части сверл (см. рис.6), зенкеров, разверток, центров, а внутренние конусы — в отверстиях шпинделей, оправок, переходных втулок, в которые эти инструменты устанавливают. Существуют семь номеров конусов Морзе (от до
Существуют семь номеров конусов Морзе (от до
Таблица 4
Стандартные размеры конусов деталей
| Конусность K | Угол конуса 2a | Угол наклона a | Обозначение конусности |
| 1:100 1:50 1:20 1:10 1:3 1:1,866 1:1,207 1:0,866 | 0 0 34¢23² 1 0 8¢45² 2 0 51¢51² 5 0 43¢29² 18 0 55¢30² 30 0 45 0 60 0 | 0 0 17¢12² 0 0 34¢23² 1 0 25¢56² 2 0 51¢45² 9 0 27¢45² 15 0 22 0 30¢ 30 0 | 1:100 1:50 1:20 1:10 1:3 30 0 45 0 60 0 |
Метрические конусы 4, 6, 80, 100, 120, 160, 200 (см. тот же стандарт) имеют одинаковую конусность 1:20 (и угол a), а номер конуса обозначает размер диаметра большого основания.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Да какие ж вы математики, если запаролиться нормально не можете. 8406 — | 7319 — или читать все.
188.64.173.93 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Источник: studopedia.ru
Угол раствора и радиус конуса
Угол раствора и радиус конуса способствуют вычислению всех возможных параметров конуса за счет двух треугольников, которые они образуют. Первый треугольник – равнобедренный, с двумя образующими и диаметром конуса, из которого можно рассчитать угол наклона конуса, между образующей и основанием. Второй треугольник – прямоугольный с высотой и радиусом в качестве катетов и образующей конуса, как гипотенузой. (рис.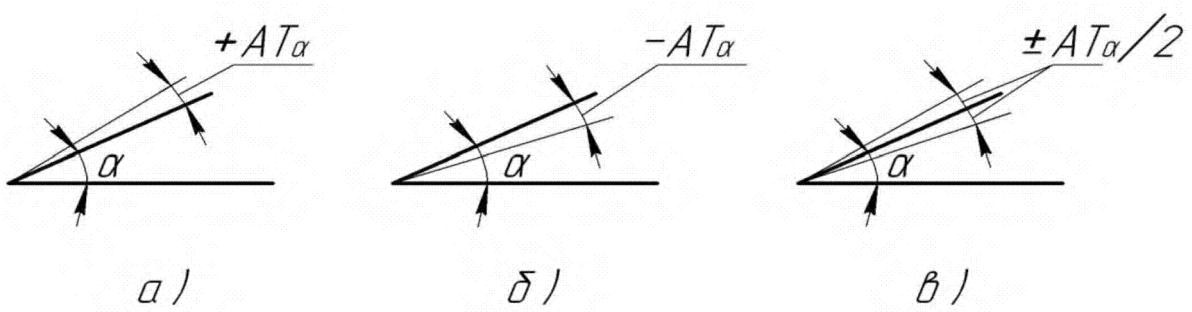 3 tanβ)/3
3 tanβ)/3
Радиус сферы вписанной в конус зависит только от радиус и угла наклона, а радиус сферы описанной вокруг конуса можно найти через угол раствора конуса и радиус основания. (рис.40.3, 40.4) r_1=r tan〖β/2〗 R=r/sinα
Источник: geleot.ru
Уклон и Конусность
Иногда, в задачах по начертательной геометрии или работах по инженерной графике, или при выполнении других чертежей, требуется построить уклон и конус. В этой статье Вы узнаете о том, что такое уклон и конусность, как их построить, как правильно обозначить на чертеже.
Что такое уклон? Как определить уклон? Как построить уклон? Обозначение уклона на чертежах по ГОСТ.
Уклон. Уклон это отклонение прямой линии от вертикального или горизонтального положения.
Определение уклона. Уклон определяется как отношение противолежащего катета угла прямоугольного треугольника к прилежащему катету, то есть он выражается тангенсом угла а. Уклон можно посчитать по формуле i=AC/AB=tga.
Построение уклона. На примере (рисунок ) наглядно продемонстрировано построение уклона. Для построения уклона 1:1, например, нужно на сторонах прямого угла отложить произвольные, но равные отрезки. Такой уклон, будет соответствовать углу в 45 градусов. Для того чтобы построить уклон 1:2, нужно по горизонтали отложить отрезок равный по значению двум отрезкам отложенным по вертикали. Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а.
Обозначение уклона на чертежах. Обозначение уклонов на чертеже выполняется в соответствии с ГОСТ 2.307—68. На чертеже указывают величину уклона с помощью линии-выноски. На полке линии-выноски наносят знак и величину уклона. Знак уклона должен соответствовать уклону определяемой линии, то есть одна из прямых знака уклона должна быть горизонтальна, а другая должна быть наклонена в ту же сторону, что и определяемая линия уклона.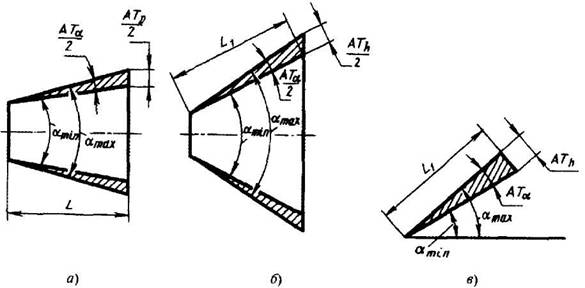 Угол уклона линии знака примерно 30°.
Угол уклона линии знака примерно 30°.
Что такое конусность? Формула для расчёта конусности. Обозначение конусности на чертежах.
Конусность. Конусностью называется отношение диаметра основания конуса к высоте. Конусность рассчитывается по формуле К=D/h, где D – диаметр основания конуса, h – высота. Если конус усеченный, то конусность рассчитывается как отношение разности диаметров усеченного конуса к его высоте. В случае усечённого конуса, формула конусности будет иметь вид: К = (D-d)/h.
Обозначение конусности на чертежах. Форму и величину конуса определяют нанесением трех из перечисленных размеров: 1) диаметр большого основания D; 2) диаметр малого основания d; 3) диаметр в заданном поперечном сечении Ds , имеющем заданное осевое положение Ls; 4) длина конуса L; 5) угол конуса а; 6) конусность с . Также на чертеже допускается указывать и дополнительные размеры, как справочные.
Размеры стандартизованных конусов не нужно указывать на чертеже. Достаточно на чертеже привести условное обозначение конусности по соответствующему стандарту.
Достаточно на чертеже привести условное обозначение конусности по соответствующему стандарту.
Конусность, как и уклон, может быть указана в градусах, дробью (простой, в виде отношения двух чисел или десятичной), в процентах.
Например, конусность 1:5 может быть также обозначена как отношение 1:5, 11°25’16», десятичной дробью 0,2 и в процентах 20.
Для конусов, которые применяются в машиностроении, OCT/BKC 7652 устанавливает ряд нормальных конусностей. Нормальные конусности — 1:3; 1:5; 1:8; 1:10; 1:15; 1:20; 1:30; 1:50; 1:100; 1:200. Также в могут быть использованы — 30, 45, 60, 75, 90 и 120°.
Источник: chertimvam.ru
Построение уклона и конусности
Построение уклона и конусности
Уклоном называют величину, характеризующую наклон одной прямой линии к другой прямой. Уклон выражают дробью или в процентах. Уклон / отрезка В С относительно отрезка ВЛ определяют отношением катетов прямоугольного треугольника ЛВС (рисунок 50, а), т.
- Для построения прямой ВС (рисунок 50. а) с заданной величиной уклона к горизонтальной прямой, например 1:4, необходимо от точки А влево отложить отрезок АВ, равный четырем единицам длины, а вверх отрезок АС, равный одной единице длины. Точки С и В соединяют прямой, которая даст направление искомого уклона.
- Уклоны применяются при вычерчивании деталей, например, стальных балок и рельсов, изготовляемых на прокатных станах, и некоторых деталей, изготовленных литьем.
При вычерчивании контура детали с уклоном сначала строится линия уклона, а затем контур. Если уклон задается в процентах, например, 20 % (рисунок 50, б)> то линия уклона строится так же, как гипотенуза прямоугольного треугольника. Длину одного из катетов принимают равной 100 %, а другого — 20 %.
Очевидно, что уклон 20 % есть иначе уклон 1:5. Г1о ГОСТ 2.307—68 перед размерным числом, определяющим уклон, наносят условный знак, острый угол которого должен быть направлен в сторону уклона (рисунок 50, а и б).
Примеры решения в задачах
| Методические указания и учебники | решения и формулы |
| задачи и методички | теория |
Конусностью называется отношение диаметра основания конуса к его высоте (рисунок 51, а). Обозначается конусность буквой С. Если конус усеченный (рисунок 51, б) решение задач по высшей математике с диаметрами оснований D и d и длиной L, то конусность определяется по формуле: Например (рисунок 51, б), если известны размеры D= 30 мм, d- 20 мм и L = 70 мм, то Если известны конусность С, диаметр одного из оснований конуса d и длина конуса можно определить второй диаметр конуса.
- Например, С- 1:7, d- 20 мм и 1 = 70 мм; D находят по формуле (рисунок 51, б). По ГОСТ 2.307—68 перед размерным числом, характеризующим конусность, необходимо наносить условный знак конусности, который имеет вид равнобедренного треугольника с вершиной, направленной в сторону вершины конуса (рисунок 51, б).

Подробнее обозначение конусности приведено в разделе 1.7 «Нанесение размеров и предельных отклонений». Вопросы для самопроверни 1. Что называется уклоном? 2. Что называется конусностью? 3. Как обозначается на чертеже конусность и уклон? 4. Как определяется конусность и уклон?
Информация расположенная на данном сайте несет информационный характер и используется для учебных целей.
© Брильёнова Наталья Валерьевна
Источник: natalibrilenova.ru
Конусность
Конусность — отношение разности диаметров двух поперечных сечений кругового конуса к расстоянию между ними.
Конусность имеет двойной Уклон: k=2i Конусность на чертеже может быть указана в градусной мере, в радианах и в процентах. Заданы конусность пробки крана 1:5, диаметр D=BC=20 мм, длина l=35 мм.
Необходимо построить очертание пробки крана одним из двух способов: Первый способ. Из формулы k=2i находим i=1:10.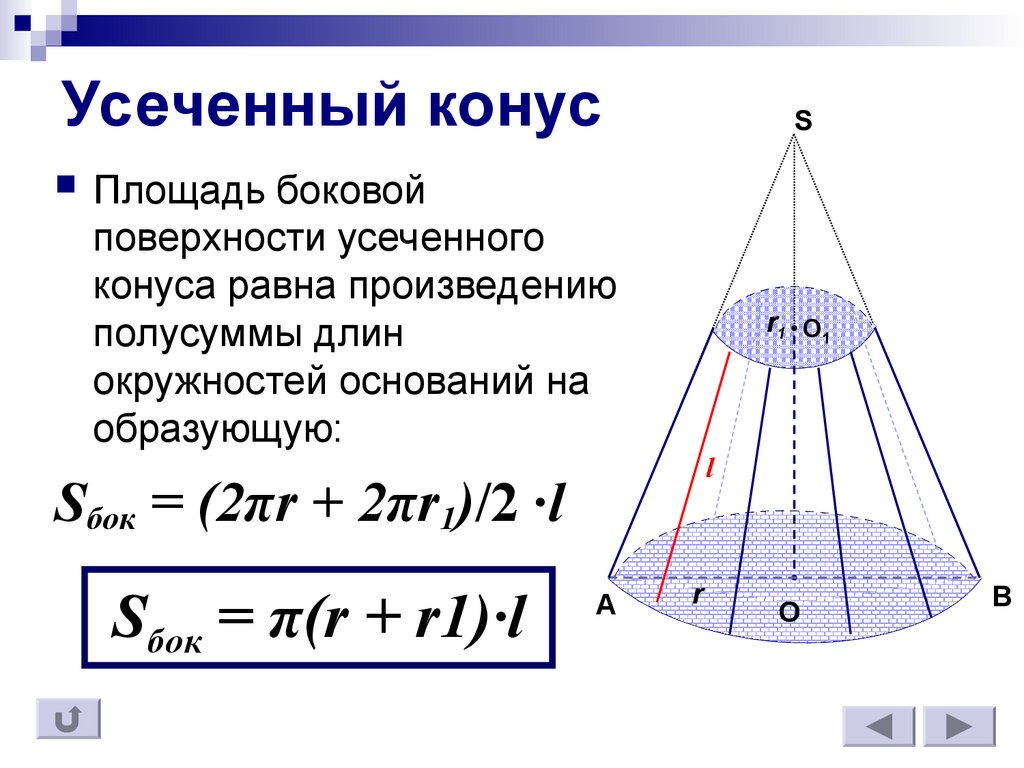 Отмечаем точки BC и строим треугольник DKP так, чтобы KP_BK=1:10. Продолжив BP до пересечения с осью конуса, получим вершину конуса S. Точку S соединяем с точкой C. Отложив по оси пробки от BC отрезок l=35 мм и проведя через конец этого отрезка прямую, перпендикулярную к оси , получим диаметр d=EF=13 мм торца пробки; Второй способ. Из формулы k=(D-d)/l находим d=EF=20-35/5=13 мм; Величина угла при вершине конуса:
Отмечаем точки BC и строим треугольник DKP так, чтобы KP_BK=1:10. Продолжив BP до пересечения с осью конуса, получим вершину конуса S. Точку S соединяем с точкой C. Отложив по оси пробки от BC отрезок l=35 мм и проведя через конец этого отрезка прямую, перпендикулярную к оси , получим диаметр d=EF=13 мм торца пробки; Второй способ. Из формулы k=(D-d)/l находим d=EF=20-35/5=13 мм; Величина угла при вершине конуса:
здесь угол φ представлен в радианах.
где L — расстояние от большого сечения до вершины S конуса, а отношение: D/(2L) = tgφ Пусть задана
Конусность стандартизована. ГОСТ 8593-81 устанавливает нормальные конусности и углы конусов
| Обозна- чение | конуса | Конус- | ность | Угол | конуса | Угол | уклона |
| Ряд 1 | Ряд 2 | Угл.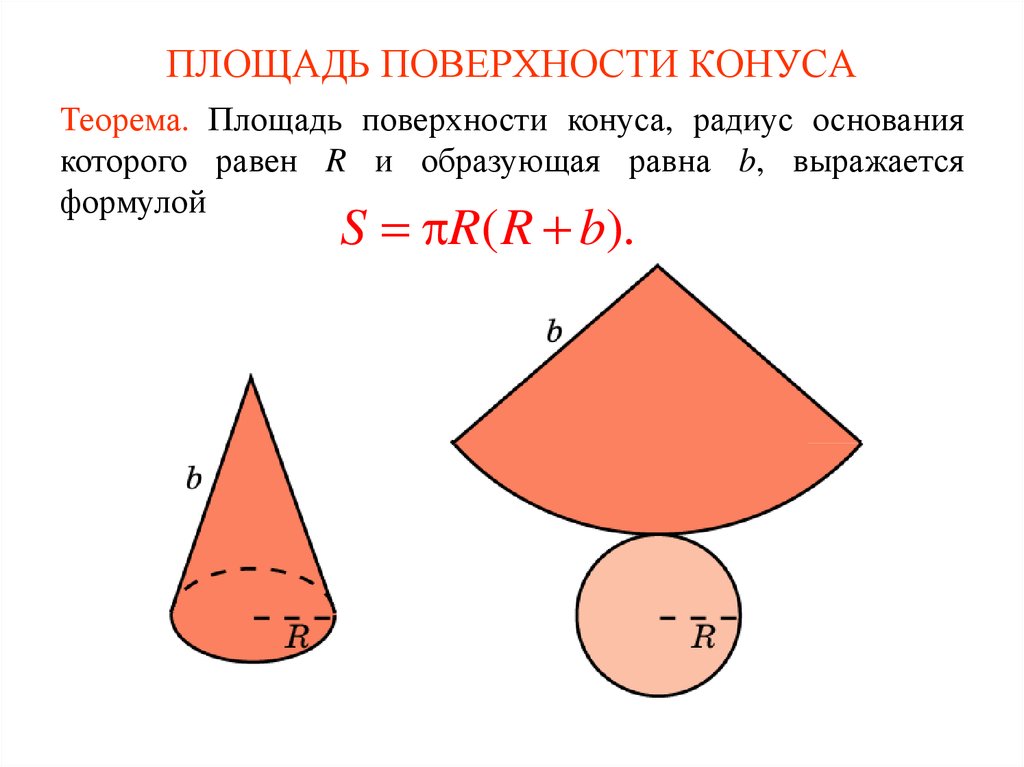 ед. ед. | Рад. | Угл. ед. | Рад. | ||
| 1:500 | 1:500 | 0,0020000 | 6`52,5″ | 0,0020000 | 3`26,25″ | 0,0010000 | |
| 1:200 | 1:200 | 0,0050000 | 17`11,3″ | 0,0050000 | 8`25,65″ | 0,0025000 | |
| 1:100 | 1:100 | 0,0100000 | 34`22,6″ | 0,0100000 | 17`11,3″ | 0,0050000 | |
| 1:50 | 1:50 | 0,0200000 | 1°8`45,2″ | 0,0199996 | 34`22,6″ | 0,0099998 | |
| 1:30 | 1:30 | 0,0333333 | 1°54`34,9″ | 0,0333304 | 57`17,45″ | 0,0166652 | |
| 1:20 | 1:20 | 0,0500000 | 2°51`51,1″ | 0,0499896 | 1°25`55,55″ | 0,0249948 | |
| 1:15 | 1:15 | 0,0666667 | 3°49`5,9″ | 0,0666420 | 1°54`32,95″ | 0,0333210 | |
| 1:12 | 1:12 | 0,0833333 | 4°46`18,8″ | 0,0832852 | 2°23`9,4″ | 0,0416426 | |
| 1:10 | 1:10 | 0,1000000 | 5°43`29,3″ | 0,0999168 | 2°51`44,65″ | 0,0499584 | |
| 1:8 | 1:8 | 0,1250000 | 7°9`9,6″ | 0,1248376 | 3°34`34,8″ | 0,0624188 | |
| 1:7 | 1:7 | 0,1428571 | 8°10`16,4″ | 0,1426148 | 4°5`8,2″ | 0,0713074 | |
| 1:6 | 1:6 | 0,1666667 | 9°31`38,2″ | 0,1662824 | 4°45`49,1″ | 0,0831412 | |
| 1:5 | 1:5 | 0,2000000 | 11°25`16,3″ | 0,1993374 | 5°42`38,15″ | 0,0996687 | |
| 1:4 | 1:4 | 0,2500000 | 14°15`0,1″ | 0,2487100 | 7°7`30,05″ | 0,1243550 | |
| 1:3 | 1:3 | 0,3333333 | 18°55`28,7″ | 0,3302972 | 9°27`44,35″ | 0,1651486 | |
| 30° | 1:1,866025 | 0,5358985 | 30° | 0,5235988 | 15° | 0,2617994 | |
| 45° | 1:1,207107 | 0,8284269 | 45° | 0,7853982 | 22°30` | 0,3926991 | |
| 60° | 1:0,866025 | 1,1547010 | 60° | 1,0471976 | 30° | 0,5235988 | |
| 75° | 1:0,651613 | 1,5346532 | 75° | 1,3089970 | 37°30` | 0,6544985 | |
| 90° | 1:0,500000 | 2,0000000 | 90° | 1,5707964 | 45° | 0,7853982 | |
| 120° | 1:0,288675 | 3,4641032 | 120° | 2,0943952 | 60° | 1,0471976 |
Конусности и углы конусов должны соответствовать указанным на чертеже и в таблице.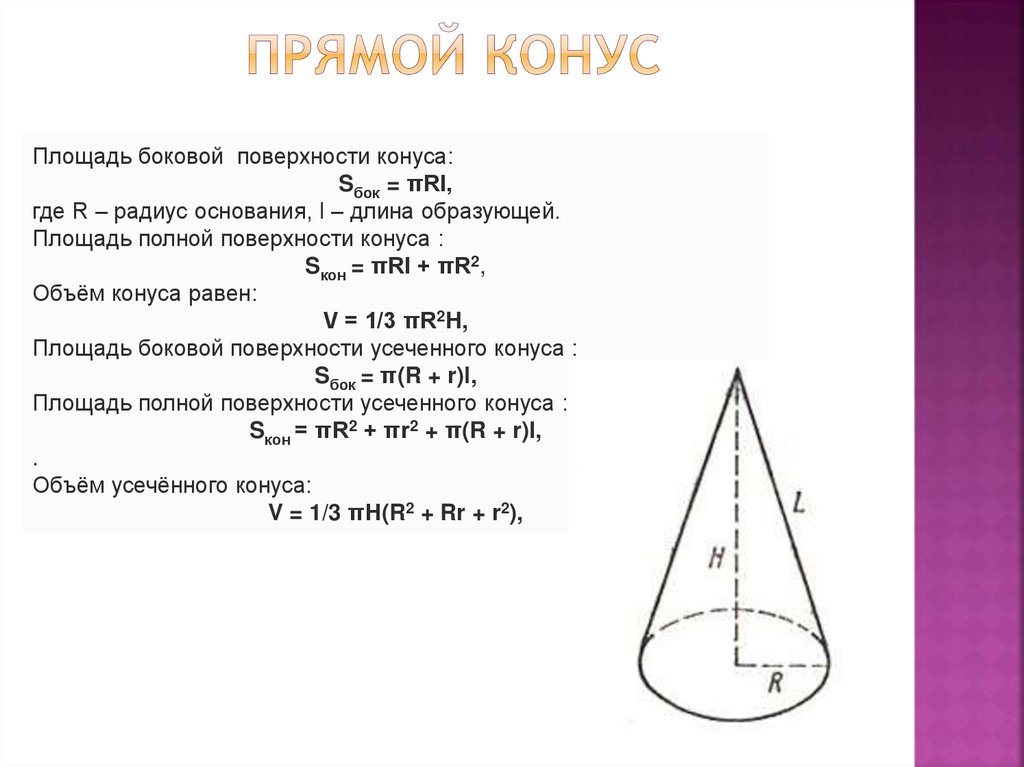 При выборе конусностей или углов конусов ряд 1 следует предпочитать ряду 2.
При выборе конусностей или углов конусов ряд 1 следует предпочитать ряду 2.
Конусность поверхности
обозначается на чертеже: — надписью Конусность с указанием ее величины; — указывающей на нее стрелкой с полкой где пишется: — Конусность с указанием ее величины; — знак конусности и ее величина.
Источник: ngeo.fxyz.ru
Оценка статьи:
Загрузка…
Сохранить себе в:
Adblock
detector
Расчет угла конуса по диаметру
Содержание
- 1. Понятие о конусе и его элементах
- 2. Способы получения конических поверхностей на токарном станке
- 3. Обработка конических поверхностей поворотом верхней части суппорта
- 4. Обработка конических поверхностей способом поперечного смещения корпуса задней бабки
- 5. Обработка конических поверхностей с применением конусной линейки
- 6.
 Обработка конических поверхностей широким резцом
Обработка конических поверхностей широким резцом - 7. Растачивание и развертывание конических отверстий
- 8. Режимы резания при обработке отверстий коническими развертками
- 9. Измерение конических поверхностей
- 10. Брак при обработке конических поверхностей и меры его предупреждения
- Рекомендованные сообщения
- Создайте аккаунт или войдите в него для комментирования
- Создать аккаунт
- Войти
- Сейчас на странице 0 пользователей
Источник: ГОСТ 8593-81
Конусность К есть отношение разности диаметров двух поперечных сечений конуса к расстоянию между ними.
Уклон “i” есть отношение разности размеров двух поперечных сечений к расстоянию между ними.
В машиностроении, наряду с цилиндрическими, широко применяются детали с коническими поверхностями в виде наружных конусов или в виде конических отверстий. Например, центр токарного станка имеет два наружных конуса, из которых один служит для установки и закрепления его в коническом отверстии шпинделя; наружный конус для установки и закрепления имеют также сверло, зенкер, развертка и т. д. Переходная втулка для закрепления сверл с коническим хвостовиком имеет наружный конус и коническое отверстие
д. Переходная втулка для закрепления сверл с коническим хвостовиком имеет наружный конус и коническое отверстие
1. Понятие о конусе и его элементах
Элементы конуса . Если вращать прямоугольный треугольник АБВ вокруг катета АБ (рис. 202, а), то образуется тело АВГ, называемое полным конусом. Линия АБ называется осью или высотой конуса, линия АВ — образующей конуса. Точка А является вершиной конуса.
При вращении катета БВ вокруг оси АБ образуется поверхность круга, называемая основанием конуса.
Угол ВАГ между боковыми сторонами АВ и АГ называется углом конуса и обозначается 2α. Половина этого угла, образуемая боковой стороной АГ и осью АБ, называется углом уклона конуса и обозначается α. Углы выражаются в градусах, минутах и секундах.
Если от полного конуса отрезать его верхнюю часть плоскостью, параллельной егооснованию (рис. 202, б), то получим тело, называемое усеченным конусом. Оно имеет два основания верхнее и нижнее. Расстояние OO1 по оси между основаниями называется высотой усеченного конуса. Так как в машиностроении большей частью приходится иметь дело с частями конусов, т. е. усеченными конусами, то обычно их просто называют конусами; дальше будем называть все конические поверхности конусами.
Расстояние OO1 по оси между основаниями называется высотой усеченного конуса. Так как в машиностроении большей частью приходится иметь дело с частями конусов, т. е. усеченными конусами, то обычно их просто называют конусами; дальше будем называть все конические поверхности конусами.
Связь между элементами конуса. На чертеже указывают обычно три основных размера конуса: больший диаметр D, меньший — d и высоту конуса l (рис. 203).
Иногда на чертеже указывается только один из диаметров конуса, например, больший D, высота конуса l и так называемая конусность. Конусностью называется отношение разности диаметров конуса к его длине. Обозначим конусность буквой K, тогда
Если конус имеет размеры: D =80 мм, d = 70 мм и l = 100 мм, то согласно формуле (10):
Это значит, что на длине 10 мм диаметр конуса уменьшается на 1 мм или на каждый миллиметр длины конуса разница между его диаметрами изменяется на
Иногда на чертеже вместо угла конуса указывается уклон конуса. Уклон конуса показывает, в какой мере отклоняется образующая конуса от его оси.
Уклон конуса показывает, в какой мере отклоняется образующая конуса от его оси.
Уклон конуса определяется по формуле
где tg α — уклон конуса;
D — диаметр большого основания конуса в мм;
d — диаметр малого основания конуса в мм;
l — высота конуса в мм.
Пользуясь формулой (11), можно при помощи тригонометрических таблиц определить угол а уклона конуса.
Уклон конуса и конусность обычно выражают простой дробью, например: 1 : 10; 1 : 50, или десятичной дробью, например, 0,1; 0,05; 0,02 и т. д.
2. Способы получения конических поверхностей на токарном станке
На токарном станке обработка конических поверхностей производится одним из следующих способов:
а) поворотом верхней части суппорта;
б) поперечным смещением корпуса задней бабки;
в) с помощью конусной линейки;
г) с помощью широкого резца.
3. Обработка конических поверхностей поворотом верхней части суппорта
При изготовлении на токарном станке коротких наружных и внутренних конических поверхностей с большим углом уклона нужно повернуть верхнюю часть суппорта относительно оси станка под углом α уклона конуса (см. рис. 204). При таком способе работы подачу можно производить только от руки, вращая рукоятку ходового винта верхней части суппорта, и лишь в наиболее современных токарных станках имеется механическая подача верхней части суппорта.
рис. 204). При таком способе работы подачу можно производить только от руки, вращая рукоятку ходового винта верхней части суппорта, и лишь в наиболее современных токарных станках имеется механическая подача верхней части суппорта.
Для установки верхней части суппорта 1 на требуемый угол можно использовать деления, нанесенные на фланце 2 поворотной части суппорта (рис. 204). Если угол α уклона конуса задан по чертежу, то верхнюю часть суппорта повертывают вместе с его поворотной частью на требуемое число делений, обозначающих градусы. Число делений отсчитывают относительно риски, нанесенной на нижней части суппорта.
Если на чертеже угол α не дан, а указаны больший и меньший диаметры конуса и длина его конической части, то величину угла поворота суппорта определяют по формуле (11)
Способ обтачивания конических поверхностей поворотом верхней части суппорта имеет следующие недостатки: он допускает обычно применение только ручной подачи, что отражается на производительности труда и чистоте обработанной поверхности; позволяет обтачивать сравнительно короткие конические поверхности, ограниченные длиной хода верхней части суппорта.
4. Обработка конических поверхностей способом поперечного смещения корпуса задней бабки
Для получения конической поверхности на токарном станке необходимо при вращении заготовки вершину резца перемещать не параллельно, а под некоторым углом к оси центров. Этот угол должен равняться углу α уклона конуса. Наиболее простой способ получения угла между осью центров и направлением подачи — сместить линию центров, сдвинув задний центр в поперечном направлении. Путем смещения заднего центра в сторону резца (на себя) в результате обтачивания получают конус, у которого большее основание направлено в сторону передней бабки; при смещении заднего центра в противоположную сторону, т. е. от резца (от себя), большее основание конуса окажется со стороны задней бабки (рис. 205).
Смещение корпуса задней бабки определяют по формуле
где S — смещение корпуса задней бабки от оси шпинделя передней бабки в мм;
D — диаметр большого основания конуса в мм;
d — диаметр малого основания конуса в мм;
L — длина всей детали или расстояние между центрами в мм;
l — длина конической части детали в мм.
Смещение корпуса задней бабки производят, используя деления 1 (рис 206), нанесенные на торце опорной плиты, и риску 2 на торце корпуса задней бабки.
Если на торце плиты делений нет, то смещают корпус задней бабки, пользуясь измерительной линейкой, как показано на рис. 207.
Преимущество обработки конических поверхностей путем смещения корпуса задней бабки заключается в том, что этим способом можно обтачивать конусы большой длины и вести обтачивание с механической подачей.
Недостатки этого способа: невозможность растачивать конические отверстия; потеря времени на перестановку задней бабки; возможность обрабатывать лишь пологие конусы; перекос центров в центровых отверстиях, что приводит к быстрому и неравномерному износу центров и центровых отверстий и служит причиной брака при вторичной установке детали в этих же центровых отверстиях.
Неравномерного износа центровых отверстий можно избежать, если вместо обычного применять специальный шаровой центр (рис. 208). Такие центры используют преимущественно при обработке точных конусов.
208). Такие центры используют преимущественно при обработке точных конусов.
5. Обработка конических поверхностей с применением конусной линейки
Для обработки конических поверхностей с углом уклона а до 10—12° современные токарные станки обычно имеют особое приспособление, называемое конусной линейкой. Схема обработки конуса с применением конусной линейки приводится на рис. 209.
К станине станка прикреплена плита 11, на которой установлена конусная линейка 9. Линейку можно поворачивать вокруг пальца 8 под требуемым углом а к оси обрабатываемой детали. Для закрепления линейки в требуемом положении служат два болта 4 и 10. По линейке свободно скользит ползун 7, соединяющийся с нижней поперечной частью 12 суппорта при помощи тяги 5 и зажима 6. Чтобы эта часть суппорта могла свободно скользить по направляющим, ее отсоединяют от каретки 3, вывинчивая поперечный винт или отсоединяя от суппорта его гайку.
Если сообщить каретке продольную подачу, то ползун 7, захватываемый тягой 5, начнет перемещаться вдоль линейки 9. Так как ползун скреплен с поперечными салазками суппорта, то они вместе с резцом будут перемещаться параллельно линейке 9. Благодаря этому резец будет обрабатывать коническую поверхность с углом уклона, равным углу α поворота конусной линейки.
Так как ползун скреплен с поперечными салазками суппорта, то они вместе с резцом будут перемещаться параллельно линейке 9. Благодаря этому резец будет обрабатывать коническую поверхность с углом уклона, равным углу α поворота конусной линейки.
После каждого прохода резец устанавливают на глубину резания с помощью рукоятки 1 верхней части 2 суппорта. Эта часть суппорта должна быть повернута на 90° относительно нормального положения, т. е. так, как это показано на рис. 209.
Если даны диаметры оснований конуса D и d и его длина l, то угол поворота линейки можно найти по формуле (11).
Подсчитав величину tg α, легко определить значение угла α по таблице тангенсов.
Применение конусной линейки имеет ряд преимуществ:
1) наладка линейки удобна и производится быстро;
2) при переходе к обработке конусов не требуется нарушать нормальную наладку станка, т. е. не нужно смещать корпус задней бабки; центры станка остаются в нормальном положении, т. е. на одной оси, благодаря чему центровые отверстия в детали и центры станка не срабатываются;
3) при помощи конусной линейки можно не только обтачивать наружные конические поверхности, но и растачивать конические отверстия;
4) возможна работа е продольным самоходом, что увеличивает производительность труда и улучшает качество обработки.
Недостатком конусной линейки является необходимость отсоединять салазки суппорта от винта поперечной подачи. Этот недостаток устранен в конструкции некоторых токарных станков, у которых винт не связан жестко со своим маховичком и зубчатыми колесами поперечного самохода.
6. Обработка конических поверхностей широким резцом
Обработку конических поверхностей (наружных и внутренних) с небольшой длиной конуса можно производить широким резцом с углом в плане, соответствующим углу α уклона конуса (рис. 210). Подача резца может быть продольная и поперечная.
Однако использование широкого резца на обычных станках возможно только при длине конуса, не превышающей примерно 20 мм. Применять более широкие резцы можно лишь на особо жестких станках и деталях, если это не вызывает вибрации резца и обрабатываемой детали.
7. Растачивание и развертывание конических отверстий
Обработка конических отверстий является одной из наиболее трудных токарных работ; она значительно труднее, чем обработка наружных конусов.
Обработку конических отверстий на токарных станках в большинстве случаев производят растачиванием резцом с поворотом верхней части суппорта и реже с помощью конусной линейки. Все подсчеты, связанные с поворотом верхней части суппорта или конусной линейки, выполняются так же, как при обтачивании наружных конических поверхностей.
Если отверстие должно быть в сплошном материале, то сначала сверлят цилиндрическое отверстие, которое затем растачивают резцом на конус или обрабатывают коническими зенкерами и развертками.
Чтобы ускорить растачивание или развертывание, следует предварительно просверлить отверстие сверлом, диаметр d, которого на 1—2 мм меньше диаметра малого основания конуса (рис. 211, а). После этого рассверливают отверстие одним (рис. 211, б) или двумя (рис. 211, в) сверлами для получения ступеней.
После чистового растачивания конуса его развертывают конической разверткой соответствующей конусности. Для конусов с небольшой конусностью выгоднее производить обработку конических отверстий непосредственно после сверления набором специальных разверток, как показано на рис.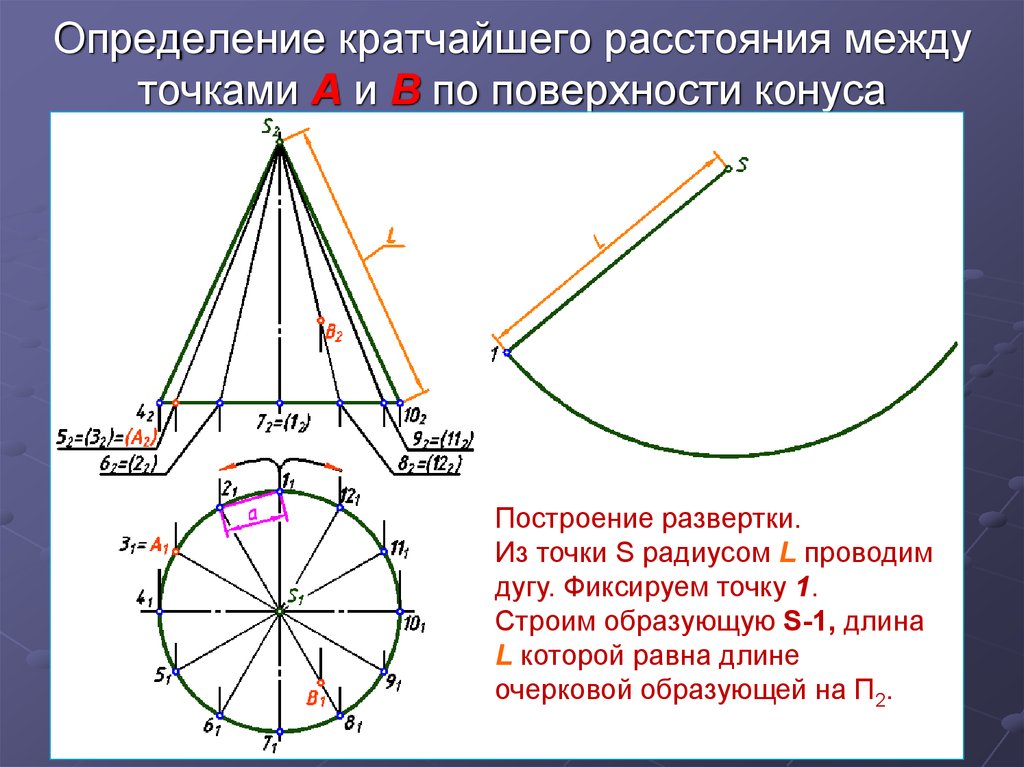 212.
212.
8. Режимы резания при обработке отверстий коническими развертками
Конические развертки работают в более тяжелых условиях, чем цилиндрические: в то время как цилиндрические развертки снимают незначительный припуск небольшими режущими кромками, конические развертки режут всей длиной их режущих кромок, расположенных на образующей конуса. Поэтому при работе коническими развертками применяют подачи и скорости резания меньше, чем при работе цилиндрическими развертками.
При обработке отверстий коническими развертками подачу производят вручную, вращая маховичок задней бабки. Необходимо следить за тем, чтобы пиноль задней бабки перемещалась равномерно.
Подачи при развертывании стали 0,1—0,2 мм/об, при развертывании чугуна 0,2—0,4 мм/об.
Скорость резания при развертывании конических отверстий развертками из быстрорежущей стали 6—10 м/мин.
Для облегчения работы конических разверток и получения чистой и гладкой поверхности следует применять охлаждение. При обработке стали и чугуна применяют эмульсию или сульфофрезол.
При обработке стали и чугуна применяют эмульсию или сульфофрезол.
9. Измерение конических поверхностей
Поверхности конусов проверяют шаблонами и калибрами; измерение и одновременно проверку углов конуса производят угломерами. На рис. 213 показан способ проверки конуса с помощью шаблона.
Наружные и внутренние углы различных деталей можно измерять универсальным угломером (рис. 214). Он состоит из основания 1, На котором на дуге 130 нанесена основная шкала. С основанием 1 жестко скреплена линейка 5. По дуге основания перемещается сектор 4, несущий нониус 3. К сектору 4 посредством державки 7 может быть прикреплен угольник 2, в котором, в свою очередь, закрепляется съемная линейка 5. Угольник 2 и съемная линейка 5 имеют возможность перемещаться по грани сектора 4.
Путем различных комбинаций в установке измерительных деталей угломера можно производить измерение углов от 0 до 320°. Величина отсчета по нониусу 2′. Отсчет, полученный при измерении углов, производится по шкале и нониусу (рис. 215) следующим образом: нулевой штрих нониуса показывает число градусов, а штрих нониуса, совпадающий со штрихом шкалы основания, — число минут. На рис. 215 со штрихом шкалы основания совпадает 11-й штрих нониуса, что означает 2’Х 11 = 22′. Следовательно, угол в данном случае равен 76°22′.
215) следующим образом: нулевой штрих нониуса показывает число градусов, а штрих нониуса, совпадающий со штрихом шкалы основания, — число минут. На рис. 215 со штрихом шкалы основания совпадает 11-й штрих нониуса, что означает 2’Х 11 = 22′. Следовательно, угол в данном случае равен 76°22′.
На рис. 216 показаны комбинации измерительных деталей универсального угломера, позволяющие производить измерение различных углов от 0 до 320°.
Для более точной проверки конусов в серийном производстве применяют специальные калибры. На рис. 217, а показан кониче-ский калибр-втулка для проверки наружных конусов, а на рис. 217, б—конический калибр-пробка для проверки конических отверстий.
На калибрах делаются уступы 1 и 2 на торцах или наносятся риски 3, служащие для определения точности проверяемых поверхностей.
На. рис. 218 приводится пример проверки конического отверстия калибром-пробкой.
Для проверки отверстия калибр (см. рис. 218), имеющий уступ 1 на определенном расстоянии от торца 2 и две риски 3, вводят с легким нажимом в отверстие и проверяют, нет ли качания калибра в отверстии. Отсутствие качания показывает, что угол конуса правилен. Убедившись, что угол конуса правилен, приступают к проверке его размера. Для этого наблюдают, до какого места калибр войдет в проверяемую деталь. Если конец конуса детали совпадает с левым торцом уступа 1 или с одной из рисок 3 или находится между рисками, то размеры конуса правильны. Но может случиться, что калибр войдет в деталь настолько глубоко, что обе риски 3 войдут в отверстие или оба торца уступа 1 выйдут из него наружу. Это показывает, что диаметр отверстия больше заданного. Если, наоборот, обе риски окажутся вне отверстия или ни один из торцов уступа не выйдет из него, то диаметр отверстия меньше требуемого.
Отсутствие качания показывает, что угол конуса правилен. Убедившись, что угол конуса правилен, приступают к проверке его размера. Для этого наблюдают, до какого места калибр войдет в проверяемую деталь. Если конец конуса детали совпадает с левым торцом уступа 1 или с одной из рисок 3 или находится между рисками, то размеры конуса правильны. Но может случиться, что калибр войдет в деталь настолько глубоко, что обе риски 3 войдут в отверстие или оба торца уступа 1 выйдут из него наружу. Это показывает, что диаметр отверстия больше заданного. Если, наоборот, обе риски окажутся вне отверстия или ни один из торцов уступа не выйдет из него, то диаметр отверстия меньше требуемого.
Для точной проверки конусности применяют следующий способ. На измеряемой поверхности детали или калибра проводят мелом или карандашом две-три линии вдоль образующей конуса, затем вставляют или надевают калибр на деталь и повертывают его на часть оборота. Если линии сотрутся неравномерно, это значит, что конус детали обработан неточно и необходимо его исправить. Стирание линий по концам калибра говорит о неправильной конусности; стирание линий в средней части калибра показывает, что конус имеет небольшую вогнутость, причиной чего обычно является неточное расположение вершины резца по высоте центров. Вместо меловых линий можно нанести на всю коническую поверхность детали или калибра тонкий слой специальной краски (синьки). Такой способ дает большую точность измерения.
Стирание линий по концам калибра говорит о неправильной конусности; стирание линий в средней части калибра показывает, что конус имеет небольшую вогнутость, причиной чего обычно является неточное расположение вершины резца по высоте центров. Вместо меловых линий можно нанести на всю коническую поверхность детали или калибра тонкий слой специальной краски (синьки). Такой способ дает большую точность измерения.
10. Брак при обработке конических поверхностей и меры его предупреждения
При обработке конических поверхностей, помимо упомянутых видов брака для цилиндрических поверхностей, дополнительно возможны следующие виды брака:
1) неправильная конусность;
2) отклонения в размерах конуса;
3) отклонения в размерах диаметров оснований при правильной конусности;
4) непрямолинейность образующей конической поверхности.
1. Неправильная конусность получается главным образом вследствие неточного смещения корпуса задней бабки, неточного поворота верхней части суппорта, неправильной установки конусной линейки, неправильной заточки или установки широкого резца. Следовательно, точной установкой корпуса задней бабки, верхней части суппорта или конусной линейки перед началом обработки можно брак предупредить. Этот вид брака исправим только в том случае, если ошибка во всей длине конуса направлена в тело детали, т. е. все диаметры у втулки меньше, а у конического стержня больше требуемых.
Следовательно, точной установкой корпуса задней бабки, верхней части суппорта или конусной линейки перед началом обработки можно брак предупредить. Этот вид брака исправим только в том случае, если ошибка во всей длине конуса направлена в тело детали, т. е. все диаметры у втулки меньше, а у конического стержня больше требуемых.
2. Неправильный размер конуса при правильном угле его, т. е. неправильная величина диаметров по всей длине конуса, получается, если снято недостаточно или слишком много материала. Предупредить брак можно только внимательной установкой глубины резания по лимбу на чистовых проходах. Брак исправим, если снято недостаточно материала.
3. Может получиться, что при правильной конусности и точных размерах одного конца конуса диаметр второго конца неправилен. Единственной причиной является несоблюдение требуемой длины всего конического участка детали. Брак исправим, если деталь излишне длинна. Чтобы избежать этого вида брака, необходимо перед обработкой конуса тщательно проверить его длину.
4. Непрямолинейность образующей обрабатываемого конуса получается при установке резца выше (рис. 219, б) или ниже (рис. 219, в) центра (на этих рисунках для большей наглядности искажения образующей конуса показаны в сильно преувеличенном виде). Таким образом, и этот вид брака является результатом невнимательной работы токаря.
Автор: starik12, 30 марта 2012 в Общий
Рекомендованные сообщения
Создайте аккаунт или войдите в него для комментирования
Вы должны быть пользователем, чтобы оставить комментарий
Создать аккаунт
Зарегистрируйтесь для получения аккаунта. Это просто!
Войти
Уже зарегистрированы? Войдите здесь.
Сейчас на странице 0 пользователей
Нет пользователей, просматривающих эту страницу.
прямой, наклонный и усеченный конус
| конус в Викисловаре |
У этого термина существуют и другие значения, см. Конус (значения).
Конус
(от др. -греч. κώνος «сосновая шишка»[1]) — тело в евклидовом пространстве, полученное объединением всех лучей, исходящих из одной точки (
-греч. κώνος «сосновая шишка»[1]) — тело в евклидовом пространстве, полученное объединением всех лучей, исходящих из одной точки (
вершины
конуса) и проходящих через плоскую поверхность. Иногда конусом называют часть такого тела, имеющую ограниченный объём и полученную объединением всех отрезков, соединяющих вершину и точки плоской поверхности (последнюю в таком случае называют
основанием
конуса, а конус называют
опирающимся
на данное основание). Если основание конуса представляет собой многоугольник, такой конус является пирамидой.
Связанные определения
- Отрезок, соединяющий вершину и границу основания, называется образующей конуса
. - Объединение образующих конуса называется образующей
(или
боковой
)
поверхностью конуса
. Образующая поверхность конуса является конической поверхностью. - Отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка), называется высотой конуса
.
- Угол раствора конуса
— угол между двумя противоположными образующими (угол при вершине конуса, внутри конуса). - Если основание конуса имеет центр симметрии (например, является кругом или эллипсом) и ортогональная проекция вершины конуса на плоскость основания совпадает с этим центром, то конус называется прямым
. При этом прямая, соединяющая вершину и центр основания, называется
осью конуса
. - Косой
(
наклонный
) конус — конус, у которого ортогональная проекция вершины на основание не совпадает с его центром симметрии. - Круговой конус
— конус, основание которого является кругом. - Прямой круговой конус
(часто его называют просто конусом) можно получить вращением прямоугольного треугольника вокруг прямой, содержащей катет (эта прямая представляет собой ось конуса). - Конус, опирающийся на эллипс, параболу или гиперболу, называют соответственно эллиптическим
,
параболическим
и
гиперболическим конусом
(последние два имеют бесконечный объём).
- Часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием, называется усечённым конусом
, или
коническим слоем
.
Что это — конус?
С точки зрения геометрии речь идет о пространственной фигуре, которая образована совокупностью прямых отрезков, соединяющих некоторую точку пространства со всеми точками плавной плоской кривой. Этой кривой может быть окружность или эллипс. На рисунке ниже показан конус.
Вам будет интересно:Советские вещи: фото и описание
Представленная фигура не обладает объемом, поскольку стенки ее поверхности имеют бесконечно малую толщину. Однако если ее заполнить веществом и ограничить сверху не кривой, а плоской фигурой, например кругом, то мы получим твердое объемное тело, которое также принято называть конусом.
Форму конуса можно часто встретить в жизни. Так, ею обладает мороженое-рожок или полосатые черно-оранжевые дорожные конусы, которые выставляют на проезжую часть для привлечения внимания участников движения.
Свойства
- Если площадь основания конечна, то объём конуса также конечен и равен трети произведения высоты на площадь основания.
V={1 \over 3} SH,
где S
— площадь основания,
H
— высота. Таким образом, все конусы, опирающиеся на данное основание (конечной площади) и имеющие вершину, находящуюся на данной плоскости, параллельной основанию, имеют равный объём, поскольку их высоты равны.
- Центр тяжести любого конуса с конечным объёмом лежит на четверти высоты от основания.
- Телесный угол при вершине прямого кругового конуса равен
2\pi \left(1 — \cos {\alpha \over 2} \right), где α — угол раствора конуса.
- Площадь боковой поверхности такого конуса равна
S = \pi R l,
а полная площадь поверхности (т. е. сумма площадей боковой поверхности и основания)
S = \pi R (l + R), где
R
— радиус основания,
l
— длина образующей.
- Объём кругового конуса равен
V={1 \over 3} \pi R^2H.
- Для усечённого конуса (не обязательно прямого и кругового) объём равен:
V={1 \over 3} (HS_2-hS_1),
где S1 и S2 — площади соответственно верхнего (ближнего к вершине) и нижнего оснований, h
и
H
— расстояния от плоскости соответственно верхнего и нижнего основания до вершины.
- Пересечение плоскости с прямым круговым конусом является одним из конических сечений (в невырожденных случаях — эллипсом, параболой или гиперболой, в зависимости от положения секущей плоскости).
Площадь поверхности
При изучении поверхности любой объемной фигуры удобно пользоваться ее разверткой на плоскость. Конус не является исключением. Для круглого конуса развертка показана ниже.
Мы видим, что развертка фигуры состоит из двух частей:
- Круга, который образует основание конуса.
- Сектора круга, являющегося конической поверхностью фигуры.
Площадь круга найти легко, и соответствующая формула известна каждому школьнику. Говоря о круговом секторе, заметим, что он является частью круга с радиусом g (длина генератрисы конуса). Длина дуги этого сектора равна длине окружности основания. Эти параметры позволяют однозначно определить его площадь. Соответствующая формула имеет вид:
Говоря о круговом секторе, заметим, что он является частью круга с радиусом g (длина генератрисы конуса). Длина дуги этого сектора равна длине окружности основания. Эти параметры позволяют однозначно определить его площадь. Соответствующая формула имеет вид:
S = pi*r2 + pi*r*g.
Первое и второе слагаемые в выражении — это конуса основания и боковой поверхности площади соответственно.
Если длина генератрисы g неизвестна, но дана высота h фигуры, тогда формулу можно переписать в виде:
S = pi*r2 + pi*r*√(r2 + h3).
Уравнение конуса
Уравнения, задающие боковую поверхность прямого кругового конуса с углом раствора 2Θ, вершиной в начале координат и осью, совпадающей с осью Oz
:
- В сферической системе координат с координатами (r
, φ, θ):
\theta = \Theta.
- В цилиндрической системе координат с координатами (r
, φ,
z
):
z = r\cdot\operatorname{ctg}\Theta или r = z\cdot\operatorname{tg}\Theta.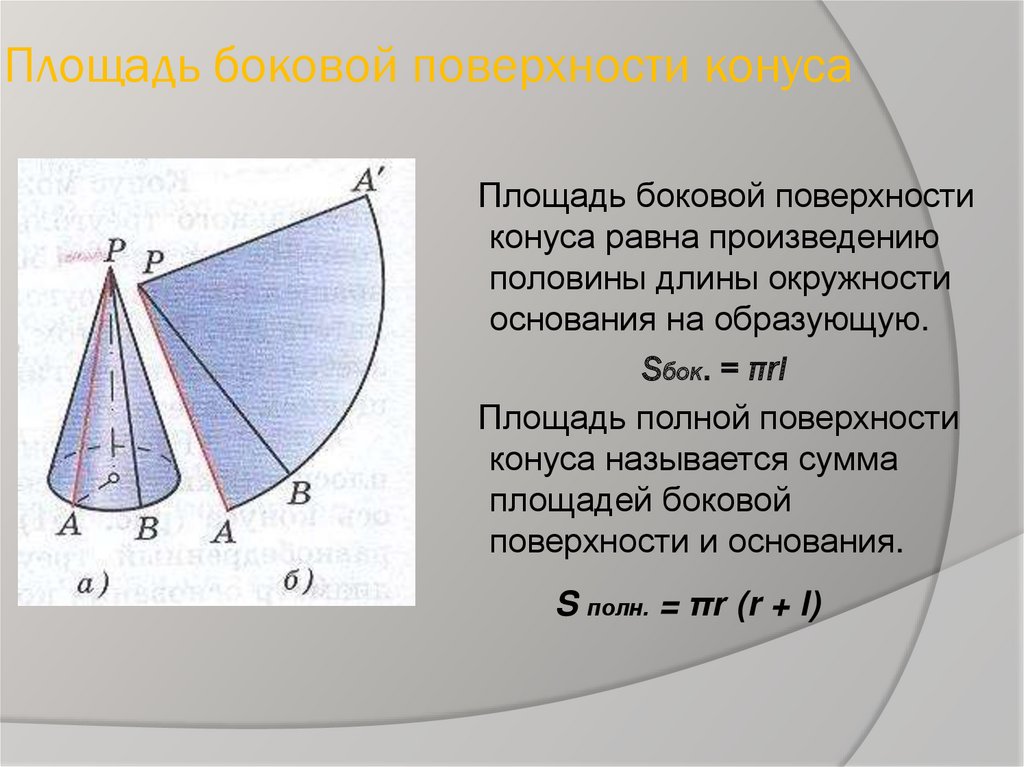 2 \]
2 \]
где: V — объем конуса H — высота конуса π — число пи (3.1415) r — радиус конуса
Развёртка
Прямой круговой конус как тело вращения образован прямоугольным треугольником, вращающимся вокруг одного из катетов, где h
— высота конуса от центра основания до вершины — является катетом прямоугольного треугольника, вокруг которого происходит вращение. Второй катет прямоугольного треугольника
r
— радиус в основании конуса. Гипотенузой прямоугольного треугольника является
l
— образующая конуса.
В создании развёртки конуса могут использоваться всего две величины r
и
l
. Радиус основания
r
определяет в развертке круг основания конуса, а сектор боковой поверхности конуса определяет образующая боковой поверхности
l
, являющаяся радиусом сектора боковой поверхности. Угол сектора \varphi в развёртке боковой поверхности конуса определяется по формуле:
φ = 360°·(r
/
l
).
Объем фигуры
Если взять прямую пирамиду и увеличивать на бесконечности число сторон ее основания, то форма основания будет стремиться к окружности, а боковая поверхность пирамиды будет приближаться к конической поверхности. Эти рассуждения позволяют использовать формулу для объема пирамиды при расчете аналогичной величины для конуса. Объем конуса может быть найден по формуле:
V = 1/3*h*So.
Справедлива эта формула всегда, независимо от того, что собой представляет основание конуса, имеющее площадь So. Более того, формула применима также для наклонного конуса.
Поскольку мы изучаем свойства прямой фигуры с круглым основанием, то для определения его объема можно пользоваться таким выражением:
V = 1/3*h*pi*r2.
Справедливость формулы очевидна.
Отрывок, характеризующий Конус
Князь Андрей приехал в квартиру генерала Бенигсена, занимавшего небольшой помещичий дом на самом берегу реки. Ни Бенигсена, ни государя не было там, но Чернышев, флигель адъютант государя, принял Болконского и объявил ему, что государь поехал с генералом Бенигсеном и с маркизом Паулучи другой раз в нынешний день для объезда укреплений Дрисского лагеря, в удобности которого начинали сильно сомневаться. Чернышев сидел с книгой французского романа у окна первой комнаты. Комната эта, вероятно, была прежде залой; в ней еще стоял орган, на который навалены были какие то ковры, и в одном углу стояла складная кровать адъютанта Бенигсена. Этот адъютант был тут. Он, видно, замученный пирушкой или делом, сидел на свернутой постеле и дремал. Из залы вели две двери: одна прямо в бывшую гостиную, другая направо в кабинет. Из первой двери слышались голоса разговаривающих по немецки и изредка по французски. Там, в бывшей гостиной, были собраны, по желанию государя, не военный совет (государь любил неопределенность), но некоторые лица, которых мнение о предстоящих затруднениях он желал знать. Это не был военный совет, но как бы совет избранных для уяснения некоторых вопросов лично для государя. На этот полусовет были приглашены: шведский генерал Армфельд, генерал адъютант Вольцоген, Винцингероде, которого Наполеон называл беглым французским подданным, Мишо, Толь, вовсе не военный человек – граф Штейн и, наконец, сам Пфуль, который, как слышал князь Андрей, был la cheville ouvriere [основою] всего дела.
Чернышев сидел с книгой французского романа у окна первой комнаты. Комната эта, вероятно, была прежде залой; в ней еще стоял орган, на который навалены были какие то ковры, и в одном углу стояла складная кровать адъютанта Бенигсена. Этот адъютант был тут. Он, видно, замученный пирушкой или делом, сидел на свернутой постеле и дремал. Из залы вели две двери: одна прямо в бывшую гостиную, другая направо в кабинет. Из первой двери слышались голоса разговаривающих по немецки и изредка по французски. Там, в бывшей гостиной, были собраны, по желанию государя, не военный совет (государь любил неопределенность), но некоторые лица, которых мнение о предстоящих затруднениях он желал знать. Это не был военный совет, но как бы совет избранных для уяснения некоторых вопросов лично для государя. На этот полусовет были приглашены: шведский генерал Армфельд, генерал адъютант Вольцоген, Винцингероде, которого Наполеон называл беглым французским подданным, Мишо, Толь, вовсе не военный человек – граф Штейн и, наконец, сам Пфуль, который, как слышал князь Андрей, был la cheville ouvriere [основою] всего дела.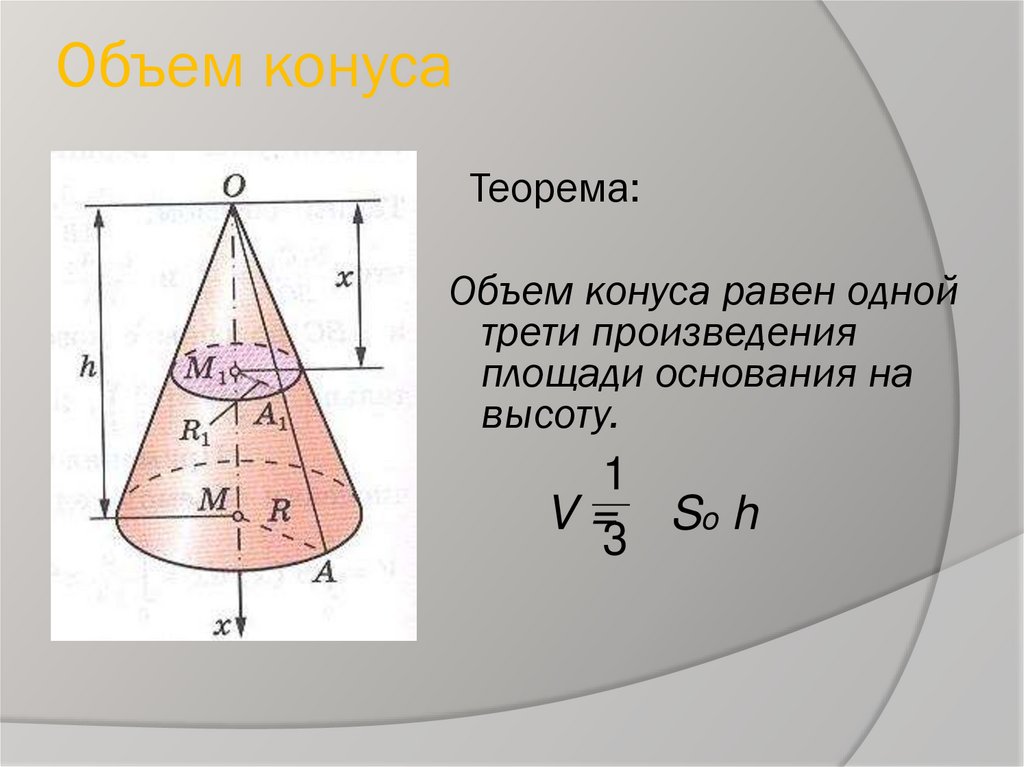 Князь Андрей имел случай хорошо рассмотреть его, так как Пфуль вскоре после него приехал и прошел в гостиную, остановившись на минуту поговорить с Чернышевым. Пфуль с первого взгляда, в своем русском генеральском дурно сшитом мундире, который нескладно, как на наряженном, сидел на нем, показался князю Андрею как будто знакомым, хотя он никогда не видал его. В нем был и Вейротер, и Мак, и Шмидт, и много других немецких теоретиков генералов, которых князю Андрею удалось видеть в 1805 м году; но он был типичнее всех их. Такого немца теоретика, соединявшего в себе все, что было в тех немцах, еще никогда не видал князь Андрей. Пфуль был невысок ростом, очень худ, но ширококост, грубого, здорового сложения, с широким тазом и костлявыми лопатками. Лицо у него было очень морщинисто, с глубоко вставленными глазами. Волоса его спереди у висков, очевидно, торопливо были приглажены щеткой, сзади наивно торчали кисточками. Он, беспокойно и сердито оглядываясь, вошел в комнату, как будто он всего боялся в большой комнате, куда он вошел.
Князь Андрей имел случай хорошо рассмотреть его, так как Пфуль вскоре после него приехал и прошел в гостиную, остановившись на минуту поговорить с Чернышевым. Пфуль с первого взгляда, в своем русском генеральском дурно сшитом мундире, который нескладно, как на наряженном, сидел на нем, показался князю Андрею как будто знакомым, хотя он никогда не видал его. В нем был и Вейротер, и Мак, и Шмидт, и много других немецких теоретиков генералов, которых князю Андрею удалось видеть в 1805 м году; но он был типичнее всех их. Такого немца теоретика, соединявшего в себе все, что было в тех немцах, еще никогда не видал князь Андрей. Пфуль был невысок ростом, очень худ, но ширококост, грубого, здорового сложения, с широким тазом и костлявыми лопатками. Лицо у него было очень морщинисто, с глубоко вставленными глазами. Волоса его спереди у висков, очевидно, торопливо были приглажены щеткой, сзади наивно торчали кисточками. Он, беспокойно и сердито оглядываясь, вошел в комнату, как будто он всего боялся в большой комнате, куда он вошел.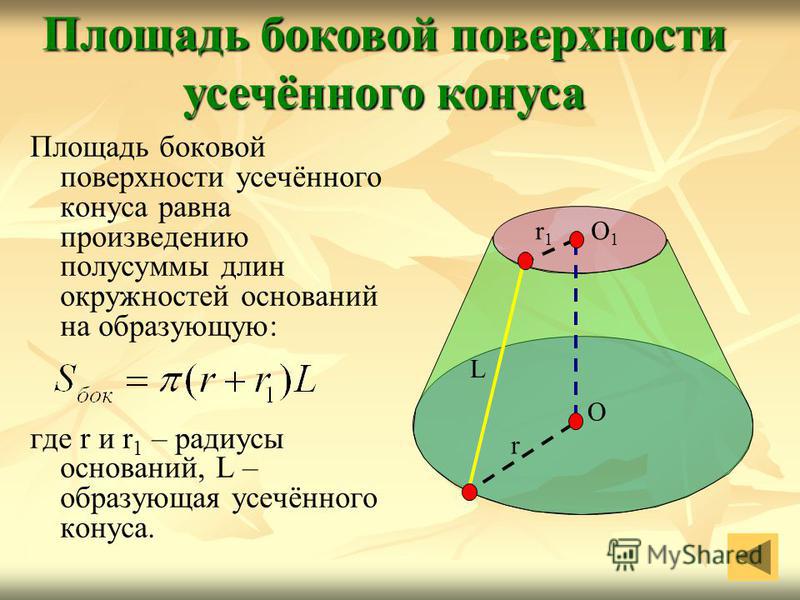 Он, неловким движением придерживая шпагу, обратился к Чернышеву, спрашивая по немецки, где государь. Ему, видно, как можно скорее хотелось пройти комнаты, окончить поклоны и приветствия и сесть за дело перед картой, где он чувствовал себя на месте. Он поспешно кивал головой на слова Чернышева и иронически улыбался, слушая его слова о том, что государь осматривает укрепления, которые он, сам Пфуль, заложил по своей теории. Он что то басисто и круто, как говорят самоуверенные немцы, проворчал про себя: Dummkopf… или: zu Grunde die ganze Geschichte… или: s’wird was gescheites d’raus werden… [глупости… к черту все дело… (нем.) ] Князь Андрей не расслышал и хотел пройти, но Чернышев познакомил князя Андрея с Пфулем, заметив, что князь Андрей приехал из Турции, где так счастливо кончена война. Пфуль чуть взглянул не столько на князя Андрея, сколько через него, и проговорил смеясь: «Da muss ein schoner taktischcr Krieg gewesen sein». [«То то, должно быть, правильно тактическая была война.» (нем.
Он, неловким движением придерживая шпагу, обратился к Чернышеву, спрашивая по немецки, где государь. Ему, видно, как можно скорее хотелось пройти комнаты, окончить поклоны и приветствия и сесть за дело перед картой, где он чувствовал себя на месте. Он поспешно кивал головой на слова Чернышева и иронически улыбался, слушая его слова о том, что государь осматривает укрепления, которые он, сам Пфуль, заложил по своей теории. Он что то басисто и круто, как говорят самоуверенные немцы, проворчал про себя: Dummkopf… или: zu Grunde die ganze Geschichte… или: s’wird was gescheites d’raus werden… [глупости… к черту все дело… (нем.) ] Князь Андрей не расслышал и хотел пройти, но Чернышев познакомил князя Андрея с Пфулем, заметив, что князь Андрей приехал из Турции, где так счастливо кончена война. Пфуль чуть взглянул не столько на князя Андрея, сколько через него, и проговорил смеясь: «Da muss ein schoner taktischcr Krieg gewesen sein». [«То то, должно быть, правильно тактическая была война.» (нем. ) ] – И, засмеявшись презрительно, прошел в комнату, из которой слышались голоса. Видно, Пфуль, уже всегда готовый на ироническое раздражение, нынче был особенно возбужден тем, что осмелились без него осматривать его лагерь и судить о нем. Князь Андрей по одному короткому этому свиданию с Пфулем благодаря своим аустерлицким воспоминаниям составил себе ясную характеристику этого человека. Пфуль был один из тех безнадежно, неизменно, до мученичества самоуверенных людей, которыми только бывают немцы, и именно потому, что только немцы бывают самоуверенными на основании отвлеченной идеи – науки, то есть мнимого знания совершенной истины. Француз бывает самоуверен потому, что он почитает себя лично, как умом, так и телом, непреодолимо обворожительным как для мужчин, так и для женщин. Англичанин самоуверен на том основании, что он есть гражданин благоустроеннейшего в мире государства, и потому, как англичанин, знает всегда, что ему делать нужно, и знает, что все, что он делает как англичанин, несомненно хорошо.
) ] – И, засмеявшись презрительно, прошел в комнату, из которой слышались голоса. Видно, Пфуль, уже всегда готовый на ироническое раздражение, нынче был особенно возбужден тем, что осмелились без него осматривать его лагерь и судить о нем. Князь Андрей по одному короткому этому свиданию с Пфулем благодаря своим аустерлицким воспоминаниям составил себе ясную характеристику этого человека. Пфуль был один из тех безнадежно, неизменно, до мученичества самоуверенных людей, которыми только бывают немцы, и именно потому, что только немцы бывают самоуверенными на основании отвлеченной идеи – науки, то есть мнимого знания совершенной истины. Француз бывает самоуверен потому, что он почитает себя лично, как умом, так и телом, непреодолимо обворожительным как для мужчин, так и для женщин. Англичанин самоуверен на том основании, что он есть гражданин благоустроеннейшего в мире государства, и потому, как англичанин, знает всегда, что ему делать нужно, и знает, что все, что он делает как англичанин, несомненно хорошо. Итальянец самоуверен потому, что он взволнован и забывает легко и себя и других. Русский самоуверен именно потому, что он ничего не знает и знать не хочет, потому что не верит, чтобы можно было вполне знать что нибудь. Немец самоуверен хуже всех, и тверже всех, и противнее всех, потому что он воображает, что знает истину, науку, которую он сам выдумал, но которая для него есть абсолютная истина. Таков, очевидно, был Пфуль. У него была наука – теория облического движения, выведенная им из истории войн Фридриха Великого, и все, что встречалось ему в новейшей истории войн Фридриха Великого, и все, что встречалось ему в новейшей военной истории, казалось ему бессмыслицей, варварством, безобразным столкновением, в котором с обеих сторон было сделано столько ошибок, что войны эти не могли быть названы войнами: они не подходили под теорию и не могли служить предметом науки. В 1806 м году Пфуль был одним из составителей плана войны, кончившейся Иеной и Ауерштетом; но в исходе этой войны он не видел ни малейшего доказательства неправильности своей теории.
Итальянец самоуверен потому, что он взволнован и забывает легко и себя и других. Русский самоуверен именно потому, что он ничего не знает и знать не хочет, потому что не верит, чтобы можно было вполне знать что нибудь. Немец самоуверен хуже всех, и тверже всех, и противнее всех, потому что он воображает, что знает истину, науку, которую он сам выдумал, но которая для него есть абсолютная истина. Таков, очевидно, был Пфуль. У него была наука – теория облического движения, выведенная им из истории войн Фридриха Великого, и все, что встречалось ему в новейшей истории войн Фридриха Великого, и все, что встречалось ему в новейшей военной истории, казалось ему бессмыслицей, варварством, безобразным столкновением, в котором с обеих сторон было сделано столько ошибок, что войны эти не могли быть названы войнами: они не подходили под теорию и не могли служить предметом науки. В 1806 м году Пфуль был одним из составителей плана войны, кончившейся Иеной и Ауерштетом; но в исходе этой войны он не видел ни малейшего доказательства неправильности своей теории.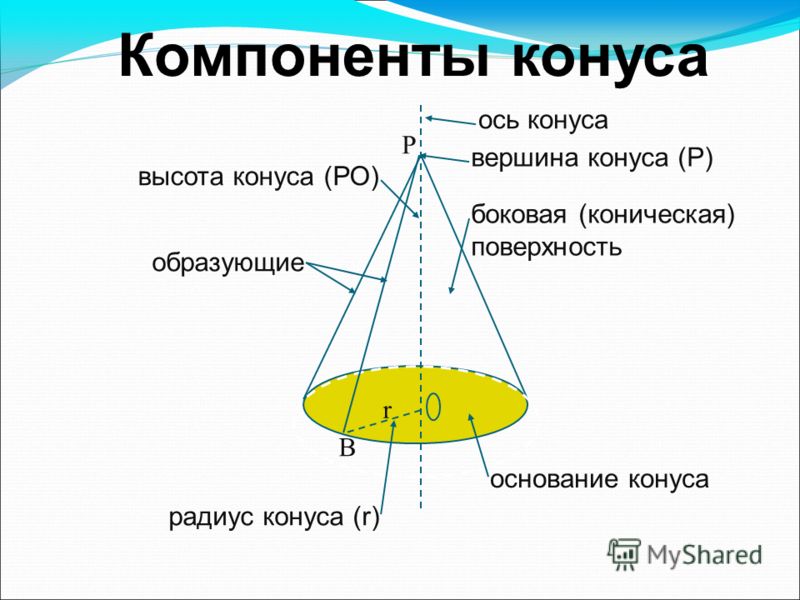 Напротив, сделанные отступления от его теории, по его понятиям, были единственной причиной всей неудачи, и он с свойственной ему радостной иронией говорил: «Ich sagte ja, daji die ganze Geschichte zum Teufel gehen wird». [Ведь я же говорил, что все дело пойдет к черту (нем.) ] Пфуль был один из тех теоретиков, которые так любят свою теорию, что забывают цель теории – приложение ее к практике; он в любви к теории ненавидел всякую практику и знать ее не хотел. Он даже радовался неуспеху, потому что неуспех, происходивший от отступления в практике от теории, доказывал ему только справедливость его теории. Он сказал несколько слов с князем Андреем и Чернышевым о настоящей войне с выражением человека, который знает вперед, что все будет скверно и что даже не недоволен этим. Торчавшие на затылке непричесанные кисточки волос и торопливо прилизанные височки особенно красноречиво подтверждали это. Он прошел в другую комнату, и оттуда тотчас же послышались басистые и ворчливые звуки его голоса. Не успел князь Андрей проводить глазами Пфуля, как в комнату поспешно вошел граф Бенигсен и, кивнув головой Болконскому, не останавливаясь, прошел в кабинет, отдавая какие то приказания своему адъютанту.
Напротив, сделанные отступления от его теории, по его понятиям, были единственной причиной всей неудачи, и он с свойственной ему радостной иронией говорил: «Ich sagte ja, daji die ganze Geschichte zum Teufel gehen wird». [Ведь я же говорил, что все дело пойдет к черту (нем.) ] Пфуль был один из тех теоретиков, которые так любят свою теорию, что забывают цель теории – приложение ее к практике; он в любви к теории ненавидел всякую практику и знать ее не хотел. Он даже радовался неуспеху, потому что неуспех, происходивший от отступления в практике от теории, доказывал ему только справедливость его теории. Он сказал несколько слов с князем Андреем и Чернышевым о настоящей войне с выражением человека, который знает вперед, что все будет скверно и что даже не недоволен этим. Торчавшие на затылке непричесанные кисточки волос и торопливо прилизанные височки особенно красноречиво подтверждали это. Он прошел в другую комнату, и оттуда тотчас же послышались басистые и ворчливые звуки его голоса. Не успел князь Андрей проводить глазами Пфуля, как в комнату поспешно вошел граф Бенигсен и, кивнув головой Болконскому, не останавливаясь, прошел в кабинет, отдавая какие то приказания своему адъютанту.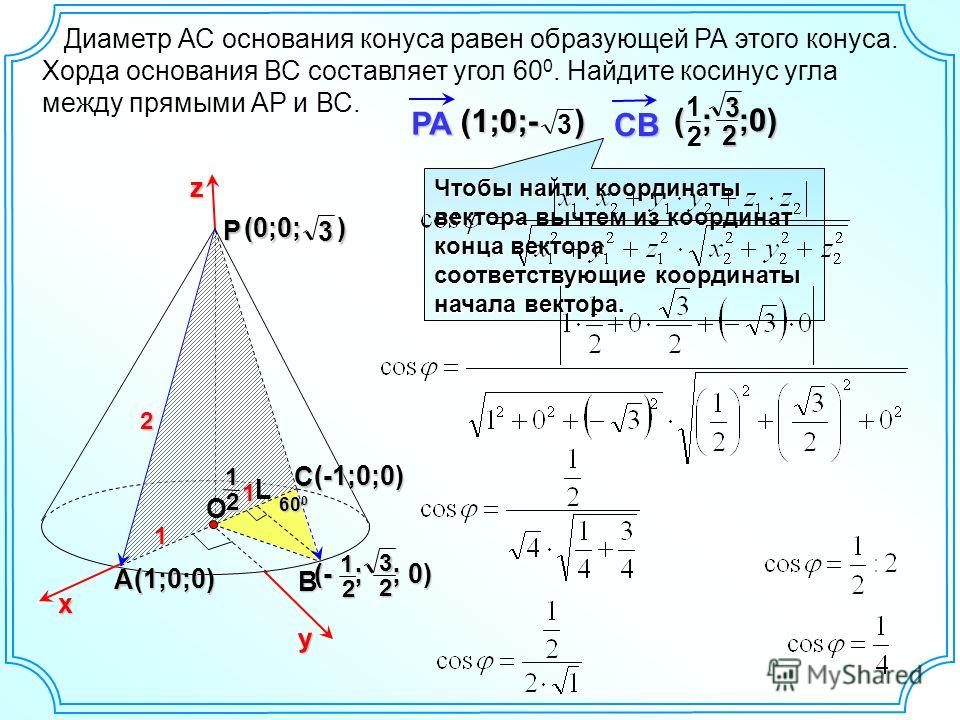 Государь ехал за ним, и Бенигсен поспешил вперед, чтобы приготовить кое что и успеть встретить государя. Чернышев и князь Андрей вышли на крыльцо. Государь с усталым видом слезал с лошади. Маркиз Паулучи что то говорил государю. Государь, склонив голову налево, с недовольным видом слушал Паулучи, говорившего с особенным жаром. Государь тронулся вперед, видимо, желая окончить разговор, но раскрасневшийся, взволнованный итальянец, забывая приличия, шел за ним, продолжая говорить:
Государь ехал за ним, и Бенигсен поспешил вперед, чтобы приготовить кое что и успеть встретить государя. Чернышев и князь Андрей вышли на крыльцо. Государь с усталым видом слезал с лошади. Маркиз Паулучи что то говорил государю. Государь, склонив голову налево, с недовольным видом слушал Паулучи, говорившего с особенным жаром. Государь тронулся вперед, видимо, желая окончить разговор, но раскрасневшийся, взволнованный итальянец, забывая приличия, шел за ним, продолжая говорить:
Как рассчитать угол конуса
Содержание
| Элементы конуса | Расчетные формулы | Элементы конуса | Расчетные формулы |
| K | K = (D-d)/ lK = 2tga | D | D = K× l + dD = 2× l×tga + d |
| a | tga = (D-d)/ 2ltga = K / 2 | d | d = D – 2× l×tgad = D – K× l |
Угол a вычисляют по тригонометрической функции тангенса.
Нормальные конические поверхности должны быть изготовлены по стандартным размерам, некоторые из которых указаны в табл.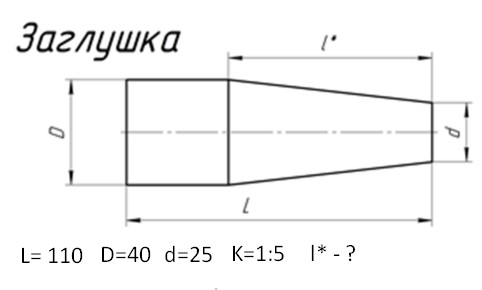 4.
4.
Кроме этих поверхностей, различают также конусы Морзе и метрические конусы. Наружные конусы Морзе выполняют на хвостовой части сверл (см. рис.6
), зенкеров, разверток, центров, а внутренние конусы – в отверстиях шпинделей, оправок, переходных втулок, в которые эти инструменты устанавливают. Существуют семь номеров конусов Морзе (от до
6
) со своими размерами и углами наклона
a
. Наименьшим является конус Морзе (
1:19,212
), наибольшим – конус Морзе
6
(
1:19,18
). Их размеры приведены в стандарте СТ СЭВ 147-75. Недостатком конусов Морзе следует считать разные углы наклона
a
у различных номеров.
Таблица 4
Стандартные размеры конусов деталей
| Конусность K | Угол конуса 2a | Угол наклона a | Обозначение конусности |
| 1:100 1:50 1:20 1:10 1:3 1:1,866 1:1,207 1:0,866 | 0 0 34¢23² 1 0 8¢45² 2 0 51¢51² 5 0 43¢29² 18 0 55¢30² 30 0 45 0 60 0 | 0 0 17¢12² 0 0 34¢23² 1 0 25¢56² 2 0 51¢45² 9 0 27¢45² 15 0 22 0 30¢ 30 0 | 1:100 1:50 1:20 1:10 1:3 30 0 45 0 60 0 |
Метрические конусы 4, 6, 80, 100, 120, 160, 200
(см. тот же стандарт) имеют одинаковую конусность
тот же стандарт) имеют одинаковую конусность
1:20
(и угол
a
), а номер конуса обозначает размер диаметра большого основания.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения:
Да какие ж вы математики, если запаролиться нормально не можете.
8256 – | 7223 – или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock! и обновите страницу (F5)
очень нужно
Конусность – отношение разности диаметров двух поперечных сечений кругового конуса к расстоянию между ними.
Конусность имеет двойной Уклон: k=2i Конусность на чертеже может быть указана в градусной мере, в радианах и в процентах. Заданы конусность пробки крана 1:5, диаметр D=BC=20 мм, длина l=35 мм.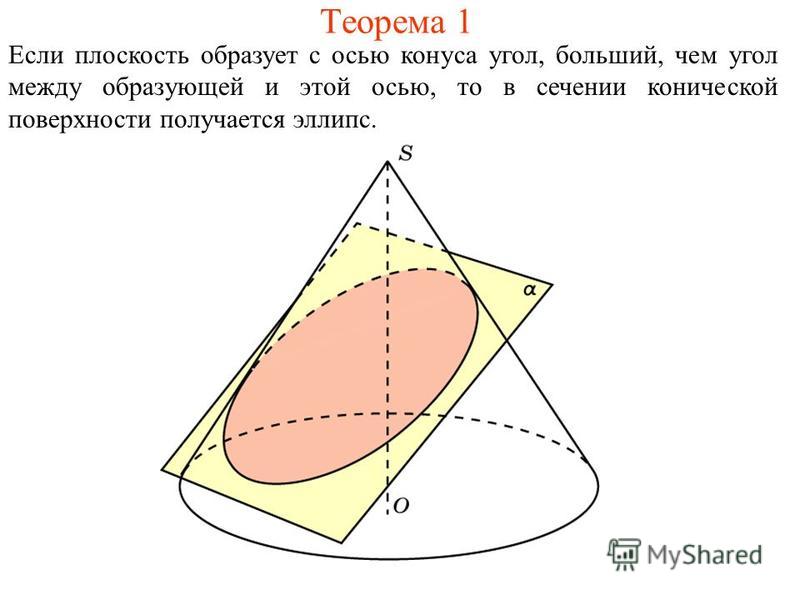
Необходимо построить очертание пробки крана одним из двух способов: Первый способ. Из формулы k=2i находим i=1:10. Отмечаем точки BC и строим треугольник DKP так, чтобы KP:BK=1:10. Продолжив BP до пересечения с осью конуса, получим вершину конуса S. Точку S соединяем с точкой C. Отложив по оси пробки от BC отрезок l=35 мм и проведя через конец этого отрезка прямую, перпендикулярную к оси , получим диаметр d=EF=13 мм торца пробки; Второй способ. Из формулы k=(D-d)/l находим d=EF=20-35/5=13 мм; Величина угла при вершине конуса:
здесь угол φ представлен в радианах.
где L – расстояние от большого сечения до вершины S конуса, а отношение: D/(2L) = tgφ Пусть задана конусность например 1 : 2,5 откуда i=1:5 и tgφ=0,2 тогда перевод ее в градусы выполняется по формулам:
Конусность стандартизована. ГОСТ 8593-81 устанавливает нормальные конусности и углы конусов
| Обозна- чение | конуса | Конус- | ность | Угол | конуса | Угол | уклона |
| Ряд 1 | Ряд 2 | Угл. ед. ед. | Рад. | Угл. ед. | Рад. | ||
| 1:500 | 1:500 | 0,0020000 | 6`52,5″ | 0,0020000 | 3`26,25″ | 0,0010000 | |
| 1:200 | 1:200 | 0,0050000 | 17`11,3″ | 0,0050000 | 8`25,65″ | 0,0025000 | |
| 1:100 | 1:100 | 0,0100000 | 34`22,6″ | 0,0100000 | 17`11,3″ | 0,0050000 | |
| 1:50 | 1:50 | 0,0200000 | 1°8`45,2″ | 0,0199996 | 34`22,6″ | 0,0099998 | |
| 1:30 | 1:30 | 0,0333333 | 1°54`34,9″ | 0,0333304 | 57`17,45″ | 0,0166652 | |
| 1:20 | 1:20 | 0,0500000 | 2°51`51,1″ | 0,0499896 | 1°25`55,55″ | 0,0249948 | |
| 1:15 | 1:15 | 0,0666667 | 3°49`5,9″ | 0,0666420 | 1°54`32,95″ | 0,0333210 | |
| 1:12 | 1:12 | 0,0833333 | 4°46`18,8″ | 0,0832852 | 2°23`9,4″ | 0,0416426 | |
| 1:10 | 1:10 | 0,1000000 | 5°43`29,3″ | 0,0999168 | 2°51`44,65″ | 0,0499584 | |
| 1:8 | 1:8 | 0,1250000 | 7°9`9,6″ | 0,1248376 | 3°34`34,8″ | 0,0624188 | |
| 1:7 | 1:7 | 0,1428571 | 8°10`16,4″ | 0,1426148 | 4°5`8,2″ | 0,0713074 | |
| 1:6 | 1:6 | 0,1666667 | 9°31`38,2″ | 0,1662824 | 4°45`49,1″ | 0,0831412 | |
| 1:5 | 1:5 | 0,2000000 | 11°25`16,3″ | 0,1993374 | 5°42`38,15″ | 0,0996687 | |
| 1:4 | 1:4 | 0,2500000 | 14°15`0,1″ | 0,2487100 | 7°7`30,05″ | 0,1243550 | |
| 1:3 | 1:3 | 0,3333333 | 18°55`28,7″ | 0,3302972 | 9°27`44,35″ | 0,1651486 | |
| 30° | 1:1,866025 | 0,5358985 | 30° | 0,5235988 | 15° | 0,2617994 | |
| 45° | 1:1,207107 | 0,8284269 | 45° | 0,7853982 | 22°30` | 0,3926991 | |
| 60° | 1:0,866025 | 1,1547010 | 60° | 1,0471976 | 30° | 0,5235988 | |
| 75° | 1:0,651613 | 1,5346532 | 75° | 1,3089970 | 37°30` | 0,6544985 | |
| 90° | 1:0,500000 | 2,0000000 | 90° | 1,5707964 | 45° | 0,7853982 | |
| 120° | 1:0,288675 | 3,4641032 | 120° | 2,0943952 | 60° | 1,0471976 |
Конусности и углы конусов должны соответствовать указанным на чертеже и в таблице. При выборе конусностей или углов конусов ряд 1 следует предпочитать ряду 2.
При выборе конусностей или углов конусов ряд 1 следует предпочитать ряду 2.
Конусность поверхности
обозначается на чертеже: – надписью Конусность с указанием ее величины; – указывающей на нее стрелкой с полкой где пишется: – Конусность с указанием ее величины; – знак конусности и ее величина.
В машиностроении, наряду с цилиндрическими, широко применяются детали с коническими поверхностями в виде наружных конусов или в виде конических отверстий. Например, центр токарного станка имеет два наружных конуса, из которых один служит для установки и закрепления его в коническом отверстии шпинделя; наружный конус для установки и закрепления имеют также сверло, зенкер, развертка и т. д. Переходная втулка для закрепления сверл с коническим хвостовиком имеет наружный конус и коническое отверстие
Читать также: Саморез кровельный размеры гост
Понятие о конусе и его элементах
Элементы конуса . Если вращать прямоугольный треугольник АБВ вокруг катета АБ (рис. 202, а), то образуется тело АВГ, называемое полным конусом
202, а), то образуется тело АВГ, называемое полным конусом
. Линия АБ называется осью или
высотой конуса
, линия АВ —
образующей конуса
. Точка А является
вершиной конуса
.
При вращении катета БВ вокруг оси АБ образуется поверхность круга, называемая основанием конуса
.
Угол ВАГ между боковыми сторонами АВ и АГ называется углом конуса
и обозначается 2α. Половина этого угла, образуемая боковой стороной АГ и осью АБ, называется
углом уклона конуса
и обозначается α. Углы выражаются в градусах, минутах и секундах.
Если от полного конуса отрезать его верхнюю часть плоскостью, параллельной егооснованию (рис. 202, б), то получим тело, называемое усеченным конусом
. Оно имеет два основания верхнее и нижнее. Расстояние OO1 по оси между основаниями называется
высотой усеченного конуса
. Так как в машиностроении большей частью приходится иметь дело с частями конусов, т. е. усеченными конусами, то обычно их просто называют конусами; дальше будем называть все конические поверхности конусами.
е. усеченными конусами, то обычно их просто называют конусами; дальше будем называть все конические поверхности конусами.
Связь между элементами конуса. На чертеже указывают обычно три основных размера конуса: больший диаметр D, меньший — d и высоту конуса l (рис. 203).
Иногда на чертеже указывается только один из диаметров конуса, например, больший D, высота конуса l и так называемая конусность. Конусностью называется отношение разности диаметров конуса к его длине. Обозначим конусность буквой K, тогда
Если конус имеет размеры: D =80 мм, d = 70 мм и l = 100 мм, то согласно формуле (10):
Это значит, что на длине 10 мм диаметр конуса уменьшается на 1 мм или на каждый миллиметр длины конуса разница между его диаметрами изменяется на
Иногда на чертеже вместо угла конуса указывается уклон конуса
. Уклон конуса показывает, в какой мере отклоняется образующая конуса от его оси. Уклон конуса определяется по формуле
где tg α — уклон конуса; D — диаметр большого основания конуса в мм; d — диаметр малого основания конуса в мм; l — высота конуса в мм.
Пользуясь формулой (11), можно при помощи тригонометрических таблиц определить угол а уклона конуса.
Уклон конуса и конусность обычно выражают простой дробью, например: 1 : 10; 1 : 50, или десятичной дробью, например, 0,1; 0,05; 0,02 и т. д.
Способы получения конических поверхностей на токарном станке
На токарном станке обработка конических поверхностей производится одним из следующих способов: а) поворотом верхней части суппорта; б) поперечным смещением корпуса задней бабки; в) с помощью конусной линейки; г) с помощью широкого резца.
Обработка конических поверхностей поворотом верхней части суппорта
При изготовлении на токарном станке коротких наружных и внутренних конических поверхностей с большим углом уклона нужно повернуть верхнюю часть суппорта относительно оси станка под углом α уклона конуса (см. рис. 204). При таком способе работы подачу можно производить только от руки, вращая рукоятку ходового винта верхней части суппорта, и лишь в наиболее современных токарных станках имеется механическая подача верхней части суппорта.
Для установки верхней части суппорта 1 на требуемый угол можно использовать деления, нанесенные на фланце 2 поворотной части суппорта (рис. 204). Если угол α уклона конуса задан по чертежу, то верхнюю часть суппорта повертывают вместе с его поворотной частью на требуемое число делений, обозначающих градусы. Число делений отсчитывают относительно риски, нанесенной на нижней части суппорта.
Если на чертеже угол α не дан, а указаны больший и меньший диаметры конуса и длина его конической части, то величину угла поворота суппорта определяют по формуле (11)
Способ обтачивания конических поверхностей поворотом верхней части суппорта имеет следующие недостатки: он допускает обычно применение только ручной подачи, что отражается на производительности труда и чистоте обработанной поверхности; позволяет обтачивать сравнительно короткие конические поверхности, ограниченные длиной хода верхней части суппорта.
Обработка конических поверхностей способом поперечного смещения корпуса задней бабки
Для получения конической поверхности на токарном станке необходимо при вращении заготовки вершину резца перемещать не параллельно, а под некоторым углом к оси центров. Этот угол должен равняться углу α уклона конуса. Наиболее простой способ получения угла между осью центров и направлением подачи — сместить линию центров, сдвинув задний центр в поперечном направлении. Путем смещения заднего центра в сторону резца (на себя) в результате обтачивания получают конус, у которого большее основание направлено в сторону передней бабки; при смещении заднего центра в противоположную сторону, т. е. от резца (от себя), большее основание конуса окажется со стороны задней бабки (рис. 205).
Этот угол должен равняться углу α уклона конуса. Наиболее простой способ получения угла между осью центров и направлением подачи — сместить линию центров, сдвинув задний центр в поперечном направлении. Путем смещения заднего центра в сторону резца (на себя) в результате обтачивания получают конус, у которого большее основание направлено в сторону передней бабки; при смещении заднего центра в противоположную сторону, т. е. от резца (от себя), большее основание конуса окажется со стороны задней бабки (рис. 205).
Смещение корпуса задней бабки определяют по формуле
где S — смещение корпуса задней бабки от оси шпинделя передней бабки в мм; D — диаметр большого основания конуса в мм; d — диаметр малого основания конуса в мм; L — длина всей детали или расстояние между центрами в мм; l — длина конической части детали в мм.
Смещение корпуса задней бабки производят, используя деления 1 (рис 206), нанесенные на торце опорной плиты, и риску 2 на торце корпуса задней бабки.
Если на торце плиты делений нет, то смещают корпус задней бабки, пользуясь измерительной линейкой, как показано на рис.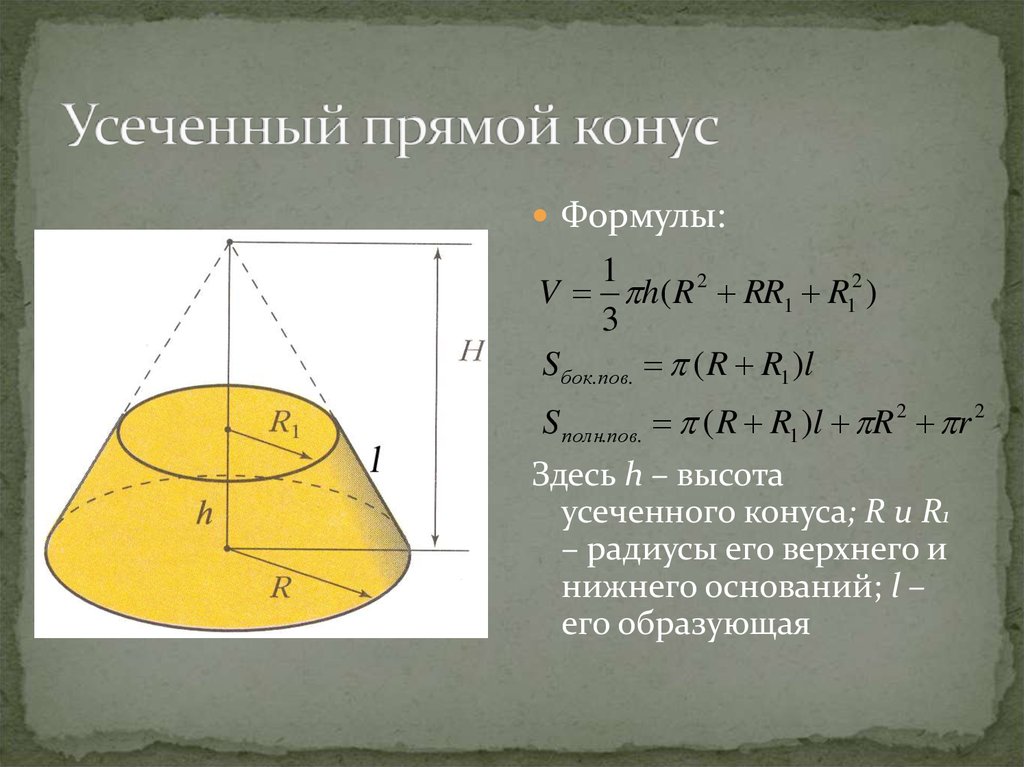 207.
207.
Читать также: Жак лебедка ручная шахтная
Преимущество обработки конических поверхностей путем смещения корпуса задней бабки заключается в том, что этим способом можно обтачивать конусы большой длины и вести обтачивание с механической подачей.
Недостатки этого способа: невозможность растачивать конические отверстия; потеря времени на перестановку задней бабки; возможность обрабатывать лишь пологие конусы; перекос центров в центровых отверстиях, что приводит к быстрому и неравномерному износу центров и центровых отверстий и служит причиной брака при вторичной установке детали в этих же центровых отверстиях.
Неравномерного износа центровых отверстий можно избежать, если вместо обычного применять специальный шаровой центр (рис. 208). Такие центры используют преимущественно при обработке точных конусов.
Обработка конических поверхностей с применением конусной линейки
Для обработки конических поверхностей с углом уклона а до 10—12° современные токарные станки обычно имеют особое приспособление, называемое конусной линейкой. Схема обработки конуса с применением конусной линейки приводится на рис. 209.
Схема обработки конуса с применением конусной линейки приводится на рис. 209.
К станине станка прикреплена плита 11, на которой установлена конусная линейка 9. Линейку можно поворачивать вокруг пальца 8 под требуемым углом а к оси обрабатываемой детали. Для закрепления линейки в требуемом положении служат два болта 4 и 10. По линейке свободно скользит ползун 7, соединяющийся с нижней поперечной частью 12 суппорта при помощи тяги 5 и зажима 6. Чтобы эта часть суппорта могла свободно скользить по направляющим, ее отсоединяют от каретки 3, вывинчивая поперечный винт или отсоединяя от суппорта его гайку.
Если сообщить каретке продольную подачу, то ползун 7, захватываемый тягой 5, начнет перемещаться вдоль линейки 9. Так как ползун скреплен с поперечными салазками суппорта, то они вместе с резцом будут перемещаться параллельно линейке 9. Благодаря этому резец будет обрабатывать коническую поверхность с углом уклона, равным углу α поворота конусной линейки.
После каждого прохода резец устанавливают на глубину резания с помощью рукоятки 1 верхней части 2 суппорта.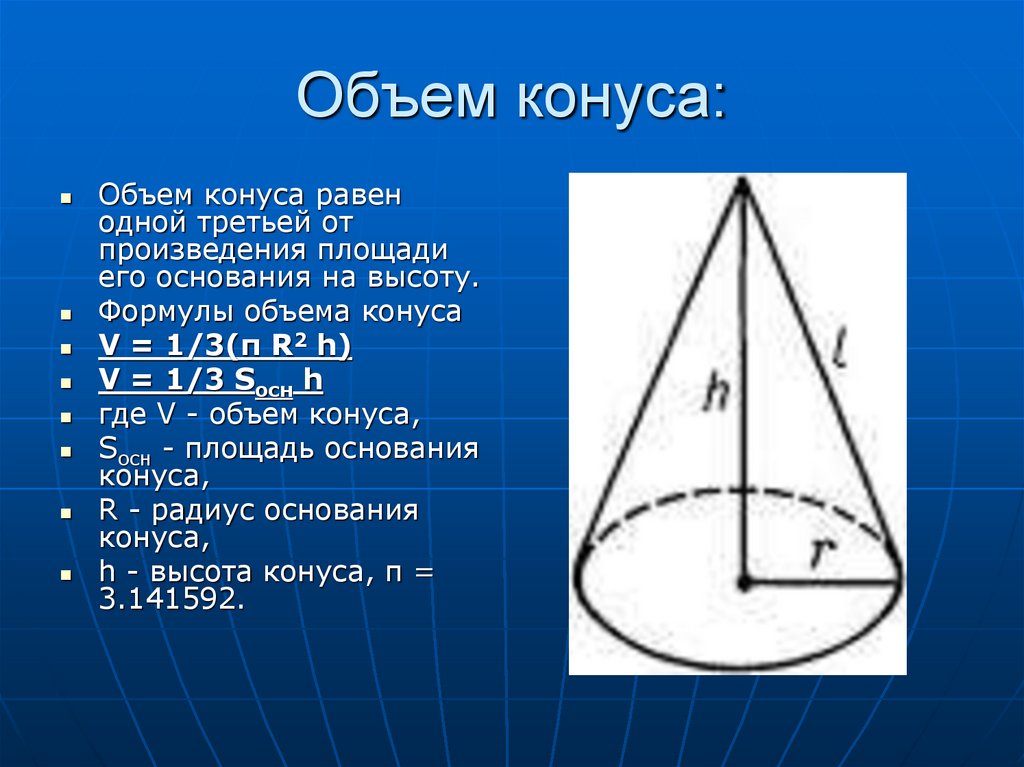 Эта часть суппорта должна быть повернута на 90° относительно нормального положения, т. е. так, как это показано на рис. 209.
Эта часть суппорта должна быть повернута на 90° относительно нормального положения, т. е. так, как это показано на рис. 209.
Если даны диаметры оснований конуса D и d и его длина l, то угол поворота линейки можно найти по формуле (11).
Подсчитав величину tg α, легко определить значение угла α по таблице тангенсов. Применение конусной линейки имеет ряд преимуществ: 1) наладка линейки удобна и производится быстро; 2) при переходе к обработке конусов не требуется нарушать нормальную наладку станка, т. е. не нужно смещать корпус задней бабки; центры станка остаются в нормальном положении, т. е. на одной оси, благодаря чему центровые отверстия в детали и центры станка не срабатываются; 3) при помощи конусной линейки можно не только обтачивать наружные конические поверхности, но и растачивать конические отверстия; 4) возможна работа е продольным самоходом, что увеличивает производительность труда и улучшает качество обработки.
Недостатком конусной линейки является необходимость отсоединять салазки суппорта от винта поперечной подачи. Этот недостаток устранен в конструкции некоторых токарных станков, у которых винт не связан жестко со своим маховичком и зубчатыми колесами поперечного самохода.
Этот недостаток устранен в конструкции некоторых токарных станков, у которых винт не связан жестко со своим маховичком и зубчатыми колесами поперечного самохода.
Обработка конических поверхностей широким резцом
Обработку конических поверхностей (наружных и внутренних) с небольшой длиной конуса можно производить широким резцом с углом в плане, соответствующим углу α уклона конуса (рис. 210). Подача резца может быть продольная и поперечная.
Однако использование широкого резца на обычных станках возможно только при длине конуса, не превышающей примерно 20 мм. Применять более широкие резцы можно лишь на особо жестких станках и деталях, если это не вызывает вибрации резца и обрабатываемой детали.
Растачивание и развертывание конических отверстий
Обработка конических отверстий является одной из наиболее трудных токарных работ; она значительно труднее, чем обработка наружных конусов.
Обработку конических отверстий на токарных станках в большинстве случаев производят растачиванием резцом с поворотом верхней части суппорта и реже с помощью конусной линейки. Все подсчеты, связанные с поворотом верхней части суппорта или конусной линейки, выполняются так же, как при обтачивании наружных конических поверхностей.
Все подсчеты, связанные с поворотом верхней части суппорта или конусной линейки, выполняются так же, как при обтачивании наружных конических поверхностей.
Если отверстие должно быть в сплошном материале, то сначала сверлят цилиндрическое отверстие, которое затем растачивают резцом на конус или обрабатывают коническими зенкерами и развертками.
Чтобы ускорить растачивание или развертывание, следует предварительно просверлить отверстие сверлом, диаметр d, которого на 1—2 мм меньше диаметра малого основания конуса (рис. 211, а). После этого рассверливают отверстие одним (рис. 211, б) или двумя (рис. 211, в) сверлами для получения ступеней.
После чистового растачивания конуса его развертывают конической разверткой соответствующей конусности. Для конусов с небольшой конусностью выгоднее производить обработку конических отверстий непосредственно после сверления набором специальных разверток, как показано на рис. 212.
Режимы резания при обработке отверстий коническими развертками
Конические развертки работают в более тяжелых условиях, чем цилиндрические: в то время как цилиндрические развертки снимают незначительный припуск небольшими режущими кромками, конические развертки режут всей длиной их режущих кромок, расположенных на образующей конуса. Поэтому при работе коническими развертками применяют подачи и скорости резания меньше, чем при работе цилиндрическими развертками.
Поэтому при работе коническими развертками применяют подачи и скорости резания меньше, чем при работе цилиндрическими развертками.
При обработке отверстий коническими развертками подачу производят вручную, вращая маховичок задней бабки. Необходимо следить за тем, чтобы пиноль задней бабки перемещалась равномерно.
Подачи при развертывании стали 0,1—0,2 мм/об, при развертывании чугуна 0,2—0,4 мм/об.
Скорость резания при развертывании конических отверстий развертками из быстрорежущей стали 6—10 м/мин.
Читать также: Масло чемпион для бензопилы
Для облегчения работы конических разверток и получения чистой и гладкой поверхности следует применять охлаждение. При обработке стали и чугуна применяют эмульсию или сульфофрезол.
Измерение конических поверхностей
Поверхности конусов проверяют шаблонами и калибрами; измерение и одновременно проверку углов конуса производят угломерами. На рис. 213 показан способ проверки конуса с помощью шаблона.
Наружные и внутренние углы различных деталей можно измерять универсальным угломером (рис. 214). Он состоит из основания 1, На котором на дуге 130 нанесена основная шкала. С основанием 1 жестко скреплена линейка 5. По дуге основания перемещается сектор 4, несущий нониус 3. К сектору 4 посредством державки 7 может быть прикреплен угольник 2, в котором, в свою очередь, закрепляется съемная линейка 5. Угольник 2 и съемная линейка 5 имеют возможность перемещаться по грани сектора 4.
214). Он состоит из основания 1, На котором на дуге 130 нанесена основная шкала. С основанием 1 жестко скреплена линейка 5. По дуге основания перемещается сектор 4, несущий нониус 3. К сектору 4 посредством державки 7 может быть прикреплен угольник 2, в котором, в свою очередь, закрепляется съемная линейка 5. Угольник 2 и съемная линейка 5 имеют возможность перемещаться по грани сектора 4.
Путем различных комбинаций в установке измерительных деталей угломера можно производить измерение углов от 0 до 320°. Величина отсчета по нониусу 2′. Отсчет, полученный при измерении углов, производится по шкале и нониусу (рис. 215) следующим образом: нулевой штрих нониуса показывает число градусов, а штрих нониуса, совпадающий со штрихом шкалы основания, — число минут. На рис. 215 со штрихом шкалы основания совпадает 11-й штрих нониуса, что означает 2’Х 11 = 22′. Следовательно, угол в данном случае равен 76°22′.
На рис. 216 показаны комбинации измерительных деталей универсального угломера, позволяющие производить измерение различных углов от 0 до 320°.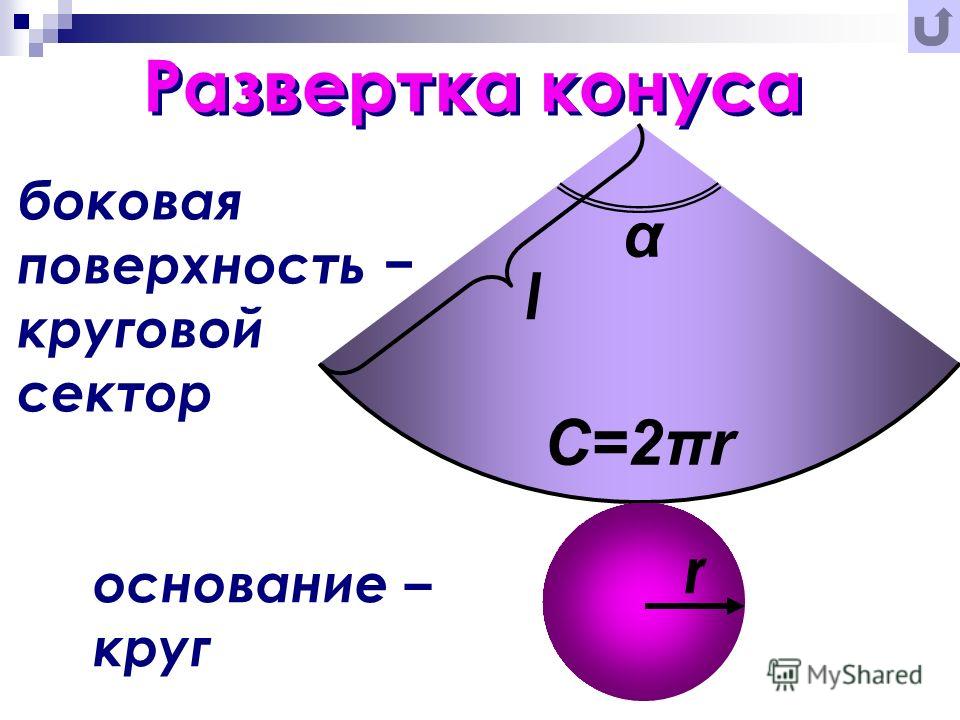
Для более точной проверки конусов в серийном производстве применяют специальные калибры. На рис. 217, а показан кониче-ский калибр-втулка для проверки наружных конусов, а на рис. 217, б—конический калибр-пробка для проверки конических отверстий.
На калибрах делаются уступы 1 и 2 на торцах или наносятся риски 3, служащие для определения точности проверяемых поверхностей.
На. рис. 218 приводится пример проверки конического отверстия калибром-пробкой.
Для проверки отверстия калибр (см. рис. 218), имеющий уступ 1 на определенном расстоянии от торца 2 и две риски 3, вводят с легким нажимом в отверстие и проверяют, нет ли качания калибра в отверстии. Отсутствие качания показывает, что угол конуса правилен. Убедившись, что угол конуса правилен, приступают к проверке его размера. Для этого наблюдают, до какого места калибр войдет в проверяемую деталь. Если конец конуса детали совпадает с левым торцом уступа 1 или с одной из рисок 3 или находится между рисками, то размеры конуса правильны.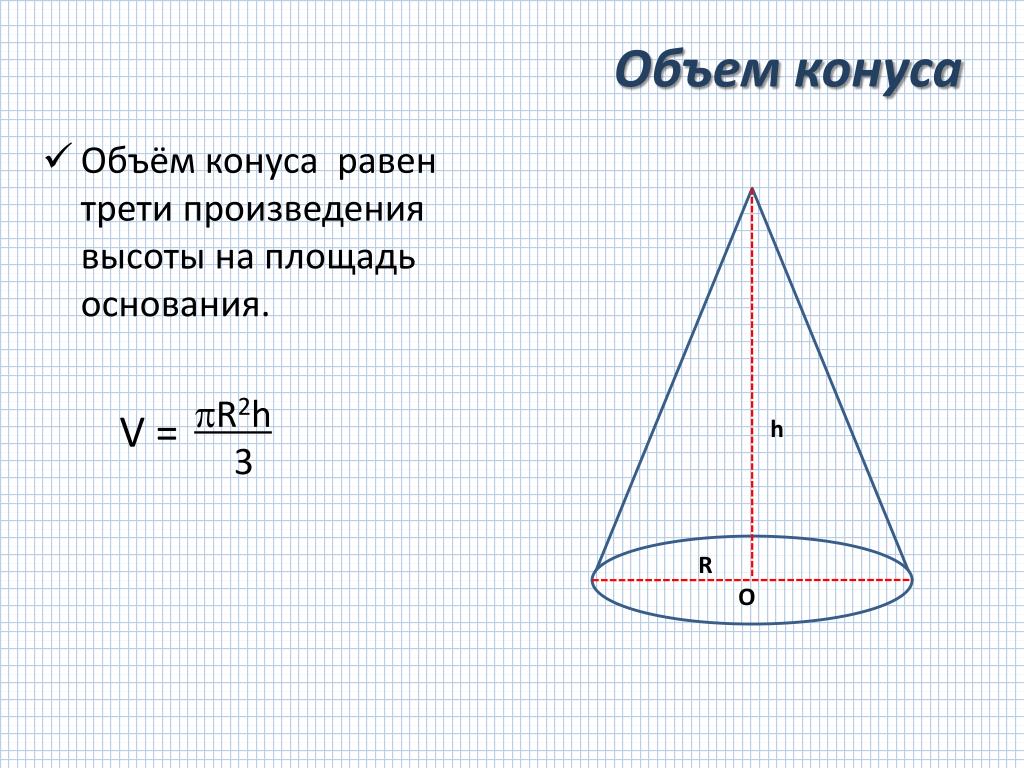 Но может случиться, что калибр войдет в деталь настолько глубоко, что обе риски 3 войдут в отверстие или оба торца уступа 1 выйдут из него наружу. Это показывает, что диаметр отверстия больше заданного. Если, наоборот, обе риски окажутся вне отверстия или ни один из торцов уступа не выйдет из него, то диаметр отверстия меньше требуемого.
Но может случиться, что калибр войдет в деталь настолько глубоко, что обе риски 3 войдут в отверстие или оба торца уступа 1 выйдут из него наружу. Это показывает, что диаметр отверстия больше заданного. Если, наоборот, обе риски окажутся вне отверстия или ни один из торцов уступа не выйдет из него, то диаметр отверстия меньше требуемого.
Для точной проверки конусности применяют следующий способ. На измеряемой поверхности детали или калибра проводят мелом или карандашом две-три линии вдоль образующей конуса, затем вставляют или надевают калибр на деталь и повертывают его на часть оборота. Если линии сотрутся неравномерно, это значит, что конус детали обработан неточно и необходимо его исправить. Стирание линий по концам калибра говорит о неправильной конусности; стирание линий в средней части калибра показывает, что конус имеет небольшую вогнутость, причиной чего обычно является неточное расположение вершины резца по высоте центров. Вместо меловых линий можно нанести на всю коническую поверхность детали или калибра тонкий слой специальной краски (синьки). Такой способ дает большую точность измерения.
Такой способ дает большую точность измерения.
Брак при обработке конических поверхностей и меры его предупреждения
При обработке конических поверхностей, помимо упомянутых видов брака для цилиндрических поверхностей, дополнительно возможны следующие виды брака: 1) неправильная конусность; 2) отклонения в размерах конуса; 3) отклонения в размерах диаметров оснований при правильной конусности; 4) непрямолинейность образующей конической поверхности.
1. Неправильная конусность получается главным образом вследствие неточного смещения корпуса задней бабки, неточного поворота верхней части суппорта, неправильной установки конусной линейки, неправильной заточки или установки широкого резца. Следовательно, точной установкой корпуса задней бабки, верхней части суппорта или конусной линейки перед началом обработки можно брак предупредить. Этот вид брака исправим только в том случае, если ошибка во всей длине конуса направлена в тело детали, т. е. все диаметры у втулки меньше, а у конического стержня больше требуемых.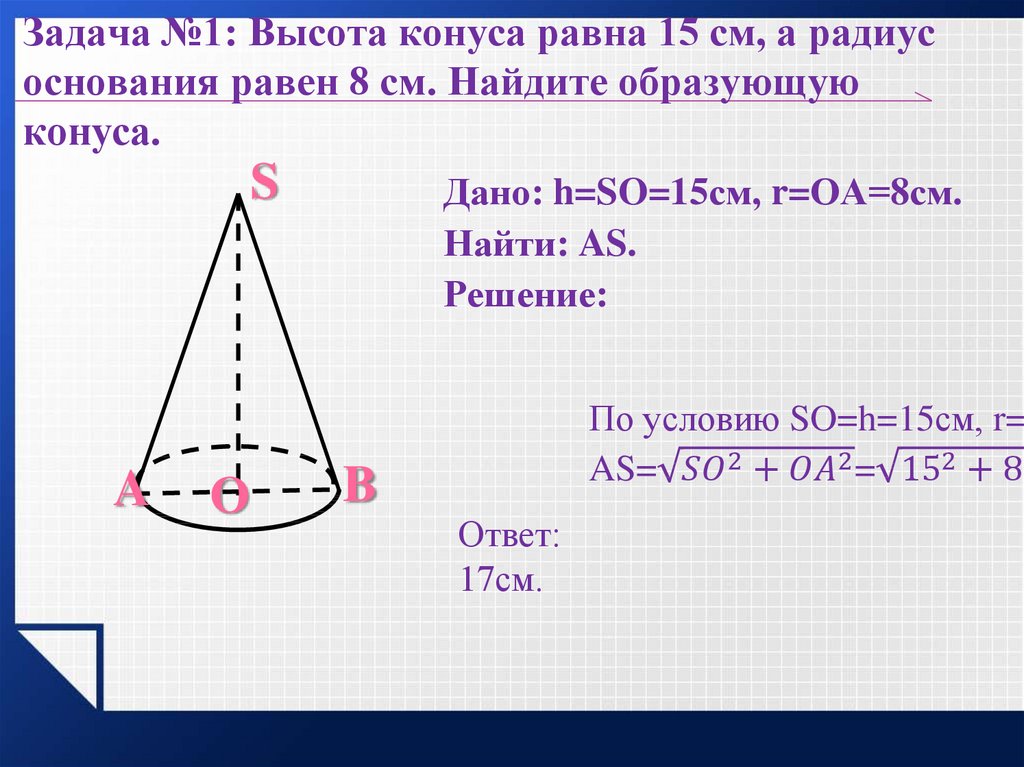
2. Неправильный размер конуса при правильном угле его, т. е. неправильная величина диаметров по всей длине конуса, получается, если снято недостаточно или слишком много материала. Предупредить брак можно только внимательной установкой глубины резания по лимбу на чистовых проходах. Брак исправим, если снято недостаточно материала.
3. Может получиться, что при правильной конусности и точных размерах одного конца конуса диаметр второго конца неправилен. Единственной причиной является несоблюдение требуемой длины всего конического участка детали. Брак исправим, если деталь излишне длинна. Чтобы избежать этого вида брака, необходимо перед обработкой конуса тщательно проверить его длину.
4. Непрямолинейность образующей обрабатываемого конуса получается при установке резца выше (рис. 219, б) или ниже (рис. 219, в) центра (на этих рисунках для большей наглядности искажения образующей конуса показаны в сильно преувеличенном виде). Таким образом, и этот вид брака является результатом невнимательной работы токаря.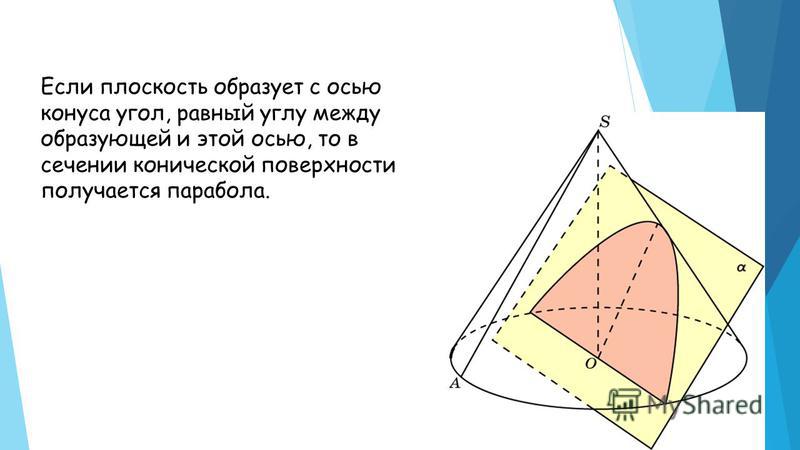
Определение фигуры
Предположим, что имеется некоторая плоская замкнутая кривая, например окружность или эллипс. В пространстве выберем некоторую точку, которая не принадлежит плоскости указанной кривой. Теперь соединим ее с каждой точкой на кривой при помощи прямых отрезков. Полученная фигура дает ответ на вопрос о том, что такое конус. На фото ниже показаны три конуса, изготовленные из бумаги.
Вам будет интересно:Подберем рифму к слову «капля»
Исходная замкнутая кривая называется директрисой или направляющей фигуры. Фиксированная точка в пространстве, упомянутая выше, называется вершиной конуса. Прямые отрезки, которые соединяют вершину с точками на директрисе, получили название генератрис, или образующих.
Рассматриваемая фигура образует некоторую поверхность, поэтому объемом не обладает. Если же внутри эту фигуру заполнить каким-либо веществом, то у нее появится некоторый объем. Полученное твердое тело также называется конусом.
Линейные характеристики круглого прямого конуса
Фигура образована кругом некоторого радиуса r и конической поверхностью.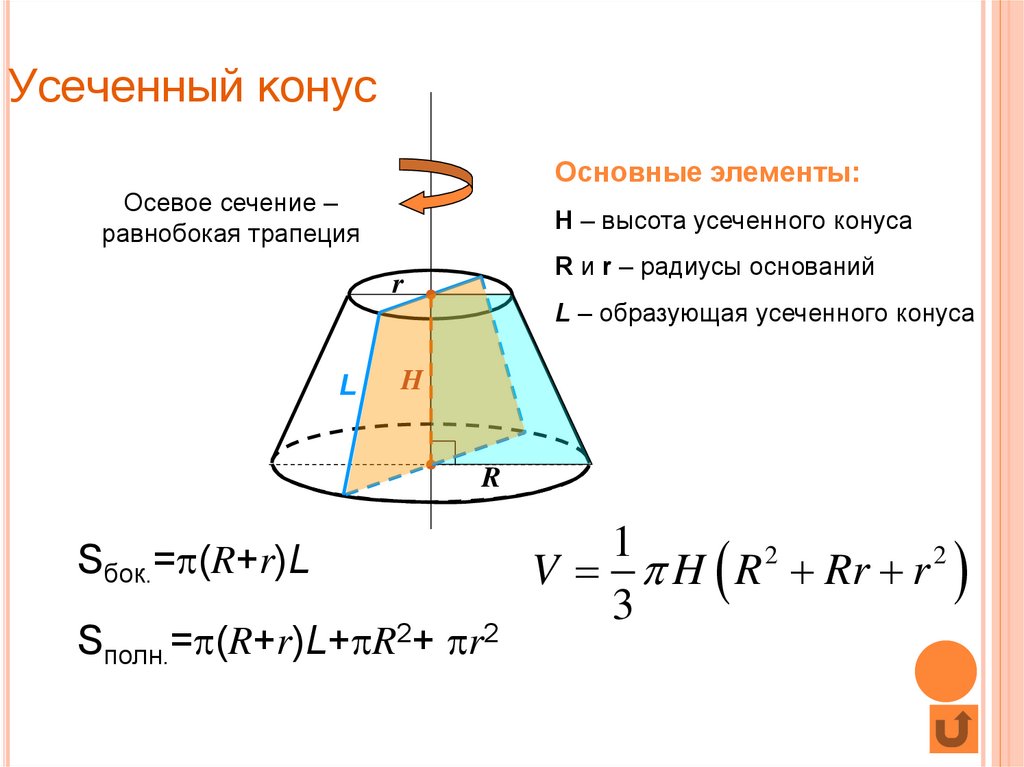 Пусть высота конуса равна h. Указанные две линейные характеристики являются основными. Их знание позволяет вычислить любые параметры фигуры, например, длину его генератрис, площадь поверхности и объем.
Пусть высота конуса равна h. Указанные две линейные характеристики являются основными. Их знание позволяет вычислить любые параметры фигуры, например, длину его генератрис, площадь поверхности и объем.
Поскольку рассматриваемая фигура является прямой, то длины всех его генератрис равны между собой. Если обозначить их длину буквой d, тогда формула для ее вычисления будет иметь вид:
d = √(h3 + r2).
Нетрудно догадаться, откуда взялась эта формула. Она является результатом применения теоремы Пифагора к соответствующему прямоугольному треугольнику. Отметим, что генератриса конуса всегда больше радиуса его основания, независимо от значения величины h.
Данное выражение позволяет по двум известным линейным величинам определить третью. Например, если известны d и h, тогда радиус круга в основании будет равен:
r = √(d2 — h3).
Сечение конуса
Осевым сечением конуса называется плоскость, проходящая по его оси либо высоте. В прямом конусе такое сечение представляет собой равнобедренный треугольник, в котором высотой треугольника является высота тела, его сторонами выступают образующие, а основание – это диаметр основания. В равностороннем геометрическом теле осевое сечение является равносторонним треугольником, так как в этом конусе диаметр основания и образующие равны.
В равностороннем геометрическом теле осевое сечение является равносторонним треугольником, так как в этом конусе диаметр основания и образующие равны.
Плоскость осевого сечения в прямом конусе является плоскостью его симметрии. Причиной этому служит то, что его вершина находится над центром его основания, то есть плоскость осевого сечения делит конус на две одинаковые части.
Так как в наклонном объемном теле высота и ось не совпадают, плоскость осевого сечения может не включать в себя высоту. Если осевых сечений в таком конусе можно построить множество, так как для этого необходимо соблюдать лишь одно условие — оно должно проходить только через ось, то осевое сечение плоскости, которому будет принадлежать высота этого конуса, можно провести лишь одно, потому что количество условий увеличивается, а, как известно, две прямые (вместе) могут принадлежать только одной плоскости.
1. Линейные размеры, углы, конусы
Нормальные утлы (по ГОСТ 8908-81)
| 1-й ряд | 2-й ряд | 3-й ряд | 1-й ряд | 2-й ряд | 3-й ряд | 1-й ряд | 2-й ряд | 3-й ряд |
| 0° | 10° | 70° | ||||||
| 0°15′ | 12° | 75° | ||||||
| 0°30′ | 15° | 80 | ||||||
| 0º45′ | 18 | 85 | ||||||
| 1° | 20 | 90° | ||||||
| 1°30′ | 22 | 100 | ||||||
| 2 | 25 | 110 | ||||||
| 2°30′ | 30 | 120 | ||||||
| 3 | 35 | 135 | ||||||
| 4 | 40 | 150 | ||||||
| 5 | 5 | 45 | 165 | |||||
| 6 | 50 | 180 | ||||||
| 7 | 55 | 270 | ||||||
| 8 | 60 | 360 | ||||||
| 9 | 65 |
Таблица не распространяется на угловые размеры конусов.
При выборе углов 1-й ряд следует предпочитать 2-му, а 2-й — 3-му.
Практическое применение
У школьников часто возникает вопрос о том, зачем учить, как рассчитывать объем разных геометрических тел, в том числе конуса.
А инженеры-конструкторы постоянно сталкиваются с необходимостью рассчитать объем конических частей деталей механизмов. Это наконечники сверл, части токарных и фрезерных станков. Форма конуса позволят сверлам легко входить в материал, не требуя первоначальной наметки специальным инструментом.
Объем конуса имеет куча песка или земли, высыпанная на землю. При необходимости, проведя несложные измерения, можно рассчитать ее объем. У некоторых вызовет затруднение вопрос о том, как узнать радиус и высоту кучи песка. Вооружившись рулеткой, измеряем окружность холмика C. По формуле R=C/2n узнаем радиус. Перекинув веревку (рулетку) через вершину, находим длину образующей. А вычислить высоту по теореме Пифагора и объем не составит труда. Конечно, такой расчет приблизителен, но позволяет определить, не обманули вас, привезя тонну песка вместо куба.
Некоторые здания имеют форму усеченного конуса. Например, Останкинская телебашня приближается к форме конуса. Ее можно представить состоящей из двух конусов, поставленных друг на друга. Купола старинных замков и соборов представляют собой конус, объем которого древние зодчие рассчитывали с удивительной точностью.
Если внимательно присмотреться к окружающим предметам, то многие из них являются конусами:
- воронки-лейки для наливания жидкостей;
- рупор-громкоговоритель;
- парковочные конусы;
- абажур для торшера;
- привычная новогодняя елочка;
- духовые музыкальные инструменты.
Как видно из приведенных примеров, умение рассчитать объем конуса, площадь его поверхности необходимо в профессиональной и повседневной жизни. Надеемся, что статья придет вам на помощь.
Нормальные конусности и углы конусов (по ГОСТ 8593-81)
Стандарт распространяется на конусности и углы конусов гладких конических элементов деталей.
C = (D — d) / L = 2tg(α/2)
| Обозначение конуса | КонусностьC | Угол конуса α | Угол уклона α / 2 | ||||
| ряд 1 | ряд 2 | утл.ед. | рад | утл.ед. | рад | ||
| 1 : 500 | 1 : 500 | 0,0020000 | 6’52,5″ | 0,0000 | 3’26,25″ | 0,0010000 | |
| 1 :200 | 1 : 200 | 0,0050000 | 1711,3″ | 0,0050000 | 8’35,55″ | 0,0025000 | |
| 1 : 100 | 1 : 100 | 0,0100000 | 34’22,6″ | 0,0100000 | 17’11,3» | 0,0050000 | |
| 1 : 50 | 1 : 50 | 0,0200000 | 1°8’45,2″ | 0,0199996 | 34’22,6″ | 0,0099998 | |
| 1 : 30 | 1 :30 | 0,0333333 | 1°54’31,9″ | 0,0333304 | 57’17,45″ | 0,0166652 | |
| 1 : 20 | 1 :20 | 0,0500000 | 2°51’51,1» | 0,0499896 | 1°25’55,55″ | 0,0249948 | |
| 1 : 15 | 1 : 15 | 0,0666667 | 3°49’5,9″ | 0,0666420 | 1°54’32,95″ | 0,0333210 | |
| 1 : 12 | 1 : 12 | 0,0833333 | 4°4618,8″ | 0,0832852 | 2°23’19,4″ | 0,0416426 | |
| 1 : 10 | 1 : 10 | 0,1000000 | 5°43’29,3″ | 0,0999168 | 2°5144,65″ | 0,0499584 | |
| 1 : 8 | 1 : 8 | 0,1250000 | 7°9’9,6″ | 0,1248376 | 3°34’34,8″ | 0,0624188 | |
| 1 : 7 | 1 :7 | 0,1428571 | 8°10’16,4″ | 0,1426148 | 4°5’8,2″ | 0,0713074 | |
| 1 : 6 | 1 :6 | 0,1666667 | 9°31’38,2″ | 0,1662824 | 4°45’49,1» | 0,0831412 | |
| 1 : 5 | 1 :5 | 0,2000000 | 11°25’16,3″ | 0,1993374 | 5º42’38,15″ | 0,0996687 | |
| 1 : 4 | 1 : 4 | 0,2500000 | 14°15’0,1» | 0,2487100 | 7°7’30,05″ | 0,1243550 | |
| 1 : 3 | 1 : 3 | 0,3333333 | 18°55’28,7″ | 0,3302972 | 9°27’44,35″ | 0,1651486 | |
| 30° | 1:1,866025 | 0,5358985 | 30° | 0,5235988 | 15° | 0,2617994 | |
| 45е | 1:1,207107 | 0,8284269 | 45° | 0,7853982 | 22°30′ | 0,3926991 | |
| 60° | 1:0,866025 | 1,1547010 | 60° | 1,0471976 | 30° | 0,5235988 | |
| 75° | 1:0,651613 | 1,5346532 | 75° | 1,3089970 | 37°30′ | 0,6544985 | |
| 90° | 1:0,500000 | 2,0000000 | 90° | 1,5707964 | 45° | 0,7853982 | |
| 120° | 1:0,288675 | 3,4641032 | 120° | 2,0943952 | 60° | 1,0471976 | |
Примечание.
Значения конусности или угла конуса, указанные в графе «Обозначение конуса», приняты за исходные при расчете других значений, приведенных в таблице.
При выборе конусностей или углов конусов ряд 1 следует предпочитать ряду 2.
Обозначение конусности на чертеже
При создании технической документации должны учитываться все установленные стандарты, так как в противном случае она не может быть использована в дальнейшем. Рассматривая обозначение конусности на чертежах следует уделить внимание следующим моментам:
- Отображается диаметр большого основания. Рассматриваемая фигура образуется телом вращения, которому свойственен диаметральный показатель. В случае конуса их может быть несколько, а изменение показателя происходит плавно, не ступенчато. Как правило, у подобной фигуры есть больший диаметр, а также промежуточной в случае наличия ступени.
- Наносится диаметр меньшего основания. Меньшее основание отвечает за образование требуемого угла.
- Рассчитывается длина конуса.
 Расстояние между меньшим и большим основанием является показателем длины.
Расстояние между меньшим и большим основанием является показателем длины. - На основании построенного изображения определяется угол. Как правило, для этого проводятся соответствующие расчеты. В случае определения размера по нанесенному изображению при применении специального измерительного прибора существенно снижается точность. Второй метод применяется в случае создания чертежа для производства неответственных деталей.
Простейшее обозначение конусности предусматривает также отображения дополнительных размеров, к примеру, справочную. В некоторых случаях применяется знак конусности, который позволяет сразу понят о разности диаметров.
Выделяют достаточно большое количество различных стандартов, которые касаются обозначения конусности. К особенностям отнесем следующее:
- Угол может указываться в градусах дробью или в процентах. Выбор проводится в зависимости от области применения чертежа. Примером можно назвать то, что в машиностроительной области указывается значение градуса.

- В машиностроительной области в особую группу выделяют понятие нормальной конусности. Она варьирует в определенном диапазоне, может составлять 30, 45, 60, 75, 90, 120°. Подобные показатели свойственны большинству изделий, которые применяются при сборке различных механизмов. При этом выдержать подобные значения намного проще при применении токарного оборудования. Однако, при необходимости могут выдерживаться и неточные углы, все зависит от конкретного случая.
- При начертании основных размеров применяется чертежный шрифт. Он характеризуется довольно большим количеством особенностей, которые должны учитываться. Для правильного отображения используется табличная информация.
- Для начала указывается значок конусности от которого отводится стрелка и отображается величина. Особенности отображения во многом зависит от того, какой чертеж. В некоторых случаях наносится большое количество различных размеров, что существенно усложняет нанесение конусности. Именно поэтому предусмотрена возможность использования нескольких различных методов отображения подобной информации.

На чертеже рассматриваемый показатель обозначается в виде треугольника. При этом требуется цифровое значение, которое может рассчитываться при применении различных формул.
Конусность наружных и внутренних конусов с резьбовым отверстием
| Обозначение величины конуса | Конусность | Угол конуса 2α |
| В7 | 1 : 19,212 = 0,05205 | 2°58’54» |
| B10; B12 | 1 : 20,047 = 0,4988 | 2°51’26» |
| В16; В18 | 1 : 20, = 0,04995 | 2°51’41» |
| В22; В24 | 1 : 19,922 = 0,05020 | 2°52’32» |
| В32 | 1 : 19,954 = 0,05194 | 2º58’31» |
| В45 | 1 : 19,002 = 0,05263 | 3°00’53» |
Угол конуса 2α подсчитан по величине конусности с округлением 1»
Рекомендуемые размеры центрового отверстия укороченного конуса
Размеры, мм
Центровые отверстия для конусов Морзе В12, В18, В24 и В45 — формы Р по ГОСТ 14034-74. Допускается изготовление центрового отверстия с размерами, указанными в таблице.
Допускается изготовление центрового отверстия с размерами, указанными в таблице.
| Обозначение конуса Морзе | d2 | d3 | d4 | L |
| В12 | М6 | 8,0 | 8,5 | 16 |
| В18 | М10 | 12,5 | 13,2 | 24 |
| В24 | М12 | 15,0 | 17,0 | 28 |
| В32 В45 | М16 М20 | 20,0 26,0 | 22,0 30,0 | 32 40 |
Capto
Конус Capto
, разработанный компанией
Sandvik Coromant
, сегодня продвигается как аналог HSK премиум-класса. С 2008 года посадка Capto вошла в международный стандарт
ISO 26623
.
В сечении он представляет собой треугольник со скругленными краями и выгнутыми сторонами. Угол поверхности посадки взят аналогично конусу Морзе.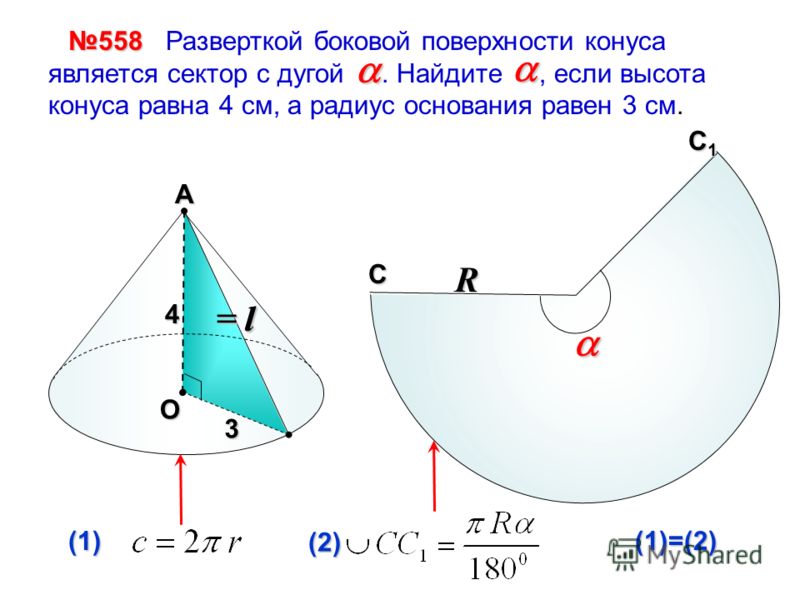 Такая форма не позволяет конусу провернуться в гнезде, обеспечивает необходимое самозаклинивание и повторяемость при разборке-сборке по всем осям. Понятно, что с одной стороны базирование на треугольник более предпочтительно ввиду гораздо большей жесткости передачи. Однако технология изготовления такого конуса несколько сложнее и следовательно дороже для конечного потребителя. При всей своей премиумной цене логически обоснованным является применение Capto для черновой, получерновой обработки.
Такая форма не позволяет конусу провернуться в гнезде, обеспечивает необходимое самозаклинивание и повторяемость при разборке-сборке по всем осям. Понятно, что с одной стороны базирование на треугольник более предпочтительно ввиду гораздо большей жесткости передачи. Однако технология изготовления такого конуса несколько сложнее и следовательно дороже для конечного потребителя. При всей своей премиумной цене логически обоснованным является применение Capto для черновой, получерновой обработки.
Главное преимущество посадки Capto по отношению к другим посадкам — жесткость соединения. Некоторые производители станков, проверив на практике возможности интерфейса Capto, стали интегрировать его в базовый шпиндель станка (WFL, Mazak). В зависимости от размера соединения Capto обозначаются C3..C10. Существуют следующие типоразмеры интерфейса (указан диаметр фланца):
- С3 — 32мм
- С4 — 40мм
- С5 — 50мм
- С6 — 63мм
- С8 — 80мм
- С10 — 100мм
При всей своей привлекательности этот конус не отвечает требованию концентрации износа.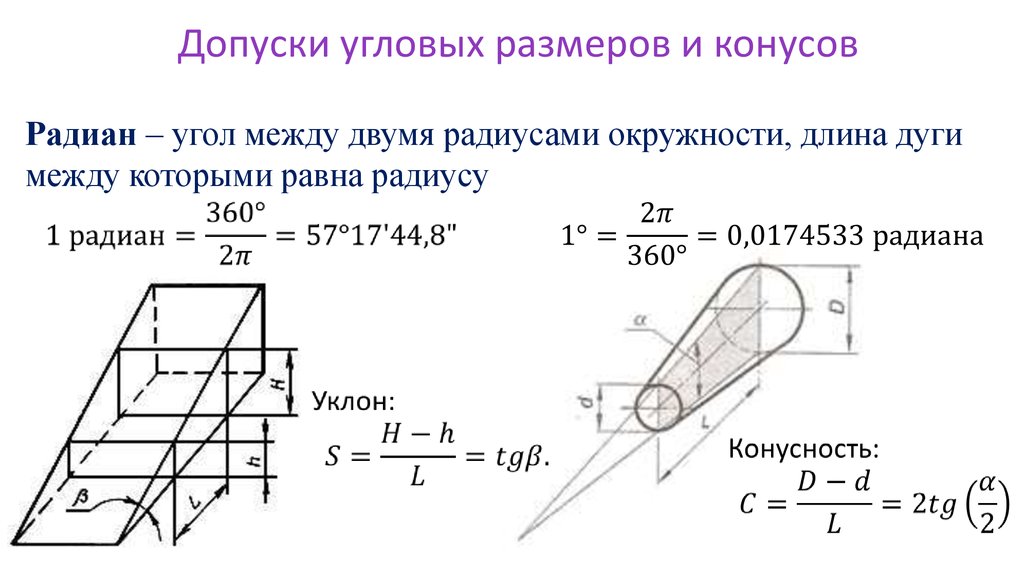 (То есть при превышении нагрузки на шпиндель — сгорит шпиндель, но Capto не провернется)
(То есть при превышении нагрузки на шпиндель — сгорит шпиндель, но Capto не провернется)
Размеры, мм
Внутренние конусы
Для конусов с лапкой
Для конусов с резьбовым отверстием
| Конус | Метрический | Морзе | Метрический | |||||||||||
| Обозначение конуса | 4 | 6 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 80 | 100 | 120 | 160 | 200 |
| Конусность | 1 : 20 = 0,05 | 1 : 19,212 = 0,05205 | 1 : 20,047 = 0,04988 | 1 : 20,020 = 0,04995 | 1 : 19,922 = 0,05 | 1 : 19,254 = 0,05194 | 1 : 19,002 = 0,05263 | 1 : 19,180 = 0,05214 | 1 : 20 = 0,05 | |||||
| D | 4 | 6 | 9,045 | 12,065 | 17,780 | 23,825 | 31,267 | 44,399 | 63,348 | 80 | 100 | 120 | 160 | 200 |
| d5 | 3 | 4,6 | 6,7 | 9,7 | 14,9 | 20,2 | 26,5 | 38,2 | 54,6 | 71,5 | 90 | 108,5 | 145,5 | 182,5 |
| d6 | — | — | — | 7 | 11,5 | 14 | 18 | 23 | 27 | 33 | 39 | 52 | ||
| l5 min | 25 | 34 | 52 | 56 | 67 | 84 | 107 | 135 | 188 | 202 | 240 | 276 | 350 | 424 |
| l6 | 21 | 29 | 49 | 52 | 62 | 78 | 98 | 125 | 177 | 186 | 220 | 254 | 321 | 388 |
| g | 2,2 | 3,2 | 3,9 | 5,2 | 6,3 | 7,9 | 11,9 | 15,9 | 19 | 26 | 32 | 38 | 50 | 62 |
| h | 8 | 12 | 15 | 19 | 22 | 27 | 32 | 38 | 47 | 52 | 60 | 70 | 90 | 110 |
1.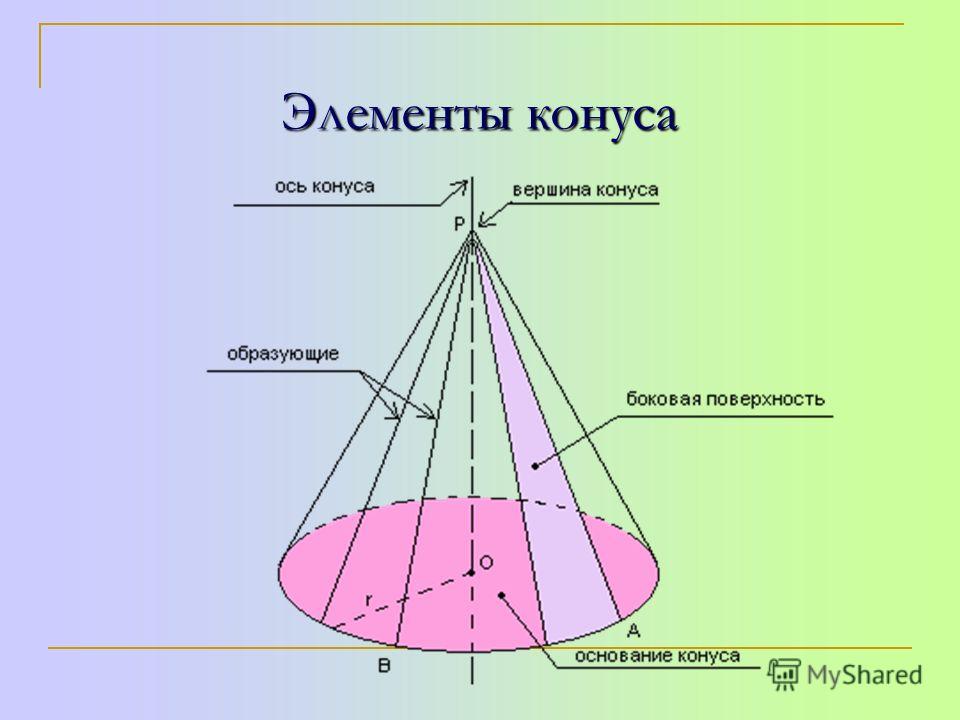 ГОСТ предусматривает размеры и для конусов инструментальных наружных.
ГОСТ предусматривает размеры и для конусов инструментальных наружных.
2. Предельные отклонения размеров конусов и допуски формы по ГОСТ 2848-75.
Как подобрать угол уклона — несколько возможных вариантов
Гост 30893.2-2002. основные нормы взаимозаменяемости. общие допуски. допуски формы и расположения поверхностей, не указанные индивидуально
Существует несколько позиций, которыми руководствуются домашние мастера:
- Сделать угол как можно более острым;
- Сделать уклон минимальным или вообще пропустить этот пункт при монтаже канализационных стоков;
- Создавать наклон согласно СНиПам, ГОСТам или специализированным справочникам.
На первый взгляд, излишне острый уклон канализационной трубы поможет воде, требующей очистки, быстрее доходить до пункта назначения. Но с другой стороны, при этом труба подвергается вредному воздействию стоков. Из-за того, что вода проходит по канализации слишком быстро, твердые частицы нечистот, пищевые остатки и прочий мусор, часто сливаемый в унитаз, остаются в трубе. Поэтому максимальный уклон трубы жестко регламентирован. Забегая вперед скажу, что он равен 15 см на 1 метр погонный.
Поэтому максимальный уклон трубы жестко регламентирован. Забегая вперед скажу, что он равен 15 см на 1 метр погонный.
Также проблемой станет заиливание трубы. Со временем канализация забьется и придется работать над её ремонтом. Срок службы такой системы значительно короче стандартного и составляет менее года.
Минимальный уклон или его отсутствие – это грубейшая ошибка при установке канализационного трубопровода. При этом труба не только заиливается, но и практически не очищается естественным путем.
Совет от эксперта: Правильнее всего работать с определенными нормативами, в которых указывается соотношение угла с диаметром и длиной трубы. Конечно, для этого требуется много времени и особая внимательность, но зато после такой кропотливой работы канализация прослужит Вам долгие годы.
Конусы внутренние и наружные конусностью 7 : 24 (по ГОСТ 15945-82)
Размеры, мм
Пример обозначения конуса 25:
Конус 25 ГОСТ 15945-82
| Обозначение конуса | D | L* (справочный) |
| 10 | 15,87 | 21,8 |
| 15 | 19,05 | 26,9 |
| 25 | 25,40 | 39,8 |
| 30 | 31,75 | 49,2 |
| 35 | 38,10 | 57,2 |
| 40 | 44,45 | 65,6 |
| 45 | 57,15 | 84,8 |
| 50 | 69,85 | 103,7 |
| 55 | 88,90 | 131,6 |
| 60 | 107,95 | 163,7 |
| 65 | 133,35 | 200,0 |
| 70 | 165,10 | 247,5 |
| 75 | 203,20 | 305,8 |
| 80 | 254,00 | 390,8 |
Размеры и допуски углов наружных и внутренних конусов
* Размер для справок.
** Z — базорасстояние конуса задается в стандартах на конкретную продукцию
1 — основная плоскость; 2 — базовая плоскость
| Обозначения конусов | D | d | Lрасч | Допуск угла, мкм, конуса ATDпо ГОСТ 8908 | ||||
| 3 | 4 | 5 | 6 | 7 | ||||
| 30 | 31,75 | 17,750 | 48 | 2,5 | 4 | 6 | 10 | 15 |
| 35 | 38,10 | 21,767 | 56 | 2,5 | 4 | 6 | 10 | 15 |
| 40 | 44,45 | 25,492 | 65 | 3,0 | 5 | 8 | 12 | 20 |
| 45 | 57,15 | 32,942 | 83 | 3,0 | 5 | 8 | 12 | 20 |
| 50 | 69,85 | 40,100 | 102 | 4,0 | 6 | 10 | 16 | 25 |
| 55 | 88,90 | 54,858 | 127 | 4,0 | 6 | 10 | 16 | 25 |
| 60 | 107,95 | 60,700 | 162 | 5,0 | 8 | 12 | 20 | 30 |
| 65 | 133,35 | 74,433 | 202 | 5,0 | 8 | 12 | 20 | 30 |
| 70 | 165,10 | 92,183 | 250 | 6,0 | 10 | 16 | 25 | 40 |
| 75 | 203,20 | 113,658 | 307 | 6,0 | 10 | 16 | 25 | 40 |
| 80 | 254,00 | 138,208 | 394 | 8,0 | 12 | 20 | 30 | 50 |
Условное обозначение конусов по ГОСТ 15945 с добавлением степени точности конуса:
Конус 50 АТ5 ГОСТ 15945-82
Предельные отклонения базорасстояния конуса Z следует выбирать из ряда: ± 0,4; ± 0,2; ± 0,1; ± 0,05мм.
Продолжение табл. 10
Как выбрать уклон
Гост 24705-2004 (исо 724:1993) основные нормы взаимозаменяемости. резьба метрическая. основные размеры
Чтобы определить какой должен быть минимальный уклон трубы, который будет оптимальным для Вас, нужно знать длину всей канализационной системы. В справочниках используются данные сразу в готовом виде, их изображают в сотых частях целого числа. Некоторым работникам сложно ориентироваться в такой информации без объяснений. Например, информация в справочниках представлена вот в таком виде как на рисунках ниже:
Таблица: необходимые уклоны и диаметры труб для слива
Таблица: уклоны отводных труб в квартире
Минимальный и максимальный уклон канализации на 1 метр погонный по СНиПу
Ниже представлена картинка, на которой показаны, минимальные уклоны в зависимости от диаметра на 1 метр погонный трубы. Например, мы видим, что для трубы диаметром 110 — угол уклона 20 мм, а для диаметра 160 мм — уже 8 мм и так далее. Запомните правило: чем больше диаметр трубы, тем меньше угол уклона.
Запомните правило: чем больше диаметр трубы, тем меньше угол уклона.
Примеры минимальных уклонов канализации на 1 метр по СНиП в зависимости от диаметра трубы
Например, уклон для трубы диаметром до 50 мм и длиною 1 метр нужен 0,03 м. Как это определили? 0,03 – это соотношение высоты уклона к длине трубы.
Важно: Максимальный уклон для канализационных труб не должен превышать 15 см на 1 метр (0,15). Исключением являются участки трубопроводов, длина которых меньше 1,5 метра
Другими словами, наш уклон всегда лежит в диапазоне от минимального (представленного на картинке выше) до 15 см (максимального).
Уклон канализационной трубы 110 мм для наружной канализации
Предположим, нужно рассчитать оптимальный уклон для распространенной трубы 110 мм, которая используется в основном в системах наружной канализации. Согласно ГОСТ уклон для трубы диаметром 110 мм составляет 0,02 м на 1 метр погонный.
Чтобы рассчитать общий угол, нужно длину трубы умножить на уклон, указанный в СНиП или ГОСТ.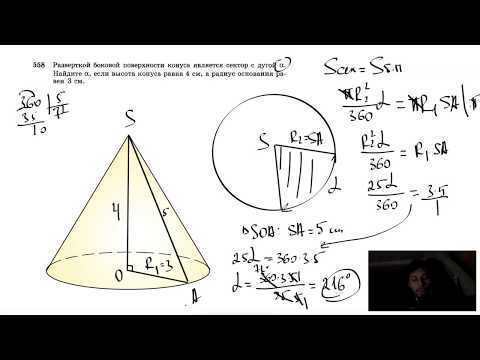 Получится: 10 м (длина канализационной системы) * 0,02 = 0,2 м или 20 см. Значит разница между уровнем установки первой точки трубы и последней – 20 см.
Получится: 10 м (длина канализационной системы) * 0,02 = 0,2 м или 20 см. Значит разница между уровнем установки первой точки трубы и последней – 20 см.
Калькулятор расчет уклона канализации для частного дома
Предлагаю вам протестировать онлайн калькулятор расчета уклона канализационных труб для частного дома. Все расчеты носят примерный характер.
| Диаметр трубы | 50мм110мм160мм200мм | Рассчитанный уклон:— Рекомендуемый уклон: |
| Выход из доманиже уровня земли | на глубине см | |
| Глубина входа трубы в септик или центральную канализацию | см | |
| Расстояние до септикат.е. длина трубы | м |
Под диаметром трубы понимается диаметр трубы, которая ведет сразу в сливную яму или общую систему канализацию (не путать с фановой).
Расчет угла конуса по диаметру – ЕГАИС
При проведении инженерных и других расчетах, а также работе с инженерной графикой и создании чертежей приходится создавать уклон.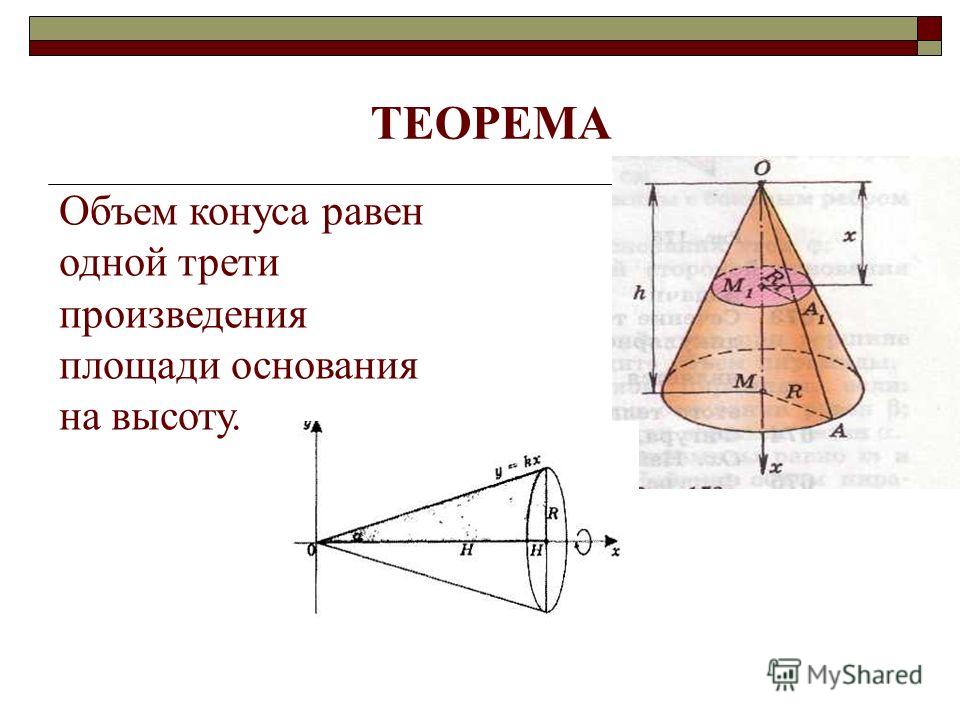
Конусность получила весьма широкое распространение, она применяется при изготовлении самых различных деталей.
Показатель конусности рассчитывается в большинстве случаев при создании деталей, которые получили широкое распространение в сфере машиностроения. Рассмотрим основные параметры, особенности начертания и многие другие моменты подробнее.
Значение конусности
Рассматривая конусность следует учитывать, что этот показатель напрямую связан с уклоном. Этот параметр определяет отклонение прямой лини от вертикального ил горизонтального положения. При этом конусность 1:3 или конусность 1:16 существенно отличается. Определение уклона характеризуется следующими особенностями:
Стоит учитывать, что нормальные конусности несколько отличаются от рассматриваемого ранее параметра. Это связано с тем, что конусностью называется соотношение диаметра основания к высоте.
Рассчитать этот показатель можно самым различным образом, наибольшее распространение получила формула K=D/h.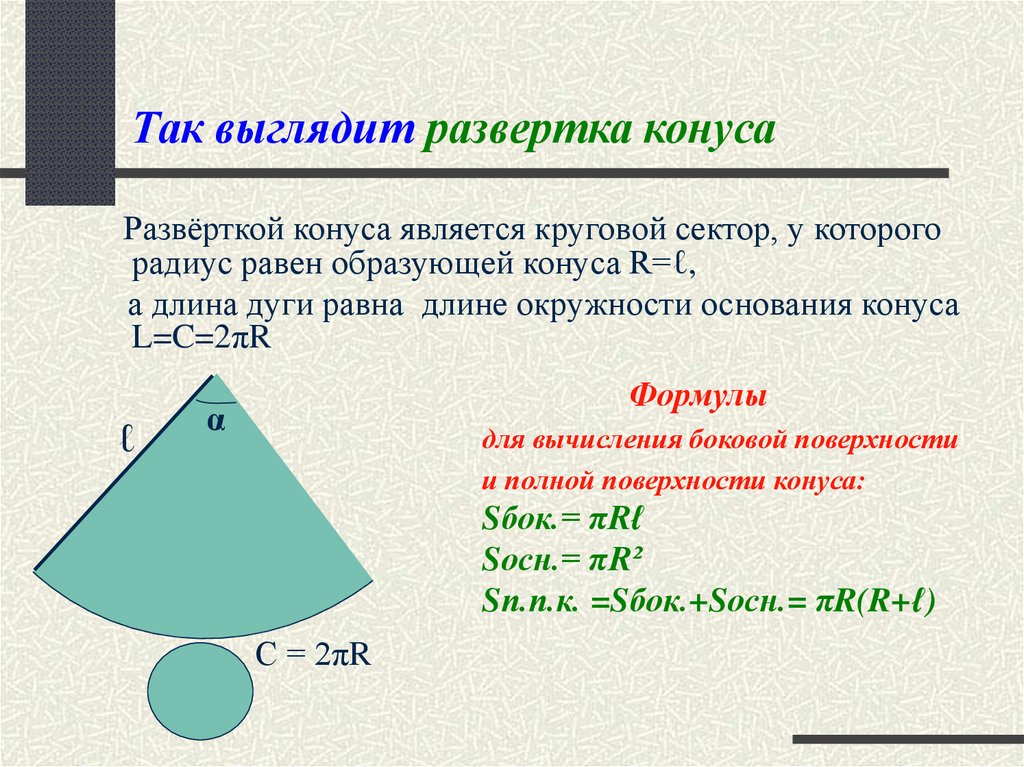 В некоторых случаях обозначение проводится в процентах, так как этот переменный показатель применяется для определения всех других параметров.
В некоторых случаях обозначение проводится в процентах, так как этот переменный показатель применяется для определения всех других параметров.
Рассматривая конусность 1:7 и другой показатель следует также учитывать особенности отображения информации на чертеже. Чаще всего подобное отображение проводится при создании технической документации в машиностроительной области.
Обозначение конусности на чертеже
При создании технической документации должны учитываться все установленные стандарты, так как в противном случае она не может быть использована в дальнейшем. Рассматривая обозначение конусности на чертежах следует уделить внимание следующим моментам:
Простейшее обозначение конусности предусматривает также отображения дополнительных размеров, к примеру, справочную. В некоторых случаях применяется знак конусности, который позволяет сразу понят о разности диаметров.
Выделяют достаточно большое количество различных стандартов, которые касаются обозначения конусности. К особенностям отнесем следующее:
К особенностям отнесем следующее:
На чертеже рассматриваемый показатель обозначается в виде треугольника. При этом требуется цифровое значение, которое может рассчитываться при применении различных формул.
Формула для определения конусности
Провести самостоятельно расчет конусности можно при применении различных формул. Стоит учитывать, что в большинстве случаев показатель указывается в градусах, но может и в процентах – все зависит от конкретного случая. Алгоритм проведения расчетов выглядит следующим образом:
На чертеже вычисления не отображаются. Как правило, для этого создается дополнительная пояснительная записка. Вычислить основные параметры довольно просто, в некоторых случаях проводится построение чертежа, после чего измеряется значение угла и другие показатели.
Угол конуса
Важным показателем при построении различных чертежей считается угол конуса. Он определяется соотношение большого диаметра к меньшему. Высчитывается этот показатель по следующим причинам:
Как ранее было отмечено, в машиностроительной области показатель стандартизирован.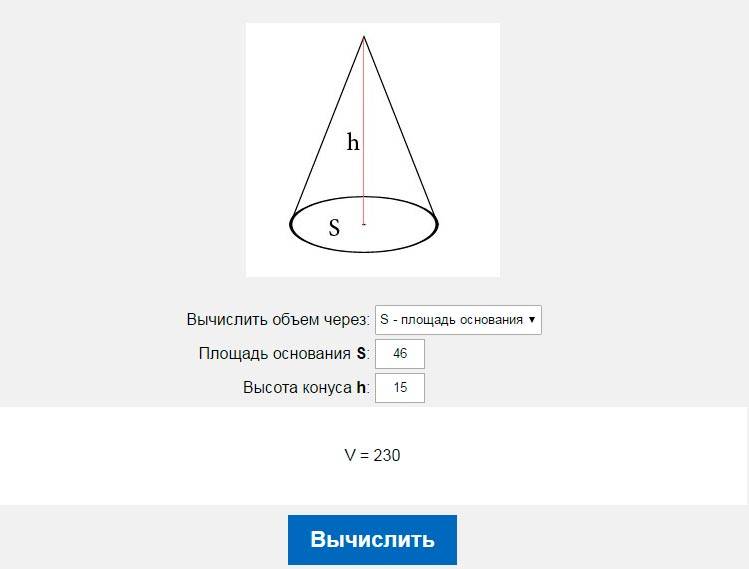 В другой области значение может существенно отличаться от установленных стандартов. Некоторые изделия характеризуются ступенчатым расположение поверхностей. В этом случае провести расчеты достаточно сложно, так как есть промежуточный диаметр.
В другой области значение может существенно отличаться от установленных стандартов. Некоторые изделия характеризуются ступенчатым расположение поверхностей. В этом случае провести расчеты достаточно сложно, так как есть промежуточный диаметр.
Что такое уклон?
Как ранее было отмечено, довольно важным показателем можно считать уклон. Он представлен линией, которая расположена под углом к горизонту. Если рассматривать конусность на чертеже, то она представлена сочетанием двух разнонаправленных уклонов, которые объединены между собой.
Понятие уклона получило весьма широкое распространение. В большинстве случаев для его отображения проводится построение треугольника с определенным углом.
Две вспомогательные стороны применяются для расчета угла, которые и определяет особенности наклона основной поверхности.
Как определить уклон
Для определения уклона достаточно воспользоваться всего одной формулой. Как ранее было отмечено, существенно упростить задачу можно при построении прямоугольного треугольника. Среди особенностей подобной работы отметим следующие моменты:
Среди особенностей подобной работы отметим следующие моменты:
Формула, которая требуется для вычисления рассматриваемого показателя указывалась выше. Стоит учитывать, что полученный показатель также переводится в градусы.
Особенности построения уклона и конусности
Область черчения развивалась на протяжении достаточно длительного периода. Она уже много столетий назад применялась для передачи накопленных знаний и навыков. Сегодня изготовление всех изделия может проводится исключительно при применении чертежей.
При этом ему больше всего внимания уделяется при наладке массового производства. За длительный период развития черчения были разработаны стандарты, которые позволяют существенно повысить степень читаемости всей информации. Примером можно назвать ГОСТ 8593-81.
Он во многом характеризует конусность и уклон, применяемые методы для их отображения. Начертательная геометрия применяется для изучения современной науки, а также создания различной техники.
Кроме этого, были разработаны самые различные таблицы соответствия, которые могут применяться при проведении непосредственных расчетов.
Различные понятия, к примеру, сопряжение, уклон и конусность отображаются определенным образом. При этом учитывается область применения разрабатываемой технической документации и многие другие моменты.
К особенностям построения угла и конусности можно отнести следующие моменты:
В целом можно сказать, что основные стандарты учитываются специалистом при непосредственном проведении работы по построению чертежа.
Часто для отображения уклона в начертательной геометрии создаются дополнительные линии, а также обозначается угол уклона.
В проектной документации, в которой зачастую отображается конусность, при необходимости дополнительная информация выводится в отдельную таблицу.
Построение уклона и конусности
Провести построение уклона и конусности достаточно просто, только в некоторых случаях могут возникнуть серьезные проблемы. Среди основных рекомендаций отметим следующее:
На сегодняшний день, когда компьютеры получили весьма широкое распространение, отображение чертежей также проводится при применении специальных программ.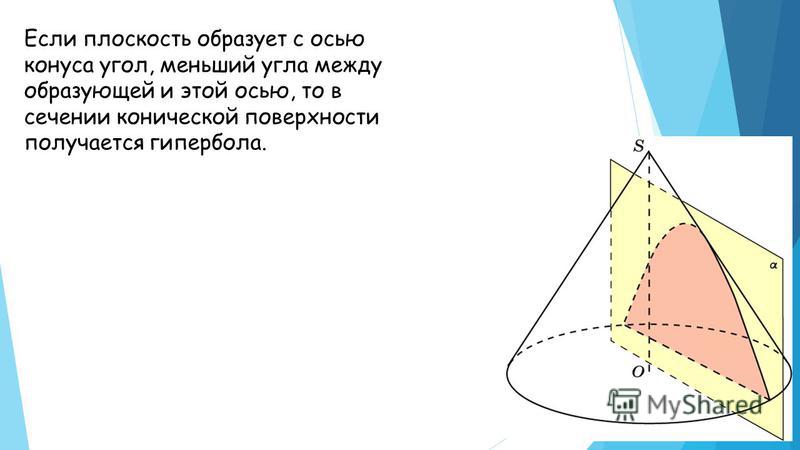 Их преимуществами можно назвать следующее:
Их преимуществами можно назвать следующее:
Процедура построения при применении подобных программ характеризуется достаточно большим количеством особенностей, которые нужно учитывать. Основными можно назвать следующее:
Есть несколько распространенных программ, которые могут применяться для построения самых различных фигур. Их применение на сегодняшний день считается стандартом.
Для работы требуются определенные навыки, а также знание установленных норм по отображению различных плоскостей и размеров.
Не стоит забывать о том, что рассматриваемое программное обеспечение является лишь инструментом, вся работа выполняется инженером.
Понятие конусности встречается в достаточно большом количестве различной технической литературы. Примером можно назвать машиностроительную область, в которой распространены конусные валы и другие изделия. На практике производство подобных изделий может создавать довольно большое количество проблем, так как выдерживать заданный угол не просто.
Источник
Формула расчета угла конуса
| Элементы конуса | Расчетные формулы | Элементы конуса | Расчетные формулы |
| K | K = (D-d)/ l K = 2tga | D | D = K× l + d D = 2× l×tga + d |
| a | tga = (D-d)/ 2l tga = K / 2 | d | d = D — 2× l×tga d = D — K× l |
Угол a вычисляют по тригонометрической функции тангенса.
Нормальные конические поверхности должны быть изготовлены по стандартным размерам, некоторые из которых указаны в табл.4.
Кроме этих поверхностей, различают также конусы Морзе и метрические конусы. Наружные конусы Морзе выполняют на хвостовой части сверл (см. рис.6), зенкеров, разверток, центров, а внутренние конусы — в отверстиях шпинделей, оправок, переходных втулок, в которые эти инструменты устанавливают.
Существуют семь номеров конусов Морзе (от до 6) со своими размерами и углами наклона a.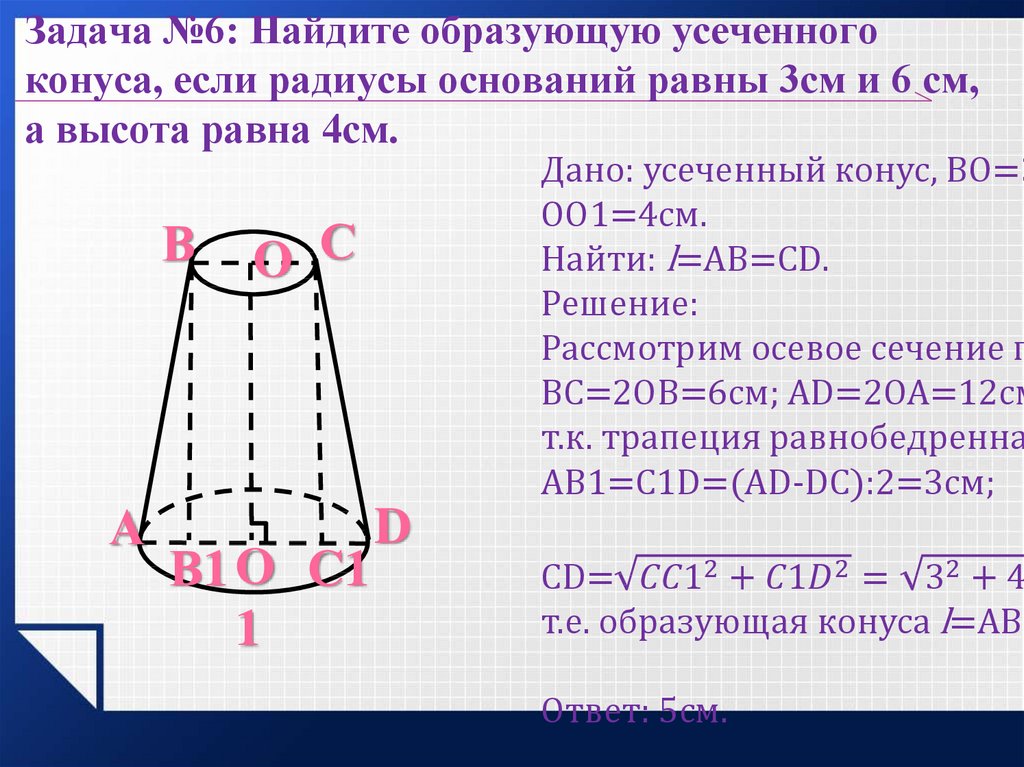 Наименьшим является конус Морзе (1:19,212), наибольшим — конус Морзе 6 (1:19,18). Их размеры приведены в стандарте СТ СЭВ 147-75.
Наименьшим является конус Морзе (1:19,212), наибольшим — конус Морзе 6 (1:19,18). Их размеры приведены в стандарте СТ СЭВ 147-75.
Недостатком конусов Морзе следует считать разные углы наклона a у различных номеров.
Таблица 4
Стандартные размеры конусов деталей
| Конусность K | Угол конуса 2a | Угол наклона a | Обозначение конусности |
| 1:100 1:50 1:20 1:10 1:3 1:1,866 1:1,207 1:0,866 | 0 0 34¢23² 1 0 8¢45² 2 0 51¢51² 5 0 43¢29² 18 0 55¢30² 30 0 45 0 60 0 | 0 0 17¢12² 0 0 34¢23² 1 0 25¢56² 2 0 51¢45² 9 0 27¢45² 15 0 22 0 30¢ 30 0 | 1:100 1:50 1:20 1:10 1:3 30 0 45 0 60 0 |
Метрические конусы 4, 6, 80, 100, 120, 160, 200 (см. тот же стандарт) имеют одинаковую конусность 1:20 (и угол a), а номер конуса обозначает размер диаметра большого основания.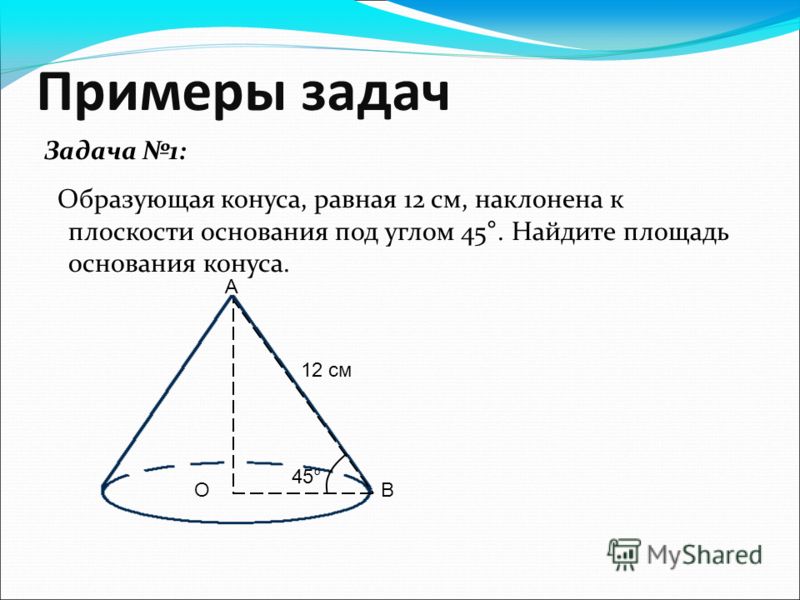
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Да какие ж вы математики, если запаролиться нормально не можете. 8406 — | 7319 — или читать все.
188.64.173.93 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock! и обновите страницу (F5)очень нужно
Угол раствора и радиус конуса
Угол раствора и радиус конуса способствуют вычислению всех возможных параметров конуса за счет двух треугольников, которые они образуют.
Первый треугольник – равнобедренный, с двумя образующими и диаметром конуса, из которого можно рассчитать угол наклона конуса, между образующей и основанием.
Второй треугольник – прямоугольный с высотой и радиусом в качестве катетов и образующей конуса, как гипотенузой. (рис. 40.2, 40.1) β=(180°-α)/2 h=r tanβ l=r/cosβ
Зная радиус конуса, можно сразу найти его диаметр, а также периметр основания и площадь, не прибегая к дополнительным заменам.
3 tanβ)/3
Радиус сферы вписанной в конус зависит только от радиус и угла наклона, а радиус сферы описанной вокруг конуса можно найти через угол раствора конуса и радиус основания. (рис.40.3, 40.4) r_1=r tan〖β/2〗 R=r/sinα
Уклон и Конусность
Иногда, в задачах по начертательной геометрии или работах по инженерной графике, или при выполнении других чертежей, требуется построить уклон и конус. В этой статье Вы узнаете о том, что такое уклон и конусность, как их построить, как правильно обозначить на чертеже.
Что такое уклон? Как определить уклон? Как построить уклон? Обозначение уклона на чертежах по ГОСТ
Уклон. Уклон это отклонение прямой линии от вертикального или горизонтального положения. Определение уклона. Уклон определяется как отношение противолежащего катета угла прямоугольного треугольника к прилежащему катету, то есть он выражается тангенсом угла а. Уклон можно посчитать по формуле i=AC/AB=tga.
Построение уклона.
На примере (рисунок ) наглядно продемонстрировано построение уклона. Для построения уклона 1:1, например, нужно на сторонах прямого угла отложить произвольные, но равные отрезки.
Такой уклон, будет соответствовать углу в 45 градусов. Для того чтобы построить уклон 1:2, нужно по горизонтали отложить отрезок равный по значению двум отрезкам отложенным по вертикали.
Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а.
Обозначение уклона на чертежах. Обозначение уклонов на чертеже выполняется в соответствии с ГОСТ 2.307—68. На чертеже указывают величину уклона с помощью линии-выноски. На полке линии-выноски наносят знак и величину уклона.
Знак уклона должен соответствовать уклону определяемой линии, то есть одна из прямых знака уклона должна быть горизонтальна, а другая должна быть наклонена в ту же сторону, что и определяемая линия уклона. Угол уклона линии знака примерно 30°.
Что такое конусность? Формула для расчёта конусности. Обозначение конусности на чертежах
Конусность. Конусностью называется отношение диаметра основания конуса к высоте. Конусность рассчитывается по формуле К=D/h, где D – диаметр основания конуса, h – высота. Если конус усеченный, то конусность рассчитывается как отношение разности диаметров усеченного конуса к его высоте. В случае усечённого конуса, формула конусности будет иметь вид: К = (D-d)/h.
Размеры стандартизованных конусов не нужно указывать на чертеже. Достаточно на чертеже привести условное обозначение конусности по соответствующему стандарту.
Конусность, как и уклон, может быть указана в градусах, дробью (простой, в виде отношения двух чисел или десятичной), в процентах. Например, конусность 1:5 может быть также обозначена как отношение 1:5, 11°25’16», десятичной дробью 0,2 и в процентах 20.
Для конусов, которые применяются в машиностроении, OCT/BKC 7652 устанавливает ряд нормальных конусностей.
Нормальные конусности — 1:3; 1:5; 1:8; 1:10; 1:15; 1:20; 1:30; 1:50; 1:100; 1:200. Также в могут быть использованы — 30, 45, 60, 75, 90 и 120°.
Уклон и Конусность — Определение, обозначение на чертеже, формула расчёта уклона и конусности
Иногда, в задачах по начертательной геометрии или работах по инженерной графике, или при выполнении других чертежей, требуется построить уклон и конус. В этой статье Вы узнаете о том, что такое уклон и конусность, как их построить, как правильно обозначить на чертеже.
Что такое уклон? Как определить уклон? Как построить уклон? Обозначение уклона на чертежах по ГОСТ
Уклон. Уклон это отклонение прямой линии от вертикального или горизонтального положения.
Определение уклона. Уклон определяется как отношение противолежащего катета угла прямоугольного треугольника к прилежащему катету, то есть он выражается тангенсом угла а. Уклон можно посчитать по формуле i=AC/AB=tga.Построение уклона.
На примере (рисунок ) наглядно продемонстрировано построение уклона. Для построения уклона 1:1, например, нужно на сторонах прямого угла отложить произвольные, но равные отрезки.
Такой уклон, будет соответствовать углу в 45 градусов. Для того чтобы построить уклон 1:2, нужно по горизонтали отложить отрезок равный по значению двум отрезкам отложенным по вертикали.
Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а.
Обозначение уклона на чертежах. Обозначение уклонов на чертеже выполняется в соответствии с ГОСТ 2.307—68. На чертеже указывают величину уклона с помощью линии-выноски. На полке линии-выноски наносят знак и величину уклона.
Знак уклона должен соответствовать уклону определяемой линии, то есть одна из прямых знака уклона должна быть горизонтальна, а другая должна быть наклонена в ту же сторону, что и определяемая линия уклона. Угол уклона линии знака примерно 30°.
Что такое конусность? Формула для расчёта конусности. Обозначение конусности на чертежах
Конусность. Конусностью называется отношение диаметра основания конуса к высоте. Конусность рассчитывается по формуле К=D/h, где D – диаметр основания конуса, h – высота. Если конус усеченный, то конусность рассчитывается как отношение разности диаметров усеченного конуса к его высоте. В случае усечённого конуса, формула конусности будет иметь вид: К = (D-d)/h.
Обозначение конусности на чертежах.
Форму и величину конуса определяют нанесением трех из перечисленных размеров: 1) диаметр большого основания D; 2) диаметр малого основания d; 3) диаметр в заданном поперечном сечении Ds , имеющем заданное осевое положение Ls; 4) длина конуса L; 5) угол конуса а; 6) конусность с . Также на чертеже допускается указывать и дополнительные размеры, как справочные.
Размеры стандартизованных конусов не нужно указывать на чертеже. Достаточно на чертеже привести условное обозначение конусности по соответствующему стандарту.
Конусность, как и уклон, может быть указана в градусах, дробью (простой, в виде отношения двух чисел или десятичной), в процентах.
Например, конусность 1:5 может быть также обозначена как отношение 1:5, 11°25’16», десятичной дробью 0,2 и в процентах 20.Для конусов, которые применяются в машиностроении, OCT/BKC 7652 устанавливает ряд нормальных конусностей. Нормальные конусности — 1:3; 1:5; 1:8; 1:10; 1:15; 1:20; 1:30; 1:50; 1:100; 1:200. Также в могут быть использованы — 30, 45, 60, 75, 90 и 120°.
Конусность и уклон — построение, расчет, обозначение — значение, формула, как определить, построение
На изображениях конических элементов деталей размеры могут быть проставлены различно: диаметры большего и меньшего оснований усеченного конуса и его длина; угол наклона образующей (или угол конуса) или величина конусности и диаметр основания, длина и т.п.
Уклон
Плоские поверхности деталей, расположенные наклонно, обозначают на чертеже величиной уклона.
Как подсчитать эту величину, покажем на примере. Клин, изображенный на рис. 6.40, я, имеет наклонную поверхность, уклон которой нужно определить. Из размера наибольшей высоты клина вычтем размер наименьшей высоты: 50 – 40 = 10 мм.
Разность между этими величинами можно рассматривать как размер катета прямоугольного треугольника, образовавшегося после проведения на чертеже горизонтальной линии (рис. 6.40, б). Величиной уклона будет отношение размера меньшего катета к размеру горизонтальной линии. В данном случае нужно разделить 10 на 100.
Величина уклона клина будет 1:10.
Рис. 6.40. Определение величины уклона
На чертеже уклоны указывают знаком и отношением двух чисел, например 1:50; 3:5.
Если требуется изобразить на чертеже поверхность определенного уклона, например 3:20, вычерчивают прямоугольный треугольник, у которого один из катетов составляет три единицы длины, а второй – 20 таких же единиц (рис. 6.41).
Рис. 6.
41. Построение уклонов и нанесение их величин
При вычерчивании деталей или при их разметке для построения линии по заданному уклону приходится проводить вспомогательные линии. Например, чтобы провести линию, уклон которой 1:4, через концевую точку вертикальной линии (рис. 6.
42), отрезок прямой линии длиной 10 мм следует принять за единицу длины и отложить на продолжении горизонтальной линии четыре такие единицы (т.е. 40 мм). Затем через крайнее деление и верхнюю точку отрезка провести прямую линию.
Рис. 6.42. Построение линии по заданному уклону
Вершина знака уклона должна быть направлена в сторону наклона поверхности детали. Знак и размерное число располагают параллельно направлению, по отношению к которому задан уклон.
Обозначение конусности на чертеже
При создании технической документации должны учитываться все установленные стандарты, так как в противном случае она не может быть использована в дальнейшем.
Рассматривая обозначение конусности на чертежах следует уделить внимание следующим моментам:
- Отображается диаметр большого основания. Рассматриваемая фигура образуется телом вращения, которому свойственен диаметральный показатель. В случае конуса их может быть несколько, а изменение показателя происходит плавно, не ступенчато. Как правило, у подобной фигуры есть больший диаметр, а также промежуточной в случае наличия ступени.
- Наносится диаметр меньшего основания. Меньшее основание отвечает за образование требуемого угла.
- Рассчитывается длина конуса. Расстояние между меньшим и большим основанием является показателем длины.
- На основании построенного изображения определяется угол. Как правило, для этого проводятся соответствующие расчеты. В случае определения размера по нанесенному изображению при применении специального измерительного прибора существенно снижается точность. Второй метод применяется в случае создания чертежа для производства неответственных деталей.
Простейшее обозначение конусности предусматривает также отображения дополнительных размеров, к примеру, справочную. В некоторых случаях применяется знак конусности, который позволяет сразу понят о разности диаметров.
Выделяют достаточно большое количество различных стандартов, которые касаются обозначения конусности. К особенностям отнесем следующее:
- Угол может указываться в градусах дробью или в процентах. Выбор проводится в зависимости от области применения чертежа. Примером можно назвать то, что в машиностроительной области указывается значение градуса.
- В машиностроительной области в особую группу выделяют понятие нормальной конусности. Она варьирует в определенном диапазоне, может составлять 30, 45, 60, 75, 90, 120°. Подобные показатели свойственны большинству изделий, которые применяются при сборке различных механизмов. При этом выдержать подобные значения намного проще при применении токарного оборудования. Однако, при необходимости могут выдерживаться и неточные углы, все зависит от конкретного случая.
- При начертании основных размеров применяется чертежный шрифт. Он характеризуется довольно большим количеством особенностей, которые должны учитываться. Для правильного отображения используется табличная информация.
- Для начала указывается значок конусности от которого отводится стрелка и отображается величина. Особенности отображения во многом зависит от того, какой чертеж. В некоторых случаях наносится большое количество различных размеров, что существенно усложняет нанесение конусности. Именно поэтому предусмотрена возможность использования нескольких различных методов отображения подобной информации.
На чертеже рассматриваемый показатель обозначается в виде треугольника. При этом требуется цифровое значение, которое может рассчитываться при применении различных формул.
Угол конуса
Важным показателем при построении различных чертежей считается угол конуса. Он определяется соотношение большого диаметра к меньшему. Высчитывается этот показатель по следующим причинам:
- На момент обработки мастер должен учитывать этот показатель, так как он позволяет получить требуемое изделие с высокой точностью размеров.
В большинстве случаев обработка проводится именно при учете угла, а не показателей большого и малого диаметра.
- Угол конуса рассчитывается на момент разработки проекта. Этот показатель наносится на чертеж или отображается в специальной таблице, которая содержит всю необходимую информацию. Оператор станка или мастер не проводит расчеты на месте производства, вся информация должна быть указана в разработанной технологической карте.
- Проверка качества изделия зачастую проводится по малому и большему основанию, но также могут применяться инструменты, по которым определяется показатель конусности.
Как ранее было отмечено, в машиностроительной области показатель стандартизирован. В другой области значение может существенно отличаться от установленных стандартов. Некоторые изделия характеризуются ступенчатым расположение поверхностей. В этом случае провести расчеты достаточно сложно, так как есть промежуточный диаметр.
Построение уклона и конусности
Уклоном называют величину, характеризующую наклон одной прямой линии к другой прямой.
Уклон выражают дробью или в процентах. Уклон / отрезка В С относительно отрезка ВЛ определяют отношением катетов прямоугольного треугольника ЛВС (рисунок 50, а), т. е.
- Для построения прямой ВС (рисунок 50. а) с заданной величиной уклона к горизонтальной прямой, например 1:4, необходимо от точки А влево отложить отрезок АВ, равный четырем единицам длины, а вверх отрезок АС, равный одной единице длины. Точки С и В соединяют прямой, которая даст направление искомого уклона.
- Уклоны применяются при вычерчивании деталей, например, стальных балок и рельсов, изготовляемых на прокатных станах, и некоторых деталей, изготовленных литьем.
При вычерчивании контура детали с уклоном сначала строится линия уклона, а затем контур. Если уклон задается в процентах, например, 20 % (рисунок 50, б)> то линия уклона строится так же, как гипотенуза прямоугольного треугольника. Длину одного из катетов принимают равной 100 %, а другого — 20 %.
Очевидно, что уклон 20 % есть иначе уклон 1:5.
Г1о ГОСТ 2.307—68 перед размерным числом, определяющим уклон, наносят условный знак, острый угол которого должен быть направлен в сторону уклона (рисунок 50, а и б). Подробнее обозначение уклона приведено в разделе 1.7 «Нанесение размеров и предельных отклонений».
Что такое уклон?
Как ранее было отмечено, довольно важным показателем можно считать уклон. Он представлен линией, которая расположена под углом к горизонту. Если рассматривать конусность на чертеже, то она представлена сочетанием двух разнонаправленных уклонов, которые объединены между собой.
Понятие уклона получило весьма широкое распространение. В большинстве случаев для его отображения проводится построение треугольника с определенным углом.
Две вспомогательные стороны применяются для расчета угла, которые и определяет особенности наклона основной поверхности.
Как определить уклон
Для определения уклона достаточно воспользоваться всего одной формулой. Как ранее было отмечено, существенно упростить задачу можно при построении прямоугольного треугольника.
Среди особенностей подобной работы отметим следующие моменты:
- Определяется начальная и конечная точка отрезка. В случае построения сложной фигуры она определяется в зависимости от особенностей самого чертежа.
- Проводится вертикальная линия от точки, которая находится выше. Она позволяет построить прямоугольный треугольник, который часто используется для отображения уклона.
- Под прямым углом проводится соединение вспомогательной линии с нижней точкой.
- Угол, который образуется между вспомогательной и основной линией в нижней точке высчитывается для определения наклона.
Формула, которая требуется для вычисления рассматриваемого показателя указывалась выше. Стоит учитывать, что полученный показатель также переводится в градусы.
Особенности построения уклона и конусности
Область черчения развивалась на протяжении достаточно длительного периода. Она уже много столетий назад применялась для передачи накопленных знаний и навыков. Сегодня изготовление всех изделия может проводится исключительно при применении чертежей.
При этом ему больше всего внимания уделяется при наладке массового производства. За длительный период развития черчения были разработаны стандарты, которые позволяют существенно повысить степень читаемости всей информации. Примером можно назвать ГОСТ 8593-81.
Он во многом характеризует конусность и уклон, применяемые методы для их отображения. Начертательная геометрия применяется для изучения современной науки, а также создания различной техники.
Кроме этого, были разработаны самые различные таблицы соответствия, которые могут применяться при проведении непосредственных расчетов.
Различные понятия, к примеру, сопряжение, уклон и конусность отображаются определенным образом. При этом учитывается область применения разрабатываемой технической документации и многие другие моменты.
К особенностям построения угла и конусности можно отнести следующие моменты:
- Основные линии отображаются более жирным начертанием, за исключением случая, когда на поверхности находится резьба.
- При проведении работы могут применяться самые различные инструменты. Все зависит от того, какой метод построения применяется в конкретном случае. Примером можно назвать прямоугольный треугольник, при помощи которого выдерживается прямой угол или транспортир.
- Отображение основных размеров проводится в зависимости от особенностей чертежа. Чаще всего указывается базовая величина, с помощью которой определяются другие. На сегодняшний день метод прямого определения размеров, когда приходится с учетом масштаба измерять линии и углы при помощи соответствующих инструментов практически не применяется. Это связано с трудностями, которые возникают на производственной линии.
В целом можно сказать, что основные стандарты учитываются специалистом при непосредственном проведении работы по построению чертежа.
Часто для отображения уклона в начертательной геометрии создаются дополнительные линии, а также обозначается угол уклона.
В проектной документации, в которой зачастую отображается конусность, при необходимости дополнительная информация выводится в отдельную таблицу.
Поделитесь в соц.сетях: Калькуляторы расчета размеров развертки конуса — с пояснениями
Иногда в ходе выполнения тех или иных хозяйственных работ мастер встаёт перед проблемой изготовления конуса – полного или усеченного. Это могут быть операции, скажем, с тонким листовым металлом, эластичным пластиком, обычной тканью или даже бумагой или картоном.
А задачи встречаются самый разные – изготовление кожухов, переходников с одного диаметра на другой, козырьков или дефлекторов для дымохода или вентиляции, воронок для водостоков, самодельного абажура.
А может быть даже просто маскарадного костюма для ребенка или поделок, заданных учителем труда на дом.
Калькуляторы расчета размеров развертки конуса
Чтобы из плоского материала свернуть объёмную фигуру с заданными параметрами, необходимо вычертить развертку. А для этого требуется рассчитать математически и перенести графически необходимые точные размеры этой плоской фигуры.
Калькуляторы расчета размеров развертки конусаНесколько слов о рассчитываемых параметрахКак это делается – рассмотрим в настоящей публикации. Помогут нам в этом вопросе калькуляторы расчета размеров развертки конуса.
Понять принцип расчета будет несложно, разобравшись со следующей схемой:
Усеченный конус с определяющими размерами и его развёртка. Показан усеченный конус, но с полным — принцип не меняется, а расчеты и построение становятся даже проще.
Итак, сам конус определяется радиусами оснований (нижней и верхней окружности) R1 и R2, и высотой Н. Понятно, что если конус не усеченный, то R2 просто равно нулю.
Буквой L обозначена длина боковой стороны (образующей) конуса. Она в некоторых случаях уже известна – например, требуется сделать конус по образцу или выкроить материал для обтяжки уже имеющегося каркаса. Но если она неизвестна – не беда, ее несложно рассчитать.
Справа показана развёртка. Она для усеченного конуса ограничена сектором кольца, образованного двумя дугами, внешней и внутренней, с радиусами Rb и Rs. Для полного конуса Rs также будет равен нулю. Хорошо видно, что Rb = Rs + L
Угловую длину сектора определяет центральный угол f, который в любом случае предстоит рассчитать.
Все расчеты займут буквально минуту, если воспользоваться предлагаемыми калькуляторами:
Шаг 1 – определение длины образующей L(Если она уже известна – шаг пропускается)
Перейти к расчётам
Шаг 2 – определение радиусов внутренней и внешней дуги разверткиРадиусы рассчитываются поочередно – с выбором в соответствующем поле калькулятора.
Шаг 3 – определение величины центрального угла fПерейти к расчётам
* * * * * * *
Итак, все данные имеются.
Остается на листе бумаги циркулем провести две дуги рассчитанных радиусов. А затем из точки центра с помощью транспортира прочертить два луча под рассчитанным углом – они ограничат развертку по угловой длине.
Существуют и чисто геометрические методы построения довольно точной развертки конуса, без проведения расчётов. Один из них подробно описан в статье нашего портала «Как сделать абажур своими руками».
Выкройка для конуса | Математика для ювелиров
19.11.2012 // Владимир Трунов
Вместо слова «выкройка» иногда употребляют «развертка», однако этот термин неоднозначен: например, разверткой называют инструмент для увеличения диаметра отверстия, и в электронной технике существует понятие развертки. Поэтому, хоть я и обязан употребить слова «развертка конуса», чтобы поисковики и по ним находили эту статью, но пользоваться буду словом «выкройка».
Построение выкройки для конуса — дело нехитрое. Рассмотрим два случая: для полного конуса и для усеченного.
На картинке (кликните, чтобы увеличить) показаны эскизы таких конусов и их выкроек. (Сразу замечу, что речь здесь пойдет только о прямых конусах с круглым основанием. Конусы с овальным основанием и наклонные конусы рассмотрим в следующих статьях).
1. Полный конус
Обозначения:
- — диаметр основания конуса;
- — высота конуса;
- — радиус дуги выкройки;
- — центральный угол выкройки.
Параметры выкройки рассчитываются по формулам:
;
;
где .2. Усеченный конус
Обозначения:
- — диаметр большего основания конуса;
- — диаметр меньшего основания конуса;
- — высота конуса;
- — радиус внешней дуги выкройки;
- — радиус внутренней дуги выкройки;
- — центральный угол выкройки.
Формулы для вычисления параметров выкройки:
;
;
;
где .
Заметим, что эти формулы подойдут и для полного конуса, если мы подставим в них .3. Угол при вершине конуса
Иногда при построении конуса принципиальным является значение угла при его вершине (или при мнимой вершине, если конус усеченный).
Самый простой пример — когда нужно, чтобы один конус плотно входил в другой. Обозначим этот угол буквой (см. картинку).
В этом случае мы можем его использовать вместо одного из трех входных значений: , или . Почему «вместо«, а не «вместе«? Потому что для построения конуса достаточно трех параметров, а значение четвертого вычисляется через значения трех остальных.
Почему именно трех, а не двух и не четырех — вопрос, выходящий за рамки этой статьи. Таинственный голос мне подсказывает, что это как-то связано с трехмерностью объекта «конус».
(Сравните с двумя исходными параметрами двухмерного объекта «сегмент круга», по которым мы вычисляли все остальные его параметры в статье Геометрия круга.)
Ниже приведены формулы, по которым определяется четвертый параметр конуса, когда заданы три.
- Заданы ; тогда .
- Заданы ; тогда .
- Заданы ; тогда .
- Заданы ; тогда .
4.
Методы построения выкройки
- Вычислить значения на калькуляторе и построить выкройку на бумаге (или сразу на металле) при помощи циркуля, линейки и транспортира.
- Занести формулы и исходные данные в электронную таблицу (например, Microsoft Exel). Полученный результат использовать для построения выкройки при помощи графического редактора (например, CorelDRAW).
- использовать мою программу Cones, которая нарисует на экране и выведет на печать выкройку для конуса с заданными параметрами. Эту выкройку можно сохранить в виде векторного файла и импортировать в CorelDRAW.
5. Не параллельные основания
- Что касается усеченных конусов, то программа Cones пока строит выкройки для конусов, имеющих только параллельные основания.
Для тех, кто ищет способ построения выкройки усеченного конуса с не параллельными основаниями, привожу ссылку, предоставленную одним из посетителей сайта:- Усеченный конус с не параллельными основаниями.
5. Расчет и проектирование спирального сверла.
Исходные данные:
Длина отверстия ;
Материал заготовки Сталь30Х;
Расчет спирального сверла.
1.Определяем диаметр сверла (согласно № варианта задания протяжки)
ГОСТ885-77
2.Определяем режим резания:
2.1подачу находим по (табл. 26. стр.277 [2])
принимаем
Корректируем подачу по станку:
2.2Определяем скорость главного движения резания:
Коэффициенты выбираем по (табл. 28. стр.278.[2]):
,,,,
Стойкость сверла .
;;
для стали 30Х
,,,
3.Осевая составляющая силы резания:
;
,,,;
4.Момент сил сопротивления резанию (крутящий момент):
;
,,,;
5.Определяем номер конуса Морзе хвостовика.
Определяем средний диаметр хвостовика
где – момент сопротивления сил резанию;
– осевая составляющая силы резания;
– коэффициент трения стали по стали;
– половина угла конуса;
;
– отклонение угла конуса;
.
По СТ СЭВ 147-75 выбираем ближайший больший конус. т.е. конус Морзе
№5.Основные конструктивные размеры конуса Морзе №5 (табл.6.4 [1])
,,,,,,,,,,,,.
6.Определяем длину сверла по ГОСТ 10903 – 77 [2]
– общая длина сверла;
– длина рабочей части;
– длина хвостовика и шейки;
7.Определяем геометрические и конструктивные параметры рабочей части сверла
Форма заточки ДП (двойная с подточкой перемычки).
Угол наклона винтовой канавки ;
Углы между режущими кромками ,;
Задний угол ;
Угол наклона поперечной кромки ;
Размеры подточенной части перемычки: ,;
Шаг винтовой канавки:
;
8.
Диаметрсердцевины сверла выбирают в зависимости от диаметра сверла: принимаем диаметр сердцевины у переднего конца сверла равной
Утолщение сердцевины по направлению к хвостовику надлины. Принимаем это утолщение равным.
9.Обратная конусность сверла надлины рабочей части по направлению к хвостовику.
10.Ширину ленточки;
Высота затылка .
11.Ширина пера
;
12.Геометрические элементы профиля фрезы для фрезерования канавки
Большой радиус профиля:
где ;
т. к. , то
При диаметре фрезы ,
Меньший радиус профиля ,
где ;
Ширина профиля
;
Режим резания при сверлении.

Обработку производим на вертикально-сверлильном станке 2Н150
1.Глубина резания
;
2.Выбираем подачу
Проверяем принятую подачу по осевой составляющей силы резания, допускаемой прочностью механизма подачи станка.
По паспортным данным станка 2Н150:
Т. к. то назначенная подачавполне допустима.
3.Период стойкости сверла
Допустимый износ сверла .
4.Скорость главного движения резания допускаемая режущими свойствами сверла
5.Частота вращения шпинделя, соответствующая найденной скорости главного движения резания:
;
Действительная скорость главного движения резания: .
Корректируем частоту вращения шпинделя по паспортным данным станка:
;
6.Крутящий момент от сил сопротивления резанию при сверлении:
Мощность затрачиваемая на резание:
;.
7.Проверим, достаточность мощность станка. Обработка возможна, если
;
8. Основное время:
;
– врезание при двойной заточке
;
– длина отверстия;
– перебег;
Конус – Калькулятор геометрии
Геометрия | Формы | Контакты и конфиденциальность Геометрические калькуляторы Немецкий: Geometriechner, Formen 1DЛиния, дуга окружности, парабола, спираль, кривая Коха 2D Правильные многоугольники:
Равносторонний треугольник, квадрат, пятиугольник, шестиугольник, семиугольник, восьмиугольник, многоугольник, десятиугольник, десятиугольник, додекагон, шестиугольник, N-угольник, кольцо многоугольникаДругие многоугольники:
треугольник, прямоугольный треугольник, равнобедренный треугольник, ИК-треугольник, четырехугольник, прямоугольник, золотой прямоугольник, ромб, параллелограмм, полуквадратный воздушный змей, прямой воздушный змей, воздушный змей, правильная трапеция, равнобедренная трапеция, трехравносторонняя трапеция, трапеция, тупая трапеция, циклический четырехугольник, касательный четырехугольник, наконечник стрелки, вогнутый четырехугольник, Перекрещенный прямоугольник, антипараллелограмм, форма дома, симметричный пятиугольник, восьмиугольник, разделенный пополам по диагонали, прямоугольник с разрезом, вогнутый пятиугольник, вогнутый правильный пятиугольник, вытянутый пятиугольник, прямой восьмиугольник, разделенный пополам, вытянутый шестиугольник, симметричный шестиугольник, параллелогон, вогнутый шестиугольник, шестиугольник со стрелкой, прямоугольный шестиугольник , L-образная форма, острый изгиб, T-образная форма, усеченный квадрат, вытянутый восьмиугольник, рамка, открытая рамка, сетка, крест, X-образная форма, H-образная форма, три звезды, F наша звезда, пентаграмма, гексаграмма, уникурсальная гексаграмма, октаграмма, звезда Лакшми, многоугольник с двойной звездой, полиграмма, многоугольникКруглые формы:
3Д Platonic Solids:
Круг, Полукруг, Круглый сектор, Круглый сегмент, Круглый слой, Круглый центральный сегмент, Круглый угол, Круглый угол, Круговая касательная стрелка, Форма капли, Полумесяц, Заостренный овал, Два круга, Стрельчатая арка, Холм , Кольцо, Сектор кольца, Изогнутый прямоугольник, Скругленный многоугольник, Скругленный прямоугольник, Эллипс, Полуэллипс, Эллиптический сегмент, Эллиптический сектор, Эллиптическое кольцо, Стадион, Спираль, Бревно.Спираль, треугольник Рело, циклоида, двойная циклоида, астроида, гипоциклоида, кардиоида, эпициклоида, параболический сегмент, сердце, треугольник, междуговой треугольник, круговой треугольник, междуговой четырехугольник, межокружной четырехугольник, круговой четырехугольник, дуговой многоугольник, коготь, полуинь -Ян, Арбелос, Салинон, Выпуклость, Луна, Три круга, Многоугольник, Круглый многоугольник, Роза, Шестерня, Овал, Яйцо-профиль, Лемниската, Сквиркл, Круглый квадрат, Дигон, Сферический треугольник
Tetrahedron, Cube, Octahedron, Dodecahedron, IcosahedronArchimedean Solids:
Truncated Tetrahedron, Cuboctahedron, Truncated Cube, Truncated Octahedron, Rhombicuboctahedron, Truncated Cuboctahedron, Icosidodecahedron, Truncated Dodecahedron, Truncated Icosahedron, Snub Cube, Rhombicosidodecahedron , Truncated Icosidodecahedron, Snub DodecahedronCatalan Solids:
Triakis Tetrahedron, Rhombic Dodecahedron, Triakis Octahedron, Tetrakis Hexahedron, Deltoidal Icositetrahedron, Hexakis Octahedron, Rhombic Triacontahedron, Triakis Icosahedron, Pentakis Dodecahedron, Pentagonal Icositetrahedron, Deltoidal Hexecontahedron, Hexakis Icosahedron, Пятиугольный шестигранникJohnson Solid:
пирамиды, куполы, ротонда, удлиненные пирамиды, гиросельные пирамиды, бипирамиды, удлиненные бипирамиды, дипирамиды 9800, дискенол, дискеноол.Столб, Треугольная Пирамида, Квадратная Пирамида, Правильная Пирамида, Пирамида, Квадратная Усеченная, Правильная Усеченная, Усеченная, Изогнутая Пирамида, Правильная Бипирамида, Бипирамида, Двуусеченная, Усеченная-Пирамида, Пандус, Прямой Клин, Клин, Половина Тетраэдра, Ромбоэдр, Параллелепипед, Правильный Призма, призма, косая призма, антикуб, антипризма, призматоид, трапецоэдр, дисфеноид, угол, общий тетраэдр, клиновидный куб, полукубовид, косой кубоид, слиток, наклонная трехгранная призма, кубовид с вырезом, усеченный кубоид, кубовид с тупыми краями, Удлиненный додекаэдр, усеченный ромбоэдр, обелиск, изогнутый куб, полый куб, полая пирамида, полая усеченная пирамида, звездчатая пирамида, звездчатый октаэдр, Sma ll Звёздчатый додекаэдр, Большой звёздчатый додекаэдр, Большой додекаэдр, Большой икосаэдр
Круглые формы:
4Д Тессеракт, Гиперсфера
Сфера, полусфера, сферический угол, цилиндр, срезанный цилиндр, косой цилиндр, изогнутый цилиндр, эллиптический цилиндр, обобщенный цилиндр, конус, усеченный конус, наклонный круговой конус, эллиптический конус, усеченный эллиптический конус, общий конус , Общий усеченный конус, двояконус, усеченный двояконус, заостренный столб, закругленный конус, капля, сфероид, эллипсоид, полуэллипсоид, сферический сектор, сферическая крышка, сферический сегмент, сферический центральный сегмент, двойной калот, сферический клин, полуцилиндр, диагонально разделенный пополам Цилиндр, Цилиндрический клин, Цилиндрический сектор, Цилиндрический сегмент, Цилиндр с плоским концом, Полуконус, Конический сектор, Конический клин, Сферическая оболочка, Полусферическая оболочка, Цилиндрическая оболочка, Вырезанная цилиндрическая оболочка, Наклонная цилиндрическая оболочка, Полый конус, Усеченный полый конус, Сферический Кольцо, тор, тор веретена, тороид, сектор тора, сектор тора, арка, тетраэдр Рело, капсула, сегмент капсулы, двойная точка, антиконус, усеченный антиконус, Sphe повторный цилиндр, линза, вогнутая линза, бочонок, форма яйца, параболоид, гиперболоид, олоид, тела Штейнмеца, тело вращенияAnzeige
Расчеты на прямом круговом конусе.
Наклонная высота — это расстояние между вершиной и краем основания, боковая поверхность — это поверхность без основания. Угол раскрытия — это угол при вершине, угол основания — это угол между наклонной линией и основанием. Введите радиус и высоту и выберите количество знаков после запятой. Затем нажмите Рассчитать. Углы рассчитываются и отображаются в градусах, здесь вы можете конвертировать единицы измерения угла. Для расчета общих конусов см. общую пирамиду.
Формулы:
s = √ h² + r²
L = r * s * π
A = r * π * ( r + s )
V = 1/3 r² * π * h
α = 2 * arcsin(r/s)
β = (180° – α)/2pi:
π = 3,141592653589793…Радиус, высота и длина имеют одну и ту же единицу измерения (например, метр), поверхности имеют эту единицу в квадрате (например, квадратный метр), объем имеет эту единицу в степени три (например, кубический метр). У аудио/видео есть этот блок -1 .
Поделиться:
© Jumk.
de Веб-проекты | Онлайн калькуляторы
Anzeige
Общие | как измерить углы конуса | Практик-механик
Бергер
Алюминий
- #1
как правильно измерить угол конуса мужского и женского пола с помощью ваших основных ручных измерительных устройств. Спасибо.
Джон в Калифорнии
Горячекатаный
- #2
Для полного охватываемого конуса, доходящего до точки, я бы измерил диаметр у основания и длину и выкрутил его. Для секции конуса (два плоских конца) для грубой проверки я бы измерил разницу между двумя диаметрами и длиной и проверил ее. Для более точного измерения я устанавливал конус на синусоидальный стержень, прислоняемый к паре стопорных штифтов или ограждению, и увеличивал длину стопки измерительных блоков до тех пор, пока я не обвел горизонт конуса с обоих концов, мой 0,0001-дюймовый DTI получил те же показания. Длина пакета, умноженная на расстояние между центрами валков на синусоидальной полосе, будет равна синусу внутреннего угла конуса.
Процедура синусоидального бара была бы одним из способов, который я мог придумать, чтобы получить хорошее, прямое количественное определение угла женской шишки. Обычно, когда мне нужно вырезать секцию охватывающего конуса, это машинное конусное гнездо, такое как Jacobs, и когда я это делаю, я на самом деле не ищу прямых измерений, потому что я подгоняю его к известному мастеру, используя Dykem, чтобы получить свидетель, пока у меня не будет подгонки, которую я хочу.
Но если бы мне действительно нужно было измерить угол, я мог бы придумать другой способ сделать это — поместить деталь в тиски на моем фрезерном станке и DTI в шпинделе. Необходимо следить за тем, чтобы ось конуса была перпендикулярна столу. Затем я бы использовал DTI, чтобы выбрать горизонт конуса на открытом конце и переместить шпиндель вниз (или колено вверх, в зависимости от обстоятельств) на известную величину, отмечая движение стрелки индикатора. . Тогда у меня было бы изменение радиуса и длины, которые я мог бы использовать для срабатывания половины прилежащего угла.
Имейте в виду, что такой способ содержит некоторые источники ошибок и, вероятно, будет неодобрительным. Во-первых, угол рычага индикатора относительно канала ствола влияет на прямые измерения. Мои Interrapids настроены так, что угол 12* относительно измеряемой поверхности дает показание 1:1. Однако для всех индикаторов может быть по-разному,
Надеюсь, это поможет,
Джон
“Я предпочитаю удачу, чем удачу в любой день.
”
Питер из Голландии
Алмаз
- #3
Если вам нужно только измерить угол на 2 разных диаметрах на известном расстоянии друг от друга и выполнить тригонометрический анализ, вы получите наилучший результат, когда это расстояние будет как можно больше
Для внутренних конусов с плоской и квадратной поверхностью вы можете использовать один из этихhttp://www.schut.com/catalog/en/en_0213.html
Если вы используете короткий и длинный измерительный рычаг, у вас есть все что вам нужно бросьте acurit
Вы также можете запустить/вычислить идентификатор на обоих концах конуса, потому что у вас есть идентификатор известного расстояния от вершины
Очень универсальный инструмент BTWПитер из Голландии
Пазузу71
Горячекатаный
- #4
Для конуса с внутренней резьбой мы используем 2 шарикоподшипника разного диаметра, вставленные в отверстие.
Затем установите угол, глубину шаров и т. д.
Это довольно просто, когда вы все это нарисуете.
Группа
Титан
- #5
Я делаю то, что сказал Пазузу, за исключением того, что я использую шарики подшипников, а не шарикоподшипники
и глубинный микрофон …. но глубинный стержень на верньере почти так же хорош
рандик
Нержавеющая сталь
- #6
Пазузу71 сказал:
Для женского конуса мы используем 2 шарикоподшипника разного диаметра, вставленные в отверстие.
Затем установите угол, глубину шаров и т. д.
Это довольно просто, когда вы все это нарисуете.Нажмите, чтобы развернуть…
это отличный совет, спасибо —
randyc
рандик
Нержавеющая сталь
- #7
Настоящая Ли сказала:
Да, идея с мячом звучит неплохо, но есть одна тонкость, на которую следует обратить внимание.
Круг контакта между мячом и конусом не находится на горизонтальной центральной линии мяча (при условии, что конус стоит на своей вершине).
Контакт существует на плоскости, определяемой точками касания двух поверхностей, которые будут ниже центральной линии.
Поскольку для точного определения этого местоположения требуется знание угла конической поверхности, а это измеряемый параметр, вы получаете круговое соотношение, которое не может быть просто решено.
– Ли
Нажмите, чтобы развернуть…
Да, ты прав. Необходима еще одна информация (например, большой или меньший диаметр конуса), прежде чем мы сможем закрыть сделку.
Группа
Титан
- #8
Я не уверен, куда делся пост Ли, он появляется только в моем (Firefox) сеансе
Это можно просто решить, если у вас есть доступ к параметрическому пакету САПР
9100
Алмаз
- #9
Это не оригинал со мной – кто-то где-то выложил эту версию. Установите диск на конец резьбового стержня и больший диск с резьбовой втулкой на стержень. Вставьте стержень в конус, пока он не сядет на меньший, затем привинтите больший, чтобы установить его. Измерьте расстояние между ними.
Рассчитайте угол, или если совсем лень, начертите в автокад и прочтите угол. Это исключает ошибку с шарами.
Что было бы действительно круто, так это циферблатный индикатор с длинным ходом с меньшим диском на стержне и большим на корпусе. Просто засуньте его в конус и читайте.
Билл
рандик
Нержавеющая сталь
- #10
Троуп сказал:
Я не уверен, куда делся пост Ли, он появляется только в моем (Firefox) сеансе
. Это можно просто решить, если у вас есть доступ к параметрическому пакету САПР.
Нажмите, чтобы развернуть…
Конечно, поскольку тангенциальные привязки так легко выполняются. На самом деле, по моему опыту, полное графическое решение занимает у меня меньше времени, чем простая настройка модели для решения тригонометрическими средствами. (И, возможно, с меньшей вероятностью ошибки.) Спасибо, AutoCAD!
9100
Алмаз
- #11
Троуп сказал:
Я не уверен, куда подевался пост Ли, он появляется только в моем (Firefox) сеансе/ЦИТАТА]
Подключен ли Cuda к какому-то новому программному обеспечению?Нажмите, чтобы развернуть.
..
Джон в Калифорнии
Горячекатаный
- #12
Я обязательно запомню трюк с шариком, потому что, даже если его нельзя использовать для непосредственного измерения угла конусности отверстия, он все равно дает хорошую проверку «да/нет». Вы можете рассчитать глубину, на которую “должен” упасть шар заданного диаметра, в верхнем и нижнем пределах допуска угловатости 9.0017 (и, как указано, один известный диаметр и глубина) и используйте микрофон глубины для проверки.
Видео: Использование сектора для формирования конуса
Стенограмма видео
В этом видео мы рассмотрим, как можно сделать конус из сектора круга.
Но сначала я хотел бы рассказать вам об уроке; Я хочу поговорить об объемах цилиндров и конусов. В начале урока мы повторим, как вычислить объем цилиндра. Сначала вам нужно проработать площадь или основание, которое представляет собой круг с радиусом 𝑟. Итак, 𝜋𝑟 в квадрате. Затем вы перетаскиваете основание вверх через пространство к вершине цилиндра, и это дает вам объем цилиндра. Поскольку высота цилиндра равна ℎ, нам нужно умножить площадь основания на ℎ, потому что это длина, на которую мы перетаскиваем основание в третьем измерении.
Пока все хорошо, затем я предложил подумать о правильном круглом конусе, который аккуратно расположен внутри этого цилиндра — с таким же радиусом основания, 𝑟, и той же высотой, ℎ. Мы собирались вычислить объем этого конуса. Очевидно, что он меньше, чем объем цилиндра, в котором он находится, потому что у нас есть все это бесполезное пространство снаружи, которое мы отрезали. Но насколько точно он будет меньше? Теперь один студент предположил, что его можно рассматривать как набор прямоугольных треугольников с высотой ℎ и основанием 𝑟, все они соединены с осью здесь, в середине цилиндра, а затем повернуты, чтобы образовать круг, так что вращаются вокруг оси.
как это делает как маленькая вещь украшения здесь. Очевидно, что таких треугольников будет очень много, так что здесь не будет много пробелов; они будут намного, намного ближе друг к другу, так что это будет приближаться к конусу.
Затем они сказали, что мы можем рассматривать цилиндр как ряд прямоугольников, расположенных почти таким же образом и снова вращающихся здесь, причем очень-очень много их очень, очень упакованных вместе, чтобы предложить цилиндр. Затем они сказали, что если мы наложим эти два прямоугольника друг на друга, для каждого прямоугольника, который у нас есть, будет соответствующий треугольник, и каждый треугольник будет ровно половиной одного из прямоугольников. Итак, если мы отбросим эту половину этого прямоугольника, если мы сделаем то же самое для каждой из этих форм, они подумали, что, возможно, объем конуса будет вдвое меньше объема цилиндра. Мы решили провести небольшой эксперимент.
Теперь у меня на столе лежит тонкая карточка в виде цилиндра шириной восемь сантиметров и высотой двенадцать целых пять десятых сантиметра и мешочек с рисом.
Ну учителя делают! Поэтому нам нужно было сделать конус точно подходящего размера, чтобы он поместился внутри цилиндра, поэтому они должны были иметь одинаковый размер основания и одинаковую высоту. Мы могли наполнить конус рисом и высыпать его в цилиндр и посмотреть, сколько раз нам нужно сделать это, прежде чем цилиндр наполнится. Если студент был прав, нам нужно сделать это два раза, но если студент ошибся, нам, возможно, придется сделать это больше или меньше раз, чем это. Итак, был цилиндр, был конус, я вставил конус в цилиндр, и конус аккуратно сидел внутри цилиндра с той же шириной, тем же радиусом и той же высотой. Итак, я наполнил конус один раз и залил его. И когда я это сделал, цилиндр был заполнен не наполовину; похоже, что студент может ошибаться. Поэтому я снова насыпал в конус рис и вылил все это в цилиндр. И после этого второго конуса, полного риса, он был полон чуть более чем наполовину. И с тремя конусами, полными риса, цилиндр был точно полным. Таким образом, мы пришли к выводу, что объем цилиндра в три раза больше, чем у конуса с тем же радиусом основания и высотой.
Теперь у нас есть еще одно видео под названием «Вычисление объема конуса», в котором более подробно объясняется, почему объем цилиндра будет в три раза больше объема конуса, а не просто в два раза больше. Но если подумать, тот треугольник, который мы получили от подсчета, если бы мы действительно сложили их кучу, они бы не пошли по кругу, чтобы образовать конус; они на самом деле шли друг перед другом и образовывали вот такую треугольную призму. Чтобы получить конус, эти треугольники на самом деле должны быть 3D-клиньями, а не 2D-треугольниками, так что клин будет бесконечно тонким здесь на оси, но немного толще здесь, на окружности конуса. И мы могли бы организовать их в большой круг здесь, и это фактически сделало бы конус. И точно так же прямоугольники не были бы двумерными прямоугольниками; они будут трехмерными клиньями, как этот, поэтому они будут иметь небольшую глубину здесь, и они будут бесконечно тонкими в середине здесь, на оси. И снова мы складывали их в большой круг, чтобы получился наш цилиндр.
Итак, если мы разрежем прямоугольный клин пополам вот так, а затем выбросим верхний, у нас останутся все эти маленькие треугольные клинья здесь внизу, чтобы сделать конус. Теперь, если мы рассмотрим высоту зеленого клина — из него получится конус — мы увидим, что самая длинная часть здесь на самом деле является бесконечно малой частью. Но что касается другой части — части, которую мы выбрасываем, — длинная часть здесь намного толще. И я думаю, вы можете видеть, что на самом деле вот этот кусочек будет больше, чем вот этот. Вот почему объем цилиндра не вдвое больше объема конуса; это более чем в два раза больше объема. Итак, это аккуратно подводит нас к сути этого видео: как сделать конус, который точно помещается внутри цилиндра с таким же радиусом основания и той же высотой?
Итак, чтобы сделать наш конус, мы вырезаем наш сектор, а затем эти два открытых радиуса перетаскиваем друг к другу. Итак, мы перетаскиваем это; мы втаскиваем это внутрь. И когда мы это делаем, вершина выскакивает, и мы получаем конус.
И мы можем видеть, что это наше заявление о том, как обойти снаружи, составляет основу конуса; так вот это расстояние — окружность всего здесь, по краю. Теперь также этот радиус, назовем его «s» для радиуса сектора. И то, что они… эти две стороны, помнишь, сошлись вот так, чтобы соединиться, – это как щель по краю нашего конуса. И поэтому эта длина тоже должна быть 𝑠. Итак, наклонная длина конуса, так что, может быть, и эта длина, и эта длина тоже; все это наклонные длины конуса и равны радиусу сектора, из которого мы создали конус.
, так что я полагаю, что решающий вопрос сейчас заключается в том, если мы хотим создать конкретный конус с радиусом основания 𝑟 и высотой ℎ, каким должен быть радиус этого сектора? и каков должен быть этот угол, мера этого угла вокруг здесь; давайте назовем его 𝜃, чтобы создать этот конкретный конус? Итак, помните, что когда мы формируем этот конус и стягиваем эти стороны вместе вот так, радиус исходного сектора теперь составляет длину наклонной стороны этого конуса.
Теперь что мы собираемся сделать, это опустить перпендикуляр вниз от кончика конуса к центру основания конуса. А потом, помните, мы говорили, что радиус равен 𝑟, а высота — ℎ; так вот это расстояние. Теперь, поскольку мы сказали, что опустили перпендикуляр, мы знаем, что этот угол здесь равен девяноста градусам. Таким образом, этот перпендикуляр находится под углом девяносто градусов к основанию конуса. Итак, у нас получился прямоугольный треугольник. Гипотенуза – это длина 𝑠 от радиуса сектора, а затем две стороны радиуса основания конуса и высота конуса. Теперь, когда у нас есть такой прямоугольный треугольник, мы начинаем думать о теореме Пифагора. А теорема Пифагора говорит нам, что в прямоугольном треугольнике квадрат наибольшей стороны равен сумме квадратов других сторон. Таким образом, в этом случае 𝑠 в квадрате равно ℎ в квадрате плюс 𝑟 в квадрате. Теперь, если мы возьмем квадратный корень из обеих частей этого уравнения, то увидим, что радиус сектора, необходимого для создания этого конуса, равен квадратному корню из ℎ в квадрате плюс 𝑟 в квадрате.
Теперь мы знаем, что ℎ в квадрате — это высота конуса, и мы знаем, что такое 𝑟 в квадрате; это радиус, который мы хотим для нашего конуса. Так что мы можем легко решить это, если нам нужно.
Теперь, чтобы определить размер угла в центре сектора, который мы пытаемся создать, нам нужно учесть некоторые пропорции. Если мы подумаем об этом расстоянии здесь, об этой длине дуги, которая, конечно же, является окружностью основания конуса, и если мы сравним это со всей окружностью этого круга для сектора, эти два измерения находятся в той же пропорции. как этот угол здесь — мера этого угла здесь — по сравнению с мерой всего угла; другими словами, на триста шестьдесят градусов по всему периметру. Теперь мы также, поскольку мы сказали, что мы хотим, чтобы радиус основания конуса был 𝑟, мы знаем, что длина окружности этого конуса в основании конуса будет в два раза больше 𝜋 раз 𝑟. Итак, у нас есть длина дуги; мы можем это вычислить. Мы только что видели, как вычислить радиус сектора. Это означает, что длина окружности всего круга будет в два раза больше радиуса 𝜋, то есть в два раза 𝜋𝑠.
И мы, очевидно, знаем триста шестьдесят, потому что это полный оборот; это мера угла полного поворота. Таким образом, знание этих трех вещей позволит нам рассчитать здесь значение 𝜃.
Хорошо, тогда давайте применим все это на практике и проведем расчеты для конуса, который я использовал в уроке, о котором только что рассказал. Таким образом, цилиндр, в который мы пытались поместить конус, имел двенадцать целых пять десятых сантиметра в высоту и восемь сантиметров в ширину. Это означает, что радиус основания здесь составлял четыре сантиметра, половина восьми сантиметров. Итак, теперь мы можем использовать часть нашей теоремы Пифагора. При построении этого прямоугольного треугольника высота составляет двенадцать целых пять десятых сантиметра; радиус, как мы сказали, был четыре сантиметра. Мы хотим знать длину этой наклонной стороны конуса. Чтобы мы могли это обработать, это будет радиус круга, который мы будем использовать для создания сектора. Итак, чтобы сделать это немного яснее, давайте вытащим это и создадим новую диаграмму.
Итак, вот наш прямоугольный треугольник с этими вещами. Мы можем сказать, что 𝑠 в квадрате, это самая длинная сторона, равна двенадцати целых пять десятых в квадрате плюс четыре в квадрате, что, когда мы оцениваем их, говорит нам, что 𝑠 в квадрате составляет сто семьдесят два целых два десятых пять. Но помните, мы не хотим, чтобы 𝑠 возводилось в квадрат; нам нужен 𝑠, радиус круга для сектора. Итак, нам нужно извлечь квадратные корни из обеих частей.
И поскольку мы собираемся рисовать это, я не буду точнее, чем с точностью до миллиметра. Таким образом, один десятичный знак в сантиметрах должен дать нам разумный ответ; таким образом, тринадцать целых один сантиметр были радиусом, который нам был нужен. На самом деле, по удивительному совпадению, когда я открыл свой компас, наибольший радиус, который я мог получить, составлял ровно тринадцать целых один сантиметр. Так что это было приятное счастливое совпадение; Я смог почти нарисовать тот круг, который мне был нужен. Итак, теперь давайте соберем информацию, которая нам нужна, чтобы определить размер угла, меру этого угла в центре сектора, который мы собираемся создать.
Основание конуса — это окружность, выделенная оранжевым цветом. Значит, радиус равен четырем. А длина окружности в два раза больше 𝜋 радиуса, равного четырем, что дает нам восемь 𝜋. На самом деле я оставлю это в этом формате, потому что, если я начну вводить десятичные разряды, я внесу ошибки округления в свои последующие вычисления. Поэтому мы просто будем использовать значение восемь 𝜋 в наших последующих вычислениях.
Итак, теперь давайте подумаем о длине всего круга, из которого будет вырезан мой сектор. Теперь помните, мы только что вычислили значение 𝑠, тринадцать целых один сантиметр. Хотя здесь у нас есть совершенно точная версия этого, квадратный корень из ста семидесяти двух целых двух десятых пяти; это значение, которое я буду использовать в своих расчетах. Таким образом, подставив эти значения, длина окружности этого круга в два раза больше, чем радиус квадратного корня из ста семидесяти двух целых двух десятых пяти, так что снова просто оставим это в хорошем формате — не очень хорошем формате; возможно, мне следует сказать два корня из ста семидесяти двух целых двух десятых пяти, умноженных на 𝜋 сантиметров.
Итак, чтобы вычислить размер угла в центре нашего сектора, нам понадобится это значение, и нам понадобится это значение.
Помните, мы говорили, что эти вещи находятся в одинаковой пропорции. Отношение длины окружности основания конуса к длине окружности сектора круга такое же, как отношение 𝜃, меры угла центрального сектора, к тремстам шестидесяти градусам полного оборота. И сопоставляя эти значения, которые мы только что вычислили, мы видим, что восемь 𝜋 больше двух корней сто семьдесят две целых две десятых пять 𝜋 равно 𝜃, деленному на триста шестьдесят. Теперь, если я разделю верх и низ левой части на два, у меня получится восемь, деленное на два, равно четырем; два разделить на два равно одному. И я разделю их обоих на 𝜋. Таким образом, 𝜋, деленное на 𝜋, равно единице, и 𝜋, деленное на 𝜋, также равно единице; это упрощает это. И если я вот так умножу обе части на триста шестьдесят, то в правой части у меня сверху будет триста шестьдесят; У меня на дне триста шестьдесят. Эти двое отменят отмену, оставив меня с 𝜃.
Ну вот и окончательный ответ; Я не смогу точно измерить это с помощью моего транспортира. Так что на самом деле значение, которое я бы использовал для измерения угла, вероятно, будет не более одного десятичного знака, сто девять и семь градусов. Итак, давайте посмотрим, что я на самом деле сделал тогда. У меня есть угол сто девять и семь десятых на полуокружности в данном случае радиусом тринадцать целых один сантиметр. Затем я вырезал его и соединил эти два радиуса вместе, чтобы получился конус, который затем аккуратно поместился внутри цилиндра.
Видео: ответы на вопросы об использовании сектора для формирования конуса
Стенограмма видео
В этом видео мы повторим основные факты о формировании правильных круглых конусов из секторов кругов, а затем продолжим отвечать на несколько вопросов о их. Чтобы сформировать правильный круглый конус из сектора, просто вырежьте сектор и соедините открытые радиусы вместе, как показано на рисунке. Центр всплывет, и у вас будет конус.
Когда вы это сделаете, радиус исходного сектора здесь окажется здесь на нашем конусе. Значит, радиус исходных секторов равен длине наклонной стороны конуса. Кроме того, дуга вокруг исходного сектора за пределами исходного сектора составляет основу конуса. Таким образом, длина дуги исходного сектора равна длине окружности основания конуса.
Если вы хотите сформировать конус с определенной высотой ℎ и радиусом основания, скажем, 𝑟, вы можете рассчитать радиус, необходимый для сектора — назовем это 𝑠 — и меру угла — назовем это 𝜃 — в центр сектора.
Теперь помните, что длина стороны радиуса 𝑠 такая же, как и наклонная сторона конуса. Так что мы можем написать это здесь. И у нас есть высота, радиус и наклонная сторона, у нас есть прямоугольный треугольник, поэтому мы можем использовать теорему Пифагора, которая гласит, что квадрат наибольшей стороны в прямоугольном треугольнике равен равно сумме квадратов двух других сторон.
Затем, взяв квадратный корень из обеих сторон, мы выяснили, что радиус сектора, который нам нужно нарисовать, равен квадратному корню из квадрата высоты конуса плюс радиус основания конуса.
в квадрате. Теперь также отношение между мерой угла в центре сектора и полным оборотом в триста шестьдесят градусов здесь такое же, как отношение длины дуги здесь к полной окружности этого сектора здесь.
И мы можем записать это таким образом, так что 𝜃 разделить на триста шестьдесят равно длине дуги на секторе, деленной на длину окружности всей окружности сектора. Но помните, длина дуги такая же, как длина окружности основания конуса; именно эта дуга была использована для создания основания конуса, то есть в два раза 𝜋 раз 𝑟.
И длина окружности сектора, которая имеет радиус 𝑠, так что это равно удвоенному 𝜋 умноженному на 𝑠. Так что, если мы впишем их, мы увидим, что мы действительно можем отменить. Если я разделю верх и низ на два 𝜋, хорошо? мы просто получаем 𝜃 больше трехсот шестидесяти равно 𝑟 больше 𝑠. И если я просто умножу обе части на триста шестьдесят, я смогу сократить те, что в левой части.
Итак, если мы знаем ℎ и 𝑟, высоту конуса, который мы ищем, и его радиус, мы можем легко вычислить радиус сектора, который нам нужно создать, и угол в центре этого сектора.
что нам нужно использовать, чтобы создать этот конус. Теперь мы собираемся использовать эту информацию в паре вопросов.
Верно, тогда первый вопрос: радиус основания конуса равен пятнадцати сантиметрам, значит, это измерение здесь равно пятнадцати сантиметрам, а длина его наклонной стороны составляет двадцать пять сантиметров, так что вот это измерение. Найдите меру угла в центре сектора, из которого образовался конус; так это здесь. Теперь мы можем просто подключить это к формуле, которую мы только что создали.
𝜃 равно тремстам шестидесятикратному радиусу основания конуса, так что это пятнадцать, разделенная на 𝑠, длину наклонной стороны, которую мы даем в вопросе, что равно двадцати пяти. И когда мы вычислим это, мы получим ответ в двести шестнадцать градусов.
Итак, если вы помните эту формулу, это был довольно простой расчет, потому что в вопросе нам дали много соответствующей информации. Давайте представим, однако, что мы не смогли вспомнить эту формулу, и попробуем разобраться в этом больше из первых принципов, взглянув на то, что мы знаем о ситуации.
Мы знаем, что отношение угла в центре ко всему витку равно отношению длины этой дуги ко всей длине окружности этого сектора. И мы можем написать, что если 𝜃 больше трехсот шестидесяти, то этот угол, деленный на триста шестьдесят, равен длине дуги сектора, деленной на длину окружности этого полного сектора.
Теперь мы также знаем, что длина дуги сектора такая же, как длина окружности основания конуса, потому что это то, что используется для формирования конуса, и мы знаем радиус основания конуса, поэтому мы можем работать с этим вне. Эта длина здесь в два раза больше радиуса 𝜋; это два раза 𝜋 умножить на пятнадцать, что равно тридцати 𝜋.
Мы также знаем, помните, что длина наклонной стороны конуса такая же, как длина радиуса сектора, который использовался для его создания, потому что помните, что эти два радиуса объединяются, чтобы сформировать эту наклонную сторону . Это означает, что радиус этого сектора составляет двадцать пять сантиметров. И снова мы можем использовать этот радиус, чтобы вычислить длину окружности всего круга этого сектора.
Это два раза 𝜋 по двадцать пять, что равно пятидесяти 𝜋. Итак, давайте подставим эти числа в расчет, который мы создали на другой стороне. И у нас есть тридцать 𝜋 разделить на пятьдесят 𝜋 равно 𝜃 более трехсот шестидесяти, поэтому мы можем немного сократить и умножить обе части на триста шестьдесят; они отменят на той стороне. Теперь у нас есть выражение для 𝜃, которое, когда мы работаем, мы получаем тот же ответ, что и раньше.
Очевидно, что второй метод был намного длиннее первого. Если вы помните формулу и просто подставляете числа, вы получите ответы очень и очень быстро. Но на самом деле такой вопрос действительно заставляет вас понять, откуда берутся цифры, понять логику ситуации. И тогда, если у вас будет небольшая паника на экзамене, и все пойдет ужасно неправильно, вы все забудете, по крайней мере, вы точно сможете воссоздать метод, поняв ситуацию, потому что вы уже проходили через это много раз.
На этот второй вопрос нам задали – нам сказали, что радиус основания конуса равен пяти сантиметрам, а мера угла в центре сектора, из которого образовался конус, равна ста и пятьдесят градусов, и мы должны найти высоту конуса.
Это то, что я называю обратным вопросом, когда мы не знаем радиуса и высоты исходного конуса, мы не возвращаемся к размерам сектора, но нам даются другие части информации. Информация. Мы должны попытаться определить высоту конуса. Но не бери в голову! Мы еще можем найти ответ.
Итак, первая очевидная вещь, которую мы можем вычислить, — это длина окружности основания конуса, поэтому у нас есть радиус, равный пяти, поэтому длина окружности в два раза больше 𝜋 радиуса. А это десять 𝜋 сантиметров. Я оставлю это в таком формате; Я не буду ставить десятичные знаки, потому что мне нужен максимально точный ответ.
Теперь вспомните, что эта длина окружности совпадает с длиной дуги сектора, на который мы смотрели. Теперь мы, кажется, не очень приблизились к тому, где хотим быть в данный момент. Помните, мы пытаемся вычислить высоту конуса, так что вот это расстояние. Теперь мы также знаем, что наклонная длина конуса совпадает с радиусом сектора здесь. И если бы мы знали, какова эта длина наклона, назовем ее 𝑠, мы смогли бы использовать теорему Пифагора, чтобы выяснить, что такое ℎ.
Прямо сейчас, чтобы мы могли вычислить выражение для длины окружности этого большого сектора, потому что это в два раза больше радиуса. Итак, это два 𝜋𝑠 сантиметра. Нет, это 𝑠, а не пятерка. Теперь мы также знаем, что отношение угла в центре к полному обороту такое же, как отношение длины дуги здесь к полной окружности окружности этого сектора, поэтому мы можем записать это уравнение.
Итак, 𝜃, что на самом деле составляет сто пятьдесят градусов, более трехсот шестидесяти, равно длине дуги сектора по окружности сектора – окружности окружности сектора. Итак, давайте подставим эти значения. Мы знаем, что длина дуги сектора равна длине окружности основания конуса, так что это десять 𝜋, и мы знаем, что длина окружности сектора равна двум 𝜋𝑠, поэтому мы можем записать и это. Теперь мы можем сделать небольшую отмену; Я могу разделить верх и низ на 𝜋; Я могу разделить верх и низ на два; и я могу разделить верх и низ здесь на тридцать, что даст мне пять на двенадцать.
Тогда я вижу, что пять больше двенадцати — это то же самое, что пять больше 𝑠, поэтому ясно, что двенадцать должно быть 𝑠.
Итак, теперь я вычислил длину наклонной стороны, так что я могу вычеркнуть ее и написать двенадцать. Итак, эта длина равна двенадцати сантиметрам. И теперь я могу использовать теорему Пифагора, чтобы вычислить значение ℎ.
Таким образом, это означает, что длина гипотенузы в квадрате, двенадцать в квадрате, равна сумме квадратов других сторон, ℎ в квадрате плюс пять в квадрате. И оценивая двенадцать в квадрате и пять в квадрате, я получил это. Теперь я могу вычесть двадцать пять из обеих частей этого уравнения, в результате чего сто девятнадцать будет равно ℎ в квадрате. Теперь, если я возьму квадратный корень из обеих сторон и извлеку квадратный корень из ста девятнадцати, ℎ будет десять целых девять десятых восемь семь один два один одна точка точка точка точка точка точка сантиметры. Но, конечно же, помните, что наш вопрос просил нас дать ответ с точностью до одного знака после запятой. Итак, если мы посмотрим на этот первый десятичный знак, десять целых девять десятых, следующая цифра будет просто нулем, поэтому мы не будем округлять ее.
Таким образом, ответ: высота конуса составляет десять целых девять десятых сантиметра с точностью до одного десятичного знака.
Итак, последний вопрос: сектор превращается в конус. Радиус круга, из которого взят сектор, равен двенадцати-десяти сантиметрам. Мера угла в центре сектора равна двумстам градусам. Найдите радиус 𝑟 и высоту ℎ образовавшегося конуса, давая ответы с точностью до одного десятичного знака.
Ну, формулы, которые мы разработали ранее, мы как бы идем в другом направлении. Они предполагали, что мы знаем ℎ и 𝑟 и можем вернуться к другим значениям. Так что мы как бы работаем в обратном направлении в этом вопросе, но давайте просто посмотрим на ситуацию и подумаем: «Что мы знаем?» Ну, мы знаем, что длина окружности основания конуса равна длине дуги сектора, и мы знаем, что радиус сектора равен наклонной длине, длине наклонной стороны конуса.
Итак, сначала давайте посмотрим на длину этой дуги. Мы знаем, что этот угол здесь равен двумстам градусам, и мы знаем, что отношение этих углов там к тремстам шестидесяти градусам такое же, как отношение длины этой дуги здесь к длине окружности всего этого круга.
Теперь у нас есть радиус этого круга, так что мы можем вычислить длину окружности.
И это два раза 𝜋 по десять, то есть двадцать 𝜋 сантиметров. Опять же, давайте сохраним это – давайте не будем использовать десятичные знаки в данный момент. Давайте сохраним эти цифры настолько точными, насколько это возможно, пока мы проводим вычисления. И, как мы только что сказали, давайте запишем это в виде уравнения. Итак, двести на триста шестьдесят, сравнение, соотношение этих двух углов такое же, как отношение длины дуги к длине окружности сектора. И помните, длина дуги такая же, как это значение здесь, длина окружности основания конуса.
Таким образом, мы можем отменить левую часть этой убывающей, сделав это с делением, так что двести на триста шестьдесят равно пяти на девять. Мы знаем, что длина окружности сектора равна двадцати 𝜋, поэтому длина дуги, напомню, здесь равна этой величине: две 𝜋𝑟. Таким образом, мы можем поставить два 𝜋𝑟 здесь.
И мы можем отменить это. Итак, если я разделю верх на 𝜋, а низ на 𝜋 с этой стороны, я смогу разделить верх на два и низ на два.
Теперь у меня есть выражение — уравнение, включающее только 𝑟. Итак, теперь я умножу обе части на десять, а это означает, что десятки в правой части сокращаются, и у меня остается 𝑟, равное пятидесяти на девять. Теперь очевидно, что вопрос ищет ответ с точностью до одного десятичного знака, так что это будет пять целых шесть десятых. Но в будущих расчетах я все равно буду использовать эту наиболее точную версию ответа для своих расчетов, чтобы не создавать ошибок округления.
Так что я могу заменить 𝑟 здесь на пятьдесят на девять. Я также знаю, помню, что радиус этого сектора был десять и что эта длина такая же, как здесь наклонная сторона, так что здесь десять сантиметров. И теперь мы знаем, что это наш перпендикуляр, так что это прямоугольный треугольник, поэтому мы можем использовать немного теоремы Пифагора, чтобы вычислить значение ℎ.
Помните, что квадрат самой длинной стороны равен сумме квадратов других сторон. Теперь, используя точное значение пятьдесят на девять, я могу расширить их, затем вычесть две тысячи пятьсот на восемьдесят один с обеих сторон, а затем извлечь квадратные корни из обеих частей этого уравнения, что даст мне мой окончательный ответ ℎ восемь точка три до одного десятичного знака.
Калькулятор высоты наклона конуса
Создано Davide Borchia
Отзыв от Luciano Mino
Последнее обновление: 30 августа 2022 г.
Содержание:
- Что такое конус?
- Элементы конуса
- Как найти наклонную высоту конуса
- Как вычислить наклонную высоту конусов другими способами
- Как использовать наш калькулятор наклонной высоты конуса
- Круговая форма
- Часто задаваемые вопросы
Наш калькулятор высоты наклона рожка ответит на один из самых насущных вопросов, которые могут у вас когда-либо возникать: какова длина стороны рожка для мороженого?
Здесь вы узнаете все, что вам нужно о конусах и их наклонных сторонах, от основания до вершины:
- Что такое конус?
- Какие элементы конуса?
- Как найти наклонную высоту конуса?
- Практические примеры!
Что такое конус?
Конус сплошная фигура возникла в результате полного вращения прямоугольного треугольника вокруг одного из его катетов.
Полученное твердое тело имеет круглое основание и непрерывную наклонную сторону, которая соединяет край основания с самой верхней точкой конуса, вершиной .
Когда мы говорим о конусах, мы обычно имеем в виду полуконус : существительное конус относится к фигуре, полученной путем поворота на 180° наклонной линии, создающей две открытые «конические» формы. Однако в этом инструменте мы будем говорить только о первом виде.
Элементы конуса
Конус идентифицируется:
- A Круглое основание с радиусом rrr; и
- A высота hhh перпендикулярно основанию.
Однако мы можем идентифицировать другой элемент:
Конус со всеми отмеченными элементами.
- наклонная сторона называемая высота наклона конуса , lll
На рисунке вы можете легко определить все элементы, упомянутые выше.
Как найти наклонную высоту конуса
Здесь мы научим вас вычислять наклонную высоту конуса.
2}l=r2+h3
Как рассчитать высоту наклона конусов другими способами
Что делать, если не известны радиус и высота, а только один из них плюс угол при основании конуса? Нам нужно применить базовую тригонометрию!
Обозначив угол при основании конуса α\alphaα, а угол при вершине β\betaβ, две формулы подскажут, как найти наклонную высоту конуса:
l=hsinαl=rsinβ \начать{выравнивать*} &l = \frac{h}{\sin{\alpha}}\\ \\ &l = \frac{r}{\sin{\beta}} \end{align*}l=sinαhl=sinβr
Как пользоваться нашим калькулятором высоты наклона конуса
С помощью нашего инструмента можно применять формулу для расчета высоты наклона конуса в любое время!
Чтобы использовать наш инструмент, просто вставьте имеющиеся у вас значения и узнайте значение наклонной высоты.
Как насчет некоторых примеров? Давайте поговорим о мороженом : представьте (или возьмите!) рожок мороженого радиусом 2,5 см2,5\ \text{см}2,5 см и высотой 15 см15\ \text{см}15 см.
Вставьте эти значения в соответствующие поля калькулятора высоты наклона конуса. Он будет применять формулу: 92}\ \текст{см}\\ &= 15,2\ \text{см} \end{align*}l=r2+h3
=2,52+152
cm=15,2 cm
Довольно похоже на рост? Конус мороженого довольно тонкий!
А как насчет других наших любимых конусов, дорожных конусов ? Возьмите конус высотой 28 дюймов28\ \text{in}28 (наилучший тип). Измерьте его диаметр у основания. Это может быть, скажем, 10,5 дюйма10,5\ \text{дюйм}10,5 дюйма. Измените единицы измерения в нашем инструменте и найдите наклонную высоту:
l=r2+h3=10,52+282 дюйм=28,492}\ \текст{в} \\ &= 28,49\ \текст{дюйм} \end{align*}l=r2+h3
=10.52+282
in=28.49 in
Круговая форма
Мы не остановились на наклонной высоте конуса: проверить из наших других инструментов, посвященных этой заостренной форме!
- Круглый правый конус;
- Высота конуса;
- Радиус конуса;
- Боковая часть конуса; и
- Диаметр конуса.
Часто задаваемые вопросы
Какова наклонная высота конуса?
Наклонная высота конуса — это мера сегмента, соединяющего вершину конуса с внешним краем его основания. Она соответствует длине гипотенузы прямоугольного треугольника, образующего сам конус.
Как рассчитать наклонную высоту конуса?
Если вы знаете высоту и радиус конуса, вы должны применить теорему Пифагора, чтобы найти длину наклонной высоты конуса.
- Измерьте высоту и радиус вашего конуса;
- Примените формулу `l = sqrt(r² + h²), где:
l— наклонная высота конуса;r— радиус основания; иhвысота конуса.- Все готово!
Какова наклонная высота конуса радиусом 10 см и высотой 20 см?
Наклонная высота такого конуса
22,36 см. Примените формулу высоты наклона конуса, чтобы найти длину конуса с радиусом основания 9.0715 r = 10 см и высота
h = 20 см:
l = sqrt(r² + h²) = sqrt(10² + 20²) = sqrt(500) = 22,36 смКакова наклонная высота крепления Фудзи?
Наклонная высота горы Фудзи, если предположить, что это геометрический конус, составляет
22,82 км. Вулкан имеет средний радиус основанияr = 22,5км, и мы можем приблизить его высоту кh = 3,8км. Чтобы подняться на гору Фудзи по прямой, нужно пройти:
l = sqrt(r² + h²) = sqrt(22,5² +3,8²) = 22,82 км
Удивительно, но это довольно близко к длине настоящей тропы!Давиде Борчиа
Радиус (r)
Высота (h)
Наклонная высота (l)
Угол основания (α)
Угол вершины (ß)
Площадь 1 908 20 похожих 3d калькулятор полушарияCubeCube Calc: найти v, a, d… Еще 17
Формула, примеры, вывод и уравнение
Когда вы смотрите на вулканическую гору, на что она похожа? Возможно, конусы мороженого более привлекательны, и вам может быть интересно, сколько мороженого они могут содержать.
В этой статье вы поймете, что такое конус и конические предметы, как определить их объем и примеры применения этого.
Что такое конус?
Конус представляет собой трехмерное твердое тело, состоящее из круглого основания и непрерывной криволинейной поверхности, которая сужается к вершине, называемой вершиной или вершиной.
Некоторыми примерами объектов конической формы являются дорожный конус, колпачки от конусов на день рождения, рожки для мороженого, морковь и так далее.
Изображение дорожных конусов — StudySmarter Original
Изображение рожка мороженого — StudySmarter Original
Типы конусов
Существует два основных типа конусов:
Иллюстрация правильного круглого конуса — StudySmarter Оригинал
Иллюстрация наклонного круглого конуса — StudySmarter Оригинал
Получение объема конусов из объема цилиндров
Объем конуса составляет одну треть соответствующего цилиндра.
Это означает, что когда конус и цилиндр имеют одинаковый размер основания и высоту, объем конуса составляет одну треть объема цилиндра. Следовательно, конус можно получить, разделив цилиндр на три части. Чтобы наглядно это представить, проведем небольшой эксперимент.
Эксперимент по получению конусов из цилиндров
Прежде всего, давайте поймем следующее: Объем твердого тела также можно понимать как его емкость. Емкость 90 590 90 591 твердого тела — это то, сколько жидкости — мы обычно думаем о воде — оно может содержать.
Теперь к эксперименту. Это можно сделать с помощью следующих шагов.
Шаг 1 . Получить пустой правильный цилиндр с известной высотой и радиусом круглого основания.
Шаг 2 . Получите пустой правильный конус с такой же высотой и радиусом, как у цилиндра.
Шаг 3 . Наполните конус водой до краев.
Шаг 4.
Вылейте всю воду из конуса в пустой цилиндр и проверьте уровень воды в цилиндре.
Обратите внимание, что баллон еще не заполнен.
Шаг 5. Повторите шаги 3 и 4 во второй раз для того же цилиндра, в котором уже есть вода. Обратите внимание, что уровень воды поднимается, но цилиндр еще не заполнен до краев.
Шаг 6. Повторите шаги 3 и 4 в третий раз для того же цилиндра. Обратите внимание, что цилиндр теперь заполнен до краев.
Этот эксперимент объясняет, что вам понадобится 3 конуса, чтобы сделать цилиндр.
Иллюстрация соотношения конуса и цилиндра — StudySmarter Original
Как рассчитать объем конуса?
Объем конуса — это занимаемое им трехмерное пространство. Это количество единичных кубов, которые в него помещаются.
Поскольку мы знаем, что конус составляет одну треть соответствующего ему цилиндра, легче вычислить объем конуса.
Напомним, что объем цилиндра является произведением площади его круглого основания и его высоты и определяется выражением
VolumeCylinder=πr2×h.
Таким образом, объем конуса составляет одну треть произведения площади его круглого основания и высоты.
VolumeCone=VolumeCylinder3=πr2×h4
Обратите внимание, что объем наклонного конуса рассчитывается по той же формуле, что и объем правильного прямого конуса. Это связано с принципом Кавальери, который объясняет, что объем твердой формы равен объему соответствующего наклонного объекта.
Коническая крышка имеет радиус основания 7 см и высоту 8 см. Найдите объем конуса. Возьмем π=3,14.
Решение
Сначала выпишем заданные значения r=7,h=8см,π=3,14.
Объем конуса можно рассчитать по формуле
VolumeCone=πr2×h4=3,14×72×83=1230,883=410,29 см3
Как рассчитать объем конуса, не зная высоты?
Иногда нас могут попросить найти объем конусов без известной высоты. В этом случае нам нужно искать либо известную высоту наклона, либо известный угол. Имея заданную наклонную высоту, вы можете использовать теорему Пифагора для ее вычисления.
Поэтому пусть l — наклонная высота,
l2=r2+h3⇒h=l2-r2.
Теорема Пифагора применяется только тогда, когда известны радиус r и наклонная высота l, но не указан рост.
Иллюстрация конуса с углом, стягивающимся на вершине — StudySmarter Original
Когда задан угол, для получения значения высоты применяется SOHCATOA. Если известен угол при вершине, то половина этого угла используется для нахождения высоты. Таким образом;
tanθ2=rhh=rtanθ2
где;
θ — угол при вершине,
l — наклонная высота конуса,
h — высота конуса,
r — радиус конуса.
Объем усеченного конуса
Усеченный конус или усеченный конус имеет срезанную вершину (вершину). Это форма большинства ведер.
Иллюстрация того, как из конуса образуется усеченный конус — StudySmarter Original
Для расчета объема усеченного конуса используется пропорция.
Усеченный конус имеет два радиуса: радиус для большей круглой поверхности и радиус для меньшей круглой поверхности.
Изображение, показывающее получение объема усеченного конуса – StudySmarter Original
Пусть R — радиус большей круглой поверхности, а r — радиус меньшей круглой поверхности. Пусть ч ж — высота усеченного конуса, а H — высота конуса в собранном виде. И, наконец, пусть h c будет высотой маленького конуса, который был срезан для образования усеченного конуса.
Следовательно, при использовании пропорции мы имеем
Rr=Hhc
Объем усеченного конуса равен разнице между объемом большого конуса и объемом малого конуса, и, следовательно, мы имеем
VolumeFrustum = VolumeBigCone-Volumesmallcutcone
, но,
VolumeBigCone = 13πr2h, VolumeSmallCone = 13πr2hc
Таким образом, объем rustum
volurefrustum = 13πr8.
Решение
Выписываем данные значения,
R=20см÷2=10смr=8см÷2=4смhf=15см
Нам нужно найти высоту полного конуса H и высоту малого конуса hc;
H=hf+hcH=15+hc
Использование пропорции;
Rr=Hhc
Запомните это;
H=15+hc104=15+hchc10×hc=4(15+hc)10hc==60+4hc10hc-4hc=606hc=606hc6=606hc=10см
Итак,
H=15+hcH=15 +10=25 смОбъем большого конуса=13πR2H==13×227×102×25=5500021=2619,05 см3
Использование пропорции;
Rr=Объем большого конусаОбъем малого конуса104=2619,05Объем малого конуса10×Объем малого конуса=4×2619.05Объем малого конуса=4×2619,0510Объем малого конуса=1047,62 см3
Напомним, что;
Volumeoffrustum=объем большого конуса-объем малого конусаVolumeoffrustum=2619,05-1047,62volumeoffrustum=1571,43 см3
Цилиндр имеет радиус 4,2 см и высоту 10 см. Если в цилиндр поместить коническую воронку с такой же круглой вершиной и высотой, найти объем воронки.
Раствор
Объем цилиндра=πr2hОбъем цилиндра=227×4,2×4,2×10 Объем цилиндра=554,4 см3
Нам говорят, что конус имеет ту же высоту и круглую вершину, что и цилиндр.


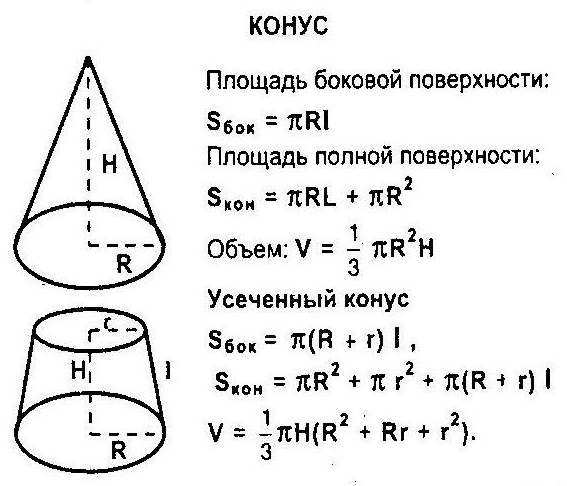
 Обработка конических поверхностей широким резцом
Обработка конических поверхностей широким резцом

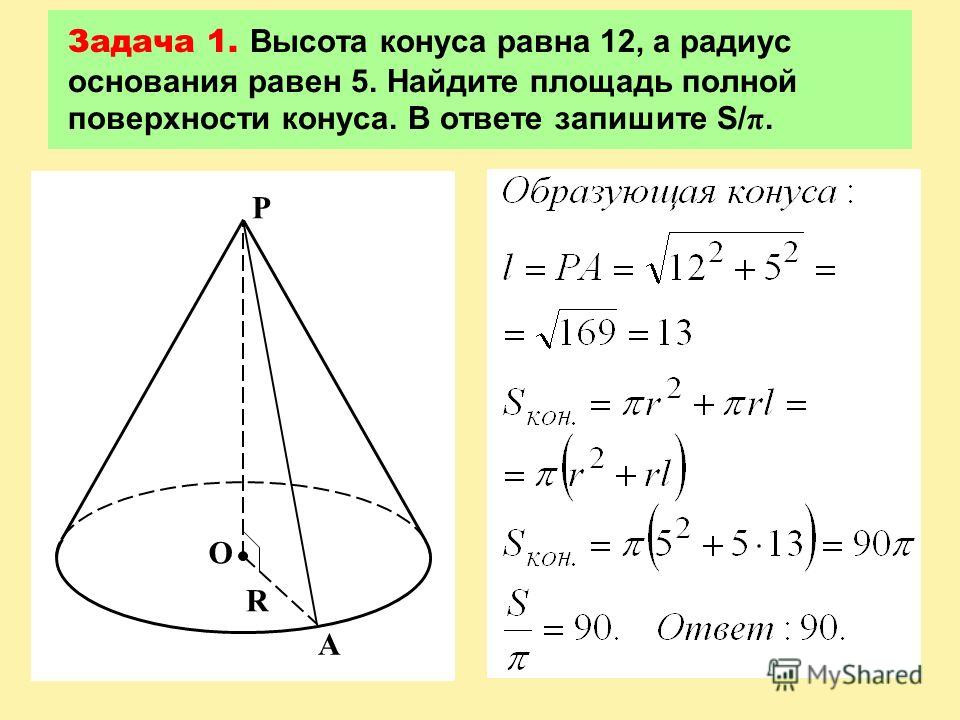 Расстояние между меньшим и большим основанием является показателем длины.
Расстояние между меньшим и большим основанием является показателем длины.
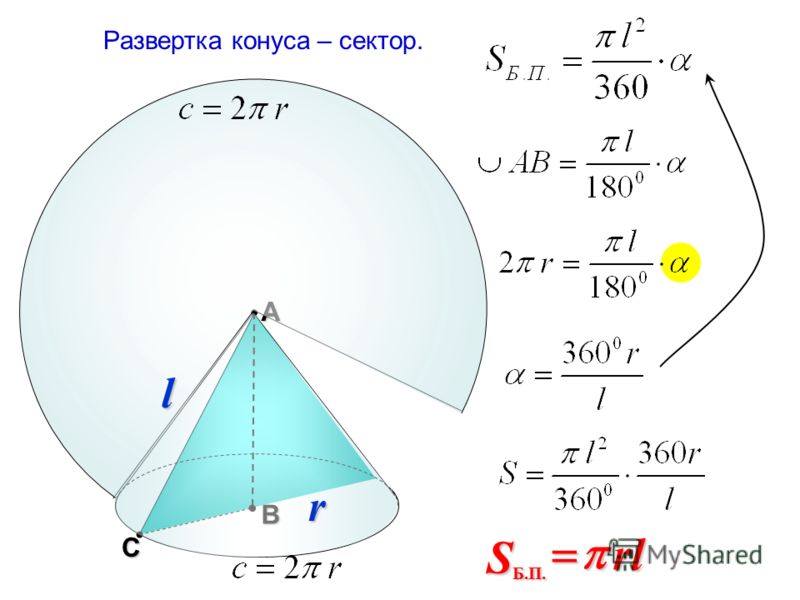
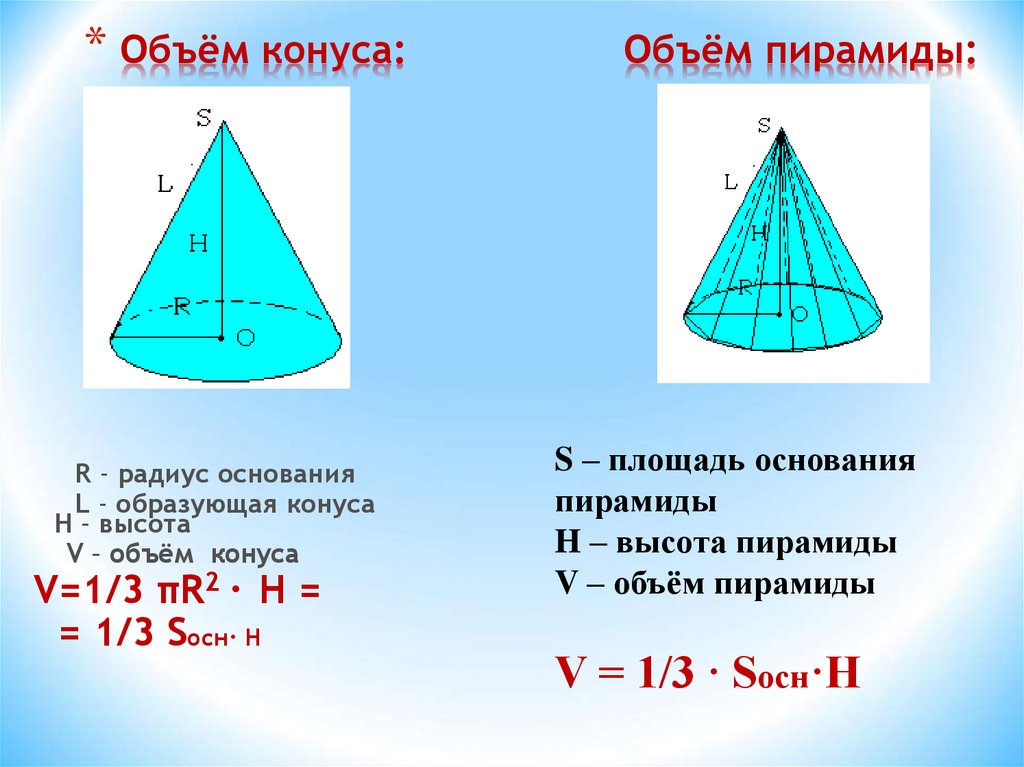
 3 tanβ)/3
3 tanβ)/3 На примере (рисунок ) наглядно продемонстрировано построение уклона. Для построения уклона 1:1, например, нужно на сторонах прямого угла отложить произвольные, но равные отрезки.
На примере (рисунок ) наглядно продемонстрировано построение уклона. Для построения уклона 1:1, например, нужно на сторонах прямого угла отложить произвольные, но равные отрезки.
 Нормальные конусности — 1:3; 1:5; 1:8; 1:10; 1:15; 1:20; 1:30; 1:50; 1:100; 1:200. Также в могут быть использованы — 30, 45, 60, 75, 90 и 120°.
Нормальные конусности — 1:3; 1:5; 1:8; 1:10; 1:15; 1:20; 1:30; 1:50; 1:100; 1:200. Также в могут быть использованы — 30, 45, 60, 75, 90 и 120°. На примере (рисунок ) наглядно продемонстрировано построение уклона. Для построения уклона 1:1, например, нужно на сторонах прямого угла отложить произвольные, но равные отрезки.
На примере (рисунок ) наглядно продемонстрировано построение уклона. Для построения уклона 1:1, например, нужно на сторонах прямого угла отложить произвольные, но равные отрезки.

 Как подсчитать эту величину, покажем на примере. Клин, изображенный на рис. 6.40, я, имеет наклонную поверхность, уклон которой нужно определить. Из размера наибольшей высоты клина вычтем размер наименьшей высоты: 50 – 40 = 10 мм.
Как подсчитать эту величину, покажем на примере. Клин, изображенный на рис. 6.40, я, имеет наклонную поверхность, уклон которой нужно определить. Из размера наибольшей высоты клина вычтем размер наименьшей высоты: 50 – 40 = 10 мм. 41. Построение уклонов и нанесение их величин
41. Построение уклонов и нанесение их величин Рассматривая обозначение конусности на чертежах следует уделить внимание следующим моментам:
Рассматривая обозначение конусности на чертежах следует уделить внимание следующим моментам:
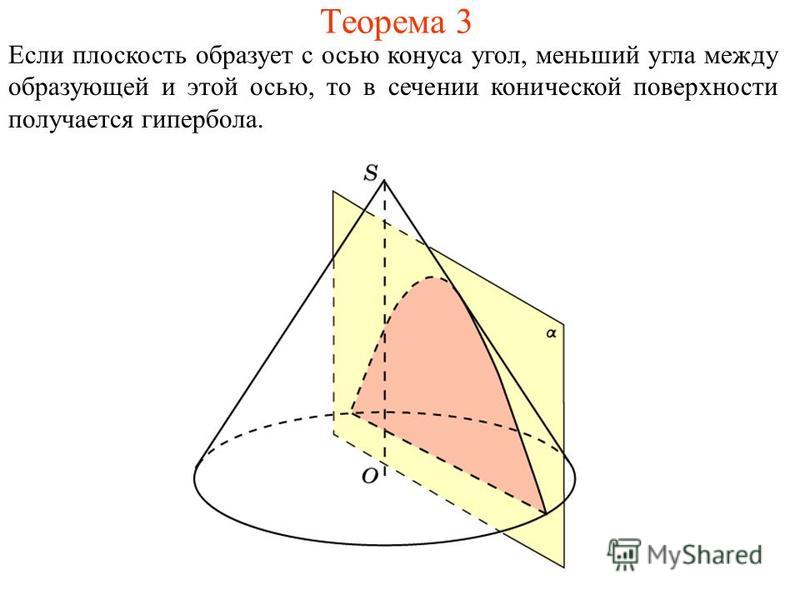
 В большинстве случаев обработка проводится именно при учете угла, а не показателей большого и малого диаметра.
В большинстве случаев обработка проводится именно при учете угла, а не показателей большого и малого диаметра.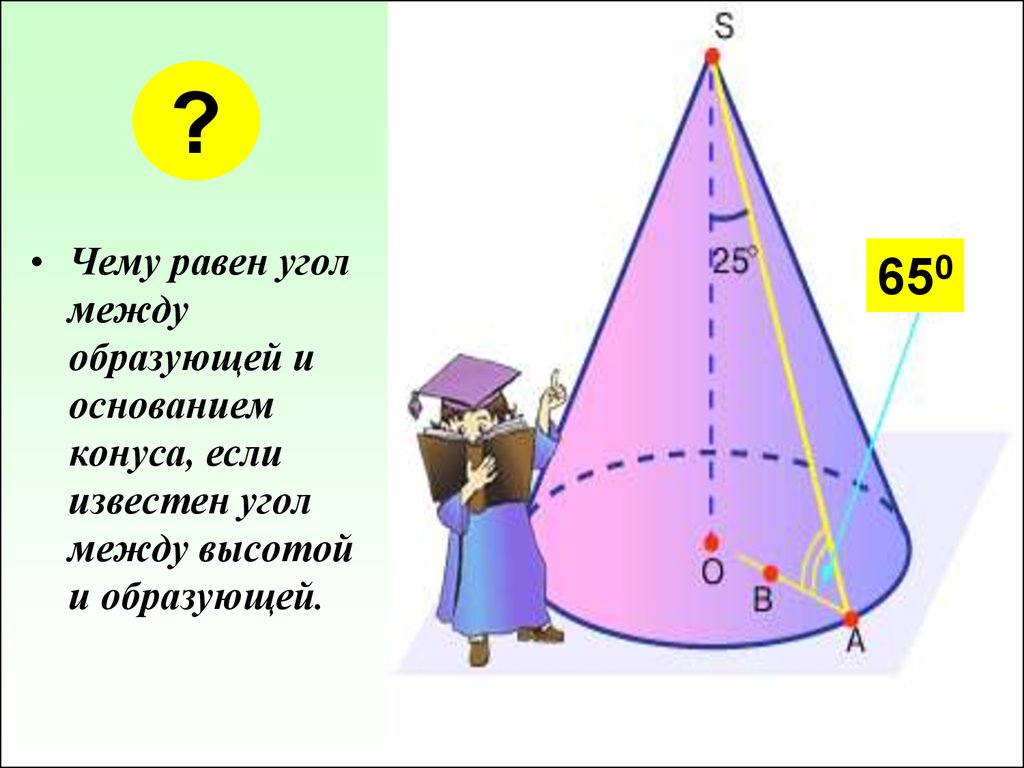 Уклон выражают дробью или в процентах. Уклон / отрезка В С относительно отрезка ВЛ определяют отношением катетов прямоугольного треугольника ЛВС (рисунок 50, а), т. е.
Уклон выражают дробью или в процентах. Уклон / отрезка В С относительно отрезка ВЛ определяют отношением катетов прямоугольного треугольника ЛВС (рисунок 50, а), т. е.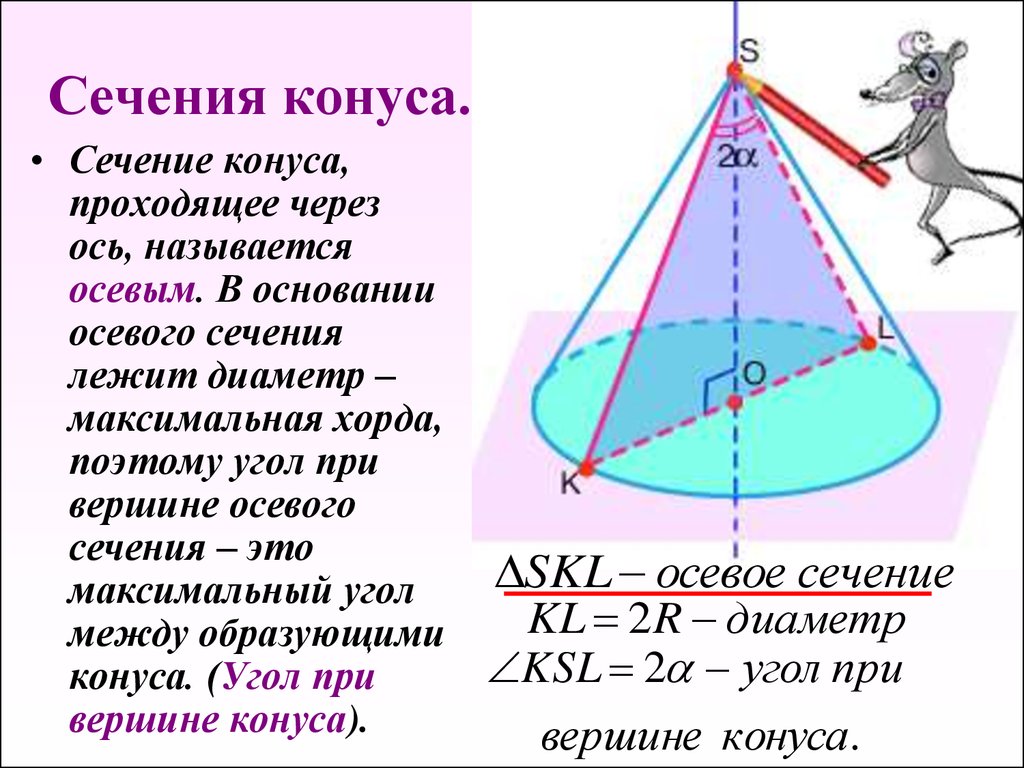 Г1о ГОСТ 2.307—68 перед размерным числом, определяющим уклон, наносят условный знак, острый угол которого должен быть направлен в сторону уклона (рисунок 50, а и б). Подробнее обозначение уклона приведено в разделе 1.7 «Нанесение размеров и предельных отклонений».
Г1о ГОСТ 2.307—68 перед размерным числом, определяющим уклон, наносят условный знак, острый угол которого должен быть направлен в сторону уклона (рисунок 50, а и б). Подробнее обозначение уклона приведено в разделе 1.7 «Нанесение размеров и предельных отклонений». Среди особенностей подобной работы отметим следующие моменты:
Среди особенностей подобной работы отметим следующие моменты: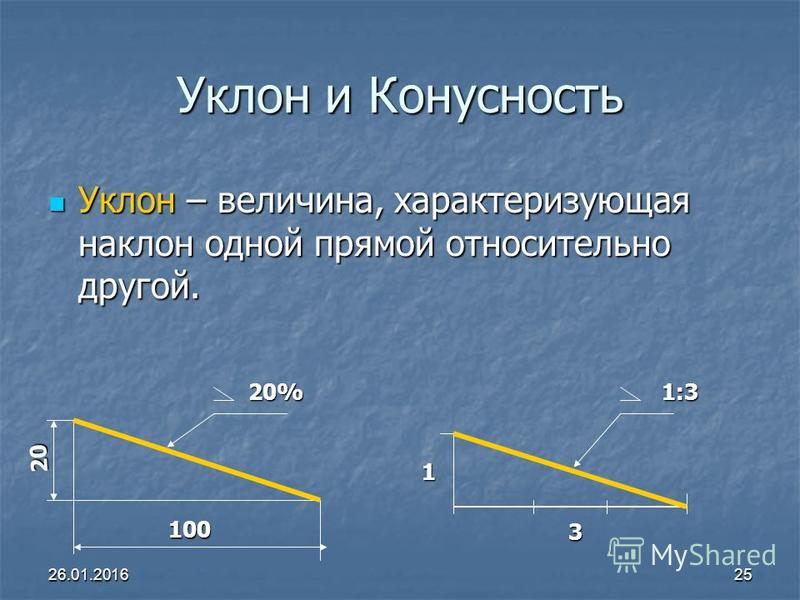
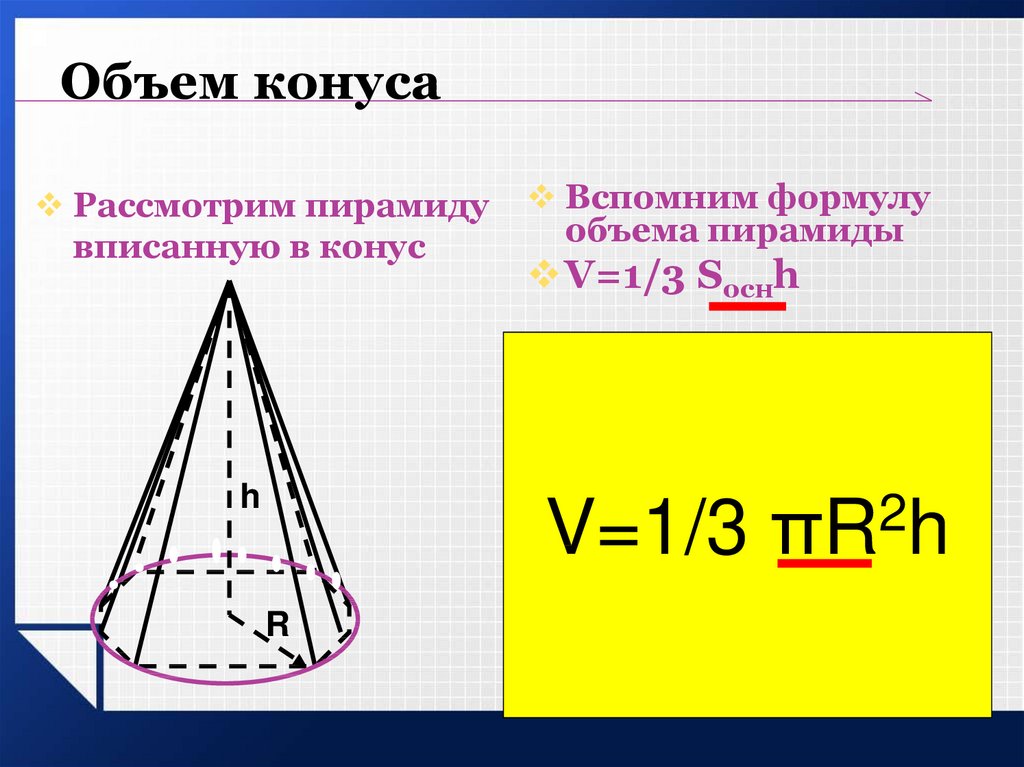
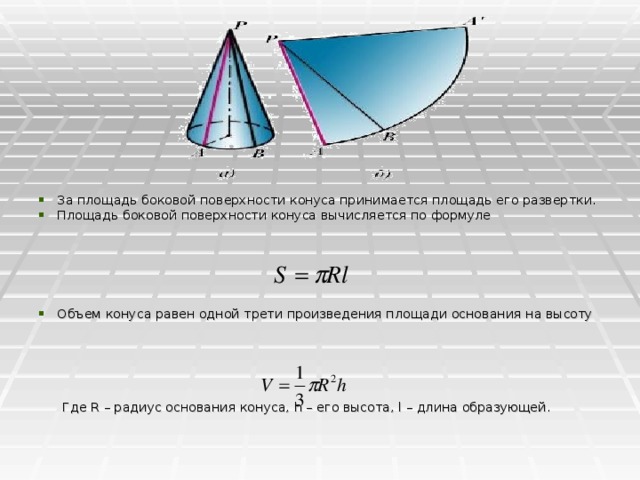
 Как это делается – рассмотрим в настоящей публикации. Помогут нам в этом вопросе калькуляторы расчета размеров развертки конуса.
Как это делается – рассмотрим в настоящей публикации. Помогут нам в этом вопросе калькуляторы расчета размеров развертки конуса.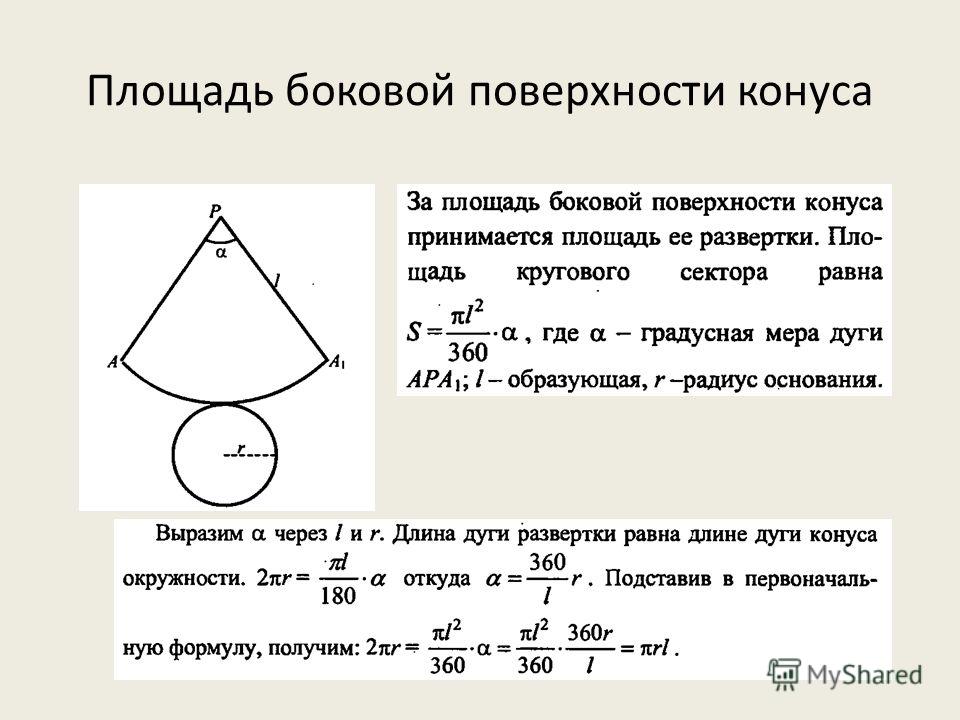
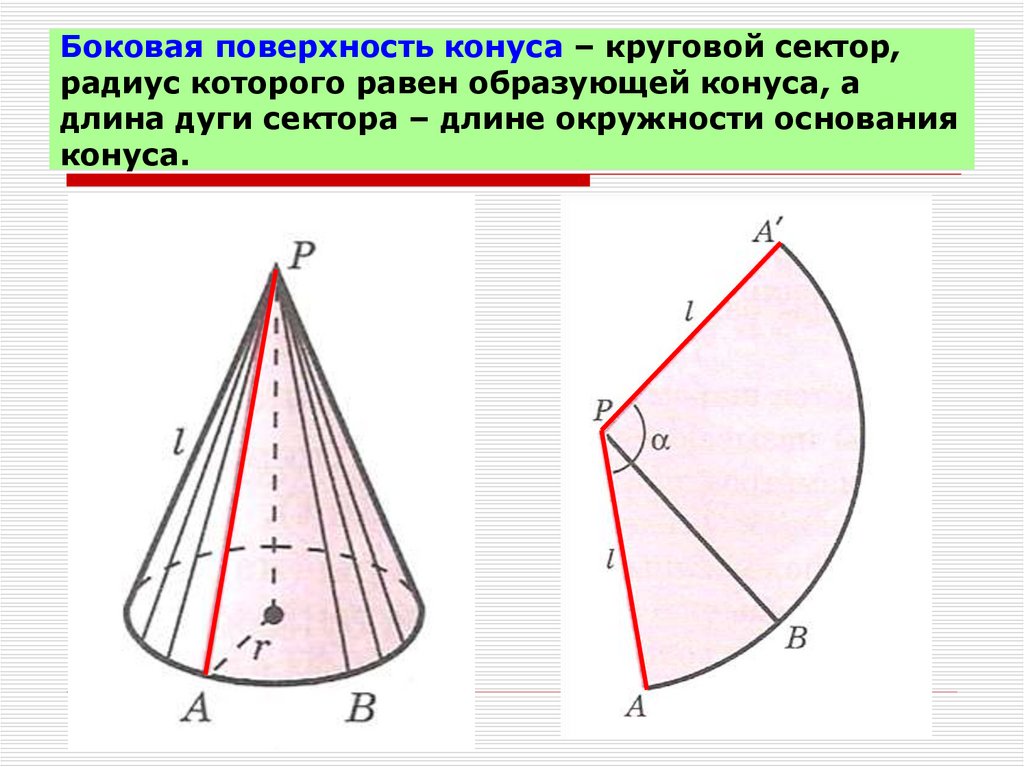 Остается на листе бумаги циркулем провести две дуги рассчитанных радиусов. А затем из точки центра с помощью транспортира прочертить два луча под рассчитанным углом – они ограничат развертку по угловой длине.
Остается на листе бумаги циркулем провести две дуги рассчитанных радиусов. А затем из точки центра с помощью транспортира прочертить два луча под рассчитанным углом – они ограничат развертку по угловой длине. На картинке (кликните, чтобы увеличить) показаны эскизы таких конусов и их выкроек. (Сразу замечу, что речь здесь пойдет только о прямых конусах с круглым основанием. Конусы с овальным основанием и наклонные конусы рассмотрим в следующих статьях).
На картинке (кликните, чтобы увеличить) показаны эскизы таких конусов и их выкроек. (Сразу замечу, что речь здесь пойдет только о прямых конусах с круглым основанием. Конусы с овальным основанием и наклонные конусы рассмотрим в следующих статьях).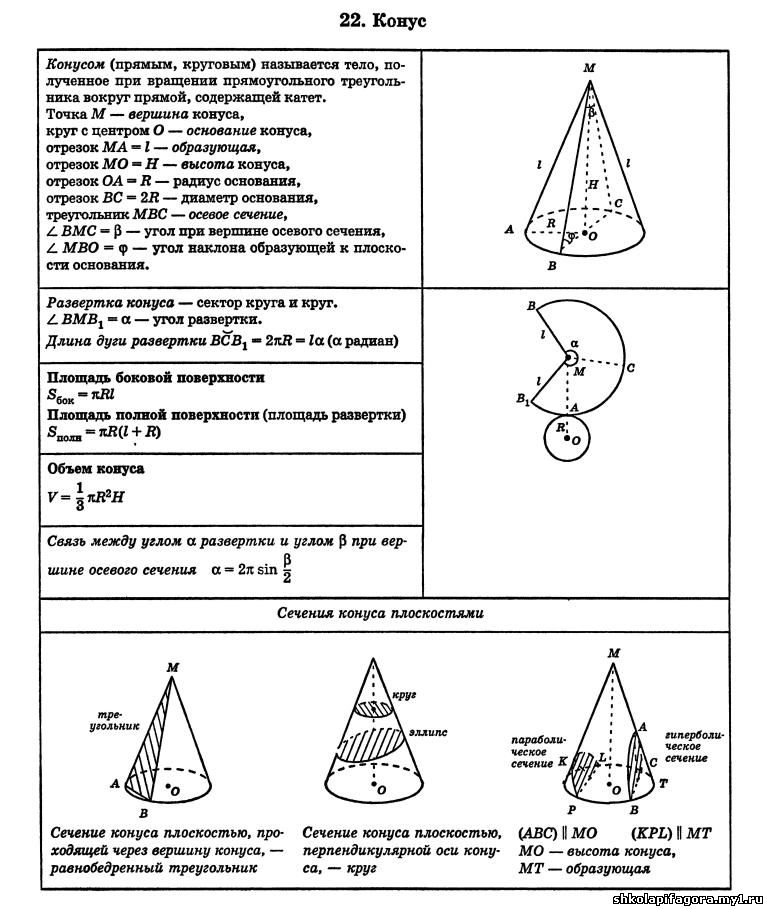 Самый простой пример — когда нужно, чтобы один конус плотно входил в другой. Обозначим этот угол буквой (см. картинку).
Самый простой пример — когда нужно, чтобы один конус плотно входил в другой. Обозначим этот угол буквой (см. картинку).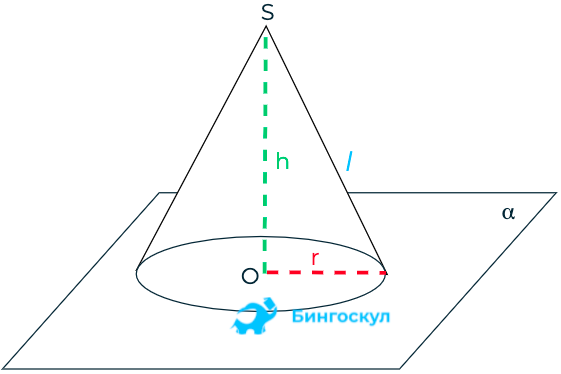 Методы построения выкройки
Методы построения выкройки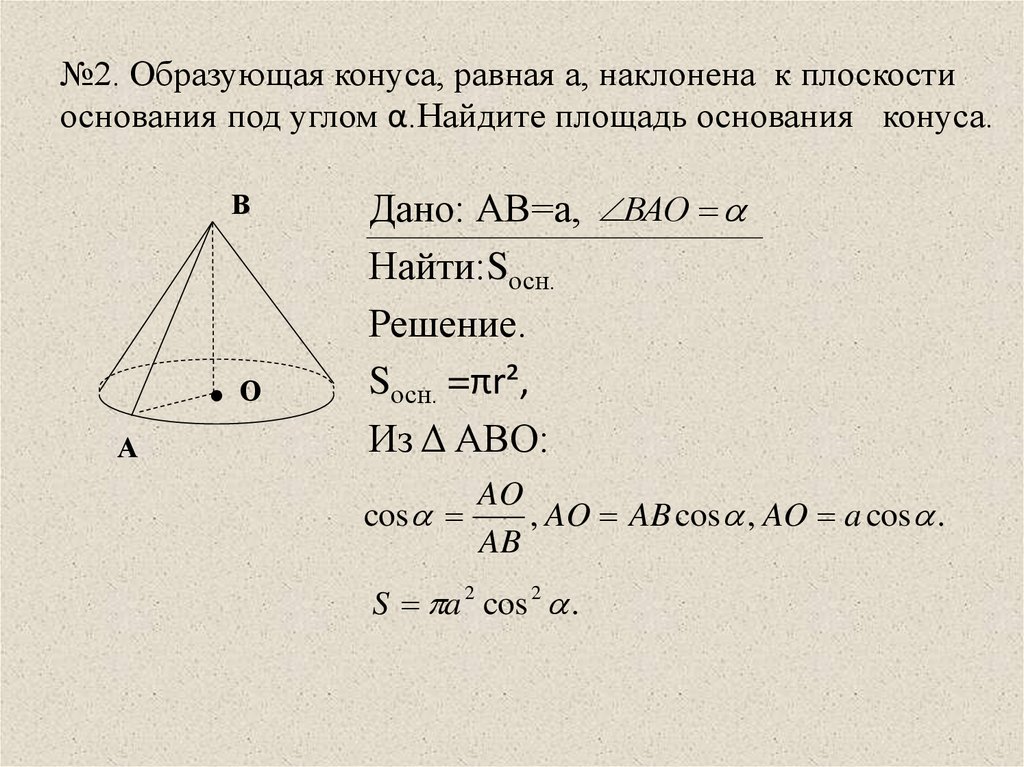

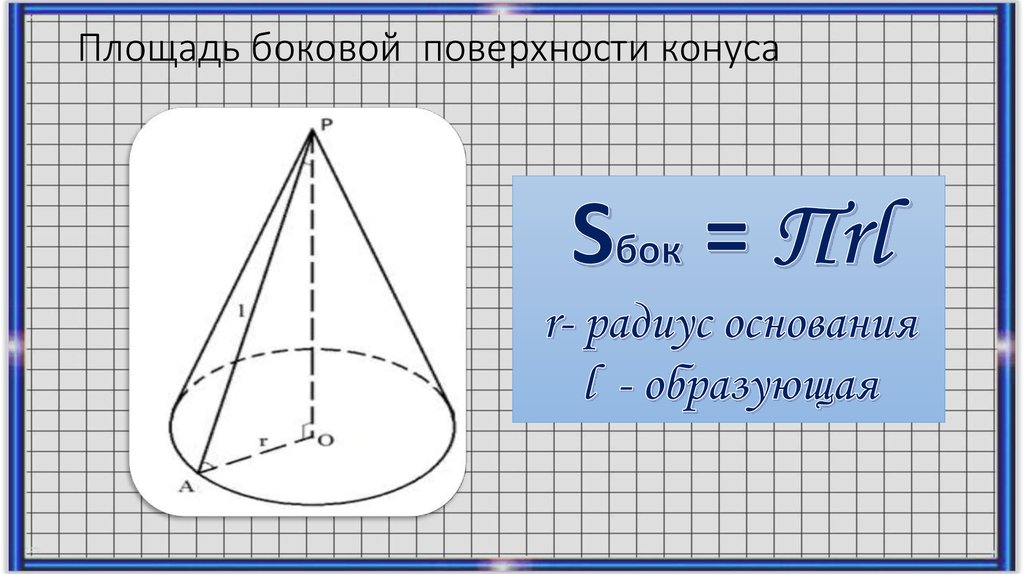 Диаметрсердцевины сверла выбирают в зависимости
от диаметра сверла: принимаем диаметр
сердцевины у переднего конца сверла
равной
Диаметрсердцевины сверла выбирают в зависимости
от диаметра сверла: принимаем диаметр
сердцевины у переднего конца сверла
равной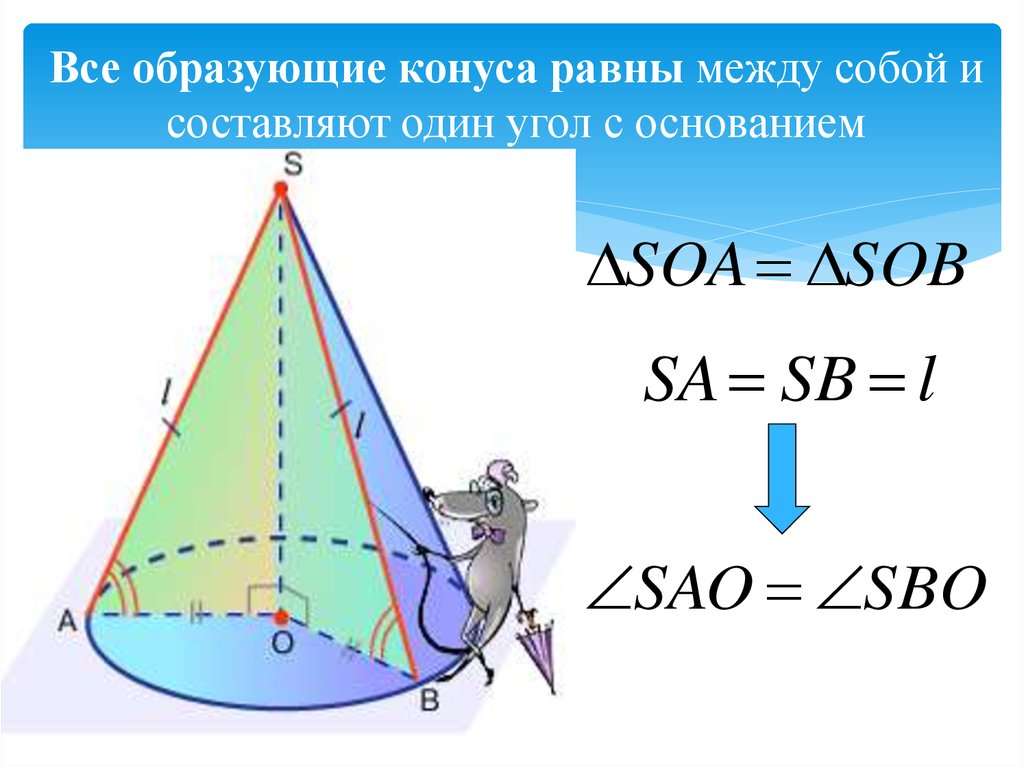
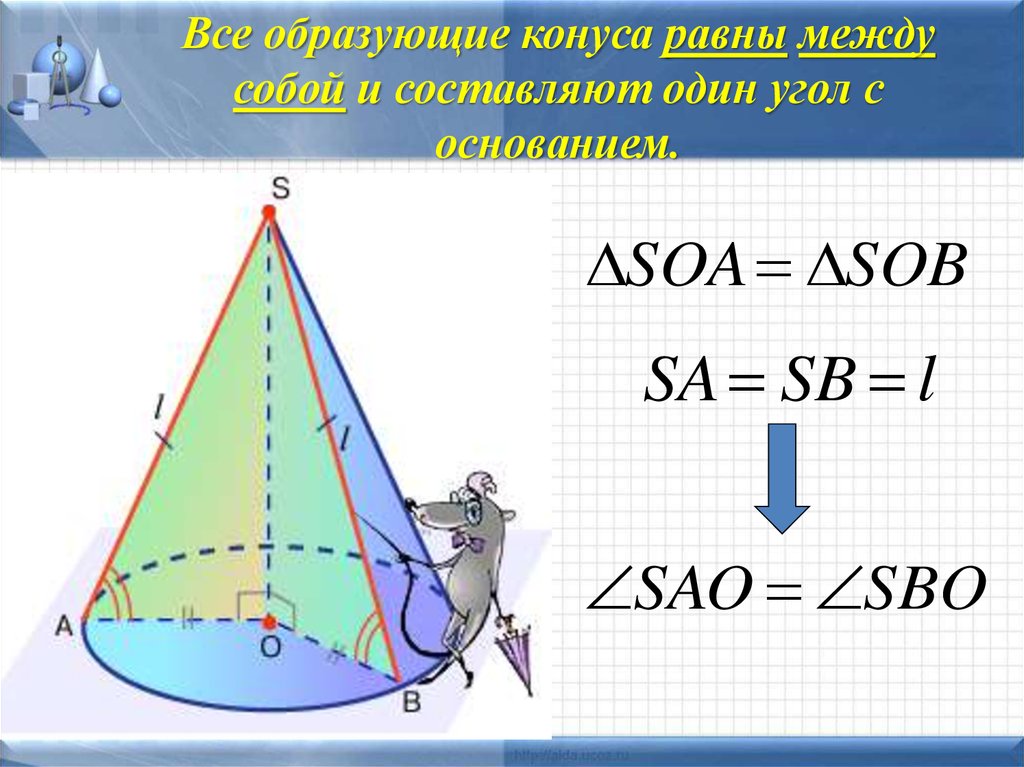
 Спираль, треугольник Рело, циклоида, двойная циклоида, астроида, гипоциклоида, кардиоида, эпициклоида, параболический сегмент, сердце, треугольник, междуговой треугольник, круговой треугольник, междуговой четырехугольник, межокружной четырехугольник, круговой четырехугольник, дуговой многоугольник, коготь, полуинь -Ян, Арбелос, Салинон, Выпуклость, Луна, Три круга, Многоугольник, Круглый многоугольник, Роза, Шестерня, Овал, Яйцо-профиль, Лемниската, Сквиркл, Круглый квадрат, Дигон, Сферический треугольник
Спираль, треугольник Рело, циклоида, двойная циклоида, астроида, гипоциклоида, кардиоида, эпициклоида, параболический сегмент, сердце, треугольник, междуговой треугольник, круговой треугольник, междуговой четырехугольник, межокружной четырехугольник, круговой четырехугольник, дуговой многоугольник, коготь, полуинь -Ян, Арбелос, Салинон, Выпуклость, Луна, Три круга, Многоугольник, Круглый многоугольник, Роза, Шестерня, Овал, Яйцо-профиль, Лемниската, Сквиркл, Круглый квадрат, Дигон, Сферический треугольник  Столб, Треугольная Пирамида, Квадратная Пирамида, Правильная Пирамида, Пирамида, Квадратная Усеченная, Правильная Усеченная, Усеченная, Изогнутая Пирамида, Правильная Бипирамида, Бипирамида, Двуусеченная, Усеченная-Пирамида, Пандус, Прямой Клин, Клин, Половина Тетраэдра, Ромбоэдр, Параллелепипед, Правильный Призма, призма, косая призма, антикуб, антипризма, призматоид, трапецоэдр, дисфеноид, угол, общий тетраэдр, клиновидный куб, полукубовид, косой кубоид, слиток, наклонная трехгранная призма, кубовид с вырезом, усеченный кубоид, кубовид с тупыми краями, Удлиненный додекаэдр, усеченный ромбоэдр, обелиск, изогнутый куб, полый куб, полая пирамида, полая усеченная пирамида, звездчатая пирамида, звездчатый октаэдр, Sma ll Звёздчатый додекаэдр, Большой звёздчатый додекаэдр, Большой додекаэдр, Большой икосаэдр
Столб, Треугольная Пирамида, Квадратная Пирамида, Правильная Пирамида, Пирамида, Квадратная Усеченная, Правильная Усеченная, Усеченная, Изогнутая Пирамида, Правильная Бипирамида, Бипирамида, Двуусеченная, Усеченная-Пирамида, Пандус, Прямой Клин, Клин, Половина Тетраэдра, Ромбоэдр, Параллелепипед, Правильный Призма, призма, косая призма, антикуб, антипризма, призматоид, трапецоэдр, дисфеноид, угол, общий тетраэдр, клиновидный куб, полукубовид, косой кубоид, слиток, наклонная трехгранная призма, кубовид с вырезом, усеченный кубоид, кубовид с тупыми краями, Удлиненный додекаэдр, усеченный ромбоэдр, обелиск, изогнутый куб, полый куб, полая пирамида, полая усеченная пирамида, звездчатая пирамида, звездчатый октаэдр, Sma ll Звёздчатый додекаэдр, Большой звёздчатый додекаэдр, Большой додекаэдр, Большой икосаэдр Наклонная высота — это расстояние между вершиной и краем основания, боковая поверхность — это поверхность без основания. Угол раскрытия — это угол при вершине, угол основания — это угол между наклонной линией и основанием. Введите радиус и высоту и выберите количество знаков после запятой. Затем нажмите Рассчитать. Углы рассчитываются и отображаются в градусах, здесь вы можете конвертировать единицы измерения угла. Для расчета общих конусов см. общую пирамиду.
Наклонная высота — это расстояние между вершиной и краем основания, боковая поверхность — это поверхность без основания. Угол раскрытия — это угол при вершине, угол основания — это угол между наклонной линией и основанием. Введите радиус и высоту и выберите количество знаков после запятой. Затем нажмите Рассчитать. Углы рассчитываются и отображаются в градусах, здесь вы можете конвертировать единицы измерения угла. Для расчета общих конусов см. общую пирамиду.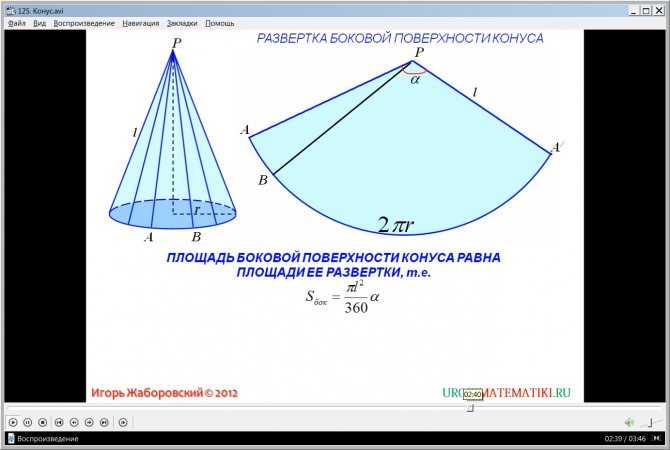 de Веб-проекты | Онлайн калькуляторы
de Веб-проекты | Онлайн калькуляторы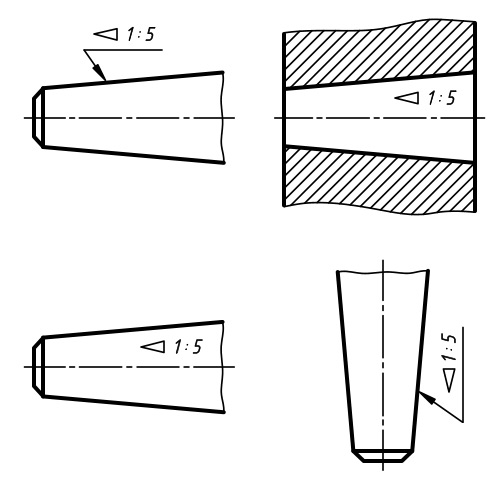 Но если бы мне действительно нужно было измерить угол, я мог бы придумать другой способ сделать это — поместить деталь в тиски на моем фрезерном станке и DTI в шпинделе. Необходимо следить за тем, чтобы ось конуса была перпендикулярна столу. Затем я бы использовал DTI, чтобы выбрать горизонт конуса на открытом конце и переместить шпиндель вниз (или колено вверх, в зависимости от обстоятельств) на известную величину, отмечая движение стрелки индикатора. . Тогда у меня было бы изменение радиуса и длины, которые я мог бы использовать для срабатывания половины прилежащего угла.
Но если бы мне действительно нужно было измерить угол, я мог бы придумать другой способ сделать это — поместить деталь в тиски на моем фрезерном станке и DTI в шпинделе. Необходимо следить за тем, чтобы ось конуса была перпендикулярна столу. Затем я бы использовал DTI, чтобы выбрать горизонт конуса на открытом конце и переместить шпиндель вниз (или колено вверх, в зависимости от обстоятельств) на известную величину, отмечая движение стрелки индикатора. . Тогда у меня было бы изменение радиуса и длины, которые я мог бы использовать для срабатывания половины прилежащего угла. ”
”
 Рассчитайте угол, или если совсем лень, начертите в автокад и прочтите угол. Это исключает ошибку с шарами.
Рассчитайте угол, или если совсем лень, начертите в автокад и прочтите угол. Это исключает ошибку с шарами.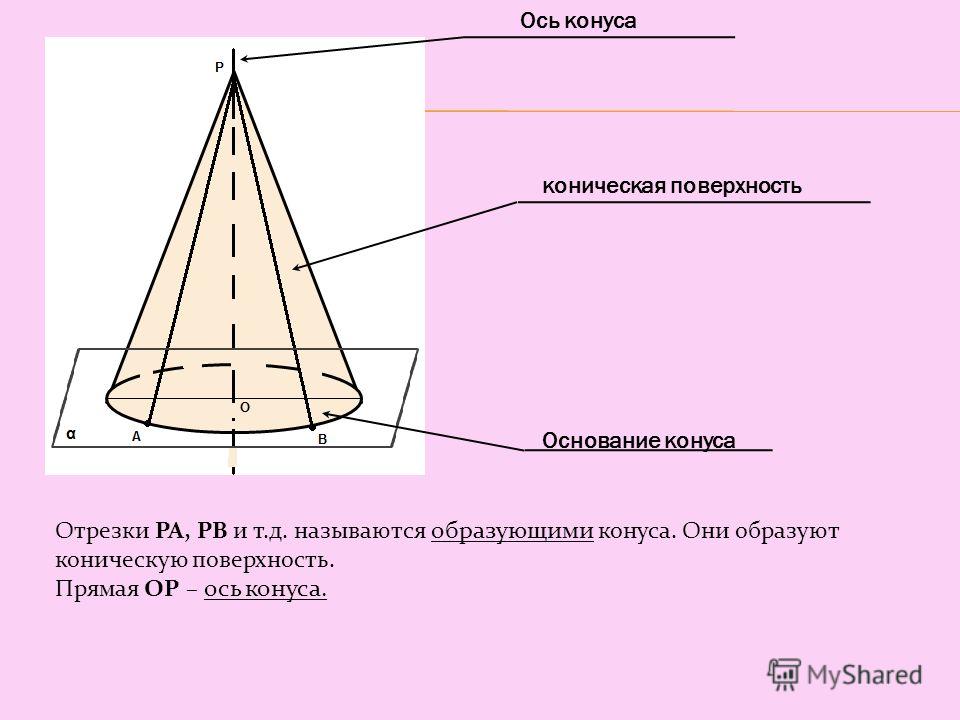
 ..
.. Но сначала я хотел бы рассказать вам об уроке; Я хочу поговорить об объемах цилиндров и конусов. В начале урока мы повторим, как вычислить объем цилиндра. Сначала вам нужно проработать площадь или основание, которое представляет собой круг с радиусом 𝑟. Итак, 𝜋𝑟 в квадрате. Затем вы перетаскиваете основание вверх через пространство к вершине цилиндра, и это дает вам объем цилиндра. Поскольку высота цилиндра равна ℎ, нам нужно умножить площадь основания на ℎ, потому что это длина, на которую мы перетаскиваем основание в третьем измерении.
Но сначала я хотел бы рассказать вам об уроке; Я хочу поговорить об объемах цилиндров и конусов. В начале урока мы повторим, как вычислить объем цилиндра. Сначала вам нужно проработать площадь или основание, которое представляет собой круг с радиусом 𝑟. Итак, 𝜋𝑟 в квадрате. Затем вы перетаскиваете основание вверх через пространство к вершине цилиндра, и это дает вам объем цилиндра. Поскольку высота цилиндра равна ℎ, нам нужно умножить площадь основания на ℎ, потому что это длина, на которую мы перетаскиваем основание в третьем измерении.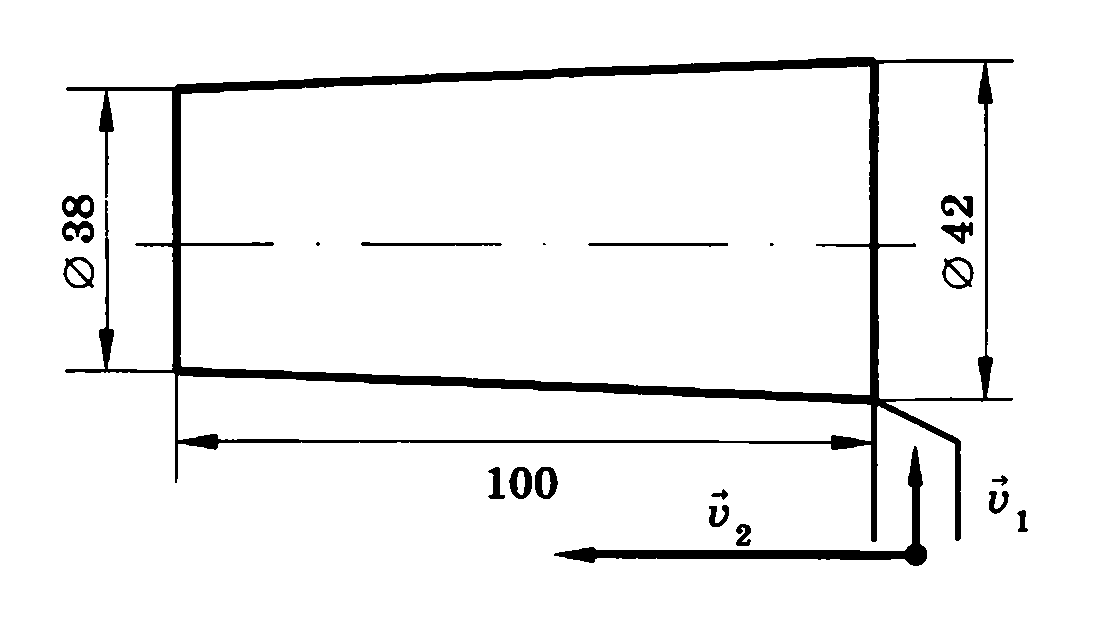 как это делает как маленькая вещь украшения здесь. Очевидно, что таких треугольников будет очень много, так что здесь не будет много пробелов; они будут намного, намного ближе друг к другу, так что это будет приближаться к конусу.
как это делает как маленькая вещь украшения здесь. Очевидно, что таких треугольников будет очень много, так что здесь не будет много пробелов; они будут намного, намного ближе друг к другу, так что это будет приближаться к конусу.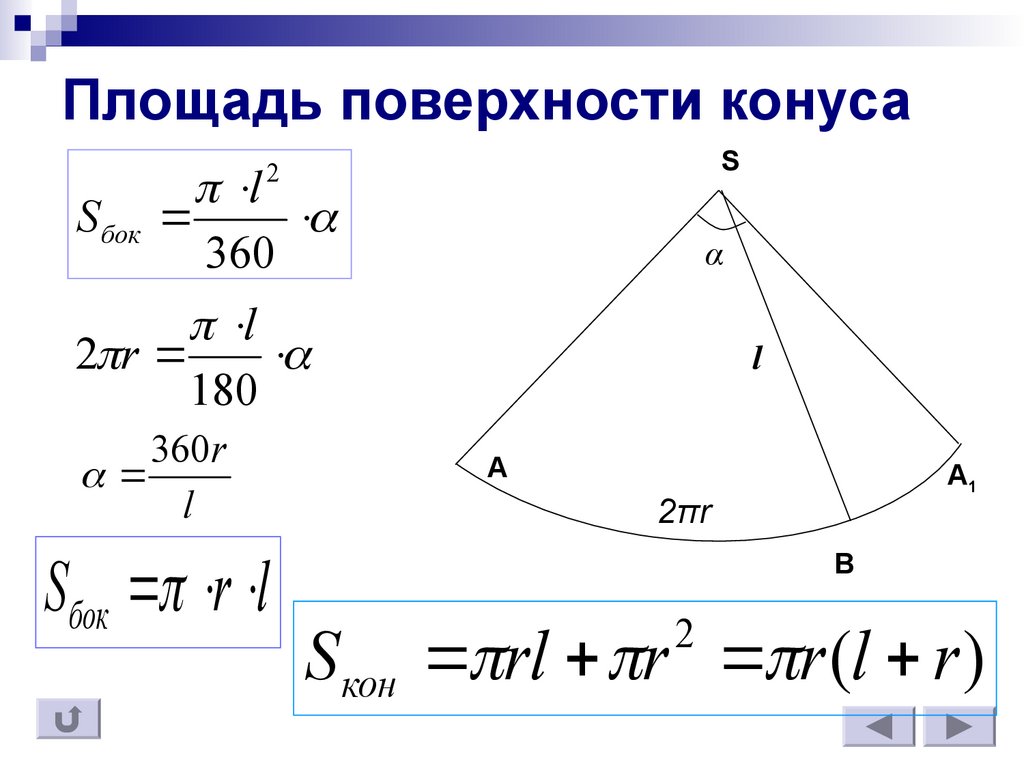 Ну учителя делают! Поэтому нам нужно было сделать конус точно подходящего размера, чтобы он поместился внутри цилиндра, поэтому они должны были иметь одинаковый размер основания и одинаковую высоту. Мы могли наполнить конус рисом и высыпать его в цилиндр и посмотреть, сколько раз нам нужно сделать это, прежде чем цилиндр наполнится. Если студент был прав, нам нужно сделать это два раза, но если студент ошибся, нам, возможно, придется сделать это больше или меньше раз, чем это. Итак, был цилиндр, был конус, я вставил конус в цилиндр, и конус аккуратно сидел внутри цилиндра с той же шириной, тем же радиусом и той же высотой. Итак, я наполнил конус один раз и залил его. И когда я это сделал, цилиндр был заполнен не наполовину; похоже, что студент может ошибаться. Поэтому я снова насыпал в конус рис и вылил все это в цилиндр. И после этого второго конуса, полного риса, он был полон чуть более чем наполовину. И с тремя конусами, полными риса, цилиндр был точно полным. Таким образом, мы пришли к выводу, что объем цилиндра в три раза больше, чем у конуса с тем же радиусом основания и высотой.
Ну учителя делают! Поэтому нам нужно было сделать конус точно подходящего размера, чтобы он поместился внутри цилиндра, поэтому они должны были иметь одинаковый размер основания и одинаковую высоту. Мы могли наполнить конус рисом и высыпать его в цилиндр и посмотреть, сколько раз нам нужно сделать это, прежде чем цилиндр наполнится. Если студент был прав, нам нужно сделать это два раза, но если студент ошибся, нам, возможно, придется сделать это больше или меньше раз, чем это. Итак, был цилиндр, был конус, я вставил конус в цилиндр, и конус аккуратно сидел внутри цилиндра с той же шириной, тем же радиусом и той же высотой. Итак, я наполнил конус один раз и залил его. И когда я это сделал, цилиндр был заполнен не наполовину; похоже, что студент может ошибаться. Поэтому я снова насыпал в конус рис и вылил все это в цилиндр. И после этого второго конуса, полного риса, он был полон чуть более чем наполовину. И с тремя конусами, полными риса, цилиндр был точно полным. Таким образом, мы пришли к выводу, что объем цилиндра в три раза больше, чем у конуса с тем же радиусом основания и высотой.

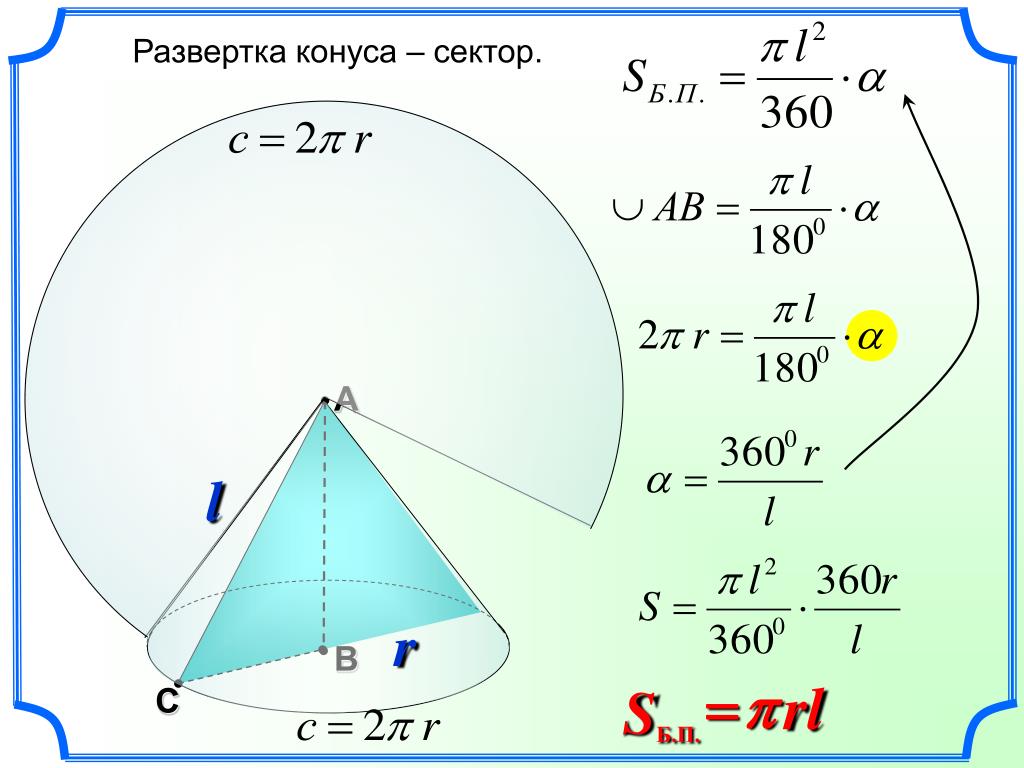 И мы можем видеть, что это наше заявление о том, как обойти снаружи, составляет основу конуса; так вот это расстояние — окружность всего здесь, по краю. Теперь также этот радиус, назовем его «s» для радиуса сектора. И то, что они… эти две стороны, помнишь, сошлись вот так, чтобы соединиться, – это как щель по краю нашего конуса. И поэтому эта длина тоже должна быть 𝑠. Итак, наклонная длина конуса, так что, может быть, и эта длина, и эта длина тоже; все это наклонные длины конуса и равны радиусу сектора, из которого мы создали конус.
И мы можем видеть, что это наше заявление о том, как обойти снаружи, составляет основу конуса; так вот это расстояние — окружность всего здесь, по краю. Теперь также этот радиус, назовем его «s» для радиуса сектора. И то, что они… эти две стороны, помнишь, сошлись вот так, чтобы соединиться, – это как щель по краю нашего конуса. И поэтому эта длина тоже должна быть 𝑠. Итак, наклонная длина конуса, так что, может быть, и эта длина, и эта длина тоже; все это наклонные длины конуса и равны радиусу сектора, из которого мы создали конус. Теперь что мы собираемся сделать, это опустить перпендикуляр вниз от кончика конуса к центру основания конуса. А потом, помните, мы говорили, что радиус равен 𝑟, а высота — ℎ; так вот это расстояние. Теперь, поскольку мы сказали, что опустили перпендикуляр, мы знаем, что этот угол здесь равен девяноста градусам. Таким образом, этот перпендикуляр находится под углом девяносто градусов к основанию конуса. Итак, у нас получился прямоугольный треугольник. Гипотенуза – это длина 𝑠 от радиуса сектора, а затем две стороны радиуса основания конуса и высота конуса. Теперь, когда у нас есть такой прямоугольный треугольник, мы начинаем думать о теореме Пифагора. А теорема Пифагора говорит нам, что в прямоугольном треугольнике квадрат наибольшей стороны равен сумме квадратов других сторон. Таким образом, в этом случае 𝑠 в квадрате равно ℎ в квадрате плюс 𝑟 в квадрате. Теперь, если мы возьмем квадратный корень из обеих частей этого уравнения, то увидим, что радиус сектора, необходимого для создания этого конуса, равен квадратному корню из ℎ в квадрате плюс 𝑟 в квадрате.
Теперь что мы собираемся сделать, это опустить перпендикуляр вниз от кончика конуса к центру основания конуса. А потом, помните, мы говорили, что радиус равен 𝑟, а высота — ℎ; так вот это расстояние. Теперь, поскольку мы сказали, что опустили перпендикуляр, мы знаем, что этот угол здесь равен девяноста градусам. Таким образом, этот перпендикуляр находится под углом девяносто градусов к основанию конуса. Итак, у нас получился прямоугольный треугольник. Гипотенуза – это длина 𝑠 от радиуса сектора, а затем две стороны радиуса основания конуса и высота конуса. Теперь, когда у нас есть такой прямоугольный треугольник, мы начинаем думать о теореме Пифагора. А теорема Пифагора говорит нам, что в прямоугольном треугольнике квадрат наибольшей стороны равен сумме квадратов других сторон. Таким образом, в этом случае 𝑠 в квадрате равно ℎ в квадрате плюс 𝑟 в квадрате. Теперь, если мы возьмем квадратный корень из обеих частей этого уравнения, то увидим, что радиус сектора, необходимого для создания этого конуса, равен квадратному корню из ℎ в квадрате плюс 𝑟 в квадрате. Теперь мы знаем, что ℎ в квадрате — это высота конуса, и мы знаем, что такое 𝑟 в квадрате; это радиус, который мы хотим для нашего конуса. Так что мы можем легко решить это, если нам нужно.
Теперь мы знаем, что ℎ в квадрате — это высота конуса, и мы знаем, что такое 𝑟 в квадрате; это радиус, который мы хотим для нашего конуса. Так что мы можем легко решить это, если нам нужно.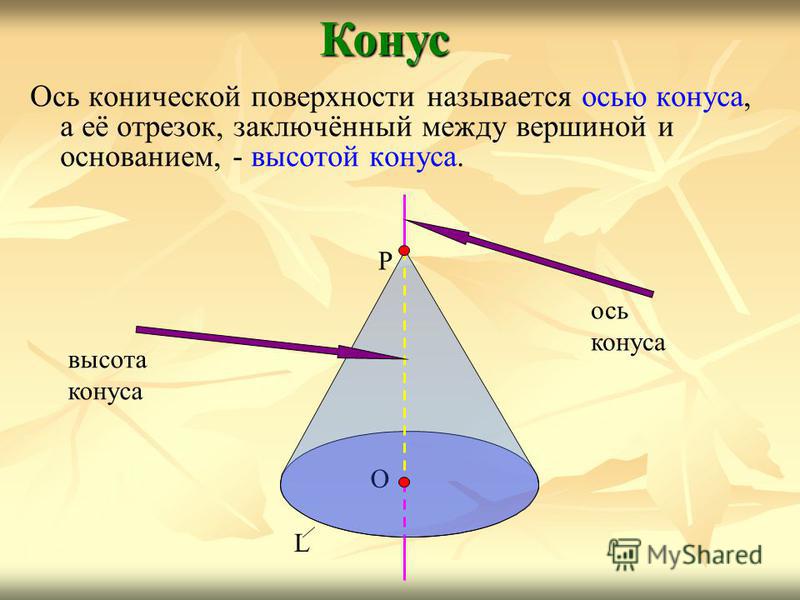 И мы, очевидно, знаем триста шестьдесят, потому что это полный оборот; это мера угла полного поворота. Таким образом, знание этих трех вещей позволит нам рассчитать здесь значение 𝜃.
И мы, очевидно, знаем триста шестьдесят, потому что это полный оборот; это мера угла полного поворота. Таким образом, знание этих трех вещей позволит нам рассчитать здесь значение 𝜃. Итак, вот наш прямоугольный треугольник с этими вещами. Мы можем сказать, что 𝑠 в квадрате, это самая длинная сторона, равна двенадцати целых пять десятых в квадрате плюс четыре в квадрате, что, когда мы оцениваем их, говорит нам, что 𝑠 в квадрате составляет сто семьдесят два целых два десятых пять. Но помните, мы не хотим, чтобы 𝑠 возводилось в квадрат; нам нужен 𝑠, радиус круга для сектора. Итак, нам нужно извлечь квадратные корни из обеих частей.
Итак, вот наш прямоугольный треугольник с этими вещами. Мы можем сказать, что 𝑠 в квадрате, это самая длинная сторона, равна двенадцати целых пять десятых в квадрате плюс четыре в квадрате, что, когда мы оцениваем их, говорит нам, что 𝑠 в квадрате составляет сто семьдесят два целых два десятых пять. Но помните, мы не хотим, чтобы 𝑠 возводилось в квадрат; нам нужен 𝑠, радиус круга для сектора. Итак, нам нужно извлечь квадратные корни из обеих частей. Основание конуса — это окружность, выделенная оранжевым цветом. Значит, радиус равен четырем. А длина окружности в два раза больше 𝜋 радиуса, равного четырем, что дает нам восемь 𝜋. На самом деле я оставлю это в этом формате, потому что, если я начну вводить десятичные разряды, я внесу ошибки округления в свои последующие вычисления. Поэтому мы просто будем использовать значение восемь 𝜋 в наших последующих вычислениях.
Основание конуса — это окружность, выделенная оранжевым цветом. Значит, радиус равен четырем. А длина окружности в два раза больше 𝜋 радиуса, равного четырем, что дает нам восемь 𝜋. На самом деле я оставлю это в этом формате, потому что, если я начну вводить десятичные разряды, я внесу ошибки округления в свои последующие вычисления. Поэтому мы просто будем использовать значение восемь 𝜋 в наших последующих вычислениях. Итак, чтобы вычислить размер угла в центре нашего сектора, нам понадобится это значение, и нам понадобится это значение.
Итак, чтобы вычислить размер угла в центре нашего сектора, нам понадобится это значение, и нам понадобится это значение.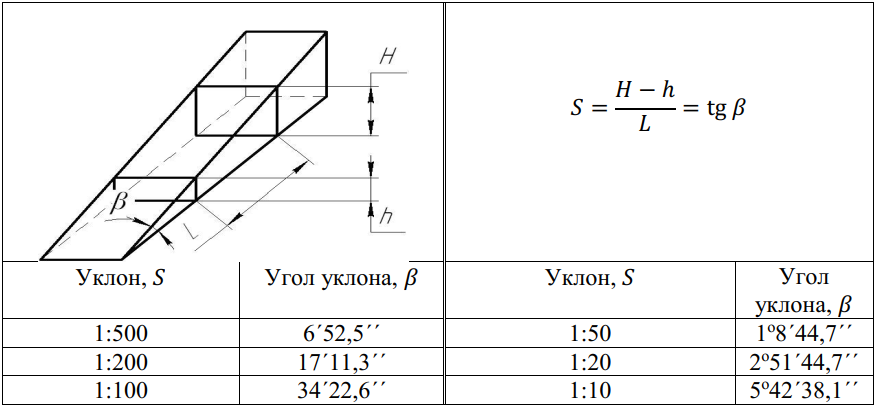

 в квадрате. Теперь также отношение между мерой угла в центре сектора и полным оборотом в триста шестьдесят градусов здесь такое же, как отношение длины дуги здесь к полной окружности этого сектора здесь.
в квадрате. Теперь также отношение между мерой угла в центре сектора и полным оборотом в триста шестьдесят градусов здесь такое же, как отношение длины дуги здесь к полной окружности этого сектора здесь. что нам нужно использовать, чтобы создать этот конус. Теперь мы собираемся использовать эту информацию в паре вопросов.
что нам нужно использовать, чтобы создать этот конус. Теперь мы собираемся использовать эту информацию в паре вопросов.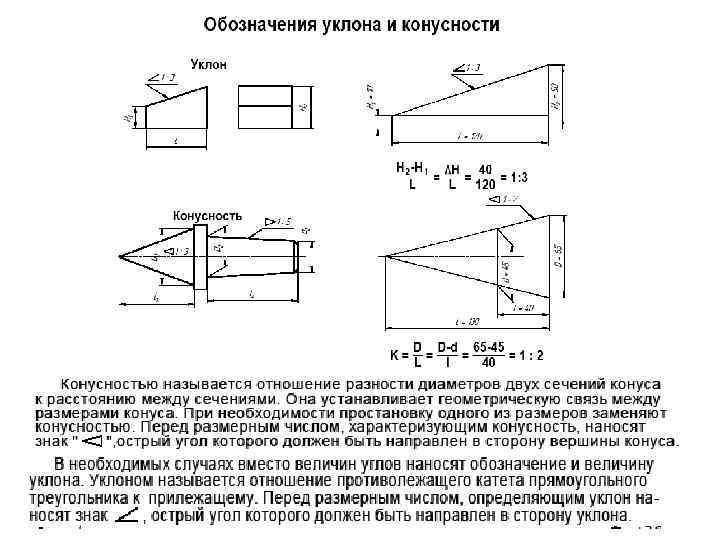

 Это то, что я называю обратным вопросом, когда мы не знаем радиуса и высоты исходного конуса, мы не возвращаемся к размерам сектора, но нам даются другие части информации. Информация. Мы должны попытаться определить высоту конуса. Но не бери в голову! Мы еще можем найти ответ.
Это то, что я называю обратным вопросом, когда мы не знаем радиуса и высоты исходного конуса, мы не возвращаемся к размерам сектора, но нам даются другие части информации. Информация. Мы должны попытаться определить высоту конуса. Но не бери в голову! Мы еще можем найти ответ.
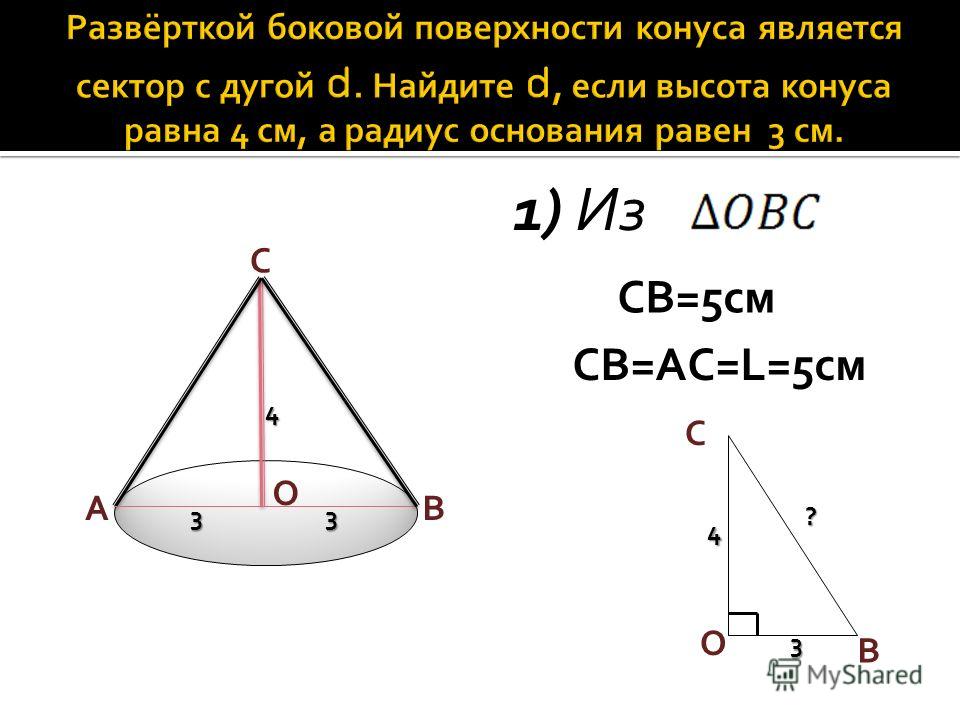 Итак, теперь я вычислил длину наклонной стороны, так что я могу вычеркнуть ее и написать двенадцать. Итак, эта длина равна двенадцати сантиметрам. И теперь я могу использовать теорему Пифагора, чтобы вычислить значение ℎ.
Итак, теперь я вычислил длину наклонной стороны, так что я могу вычеркнуть ее и написать двенадцать. Итак, эта длина равна двенадцати сантиметрам. И теперь я могу использовать теорему Пифагора, чтобы вычислить значение ℎ.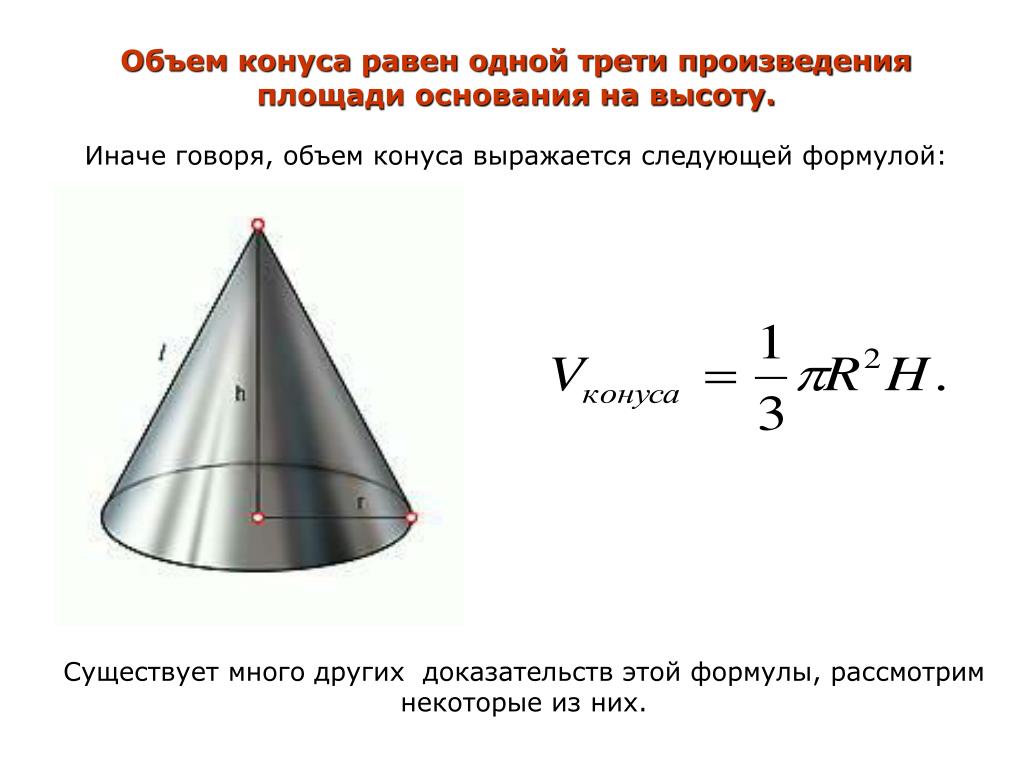 Таким образом, ответ: высота конуса составляет десять целых девять десятых сантиметра с точностью до одного десятичного знака.
Таким образом, ответ: высота конуса составляет десять целых девять десятых сантиметра с точностью до одного десятичного знака.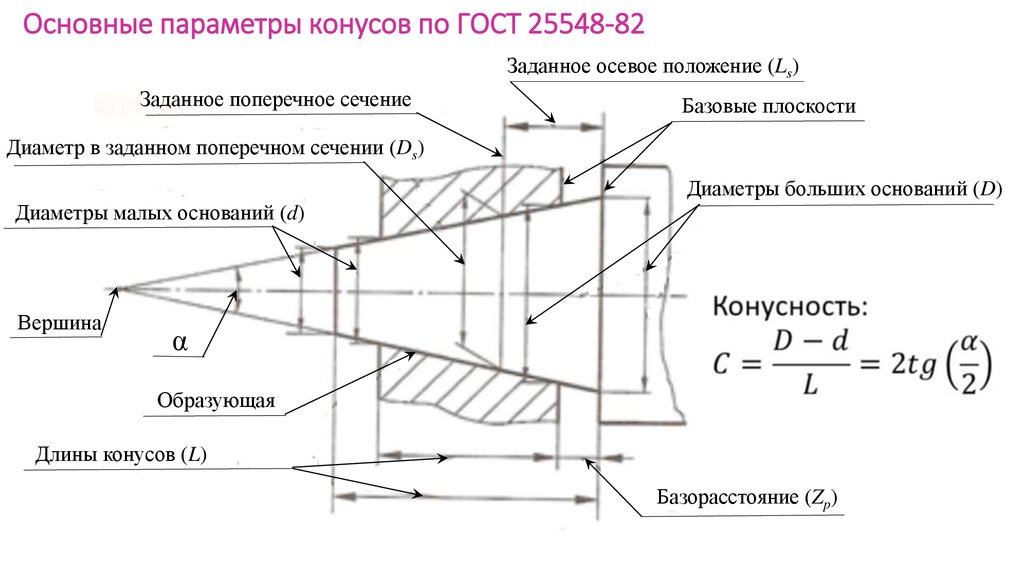 Теперь у нас есть радиус этого круга, так что мы можем вычислить длину окружности.
Теперь у нас есть радиус этого круга, так что мы можем вычислить длину окружности. Теперь у меня есть выражение — уравнение, включающее только 𝑟. Итак, теперь я умножу обе части на десять, а это означает, что десятки в правой части сокращаются, и у меня остается 𝑟, равное пятидесяти на девять. Теперь очевидно, что вопрос ищет ответ с точностью до одного десятичного знака, так что это будет пять целых шесть десятых. Но в будущих расчетах я все равно буду использовать эту наиболее точную версию ответа для своих расчетов, чтобы не создавать ошибок округления.
Теперь у меня есть выражение — уравнение, включающее только 𝑟. Итак, теперь я умножу обе части на десять, а это означает, что десятки в правой части сокращаются, и у меня остается 𝑟, равное пятидесяти на девять. Теперь очевидно, что вопрос ищет ответ с точностью до одного десятичного знака, так что это будет пять целых шесть десятых. Но в будущих расчетах я все равно буду использовать эту наиболее точную версию ответа для своих расчетов, чтобы не создавать ошибок округления.
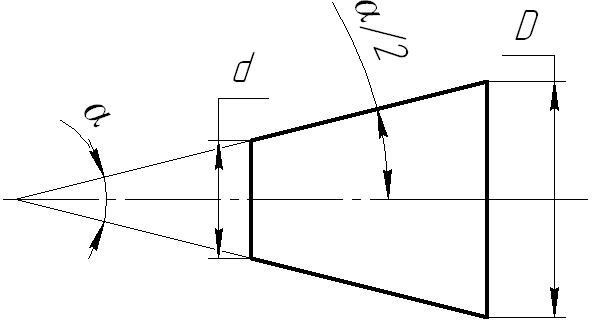
 2}l=r2+h3
2}l=r2+h3 Вставьте эти значения в соответствующие поля калькулятора высоты наклона конуса. Он будет применять формулу: 92}\ \текст{см}\\
&= 15,2\ \text{см}
\end{align*}l=r2+h3
Вставьте эти значения в соответствующие поля калькулятора высоты наклона конуса. Он будет применять формулу: 92}\ \текст{см}\\
&= 15,2\ \text{см}
\end{align*}l=r2+h3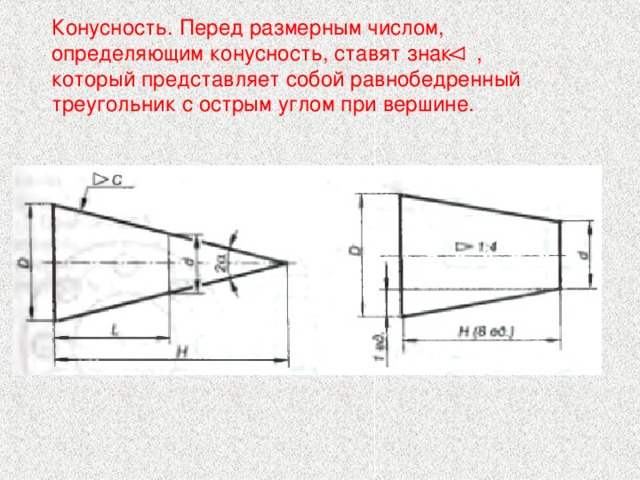
 0715 r = 10 см и высота
0715 r = 10 см и высота 
 Это означает, что когда конус и цилиндр имеют одинаковый размер основания и высоту, объем конуса составляет одну треть объема цилиндра. Следовательно, конус можно получить, разделив цилиндр на три части. Чтобы наглядно это представить, проведем небольшой эксперимент.
Это означает, что когда конус и цилиндр имеют одинаковый размер основания и высоту, объем конуса составляет одну треть объема цилиндра. Следовательно, конус можно получить, разделив цилиндр на три части. Чтобы наглядно это представить, проведем небольшой эксперимент.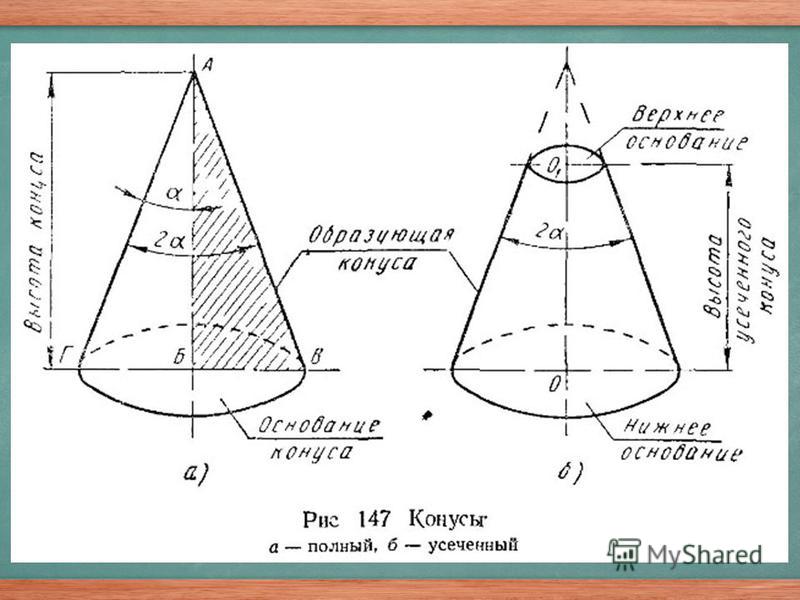 Вылейте всю воду из конуса в пустой цилиндр и проверьте уровень воды в цилиндре.
Вылейте всю воду из конуса в пустой цилиндр и проверьте уровень воды в цилиндре.
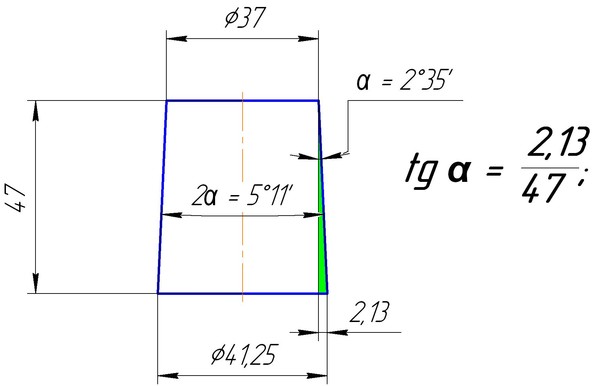 Поэтому пусть l — наклонная высота,
Поэтому пусть l — наклонная высота, Усеченный конус имеет два радиуса: радиус для большей круглой поверхности и радиус для меньшей круглой поверхности.
Усеченный конус имеет два радиуса: радиус для большей круглой поверхности и радиус для меньшей круглой поверхности.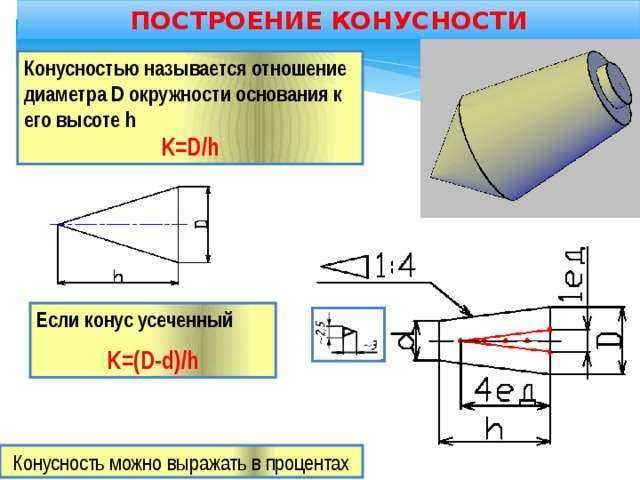 Решение
Решение 