Как уклон считается: Калькулятор уклонов – посчитать онлайн
alexxlab | 17.01.2023 | 0 | Разное
как посчитать, методы, как перевести градусы в промилле
Существуют нормативы на уклоны при проектировании различных коммуникаций и сооружений, которыми руководствуются в своей работе архитекторы и строители. Пользоваться можно любыми размерностями, в том числе и градусами. На практике принято крутые склоны обозначать в градусах, а пологие — в процентах и промилле.
- Способы вычисления склона в процентах
- Определение угла наклона через тангенс
- Соотношение величин с уклоном крыши
Способы вычисления склона в процентах
Единицей измерения крена, в зависимости от его величины, бывают градус, процент, промилле — тысячная доля целого числа: 1‰ = 1/10% = 1/1000 от 1. Физический смысл уклона — отношение перепада высот к длине участка, на котором это наблюдается. По сути — тангенс угла: превышение 12 метров на отрезке дороги в сто метров выражается величиной 0,12 (тангенс) = 12% = 120 ‰. То есть чтобы сделать расчёт уклона в промилле, надо умножить процентный показатель на десять.
При выполнении планировочных работ на земельном участке приходится прибегать к измерениям крутизны косогоров. Сделать это можно несколькими методами:
- С помощью нивелира выполняются все необходимые измерения, а потом несложными вычислениями формируется уклон в процентах. Как считать: перепад высот делится на расстояние между точками замеров, и результат умножается на сто процентов.
- По плану земельного участка, если на нём вынесены отметки рельефа местности. Разница высот между необходимыми точками считывается с рисунка, а расстояние замеряется масштабной линейкой. Дальнейшие вычисления аналогичны предыдущему способу.
Кровельщики часто сталкиваются с необходимостью определить фактический скат крыши, и знают, как рассчитать уклон с помощью специального инструмента, называемого уклономер. Конструкция приспособления несложная: на рейке закреплена рамка с закреплённым внутри транспортиром и маятником, имеющим груз и указатель.
Определение угла наклона через тангенс
Из тригонометрии известно, что тангенс — дробь, в основании которой прилежащий к углу катет, а поверх — противолежащий (перепад высот). Чтобы определить уклон кровли в процентах и градусах через тангенс, понадобится выполнить замеры:
- высоты от потолочного перекрытия до конька кровли;
- расстояния от края ската до проекции верхней линии смыкания двух плоскостей.
Сделав несложные расчёты, получают некоторое значение и по таблице Брадиса или с помощью инженерного калькулятора находят соответствующее число градусов для искомого угла. Как посчитать уклон в процентах —  Можно заметить, что это и есть тангенс уже определённого в градусах угла. Чтобы перейти к процентному выражению уклона, надо выполнить действие: значение tg *100, и результат получится в процентах.
Можно заметить, что это и есть тангенс уже определённого в градусах угла. Чтобы перейти к процентному выражению уклона, надо выполнить действие: значение tg *100, и результат получится в процентах.
Соотношение величин с уклоном крыши
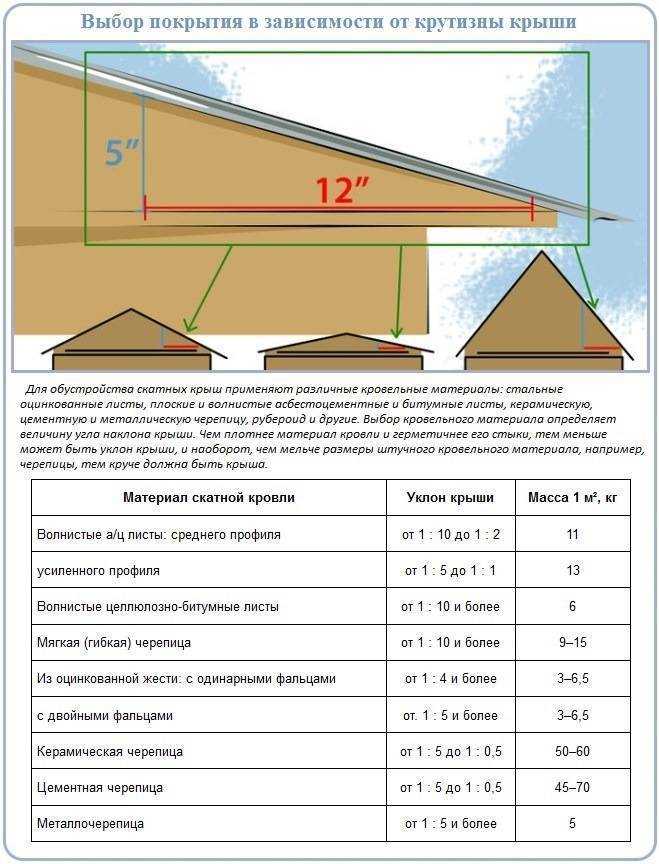
Для каждого кровельного материала установлены допуски по наименьшему уклону. Другие факторы, влияющие на выбор угла скатов крыши:
- способность комплексно защищать строение от внешних воздействий — техногенных и природных;
- стойкость к ветровой нагрузке — крутые поверхности увеличивают парусность сооружения, это делает конструкцию уязвимой;
- преобладание определённых решений архитекторов в отдельных регионах;
- количество атмосферных осадков и загрязнений — на кровле с большим уклоном груз накапливаться не будет.
Строительные нормы и правила — СНиП II -26−76 регламентируют пологость скатов в процентах. Соотношение процентов и градусов для некоторых углов приведено в таблице.
Соотношение процентов и градусов для некоторых углов приведено в таблице.
| Градус º | Тангенс | Процент, % | Промилле, ‰ | Градус º | Тангенс | Процент, % | Промилле, ‰ |
| 1 | 0,0175 | 1,75 | 17,5 | 22 | 0,4040 | 40,40 | — |
| 5 | 0,0875 | 8,75 | 87,5 | 24 | 0,4452 | 44,52 | — |
| 10 | 0,1740 | 17,40 | 174 | 26 | 0,4878 | 48,78 | — |
| 12 | 0,2125 | 21,25 | — | 28 | 0,5318 | 53,18 | — |
| 14 | 0,2494 | 24,94 | — | 30 | 0,5773 | 57,73 | — |
| 16 | 0,2868 | 28,68 | — | 35 | 0,7001 | 70,01 | — |
| 18 | 0,3250 | 32,50 | — | 40 | 0,8390 | 83,90 | — |
| 20 | 0,3828 | 38,28 | — | 45 | 1,0000 | 100,0 | — |
Математические способы расчёта уклона применяются, когда особая точность не нужна, и измерения делают приблизительные.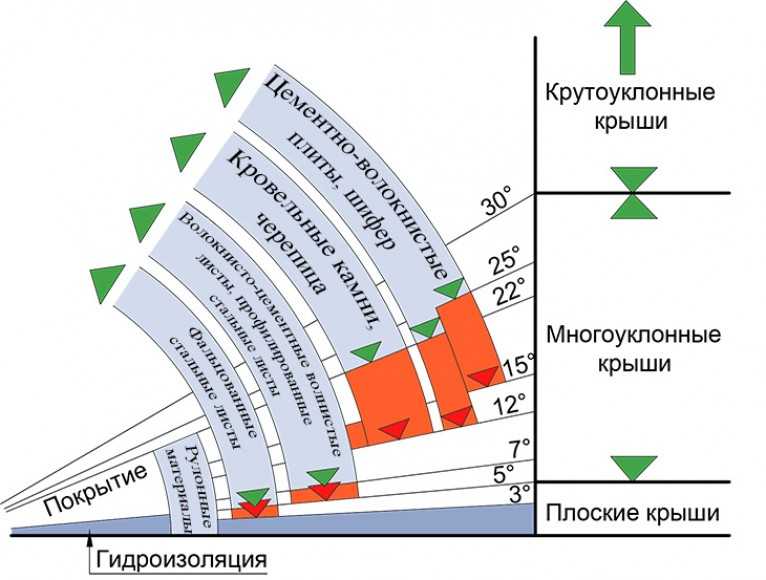
Пример вычисления: расстояние от края ската кровли до проекции линии сопряжения сторон — длина заложения, 5,2 м. Высота от чердачного перекрытия до верхней отметки кровли 2 метра. Уклон (тангенс угла) определяется действием: 2/5,2 = 0,3846. Ближайшее значение из таблицы — 20 градусов, что соответствует примерно 38%.
Другой вариант — с помощью угломера определили угол наклона кровли, его значение 5º. По соответствующей строке уклон поверхности составит 8,75 процента или 87,5 промилле.
Как расшифровать знаки с изображением уклона в процентах? | ГИБДД | Авто
Владимир Гаврилов
Примерное время чтения: 4 минуты
9695
Категория: ПДД и ГИБДД
По международным стандартам крутизна уклонов на знаках обозначается всегда в процентах. Перед въездом на холмы и горки устанавливаются треугольные знаки 1.14 «Крутой подъем», которые содержат цифровое обозначение, содержащее надпись типа «7%», «10%» или «12%», а в очень редких случаях «30%», а на автополигонах есть даже знаки «100%». Как понять эти обозначения?
Перед въездом на холмы и горки устанавливаются треугольные знаки 1.14 «Крутой подъем», которые содержат цифровое обозначение, содержащее надпись типа «7%», «10%» или «12%», а в очень редких случаях «30%», а на автополигонах есть даже знаки «100%». Как понять эти обозначения?
Тангенс и расстояние
Процентное обозначение уклона дороги отражает тангенс угла наклона. Оно потребовалось для упрощения понимания уровня возвышения и расчетов для водителей. Смысл этой маркировки основан на тригонометрических вычислениях треугольников. Если представить горку в виде геометрической фигуры, то в ней можно выделить два катета и гипотенузу. Из школьного курса мы помним, что отношения сторон треугольника отражаются в значениях синуса и косинуса. Они помогают высчитать по углу наклона гипотенузы одну из сторон. Между тем в вычислениях часто применяют отношение синуса к косинусу, которое называется тангенсом. Если вы установите гипотенузу под углом 45 градусов, то синус и косинус будут совершенно одинаковы, а тангенс равен 1.
Для расчета уклонов дорог за основу принято именно это соотношение. Угол в 45 градусов принимается за 100%, а длина прилежащего катета, то есть горизонтальная проекция дороги, идущей на возвышение, за 100 м. Забраться на такой уклон могут не все автомобили, а лишь те, что обладают идеальной развесовкой, хорошими покрышками и мощным мотором.
Практичные вычисления
Тем самым цифра на дорожном знаке — это тангенс угла наклона проезжей части, выраженный в процентах. Звучит сложно, но на практике обозначения в процентах очень удобны и помогают быстро оценить крутизну подъема и опасности для транспортного средства в непогоду и гололед.
Если стоит знак «10%», то это значит, что, проехав примерно 100 м по дороге на горку с крутизной уклона в 10%, машина поднимется на высоту 10 метров. Тем самым проценты на знаках можно представить и как количество метров, на которые проезжая часть опустится или поднимется через расстояние, кратное 100 м.
Или еще пример. 12% означает, что, проехав 1 километр по дороге с уклоном 12%, машина поднимется на 120 метров.
Как проценты перевести в градусы?
В целом для автомобиля могут начинаться проблемы, когда возвышение составляет «10%» и более. На таких горках в гололед буксуют грузовики.
Иногда во время путешествия на внедорожниках бывает важно понять, какой все-таки угол зашифрован на знаке. Тогда можно понять, насколько поверхность способна держать автомобиль. В этом случае необходимо взять калькулятор и высчитать угол через тангенс. Это отношение противолежащего катета к прилежащему, который находится рядом с углом.
Берем число на знаке, делим на 100 и по таблице тангенсов находим угол. Если на знаке указано 12%, то по таблице необходимо смотреть угол для значения 0,12. В итоге получится 7 градусов.
ПДДдорожные знаки
Следующий материал
Новости СМИ2
9. Уклон
Уклон – это мера изменения высоты. Это важный параметр в нескольких известных прогностических моделях, используемых для управления окружающей средой, включая универсальное уравнение потери почвы и сельскохозяйственные модели загрязнения из неточечных источников.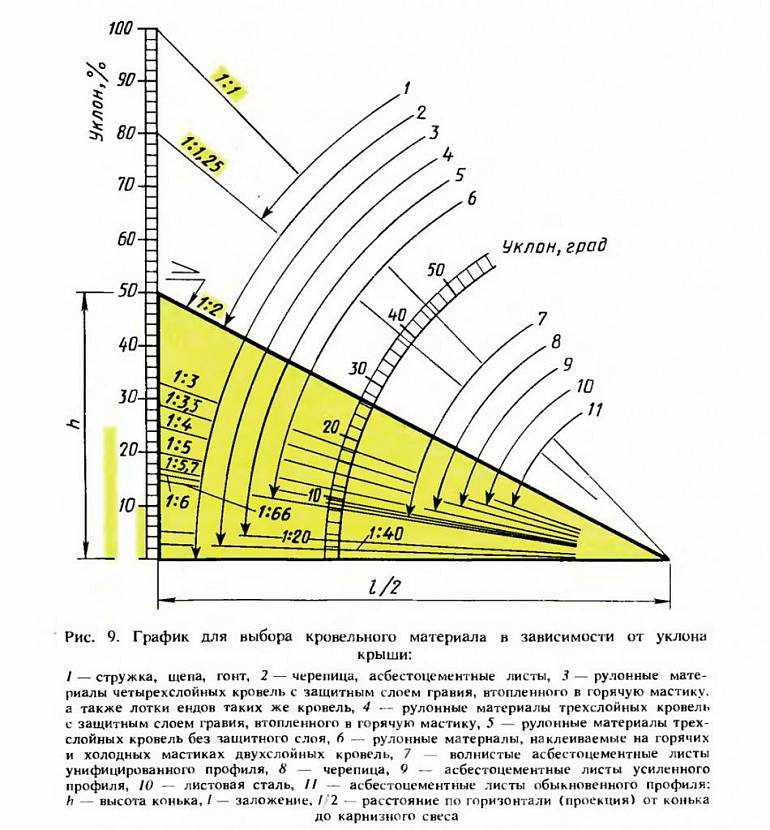
Один из способов выразить наклон в процентах. Чтобы вычислить уклон в процентах, разделите разницу между высотами двух точек на расстояние между ними, а затем умножьте частное на 100. Разница в высотах между точками называется подъемом. Расстояние между точками называется пробегом. Таким образом, процент уклона равен (подъем/спуск) x 100.
Рисунок 7.10.1 Расчет наклона в процентах. Подъем на 100 футов над пробегом в 100 футов дает 100-процентный уклон. Подъем на 50 футов над 100-футовым пробегом дает 50-процентный уклон.
Еще один способ выразить наклон – это угол наклона или градус наклона. Как показано ниже, если вы визуализируете подъем и бег как стороны прямоугольного треугольника, то градус наклона — это угол, противоположный подъему. Поскольку степень наклона равна тангенсу дроби подъем/набег, ее можно рассчитать как арктангенс подъема/набега.
Рисунок 7.10.2 Подъем на 100 футов на участке длиной 100 футов дает угол наклона 45°. Подъем на 50 футов на протяжении 100 футов дает угол наклона 26,6°.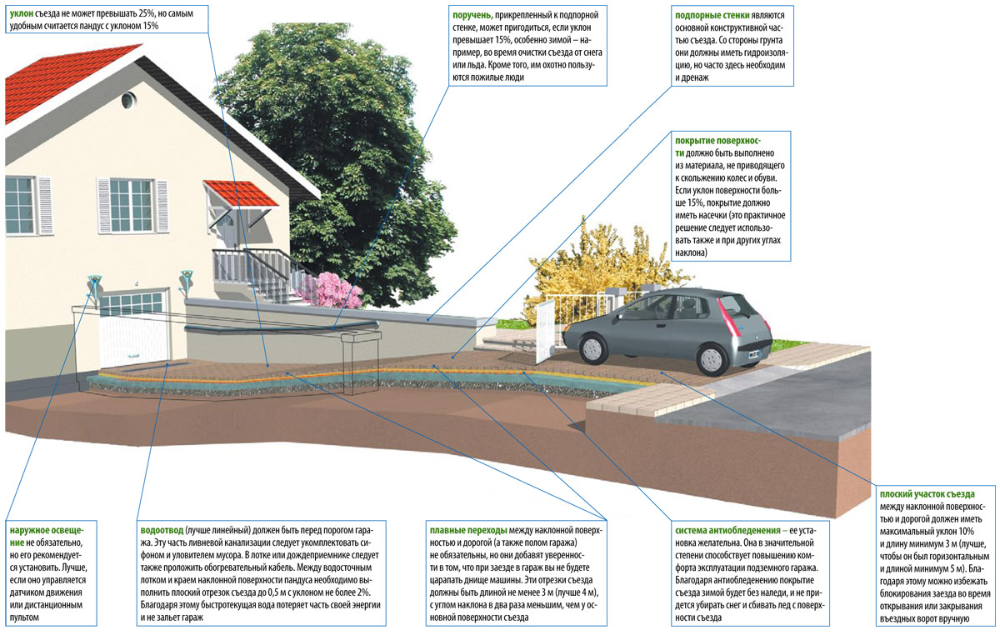
Вы можете рассчитать уклон на контурной карте, анализируя расстояние между горизонталями. Однако, если вам нужно рассчитать много значений уклона, вы захотите автоматизировать процесс. Оказывается, расчеты уклона гораздо проще выполнять для данных высот с координатной сеткой, чем для векторных данных, поскольку высоты более или менее равномерно распределены в растровых сетках.
Было разработано несколько алгоритмов для расчета процента наклона и степени наклона. Самый простой и распространенный метод называется методом соседства . Метод соседства вычисляет уклон в одной точке сетки путем сравнения высот восьми точек сетки, которые ее окружают.
Рисунок 7.10.3 Алгоритм соседства оценивает процентный уклон в ячейке 5 путем сравнения высот соседних ячеек сетки.
Алгоритм соседства оценивает процентный уклон в ячейке сетки 5 (Z 5 ) в виде суммы абсолютных значений уклона восток-запад и уклона север-юг и умножения суммы на 100.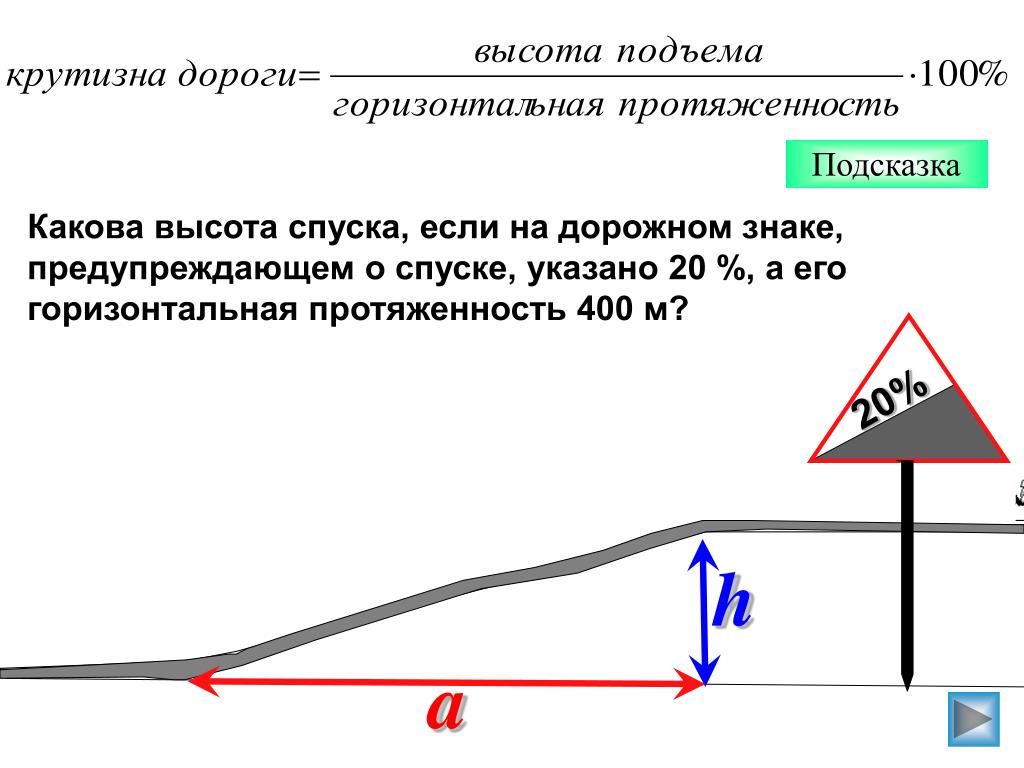
Рисунок 7.10.4 Алгоритм соседства для расчета процентного уклона.
Щелкните здесь, чтобы просмотреть текстовую версию уравнения, показанного на изображении выше.
На иллюстрации показано, как уклон местности в заданной ячейке сетки высот можно рассчитать на основе высот восьми окружающих ее ячеек сетки. Во-первых, наклон север-юг рассчитывается из столбцов сетки. Затем по рядам сетки рассчитывается уклон с востока на запад. Квадратный корень из суммы наклона с севера на юг и уклона с востока на запад, умноженный на 100, равен наклону в процентах в исходной ячейке сетки.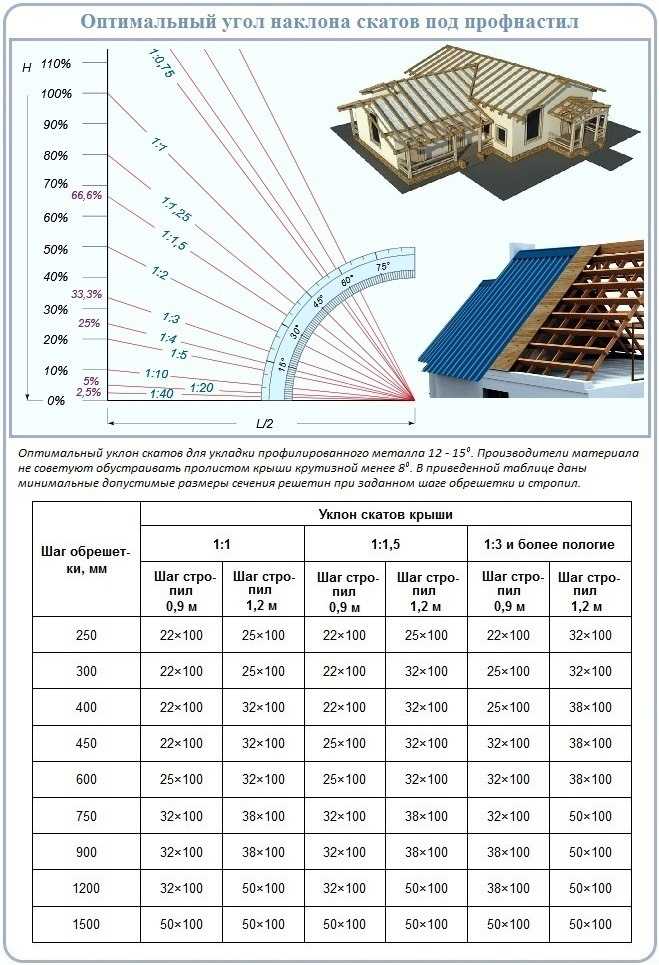 Причудливый технический термин для этой процедуры — «алгоритм соседства».
Причудливый технический термин для этой процедуры — «алгоритм соседства».
Алгоритм окрестности вычисляет уклон для каждой ячейки в сетке высот путем анализа каждой окрестности 3 x 3. Процентный уклон можно преобразовать в градусы позже. Результатом является сетка значений уклона, подходящая для использования в различных моделях потери почвы и гидрологических моделях.
Как использовать формулу наклона и найти наклон линии, независимо от того, является ли наклон положительным, отрицательным или неопределенным.
Рабочий лист по наклону линии
Апплет наклона (html5)
Калькулятор формулы уклона (Бесплатный онлайн-инструмент вычисляет уклон по 2 точкам)
Наклон линии характеризует направление линии. Чтобы найти наклон, вы делите разницу координат y двух точек на прямой на разницу координат x тех же двух точек.
Разные слова, та же формула
Учителя используют разные слова для координат y и координат x.
- Некоторые называют координаты у подъемом, а координатами х — бег.
- Другие предпочитают использовать нотацию $$\Delta$$ и называть y-координаты $$\Delta y$$ , а x-координаты $$\Delta x$$ .
Все эти слова означают то же самое, что и , то есть значения y находятся вверху формулы (числитель), а значения x внизу формулы (знаменатель)!
Пример 1
Наклон прямой , проходящей через точку (1, 2) и точку (4, 3), равен $$ \frac{1}{3}$$.
Помните: разница в значениях y идет в числителе формулы, а разница в значениях x идет в знаменателе формулы.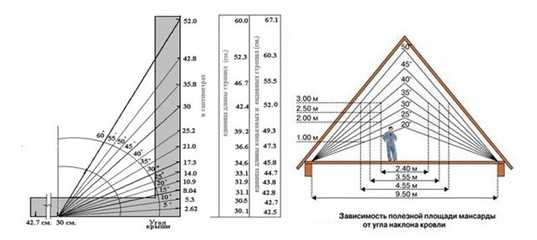
Может ли любая из точек быть $$( x_1 , y_1 ) $$ ?
Есть только один способ узнать!
Во-первых, мы будем использовать точку (1, 2) как $$x_1, y_1$$, и, как вы можете видеть: наклон: $ \boxed {\frac{1}{3} }$ .
Теперь давайте используем точку (4, 3) как $$x_1, y_1$$, и, как вы можете видеть, наклон упрощается до того же значения: $ \boxed {\frac{1}{3} }$ .
Работа рядом
точка (4, 3) как $$ (x_1, y_1 )$$
Наклон $$ = \frac{y_{2}-y_{1}}{x_{2}-x_{1}} = \frac{3-2}{4-1} = \frac{1}{3} $$
точка (1, 2) как $$ (x_1, y_1 )$$
Наклон $$ = \frac{y_{2}-y_{1}}{x_{2}-x_{1}} = \frac{2-3}{1-4} = \frac{-1}{- 3} = \frac{1}{3} $$
Ответ: , а не не имеет значения, какую точку поставить первой. Вы можете начать с (4, 3) или с (1, 2), и в любом случае вы закончите точно таким же числом!
$$ \фракция{1}{3} $$
Вы можете начать с (4, 3) или с (1, 2), и в любом случае вы закончите точно таким же числом!
$$ \фракция{1}{3} $$
Пример 2 наклона линии А
Наклон прямой , проходящей через точки (3, 4) и (5, 1), равен $$- \frac{3}{2}$$, потому что каждый раз, когда линия опускается на 3 (изменение y или подъем) линия смещается вправо (разбег) на 2.
Эта страница:
- Формула
- Пример
- Видео
- Заказать?
- Любые две точки определяют наклон линии?
- Наклон вертикальной линии
- Наклон горизонтальной линии
- Практические задачи
Наклон вертикальных и горизонтальных линий
Наклон вертикальной линии не определен
Это связано с тем, что любая вертикальная линия имеет $$\Delta x$$ или «пробег» нуля. Всякий раз, когда ноль является знаменателем дроби в этом случае дроби, представляющей наклон линии, дробь не определена. На рисунке ниже показана вертикальная линия (x = 1).
Наклон горизонтальной линии равен нулю
Это потому, что любая горизонтальная линия имеет $$\Delta y$$ или «подъем» нуля. Следовательно, независимо от того, каков пробег (при условии, что он не равен нулю!), дробь, представляющая уклон, имеет в числителе ноль. Следовательно, наклон должен оцениваться как нулевой. Ниже приведено изображение горизонтальной линии — вы можете видеть, что у нее нет «подъема».
Следовательно, наклон должен оцениваться как нулевой. Ниже приведено изображение горизонтальной линии — вы можете видеть, что у нее нет «подъема».
Любые две точки на прямой имеют одинаковый наклон?
Ответ: Да, и это фундаментальный момент, который следует помнить при расчете уклона.
Каждая линия имеет постоянный наклон. Другими словами, наклон линии никогда не меняется. Эта фундаментальная идея означает, что вы можете выбрать 90 155 любых 90 156 2 точек на линии.
Подумайте об идее прямой линии. Если бы наклон линии изменился, то это была бы зигзагообразная линия, а не прямая линия, как вы можете видеть на рисунке выше.
Как вы можете видеть ниже, наклон одинаков независимо от того, какие 2 точки вы выбрали.
Наклон линии
Никогда не меняетсяЭта страница:
- Формула
- Пример
- Видео
- Заказать?
- Любые две точки определяют наклон линии?
- Наклон вертикальной линии
- Наклон горизонтальной линии
- Практические задачи
Рабочий лист по наклону линии
Апплет наклона (html5)
Калькулятор формулы уклона (Бесплатный онлайн-инструмент вычисляет уклон по 2 точкам)
Практика ПроблемыПроблема 1
Каков наклон прямой, проходящей через точки (10,3) и (7, 9)?
$ \frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}} $
Используя $$ \red{ (10,3)}$$ как $$x_1, y_1$$
$ \frac{9- \red 3}{7- \red{10}} \\ = \frac{6}{-3} \\ = \ в коробке {-2 } $
Используя $$ \red{ (7,9)} $$ как $$x_1, y_1$$
$ \frac{3- \red 9{10- \красное 7} \\ =\ гидроразрыв{-6}{3} \\ = \в коробке{-2} $
Проблема 2
Прямая проходит через (4, -2) и (4, 3). Каков его наклон?
Каков его наклон?
$ \frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}} $
Используя $$ \red{ ( 4,3 )}$$ как $$x_1, y_1$$
$ = \frac{-2 – \red 3}{4- \red 4} знак равно \frac{-5}{\color{red}{0}} \\ = \text{неопределенный} $
Используя $$ \red{ ( 4, -2 )}$$ как $$x_1, y_1$$
$ = \frac{3- \red{-2}}{4- \red 4} знак равно \frac{5}{\color{red}{0}} \\ = \текст{неопределенный} $
Всякий раз, когда длина линии равна нулю, наклон не определен. Это потому, что в знаменателе наклона стоит ноль! Любой наклон любой вертикальной линии не определен.
Проблема 3
Прямая проходит через (2, 10) и (8, 7). Каков его наклон?
Каков его наклон?
$ \frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}} $
Используя $$ \red{ ( 8, 7 )}$$ как $$x_1, y_1$$
$ \frac{10 – \red 7}{2 – \red 8} \\ = \ гидроразрыва {3}{-6} \\ = -\фракция{1}{2} $
Используя $$ \red{ ( 2,10 )}$$ как $$x_1, y_1$$
$ \frac{7 – \red {10}}{8- \red 2} \\ = \ гидроразрыв {-3} {6} \\ = -\фракция{1}{2} $
Проблема 4
Прямая проходит через (7, 3) и (8, 5). Каков его наклон?
$ \frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}} $
Используя $$ \red{ (7,3 )}$$ как $$x_1, y_1$$
$$ \frac{ 5- \red 3}{8- \red 7} \\ = \ гидроразрыва {2} {1} \\ = 2 $$
Используя $$ \red{ ( 8,5 )}$$ как $$x_1, y_1$$
$$ \frac{ 3- \red 5}{7- \red 8} \\= \фракция{-2}{-1} \\ = 2 $$
Проблема 5
Прямая проходит через (12, 11) и (9, 5) . Каков его наклон?
Каков его наклон?
$ \frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}} $
Используя $$ \red{ ( 5, 9)}$$ как $$x_1, y_1$$
$$ \frac{ 11 – \red 5}{12- \red 9} \\ = \ гидроразрыва {6} {3} \\ =2 $$
Используя $$ \red{ (12, 11 )}$$ как $$x_1, y_1$$
$$ \frac{ 5- \red{ 11} }{9- \red { 12}} \\ = \фракция{-6}{-3} \\ = 2$$
Проблема 6
Каков наклон линии, проходящей через (4, 2) и (4, 5)?
$ \frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}} $
Используя $$ \red{ ( 4,5 )}$$ как $$x_1, y_1$$
$$ \frac{ 2 – \red 5}{4- \red 4} \\ = \frac{-3}{\color{red}{0}} \\ = не определено $$
Используя $$ \red{ ( 4,2 )}$$ как $$x_1, y_1$$
$$ \frac{ 5 – \red 2}{4- \red 4} \\ = \frac{ 3}{\color{red}{0}} \\ = не определено $$
ПРЕДУПРЕЖДЕНИЕ! Уловите ошибку в следующей задаче: Дженнифер пыталась найти наклон, проходящий через точки $$(\color{blue}{1},\color{red}{3})$$ и $$ (\color {синий}{2}, \цвет{красный}{6})$$ . У нее были небольшие проблемы с применением формулы наклона, она пыталась вычислить наклон 3 раза и дала 3 разных ответа. Сможете ли вы определить правильный ответ?
У нее были небольшие проблемы с применением формулы наклона, она пыталась вычислить наклон 3 раза и дала 3 разных ответа. Сможете ли вы определить правильный ответ?
Задача-вызов
Найдите наклон прямой через две точки.
Попытка №1
$ наклон = \ гидроразрыв {подъем} {бег} \\= \ frac{\ color {red} {y_ {2} -y_ {1}}} {\ color {blue} {x_ {2} -x_ {1}}} знак равно \ гидроразрыв {6-3} {1-2} \\= \фракция{3}{-1} =\в коробке{-3} $
Попытка №2
$$ наклон = \ гидроразрыв {подъем} {бег} \\= \ frac{\ color {red} {y_ {2} -y_ {1}}} {\ color {blue} {x_ {2} -x_ {1}}} знак равно \фракция{6-3}{2-1} \\= \фракция{3}{1} \\ = \в коробке{3} $$
Попытка №3
$$ уклон = \ гидроразрыв {подъем} {бег} \\= \ frac{\ color {red} {y_ {2} -y_ {1}}} {\ color {blue} {x_ {2} -x_ {1}}} \\ =\ гидроразрыва {2-1} {6-3} \\ =\в коробке{ \frac{1}{3}} $$
Правильный ответ — попытка №2.
В попытке №1 она не всегда использовала очки. В первой попытке она сделала следующее:
$$ \frac{\color{red}{y{\boxed{_2}}-y_{1}}}{\color{blue}{x\boxed{_{1}}-x_{2}}} $$
Проблема с попыткой №3 заключалась в обратном подъеме и беге. Она поместила значения x в числитель (сверху), а значения y в знаменатель, что, конечно же, противоположно!
$$ \ отмена {\ frac {\ color {синий} {x_ {2} -x_ {1}}} {\ color {red} {y_ {2} -y_ {1}}}} $$
Slope Practice Генератор проблем Вы можете сколько угодно практиковаться в решении подобных задач с помощью приведенного ниже генератора задач на уклон.