Какие шкалы бывают: Измерение. Шкалы измерений

alexxlab | 29.11.2022 | 0 | Разное

Шкала в психологии. Виды шкал и их характеристика

Измерительная шкала — основное понятие, также введенное в психологию С.С. Стивенсом в 1950 г.; его трактовка шкалы и сегодня используется в научной литературе. Итак, приписывание чисел объектам создает шкалу. Шкала (лат. scala — лестница) в буквальном значении есть измерительный инструмент.

Числовое значение, приписанное объекту, должно представлять (репрезентировать) ту характеристику объекта, которая интересует исследователя. Репрезентировать в данном случае означает, что по приписанному значению исследователь будет вправе сделать вывод об изучаемом свойстве.

Существует четыре группы правил, по которым свойства объекта в разной степени передаются его числовому значению (номеру). Каждому из четырех наборов правил соответствует свой вид измерения или шкала: номинативная (номинальная или шкала наименований), порядковая, интервальная и шкала отношений. Несколько упрощая, различия между шкалами примерно следующие:

• если все, что мы можем сказать об объекте, – это то, что он отличается от другого, то мы имеем номинативную шкалу;
• если мы можем сказать, что один объект больше или лучше, или в чем-то превосходит другой, мы имеем порядковую шкалу;
• если мы можем сказать, что один объект на сколько-то единиц (градусов, сантиметров) больше, чем другой, мы имеем интервальную шкалу;
• если мы можем сказать, что один объект в какое-то количество раз больше, чем другой, мы имеем шкалу отношений.

Четыре типа шкал образуют иерархию, в которой каждая последующая шкала включает в себя свойства нижележащих шкал (табл. 3).

С каждой из шкал связан определенный диапазон допустимых математико-статистических преобразований. Выход за пределы этого диапазона приводит к тому, что получаемые результаты оказываются лишенными смысла. Об этом необходимо помнить на этапе планирования работы по сбору данных. Именно от типа шкалы зависят все дальнейшие процедуры подсчета.

Рассмотрим свойства каждой шкалы более подробно.

Номинативная шкала

Номинативная шкала (лат. потеп – имя, название) – это шкала, классифицирующая по названию. Название не измеряется количественно, оно лишь позволяет отличить один объект от другого или одного субъекта от другого. Простейший случай номинативной шкалы -дихотомическая шкала, состоящая из двух наименований, например «имеет братьев и сестер – единственный ребенок в семье»; «иностранец – соотечественник»; «проголосовал “за” – проголосовал “против”» и т. п.

Телефонные и автомобильные номера, цветные фигурки на шкафчиках в детском саду – это примеры имен, которыми мы наделяем различные объекты. При этом неважно, что будет использоваться в качестве имени – цифры, буквенные сочетания, условные обозначения или другое. Основное правило – не присваивать одно и то же имя двум разным объектам. Однако если мы имеем дело с одинаковыми объектами, обладающими одинаковыми свойствами, то они должны в шкале наименований получать одинаковые имена. Количество используемых имен должно быть не меньше числа типов объектов или их свойств. Например, три имени для обозначения семейного положения (холост, женат/замужем, разведен) может оказаться недостаточно в случае наличия в выборке вдов/вдовцов.

Если для обозначения классов (типов) объектов выбраны числа, то формальные правила арифметики в этом случае не используются. Возьмем, к примеру, опросник, где мы приписываем 1 балл ответу «да», 2 – ответу «нет», 3 – «не знаю». Предположим также, что все три ответа выбираются одинаково часто. Допустим, теперь мы хотим найти, что является средним ответом. Среднее этих чисел дает нам «2» – как средний ответ. Можем мы теперь заключить, что средний ответ – «нет»? Такой вывод будет бессмысленным. Числа могут суммироваться и вычитаться, названия классов объектов не могут быть сложены или вычтены.

Статистическая обработка данных, представленных в шкале наименований, чаще всего начинается с построения таблицы сопряженности, показывающей распределение имен в соответствии с числом объектов и/или их свойств. Расклассифицировав все объекты, реакции или всех испытуемых по ячейкам классификации мы получаем возможность от наименований перейти к числам, подсчитав количество наблюдений в каждой из ячеек.

Таким образом, номинативная шкала позволяет нам подсчитывать частоты встречаемости разных наименований, или значений признака, и затем работать с этими частотами с помощью математических методов (метода %2, биноминального критерия m и углового преобразования Фишера ф).

Шкала порядка

В том случае, когда между объектами возможно установление отношений типа «быстрее», «успешнее», «вкуснее», «ярче», «громче», «тверже» и др. , появляется возможность расположить объекты в порядке возрастания или убывания определенного признака. После этого остается наделить упорядоченную последовательность числами таким образом, чтобы, например, большее число соответствовало большей степени выраженности признака. В результате получим шкалу порядка, в которой отношения между числами будут соответствовать отношениям между объектами.

Порядковая шкала – это шкала, которая допускает возможность расположить пункты (или объекты) в порядке отношений между ними.

В порядковой шкале должно быть не менее трех объектов, например «положительная реакция – нейтральная реакция – отрицательная реакция».

Если расположить объекты по порядку возрастания интересующего нас признака, то можно обозначить эти объекты или А, В, С, или 1, 2, 3, или 50, 60, 70. Однако им нельзя приписать, например, такую последовательность цифр: 7, 90, 4, потому что эти цифры не соответствовали бы тому порядку, в котором данное свойство изменяет свое значение от объекта к объекту.

Примерами порядковых шкал могут являться школьные оценки (отлично, хорошо, удовлетворительно), призовые места по итогам соревнований (1 -е, 2-е и 3-е), градация званий в спорте (перворазрядник, кандидат в мастера спорта, мастер спорта). Из психологического инструментария самым ярким примером порядковой шкалы являются опросники установок и отношений, когда нужно выразить свое отношение в терминах больше – меньше, чаще – реже, и многие другие виды рейтинговых шкал.

В то же время расположение объектов в порядке возрастания определенного свойства еще не дает ответа на вопрос: насколько больше? Шкала порядка не позволяет определить «расстояние» между объектами. Об этом особенно необходимо помнить в тех случаях, когда из соображений удобства шкальные значения отделяют друг от друга равные интервалы. Например, четыре студента получили на экзамене оценки 75, 85, 90 и 100 баллов. Оценка второго студента отличается от оценки первого так же, как оценка четвертого студента отличается от оценки третьего, – на 10 баллов.

Но из этого не следует, что знания второго студента больше знаний первого настолько же, насколько знания четвертого больше знаний третьего.

Рассмотрим еще один пример. Предположим, есть четыре игрока в теннис. Первый – профессиональный спортсмен, обладатель кубка Дэвиса. Второй игрок – любитель, но все свое свободное время он отдает теннису и в результате играет очень хорошо. Третий играет изредка, а четвертый взял в руки ракетку второй раз в жизни. Расположив игроков по степени мастерства, получаем порядковую шкалу, где под № 4 будет стоять первый игрок, а под № 1 – четвертый игрок, с трудом попадающий ракеткой по мячу. Теперь игрокам приписаны номера 4, 3, 2, 1. Если мы организуем игру парами и расставим игроков так: № 1 и № 4 – на одной стороне корта, № 2 и № 3 – на другой, то можем ли мы быть уверенными, что игра пройдет вничью? Ведь равенство 1 + 4 = 2 + 3 истинно. В этом примере мы имеем дело с порядковыми номерами, а не с числами, поэтому игра вничью не гарантируется такой расстановкой игроков.

Разница в умении играть между № 1 и № 2 не равна разнице между № 2 и № 3.

Таким образом, выбор чисел используемых в шкале порядка в известных пределах произволен. Числа могут быть любыми, но они должны подчиняться основному требованию: объекту с большей выраженностью признака должно быть приписано большее число. Абсолютное значение числа не имеет смысла в порядковой шкале; смысл имеет только порядок чисел.

Со шкалами порядка связана одна из наиболее популярных в непараметрической статистике процедур – процедура ранжирования. Ранжирование – это процедура определения места, которое должен занять данный результат в упорядоченной последовательности всех результатов.

Особенности шкалы порядка позволяют определить для нее группу допустимых математико-статистических преобразований. Результаты, представленные в шкале порядка, нельзя использовать для пропорций (знания, оцененные на 100, не являются вдвое больше знаний, оцененных на 50). Эти результаты нельзя складывать (знания получившего на экзамене 100 баллов не равны сумме знаний получивших 40 и 60 баллов).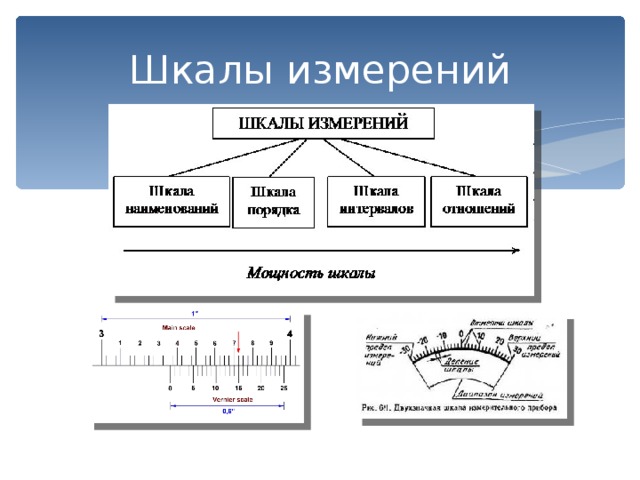 Если говорить о мерах центральной тенденции, то из них можно применять только моду и медиану. Вычисление среднего является недопустимой операцией для шкалы порядка.

Интервальная шкала

Интервальная шкала – это шкала, классифицирующая объекты по принципу «больше на определенное количество единиц – меньше на определенное количество единиц». Каждое из возможных значений признака отстоит от другого на равном расстоянии. Это расстояние и называется интервалом. Размер интервала – величина, фиксированная и равная для всех сравниваемых объектов.

Особенность этой шкалы в том, что она не предполагает абсолютного нуля (нуль здесь условен и не указывает на отсутствие свойства). Например, когда говорят, что на улице температура 00С, то не имеют в виду, что температуры нет вообще. Этим хотят сказать, что на улице достаточно холодно, может лежать мокрый снег и могут быть лужи.

Другая популярная шкала интервалов – календарное летоисчисление. Как известно, христианское (европейское) летоисчисление берет начало от произвольно выбранной точки отсчета («рождение Христа»). Величина интервалов (день, месяц, год) привязана к видимому движению Солнца, а выражение «до нашей эры» означает, по сути, что в этой точке летоисчисление меняет свой знак.

В случае психологических измерений главная трудность – в обосновании равности интервалов. Психологические характеристики, выраженные в тестовых показателях, – это непрерывные величины, выраженные через дискретные. Допустим, первый испытуемый по тесту тревожности получил показатель со значением 20, второй получил по тому же тесту 25, третий – 30. Первый испытуемый отличается от второго настолько же, насколько второй отличается от третьего. Но означает ли это, что первый тревожен меньше, чем второй, ровно настолько же, насколько второй – по сравнению с первым? Можно ли поставить знак равенства между разностью в показателях и разностью в степени тревожности? Эти вопросы встают всякий раз, когда психолог начинает интерпретировать индивидуальные различия по тестовым показателям.

Поскольку множество психологических конструктов не может наблюдаться непосредственно, большинство измерений в психологии – скорее порядковые. Установки, потребности, мнения, личностные характеристики, психологическое благополучие – все это конструкты, имеющие различную степень выраженности у разных людей. Но все они допускают только непрямое порядковое измерение.

В психологической науке существует определенная конвенция о том, что в случае применения стандартизованных тестов исследователи могут трактовать показатели, полученные в порядковой шкале, так, как если бы они были получены в шкале интервалов. Эта договоренность распространяется только на действительно стандартизованные тесты и связана с необходимостью использовать статистические вычисления с полученными данными. Хорошо известный пример трактовки порядковых данных как данных интервальной шкалы – использование тестов IQ.

Шкала интервалов позволяет применять большинство математико-статистических методов для обработки и анализа данных, полученных с ее помощью. Можно использовать все меры центральной тенденции и рассеяния, коэффициент корреляции Пирсона и др. Имеющиеся здесь ограничения в первую очередь связаны с исключением пропорций. Отвечая на вопрос «Насколько больше?», шкала интервалов не дает ответа на вопрос «Во сколько больше?». Например, нельзя утверждать, что человек с IQ = 140 в два раза более интеллектуально развит, чем тот, у кого IQ = 70.

Шкала отношений

Шкала равных отношений – это шкала, классифицирующая объекты или субъектов пропорционально степени выраженности измеряемого свойства. В шкалах отношений классы обозначаются числами, которые пропорциональны друг другу: 2 так относится к 4, как 4 к 8. Это предполагает наличие абсолютной нулевой точки отсчета. В физике абсолютная нулевая точка отсчета встречается при измерении длин отрезков или физических объектов и при измерении температуры по шкале Кельвина с абсолютным нулем температур. Считается, что в психологии примерами шкал равных отношений являются шкалы порогов абсолютной чувствительности (С. Стивенс, 1960; В.К. Гайда, В.П. Захаров, 1982).

Примерами измерений в шкале отношений могут быть измерения массы и роста, скорости и ускорения, времени реакции, и вообще любые измерения, предполагающие в качестве точки отсчета абсолютный нуль и имеющие равные интервалы – единицы измерения.

Следует иметь в виду, что одно и то же исследование может давать данные по разным шкалам. Если сравнивать количество решенных задач в тесте, то работа ведется в шкале отношений. Но если речь идет о сравнении участников по этому тесту, – то в шкале порядка, ведь нулевой показатель не может отражать абсолютно «нулевую» математическую способность человека. Шкалы отношений наиболее широко используются при проведении физических измерений. Их применение в психологии ограничено двумя существенными обстоятельствами. Во-первых, в психологии объект и их свойства нельзя объединить. Можно объединить два тела и сложить их массы, но объединить двух людей со средним IQ с целью получения IQ гения нельзя. Во-вторых, для объектов измерений в психологии практически невозможно указать «естественное» начало отсчета, абсолютный нуль.

Математико-статистические методы, используемые для обработки и анализа данных в шкале отношении, можно применять без каких-либо ограничений.

Типы статистических шкал

Иллюстрированный самоучитель по SPSS > Основы статистики > Типы статистических шкал

gif”/>

5.2. Типы статистических шкал В эмпирическом исследовании могут встречаться, к примеру, следующие переменные (указано их наиболее вероятное кодирование): Пол 1 = мужской 2 = женский Семейное положение 1 = холост/не замужем 2 = женат/замужем 3 = вдовец/вдова 4 = разведен(а) Курение 1 = некурящий 2 = изредка курящий 3 = интенсивно курящий 4 = очень интенсивно курящий Месячный доход 1 = до 3000 DM 2 = 3001 – 5000 DM 3 = более 5000 DM Коэффициент интеллекта (I.Q.) Возраст (лет) Рассмотрим сначала графу “Пол”. Мы видим, что назначение соответствия цифр 1 и 2 обоим полам абсолютно произвольно, их можно было поменять местами или обозначить другими цифрами. Мы, конечно, не имеем в виду, что женщины стоят на ступеньку ниже мужчин, или мужчины значат меньше, чем женщины. Следовательно, отдельным числам не соответствует никакою эмпирического значения. В этом случае говорят о переменных, относящихся к номинальной шкале. В нашем примере рассматривается переменная с номинальной шкалой, имеющая две категории. Такая переменная имеет еще одно название – дихотомическая. Такая же ситуация и с переменной “Семейное положение”. Здесь также соответствие – между числами и категориями семейного положения не имеет никакого эмпирического значения. Но в отличии от Пола, эта переменная не является дихотомической — у нее четыре категории вместо двух. Возможности обработки переменных, относящихся к номинальной шкале очень ограничены. Собственно говоря, можно провести только частотный анализ таких переменных. К примеру, расчет среднего значения для переменной Семейное положение, совершенно бессмысленен. Переменные, относящиеся к номинальной шкале часто используются для группировки, с помощью которых совокупная выборка разбивается по категориям этих переменных. В частичных выборках проводятся одинаковые статистические тесты, результаты которых затем сравниваются друг с другом. В качестве следующего примера рассмотрим переменную “Курение”. Здесь кодовым цифрам присваивается эмпирическое значение в том порядке, в котором они расположены в списке. Переменная Курение, в итоге, сортирована в порядке значимости снизу вверх: умеренный курильщик курит больше, нежели некурящий, а сильно курящий — больше, чем умеренный курильщик и т.д. Такие переменные, для которых используются численные значения, соответствующие постепенному изменению эмпирической значимости, относятся к порядковой шкале. Однако эмпирическая значимость этих переменных не зависит от разницы между соседними численными значениями. Так, несмотря на то, что разница между значениями кодовых чисел для некурящего и изредка курящего и изредка курящего и интенсивно курящего в обоих случаях равна единице, нельзя утверждать, что фактическое различие между некурящим и изредка курящим и между изредка курящим и интенсивно курящим одинаково. Для этого данные понятия слишком расплывчаты. К классическими примерами переменных с порядковой шкалой относятся также переменные, полученные в результате объединения величин в классы, как “Месячный доход” в нашем примере. Кроме частотного анализа, переменные с порядковой шкалой допускают также вычисление определенных статистических характеристик, таких как медианы. В некоторых случаях возможно вычисление среднего значения. Если должна быть установлена связь (корреляция) с другими переменными такого рода, для этой цели можно использовать коэффициент ранговой корреляции. Для сравнения различных выборок переменных, относящихся к порядковой шкале, могут применяться непараметрические тесты, формулы которых оперируют рангами. Рассмотрим теперь “Коэффициент интеллекта (IQ)“. Не только его абсолютные значения отображают порядковое отношение между респондентами, но и разница между двумя значениями также имеет эмпирическую значимость. Например, если у Ганса IQ равен 80, у Фрица — 120 и у Отто — 160, можно сказать, что Фриц в сравнении с Гансом настолько же интеллектуальнее насколько Отто в сравнении с Фрицем (а именно — на 40 единиц IQ). Однако, основываясь только на том, что значение IQ у Ганса в два раза меньше, чем у Отто, исходя из определения IQ нельзя сделать вывод, что Отто вдвое умнее Ганса. Такие переменные, у которых разность (интервал) между двумя значениями имеет эмпирическую значимость, относятся к интервальной шкале. Они могут обрабатываться любыми статистическим методами без ограничений. Так, к примеру, среднее значение является полноценным статистическим показателем для характеристики таких переменных. Наконец, мы достигли наивысшей статистической шкалы, на которой эмпирическую значимость приобретает и отношение двух значений. Примером переменной, относящейся к такой шкале является “Возраст“: если Максу 30 лет, а Морицу 60, можно сказать, что Мориц вдвое старше Макса. Шкала, к которой относятся данные называется шкалой отношений. К этой шкале относятся все интервальные переменные, которые имеют абсолютную нулевую точку. Поэтому переменные относящиеся к интервальной шкале, как правило, имеют и шкалу отношений. Подводя итоги, можно сказать, что существует четыре вида статистических шкал, на которых могут сравниваться численные значения: Статистическая шкала Эмпирическая значимость Примеры Номинальная Нет Пол, семейное положение Порядковая Порядок чисел Курение, месячный доход Интервальная Разность чисел Коэффициент интеллекта (I.Q.) Шкала отношений Отношение чисел Возраст (лет) На практике, в том числе в SPSS, различие между переменными, относящимися к интервальной шкале и шкале отношений обычно несущественно. То есть в дальнейшем практически всегда речь будет идти о переменных, относящихся к интервальной шкале. Пользователь SPSS должен четко разбираться в видах статистических шкал и при выборе метода обращать внимание на то, чтобы были определены надлежащие виды шкал. Мы уже указывали, что переменные, относящиеся к номинальной шкале допускают весьма ограниченные возможности для проведения анализа. Исключение в некоторых ситуациях составляют дихотомические переменные. Для них можно, по крайней мере, определять ранговую корреляцию. Если, например, обнаруживается корреляция коэффициента интеллекта с полом, то положительный коэффициент корреляции означает, что женщины интеллектуальнее, чем мужчины. Однако если переменные, относящиеся к номинальной шкале не являются дихотомическими, вычисление коэффициентов ранговой корреляции не имеет смысла.

Музыкальные гаммы: руководство для начинающих

Если вы учитесь играть на музыкальном инструменте, то довольно часто одной из первых вещей, которую вы изучаете, является игра на мажорной гамме, но на самом деле существует множество различных типов гамм.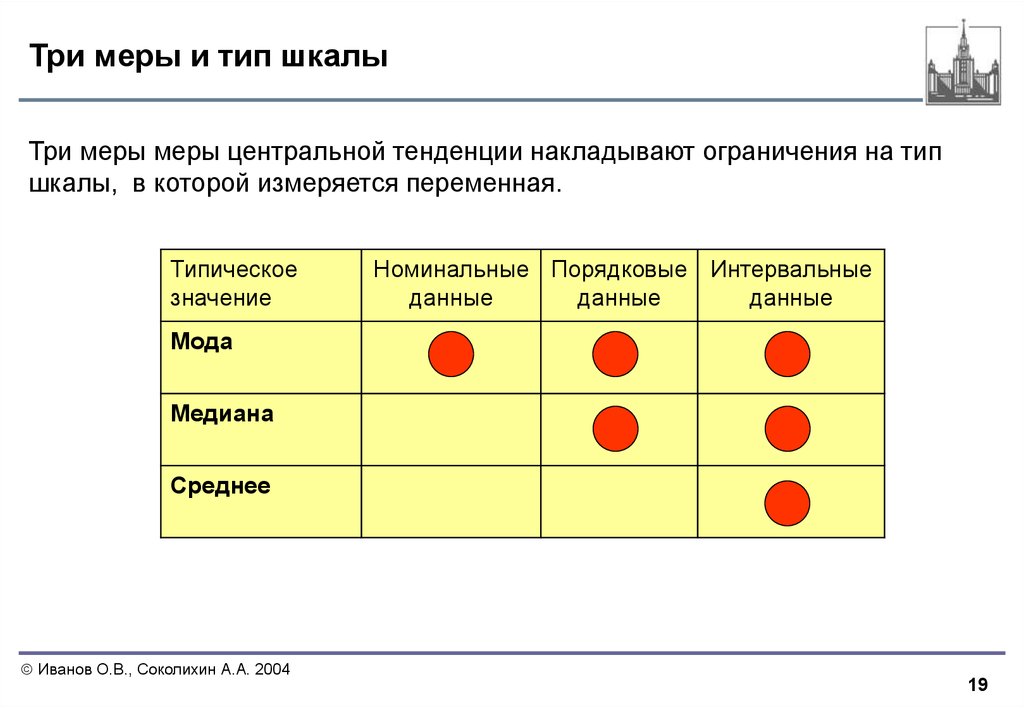 Одни звучат радостно, другие — грустно, у одних пять нот, у других — двенадцать.

В этом посте мы рассмотрим все различные типы музыкальных гамм, их теорию и способы их формирования. Давайте начнем.

Содержание

Что такое гамма в музыке?

Гамма  – это группа нот, расположенных в порядке возрастания или убывания высоты тона.

В восходящей шкале каждая нота выше по высоте, чем предыдущая, а в нисходящей шкале каждая нота ниже по высоте, чем предыдущая.

Степени шкалы

Слово шкала происходит от латинского слова, означающего лестницу.

Итак, вы можете представить шкалу восхождения по ступеням лестницы, которая представлена ​​посохом.

Степени шкалы

Вы должны иметь пометку на каждой строке или пробеле.

Каждая ступень звукоряда имеет особое название:

• 1-я ступень: тоника
• 2-я ступень: супертоника
• 3-я ступень: медианта
• 4-я ступень: субдоминанта
90:28 доминанта 5-я ступень 6-я ступень: субмедианта
• 7-я ступень: ведущая нота (или ведущий тон)

8-я ступень гаммы на самом деле является тоникой, но на октаву выше.

По этой причине, называя ступени гаммы, всегда следует называть ее 1-й ступенью.

Для получения дополнительной информации ознакомьтесь с моим подробным руководством по шкале имен градусов здесь.

Мажорные гаммы

Одним из наиболее распространенных типов гамм является мажорная гамма .

Мажорные гаммы определяются комбинацией полутонов и тонов (целые тона и полутона):

Тон – Тон – Полутон – Тон – Тон – Тон – Semitone

или в целых шагах и наполовину шагах, это будет:

ВСЕГО – ЦЕЛЕЙ – Половина – ВСЕ – ЦЕЛЕЙ . – Весь – Половина

Формула мажорной гаммы Гамма соль мажор

Вы можете использовать эту формулу целых шагов и полутонов для формирования мажорной гаммы, начиная с любой ноты.

Для более подробного ознакомления с формированием мажорных гамм прочтите этот пост, где мы рассмотрим все 12 мажорных гамм.

Минорные гаммы

Второй тип гаммы, который мы собираемся рассмотреть, это минорная гамма .

Минорные гаммы также имеют семь нот, как и мажорные, но они определяются сглаженной терцией.

Это означает, что третья нота звукоряда находится на три полутона выше первой, в отличие от мажорных звукорядов, где третья нота звукоряда находится на четыре полутона выше.

Мелодическая минорная гамма

Существует три различных типа минорной гаммы:

• натуральный минор
• гармонический минор
• мелодический минор

Каждый тип минорной гаммы использует немного отличающуюся формулу полутонов и тонов, но все они имеют минорную терцию.

Подробнее о типах минорных гамм читайте в моем посте здесь.

Мажорные тональности довольно часто ассоциируются с музыкой, которая кажется счастливой или радостной, тогда как минорные тональности известны для музыки, которая звучит грустно или меланхолично.

Вот видео Прелюдии ми минор Шопена для демонстрации.

Прелюдия Шопена ми минор

Хроматические гаммы

Две рассмотренные нами гаммы называются диатоническими.

Это означает, что они находятся в «тональности», а первая нота звукоряда — это тоника.

Диатонические гаммы также являются гептатоническими (это означает, что они имеют семь нот) с двумя интервалами в полтона (полутона) и пятью интервалами, представляющими собой целые тона (тона).

Хроматическая гамма сильно отличается от диатонической гаммы, поскольку состоит из всех 12 нот западной музыки.

Каждая нота в хроматической гамме представляет собой интервал в полтона (полутона) отдельно от других.

Другими словами, чтобы сыграть хроматическую гамму, вы выбираете ноту, затем играете ноту на полшага выше и продолжаете, пока не дойдете до ноты, с которой начали.

Например, вот восходящая хроматическая гамма, начинающаяся с C:

Восходящая хроматическая гамма, C Хроматическая гамма, начинающаяся с C

А вот нисходящая хроматическая гамма, начинающаяся с Gb:

Нисходящая хроматическая гамма, соль-бемоль

Поскольку хроматические гаммы используют каждую отдельную ноту, мы не говорим, что хроматическая гамма находится в определенной тональности.

Мы просто используем примечание, с которого начинается шкала, чтобы назвать его.

Чтобы узнать больше, ознакомьтесь с моим руководством по хроматическим гаммам здесь.

Шкалы целых тонов

Гамма целого тона — это тип гаммы, в которой каждая нота представляет собой интервал, равный целому шагу (тону) друг от друга.

Это полная противоположность хроматической гамме, где каждая нота отстоит на полтона (полутона).

Полная шкала тонов является типом гексатонической шкалы, что означает, что она имеет только шесть нот.

Это связано с тем, что в целой шкале тонов нет интервалов в полшага.

Полная шкала тонов, начинающаяся с C

Целая шкала тонов имеет очень характерный звук, и с ней можно весело поиграть.

Чтобы узнать о них больше, я написал более подробный пост о шкалах целых тонов здесь.

Пентатоника

Следующий тип гаммы, который мы собираемся рассмотреть, это 9-й.0011 пентатоника .

Пентатонические гаммы являются одним из самых простых типов гамм и существуют уже очень давно.

Считается, что им может быть даже 50 000 лет!

Слово пентатоника происходит от греческого слова «пенте», означающего пять.

Это то же самое греческое слово, от которого мы получили «пятиугольник», означающее пятигранную форму.

Пять нот мажорной пентатоники:

• Первая ступень – тоника
• Вторая ступень – супертоника
• Третья ступень – медиана
• Пятая ступень – доминанта
• Шестая ступень – субмедианта

Вот пентатоника до мажор, чтобы вы могли видеть:

Пентатоника до мажор

Пентатоника до мажор гамма очень распространена во многих музыкальных произведениях, с которыми вы будете знакомы, от блюза и джаза до фолка и рока. Простота пентатоники делает ее очень универсальной.

Вот одно из моих любимых видео, в котором Бобби Макферрин использует пентатоническую гамму, чтобы создать музыку для публики.

Бобби МакФеррин демонстрирует пентатоническую гамму

Музыкальные лады

У каждой мажорной гаммы есть семь ладов. Иногда их называют церковными модусами или греческими модусами.

Имии из них:

• Иония (I)
• Дориан (II)
• Фригиан (III)
• Lydian (IV)
• Mixolyian (V)
• AEOLIAN (VI)
8888888888888888888888888888888888888888888888888888887 )

Музыкальные режимы

Несмотря на то, что они могут быть довольно запутанными, вы, вероятно, уже знакомы по крайней мере с одним из них.

Ионический лад — это просто другое название мажорной гаммы, а эолийский лад — это то же самое, что и натуральный минорный лад.

Каждый режим имеет разное звучание, некоторые из них мажорные, а некоторые минорные.

Для получения дополнительной информации об их использовании ознакомьтесь с этой статьей о музыкальных режимах здесь.

Суммирование гамм в музыке

Надеюсь, это поможет лучше понять гаммы.

В ближайшее время я дополню этот пост и надеюсь охватить диатонические гаммы, уменьшенные гаммы и гаммы из других культур.

Если у вас есть какие-либо вопросы по поводу чего-либо, просто отправьте мне сообщение, и я свяжусь с вами!

Музыкальные гаммы: как создавать, играть и использовать все важные гаммы

Усовершенствованные музыкальные гаммы

Этот урок является шагом 1 / 7 плана урока LANDR. Нажмите здесь, чтобы начать с самого начала, или просто продолжайте читать.

Гаммы являются одним из важнейших строительных блоков музыки.

Наряду с аккордами, интервалами и последовательностями, гаммы являются важной концепцией теории музыки, если вы хотите писать песни или создавать треки.

• 
  Что такое музыкальные гаммы?
  
• 
  Зачем учить гаммы?
  
• 
  Types of scales
  
• 
  Major Scales
  
• 
  Minor Scales
  
• 
  Pentatonic scales
  
• 
  Blues scales
  
• 
  Modes of the major scale
  
• 
  Другие гаммы
  

Но музыкальные гаммы могут пугать, если вы только начинаете.

В этом подробном руководстве я расскажу все, что вам нужно знать о гаммах: что это такое, как их использовать и какие из них наиболее важны для создания музыки.

Что такое музыкальные гаммы?

Гаммы в музыке представляют собой набор нот, воспроизводимых одна за другой в соответствии с установленным интервалом. Паттерн определяет качество гаммы и повторяется с одним и тем же набором высоты тона в каждой октаве.

Гаммы чаще всего используются как мелодическая форма набора нот в тональности, но возможны и многие другие наборы нот за пределами двенадцати тональностей.

Зачем учить гаммы?

Гаммы могут показаться сухой и скучной теоретической темой, но они являются невероятно важным инструментом для сочинения, импровизации и написания песен.

Гамма похожа на основу, которую вы можете использовать для создания идей для мелодий, хуков, басовых партий или соло.

А если вы любите импровизировать, гаммы — это паттерны, которые вы используете для выбора нот.

Гаммы необходимо знать, чтобы играть вместе с другими музыкантами и держать свой инструмент в тональности песни.

Со всеми этими разнообразными приложениями неудивительно, что гаммы преподаются как основа теории музыки.

Если вы хотите перейти к использованию таких понятий теории музыки, как аккорды и гармонические последовательности, гаммы — один из самых полезных навыков.

Какие виды весов существуют?

Гаммой в музыке может быть почти любой набор нот.

Самые важные гаммы для музыкантов:

• Мажорные гаммы
• Минорные гаммы
• Пентатонные гаммы
• Блюзовые гаммы
• Лады мажорной гаммы
90 объясните, как они работают, и предоставьте ресурсы, которые помогут вам их изучить.

Гаммы мажор

Гамма мажор является самой основной из всех музыкальных гамм. Если вы когда-либо получали музыкальное образование, вы, вероятно, видели их раньше.

Мажорные гаммы происходят от мажорных тональностей и содержат ноты, необходимые для мажорных аккордов. Звучание мажорной гаммы обычно ассоциируется со счастливыми чувствами и ярким согласным тоном.

Звук исходит из характерного мажорного третьего интервала, образующего третью ступень звукоряда.

Если вам нужно освежить в памяти интервалы, ознакомьтесь с нашим руководством.

Вот образец тонов и полутонов, используемых для построения мажорной гаммы.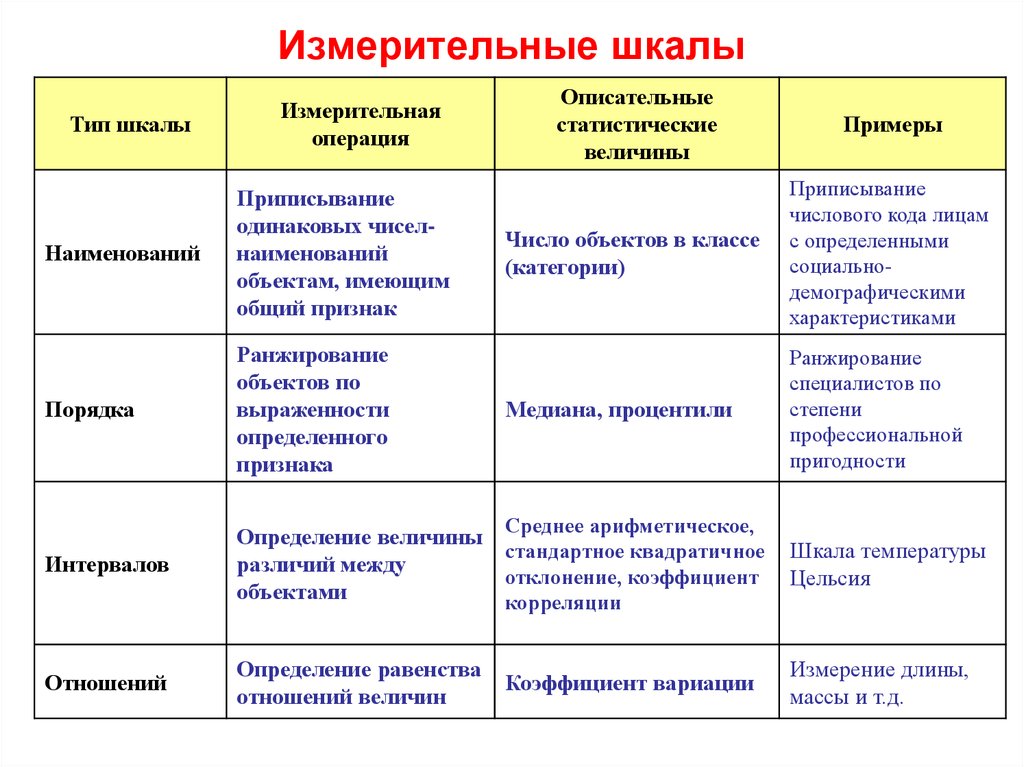





Мажорные гаммы: как использовать самый важный музыкальный строй

Минорные гаммы

Минорные гаммы — следующий по важности тип гаммы в музыке.

Эти гаммы происходят от минорных тональностей и содержат минорную терцию, которую мы часто ассоциируем с грустной музыкой.

Но, в отличие от мажорной гаммы, минорные гаммы могут принимать несколько различных форм в зависимости от того, как они используются в песне.

Три разных типа минорных гамм:

• Натуральный минор (иногда называемый эоловым ладом)
• Мелодический минор
• Гармонический минор

Гамма натурального минора является самой простой и содержит следующий образец тона и полутона:

Если вы внимательно посмотрите, то заметите, что эта минорная гамма содержит ту же формулу гаммы, что и мажорная гамма, если она начинается с шестой ступени гаммы!

Это явление называется относительным мажором, и оно может помочь вам построить минорные гаммы и определить минорные тональности.

Но гамма натурального минора создает проблемы в некоторых мелодиях и гармонических прогрессиях.

Без повышенного ведущего тона (седьмая ступень гаммы) натуральный минор не содержит нот, необходимых для создания доминирующего септаккорда из его пятой ступени.

Повышение седьмой ступени натурального минора решает проблему и дает гармонический минор. Вот образец интервала:

Но гармонический минор имеет свою особенность, на которую следует обратить внимание. Приподнятая седьмая ступень создает очень широкий шаг между шестой и седьмой ступенью шкалы.

Мелодический минорный лад был создан, чтобы ступенчатые мелодии звучали более плавно в миноре.

В этой гамме шестая и седьмая ступени поднимаются вверх при воспроизведении в порядке возрастания и сглаживаются при воспроизведении в порядке убывания.

Вот паттерн по возрастанию:

И по убыванию:





Минорные гаммы:


Как сочинять грустную музыку

Пентатонические гаммы

Пентатонные гаммы с пятью уникальными нотами. Вы можете думать о них как о сокращенной версии мажорной или минорной гаммы.

Пенатоника делится на мажорную пентатонику и минорную пентатонику.

Это одни из самых ранних музыкальных гамм, когда-либо использовавшихся, и они до сих пор неподвластны времени.

Характерные пропуски и промежутки, разделяющие октаву на пять шагов, дают вам прекрасную платформу для написания запоминающихся мелодий и риффов.

Вот образец тон-полутон для мажорной пентатоники:

И минорной пентатоники:

Как только вы возьмете эти гаммы под свои пальцы, вы начнете видеть их повсюду в популярной музыке — от госпела до хэви-метала. .

Чтобы поближе познакомиться с пентатоникой, перейдите к нашему полному руководству




Пентатонические гаммы: как использовать самый универсальный музыкальный строй

Блюзовые гаммы заслуживает отдельной категории, так как он так широко используется в музыке.

На самом деле есть две блюзовые гаммы — одна мажорная и одна минорная. Они связаны с мажорной и минорной пентатоникой.

Мажорная блюзовая гамма состоит из следующих нот:

Мажорная блюзовая гамма содержит минорную терцию минорной гаммы. В этом контексте он известен как синяя нота.

Мажорную блюзовую гамму иногда называют госпел-гаммой, и она используется немного реже, чем ее минорный аналог.

Но минорная блюзовая гамма чрезвычайно распространена во многих жанрах.

Как только вы услышите минорную блюзовую гамму, вы сразу ее узнаете. Вот шаблон:

Эта шкала встречается во всей популярной музыке, от раннего кантри и блюза до классического рока и современного R&B.

Если бы вам нужно было выбрать только одну гамму для обучения импровизации, это, вероятно, была бы блюзовая гамма.

Работает как с мажорными, так и с минорными прогрессиями, особенно с 12-тактовым блюзом.

Блюзовая гамма особенно хорошо подходит для запоминающихся мелодий, хуков и риффов. Если вы хотите узнать, как это работает более подробно, ознакомьтесь с этой статьей.




Блюзовый лад: как использовать его в музыке

Гаммы мажорной гаммы

Гадии мажорной гаммы представляют собой набор гамм с уникальными свойствами, которые вы можете построить из базовой формулы мажора.

Каждый из них имеет различную структуру тонов и полутонов.

Вы получаете паттерн для каждого лада, строя семинотную гамму, начиная с каждой ступени мажорной гаммы в соответствии с формулой мажорной гаммы.

Если это звучит сложно, перейдите к нашему подробному обзору музыкальных режимов, чтобы получить полное руководство.

Если вам просто нужно освежить в памяти, чем лады отличаются от мажорных и минорных гамм, на которые они похожи, эти удобные таблицы могут дать вам быструю справку.

Вот лады, которые тесно связаны с мажорной гаммой:

А вот лады, похожие на минорную гамму:

Хитрость правильного использования ладов состоит в том, чтобы думать о них как о цветах в спектре света. к темноте.

Гаммы с наиболее приподнятыми нотами типа Lydian имеют самое яркое и стабильное звучание.

Лады с более низкими нотами, такие как фригийский, самые темные.

Режимы могут помочь вам добиться звучания, которое даже более радостно, чем мажор, или даже более задумчиво, чем минор.




Музыкальные лады: как обогатить ваши песни модальным цветом

Другие гаммы

Вы можете использовать только гаммы, которые мы рассмотрели до сих пор в этой статье, и никогда не исчерпать материал для написания отличных песен.

Но если вы любите приключения, есть целый мир других весов, с которыми можно поэкспериментировать.

Это странные и удивительные гаммы, используемые в джазе, мировой музыке и других жанрах. Они могут добавить уникальное ощущение изысканности и направить вас в новые музыкальные направления.

Слишком много других гамм, чтобы перечислять их здесь, так что переходите к нашему пошаговому обзору некоторых из лучших вариантов звучания.




6 странных гамм, которые сделают ваши песни особенными

Масштабная модель

Изучение гамм — важный первый шаг в вашем путешествии по теории музыки.