Какие существуют способы обозначения классов точности – 37. Способы обозначения классов точности си

alexxlab | 25.06.2020 | 0 | Разное

5Бил. Класс точности си и его обозначение

Установление рядов пределов допускаемых погрешностей позволяет упорядочить требования к средствам измерений по точности. Это упорядочивание осуществляется путем установления классов точности СИ. Класс точности СИ – обобщенная характеристика данного типа СИ, отражающая уровень их точности, выражаемая пределами допускаемой основной, а в некоторых случаях и дополнительных погрешностей, а также другими характеристиками, влияющими на точность. Класс точности применяется для средств измерений, используемых в технических измерениях, когда нет необходимости или возможности выделить отдельно систематические и случайные погрешности, оценить вклад влияющих величин с помощью дополнительных погрешностей. Класс точности позволяет судить о том, в каких пределах находится погрешность средств измерений одного типа, но не является непосредственным показателем точности измерений, выполняемых с помощью

каждого из этих средств. Класс точности СИ конкретного типа устанавливают в стандартах технических требований или других нормативных документах. При выражении предела допускаемой основной погрешности в форме абсолютной погрешности класс точности в документации и на средствах измерения обозначается прописными буквами латинского алфавита или римскими цифрами. Чем дальше буква от начала алфавита, тем больше погрешность. Расшифровка соответствия букв значению абсолютной погрешности осуществляется в технической документации на средство измерения. Выражение класса точности через относительные и приведенную погрешности рассмотрено в предыдущем разделе В настоящее время по отношению к современным средствам измерений понятие класс точности применяется довольно редко. В основном он чаще всего используется для описания характеристик электроизмерительных приборов, аналоговых стрелочных приборов всех типов, некоторых мер длины, весов, гирь общего назначения, манометров. Примеры обозначение классов точности для различных форм выражения погрешности приведены в таблице.

Обозначение классов точности

Пределы допускаемой основной погрешности	Обозначения		Форма выражения погрешности
	в документации	на приборе
γ = ± 1,5	Класс точности 1,5	1,5	Приведенная погрешность
δ = ± 0,5	Класс точности 0,5	0,5	Относительная погрешность, постоянная
δ = ± [ 0,02 + 0,01( xk /x –1)]	Класс точности 0,02/0,01	0,02/0,01	Относительная погрешность, возрастает с уменьшением х

4бил

Понятие погрешности измерений Непосредственной задачей измерения является определение значений измеряемой величины. В результате измерения физической величины с истинным значением Х_и мы получаем оценку этой величины Х_изм. – результат измерений. При этом следует четко различать два понятия: истинные значения физических величин и их эмпирические проявления – действительные значения, которые являются результатами измерений и в конкретной измерительной задаче могут приниматься в качестве истинных значений. Истинное значение величины неизвестно и оно применяют только в теоретических исследованиях. Результаты измерений являются продуктами нашего познания и представляют собой приближенные оценки значений величин, которые находятся в процессе измерений. Степень приближения полученных оценок к истинным (действительным) значениям измеряемых величин зависит от многих факторов: метода измерений, использованных средств измерений и их погрешностей, от свойств органов чувств операторов, проводящих измерения, от условий, в которых проводятся измерения и т.д. Поэтому между истинным значением физической величины и результатом измерений всегда имеется различие, которое выражается погрешностью измерений (то же самое, что погрешностью результата измерений).

Погрешность результата измерения — отклонение результата измерения от истинного (действительного) значения измеряемой величины:

∆X = X_изм – X_ист

Так как истинное значение измеряемой величины всегда неизвестно и на практике мы имеем дело с действительными значениями величин Х_д, то формула для определения погрешности в связи с этим приобретает вид:

∆X = X_изм – X_д

Погрешность СИ — разность между показанием средства измерений –

Х_п и истинным (действительным) значением измеряемой величины – Х_д. Существует распространенная классификация погрешностей средств измерений. Ниже приводятся примеры их наиболее часто используемых видов. Абсолютная погрешность СИ – погрешность средства измерений, выраженная в единицах измеряемой величины: ∆Х = Х_п – Х_д. Абсолютная погрешность удобна для практического применения, т.к. дает значение погрешности в единицах измеряемой величины. Но при ее использовании трудно сравнивать по точности приборы с разными диапазонами измерений. Эта проблема снимается при использовании относительных погрешностей. Если абсолютная погрешность не изменяется во всем диапазоне измерения, то она называется аддитивной, если она изменяется пропорционально измеряемой величине (увеличивается с ее увеличением), то она называется мультипликативной Относительная погрешность СИ – погрешность средства измерений, выраженная отношением абсолютной погрешности СИ к результату измерений или к действительному значению измеренной величины: δ = ∆Х / Х_д. Относительная погрешность дает наилучшее из всех видов погрешностей представление об уровне точности измерений, который может быть достигнут при использовании данного средства измерений. Однако она обычно существенно изменяется вдоль шкалы прибора, например, увеличивается с уменьшением значения измеряемой величины. В связи с этим часто используют приведенную погрешность. Приведенная погрешность СИ – относительная погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины Х_N, которое называют нормирующим: γ = ∆Х / Х_N. Относительные и приведенные погрешности обычно выражают либо в процентах, либо в относительных единицах (долях единицы). Для показывающих приборов нормирующее значение устанавливается в зависимости от особенностей и характера шкалы. Приведенные погрешности позволяют сравнивать по точности средства измерений, имеющие разные пределы измерений, если абсолютные погрешности каждого из них не зависят от значения измеряемой величины. По условиям проведения измерений погрешности средств измерений подразделяются на

основные и дополнительные. Основная погрешность СИ – погрешность средства измерений, применяемого в нормальных условиях, т.е. в условиях, которые определены в НТД не него как нормальные. Нормальные значения влияющих величин указываются в стандартах или технических условиях на средства измерений данного вида в форме номиналов с нормированными отклонениями. Наиболее типичными нормальными условиями являются:

• температура (20 ± 5)ºС;

• относительная влажность (65±15) %;

• атмосферное давление (100 ± 4) кПа или (750 ± 30) мм рт. ст.;

• напряжение питания электрической сети 220 В ± 2% с частотой 50 Гц.

Иногда вместо номинальных значений влияющих величин указывается нормальная область их значений. Например, влажность (30–80)%. Дополнительная погрешность СИ – составляющая погрешности СИ, возникающая дополнительно к основной погрешности вследствие отклонения какой-либо из влияющих величин от нормального ее значения. Деление погрешностей на основные и дополнительные обусловлено тем, что свойства средств измерений зависят от внешних условий. Погрешности по своему происхождению разделяются на систематические и случайные. Систематическая погрешность СИ – составляющая погрешности средства измерений, принимаемая за постоянную или закономерно изменяющуюся. Систематические погрешности являются в общем случае функциями измеряемой величины и влияющих величин (температуры, влажности, давления, напряжения питания и т.п.). Случайная погрешность СИ – составляющая погрешности средства измерений, изменяющаяся случайным образом. Случайные погрешности средств измерений обусловлены случайными изменениями параметров составляющих эти СИ элементов и случайными погрешностями отсчета показаний приборов. При конструировании прибора его случайную погрешность стараются сделать незначительной в сравнении с другими погрешностями. У хорошо сконструированного и выполненного прибора случайная погрешность незначительна. Однако при увеличении чувствительности средств измерений обычно наблюдается увеличение случайной погрешности. Тогда при повторных измерениях одной и той же величины в одних и тех же условиях результаты будут различными. В таком случае приходится прибегать многократным измерениям и к статистической обработке получаемых результатов. Как правило, случайную погрешность приборов снижается до такого уровня, что проводить многократные измерений нет необходимости.

Стабильность СИ — качественная характеристика средства измерений, отражающая неизменность во времени его метрологических характеристик.

Градуировочная характеристика СИ – зависимость между значениями величин на входе и выходе средства измерений, полученная экспериментально. Может быть выражена в виде формулы, графика или таблицы.

9бил.

Классификация погрешностей измерений Представленная классификация погрешностей измерений связана с причинами их возникновения. Кроме этого существуют и другие признаки, по которым классифицируются погрешности. По характеру проявления (свойствам погрешностей) они разделяются на систематические и случайные, по способам выражения – на абсолютные и относительные. Абсолютная погрешность выражается в единицах измеряемой величины, а относительная погрешность представляет собой отношение абсолютной погрешности к измеренному (действительному) значению величины и ее численное значение выражается либо в процентах, либо в долях единицы. Опыт проведения измерений показывает, что при многократных измерениях одной и той же неизменной физической величины при постоянных условиях погрешность измерений можно представить в виде двух слагаемых, которые по-разному проявляются от измерения к измерению. Существуют факторы, постоянно или закономерно изменяющиеся в процессе проведения измерений и влияющие на результат измерений и его погрешность. Погрешности, вызываемые такими факторами, называются систематическими. Систематическая погрешность – составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины. В зависимости от характера изменения систематические погрешности подразделяются на постоянные, прогрессирующие, периодические, изменяющиеся по сложному закону. Близость к нулю систематической погрешности отражает правильность измерений. Систематические погрешности обычно оцениваются либо путем теоретического анализа условий измерения, основываясь на известных свойствах средств измерений, либо использованием более точных средств измерений. Как правило, систематические погрешности стараются исключить с помощью поправок. Поправка представляет собой значение величины, вводимое в неисправленный результат измерения с целью исключения систематической погрешности. Знак поправки противоположен знаку величины. На возникновение погрешностей влияют также и факторы, нерегулярно появляющиеся и неожиданно исчезающие. Причем интенсивность их тоже не остается постоянной. Результаты измерения в таких условиях имеют различия, которые индивидуально непредсказуемы, а присущие им закономерности проявляются лишь при значительном числе измерений. Погрешности, появляющиеся в результате действия таких факторов, называются случайными погрешностями. Случайная погрешность – составляющая погрешности измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях одной и той же величины, проведенных с одинаковой тщательностью. Незначительность случайных погрешностей говорит о хорошей сходимости измерений, то есть о близости друг к другу результатов измерений, выполненных повторно одними и теми же средствами, одним и тем же методом, в одинаковых условиях и с одинаковой тщательностью. Обнаруживаются случайные погрешности путем повторных измерений одной и той же величины в одних и тех же условиях. Они не могут быть исключены опытным путем, но могут быть оценены при обработке результатов наблюдений. Деление погрешностей измерений на случайные и систематические очень важно, т.к. учет и оценка этих составляющих погрешности требует разных подходов. Факторы, вызывающие погрешности, как правило, можно свести к общему уровню, когда влияние их на формирование погрешности является более или менее одинаковым. Однако некоторые факторы могут проявляться неожиданно сильно, например, резкое падение напряжения в сети. В таком случае могут возникать погрешности, существенно превышающие погрешности, оправданные условиями измерений, свойствами средств измерений и метода измерений, квалификацией оператора. Такие погрешности называются грубыми, или промахами. Грубая погрешность (промах) – погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных значений погрешности. Грубые погрешности необходимо всегда исключать из рассмотрения, если известно, что они являются результатом очевидных промахов при проведении измерений. Если же причины появления резко выделяющихся наблюдений установить нельзя, то для решения вопроса об их исключении используют статистические методы. Существует несколько критериев, которые позволяют выявить грубые погрешности. Некоторые из них рассмотрены ниже в разделе об обработке результатов измерений.

8

Виды измерений По характеру зависимости измеряемой величины от времени измерения разделяются на: статические, при которых измеряемая величина остается постоянной во времени; динамические, в процессе которых измеряемая величина изменяется и является непостоянной во времени. Статическими измерениями являются, например, измерения размеров тела, постоянного давления, электрических величин в цепях с установившемся режимом, динамическими – измерения пульсирующих давлений, вибраций, электрических величин в условиях протекания переходного процесса. По способу получения результатов измерений их разделяют на: прямые; косвенные; совокупные; совместные. Прямые – это измерения, при которых искомое значение физической величины находят непосредственно из опытных данных. Прямые измерения можно выразить формулой , где- искомое значение измеряемой величины, а- значение, непосредственно получаемое из опытных данных. При прямых измерениях экспериментальным операциям подвергают измеряемую величину, которую сравнивают с мерой непосредственно или же с помощью измерительных приборов, градуированных в требуемых единицах. Примерами прямых служат измерения длины тела линейкой, массы при помощи весов и др.Косвенные – это измерения, при которых искомую величину определяют на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям, т.е. измеряют не собственно определяемую величину, а другие, функционально с ней связанные. Значение измеряемой величины находят путем вычисления по формуле , где- функциональная зависимость, которая заранее известна,- значения величин, измеренных прямым способом. Примеры косвенных измерений: определение объема тела по прямым измерениям его геометрических размеров, нахождение удельного электрического сопротивления проводника по его сопротивлению, длине и площади поперечного сечения. Косвенные измерения широко распространены в тех случаях, когда искомую величину невозможно или слишком сложно измерить непосредственно или когда прямое измерение дает менее точный результат. Роль их особенно велика при измерении величин, недоступных непосредственному экспериментальному сравнению, например размеров астрономического или внутриатомного порядка.Совокупные – это производимые одновременно измерения нескольких одноименных величин, при которых искомую величину определяют решением системы уравнений, получаемых при прямых измерениях различных сочетаний этих величин. Примером совокупных измерений является определение массы отдельных гирь набора (калибровка по известной массе одной из них и по результатам прямых сравнений масс различных сочетаний гирь). Совместные – это производимые одновременно измерения двух или нескольких неодноименных величин для нахождения зависимостей между ними. В качестве примера можно назвать измерение электрического сопротивления при 200С и температурных коэффициентов измерительного резистора по данным прямых измерений его сопротивления при различных температурах.

Методы измерений Метод измерения – это способ экспериментального определения значения физической величины, т. е. совокупность используемых при измерениях физических явлений и средств измерений. 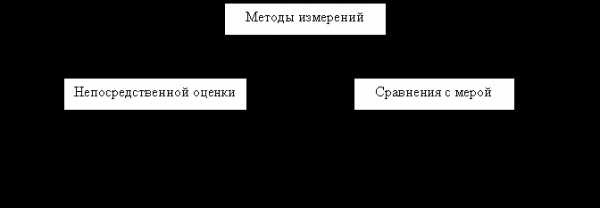Метод непосредственной оценки заключается в определения значения физической величины по отсчетному устройству измерительного прибора прямого действия. Например – измерение напряжения вольтметром. Этот метод является наиболее распространенным, но его точность зависит от точности измерительного прибора. Метод сравнения с мерой – в этом случае измеряемая величина сравнивается с величиной, воспроизводимой мерой. Точность измерения может быть выше, чем точность непосредственной оценки. Различают следующие разновидности метода сравнения с мерой: Метод противопоставления, при котором измеряемая и воспроизводимая величина одновременно воздействуют на прибор сравнения, с помощью которого устанавливается соотношение между величинами. Пример: измерение веса с помощью рычажных весов и набора гирь. Дифференциальный метод, при котором на измерительный прибор воздействует разность измеряемой величины и известной величины, воспроизводимой мерой. При этом уравновешивание измеряемой величины известной производится не полностью. Пример: измерение напряжения постоянного тока с помощью дискретного делителя напряжения, источника образцового напряжения и вольтметра. Нулевой метод, при котором результирующий эффект воздействия обеих величин на прибор сравнения доводят до нуля, что фиксируется высокочувствительным прибором – нуль-индикатором. Пример: измерение сопротивления резистора с помощью четырехплечевого моста, в котором падение напряжения на резисторе с неизвестным сопротивлением уравновешивается падением напряжения на резисторе известного сопротивления. Метод замещения, при котором производится поочередное подключение на вход прибора измеряемой величины и известной величины, и по двум показаниям прибора оценивается значение измеряемой величины, а  затем подбором известной величины добиваются, чтобы оба показания совпали. При этом методе может быть достигнута высокая точность измерений при высокой точности меры известной величины и высокой чувствительности прибора. Пример: точное точное измерение малого напряжения при помощи высокочувствительного гальванометра, к которому сначала подключают источник неизвестного напряжения и определяют отклонение указателя, а затем с помощью регулируемого источника известного напряжения добиваются того же отклонения указателя. При этом известное напряжение равно неизвестному. Метод совпадения, при котором измеряют разность между измеряемой величиной и величиной, воспроизводимой мерой, используя совпадение отметок шкал или периодических сигналов. Пример: измерение частоты вращения детали с помощью мигающей лампы стробоскопа: наблюдая положение метки на вращающейся детали в моменты вспышек лампы, по известной частоте вспышек и смещению метки определяют частоту вращения детали.

2 И 3

1. Статическая погрешность измерений

Погрешность результата измерений, свойственная условиям статического измерения

2. Динамическая погрешность измерений

Погрешность результата измерений, свойственная условиям динамического измерения.

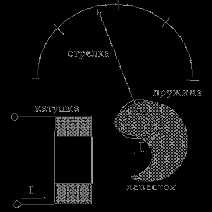
20 Б Элекродинамические измерительные приборы

Устройство электродинамического механизма и векторная диаграмма, поясняющая его работу, приведены на рисунке:

Электродинамический измерительный механизм работает по принципу взаимодействия магнитных потоков двух катушек. Электродинамический механизм состоит из двух катушек. Одна из них подвижная, а другая укреплена неподвижно. Токи, протекающие по этим катушкам и магнитные потоки ими образуемые при своем взаимодействии создают вращающий момент.

Приборы электродинамической системы имеют малую чувствительность и большое самопотребление. Применяются в основном при токах 0.1…10А и напряжениях до 300 В.

19 Б

Электромагнитные измерительные приборы

Устройство измерительного механизма электромагнитного типа показано на рисунке:

В электромагнитных измерительных механизмах для создания вращающего момента используется действие магнитного поля катушки с током на подвижный ферромагнитный (чаще пермоллоевый) лепесток. Достоинства электромагнитных механизмов: пригодность для работы в цепях постоянного и переменного тока; большая перегрузочная способность; возможность непосредственного измерения больших токов и напряжений; простота конструкции. Недостатки электромагнитных механизмов: неравномерная шкала; невысокая чувствительность; большое самопотребление мощности; подверженность влиянию изменения частоты; подверженность влиянию внешних магнитных полей и температуры.

21БИЛ

Электростатические измерительные приборы

Схемы механизмов различных конструкций показаны на рисунке. На рисунке а приведена схема с изменяющейся площадью электродов, а на рисунке б- с изменяющимся расстоянием между электродами.

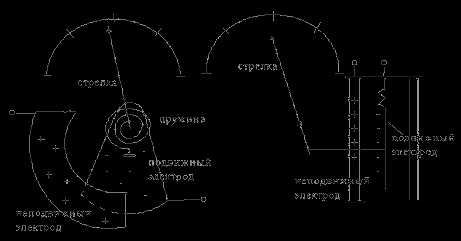
Принцип действия электростатического измерительного механизма основан на взаимодействии сил, возникающих между двумя разнозаряженными пластинами. Достоинства электростатических приборов: высокое входное сопротивление, малую входную емкость, малую мощность самопотребления, широкий частотный диапазон, могут использоваться в цепях переменного и постоянного тока, показания не зависят от формы кривой измеряемого сигнала. Недостатки электростатических приборов: приборы имеют малую чувствительность и невысокую точность.

31БИЛ

. Цифровые измерительные устройства.

Это устройства, автоматически вырабатывающие дискретные сигналы цифровой информации и показания представляются в цифровом виде.

Вырабатывает цифровой код в соответствии с измеряемой величиной, при этом непрерывная аналоговая величина квантуется по уровню и дискретизируется во времени.

Дискретизация во времени – преобразование, при котором значение величины отличается от 0 и совпадает с соответствующим значением измеряемой величины только в определенные моменты времени. Промежутки между этими значениями – шаг дискретизации.

Квантование по уровню – преобразование, при котором непрерывная аналоговая величина принимает фиксированные, квантованные значения. Эти значения – уровни квантования или кванты.

Важной характеристикой является правило отождествления измеряемой величины и уровней квантования. —————-

studfiles.net

Обозначение классов точности.

1.5 –

0.5 –

Для СИ с существенно неравномерной шкалой; 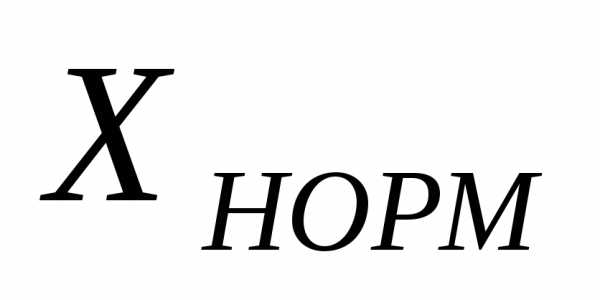принято равным длине шкалы.

1.0 –

0.05/0.01 –

Если дополнительные погрешности малы, то погрешность СИ не разделяют на основную и дополнительную и нормируют ее для рабочих условий.

Итак, класс точности является обобщенным показателем точности СИ, учитывающим погрешность СИ в нормальных условиях и ее изменения в рабочих условиях. Однако, он является такой характеристикой, которая необходима но в общем случае недостаточна для определения погрешности измерения.

Он не отражает погрешности взаимодействия СИ с объектом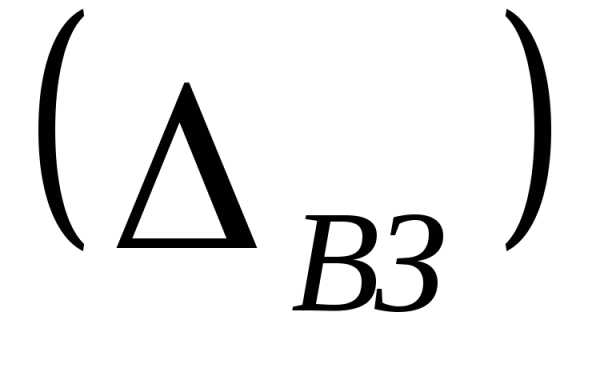. Поэтому в дополнение к классу точности указывают сопротивление Vи A.

При наличии сведений о выходном сопротивлении объекта это позволяет рассчитать погрешность от взаимодействия СИ с объектом, которая относится к числу методических.

Замечание.Отнесение к той или иной категории спорно. Так, например, погрешность от взаимодействия принято относить к категории методических. Но по Маликову, методическая –0 это такая, которая остается. Как бы ни усовершенствовали само средство измерения.

Если повышать входное сопротивление V и понижать у А, то будет уменьшаться. Таким образом, усовершенствование СИ ведет к уменьшению. По Маликову – это инструментальная. Вообще, в широком смысле, методическая – это от несоответствия модели и действительности. В конечном счете не так важно, куда отнести, а важно учесть и уметь вычислить.

На переменном токе недостаточно указать сопротивление, ибо сказываются реактивные элементы. Поэтому говорят входные и выходные импедансы.

2.1.3.Тенденция развития комплексов нмх.

Рассмотренных НМХ оказывается недостаточно, если:

-СИ применяется в условиях с широкими диапазонами значений влияющих величин;

-СИ предназначается для динамических измерений;

-СИ имеет не автономное, а системное применение.

В связи с этим разработан ГОСТ 8.009-84 «Государственная система обеспечения единства измерений. Нормируемые метрологические характеристики средств измерений». С 1.1.86.

Номенклатура НМХ расширяется по следующим направлениям:

1. В погрешности СИ выделяют систематическую 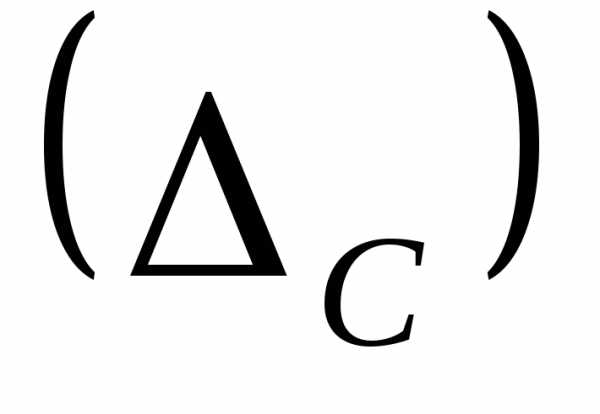и центрированную случайнуюсоставляющие, еслисущественна. Характеристиками являются СКО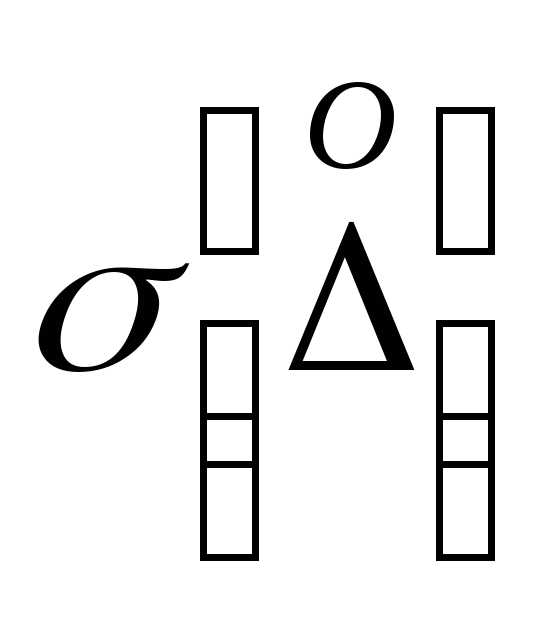и иногда некоторые более сложные характеристики, т.н. автокорреляционная функция или же спектральная плотность. Нормируют пределы допускаемых значений: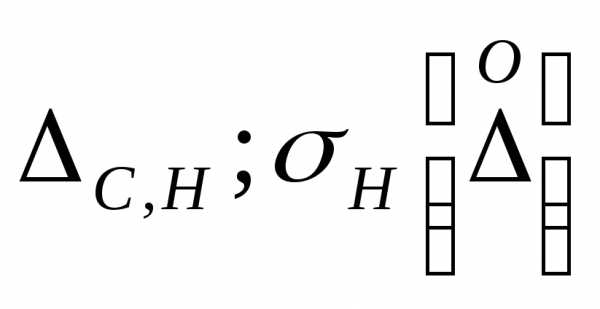и номинальную автокорреляционную функцию или номинальную спектральную плотность.

2. Действие характеризуют более полно и детально по сравнению с нормированием дополнительных погрешностей. Для этого нормируют функции влияния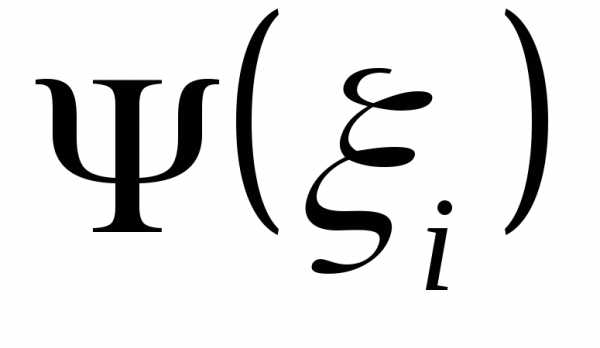не только на погрешность, но на любую МХ, и только если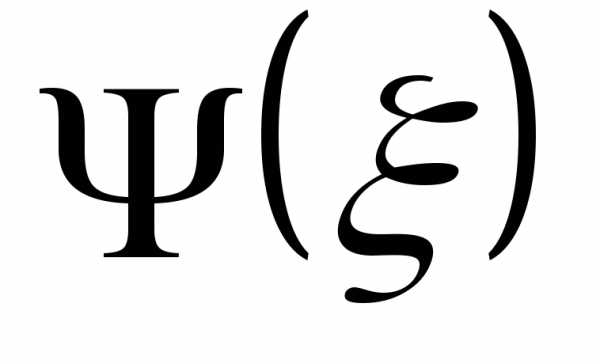линейна, ее заменяют коэффициентом влияния. Нормируютв виде формулы, таблицы, графика.

3. Для обеспечения возможности оценки динамической составляющей погрешности измерения вводят какую-либо из т.н. полных динамических характеристик, например, переходную характеристику h(t), т.е. реакцию СИ на ступенчатое входное воздействие:

Только в тех случаях, когда этого достаточно для раcчета 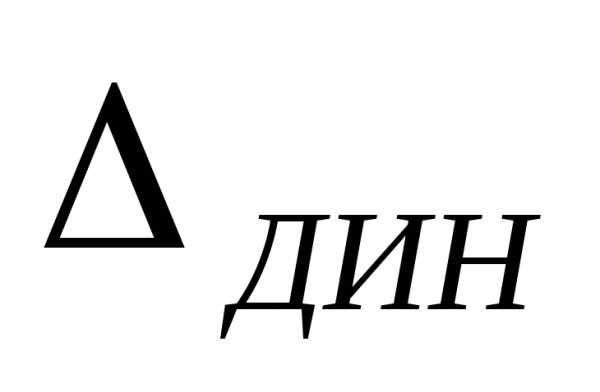, вместо полных динамических характеристик можно давать частные, например, если СИ в динамическом отношении можно считать инерционным звеном первого порядка, то однозначно характеризуется постоянной времени.

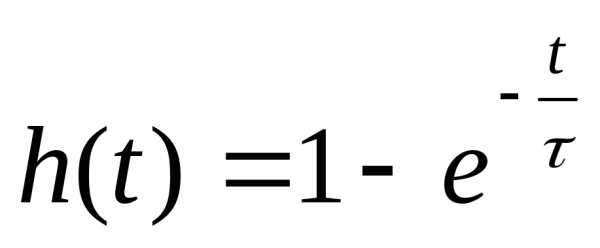
В этом случае – частная динамическая характеристика, достаточная для расчета.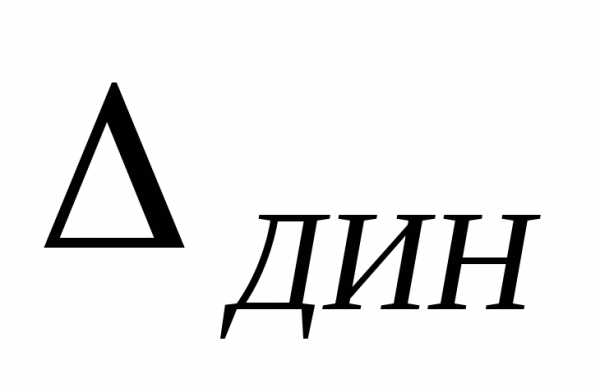

Нормируют динамические характеристики также, как функции влияния. Для каждого данного типа СИ формируют комплексы НМХ. Эти комплексы разделяют на две группы в соответствии с принятой моделью расчета погрешности.

Модель 1 – предполагает статистическое суммирование составляющих погрешности, а

Модель 2 – арифметическое суммирование.

Модель 2 предназначена в основном для таких СИ, у которых не существенна .

Критерий существенности (для СИ, у которых нет вариаций).

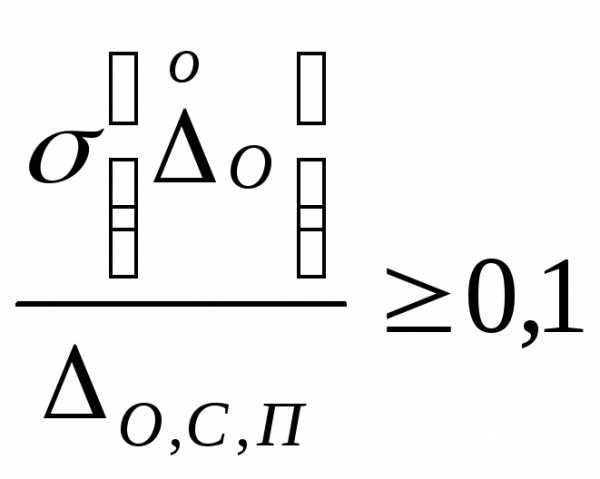
Выбор модели? С одной стороны модель2 требует меньше исходных данных, она проще. С другой, дает завышенную оценку погрешности измерения. Для модели 2 доверительная вероятность может быть принята Р=1. Другими словами, модель2 «неэкономична»: она завышает требования к НМХ СИ при заданной погрешности измерения.

Тем не менее, если ни в коем случае нельзя допустить, чтобы действительная погрешность измерений хотя бы изредка превышала значение, рассчитанное по НМХ (возможность катастрофических последствий, угроза здоровью людей и т.п.), то должна быть принята модель 2.

Модель 1 дает более правильную, т.е. не столь завышенную оценку погрешности измерений с любой вероятностью, близкой к 1, но не равной 1.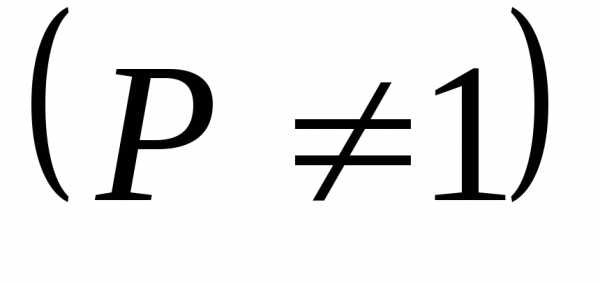

При небольшом числе суммируемых составляющих погрешностей – до трех выигрыш от применения модели 1 получается несущественным.

Для каждой из двух моделей комплекса НМХ сформированы согласно рассматриваемому ГОСТу для трех видов СИ:

-меры

-измерительные приборы

-измерительные преобразователи.

Возьмем только измерительные приборы. Согласно модели 2 для них нормируются:

-ЦДШ (цена деления шкалы)

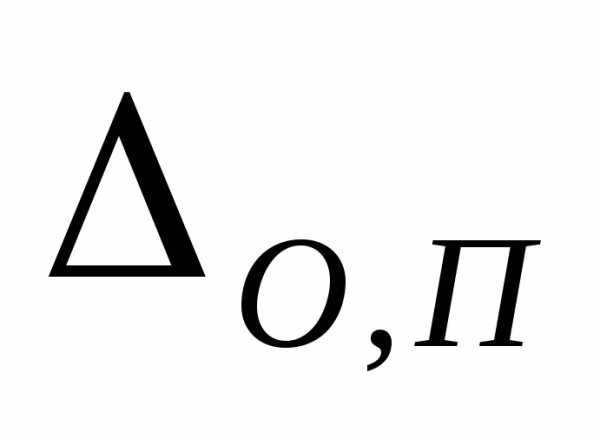–(в любой форме:,,)

-предел допускаемой вариации (если она есть)

-пределы дополнительных погрешностей

– характеристики взаимодействия

-динамические характеристики.

Согласно модели 1:

-ЦДШ

–

–

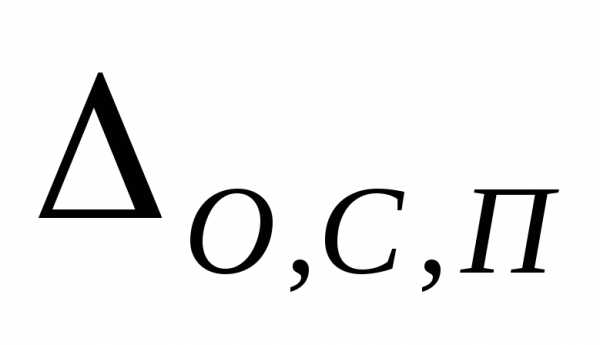
-предел допускаемой вариации

–

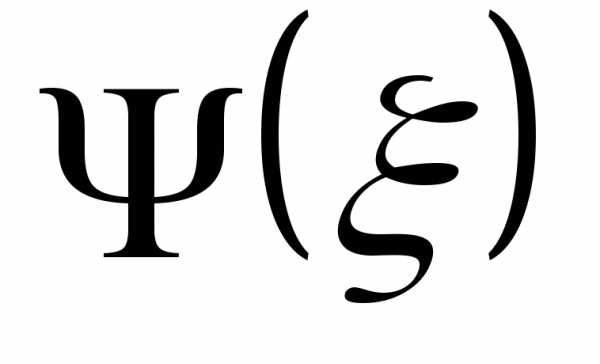
-характеристики взаимодействия

динамические характеристики.

2.2.Оценка погрешностей прямых измерений с однократными наблюдениями.

studfiles.net

3.5 Класс точности си и его обозначение

Установление рядов пределов допускаемых погрешностей позволяет упорядочить требования к средствам измерений по точности. Это упорядочивание осуществляется путем установления классов точностиСИ.

Класс точности СИ – обобщенная характеристика данного типа СИ, отражающая уровень их точности, выражаемая пределами допускаемой основной, а в некоторых случаях и дополнительных погрешностей (они рассмотрены выше), а также другими характеристиками, влияющими на точность. Класс точности применяется для средств измерений, используемых в технических измерениях, когда нет необходимости или возможности выделить отдельно систематические и случайные погрешности, оценить вклад влияющих величин с помощью дополнительных погрешностей. Класс точности позволяет судить о том, в каких пределах находится погрешность средств измерений одного типа, но не является непосредственным показателем точности измерений, выполняемых с помощью каждого из этих средств. Класс точности СИ конкретного типа устанавливают в стандартах технических требований или других нормативных документах.

При выражении предела допускаемой основной погрешности в форме абсолютной погрешности класс точности в документации и на средствах измерения обозначается прописными буквами латинского алфавита или римскими цифрами. Чем дальше буква от начала алфавита, тем больше погрешность. Расшифровка соответ-ствия букв значению абсолютной погрешности осуществляется в технической документации на средство измерения.

Выражение класса точности через относительные и приведенную погрешности рассмотрено в предыдущем разделе

В настоящее время по отношению к современным средствам измерений понятие класс точности применяется довольно редко. В основном он чаще всего используется для описания характеристик электроизмерительных приборов, аналоговых стрелочных приборов всех типов, некоторых мер длины, весов, гирь общего назначения, манометров.

Примеры обозначение классов точности для различных форм выражения погрешности приведены в таблице.

Обозначение классов точности

___________________________________________________________

Пределы допускаемой Обозначения Форма выраже-

основной погрешности ния погрешности

в документации на приборе

=  1,5 Класс точности 1,5 1,5 Приведенная

погрешность

 =  0,5 Класс точности 0,5 0,5 Относительная

погрешность,

постоянная

 =  [ 0,02 + 0,01( x_k/x –1)] Класс точности 0,02/0,01 Относительная

0,02/0,01 погрешность,

возрастает с

уменьшением х

6. Эталоны и их использование

Решение задачи обеспечения единства измерений требует тождественности единиц одной и той же величины, которые передаются средствам измерения. Это достигается путем точного воспроизведения и хранения единиц физических величин и передачи их размеров используемым средствам измерений. Воспроизведение, хранение и передача размеров единиц осуществляется с помощью эталонов. Под воспроизведением единицы физической величины понимается совокупность операций по ее материализации путем создания фиксированной по размеру физической величины в соответствии с ее определением. Эталоны классифицируются по различным признакам. Так, они делятся на первичные, вторичные и рабочие. Первичный эталон воспроизводит единицу с наивысшей (по сравнению с другими эталонами той же величины) точностью. Государственный первичный эталон  это эталон, признанный в качестве исходного натерритории государства. Вторичный эталон получает размер единицы от первичного эталона. Рабочий эталон предназначен для передачи размера единицы рабочим средствам измерений, так как для поверки многочисленных рабочих средств измерений нецелесообразно использовать очень точный и дорогой первичный эталон. Этот термин заменяет применявшийся ранее термин образцовое средство измерений. Рабочие эталоны подразделяют на разряды: 1-й, 2-й и т.д.

Эталонная база РФ состоит из 118 государственных эталонов и более 300 вторичных эталонов. Государственные эталоны служат для воспроизведения физических величин, поэтому структура эталонной базы соответствует структуре единиц СИ. Основа этой базы — эталоны основных единиц СИ кроме эталона единицы количества вещества (моль). Одной из причин того, что эталон единицы количества вещества не создан, является недостаточная четкость определения этой единицы и отсутствует метод ее измерения в соответствии с определением. Тем более, эту единицу трудно назвать основной, так как в ее определение связано с единицей массы. Вполне возможно, что эта единица будет переведена в разряд специальных единиц массы.

Большинство эталонов сосредоточено в двух метроло-гических институтах РФ  Всероссийском научно-исследователь-ском институте метрологии им. Д.И. Менделеева (ВНИИМ) и Всероссийском научно-исследовательском институте физико-технических и радиотехнических измерений (ВНИИФТРИ).

В области измерения параметров ионизирующих излучений применяются 14 государственных эталонов: 9 во ВНИИМ, 5 во ВНИИФТРИ.

Эталоны предназначены не только для воспроизведения единицы физической величины, но и для передачи ее размера другим эталонам и рабочим средствам измерений. Под передачей размера единицы величины понимается приведение размера величины, хранимой средством измерений, к размеру единицы, воспроизводимой эталоном. Эта процедура осуществляется при поверке средств измерений.

Поверка средств измерений – установление органом государственной метрологической службы (или другим официально уполномоченным органом, организацией) пригодности СИ к применению на основе экспериментально определяемых метрологических характеристик и подтверждения их соответствия установленным обязательным требованиям.

Поверке подвергают СИ, подлежащие государственному метрологическому контролю и надзору и используемые в здравоохранении, охране окружающей среды, обеспечении безопасности труда, обороны, в торговых, банковских, почтовых операциях, при испытаниях контроля качества продукции и в других важных сферах деятельности.

При поверке рабочих средств измерений используют эталон, как правило, рабочий эталон, а процедура проведения поверки регламентируется обязательными требованиями, которые устанавливаются нормативными документами по поверке. В качестве таких документов используются либо методические указания по поверке, либо государственные (национальные) стандарты. Например, ГОСТ 8.355-79. «Радиометры нейтронов. Методы и средства поверки».

Общие вопросы организации и проведения поверки регламентируются Правилами по метрологии Государственной системы обеспечения единства измерений (ГСИ). Например, «ПР 50.2.006-94. Правила по метрологии. Порядок проведения поверки средств измерений».

Проводят поверку специально обученные специалисты, аттестованные в качестве поверителей органами Государственной метрологической службы.

Результаты поверки средств измерений, признанных годными к применению, оформляют выдачей свидетельства о поверке, нанесением поверительного клейма на приборы или в техническую документацию (паспорт) прибора. Поверку СИ могут проводить также метрологические службы юридических лиц, аккредитованные на право поверки средств измерений в государственных метрологических органах.

Поверка подразделяется на первичную (при выпуске средств измерений), периодическую (при их эксплуатации), внеочередную, инспекционную (при различных проверках), комплектную (всей измерительной установки или системы целиком), поэлементную (отдельных элементов установки или системы), выборочную (отдельных экземпляров средств измерений).

Передача размера единицы от эталона к рабочим средствам измерений регламентируется поверочными схемами.

Поверочная схема для СИ – нормативный документ, устанавливающий соподчинение средств измерений, участвующих в передаче размера единицы от эталона к рабочим средствам измерений, с указанием методов и погрешности при передаче.. Различают государственные (на все средства измерений данной величины в стране) и локальные поверочные схемы (на средства измерений в регионе, отрасли, предприятии). Требования к поверочным схемам определены стандартом ГСИ «ГОСТ 8.061-80. Поверочные схемы. Содержание и построение».

В качестве примера стандарта на поверочную схему для средств измерений конкретного типа можно привести Межгосудар-ственный стандарт ГСИ «ГОСТ 8.033-96. Государственная повероч-ная схема для средств измерений активности радионуклидов, потока и плотности потока альфа-, бета-частиц и фотонов радионуклидных источников».

Средства измерений, не входящие в сферу государственного метрологического контроля, могут подвергаться калибровке.

Калибровка СИ – совокупность операций, устанавливающих соотношение между значением величины, полученным с помощью данного СИ и соответствующим значением величины, определенной с помощью эталона, с целью определения действительных метрологических характеристик этого СИ.

Результаты калибровки позволяют определять:

• действительные значения измеряемой величины;

• поправки к показаниям средств измерений;

• погрешность средств измерений.

Результаты калибровки удостоверяются калибровочным знаком, наносимым на СИ, или сертификатом о калибровке. Калибровке присущ ряд особенностей по сравнению с поверкой. Это добровольная процедура и она может выполняться любой метрологической службой. При этом аккредитация на право калибровки также является добровольной (не обязательной) процедурой.

Отмеченные особенности калибровки являются следствием разгосударствления процессов контроля за метрологической исправностью средств измерений – отказом от их всеобщей обязательности поверки.

Хотя калибровка может проводиться любой метрологической службой и является добровольной процедурой, для ее проведения необходимы определенные условия. Основное из них – прослеживание измерений, т.е. обязательная передача размера единицы от эталона к калибруемому рабочему средству измерений.

Для организации работ по калибровке в РФ создана Российская система калибровки (РСК), в которую входят государственные научные метрологические центры, органы ГМС, метрологические службы юридических лиц, объединенные целью ОЕИ в сферах, не подлежащих государственному метрологическому контролю и надзору.

Российская система калибровки базируется на следующих принципах:

• обязательность передачи размеров единиц от государственных эталонов к рабочим СИ;

• профессионализм и техническая компетентность;

• самоокупаемость.

studfiles.net

Обозначение классов точности

Обычно класс точности указывается в виде арабских или римских цифр, а также букв латинского алфавита. Обозначения классов точности наносят на циферблаты, щитки и корпуса средств измерений (рис. 2.9), приводят в нормативных и технических документах.   Рис. 2.9. Внешний вид шкал средств измерений: а – вольтметр, б – амперметр, в – частотомер, г – мегаомметр Согласно ГОСТ 8.401 обозначение классов точности вводится в зависимости от способов задания пределов допускаемых погрешностей. Возможны четыре варианта обозначения класса точности. 1) Если пределы допускаемой основной погрешности выражены в абсолютной форме (формулы 2.17, 2.18), то класс точности средства измерения обозначают заглавными буквами латинского алфавита (например: А, В, С) или римскими цифрами (I, II, III и т. д.). Соответствие букв значению абсолютной погрешности раскрывается в технической документации на данное средство измерения. Обычно чем дальше буква от начала алфавита, тем больше значение допускаемой абсолютной погрешности (например, прибор класса В более точен, чем класса С). 2) Если пределы допускаемой основной погрешности выражены в приведенной форме (формула 2.19), то класс точности средств измерений обозначается арабской цифрой (возможны дополнительные условные знаки), указывающей предел допускаемой погрешности. Например, класс точности прибора 1,5 означает, что g = ±1,5 %. 3) Если пределы допускаемой основной погрешности выражены в относительной форме (формула 2.20), то класс точности средств измерений обозначается арабской цифрой в окружности, указывающей предел допускаемой погрешности. Например, класс точности прибора 0,5 означает, что d = ±0,5 %. 4) Если пределы допускаемой основной погрешности выражены в относительной форме (формула 2.21), то класс точности средств измерений обозначается двумя цифрами, соответствующими значениям c и d. Например, класс точности прибора 0,02/0,01 означает, что с = 0,02, d = 0,01. В таблице 2.2 приведены примеры обозначения классов точности в документации и на средствах измерения.     Таблица 2.2   Классы точности средств измерений Формула для определения пределов допускаемой погрешности Примеры пределов допускаемой основной погрешности, % Обозначение класса точности в документации на средстве измерения D = ± a или D = ± (a + bХ) - Класс точности М или класс точности III M III g = ± 1,5 Класс точности 1,5 1,5 g = ± 0,5 Класс точности 0,5 d = ± 0,5 Класс точности 0,5   Класс точности 0,02/0,01 0,02/0,01   Пределы допускаемых дополнительных погрешностей непосредственно не учитывают при установлении класса точности средства измерения. В технической документации их устанавливают обычно в виде дольного (кратного) значения предела допускаемой основной погрешности. Пределы всех основных и дополнительных допускаемых погрешностей выражаются не более чем двумя значащими цифрами. Ниже приведены примеры определения пределов допускаемой погрешности средств измерения с использованием классов точности.   Пример 1. Термоэлектрический преобразователь ТХА-9310 выпускают трех классов точности: А, В и С. Пределы допускаемых погрешностей составляют: DА = 0,004×t, DВ = 0,0075×t, DС = 0,015×t (t – текущая температура). Необходимо определить значения пределов допускаемых абсолютных погрешностей для преобразователей этих классов точности при результате измерения температуры t = 200 °С. Решение. DА = ±(0,004 × 200) = ±0,8 °С, аналогично DВ = ±1,5 °С, DС = ±3 °С.   Пример 2. На рис. 2.9 представлены шкалы средств измерений с указанием значений измеряемых величин и классов точности. Необходимо определить пределы допускаемых абсолютных погрешностей указанных приборов. Решение. Класс точности вольтметра, равный 0,5 (рис. 2.9, а) означает, что нормированы пределы допускаемой приведенной погрешности прибора, т.е. g = ±0,5 %. Следовательно, необходимо воспользоваться формулой 2.19 для определения пределов допускаемой абсолютной погрешности. Нормирующее значение равно верхнему пределу измерений (ХN =100 В), т.к. нулевое значение равномерной шкалы находится на краю диапазона измерений. Отсюда: Следовательно, предел допускаемой погрешности вольтметра не превышает 0,5 В, а измеряемое напряжение U при показании 65 В составляет (65,0 ± 0,5) В.   Класс точности амперметра, равный 1,5 (рис. 2.9, б), означает также нормирование пределов допускаемой приведенной погрешности прибора, т.е. g = ±1,5 %. Нормирующее значение равно сумме модулей пределов измерений (ХN =25 А), т.к. нулевая отметка находится внутри диапазона измерений. Поэтому в соответствии с формулой 2.19 допускаемая погрешность равна Таким образом, предел допускаемой погрешности амперметра составляет ±0,38 А.   На рис. 2.9, в рядом с цифровым табло частотомера указан класс точности 2. Это указывает на нормирование пределов допускаемой приведенной погрешности прибора (g = ±2 %). Нормирующее значение равно номинальному значению (ХN =50 Гц), поэтому и измеряемая частота равна (47 ±1) Гц. Класс точности мегаомметра с неравномерной шкалой, равный 2,5 (рис. 2.9, г), свидетельствует о том, что допускаемая относительная погрешность d прибора не превышает 2,5 %. Следовательно, необходимо воспользоваться формулой 2.20 для определения абсолютной погрешности.   R= (40 ± 1) МОм.   Пример 3. Амперметр с диапазоном измерения -50…50 А имеет класс точности, равный 0,02/0,01. Необходимо определить, чему равна сила тока в цепи при показании 25,625 А. Решение. Класс точности прибора указывает на нормирование пределов допускаемой относительной погрешности прибора. Вначале определим значение этих пределов по формуле 3.21 (с=0,02, d=0,01, Хk=50 А). Затем вычислим пределы допускаемой абсолютной погрешности, используя формулу 2.20 Следовательно, сила тока в цепи с учетом правил округления равна (25,625 ± 0,008) А.   Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:

zdamsam.ru

Классы точности

В зависимости от требований, предъявляемых к тому или другому механизму, узлу, машине, их детали могут быть выполнены с различной степенью точности. Так, например, детали сельскохозяйственных машин можно изготовлять менее точно, чем детали токарных станков, которые изготовляются в свою очередь с меньшей

точностью, чем детали измерительных приборов. Иначе говоря, одна и та же посадка может быть выполнена с различной точностью.

Государственным стандартом в системе допусков для машиностроения предусмотрено 10 классов точности (для размеров от 1 до 500 мм).

Пять из них 1,2,2а, 3, За — более точные, имеющие наименьшие допуски; два класса — 4 и 5 — менее точные;

остальные три — 7, 8 и 9 (6-й класс в системе отсутствует) — имеют наибольшие допуски и предназначаются для несопрягаемых размеров.

Способы обработки деталей в зависимости от классов точности

Класс точности	Применение	Способы обработки				Посадки		Примечание
		отверстий		валов
2а	В ответственных сопряжениях весьма высокой точности {подшипники качения, шарики и ролики подшипников, детали точных измерительных машин и приборов) В машинах и механизмах, работающих на больших скоростях (детали станков, тракторных, автомобильных и авиационных двигателей, электромашин и т. д.) То же для малоответственных деталей автомобилей, тракторов, сельско-	Калибровка и доводка малых отверстии, хонингование, тонкая расточка,   притирка и доводка   больших отверстий Чистовое развертывание, точное чистовое шлифование, протягивание,   прошивание и хонннгование Развертывание, протягивание, шлифование Расточка чистовым резцом, развертывание, шлифование –		Тонкое шлифование, притирка, доводка, полирование Точное чистовое шлифование, чистовая обточка Чистовое шлифование и обтачка Чистовая обточка		Прессовая   1 -я, 2-я, глухая, тугая, плотная, напряженная, скользящая и движения Все посадки, кроме прессовок 1- й  и прессовой Глухая, тугая, напряжения, плотная и скользящая Прессовая 1-я, 2-   я, 3-я, скользящая, ходовая и широкоходовая		Высший из классов, применяемых в машиностроении Наиболее распространенный в машиностроении класс точности 2
Продолжение табл. 3
Класс точности	Применение хозяйственных, текстильных машин и т. п	Способы обработки			Посадки		Примечание
		отверстий	валов
За	Для малоответственных деталей автомобилей, тракторов, сельскохозяйственных, текстильных машин и т. п.	Расточка резцом, черновое развертывание, шлифование	Чистовая обточка   валов больших диаметров и шлифование малых диаметров		Скользящая
4	В сельскохозяйственном машиностроении, паровозо – и вагоностроении, в сопряжениях штампованных деталей и т. д.	Точное сверление одним сверлом по кондуктору, двумя сверлами, зенкерование	Чистовая обточка		Прессовая скользящая, ходовая, широкоходовая, легкоходовая
5	То же	То же	То же		Скользящая и ходовая
7	Для сопрягаемых де-	Горячая штамповка,	Ковка, штам-		Не ИМЕЮТ		По этим классам
8	талей не применяют	отливка в землю	повка, прокатка,				устанавливают до-
	Применяют только при изготовлении дета-		обдирка, отливка, отрезка				пуски на свободные (несопрягае-
9	лей с допускаемыми грубыми отклонениями от номинальных размеров						мые) размеры

Для определения, к какому классу точности относится та или иная посадка, у ее условного обозначения проставляется в виде индекса соответствующая цифра. Например, глухая посадка первого класса точности обозначается Г1; ходовая четвертого класса точности — Х4; прессовая 2-я третьего класса — Пр2з и т. д.

Только посадки второго класса точности не имеют цифрового обозначения; например обозначение Пр указывает на прессовую посадку второго класса точности;

обозначение Т — на тугую и т. д. Но посадки класса точности 2а, как и других классов, имеют условное обозначение и цифру; например тугая посадка класса точности 2а обозначается Т2а

1. Виды погрешности обработки. Понятие о случайных и систематических погрешностях.

Для правильного функционирования изделий необходимо чтобы назначались отклонения не только на размеры, но и на форму и расположение поверхностей.

Под отклонением от правильной геометрической формы или расположения поверхности понимают отклонение реальной детали от номинальной, т.е. заданной чертежом: ∆=А_изм-А_треб.

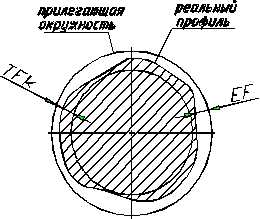
В основу нормирования положен принцип прилегающих прямых, окружностей, плоскостей, поверхностей и т.д.

Само отклонение оценивается наибольшим расстоянием от прилегающей поверхности до реальной по перпендикуляру.

Причины возникновения отклонений формы:

Овальность – износ посадочных поверхностей подшипников.

Огранка – бесцентровое шлифование.

Конусность – износ инструмента.

Бочкообразность – при обработке длинных тонких валов.

Седлообразность – при обработке коротких толстых валов.

Обозначение отклонений формы и расположения поверхности.

А – нормальная точность – 60%Т

В – средняя точность – 40%Т

С – высокая точность – 25%Т

Допуск формы:

Допуск расположения:

Примеры:

Отклонения формы цилиндрических поверхностей, их нормирование и примеры обозначения на чертежах допусков формы цилиндрических поверхностей.

Поперечное сечение:

Овальность Огранка Некруглость

Продольное сечение:

Конусообразность Бочкообразность Седлообразность

studfiles.net

Точность обработки деталей. Классы точности

Взаимозаменяемость деталей.

Выпуск велосипедов, мотоциклов, тракторов, автомобилей, электродвигателей, швейных и других машин осуществляется на заводах такими темпами, когда счет времени обработки и сборки ведется не только минутами, но и секундами. Детали этих машин должны быть изготовлены точно по чертежам и техническим условиям так, чтобы при сборке они подходили одна к другой без слесарной подгонки, что сокращает время на сборку и удешевляет стоимость изделия. Важно также, чтобы при ремонте машины новая деталь, заменяющая изношенную, могла быть установлена на ее место без подгонки. Детали, удовлетворяющие таким требованиям, называются взаимозаменяемыми. Взаимозаменяемость – это свойство деталей занимать свои места в узлах и изделиях без предварительного подбора или подгонки по месту.

Сопряжение деталей.

Две детали, подвижно или неподвижно соединяемые друг с другом, называют сопрягаемыми. Размеры, по которым происходит соединение этих деталей, называют сопрягаемыми размерами. Размеры, по которым не происходит соединение деталей, называют свободными размерами. Примером сопрягаемых размеров может служить наружный диаметр фрезерной оправки и соответствующий ему диаметр отверстия в насадной фрезе, диаметр шейки оправки и соответствующий ему диаметр отверстия в подшипнике подвески. Примером свободных размеров может служить наружный диаметр установочных колец фрезерной оправки, длина фрезерной оправки, ширина цилиндрической фрезы.

Сопрягаемые детали должны быть выполнены взаимозаменяемыми.

Понятие о точности обработки.

Изготовить партию взаимозаменяемых деталей абсолютно одинакового размера невозможно, так как на точность обработки влияют неточность и износ станка, износ фрезы, неточности при установке и закреплении заготовки и другие причины. Как правило, все детали данной партии при обработке имеют отклонения от заданных размеров и формы. Но величины этих отклонений должны быть назначены таким образом, чтобы сопрягаемые размеры могли обеспечить сборку деталей без подгонки, т.е. чтобы детали были взаимозаменяемыми.

Конструкторы изделий при назначении величины допускаемых отклонений на сопрягаемые детали руководствуются установленными государством стандартами – ГОСТ. Ниже вкратце излагаются основные понятия о допусках и предельных отклонениях, вытекающие их ГОСТ 7713-55.

Понятие о допуске и предельных отклонениях. Величина допустимых отклонений указывается в чертежах детали со знаками плюс и минус.

Знак минус показывает, что деталь может быть изготовлена с отклонением в меньшую сторону; знак плюс показывает, что деталь может быть изготовлена с отклонением в большую сторону. Например, поставленный в чертеже бруска размер 10_-0,1 мм показывает, что брусок может быть отфрезерован так, чтобы после его обработки его размер лежал в пределах между 10 мм и 9,9 мм. Точно также поставленный в чертеже диаметр паза 10^+0,2 мм показывает, что паз может быть отфрезерован так, чтобы после обработки его размер лежал в пределах между 10 мм и 10,2 мм.

Поставленный в чертеже размер 10^+0,2_-0,1 мм показывает, что обработанная деталь будет годной, если ее размер составляет не менее 9,9 мм и не более 10,2 мм, т.е. лежит в этих пределах.

Номинальным размером называется основной расчетный размер, от которого исходят при назначении отклонений. Если в чертеже указан размер 10^+0,2_-0,1 мм, то размер 10 мм называется номинальным.

Действительным размером называется размер, полученный при измерении обработанной детали. Размеры, между которыми может находиться действительный размер годной детали, называются предельными размерами. Действительный размер детали с размерами 10^+0,2_-0,1 мм может лежать в пределах 10+0,2 = 10,02 мм и 10-0,1 =9,9 мм. Больший размер называется наибольшим предельным размером, а меньший – наименьшим предельным размером.

Разность между наибольшим и наименьшим предельными размерами называется допуском размера.

• Верхним предельным отклонением называется разность между наибольшим предельным размером и номинальным размером.
• Нижним предельным отклонением называется разность между наименьшим предельным размером и номинальным размером.

Допуск можно также определить, как разность между верхним и нижним предельными отклонениями.

Действительным отклонением называется разность между действительным и номинальным размерами.

При графическом изображении допусков отклонения размеров откладываются от линии, соответствующей номинальному размеру и называемой нулевой линией; положительные отклонения откладываются вверх от нулевой линии, а отрицательные – вниз.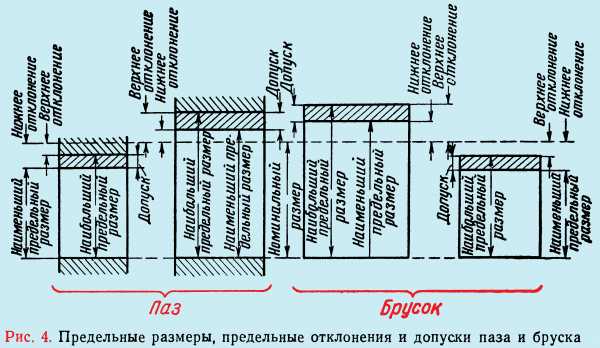

Зазоры и натяги.

Если брусок с размерами грани 10_-0,1 мм посадить в паз с размерами грани 10^+0,2_+0,1 мм, то в соединении бруска с пазом получится зазор, и брусок можно будет передвигать вдоль паза. Такая посадка (сопряжение двух деталей) называется свободной. Наибольший зазор в этом случае составит 0,3 мм, а наименьший будет равен 0,1 мм.

Если же размер бруска будет 10^+0,2_+0,1 мм, а паза 10_-0,1 мм, то брусок не войдет свободно в паз и его придется вставлять с силой или запрессовывать. В соединении получится натяг или отрицательный зазор, наименьшая величина которого равна 0,1 мм. А наибольшая 0,3 мм. Такая посадка называется неподвижной, так как брусок нельзя будет передвигать вдоль паза.

Таким образом, можно сделать следующие заключения.

• Зазором называется положительная разность между размером паза и размером бруска, обеспечивающая свободу их движения относительно друг друга.
• Натягом называется отрицательная разность между размером паза и размером бруска (размер бруска больше размера паза), которая после посадки бруска в паз создает неподвижное их соединение.

Посадки.

Посадкой называется характер соединения сопрягаемых деталей, определяемый разностью между размерами паза и бруска, создающий большую или меньшую свободу (зазор или натяг) их относительного перемещения или степень сопро­тивления взаимному перемещению. В зависимости от наличия в сопряжении бруска и паза зазора или натяга различают посадки с зазором, с натягом и переходные.

Посадками с зазором, или свободными, называют такие посадки, при которых обеспечивается возможность относительного перемещения сопряженных деталей во время работы. В зависимости от величины зазора степень относительного перемещения деталей, сопряженных свободной посадкой, может быть различной. Для вращения шпинделя фрезерного станка в подшипниках зазор должен быть меньшим и, следовательно, посадка более тугой, чем для посадки колец на фрезерную оправку.

Посадками с натягом, или неподвижными, называют посадки, при которых во время работы не должно происходить перемещения сопряженных деталей относительно друг друга. В зависимости от величины натяга степень свободы сопряженных деталей неподвижной посадки может быть различной. Так, посадку шейки вала в кольцо шарикоподшипника производят с меньшим натягом, чем посадку колеса железнодорожного вагона на шейку оси.

При переходных посадках возможно получение, как натягов, так и зазоров. При наибольшем предельном размере бруска и наименьшем предельном размере паза получается натяг, а при наименьшем предельном размере бруска и наибольшем предельном размере паза получается зазор (в таблицах допусков в графе «натяг» обозначен знаком минус).

Ниже приводятся посадки, относящиеся к рассмотренным трем группам; в скобках даются их сокращенные обозначения.

Наибольший натяг получается при горячей посадке, меньший — при прессовых посадках; наименьший зазор получается при скользящей посадке, немного больший — при посадке движения, почти втрое больший при ходовой, затем еще больший при легкоходовой и, наконец, наибольший при широкоходовой посадке.

При глухой, тугой, напряженной и плотной посадках, как указывалось выше, возможны натяги и зазоры в зависимости от получающихся отклонений размера.

Классы точности.

Точность изготовления характеризуется величиной допускаемых отклонений от заданных размеров и формы. Для разных машин требуются детали с различной точностью обработки. Очевидно, что детали плуга, дорожного катка и других сельскохозяйственных и дорожных машин могут быть изготовлены менее точно, чем детали фрезерного станка, а детали фрезерного станка требуют меньшей точности, чем детали измерительного прибора. В связи с этим в машиностроении детали разных машин изготовляют по разным классам точности. В СССР (были) приняты десять классов точности.

• пять из них: 1-й, 2-й, 2а, 3-й, За — требуют наибольшей точности обработки;
• два других: 4-й и 5-й — меньшей;
• три остальных: 7-й, 8-й, 9-й — еще меньшей.

Применение классов точности в различных областях

• 1-й класс точности применяют при изготовлении особо точных изделий. Вследствие очень малых допусков работа по 1-му классу точности требует высокой квалификации рабочего и точного оборудования, приспособлений и инструмента.
• 2-й и 2а классы точности применяют наиболее часто. По ним изготовляют ответственные детали станков, автомобильных, тракторных, авиационных и электрических двигателей, текстильных и других машин.Наряду с этим в отраслях машиностроения, выпускающих указанные машины, детали менее ответственных соединений из­готовляют по 3-му, 4-му, 5-му и другим более грубым классам точности.
• 3-й и За классы точности применяют главным образом в тяжелом машиностроении при производстве турбин, паровых машин, двигателей внутреннего сгорания, трансмиссионных деталей и т. д.
• По 4-му классу точности изготовляют детали сельскохозяйственных машин, паровозов, железнодорожных вагонов и т. д.
• 5-й класс точности применяют в машиностроении для неответственных деталей менее точных механизмов.
• 7-й, 8-й и 9-й классы точности применяют при изготовлении более грубых деталей и особенно при заготовительных операциях: литье, штамповке, медницко-слесарных работах и т. д.
• Свободные размеры деталей выполняют обычно по 5-му или 7-му классам точности.

Чтобы показать, с какой посадкой и по какому классу точности нужно изготовить деталь, в чертежах на номинальных сопрягаемых размерах ставится буква, обозначающая посадку, и цифра, соответствующая классу точности. Например, С₄ означает: скользящая посадка 4-го класса точности; Х₃ — ходовая посадка 3-го класса точности и т. п. Для посадок 2-го класса точности (особенно широко распространенных) цифра 2 не ставится. Поэтому, если в чертеже на сопрягаемом размере рядом с буквой посадки нет цифры, то это значит, что деталь надо изготовить по 2-му классу точности. Например, Л означает легкоходовая посадка 2-го класса точности.

---

 

Автор: С. В. Аврутин
Источник: Основы фрезерного дела, С. В. Аврутин, 1962г
Дата в источнике: 1962г

mplast.by

Классы точности (средств измерений) – это… Что такое Классы точности (средств измерений)?



Классы точности (средств измерений)

Классы точности средств измерений, обобщённая характеристика средств измерений, служащая показателем установленных для них государственными стандартами пределов основных и дополнительных погрешностей и др. параметров, влияющих на точность. Например, для концевых мер длины К. т. характеризуют пределы допускаемых отклонений от номинального размера и влияние изменений температуры, а также допустимую непараллельность рабочих поверхностей и отклонение их от идеальной плоскости. Введение К. т. облегчает стандартизацию средств измерений и их подбор для измерений с требуемой точностью.

Из-за разнообразия измеряемых величин и средств измерений нельзя ввести единый способ выражения пределов допускаемых погрешностей и единые обозначения К. т. Если пределы погрешностей выражены в виде приведенной погрешности (т. е. в процентах от верхнего предела измерений, диапазона измерений или длины шкалы прибора), а также в виде относительной погрешности (т. е. в процентах от действительного значения величины), то К. т. обозначают числом, соответствующим значению погрешности. Например: К. т. 0,1 соответствует погрешность 0,1%. Многие показывающие приборы (амперметры, вольтметры, манометры и др.) формируются по приведённой погрешности, выраженной в процентах от верхнего предела измерений. В этих случаях применяется ряд К. т.: 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0. При нормировании по относительной погрешности обозначение К. т. заключают в кружок.

Для гирь, мер длины и приборов, для которых предел погрешности выражают в единицах измеряемой величины, К. т. принято обозначать номером (1-й, 2-й и т.д. ‒ в порядке снижения К. т.). При указании конкретного К. т. слово «точность» обычно опускается, например гири 3-го класса. Ряды К. т., их обозначения и соответствующие требования к средствам измерений включаются в стандарты (ГОСТ) на отдельные их виды.

Лит.: ГОСТ 13600‒68. Государственная система обеспечения единства измерений. Средства измерений. Классы точности. Общие требования: Широков К. П. и Раинович С. Г., О классах точности средств измерений, «Измерительная техника», 1969, № 4.

К. П. Широков.

Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.

• Классы точности (в машиностроении)
• Классы чистоты

Смотреть что такое “Классы точности (средств измерений)” в других словарях:

• КЛАССЫ ТОЧНОСТИ (средств измерений) — КЛАССЫ ТОЧНОСТИ средств измерений, обобщенная характеристика средств измерений (см. СРЕДСТВА ИЗМЕРЕНИЙ), служащая показателем установленных для них государственными стандартами пределов основных и дополнительных погрешностей и других параметров,… …   Энциклопедический словарь

• Классы точности (средств измерений) — Класс точности средства измерений обобщенная характеристика прибора, характеризующая допустимые по стандарту значения основных и дополнительных погрешностей, влияющих на точность измерения. Погрешность может нормироваться, в частности, по… …   Википедия

• КЛАССЫ ТОЧНОСТИ — средств измерений, обобщённая хар ка средств измерений (мер, измерительных приборов), служащая показателем установленных для них гос. стандартами пределов осн. и дополнит. погрешностей и др. параметров, влияющих на точность. Напр., для концевых… …   Физическая энциклопедия

• КЛАССЫ ТОЧНОСТИ — средств измерений обобщенная характеристика средств измерений, служащая показателем установленных для них государственными стандартами пределов основных и дополнительных погрешностей и других параметров, влияющих на точность …   Большой Энциклопедический словарь

• Классы точности — I Классы точности         средств измерений, обобщённая характеристика средств измерений, служащая показателем установленных для них государственными стандартами пределов основных и дополнительных погрешностей и др. параметров, влияющих на… …   Большая советская энциклопедия

• классы точности — I средств измерений, обобщённая характеристика средств измерений, служащая показателем установленных для них государственными стандартами пределов основной и дополнительной погрешностей и других параметров, влияющих на точность. II (в… …   Энциклопедический словарь

• КЛАССЫ ТОЧНОСТИ — средств измерений, обобщённая характеристика средств измерений, служащая показателем установленных для них гос. стандартами пределов осн. и доп. погрешностей и др. параметров, влияющих на точность …   Естествознание. Энциклопедический словарь

• Погрешности средств измерений —         отклонения метрологических свойств или параметров средств измерений от номинальных, влияющие на погрешности результатов измерений, получаемых при помощи этих средств. Составляющие этих погрешностей, зависящие от П. с. и., называются… …   Большая советская энциклопедия

• ПОГРЕШНОСТИ СРЕДСТВ ИЗМЕРЕНИЙ — отклонения метрологич. св в или параметров средств измерений от номинальных, влияющие на погрешности результатов измерений, получаемых при помощи этих средств. Составляющие этих погрешностей, зависящие от П. с. и., наз. и н с т р у м е н т а л ь… …   Физическая энциклопедия

• точности классы — см. Классы точности. * * * ТОЧНОСТИ КЛАССЫ ТОЧНОСТИ КЛАССЫ, см. Классы точности (см. КЛАССЫ ТОЧНОСТИ (средств измерений)) …   Энциклопедический словарь

dic.academic.ru