Калькулятор расчет массы уголка: Калькулятор веса уголка | расчет веса стального уголка онлайн
alexxlab | 11.01.2023 | 0 | Разное
Калькулятор веса уголка. Торговый Дом “Профиль”
Квадратная
Прямоугольная
Круглая
Уголок
Швеллер
Полоса
Лист
Арматура
Квадрат
Балка
Круг
Калькулятор металлопроката
Уголковые стальные профили прокатывают в виде неравнополочных и равнополочных. От вида и способа проката зависит и вес погонного метра уголка. При расчетах горячекатаных уголков важно знать не только ширину и толщину полки, но и радиусы внутреннего и внешнего закругления. Для расчета массы горячекатаных уголков применяется формула:
ρу= [(A+B-t)·t+(1-π/4)·(r2
где t — толщина полок; А — ширина большей полки; B — ширина меньшей полки; ρ — плотность материала; rвнешн— радиус внешнего закругления полок; rвнутр— радиус внутреннего закругления.
Так как вес погонного метра уголка является справочной величиной, калькулятор металлопроката в первую очередь сверится с информацией в таблицах ГОСТ, в случае если в справочнике не будет найден уголок нужного вам размера, то вес будет вычислен по приблизительной формуле.
Таблицы веса металлических уголков различных ГОСТ и размеров
- ОСТ 8509-93 — Уголки стальные горячекатаные равнополочные
Теоретическая масса 1 погонного метра уголка по ГОСТ 8509-93
Наименование Размеры уголка, мм Толщина стенки s, мм Вес метра, кг Метров в тонне a b Уголок 20×3 20 3 0.890 1123.6 Уголок 20×4 20 4 1.150 869.57 Уголок 25×3 25 3 1.  120
120892.86 Уголок 25×4 25 4 1.460 684.93 Уголок 25×5 25 5 1.780 561.8 Уголок 28×3 28 3 1.270 787.4 Уголок 30×3 30 3 1.360 735.29 Уголок 30×4 30 4 1.780 561.8 Уголок 30×5 30 5 458.72 Уголок 32×3 32 3 1.460 684.93 Уголок 32×4 32 4 1.910 523.56 Уголок 35×3 35 3 1.  600
600625 Уголок 35×4 35 4 2.100 476.19 Уголок 35×5 35 5 2.580 387.6 Уголок 40×3 40 3 1.850 540.54 Уголок 40×4 40 4 2.420 413.22 Уголок 40×5 40 5 2.980 335.57 Уголок 40×6 40 6 3.520 284.09 Уголок 45×3 45 3 2.080 480.77 Уголок 45×4 45 4 2.730 366.3 Уголок 45×5 45 5 3.  370
370296.74 Уголок 45×6 45 6 3.990 250.63 Уголок 50×3 50 3 2.320 431.03 Уголок 50×4 50 4 3.050 327.87 Уголок 50×5 50 5 3.770 265.25 Уголок 50×6 50 6 4.470 223.71 Уголок 50×7 50 7 5.150 194.17 Уголок 50×8 50 8 5.820 171.82 Уголок 56×4 56 4 3.440 290.7 Уголок 56×5 56 5 4.  250
250235.29 Уголок 60×4 60 4 3.710 269.54 Уголок 60×5 60 5 4.580 218.34 Уголок 60×6 60 6 5.430 184.16 Уголок 60×8 60 8 7.100 140.85 Уголок 60×0 60 10 8.700 114.94 Уголок 63×4 63 4 3.900 256.41 Уголок 63×5 63 5 4.810 207.9 Уголок 63×6 63 6 5.720 174.83 Уголок 65×6 65 6 5.  910
910169.2 Уголок 65×8 65 8 7.730 129.37 Уголок 70×4 70 4,5 4.870 205.34 Уголок 70×5 70 5 5.380 185.87 Уголок 70×6 70 6 6.390 156.49 Уголок 70×7 70 7 7.390 135.32 Уголок 70×8 70 8 8.370 119.47 Уголок 70×0 70 10 10.290 97.18 Уголок 75×5 75 5 5.800 172.41 Уголок 75×6 75 6 6.  890
890145.14 Уголок 75×7 75 7 7.960 125.63 Уголок 75×8 75 8 9.020 110.86 Уголок 75×9 75 9 10.070 99.3 Уголок 80×5 80 5,5 6.780 147.49 Уголок 80×6 80 6 7.360 135.87 Уголок 80×7 80 7 8.510 117.51 Уголок 80×8 80 8 9.650 103.63 Уголок 80×10 80 10 11.880 84.18 Уголок 80×12 80 12 14.  050
05071.17 Уголок 90×6 90 6 8.330 120.05 Уголок 90×7 90 7 9.640 103.73 Уголок 90×8 90 8 10.930 91.49 Уголок 90×9 90 9 12.200 81.97 Уголок 90×10 90 10 13.480 74.18 Уголок 90×12 90 12 15.960 62.66 Уголок 100×6.5 100 6,5 10.060 99.4 Уголок 100×7 100 7 10.790 92.68 Уголок 100×8 100 8 12.  250
25081.63 Уголок 100×10 100 10 15.100 66.23 Уголок 100×12 100 12 17.900 55.87 Уголок 100×14 100 14 20.630 48.47 Уголок 100×15 100 15 21.970 45.52 Уголок 100×16 100 16 23.300 42.92 Уголок 110×7 110 7 11.890 84.1 Уголок 110×8 110 8 13.500 74.07 Уголок 120×8 120 8 14.760 67.75 Уголок 120×10 120 10 18.  240
24054.82 Уголок 120×12 120 12 21.670 46.15 Уголок 120×15 120 15 26.680 37.48 Уголок 125×8 125 8 15.460 64.68 Уголок 125×9 125 9 17.300 57.8 Уголок 125×10 125 10 19.100 52.36 Уголок 125×12 125 12 22.680 44.09 Уголок 125×14 125 14 26.200 38.17 Уголок 125×16 125 16 29.650 33.73 Уголок 140×9 140 9 19.  410
41051.52 Уголок 140×10 140 10 21.450 46.62 Уголок 140×12 140 12 25.500 39.22 Уголок 150×10 150 10 23.020 43.44 Уголок 150×12 150 12 27.390 36.51 Уголок 150×15 150 15 33.820 29.57 Уголок 150×18 150 18 40.110 24.93 Уголок 160×10 160 10 24.670 40.54 Уголок 160×11 160 11 27.020 37.01 Уголок 160×12 160 12 28.  350
35035.27 Уголок 160×14 160 14 33.970 29.44 Уголок 160×16 160 16 38.520 25.96 Уголок 160×18 160 18 43.010 23.25 Уголок 160×20 160 20 47.440 21.08 Уголок 180×11 180 11 30.470 32.82 Уголок 180×12 180 12 33.120 30.19 Уголок 180×15 180 15 40.960 24.41 Уголок 180×18 180 18 48.660 20.55 Уголок 180×20 180 20 53.  720
72018.62 Уголок 200×12 200 12 36.970 27.05 Уголок 200×13 200 13 39.920 25.05 Уголок 200×14 200 14 42.800 23.36 Уголок 200×16 200 16 48.650 20.55 Уголок 200×18 200 18 54.400 18.38 Уголок 200×20 200 20 60.080 16.64 Уголок 200×24 200 24 71.260 14.03 Уголок 200×25 200 25 74.020 13.51 Уголок 200×30 200 30 87.  560
56011.42 Уголок 220×14 220 14 47.400 21.1 Уголок 220×16 220 16 53.830 18.58 Уголок 250×16 250 16 61.550 16.25 Уголок 250×18 250 18 68.860 14.52 Уголок 250×20 250 20 76.110 13.14 Уголок 250×22 250 22 83.310 12 Уголок 250×25 250 25 93.970 10.64 Уголок 250×28 250 28 104.500 9.57 Уголок 250×30 250 30 111.  440
4408.97 Уголок 250×35 250 35 128.510 7.78 - ГОСТ 8510-86 — Уголки стальные горячекатаные неравнополочные
Теоретическая масса 1 погонного метра уголка по ГОСТ 8510-86
Наименование Размеры уголка, мм Толщина стенки s, мм Вес метра, кг Метров в тонне a b Уголок 25×16×3 25 16 3 0.910 1098.9 Уголок 30×20×3 30 20 3 1.120 892.86 Уголок 30×20×4 30 20 4 1.450 689.66 Уголок 32×20×3 32 20 3 1.  170
170854.7 Уголок 32×20×4 32 20 4 1.520 657.89 Уголок 40×25×3 40 25 3 1.480 675.68 Уголок 40×25×4 40 25 4 1.940 515.46 Уголок 40×25×5 40 25 5 2.370 421.94 Уголок 40×30×4 40 30 4 2.260 442.48 Уголок 40×30×5 40 30 5 2.460 406.5 Уголок 45×28×3 45 28 3 1.680 595.24 Уголок 45×28×4 45 28 4 2.200 454.55 Уголок 50×32×3 50 32 3 1.  900
900526.32 Уголок 50×32×4 50 32 4 2.400 416.67 Уголок 56×36×4 56 36 4 2.810 355.87 Уголок 56×36×5 56 36 5 3.460 289.02 Уголок 63×40×4 63 40 4 3.170 315.46 Уголок 63×40×5 63 40 5 3.910 255.75 Уголок 63×40×6 63 40 6 4.630 215.98 Уголок 63×40×8 63 40 8 6.030 165.84 Уголок 65×50×5 65 50 5 4.360 229.36 Уголок 65×50×6 65 50 6 5.  180
180193.05 Уголок 65×50×7 65 50 7 5.930 168.63 Уголок 65×50×8 65 50 8 6.770 147.71 Уголок 70×45×5 70 45 5 4.300 232.56 Уголок 75×60×5 75 60 5 4.790 208.77 Уголок 75×60×6 75 60 6 5.690 175.75 Уголок 75×60×7 75 60 7 6.570 152.21 Уголок 75×60×8 75 60 8 7.430 134.59 Уголок 80×50×5 80 50 5 4.490 222.72 Уголок 80×50×6 80 50 6 5.  920
920168.92 Уголок 80×60×6 80 60 6 6.390 156.49 Уголок 80×60×7 80 60 7 7.390 135.32 Уголок 80×60×8 80 60 8 8.370 119.47 Уголок 90×56×5 90 56 5,5 6.170 162.07 Уголок 90×56×6 90 56 6 6.700 149.25 Уголок 90×56×8 90 56 8 8.770 114.03 Уголок 100×63×6 100 63 6 7.530 132.8 Уголок 100×63×7 100 63 7 8.700 114.  94
94Уголок 100×63×8 100 63 8 9.870 101.32 Уголок 100×63×10 100 63 10 12.140 82.37 Уголок 100×65×7 100 65 7 8.810 113.51 Уголок 100×65×8 100 65 8 9.990 100.1 Уголок 100×65×10 100 65 10 12.300 81.3 Уголок 110×70×6 110 70 6,5 8.980 111.36 Уголок 110×70×8 110 70 8 10.930 91.49 Уголок 125×80×7 125 80 7 11.040 90.58 Уголок 125×80×8 125 80 8 12.  580
58079.49 Уголок 125×80×10 125 80 10 15.470 64.64 Уголок 125×80×12 125 80 12 18.340 54.53 Уголок 140×90×8 140 90 8 14.130 70.77 Уголок 140×90×10 140 90 10 17.460 57.27 Уголок 160×100×9 160 100 9 17.960 55.68 Уголок 160×100×10 160 100 10 19.850 50.38 Уголок 160×100×12 160 100 12 23.580 42.41 Уголок 160×100×14 160 100 14 27.  260
26036.68 Уголок 180×110×10 180 110 10 22.200 45.05 Уголок 180×110×12 180 110 12 26.400 37.88 Уголок 200×125×11 200 125 11 27.370 36.54 Уголок 200×125×12 200 125 12 29.740 33.62 Уголок 200×125×14 200 125 14 34.430 29.04 Уголок 200×125×16 200 125 16 39.070 25.6
Телефоны
8 800 100 17 62 (бесплатно по всей территории России)
+7 495 543 91 20 (многоканальный)
+7 985 739 17 20
Поделиться:
Корзина
0 элементов
Калькулятор веса уголка (метр / кг) стального
Таблица веса равнополочного уголка ГОСТ 8509-93
Таблица веса стального уголка с одинаковым размером полок ГОСТ 8509-93 “Уголки стальные горячекатаные равнополочные”:
| Размер, мм | Вес 1 метра, кг | Метров в тонне |
|---|---|---|
| 20x20x3 | 0,89 | 1123,6 |
| 20x20x4 | 1,15 | 869,57 |
| 25x25x3 | 1,12 | 892,86 |
| 25x25x4 | 1,46 | 684,93 |
| 25x25x5 | 1,78 | 561,8 |
| 28x28x3 | 1,27 | 787,4 |
| 30x30x3 | 1,36 | 735,29 |
| 30x30x4 | 1,78 | 561,8 |
| 30x30x5 | 2,18 | 458,72 |
| 32x32x3 | 1,46 | 684,93 |
| 32x32x4 | 1,91 | 523,56 |
| 35x35x3 | 1,6 | 625 |
| 35x35x4 | 2,1 | 476,19 |
| 35x35x5 | 2,58 | 387,6 |
| 40x40x3 | 1,85 | 540,54 |
| 40x40x4 | 2,42 | 413,22 |
| 40x40x5 | 2,98 | 335,57 |
| 40x40x6 | 3,52 | 284,09 |
| 45x45x3 | 2,08 | 480,77 |
| 45x45x4 | 2,73 | 366,3 |
| 45x45x5 | 3,37 | 296,74 |
| 45x45x6 | 3,99 | 250,63 |
| 50x50x3 | 2,32 | 431,03 |
| 50x50x4 | 3,05 | 327,87 |
| 50x50x5 | 3,77 | 265,25 |
| 50x50x6 | 4,47 | 223,71 |
| 50x50x7 | 5,15 | 194,17 |
| 50x50x8 | 5,82 | 171,82 |
| 56x56x4 | 3,44 | 290,7 |
| 56x56x5 | 4,25 | 235,29 |
| 60x60x4 | 3,71 | 269,54 |
| 60x60x5 | 4,58 | 218,34 |
| 60x60x6 | 5,43 | 184,16 |
| 60x60x8 | 7,1 | 140,85 |
| 60x60x10 | 8,7 | 114,94 |
| 63x63x4 | 3,9 | 256,41 |
| 63x63x5 | 4,81 | 207,9 |
| 63x63x6 | 5,72 | 174,83 |
| 65x65x6 | 5,91 | 169,2 |
| 65x65x8 | 7,73 | 129,37 |
| 70x70x4,5 | 4,87 | 205,34 |
| 70x70x5 | 5,38 | 185,87 |
| 70x70x6 | 6,39 | 156,49 |
| 70x70x7 | 7,39 | 135,32 |
| 70x70x8 | 8,37 | 119,47 |
| 70x70x10 | 10,29 | 97,18 |
| 75x75x5 | 5,8 | 172,41 |
| 75x75x6 | 6,89 | 145,14 |
| 75x75x7 | 7,96 | 125,63 |
| 75x75x8 | 9,02 | 110,86 |
| 75x75x9 | 10,07 | 99,3 |
| 80x80x5,5 | 6,78 | 147,49 |
| 80x80x6 | 7,36 | 135,87 |
| 80x80x7 | 8,51 | 117,51 |
| 80x80x8 | 9,65 | 103,63 |
| 80x80x10 | 11,88 | 84,18 |
| 80x80x12 | 14,05 | 71,17 |
| 90x90x6 | 8,33 | 120,05 |
| 90x90x7 | 9,64 | 103,73 |
| 90x90x8 | 10,93 | 91,49 |
| 90x90x9 | 12,2 | 81,97 |
| 90x90x10 | 13,48 | 74,18 |
| 90x90x12 | 15,96 | 62,66 |
| 100x100x6,5 | 10,06 | 99,4 |
| 100x100x7 | 10,79 | 92,68 |
| 100x100x8 | 12,25 | 81,63 |
| 100x100x10 | 15,1 | 66,23 |
| 100x100x12 | 17,9 | 55,87 |
| 100x100x14 | 20,63 | 48,47 |
| 100x100x15 | 21,97 | 45,52 |
| 100x100x16 | 23,3 | 42,92 |
| 110x110x7 | 11,89 | 84,1 |
| 110x110x8 | 13,5 | 74,07 |
| 120x120x8 | 14,76 | 67,75 |
| 120x120x10 | 18,24 | 54,82 |
| 120x120x12 | 21,67 | 46,15 |
| 120x120x15 | 26,68 | 37,48 |
| 125x125x8 | 15,46 | 64,68 |
| 125x125x9 | 17,3 | 57,8 |
| 125x125x10 | 19,1 | 52,36 |
| 125x125x12 | 22,68 | 44,09 |
| 125x125x14 | 26,2 | 38,17 |
| 125x125x16 | 29,65 | 33,73 |
| 140x140x9 | 19,41 | 51,52 |
| 140x140x10 | 21,45 | 46,62 |
| 140x140x12 | 25,5 | 39,22 |
| 150x150x10 | 23,02 | 43,44 |
| 150x150x12 | 27,39 | 36,51 |
| 150x150x15 | 33,82 | 29,57 |
| 150x150x18 | 40,11 | 24,93 |
| 160x160x10 | 24,67 | 40,54 |
| 160x160x11 | 27,02 | 37,01 |
| 160x160x12 | 28,35 | 35,27 |
| 160x160x14 | 33,97 | 29,44 |
| 160x160x16 | 38,52 | 25,96 |
| 160x160x18 | 43,01 | 23,25 |
| 160x160x20 | 47,44 | 21,08 |
| 180x180x11 | 30,47 | 32,82 |
| 180x180x12 | 33,12 | 30,19 |
| 180x180x15 | 40,96 | 24,41 |
| 180x180x18 | 48,66 | 20,55 |
| 180x180x20 | 53,72 | 18,62 |
| 200x200x12 | 36,97 | 27,05 |
| 200x200x13 | 39,92 | 25,05 |
| 200x200x14 | 42,8 | 23,36 |
| 200x200x16 | 48,65 | 20,55 |
| 200x200x18 | 54,4 | 18,38 |
| 200x200x20 | 60,08 | 16,64 |
| 200x200x24 | 71,26 | 14,03 |
| 200x200x25 | 74,02 | 13,51 |
| 200x200x30 | 87,56 | 11,42 |
| 220x220x14 | 47,4 | 21,1 |
| 220x220x16 | 53,83 | 18,58 |
| 250x250x16 | 61,55 | 16,25 |
| 250x250x18 | 68,86 | 14,52 |
| 250x250x20 | 76,11 | 13,14 |
| 250x250x22 | 83,31 | 12 |
| 250x250x25 | 93,97 | 10,64 |
| 250x250x28 | 104,5 | 9,57 |
| 250x250x30 | 111,44 | 8,97 |
| 250x250x35 | 128,51 | 7,78 |
С помощью нашего калькулятора вы можете рассчитать
следующие уголки стальные:
20x20x3 мм,
20x20x4 мм,
25x25x3 мм,
25x25x4 мм,
25x25x5 мм,
28x28x3 мм,
30x30x3 мм,
30x30x4 мм,
30x30x5 мм,
32x32x3 мм,
32x32x4 мм,
35x35x3 мм,
35x35x4 мм,
35x35x5 мм,
40x40x3 мм,
40x40x4 мм,
40x40x5 мм,
40x40x6 мм,
45x45x3 мм,
45x45x4 мм,
45x45x5 мм,
45x45x6 мм,
50x50x3 мм,
50x50x4 мм,
50x50x5 мм,
50x50x6 мм,
50x50x7 мм,
50x50x8 мм,
56x56x4 мм,
56x56x5 мм,
60x60x4 мм,
60x60x5 мм,
60x60x6 мм,
60x60x8 мм,
60x60x10 мм,
63x63x4 мм,
63x63x5 мм,
63x63x6 мм,
65x65x6 мм,
65x65x8 мм,
70x70x4,5 мм,
70x70x5 мм,
70x70x6 мм,
70x70x7 мм,
70x70x8 мм,
70x70x10 мм,
75x75x5 мм,
75x75x6 мм,
75x75x7 мм,
75x75x8 мм,
75x75x9 мм,
80x80x5,5 мм,
80x80x6 мм,
80x80x7 мм,
80x80x8 мм,
80x80x10 мм,
80x80x12 мм,
90x90x6 мм,
90x90x7 мм,
90x90x8 мм,
90x90x9 мм,
90x90x10 мм,
90x90x12 мм,
100x100x6,5 мм,
100x100x7 мм,
100x100x8 мм,
100x100x10 мм,
100x100x12 мм,
100x100x14 мм,
100x100x15 мм,
100x100x16 мм,
110x110x7 мм,
110x110x8 мм,
120x120x8 мм,
120x120x10 мм,
120x120x12 мм,
120x120x15 мм,
125x125x8 мм,
125x125x9 мм,
125x125x10 мм,
125x125x12 мм,
125x125x14 мм,
125x125x16 мм,
140x140x9 мм,
140x140x10 мм,
140x140x12 мм,
150x150x10 мм,
150x150x12 мм,
150x150x15 мм,
150x150x18 мм,
160x160x10 мм,
160x160x11 мм,
160x160x12 мм,
160x160x14 мм,
160x160x16 мм,
160x160x18 мм,
160x160x20 мм,
180x180x11 мм,
180x180x12 мм,
180x180x15 мм,
180x180x18 мм,
180x180x20 мм,
200x200x12 мм,
200x200x13 мм,
200x200x14 мм,
200x200x16 мм,
200x200x18 мм,
200x200x20 мм,
200x200x24 мм,
200x200x25 мм,
200x200x30 мм,
220x220x14 мм,
220x220x16 мм,
250x250x16 мм,
250x250x18 мм,
250x250x20 мм,
250x250x22 мм,
250x250x25 мм,
250x250x28 мм,
250x250x30 мм,
250x250x35 мм.
Калькулятор треугольника
Введите 3 значения, включая хотя бы одну сторону, в следующие 6 полей и нажмите кнопку «Рассчитать». Если в качестве единицы измерения угла выбран радиан, он может принимать такие значения, как пи/2, пи/4 и т. д.
Треугольник — это многоугольник с тремя вершинами. Вершина — это точка, в которой встречаются две или более кривых, линий или ребер; в случае треугольника три вершины соединены тремя отрезками, называемыми ребрами. Треугольник обычно называют его вершинами. Следовательно, треугольник с вершинами a, b и c обычно обозначается как Δabc. Кроме того, треугольники, как правило, описываются на основе длины их сторон, а также их внутренних углов. Например, треугольник, в котором все три стороны имеют одинаковую длину, называется равносторонним треугольником, а треугольник, в котором две стороны имеют одинаковую длину, называется равнобедренным. Когда ни одна из сторон треугольника не имеет одинаковой длины, он называется разносторонним, как показано ниже.
Когда ни одна из сторон треугольника не имеет одинаковой длины, он называется разносторонним, как показано ниже.
Засечки на ребрах треугольника — общепринятое обозначение, отражающее длину стороны, где одинаковое количество засечек означает одинаковую длину. Аналогичные обозначения существуют для внутренних углов треугольника, обозначаемых разным количеством концентрических дуг, расположенных в вершинах треугольника. Как видно из приведенных выше треугольников, длина и внутренние углы треугольника напрямую связаны, поэтому имеет смысл, что равносторонний треугольник имеет три равных внутренних угла и три стороны одинаковой длины. Обратите внимание, что треугольник, представленный в калькуляторе, показан не в масштабе; хотя он выглядит равносторонним (и имеет маркировку углов, которые обычно читаются как равные), он не обязательно является равносторонним и представляет собой просто изображение треугольника. При вводе фактических значений выходные данные калькулятора будут отражать форму входного треугольника.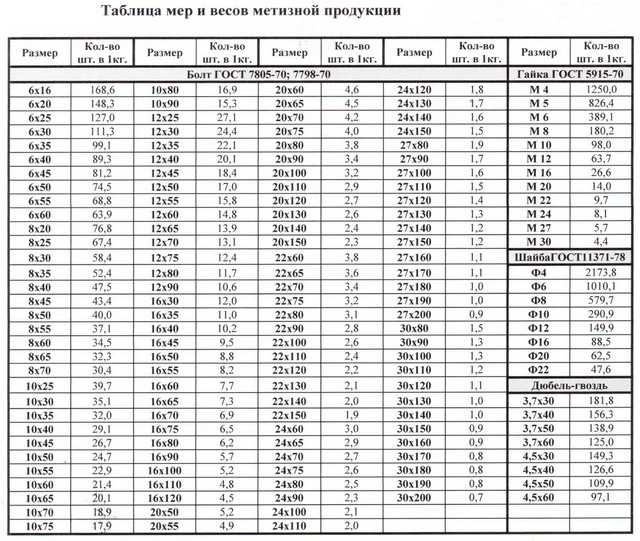
Треугольники, классифицированные по их внутренним углам, делятся на две категории: прямоугольные и косоугольные. Прямоугольный треугольник — это треугольник, в котором один из углов равен 90°, и обозначается двумя отрезками, образующими квадрат в вершине, составляющей прямой угол. Самая длинная сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой. Любой треугольник, который не является прямоугольным, классифицируется как косоугольный и может быть либо тупоугольным, либо остроугольным. В тупоугольном треугольнике один из углов треугольника больше 90°, а в остроугольном треугольнике все углы меньше 90°, как показано ниже.
Факты, теоремы и законы треугольника
- Зная длины всех трех сторон любого треугольника, каждый угол можно вычислить с помощью следующего уравнения. Обратитесь к треугольнику выше, предполагая, что значения a, b и c известны.
Площадь треугольника
Существует несколько различных уравнений для расчета площади треугольника, в зависимости от того, какая информация известна. Вероятно, наиболее известное уравнение для вычисления площади треугольника включает его основание, b и высота h . «Основание» относится к любой стороне треугольника, где высота представлена длиной отрезка, проведенного от вершины, противоположной основанию, к точке на основании, образующей перпендикуляр.
Вероятно, наиболее известное уравнение для вычисления площади треугольника включает его основание, b и высота h . «Основание» относится к любой стороне треугольника, где высота представлена длиной отрезка, проведенного от вершины, противоположной основанию, к точке на основании, образующей перпендикуляр.
Зная длину двух сторон и угол между ними, можно использовать следующую формулу для определения площади треугольника. Обратите внимание, что используемые переменные относятся к треугольнику, показанному в калькуляторе выше. Учитывая а = 9, b = 7 и C = 30°:
Другой метод вычисления площади треугольника использует формулу Герона. В отличие от предыдущих уравнений, формула Герона не требует произвольного выбора стороны в качестве основания или вершины в качестве начала координат. Однако для этого требуется, чтобы длины трех сторон были известны. Опять же, в отношении треугольника, представленного в калькуляторе, если a = 3, b = 4 и c = 5:
Медиана, внутренний радиус и радиус описанной окружности
Медиана
Медиана треугольника определяется как длина отрезка, проходящего от вершины треугольника до середины противоположной стороны. Треугольник может иметь три медианы, каждая из которых будет пересекаться в центре тяжести (среднее арифметическое положение всех точек треугольника) треугольника. Обратитесь к приведенному ниже рисунку для пояснения.
Треугольник может иметь три медианы, каждая из которых будет пересекаться в центре тяжести (среднее арифметическое положение всех точек треугольника) треугольника. Обратитесь к приведенному ниже рисунку для пояснения.
Медианы треугольника представлены отрезками m a , m b и m c . Длину каждой медианы можно рассчитать следующим образом:
Где a, b и c представляют длину стороны треугольника, как показано на рисунке выше.
Например, учитывая, что a=2, b=3 и c=4, медиана m a может быть рассчитана следующим образом: круг, который поместится внутри заданного многоугольника, в данном случае треугольника. Внутренний радиус перпендикулярен каждой стороне многоугольника. В треугольнике внутренний радиус можно определить, построив две биссектрисы угла, чтобы определить центр треугольника. Внутренний радиус — это расстояние по перпендикуляру между центром вписанной стороны и одной из сторон треугольника.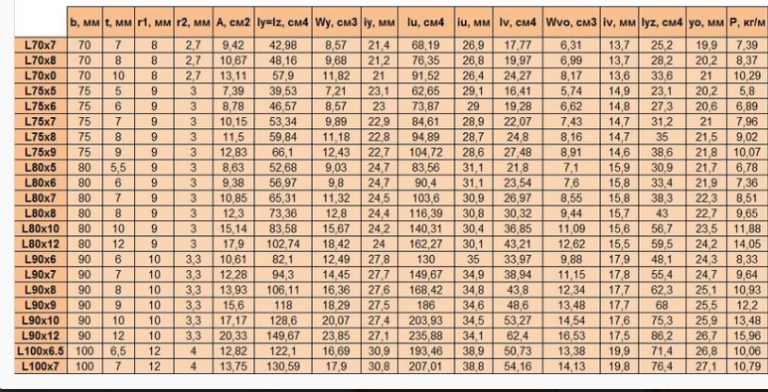 Можно использовать любую сторону треугольника, если определено перпендикулярное расстояние между стороной и центром вписанной стороны, поскольку центр вписанной стороны по определению равноудален от каждой стороны треугольника.
Можно использовать любую сторону треугольника, если определено перпендикулярное расстояние между стороной и центром вписанной стороны, поскольку центр вписанной стороны по определению равноудален от каждой стороны треугольника.
Для целей этого калькулятора внутренний радиус рассчитывается с использованием площади (Area) и полупериметра (s) треугольника по следующим формулам:
| внутренний радиус = |
| с = |
|
где a, b и c — стороны треугольника
Радиус окружности
Радиус окружности определяется как радиус окружности, проходящей через все вершины многоугольника, в данном случае треугольника. Центр этой окружности, где встречаются все серединные перпендикуляры каждой стороны треугольника, является центром описанной окружности треугольника и является точкой, от которой измеряется радиус описанной окружности.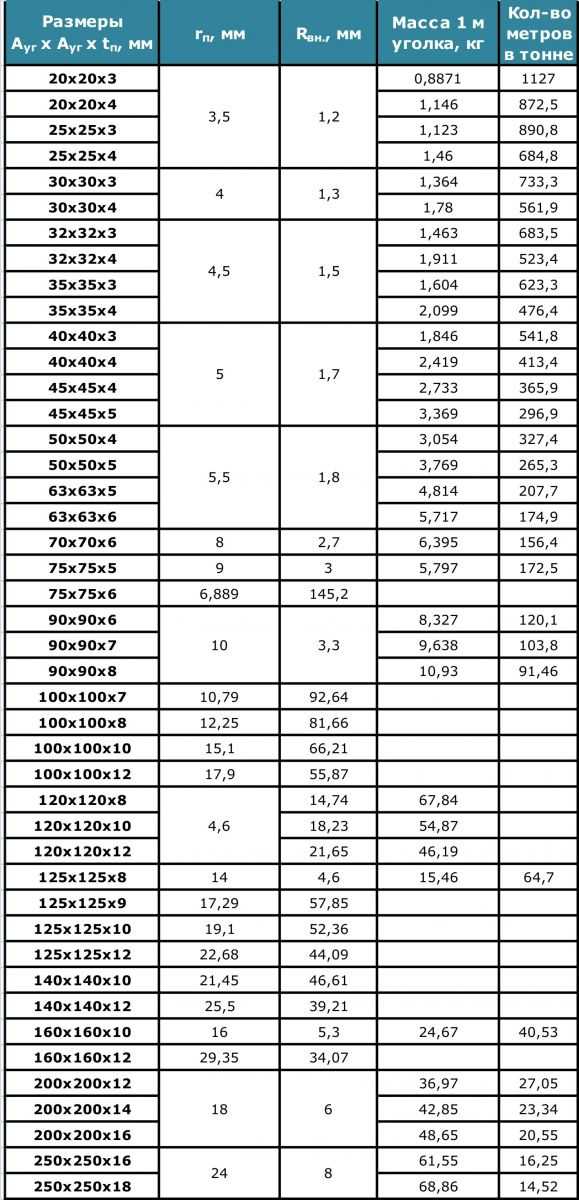 Центр описанной окружности треугольника не обязательно должен находиться внутри треугольника. Стоит отметить, что у всех треугольников есть описанная окружность (окружность, проходящая через каждую вершину) и, следовательно, радиус описанной окружности.
Центр описанной окружности треугольника не обязательно должен находиться внутри треугольника. Стоит отметить, что у всех треугольников есть описанная окружность (окружность, проходящая через каждую вершину) и, следовательно, радиус описанной окружности.
Для целей данного калькулятора радиус описанной окружности рассчитывается по следующей формуле:
| радиус описанной окружности = |
|
Где а — сторона треугольника, а А — угол, противоположный стороне а
Хотя сторона а и угол А используются, в формуле можно использовать любую из сторон и соответствующие им противоположные углы.
Калькулятор угла прямоугольного треугольника
Этот калькулятор угла прямоугольного треугольника поможет вам определить, каковы углы прямоугольного треугольника, то есть если вы знаете измерения по крайней мере двух его сторон или хотя бы одной его сторон вместе с его площадью. Продолжайте читать, чтобы узнать о:
Продолжайте читать, чтобы узнать о:
- Как найти углы прямоугольного треугольника ;
- Как пользоваться этим калькулятором ; и
- Другие наши калькуляторы треугольников .
Как найти углы прямоугольного треугольника?
Поскольку сумма внутренних углов треугольника составляет 180°, то, если один угол имеет угол, равный 90°, это означает, что оставшиеся два других угла должны иметь в сумме 90°. При этом мы можем сказать, что два оставшихся угла α\alphaα и β\betaβ являются дополнительными углами. В форме уравнения мы выражаем это как:
α+β=90°\альфа + \бета = 90\градусα+β=90°
Итак, если мы знаем один из этих двух углов, как найти недостающие углы прямоугольного треугольника так же просто, как вычесть наш известный угол из 90° 🙂.
С другой стороны, если мы не знаем ни одного из двух углов, мы все равно можем найти их с помощью некоторых основных тригонометрических функций.
Чтобы найти угол α\alphaα, мы можем использовать следующие уравнения:
- α=arctan(a/b)\alpha = \arctan(a / b)α=arctan(a/b)
- α=arccos(b/c)\alpha = \arccos(b/c)α=arccos(b/c)
- α=arcsin(a/c)\alpha = \arcsin(a/c)α=arcsin(a/c)
Для определения угла β\betaβ можно использовать следующие уравнения:
- β=arctan(b/a)\beta = \arctan(b/a)β=arctan(b/a)
- β=arccos(a/c)\beta = \arccos(a/c)β=arccos(a/c)
- β=arcsin(b/c)\бета = \arcsin(b/c)β=arcsin(b/c)
С помощью этих уравнений мы можем видеть, что если у нас есть измерения по крайней мере двух сторон нашего прямоугольного треугольника, мы можем определить, каковы углы прямоугольного треугольника.
Что, если вы знаете размер только одной ноги? Для этого нужно хотя бы знать площадь вашего прямоугольного треугольника, чтобы получить другую сторону вашего треугольника, используя одно из следующих уравнений:
Чтобы найти aaa, зная площадь\текст{площадь}площадь и bbb:
a=2×area/ba = 2 \ times \text{area} / ba=2×area/b
Чтобы найти bbb по заданным \text{area} и aaa:
b=2×area/ab = 2 \times \text{area} / ab= 2×площадь/а
Затем вы можете использовать формулы, которые мы обсуждали ранее, чтобы найти недостающие углы вашего прямоугольного треугольника.
Самое интересное, что мы уже использовали эти уравнения в этом калькуляторе для вашего удобства. Перейдите к следующему разделу этого текста, чтобы узнать, как использовать этот инструмент для расчета угла прямоугольного треугольника 🙂.
🙋 Обратите внимание, что мы не можем найти углы прямоугольного треугольника, если мы знаем только его гипотенузу ccc и его площадь \ текст {площадь}, потому что разные прямоугольные треугольники могут иметь одну и ту же гипотенузу, но с разными площадями.
Как использовать наш калькулятор угла прямоугольного треугольника
Чтобы использовать наш калькулятор угла прямоугольного треугольника, все, что вам нужно сделать, это ввести любые две известные стороны вашего прямоугольного треугольника . Это могут быть измерения двух сторон вашего прямоугольного треугольника (aaa и bbb) или измерения одной стороны и гипотенузы (aaa и ccc или bbb и ccc). Вы также можете ввести одну из сторон вашего треугольника (aaa, bbb или ccc) и площадь\текст{площадь}прямоугольного треугольника .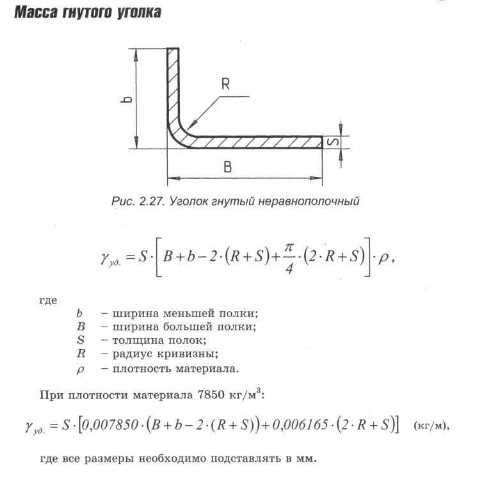
После этого вы сразу увидите углы вашего прямоугольного треугольника: оба угла α\alphaα и угол β\betaβ. Это так просто!
Если вы хотите еще больше расширить свои знания о треугольниках, вот список других наших калькуляторов треугольников, которые вы можете проверить:
- Калькулятор стороны и угла прямоугольного треугольника;
- Сторона треугольника;
- Отсутствует сторона треугольника;
- Длина треугольника;
- Градус треугольника;
- Сторона и угол треугольника;
- Подобные прямоугольные треугольники;
- треугольник abc;
- Прямоугольный треугольник; и
- Проверка подобия прямоугольных треугольников.
Часто задаваемые вопросы
Каковы углы прямоугольного треугольника?
Допустим, прямоугольный треугольник имеет площадь 20 см² и один из его катетов равен 4 см. Чтобы найти углы этого прямоугольного треугольника:
- Сначала мы найдем другую сторону треугольника , используя это уравнение:
b = 2 × площадь / a, гдеa = 4 см.


 120
120 600
600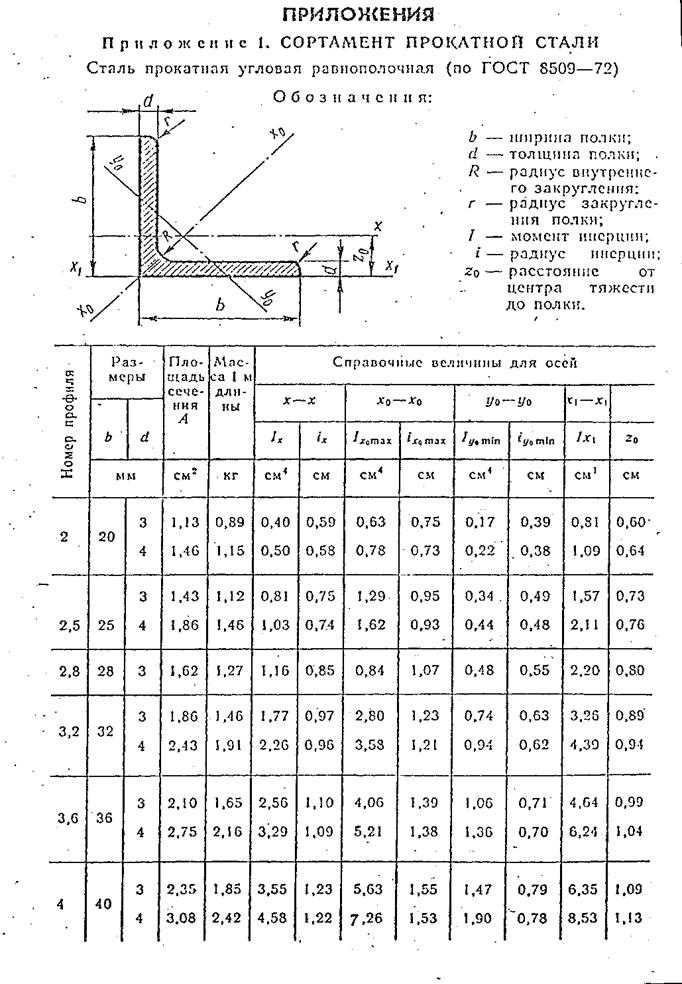 370
370 250
250 910
910 890
890 050
050 250
250 240
240 410
410 350
350 720
720 560
560 440
440 170
170 900
900 180
180 920
920 94
94 580
580 260
260