Кинематика схема: КИНЕМАТИЧЕСКАЯ СХЕМА | это… Что такое КИНЕМАТИЧЕСКАЯ СХЕМА?
alexxlab | 26.03.2023 | 0 | Разное
|
| ||||||||||||||||||
Псков, 2009 | Вернуться |
Возможные кинематические схемы цилиндрического бипланетарного механизма
Автор: Закирова Дилором Ахмедовна
Рубрика: Технические науки
Опубликовано в Молодой учёный №6 (140) февраль 2017 г.
Дата публикации: 13.02.2017 2017-02-13
Статья просмотрена: 52 раза
Скачать электронную версию
Скачать Часть 1 (pdf)
Библиографическое описание: Закирова, Д. А. Возможные кинематические схемы цилиндрического бипланетарного механизма / Д. А. Закирова. — Текст : непосредственный // Молодой ученый. — 2017. — № 6 (140). — С. 40-41. — URL: https://moluch.ru/archive/140/38669/ (дата обращения: 03.02.2023).
А. Возможные кинематические схемы цилиндрического бипланетарного механизма / Д. А. Закирова. — Текст : непосредственный // Молодой ученый. — 2017. — № 6 (140). — С. 40-41. — URL: https://moluch.ru/archive/140/38669/ (дата обращения: 03.02.2023).
На рисунке, а представлен бипланетарный механизм, состоящий из трех планетарных контуров [1]. Обозначим эти контуры А, В, С соответственно. Планетарный механизм А образуется из звеньев 1, 4 и 6; В ― из звеньев 1, 2 и 5;С―из звеньев 2, 3, и 4, в котором водило-сателлит 2 является сателлитом первой ступени, 3―сателлитом второй.
Кинематические схемы бипланетарных механизмов, аналогичных указанному на рисунке, а, будем считать полными. Наряду с полными существуют частные кинематические схемы. Например, при отсутствии планетарного контура А (за счет ликвидации звена 4) или В (за счет ликвидации звеньев 5 и 2) механизм также будет бипланетарным.
Каждый из приведенных планетарных контуров может иметь три варианта сцепления сателлита с центральным колесом [2]:
Комплекс вариантов позволяет создать следующие неповторяющиеся варианты кинематических схем полного бипланетарного механизма (рисунок, а):
A1 B1 C1 | A2 B1 C1 | A3 B1 C1 |
A1 B2 C1 | A2 B2 C1 | A3 B2 C1 |
A1 B3 C1 | A2 B3 C1 | A3 B3 C1 |
A1 B1 C2 | A2 B1 C2 | A3 B1 C2 |
A1 B2 C2 | A2 B2 C2 | A3 B2 C2 |
A1 B3 C2 | A2 B3 C2 | A3 B3 C2 |
A1 B1 C3 | A2 B1 C3 | A3 B1 C3 |
A1 B2 C3 | A2 B2 C3 | A3 B2 C3 |
A1 B3 C3 | A2 B3 C3 | A3 B3 C3 |
Например, рисунок, а соответствует кинематической схеме A1 B2 C1.
Частный бипланетарный механизм, представленный на рисунке, б, состоит из двух (ранее рассмотренных) планетарных контуров А и С. Его возможные варианты следующие:
A1 C1 | A2 C1 | A3 C1 |
A1 C2 | A2 C2 | A3 C2 |
A1 C3 | A2 C3 | A3 C3 |
Нетрудно заметить, что указанные варианты получаются из приведенных выше путем подстановки в них В=0.
На основе данных вариантов формулу для определения числа возможных кинематических схем бипланетарного механизма можно выразить в виде В=Кn, где В―число возможных кинематических схем бипланетарного механизма; К―количество возможных кинематических схем каждого планетарного контура; n―число планетарных контуров, участвующих в бипланетарном механизме.
На рисунке, аК=3, n=3, поэтому В=33=27, что соответствует комплексу вариантов, на рисунке, бК=3,n=2, следовательно, В=32=9, что согласуется с вариантами для частного бипланетарного механизма.
Возможные варианты схем бипланетарных механизмов можно увеличивать только за счет механизмов, подобных рассмотренным. При этом в кинематической схеме происходит количественное наращивание, а не качественные изменения. Для необходимого и достаточного обьёма исследований можно ограничиться тремя контурами с их тремя возможными сцеплениями.
Литература:
- Файзиев И. Х. Вопросы киберн. и вычисл. матем. Ташкент: Фан. 1996. С. 96–103.
- Файзиев И. Х. ДАН УзССР. 1969. № 1. Институт механики и сейсмостойкости сооружений им. М. Т. Уразбаева АН УзССР УзССР 1969.№ 1.
Основные термины (генерируются автоматически): бипланетарный механизм, кинематическая схема, комплекс вариантов, планетарный контур А, рисунок, схема, частный бипланетарный механизм.
Похожие статьи
Дифференциальное уравнение движения
бипланетарного…Рассмотрим бипланетарный механизм (рисунок).
Кинематическая схема бипланетарного механизма: 1-водило H; 2-водило h; 3,4- сателлиты; 5,6- неподвижные центральные колеса.
Структура и
кинематика планетарного механизма со…Рассмотрим кинематику планетарного механизма со ступенчатым сателлитом (схему определения линейных и угловых скоростей характерных точек механизма см.на рисунке, б). Угловые скорости и (см. рисунок, а)…
Закирова Дилором Ахмедовна — Информация об авторе
Возможные кинематические схемы цилиндрического бипланетарного механизма.
Бидифференциальный механизм.
Структура и кинематика планетарного механизма со ступенчатым сателлитом.
Кинематическое исследование гибкого планетарного механизма…Рис. 1. Кинематическая схема (а) эпи-гипоциклоидального планетарного механизма и
Спроектировав соответствующие радиусы звеньев механизма на выбранные координатные оси (рисунок 1, б), получим параметрическое уравнение траектории движении точки сателлита
Работа
механизма нитепритягивателя универсальной швейной…Рис. 1. Кинематическая схема механизма нитепритягивателя машины 22-А класса: 1-соединительное звено, 2-шпилька, 3-рычаг нитепритягивателя.
Регулировка механизма показана на рисунке стрелками (Р). Механизм не требует смазки.
Кинематический и силовой анализ схемы зубчатого вариатора…Кинематическая схема зубчатого вариатора момента с несимметричным дифференциалом представлена на рисунке 1.
При неподвижном выходном вале 2 движение центрального колеса 5 передается на водило планетарного механизма 6, которое вместе с блоком…
Моделирование результатов решения задачи по определению…
По полученным результатам выполняем компьютерное моделирование всех вариантов симметричных структурных схем
1. Мерко М. А. Кинематические и геометрические характеристики эксцентрикового механизма качения: автореф. дис. канд. техн. наук: 05.02.02.
дис. канд. техн. наук: 05.02.02.
К вопросу исследования карданного
механизмаДифференциальное уравнение движения бипланетарного механизма.
Структура и кинематика планетарного механизма со ступенчатым сателлитом. Задачи проектирования механизма иглы швейной машины.
Дифференциальное уравнение движения
бипланетарного…Рассмотрим бипланетарный механизм (рисунок).
Кинематическая схема бипланетарного механизма: 1-водило H; 2-водило h; 3,4- сателлиты; 5,6- неподвижные центральные колеса.
Структура и
кинематика планетарного механизма со…Рассмотрим кинематику планетарного механизма со ступенчатым сателлитом (схему определения линейных и угловых скоростей характерных точек механизма см. на рисунке, б). Угловые скорости и (см. рисунок, а)…
на рисунке, б). Угловые скорости и (см. рисунок, а)…
Закирова Дилором Ахмедовна — Информация об авторе
Возможные кинематические схемы цилиндрического бипланетарного механизма.
Бидифференциальный механизм.
Структура и кинематика планетарного механизма со ступенчатым сателлитом.
Кинематическое исследование гибкого планетарного механизма…Рис. 1. Кинематическая схема (а) эпи-гипоциклоидального планетарного механизма и
Спроектировав соответствующие радиусы звеньев механизма на выбранные координатные оси (рисунок 1, б), получим параметрическое уравнение траектории движении точки сателлита
Работа
механизма нитепритягивателя универсальной швейной. ..
..Рис. 1. Кинематическая схема механизма нитепритягивателя машины 22-А класса: 1-соединительное звено, 2-шпилька, 3-рычаг нитепритягивателя.
Регулировка механизма показана на рисунке стрелками (Р). Механизм не требует смазки.
Кинематический и силовой анализ схемы зубчатого вариатора…Кинематическая схема зубчатого вариатора момента с несимметричным дифференциалом представлена на рисунке 1.
При неподвижном выходном вале 2 движение центрального колеса 5 передается на водило планетарного механизма 6, которое вместе с блоком…
Моделирование результатов решения задачи по определению…
По полученным результатам выполняем компьютерное моделирование всех вариантов симметричных структурных схем
1. Мерко М. А. Кинематические и геометрические характеристики эксцентрикового механизма качения: автореф. дис. канд. техн. наук: 05.02.02.
Мерко М. А. Кинематические и геометрические характеристики эксцентрикового механизма качения: автореф. дис. канд. техн. наук: 05.02.02.
К вопросу исследования карданного
механизмаДифференциальное уравнение движения бипланетарного механизма.
Структура и кинематика планетарного механизма со ступенчатым сателлитом. Задачи проектирования механизма иглы швейной машины.
Похожие статьи
Дифференциальное уравнение движения
бипланетарного…Рассмотрим бипланетарный механизм (рисунок).
Кинематическая схема бипланетарного механизма: 1-водило H; 2-водило h; 3,4- сателлиты; 5,6- неподвижные центральные колеса.
Структура и
кинематика планетарного механизма со…Рассмотрим кинематику планетарного механизма со ступенчатым сателлитом (схему определения линейных и угловых скоростей характерных точек механизма см.на рисунке, б). Угловые скорости и (см. рисунок, а)…
Закирова Дилором Ахмедовна — Информация об авторе
Возможные кинематические схемы цилиндрического бипланетарного механизма.
Бидифференциальный механизм.
Структура и кинематика планетарного механизма со ступенчатым сателлитом.
Кинематическое исследование гибкого планетарного механизма. ..
..Рис. 1. Кинематическая схема (а) эпи-гипоциклоидального планетарного механизма и
Спроектировав соответствующие радиусы звеньев механизма на выбранные координатные оси (рисунок 1, б), получим параметрическое уравнение траектории движении точки сателлита
Работа
механизма нитепритягивателя универсальной швейной…Рис. 1. Кинематическая схема механизма нитепритягивателя машины 22-А класса: 1-соединительное звено, 2-шпилька, 3-рычаг нитепритягивателя.
Регулировка механизма показана на рисунке стрелками (Р). Механизм не требует смазки.
Кинематический и силовой анализ схемы зубчатого вариатора…Кинематическая схема зубчатого вариатора момента с несимметричным дифференциалом представлена на рисунке 1.
При неподвижном выходном вале 2 движение центрального колеса 5 передается на водило планетарного механизма 6, которое вместе с блоком…
Моделирование результатов решения задачи по определению…
По полученным результатам выполняем компьютерное моделирование всех вариантов симметричных структурных схем
1. Мерко М. А. Кинематические и геометрические характеристики эксцентрикового механизма качения: автореф. дис. канд. техн. наук: 05.02.02.
К вопросу исследования карданного
механизмаДифференциальное уравнение движения бипланетарного механизма.
Структура и кинематика планетарного механизма со ступенчатым сателлитом. Задачи проектирования механизма иглы швейной машины.
Дифференциальное уравнение движения
бипланетарного…Рассмотрим бипланетарный механизм (рисунок).
Кинематическая схема бипланетарного механизма: 1-водило H; 2-водило h; 3,4- сателлиты; 5,6- неподвижные центральные колеса.
Структура и
кинематика планетарного механизма со…Рассмотрим кинематику планетарного механизма со ступенчатым сателлитом (схему определения линейных и угловых скоростей характерных точек механизма см.на рисунке, б). Угловые скорости и (см. рисунок, а)…
Закирова Дилором Ахмедовна — Информация об авторе
Возможные кинематические схемы цилиндрического бипланетарного механизма.
Бидифференциальный механизм.
Структура и кинематика планетарного механизма со ступенчатым сателлитом.
Кинематическое исследование гибкого планетарного механизма…Рис. 1. Кинематическая схема (а) эпи-гипоциклоидального планетарного механизма и
Спроектировав соответствующие радиусы звеньев механизма на выбранные координатные оси (рисунок 1, б), получим параметрическое уравнение траектории движении точки сателлита
Работа
механизма нитепритягивателя универсальной швейной…Рис. 1. Кинематическая схема механизма нитепритягивателя машины 22-А класса: 1-соединительное звено, 2-шпилька, 3-рычаг нитепритягивателя.
Регулировка механизма показана на рисунке стрелками (Р). Механизм не требует смазки.
Кинематический и силовой анализ схемы зубчатого вариатора…Кинематическая схема зубчатого вариатора момента с несимметричным дифференциалом представлена на рисунке 1.
При неподвижном выходном вале 2 движение центрального колеса 5 передается на водило планетарного механизма 6, которое вместе с блоком…
Моделирование результатов решения задачи по определению…
По полученным результатам выполняем компьютерное моделирование всех вариантов симметричных структурных схем
1. Мерко М. А. Кинематические и геометрические характеристики эксцентрикового механизма качения: автореф. дис. канд. техн. наук: 05.02.02.
дис. канд. техн. наук: 05.02.02.
К вопросу исследования карданного
механизмаДифференциальное уравнение движения бипланетарного механизма.
Структура и кинематика планетарного механизма со ступенчатым сателлитом. Задачи проектирования механизма иглы швейной машины.
Кинематические уравнения и кинематические графики
Урок 4 этого раздела в классе физики был посвящен использованию графиков скорость-время для описания движения объектов. В этом Уроке подчеркивалось, что наклон линии на графике скорость-время равен ускорению объекта, а площадь между линией и осью времени равна смещению объекта. Таким образом, графики зависимости скорости от времени можно использовать для определения числовых значений и отношений между величинами перемещения (d), скорости (v), ускорения (a) и времени (t). В Уроке 6 основное внимание уделялось использованию четырех кинематических уравнений для описания движения объектов и предсказания численных значений одного из четырех параметров движения — смещения (d), скорости (v), ускорения (a) и время (т). Таким образом, теперь есть два метода решения задач, связанных с числовыми соотношениями между перемещением, скоростью, ускорением и временем. В этой части Урока 6 мы исследуем отношения между этими двумя методами.
Таким образом, теперь есть два метода решения задач, связанных с числовыми соотношениями между перемещением, скоростью, ускорением и временем. В этой части Урока 6 мы исследуем отношения между этими двумя методами.
Рассмотрим объект, который движется с постоянной скоростью +5 м/с в течение 5 секунд, а затем ускоряется до конечной скорости +15 м/с в течение следующих 5 секунд. секунды. Такое словесное описание движения может быть представлено графиком скорость-время. График показан ниже.
Горизонтальная часть графика изображает движение с постоянной скоростью, что соответствует словесному описанию. Участок графика с положительным наклоном (т. е. с наклоном вверх) изображает положительное ускорение, соответствующее словесному описанию объекта, движущегося в положительном направлении и ускоряющегося с 5 м/с до 15 м/с. Наклон линии можно вычислить, используя коэффициент подъема относительно пробега. Между 5 и 10 секундами скорость линии увеличивается с 5 м/с до 15 м/с и продолжается от 5 до 10 с. Это общий подъем +10 м/с и общий пробег 5 с. Таким образом, уклон (соотношение подъем/спуск) равен (10 м/с)/(5 с) = 2 м/с 2 . По графику скорость-время определено ускорение объекта, равное 2 м/с 2 в течение последних пяти секунд движения объекта. Смещение объекта также можно определить с помощью графика зависимости скорости от времени. Площадь между линией на графике и осью времени представляет смещение; эта область принимает форму трапеции. Как обсуждалось в Уроке 4, площадь трапеции можно приравнять к площади треугольника, лежащего на вершине площади прямоугольника. Это показано на диаграмме ниже.
Между 5 и 10 секундами скорость линии увеличивается с 5 м/с до 15 м/с и продолжается от 5 до 10 с. Это общий подъем +10 м/с и общий пробег 5 с. Таким образом, уклон (соотношение подъем/спуск) равен (10 м/с)/(5 с) = 2 м/с 2 . По графику скорость-время определено ускорение объекта, равное 2 м/с 2 в течение последних пяти секунд движения объекта. Смещение объекта также можно определить с помощью графика зависимости скорости от времени. Площадь между линией на графике и осью времени представляет смещение; эта область принимает форму трапеции. Как обсуждалось в Уроке 4, площадь трапеции можно приравнять к площади треугольника, лежащего на вершине площади прямоугольника. Это показано на диаграмме ниже.
Общая площадь равна площади прямоугольника плюс площадь треугольника. Расчет этих площадей показан ниже.
| Прямоугольник | Треугольник |
|---|---|
| Площадь = основание * высота Площадь = (10 с) * (5 м/с) Площадь = 50 м | Площадь = 0,5 * основание * высота Площадь = 0,5 * (5 с) * (10 м/с) Площадь = 25 м |
Общая площадь (прямоугольник плюс треугольник) равна 75 м. кв. Таким образом, перемещение объекта за 10 секунд движения составляет 75 метров.
кв. Таким образом, перемещение объекта за 10 секунд движения составляет 75 метров.
Приведенное выше обсуждение иллюстрирует, как графическое представление движения объекта может использоваться для извлечения числовой информации об ускорении и смещении объекта. После построения график зависимости скорости от времени можно использовать для определения скорости объекта в любой момент времени в течение 10 секунд движения. Например, скорость объекта в 7 секунд может быть определена путем считывания значения координаты y в координате x 7 секунд. Таким образом, графики скорость-время могут быть использованы для выявления (или определения) числовых значений и взаимосвязей между величинами смещения (d), скорости (v), ускорения (a) и времени (t) для любого заданного движения.
Пример задачи — решение с использованием кинематического уравнения
Теперь рассмотрим то же словесное описание и соответствующий анализ с использованием кинематического уравнения. Вербальное описание движения было следующим:
Вербальное описание движения было следующим:
Объект, который движется с постоянной скоростью +5 м/с в течение 5 секунд, а затем ускоряется до конечной скорости +15 м/с в течение следующих 5 секунд
Кинематические уравнения могут быть применены к любому движению, для которого ускорение является постоянным. Поскольку это движение имеет две отдельные стадии ускорения, любой кинематический анализ требует, чтобы параметры движения для первых 5 секунд не смешивались с параметрами движения для последних 5 секунд. В таблице ниже перечислены заданные параметры движения.
| t = 0 с – 5 с | т = 5 с – 10 с |
|---|---|
| v i = 5 м/с v f = 5 м/с t = 5 с a = 0 м/с 2 | v i = 5 м/с v f = 15 м/с t = 5 с |
Обратите внимание, что ускорение в течение первых 5 секунд указано как 0 м/с 2 , несмотря на то, что это явно не указано. Фраза постоянная скорость указывает на движение с нулевым ускорением. Ускорение объекта за последние 5 секунд можно рассчитать с помощью следующего кинематического уравнения.
Фраза постоянная скорость указывает на движение с нулевым ускорением. Ускорение объекта за последние 5 секунд можно рассчитать с помощью следующего кинематического уравнения.
v f = v i + a*t
Здесь показаны подстановка и алгебра.
15 м/с = 5 м/с + а*(5 с)
15 м/с – 5 м/с = a*(5 с)
10 м/с = a*(5 с)
(10 м/с)/(5 с) = a
a = 2 м /с 2
Это значение ускорения объекта за время от 5 с до 10 с согласуется со значением, определяемым по наклону линии на графике скорость-время.
Смещение объекта за все 10 секунд также можно рассчитать с помощью кинематических уравнений. Поскольку эти 10 секунд включают в себя два совершенно разных интервала ускорения, расчеты для каждого интервала необходимо выполнять отдельно. Это показано ниже.
| t = 0 с – 5 с | т = 5 с – 10 с |
|---|---|
| d = v i *t + 0,5*a*t 2 d = (5 м/с)*(5 с) +0,5*(0 м/с 2 )*(5 с) 2 d = 25 м + 0 м д = 25 м | d = ((v i + v f )/2)*t d = ((5 м/с + 15 м/с)/2)*(5 с) d = (10 м/с)*(5 с) д = 50 м |
Общее перемещение за первые 10 секунд движения составляет 75 метров, что соответствует значению, определенному по площади под линией на графике скорость-время.
Анализ этого простого движения иллюстрирует значение этих двух представлений движения – графика скорость-время и кинематических уравнений. Каждое представление можно использовать для извлечения числовой информации о неизвестных величинах движения для любого заданного движения. Приведенные ниже примеры предоставляют полезную возможность для тех, кому требуется дополнительная практика.
Проверьте свое понимание
1. Rennata Gas движется по городу со скоростью 25,0 м/с и начинает ускоряться с постоянной скоростью -1,0 м/с 2 . В конце концов Ренната полностью останавливается.
а. Представьте ускоренное движение Реннаты, нарисовав график зависимости скорости от времени. Используйте график зависимости скорости от времени, чтобы определить это расстояние.
б. Используйте кинематические уравнения для расчета расстояния, которое проходит Ренната при замедлении.
См. график и ответ
2. Отто Эмиссионс едет на своей машине со скоростью 25,0 м/с. Отто ускоряется со скоростью 2,0 м/с 2 в течение 5 секунд. Затем Отто поддерживает постоянную скорость еще 10,0 секунд.
Отто Эмиссионс едет на своей машине со скоростью 25,0 м/с. Отто ускоряется со скоростью 2,0 м/с 2 в течение 5 секунд. Затем Отто поддерживает постоянную скорость еще 10,0 секунд.
а. Представьте 15 секунд движения Отто Эмиссион, нарисовав график зависимости скорости от времени. Используйте график, чтобы определить расстояние, пройденное Отто за все 15 секунд.
б. Наконец, разбейте движение на два сегмента и используйте кинематические уравнения для расчета общего расстояния, пройденного за все 15 секунд.
См. график и ответ
3. Люк Отбелоу, человек, мастер по стрельбе из пушечного ядра, был сброшен с края обрыва с начальной восходящей скоростью +40,0 м/с. Люк ускоряется с постоянным нисходящим ускорением -10,0 м/с 2 (приблизительное значение ускорения свободного падения).
а. Нарисуйте график зависимости скорости от времени для первых 8 секунд движения Люка.
б. Используйте кинематические уравнения, чтобы определить время, необходимое Люку Отбело, чтобы вернуться на исходную высоту скалы. Укажите это время на графике.
См. график и ответ
4. Чак Вагон движется с постоянной скоростью 0,5 мили/мин в течение 10 минут. Затем Чак замедляется со скоростью -0,25 мили/мин 2 в течение 2 минут.
а. Нарисуйте график скорости во времени для движения Чака Вагона. Используйте график зависимости скорости от времени, чтобы определить общее расстояние, пройденное Чаком Вагоном за 12 минут движения.
б. Наконец, разбейте движение на два сегмента и используйте кинематические уравнения, чтобы определить общее расстояние, пройденное Чаком Вагоном.
См. график и ответ
5. Вера Сайд мчится по межштатной автомагистрали со скоростью 45,0 м/с. Вера смотрит вперед и наблюдает за аварией, в результате которой посреди дороги образовалась авария. К моменту, когда Вера бьет по тормозам, она находится в 50,0 м от пайлапа. Она замедляется со скоростью -10,0 м/с 2 .
К моменту, когда Вера бьет по тормозам, она находится в 50,0 м от пайлапа. Она замедляется со скоростью -10,0 м/с 2 .
а. Постройте график зависимости скорости от времени для движения Веры Сайд. Используйте график, чтобы определить расстояние, которое Вера преодолела бы до полной остановки (если бы она не столкнулась с нагромождением).
б. Используйте кинематические уравнения, чтобы определить расстояние, которое Вера Сайд преодолела бы до полной остановки (если бы она не столкнулась с нагромождением). Столкнется ли Вера с машинами в толпе? То есть проедет ли Вера больше 50,0 метров?
См. график и ответ
6. Эрл Э. Берд движется со скоростью 30,0 м/с за 10,0 секунд. Затем он ускоряется со скоростью 3,00 м/с 2 в течение 5,00 секунд.
a.Построить график зависимости скорости от времени для движения Эрла Э. Бёрда. Используйте график, чтобы определить общее пройденное расстояние.
б. Разделите движение Earl E. Bird на два временных сегмента и используйте кинематические уравнения для расчета полного перемещения.
См. график и ответ
Ответы на вышеуказанные вопросы
Ответ на вопрос 1
а. График скорость-время для движения:
Пройденное расстояние можно определить путем вычисления площади между линией на графике и осью времени.
Площадь = 0,5*b*h = 0,5*(25,0 с)*(25,0 м/с)
Площадь = 313 м
б. Пройденное расстояние можно рассчитать с помощью кинематического уравнения. Решение показано здесь.
Дано:
| Найти: д = ?? |
v f 2 = v i 2 + 2*a*d
(0 м/с) 2 = (25,0 м/с) 2 + 2 * (-1,0 м/с 2 )*д
0,0 м 2 /с 2 = 625,0 м 2 /с 2 + (-2,0 м/с 2 )*d
0,0 м 2 /с 2 – 625,0 м 2 /с 2 = (-2,0 м/с 2 )*d
(-625,0 м 2 /с 2 )/(-2,0 м/с 2 ) = d
313 м = д
Вернуться к вопросу 1
Ответ на вопрос 2
а. График скорости во времени для движения:
График скорости во времени для движения:
Пройденное расстояние можно определить путем вычисления площади между линией на графике и осью времени. Эта площадь будет равна площади треугольника плюс площадь прямоугольника 1 плюс площадь прямоугольника 2.
Площадь = 0,5*b tri *h tri + b rect1 *h rect1 + b rect2 *h rect2
Площадь = 0,5*(5,0 с)*(10,0 м/с) + (5,0 с)*(25,0 м/с) + (10,0 с)*(35,0 м/с)
Площадь = 25 м + 125 м + 350 м
Площадь = 500 м
б. Пройденное расстояние можно рассчитать с помощью кинематического уравнения. Решение показано здесь.
Сначала найдите d за первые 5 секунд:
Дано:
| Найти: д = ?? |
d = v i *t + 0,5*a*t 2
d = (25,0 м/с)*(5,0 с) + 0,5*(2,0 м/с 2 )*(5,0 с) 2
d = 125 м + 25,0 м
д = 150 м
Теперь найдите d за последние 10 секунд:
Дано:
| Найти: д = ?? |
(Примечание: скорость на 5-й секунде можно найти, зная, что автомобиль ускоряется с 25,0 м/с до +2,0 м/с 2 на 5 секунд. Это приводит к изменению скорости a*t = 10 м/с и, следовательно, к скорости 35,0 м/с.)
Это приводит к изменению скорости a*t = 10 м/с и, следовательно, к скорости 35,0 м/с.)
d = v i *t + 0,5*a*t 2
d = (35,0 м/с)*(10,0 с) + 0,5*(0,0 м/с 2 )*(10,0 с) 2
d = 350 м + 0 м
d =350 м
Общее расстояние за 15 секунд движения равно сумме этих двух расчетов расстояния (150 м + 350 м):
расстояние = 500 м
Вернуться к вопросу 2
Ответ на вопрос 3
а. График скорость-время для движения:
б. Время подъема и падения на исходную высоту в два раза превышает время подъема на пик. Таким образом, решение заключается в том, чтобы найти время, чтобы подняться до пика, а затем удвоить его.
Дано:
| Найти: т до = ?? 2*t вверх = ?? |
v f = v i + a*t вверх
0 м/с = 40 м/с + (-10 м/с2)*t вверх
(10 м/с 2 )*t до = 40 м/с
t up = (40 м/с)/(10 м/с 2 )
т до = 4,0 с
2*t до = 8,0 с
Вернуться к вопросу 3
Ответ на вопрос 4
а. График скорость-время для движения:
График скорость-время для движения:
Пройденное расстояние можно определить путем вычисления площади между линией на графике и осью времени. Эта площадь будет равна площади прямоугольника плюс площадь треугольника.
Площадь = b прямоугольная *h прямоугольная + 0,5*b тройная *h тройная
Площадь = (10,0 мин)*(0,50 мили/мин) + 0,5*(2,0 мин)*(0,50 мили/мин)
Площадь = 5 миль + 0,5 мили
Площадь = 5,5 мили
б. Пройденное расстояние можно рассчитать с помощью кинематического уравнения. Решение показано здесь.
Сначала найдите d за первые 10 минут:
Дано:
| Найти: д = ?? |
d = v i *t + 0,5*a*t 2
d = (0,50 миль/мин)*(10,0 мин) + 0,5*(0,0 миль/мин 2 )*(10,0 мин) 2
d = 5,0 миль + 0 миль
d = 5,0 миль
Теперь найдите d за последние 2 минуты:
Дано:
| Найти: д = ?? |
d = v i *t + 0,5*a*t 2
d = (0,50 миль/мин)*(2,0 мин) + 0,5*(-0,25 м/с 2 )*(2,0 мин) 2
d = 1,0 мили + (-0,5 мили)
d = 0,5 мили
Общее расстояние за 12 минут движения равно сумме этих двух расчетов расстояния (5,0 миль + 0,5 мили):
расстояние = 5,5 мили
Вернуться к вопросу 4
Ответ на вопрос 5
а. График скорость-время для движения:
График скорость-время для движения:
Пройденное расстояние можно определить путем вычисления площади между линией на графике и осью времени.
Площадь = 0,5*b*h = 0,5*(4,5 с)*(45,0 м/с)
Площадь = 101 м
б.
Дано:
| Найти: д = ?? |
v f 2 = v i 2 + 2*a*d
(0 м/с) 2 = (45,0 м/с) 2 + 2 * (-10,0 м/с 2 )*d
0,0 м 2 /с 2 = 2025,0 м 2 /с 2 + (-20,0 м/с 2 )*d
0,0 м 2 /с 2 – 2025,0 м 2 /с 2 = (-20,0 м/с 2 )*d
(-2025,0 м 2 /с 2 )/(-20,0 м/с 2 ) =d
101 м =d
Так как место аварии находится менее чем в 101 м от Веры, она действительно врежется в нагромождение перед полной остановкой (если не отклонится в сторону).
Вернуться к вопросу 5
Ответ на вопрос 6
а. График скорость-время для движения:
Пройденное расстояние можно определить путем вычисления площади между линией на графике и осью времени. Эта площадь будет равна площади треугольника плюс площадь прямоугольника 1 плюс площадь прямоугольника 2.
Площадь = 0,5*b tri *h tri + b 1 *ч 1 + б 2 *ч 2
Площадь = 0,5*(5,0 с)*(15,0 м/с) + (10,0 с)*(30,0 м/с) + (5,0 с)*(30,0 м/с)
Площадь = 37,5 м + 300 м + 150 м
Площадь = 488 м
б. Пройденное расстояние можно рассчитать с помощью кинематического уравнения. Решение показано здесь.
Сначала найдите d за первые 10 секунд:
Дано:
| Найти: д = ?? |
d = v i *t + 0,5*a*t 2
d = (30,0 м/с)*(10,0 с) + 0,5*(0,0 м/с 2 )*(10,0 с) 2
d = 300 м + 0 м
d =300 м
Теперь найдите d за последние 5 секунд:
Дано:
| Найти: д = ?? |
d = v i *t + 0,5*a*t 2
d = (30,0 м/с)*(5,0 с) + 0,5*(3,0 м/с 2 )*(5,0 с) 2
d = 150 м + 37,5 м
д = 187,5 м
Общее расстояние за 15 секунд движения равно сумме этих двух расчетов расстояния (300 м + 187,5 м):
расстояние = 488 м
Вернуться к вопросу 6
Графическая кинематика, визуальная виртуальная работа и эластография
. 2017 24 мая; 4(5):170202.
2017 24 мая; 4(5):170202.
doi: 10.1098/rsos.170202. Электронная коллекция 2017 май.
Аллан МакРоби 1 , Марина Константину 1 , Георгиос Атанасопулос 1 , Лаура Ханниган 2
Принадлежности
- 1 Инженерный факультет Кембриджского университета, Трампингтон-стрит, Кембридж CB2 1PZ, Великобритания.
- 2 aktII, 100 St John Street, Лондон EC1M 4EH, Великобритания.
- PMID: 28573030
- PMCID: PMC5451831
- DOI:
10.
 1098/rsos.170202
1098/rsos.170202
Бесплатная статья ЧВК
Аллан МакРоби и др. R Soc Open Sci. .
Бесплатная статья ЧВК
. 2017 24 мая; 4(5):170202.
doi: 10.1098/rsos.170202. Электронная коллекция 2017 май.
Авторы
Аллан МакРоби 1 , Марина Константину 1 , Георгиос Атанасопулос 1 , Лаура Ханниган 2
Принадлежности
- 1 Инженерный факультет Кембриджского университета, Трампингтон-стрит, Кембридж CB2 1PZ, Великобритания.

- 2 aktII, 100 St John Street, Лондон EC1M 4EH, Великобритания.
- PMID: 28573030
- PMCID: PMC5451831
- DOI: 10.1098/rsos.170202
Абстрактный
В этой статье последние достижения в графической статике объединены с диаграммами перемещений Уиллиота для создания графического описания как статики, так и кинематики для двух- и трехмерных ферм с шарнирным соединением. Начнем с обратной формы и силовых диаграмм. Силовая диаграмма разбивается на составные ячейки, которые затем переводятся друг относительно друга. Это определяет диаграмму смещения, которая топологически эквивалентна диаграмме формы (структуре). Различные вклады в общую Виртуальную Работу проявляются в виде параллелограммов (для двумерных ферм) или параллелепипедов (для трехмерных ферм), которые разделяют силы и смещения. Структурные механизмы могут быть идентифицированы путем перемещения силовых ячеек таким образом, чтобы их общие поверхности скользили друг по другу, не разделяясь. Упругие решения можно получить, выбрав параллелограммы или параллелепипеды соответствующего соотношения сторон. Наконец, представлен новый тип «эластографической» диаграммы, называемой деформированной диаграммой Максвелла-Виллиота (двумерной) или деформированной диаграммой Ренкина-Виллиота (трехмерной), которая сочетает в себе деформированную конструкцию с силами, переносимыми ее элементами. .
Это определяет диаграмму смещения, которая топологически эквивалентна диаграмме формы (структуре). Различные вклады в общую Виртуальную Работу проявляются в виде параллелограммов (для двумерных ферм) или параллелепипедов (для трехмерных ферм), которые разделяют силы и смещения. Структурные механизмы могут быть идентифицированы путем перемещения силовых ячеек таким образом, чтобы их общие поверхности скользили друг по другу, не разделяясь. Упругие решения можно получить, выбрав параллелограммы или параллелепипеды соответствующего соотношения сторон. Наконец, представлен новый тип «эластографической» диаграммы, называемой деформированной диаграммой Максвелла-Виллиота (двумерной) или деформированной диаграммой Ренкина-Виллиота (трехмерной), которая сочетает в себе деформированную конструкцию с силами, переносимыми ее элементами. .
Ключевые слова: взаимные диаграммы Максвелла; взаимные диаграммы Ренкина; диаграммы Уиллиота; графическая статика; кинематика; виртуальная работа.
Заявление о конфликте интересов
У авторов нет конкурирующих финансовых интересов.
Цифры
Рисунок 1.
( a ) Форма…
Рисунок 1.
( a ) Схема формы, показывающая загруженную структуру. ( б )…
Рисунок 1. ( a ) Диаграмма формы, показывающая загруженную структуру. ( b ) Диаграмма обратной силы. ( c ) Этапы строительства. Силовые треугольники N 2 and N 3 are offset from force triangle N 4 by distances equal to the extensions of the bars joining nodes N 2 , N 3 and N 4 . Треугольник силы Н 1 смещен от Н 2 и Н 3 . ( d ) Завершенная диаграмма Максвелла – Виллиота. ( e ) Созданная таким образом диаграмма смещения.
Треугольник силы Н 1 смещен от Н 2 и Н 3 . ( d ) Завершенная диаграмма Максвелла – Виллиота. ( e ) Созданная таким образом диаграмма смещения.
Рисунок 2.
( a ) Рабочий объем…
Рисунок 2.
( a ) Диаграмма смещения. ( b ) Векторы узловых…
Фигура 2.( a ) Диаграмма смещения. ( b ) Векторы узловых перемещений u относительно опорного узла N 4 .
Рисунок 3.
Параллелограмм виртуальной работы…
Рисунок 3.
Параллелограмм виртуальной работы, соединяющий полигоны сил и перемещений.
Рисунок 3.Параллелограмм виртуальной работы, соединяющий полигоны сил и перемещений.
Рисунок 4.
( a ) Двойной…
Рисунок 4.
( a ) Двойное покрытие диаграммы Максвелла – Виллиота. Начиная с районов N…
Рисунок 4. ( a ) Двойное покрытие диаграммы Максвелла – Виллиота. Начиная с областей N 1 + N 2 + N 3 = N 4 and a 1 + a 4 = a 2 + a 3 (из двойных покрытий индивидуальных форм и диаграмм сил) сразу следует, что внешняя виртуальная работа должна равняться сумме площадей параллелограммов внутренней виртуальной работы. ( b ) Двойное покрытие диаграммы Максвелла – Минковского.
( b ) Двойное покрытие диаграммы Максвелла – Минковского.
Рисунок 5.
Пример моста.
Рисунок 5.
Пример моста.
Рисунок 5.Пример моста.
Рисунок 6.
( и ) Фуникулер…
Рисунок 6.
( a ) Под мостом добавлен многоугольник фуникулера для применения…
Рисунок 6. ( a ) Под мостом добавлен многоугольник фуникулера для приложения нагрузок. ( b ) Многогранная функция напряжения Эйри и нормали к ее граням.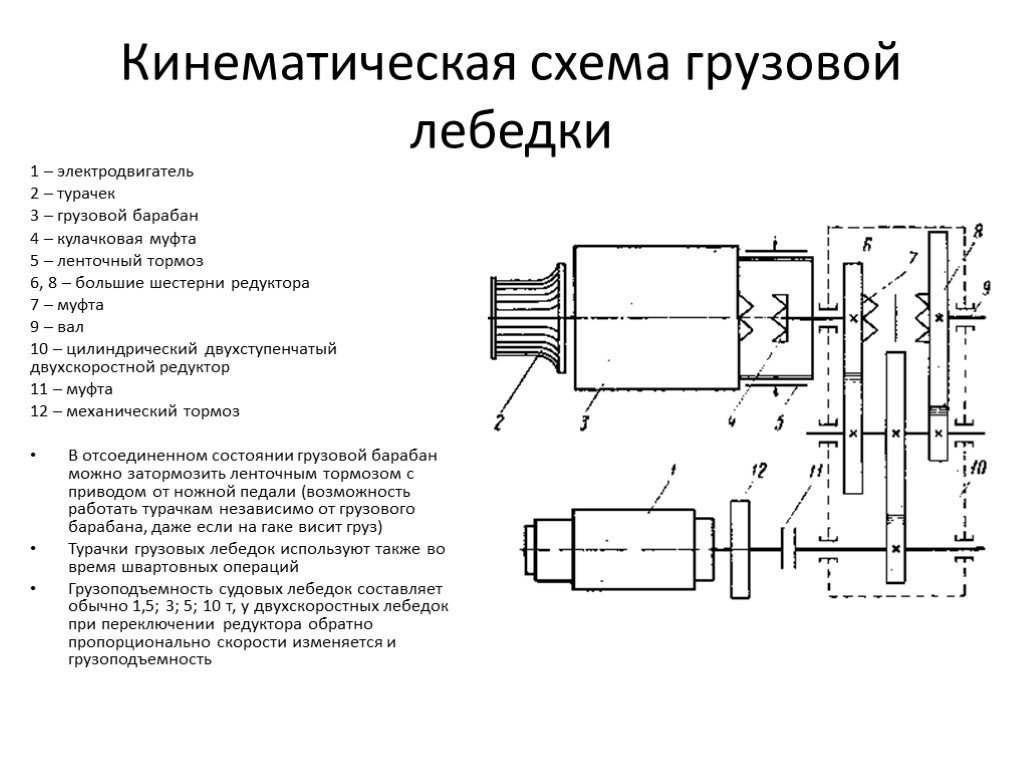 ( c ) Диаграмма силы, определяемая нормалями.
( c ) Диаграмма силы, определяемая нормалями.
Рисунок 7.
Многоугольные детали…
Рисунок 7.
Многоугольные части силовой диаграммы.
Рисунок 7.Многоугольные части силовой диаграммы.
Рис. 8.
Силовая диаграмма и два…
Рисунок 8.
Силовая диаграмма и две искусственные диаграммы Максвелла–Виллиота для различных смещений B…
Рисунок 8. Силовая диаграмма и две искусственные диаграммы Максвелла-Виллиота для различных смещений B параллельно ребру AB.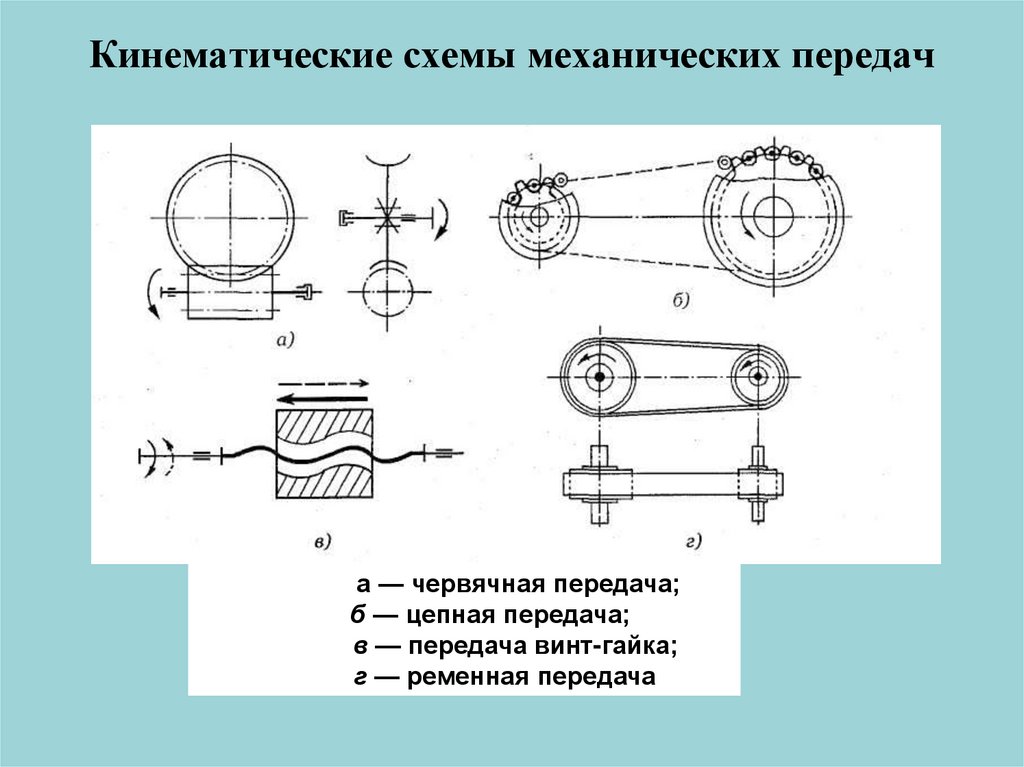 С помощью линейной интерполяции смещение B, которое дает нулевое относительное вертикальное смещение между опорами A и G, приводит к окончательной диаграмме Максвелла-Виллиота.
С помощью линейной интерполяции смещение B, которое дает нулевое относительное вертикальное смещение между опорами A и G, приводит к окончательной диаграмме Максвелла-Виллиота.
Рисунок 9.
Узловые смещения определяются по формуле…
Рисунок 9.
Узловые смещения задаются переводами частей между силами…
Рисунок 9.Узловые смещения задаются переводами частей между диаграммой сил и окончательной диаграммой Максвелла-Виллиота.
Рисунок 10.
Деформированная форма (красная).
Рисунок 10.
Деформированная форма (красная).
Рисунок 10.Деформированная фигура (красная).
Рисунок 11.
( a ) Форма и…
Рисунок 11.
( a ) Диаграммы форм и сил. ( b ) Раздвижной механизм…
Рисунок 11.( a ) Диаграммы форм и сил. ( b ) Раздвижной механизм силовой диаграммы. ( c ) Параллелограммы искусственно открыты для наглядности. ( d ) Смещения, определяемые скольжением. ( e ) Диаграмма смещения. ( ф ) Структурный механизм.
Рисунок 12.
( a ) Схема формы…
Рисунок 12.
( a ) Схема формы для варианта моста Бегини. ( б )…
Рисунок 12.( a ) Схема формы для варианта моста Бегини. ( b ) Соответствующая диаграмма силы, разложенная на двойное покрытие. ( c ) Симметричный механизм. ( d ) Антисимметричный механизм.
Рисунок 13.
Как форма, сила и…
Рисунок 13.
Как сочетание диаграмм формы, силы и перемещения дает диаграммы Максвелла–Минковского, Максвелла–Виллиота…
Рисунок 13. Как диаграммы формы, силы и смещения в совокупности дают диаграммы Максвелла-Минковского, Максвелла-Виллиота и деформированные диаграммы Максвелла-Виллиота. (Для трехмерных ферм «Максвелл» везде заменен на «Ранкин».)
(Для трехмерных ферм «Максвелл» везде заменен на «Ранкин».)
Рисунок 14.
Деформированная диаграмма Максвелла–Виллиота для…
Рисунок 14.
Деформированная диаграмма Максвелла–Виллиота для нагруженного асимметричного ферменного моста.
Рисунок 14.Деформированная диаграмма Максвелла–Виллиота для нагруженного асимметричного ферменного моста.
Рисунок 15.
( a ) Обычный…
Рисунок 15.
( a ) Правильный тетраэдр с радиальными спицами, нагруженный по линии…
Рисунок 15.
( a ) Правильный тетраэдр с радиальными спицами, нагруженный по линии отсутствующей спицы N 4 – N 5 . ( b ) Силовая диаграмма и составляющие ее тетраэдры. ( c ) Переводы частей диаграммы сил в соответствии с деформациями стержня и полученная диаграмма Ренкина-Виллиота, из которой может быть извлечена диаграмма узловых перемещений.
Рисунок 16.
( a ) Родственник…
Рисунок 16.
( a ) Диаграмма относительного перемещения нагруженного симплекса. ( б…
Рисунок 16. ( a ) Диаграмма относительного перемещения нагруженного симплекса. ( б ) Абсолютные узловые смещения (относительно узла N 5 ).
Рисунок 17.
Деформированная диаграмма Ренкина–Уиллиота, показывающая…
Рисунок 17.
Деформированная диаграмма Ренкина-Виллиота, показывающая изогнутую форму конструкции.
Рисунок 17.Деформированная диаграмма Ренкина-Виллиота, показывающая изогнутую форму конструкции.
Рисунок 18.
( a ) Форма…
Рисунок 18.
( a ) Схема формы куба со спицами. ( б )…
Рисунок 18. ( a ) Схема формы куба со спицами. ( b ) Силовая диаграмма представляет собой октаэдр со спицами. ( c ) Механизм куба со спицами. ( d ) Механизм куба без спиц.
( b ) Силовая диаграмма представляет собой октаэдр со спицами. ( c ) Механизм куба со спицами. ( d ) Механизм куба без спиц.
Рисунок 19.
( a ) Джессен…
Рисунок 19.
( a ) Икосаэдрический тенсегрити Джессена. ( b ) Один из…
Рисунок 19.( a ) Икосаэдрический тенсегрити Джессена. ( b ) Одна из ячеек реципроки Ренкина. ( c ) Все ячейки реципрокной системы Ренкина. ( d ) Механизм скользящего блока взаимных ячеек, но позволяющий сторонам, нормальным к радиальным спицам, терять контакт. ( e ) Трехмерный ферменный механизм.
См. это изображение и информацию об авторских правах в PMC
Похожие статьи
Устойчивость ферм по графической статике.

МакРоби А., Миллар С., Бейкер В.Ф. Макроби А. и др. R Soc Open Sci. 2021 9 июня; 8 (6): 201970. doi: 10.1098/rsos.201970. R Soc Open Sci. 2021. PMID: 34113449 Бесплатная статья ЧВК.
Геометрия структурного равновесия.
МакРоби А. Макроби А. R Soc Open Sci. 2017 22 марта; 4(3):160759. doi: 10.1098/rsos.160759. Электронная коллекция 2017 март. R Soc Open Sci. 2017. PMID: 28405361 Бесплатная статья ЧВК.
ты? Диаграмма, мощный метод оптического проектирования для лазерных систем.
Кесслер Д., Хижина Р.В. Кесслер Д. и соавт. Прил. опт. 1992 20 мая; 31(15):2692-707. doi: 10.1364/AO.31.002692. Прил. опт. 1992. PMID: 20725196
Диаграммы Венна в биоинформатике.

Цзя А., Сюй Л., Ван Ю. Цзя А. и др. Кратко Биоинформ. 2021 сен 2; 22 (5): bbab108. дои: 10.1093/биб/ббаб108. Кратко Биоинформ. 2021. PMID: 33839742 Обзор.
Вольф: прямой, не изогнутый.
Хаммер А. Хаммер А. Ir J Med Sci. 2017 ноябрь; 186(4):939-946. doi: 10.1007/s11845-016-1506-7. Epub 2016 24 сентября. Ir J Med Sci. 2017. PMID: 27665092 Обзор.
Посмотреть все похожие статьи
Цитируется
Устойчивость ферм по графической статике.
МакРоби А., Миллар С., Бейкер В.Ф. Макроби А. и др. R Soc Open Sci. 2021 9 июня;8(6):201970. doi: 10.1098/rsos.201970. R Soc Open Sci. 2021. PMID: 34113449 Бесплатная статья ЧВК.

использованная литература
- Максвелл Дж. 1864. Об обратных фигурах и диаграмме сил. Филос. Маг. 26, 250–261. (DOI: 10.1017/S0080456800026351) – DOI
- Рэнкин WJM. 1864. Принцип равновесия многогранных реперов. Филос. Маг. J. Sci. ХХVII, 92.
- Митчелл Т., Бейкер В., МакРоби А., Мазурек А. 2016. Механизмы и состояния самонапряжения плоских ферм с использованием графической статики, Часть I. Межд. J. Космическая структура. 31, 85–101. (дои: 10.1177/0266351116660790) – DOI
- МакРоби А.

- МакРоби А.



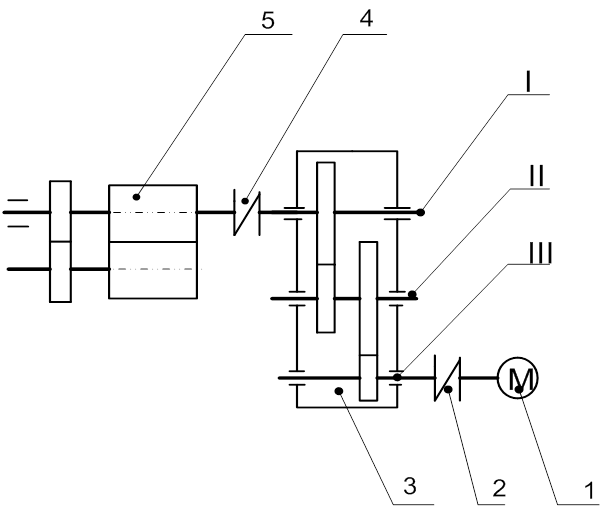
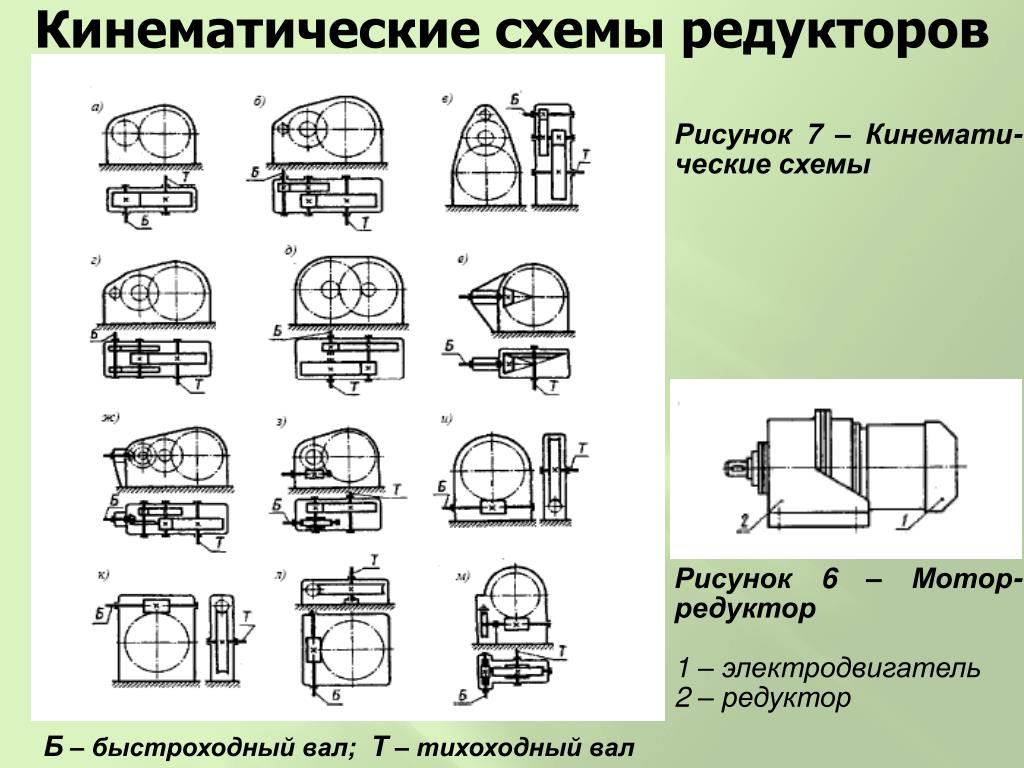 Упрощенная кинематическая схема механизма представлена на рисунке.
Упрощенная кинематическая схема механизма представлена на рисунке.
 Была произведена модификация путем добавления второго вращающегося рычага. На рисунке 3.22 представлена упрощенная кинематическая схема механизма.
Была произведена модификация путем добавления второго вращающегося рычага. На рисунке 3.22 представлена упрощенная кинематическая схема механизма. Траектория движения точек A, B, C, D определяется формой кулачка. Длина рычагов-лопастей равна 2*L1, длина плеч равна L2. Входной момент подается на рычаги-лопасти, выходной момент может сниматься с диагоналей A-C и B-D.
Траектория движения точек A, B, C, D определяется формой кулачка. Длина рычагов-лопастей равна 2*L1, длина плеч равна L2. Входной момент подается на рычаги-лопасти, выходной момент может сниматься с диагоналей A-C и B-D.
 е. возможность передачи момента как с входа на выход, так и с выхода на вход
е. возможность передачи момента как с входа на выход, так и с выхода на вход
 1098/rsos.170202
1098/rsos.170202