Кинетическая энергия пружинного маятника формула: Превращение энергии при колебаниях пружинного маятника

Кинетическая энергия пружинного маятника формула: Превращение энергии при колебаниях пружинного маятника — урок. Физика, 9 класс.

alexxlab | 29.11.1995 | 0 | Разное

2_0=\frac{k}{m}$ – циклическая частота колебаний пружинного маятника. Решением уравнения (1) является функция:

\[x=A{\cos \left({\omega }_0t+\varphi \right)=A{\sin \left({\omega }_0t+{\varphi }_1\right)\ }\ }\left(2\right),\]

где ${\omega }_0=\sqrt{\frac{k}{m}}>0$- циклическая частота колебаний маятника, $A$ – амплитуда колебаний; ${(\omega }_0t+\varphi )$ – фаза колебаний; $\varphi $ и ${\varphi }_1$ – начальные фазы колебаний.

В экспоненциальном виде колебания пружинного маятника можно записать как:

\[Re\ \tilde{x}=Re\left(A\cdot exp\ \left(i\left({\omega }_0t+\varphi \right)\right)\right)\left(3\right).\]

Содержание

Формулы периода и частоты колебаний пружинного маятника

Если в упругих колебаниях выполняется закон Гука, то период колебаний пружинного маятника вычисляют при помощи формулы:

\[T=2\pi \sqrt{\frac{m}{k}}\left(4\right).\]

Так как частота колебаний ($\nu $) – величина обратная к периоду, то:

\[\nu =\frac{1}{T}=\frac{1}{2\pi }\sqrt{\frac{k}{m}}\left(5\right). 2_0}}\left(6\right),\]

начальная фаза при этом:

\[tg\ \varphi =-\frac{v_0}{x_0{\omega }_0}\left(7\right),\]

где $v_0$ – скорость груза при $t=0\ c$, когда координата груза равна $x_0$.

Энергия колебаний пружинного маятника

При одномерном движении пружинного маятника между двумя точками его движения существует только один путь, следовательно, выполняется условие потенциальности силы (любую силу можно считать потенциальной, если она зависит только от координат). Так как силы, действующие на пружинный маятник потенциальны, то можно говорить о потенциальной энергии.

Пусть пружинный маятник совершает колебания в горизонтальной плоскости (рис.2). За ноль потенциальной энергии маятника примем положение его равновесия, где поместим начало координат. Силы трения не учитываем. Используя формулу, связывающую потенциальную силу и потенциальную энергию для одномерного случая:

\[E_p=-\frac{dF}{dx}(8)\]

учитывая, что для пружинного маятника $F=-kx$,

тогда потенциальная энергия ($E_p$) пружинного маятника равна:

\[E_p=\frac{kx^2}{2}=\frac{m{{\omega }_0}^2x^2}{2}\left(9\right). 2}{2}$ – кинетическая энергия маятника.

Из формулы (10) можно сделать следующие выводы:

Максимальная кинетическая энергия маятника равна его максимальной потенциальной энергии.
Средняя кинетическая энергия по времени осциллятора равна его средней по времени потенциальной энергии.

Примеры задач с решением

Пример 1

Задание. Маленький шарик, массой $m=0,36$ кг прикреплен к горизонтальной пружине, коэффициент упругости которой равен $k=1600\ \frac{Н}{м}$. Каково было начальное смещение шарика от положения равновесия ($x_0$), если он при колебаниях проходит его со скоростью $v=1\ \frac{м}{с}$?

Решение. Сделаем рисунок.

По закону сохранения механической энергии (так как считаем, что сил трения нет), запишем:

\[E_{pmax}=E_{kmax\ }\left(1.1\right),\]

где $E_{pmax}$ – потенциальная энергия шарика при его максимальном смещении от положения равновесия; $E_{kmax\ }$ – кинетическая энергия шарика, в момент прохождения положения равновесия.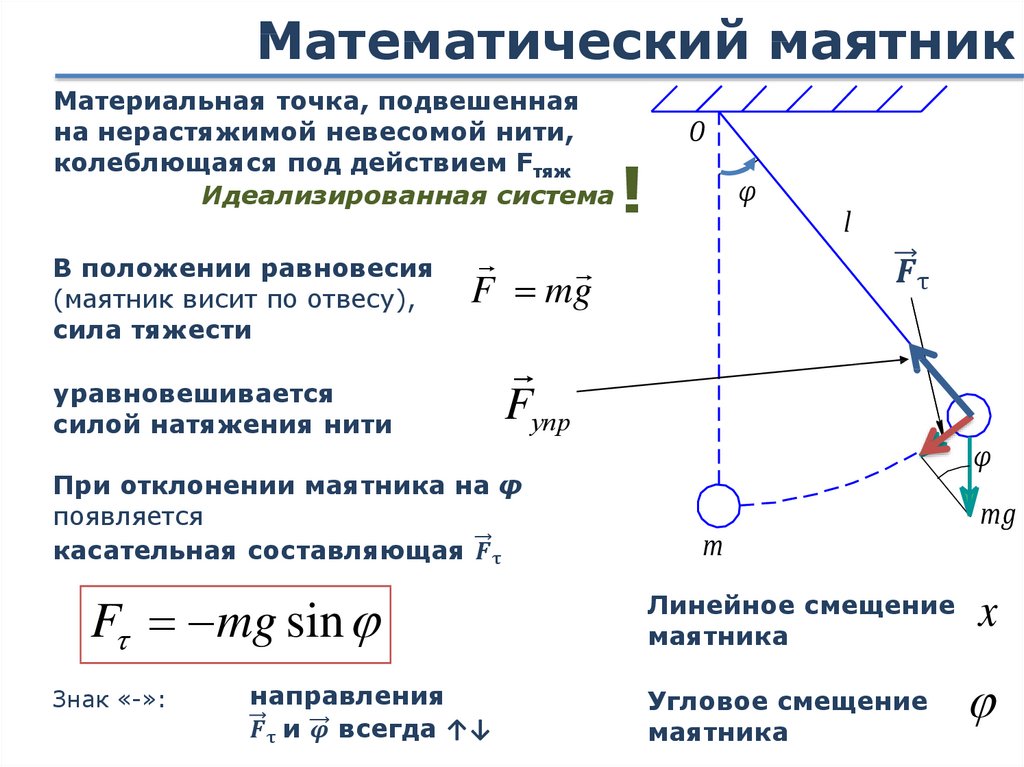 2 \left(\omega t\right)\ }}{2}\left(2.2\right).\]

В момент времени, который следует найти $F=F_0$; $E_p=E_{p0}$, значит:

\[\frac{E_{p0}}{F_0}=-\frac{A}{2}{\cos \left(\omega t\right)\ }\to t=\frac{1}{\omega }\ arc{\cos \left(-\frac{2E_{p0}}{AF_0}\right)\ }.\]

Ответ. $t=\frac{1}{\omega }\ arc{\cos \left(-\frac{2E_{p0}}{AF_0}\right)\ }$

Читать дальше: формулы равноускоренного прямолинейного движения.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

1.3. Сохранение энергии при гармонических колебаниях

Умножим уравнение (1.18) гармонических колебаний на скорость изменения переменной x:

(1. 28)

Каждое из слагаемых можно представить как соответствующую производную:

так что уравнение (1.28) записывается в виде:

(1.29)

Отсюда следует, что величина в скобках не зависит от времени, то есть сохраняется в процессе колебаний:

(1.30)

Для выяснения физического смысла сохраняющейся величины применим эти соотношения к пружинному маятнику, когда

Видим, что уравнение (1. 30) можно записать в виде суммы кинетической энергии груза и потенциальной энергии деформированной (сжатой или растянутой) пружины:

(1.31)

Таким образом, найденный закон сохранения есть не что иное, как закон сохранения полной энергии системы.

Аналогично, для электромагнитного контура переменная

В этом случае соотношение (1.30) принимает вид:

(1. 32)

Первый член — это энергия магнитного поля в катушке, а второй — энергия электрического поля в конденсаторе. Снова мы получили, что сохраняется полная энергия системы.

Возвращаясь к общей форме (1.30) закона сохранения энергии и подставляя сюда общее решение (1.23), получаем законы изменения во времени кинетической и потенциальной энергий (или их аналогов) и выражение для сохраняющейся полной энергии:

(1.33)

Отсюда следует, что

кинетическая и потенциальная энергии — периодические функции времени с периодом, равным половине периода колебаний;
кинетическая и потенциальная энергии колеблются в противофазе: когда кинетическая энергия достигает максимума, значение потенциальной энергии минимально и наоборот;
в колебательной системе энергия периодически «перекачивается» из одной формы в другую, а полная энергия Е = К + П сохраняется;
полная энергия колебаний пропорциональна квадрату их амплитуды и квадрату частоты.

Видео 1.9 Сохранение энергии при почти гармонических колебаниях – маятник Галилея.

Сказанное проиллюстрировано на рис. 1.11, на котором показаны изменения кинетической и потенциальной энергий для пружинного маятника и электромагнитного контура.

Рис. 1.11. Изменения во времени различных форм энергии в колебательной системе:
1 –

пружинный маятник; 2 – электромагнитный колебательный контур

Видео 1.10 Cохранение энергии при механических колебаниях — маятник Максвелла

Видео 1.11 Cохранение энергии (и не только) при механических колебаниях — баллистический маятник

Энергия в маятнике | Блог Гэри Гарбера

Энергия в маятнике

В простом маятнике без трения сохраняется механическая энергия. Полная механическая энергия представляет собой комбинацию кинетической энергии и гравитационной потенциальной энергии. Когда маятник качается вперед и назад, происходит постоянный обмен между кинетической энергией и гравитационной потенциальной энергией.

Потенциальную энергию маятника можно смоделировать с помощью основного уравнения

PE = mgh

, где g — ускорение свободного падения, а h — высота. Мы часто используем это уравнение для моделирования объектов в свободном падении.

Однако маятник удерживается стержнем или струной и не находится в свободном падении. Таким образом, мы должны выразить высоту через θ , угол и L, длину маятника. Таким образом, h = L(1 – COS θ)

Когда θ = 90 ° маятник находится в высшей точке. COS 90 ° = 0 и h = L(1-0) = L, и PE = mgL(1 – COS θ) = mgL

Когда маятник находится в самой нижней точке, θ = 0 ° COS 0 ° = 1 и h = L (1-1) = 0, и PE = mgL(1 –1) = 0

Во всех точках в -между потенциальной энергией можно описать с помощью PE = mgL(1 – COS θ)

Пренебрегая трением и другими неконсервативными силами, мы находим, что в простом маятнике сохраняется механическая энергия. Кинетическая энергия будет равна KE = ½mv ² , где м — масса маятника, а v — скорость маятника.

В своей высшей точке (точка А) маятник моментально неподвижен. Вся энергия маятника представляет собой гравитационную потенциальную энергию, а кинетическая энергия отсутствует. В самой нижней точке (точка D) маятник имеет наибольшую скорость. Вся энергия маятника представляет собой кинетическую энергию, а гравитационная потенциальная энергия отсутствует. Однако полная энергия постоянна как функция времени. Вы можете наблюдать это в следующем БУ Физлет об энергии в маятнике.

Если есть трение, мы имеем затухающий маятник, который демонстрирует затухающее гармоническое движение. Вся механическая энергия в конечном итоге становится другими формами энергии, такими как тепло или звук.

Ваши исследования должны были показать, что масса не влияет на период маятника. Одной из причин, объясняющих это, является использование закона сохранения энергии.

Если мы рассмотрим уравнения сохранения энергии в маятниковой системе, мы обнаружим, что масса исключается из уравнений.

KE _I + PE _I = KE _F + PE _F

[½MV ² + MGL (1-COSQ)] _I = [½MV ² + МЛИ COSq) ] _f

Существует прямая зависимость между углом θ и скоростью. Благодаря этому масса не влияет на поведение маятника и не изменяет его период.

15.2 Энергия в простом гармоническом движении

Цели обучения

К концу этого раздела вы сможете:

Описывать сохранение энергии системы массы и пружины
Объяснить концепции устойчивых и неустойчивых точек равновесия

Чтобы произвести деформацию объекта, мы должны совершить работу. То есть, дергаете ли вы струну гитары или сжимаете амортизатор автомобиля, сила должна действовать на расстоянии. Если единственным результатом является деформация и никакая работа не превращается в тепловую, звуковую или кинетическую энергию, то вся работа первоначально хранится в деформированном объекте в виде некоторой формы потенциальной энергии.

Рассмотрим пример блока, прикрепленного к пружине на столе без трения, колеблющегося в СТМ. Сила пружины является консервативной силой (которую вы изучали в главе о потенциальной энергии и сохранении энергии), и мы можем определить для нее потенциальную энергию. Эта потенциальная энергия представляет собой энергию, запасенную в пружине, когда пружина растягивается или сжимается. В этом случае брусок колеблется в одном измерении с силой пружины, действующей параллельно движению:
9{2}[/latex] хранится весной. В СГМ системы масса-пружина диссипативные силы отсутствуют, поэтому полная энергия представляет собой сумму потенциальной энергии и кинетической энергии. В этом разделе мы рассмотрим сохранение энергии системы. Рассмотренные концепции справедливы для всех простых гармонических осцилляторов, в том числе и для тех, в которых играет роль гравитационная сила.
Рассмотрим (рисунок), на котором показан колеблющийся блок, прикрепленный к пружине. В случае незатухающего SHM энергия колеблется между кинетической и потенциальной, полностью переходя от одной формы энергии к другой по мере колебаний системы.
Таким образом, для простого примера объекта на поверхности без трения, прикрепленной к пружине, движение начинается со всей энергии, запасенной в пружине, как упругая потенциальная энергия . Когда объект начинает двигаться, упругая потенциальная энергия преобразуется в кинетическую энергию, становясь полностью кинетической энергией в положении равновесия. Затем энергия преобразуется пружиной обратно в упругую потенциальную энергию по мере ее растяжения или сжатия. Скорость становится равной нулю, когда кинетическая энергия полностью преобразуется, и затем этот цикл повторяется. Понимание сохранения энергии в этих циклах даст дополнительную информацию здесь и в более поздних применениях SHM, таких как переменные цепи. 9{2}. [/latex] Полная энергия системы постоянна.

Более пристальный взгляд на энергию системы показывает, что кинетическая энергия колеблется как функция квадрата синуса, а потенциальная энергия колеблется как функция квадрата косинуса. Однако полная энергия системы постоянна и пропорциональна квадрату амплитуды.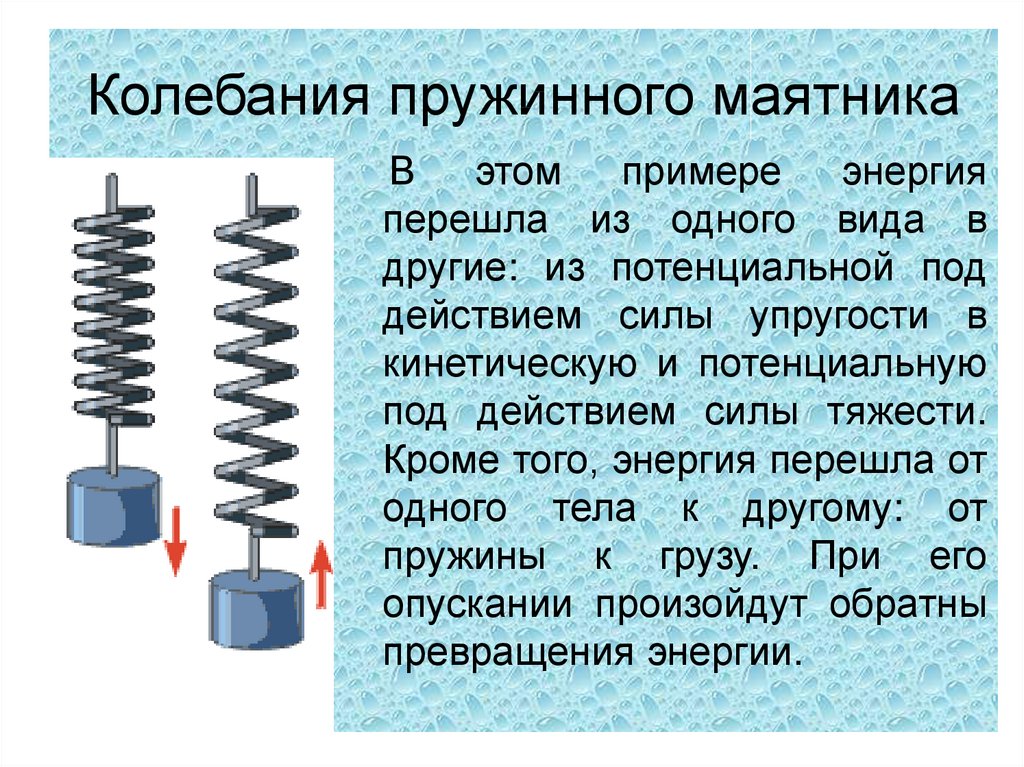 {2} [/latex], а сила, действующая на блок, максимальна и указывает на минус x -направление [латекс] ({F}_{S}=\text{−}kA) [/латекс]. Скорость и кинетическая энергия блока равны нулю в момент времени [латекс] t=0.00\,\text{s}\text{.} [/latex] В момент времени [латекс] t=0.00\,\text{с,} [/latex] блок выходит из состояния покоя.
Рисунок 15.12 График кинетической энергии, потенциальной энергии и полной энергии блока, колеблющегося на пружине в СГМ. Также показаны графики зависимости положения от времени и скорости от времени. Полная энергия остается постоянной, но энергия колеблется между кинетической и потенциальной энергией. Когда кинетическая энергия максимальна, потенциальная энергия равна нулю. Это происходит, когда скорость максимальна, а масса находится в положении равновесия. Потенциальная энергия максимальна, когда скорость равна нулю. Полная энергия представляет собой сумму кинетической энергии плюс потенциальная энергия, и она постоянна.

Колебания около положения равновесия
Мы только что рассмотрели энергию СГМ как функцию времени.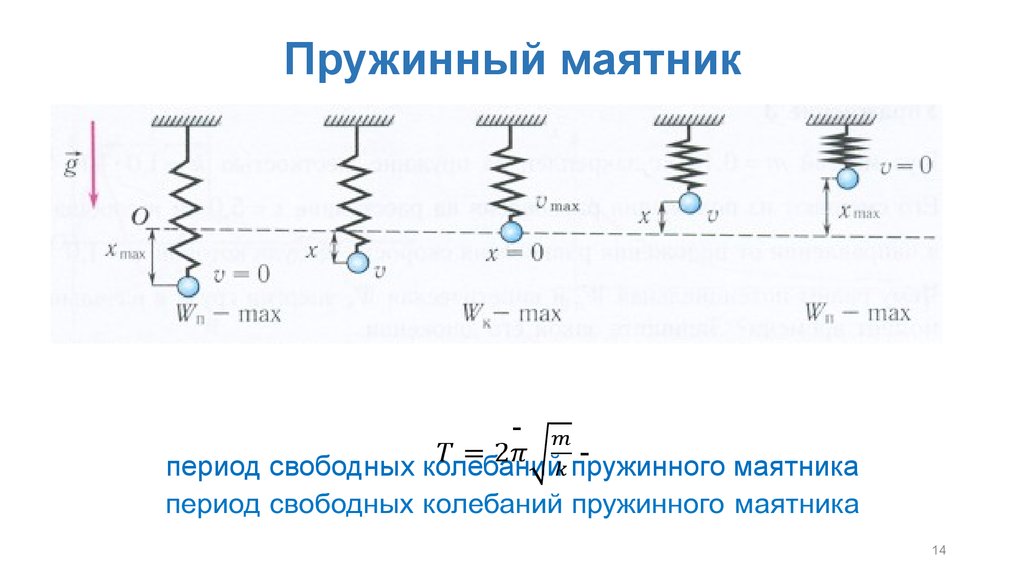 Другой интересный взгляд на простой гармонический осциллятор состоит в том, чтобы рассматривать энергию как функцию положения. (Рисунок) показывает график зависимости энергии от положения системы, подвергающейся СГМ.
Рисунок 15.13 График кинетической энергии (красный), потенциальной энергии (синий) и полной энергии (зеленый) простого гармонического осциллятора. Сила равна [латекс] F=-\frac{dU}{dx} [/латекс]. Положение равновесия показано черной точкой и представляет собой точку, в которой сила равна нулю. Сила положительна, когда [латекс] x<0 [/латекс], отрицательна, когда [латекс] х>0 [/латекс], и равна нулю, когда [латекс] х=0 [/латекс].
Кривая потенциальной энергии на (рис.) напоминает чашу. Когда шарик помещают в чашу, он достигает положения равновесия в самой нижней точке чаши [латекс] (х=0) [/латекс]. Это происходит потому, что возвращающая сила направлена в сторону точки равновесия. Эту точку равновесия иногда называют фиксированной точкой . Когда шарик перемещается в другое положение [латекс] (x=+A) [/латекс], шарик колеблется вокруг положения равновесия. Оглядываясь назад на график потенциальной энергии, силу можно найти, посмотрев на наклон графика потенциальной энергии [латекс] (F=-\frac{dU}{dx}) [/латекс]. Поскольку сила по обе стороны от неподвижной точки направлена обратно к точке равновесия, точка равновесия называется устойчивая точка равновесия . Точки [latex] x=A [/latex] и [latex] x=\text{−}A [/latex] называются точками поворота. (См. «Потенциальная энергия» и «Сохранение энергии».)
Стабильность — важная концепция. Если точка равновесия устойчива, небольшое возмущение объекта, который изначально находится в точке устойчивого равновесия, заставит объект колебаться вокруг этой точки. Точка устойчивого равновесия возникает потому, что к ней направлена сила с обеих сторон. Для неустойчивой точки равновесия, если объект слегка потревожить, он не возвращается в точку равновесия.
Рассмотрим пример с мрамором в чаше. Если чаша находится правильной стороной вверх, шарик, если его слегка поколебать, будет колебаться вокруг точки стабильного равновесия. Если чашу перевернуть вверх дном, шарик можно уравновесить сверху, в точке равновесия, где результирующая сила равна нулю. Однако, если шарик слегка потревожить, он не вернется в точку равновесия, а вместо этого скатится с чаши. Причина в том, что сила по обе стороны от точки равновесия направлена от этой точки. Эта точка является неустойчивой точкой равновесия.
(рисунок) показывает три состояния. Первая представляет собой устойчивую точку равновесия (а), вторая — неустойчивую точку равновесия (б), а последняя — также неустойчивую точку равновесия (в), поскольку сила только с одной стороны направлена в сторону точки равновесия.
Рисунок 15.14 Примеры точек равновесия. а) точка устойчивого равновесия; (б) неустойчивая точка равновесия; в) точка неустойчивого равновесия (иногда называемая точкой полуустойчивого равновесия).
Процесс определения того, является ли точка равновесия устойчивой или нестабильной, можно формализовать. Рассмотрим кривые потенциальной энергии, показанные на (рис.). Силу можно найти, анализируя наклон графика. Сила равна [латекс] F=-\frac{dU}{dx}. [/latex] В (a) фиксированная точка находится в точке [латекс] x=0,00\,\text{m}\text{.} [/latex] Когда [латекс] x<0,00\,\text{m, } [/latex] сила положительна. Когда [латекс] х>0,00\,\текст{м,} [/латекс] сила отрицательна. Это стабильная точка. В (b) фиксированная точка находится в точке [латекс] x=0,00\,\text{m}\text{.} [/latex]. Когда [латекс] x<0,00\,\text{m,} [/latex ] сила отрицательна. Когда [латекс] х>0,00\,\текст{м,} [/латекс] сила также отрицательна. Это нестабильная точка.
Рис. 15.15 Два примера функции потенциальной энергии. Сила в положении равна отрицательному наклону графика в этом положении. (а) Функция потенциальной энергии с устойчивой точкой равновесия. (b) Функция потенциальной энергии с неустойчивой точкой равновесия. Эту точку иногда называют полуустойчивой, потому что сила с одной стороны направлена в сторону неподвижной точки.
Практическое применение концепции устойчивых точек равновесия — сила между двумя нейтральными атомами в молекуле. Если две молекулы находятся в непосредственной близости друг от друга на расстоянии нескольких атомных диаметров, они могут испытывать силу притяжения. Если молекулы движутся достаточно близко, так что электронные оболочки других электронов перекрываются, сила между молекулами становится отталкивающей. Сила притяжения между двумя атомами может привести к тому, что атомы образуют молекулу. Сила между двумя молекулами не является линейной силой и не может быть смоделирована просто как две массы, разделенные пружиной, но атомы молекулы могут колебаться вокруг точки равновесия при небольшом смещении от положения равновесия. Атомы колеблются из-за силы притяжения и силы отталкивания между двумя атомами. 9{6}]. [/latex]
График этой функции показан на (Рисунок). Два параметра [латекс]\эпсилон[/латекс] и [латекс]\сигма[/латекс] находятся экспериментально.
Рис. 15.16 Функция потенциальной энергии Леннарда-Джонса для системы двух нейтральных атомов. Если энергия ниже некоторой максимальной энергии, система колеблется вблизи положения равновесия между двумя точками поворота.
На графике видно, что имеется яма потенциальной энергии, которая имеет некоторое сходство с ямой потенциальной энергии функции потенциальной энергии простого гармонического осциллятора, обсуждаемой на (рис.). Потенциал Леннарда-Джонса имеет устойчивую точку равновесия, в которой потенциальная энергия минимальна, а сила по обе стороны от точки равновесия направлена к точке равновесия. Обратите внимание, что в отличие от простого гармонического осциллятора потенциальная яма потенциала Леннарда-Джонса не симметрична. Это связано с тем, что сила между атомами не является силой закона Гука и не является линейной. Атомы все еще могут колебаться вокруг положения равновесия [латекс] {x}_{\text{мин}} [/латекс], потому что, когда [латекс] х<{х}_{\текст{мин}} [/латекс], сила положительная; когда [латекс] х>{х}_{\текст{мин}} [/латекс], сила отрицательна. Обратите внимание, что как x приближается к нулю, наклон довольно крутой и отрицательный, а значит сила большая и положительная. Это говорит о том, что требуется большая сила, чтобы попытаться сблизить атомы. По мере того, как x становится все больше, наклон становится менее крутым, а сила меньше и отрицательна. Это говорит о том, что при достаточно большой энергии атомы можно разделить.
Если вас интересует это взаимодействие, найдите силу между молекулами, взяв производную функции потенциальной энергии. Вы сразу увидите, что сила не похожа на силу закона Гука [латекс] (F=\text{−}kx) [/латекс], но если вы знакомы с биномиальной теоремой: 9{3}+\cdots , [/latex]
сила может быть аппроксимирована силой закона Гука.
Скорость и сохранение энергии
Возвращаясь к системе блока и пружины (рисунок), после выхода блока из состояния покоя он начинает двигаться в отрицательном направлении к положению равновесия. Потенциальная энергия уменьшается, а величина скорости и кинетическая энергия увеличиваются. {2} [/латекс ]. При колебаниях полная энергия постоянна и равна сумме потенциальной энергии и кинетической энергии системы, 9{2})}. [/latex]
Энергия в простом гармоническом осцилляторе пропорциональна квадрату амплитуды. При рассмотрении многих форм колебаний вы обнаружите, что энергия пропорциональна квадрату амплитуды.
Проверьте свое понимание
Почему будет больнее, если вы щелкнете рукой по линейке, чем по ослабленной пружине, даже если смещение каждой системы одинаково?
Показать решение
Проверьте свое понимание
Определите, как можно уменьшить максимальную скорость простого гармонического осциллятора.
Показать решение
Резюме
Колебания простейшего типа относятся к системам, описываемым законом Гука, F = − kx , где F – возвращающая сила, x – смещение от равновесия или деформации, а k — силовая постоянная системы. {2}. [/латекс] 9{2})}. [/латекс]
Концептуальные вопросы
Опишите систему, в которой запасается упругая потенциальная энергия.
Показать решение
Объясните с точки зрения энергии, как диссипативные силы, такие как трение, уменьшают амплитуду гармонического осциллятора. Также объясните, как приводной механизм может компенсировать. (Такой системой являются маятниковые часы.)
Температура атмосферы колеблется от максимума около полудня до минимума перед восходом солнца. Считаете ли вы, что атмосфера находится в устойчивом или неустойчивом равновесии?
Показать решение
Проблемы
Рыбу подвешивают на пружинных весах для определения ее массы. а) Какова постоянная силы пружины в таком масштабе, если пружина растягивается на 8,00 см при нагрузке 10,0 кг? б) Какова масса рыбы, растянувшей пружину на 5,50 см? в) Какое расстояние между полукилограммовыми отметками на весах?
Пришло время взвешивания местной команды по регби до 85 кг. Ванные весы, используемые для оценки соответствия критериям, описываются законом Гука, и их максимальная нагрузка в 120 кг опускается на 0,75 см. а) Какова постоянная эффективной силы пружины? б) Игрок встает на весы и опускает их на 0,48 см. Имеет ли он право играть в этой команде до 85 кг?
Показать решение
В одном типе пневматического оружия используется поршень с пружинным приводом для выдувания пули из ствола. (a) Рассчитайте силовую постоянную пружины его поршня, если вы должны сжать ее на 0,150 м, чтобы привести поршень массой 0,0500 кг к максимальной скорости 20,0 м/с. б) Какую силу надо приложить, чтобы сжать пружину?
Когда человек массой 80,0 кг стоит на пого-стике, пружина сжимается на 0,120 м. а) Чему равна постоянная силы пружины? б) Будет ли пружина сжата сильнее, когда он будет прыгать по дороге? 9{4}\,\text{Н/м} [/латекс]. (a) Какова частота, с которой он отскакивает, учитывая его массу плюс и массу его снаряжения 90,0 кг? (b) Насколько растянется эта веревка, чтобы предотвратить падение альпиниста, если он пролетит 2,00 м в свободном падении до того, как веревка натянется? ( Подсказка: Используйте закон сохранения энергии.