Коэффициент упругости формула: Коэффициент упругости, формула и примеры
alexxlab | 02.01.2023 | 0 | Разное
Лабораторная работа 116
Лабораторная работа № 116
Определение
коэффициента упругости
Цель работы: Экспериментальное определение коэффициента упругости стальной пружины методом колебаний.
Приборы и принадлежности: пружинный маятник, секундомер, грузы, технические весы.
Теоретическое введение
Под действием приложенных к нему сил всякое реальное тело деформируется, т.е. изменяет свои размеры и форму. Если после прекращения действия сил тело принимает первоначальные размеры и форму, деформация называется упругой. Упругие деформации наблюдаются в том случае, если сила, обусловившая деформацию, не превосходит некоторый, определенный для каждого тела, предел.
Опыт показывает, что при упругой деформации
для тела выполняется закон Гука, который гласит: упругая сила пропорциональна
абсолютному удлинению тела, т.
,
где k – коэффициент упругости тела; Dl – абсолютное удлинение.
Рассмотрим пружинный маятник, представляющий собой упругую пружину с коэффициентом упругости k, на одном конце которой подвешено тело массой m, а другой конец закреплен (рис.1).
В свободном состоянии
маятника на тело массой m действуют
сила тяжести и упругая сила ,
которые равны по величине и противоположны по направлению. Поэтому тело
массой m будет находиться в
состоянии покоя (равновесия) (рис.1). Приложим к телу массой m внешнюю силу ,
которая сместит тело из положения равновесия вниз на расстояние х (рис.2), затем уберем эту силу и
предоставим маятник самому себе. Под действием упругой силы тело
возвращается в положение равновесия, по достижению его тело по инерции будет
двигаться вверх, сжимая пружину.
|
|
||
|
Рис. 1 |
Рис. |
Рис. 3 |
Найдем уравнение колебания пружинного маятника и период колебания. Для этого используем закон сохранения механической энергии. В любой момент времени полная механическая энергия пружинного маятника остается постоянной, если отсутствуют диссипативные силы и система изолирована. Тогда сумма кинетической энергии и потенциальной энергии - постоянна
где υ – скорость тела, х – смещение тела от положения равновесия, причем
.
Продифференцировав (1) по времени, получим
,
Откуда
.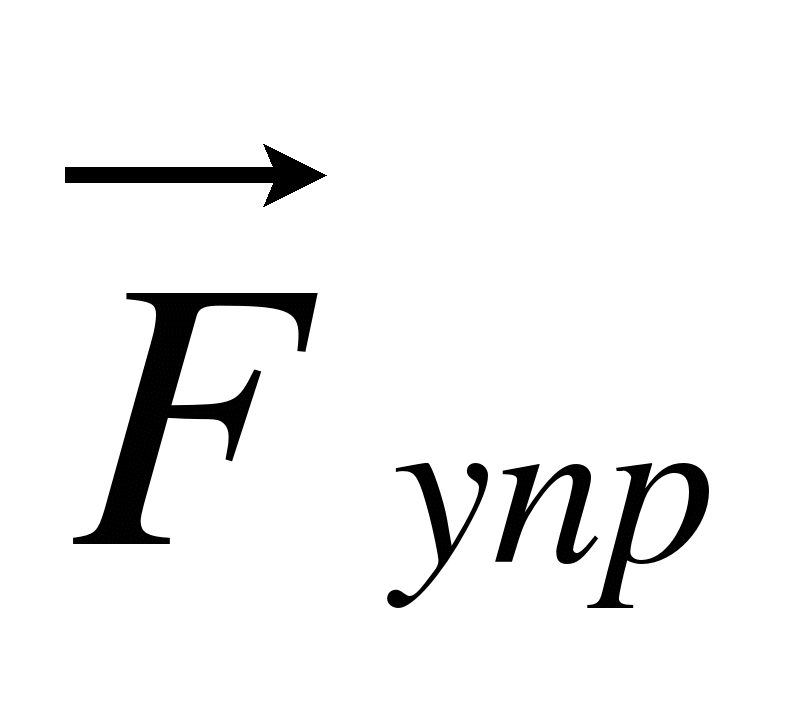
Обозначив
,
получим
Соотношение (3) является дифференциальным уравнением гармонического колебания пружинного маятника, совершающегося с циклической частотой w
Решением дифференциального уравнения (3) служит уравнение гармонического колебания
где х – смещение колеблющегося тела от положения равновесия в момент времени t; А – амплитуда колебания, равная наибольшему смещению тела от положения равновесия; j0 – начальная фаза колебания.
Период колебания, равный времени, за которое совершается одно полное колебание, определяется формулой
Период колебания
пружинного маятника зависит от коэффициента упругости пружины и массы
колеблющегося тела.
Из формулы (5) коэффициент упругости пружины равен
Описание рабочей установки и метода измерений
Рабочая установка представляет собой пружинный маятник (рис.3), состоящий из груза Г, подвешенного к пружине б. Пружина крепится к перекладине, закрепленной на двух штативах а.
Если груз вывести из состояния покоя, то под действием упругой силы пружины он начнет совершать гармонические колебания. Зная массу груза m и период колебаний Т, по формуле (6) легко находится коэффициент упругости пружины k.
Правильность найденного значения коэффициента упругости k проверяется по формуле, являющейся выражением закона Гука:
где P = mg
– вес груза, под действием которого пружина удлиняется на величину Dl. Значение Dl отсчитывают по смещению миллиметровой
линейки в, укрепленной с пружиной
относительно указателя смещения g.
Значение Dl отсчитывают по смещению миллиметровой
линейки в, укрепленной с пружиной
относительно указателя смещения g.
Ход работы
1. Подобрать массу груза так, чтобы можно было легко считать число колебаний маятника. Определить массу груза m взвешиванием на технических весах.
2. Исходя из 30-50 полных колебаний, определить период колебаний груза
,
где <t>
– среднее время n полных колебаний.Время t измерить секундомером. С данным грузом время t измерить не менее 5 раз для одного и того же числа колебаний и определить среднее значение времени <t>.
3.
По формуле (6) найти значение коэффициента упругости k.
4. Грузы привести в статическое состояние, и, по смещению линейки относительно указателя, определить удлинение пружины Dl под действием веса груза.
5. По формуле (7) найти среднее значение kпров.
6. Опыт повторить при другой массе груза.
7. Вычислить абсолютную и относительную погрешности коэффициента упругости k.
8. Данные занести в таблицу.
Таблица
|
№ |
т |
п |
t |
<t> |
T |
<k> |
Dl |
P |
k пров |
Е |
|
|
кг |
|
с |
с |
с |
Н/м |
м |
Н |
Н/м |
% |
|
|
|
|
|
|
|
|
|
|
|
Вопросы для допуска к работе
1.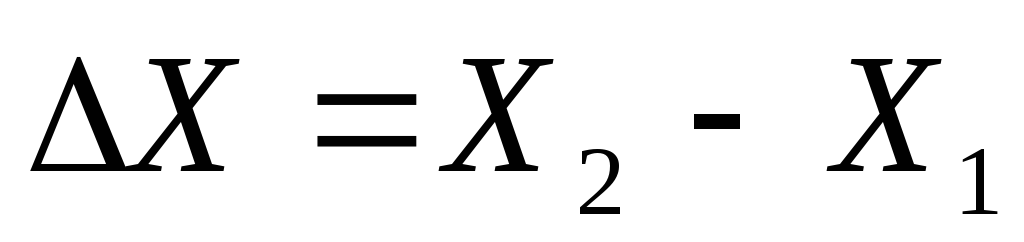 Какова цель работы?
Какова цель работы?
2. Запишите рабочую формулу и поясните величины, входящие в нее.
3. Опишите рабочую установку и ход эксперимента.
4. Оцените погрешность метода измерений коэффициента упругости.
Вопросы для защиты работы
1. Опишите колебания пружинного маятника.
2. Выведите дифференциальное уравнение гармонического колебания для пружинного маятника.
3. Напишите уравнение гармонического колебания пружинного маятника и поясните физический смысл всех величин.
4. Дайте определение циклической частоты и периода колебания.
5. От чего зависят циклическая частота и период колебания пружинного маятника?
6. Выведите рабочую формулу.
7. Каков физический смысл коэффициента упругости?
Каков физический смысл коэффициента упругости?
8. Какие колебания называются свободными? Вынужденными?
9. Вычислите погрешность результата эксперимента, пользуясь дифференцированным методом.
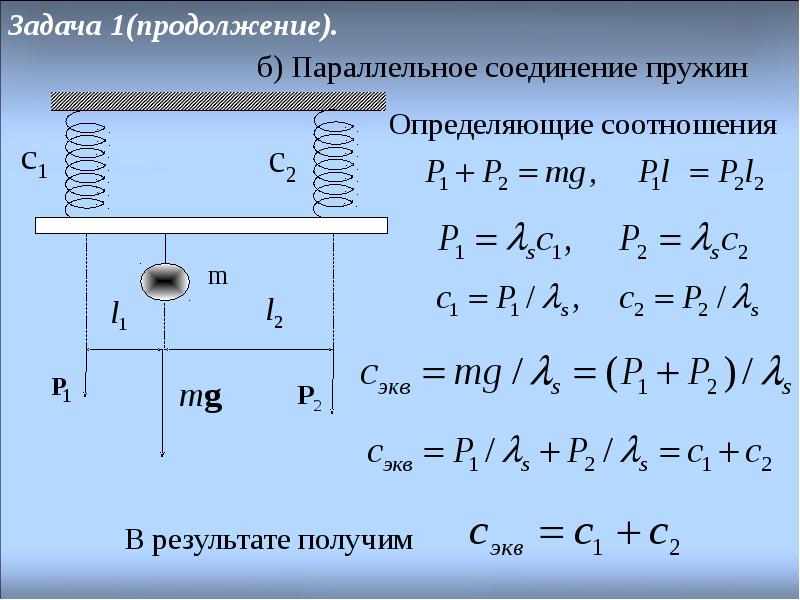
Цель работы.Определить: 1) угловой коэффициент упругости спиральной пружины;2) момент инерции двух полых цилиндров.Проверить аддитивность момента инерции и теорему Штейнера. Оборудование. В комплект экспериментальной установки входят: вращающийся вал, на который устанавливают стержень или диск; два полых толстостенных цилиндра; динамометр; масштабная линейка; световой барьер со счетчиком; источник питания (рис.1).
(1) где: G- угловой коэффициент упругости спиральной пружины; I-момент инерции диска; m – максимальная угловая скорость диска. При слабом затухании механические колебания можно считать гармоническими. Угловое перемещение в момент времени t описывает-ся уравнением (2) где 0 – собственная циклическая частота свободных колебаний диска. Циклическая частота связана с периодом Т свободных колебаний соотношением . (3) Модуль угловой скорости маятника определим как первую производную от углового перемещения (2) (4) где – максимальная угловая скорость диска. Если подставить максимальную скорость диска в уравнение (1) , то получим формулу, с помощью которой можно определить момент инерции диска (6) Совместное решение уравнений (3) и (6) позволяет определить момент инерции диска по его периоду крутильных колебаний: (7) Формул (7) является универсальной, с ее помощью можно определить момент инерции любого твердого тела, способного совершать крутильные колебания. Z Z CC/Рис. 2. Принципиальная схема установки для проверки теоремы Штейнера. (8) где I0 – момент инерции диска с цилиндрами, I – момент инерции диска без цилиндров. (9) где R и r – внешний и внутренний радиусы цилиндров, соответственно, m – масса цилиндра, а – расстояние от оси симметрии цилиндров Z до оси вращения СС/. Выполнение работы 2. Измерьте силу при помощи динамометра для углов поворота стержня π, 2π, 3π, 4π. Исходя из требований к безопасности и устойчивости, не рекомендуется перегибать пружину на ± 720º. 3. Задание 2. Определение момента инерции двух полых толстостенных цилиндров. 2. Несколько раз (5-7) измерьте период колебаний диска. Для измерения периода колебаний на диск прикрепите листок бумаги (ширина ≤ 3 мм). Разместите диск так, чтобы листок находился точно под световым барьером. Для светового барьера выберите режим . Отклоните диск на 90º. Измерьте величину периода для каждого случая. 3. По среднему значению периода определите по формуле (7) момент инерции однородного диска I. 4. Установите в центр диска два полых цилиндра и повторите пункт 2. 5. По среднему значению периода Т0 определите момент инерции I0 диска с цилиндрами. 6. Вычислите момент инерции двух цилиндров относительно их оси симметрии Z: Iz= I0 – I. 7. С помощью динамометра измерьте вес цилиндра и определите его массу m. 8. Найдите теоретическое значение момента инерции цилиндров, по формуле: 9. Результаты измерений и вычислений занесите в таблицу1. Таблица 1
9. Сравните результаты эксперимента с теоретическим значением момента инерции цилиндров, оцените погрешность и сделайте вывод. Задание 3. Проверка теоремы Штейнера. 2. Несколько раз (5-7) измерьте период колебаний диска с цилиндрами. 3. По среднему значению периода Т0 определите по формуле (7) момент инерции диска с цилиндрами. 4. Вычислите момент инерции двух цилиндров относительно оси CC/: I CC ’= I0 – I, где I – момент инерции диска (см. задание 2). 5. Найдите теоретическое значение момента инерции цилиндров, по формуле: 6. Результаты измерений и вычислений занесите в таблицу 2. Таблица 2
7. Сравните результаты эксперимента с теоретическим значением момента инерции цилиндров, оцените погрешность и сделайте вывод. 2. В чем состоит смысл аддитивности момента инерции? 3. Сформулируйте теорему Штейнера. 4. Какие энергетические преобразования происходят в системе, совершающей крутильные колебания? 5. Выведите формулу, позволяющую определить момент инерции твердого тела методом крутильных колебаний. Рекомендуемая литература 1. Савельев И.В. Курс физики. Т2. М.: Наука. 1989. §§ 64. 2. Савельев И.В. Курс физики. Т1. М.: Наука. 1989. §§ 32,33. 3. Трофимова Т. И. Курс физики. М.: Высшая школа. 2003. §§ 16, 17, 141. 4. Федосеев В.Б. Физика 5. Инструкция по эксплуатации оборудования фирмы “PHYWE”. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Исследование зависимости силы упругости от удлинения пружины. Измерение жёсткости пружины Измерение жёсткости пружиныИзучение зависимости пути от времени при прямолинейном равномерном движении. Измерение скорости | 1. Землеустройство Цель работы – определить сущность, типы и этапы землеустройства, изучить предмет и задачи геодезии, дать определения основным её… | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Руководство по эксплуатации и паспорт изделия гайковерт угловой Мы прилагаем все усилия, чтобы улучшить качество и срок службы инструментов, а также снизить вибрации и шум при работе инструмента…. | Осторожно, кNiГа! Разработчики Регионального сайта детских библиотек преследовали цель привлечения детей к чтению, выработки привычки и устойчивых… | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Эти отверстия с номерами 0,3,6,9 означают преднатяг пружины ведомого… Я обычно, в марте, когда температура поднимается к 0 и выше переставляю пружину на 6-ку. На “0” ставить вообще не рекомендую! Максималка… | Работы Исследование зависимости периода колебаний пружинного маятника от массы груза и жёсткости пружины | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1.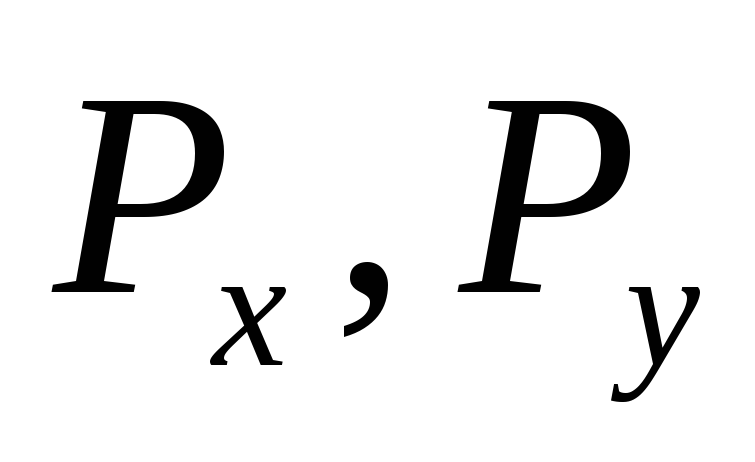 Цель и задачи работы Цель и задачи работыЦель работы – изучение конкурентных практических умений и навыков безопасной работы с торговым оборудованием, законодательными и… | Моу «Ломоватская средняя общеобразовательная школа» Цель паспортизации медицинского кабинета Проанализировать состояние кабинета, его готовность к обеспечению требований стандартов, определить основные направления работы по… | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Программатор тахографов cd400 паспорт руководство по эксплуатации cd concept S. P. R. L. Бельгия Прибор позволяет определять характеристический коэффициент транспортного средства (W), коэффициент тахографа (К), может использоваться… | 1. По доплеровскому смещению частоты опреде-лить скорость ультразвука… Цель работы. По доплеровскому смещению частоты опреде-лить скорость ультразвука (звука) в воздухе. Определить основные характеристики… | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Инструкция: «Ответь на вопросы» Цель: определить уровень развития социальных качеств, связь с общей осведомлённостью ребёнка и развитие мыслительных операций | Яс нител ь н а я з а пи с ка Вступительное испытание «Священное Писание Ветхого и Нового Завета» проводится в устной форме.  Цель испытания определить уровень… Цель испытания определить уровень… | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| И цель лабораторной работы Цель работы – изучение физических процессов, происходящих в волоконно-оптической линии связи, изучение процессов модуляции и демодуляции… | Анализ методической работы школы за 2013-2014 учебный год Цель анализа … | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Техническое задание на проектирование блочной трансформаторной подстанции… Строительство блочной трансформаторной подстанции напряжением 10 4Kb., тип трансформаторной подстанции, исполнение вводов, мощность… | Магистерская диссертация Цель. Цель работы состояла в разработке нового подхода к оценке стоимости брэнда компании |
Коэффициент эластичности – определение, формула, примеры
Коэффициент эластичности – это экономическая мера, которая используется для определения процентного колебания одной переменной по отношению к 1%-ной вариации другой переменной.
Это скорость изменения объема спроса в ответ на изменение цены товара на 1%.
Термин эластичность относится к степени изменения зависимой переменной при приложении к ней внешней силы (изменение независимой переменной). Таким образом, коэффициент ценовой эластичности спроса показывает, насколько спрос на товар чувствителен к изменению цены.
СОДЕРЖАНИЕ
- Коэффициент эластичности Определение
- Коэффициент эластичности объяснил
- Формула
- Интерпретация
- Примеры
- Пример № 1
- Пример № 2
- Зачатывание. Зачатываемые вопросы.
- Коэффициент эластичности представляет собой числовую меру степени вариации одной переменной (зависимой) в ответ на изменение другой переменной (независимой переменной) на 1%.
- Коэффициент указывает на процентное изменение величины спроса, вызванное изменением цены на 1%.
- Коэффициент эластичности выражается следующим образом:
‘E = (%∆y) / (%∆x), или E = (%∆Q) / (%∆P)’ - Когда, E = 0 наблюдается совершенная неэластичность, E < 1 показывает неэластичность, E = 1 означает унитарную эластичность, E > 1 напоминает эластичность, а E = ∞ указывает идеальную эластичность.

Объяснение коэффициента эластичности
Коэффициент эластичности – это мера степени, в которой значение одной переменной колеблется из-за изменений другой переменной. Например, если у — зависимая переменная, а х — независимая переменная, то значение у зависит от увеличения или уменьшения значения х.
Вы можете использовать это изображение на своем веб-сайте, в шаблонах и т. д. Пожалуйста, предоставьте нам ссылку с указанием авторства. Как указать авторство? Ссылка на статью должна быть гиперссылкой
Например:
Источник: Коэффициент эластичности (wallstreetmojo.com)
В экономике существует четыре типа эластичности: эластичность спроса, эластичность предложения по цене, эластичность по доходу и перекрестная эластичность. Но для понимания коэффициента основное внимание уделяется «эластичности спроса».
Товар считается «эластичным по цене», когда спрос на товар увеличивается при падении цен или уменьшается при повышении цены. Напротив, если изменения цен вызывают незначительное изменение или отсутствие изменений в спросе на товар, товар считается неэластичным по цене.
Напротив, если изменения цен вызывают незначительное изменение или отсутствие изменений в спросе на товар, товар считается неэластичным по цене.
Формула коэффициента эластичности
Коэффициент измеряет степень изменения спроса на определенный товар при изменении цены на 1%.
Для расчета коэффициента эластичности используется следующая формула:
Здесь
- E – коэффициент эластичности.
- %∆y — процентное изменение значения зависимой переменной.
- %∆x — процентное изменение значения независимой переменной.
- %∆Q — процентное изменение количества требуемого продукта.
- %∆P — процентное изменение цены продукта.
Интерпретация
Закон спроса гласит, что изменения цен на товары вызывают изменения в спросе на товары. Давайте обсудим пять различных интерпретаций коэффициента:
Случай 1: Если E = 0
Коэффициент эластичности равен 0, когда изменение цен не влияет на спрос на продукцию. В таком сценарии спрос на продукт совершенно неэластичен (по цене). Однако это обычное дело; спрос на необходимые товары и услуги остается постоянным, несмотря на колебания цен.
В таком сценарии спрос на продукт совершенно неэластичен (по цене). Однако это обычное дело; спрос на необходимые товары и услуги остается постоянным, несмотря на колебания цен.
Случай 2: Если E < 1
Когда процентное увеличение или падение спроса на товар сравнительно меньше, чем изменение цены товара, тогда спрос на товар неэластичен по цене.
Случай 3: E = 1
Когда коэффициент равен 1, спрос на товар изменяется с той же скоростью, с которой колеблется цена. В таком сценарии товарный спрос унитарно эластичен (по цене).
Случай 4: E > 1
Если спрос на продукт значительно возрастает или падает — в ответ даже на незначительное изменение его цены, то спрос на продукт эластичен по цене. Например, предметы роскоши очень чувствительны к цене — даже незначительные изменения цен вызывают значительный рост или падение спроса.
Случай 5: E = ∞
Когда изменение спроса на продукт бесконечно в ответ на незначительное изменение цен, продукт считается абсолютно эластичным (по цене). Это крайний сценарий и, следовательно, теоретический.
Это крайний сценарий и, следовательно, теоретический.
Примеры
Поясним коэффициент эластичности на следующих примерах:
Пример #1
Цена на рис повышается с 0,67 долл./кг до 0,71 долл./кг, но спрос на рис (количество спроса) сохраняется. то же, на 10000 ц. Теперь на основе заданных значений оцените коэффициент ценовой эластичности спроса.
Решение :
Дано:
%∆Q = 0%
%∆P = [(0,71 – 0,67)/0,67] × 100 = 5,97%
E = (%∆Q) / (%∆P)
E = 0 / 5,97 = 0
Таким образом, в данном сценарии спрос на рис совершенно неэластичен по цене.
Пример #2
В автосалоне ABC произошло падение спроса на роскошные автомобили. Спрос на продукцию упал с 540 единиц до 386 единиц в течение года. За тот же период цены на автомобили выросли с 92 000 до 96 000 долларов. По заданным значениям определите коэффициент ценовой эластичности спроса.
Решение :
Дано:
%∆Q = [(386 – 540) / 540] × 100 = 28,52%
%∆P = [(96000 – 92000) / 92000] × 100 = 4,35%
E = (% ∆Q) / (%∆P)
E = 28,52 / 4,35 = 6,56
Поскольку E > 1, спрос на роскошные автомобили считается высокоэластичным по цене.
Часто задаваемые вопросы (FAQ)
Что такое коэффициент эластичности?
Это степень вариации в количестве требуемого товара по отношению к (процентному) изменению цен.
Как рассчитать коэффициент эластичности?
Если Е – коэффициент; %∆Q — процентное изменение объема спроса, а %∆P — процентное изменение цены продукта, тогда коэффициент эластичности выражается следующим образом:
E = %∆Q / %∆P
интерпретировать коэффициент эластичности?
Ниже приведены различные интерпретации:
E = 0, тогда спрос на продукт совершенно неэластичен по цене.
E < 1, то спрос на товар неэластичен по цене.
E = 1, то спрос на продукт унитарно эластичен (по цене).
E > 1, то спрос на продукцию эластичен по цене.
E = ∞, то спрос на товар абсолютно эластичен по его цене.
Что означает нулевой коэффициент эластичности?
Если коэффициент равен нулю, то колебания цен на товары не вызывают изменения спроса на товары. В таком сценарии спрос на продукт совершенно неэластичен по цене.
Рекомендуемые статьи
Это руководство о том, что такое коэффициент эластичности. Мы объясняем «ценовую эластичность коэффициента спроса», его определение, формулу, интерпретацию и примеры. Вы можете узнать больше об экономике из следующих статей –
- Неэластичные товары
- Неэластичный спрос
- Эластичный спрос
Что вам нужно знать о коэффициентах эластичности
Обновлено 25 августа 2022 г. Джейкоб Рид
На экзаменах по микроэкономике 2015 и 2016 годов FRQ были сосредоточены на эластичности и расчете коэффициентов эластичности. Некоторые из моих учеников чувствовали себя недостаточно подготовленными к решению этих сложных вопросов. Чтобы убедиться, что это больше не повторится, я создал приведенный ниже обзор эластичности вместе с 15 вопросами Расчеты и интерпретации коэффициента эластичности , чтобы проверить ваши навыки. Если повезет, он предоставит вам все, что вам нужно знать об эластичности, чтобы вы не были застигнуты врасплох, когда в мае начнется экзамен AP.
Чтобы убедиться, что это больше не повторится, я создал приведенный ниже обзор эластичности вместе с 15 вопросами Расчеты и интерпретации коэффициента эластичности , чтобы проверить ваши навыки. Если повезет, он предоставит вам все, что вам нужно знать об эластичности, чтобы вы не были застигнуты врасплох, когда в мае начнется экзамен AP.
Основы и эластичность спроса по цене
Эластичность – это степень, в которой одно изменение вызывает другое изменение. Поскольку эластичность спроса по цене проще всего понять, мы начнем с этого. Мы знаем, что когда цены растут, объем спроса уменьшается. Эластичность говорит нам, насколько уменьшается величина спроса.
Когда большое изменение цены вызывает небольшое изменение объема спроса, кривая спроса относительно IN эластична. То есть потребители относительно IN чувствителен к изменению цены. Относительно неэластичные кривые спроса имеют тенденцию быть более вертикальными, чем горизонтальными. Если потребители требуют одинаковое количество товара независимо от цены, кривая спроса совершенно неэластична; потребители совершенно IN чувствительны к изменению цен. Совершенно неэластичные кривые спроса вертикальны.
Если потребители требуют одинаковое количество товара независимо от цены, кривая спроса совершенно неэластична; потребители совершенно IN чувствительны к изменению цен. Совершенно неэластичные кривые спроса вертикальны.
Товары с неэластичными кривыми спроса, как правило, являются:
- Товары первой необходимости.
- Продукты, у которых мало заменителей.
- Относительно недорогие товары.
Когда небольшое изменение цены вызывает большое изменение объема спроса, кривая спроса является относительно E эластичной. То есть E потребители особенно чувствительны к изменению цены. Кривые относительно эластичного спроса имеют тенденцию быть более горизонтальными, чем вертикальными. Если потребители будут требовать любое количество по одной максимальной цене, кривая спроса будет совершенно эластичной; потребители совершенно чувствительны к изменению цен. Кривые абсолютно эластичного спроса горизонтальны.
Товары, которые имеют эластичные кривые спроса, тогда будут:
- Товары, которые не являются необходимостью.
- Продукты, имеющие множество заменителей.
- Относительно дорогие продукты
Существует еще один тип упругости, и он называется единичной эластичностью. Кривая единичной эластичности спроса будет иметь рост цен, вызывающий пропорциональное уменьшение объема спроса.
Примечание. Глядя на форму кривой спроса, нельзя определить эластичность. Эластичность линейной кривой спроса уменьшается по мере увеличения количества (см. тест TR ниже)
Проверка общей выручки
Когда речь идет об эластичности спроса по цене, самым простым способом определения эластичности является проверка совокупной выручки (TR). Формула общего дохода: P x Q. На кривой спроса объемы падают по мере роста цен, а объемы растут по мере снижения цен. Если цена растет, а TR увеличивается (P и TR движутся в одном направлении), кривая спроса неэластична. Если цена падает, а TR уменьшается (опять же P и TR идут в одном направлении, кривая спроса также неэластична. Если цена растет, а TR падает (P и TR идут в противоположных направлениях, кривая спроса эластична. Если цена падает, а TR растет (снова PR и TR движутся в противоположных направлениях, кривая спроса также эластична. Если изменения цены не изменяют TR, кривая спроса является единично эластичной (увеличение или снижение цены сохраняет TR неизменной)9.0004
Если цена падает, а TR уменьшается (опять же P и TR идут в одном направлении, кривая спроса также неэластична. Если цена растет, а TR падает (P и TR идут в противоположных направлениях, кривая спроса эластична. Если цена падает, а TR растет (снова PR и TR движутся в противоположных направлениях, кривая спроса также эластична. Если изменения цены не изменяют TR, кривая спроса является единично эластичной (увеличение или снижение цены сохраняет TR неизменной)9.0004
Прямолинейная кривая спроса имеет эластичный участок вверху, неэластичный участок внизу и точку единичной эластичности в середине. Если на графике есть кривая предельного дохода (вы увидите ее, узнавая о монополиях и фирмах с монополистической конкуренцией), она может помочь вам определить эластичность. Снижение цены увеличивает общий доход по мере увеличения количества, пока предельный доход больше нуля. Участок единичной эластичности кривой спроса находится там, где MR=0. Тогда снижение цены уменьшает общую выручку, поскольку предельная выручка отрицательна. В этом диапазоне кривая спроса неэластична.
В этом диапазоне кривая спроса неэластична.
Примечание: ТЕСТ ОБЩЕГО ДОХОДА ПРИМЕНЯЕТСЯ ТОЛЬКО К ЭЛАСТИЧНОСТИ СПРОСА ПО ЦЕНЕ.
Коэффициент эластичности
Другим способом определения эластичности является расчет коэффициента. Коэффициент говорит нам о пропорциях, в которых изменение цены изменяет количество. Например, коэффициент -2 говорит нам о том, что повышение цены на заданный процент вызовет вдвое большее уменьшение количества. С другой стороны, коэффициент -0,5 вызовет уменьшение объема спроса на половину (поскольку 0,5 составляет 1/2) процента повышения цены. Основная формула для расчета коэффициента – это %∆Q/%∆P (∆ означает изменение). После расчета коэффициента абсолютное значение (то есть положительное или отрицательное значение не имеет значения) можно использовать для определения эластичности. Значения эластичности следующие:
- Абсолютное значение коэффициента = 0: совершенно неэластичный
- Абсолютное значение коэффициента <1 (но не ноль): относительно неэластичный
- Абсолютное значение коэффициента = 1: единичная эластичность ∞ или неопределенный): относительно эластичный
- Абсолютное значение коэффициента = ∞ или неопределенный: абсолютно эластичный.

Примечание. Это значения эластичности для всех типов эластичности.
Формулы процентного изменения коэффициента эластичности: Метод конечной точки
Метод конечной точки для расчета процентного изменения является самым простым и прямым. Кроме того, это (пока что) все, что нужно для расчета коэффициентов на опубликованных экзаменах по микроэкономике Advanced Placement Exams. Проблема с этим методом заключается в том, что он не так точен, как формула средней точки, и направление изменения может вызвать у вас проблемы.
Формула конечной точки для %∆ Пример: если количество увеличится со 100 до 150, это будет увеличение на 50 %, поскольку (150 – 100)/100 x 100 = 50 %. Но если вы пойдете в обратном направлении (от 150 до 100), вы получите изменение на 33 ⅓.%. Эта разница будет означать, что вы получите 2 разных коэффициента в зависимости от того, какое число вы считаете новым и старым. Хитрость заключается в том, чтобы следовать направлению вопроса. Таким образом, если количество увеличится со 100 до 150 при снижении цены со 100 до 75 долларов, процентное изменение количества составит 50%, а процентное изменение цены составит -25%. И %∆Q/%∆P=50%/-25%=-2, поэтому эта кривая спроса эластична по цене.
Таким образом, если количество увеличится со 100 до 150 при снижении цены со 100 до 75 долларов, процентное изменение количества составит 50%, а процентное изменение цены составит -25%. И %∆Q/%∆P=50%/-25%=-2, поэтому эта кривая спроса эластична по цене.
Формулы процентного изменения коэффициента эластичности: Метод средней точки
Метод средней точки расчета процентного изменения устраняет проблемы направленности, связанные с вычислением процентного изменения. Это связано с тем, что для расчета процентного изменения требуется средняя средняя точка между новой и старой ценой/количеством.
Недостатком этого метода является то, что экзамен AP по микроэкономике не позволяет учащимся использовать калькуляторы, а математические расчеты с помощью этого метода часто более сложны. Какой метод вы предпочитаете, действительно зависит от вас. Но выбирайте с умом.
Формула средней точки для %∆Ценовая эластичность
Как упоминалось выше, %∆Q/%∆P даст вам коэффициент ценовой эластичности. Кривые спроса имеют отрицательный коэффициент ценовой эластичности из-за обратной зависимости кривой спроса между ценой и количеством. Кривые предложения имеют положительный коэффициент ценовой эластичности из-за прямой зависимости между ценой и количеством. Эластичность спроса по цене определяется количеством заменителей, тем, насколько необходим товар и какой частью дохода потребителя требуется оплатить этот товар. Эластичность предложения по цене определяется ценами на альтернативные ресурсы, наличием ресурсов, временем, необходимым для производства продукта, и т. д.
Кривые спроса имеют отрицательный коэффициент ценовой эластичности из-за обратной зависимости кривой спроса между ценой и количеством. Кривые предложения имеют положительный коэффициент ценовой эластичности из-за прямой зависимости между ценой и количеством. Эластичность спроса по цене определяется количеством заменителей, тем, насколько необходим товар и какой частью дохода потребителя требуется оплатить этот товар. Эластичность предложения по цене определяется ценами на альтернативные ресурсы, наличием ресурсов, временем, необходимым для производства продукта, и т. д.
Эластичность по доходу
Эластичность по доходу показывает, насколько изменение дохода потребителя вызывает изменение величины спроса. Нормальные товары (большинство товаров попадают в эту категорию) — это товары, которые потребители покупают больше, когда их доходы растут, и меньше, когда их доходы падают. Товары низшего качества — это такие товары, как однослойная туалетная бумага, рамен высшего качества или непатентованные брендовые продукты. Когда доходы потребителей растут, потребители покупают меньше этих товаров, а когда доходы падают, они покупают больше.
Когда доходы потребителей растут, потребители покупают меньше этих товаров, а когда доходы падают, они покупают больше.
Одним из неценовых определяющих факторов спроса является изменение дохода. Эластичность дохода говорит нам, насколько изменение дохода изменит спрос на товар или услугу. Формула эластичности дохода: %∆Q/%∆Income. Нормальные товары имеют положительный коэффициент эластичности по доходу, поскольку увеличение доходов вызывает увеличение спроса на нормальные товары. Некачественные товары имеют отрицательный коэффициент эластичности по доходу. Это связано с тем, что рост доходов вызывает снижение спроса на товары низшего качества.
Перекрестная эластичность
Перекрестная ценовая эластичность связана с заменителями и дополнениями. Заменители — это товары, которые можно использовать вместо друг друга; как масло и маргарин, или варенье и желе. Когда цена одного увеличивается, спрос на другой также увеличивается. Дополнения — это товары, которые используются вместе; как хлеб с маслом или зубные щетки и зубная паста.


 2
2 Если предоставить систему самой себе, то в ней возникнут свободные крутильные колебания: потенциальная энергия спиральной пружины будет переходить в кинетическую энергию диска и наоборот. В реальных условиях под действием моментов сил трения в подшипниках и сопротивления воздуха диск совершает затухающие колебания. При слабом затухании в пределах одного периода потерями механической энергии можно пренебречь, ввиду их малости, а закон сохранения механической энергии имеет вид
Если предоставить систему самой себе, то в ней возникнут свободные крутильные колебания: потенциальная энергия спиральной пружины будет переходить в кинетическую энергию диска и наоборот. В реальных условиях под действием моментов сил трения в подшипниках и сопротивления воздуха диск совершает затухающие колебания. При слабом затухании в пределах одного периода потерями механической энергии можно пренебречь, ввиду их малости, а закон сохранения механической энергии имеет вид (5)
(5)
 Построить график зависимос-ти момента силы спиральной пружины от угла ее закручи-вания. Из графика (рис.3) находим тангенс угла наклона, численное значение которого равно угловому коэффициенту упругости пружины.
Построить график зависимос-ти момента силы спиральной пружины от угла ее закручи-вания. Из графика (рис.3) находим тангенс угла наклона, численное значение которого равно угловому коэффициенту упругости пружины.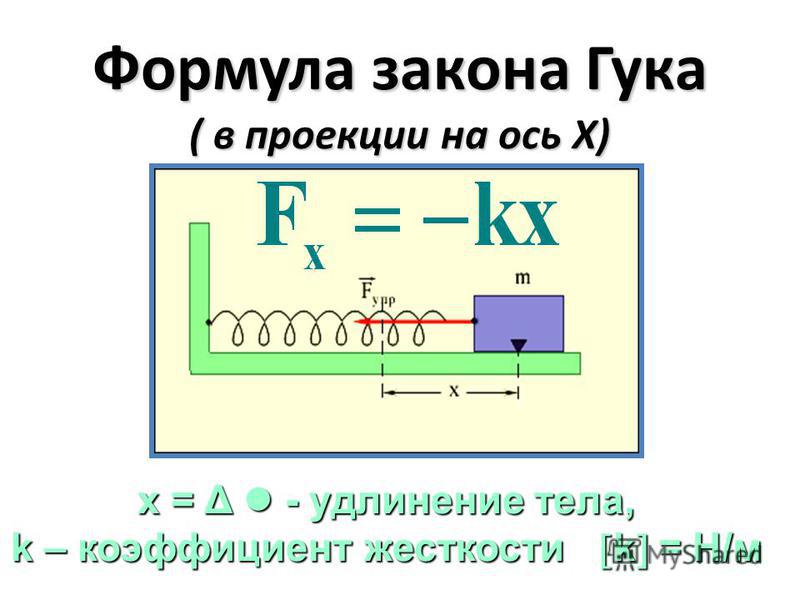

 Это скорость изменения объема спроса в ответ на изменение цены товара на 1%.
Это скорость изменения объема спроса в ответ на изменение цены товара на 1%.