Коэффициент упругости пружины: Коэффициент упругости | это… Что такое Коэффициент упругости?

alexxlab | 01.04.2023 | 0 | Разное

PhysBook:Электронный учебник физики — PhysBook

Содержание

• 1 Учебники
• 2 Механика
  • 2.1 Кинематика
  • 2.2 Динамика
  • 2.3 Законы сохранения
  • 2.4 Статика
  • 2.5 Механические колебания и волны
• 3 Термодинамика и МКТ
  • 3.1 МКТ
  • 3. 2 Термодинамика
• 4 Электродинамика
  • 4.1 Электростатика
  • 4.2 Электрический ток
  • 4.3 Магнетизм
  • 4.4 Электромагнитные колебания и волны
• 5 Оптика. СТО
  • 5.1 Геометрическая оптика
  • 5.2 Волновая оптика
  • 5. 3 Фотометрия
  • 5.4 Квантовая оптика
  • 5.5 Излучение и спектры
  • 5.6 СТО
• 6 Атомная и ядерная
  • 6.1 Атомная физика. Квантовая теория
  • 6.2 Ядерная физика
• 7 Общие темы
• 8 Новые страницы

Здесь размещена информация по школьной физике:

1. материалы из учебников, лекций, рефератов, журналов;
2. разработки уроков, тем;
3. flash-анимации, фотографии, рисунки различных физических процессов;
4. ссылки на другие сайты

и многое другое.

Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.

Учебники

Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –

Механика

Кинематика

Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве

Динамика

Законы Ньютона – Силы в механике – Движение под действием нескольких сил

Законы сохранения

Закон сохранения импульса – Закон сохранения энергии

Статика

Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика

Механические колебания и волны

Механические колебания – Механические волны

---

Термодинамика и МКТ

МКТ

Основы МКТ – Газовые законы – МКТ идеального газа

Термодинамика

Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение

---

Электродинамика

Электростатика

Электрическое поле и его параметры – Электроемкость

Электрический ток

Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках

Магнетизм

Магнитное поле – Электромагнитная индукция

Электромагнитные колебания и волны

Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны

---

Оптика.

СТО

Геометрическая оптика

Прямолинейное распространение света. Отражение света – Преломление света – Линзы

Волновая оптика

Свет как электромагнитная волна – Интерференция света – Дифракция света

Фотометрия

Фотометрия

Квантовая оптика

Квантовая оптика

Излучение и спектры

Излучение и спектры

СТО

СТО

---

Атомная и ядерная

Атомная физика. Квантовая теория

Строение атома – Квантовая теория – Излучение атома

Ядерная физика

Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы

---

Общие темы

Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ – Репетитор по физике

Новые страницы

Запрос не дал результатов.

LAB10

Лабораторная работа № 10

Изучение упругих свойств пружины

Цель работы: изучение упругих свойств пружины, изготовленной из проволоки круглого сечения; определение двумя методами коэффициента жесткости пружины и расчет модуля сдвига материала проволоки.

Оборудование: установка, пружина, платформа с грузами, ручной секундомер, штангенциркуль, микрометр.

Продолжительность работы – 4 часа.

Рассмотрим спиральную пружину, один конец которой закреплен, а к другому подвешен груз массой Под действием силы тяжести груза пружина растягивается на некоторую величину При этом возникает сила упругости пружины , которая согласно закону Гука пропорциональна удлинению пружины:

(1)

Коэффициент пропорциональности называется коэффициентом жесткости пружины.

Если груз находится в равновесии, то сила тяжести груза уравновешивается силой упругости пружины (пружину считаем невесомой). Из условия равновесия груза следует, что

(2)

Выражение (2) можно использовать для определения коэффициента жесткости пружины. Такой метод определения называется статическим.

Если груз вывести из состояния равновесия и затем отпустить, то он начнет совершать колебания в вертикальном направлении. При малых отклонениях груза от положения равновесия колебания будут гармоническими. Период таких колебаний определяется выражением

(3)

Измерив период колебаний груза известной массы, с помощью формулы (3) можно определить коэффициент жесткости пружины. Этот метод определения называется

динамическим.

Зная коэффициент жесткости пружины, ее радиус , число витков пружины и радиус проволоки можно рассчитать модуль сдвига материала проволоки из которой изготовлена пружина:

(4)

Вывод формулы (4) приведен в приложении.

Экспериментальная часть

Упражнение 1. Определение коэффициента жесткости пружины статическим методом.

Подвесьте к пружине пустую платформу. По линейке определите координату нижнего края платформы. Помещая на платформу грузы разной массы определите с помощью линейки удлинения пружиныи постройте график зависимости от (согласно выражению (2) эта зависимость должна быть линейной). По угловому коэффициенту прямой рассчитайте коэффициент жесткости пружины.

Упражнение 2. Определение коэффициента жесткости пружины динамическим методом.

Подвесьте к пружине пустую платформу известной массы; измерьте с помощью секундомера время, за которое она совершают 50 колебаний; рассчитайте период этих колебаний. Нагружая платформу грузами, повторите измерения.

Постройте график зависимости от массы грузиков (зависимость, как следует из формулы (3), должна быть линейной). Определите угловой коэффициент и рассчитайте коэффициент жесткости пружины.

Применив выражение (4), определите модуль сдвига материала проволоки, из которой изготовлена пружина.

Литература

1. Сивухин Д.В. Общий курс физики. – М.: Наука, 1979. – Т. 1. -§§ 39, 40, 78, 79.

2. Савельев И.В. Курс физики. – М.: Наука, 1989. – Т. 1. – § 13.

3. Савельев И.В. Курс общей физики. – М.: Астрель, 2001. – Т. 1. -§§ 2.9, 8.1, 8.4.

4. Иродов И.Е. Механика. Основные законы. – М.: Физматлит,

2001. – § 6.1.

Приложение

Вывод зависимости коэффициента жесткости пружины от ее параметров

Рассмотрим спиральную пружину, изготовленную из проволоки круглого сечения, растянутую силой действующей вдоль ее оси (рис.П1). Шаг пружины будем считать малым по сравнению с ее радиусом.

Мысленно разрежем проволоку пружины в произвольной точке А.

Пусть – сила, с которой верхняя часть пружины действует на нижнюю в месте разреза. Для равновесия нижней части пружины необходимо, чтобы силы ибыли равны по величине (пружину считаем невесомой).

Силы и образуют пару сил, а момент пары сил не зависит от точки, относительно которой он вычисляется. Относительно точки модуль момента этих сил равен

(П1)

Рис.П1. Возникновение кру- Из-за малости шага витков пружины можно тящего момента проволоки считать, что момент в точке направ-

при растяжении пружины лен вдоль оси проволоки. Для сохранения

рассматриваемой части пружины в равновесии необходимо, чтобы возникало кручение проволоки вокруг ее оси, компенсирующее момент Так как растягивающая сила действует вдоль оси пружины, величина момента не меняется вдоль проволоки. Поэтому кручение проволоки является равномерным.

Установим связь между растяжением пружины и полным углом закручивания проволоки.

Мысленно разрежем пружину вертикальной плоскостью, проходящей через ее ось (рис. П2,а). Теперь каждый из участков пружи-

Рис.П2. Разрез пружины: а – в нерастянутом состоянии;

б – в растянутом состоянии

ны, прилегающих к местам разреза (на рисунке – темные точки), закрутим на малый угол (остальные участки пока будем считать недеформированными). Так как на каждый виток пружины приходится по два таких участка (рис.П2,б), то суммарный угол закручивания проволоки будет определяться следующим образом:

, (П2)

где- число витков пружины.

При таком закручивании длина пружины увеличивается на величину

, ( П3)

где – изменение шага пружины, равное (см. рис.П2,б)

(П4)

Из выражений (П2) – (П4) получим зависимость между удлинением пружины и углом закручивания проволоки:

.

Повторив эти рассуждения для других участков пружины и просуммировав удлинения, найдем, что растяжение пружины и полный угол закручивания проволоки связаны следующим соотношением:

. (П5)

Определим, как угол закручивания связан с растягивающей силой Для этого выделим из проволоки цилиндрическую трубку радиусом длиной и толщиной Вырежем из трубки малый элемент, площадь верхней грани которого, определяемая углом , равна (рис.П3,а).

Рис.П3. Положение элемента проволоки до закручивания (а)

и после закручивания (б)

Повернем верхнее основание трубки относительно нижнего на малый угол . При этом боковые грани элемента, лежащие в сечении трубки, повернутся на малый угол (рис.П3,б).

Углы и малы, поэтому нетрудно найти связь между ними:

(П6)

В результате закручивания трубки элемент будет испытывать деформацию сдвига.

Закон Гука для деформации сдвига (где – касательное напряжение) можно записать в виде

, (П7)

где – касательная сила, возникающая при сдвиге и стремящаяся вернуть элемент в исходное положение; – площадь верхней грани элемента; – модуль сдвига.

Подставив соотношение (П6) в выражение (П7) и приняв во внимание, что , для силы получим:

.

Момент этой силы относительно оси трубки равен

.

Просуммировав моменты касательных сил по верхнему основанию рассматриваемой трубки (т.е. проинтегрировав по углу ) и по радиусу проволоки (т.е. проинтегрировав по ), найдем результирующий момент всех касательных сил, действующих в сечении проволоки:

.

При равновесии пружины этот момент равен моменту силы, растягивающей пружину, определяемому выражением (П1)

. (П8)

Производная представляет собой угол закручивания, приходящийся на единицу длины проволоки. Согласно выражению (П8) величина постоянна и, следовательно, равна

, (П9)

где – длина проволоки; – полный угол закручивания проволоки (см. формулу (П5)).

С учетом соотношения (П9) выражение (П8) можно переписать в виде

,

где – коэффициент жесткости пружины.

Из последнего уравнения следует выражение (4) для модуля сдвига проволоки, используемое в работе.

74

Аналитическая модель для точной калибровки жесткости прямоугольных кантилеверов атомно-силового микроскопа

Калибровка жесткости прямоугольных кантилеверов атомно-силового микроскопа (АСМ) имеет фундаментальное значение при измерении сил пико/нано-ньютоновского масштаба с помощью АСМ с приложениями к многие новые технологии, такие как атомные манипуляции ¹ , визуализация молекул с атомарным разрешением ² , характеристика сложных механических свойств ³ и измерение одной неровности ⁴ . Однако номинальные постоянные пружины часто неточны, и производители могут предложить только широкий диапазон их значений ⁵ . Хотя измерение жесткости пружины не является простой задачей, было разработано несколько широко используемых методов статической или динамической экспериментальной калибровки, таких как метод подвешивания статической массы ⁶ , метод эталонного кантилевера/пружины ^7,8,9 , динамическое крепление массы метод ¹⁰ , метод резонансной частоты ¹¹ и метод теплового шума ¹² . Совсем недавно были предложены некоторые варианты вышеупомянутых методов калибровки, такие как метод Сэдера для кантилеверов с модифицированной поверхностью ¹³ , метод прямого теплового шума для кантилеверов с коллоидным зондом ¹⁴ , метод на основе калибровочных структур ¹⁵ и микроканальный метод. вспомогательный метод ¹⁶ . Некоторые тесно связанные темы также привлекают внимание, например эластичность с наноразмерным разрешением ¹⁷ и влияние поверхностного напряжения на жесткость микро/нано кантилевера ¹⁸ , что помогает лучше понять интерпретацию измерений. Следует отметить, что широко используется метод теоретических размеров ¹⁹ , который основан на теории балок или основан на теории пластин с приближенными или численными решениями ^20,21 .

Согласно размерному методу уравнение жесткости пружины прямоугольного кантилевера, основанное на теории балок, составляет ¹⁹

где E — модуль Юнга материала, , а t — ширина, длина и толщина кантилевера соответственно. Хорошо известно, что уравнение (1) не учитывает изгиб кантилевера по ширине, поэтому применимо только к кантилеверам с  << b . Для относительно широких консолей для получения более точных результатов следует использовать теорию пластин вместо теории балок. Однако получить точное аналитическое решение основного уравнения прямоугольной консольной пластины было чрезвычайно сложно из-за сложности математической модели. Соответственно, необходимо было разработать приблизительные/численные решения для калибровки параметров пружины АСМ в каждом конкретном случае. Очевидно, что аналитические решения необходимы для улавливания сути проблемы путем количественной реализации связи между ключевыми параметрами/величинами, что не может быть реализовано приближенным/численным решением.

В соответствии с классической теорией тонкой пластины Кирхгофа ²² основное уравнение для статической задачи тонкой пластины имеет вид

где обозначают координаты в плоскости, где лежит пластина, – поперечное отклонение средней плоскости пластины , – распределенная поперечная нагрузка, – изгибная жесткость плиты, в которой – коэффициент Пуассона. Используя классические методы, аналитическое решение уравнения (2) может быть получено только для прямоугольной пластины, у которой хотя бы пара противоположных ребер свободно оперты. Для прямоугольного кантилевера АСМ, который моделируется как пластина с одним защемленным краем и тремя свободными краями, т.е. консольной пластины, точное аналитическое моделирование было недоступно. Острая необходимость решения этого вопроса мотивирует настоящую работу.

Мы исследуем механическое поведение прямоугольного кантилевера АСМ путем построения вариационного принципа Гамильтона на основе исходного вариационного принципа Хеллингера-Рейсснера для задачи изгиба тонкой пластины. Соответствующее управляющее матричное уравнение на основе гамильтоновой системы выводится (подробности см. в дополнительной информации) как

здесь , , в котором , и ; , противоположна эквивалентной поперечной силе и является изгибающим моментом. Соблюдая , где – симплектическая матрица, в которой – единичная матрица, является гамильтоновой операторной матрицей ²³ Таким образом, уравнение (3) представляет собой управляющее уравнение на основе системы Гамильтона для изгиба тонкой пластины.

Мы разрабатываем современный метод суперпозиции ²⁴ , чтобы предложить рациональный способ точного получения аналитического решения прямоугольного кантилевера АСМ с длиной и шириной под точечной нагрузкой P при , как показано на рис. 1. Получено решение нормированного прогиба в точке нагрузки и обозначено безразмерной функцией , которая явно представлена ​​как

Рисунок 1

Теоретическая модель прямоугольного кантилевера АСМ под действием точечной нагрузки.

Изображение в натуральную величину

где и , в котором расстояние точки нагрузки от конца свободного конца и может принимать значения от 0 до b . Нормированные константы , , и определяются уравнениями (S22)-(S26) дополнительной информации.

Таким образом, мы находим закон масштабирования при определении жесткости пружины :

Уравнение (5) ясно показывает, что константа пружины , нормированная на , зависит только от коэффициента Пуассона , нормированного размера и нормированной координаты нагрузки . Чтобы проиллюстрировать эту зависимость, для прямоугольного кантилевера с торцевой нагрузкой (т.е.) построен график зависимости и для различных и соответственно, как показано на рис. 2а, б. 9Рисунок 2

Полноразмерное изображение

Наш вывод должен быть подтвержден общепринятым методом конечных элементов (МКЭ). Нормированные прогибы в точке нагрузки приведены в таблице 1 для прямоугольной консоли с соотношением сторон   1/5, 2/9, 1/4, 2/7, 1/3, 2/5, 1/2, 2/3. , 1 и 2 соответственно, а коэффициент Пуассона  0, 0,25 и 0,4 соответственно. Показано сравнение с МКЭ от пакета программ ABAQUS, где используется 4-узловой элемент оболочки общего назначения S4R и равномерная сетка с шагом сетки. Количество членов для решения настоящего ряда выбирается таким, чтобы результаты сходились до последней значащей цифры из четырех. Из таблицы 1 видно, что наши аналитические решения полностью согласуются с решениями FEM, которые считаются эталонными ввиду отсутствия сопоставимых аналитических решений, а наши результаты, основанные на теории пластин, дают очевидное улучшение точности по сравнению с балочной теорией ²⁵ . Следует отметить, что приближенные методы должны были быть разработаны в прошлом, когда был необходим теоретический анализ ²⁰ , который, однако, не может дать столь точных результатов, как представлено здесь. Следует отметить, что случай с в табл. 1 редко встречается на практике, но мы все же приводим результаты, чтобы продемонстрировать лучшую точность, а также более широкую применимость теории пластин, которая лучше описывает поведение консолей при любых масштабах, то есть в масштабах, которые не ограничиваются только кантилеверами АСМ. Вариации ошибок теории луча с и для различных и соответственно показаны на рис. 3а,б, чтобы можно было быстро оценить, какие ситуации могут привести к значительной коррекции. Интересно отметить, что как в Таблице 1, так и на Рисунке 3 очень малы ошибки для кантилеверов с относительно более низким значением . Чтобы объяснить это наблюдение, а также механизм повышения точности нашей модели, мы хотели бы подробнее объяснить разницу между двумя теориями. С физической точки зрения для кантилевера, изображенного на рис. 1, балочная теория фактически описывает такую ​​консольную пластину с нулевым коэффициентом Пуассона: вдоль нее приложена равномерно распределенная линейная нагрузка с интенсивностью направлении, в то время как вращение вокруг оси не допускается для ребер и . Это можно было бы строго доказать с математической точки зрения. Аналитическое решение нормированного прогиба в точке нагрузки для такой конкретной пластины получается путем решения основного уравнения , с наложенными граничными условиями и , где – дельта-функция Дирака; таким образом, мы можем получить

Таблица 1 Нормированные точечные прогибы прямоугольного кантилевера с точечной нагрузкой P , приложенной к концевому наконечнику (a/2,0).

Полноразмерная таблица

Рис. 3

( a ) Относительная погрешность балочной теории по сравнению с другими и (b) погрешность по сравнению с другими для прямоугольного кантилевера, нагруженного на конце.

Полноразмерное изображение

, которое сводится к решению балочной модели. Таким образом, по сравнению с трехмерной моделью теории пластин, учитывающей эффект Пуассона, балочная теория дает гораздо более упрощенную плоскую модель и игнорирует эффект Пуассона, который численно выявляется в табл. 1 независимостью балочной теории: на основании результатов по тому же . Способность теории пластин отображать распределение полей механических величин по кантилеверу ясно отражена на рис. 4а по сравнению с теорией балок на рис. 4б. Кроме того, как из таблицы 1, так и из рис. 3b видно, что теория пластин предсказывает либо увеличение, либо уменьшение жесткости пружины по сравнению с теорией балок, но на самом деле следует сделать важный вывод о том, что теория пластин всегда предсказывает уменьшение жесткости пружины по балочной теории при коэффициенте Пуассона. Это можно объяснить простым выводом. Как показано на рис. 5, для кантилевера с модель пластины под точечной нагрузкой P на центральной линии (рис. 5а) дает меньшую упругую жесткость, чем та же пластина при равномерно распределенной линейной нагрузке с интенсивностью (рис. 5б), так как прежний прогиб в точке нагрузки заведомо больше, чем последний в том же месте. С другой стороны, эта последняя модель (рис. 5b) дает более низкую жесткость пружины, чем та же модель, плюс ограничение, запрещающее вращение вокруг двух боковых краев (рис. 5c), потому что добавление ограничения повысит жесткость. Мы показали, что модель пластины на рис. 5в аналогична модели балки при той же точечной нагрузке P как на рис. 5а (см. рис. 5г). Поэтому, если константы пружины на рис. 5a–d обозначить , , и , соответственно, мы заключаем, что . Рис. следует из теории пластин. (b) Результаты теории пучков.

Полноразмерное изображение

Рисунок 5

Схематическая диаграмма для сравнения жесткости пружины между теорией пластины и теорией балки для кантилевера с v  = 0,

(a) Модель пластины под точечной нагрузкой P . (б) Модель пластины под действием равномерно распределенной линейной нагрузки интенсивностью . (c) Модель пластины со связями при той же нагрузке, что и в (b) . (d) Модель балки при той же точечной нагрузке P, что и в (а) .

Изображение полного размера

Мы используем разработанные решения для калибровки жесткости пружины для реальных кантилеверов. Три комплекта прямоугольных кантилеверов с торцевой нагрузкой, изготовленных из плексигласа ²¹ (ПММА, модуль Юнга   3 ГПа, коэффициент Пуассона   0,35), длиной 20 см, толщиной  3 мм и шириной  9,31, 6,53 и 3,29 см соответственно. , которые считаются. Как показано в Таблице 2, нормированные пружинные константы настоящего аналитического решения очень хорошо согласуются с численными результатами из ссылки. 21. Мы также рассмотрели несколько коммерческих прямоугольных кантилеверов АСМ в таблице 3 с   169ГПа и   0,408 ²⁶ , из которых размеры , и указаны в таблице. Мы подчеркиваем, что с помощью настоящей модели может быть достигнуто значительное улучшение точности (например, 5,7%), даже если кантилеверы имеют тенденцию к < .

Таблица 2 Нормированные жесткости нескольких прямоугольных кантилеверов с торцевой нагрузкой, изготовленных из плексигласа.

Полноразмерный стол

Таблица 3. Жесткость некоторых коммерческих прямоугольных кантилеверов на концах.

Полноразмерный стол

В заключение мы рассмотрели аналитический подход к точной калибровке жесткости прямоугольных кантилеверов АСМ на основе теории тонких пластин, что подтверждает важность трехмерного эффекта, а также эффекта Пуассона. Полученные решения устраняют ошибки классической балочной теории и справедливы для прямоугольных консолей с любым соотношением сторон. Деформация кантилевера АСМ включает семь величин нагрузки, материала и геометрии: точечная нагрузка, коэффициент Пуассона, модуль Юнга, длина, ширина, толщина и положение нагрузки. Закон масштабирования в уравнении (5), подтвержденный МКЭ, показывает, что нормированная жесткость пружины зависит только от трех нормированных величин, т. е. , и . Этот закон масштабирования может служить теоретической основой для аналитической калибровки пружинных констант прямоугольных кантилеверов АСМ. Следует отметить, что в некоторых приложениях кантилеверы АСМ покрываются трехмерными слоями, и влияние этих слоев на калибровку жесткости пружины не является незначительным. Это особенно важно для приложений, требующих одновременного сбора токов, таких как проводящий AFM 9.0003 27,28,29 . Одной из возможных простых обработок является использование эквивалентной жесткости, которая соответствующим образом учитывает влияние слоев ³⁰ . Наша текущая работа заключается в том, чтобы получить достаточно точную эквивалентную жесткость, чтобы настоящая модель также была применима к кантилеверам со слоями.

Видео с вопросами: определение жесткости пружины с помощью графика

Стенограмма видео

На графике показана длина пружина при изменении приложенной к ней силы. Какова жесткость пружины?

Итак, как мы видим здесь, в на графике нам дана длина струны по горизонтальной оси и усилие, приложенное к пружине по вертикальной оси. Теперь мы ясно видим, что когда к пружине не приложено усилие — нулевое усилие, длина пружины 0,5 метров. Поэтому вот какая весна выглядит так, как если бы к нему не прикладывались никакие силы.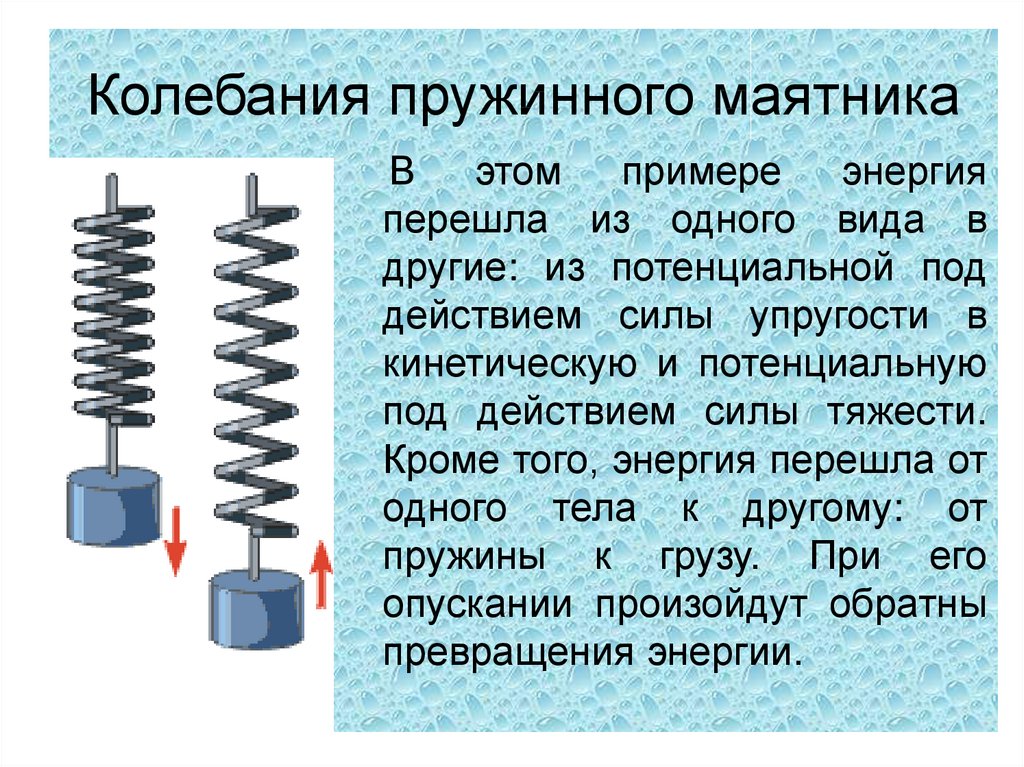

Вот пружина и ее длина составляет 0,5 метра. Теперь, впоследствии, сила применительно к весенним увеличениям. И мы можем видеть это как силу применяется увеличивается, так же как и длина пружины. Другими словами, мы прикладываем силу к пружина — скажем, на правом конце пружины — и мы называем эту силу 𝐹.

Теперь из-за этого длина пружина увеличивается. Итак, теперь общая длина весна отсюда сюда. Теперь, если нас попросят найти упругая постоянная пружины, то надо вспомнить закон Гука.

Закон Гука говорит нам, что сила применительно к пружине 𝐹 равна жесткости пружины 𝑘, умноженной на удлинением пружины 𝑥. Теперь обратите внимание, что мы говорим о расширение пружины, а не длина пружины. Другими словами, когда сила 𝐹 к пружине приложена эта сила, прямо пропорциональная расширение; вот эта длина. Итак, давайте назовем эту длину 𝑥.

Сила не напрямую пропорциональна всей длине пружины, которую мы будем называть 𝐿. Но поскольку нам дали длину пружины по горизонтальной оси, нам нужно найти зависимость между длина пружины и расширение, чтобы мы могли выработать пружину постоянный.

Мы делаем это, говоря, что общая длина пружины — здесь все это расстояние — равна 0,5 — т. е. естественная длина пружины, когда на нее не действует сила — плюс 𝑥, расширение. И поэтому мы можем сказать, что 𝐿 равно до 𝑥 плюс 0,5 метра или, если мы переставим это, 𝑥 равно 𝐿 минус 0,5 метров.

Это означает, что для любой точки на график, теперь мы можем вычислить силу, действующую на пружину, которую мы можем просто считывайте, перемещая влево по вертикальной оси. И мы можем разработать расширение весны.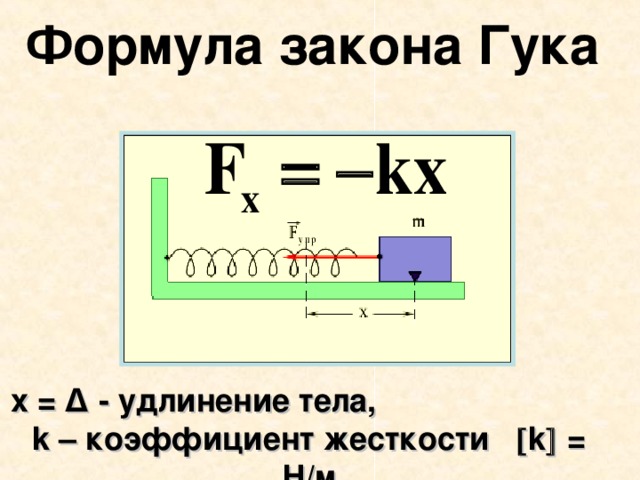 Так как мы знаем длину пружина в этой точке, и если мы отнимем от нее 0,5 метра, то мы будем иметь расширение.

Итак, давайте просто выберем любую случайную точку и измените закон Гука, чтобы определить постоянную пружины. Мы собираемся разделить обе стороны уравнение на 𝑥, расширение, так что расширение сокращается на Правая сторона. То, что у нас осталось, это то, что жесткость пружины 𝑘 равна приложенной силе 𝐹, деленной на удлинение 𝑥.

А теперь предположим, что мы учитывая этот момент здесь. Ну, мы видим, что сила применяемая в этой точке, если мы идем влево по вертикальной оси, составляет 200 ньютонов. Таким образом, мы можем сказать, что когда сила 𝐹 составляет 200 ньютонов, длина пружины 𝐿 составит 3,0 метра, что то, что мы записываем здесь. Но тогда мы можем использовать это уравнение чтобы дать нам расширение весны.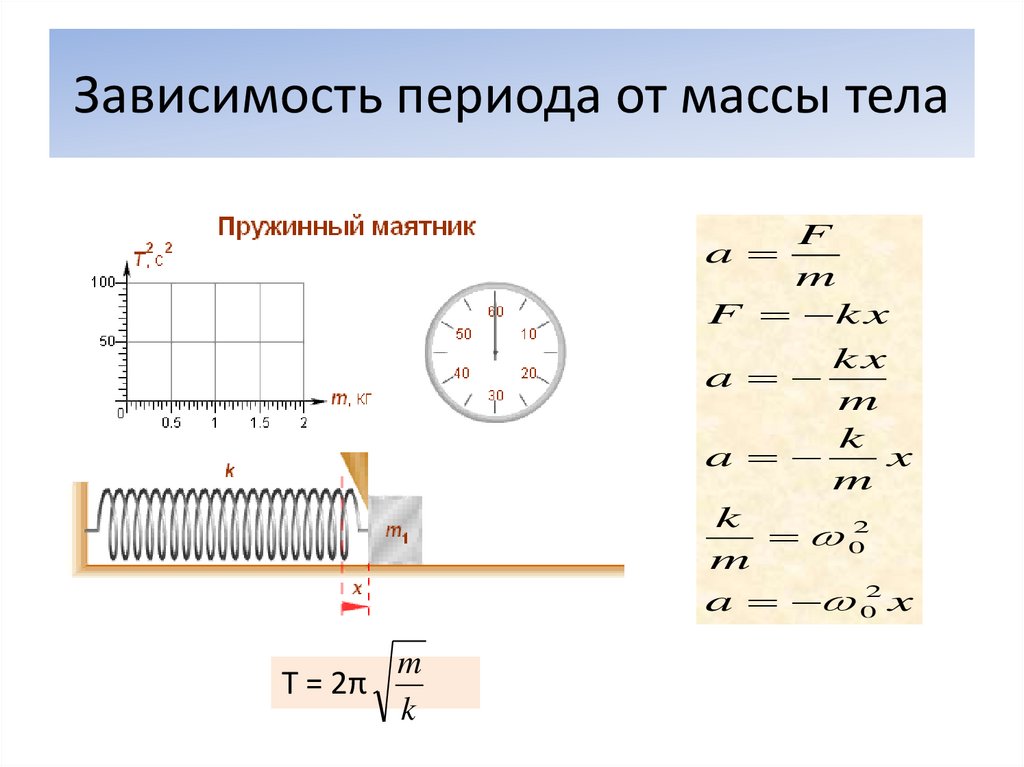

По сути, вычитаем 0,5 метра от длины 𝐿. И поэтому мы говорим, что 𝑥, удлинение, равное 3,0 метра, длина, минус 0,5 метра, естественная длина весны. И когда мы оцениваем это, мы находим что расширение 2,5 метра.

Итак, мы применили силу к пружине в одной точке графика и удлинению пружины в той же точка. Поэтому мы можем заменить в значения, чтобы найти значение 𝑘. Теперь обратите внимание, что мы в основном нужно найти градиент этой линии наилучшего соответствия, потому что то, что мы делаем здесь говорит, что 𝑘 равно силе, приложенной к пружине, равной 200 ньютоны. Но это также эквивалентно 200 минус ноль ньютонов. И мы делим это на 3,0 — это длина пружины – минус 0,5 – это естественная длина пружины весна.

Так совпало, сделав это вычисления, мы на самом деле находим градиент линии наилучшего соответствия.