Коэффициент жесткости в чем измеряется: Жесткость пружины, теория и онлайн калькуляторы
alexxlab | 08.04.1986 | 0 | Разное
области применения, формула расчета и единицы измерения
Самым важным показателем, определяющим упругость металлических изделий, предназначенных для различного пользования, считается коэффициент пружинной жесткости. Он определяет устойчивость пружинного механизма к различным трансформациям и воздействиям с другими элементами. Также важно сопротивление пружины при ее взаимодействии с различными телами. Как правило, коэффициент жесткости равняется силе сопротивления.
Содержание:
- Применение и разновидности пружин
- Единицы измерения коэффициента
- Определение жесткости пружины
- Видео
Применение и разновидности пружин
Пружина является упругим изделием, что обеспечивает трансформацию нарастающих двигательных импульсов к приборным и механизменным составляющим собственного звена. Встречается устройство во многих изделиях как в бытовых приборах, так и в производственных элементах. А степень надежности работы механизмов на производстве зависит от коэффициента пружинной жесткости. Эту величину следует соизмерять с усилием, приложенным к пружине, что определяет ее сжатие или растяжение. Пружинное вытяжение зависит от свойств металла, который ее составляет, а не от коэффициента упругости.
Эту величину следует соизмерять с усилием, приложенным к пружине, что определяет ее сжатие или растяжение. Пружинное вытяжение зависит от свойств металла, который ее составляет, а не от коэффициента упругости.
Пружинный элемент имеет разнообразные структуры. Все зависит от того, для чего он предназначен. По деформационным особенностям и структурным характеристикам пружина бывает:
- спиральной;
- канонической;
- цилиндрической.
Коэффициентный показатель жесткости определенного элемента зависит от способа деформационной передачи. Параметры деформации подразделяют все механизмы на такие:
- ввинчивающиеся;
- крутящиеся;
- изогнутые;
- растягивающиеся.
При одновременном применении нескольких пружинных механизмов в одном изделии жесткостный показатель будет обусловлен крепежным элементом. Если все соединено параллельным креплением, то показатель будет расти, а последовательное крепление предусматривает уменьшение.
Единицы измерения коэффициента
Показатель жесткости изделия является важной величиной, который имеет свойства определять срок изнашиваемости механизма. Рассчитать требуемый коэффициент можно по такой формуле:
С = (d * G) : ( n * 8 * D³ ср ), где:
- С — коэффициент жесткости;
- d — пружинный диаметр;
- G — модуль сдвига пружины;
- n — количество витков;
- D ср — сила упругости.
Расчет коэффициентного показателя может быть произведен и в электронном вычислении. Для этого применяется калькулятор пружинных расчетов. При этом стоит учитывать, что эксплуатационные характеристики пружинного механизма будут зависеть от качества сборки изделия и от материала, который использовался в производстве прибора.
Коэффициент жесткости в физике зачастую именуют коэффициентом упругости или Гука. Все эти величины отвечают за жесткость пружины. Это механический показатель, применяемый для определения твердых величин. Коэффициент упругости равняется силовому полю, приложенному к пружинному механизму для изменения длины на определенном расстоянии.
Все эти величины отвечают за жесткость пружины. Это механический показатель, применяемый для определения твердых величин. Коэффициент упругости равняется силовому полю, приложенному к пружинному механизму для изменения длины на определенном расстоянии.
Коэффициент Гука рассчитывается путем соотношения силы упругости к длине пружинящего механизма. Эта величина будет зависеть от качества материалов и от размерных составляющих твердого тела. Упругость пружины будет зависеть от ее длины и площади. Эти величины определяются как Модуль Юнги и зависят от составляющих и свойственных параметров материала, из которых изготовлена пружина.
Основные теории упругости – в этом видео.
Определение жесткости пружины
Как и любой другой механизм, пружина может соединяться:
- параллельным соединением;
- последовательным соединением.
Соединяясь в одно целое, несколько механизмов при деформации меняют свою жесткость. Параллельное соединение предусматривает увеличение упругости, а последовательное — уменьшение.
Параллельное соединение предусматривает увеличение упругости, а последовательное — уменьшение.
Параллельное соединение вычисляется такой формулой:
k = k 1 + k 2 + k 3 + …+ k n, где:
- k — показатель жесткости системы;
- n — соединение пружинных механизмов.
Последовательное соединение пружин рассчитывается по такой формуле:
1: k = (1: k 1 + 1: k 2 + 1: k 3 + … + 1: k n).
Кроме этого, существует множество расчетов показателей упругости при деформации, но на каждый из них приходится соответствующая формула. Все расчеты ведутся обычно в определенных программных комплексах на предприятиях, изготавливающих механизмы из пружин. Так что формулы уже запрограммированы, а для расчета вводятся только известные данные.
Итак, коэффициент жесткости пружины является постоянной величиной, которая рассчитывается для определения срока эксплуатации прибора на практике. Кроме того, определяются свойства пружинного механизма и его работы в целом, что помогает улучшить качество изготавливаемого изделия.
Видео
Из этого видео вы узнаете, как определить жесткость пружины.
формула, как найти, коэффициент, обозначение
Содержание:
-
От чего зависит жесткость
- Геометрия пружины
- Тип материала
- Коэффициент
- Срок эксплуатации
-
В чем измеряется жесткость
- Как обозначается
-
Коэффициент жесткости пружины
- Формула расчета через массу и длину
-
Как можно измерить жесткость
- Измерительные приборы
- Практическая задача
- Альтернативные способы определения жесткости
Содержание
-
От чего зависит жесткость
- Геометрия пружины
- Тип материала
- Коэффициент
- Срок эксплуатации
-
В чем измеряется жесткость
- Как обозначается
-
Коэффициент жесткости пружины
- Формула расчета через массу и длину
-
Как можно измерить жесткость
- Измерительные приборы
- Практическая задача
- Альтернативные способы определения жесткости
Определение
Жесткость — способность твёрдого тела, конструкции или её элементов сопротивляться деформации от приложенного усилия вдоль выбранного направления в заданной системе координат.
Сила жесткости — сила, возникающая в теле в результате его деформации и стремящаяся вернуть его в исходное состояние.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
От чего зависит жесткость
Жесткость пружины зависит от нескольких параметров:
- геометрии пружины;
- типа материала;
- коэффициента;
- срока эксплуатации.
Геометрия пружины
На жесткость витой пружины влияет:
- количество витков;
- их диаметр;
- диаметр проволоки.
Диаметр намотки измеряется от оси пружины. Так как длина проволоки в пружине значительно больше длины упругого стержня, сопротивляемость внешней деформации многократно возрастает.
Волновые пружины состоят из металлических лент, навитых ребром по окружности заданного диаметра.
Их основные геометрические параметры:
- количество витков;
- количество волн на виток;
- сечение ленты.
Тип материала
У каждого материала есть условный предел упругости, характеризующий его способность восстанавливаться после деформации. Если этот предел превышается, в структуре материала возникают необратимые изменения.
Определение
Предел упругости — механическая характеристика материала, показывающая максимальное напряжение, при котором имеют место только упругие, обратимые деформации.
Предел упругости измеряют в паскалях и определяют по формуле:
\(\sigma_{у\;}=\;\frac FS\)
где F — действие внешней силы на исследуемый образец, приводящее к повреждениям, а S — его площадь.
Кроме предела упругости, существуют такие характеристики упругости материалов, как модули упругости (модуль Юнга) и сдвига, коэффициент жесткости и другие.
Коэффициент
Определение
Согласно закону Гука, при малой деформации абсолютная величина силы упругости прямо пропорциональна величине деформации.
Эта линейная зависимость описывается формулой:
\(F=\;k\;\times\;x\)
где k — коэффициент жесткости, а х — величина, на которую сжалась или растянулась пружина.
Примечание
Деформация считается малой в том случае, когда изменение размеров тела значительно меньше его первоначальных размеров.
Срок эксплуатации
Нахождение под напряжением приводит к постепенной необратимой деформации, называемой ослаблением пружины.
Жесткость пружины влияет на срок ее эксплуатации, как и сила воздействия. Конструкторы пружин, предварительно рассчитав эти параметры, проводят тесты на прототипах, прежде чем начать массовое производство. В специальных установках для испытания на усталость материала их сжимают и отпускают определенное количество циклов, отдельно проверяя поведение пружин при максимальной и минимальной нагрузке.
В специальных установках для испытания на усталость материала их сжимают и отпускают определенное количество циклов, отдельно проверяя поведение пружин при максимальной и минимальной нагрузке.
В чем измеряется жесткость
Жесткость пружины в системе СИ измеряется в ньютонах на метр, Н/м. Также встречается единица измерения ньютон на миллиметр, Н/мм. Численно жесткость равна величине силы, изменяющей размер пружины на метр длины.
Как обозначается
Коэффициент жесткости пружины обозначают буквой k.
Коэффициент жесткости пружины
Определение
Коэффициент жесткости — коэффициент, связывающий в законе Гука удлинение упругого тела и возникающую вследствие этого удлинения силу жесткости.
Применяется в механике твердого тела в разделе упругости.
Формула расчета через массу и длину
Используя закон Гука, коэффициент жесткости можно вычислить по формуле:
\(k\;=\;\frac Fx\)
Чтобы выяснить силу тяжести, воздействующую на пружину, нужно воспользоваться формулой:
\(F\;=\;m\;\times\;g\)
где m — масса подвешенного на пружине тела, а g — величина свободного ускорения, равная 9,8.
Чтобы найти х, нужно дважды измерить длину пружины и вычислить разницу между этими двумя значениями.
При соединении нескольких пружин общая жесткость системы меняется. Коэффициенты каждой из пружин суммируются при параллельном соединении. При последовательном соединении общая жесткость вычисляется по формуле:
\(\frac1k\;=\;(\frac1{k_1}\;+\;\frac1{k_2}\;+\;…\;+\;\frac1{k_n})\)
Как можно измерить жесткость
Измерительные приборы
Приборы для испытания пружин на сжатие-растяжение контролируют приложенное усилие с помощью тензометрического датчика, а также изменение их длины, выводя показатели на дисплей. Без специального прибора измерить осевую жесткость можно, используя динамометр и линейку.
Существуют приборы и для измерения поперечной жесткости пружин. Для этого нужно измерить смещение нескольких точек пружины, определив расстояние и угол между ними.
Практическая задача
Самый простой способ измерить жесткость пружины — провести стандартный школьный опыт со штативом и подвешенными на пружине грузиками.
Для измерения осевой жесткости спиральной пружины используют:
- штатив, на котором закрепляют пружину;
- крючок, который крепят на свободный ее конец;
- грузики с известной массой, которые подвешивают на свободный конец пружины;
- линейку, чтобы измерить длину пружины с грузом и без груза.
Проведя несколько измерений с грузиками разной массы и вычислив силу тяжести, воздействовавшую на пружину в каждом из них, можно построить график зависимости длины пружины от приложенного усилия и узнать среднее значение коэффициента жесткости.
Альтернативные способы определения жесткости
Жесткость пружины можно определить и через период ее колебания, воспользовавшись формулой:
\(Т\;=\;2\mathrm\pi\sqrt{\frac{\mathrm m}{\mathrm k}}\)
Или через частоту колебаний по формуле:
\(\omega=\;\sqrt{\frac{\mathrm k}{\mathrm m}}\)
Проводя опыт с пружиной, закрепленной на штативе, и грузиками с известной массой, можно не измерять длину пружины, а привести ее в колебательное движение и сосчитать количество колебаний в период времени. 3\;\times\;25}\)
3\;\times\;25}\)
\(k = 100 \frac Нм\)
Жесткость при деформации кручения существенно отличается от жесткости сжатия-растяжения. Предел прочности при кручении у любого материала будет меньше, чем предел прочности при сжатии-растяжении или изгибе. Торсионная жесткость, также называемая крутильной, в системе СИ измеряется в ньютон-метрах на радиан, сокращенно Н-м/рад. Ее можно определить по формуле:
\(k\;=\;\frac M\alpha\)
где \(М\) — крутящий момент, приложенный к телу, а \(\alpha\) — угол закручивания тела по оси приложения крутящего момента.
Насколько полезной была для вас статья?
Рейтинг: 3.50 (Голосов: 4)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
Калькулятор жесткости воды – Мосводоканал
Одним из наиболее часто задаваемых вопросов жителями города Москвы является вопрос о величине жесткости питьевой воды. Это обусловлено широким распространением в быту посудомоечных и стиральных машин, для которых расчет загрузки моющих средств осуществляется исходя из фактического значения жесткости используемой воды.
Это обусловлено широким распространением в быту посудомоечных и стиральных машин, для которых расчет загрузки моющих средств осуществляется исходя из фактического значения жесткости используемой воды.
Узнать значение жесткости воды по своему адресу вы можете с помощью нашего электронного сервиса “Качество воды в районах Москвы”.
В России жесткость измеряют в “градусах жесткости”, а мировые производители используют принятые в своих странах единицы измерения. Поэтому для удобства жителей создан “Калькулятор жесткости”, с помощью которого можно перевести значения жесткости из одной системы измерения в другую, чтобы правильно настроить свою бытовую технику.
°Ж °DH °Clark °F Ppm | = | °Ж °DH °Clark °F Ppm |
Все, что вы хотели знать про жесткость московской воды
Жесткостью называют совокупность свойств воды, связанных с содержанием в ней растворённых солей, главным образом, кальция и магния, так называемых “солей жесткости”. Общая жесткость складывается из временной и постоянной. Временную жесткость можно устранить кипячением воды, что обусловлено свойством некоторых солей выпадать в осадок, образуя так называемую накипь на бытовых кухонных приборах.
Общая жесткость складывается из временной и постоянной. Временную жесткость можно устранить кипячением воды, что обусловлено свойством некоторых солей выпадать в осадок, образуя так называемую накипь на бытовых кухонных приборах.
Жесткость воды является характеристикой конкретного источника водоснабжения и не изменяется в процессе подготовки питьевой воды.
Согласно ГОСТ 31865-2012 «Вода. Единицы жесткости», единица измерения жесткости – градус жесткости (оЖ), величина которого соответствует 1 мг-экв./л. По рекомендации Всемирной организации здравоохранения человек получает магний и кальций в достаточном количестве при условии потребления воды жесткостью примерно 5ºЖ.
Московская водопроводная вода не нуждается в дополнительном умягчении, поскольку ее жесткость находится именно в этих пределах. Не стоит забывать, что магний и кальций – два необходимых элемента, поступающих в организм человека из воды.
Нормативные требования и рекомендации
Рекомендации всемирной организации здравоохранения (ВОЗ) для питьевой воды: кальций – 20-80 мг/л; магний – 10-30 мг/л. Для жесткости какой-либо рекомендуемой величины не предлагается. Московская питьевая вода по данным показателям соответствует рекомендациям ВОЗ.
Для жесткости какой-либо рекомендуемой величины не предлагается. Московская питьевая вода по данным показателям соответствует рекомендациям ВОЗ.
Российские нормативные документы (СанПиН 1.2.3685-21, СанПиН 2.1.3684-21) для питьевой воды регламентируют: кальций – норматив не установлен; магний – не более 50 мг/л; жесткость – не более 7°Ж.
Норматив физиологической полноценности бутилированной воды (СанПиН 2.1.4.1116-02): кальций – 25-130 мг/л; магний – 5-65 мг/л; жесткость – 1,5-7°Ж.
По содержанию кальция и магния бутилированная вода высшей категории ничем не лучше воды из-под крана!
В целом московская вода централизованной системы питьевого водоснабжения относится к водам средней жесткости и по фактическим значениям соответствует показателю физиологической полноценности, установленного для бутилированных вод высшей категории качества. Вода не содержит вредных для здоровья человека соединений и безопасна для потребления.
Изменяется ли жесткость воды в течение года?
Основной фактор, влияющий на величину жесткости – растворение горных пород, содержащих кальций и магний (известняки, доломиты), при прохождении через них природной воды.
Основой водоснабжения Москвы являются в поверхностные воды – водные ресурсы рек и водохранилищ. Поверхностные воды, в целом, более мягкие, чем подземные, в частности из артезианских источников.
Жесткость поверхностных вод подвержена заметным сезонным колебаниям, достигая максимума в зимний период. Во всех районах города Москвы ее минимальные и максимальные значения колеблются от 1,9 до 5-5,7 градусов жесткости в зависимости от времени года. Минимальные величины жесткости типичны для периодов половодья или паводка, когда происходит интенсивное поступление в источники водоснабжения мягких талых или дождевых вод.
Можно ли пить жесткую воду?
Не стоит забывать, что магний и кальций – два необходимых элемента для организма человека. А питьевая вода является одним из ценных источников, поскольку обусловливающие жесткость воды соли кальция и магния в значительной мере поступают в наш организм вместе с водой.
А питьевая вода является одним из ценных источников, поскольку обусловливающие жесткость воды соли кальция и магния в значительной мере поступают в наш организм вместе с водой.
Так, с питьем в организм поступает до 10-15% суточной нормы кальция – он, как известно, залог крепких костей и зубов. А магний – ключевой участник более чем 250 химических реакций в теле человека; он входит в состав всех тканей и клеток. При этом организм не может самостоятельно вырабатывать магний – для этого нужна магниесодержащая вода и пища.
Соответственно, вода не может быть абсолютно мягкой, в ней обязательно должны присутствовать соли магния и кальция. Если постоянно пить чересчур мягкую воду, организму очень скоро может потребоваться фармацевтическая поддержка – витамины, препараты.
Дополнительное умягчение московской воды не требуется для питья и приготовления еды!
Нам с Вами, как жителям средней полосы России, природа подарила оптимальный состав солей жесткости воды, которые нужны для нормальной работы нашего организма, в том числе сердечно-сосудистой системы. Этот состав природной воды из рек и водохранилищ – источников водоснабжения Москвы – сохраняется в процессе подготовки питьевой воды на станциях водоподготовки. Бесконтрольное же умягчение такой воды на бытовой установке доочистки может привести к снижению величины жесткости до слишком маленьких величин, что будет медленно, но неуклонно негативно отражаться на здоровье, и в перспективе потребует приема фармацевтических препаратов, содержащих кальций и магний.
Этот состав природной воды из рек и водохранилищ – источников водоснабжения Москвы – сохраняется в процессе подготовки питьевой воды на станциях водоподготовки. Бесконтрольное же умягчение такой воды на бытовой установке доочистки может привести к снижению величины жесткости до слишком маленьких величин, что будет медленно, но неуклонно негативно отражаться на здоровье, и в перспективе потребует приема фармацевтических препаратов, содержащих кальций и магний.
Как настроить работу бытовой техники под жесткость воды?
Это тоже один из популярных вопросов жителей города, вызванный широким распространением в быту посудомоечных и стиральных машин, для которых расчет загрузки моющих средств осуществляется исходя из фактического значения жесткости используемой воды.
В России жесткость измеряют в “градусах жесткости”, а мировые производители используют принятые в своих странах единицы измерения.
Поэтому для удобства жителей на сайте Мосводоканала и создан “Калькулятор жесткости”, с помощью которого можно перевести значения жесткости из одной системы измерения в другую, чтобы правильно настроить свою бытовую технику.
Узнав на сайте Мосводоканала жесткость воды в своем доме с помощью сервиса «Качество воды в районах Москвы», вы вводите этот показатель в «Калькулятор жесткости». Выбрав требуемую единицу измерения, которая указана в инструкции для вашей техники, вы получите в результате расчета калькулятора значение, которое необходимо выставить на шкале бытового прибора для оптимального режима работы той же посудомоечной машины.
Коэффициент жесткости пружины: определение, формулы, измерение
Пружины можно назвать одной из наиболее распространенных деталей, которые являются частью простых и сложных механизмов. При ее изготовлении применяется специальная проволока, накручиваемая по определенной траектории. Выделяют довольно большое количество различных параметров, характеризующих это изделие. Наиболее важным можно назвать коэффициент жесткости. Он определяет основные свойства детали, может рассчитываться и применяться в других расчетах. Рассмотрим особенности подобного параметра подробнее.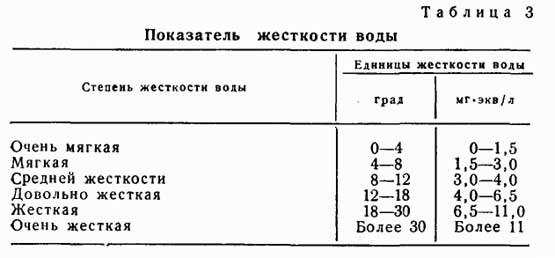
Содержание
Определение и формула жесткости пружины
При рассмотрении того, что такое коэффициент жесткости пружины следует уделить внимание понятию упругости. Для ее обозначения применяется символ F. При этом сила упругости пружины характеризуется следующими особенностями:
- Проявляется исключительно при деформации тела и исчезает в случае, если деформация пропадает.
- При рассмотрении, что такое жесткость пружины следует учитывать, после снятия внешней нагрузки тело может восстанавливать свои размеры и форму, частично или полностью. В подобном случае деформация считается упругой.
Не стоит забывать о том, что жесткость – характеристика, свойственная упругим телам, способным деформироваться. Довольно распространенным вопросом можно назвать то, как обозначается жесткость пружины на чертежах или в технической документации. Чаще всего для этого применяется буква k.
Слишком сильная деформация тела становится причиной появления различных дефектов. Ключевыми особенностями можно назвать следующее:
Ключевыми особенностями можно назвать следующее:
- Деталь может сохранять свои геометрические параметры при длительной эксплуатации.
- При увеличении показателя существенно снижается сжатие пружины под воздействие одинаковой силы.
- Наиболее важным параметром можно назвать коэффициент жесткости. Он зависит от геометрических показателей изделия, типа применяемого материала при изготовлении.
Довольно большое распространение получили красные пружины и другого типа. Цветовое обозначение применяется в случае производства автомобильных изделий. Для расчета применяется следующая формула: k=Gd4/8D3n. В этой формуле указываются нижеприведенные обозначения:
- G – применяется для определения модуля сдвига. Стоит учитывать, что это свойство во многом зависит от применяемого материала при изготовлении витков.
- d – диаметральный показатель проволоки. Она производится путем проката. Этот параметр указывается также в технической документации.

- D – диаметр создаваемых витков при накручивании проволоки вокруг оси. Он подбирается в зависимости от поставленных задач. Во многом диаметр определяет то, какая нагрузка оказывается для сжатия устройства.
- n – число витков. Этот показатель может варьировать в достаточно большом диапазоне, также влияет на основные эксплуатационные характеристики изделия.
Рассматриваемая формула применяется в случае расчета коэффициента жесткости для цилиндрических пружин, которые устанавливаются в самых различных механизмах. Подобная единица измеряется в Ньютонах. Коэффициент жесткости для стандартизированных изделий можно встретить в технической литературе.
Формула жесткости соединений пружин
Не стоит забывать о том, что в некоторых случаях проводится соединение тела нескольким пружинами. Подобные системы получили весьма широкое распространение. Определить жесткость в этом случае намного сложнее. Среди особенностей соединения можно отметить нижеприведенные моменты:
- Параллельное соединение характеризуется тем, что детали размещаются последовательно.
 Подобный метод позволяет существенно повысить упругость создаваемой системы.
Подобный метод позволяет существенно повысить упругость создаваемой системы. - Последовательный метод характеризуется тем, что деталь подключаются друг к другу. Подобный способ подсоединения существенно снижает степень упругости, однако позволяет существенно увеличить максимальное удлинение. В некоторых случаях требуется именно максимальное удлинение.
В обеих случаях применяется определенная формула, которая определяет особенности подключения. Модуль силы упругости может существенно отличаться в зависимости от особенностей конкретного изделия.
При последовательном соединении изделий показатель рассчитывается следующим образом: 1/k=1/k1+1/k2+…+1/kn. Рассматриваемый показатель считается довольно важным свойством, в данном случае он снижается. Параллельный метод подключения рассчитывается следующим образом: k=k1+k2+…kn.
Подобные формулы могут использоваться при самых различных расчетах, чаще всего на момент решения математических задач.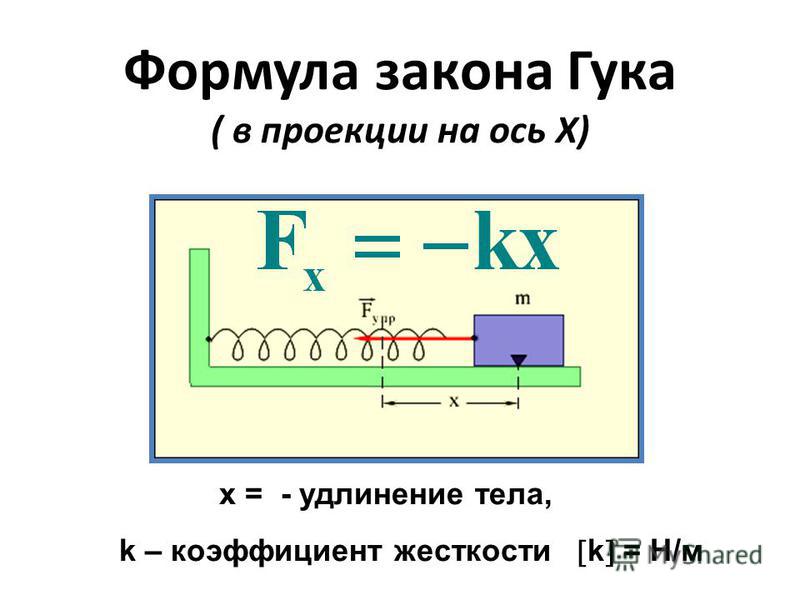
Коэффициент жесткости соединений пружин
Приведенный выше показатель коэффициента жесткости детали при параллельном или последовательном соединении определяет многие характеристики соединения. Довольно часто проводится определение тому, чему равно удлинение пружины. Среди особенностей параллельного или последовательного соединения можно отметить нижеприведенные моменты:
- При параллельном подключении удлинение обоих изделий будет равным. Не стоит забывать о том, что оба варианта должны характеризоваться одинаковой длиной в свободном положении. При последовательном показатель увеличивается в два раза.
- Свободное положение – ситуация, в которой деталь находится без прикладывания нагрузки. Именно оно в большинстве случаев учитывается при проведении расчетов.
- Коэффициент жесткости изменяется в зависимости от применяемого способа подсоединения. В случае параллельного соединения показатель увеличивается в два раза, при последовательном уменьшается.
Для проведения расчетов нужно построить схему подключения всех элементов. Основание представлено линией со штриховкой, изделие обозначается схематически, а тело в упрощенном виде. Кроме этого, от упругой деформации во многом зависит кинетическая и другая энергия.
Основание представлено линией со штриховкой, изделие обозначается схематически, а тело в упрощенном виде. Кроме этого, от упругой деформации во многом зависит кинетическая и другая энергия.
Коэффициент жесткости цилиндрической пружины
На практике и в физике довольно большое распространение получили именно цилиндрические пружины. Их ключевыми особенностями можно назвать следующие моменты:
- При создании указывается центральная ось, вдоль которой и действует большинство различных сил.
- При производстве рассматриваемого изделия применяется проволока определенного диаметра. Она изготавливается из специального сплава или обычных металлов. Не стоит забывать о том, что материал должен обладать повышенной упругостью.
- Проволока накручивается витками вдоль оси. При этом стоит учитывать, что они могут быть одного или разного диаметра. Довольно большое распространение получил вариант исполнения цилиндрического типа, но большей устойчивостью характеризуется цилиндрический вариант исполнения, в сжатом состоянии деталь обладает небольшой толщиной.

- Основными параметрами можно назвать больший, средний и малый диаметр витков, диаметр проволоки, шаг расположения отдельных колец.
Не стоит забывать о том, что выделяют два типа деталей: сжатия и растяжения. Их коэффициент жесткости определяется по одной и той же формуле. Разница заключается в следующем:
- Вариант исполнения, рассчитанный на сжатие, характеризуется дальним расположением витков. За счет расстояние между ними есть возможность сжатия.
- Модель, рассчитанная на растяжение, имеет кольца, расположенные практически вплотную. Подобная форма определяет то, что при максимальная сила упругости достигается при минимальном растяжении.
- Также есть вариант исполнения, который рассчитан на кручение и изгиб. Подобная деталь рассчитывается по определенным формулам.

Расчет коэффициента цилиндрической пружины может проводится при использовании ранее указанной формулы. Она определяет то, что показатель зависит от следующих параметров:
- Наружного радиуса колец. Как ранее было отмечено, при изготовлении детали применяется ось, вокруг которой проводится накручивание колец. При этом не стоит забывать о том, что выделяют также средний и внутренний диаметр. Подобный показатель указывается в технической документации и на чертежах.
- Количества создаваемых витков. Этот параметр во многом определяет длину изделия в свободном состоянии. Кроме этого, количество колец определяет коэффициент жесткость и многие другие параметры.
- Радиуса применяемой проволоки. В качестве исходного материала применяется именно проволока, которая изготавливается из различных сплавов. Во многом ее свойства оказывают влияние на качества рассматриваемого изделия.
- Модуля сдвига, который зависит от типа применяемого материала.
Коэффициент жесткости считается одним из наиболее важных параметров, который учитывается при проведении самых различных расчетов.
Единицы измерения
При проводимых расчетах также должно учитываться то, в каких единицах измерениях проводятся вычисления. При рассмотрении того, чему равно удлинение пружины уделяется внимание единице измерения в Ньютонах.
Для того чтобы упростить выбор детали многие производители указывают его цветовым обозначением.
Разделение пружины по цветам проводится в сфере автомобилестроения.
Среди особенностей подобной маркировки отметим следующее:
- Класс А обозначается белым, желтым, оранжевым и коричневым оттенками.
- Класса В представлен синим, голубым, черным и желтым цветом.
Как правило, подобное свойство отмечается на внешней стороне витка. Производители наносят небольшую полоску, которая и существенно упрощает процесс выбора.
Особенности расчета жесткости соединений пружин
Приведенная выше информация указывает на то, что коэффициент жесткости является довольно важным параметром, который должен рассчитываться при выборе наиболее подходящего изделия и во многих других случаях. Именно поэтому довольно распространенным вопросом можно назвать то, как найти жесткость пружины. Среди особенностей соединения отметим следующее:
Именно поэтому довольно распространенным вопросом можно назвать то, как найти жесткость пружины. Среди особенностей соединения отметим следующее:
- Провести определение растяжения пружины можно при вычислении, а также на момент теста. Этот показатель может зависеть в зависимости от проволоки и других параметров.
- Для расчетов могут применяться самые различные формулы, при этом получаемый результат будет практически без погрешностей.
- Есть возможность провести тесты, в ходе которых и выявляются основные параметры. Определить это можно исключительно при применении специального оборудования.
Как ранее было отмечено, выделяют последовательный и параллельный метод соединения. Оба характеризуются своими определенными особенностями, которые должны учитываться.
В заключение отметим, что рассматриваемая деталь является важной частью конструкции различных механизмов. Неправильный вариант исполнения не сможет прослужить в течение длительного периода. При этом не стоит забывать о том, что слишком сильная деформация становится причиной ухудшения эксплуатационных характеристик.
Лабораторная работа № 2 «Измерение жесткости пружины»
Цель работы: найти жесткость пружины из измерений удлинения пружины при различных значениях силы тяжести
уравновешивающей силу упругости на основе закона Гука:
В каждом из опытов жесткость определяется при разных значениях силы упругости и удлинения, т. е. условия опыта меняются. Поэтому для нахождения среднего значения жесткости нельзя вычислить среднее арифметическое результатов измерений. Воспользуемся графическим способом нахождения среднего значения, который может быть применен в таких случаях. По результатам нескольких опытов построим график зависимости модуля силы упругости Fупр от модуля удлинения |x|. При построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле
При построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле
Это связано с погрешностями измерения. В этом случае график надо проводить так, чтобы примерно одинаковое число точек оказалось по разные стороны от прямой. После построения графика возьмите точку на прямой (в средней части графика), определите по нему соответствующие этой точке значения силы упругости и удлинения и вычислите жесткость k. Она и будет искомым средним значением жесткости пружины kср.
Результат измерения обычно записывается в виде выражения k = = kcp±Δk, где Δk — наибольшая абсолютная погрешность измерения. Из курса алгебры (VII класс) известно, что относительная погрешность (εk) равна отношению абсолютной погрешности Δk к значению величины k:
откуда Δk — εkk. Существует правило для расчета относительной погрешности: если определяемая в опыте величина находится в результате умножения и деления приближенных величин, входящих в расчетную формулу, то относительные погрешности складываются. В данной работе
В данной работе
Поэтому
Средства измерения: 1) набор грузов, масса каждого равна m0 = 0,100 кг, а погрешность Δm0 = 0,002 кг; 2) линейка с миллиметровыми делениями.
Материалы: 1) штатив с муфтами и лапкой; 2) спиральная пружина.
Порядок выполнения работы
1. Закрепите на штативе конец спиральной пружины (другой конец пружины снабжен стрелкой-указате-лем и крючком — рис. 176).
2. Рядом с пружиной или за ней установите и закрепите линейку с миллиметровыми делениями.
3. Отметьте и запишите то деление линейки, против которого приходится стрелка-указатель пружины.
4. Подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины.
5. К первому грузу добавьте второй, третий и т. д. грузы, записывая каждый раз удлинение |х| пружины. По результатам измерений заполните таблицу:
|
Номер опыта |
m, кг |
mg1, Н |
|х|, м |
6. По результатам измерений постройте график зависимости силы упругости от удлинения и, пользуясь им, определите среднее значение жесткости пружины kcp.
По результатам измерений постройте график зависимости силы упругости от удлинения и, пользуясь им, определите среднее значение жесткости пружины kcp.
7. Рассчитайте наибольшую относительную погрешность, с которой найдено значение kср (из опыта с одним грузом). В формуле (1)
так как погрешность при измерении удлинения Δx=1 мм, то
8. Найдите
и запишите ответ в виде:
1 Принять g≈10 м/с2.
Закон Гука: «Сила упругости, возникающая при деформации тела, пропорциональна его удлинению и направлена противоположно направлению перемещения частиц тела при деформации».
Закон Гука
Жесткостью называют коэффициент пропорциональности между силой упругости и изменением длины пружины под действием приложенной к ней силы. Согласно третьему закону Ньютона, приложенная к пружине сила по модулю равна возникшей в ней силе упругости. Таким образом жесткость пружины можно выразить как:
где F – приложенная к пружине сила, а х – изменение длины пружины под ее действием. Средства измерения: набор грузов, масса каждого равна m0 = (0,1±0,002) кг.
Средства измерения: набор грузов, масса каждого равна m0 = (0,1±0,002) кг.
Линейка с миллиметровыми делениями (Δх = ±0,5 мм). Порядок выполнения работы описан в учебнике и комментариев не требует.
|
№ опыта |
масса, кг |
удлинение |х|, |
К, Н/м | |
|
м | ||||
|
1 |
0,1 |
1 |
0,036 |
27,78 |
|
2 |
0,2 |
2 |
0,074 |
27,03 |
|
3 |
0,3 |
3 |
0,112 |
26,79 |
|
4 |
0,4 |
4 |
0,155 |
25,81 |
* Ускорение свободного падения примем равным 10 м/с2.
Вычисления:
Вычисление погрешности измерения:
εх максимально когда х – наименьшее, т.е., в нашем случае, для опыта с одним грузом
Можно записать результат измерений как:
или округляя:
т.к. в нашем случае отклонения вычисленных R1; R2; R3; R4 от Rср велики из-за разности условий опытов принимаем
Источник:
Решебник
по
физике
за 9 класс (И.К.Кикоин, А.К.Кикоин, 1999 год),
задача №2
к главе «ЛАБОРАТОРНЫЕ РАБОТЫ».
Все задачи
← Лабораторная работа № 1 «Измерение ускорения тела при равноускоренном движении»
Лабораторная работа № 3 «Измерение коэффициента трения скольжения» →
14. Измерение жесткости пружины
Оборудование: штатив с лапкой и муфтой набор грузов динамометр
направляющая прибора для изучения
прямолинейного движения.
Цель работы состоит в том, чтобы определить коэффициент жесткости пружины динамометра.
Способ измерения жесткости пружины, которым пользуются в работе, основан на использовании графика зависимости силы упругости, возникающей в пружине при ее растяжении от величины удлинения.
Удлиняться пружина динамометра будет под действием веса подвешенных к нему грузов. Удлинение происходит до тех пор, пока вес груза не уравновесится силой упругости пружины.
Удлинение пружины измеряется непосредственно по шкале направляющей.
Величину силы упругости определяют по показаниям динамометра.
1. Подготовьте таблицу для записи результатов измерений:
№ опыта | Модуль силы упругости, Н | Модуль удлинения, *10-3м |
2. Закрепите муфту
с лапкой на стержне штатива на высоте
около 30 см от поверхности стола. В лапке
зажмите динамометр, как показано на
рисунке. Направляющую рейку установите
вертикально. Ее шкала должна располагаться
вблизи указателя динамометра.
Закрепите муфту
с лапкой на стержне штатива на высоте
около 30 см от поверхности стола. В лапке
зажмите динамометр, как показано на
рисунке. Направляющую рейку установите
вертикально. Ее шкала должна располагаться
вблизи указателя динамометра.
3. Заметьте положение стрелки динамометра относительно шкалы.
4. Подвесьте к динамометру один груз и по шкале с миллиметровыми делениями определите удлинение его пружины в миллиметрах. Удлинение находят как разницу двух положений указателя динамометра на шкале при нагруженном и ненагруженном динамометре.
5. По шкале динамометра измерьте величину силы упругости.
6. Результаты измерений занесите в таблицу.
7.Подвесьте к динамометру два груза и вновь определите удлинение пружины и величину силы упругости.
8. Повторите опыт с тремя и четырьмя грузами.
9. Начертите
координатные оси для построения графика
зависимости силы упругости от величины
удлинения.
10. нанесите на координатной плоскости соответствующие результатам каждого опыта точки.
11. Постройте график зависимости силы упругости от величины удлинения пружины. Если точки не ложатся на одну прямую, то провести линию графика надо так, чтобы половина точек расположилась по одну сторону от нее, а другая половина – по другую.
12. По графику определите коэффициент жесткости пружины. Для этого в средней части графика возьмите произвольную точку, опустите от нее перпендикуляры на координатные оси и определите соответствующие этой точке величины удлинения и силы упругости. По полученным значениям этих величин на основании закона Гука вычислите коэффициент жесткости (или, короче, жесткость) пружины: k = .
Оборудование: прибор для изучения прямолинейного движения динамометр набор грузов.
Цель работы состоит
в определении коэффициента трения между
пластиковыми
поверхностями направляющей
рейки и каретки.
Измеряют эту величину по графику зависимости силы трения от силы нормального давления.
Силу трения можно определить, если к каретке, лежащей на горизонтальной поверхности, присоединить динамометр и потянуть за него вдоль поверхности так, чтобы каретка стала бы двигаться равномерно. При равномерном скольжении сила трения, действующая на каретку, будет равна силе упругости растянутой пружины динамометра. Следовательно, динамометр будет при этом показывать величину силы трения.
Сила нормального давления тела на горизонтальную поверхность, на которой тело покоится или движется, равна весу этого тела. Таким образом эту силу можно измерить, определив с помощью того же динамометра вес каретки.
Порядок выполнения работы:
1. Подготовьте таблицу для записи результатов измерений.
№ опыта | Вес каретки Рк, Н | Вес грузов Рг, Н | Вес каретки с грузами Р=Рк+Рг , Н | Сила трения Fтр, Н |
2. Направляющую рейки
прибора для изучения прямолинейного
движения положите на стол горизонтально
(см. рисунок в эксперименте 2 “Измерение
силы трения скольжения
и сравнение
ее с весом тела”)
Направляющую рейки
прибора для изучения прямолинейного
движения положите на стол горизонтально
(см. рисунок в эксперименте 2 “Измерение
силы трения скольжения
и сравнение
ее с весом тела”)
3. Подвесьте каретку к динамометру и определите ее вес.
4. Разместите каретку на одном из концов направляющей рейки крючком по ходу движения. К крючку прицепите динамометр. Плавно потяните за динамометр вдоль направляющей рейки так, чтобы каретка стала перемещаться с постоянной скоростью.
5. По показанию динамометра при равномерном движении каретки определите действующую на нее силу трения.
6. Данные измерений первого опыта занесите в первую строчку таблицы. Вес груза в этом опыте был равен нулю (Рг = 0).
7. Отсоедините динамометр от каретки, подвесьте к нему один груз и определите его вес.
8.
Укрепите груз на каретке, подцепите к
ней динамометр и повторите опыт для
измерения силы трения, действующую на
каретку нагруженную одним грузом. Данные
всех измерений этого опыта занесите во
вторую строчку таблицы.
Данные
всех измерений этого опыта занесите во
вторую строчку таблицы.
9. Проведите третий, а затем и четвертый опыт, нагружая каретку соответственно двумя и тремя грузами.
10. По данным таблицы постройте график зависимости силы трения от веса каретки. При проведении линии графика следует стремиться к тому, чтобы она прошла симметрично относительно точек, нанесенных на координатную плоскость. (Точки поровну должны распределиться по обе стороны линии.)
11.Возьмите произвольную точку А на линии графика, опустите из нее перпендикуляры на оси координат и определите значение силы трения FтрА при данном весе каретки РА.
12. Вычислите по этим данным коэффициент трения = .
Как рассчитывается коэффициент жесткости?
Коэффициент жесткости k можно рассчитать, используя соотношения k = сила/перемещение . .
.
Просмотр полный ответ на encyclopedia2.thefreedictionary.com
Что такое коэффициент жесткости?
[′stif·nəs ‚kō·i‚fish·ənt] (механика) Отношение силы, действующей на линейную механическую систему, такую как пружина, к ее смещению от равновесия.
Просмотр полный ответ на encyclopedia2.thefreedictionary.com
Что такое жесткость и ее формула?
Жесткость — это сопротивление упругого тела прогибу или деформации под действием приложенной силы — и может быть выражена как. k = F/δ (1) где. k = жесткость (Н/м, фунт/дюйм)
Просмотр полный ответ на сайте engineeringtoolbox.com
Какова единица измерения коэффициента жесткости?
Что такое единица жесткости в СИ? Пояснение: Жесткость – это сопротивление прогибу. Это отношение силы (единица Н) к удлинению (м). Следовательно, его единицей является Н/м.
Просмотр
полный ответ
на sanfoundry. com
com
Как измерить жесткость материала?
Он рассчитывается путем деления продольного напряжения на деформацию и определяется путем определения наклона упругого участка кривой напряжения-деформации для данного материала. Модуль упругости является основным свойством, которое классифицирует жесткость материала.
Просмотр полный ответ on fictiv.com
Динамика конструкций, Урок 1d: Основы, коэффициенты жесткости элементов каркаса
Равна ли жесткость модулю Юнга?
Жесткость – это сопротивление упругой деформации. Модуль Юнга Y=напряжение/деформация. так, для данного напряжения, если модуль Юнга высок, то упругая деформация мала. Итак, жесткость и модуль Юнга пропорциональны друг другу.
Итак, жесткость и модуль Юнга пропорциональны друг другу.
Просмотр полный ответ на researchgate.net
Является ли жесткость такой же, как модуль Юнга?
Модуль Юнга (или модуль упругости) — это, по сути, жесткость материала. Другими словами, насколько легко он сгибается или растягивается.
Просмотр полный ответ на depts.washington.edu
Является ли жесткость такой же, как постоянная пружины?
Постоянная пружины, k, является мерой жесткости пружины. Для разных пружин и материалов она разная. Чем больше жесткость пружины, тем жестче пружина и тем труднее ее растянуть.
Просмотр полный ответ на bbc.co.uk
Как рассчитать вращательную жесткость?
Как рассчитать вращательную жесткость? Чтобы рассчитать вращательную жесткость: Разделите приложенный момент на угол поворота.
Просмотр полный ответ на omnicalculator.com
Что такое вращательная жесткость?
Определение вращательной жесткости (которая является вращательным аналогом жесткости пружины при вертикальной нагрузке) представляет собой отношение приложенного момента к угловому повороту. Для жесткого круглого основания, покоящегося на упругом полупространстве и подвергающегося качательному движению, Richart et al. (
Для жесткого круглого основания, покоящегося на упругом полупространстве и подвергающегося качательному движению, Richart et al. (
Просмотр полный ответ на sciencedirect.com
Почему жесткость является константой?
Любой из коэффициентов соотношения в обобщенном законе Гука используется для выражения компонентов напряжений как линейных функций компонентов деформации. Также известна как константа упругости.
Просмотр полный ответ на encyclopedia2.thefreedictionary.com
Каково значение K пружины?
Буква k представляет собой «постоянную пружины», число, которое, по сути, говорит нам, насколько «жесткой» является пружина. Если у вас большое значение k, это означает, что для растяжения пружины на определенную длину требуется больше усилий, чем для растяжения менее жесткой пружины на ту же длину.
Просмотр полный ответ на austincc.edu
Какая связь между жесткостью и эластичностью?
Жесткость (F=Kx) — это степень, в которой объект сопротивляется деформации в ответ на приложенную силу. Модуль упругости (E=напряжение/деформация) — это величина, которая измеряет сопротивление объекта или вещества упругой деформации при воздействии на него напряжения. В механике твердого тела мы можем связать эти K = AE / L.
Модуль упругости (E=напряжение/деформация) — это величина, которая измеряет сопротивление объекта или вещества упругой деформации при воздействии на него напряжения. В механике твердого тела мы можем связать эти K = AE / L.
Просмотр полный ответ на engineering.stackexchange.com
Связана ли жесткость с эластичностью?
Жесткость компонента зависит как от материала, так и от геометрии. Со стороны материала жесткость зависит от модуля упругости, также известного как модуль Юнга и сокращенно E. Модуль Юнга представляет собой отношение напряжения к деформации при очень малых деформациях.
Просмотр полный ответ на thefabricator.com
Как рассчитать жесткость пружины?
F = -кх. Пропорциональная константа k называется жесткостью пружины. Это показатель жесткости пружины. Когда пружину растягивают или сжимают так, что ее длина изменяется на величину х по сравнению с ее равновесной длиной, тогда она оказывает силу F = -kx в направлении своего положения равновесия.
Просмотр полный ответ на labman.phys.utk.edu
Как рассчитать пружину k?
Ответ: Когда пружина растягивается, прилагаемая сила пропорциональна увеличению длины по сравнению с равновесной длиной в соответствии с законом Гука. Жесткость пружины можно рассчитать по следующей формуле: k = -F/x, где k — жесткость пружины.
Просмотр полный ответ на geeksforgeeks.org
Почему K отрицательно в законе Гука?
Хотя мы явно не установили здесь направление силы, обычно добавляется знак минус. Это означает, что восстанавливающая сила пружины направлена в противоположную сторону по отношению к силе, вызвавшей смещение.
Просмотр полный ответ на khanacademy.org
Что вы подразумеваете под жесткостью 1?
Жесткость определяется как сопротивление силе, вызывающей изгиб элемента. Жесткость очень важна для конечного использования многих видов бумаги.
Просмотр полный ответ на sciencedirect.com
Что такое жесткость и ее единицы?
В Международной системе единиц жесткость обычно измеряется в ньютонах на метр ( ). В имперских единицах жесткость обычно измеряется в фунтах на дюйм.
Просмотр полный ответ на en.wikipedia.org
Что является примером жесткости?
Жесткость – это жесткость любого объекта или материала. Объекты с высокой жесткостью будут сопротивляться изменению формы при воздействии на них физической силы. Например, рыхлая, влажная глина имеет низкую жесткость и меняет форму всего за несколько фунтов давления. Жесткость алюминия значительно выше, чем у влажной глины.
Просмотр полный ответ на marlinwire.com
В чем разница между жесткостью и прочностью?
Жесткость — это показатель тенденции элемента возвращаться в свою первоначальную форму после воздействия силы. Прочность измеряет, какое напряжение может быть приложено к элементу, прежде чем он необратимо деформируется или сломается.
Прочность измеряет, какое напряжение может быть приложено к элементу, прежде чем он необратимо деформируется или сломается.
Просмотр полный ответ на fictiv.com
Является ли жесткость такой же, как прочность на растяжение?
Прочность измеряет напряжение или силу, приложенную к материалу до того, как он сломается (предел прочности) или необратимо деформируется (предел текучести). Однако жесткость материала определяет, как материал изгибается, чтобы противостоять приложенной силе, возвращаясь к своей первоначальной форме после снятия силы.
Просмотр полный ответ на rapiddirect.com
Влияет ли толщина на жесткость?
Жесткость увеличивается с увеличением толщины панели, а жесткость удваивается при увеличении толщины на 0,1 мм. Влияние толщины на жесткость намного больше, чем влияние удерживающей силы бланка. Чем больше высота дуги пуансона, тем больше жесткость.
Просмотр
полный ответ на matec-conferences. org
org
Как повысить жесткость?
- Центральное ядро. Жесткость зданий может быть существенно увеличена за счет строительства центрального ядра. …
- Стены сдвига. Стена сдвига – это элемент конструкции, используемый для сопротивления боковым силам. …
- Раскосная рама. …
- Трубная система. …
- Двухтрубная система.
Посмотреть полный ответ на theconstructor.org
Какое другое слово для жесткости?
На этой странице вы можете найти 32 синонима, антонима, идиоматического выражения и родственных слов жесткости, таких как: жесткость, негибкость, формальность, скромность, ограничение, твердость, точность, строгость, кривизна, строгость и строгость.
Просмотр полный ответ на thesaurus.yourdictionary.com
← Предыдущий вопрос
Можно ли убрать тазобедренные суставы?
Следующий вопрос →
Что вызывает белую мокроту?
Стандартный метод испытаний для измерения динамической жесткости (DS) и цилиндрического коэффициента восстановления (CCOR) бейсбольных и софтбольных мячей
Лицензионное соглашение ASTM
ВАЖНО – ВНИМАТЕЛЬНО ПРОЧИТАЙТЕ ЭТИ УСЛОВИЯ ПЕРЕД ВХОДОМ В ЭТОТ ПРОДУКТ ASTM.
Приобретая подписку и нажимая на это соглашение, вы вступаете в
контракт, и подтверждаете, что прочитали настоящее Лицензионное соглашение, что вы понимаете
его и соглашаетесь соблюдать его условия. Если вы не согласны с условиями настоящего Лицензионного соглашения,
немедленно покиньте эту страницу, не входя в продукт ASTM.
1. Право собственности:
Этот продукт защищен авторским правом как
компиляции и в виде отдельных стандартов, статей и/или документов («Документы») ASTM
(«ASTM»), 100 Barr Harbour Drive, West Conshohocken, PA 19.428-2959 США, если не указано иное
прямо указано в тексте отдельных документов. Все права защищены. Ты
(Лицензиат) не имеет прав собственности или иных прав на Продукт ASTM или Документы.
Это не продажа; все права, право собственности и интерес к продукту или документам ASTM
(как в электронном, так и в печатном виде) принадлежат ASTM. Вы не можете удалять или скрывать
уведомление об авторских правах или другое уведомление, содержащееся в Продукте или Документах ASTM.
Вы не можете удалять или скрывать
уведомление об авторских правах или другое уведомление, содержащееся в Продукте или Документах ASTM.
2. Определения.
A. Типы лицензиатов:
(i) Индивидуальный пользователь:
один уникальный компьютер с индивидуальным IP-адресом;
(ii) Одноместный:
одно географическое местоположение или несколько
объекты в пределах одного города, входящие в состав единой организационной единицы, управляемой централизованно;
например, разные кампусы одного и того же университета в одном городе управляются централизованно.
(iii) Multi-Site:
организация или компания с
независимое управление несколькими точками в одном городе; или организация или
компания, расположенная более чем в одном городе, штате или стране, с центральным управлением для всех местоположений.
B. Авторизованные пользователи:
любое лицо, подписавшееся
к этому Продукту; если Site License также включает зарегистрированных студентов, преподавателей или сотрудников,
или сотрудник Лицензиата на Одном или Множественном Сайте.
3. Ограниченная лицензия.
ASTM предоставляет Лицензиату ограниченное,
отзывная, неисключительная, непередаваемая лицензия на доступ посредством одного или нескольких
авторизованные IP-адреса и в соответствии с условиями настоящего Соглашения использовать
разрешенных и описанных ниже, каждого Продукта ASTM, на который Лицензиат подписался.
A. Конкретные лицензии:
(i) Индивидуальный пользователь:
(a) право просматривать, искать, извлекать, отображать и просматривать Продукт;
(b) право скачивать, хранить или распечатывать отдельные копии
отдельных Документов или частей таких Документов исключительно для собственного использования Лицензиатом. То есть Лицензиат может получить доступ к электронному файлу Документа (или его части) и загрузить его.
Документа) для временного хранения на одном компьютере в целях просмотра и/или
печать одной копии документа для личного пользования. Ни электронный файл, ни
единственный печатный отпечаток может быть воспроизведен в любом случае. Кроме того, электронный
файл не может распространяться где-либо еще по компьютерным сетям или иным образом. Это
электронный файл нельзя отправить по электронной почте, загрузить на диск, скопировать на другой жесткий диск или
в противном случае разделены. Одна печатная копия может быть распространена среди других только для их
внутреннее использование в вашей организации; его нельзя копировать. Индивидуальный загруженный документ
иным образом не может быть продана или перепродана, сдана в аренду, сдана в аренду, одолжена или сублицензирована.
То есть Лицензиат может получить доступ к электронному файлу Документа (или его части) и загрузить его.
Документа) для временного хранения на одном компьютере в целях просмотра и/или
печать одной копии документа для личного пользования. Ни электронный файл, ни
единственный печатный отпечаток может быть воспроизведен в любом случае. Кроме того, электронный
файл не может распространяться где-либо еще по компьютерным сетям или иным образом. Это
электронный файл нельзя отправить по электронной почте, загрузить на диск, скопировать на другой жесткий диск или
в противном случае разделены. Одна печатная копия может быть распространена среди других только для их
внутреннее использование в вашей организации; его нельзя копировать. Индивидуальный загруженный документ
иным образом не может быть продана или перепродана, сдана в аренду, сдана в аренду, одолжена или сублицензирована.
(ii) Односайтовые и многосайтовые лицензии:
(a) право просматривать, искать, извлекать, отображать и просматривать Продукт;
(b) право скачивать, хранить или распечатывать отдельные копии отдельных Документов или частей таких Документов для личных целей Авторизованного пользователя. использовать и передавать такие копии другим Авторизованным пользователям Лицензиата в компьютерной сети Лицензиата;
(c) если образовательное учреждение, Лицензиату разрешается предоставлять печатная копия отдельных Документов отдельным учащимся (Авторизованные пользователи) в классе по месту нахождения Лицензиата;
(d) право на отображение, загрузку и распространение печатных копий
Документов для обучения Авторизованных пользователей или групп Авторизованных пользователей.
(e) Лицензиат проведет всю необходимую аутентификацию и процессы проверки, чтобы гарантировать, что только авторизованные пользователи могут получить доступ к продукту ASTM.
(f) Лицензиат предоставит ASTM список авторизованных IP-адреса (числовые IP-адреса домена) и, если многосайтовый, список авторизованных сайтов.
B. Запрещенное использование.
(i) Настоящая Лицензия описывает все разрешенные виды использования. Любой другой использование запрещено, является нарушением настоящего Соглашения и может привести к немедленному прекращению действия настоящей Лицензии.
(ii) Авторизованный пользователь не может производить этот Продукт, или
Документы, доступные любому, кроме другого Авторизованного Пользователя, будь то по интернет-ссылке,
или разрешив доступ через его или ее терминал или компьютер; или другими подобными или отличными средствами или договоренностями.
(iii) В частности, никто не имеет права передавать, копировать,
или распространять любой Документ любым способом и с любой целью, за исключением случаев, описанных в Разделе
3 настоящей Лицензии без предварительного письменного разрешения ASTM. Особенно,
за исключением случаев, описанных в Разделе 3, никто не может без предварительного письменного разрешения
ASTM: (a) распространять или пересылать копию (электронную или иную) любой статьи, файла,
или материал, полученный из любого продукта или документа ASTM; (b) воспроизводить или фотокопировать любые
стандарт, статья, файл или материал из любого продукта ASTM; в) изменять, видоизменять, приспосабливать,
или переводить любой стандарт, статью, файл или материал, полученный из любого продукта ASTM;
(d) включать любой стандарт, статью, файл или материал, полученный из любого продукта ASTM или
Документировать в других произведениях или иным образом создавать любые производные работы на основе любых материалов. получено из любого продукта или документа ASTM; (e) взимать плату за копию (электронную или
иным образом) любого стандарта, статьи, файла или материала, полученного из любого продукта ASTM или
Документ, за исключением обычных расходов на печать/копирование, если такое воспроизведение разрешено
по разделу 3; или (f) систематически загружать, архивировать или централизованно хранить существенные
части стандартов, статей, файлов или материалов, полученных из любого продукта ASTM или
Документ. Включение печатных или электронных копий в пакеты курсов или электронные резервы,
или для использования в дистанционном обучении, не разрешено настоящей Лицензией и запрещено без
Предварительное письменное разрешение ASTM.
получено из любого продукта или документа ASTM; (e) взимать плату за копию (электронную или
иным образом) любого стандарта, статьи, файла или материала, полученного из любого продукта ASTM или
Документ, за исключением обычных расходов на печать/копирование, если такое воспроизведение разрешено
по разделу 3; или (f) систематически загружать, архивировать или централизованно хранить существенные
части стандартов, статей, файлов или материалов, полученных из любого продукта ASTM или
Документ. Включение печатных или электронных копий в пакеты курсов или электронные резервы,
или для использования в дистанционном обучении, не разрешено настоящей Лицензией и запрещено без
Предварительное письменное разрешение ASTM.
(iv) Лицензиат не может использовать Продукт или доступ к
Продукт в коммерческих целях, включая, помимо прочего, продажу Документов,
материалы, платное использование Продукта или массовое воспроизведение или распространение Документов
в любой форме; а также Лицензиат не может взимать с Авторизованных пользователей специальные сборы за использование
Продукт сверх разумных расходов на печать или административные расходы.
C. Уведомление об авторских правах . Все копии материала из ASTM Продукт должен иметь надлежащее уведомление об авторских правах от имени ASTM, как показано на начальной странице. каждого стандарта, статьи, файла или материала. Сокрытие, удаление или изменение уведомление об авторских правах не допускается.
4. Обнаружение запрещенного использования.
A. Лицензиат несет ответственность за принятие разумных мер
для предотвращения запрещенного использования и незамедлительного уведомления ASTM о любых нарушениях авторских прав или
запрещенное использование, о котором Лицензиату стало известно. Лицензиат будет сотрудничать с ASTM
при расследовании любого такого запрещенного использования и предпримет разумные шаги для обеспечения
прекращение такой деятельности и предотвращение ее повторения.
B. Лицензиат должен прилагать все разумные усилия для защиты Продукт от любого использования, не разрешенного настоящим Соглашением, и уведомляет ASTM о любом использовании, о котором стало известно или о котором было сообщено.
5. Постоянный доступ к продукту.
ASTM резервирует
право прекратить действие настоящей Лицензии после письменного уведомления, если Лицензиат существенно нарушит
условия настоящего Соглашения. Если Лицензиат не оплачивает ASTM какую-либо лицензию или
абонентской платы в установленный срок, ASTM предоставит Лицензиату 30-дневный период в течение
что бы вылечить такое нарушение. Для существенных нарушений период устранения не предоставляется
связанные с нарушениями Раздела 3 или любыми другими нарушениями, которые могут привести к непоправимым последствиям ASTM. вред. Если подписка Лицензиата на Продукт ASTM прекращается, дальнейший доступ к
онлайн-база данных будет отклонена. Если Лицензиат или Авторизованные пользователи существенно нарушают
настоящую Лицензию или запрещать использование материалов в любом продукте ASTM, ASTM оставляет за собой право
право отказать Лицензиату в любом доступе к Продукту ASTM по собственному усмотрению ASTM.
вред. Если подписка Лицензиата на Продукт ASTM прекращается, дальнейший доступ к
онлайн-база данных будет отклонена. Если Лицензиат или Авторизованные пользователи существенно нарушают
настоящую Лицензию или запрещать использование материалов в любом продукте ASTM, ASTM оставляет за собой право
право отказать Лицензиату в любом доступе к Продукту ASTM по собственному усмотрению ASTM.
6. Форматы доставки и услуги.
A. Некоторые продукты ASTM используют стандартный интернет-формат HTML.
ASTM оставляет за собой право изменить такой формат с уведомлением Лицензиата за три [3] месяца,
хотя ASTM приложит разумные усилия для использования общедоступных форматов.
Лицензиат и Авторизованные пользователи несут ответственность за получение за свой счет
подходящие подключения к Интернету, веб-браузеры и лицензии на любое необходимое программное обеспечение
для просмотра продуктов ASTM.
B. Продукты ASTM также доступны в Adobe Acrobat (PDF) Лицензиату и его Авторизованным пользователям, которые несут единоличную ответственность за установку и настройка соответствующего программного обеспечения Adobe Acrobat Reader.
C. ASTM приложит разумные усилия для предоставления онлайн-доступа
доступны на постоянной основе. Доступность будет зависеть от периодического
перерывы и простои для обслуживания сервера, установки или тестирования программного обеспечения,
загрузка новых файлов и причины, не зависящие от ASTM. ASTM не гарантирует доступ,
и не несет ответственности за ущерб или возврат средств, если Продукт временно недоступен,
или если доступ становится медленным или неполным из-за процедур резервного копирования системы,
объем трафика, апгрейды, перегрузка запросов к серверам, общие сбои сети
или задержки, или любая другая причина, которая может время от времени делать продукт недоступным
для Лицензиата или Авторизованных пользователей Лицензиата.
7. Условия и стоимость.
A. Срок действия настоящего Соглашения _____________ (“Период подписки”). Доступ к Продукту предоставляется только на Период Подписки. Настоящее Соглашение останется в силе после этого для последовательных Периодов подписки при условии, что ежегодная абонентская плата, как таковая, может меняются время от времени, оплачиваются. Лицензиат и/или ASTM имеют право расторгнуть настоящее Соглашение. в конце Периода подписки путем письменного уведомления, направленного не менее чем за 30 дней.
B. Сборы:
8. Проверка.
ASTM имеет право проверять соответствие
с настоящим Соглашением, за свой счет и в любое время в ходе обычной деятельности
часы. Для этого ASTM привлечет независимого консультанта при соблюдении конфиденциальности. соглашение, для проверки использования Лицензиатом Продукта и/или Документов ASTM. Лицензиат соглашается
разрешить доступ к своей информации и компьютерным системам для этой цели. Проверка
состоится после уведомления не менее чем за 15 дней, в обычные рабочие часы и в
таким образом, чтобы не создавать необоснованного вмешательства в деятельность Лицензиата. Если
проверка выявляет нелицензионное или запрещенное использование продуктов или документов ASTM,
Лицензиат соглашается возместить ASTM расходы, понесенные при проверке и возмещении
ASTM для любого нелицензированного/запрещенного использования. Применяя эту процедуру, ASTM не отказывается от
любое из своих прав на обеспечение соблюдения настоящего Соглашения или на защиту своей интеллектуальной собственности путем
любым другим способом, разрешенным законом.
соглашение, для проверки использования Лицензиатом Продукта и/или Документов ASTM. Лицензиат соглашается
разрешить доступ к своей информации и компьютерным системам для этой цели. Проверка
состоится после уведомления не менее чем за 15 дней, в обычные рабочие часы и в
таким образом, чтобы не создавать необоснованного вмешательства в деятельность Лицензиата. Если
проверка выявляет нелицензионное или запрещенное использование продуктов или документов ASTM,
Лицензиат соглашается возместить ASTM расходы, понесенные при проверке и возмещении
ASTM для любого нелицензированного/запрещенного использования. Применяя эту процедуру, ASTM не отказывается от
любое из своих прав на обеспечение соблюдения настоящего Соглашения или на защиту своей интеллектуальной собственности путем
любым другим способом, разрешенным законом. Лицензиат признает и соглашается с тем, что ASTM может внедрять
определенная идентифицирующая или отслеживающая информация в продуктах ASTM, доступных на Портале.
Лицензиат признает и соглашается с тем, что ASTM может внедрять
определенная идентифицирующая или отслеживающая информация в продуктах ASTM, доступных на Портале.
9. Пароли:
Лицензиат должен немедленно уведомить ASTM
о любом известном или предполагаемом несанкционированном использовании(ях) своего пароля(ей) или о любом известном или предполагаемом
нарушение безопасности, включая утерю, кражу, несанкционированное раскрытие такого пароля
или любой несанкционированный доступ или использование Продукта ASTM. Лицензиат несет исключительную ответственность
для сохранения конфиденциальности своего пароля (паролей) и для обеспечения авторизованного
доступ и использование Продукта ASTM. Личные учетные записи/пароли не могут быть переданы.
10. Отказ от гарантии:
Если не указано иное в настоящем Соглашении,
все явные или подразумеваемые условия, заверения и гарантии, включая любые подразумеваемые
гарантия товарного состояния, пригодности для определенной цели или ненарушения прав
отказываются от ответственности, за исключением случаев, когда такие отказы признаются юридически недействительными.
11. Ограничение ответственности:
В случаях, не запрещенных законом,
ни при каких обстоятельствах ASTM не несет ответственности за любые потери, повреждения, потерю данных или за особые, косвенные,
косвенные или штрафные убытки, независимо от теории ответственности,
возникающие в результате или в связи с использованием продукта ASTM или загрузкой документов ASTM.
Ни при каких обстоятельствах ответственность ASTM не будет превышать сумму, уплаченную Лицензиатом по настоящему Лицензионному соглашению.
12. Общие.
A. Прекращение действия:
Настоящее Соглашение действует до
прекращено. Лицензиат может расторгнуть настоящее Соглашение в любое время, уничтожив все копии
(на бумажном, цифровом или любом носителе) Документов ASTM и прекращении любого доступа к Продукту ASTM.
B. Применимое право, место проведения и юрисдикция:
Это
Соглашение должно толковаться и толковаться в соответствии с законодательством
Содружество Пенсильвании. Лицензиат соглашается подчиняться юрисдикции и месту проведения
в суды штата и федеральные суды Пенсильвании по любому спору, который может возникнуть в соответствии с настоящим
Соглашение. Лицензиат также соглашается отказаться от любых претензий на неприкосновенность, которыми он может обладать.
C. Интеграция:
Настоящее Соглашение представляет собой полное соглашение
между Лицензиатом и ASTM в отношении его предмета. Он заменяет все предыдущие или
одновременные устные или письменные сообщения, предложения, заверения и гарантии
и имеет преимущественную силу над любыми противоречащими или дополнительными условиями любой цитаты, заказа, подтверждения,
или другое сообщение между сторонами, относящееся к его предмету в течение срока действия
настоящего Соглашения. Никакие изменения настоящего Соглашения не будут иметь обязательной силы, если они не будут в письменной форме
и подписан уполномоченным представителем каждой стороны.
Никакие изменения настоящего Соглашения не будут иметь обязательной силы, если они не будут в письменной форме
и подписан уполномоченным представителем каждой стороны.
D. Назначение:
Лицензиат не может назначать или передавать
свои права по настоящему Соглашению без предварительного письменного разрешения ASTM.
E. Налоги.
Лицензиат должен платить все применимые налоги,
за исключением налогов на чистый доход ASTM, возникающий в результате использования Лицензиатом Продукта ASTM.
и/или права, предоставленные по настоящему Соглашению.
Измерение структурной жесткости и коэффициентов демпфирования в металлическом сетчатом фольгированном подшипнике | Дж. Инж. Газовые турбины Power
Пропустить пункт назначения навигации
Научно-исследовательские работы
Луис Сан Андрес,
Томас Абрахам Чиратадам,
Тэ-Хо Ким
Информация об авторе и статье
Дж. Инж. Газовые турбины Power . март 2010 г., 132(3): 032503 (7 страниц)
Инж. Газовые турбины Power . март 2010 г., 132(3): 032503 (7 страниц)
https://doi.org/10.1115/1.3159379
Опубликовано в Интернете: 3 декабря 2009 г.
История статьи
Получен:
23 марта 2009 г.
Пересмотренный Просмотры
- Содержание артикула
- Рисунки и таблицы
- Видео
- Аудио
- Дополнительные данные
- Экспертная оценка
- MailTo
- Твиттер
Иконка Цитировать Цитировать
Разрешения
Citation
Сан-Андрес, Л. , Чиратхадам, Т.А., и Ким, Т. (3 декабря 2009 г.). «Измерение структурной жесткости и коэффициентов демпфирования в подшипнике с металлической сеткой». КАК Я. Дж. Инж. Газовые турбины Power . март 2010 г.; 132(3): 032503. https://doi.org/10.1115/1.3159379
, Чиратхадам, Т.А., и Ким, Т. (3 декабря 2009 г.). «Измерение структурной жесткости и коэффициентов демпфирования в подшипнике с металлической сеткой». КАК Я. Дж. Инж. Газовые турбины Power . март 2010 г.; 132(3): 032503. https://doi.org/10.1115/1.3159379
Скачать файл цитаты:
- Рис (Зотеро)
- Менеджер ссылок
- EasyBib
- Подставки для книг
- Менделей
- Бумаги
- Конечная примечание
- РефВоркс
- Бибтекс
- Процит
- Медларс
Расширенный поиск
Фольгированные подшипники с металлической сеткой (MMFB) представляют собой многообещающую недорогую технологию подшипников для безмасляных микротурбомашин. В MMFB металлическая сетка в форме кольца обеспечивает мягкую эластичную опору для гладкой изогнутой фольги, обернутой вокруг вращающегося вала. В этом документе подробно описывается конструкция MMFB, а также испытания подшипника на статическую и динамическую нагрузку для оценки его структурной жесткости и эквивалентного вязкостного демпфирования. Подшипник диаметром 28,00 мм и длиной 28,05 мм с металлическим сетчатым кольцом из медной проволоки диаметром 0,3 мм и компактностью 20 % устанавливают на испытательный вал с небольшим предварительным натягом. Измерения статической нагрузки в зависимости от прогиба подшипника показывают кубическую нелинейность с большим гистерезисом. Прогиб подшипника изменяется линейно при нагрузке и нелинейно при разгрузке. Электромагнитный вибратор прикладывает к испытательному подшипнику нагрузки контролируемой амплитуды в диапазоне частот. В частотной области отношение приложенной силы к прогибу подшипника дает механический импеданс подшипника, чья действительная и мнимая части дают жесткость конструкции и коэффициенты демпфирования соответственно. Как и в случае известного уровня техники, опубликованного в литературе, жесткость подшипника значительно уменьшается с увеличением амплитуды движения и имеет тенденцию к постепенному увеличению с увеличением частоты.
В этом документе подробно описывается конструкция MMFB, а также испытания подшипника на статическую и динамическую нагрузку для оценки его структурной жесткости и эквивалентного вязкостного демпфирования. Подшипник диаметром 28,00 мм и длиной 28,05 мм с металлическим сетчатым кольцом из медной проволоки диаметром 0,3 мм и компактностью 20 % устанавливают на испытательный вал с небольшим предварительным натягом. Измерения статической нагрузки в зависимости от прогиба подшипника показывают кубическую нелинейность с большим гистерезисом. Прогиб подшипника изменяется линейно при нагрузке и нелинейно при разгрузке. Электромагнитный вибратор прикладывает к испытательному подшипнику нагрузки контролируемой амплитуды в диапазоне частот. В частотной области отношение приложенной силы к прогибу подшипника дает механический импеданс подшипника, чья действительная и мнимая части дают жесткость конструкции и коэффициенты демпфирования соответственно. Как и в случае известного уровня техники, опубликованного в литературе, жесткость подшипника значительно уменьшается с увеличением амплитуды движения и имеет тенденцию к постепенному увеличению с увеличением частоты. Эквивалентное вязкое демпфирование подшипника обратно пропорционально частоте возбуждения и амплитуде движения. Следовательно, лучше всего описывать характеристики рассеивания механической энергии MMFB с помощью коэффициента структурных потерь (материального демпфирования). Экспериментальные результаты показывают, что коэффициент потерь достигает 0,7, хотя и зависит от амплитуды движения. Эмпирически обоснованные формулы, первоначально разработанные для металлических сетчатых колец, позволяют прогнозировать жесткость несущей конструкции и коэффициенты демпфирования, которые хорошо согласуются с экспериментально оцененными параметрами. Обратите внимание, однако, что металлическое сетчатое кольцо после продолжительной эксплуатации и различных процессов демонтажа и повторной сборки показало значительную ползучесть или провисание, что привело к постепенному снижению его коэффициентов структурной силы.
Эквивалентное вязкое демпфирование подшипника обратно пропорционально частоте возбуждения и амплитуде движения. Следовательно, лучше всего описывать характеристики рассеивания механической энергии MMFB с помощью коэффициента структурных потерь (материального демпфирования). Экспериментальные результаты показывают, что коэффициент потерь достигает 0,7, хотя и зависит от амплитуды движения. Эмпирически обоснованные формулы, первоначально разработанные для металлических сетчатых колец, позволяют прогнозировать жесткость несущей конструкции и коэффициенты демпфирования, которые хорошо согласуются с экспериментально оцененными параметрами. Обратите внимание, однако, что металлическое сетчатое кольцо после продолжительной эксплуатации и различных процессов демонтажа и повторной сборки показало значительную ползучесть или провисание, что привело к постепенному снижению его коэффициентов структурной силы.
Раздел выпуска:
Газовые турбины: конструкции и динамика
Ключевые слова:
ползучесть, демпфирование, динамическое тестирование, эластичность, фольга, подшипники машин, микромеханические устройства, кольца (конструкции), валы, турбомашиностроение
Темы:
Подшипники, Демпфирование, Возбуждение, Фольгированные подшипники, Металлы, Жесткость, Stress
1.
Agrawal
,
G.
, 1997, «
Фольгированные воздушные/газовые подшипники – обзор
», ASMEG Paper No. 37-47.
2.
Аль-Хатиб
,
Э. М.
, 2002, «
Проектирование, моделирование и экспериментальное исследование виброгасителей из проволочной сетки
», кандидат наук. диссертация, Техасский университет A&M, Колледж-Стейшн, Техас.
3.
Lee
,
Y. B.
,
Kim
,
C. H.
,
Jo
,
J. H.
, and
Ryu
,
K
, 2006, “
Подшипник с воздушной фольгой, имеющий пористую фольгу
», Международный патент № WO 2006/043736 A1.
4.
AO
,
H.
,
Jiang
,
H.
,
WEI
,
W.
, и
95955
W.
, и
9955
7,
, и
W.
, и
9955
.
AM
, 2006, «
Исследование демпфирующих характеристик демпфера MR в гибкой опоре ротора турбонасоса для двигателя
»,
Первый международный симпозиум по системам и средствам управления в аэрокосмической и космонавтике
, Харбин, Китай, стр.
618
–
622
.
5.
Zarzour
,
M. J.
, 2000, «
Экспериментальная оценка демпфера для подшипника с мешами металлов в высокоскоростной тестовой установке
»,
Asme J. Eng. Газовые турбины Энергия
0742-4795,
122
(
2
), стр.
326
– 9090
320 900
6.
OKASU
,
A.
,
OHTA
,
T.
,
Azuma
,
T.
,
9
,
,
,
9
,
,
,
,
,
,
,
,
,
T.
,
,
,
.
T.
, и
Aoki
,
H.
, 1990, «
Проблемы с вибрацией в жидководородном турбонасосе LE-7», AI 509 No.
7.
Al-Khateeb
,
E. M. M.
и
Vance
,
J. M.
, 2001, «
Экспериментальная оценка на металлическом матче Документ № 2001-GT-0247.
8.
ERTAS
,
B. H.
,
Al-Khateeb
,
E. M.
и
Vance
,
. 0005
0005
J.M.
, 2003, «
Демпферы подшипников ротора для турбонасосов криогенных ракетных двигателей
»,
J. Propul. Мощность
0748-4658,
19
(
4
), стр.
674
–
026 089.
Буршид
,
С. М.
, 1990, “
Экспериментальная оценка ротородинамических коэффициентов для гибридных металлических сетчатых демпферных уплотнений в турбомашинах
», магистерская диссертация, Техасский университет A&M, Колледж-Стейшн, Техас.
10.
Choudhry
,
V.
и
Vance
,
J. M.
M.
, 2005, «
. № ГТ 2005-68641.
11.
Ertas
,
Б. Х.
, и
Луо
,
Х.
, 2008, «
Нелинейная динамическая характеристика безмасляных сетчатых демпферов
»,
ASME J. Eng. Газовые турбины Энергетика
0742-4795,
130
(
3
), с.
032503
.
12.
Ertas
,
B. H.
, 2008, «Гибридные опорные подшипники, совместимые с
, использующие встроенные демпферы из проволочной сетки», GT 5-20ME №
, бумага84.
13.
San Andrés
,
L.
и
KIM
,
T. H.
, 2008, «
. Вынужденный нелинейный ответ газовой фармий
Трибол. Междунар.
0301-679X,
41
, стр.
704
–
715
.
14.
ДеллаКорте
,
С.
,
Radil
,
K. C.
,
Bruckner
,
J. R.
, and
Howard
,
S. A.
, 2007, “
Design, Fabrication and Performance of Open Source Гидродинамические газовые фольговые подшипники, соответствующие поколениям I и II
», отчет № NASA / TM-2007-214691.
15.
ЛаРю
,
Г. Д.
,
Кан
,
S. G.
и
Wick
,
W.
, 2006, «
Turbocharger с гидродинамическими подшипниками фольги
», патент США № 7108488 B2.
16.
Dodge
,
H. L.
, 1913,
Физический обзор
,
AIP
,
New York
, p.
439
.
17.
Boyd
,
J. E.
, 1917,
Прочность материалов
,
McGraw-Hill
,
New York
, с.
16
.
18.
Бридлав
,
A. W.
, 2007, «
Experimental Identification of Structural Force Coefficients in a Bump-Type Foil Bearing», Техасский университет, AMsis
5 90
19.
Ginsberg
,
J. H.
, 2001,
Механическая и структурная вибрация – теория и применение
,
,
, стр.
–
137
.
20.
San Andrés
,
L.
,
KIM
,
T. H.
,
Chirathadam
,
T. A.
и
Martinez
,
A.
, 2008, «
ИЗМЕРЕНИЯ Структурной жесткости и демпфирования.
», Техасский университет A&M, Колледж-Стейшн, Техас, Технический отчет № TRC-B&C-5-08.
21.
Сан Андрес
,
Л.
,
Ким
,
T. H.
,
Ryu
,
K.
,
Chirathadam
,
T. A.
,
Hagen
,
K.
,
Martinez
,
A.
,
Rice
B.
,
Niedbalski
,
N.
,
,
W.
, и
9000,
W.
,
,
Вт.0006 Johnson
,
M.
, 2009, «
Газоподшипниковая технология для безмасляных микротурбомашин – Опыт исследований для программы бакалавриата (REU) в Техасском университете A&M
», ASME Paper No. GT 99209-5 .
GT 99209-5 .
В настоящее время у вас нет доступа к этому содержимому.
25,00 $
Покупка
Товар добавлен в корзину.
Проверить Продолжить просмотр Закрыть модальныйОпределение коэффициентов жесткости, демпфирования и массы роторно-подшипниковой системы импульсным методом | Extrica
Ключевые слова: силовые коэффициенты, масса, коэффициенты жесткости и демпфирования, импульсная характеристика, опорный подшипник.
1. Введение
Значения коэффициентов жесткости и демпфирования оказывают решающее влияние на вибрацию вращающейся системы [1-2]. При динамическом анализе ротора необходимо создать геометрию и сетку, установить граничные условия и отдельные силы, приложенные к ротору, включая численные значения этих коэффициентов. Значения коэффициентов жесткости и демпфирования изменяются в зависимости от скорости вращения. Для большинства типов подшипников наблюдается их нелинейность, означающая, что их значения меняются со временем, а также зависят от возбуждающей силы [3]. Для большинства работ, а также для данной статьи коэффициенты линеаризованы, что на практике означает, что они имеют фиксированные значения при постоянной скорости и не изменяются при приложении различных значений возбуждающей силы. При этом следует отметить, что значения динамических коэффициентов зависят от давления подачи, температуры и нагрузки на подшипник [4].
Для большинства работ, а также для данной статьи коэффициенты линеаризованы, что на практике означает, что они имеют фиксированные значения при постоянной скорости и не изменяются при приложении различных значений возбуждающей силы. При этом следует отметить, что значения динамических коэффициентов зависят от давления подачи, температуры и нагрузки на подшипник [4].
Имеется возможность численного определения коэффициентов жесткости и демпфирования на основе известной геометрии и путем решения уравнений движения Рейнольдса. Такие расчеты можно выполнять для линейных систем с известными параметрами с высокой точностью. В случае нелинейных систем и систем сложной конструкции, где некоторые параметры неизвестны, расчеты усложняются и могут привести к расчетной ошибке [5].
Ввиду трудностей, возникающих при расчете коэффициентов жесткости и демпфирования подшипников с использованием численных моделей, было предложено несколько экспериментальных методов, облегчающих определение этих коэффициентов. Определение динамических коэффициентов может выполняться во временной области и в частотной области. Метод импульсного возбуждения применялся для определения динамических коэффициентов для подшипников, рассматриваемых в данной статье, в частотной области. Этот метод был предложен Нордманом и Шолльхорном [6]. Чжан и др. [8] и Чан вместе с Уайтом [9] определили коэффициенты жесткости и демпфирования для двух симметричных подшипников путем сопоставления кривых частотной характеристики. Этот подход охватывает ротор с двумя одинаковыми подшипниками и позволяет определить 8 динамических коэффициентов (4 коэффициента жесткости и 4 коэффициента демпфирования). Поскольку многие системы подшипников ротора несимметричны, а их траектории более сложны, чем траектории с одним подшипником, допущение о симметрии во многих случаях нельзя использовать. Метод сопоставления кривых также требует значительной вычислительной мощности.
Определение динамических коэффициентов может выполняться во временной области и в частотной области. Метод импульсного возбуждения применялся для определения динамических коэффициентов для подшипников, рассматриваемых в данной статье, в частотной области. Этот метод был предложен Нордманом и Шолльхорном [6]. Чжан и др. [8] и Чан вместе с Уайтом [9] определили коэффициенты жесткости и демпфирования для двух симметричных подшипников путем сопоставления кривых частотной характеристики. Этот подход охватывает ротор с двумя одинаковыми подшипниками и позволяет определить 8 динамических коэффициентов (4 коэффициента жесткости и 4 коэффициента демпфирования). Поскольку многие системы подшипников ротора несимметричны, а их траектории более сложны, чем траектории с одним подшипником, допущение о симметрии во многих случаях нельзя использовать. Метод сопоставления кривых также требует значительной вычислительной мощности.
В статье [7] представлен способ расширения метода идентификации 8 коэффициентов, соответствующих одному подшипнику, для возможности определения 16 коэффициентов жесткости и демпфирования, соответствующих паре различных гидродинамических подшипников. Описан метод определения линеаризованных коэффициентов. Это представляет собой расширение импульсного метода, используемого для идентификации шестнадцати коэффициентов двух различных пеленгов. Существуют различные способы возбуждения ротора. Наиболее распространенным методом возбуждения является использование модального ударного молота для приложения импульсной силы к вращающемуся валу. Другие такие методы включают использование дополнительных возбудителей дисбаланса ротора или вибровозбудителей. Кью и Тиу считают импульсный метод наиболее экономичным и удобным для определения этих коэффициентов. Коэффициенты рассчитываются на основе сигнала реакции системы на возбуждение ротора в его центральной части модальным молотком. Затем сигналы в частотной области используются для дальнейших вычислений. В статье представлена методика экспериментального исследования, измеренные сигналы и расчетные значения коэффициентов пеленга. Коэффициенты могут быть рассчитаны за одну операцию с помощью модели, основанной на методе наименьших квадратов.
Описан метод определения линеаризованных коэффициентов. Это представляет собой расширение импульсного метода, используемого для идентификации шестнадцати коэффициентов двух различных пеленгов. Существуют различные способы возбуждения ротора. Наиболее распространенным методом возбуждения является использование модального ударного молота для приложения импульсной силы к вращающемуся валу. Другие такие методы включают использование дополнительных возбудителей дисбаланса ротора или вибровозбудителей. Кью и Тиу считают импульсный метод наиболее экономичным и удобным для определения этих коэффициентов. Коэффициенты рассчитываются на основе сигнала реакции системы на возбуждение ротора в его центральной части модальным молотком. Затем сигналы в частотной области используются для дальнейших вычислений. В статье представлена методика экспериментального исследования, измеренные сигналы и расчетные значения коэффициентов пеленга. Коэффициенты могут быть рассчитаны за одну операцию с помощью модели, основанной на методе наименьших квадратов. В рамках данной работы были проведены тесты компьютерного моделирования с целью проверки расчетных коэффициентов. В ходе экспериментальных анализов было обнаружено явление неустойчивости нефтяного вихря. Авторы предполагают, что повышение воспроизводимости результатов тестирования может быть обеспечено за счет проведения расчетов для более широкого диапазона идентификации.
В рамках данной работы были проведены тесты компьютерного моделирования с целью проверки расчетных коэффициентов. В ходе экспериментальных анализов было обнаружено явление неустойчивости нефтяного вихря. Авторы предполагают, что повышение воспроизводимости результатов тестирования может быть обеспечено за счет проведения расчетов для более широкого диапазона идентификации.
Тивари и Чакраварти [10] предложили усовершенствовать алгоритм оценки динамических параметров подшипника таким образом, чтобы он дополнительно позволял оценивать остаточный дисбаланс. В работе представлены численные и экспериментальные методы его идентификации. В статье описаны два метода: импульсный метод и метод, связанный с использованием трех значений небаланса. Оказалось, что методы эффективны, даже если шумовая составляющая относительно высока. Достигнут хороший уровень сопоставимости экспериментальных результатов с результатами численного моделирования.
Меруан и Паскуаль [11] описали методологию расчета коэффициентов нелинейной жесткости и демпфирования в гидродинамических подшипниках. Нелинейное численное моделирование коэффициентов масляной пленки было выполнено для больших перемещений в подшипнике (20-60 % зазора подшипника). Нелинейный эффект определялся путем применения нелинейных уравнений третьего порядка, которые впоследствии решались путем разложения в ряд Тейлора. Нелинейная модель создана на базе тестового стенда. В данном случае доказано влияние линеаризованных коэффициентов на динамику исследуемой системы. Установлено, что нелинейное поведение проявляется в появлении масляных вихрей, которые не возникают при использовании классических линейных моделей (которые, безусловно, более распространены в инженерной практике).
Нелинейное численное моделирование коэффициентов масляной пленки было выполнено для больших перемещений в подшипнике (20-60 % зазора подшипника). Нелинейный эффект определялся путем применения нелинейных уравнений третьего порядка, которые впоследствии решались путем разложения в ряд Тейлора. Нелинейная модель создана на базе тестового стенда. В данном случае доказано влияние линеаризованных коэффициентов на динамику исследуемой системы. Установлено, что нелинейное поведение проявляется в появлении масляных вихрей, которые не возникают при использовании классических линейных моделей (которые, безусловно, более распространены в инженерной практике).
В настоящее время ведутся работы по модификации экспериментальных методов с целью достижения большей точности. Миллер и Ховард [12] описали метод идентификации коэффициентов динамики ротора подшипника с использованием расширенного фильтра Калмана. Этот фильтр был разработан для оценки линеаризованных коэффициентов жесткости и демпфирования в роторно-подшипниковых системах с учетом шума и дисбаланса. В системе применялось импульсное возбуждение. В этом методе свойства подшипника моделируются стохастически с использованием линейной модели Гаусса-Маркова. Часть, связанная с шумом, вводится в систему как ошибка оценки с учетом неопределенности для моделирования, а также неопределенности измерения. Система содержит два параметра, созданных пользователем для настройки эффективности фильтра. Они связаны с ковариацией и шумовыми переменными. Фильтр тестировался с использованием данных численного моделирования, выполненного для системы, содержащей два одинаковых подшипника, что уменьшает количество неизвестных коэффициентов до восьми. Метод успешно применялся для оценки основных коэффициентов жесткости, тогда как коэффициенты поперечного демпфирования были получены с меньшей точностью.
В системе применялось импульсное возбуждение. В этом методе свойства подшипника моделируются стохастически с использованием линейной модели Гаусса-Маркова. Часть, связанная с шумом, вводится в систему как ошибка оценки с учетом неопределенности для моделирования, а также неопределенности измерения. Система содержит два параметра, созданных пользователем для настройки эффективности фильтра. Они связаны с ковариацией и шумовыми переменными. Фильтр тестировался с использованием данных численного моделирования, выполненного для системы, содержащей два одинаковых подшипника, что уменьшает количество неизвестных коэффициентов до восьми. Метод успешно применялся для оценки основных коэффициентов жесткости, тогда как коэффициенты поперечного демпфирования были получены с меньшей точностью.
Численная оценка динамических коэффициентов может быть очень сложной задачей для подшипников сложной конструкции, например, в случае фольгированных подшипников [13]. Результаты экспериментальной идентификации динамических коэффициентов гибридного фольгированного подшипника большого диаметра представлены в работе [14]. В статье приведены гидростатические и гидродинамические характеристики подшипника диаметром 101,6 мм и длиной 82,6 мм. Коэффициенты жесткости оценивались с использованием двух различных подходов: во-первых, квазистатическим методом с построением кривых, представляющих прогиб во временной области; во-вторых, импульсным методом в частотной области. Коэффициенты демпфирования оценивались только импульсным методом. Значения коэффициентов жесткости, полученные двумя методами, были схожими, а различия достигали 4-7 МН/м в зависимости от скорости, нагрузки и давления подачи. Расчеты в частотной области привели к большим расхождениям между результатами. Кроме того, создана численная модель, использующая линейный метод возмущений. Видно хорошее совпадение результатов расчета с результатами эксперимента, сделанное на основании изгиба вала.
В статье приведены гидростатические и гидродинамические характеристики подшипника диаметром 101,6 мм и длиной 82,6 мм. Коэффициенты жесткости оценивались с использованием двух различных подходов: во-первых, квазистатическим методом с построением кривых, представляющих прогиб во временной области; во-вторых, импульсным методом в частотной области. Коэффициенты демпфирования оценивались только импульсным методом. Значения коэффициентов жесткости, полученные двумя методами, были схожими, а различия достигали 4-7 МН/м в зависимости от скорости, нагрузки и давления подачи. Расчеты в частотной области привели к большим расхождениям между результатами. Кроме того, создана численная модель, использующая линейный метод возмущений. Видно хорошее совпадение результатов расчета с результатами эксперимента, сделанное на основании изгиба вала.
В статье [15] представлены экспериментальные исследования гибридного газового подшипника, характеризующегося сложной конструкцией фольги, достаточно устойчивой к высоким давлениям. В подшипнике используются две смазывающие пленки: гидростатическая и гидродинамическая. Такое изготовление обеспечивает соответствующую грузоподъемность и жесткость всей системы. В работе описана экспериментальная проверка коэффициентов жесткости и демпфирования подшипника диаметром 110 мм. Измерения проводились на специально подготовленном стенде. В ходе эксперимента варьировались следующие параметры: гидростатическое давление подачи, частота возбуждающей силы и частота вращения ротора. Исследования направлены на оценку возможностей использования подшипника в мощных энергетических машинах. Результаты испытаний выявили низкую чувствительность основных коэффициентов жесткости к большинству тестируемых параметров, кроме частоты и скорости вращения. Чем больше частота вращения и частота возмущающей силы, тем ниже будут расчетные коэффициенты жесткости.
В подшипнике используются две смазывающие пленки: гидростатическая и гидродинамическая. Такое изготовление обеспечивает соответствующую грузоподъемность и жесткость всей системы. В работе описана экспериментальная проверка коэффициентов жесткости и демпфирования подшипника диаметром 110 мм. Измерения проводились на специально подготовленном стенде. В ходе эксперимента варьировались следующие параметры: гидростатическое давление подачи, частота возбуждающей силы и частота вращения ротора. Исследования направлены на оценку возможностей использования подшипника в мощных энергетических машинах. Результаты испытаний выявили низкую чувствительность основных коэффициентов жесткости к большинству тестируемых параметров, кроме частоты и скорости вращения. Чем больше частота вращения и частота возмущающей силы, тем ниже будут расчетные коэффициенты жесткости.
В работе [16] представлены результаты расчета аэростатических подшипников скольжения на примере испытательного стенда Bentley Nevada. Были проведены испытания с различными типами подшипников для получения их статических и динамических характеристик. Было применено несколько методов определения динамических коэффициентов подшипника. Рассчитывались только основные коэффициенты жесткости и демпфирования. Влияние перекрестной жесткости и коэффициентов демпфирования на результаты оценивалось на основе численного моделирования. При расчетах элементы матрицы масс считались известными параметрами. Необходимо было рассчитать матрицы жесткости и демпфирования. Авторы рекомендуют оценивать значения основных коэффициентов в начале эксперимента. На следующем шаге нужно рассчитать коэффициенты перекрестной связи, так как они более уязвимы для ошибок. По мнению авторов данной статьи, увеличение давления питания или частоты возбуждающей силы негативно влияет на значения динамических коэффициентов.
Были проведены испытания с различными типами подшипников для получения их статических и динамических характеристик. Было применено несколько методов определения динамических коэффициентов подшипника. Рассчитывались только основные коэффициенты жесткости и демпфирования. Влияние перекрестной жесткости и коэффициентов демпфирования на результаты оценивалось на основе численного моделирования. При расчетах элементы матрицы масс считались известными параметрами. Необходимо было рассчитать матрицы жесткости и демпфирования. Авторы рекомендуют оценивать значения основных коэффициентов в начале эксперимента. На следующем шаге нужно рассчитать коэффициенты перекрестной связи, так как они более уязвимы для ошибок. По мнению авторов данной статьи, увеличение давления питания или частоты возбуждающей силы негативно влияет на значения динамических коэффициентов.
В публикации [17] представлен новый способ определения характеристик жесткости и демпфирования подшипников с использованием фазовых диаграмм. Авторы подчеркивают, что надежная оценка динамических коэффициентов подшипника является серьезной проблемой, особенно для нелинейных систем. Они утверждают, что не существует единой универсальной модели расчета параметров системы, поскольку их идентификация зависит от данных измерений и эталонной модели. Описанная модель, содержащая диаграммы фазовой плоскости, хорошо работает, когда коэффициенты сильно зависят от частоты.
Авторы подчеркивают, что надежная оценка динамических коэффициентов подшипника является серьезной проблемой, особенно для нелинейных систем. Они утверждают, что не существует единой универсальной модели расчета параметров системы, поскольку их идентификация зависит от данных измерений и эталонной модели. Описанная модель, содержащая диаграммы фазовой плоскости, хорошо работает, когда коэффициенты сильно зависят от частоты.
Экспериментальные расчеты жесткости подшипников и параметров демпфирования проводятся не только для подшипников скольжения, но и для осевых подшипников. Экспериментальное определение коэффициентов жесткости и демпфирования осевого фольгированного подшипника показано в статье [18]. В работу включены схема процедуры идентификации этих коэффициентов, испытательный стенд и графики коэффициентов/скорости.
Метод импульсного возбуждения используется для оценки жесткости подшипников и коэффициентов демпфирования. Он может применяться ко многим типам подшипников, таким как гидродинамические, аэродинамические, магнитные и фольговые подшипники. В этой статье описывается модификация метода, используемого для определения жесткости подшипника и коэффициентов демпфирования, который был разработан Qiu и Tieu. Этот метод, кратко заключающийся в применении импульсного возбуждения, а затем в использовании метода аппроксимации (метода наименьших квадратов), был дополнен новой функциональностью – вычислением массовых коэффициентов. Расчет жесткости, демпфирования и массовых коэффициентов (происходит за один шаг) позволяет проверить результаты на начальном этапе работы, так как массовые коэффициенты можно сравнивать с известной массой вала. На основе массовых коэффициентов можно легко рассчитать массу ротора, что позволяет, например, оценка влияния муфты на уровень вибрации. Такой подход способствует полной идентификации всех динамических параметров роторно-подшипниковой системы.
В этой статье описывается модификация метода, используемого для определения жесткости подшипника и коэффициентов демпфирования, который был разработан Qiu и Tieu. Этот метод, кратко заключающийся в применении импульсного возбуждения, а затем в использовании метода аппроксимации (метода наименьших квадратов), был дополнен новой функциональностью – вычислением массовых коэффициентов. Расчет жесткости, демпфирования и массовых коэффициентов (происходит за один шаг) позволяет проверить результаты на начальном этапе работы, так как массовые коэффициенты можно сравнивать с известной массой вала. На основе массовых коэффициентов можно легко рассчитать массу ротора, что позволяет, например, оценка влияния муфты на уровень вибрации. Такой подход способствует полной идентификации всех динамических параметров роторно-подшипниковой системы.
2. Оценщик коэффициентов
Движение точки можно описать уравнением. (1). Получив преобразование Лапласа и уравнения Эйлера, мы получаем уравнения (2), (3) и (4):
(1)
м∙x¨+c∙x˙+k∙x=ft,
(2)
mjω2Xs+cjωXs+kXs=Fs,
(3)
k-mω2+djωX0ej∅x=F0ej∅F,
(4)
k-mω2+djωX0cos∅x+jsin∅x=F0cos∅F+jsin∅.
Уравнение движения для одиночного подшипника (для модели, показанной на рис. 1(b)) может быть описано уравнением. (5). Это уравнение можно записать в матричной форме. (6). Описанная таким образом система ведет себя иначе, когда ее возбуждают в направлениях X и Y, используя возбуждающую силу соответственно FX и FY. Отклик системы в направлении X после возбуждения в направлении Y описывается XY:
(5)
-mxxω2Xx-mxyω2Xy+kxxXx+cxxjωXx+kxyXy+cxyjωXy=Fx,
-myyω2Yy-mxyω2Yx+kyyYy+cyyjωYy+kyxYx+cyxjωYx=Fy,
(6)
kxx-mxxω2+cxxjωkxy -mxyω2+cxyjωkyx-myxω2+cyxjωkyy-myyω2+cyyjωXxXyYxYy=Fx00Fy.
Рис. 1. а) Модель ротора, подготовленная в Samcef Rotors, б) модель одного из подшипников
а)
б)
Первая часть уравнения. (6) определяется как импеданс и может быть разделен на параметры массы, жесткости и демпфирования (уравнение). (7):
(7)
kxx-mxxω2+cxxjωkxy-mxyω2+cxyjωkyx-myxω2+cyxjωkyy-myyω2+cyyjω10-ω20jω0010-ω20jω
=kxxkxykyxkyymxxmxymyxmyycxxcxycyxcyy.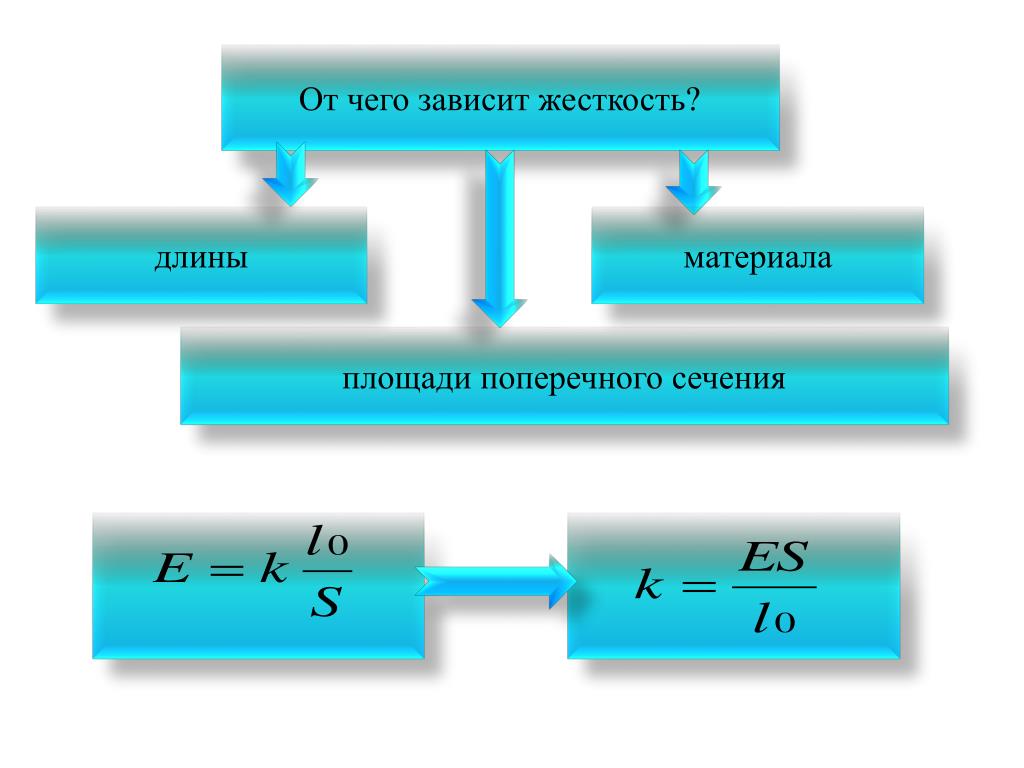
Метод наименьших квадратов используется для решения уравнений и требует использования сигнала в частотной области. Это достигается преобразованием Фурье силового сигнала и отклика системы во временной области. Вектор D представляет собой ответный сигнал в частотной области, матрица F состоит из составляющих возбуждающей силы (Fx(t) и Fy(t)) в частотной области. Принимая во внимание матрицы D и F, уравнение. (6) можно представить в виде уравнения. (8). Если мы рассмотрим систему с двумя подшипниками (показана на рис. 1 (б)) уравнение. (8) можно определить как уравнение (9). Расширение математического описания системы с двумя подшипниками (модель показана на рис. 1(а)) представлено уравнениями. (9)–(15):
(8)
HxxiHxyiHyxiHyyiDxxiDxyiDyxiDyyi= Fxi00Fyi.
Индексы «1» и «2» в уравнении (9) обозначают первый и второй подшипники. Индекс ‘i ’ обозначает диапазон частот. Первый двойной индекс указывает направление реакции системы, второй индекс указывает направление силы возбуждения.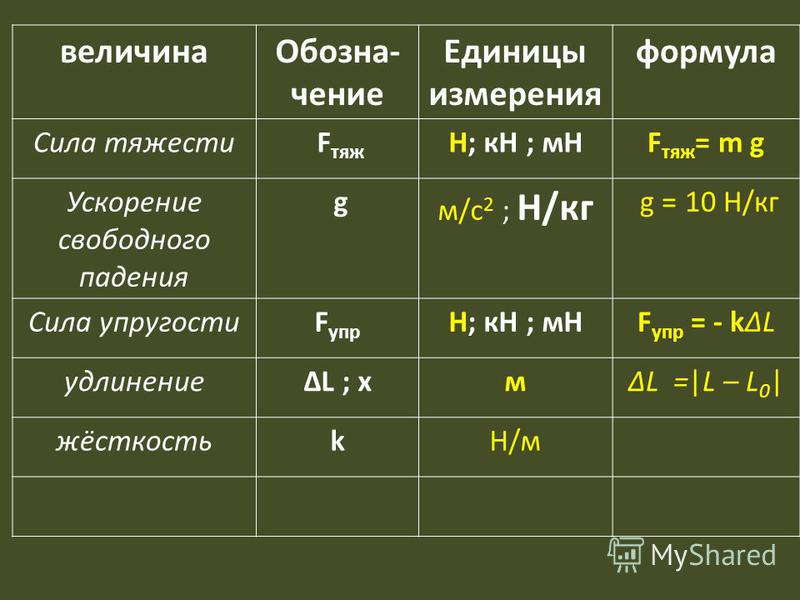 Например, элемент Dyx1 определяет колебания ротора на первом подшипнике в направлении x после возбуждения в направлении Y:
Например, элемент Dyx1 определяет колебания ротора на первом подшипнике в направлении x после возбуждения в направлении Y:
(9)
Hxxi1Hxyi1Hyxi1Hyyi1=Fxi100Fyi1Dxxi1Dxxi1Dxxi1Dxxi1-1, Hxxi2Hxyi2Hyxi2Hyyi1=Fxi200Fyi2Dxxi2Dxxi2Dxxi2Dxxi2-1.
Гибкость определяется как величина, обратная механическому импедансу, и представлена в уравнении. (10):
(10)
К уравнению можно применить метод наименьших квадратов. (10), тогда необходимо сформулировать уравнение (11). Значения матрицы Z можно определить из уравнения (12). В этом уравнении Ai представляет собой матрицу, в которой сигналы являются элементами матрицы гибкости и частотного вектора. Он был сформирован путем разложения действительной и мнимой частей уравнения. (13). Матрица I определяется уравнением. (14), а матрица Z состоит из коэффициентов жесткости, демпфирования и массы системы ротор – подшипники. Если считать, что параметры получены для 100 частотных отсчетов (определяется индексом i), то матрица A будет иметь размерность 800×12, матрица I будет иметь размерность 800×2, а матрица Z будет иметь размерность размеры 2×12:
(11)
AI · z = II,
(12)
z = (AITAI) -1aitii,
(13)
AI = Realfi1 · 1000- (ωi) 2000 ОДВО · 001000- (ωi) 2000,–200001000- (ωi) 2000ωi Imagfi1 · 1000- (ωi) 2000ωi0000001000- (ωi) 2000 Ом й Imagfi2 · 001000- (ωi) 2000,2001000- (ωi) 2000 ОД,
(140006 (140006100100100100100100100100100100100 гг.
Порядок масс, коэффициентов жесткости и демпфирования в системе ротор-подшипник показан ниже. (15):
(15)
Z=kxx1kxy1kxy2kyx1kyy1kyx2 kxy2mxx1mxy1kyy2myx1myy1 mxx2mxy2cxx1myx2myy2cyx1 cxy1cxx2cxy2cyy1cyx2cyy2T.
3. Численная модель и валидация
Для проверки предложенного метода была создана численная модель ротора в программе Samcef Rotors (рис. 1(а)). Модель состоит из вала, вращающегося со скоростью 8000 об/мин, и подшипников, смоделированных с использованием коэффициентов жесткости и демпфирования в ортогональном и поперечном направлениях. Ротор при моделировании возбуждался известным значением силы возбуждения в центральной части в направлении X. Затем измеряли амплитуду колебаний ротора в каждом подшипнике в направлениях X и Y. Затем моделирование было повторено, на этот раз с использованием той же возбуждающей силы, но модель была возбуждена в направлении Y. При этом измерялась амплитуда вибрации ротора в подшипниках в направлении X и Y. При измерении вибрации в направлении X в первом подшипнике после возбуждения в направлении Y сигнал описывался как 1XY. На основе сигналов возбуждения и сигнала отклика, генерируемого программой Samcef Rotors, были рассчитаны коэффициенты жесткости, демпфирования и массы подшипников. Поскольку коэффициенты жесткости и демпфирования были определены в программе Samcef Rotors, это позволяет сравнивать коэффициенты, рассчитанные с использованием предложенного алгоритма, и фактические значения.
При измерении вибрации в направлении X в первом подшипнике после возбуждения в направлении Y сигнал описывался как 1XY. На основе сигналов возбуждения и сигнала отклика, генерируемого программой Samcef Rotors, были рассчитаны коэффициенты жесткости, демпфирования и массы подшипников. Поскольку коэффициенты жесткости и демпфирования были определены в программе Samcef Rotors, это позволяет сравнивать коэффициенты, рассчитанные с использованием предложенного алгоритма, и фактические значения.
Создана симметричная модель ротора (рис. 1(а)), длина L= 0,92 м. Расстояние между опорами 2l1=0,58 м. Диаметр вала ротора d= 19,05 мм. В центре ротора находится диск диаметром D=152,4 мм. Материал ротора – сталь с модулем Юнга 205·10 9 Па, коэффициентом Пуассона 0,3, плотностью материала 7800 кг/м 3 . Принятые значения жесткости подшипника и параметров демпфирования в основных направлениях xx, yy и направлениях перекрестной связи xy, yx приведены в таблицах 1 и 2. Это стандартная процедура численного моделирования систем подшипник-вал.
Рис. 2. Схема обработки данных
В ответном сигнале есть часть, связанная с дисбалансом, вызывающим постоянную составляющую вибрации. На практике нам нужно извлечь этот компонент из нашего ответного сигнала. Схема обработки данных, показывающая всю процедуру, показана на рис. 2. В численной модели при вращении ротора его возбуждала известная сила F в направлении X и направлении Y соответственно. Силовой сигнал в направлении X показан на рис. 3(а). Такой же метод возбуждения необходимо использовать в экспериментальных исследованиях. Затем измерялись амплитуды колебаний в подшипниках. Амплитуда первого пеленга показана на рис. 3(b). Поскольку в описанном алгоритме определения коэффициентов жесткости, демпфирования и массовых коэффициентов системы ротор-подшипник используется сигнал в частотной области, необходимо выполнить быстрое преобразование Фурье (БПФ) сигналов. Возбуждение и смещение в первом сигнале пеленга в частотной области показаны на рис. 4. Показанная на графике функция соответствует сигналу полного опознавательного диапазона (0-87,5 Гц).
Показанная на графике функция соответствует сигналу полного опознавательного диапазона (0-87,5 Гц).
Рис. 3. а) Сила в направлении Х как функция времени, б) перемещение в подшипнике № 1 как функция времени
а)
б)
Результаты а) амплитуда, б) фаза податливости показаны на рис. 5. Сигналы податливости используются в описанном алгоритме расчета жесткости, демпфирования и массовых коэффициентов системы ротор – подшипник. Резонанс, видимый на графике, происходит около 46 Гц и соответствует собственной частоте описываемого ротора. Форма колебаний ротора показана на рис. 6.9.0005
Рис. 4. а) Сила в частотной области, б) перемещение в подшипнике № 1 в частотной области
а)
б)
Рис. – амплитуда, б) податливость первого подшипника – фаза
а)
б)
Рис. 6. Форма первой моды ротора на частоте 46 Гц
Программа Samcef была использована для расчета коэффициентов жесткости, демпфирования и массы системы ротор-подшипник.
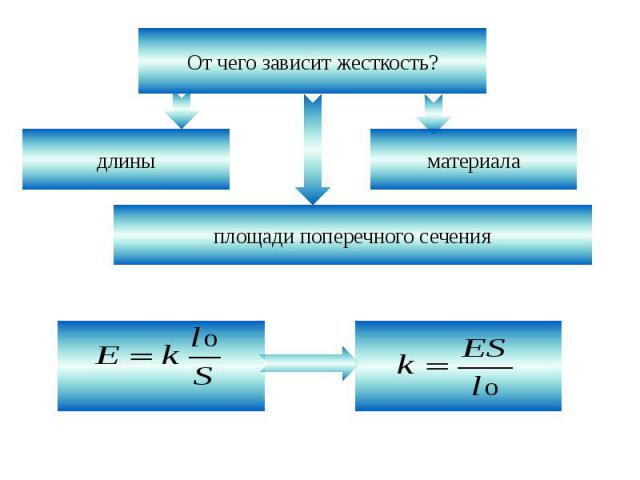 Рассматривалась модель симметричного ротора, но коэффициенты жесткости и демпфирования (включая значения кросс-связей) имеют разные значения. В гидродинамических подшипниках перекрестная часть коэффициентов демпфирования Cxy и Cyx имеет одинаковые значения [10], в данном случае это разные значения, чтобы показать, как работает предложенный метод. Поскольку значения коэффициентов жесткости и демпфирования были известны из численной модели, можно было напрямую их сравнивать и на этой основе можно было оценить погрешность расчета коэффициентов несущей способности. Результаты расчета коэффициентов жесткости, демпфирования и массы показаны для двух диапазонов идентификации. Первая из них от 0 Гц до 3,1250 Гц, что соответствует значению первых трех частот. Второй диапазон идентификации от 0 Гц до 87,5 Гц, в этот диапазон вошли первые 57 значений частоты. Второй диапазон идентификации включал весь резонансный диапазон. Были рассмотрены два различных диапазона идентификации, поскольку в теоретическом примере достаточно лишь небольшого фрагмента частот.
Рассматривалась модель симметричного ротора, но коэффициенты жесткости и демпфирования (включая значения кросс-связей) имеют разные значения. В гидродинамических подшипниках перекрестная часть коэффициентов демпфирования Cxy и Cyx имеет одинаковые значения [10], в данном случае это разные значения, чтобы показать, как работает предложенный метод. Поскольку значения коэффициентов жесткости и демпфирования были известны из численной модели, можно было напрямую их сравнивать и на этой основе можно было оценить погрешность расчета коэффициентов несущей способности. Результаты расчета коэффициентов жесткости, демпфирования и массы показаны для двух диапазонов идентификации. Первая из них от 0 Гц до 3,1250 Гц, что соответствует значению первых трех частот. Второй диапазон идентификации от 0 Гц до 87,5 Гц, в этот диапазон вошли первые 57 значений частоты. Второй диапазон идентификации включал весь резонансный диапазон. Были рассмотрены два различных диапазона идентификации, поскольку в теоретическом примере достаточно лишь небольшого фрагмента частот. В экспериментальной практике исследователи предлагают учитывать весь диапазон частот, в котором возникают резонансы [7], такая процедура позволяет получать воспроизводимые результаты. Результаты расчета коэффициентов жесткости приведены в табл. 1, коэффициентов демпфирования — в табл. 2, массовых — в табл. 3.
В экспериментальной практике исследователи предлагают учитывать весь диапазон частот, в котором возникают резонансы [7], такая процедура позволяет получать воспроизводимые результаты. Результаты расчета коэффициентов жесткости приведены в табл. 1, коэффициентов демпфирования — в табл. 2, массовых — в табл. 3.Относительная погрешность оценки коэффициентов жесткости подшипника в первом диапазоне идентификации не превышает 0,02 %. Относительная погрешность оценки коэффициентов жесткости подшипника во втором диапазоне идентификации – на более длинном диапазоне частот не превышает 0,5 %. Это достаточно точная оценка коэффициентов жесткости подшипников, особенно с учетом того, что погрешность расчета коэффициентов жесткости в пределах второго диапазона идентификации в основных координатах (более значимых при дальнейшем моделировании динамики системы) не превышает 0,04 %.
Table 1. The stiffness coefficients
kxx1 | kyy1 | kxy1 | kyx1 | kxx2 | kyy2 | kxy2 | KYX2 | ||
Фактические значения N/M | 500 000 | 450,000 | 250,0009 | 250. 450,000 | 240 000 | 550 000 | 470 000 | 270 000 | 260 000 |
Calculated values N/m Identification range 0-3.125 Hz | 499 913 | 449 922 | 249 957 | 239 959 | 549 905 | 469 919 | 269 953 | 259 955 | |
Relative error % Identification range 0-3.125 Hz | 0.02 | 0.02 | 0.02 | 0.02 | 0,02 | 0,02 | 0,02 | 0,02 | |
Расчеты.0005 | 499 949 | 449 999 | 249 630 | 241 198 | 550 192 | 469 822 | 270 271 | 259 138 | |
Относительная ошибка % . | 0,03 | 0,04 | 0,10 | 0,33 |
. Ошибка. Необходимость. Эта ошибка возникает только при расчете перекрестной части коэффициентов демпфирования. Погрешность расчета коэффициентов демпфирования во втором диапазоне идентификации составляет около 2 %.
Table 2. Damping coefficients
cxx1 | cyy1 | cxy1 | cyx1 | cxx2 | cyy2 | cxy2 | Cyx2 | ||
Фактические значения N/M | 500 | 550 | 250 | 6666666903 250 | 66666666666903 250 | .0005550 | 560 | 260 | 270 |
Calculated values N/(m/s) Identification range 0-3. | 500 | 550 | 250 | 259 | 550 | 560 | 260 | 271 | |
Relative error % Identification range 0-3.125 Hz | 0.00 | 0.00 | 0.00 | 0.38 | 0.00 | 0.00 | 0.00 | 0,37 | |
Расчетные значения N/(м/с) Диапазон идентификации 0-87,5 Гц | 66 090 0006 545 | 248 | 260 | 562 | 565 | 262 | 270 | ||
Relative error % Identification range 0-87.5 Hz | 2.00 | 0.91 | 0. | 0.00 | 2.18 | 0.89 | 0,77 | 0,00 |
Вес вала, смоделированного в программе Samcef Rotors, составляет 4,845 кг. Расчетная масса вала на основе описанного алгоритма (и численной модели вала) для первого диапазона идентификации составляет 4,851 кг, а для второго диапазона идентификации – 4,855 кг. Эта масса была рассчитана путем сложения массовых коэффициентов на главной диагонали (XX и YY) и деления этого значения на два. Интерпретация значений массового коэффициента следующая: массовый коэффициент mxx1 представляет собой массу части вала, вовлеченной в вибрацию в направлении X, отнесенную к первому подшипнику после возбуждения в направлении X. Напротив, массовый коэффициент myy1 представляет собой массу части вала, вовлеченной в вибрацию в направлении Y, относящуюся к первому подшипнику после возбуждения в направлении Y. Разделение суммы весовых коэффициентов на два для расчета массы вала применено, так как система возбуждалась дважды. Массовые коэффициенты перекрестной связи (xyyx) должны быть близки к нулю. Погрешность расчета весового коэффициента для первого диапазона идентификации составляет 0,12 %, для второго диапазона идентификации 0,21 %. Эти результаты означают, что вес ротора 4,845 кг может быть оценен с точностью ± 0,01 кг (со вторым диапазоном идентификации с более высокими значениями относительной ошибки).
Массовые коэффициенты перекрестной связи (xyyx) должны быть близки к нулю. Погрешность расчета весового коэффициента для первого диапазона идентификации составляет 0,12 %, для второго диапазона идентификации 0,21 %. Эти результаты означают, что вес ротора 4,845 кг может быть оценен с точностью ± 0,01 кг (со вторым диапазоном идентификации с более высокими значениями относительной ошибки).
Table 3. Mass coefficients
mxx1 | myy1 | mxy1 | myx1 | mxx2 | myy2 | mxy2 | Myx2 | ∑m | |
Фактические значения кг | 4,845 | ||||||||
9000 Identification range 0-3. | 2.35 | 2.4 | –0.02 | 0.01 | 2.51 | 2.45 | 0.02 | –0.01 | 4.851 |
Относительная ошибка % Диапазон идентификации 0-3,125 Гц | 0,12 | 0,12 | 0,12 | 0,12 | 0,12 | 0,12 | 0,12 | 0,12 | 1401 | Calculated values kg Identification range 0-87.5 Hz | 2.33 | 2.40 | –0.02 | 0.04 | 2.54 | 2.45 | 0.02 | –0,03 | 4,855 |
Относительная ошибка %1403 0,21 | |||||||||
В процессе проверки описанного алгоритма, используемого для расчета коэффициентов несущей способности, были проверены два диапазона идентификации. Первый диапазон идентификации включал только первые три частоты из частотного диапазона, второй включал весь диапазон, в котором имели место резонансы. При расширении диапазона идентификации ошибка в большинстве случаев увеличивается незначительно, но все же находится на относительно низком уровне. Расширение диапазона идентификации влечет за собой меньшее влияние дополнительных факторов на расчетные значения коэффициентов массы, жесткости и демпфирования. Автор предлагает в случае расчета одного пеленга (такие расчеты часто выполняются с учетом близко расположенного к пеленгу возбуждения) следует применять узкий диапазон идентификации предпочтительно из исходного диапазона частот.
Первый диапазон идентификации включал только первые три частоты из частотного диапазона, второй включал весь диапазон, в котором имели место резонансы. При расширении диапазона идентификации ошибка в большинстве случаев увеличивается незначительно, но все же находится на относительно низком уровне. Расширение диапазона идентификации влечет за собой меньшее влияние дополнительных факторов на расчетные значения коэффициентов массы, жесткости и демпфирования. Автор предлагает в случае расчета одного пеленга (такие расчеты часто выполняются с учетом близко расположенного к пеленгу возбуждения) следует применять узкий диапазон идентификации предпочтительно из исходного диапазона частот.
5. Заключительные замечания
В статье автор расширил метод оценки 16 коэффициентов жесткости и демпфирования гидродинамических подшипников, предложенный Qiu и Tieu, и оценил еще 8 массовых коэффициентов. Все силовые коэффициенты рассчитываются за одну операцию по методу наименьших квадратов. Рассчитанные массовые коэффициенты соответствуют весу ротора, участвующего в вибрации подшипников.
Рассчитанные массовые коэффициенты соответствуют весу ротора, участвующего в вибрации подшипников.
Для проверки описанного метода была построена численная модель ротора. По известным значениям возбуждающей силы и отклика системы в каждой опорной точке были рассчитаны коэффициенты жесткости, демпфирования и массы системы ротор-подшипник.
В ходе работы сравнивались два диапазона идентификации. Первый диапазон идентификации включал только диапазон начальных частот, второй диапазон идентификации охватывал весь резонансный диапазон. Получается, что при увеличении дальности идентификации ошибка несколько увеличивается, но все же допустима. Расширение диапазона идентификации на резонансных частотах может обеспечить хорошую воспроизводимость результатов экспериментальных исследований.
Часть работы, описанной в этой статье, была реализована в рамках проекта STA-DY-WI-CO, это программа передачи знаний Марии Кюри IAPP. Я хотел бы поблагодарить г-на Барта Питерса за то, что он руководил мной во время моей годичной практики в LMS International и за возможность использования программы Samcef Rotors. Я хотел бы также поблагодарить г-на Гжегожа Живицу за ценные комментарии и предложения.
Я хотел бы также поблагодарить г-на Гжегожа Живицу за ценные комментарии и предложения.
Экспериментальный анализ прочности и моделирование материалов 3D-печатных деталей
(1)
Ander s Dahl e Thor sen Experiment al Str ength Anal ysis and Mat erial Modelling of 3D Print ed P arts NTNU Norw egian Univ er sity of Science e and T echnol ogy Faculty of Engineering Department of Oc ean Oper ations and Civil Engineering
Mas ter’ s thesisAnders Dahle Thorsen
Экспериментальный анализ прочности и моделирование материалов 3D-печатных деталей
Магистерская работа по проектированию продуктов и систем Супервайзер: Генри Питер Пиль
июнь 2019 г.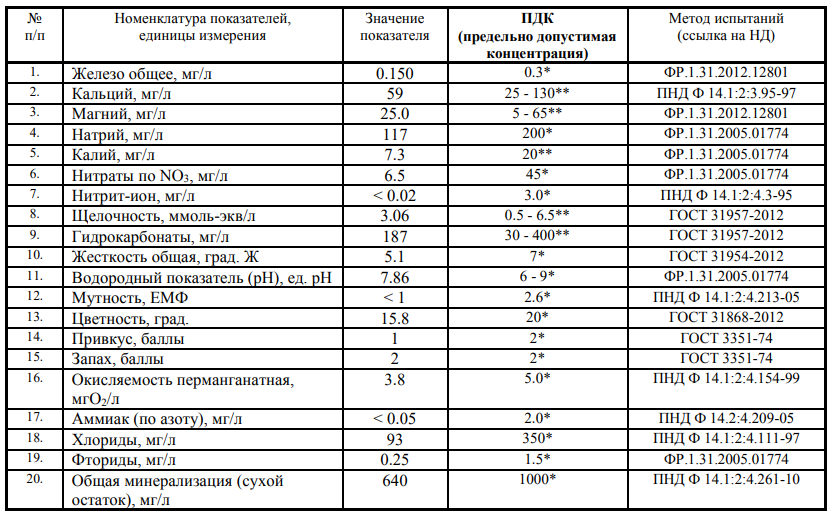
(2)
(3)
Anders Dahle Thorsen
Экспериментальный анализ прочности и моделирование материалов 3D-печатных деталей
Магистерская работа по проектированию продуктов и систем Супервайзер: Генри Питер Пиль
июнь 2019 г.
Норвежский университет науки и технологий Инженерный факультет
Департамент морских операций и гражданского строительства
(4)
(5)
Реферат
Мир инженерии наполнен глубокими знаниями традиционного анализа прочности
методы, восходящие к десятилетиям. По мере того, как мир движется вперед, начинают появляться новые вещи
от людей, пробующих новые вещи, чтобы увидеть, возможно ли совместить традиционные методы и
новые технологии для расширения наших знаний. Следующая магистерская диссертация представляет собой глубокое погружение в
3D-печать и оценка прочностных характеристик 3D-печатного материала.
В частности, определение модуля Юнга напечатанной на 3D-принтере полимолочной кислоты.
Сочетание традиционных методов с новыми технологиями может выявить новые аспекты, которые раньше не видел. Экспериментальные испытания проводятся с использованием традиционной прочности на растяжение. методы. Наряду с экспериментальной проверкой в качестве численного метода использовался метод конечных элементов. инструмент для анализа, поставляемый Siemens NX. Был проведен численный анализ, чтобы определить соотношение коэффициентов жесткости выбранных геометрий.
Результаты испытаний были статистически проанализированы с использованием MATLAB и подтверждены с результатами из других независимых источников, чтобы сделать вывод о возможности применения метода.
(6)
(7)
Sammendrag
Ingeniørens omfattende kunnskaper om styrkeanalyser er i all hovedsak basert på tradis-
Jonell analysemetodikk fra langt tilbake i tid. Nå som verden beveger seg fremover,
popper det stadig opp nye technologier, produkter, krav og Problemstillinger, hvor en kan
undersøke mulighetene for å kombinere tradisjonelle metoder med ny teknologi, for å
komme и др kunnskapsmessig стег видере. Masteroppgaven er et dypdykk i 3D-печать и
оценка качества материалов для 3D-печати. Nærmere bestemt, идент.
Тифические эластичные модули с 3D-печатью Полимолочная кислота.
Nå som verden beveger seg fremover,
popper det stadig opp nye technologier, produkter, krav og Problemstillinger, hvor en kan
undersøke mulighetene for å kombinere tradisjonelle metoder med ny teknologi, for å
komme и др kunnskapsmessig стег видере. Masteroppgaven er et dypdykk i 3D-печать и
оценка качества материалов для 3D-печати. Nærmere bestemt, идент.
Тифические эластичные модули с 3D-печатью Полимолочная кислота.
Å комбинат традиционных методов с использованием технологий, который может использоваться в качестве альтернативы аспек- ter som tidligere ikke er registrert. Forsøkstestene er gjort ved hjelp av tradisjonelle strekkfasthets-methoder. Ведение экспериментов с конечными элементами Метод анализа числового риска, основанный на Siemens NX. Числовой анализ ysen ble utført for å identifisere et stivhetskoeefsientforhold mello de valgte geometriene.
Resultat fra testene er statistisk analysert ved hjelp av MATLAB og validert med res-
tater fra andre uavhengige kilder, для å konkludere metodens gjennomførbarhet.
(8)
(9)
Предисловие
Эта магистерская диссертация написана от имени Департамента океанического и гражданского строительства. в Норвежском университете науки и технологии в Олесунне. Он завершает 2-летний степень магистра в области проектирования продуктов и систем и является конечным результатом проделанной работы в течение весеннего семестра 2019 года. Со всеми новыми технологиями, Из разных секторов промышленности я считаю 3D-печать наиболее интересной. 3D печать сама по себе не нова, но с точки зрения изготовления 3D-печатных промышленных деталей, это относительно новое. Этот тезис включает в себя исследование оценки модуля Юнга 3D печатных материалов. Для этого тезиса была использована полимолочная кислота. Диссертация была представлено и написано под руководством доцента Генри Питера Пиля в NTNU Олесунн.
Предполагается, что читатель обладает базовыми знаниями в области инженерии, но мы надеемся, что диссертация
написан таким образом, что за ним относительно легко следовать, если это не так.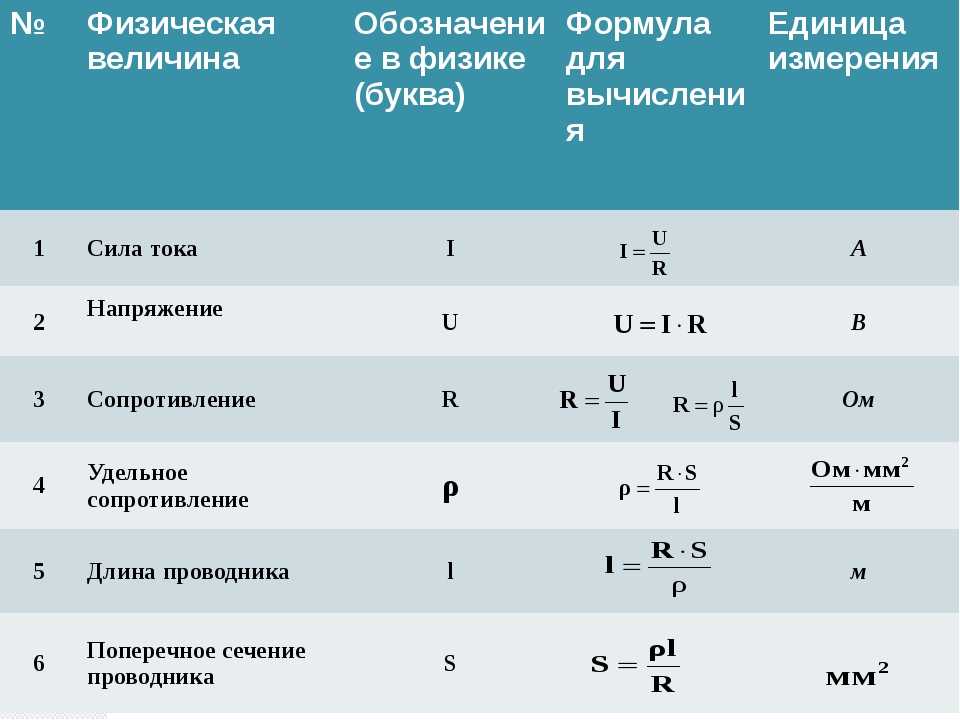 Работающий
в течение семестра с этой диссертацией я приобрел большой опыт в организации
работа, 3D-печать, программирование в MATLAB и экспериментальные методы. При выборе-
Работая над магистерской диссертацией, я хотел сделать что-то, что включало бы реальные физические эксперименты.
и что-то связанное с 3D-печатью. В этой диссертации мне посчастливилось получить
оба. Магистерская диссертация была сложной и полезной, и я доволен своим
выбор. Я благодарен за полученные знания, и мое личное развитие на протяжении всего
семестр.
Работающий
в течение семестра с этой диссертацией я приобрел большой опыт в организации
работа, 3D-печать, программирование в MATLAB и экспериментальные методы. При выборе-
Работая над магистерской диссертацией, я хотел сделать что-то, что включало бы реальные физические эксперименты.
и что-то связанное с 3D-печатью. В этой диссертации мне посчастливилось получить
оба. Магистерская диссертация была сложной и полезной, и я доволен своим
выбор. Я благодарен за полученные знания, и мое личное развитие на протяжении всего
семестр.
(10)
(11)
Благодарности
Есть много людей, которым я должен выразить свою благодарность. Прежде всего, я выражаю глубочайшую признательность моему научному руководителю, доценту Генри Питеру Пилю. Ваш руководство и знания были неоценимы для этой диссертации. Ты меня так выучил много за те два года, что я тебя знаю. Ты всегда уделял мне время, даже когда вы заняты, и я хочу сказать спасибо!
Кроме того, хочу выразить особую благодарность Андре Транвогу – главному инженеру NTNU. Олесунн. Вы были одним из первых учителей, с которым я познакомился в NTNU, и у вас есть
многому меня научил. Вы всегда готовы помочь, и, как и ожидалось, вы стремились
помогите мне провести эксперименты в моем исследовании. Благодарю вас!
Олесунн. Вы были одним из первых учителей, с которым я познакомился в NTNU, и у вас есть
многому меня научил. Вы всегда готовы помочь, и, как и ожидалось, вы стремились
помогите мне провести эксперименты в моем исследовании. Благодарю вас!
Я также хочу поблагодарить Ларса Петтера Брюна, доцента NTNU Ålesund. То есть за вашу проницательность и знания в области машиностроения, а также за то, что дверь вашего офиса всегда открыт для любых вопросов, которые у меня были за все пять лет, что я знаю тебя.
Я хочу поблагодарить NTNU Ålesund за пять лет моего обучения здесь за предоставление необходимые инструменты и рабочее место для нас, студентов, чтобы преуспеть в качестве студентов. А также для давняя дружба, которую я приобрел за все время, проведенное здесь.
Наконец, я хочу выразить благодарность моей семье и девушке.
Всем спасибо!
АДТ
(12)
(13)
Содержание
Резюме i
Саммендраг III
Предисловие v
Благодарности vii
Содержание ix
Список иллюстраций xiii
Список таблиц xv
Номенклатура xvii
1 Введение 1
1. 1 Проблема . . . 1
1 Проблема . . . 1
1.2 Мотивация . . . 3
1.3 Область применения . . . 4
1.4 Цели и вопросы исследования . . . 5
1.5 Структура отчета . . . 6
2 Обзор литературы 7 2.1 3D-печать. . . 7
2.2 Экспериментальные методы . . . 18
2.3 Численные методы . . . 23
2.4 Сопутствующая работа . . . 25
3 Методология 27
(14)
3.3 Экспериментальное испытание – установка для испытания на растяжение . . . 34
3.3.1 Экспериментальный тест 1 – Особенности . . . 34
3.3.2 Экспериментальный тест 2 – Особенности . . . 35
3.4 Статистический анализ . . . 36
3.4.1 Сглаживание необработанных данных . . . 36
3.4.2 Линейная область . . . 38
3.5 Структурный анализ . . . 41
3.5.1 Коэффициент жесткости . . . 41
3.5.2 Сетка . . . 43
3.5.3 Ограничения . . . 45
3.5.4 Загрузка . . . 46
3.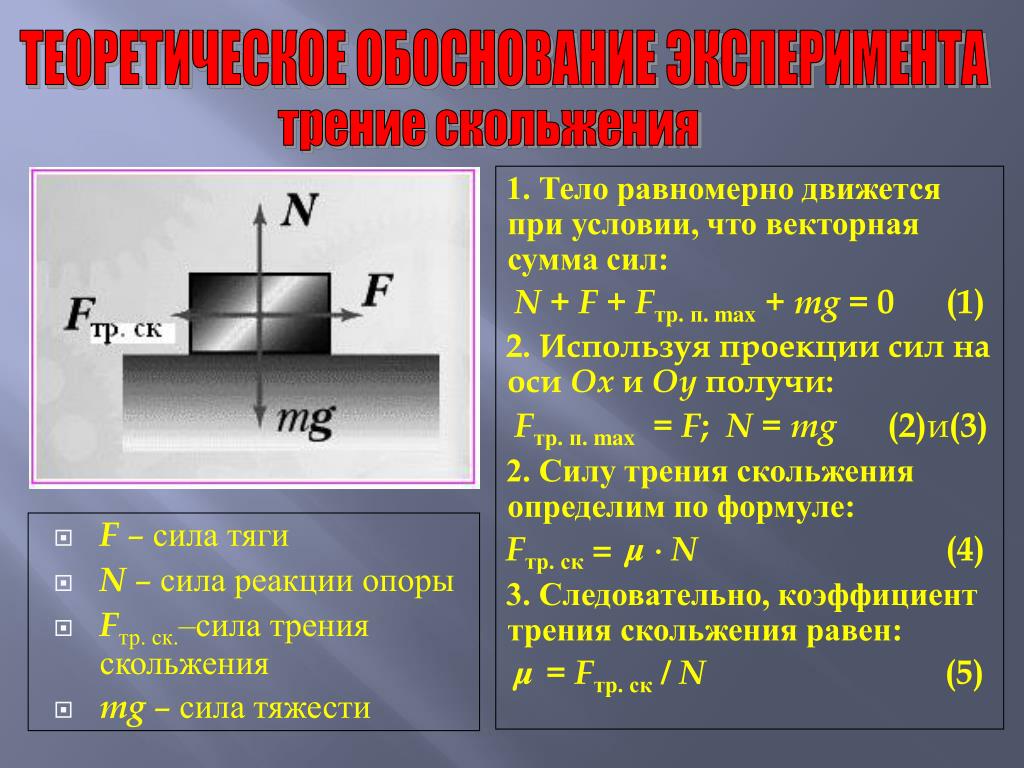 5.5 Деформация . . . 48
5.5 Деформация . . . 48
4 Результаты и обсуждение 51 4.1 Экспериментальные испытания Анализ разрушения . . . 51
4.2 Модуль Юнга PLA . . . 52
4.2.1 Начальный модуль Юнга из экспериментальных тестов . . . 52
4.2.2 Модуль Юнга из экспериментальных испытаний с коэффициентом жесткости . . 55
5 Заключение и будущая работа 61 5.1 Заключение. . . 61
5.2 Будущая работа . . . 62
Библиография 63 Приложение 66 Образцы для испытаний 67 A.1 Экспериментальный тест 1 – Обзор сравнения. . . 68
A.1.1 Тест 2.1 – Тест 2.5, напечатано под углом 0°. . . 70
A.1.2 Тест 3.1 – Тест 3.5, печать под углом 45° . . . 75
A.1.3 Тест 3.6 – Тест 3.11, напечатано под углом 90° . . . 80
A.2 Экспериментальный тест 2 — Обзор сравнения . . . 86
A.2.1 Тест 4.1 – Тест 4.5, напечатано под углом 0°. . . 88
A.2.2 Тест 4.6 – Тест 4.10, напечатано под углом 45° . . . 93
A.2.3 Тест 4.11 – Тест 4. 15, напечатано под углом 90° . . . 98
15, напечатано под углом 90° . . . 98
(15)
B.3 Размер элемента сетки 2 мм . . . 104
B.4 Размер элемента сетки 4 мм . . . 105
B.5 Размер элемента сетки 8 мм . . . 105
Скрипты C MATLAB 107 C.1 Основной сценарий, пример T3.1. . . 108
C.2 Начальное сравнение модулей Юнга . . . 115
C.3 Сравнение модулей Юнга . . . 117
C.4 Исследование конвергенции сетки . . . 121
D Листы данных 123
(16)
(17)
Список рисунков
1.1 Направление сборки – [1] . . . 2
1.2 Разрушение прочности – [3] . . . 3
1.3 Область применения . . . 4
2.1 Классификация технологий 3D-печати – [5] . . . 8
2.2 Процесс экструзии материала – [6] . . . 9
2.3 Процесс SLA – [7] . . . 10
2.4 Процесс плавки в порошковом слое – [8] . . . 11
2.5 HP Jet Fusion Process — [10] . . . 12
. . 12
2.6 Аддитивное производство – [12] . . . 13
2.7 Нить для 3D-печати на барабане — [14] . . . 14
2.8 Ориентация слоя . . . 15
2.9 Напечатано под углом 0°. . . 15
2.10 Напечатано под углом 45° . . . 15
2.11 Напечатано под углом 90° . . . 15
2.12 Геометрия заполнения – [15] . . . 16
2.13 Образец для испытаний на растяжение. . . 19
2.14 Установка для испытаний на растяжение. . . 19
2.15 Кривая хрупкого и пластичного материала. . . 20
2.16 Кривая деформации стали . . . 21
2.17 Закон Гука – [18] . . . 22
2.18 Визуальное представление шагов анализа – [21] . . . 23
2.19 Размер элемента и напряжение фон Мизеса – [23] . . . 24
3.1 CAD-модель . . . 28
3.2 Модель Cura. . . 28
3.3 Готовая модель. . . 28
3.4 Геометрия 1 . . . 29
(18)
3.11 Сглаженные данные увеличены . . . 37
. . 37
3.12 Сглаженные необработанные данные Test3.1. . . 37
3.13 Линейная область . . . 38
3.14 Дифференцированный . . . 38
3.15 Распространение ядра . . . 39
3.16 Среднее значение градиента . . . 39
3.17 Расчетный линейный диапазон . . . 39
3.18 Диапазон укороченной силы – кривая удлинения. . . 39
3.19 Пример длины . . . 41
3.20 Экстензометр – [28] . . . 41
3.21 Модельный ряд . . . 42
3.22 Разделенная CAD-модель модели 4 . . . 43
3.23 Сетка модели 4 . . . 43
3.24 Схождение сетки . . . 44
3.25 Ссылка на систему координат . . . 45
3.26 Ограничение поверхности . . . 46
3.27 Ограничение узлов . . . 46
3.28 Приложенная сила . . . 46
3.29 Модель 4 с поддержкой FEM . . . 47
3.30 Жесткость k . . . 48
4.1 Чистый излом по шаблону. . . 51
4.2 Диагональный излом по рисунку . . . 51
4. 3 Геометрия 1 – Печатается под углом 0° . . . 52
3 Геометрия 1 – Печатается под углом 0° . . . 52
4.4 Геометрия 2 – Печатается под углом 0° . . . 52
4.5 Геометрия 1 – Печатается под углом 45° . . . 53
4.6 Геометрия 2 – Печатается под углом 45°. . . 53
4.7 Геометрия 1 – Печатается под углом 90° . . . 53
4.8 Геометрия 2 – Печатается под углом 90° . . . 53
4.9 Начальный модуль Юнга . . . 54
4.10 Модуль Юнга . . . 56
4.11 Отдельная прямоугольная диаграмма модуля Юнга . . . 57
4.12 Изготовление образцов для испытаний. . . 58 привет
(19)
Список таблиц
2.1 Экструзия материалов – за и против . . . 9
2.2 НДС Полимеризация – плюсы и минусы. . . 10
2.3 Fusion с порошковым покрытием – плюсы и минусы. . . 11
2.4 Multi Jet Fusion – плюсы и минусы. . . 12
3.1 Настройки печати Ultimaker Cura . . . 30
3.2 Тестовая матрица . . . 32
4.1 Независимые источники . . . 59
. . 59
(20)
(21)
Номенклатура
Сокращения
АБС-акрилонитрил-бутадиен-стирол
ASTM Американское общество испытаний и материалов Автоматизированное проектирование САПР
Компьютерное проектирование CAE Автоматизированное производство CAM Обработка прямого света DLP
Анализ конечных элементов методом конечных элементов Метод конечных элементов FEM Моделирование плавленого осаждения FDM Изготовление плавленых нитей FFF
ISO Международная организация по стандартизации LS лазерное спекание
PDF Порошковая кровать Fusion PLA-полимолочная кислота SLA-стереолитография
Селективное лазерное спекание SLS
(22)
Удлинение мм
F Сила N
L Длина мм
мкм Микро 10 3
k Жесткость Н/мм
✏ Штамм [ ]
Напряжение Н/мм 2
E Модуль Юнга, МПа
(23)
(24)
(25)
Глава 1.
 Введение
Введение1.1 Проблема
производство продуктов в результате доступных технологий 3D-печати. Некоторые из продукты, которые производятся сейчас, раньше были невозможны из-за ограничений старого методы изготовления. Растущее использование 3D-печати в качестве производственного метода в современной промышленности, требует более глубокого понимания механического поведение 3D-печатных деталей. Образ мышления относительно производства новых продуктов необходимо изменить в результате быстрого темпа новых производственных процессов, которые де- развивается. Проверка прочностных характеристик деталей, напечатанных на 3D-принтере, проблематична. В В некоторых случаях производитель материалов для 3D-печати предоставляет результаты испытаний на прочность конкретный материал, который они предоставляют, но эти результаты часто различаются между производителями.
Кроме того, трудно сказать, проводятся ли эти тесты для небольшой партии или для тысяч.
Технология 3D-печати не нова, а является воплощением 3D-технологий промышленного качества. печатные детали являются новыми, если, например, сравнивать их со сталью. Сталь имеет изотропную
свойство материала в отличие от полимолочной кислоты (PLA), которая является анизотропным материалом.
печатные детали являются новыми, если, например, сравнивать их со сталью. Сталь имеет изотропную
свойство материала в отличие от полимолочной кислоты (PLA), которая является анизотропным материалом.
Анизотропный материал означает, что свойства материала в объекте неодинаковы во всех направления и, следовательно, более уязвимы для отказа при приложении нагрузки. это усиливается тем фактом, что ориентация деталей, напечатанных на 3D-принтере, также имеет большое влияние. на прочность отдельной детали, отображенной на рис. 1.1. Стальная проволока и сталь куб имеет те же свойства материала, тогда как 3D-печатная проволока и куб из PLA отличается. Работа с анизотропным материалом является сложной задачей, а также потенциально опасно, если не сделано правильно. Инженеры до сегодняшнего дня использовали сталь на протяжении веков.
(26)
анализ не простая задача. Кроме того, как 3D-печатный объект печатается с точки зрения
ориентации влияет на прочность. Несмотря на то, что модуль Юнга материала
может быть известен, он может не полностью отражать характеристики модуля Юнга
при выполнении теста на различных 3D-печатных объектах.
Несмотря на то, что модуль Юнга материала
может быть известен, он может не полностью отражать характеристики модуля Юнга
при выполнении теста на различных 3D-печатных объектах.
Рисунок 1.1: Направление сборки — [1]
(27)
1.2. МОТИВАЦИЯ
1.2 Мотивация
Мотивация, стоящая за этим исследованием, состоит в том, чтобы точнее сделать функциональные 3D
печатных компонентов, таким образом изучите свойства их материалов. При изготовлении компо-
Для клиентов, как инженеру, вам нужно знать, насколько прочен сам материал,
потому что это повлияет на дизайн компонента. В противном случае компоненты могут
должны быть чрезмерно построены, что противоречит всей цели создания конкретных
оптимизированные 3D-печатные детали. Для этого требуется процедура тестирования,
поступающий материал и его исполнение. В случае успеха это сделает работу инженеров более
эффективным и точным. Это даст инженеру более быстрые и точные расчеты на основе
их расчеты того, насколько толстым или тонким должен быть или может быть изготовлен данный компонент.
Изменение свойств материала из-за изменения способа его изготовления может иметь огромные последствия неправильного выполнения, представленные на рис. 1.2. Есть много компаний участие, и большая деятельность, связанная с 3D-печатью промышленного назначения, что делает эта магистерская диссертация весьма актуальна [2].
Рисунок 1.2: Разрушение прочности — [3]
(28)
1.3 Объем
Объем данной магистерской диссертации будет в основном состоять из трех частей, показанных на рисунке 1.3.
Секция 3D-печати будет состоять из изготовления тестовых образцов,
подсчет проверен в этом исследовании. Это было сделано в соответствии с конкретными измерениями, представленными
далее в диссертации. Тестовые образцы были изготовлены на Ultimaker 2+, который представляет собой 3D-принтер.
принтер, поставляемый Ultimaker. В этом принтере используется метод наплавления (FDM) — технология.
нология и материал, который был использован, называется PLA.
Раздел «Экспериментальные методы» состоит из экспериментальных тестов, проведенных в рамках данного исследования.
Для определения прочностных свойств материала проводятся традиционные испытания прочности на растяжение. б/у, находится в мастерской NTNU Ålesund. Испытания проводятся в соответствии с рекомендациями ISO. и под руководством главного инженера Андре Транвога в NTNU.
Численные методы будут выполняться с использованием решателя FEM Nastran в Siemens NX.
Анализ методом конечных элементов будет использоваться для определения соотношения коэффициентов жесткости между вантовые геометрии.
Рисунок 1.3: Область применения
(29)
1.4. ЦЕЛЬ И ИССЛЕДОВАНИЕ ВОПРОСЫ
1.4 Цель и вопросы исследования
Основная цель данной диссертации — изучить возможность разработки процедуры тестирования.
во время измерения свойств материала 3D-печатных деталей, изготовленных из PLA. Подтвердить
результаты, полученные из диссертации, в независимые источники.
Вопросы исследования, на которых будет основываться эта диссертация, и над которой она работала:
• Вопрос 1: Как измерить прочность детали, напечатанной на 3D-принтере из PLA?
• RQ 2: Как можно экспериментально и численно оценить прочность свойства напечатанных на 3D-принтере деталей из PLA?
• RQ 3: Каковы процедуры экспериментальной и численной оценки правильности оценка прочности?
(30)
1.5 Структура отчета
Эта магистерская диссертация разделена на пять глав и содержит следующее:
Глава 1 – Введение:
– В первой главе введение, содержащее проблему, мотивацию, объем, цель и представлены исследовательские вопросы, касающиеся этой диссертации.
Глава 2. Обзор литературы:
– Во второй главе текущий старт арта по быстрому прототипированию, измерение прочности представлены предположения и экспериментальный анализ.
Глава 3 – Методология:
– Третья глава содержит прототипирование, экспериментальные испытания, статистические и структурные
анализ.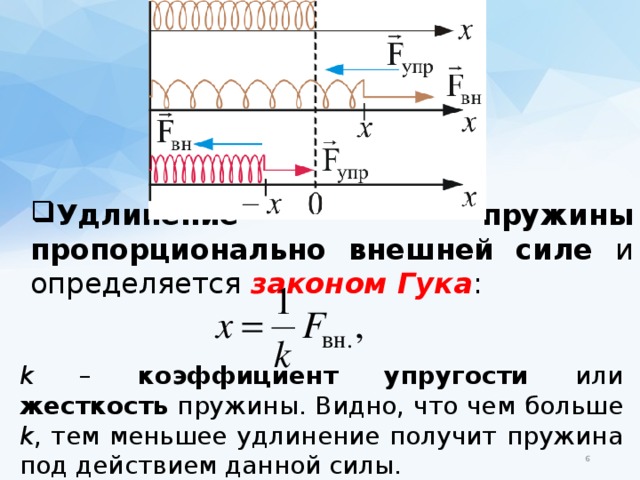
Глава 4 – Результаты и обсуждение:
Глава 5 – Заключение и будущая работа:
Приложение:
— содержит все отдельные экспериментальные тесты, исследование сходимости сетки, MATLAB скрипты и соответствующие таблицы данных.
(31)
Глава 2
Обзор литературы
2.1 3D-печать
3D-печать — это производственный процесс, при котором деталь создается слой за слоем. 3D печать-
ing имеет множество различных вариаций и в настоящее время встречается во многих различных отраслях промышленности с
его индивидуальные преимущества и ограничения. Они используются в промышленности, медицине, высоких технологиях,
и коммерческие товары. Некоторые из них дешевые, а некоторые очень дорогие. Материалы
может быть в диапазоне пластика, смолы, металла, бумаги и т. д. 3D-печать сильно развилась
быстро за последние 10-15 лет из более или менее бесполезного превратился в весьма ценный
инструмент многих производителей.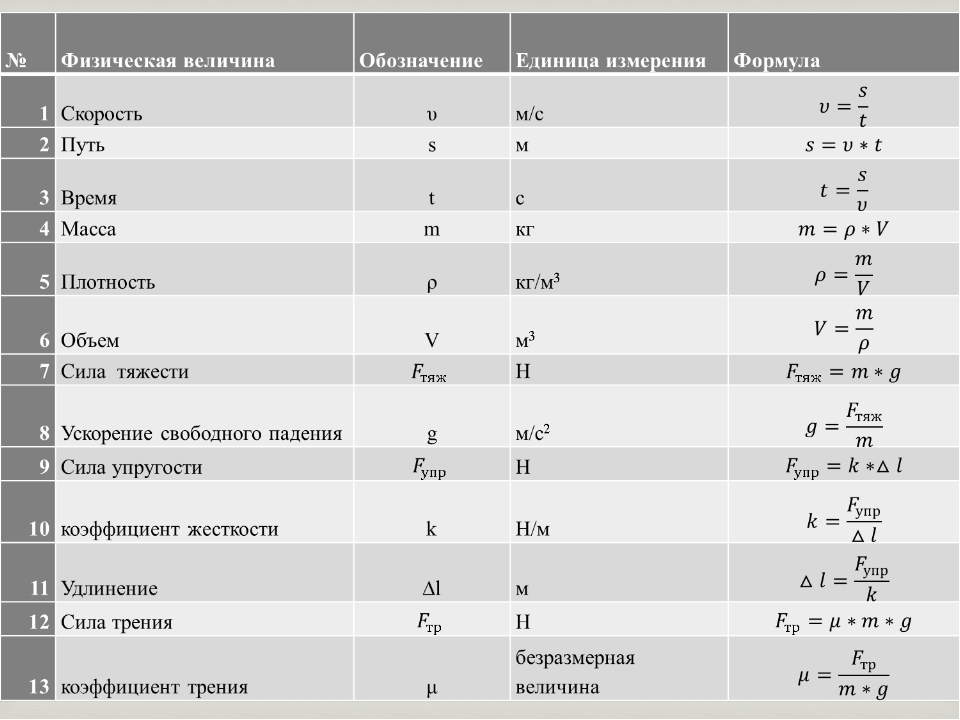 Особенно после 2009 годакогда патент
для FDM-печати истек и сделал ее доступной для всех [4].
Особенно после 2009 годакогда патент
для FDM-печати истек и сделал ее доступной для всех [4].
Спрос на высококачественные детали и простые в использовании машины постоянно растет.
Инженеры в различных секторах используют его для создания прототипов на ранней стадии проектирования для наиболее
часть, но из-за растущего развития более качественных и быстрых 3D-принтеров они
медленно выводят инженерный мир к новым возможностям. Наиболее существенной причиной
исследования по внедрению 3D-печати в машиностроение не должны ограничиваться
традиционными способами изготовления. Как уже было сказано во вступлении, есть части, которые
вы можете создать с помощью 3D-печати то, что невозможно произвести при использовании традиционной
методы изготовления. В 2015 году ISO/ASTM 52900 Стандарт был создан, чтобы
dardize всю терминологию, а также классификацию различных процессов 3D-печати
категории. Всего в этом стандарте установлено семь технологий. Все
они и связанные с ними процессы описаны на рис. 2.1.
2.1.
(32)
Рисунок 2.1: Классификация технологий 3D-печати – [5]
(33)
2.1. 3D ПЕЧАТЬ
Технологии
Экструзия материалов
Наиболее распространенной технологией экструзии материалов является производство плавленых нитей или FFF.
(обычно называемое моделированием наплавленного осаждения или FDM) [5]. FDM – это метод,
материал загружается в принтер и нагревается до точки плавления, а затем
проходил через тонкое сопло, показанное на рис. 2.2. Экструзионное сопло крепится к
3-осевая система, позволяющая перемещаться в направлениях X, Y и Z. Это создает строку
материал, который наносится слой за слоем в заранее определенных местах, где затем охлаждается
и затвердевает. FDM — очень распространенный способ 3D-печати, поскольку он относительно дешев, но
имеет некоторое ограничение, в котором прочностные характеристики не указаны должным образом. Таким образом, это
имеет путь к тому, чтобы стать надежным производственным инструментом для промышленных деталей, как его стенды
в настоящее время. Наиболее существенные плюсы и минусы этой технологии представлены в таблице 2.1.
Наиболее существенные плюсы и минусы этой технологии представлены в таблице 2.1.
Рисунок 2.2: Процесс экструзии материала — [6]
Таблица 2.1: Экструзия материалов – плюсы и минусы Экструзия материала
Плюсы Минусы
Экономичность Требует много времени Удобные для пользователя ограничения сборки Высокое визуальное качество Анизотропный
(34)
НДС Полимеризация – SLA/DLP
При этом методе структура изготавливается путем селективного послойного отверждения полимерной смолы.
Материалы, используемые в стереолитографии (SLA), представляют собой светочувствительные термореактивные полимеры.
которые бывают в жидком виде. Это делается с помощью ультрафиолетового лазерного луча. Соглашение об уровне обслуживания
процесс известен как первая технология 3D-печати, созданная еще в 1986. СУО
имеет много общих характеристик с технологией Direct Light Processing (DLP), еще одной фотокамерой Vat.
Технология тополимеризационной 3D печати. Для простоты эти две технологии могут быть
на равных [7]. Сам по себе процесс SLA можно разделить на восходящий и верхний.
вниз. Именно так ориентируется рабочая пластина, которая определяет способ расположения объектов.
печататься. Используя человеческое тело в качестве примера, технология «сверху вниз» сначала
напечатайте ноги и закончите в голове, тогда как снизу вверх сначала напечатает голову и
наконец ноги. Из-за этого существуют разные атрибуты относительно их плюсов и минусов.
представлены в таблице 2.2.
Для простоты эти две технологии могут быть
на равных [7]. Сам по себе процесс SLA можно разделить на восходящий и верхний.
вниз. Именно так ориентируется рабочая пластина, которая определяет способ расположения объектов.
печататься. Используя человеческое тело в качестве примера, технология «сверху вниз» сначала
напечатайте ноги и закончите в голове, тогда как снизу вверх сначала напечатает голову и
наконец ноги. Из-за этого существуют разные атрибуты относительно их плюсов и минусов.
представлены в таблице 2.2.
Рисунок 2.3: Процесс SLA — [7]
Таблица 2.2: Полимеризация НДС – плюсы и минусы НДС Полимеризация
Снизу вверх Сверху вниз
Плюсы Минусы Плюсы Минусы
Стоимость Объем сборки Скорость Стоимость
Доступность Ассортимент материалов Объем сборки Специальное обучение Срок постобработки
для поддержки
Переключение материалов создает отходы из-за снятия бака
(35)
2. 1. 3D ПЕЧАТЬ
1. 3D ПЕЧАТЬ
Порошковая кровать Fusion
В индустрии 3D-печати с использованием технологии Powder Bed Fusion (PBF) с поли- полимерного порошка для производства компонентов, которые обычно называют селективным лазерным спеканием. ing(SLS) или просто Laser Sintering(LS) [5]. Эта технология использует высокоточные лазерные лучи. чтобы расплавить и соединить зерна материала, чтобы создать твердый объект, визуализированный на рисунке 2.4. материал распределяется по заданной платформе сборки, куда направляется лазерный луч данный шаблон слоя для формирования объекта. Когда объект создается, он использует все свои пространство для постройки, а значит много лишнего материала. Этот избыточный материал используется в качестве опорной конструкции на протяжении всего процесса. Этот избыточный материал затем позже удалено, чтобы сформировать конкретный объект. Наиболее существенные плюсы и минусы относительно этого технология представлена в таблице 2.3.
Рисунок 2. 4: Процесс плавки в порошковом слое — [8]
4: Процесс плавки в порошковом слое — [8]
Таблица 2.3: Сплав в порошковом слое – плюсы и минусы Порошковая кровать Fusion
Плюсы Минусы
Высокая точность Дорогой
Несколько ограничений сборки Неудобный для пользователя
Твердый Хрупкий
(36)
HP Multi Jet Fusion
Эта конкретная технология добавлена из-за ее положения в маркировке. Этот конкретный
Технология разработана HP. Это относится к той же категории, что и метод SLS,
PBF-технология. Этот метод подобен обычному копировальному аппарату, визуализируемому в
Рисунок 2.5. Это, в отличие от чернил, связующее, которое будет работать как клей для соединения
зерна материала для формирования объекта. При размещении связующего источник тепла нагревает
связующее для соединения его с твердым телом слой за слоем. После этого сделано все лишнее
материал удаляется, а твердая часть помещается в печь для удаления любых внутренних и
внешние напряжения [9].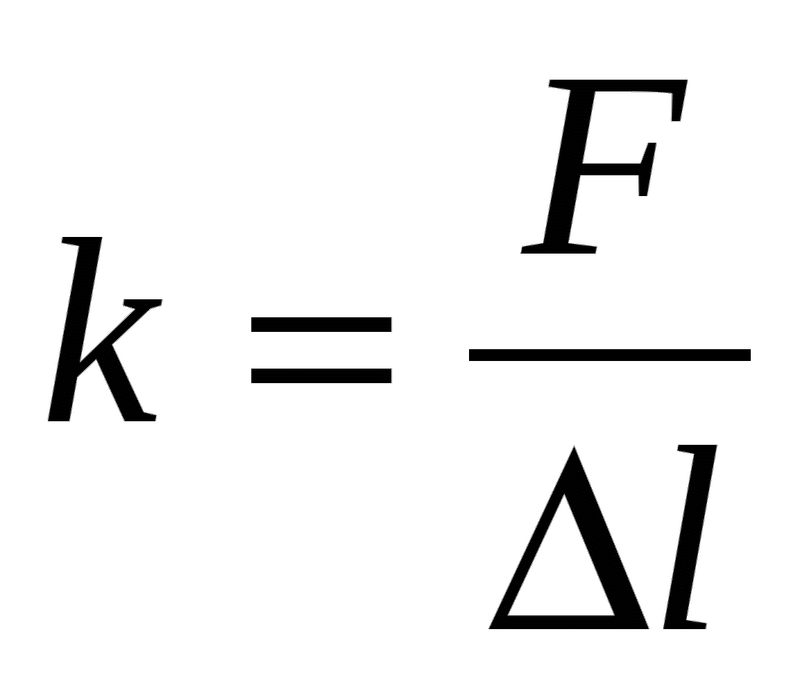 Плюсы и минусы этой технологии показаны в таблице 2.4.
Плюсы и минусы этой технологии показаны в таблице 2.4.
Рисунок 2.5: Процесс HP Jet Fusion — [10]
Таблица 2.4: Multi Jet Fusion – плюсы и минусы HP Multi Jet Fusion
Плюсы Минусы
Высокая точность Дорогой
Прочность материала Неудобен в использовании
Пространство скорости
Все эти технологии относятся к термину 3D-печать, но они также относятся к более широкий термин «аддитивное производство». Аддитивное производство часто неправильно воспринимается как 3D-печать, но это не одно и то же [11]. На рис. 2.6 все разные производственные технологии, которые подпадают под общий термин «аддитивное производство». отображаются.
(37)
2.1. 3D ПЕЧАТЬ
ADDITIVE MANUF A CTURING TECHNOL OGIES Fused Deposition Modeling FDM MJF Multi Jet Fusion Fused with agent и энергия Пластик Пластик Металл
Material e xtrusion Powder bed fusion Binder jetting NanoP article Jetting NP J
Струйная обработка материала Отверждение нагревание DLP
Цифровая обработка света
CDLP
Непрерывная цифровая обработка света
Материал Струйная обработка MJ
Ванная фотополимеризация
Отверждение с помощью проектора Отверждение светодиодом и o
кислород Пластик Пластик
Отверждение УФ-светом Пластик
BJ Распылитель связующего
Соединение клеем Гипс, песок Металл
Пластик Композит (CFF)
Бумага Композит
Металл Гипс, Песок
Селективный Лазерное спекание SLS
Сплав с лазером Прямой металл L aser Sintering 0003 Selective L Плавка aser DMLS/SLM Металл
Электрон Лучевая плавка ЭБМ
Сплавленный с электронно-лучевой Металл
Сплав с лазер Металл
Прямое осаждение энергии Лазерная техника Форма сетки ЛИНЗА
Сплавленный с электронно-лучевой Металл
Электронно-лучевой Аддитивное производство EBAM
Листовое ламинирование Laminated Object Manufacturing LOM Drop On Demand DOD Milled to form W ax 3D-ХАБ S
Пластик Композит Бумага Композит ПРУСА по ЙОЗЕФ ПРУСА
(38)
Материал
PLA
Материал, который будет использоваться в этом исследовании, представляет собой материал PLA, который является одним из
наиболее часто используемые материалы для 3D-печати в мире. Он очень универсален и прост в использовании,
а также обеспечивает хорошую точность. Из-за того, как он построен, существует множество
цвета на выбор, которые не оказывают заметного влияния на его производительность. Это дешево и
также один из самых экологически чистых материалов по маркировке. PLA является производным
из кукурузы и сахарного тростника, что также делает материал возобновляемым и биоразлагаемым
[13]. Наличие материала, который восстанавливается путем нагревания его до точки плавления, является
огромное преимущество и сведет чрезмерные потери к минимуму, если все сделано правильно. В качестве
как уже говорилось в предыдущих разделах, материал является анизотропным, а свойства материала
связи будут иметь разные значения при воздействии на них силы. Материал большей частью
поставляется от производителей в небольших бочках, представленных на рис. 2.7. Материал, который
был использован в исследованиях, предоставленных RS и 3DNet.
Он очень универсален и прост в использовании,
а также обеспечивает хорошую точность. Из-за того, как он построен, существует множество
цвета на выбор, которые не оказывают заметного влияния на его производительность. Это дешево и
также один из самых экологически чистых материалов по маркировке. PLA является производным
из кукурузы и сахарного тростника, что также делает материал возобновляемым и биоразлагаемым
[13]. Наличие материала, который восстанавливается путем нагревания его до точки плавления, является
огромное преимущество и сведет чрезмерные потери к минимуму, если все сделано правильно. В качестве
как уже говорилось в предыдущих разделах, материал является анизотропным, а свойства материала
связи будут иметь разные значения при воздействии на них силы. Материал большей частью
поставляется от производителей в небольших бочках, представленных на рис. 2.7. Материал, который
был использован в исследованиях, предоставленных RS и 3DNet.
Рисунок 2.7: Нить для 3D-печати на барабане — [14]
Ориентация
В технологии FDM, как указано выше, используется сопло для выдавливания материала и
строить деталь слой за слоем. Благодаря этому способу изготовления деталь будет иметь
различные прочностные характеристики в зависимости от ориентации детали.
печатается внутри. Поскольку печатный материал выкладывается слой за слоем в длинную цепочку материала
заставит струны материала действовать как струны материальных волокон. Наличие продольных волокон
при воздействии на волокна сила вдоль волокон значительно сильнее, чем при воздействии на поперечные волокна.
Благодаря этому способу изготовления деталь будет иметь
различные прочностные характеристики в зависимости от ориентации детали.
печатается внутри. Поскольку печатный материал выкладывается слой за слоем в длинную цепочку материала
заставит струны материала действовать как струны материальных волокон. Наличие продольных волокон
при воздействии на волокна сила вдоль волокон значительно сильнее, чем при воздействии на поперечные волокна.
В упрощенном виде это показано на рис. 2.8.
(39)
2.1. 3D ПЕЧАТЬ
Рисунок 2.8: Ориентация слоя
Разъяснение ориентации
Различные ориентации, в которых напечатаны тестовые образцы, показаны на рисунке.
2.9 – Рисунок 2.11. Благодаря тому, как 3D-принтер от Ultimaker 2+ укладывает нить
экструдированный материал на рабочей пластине, это повлияет на то, как будет выглядеть испытуемый образец.
построен. Когда тестовый образец печатается под углами 0° и 9°0°, принтер применяет
экструдированный материал в поперечном направлении под углом 45°. При этом, когда испытательный образец
помещается под углом 45 ° в рабочую пластину, что приводит к продольному и поперечному отпечатку
шаблон. Это делается для выявления различий в силе, которые могут возникнуть из-за
Ориентация печатного материала. Позже, когда будет представлен экспериментальный тест,
этот метод объяснения того, как построены отдельные части, будет использоваться.
При этом, когда испытательный образец
помещается под углом 45 ° в рабочую пластину, что приводит к продольному и поперечному отпечатку
шаблон. Это делается для выявления различий в силе, которые могут возникнуть из-за
Ориентация печатного материала. Позже, когда будет представлен экспериментальный тест,
этот метод объяснения того, как построены отдельные части, будет использоваться.
Рисунок 2.9: Напечатано под углом 0° Рисунок 2.10: Напечатано под углом 45° Рисунок 2.11: Напечатано под углом 90°
(40)
Заполнение
Заполнение — это шаблон, по которому 3D-принтер укладывает материал внутрь самого компонента. Там
в большинстве случаев есть множество различных геометрий и процентных соотношений, из которых можно выбирать при печати.
компонент. Процент заполнения, который применяется, имеет сильную корреляцию с
прочность и вес отдельных компонентов. Компонент с 90% заполнением будет
почти в каждом случае будет прочнее, чем компонент с 20% заполнением, но также будет
тяжелее. Именно здесь проявляется мастерство инженера и его понимание функций.
Состояние конечного печатного компонента имеет решающее значение. Прототип, где форма важнее всего
важная особенность, компонент может быть напечатан с очень низким заполнением, что значительно экономит
стоимость и время. Принимая во внимание, что кронштейн, который будет испытывать нагрузку, потребует более высокого заполнения.
процент. На рис. 2.12 показан выбор различных геометрий заполнения, чтобы получить
лучшее понимание того, как 3D-печатные компоненты могут быть внутри.
Именно здесь проявляется мастерство инженера и его понимание функций.
Состояние конечного печатного компонента имеет решающее значение. Прототип, где форма важнее всего
важная особенность, компонент может быть напечатан с очень низким заполнением, что значительно экономит
стоимость и время. Принимая во внимание, что кронштейн, который будет испытывать нагрузку, потребует более высокого заполнения.
процент. На рис. 2.12 показан выбор различных геометрий заполнения, чтобы получить
лучшее понимание того, как 3D-печатные компоненты могут быть внутри.
Рисунок 2.12: Геометрия заполнения – [15]
(41)
2.1. 3D ПЕЧАТЬ
Потенциальные проблемы
Поскольку в этом исследовании будет использоваться технология FDM, есть некоторые потенциальные проблемы, которые необходимо решить.
быть адресовано. Наиболее распространенные проблемы при использовании FDM — это по большей части адгезия слоев.
модели и ее возможности деформации. Так как есть много потенциальных проблем список
делается с кратким пояснением ниже.
Так как есть много потенциальных проблем список
делается с кратким пояснением ниже.
• Не прилипает к платформе — первый слой не прилипает к платформе, и печать терпит неудачу.
• Недостаточное выдавливание — принтер выдавливает недостаточно материала, что приводит к образованию зазоров в модели.
• Чрезмерная экструзия — принтер выдавливает слишком много материала, что делает модель грязной и размерность неправильная.
• Натяжение – Небольшие нити материала, возникающие при движении головки экструдера. по разным частям модели.
• Перегрев. Секции модели нагреваются слишком сильно, что приводит к их плавлению и деформации.
• Смещение слоев — слои смещены и смещены из-за ошибки в файле или механических отказ.
• Разделение слоев — Слои разделяются во время печати, разделяя модель.
• Замятие экструдера — головка экструдера заклинила и не выдавливает материал.
• Скручивание — углы модели имеют тенденцию скручиваться и деформироваться при печати.
• Мелкие элементы не напечатаны. Если модель имеет слишком мелкие детали, принтер может не печатать их. Например, уменьшение большого файла модели может привести к такому происходит.
• Деформация — деформация печатной модели из-за непостоянства и слишком высокой температуры. температура во время печати.
• Размерная точность — как следствие того, как технология FDM использует круглая нить материала для изготовления модели, во многих случаях она не будет полностью представлять его первоначальные размеры.
(42)
2.2 Экспериментальные методы
Методический подход
Проектирование любых деталей или конструкций требует от инженера понимания механическое поведение материала, который будет использоваться. Проверенный способ определения то, как материалы работают и ведут себя при воздействии нагрузок, определяется экспериментально.
Делая это, инженер может определить ограничения и сильные стороны мате-
риал, таким образом, будьте более уверены, что расчетные результаты подобны реальным. Тестировать
материалов есть разработанные международные стандарты (ISO) для того, как эти типы испытаний
должны быть выполнены. Стандарт ISO, на котором будет основано это исследование,
ИСО 527:2012 [16]. Название этого стандарта: «Пластмассы. Определение прочности на растяжение».
Это стандарт, который содержит различные методы исследования поведения при растяжении.
образцов для испытаний, а также для определения предела прочности при растяжении, модуля упругости и других
аспекты отношения напряжения/деформации при растяжении в конкретных условиях. Конкретная гео-
испытания образцов, температуры, скорости тяги машины и т. д. Это делается
чтобы результаты можно было сравнить с более ранними тестами, а также, при необходимости, воспроизвести. В
На рисунках 2.13 и 2.14 показаны типичная геометрия испытания на растяжение и установка испытания на растяжение.
Тестировать
материалов есть разработанные международные стандарты (ISO) для того, как эти типы испытаний
должны быть выполнены. Стандарт ISO, на котором будет основано это исследование,
ИСО 527:2012 [16]. Название этого стандарта: «Пластмассы. Определение прочности на растяжение».
Это стандарт, который содержит различные методы исследования поведения при растяжении.
образцов для испытаний, а также для определения предела прочности при растяжении, модуля упругости и других
аспекты отношения напряжения/деформации при растяжении в конкретных условиях. Конкретная гео-
испытания образцов, температуры, скорости тяги машины и т. д. Это делается
чтобы результаты можно было сравнить с более ранними тестами, а также, при необходимости, воспроизвести. В
На рисунках 2.13 и 2.14 показаны типичная геометрия испытания на растяжение и установка испытания на растяжение.
Во время испытания образец для испытаний, показанный на рис. 2.13, зажимается между двумя
захваты, а затем загружаются с напряжением. Чтобы определить, как работает образец,
несколько измерительных устройств, чтобы увидеть деформацию. Некоторые устройства подключены снаружи
если машина не способна сделать это сама. Образец для испытания на растяжение изготавливается в этом
способ гарантировать, что разрушение образца произойдет внутри светло-синей области. Это будет
убедитесь, что область подвергается чистому растяжению только в продольном направлении. Следовательно,
внешние части, на которых будут зажиматься захваты для удержания образца, сделаны дополнительно
большой, это для того, чтобы они не сломались в этом регионе. Причина этого в том, что
в этих внешних зонах распределение напряжения неравномерно и не обеспечит правильного
результаты, если это где разбить в этой области [17].
Чтобы определить, как работает образец,
несколько измерительных устройств, чтобы увидеть деформацию. Некоторые устройства подключены снаружи
если машина не способна сделать это сама. Образец для испытания на растяжение изготавливается в этом
способ гарантировать, что разрушение образца произойдет внутри светло-синей области. Это будет
убедитесь, что область подвергается чистому растяжению только в продольном направлении. Следовательно,
внешние части, на которых будут зажиматься захваты для удержания образца, сделаны дополнительно
большой, это для того, чтобы они не сломались в этом регионе. Причина этого в том, что
в этих внешних зонах распределение напряжения неравномерно и не обеспечит правильного
результаты, если это где разбить в этой области [17].
(43)
2.2. ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ
Рисунок 2.13: Образец для испытания на растяжение Рисунок 2.14: Установка для испытания на растяжение
Напряжение
Напряжение, действующее на конструкцию, можно рассчитать с помощью уравнения 2. 1. стресс это
мера единиц силы на единицу площади. Когда стержень, цилиндр или любой другой
конструкция растягивается под действием силы F, напряжения называются растягивающими. Если бы это было
сжать с силой F, полученные напряжения будем называть сжимающими.
1. стресс это
мера единиц силы на единицу площади. Когда стержень, цилиндр или любой другой
конструкция растягивается под действием силы F, напряжения называются растягивающими. Если бы это было
сжать с силой F, полученные напряжения будем называть сжимающими.
Однако уравнение справедливо только в том случае, если напряжения равномерно распределены поперек площадь сечения нагруженной детали [17], показанная на рис. 2.13.
= Ф
А (2.1)
(44)
Деформация ✏
Деформация ✏, которой подвергается объект, может быть выражена с помощью уравнения 2.2. Когда
на часть действует сила, она изменит свое начальное поперечное сечение. Удлинение стержня
является результатом растяжения всех элементов материала по всему объему
стержень, при условии, что стержень изготовлен из одного материала. Например, когда штанга прикладывается к
сила в осевом направлении, длина стержня будет либо растягиваться, либо сжиматься.
В общем случае удлинение сегмента равно его длине, деленной на общая длина L и умножается на полное удлинение . Следовательно, единица длины стержня будет иметь удлинение, равное 1/L раз. Это количество равно называется удлинением на единицу длины, или деформацией, и обозначается греческим буква ✏ (эпсилон) [17].
“=
л (2,2)
Результаты, полученные в результате испытаний, основаны на специфической геометрии тестовых спецификаций. имени, в котором она была исполнена. Чтобы сделать эти результаты жизнеспособными для любых других геометрий для конкретного материала можно преобразовать эти результаты в диаграммы напряжения-деформации.
Эти диаграммы могут предоставить данные о поведении материалов при воздействии на них
сила. Свойства материала в отношении максимальной прочности на растяжение, предела текучести,
Модуль Юнга, предел упругости и предел прочности — это свойства, которые можно
определить с помощью диаграмм напряжения-деформации. И они также покажут, например, если материал
является хрупким или пластичным, как показано на рис. 2.15.
И они также покажут, например, если материал
является хрупким или пластичным, как показано на рис. 2.15.
(45)
2.2. ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ
Линейная эластичность
Когда поведение материала ведет себя как упругое при воздействии нагрузки, а также отображает линейная зависимость между напряжением и деформацией, она называется линейно-упругой [17]. Это показано на рис. 2.16. Инженеру это очень важно знать при проектировании новой конструкции/изделия, чтобы избежать остаточной деформации, в результате податливость из-за специфических свойств материала.
После этой точки пропорциональности между напряжением и деформацией больше не существует; следовательно
напряжение в точке называется пределом пропорциональности. Наклон прямой линии от ориго
пределу пропорциональности называется модулем упругости или более известен как
Модуль Юнга E. Модуль Юнга действителен только в диапазоне, в котором напряжение
пропорциональна деформации, что означает, что материал вернется к своим первоначальным размерам
при снятии приложенной силы. Другими словами, в области линейной упругости. превосходящий
в этой области модуль Юнга в большинстве случаев не будет оставаться постоянным. Чем круче
уклон есть, значит материал более устойчив к растяжению, куры обладают большей жесткостью.
Другими словами, в области линейной упругости. превосходящий
в этой области модуль Юнга в большинстве случаев не будет оставаться постоянным. Чем круче
уклон есть, значит материал более устойчив к растяжению, куры обладают большей жесткостью.
Поскольку линейный уклон имеет единицы измерения напряжения, деленные на деформацию, модуль упругости имеет в тех же единицах, что и напряжение, т.е. МПа / [Н/мм 2 ]. На рисунке 2.16 показан пример мягкой стали. визуализируется кривая напряжение-деформация.
1. Линейная упругая 2. Пропорциональный предел 3. Предел текучести
4. Предел прочности при растяжении 5. Перелом
Рисунок 2.16: Кривая напряжения-деформации стали
(46)
Закон Гука
Закон определяется прямой пропорциональностью между сжатием или удлинением пружины,
и последующая восстанавливающая сила. Это соотношение определяется уравнением 2.3, где x
это расстояние, на которое растянулась пружина под действием силы F, действующей на пружину. весна. k — жесткость пружины, характеризующая упругие свойства пружины.
материал. Это показано на рис. 2.17. Этот закон справедлив только в пределах упругости
линейной системы. Глядя на другие материалы, становится ясно, что большинство материалов действует
как пружины при приложении силы, где сила пропорциональна смещению.
весна. k — жесткость пружины, характеризующая упругие свойства пружины.
материал. Это показано на рис. 2.17. Этот закон справедлив только в пределах упругости
линейной системы. Глядя на другие материалы, становится ясно, что большинство материалов действует
как пружины при приложении силы, где сила пропорциональна смещению.
Но по сравнению с пружинами другие материалы обладают площадью, в которой необходимо учитывать для которого можно выразить уравнением 2.4. Переписав исходное уравнение 2.3, заменив силы с мерой напряжения и смещения деформации, выводится комбинированное уравнение, отображается в уравнении 2.5. В котором осевое напряжение, ✏ осевая деформация и E – модуль упругости для конкретного материала [17]. Эти уравнения имеют решающее значение в это исследование.
Рисунок 2.17: Закон Гука – [18]
F = к· х (2.3)
шт.
(47)
2.3. ЧИСЛЕННЫЕ МЕТОДЫ
2.3 Численные методы
МКЭ — это численный метод, который используется для решения сложных, в основном, инженерно-технических задач. и задачи по физике. Это математическая основа конечных элементов.
Анализ (FEA), который больше подходит для решения и практического применения FEM. В этом
метод задача под рукой математически выражается таким образом, что это возможно
провести анализ со всеми данными, необходимыми для получения точного виртуального представления.
насущной проблемы. Инженеры в современном промышленном мире используют его, чтобы уменьшить
количества физических прототипов, количества необходимых экспериментов, а также для оптимизации
компонентов на ранней стадии проектирования [19]. Это возможно во многих различных компьютерах.
Программное обеспечение Aided Engineering (CAE). Некоторые из них Nastran (Siemens NX), Autodesk
Моделирование, ANSYS и многие другие.
и задачи по физике. Это математическая основа конечных элементов.
Анализ (FEA), который больше подходит для решения и практического применения FEM. В этом
метод задача под рукой математически выражается таким образом, что это возможно
провести анализ со всеми данными, необходимыми для получения точного виртуального представления.
насущной проблемы. Инженеры в современном промышленном мире используют его, чтобы уменьшить
количества физических прототипов, количества необходимых экспериментов, а также для оптимизации
компонентов на ранней стадии проектирования [19]. Это возможно во многих различных компьютерах.
Программное обеспечение Aided Engineering (CAE). Некоторые из них Nastran (Siemens NX), Autodesk
Моделирование, ANSYS и многие другие.
Обычно процесс начинается с создания компонента системы автоматизированного проектирования (САПР) для
провести анализ на. На основе этой модели создается сетка для представления модели САПР.
по узлам и элементам, которые будут использоваться для запуска анализа [20]. Пример этого
показан на рисунке 2.18, где представлены CAD, сетка и модель FEA.
Пример этого
показан на рисунке 2.18, где представлены CAD, сетка и модель FEA.
Рисунок 2.18: Визуальное представление шагов анализа — [21]
Здесь указываются материальные и структурные свойства модели. На основе
(48)
ультратонкая сетка на всей модели была бы полезной, но тогда вычислительная мощность, необходимая для ее решения, была бы огромной, и на ее решение ушло бы огромное количество времени.
Другая проблема, которая может возникнуть, заключается в том, что модель будет испытывать большие концентрации напряжения, которые не являются репрезентативными для фактического напряжения в пораженной области.
Такое бывает вокруг, причем с острыми углами и краями. Проблема возникает, когда
Модель САПР с острыми внутренними углами/краями и точечными нагрузками заключается в том, что они являются источниками
числовых особенностей. Это означает, что эти местоположения не способны предсказать
точные результаты даже при точных входных данных и очень мелкой сетке. Причина этого
что численно анализ конечных элементов рассчитывает напряжение в углах на основе локальной
размер элемента, при этом меньшие элементы создают более высокие напряжения. Как следствие, увеличение
измельчение сетки будет способствовать только увеличению напряжения без ограничений [22]. А
визуализация этого показана на рис. 2.19..
Причина этого
что численно анализ конечных элементов рассчитывает напряжение в углах на основе локальной
размер элемента, при этом меньшие элементы создают более высокие напряжения. Как следствие, увеличение
измельчение сетки будет способствовать только увеличению напряжения без ограничений [22]. А
визуализация этого показана на рис. 2.19..
Рисунок 2.19: Размер элемента и напряжение фон Мизеса – [23]
(49)
2.4. СВЯЗАННЫХ С РАБОТОЙ
2.4 Связанная работа
Одним из самых интересных найденных ссылок был эксперимент, в котором они использовали
3D-печать FDM для определения свойств материала ABS. Они использовали разн.
ent стандартов для достижения своих результатов, и все объясняется в краткой и хорошо организованной
поместье. Они также изучали ориентацию печатного материала и ее эффекты.
это может вызвать. Это исследовательская работа, у которой 6 авторов, так что это значительный объем
работа сделана. Большой недостающей частью является проверка результатов в FEM и проверка того,
значения дали бы те же самые результаты отклонения там, но это не было частью исследования.
Однако они заключили это:
Из плана эксперимента для FDM ABS (P400) было обнаружено, что воздушный зазор и ориентация растра влияют на прочность на растяжение детали FDM сильно. Ширина валика, температура модели и цвет не имеют большого значения. измеренные свойства материала показали, что детали, изготовленные методом FDM, имеют анизотропную характеристики. Измеренная прочность на растяжение типичного растра Criss-Cross [458/2458] и перекрестный растр [08/908] с воздушным зазором 2 0,003 находились между 65 и 72 процента измеренной прочности FDM ABS, полученного литьем под давлением. прочность на сжатие материала FDM была выше, чем прочность на растяжение и направление сборки не сильно повлияло. Из-за анизотропного поведения деталей, изготовленных методом FDM, прочность локального участка в детали зависит от направления растра [24].
Еще одна, магистерская диссертация под названием «Валидация модели материала для полипропилена».
lene». Диссертация написана в 2012 году в NTNU Кьетилом Ванге. Благодаря использованию, в
время, новый материал был исследован, если было возможно вывести модель материала
и проверка его с помощью FEM-анализа. В диссертации используются экспериментальные методы растяжения
испытание на прочность и сжатие для определения свойств материала. Оттуда эти значения
UE используются для проверки результатов с помощью FEM. Он завершил исследование следующим образом:
Благодаря использованию, в
время, новый материал был исследован, если было возможно вывести модель материала
и проверка его с помощью FEM-анализа. В диссертации используются экспериментальные методы растяжения
испытание на прочность и сжатие для определения свойств материала. Оттуда эти значения
UE используются для проверки результатов с помощью FEM. Он завершил исследование следующим образом:
В заключение можно констатировать, что модель материала успешно в возрасте для представления полипропилена, рассматриваемого в данной диссертации. Несмотря на то, что кал- процедура фибрирования достаточно проста, она не остановила материальную модель от представляющие сложные проблемы. Дальнейшим усовершенствованием будет включение вязкоупругое поведение и критерий разрушения. Добавляя эти собственные
(50)
Оглядываясь на поставленные в начале вопросы исследования. Измерения
Прочность напечатанной на 3D-принтере детали возможна, если посмотреть на проделанную ранее работу. Но они
использовал другой материал, который может иметь значение, так как это большая переменная, которую нужно изменить,
однако это показывает, что можно генерировать данные из 3D-печатных деталей. Связанные
проделанная работа и теория, лежащая в основе, дают хорошую платформу для дальнейшего изучения возможности
разработать процедуру функционального тестирования.
Но они
использовал другой материал, который может иметь значение, так как это большая переменная, которую нужно изменить,
однако это показывает, что можно генерировать данные из 3D-печатных деталей. Связанные
проделанная работа и теория, лежащая в основе, дают хорошую платформу для дальнейшего изучения возможности
разработать процедуру функционального тестирования.
(51)
Глава 3
Методология
3.1 Тезисный подход
Основная цель состоит в том, чтобы разработать процедуру испытаний для измерения свойств материала, подробнее
в частности, модуль Юнга 3D-печатного PLA. Предварительным этапом было собрать
информация и знания о различных методах расчета прочности и основах
3D-печати. С учетом этого было остановлено изготовление опытных образцов.
канальный. То, как должно проводиться экспериментальное испытание, также было существенной частью этого
исследовательская работа. Был протестирован простой печатный тестовый образец, чтобы убедиться, что предполагаемый экспериментальный
процедура тестирования для этого исследования даст какие-либо измеримые результаты. Как это было найдено
Для достижения этой цели было напечатано больше образцов с различной геометрией и печатью.
ориентации, которые далее представлены в данной диссертации. Это было сделано для того, чтобы выявить
важность метода производства и то, как его изменение может иметь последствия
на результаты. Все результаты были статистически проанализированы с использованием MATLAB.
Как это было найдено
Для достижения этой цели было напечатано больше образцов с различной геометрией и печатью.
ориентации, которые далее представлены в данной диссертации. Это было сделано для того, чтобы выявить
важность метода производства и то, как его изменение может иметь последствия
на результаты. Все результаты были статистически проанализированы с использованием MATLAB.
Кроме того, наряду с экспериментальными испытаниями был проведен анализ прочности в МКЭ. используется для получения соотношения коэффициентов жесткости между различными геометриями. Это было сделано с помощью решателя Siemens NX Nastran для более точного расчета модуля Юнга материал.
(52)
3.2 Прототипирование
Изготовление 3D-печатных тестовых образцов осуществляется с использованием следующей процедуры:
в этом разделе. Все этапы от модели САПР до окончательного образца психического теста
будут представлены в этом разделе. Наглядное представление этой процедуры визуализируется
на рис. 3.1 – 3.3.
3.1 – 3.3.
Рисунок 3.1: Модель CAD Рисунок 3.2: Модель Cura Рисунок 3.3: Готовая модель
3.2.1 Автоматизированное проектирование
Образцы для испытаний созданы в Siemens NX, передовом программном обеспечении CAE высокого класса. ware, которое является одним из программ, доступных в NTNU Ålesund. Сименс NX также включает, помимо других режимов, решатель анализа FEM, который будет использоваться позже в раздел структурного анализа. Образцы для испытаний были вдохновлены ISO Стандарт 527 представлен ранее. Там сделаны две разные геометрии, и они визуализированы на рис. 3.4 и рис. 3.5. Геометрия основана, как упоминалось ранее, на стандарт ISO, но он нуждался в некоторых изменениях из-за размера принтера. Как поясняется в Раздел 2.2 они сделаны таким образом, чтобы образец подвергался чистому растяжению в меньшей области, и что перелом, скорее всего, произойдет здесь.
После установки геометрии они были экспортированы в виде файла STL для дальнейшего изготовления.
В файле STL хранится информация о геометрии экспортированной модели САПР. Формат описывает только геометрию поверхности модели САПР без какого-либо представления
(53)
3.2. ПРОТОТИПИРОВАНИЕ
Рисунок 3.4: Геометрия 1
Рисунок 3.5: Геометрия 2
(54)
3.2.2 Автоматизированное производство
Экспортированные STL-файлы моделей САПР необходимо дополнительно обработать, чтобы в конечном итоге
3D печать. Программное обеспечение, используемое для чтения этих файлов и установки начальных настроек 3D-печати.
называется Ultimaker Cura. Это бесплатно загружаемое программное обеспечение, которое относительно просто в использовании.
и имеет 3D-принтер, который будет использоваться в его библиотеке, судя по названию. Ультимейкер Кура
используется для создания файла STL и разделения модели на несколько слоев, создавая
Путь экструзии 3D-принтеров. Вся эта информация затем сохраняется и экспортируется с использованием
формат файла g-кода, который автоматически создается в Ultimaker Cura. G-код является одним из
производственные языки, понятные 3D-принтерам. Этот код описывает
как 3D-принтер должен печатать модель слой за слоем. Хранит информацию в текстовом файле
были все задачи, которые должен выполнять 3D-принтер. Все настройки, начиная с того, насколько быстро принтер
должна печатать, до какой температуры должно быть сопло, хранится в этих файлах. 3D
печать требует большого количества инструкций для точной печати, поэтому она разделяет
оценивает задачу в несколько слоев.
G-код является одним из
производственные языки, понятные 3D-принтерам. Этот код описывает
как 3D-принтер должен печатать модель слой за слоем. Хранит информацию в текстовом файле
были все задачи, которые должен выполнять 3D-принтер. Все настройки, начиная с того, насколько быстро принтер
должна печатать, до какой температуры должно быть сопло, хранится в этих файлах. 3D
печать требует большого количества инструкций для точной печати, поэтому она разделяет
оценивает задачу в несколько слоев.
В Ultimaker Cura доступно множество различных настроек, но все настройки всплывающее информационное окно при наведении курсора на отдельную настройку для быстрого объяснения.
Для большего контроля над настройками использовался расширенный режим, в котором различные настройки могут быть применены вручную. Настройки, применяемые вручную в Ultimaker Cura и используемые на всех распечатанных тестовых образцах, показаны в Таблице 3.1.
Таблица 3.1: Настройки печати Ultimaker Cura Общий PLA
Диаметр нити 2,85 мм Высота слоя 0,1 мм Толщина стенки 0,4 мм Толщина верха 0,8 мм Толщина дна 0,8 мм Плотность заполнения 100%
Линии шаблона заполнения Скорость печати 50 мм/с
Край рабочей пластины Рисунок 3. 6: Ultimaker Cura
6: Ultimaker Cura
(55)
3.2. ПРОТОТИПИРОВАНИЕ
3.2.3 3D-печать
Все испытательные образцы, напечатанные на 3D-принтере, были напечатаны на одном и том же принтере, чтобы
производственный процесс как можно более похожим и избегать возможных несоответствий между
несколько принтеров. В этом проекте используется принтер Ultimaker 2+,
показано на рис. 3.7. Он очень надежен, удобен в использовании и в большинстве случаев создает
хорошие результаты. В таблице 3.2 все испытанные образцы с индивидуальными настройками 3D-принтера
визуализируется. Единственная заметная разница в настройках принтера, кроме сек-
Площадь испытуемых образцов и ориентация оттиска — температура стола. Из-за
длины и ширины испытательного образца от Т4.1 до Т4.15 стало очевидно, что
размер моделей вызывал их деформацию. Решение для этого состояло в том, чтобы отказаться
температура печатной платформы 8°С. Это оказывает незначительное влияние на конечный результат, т. но это снижает вероятность неудачных отпечатков.
но это снижает вероятность неудачных отпечатков.
Частью исследования является выявление различий в том, как 3D-печатные образцы были напечатаны с точки зрения ориентации и ее влияния на силу. Дис- В Таблице 3.2 показан 31 образец для испытаний, 10 из которых напечатаны под углом 0°, 10 напечатаны под углом 45° и 11 напечатано под углом 90°. Причина нечетного числа в том, что произошел сбой в первое экспериментальное испытание, из-за которого T3.6 не сработал, что можно увидеть в приложении А.1. Но, к счастью, в той же партии был изготовлен и испытан один дополнительный образец. с маркировкой T3.11, которая работала вместо T3.6.
(56)
Таблица 3.2: Тестовая матрица
Имя Время печати часов
Форсунка Размер [мм]
Форсунка Температура [°C]
Кровать Температура [°C]
Раздел Площадь [мм 2 ]
Печать Ориентация [°]
T2. 1 7 0,4 205 60 40 0
1 7 0,4 205 60 40 0
T2.2 7 0,4 205 60 40 0
T2.3 7 0,4 205 60 40 0
T2.4 7 0,4 205 60 40 0
T2.5 7 0,4 205 60 40 0
T3.1 7 0,4 205 60 40 45
T3.2 7 0,4 205 60 40 45
T3. 3 7 0,4 205 60 40 45
3 7 0,4 205 60 40 45
T3.4 7 0,4 205 60 40 45
T3.5 7 0,4 205 60 40 45
T3.6 7 0,4 205 60 40 90
Т3.7 7 0,4 205 60 40 90
T3.8 7 0,4 205 60 40 90
T3.9 7 0,4 205 60 40 90
T3. 10 7 0,4 205 60 40 90
10 7 0,4 205 60 40 90
T3.11 7 0,4 205 60 40 90
T4.1 8 0,4 205 52 80 0
T4.2 8 0,4 205 52 80 0
T4.3 8 0,4 205 52 80 0
T4.4 8 0,4 205 52 80 0
T4.5 8 0,4 205 52 80 0
T4. 6 8 0,4 205 52 80 45
6 8 0,4 205 52 80 45
Т4.7 8 0,4 205 52 80 45
T4.8 8 0,4 205 52 80 45
T4.9 8 0,4 205 52 80 45
T4.10 8 0,4 205 52 80 45
Т4.11 8 0,4 205 52 80 90
T4.12 8 0,4 205 52 80 90
T4. 13 8 0,4 205 52 80 90
13 8 0,4 205 52 80 90
T4.14 8 0,4 205 52 80 90
T4.15 8 0,4 205 52 80 90
(57)
3.2. ПРОТОТИПИРОВАНИЕ
3.2.4 Постобработка
После того, как тестовые образцы были напечатаны, необходимо было внести небольшие завершающие штрихи, и
размерная проверка. Это делается для того, чтобы на всех распечатанных тестовых образцах не было
лишнего материала и иметь правильные размеры. На печатных экземплярах было
добавил кромку вокруг базового слоя модели, как показано на рис. 3.8. Готово
для обеспечения хорошей адгезии к печатной платформе и снижения вероятности деформации. Этот
это просто очень тонкий слой, который легко удаляется впоследствии. Каждый отдельный испытательный образец
был измерен и проанализирован, чтобы убедиться, что исходная геометрия соответствует остальным
партии с очень низким отклонением +/- 0,5%. Кроме того, всякий раз, когда появляется новый экземпляр
была закончена, их положили и хранили в одном ящике-контейнере с влажным редуцентом
сумку до тех пор, пока они в конце концов не будут проверены.
Этот
это просто очень тонкий слой, который легко удаляется впоследствии. Каждый отдельный испытательный образец
был измерен и проанализирован, чтобы убедиться, что исходная геометрия соответствует остальным
партии с очень низким отклонением +/- 0,5%. Кроме того, всякий раз, когда появляется новый экземпляр
была закончена, их положили и хранили в одном ящике-контейнере с влажным редуцентом
сумку до тех пор, пока они в конце концов не будут проверены.
Рисунок 3.8: Край
(58)
3.3 Экспериментальное испытание – установка для испытания на растяжение
Экспериментальное испытание, проведенное для определения свойств материала PLA, было
испытание на прочность при растяжении. Как конкретно проводится тест, не рассматривается.
здесь, благодаря этому все готово было объяснено в разделе 2.2. В мастерской НТНУ
Олесунн, есть машина Galdabini Quasar 200, которая использовалась для тестирования 3D-печати.
пробные образцы. Машина имеет максимальную мощность 200 кН, курицы название,
и подходит для металлов, пластмасс, композитов и других материалов. Ключевая особенность
эта конкретная машина, по словам самого Галдабини, имеет «чрезвычайно высокое разрешение
показаний нагрузки и хода». Технический паспорт самой машины добавлен в Приложение D.
Ключевая особенность
эта конкретная машина, по словам самого Галдабини, имеет «чрезвычайно высокое разрешение
показаний нагрузки и хода». Технический паспорт самой машины добавлен в Приложение D.
Экспериментальное испытание различных образцов было разделено на два эксперимента. Этот в основном из-за количества часов, необходимых для печати самих образцов. Как принтеры расположены в лабораториях, и студенты имеют ограниченный доступ в эти комнаты, сам процесс печати был немного более утомительным, чем хотелось бы. Кроме того, было также сделано таким образом, чтобы иметь больше контроля и сократить количество времени с момента, когда образцы были напечатаны до точки, где они были испытаны.
Все экспериментальные испытания были проведены и под наблюдением:
Андре Транвог — главный инженер NTNU Ålesund.
3.3.1 Экспериментальное испытание 1. Особенности
Испытание на растяжение 15 образцов с различной ориентацией.
5 экземпляров с диагональным печатным рисунком 45°, напечатанным под углом 0°.
5 экз. с продольным и поперечным печатным рисунком, отпечатанным под углом 45°.
5 экз. с печатным рисунком по диагонали 45°, отпечатанным на 90°.
Площадь поперечного сечения испытуемого образца: 40 мм 2 – ширина 10 мм и толщина 4 мм Ориентация печати T2.1 – T2.5: 0°
Ориентация печати T3.1 – T3.5: 45°
Ориентация печати T3.6 – T3.11: 90°
Место: Мастерская в NTNU Ålesund Комнатная температура: 18-22°С
(59)
3.3. ЭКСПЕРИМЕНТАЛЬНОЕ ИСПЫТАНИЕ – УСТАНОВКА ДЛЯ ИСПЫТАНИЙ НА РАСТЯЖЕНИЕ
3.3.2 Экспериментальное испытание 2. Особенности
Испытание на растяжение 15 образцов с различной ориентацией 5 образцов с печатным рисунком по диагонали 45°, напечатанным под углом 0°
5 экз. с продольным и поперечным печатным рисунком, отпечатанным под углом 45°.
5 экземпляров с печатным рисунком с диагональю 45°, напечатанным под углом 90°.
Площадь поперечного сечения испытуемого образца: 80 мм 2 – ширина 20 мм и толщина 4 мм Ориентация печати T4.1 – T4.5: 0°
Ориентация печати T4.6 – T4.10: 45°
Ориентация печати T4.11 – T4.15: 90°
Место: Мастерская в NTNU Ålesund Комнатная температура: 18-22°С
Мониторинг испытаний и контроль первоначальных результатов осуществлялся с помощью собственного
интегрированное программное обеспечение, Graphwork. В программе есть график, на котором можно
имеют начальный пик на кривой сила-деформация. Пока проходят испытания
программа строит простые кривые сила-деформация друг над другом. Это очень
полезно, так как легко очень быстро определить, как прошел тест, а также посмотреть,
есть какие-либо первоначальные нарушения между тестами. Единственная начальная установка, которая была
Перед испытанием требовалось установить ширину испытуемых образцов, как показано
в разделе 3.2.1 это были 10- и 20 мм. Скорость хода, используемая во всех тестах
выполненные в данной диссертации, были установлены со скоростью 4 мм/мин. После индивидуальных испытаний
данные были экспортированы в файлы Excel, которые впоследствии будут обработаны в MATLAB.
для статистического анализа в разделе 3.4.
После индивидуальных испытаний
данные были экспортированы в файлы Excel, которые впоследствии будут обработаны в MATLAB.
для статистического анализа в разделе 3.4.
(60)
3.4 Статистический анализ
3.4.1 Сглаживание исходных данных
Экспорт данных из Graphwork сначала выполняется в файлы Excel. Из Graphwork это
можно решить, какие данные вы хотите экспортировать, в некоторой степени. Все зависит от
тест. Однако для этого исследования важными данными экспериментальной проверки были
сила и скорость деформации от каждого отдельного испытания. Эти данные, помимо
поперечный ход самой машины был экспортирован. В среднем экспортируемые данные
состоял примерно из 30 000 строк необработанных данных, которые необходимо было проанализировать. Путь
обработка и анализ данных осуществляется с помощью MATLAB. Сценарий предназначен для непосредственного воспроизведения
портировать Excel-файлы для дальнейшего анализа, который прилагается в Приложении C. 1. Держите в
Имейте в виду, что все дальнейшее кодирование основано на силе-деформации данных каждого испытания.
1. Держите в
Имейте в виду, что все дальнейшее кодирование основано на силе-деформации данных каждого испытания.
Как было сказано ранее, нужно было обработать много данных, первоначально сила-деформация выглядела
как на рис. 3.9. Красные точки на Рисунке 3.10 представляют зарегистрированные выходные данные из
машина и программное обеспечение Graphwork, и представляет собой то же изображение, что и на рис. 3.9, только в увеличенном масштабе.
чтобы увидеть несколько записей силы. График исходных исходных данных показывает, что
данные нуждаются в сглаживании, чтобы лучше представить значения силы и удлинения. Интерпретация
исходные данные заключаются в том, что существует множество точек данных силы на одном и том же точном удлинении
уровень. Функция прямого сглаживания не работает для этих начальных точек данных, потому что
слишком много точек данных силы на одном уровне удлинения. Каждая красная точка инди-
охват одной точки измерения. Решением этого было для каждой множественной записи среднее значение
вычисляется и отображается зелеными точками, как показано на рис. 3.11.
3.11.
Благодаря новым зеленым точкам применяется сильная функция сглаживания, которая представлена синей линией на рис. 3.11 и полностью визуализируется на рис. 3.12. Чтобы показать это, и процесса, в качестве примера используются данные Test3.1, которые добавлены в Приложение A.1, наряду со всеми другими тестами.
(61)
3.4. СТАТИСТИЧЕСКИЙ АНАЛИЗ
0 500 1000 1500 2000 2500 3000 3500 4000
Удлинение [м]
0 200 400 600 800 1000 1200 1400 1600 1800 2000 2200 2400 2600
Сила [Н]
Удлинение [м]
Сила [Н]
Рисунок 3. 9: Кривая исходных данных Test3.1 Рисунок 3.10: Кривая исходных данных увеличена
9: Кривая исходных данных Test3.1 Рисунок 3.10: Кривая исходных данных увеличена
Удлинение [м]
Сила [Н]
0 500 1000 1500 2000 2500 3000 3500 4000
Удлинение [м]
0 200 400 600 800 1000 1200 1400 1600 1800 2000 2200 2400 2600
Сила [Н]
Рисунок 3.11: Сглаженные данные, увеличенные Рисунок 3.12: Сглаженные необработанные данные Тест3.1
– Видно, что сглаживание не полностью отображает необработанные данные, когда происходит перелом
показано на рис. 3.12. Поскольку это исследование будет основываться на упругой области, а это не
иметь влияние в дальнейшем, кроме как на изображения.
3.12. Поскольку это исследование будет основываться на упругой области, а это не
иметь влияние в дальнейшем, кроме как на изображения.
(62)
3.4.2 Линейная область
Теперь, когда исходные необработанные данные очищены, пришло время их использовать. Модуль Юнга может быть получен из площади упругости по кривой сила-удлинение.
Измерив вручную, его можно получить, но это будет не очень точно,
а также, как мы увидим позже, не полностью представляют модуль Юнга из-за геометрии
образцы для испытаний. Однако из всех тестов можно вывести процедуру
чтобы в конечном итоге получить начальный модуль Юнга. Чтобы получить начальный модуль Юнга
как можно точнее, нужно было найти, где находится область, в которой действует сила – удлинн.
кривая гации ведет себя наиболее линейно. Из экспериментов и просмотра кривых это было
Ясно, что в начале кривой была нелинейная область и, очевидно, вблизи
точка текучести кривой. Это требовало, чтобы регион находился где-то посередине,
показан красным квадратом на рис. 3.13. Чтобы найти уклон наклона силы –
кривая удлинения была дифференцирована, что делает ее похожей на рис. 3.14. Горизонтальный
часть кривой на рис. 3.14 представляет собой диапазон, в котором градиент силы – удлинн.
кривая градаций наиболее постоянна, кур — наиболее линейна, что в данном случае находится где-то около
1.25, если смотреть только на кривую на рис. 3.14.
3.13. Чтобы найти уклон наклона силы –
кривая удлинения была дифференцирована, что делает ее похожей на рис. 3.14. Горизонтальный
часть кривой на рис. 3.14 представляет собой диапазон, в котором градиент силы – удлинн.
кривая градаций наиболее постоянна, кур — наиболее линейна, что в данном случае находится где-то около
1.25, если смотреть только на кривую на рис. 3.14.
0 500 1000 1500 2000 2500
0 0,2 0,4 0,6 0,8 1 1,2 1,4 1,6
Рисунок 3.13: Линейная область Рисунок 3.14: Дифференцированный
Чтобы лучше контролировать диапазон, в котором рассчитывается градиент кривой, ядро
используется распределение значений. Это берет все данные из дифференцированной кривой
и распределите его соответствующим образом, как показано на рис. 3.15. Из дистрибутива ядра
найдено среднее значение 1,2658 из всех исходных данных, которые будут использоваться в качестве исходных
для линейной области T3.1, представленной на рис. 3.16. Затем среднее значение используется для
сделать диапазон интервалов, в котором градиент кривой постоянен до необязательного
3.15. Из дистрибутива ядра
найдено среднее значение 1,2658 из всех исходных данных, которые будут использоваться в качестве исходных
для линейной области T3.1, представленной на рис. 3.16. Затем среднее значение используется для
сделать диапазон интервалов, в котором градиент кривой постоянен до необязательного
(63)
3.4. СТАТИСТИЧЕСКИЙ АНАЛИЗ
линия проходит слева направо под розовой линией и еще раз, когда она проходит под красной линия. Используя диапазон внутри розовой и красной линии, в котором градиент является «постоянным», построена обрезанная кривая кривой силы удлинения, это показано на рис. 3.18.
Представляет собой новую обрезанную кривую силы – удлинения, в которой модуль Юнга будет извлекаться из.
0 0,5 1 1,5
0 100 200 300 400 500 600
0 0,2 0,4 0,6 0,8 1 1,2 1,4 1,6
0 50 100 150 200 250 300 350
Рисунок 3. 15: Ядерное распределение Рисунок 3.16: Среднее значение градиента
15: Ядерное распределение Рисунок 3.16: Среднее значение градиента
0 500 1000 1500 2000 2500 3000
Сила [Н]
0 0,2 0,4 0,6 0,8 1 1,2 1,4 1,6
Градиент
+5% от макс. -5% от макс.
200 300 400 500 600 700 800 900 1000 1100 1200 1300 Удлинение [м]
200 300 400 500 600 700 800 900 1000 1100 1200 1300 1400 1500 1600 1700 1800
Сила [Н]
Рисунок 3. 17: Расчетный линейный диапазон Рисунок 3.18: Сила обрезки диапазона — удлинение
кривая градации
17: Расчетный линейный диапазон Рисунок 3.18: Сила обрезки диапазона — удлинение
кривая градации
(64)
Сценарий также регистрирует начало и конец кривой усилия обрезки и удлинения, которые, очевидно, будут разными для каждого теста, представленного на рис. 3.18. Для T3.1 удлинение начинается с 209и доходит до 1310 мкм, так как усилие увеличивается от 309 и выше до 1705 Н. При этих значениях и геометрии образца для испытаний можно выведите начальный модуль Юнга, представленный в уравнении 3.1.
Где геометрия Т3.1:
Д = 170 мм А = 40 мм 2
Э =
✏ =
Ф А л
=
(1703 309)Н 40 мм 2 (1310 209) мкм
170 · 10 3 мкм
⇡5390M Па (3. 1)
1)
Из всех представленных шагов становится ясно, что этот метод позволяет получить критерий Юнга. модуль, но становится очевидным, что этот модуль Юнга не полностью отражает материал. Это связано с геометрией испытательного образца и будет дополнительно уточнено. оценивается в разделе 3.5.
Engineering at Alberta Courses » Коэффициенты влияния
До сих пор мы использовали законы Ньютона для получения уравнений движения для систем с несколькими степенями свободы. Еще один способ их получить — использовать коэффициентов влияния . (Они также основаны на законах Ньютона, но их часто легче применять.) Коэффициенты влияния связывают воздействие сил и перемещений на одну часть конструкции на другую и широко используются в проектировании конструкций. По существу, с каждой матрицей, входящей в уравнения движения, может быть связан один набор коэффициентов влияния. Как и в случае с уравнениями движения, коэффициенты влияния напрямую связаны с выбором координат в задаче. Другой набор координат для одной и той же задачи приведет к совершенно другому набору коэффициентов влияния.
Другой набор координат для одной и той же задачи приведет к совершенно другому набору коэффициентов влияния.
Для матрицы жесткости можно использовать два (связанных) набора коэффициентов влияния
- Коэффициенты влияния жесткости и
- Коэффициенты влияния гибкости.
Для матрицы масс мы можем использовать
- Коэффициенты влияния инерции.
Коэффициенты влияния гибкости
Коэффициенты влияния гибкости определены как
= отклонение координаты в положительном направлении из-за приложения единичной нагрузки к координате в положительном направлении.
Обратите внимание, что для системы с одной степенью свободы это упрощает наше предыдущее определение эквивалентной жесткости. Для системы с несколькими степенями свободы эти коэффициенты определяются на практике путем приложения к системе единичной нагрузки в положительном направлении координат и определения смещения всех координат в системе. Это проблема статики. Тогда – отклонение системы в (положительном) направлении координат в этом случае.
Тогда – отклонение системы в (положительном) направлении координат в этом случае.
Коэффициенты влияния гибкости также могут применяться к торсионным системам, где
= поворот по координате в положительном направлении из-за приложения единичного крутящего момента по координате в положительном направлении.
Мы также можем использовать коэффициенты влияния гибкости в смешанных системах как с линейными, так и с вращательными координатами. Затем единицы будут меняться в зависимости от того, являются ли и линейными или угловыми координатами.
Коэффициенты влияния жесткостиКоэффициенты влияния жесткости определены как
= сила, необходимая для координаты в положительном направлении, чтобы поддерживать единичное отклонение координаты в положительном направлении при сохранении нулевого смещения для всех других координат.
Обратите внимание, что для системы с одной степенью свободы это упрощает наше предыдущее определение эквивалентной жесткости. Для системы с несколькими степенями свободы эти коэффициенты определяются на практике при рассмотрении системы, когда координата имеет положительное единичное смещение, а все остальные координаты фиксируются с нулевым смещением. Силы, необходимые для поддержания конструкции в этой деформированной конфигурации, затем вычисляются статически. это сила, необходимая в положительном направлении координат для поддержания этой деформированной конфигурации.
Для системы с несколькими степенями свободы эти коэффициенты определяются на практике при рассмотрении системы, когда координата имеет положительное единичное смещение, а все остальные координаты фиксируются с нулевым смещением. Силы, необходимые для поддержания конструкции в этой деформированной конфигурации, затем вычисляются статически. это сила, необходимая в положительном направлении координат для поддержания этой деформированной конфигурации.
Коэффициенты влияния жесткости также могут применяться к торсионным системам, где
= крутящий момент , необходимый для координаты в положительном направлении для поддержания статической единицы вращения координаты в положительном направлении при сохранении нулевого вращения для всех других координат.
Мы также можем использовать одну степень свободы в смешанных системах как с линейными, так и с вращательными координатами. Затем единицы будут меняться в зависимости от того, являются ли и линейными или угловыми координатами.
Коэффициенты влияния инерции определены как
= импульс, который должен быть приложен к координате в положительном направлении, чтобы создать единичную скорость в координате в положительном направлении, сохраняя при этом нулевую скорость во всех других координатах.
Альтернативное эквивалентное определение:
.= сила, которая должна быть приложена к координате в положительном направлении, чтобы создать единичное ускорение в координате в положительном направлении, сохраняя при этом нулевое ускорение во всех других координатах.
Коэффициенты влияния инерциитакже могут применяться к торсионным системам, где
= крутящий момент по координате в положительном направлении, который необходимо приложить для создания единичного углового ускорения по координате в положительном направлении при поддержании нулевого углового ускорения по всем другим координатам.
Мы также можем использовать коэффициенты влияния инерции в смешанных системах как с линейными, так и с вращательными координатами. Затем единицы будут меняться в зависимости от того, являются ли и линейными или угловыми координатами.
Затем единицы будут меняться в зависимости от того, являются ли и линейными или угловыми координатами.
Свойства коэффициентов влияния жесткости и гибкости
Суммарная сила, действующая в направлении координат, может быть определена из всех перемещений () в системе из
или в матричной форме
(8,32)
где – вектор-столбец сил, действующих на систему в положительных направлениях координат, – матрица одной степени свободы. (Обратите внимание, что если одна из координат представляет собой угловое смещение, соответствующий член будет представлять собой крутящий момент). Аналогично полное перемещение в направлении координат можно определить по всем силам, действующим в положительных направлениях координат () для системы из
или снова в матричной форме
(8,33)
где – матрица коэффициентов влияния гибкости. (Обратите внимание, что если одна из координат является угловым смещением, соответствующий член будет поворотом).



 Подобный метод позволяет существенно повысить упругость создаваемой системы.
Подобный метод позволяет существенно повысить упругость создаваемой системы.

 000
000 0005
0005 125 Hz
125 Hz 80
80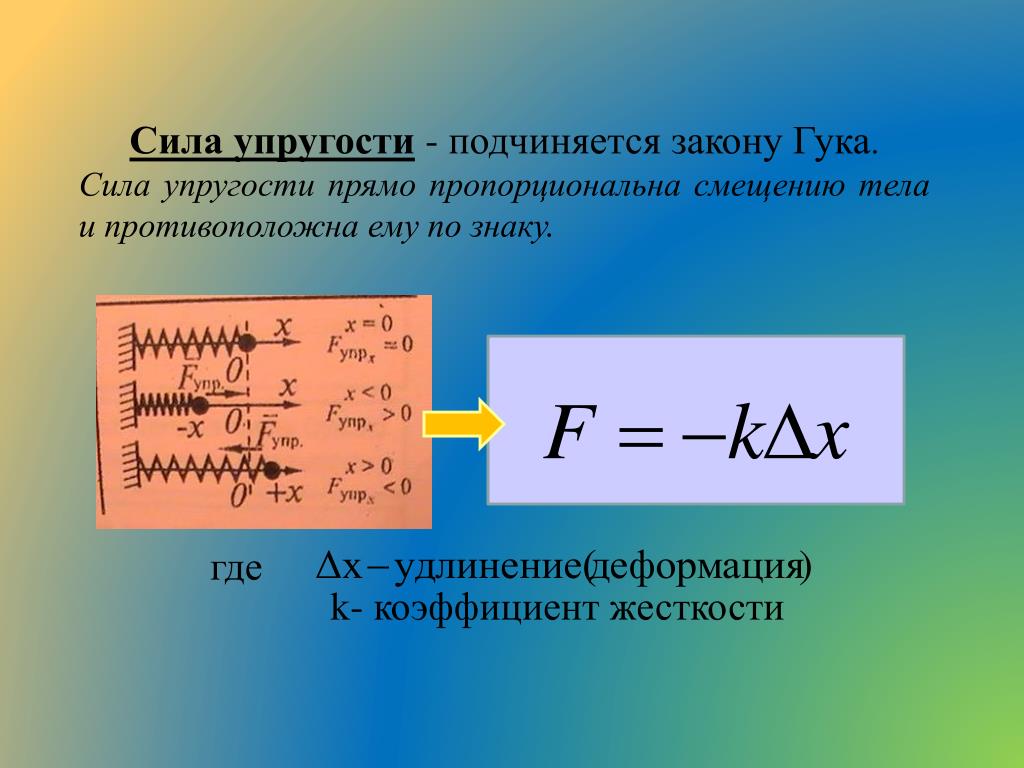 125 Hz
125 Hz