Колеса зубчатые основные параметры: 8.8. Основные параметры зубчатых колёс – скачать лекцию, скачать реферат
alexxlab | 28.04.1984 | 0 | Разное
Основные параметры зубчатого цилиндрического колеса
Геометрические параметры | Обозначение | Расчетная формула |
Высота головки | ha | ha = m |
Высота ножки | hr | hf=1.25m |
Высота зуба | h | h = h. + h= 2,25m |
Делительный диаметр | d | d=mz |
Диаметр вершин зубьев | da=d+2ha=m(z+2) | |
Диаметр впадин зубьев | df | df=d-2hf=m(z-2,5) |
Окружной шаг | Pt | Pt= π m |
Окружная толщина зуба | St | St=0. |
Окружная ширина впадины | et | et=0.5Pt= 0.5π m |
Радиус кривизны переходной цилиндрической поверхности | Rf | Rf= 0,25m |
Табл.3
Конструктивные параметры | Расчетная формула |
Ширина зубчатого венца | b=(6/8)m |
Толщина обода зубчатого венца | δ1=(2,5/3)m |
Наружный диаметр ступицы | Dст=(1,6/1,8)DB |
Толщина диска | δ2=(3/3,6)m |
Диаметр, определяющий расположение отверстий в диске | D1=0,5(DK+Dст) |
Диаметр отверстий в диске | D0=(DK-Dст)/2,5/3 |
Длина ступицы | Lст=1,5DB |
Фаска | 0,5mX45o |
Размеры паза под шпонку | Выбираются по таблицам ГОСТ 23360-78 в зависимости от |
Примечание. | |
Если зубчатое колесо изготовлено так, что высота зуба h=2,25m, то колесо называется выполненным без смещения исходного контура (некоррегированное колесо). Если колесо изготовлено с высотой зуба h=2,25m, то колесо называется выполненным со смещением исходного контура (корригированное колесо).
Смещение исходного контура характеризуется коэффициентом смещения исходного контура, обозначаемым по ГОСТ 16531-70 буквой х. Для некоррегированного колеса коэффициент смещения исходного контура х=0.
В современном
машиностроении применяются зубчатые
колеса самых разнообразных конструкций,
отличающиеся друг от друга технологией
изготовления, материалом и конструктивными
особенностями.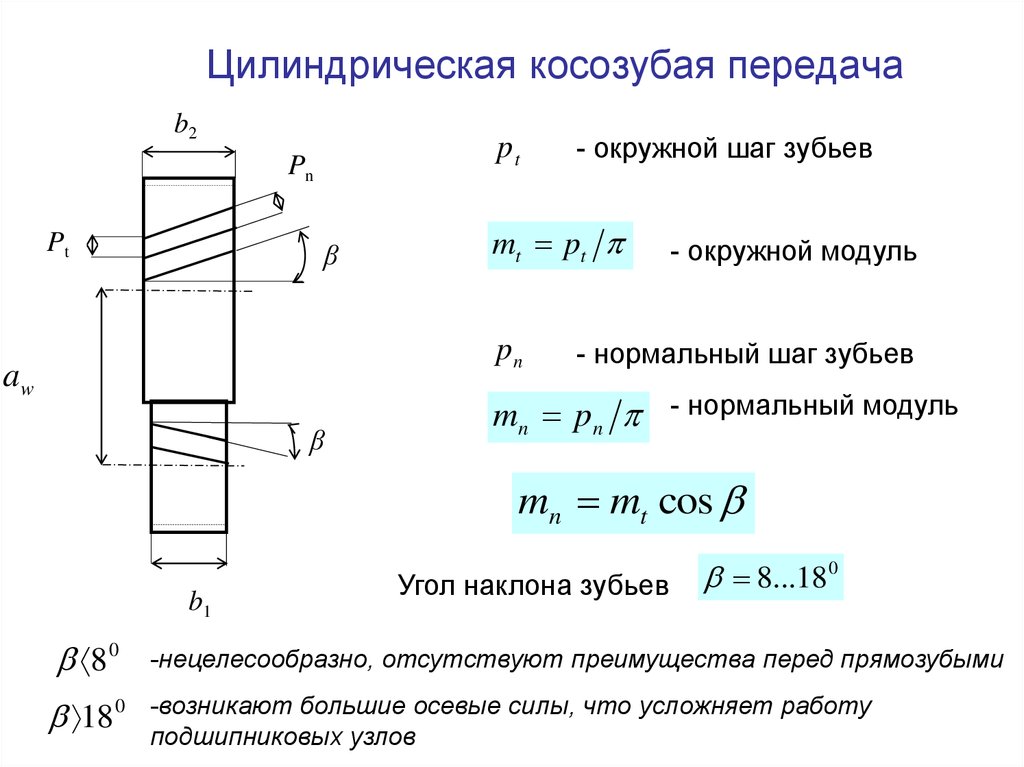
Конструктивные форма и размеры зубчатого колеса зависят от нагрузок, действующих на его зубья, требований технологии их изготовления, удобства монтажа и эксплуатации, уменьшения массы (веса) зубчатых колес, бесшумности работы и др.
Наиболее часто встречающиеся формы цилиндрических зубчатых колес с прямыми зубьями представлены на рис. 1, д-ж.
Цилиндрическое зубчатое колесо малого диаметра (рис. 1, д-ж) обычно имеет форму сплошного цилиндра с отверстием для установки на вал.
При несколько большем диаметре колеса для облегчения его конструкции выполняются массивными только обод и ступица (втулка) с отверстием для вала. Остальная часть колеса представляет собой тонкий диск с отверстиями (или без отверстий). Диск может выполняться с ребрами жесткости.
Если диаметр колеса
достаточно велик, диск заменяется
несколькими спицами, соединяющими обод со ступицей.
Форма спиц может быть различной.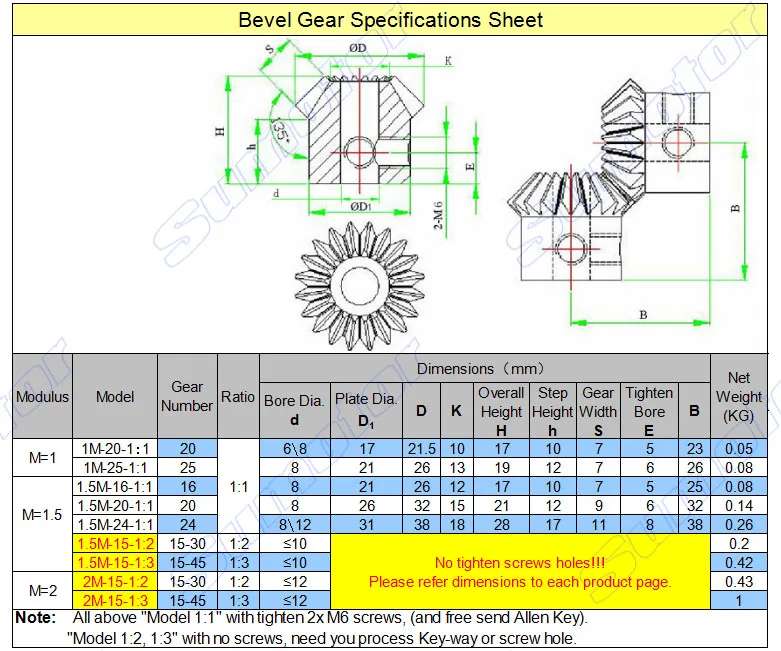 Форма
поперечного сечения спиц тоже различна:
круглая, овальная, прямоугольная,
двутавровая, крестообразная и др.
Форма
поперечного сечения спиц тоже различна:
круглая, овальная, прямоугольная,
двутавровая, крестообразная и др.
Колеса большого диаметра для удобства монтажа’и упрощения технологии изготовления иногда выполняют разъемными из двух половин, скрепляемых болтами (рис. 5, а).
Рис.5
Зубья колес могут быть прямыми (рис. 5, а-в) косыми (рис. 5, г), шевронными и криволинейными (рис. 5, д). Термины, определения и обозначения элементов зубчатых передач установлены ГОСТ 16536-78 и ГОСТ 16561-76.
Рис. 5
ГОСТ, параметры, виды, типы, расчет
Основу конструкции любого механизма составляют элементы, призванные передать механическое усилие от двигателя на рабочий орган. В зависимости от принципа действия принято различать несколько видов таких передач: клиноременные, фрикционные или червячные. Но самое широкое распространение в технике получили зубчатые передачи.
Но самое широкое распространение в технике получили зубчатые передачи.
Такие механизмы в простейшем случае использующие сопрягаемую пару, включающую ведущую шестерню и колесо зубчатое. Благодаря зубчатой форме поверхности эти элементы входят в зацепление между собой и за счет этого передают вращение с одного вала на другой. Кроме возможности передать механическую мощность, такая передача способна обеспечить изменение скорости вращения выходного вала, относительно входного. Благодаря таким свойствам, практически в каждом промышленном механическом устройстве встречается редуктор, понижающий скорость вращения или мультипликатор, наоборот увеличивающий ее. В более сложных механизмах, так называемых коробках передач, группа зубчатых колес способна выполнить ступенчатое изменение скорости.
Широкое распространение зубчатые передачи получили благодаря высокой надежности и способности передавать момент в большом диапазоне нагрузок и скоростей вращения. При этом конструкция таких механизмов отличается относительной простотой и компактностью. Зубчатые передачи не предъявляют высоких требований к обслуживанию и характеризуются длительным сроком службы.
Зубчатые передачи не предъявляют высоких требований к обслуживанию и характеризуются длительным сроком службы.
Наряду с очевидными достоинствами, этим механизмам присущ и ряд недостатков. В отличие от других типов передач, они более сложны в изготовлении, требуют более высокой точности обработки и применения специализированного обрабатывающего оборудования. Выбор материалов для зубчатых колес должен обеспечить сопротивляемость значительным механическим усилиям. Высокая жесткость, реализуемая зубчатой передачей, способствует минимизации потерь при передаче механической энергии. КПД таких механизмов приближаются к абсолютным значениям. Но при этом конструкция не позволяет преодолевать большие значения динамической нагрузки, что часто приводит к разрушению механизма. Еще одним негативным явлением, возникающим в процессе работы зубчатой пары, становится шум. Его уровень напрямую связан частотой вращения механизма и зависит от качества изготовления колес.
Содержание
Виды зубчатых колес
Само название зубчатой передачи отражает ее конструкцию. В простейшем случае в состав такого механизма входят два вращающихся диска, на боковой поверхности, которых выполнены зубья. В процессе работы эти зубья зацепляются между собой. Колесо, связанное с источником вращающего момента, увлекает за собой второе. В итоге ведомый вал начинает вращаться.
В простейшем случае в состав такого механизма входят два вращающихся диска, на боковой поверхности, которых выполнены зубья. В процессе работы эти зубья зацепляются между собой. Колесо, связанное с источником вращающего момента, увлекает за собой второе. В итоге ведомый вал начинает вращаться.
В зависимости от направления передачи энергии используются разные обозначения зубчатых колес. Элемент, к которому присоединен вал двигателя, называется ведущим зубчатым колесом. В понижающих передачах оно характеризуется небольшим диаметром и малым числом зубьев. В технической литературе этот элемент часто называют шестерней. Сопрягаемое с ней колесо большого диаметра с большим числом зубьев называется ведомым. Вал этого колеса используется для передачи мощности на рабочий орган исполнительного механизма. Более сложные виды передач используют большее количество зубчатых колес. Например, такие устройства используются для реализации возможности отбора мощности от одного вала на несколько устройств или переключения скоростей вращения.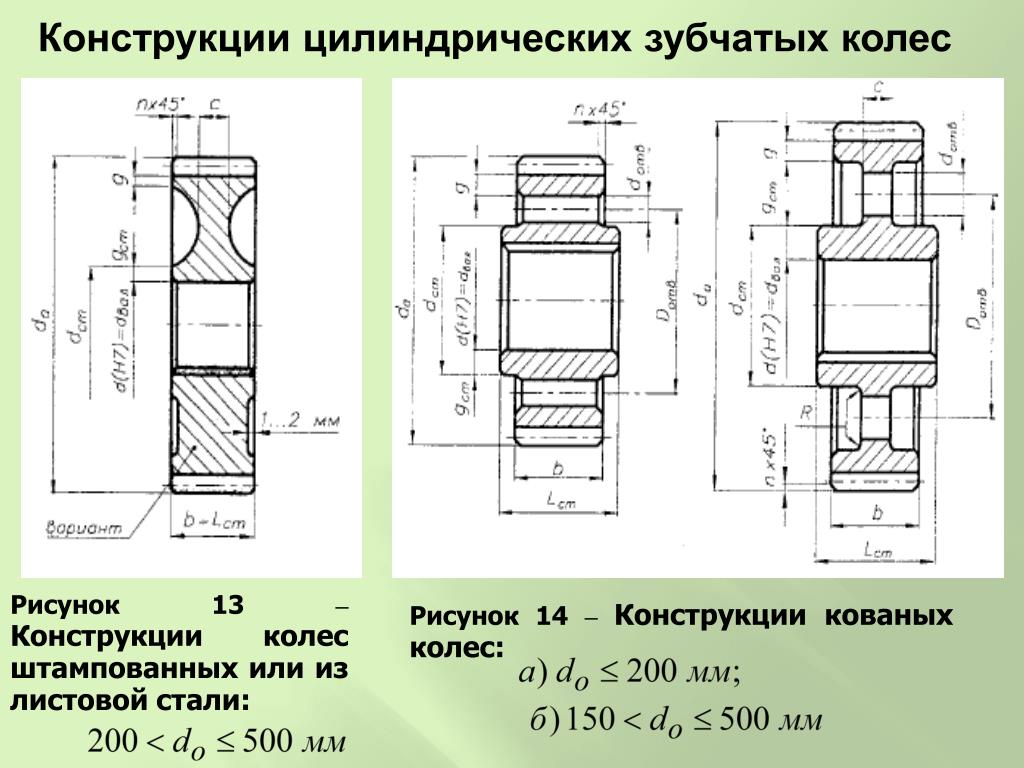
Высокие технические характеристики передачи и различные направления применения привели к созданию большого числа вариантов зубчатых колес. Наиболее простыми и распространенными из них являются цилиндрические прямозубые колеса. Зуб такой детали расположен на боковой поверхности колеса, параллельно оси. Второе колесо механической передачи имеет аналогичную геометрию. Оси обеих колес должны располагаться параллельно, на строго заданном расстоянии. Высокая технологичность изготовления этого типа деталей способствует массовому применению прямозубых передач в различных отраслях промышленности.
Из недостатков следует отметить только невысокий предельный момент. В сложных условиях работы используют другие виды зубчатых колес. Благодаря изменению геометрии зацепления, такие передачи обладают улучшенными свойствами. Например, для передач повышенной мощности проектируют косозубые колеса. В них ось зуба расположена под углом к оси вращения, за счет чего достигается большая зона контакта сопрягаемых деталей. В механизмах, характеризующихся сверхтяжелыми нагрузками, применяют шевронные модели. Зацепление в такой передаче выполняется на основе V-образных зубьев, чем обеспечивается оптимальное распределение нагрузки. Еще один вид зуба, называемый, круговым или криволинейным, выполняется в виде дуги. Он обеспечивает улучшенные механические характеристики, но достаточно трудоемок в изготовлении, поэтому большого распространения не получил.
В механизмах, характеризующихся сверхтяжелыми нагрузками, применяют шевронные модели. Зацепление в такой передаче выполняется на основе V-образных зубьев, чем обеспечивается оптимальное распределение нагрузки. Еще один вид зуба, называемый, круговым или криволинейным, выполняется в виде дуги. Он обеспечивает улучшенные механические характеристики, но достаточно трудоемок в изготовлении, поэтому большого распространения не получил.
Профиль или поперечное сечение зуба в механических передачах может быть практически любым. Встречаются варианты с треугольным, трапециевидным, прямоугольным или круглым профилем. Всем им, несмотря на простоту изготовления, свойственны недостатки, связанные с неравномерностью зацепления. Поэтому, в современных механических передачах, профиль чаще всего выполняется эвольвентным. Он представляет собой сложную кривую, обеспечивающую постоянное качество зацепления, вне зависимости от углового положения отдельных деталей и как следствие постоянство передаточного отношения.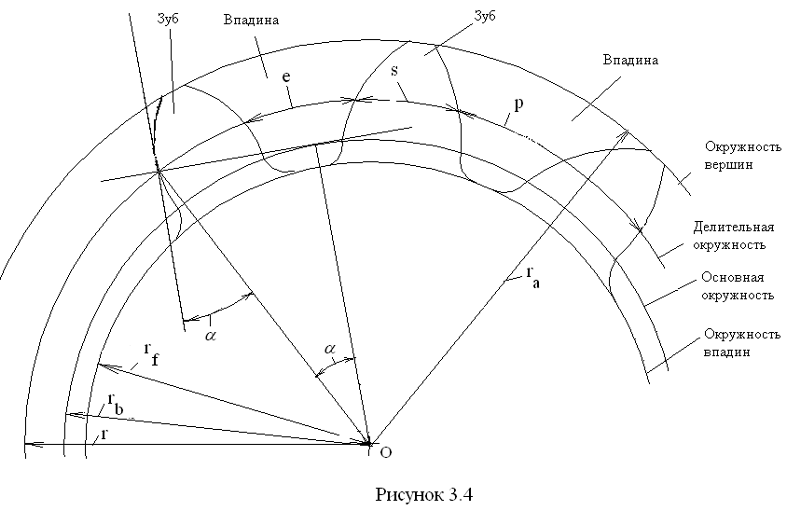 Такой профиль показывает оптимальные характеристики и относительно прост в изготовлении.
Такой профиль показывает оптимальные характеристики и относительно прост в изготовлении.
Кроме вида и профиля зуба, принято выделять и место его расположения. В зависимости от назначения, элементы зацепления могут быть расположены на внешней или внутренней части колеса. Также встречаются колеса с расположением зацепляющихся элементов со стороны торцевой части. Подобные шестерни называют корончатыми. Область их применения достаточно узка, поэтому встречаются они сравнительно редко. Гораздо более широкое применение получили передачи конического типа. Элементы зацепления в таких механизмах выполнены на поверхности усеченного конуса. Результирующее расположение конических шестерен подразумевает разное положение их осей в пространстве.
Еще один вид зубчатой передачи применяется в механизмах, преобразующих вращательное движение в возвратно-поступательное.
Общее название таких устройств — рейка-шестерня.
Ведущий элемент такой передачи выполнен в виде обычного зубчатого колеса. Ведомая деталь представляет собой рейку, с нанесенными на одной из граней, зубьями. Вращение шестерни приводит к продольному перемещению рейки. Подобные передачи широко распространены в станочном оборудовании.
С зубчатыми колесами часто сравнивают звездочки цепных передач. Схожая форма деталей приводит к путанице. На самом деле цепная передача имеет иной принцип действия, а конструкция звездочки рассчитывается по собственным формулам.
Редкие модели
В общем случае считается, что зубчатое колесо должно иметь цилиндрическую форму. Но встречаются модели и некруглого типа. Главной их особенностью является переменное передаточное отношение, зависящее от угла поворота детали. Сегодня разработаны модели треугольной и квадратной формы, а также эллиптические шестерни. При постоянном вращении ведущего вала эти модели обеспечивают неравномерную скорость выходного. Высокая сложность изготовления и ограниченная область применения не дали подобным конструкциям широкого распространения. Тем не менее, сегодня встречаются отдельные устройства, в составе которых можно встретить некруглые шестерни. Примером могут служить редукторы некоторых насосов или специфические измерительные приборы.
Высокая сложность изготовления и ограниченная область применения не дали подобным конструкциям широкого распространения. Тем не менее, сегодня встречаются отдельные устройства, в составе которых можно встретить некруглые шестерни. Примером могут служить редукторы некоторых насосов или специфические измерительные приборы.
Конструкция зубчатого колеса
Несмотря на кажущуюся простоту, в технике принято выделять несколько отдельных частей зубчатого колеса. Как и любое другое колесо, зубчатый вариант в своей основе имеет диск необходимого диаметра. Основной частью является обод, на боковой или торцевой поверхности которого выполнены зубья. Все вместе они образуют так называемый венец зубчатого колеса. Геометрия зубьев различна у разных типов зубчатой передачи. Сам зуб условно разбивается на несколько частей. Наружная часть называется вершиной. Прилегающие к ней боковые поверхности носят название головки зуба. Внутренняя часть именуется ножкой зуба. Две соседние ножки образуют впадину зубчатого колеса.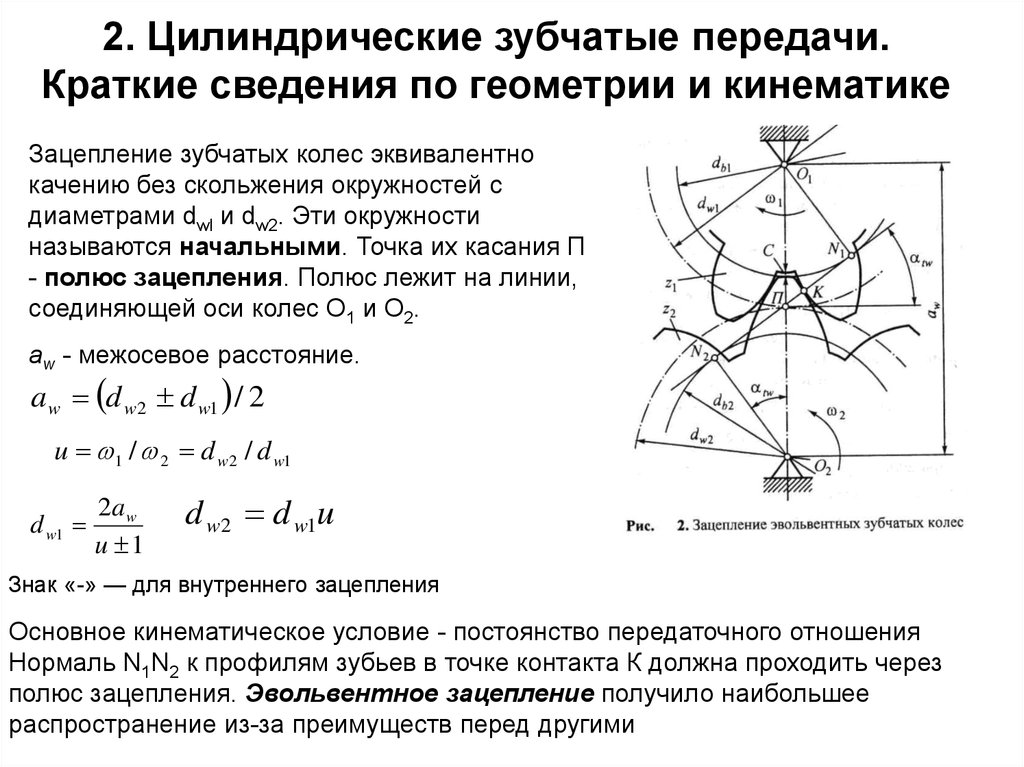
Для крепления на валу механизма в центре диска изготавливается ступица со сквозным отверстием. Форма отверстия зависит от геометрии сечения вала и может быть цилиндрической, квадратной или многоугольной. При использовании цилиндрических валов, в ступице обычно выполняют шпоночный паз.
С целью уменьшения веса толщина диска колеса выполняется обычно меньше, чем толщина ступицы или обода. Также для этого в теле диска могут присутствовать окна разнообразной формы.
Основные параметры
Для обеспечения подвижности и работоспособности, конструкция отдельных деталей механической передачи должна быть согласована по размерам и геометрии. Для этого при описании подобных устройств принято использовать систему специальных параметров. В их число входят геометрические, массогабаритные и прочностные величины, закрепленные стандартами. Применение стандартных параметров позволяет сравнительно просто производить расчет унифицированных зубчатых передач и обеспечивает гарантированное сопряжение всех изделий между собой. Естественно, что для разных видов, параметры будут несколько отличаться. Далее рассматриваются термины, связанные с конструкцией эвольвентного цилиндрического колеса. Эти параметры, в своем большинстве, описывают основные характеристики и других вариантов колес.
Естественно, что для разных видов, параметры будут несколько отличаться. Далее рассматриваются термины, связанные с конструкцией эвольвентного цилиндрического колеса. Эти параметры, в своем большинстве, описывают основные характеристики и других вариантов колес.
В основе сечения зуба большинства шестерен лежит эвольвентный профиль, который получается на основе одноименной кривой. Его применение легко стандартизируется, характеризуется высокой технологичностью изготовления и низкими требованиями к качеству сборки механизма. Основными параметры эвольвентного зубчатого колеса считаются модуль зацепления и количество зубьев зубчатого колеса. При одном и том же наружном диаметре деталей значения этих величин могут существенно отличаться в разных вариантах конструкции.
Число зубьев определяет коэффициент передачи и геометрические размеры зубьев. На ведущем колесе редуктора оно выполняется меньшим, чем на ведомом. В итоге один нормальный оборот ведущей шестерни приводит к повороту ведомого колеса только на определенный угол. Отношение числа зубьев двух колес дает значение передаточного коэффициента. Размеры зубьев определяются как отношение их количества к длине окружности колеса. С целью упрощения расчетов и гарантированного обеспечения зацепления между разными колесами, предусмотрен дополнительный параметр, называемый модулем зацепления. Любые шестерни с одинаковым модулем обеспечивают взаимодействие между собой и могут использоваться для построения механизмов, без дополнительной обработки.
Отношение числа зубьев двух колес дает значение передаточного коэффициента. Размеры зубьев определяются как отношение их количества к длине окружности колеса. С целью упрощения расчетов и гарантированного обеспечения зацепления между разными колесами, предусмотрен дополнительный параметр, называемый модулем зацепления. Любые шестерни с одинаковым модулем обеспечивают взаимодействие между собой и могут использоваться для построения механизмов, без дополнительной обработки.
Сумма ширины зуба и впадины совместно дают шаг зубчатого колеса. Учитывая неравномерность профиля по радиусу и зависимость длины дуги от диаметра, в каждом колесе можно определить бесконечное число значений этого параметра. С целью стандартизации принято рассматривать шаг по делительной окружности, называемый так же окружным шагом. Отношение этого шага к числу пи дает модуль зацепления. В некоторых случаях для описания шестерен используют угловой шаг, измеряемый в градусах. Стандартами предусмотрены и несколько других угловых величин. Например, для упрощения настройки оборудования при изготовлении колес рассматривают угловую ширину зуба и угловую ширину впадины. Определяются они также на основе делительной окружности.
Например, для упрощения настройки оборудования при изготовлении колес рассматривают угловую ширину зуба и угловую ширину впадины. Определяются они также на основе делительной окружности.
Диаметры окружностей
Рассмотрение геометрии зубчатых пар невозможно без определения диаметров. На каждой детали их выделяется несколько. Широкое распространение имеет диаметр окружности по выступам, иногда называемый диаметром вершин. Он определяет максимальные габариты диска колеса. Его противоположностью считается диаметр окружности впадин. Разность этих величин, поделенная пополам, дает полную длину зуба. Но этот параметр в чистом виде не используется. При расчетах принято выделять высоту головки и ножки зуба. Граница, отделяющая два этих понятия, называется делительной окружностью зубчатого колеса. Диаметр данной окружности выполняет функцию опорного параметра при выполнении расчетов геометрии, так как именно по ней определяется окружной шаг и модуль зацепления. Еще один диаметральный параметр, называемый основной окружностью, описывает теоретическую кривую, которая является базой при построении эвольвенты. Диаметр основной окружности используется для построения конкретного профиля зуба.
Диаметр основной окружности используется для построения конкретного профиля зуба.
Модуль зубчатого колеса
Универсальным понятием, позволяющим определить геометрические параметры деталей, выступает модуль зубчатой передачи. Его значение равно длине дуги в миллиметрах, приходящейся на один зуб колеса. Конкретное значение определяется по делительной окружности. Ее численно подбирают таким образом, что бы значение модуля совпадало с одним из общепринятых значений, найти которые можно в специальной литературе. В отечественной практике стандартные модули зубчатых колес нормированы в ГОСТ 9563-60. При проектировании шестерен обычно задаются значением этого параметра, а от него легко рассчитают все множество других. Исходными данными для определения требуемого модуля зубчатого колеса выступают расчеты прочности, призванные обеспечить требуемую мощность механической передачи.
Скачать ГОСТ 9563-60
Модуль зубчатого колеса связан с целым набором производных параметров. Используя несложные формулы расчета и значение необходимого числа зубьев, можно получить окружной шаг, диаметры верши и впадин, толщину зуба и ширину впадины по делительной окружности.
Используя несложные формулы расчета и значение необходимого числа зубьев, можно получить окружной шаг, диаметры верши и впадин, толщину зуба и ширину впадины по делительной окружности.
В зарубежной литературе аналогом отечественного модуля выступает питч. По своей сути это обратная к модулю зацепления величина, приведенная к дюймовой системе измерений. Аналогично для питчей разработаны специальные таблицы, содержащие нормированные значения параметра.
Расчет параметров
Расчет параметров зубчатых колес выполняют комплексно, для всей передачи. Необходимость расчета отдельного колеса возникает только в процессе ремонта оборудования с неизвестными данными. Расчет начинают с определения требуемого числа зубьев и модуля зацепления. Для того чтобы узнать значение модуля, предварительно проводят расчеты на прочность, исходя из срока службы и выбранного материала будущего механизма. Также на этом этапе рассчитывают межосевое расстояние между колесами. На основе полученных данных выносливости зубьев вычисляется минимально допустимая величина модуля зацепления. Конкретное его значение выбирается на основе таблиц, приведенных в справочной литературе. Далее, используя требуемое передаточное отношение, производится вычисление числа зубьев на сопрягаемых колесах.
Конкретное его значение выбирается на основе таблиц, приведенных в справочной литературе. Далее, используя требуемое передаточное отношение, производится вычисление числа зубьев на сопрягаемых колесах.
При известном модуле зацепления и количестве зубьев шестерни и колеса, доступно произвести вычисление геометрических размеров отдельных деталей. Основные диаметры и профиль зуба передачи рассчитываются с использованием несложных арифметических действий. Сложные операции потребуются только для ограниченного числа параметров. Для цилиндрического прямозубого колеса тригонометрические функции содержат только формулы расчета делительного диаметра. При проектировании других типов зубчатых колес, используют тот же математический аппарат, что и для прямозубых, но с добавлением расчетов, учитывающих иную геометрию деталей. Результаты расчетов используют для построения чертежей будущих шестерен, а также при вычислении параметров редукторов.
Заключительным этапом расчета зубчатой передачи становится окончательная проверка механизма на прочность. Если результаты этих вычислений укладываются в принятые нормативы, то полученные значения величин можно использовать для изготовления готового механизма. В противном случае может потребоваться выполнить новый расчет, изменив исходные данные, например, увеличить геометрические размеры, либо поменять тип зубчатой передачи или количество ступеней редуктора.
Если результаты этих вычислений укладываются в принятые нормативы, то полученные значения величин можно использовать для изготовления готового механизма. В противном случае может потребоваться выполнить новый расчет, изменив исходные данные, например, увеличить геометрические размеры, либо поменять тип зубчатой передачи или количество ступеней редуктора.
Применение
Высокие свойства зубчатых передач нашли отражение в широком спектре применений. Во многих промышленных механизмах используются редукторы, призванные понизить число оборотов вращения вала двигателя, для передачи на технологическое оборудование. Помимо изменения скорости, такое устройство также увеличивает механический момент. В итоге маломощный двигатель с большой скоростью вращения, способен приводить в движение медленный и тяжелый механизм.
С целью уменьшения габаритов редуктора его часто выполняют многоступенчатым.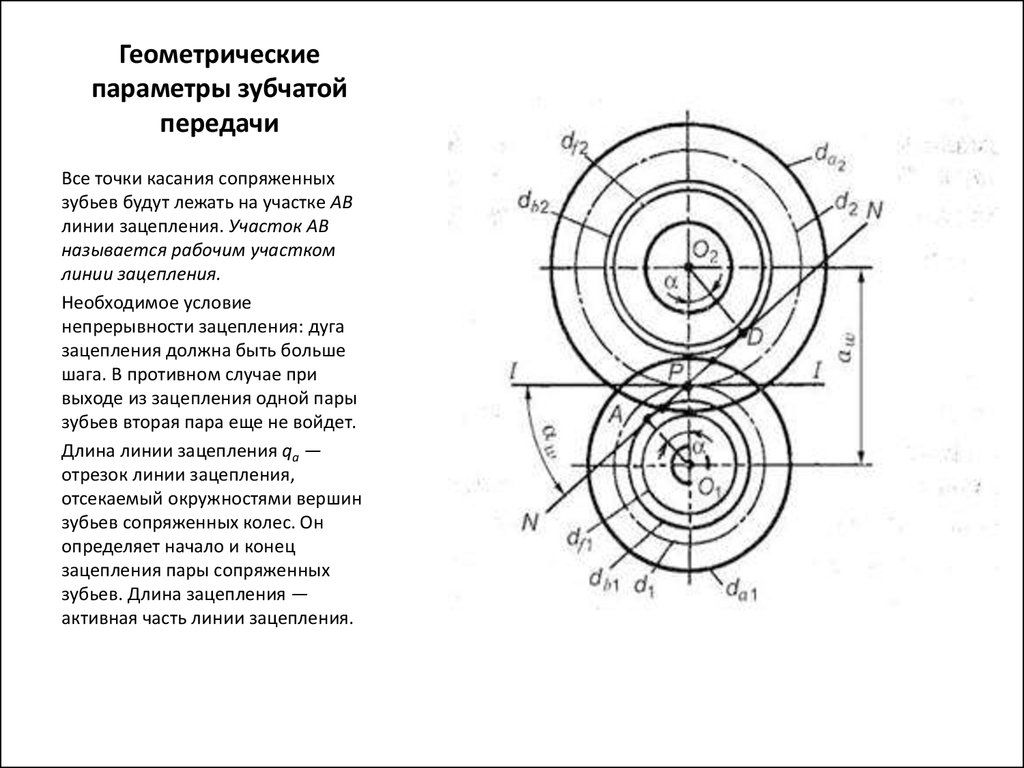 Большое количество зубчатых колес входят в последовательное зацепление между собой, обеспечивая высокое передаточное число. Классическим примером подобного устройства являются обычные механические часы. Благодаря множеству специально подобранных передач, скорости движения секундной, минутной и часовой стрелок отличаются друг от друга ровно в 60 раз.
Большое количество зубчатых колес входят в последовательное зацепление между собой, обеспечивая высокое передаточное число. Классическим примером подобного устройства являются обычные механические часы. Благодаря множеству специально подобранных передач, скорости движения секундной, минутной и часовой стрелок отличаются друг от друга ровно в 60 раз.
Зубчатые передачи позволяют реализовать и функцию регулирования скорости. Для этого применяются сменные комплекты колес, имеющих одинаковое межосевое расстояние и разное передаточное отношение.
Меняя один комплект на другой, можно получить разные скорости выходного вала. Этот принцип действия лег в основу коробок переключения передач, широко используемых в автомобилестроении, станкостроении и других отраслях.
Обычное зубчатое колесо допускает применение и для повышения скорости выходного вала относительно входного. В общем случае для этого достаточно развернуть редуктор или поменять местами точки подключения двигателя и конечного механизма. Называется подобное устройство мультипликатор. Из особенностей его применения необходимо учитывать запас по мощности двигателя, сопоставимый с передаточным числом механизма.
Называется подобное устройство мультипликатор. Из особенностей его применения необходимо учитывать запас по мощности двигателя, сопоставимый с передаточным числом механизма.
Зубчатые колеса используются также для изменения направления движения. Две цилиндрические шестерни с одинаковым числом зубьев реализуют функцию смены направления вращения вала. Передачи конической или корончатой конструкции используются в случае необходимости смены положения оси в пространстве. Ведущая и ведомая шестерни в таких механизмах развернуты друг относительно друга на какой-либо угол, значение которого может достигать 90 градусов. При этом передаточное отношение часто равно единице, что обеспечивает одинаковые скорости валов.
Наряду с простыми вариантами передач, содержащих зубчатые колеса, разработаны несколько специальных моделей. С целью снижения материалоемкости, в механизмах с ограниченным углом поворота, используют только часть зубчатого колеса. Такой сектор, обладая всеми основными свойствами зубчатого зацепления, отличается более низкой массой и стоимостью.
Еще один вариант, называемый планетарной передачей, также характеризуется малым весом и габаритами. При этом устройство обеспечивает высокое значение передаточного числа и пониженный уровень шума в процессе работы. Конструктивно такая передача состоит из нескольких шестерен, имеющих разную степень свободы. За счет этого механизм может не только передавать вращение, но и складывать или выделять угловые скорости разных валов, находящихся на одной оси. Сегодня разработано большое число вариантов планетарных передач, отличающихся типом и взаимным расположением зубчатых колес. Планетарные передачи широко применяются в автомобильной и авиационной технике, тяжелом металлорежущем оборудовании. Среди недостатков, сдерживающих распространение передач данного типа, следует отметить низкий КПД и высокие конструктивные требования к точности изготовления отдельных деталей.
Зубчатое колесо: виды, типы, классификация, области применения
- Что такое зубчатые колеса
- Виды зубчатых колес
- Конструкция зубчатого колеса
- Основные параметры
- Диаметры окружностей
- Модули зубчатых колес
- Расчет параметров
- Применение
- Зубчатое колесо и шестерня — отличия
- Особенности зубчатых колес и шестерней
Зубчатые передачи весьма широко и продуктивно применяются в конструкциях современных машин, механизмов и устройств. Транспортные средства, энергетические установки, грузоподъемные устройства, авиационные установки, сельскохозяйственные машины, точные приборы — во всех них найдутся те или иные варианты зубчатого колеса. В технике зубчатая передача используется с целью распространения вращательного движения между осями валов, которые могут быть расположены параллельно, скрещиваться или пересекаться. Также, при помощи подобной передачи легко преобразовать вращательное движение, например, в поступательное, или реализовать эффективное преобразование крутящего момента и оборотов валов. Благодаря последнему свойству их используют в редукторах или мультипликаторах различных типов, а также коробках передач.
Транспортные средства, энергетические установки, грузоподъемные устройства, авиационные установки, сельскохозяйственные машины, точные приборы — во всех них найдутся те или иные варианты зубчатого колеса. В технике зубчатая передача используется с целью распространения вращательного движения между осями валов, которые могут быть расположены параллельно, скрещиваться или пересекаться. Также, при помощи подобной передачи легко преобразовать вращательное движение, например, в поступательное, или реализовать эффективное преобразование крутящего момента и оборотов валов. Благодаря последнему свойству их используют в редукторах или мультипликаторах различных типов, а также коробках передач.
Основными преимуществами подобного способа передачи мощностей являются высокий КПД; компактный конструктив; плавная работа; точность; долговечность; надежность; возможность осуществления передачи силы с использованием любого угла, передаточного числа (до нескольких тысяч) и большого диапазона скоростей (до 150 м/с).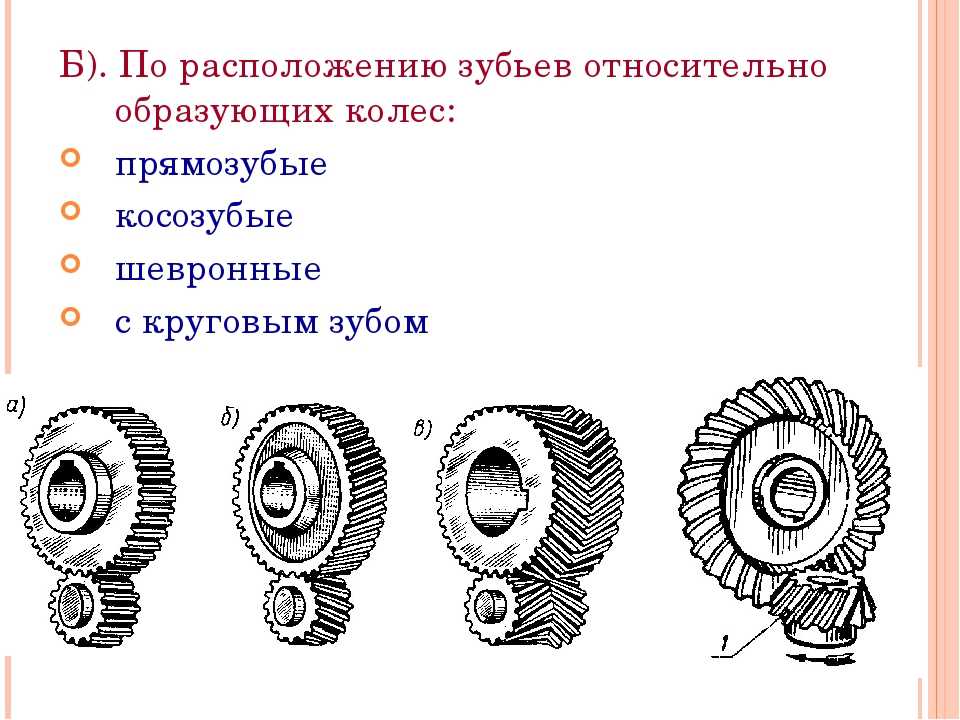 Эти качества и обусловили распространение использования зубчатых передач в технике. К негативным моментам можно отнести технологическую сложность производства; требовательность к точности обработки, материалам и обрабатывающему оборудованию. Выбор материала для зубчатого колеса один из наиболее важных критериев надежности и долговечности в дальнейшей его работе. Жесткость конструкции, обеспечивающая передаче высокую эффективность, к сожалению, не позволяет ей держать высокие значения динамических нагрузок, часто являющихся причиной разрушения механизма. В дополнение, этим передачам характерна повышенная шумность, снижения которой можно достичь повышением качества и точности при производстве изделий.
Эти качества и обусловили распространение использования зубчатых передач в технике. К негативным моментам можно отнести технологическую сложность производства; требовательность к точности обработки, материалам и обрабатывающему оборудованию. Выбор материала для зубчатого колеса один из наиболее важных критериев надежности и долговечности в дальнейшей его работе. Жесткость конструкции, обеспечивающая передаче высокую эффективность, к сожалению, не позволяет ей держать высокие значения динамических нагрузок, часто являющихся причиной разрушения механизма. В дополнение, этим передачам характерна повышенная шумность, снижения которой можно достичь повышением качества и точности при производстве изделий.
Что такое зубчатые колеса
В общем случае, шестерня, или зубчатое колесо — главная деталь одноименной передачи, имеет вид диска с расположенными на цилиндрической или конической поверхности зубьями. При помощи этих зубьев в процессе вращения происходит зацепление колес между собой, что позволяет реализовать перенос вращательного момента от одного вала, на котором расположено колесо, к другому. Зуб зубчатого колеса при вращении толкает зуб другого, сопряженного с ним, колеса, которое вследствие этого тоже начинает совершать вращательное движение.
Зуб зубчатого колеса при вращении толкает зуб другого, сопряженного с ним, колеса, которое вследствие этого тоже начинает совершать вращательное движение.
Сопряженная зубчатая передача должна всегда состоять из двух типов элементов: ведущих и ведомых. При этом ведущим, по определению, называют колесо передающее (сообщающее) вращение, ведомым — то зубчатое колесо, которое имеет большой диаметр с большим количеством зубьев и приводит во вращение. В большинстве случаев используется пара зубчатых колес, одно из которых с большим числом зубьев, а другое с меньшим. Иногда элемент, несущий меньше зубьев, считается шестерней, тогда колесом считают тот, у которого зубьев больше.
Виды зубчатых колес
Все зубчатые колеса, виды которых также многочисленны, как и варианты их применения, делятся на основные типы по расположению осей валов и геометрии формы зубьев. Выделяют цилиндрические, конические, червячные, винтовые передачи. На практике, исходя из формы профиля зубьев, выделяют эвольвентные и круговые колеса, а по расположению — прямозубые и косозубые типы зубчатых колес.
Для параллельного случая расположения осей валов применяют цилиндрические передачи:
- прямозубые;
- с круговыми зубьями;
- шевронные;
- косозубые.
Конические передачи подходят для пересекающихся осей:
- с криволинейными зубьями;
- косозубые;
- с нулевым углом наклоном;
- прямозубые.
Когда оси перекрещиваются, тогда используют передачи:
- спироидные;
- гипоидные;
- винтовые;
- червячные.
Наибольшую распространенность среди машин и механизмов обрели цилиндрические зубчатые колеса. Им свойственна простота изготовления, надежность, малые габариты. Конические, червячные и винтовые виды зубчатых колес используют лишь тогда, когда компоновка машины предъявляет особые условия. Цилиндрические зубчатые передачи делятся на два существенных вида: внешнего и внутреннего зацепления. В первом варианте реализации колесо и шестерня, у которой внешнее зацепление, крутятся в направлениях, которые противоположны друг другу. Во втором — колесо внутреннего зацепления и шестерня внешнего зацепления совершают вращательное движение со направленно. Существует также реечная передача — в ней рейка с зубьями сопрягается с имеющей внешнее зацепление шестерней.
Во втором — колесо внутреннего зацепления и шестерня внешнего зацепления совершают вращательное движение со направленно. Существует также реечная передача — в ней рейка с зубьями сопрягается с имеющей внешнее зацепление шестерней.
Косозубые цилиндрические колеса имеют расположенные под углом к оси зубья. Сопряженные колеса имеют одинаковый наклон зубьев, но различные его направления. У одного наклон будет правым, у другого же — левым. Наличие наклона дает возможность передавать большие, по сравнению с прямозубыми, нагрузки, способствует плавному зацеплению зубьев и снижению шума.
Шевронные колеса представляют собой пару соединенных колес с косыми зубьями, имеющими равный угол наклона, но расположенными противоположно: одно с правым, второе с левым наклоном. Это позволяет уравновесить осевые силы, тем самым снизив нагрузку на подшипник. Колеса могут иметь в середине канавку. Колеса без канавки более прочны, но сложны в изготовлении.
Винтовые цилиндрические передачи, в свою очередь, применяют для вращения валов, когда угол их перекрещивания лежит в пределах от 0 до 90 градусов. Они похожи на косозубые колеса, однако винтовая передача имеет контакт точечный, а не линейный, как косозубая. Направление наклона зубьев у всех таких сопряженных колес одинаковое. Точечный контакт зубов вызывает повышение их износа, как следствие их используют только на небольших нагрузках.
Они похожи на косозубые колеса, однако винтовая передача имеет контакт точечный, а не линейный, как косозубая. Направление наклона зубьев у всех таких сопряженных колес одинаковое. Точечный контакт зубов вызывает повышение их износа, как следствие их используют только на небольших нагрузках.
Реечные передачи составляются из зубчатых колес и реек, которые также имеют зубья. Вращаясь, цилиндрическое колесо, перемещает сопряженную рейку по перпендикулярной оси колеса прямой. Таким способом движение из вращательного превращается в поступательное. Подобная передача бывает как с косыми зубьями, так и с прямыми.
Прямозубые конические колеса обладают зубьями, пересекающими оси этих колес. Коническое расположение позволяет вращать пересекающиеся или скрещивающиеся оси. Зубья также могут быть косыми, т.е. касательными к окружности. Угол наклона зубьев у таких колес составляет не больше тридцати градусов. Снабжение конических колес зубьями с нулевым углом наклона обеспечивает первым невысокие осевые и радиальные нагрузки, дает возможность применения подшипников скольжения. Эти качества делают передачи с использованием таких колес компактными, а изготовление не затратным.
Эти качества делают передачи с использованием таких колес компактными, а изготовление не затратным.
Использование криволинейных зубьев для применения в конических зубчатых колесах резко снижает шумность передач и повышает прочность. Конические передачи подобного рода всегда имеют в зацеплении как минимум два зуба, что дает им возможность выдерживать нагрузку, которая выше на 30% относительно идентичных прямозубых и колес, имеющих нулевой наклон.
Гипоидные зубчатые колеса подобны коническим, но ось ведущей шестерни у них смещена выше или ниже относительно оси колеса, которое она ведет. У таких передач шестерни имеют наклон зубьев больший, чем у колес. Нормальный шаг при этом у шестерни и зубчатого колеса будет одинаковый, а торцовый — у шестерни больше. Гипоидной передаче не присуще чистое качение или скольжение, все ее точки подвержены скольжению. Это придает ей плавность и повышенную бесшумность. Кроме того, притирка происходит быстрее и качественней. Минус — присутствие скольжения вызывает повышенный износ поверхности зубов, что требует применения для таких передач специализированных масел.
Червячные передачи цилиндрические имеют червяк, имеющий геометрию цилиндра, на котором нарезаются витки, идущие вдоль направления винтовой линии. Червячное колесо должно иметь вогнутые зубья. Линейный контакт таких зубьев обеспечивает передачу больших нагрузок. Скольжение у червячных значительно выше, чем у прочих зубчатых передач. В глобоидной передаче червяк обладает вогнутой формой. Эта особенность позволяет участвовать в процессе зацепления большему числу зубьев, что повышает величину передаваемых такой передачей нагрузок.
Спироидные передачи занимают промежуточное место между червячными и гипоидными вариантами. В отличие от червячной, у гипоидной передачи червяк имеет форму конуса и зацепляется с колесом, на котором зубья располагаются на торцевой стороне.
Конструкция зубчатого колеса
Металлические зубчатые колеса, чертеж которых иногда довольно сложен, имеют разнообразные варианты конструкций, однако в них можно выделить три основных компоненты: венец с зубьями, ступицу и сам колесный диск. Венец зубчатого колеса является основным компонентом и на него приходится основная нагрузка. Зубья имеют различную геометрию. Наружная часть у зуба — это вершина, прилегающие к ней боковые части — головка зуба. Внутренняя часть зуба называется его ножкой. Пространство между двумя ближними ножками образует впадину колеса. Чтобы крепить шестерню или колесо на валу, в центре диска располагается ступица, имеющая сквозное отверстие, форма которого напрямую зависит от сечения вала: она может иметь форму цилиндра, квадрата или любого другого многоугольника. В случае цилиндрических валов, ступица часто имеет т.н. шпоночный паз. В целях экономии материалов и веса колеса, его диск имеет толщину, меньшую по сравнению с толщиной обода и ступицы. Часто в диске для этих целей еще выполняют различные отверстия.
Венец зубчатого колеса является основным компонентом и на него приходится основная нагрузка. Зубья имеют различную геометрию. Наружная часть у зуба — это вершина, прилегающие к ней боковые части — головка зуба. Внутренняя часть зуба называется его ножкой. Пространство между двумя ближними ножками образует впадину колеса. Чтобы крепить шестерню или колесо на валу, в центре диска располагается ступица, имеющая сквозное отверстие, форма которого напрямую зависит от сечения вала: она может иметь форму цилиндра, квадрата или любого другого многоугольника. В случае цилиндрических валов, ступица часто имеет т.н. шпоночный паз. В целях экономии материалов и веса колеса, его диск имеет толщину, меньшую по сравнению с толщиной обода и ступицы. Часто в диске для этих целей еще выполняют различные отверстия.
Основные параметры
Чтобы обеспечивать возможность конструирования работоспособных зубчатых передач, размеры колес и шестерен, а также их прочностные и массогабаритные характеристики описываются специальными параметрами, величины которых хорошо стандартизированы ГОСТ.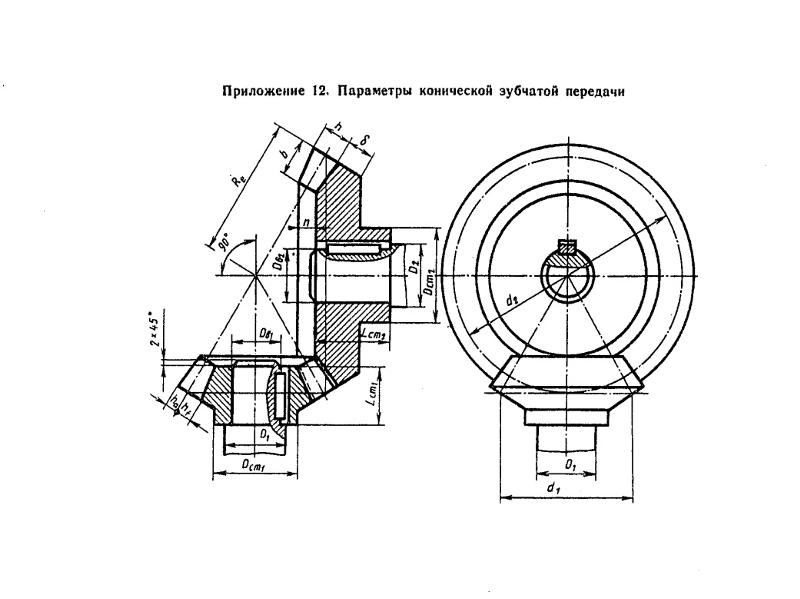 Так, эвольвентный профиль, положенный в основу сечения зуба подавляющего большинства колес, характеризуется модулем зацепления и имеющимся количеством зубьев на колесе или шестерне. Довольно часто, эвольвентные зубчатые колеса, имея один и тот же диаметр, могут иметь существенно различающие значения данных величин. Окружной модуль, служащий основной характеристикой для зубьев, по стандарту может иметь значения в диапазоне от 0,05 до 100 мм. Главными параметрами геометрии у различных зубчатых колес являются следующие диаметры: начальный, основной и делительный. Шагом зубчатого колеса называется общее расстояние ширины зуба и впадины. Так же важным параметром является радиус колеса. Радиуса зубчатых колес делятся: радиус окружности вершин, радиус делительной окружности, радиус основной окружности, радиус окружности впадин.
Так, эвольвентный профиль, положенный в основу сечения зуба подавляющего большинства колес, характеризуется модулем зацепления и имеющимся количеством зубьев на колесе или шестерне. Довольно часто, эвольвентные зубчатые колеса, имея один и тот же диаметр, могут иметь существенно различающие значения данных величин. Окружной модуль, служащий основной характеристикой для зубьев, по стандарту может иметь значения в диапазоне от 0,05 до 100 мм. Главными параметрами геометрии у различных зубчатых колес являются следующие диаметры: начальный, основной и делительный. Шагом зубчатого колеса называется общее расстояние ширины зуба и впадины. Так же важным параметром является радиус колеса. Радиуса зубчатых колес делятся: радиус окружности вершин, радиус делительной окружности, радиус основной окружности, радиус окружности впадин.
Диаметры окружностей
Зубчатое колесо описывается несколькими окружностями, являющимися важными характеристиками их геометрии. Так, диаметр вершин дает максимальные размеры зубчатого колеса. Ему противоположен диаметр окружности впадин. Высчитав разность между этими двумя величинами и разделив ее пополам, получим полную длину зуба. Важным параметром считается диаметр делительной окружности, имеющий формулу d=pz/3,14, по нему можно определить окружной шаг p расположенных на колесе зубьев, иначе называемый шагом зацепления, имеющий геометрический смысл части длины этой окружности, приходящейся на каждый зуб. В общем случае, диаметр делительной окружности отделяет высоту головок и высоту ножек зуба. Он также задает кривую, являющуюся необходимой базой для построения самой эвольвенты, и используется для построения требуемого в конкретной задаче профиля зубьев колес и шестерен.
Ему противоположен диаметр окружности впадин. Высчитав разность между этими двумя величинами и разделив ее пополам, получим полную длину зуба. Важным параметром считается диаметр делительной окружности, имеющий формулу d=pz/3,14, по нему можно определить окружной шаг p расположенных на колесе зубьев, иначе называемый шагом зацепления, имеющий геометрический смысл части длины этой окружности, приходящейся на каждый зуб. В общем случае, диаметр делительной окружности отделяет высоту головок и высоту ножек зуба. Он также задает кривую, являющуюся необходимой базой для построения самой эвольвенты, и используется для построения требуемого в конкретной задаче профиля зубьев колес и шестерен.
Модули зубчатых колес
Чтобы упростить расчеты элементов, использующихся для зацепления, для зубчатых колес была введена стандартизованная ГОСТ величина, названная модулем. Модуль зубчатого колеса является частью от диаметра имеющейся делительной окружности зубчатого колеса, которая приходится на зуб: m=d/z. Таким образом, количество зубьев колеса, его собственный делительный диаметр и его модуль — во взаимовлиянии. Модуль можно расписать как отношение шага зацепления колеса и числа Пи: m=d/3,14. Когда передаваемая зубчатыми колесами нагрузка невелика, то лучше использовать малые модули. Малый модуль дает более длительный срок эксплуатации и упрощается обработка зубчатых колес. В данном случае на делительном диаметре разместится больше зубьев, а значит и зацепление будет происходить с большим их числом, что уменьшит нагрузку на отдельные зубья шестерен. У прямозубых цилиндрических колес бывает всего только один модуль, у косозубых — два: нормальный и окружной. В расчетах используют первый.
Таким образом, количество зубьев колеса, его собственный делительный диаметр и его модуль — во взаимовлиянии. Модуль можно расписать как отношение шага зацепления колеса и числа Пи: m=d/3,14. Когда передаваемая зубчатыми колесами нагрузка невелика, то лучше использовать малые модули. Малый модуль дает более длительный срок эксплуатации и упрощается обработка зубчатых колес. В данном случае на делительном диаметре разместится больше зубьев, а значит и зацепление будет происходить с большим их числом, что уменьшит нагрузку на отдельные зубья шестерен. У прямозубых цилиндрических колес бывает всего только один модуль, у косозубых — два: нормальный и окружной. В расчетах используют первый.
Расчет параметров
Для всех зубчатых колес инженерный расчет их параметров является задачей комплексной, в ходе решения которой принимается во внимание конструкция всей передачи. Вначале нужно определиться с числом зубьев и необходимым в задаче модулем зацепления. Для выбора последнего необходимы параметры прочности и предполагаемого срока службы колес; материала, из которого оно будет изготовлено. На основе этих данных рассчитывается минимально возможная в данной задаче величина модуля зацепления, которое затем приводится к стандартизованным значениям, находящимся из соответствующих таблиц. Передаточное отношение высчитывается с применением формулы u=z2z1, где z2 — это количество колесных зубьев, а z1 — количество зубьев, находящихся на шестерне. Оно позволяет понять, сколько всего нужно зубьев на колесах, подлежащих сопряжению. Зная модули и полученное число зубьев для всех колес и шестерней, можно произвести дальнейшие расчеты размеров требуемых деталей, используя стандартный метод для их расчетов.
На основе этих данных рассчитывается минимально возможная в данной задаче величина модуля зацепления, которое затем приводится к стандартизованным значениям, находящимся из соответствующих таблиц. Передаточное отношение высчитывается с применением формулы u=z2z1, где z2 — это количество колесных зубьев, а z1 — количество зубьев, находящихся на шестерне. Оно позволяет понять, сколько всего нужно зубьев на колесах, подлежащих сопряжению. Зная модули и полученное число зубьев для всех колес и шестерней, можно произвести дальнейшие расчеты размеров требуемых деталей, используя стандартный метод для их расчетов.
Применение
Каждый из видов передач имеет свои преимущества и отрицательные качества. Нарезание прямозубых колес — довольно простой технологический процесс, поэтому они широко применяются в промышленности. Косозубые, как и прямозубые цилиндрические колеса, используются в тракторах, станках, коробках передач автотранспорта. Цилиндрические колеса с использованием внутреннего зацепления, благодаря компактности и прочности, нашли себя в самолетах, трансмиссиях автомобилей, редукторах, в шлицевых соединениях и сложных планетарных передачах, которые славятся своим особенно малым весом и габаритными размерами. При этом они предоставляют высокие передаточные числа и значительно сниженные уровни шумов при своей работе. Шевронные колеса, будучи трудоемкими в производстве, используются в больших редукторах и их ремонте, где требуется плавная и бесшумная передача значительных нагрузок. Конические колеса с нулевым наклоном и их прямозубые аналоги, имея высокую компактность и невысокую себестоимость изготовления, эксплуатируются в дифференциалах автомашин и станков. Криволинейные зубья обеспечивают коническим колесам особую прочность и малошумность, поэтому их можно найти в ответственных и скоростных передачах. Их используют практически везде: от самолетов до тракторов. Гипоидные зубчатые пары можно делать с большим передаточными числами (до 100:1), они часто используются в металлорежущем оборудовании.
Цилиндрические колеса с использованием внутреннего зацепления, благодаря компактности и прочности, нашли себя в самолетах, трансмиссиях автомобилей, редукторах, в шлицевых соединениях и сложных планетарных передачах, которые славятся своим особенно малым весом и габаритными размерами. При этом они предоставляют высокие передаточные числа и значительно сниженные уровни шумов при своей работе. Шевронные колеса, будучи трудоемкими в производстве, используются в больших редукторах и их ремонте, где требуется плавная и бесшумная передача значительных нагрузок. Конические колеса с нулевым наклоном и их прямозубые аналоги, имея высокую компактность и невысокую себестоимость изготовления, эксплуатируются в дифференциалах автомашин и станков. Криволинейные зубья обеспечивают коническим колесам особую прочность и малошумность, поэтому их можно найти в ответственных и скоростных передачах. Их используют практически везде: от самолетов до тракторов. Гипоидные зубчатые пары можно делать с большим передаточными числами (до 100:1), они часто используются в металлорежущем оборудовании.
Зубчатое колесо и шестерня — отличия
Главными деталями в зубчатой передаче – зубчатое колесо и шестерня. Они применяются во многих промышленных узлах, машинах. Многие полагают, что зубчатое колесо и шестерня это одна и та же деталь и у них нет различий между собой. Специалисты, которые тесно связаны с промышленностью и машиностроением так не считают и уверяю, что это разные детали хоть и выполняют по сути одну и ту же функцию передачу вращательного движения. Давайте разберем основные моменты по данному вопросу.
Особенности зубчатых колес и шестерней
Внешне зубчатое колесо и шестерня имеют схожесть в виде диска с расположенными на нем зубцами. Их расположение может быть как на конической, так и цилиндрической поверхности. Основной задачей данных деталей является передача крутящего момента. Для того чтобы получить и передать крутящий момент, нужна ответная шестерня, то есть пара. Мы разобрали выше, что существует ведомая деталь и ведущая. С ведущей начинается движение и дальнейшая передача крутящего момента на ведомую деталь.
Отметим что при работе двух зубчатых колес, колесо, которое имеет большее количество зубьев, называют шестерней. В ГОСТ 16530-83 есть пояснение, что зубчатое колесо и шестерня являются словами синонимами, шестерня является главным и ведущим зубчатым колесом. Существуют специалисты работающие в определенных областях промышленности и машиностроения, которые четко разделяют разницу между зубчатым колесом и шестерней. Они убеждены, что изготовление зубчатых колес это одно, а производство шестерней это другое, так как между ними есть различия.
Наша компания работает на своих станочных мощностях, что позволяет выполнять работы не только быстрее посредников, но и с более выгодными условиями на изготовление червячных зубчатых колес.
Работаем с любыми видами стали:
- Черные виды сталей;
- Цветные стали;
- Нержавеющие стали;
- Чугун.

Мы оказываем полный спектр услуг по металлообработке на современном, точном оборудовании с помощью качественного режущего инструмента, что позволяет нашим специалистам получать максимальной точности детали с чертежом заказчика.
Наши специалисты отдела металлообработки готовы принять заказы, обсудить с заказчиком все нюансы и пожелания, рассчитать заявку по срокам и стоимости изготовления в течение одного рабочего дня. Механическую обработку металла можно заказать на сайте https://metall-servise.ru/
Отправляйте заявку для расчета
Введите ваше имя*
E-mail*
Телефон для связи*
Комментарий к заявке
Прикрепите чертеж, эскиз или фото детали*
– Я не робот
Другие статьи:
Запись опубликована в рубрике Детали из металла. Добавьте в закладки постоянную ссылку.
Тема 1.3. Коронное зубчатое колесо.
Механическое преимущество: крутящий момент против скорости вращения
Зубчатые передачи работают по принципу механического преимущества. Это значит, что с помощью использования шестерен различных диаметров вы можете изменять скорость вращения выходного вала и вращающий момент, развиваемый приводным двигателем.
Это значит, что с помощью использования шестерен различных диаметров вы можете изменять скорость вращения выходного вала и вращающий момент, развиваемый приводным двигателем.
Любой электродвигатель имеет определенную скорость вращения и соответствующий его мощности крутящий момент. Но, к сожалению, для многих механизмов предлагаемые на рынке и подходящие по стоимости асинхронные двигатели обычно не обладают желаемым соотношением между скоростью и моментом (исключением являются сервоприводы и мотор-редукторы с высоким моментом). Например, вы действительно хотите, чтобы колеса вашего робота-уборщика вращались со скоростью 3000 об/мин при низком крутящем моменте? Нет конечно, поэтому последний зачастую предпочтительнее скорости.
Уравнение зубчатой передачи
Она обменивает высокую входную скорость на больший выходной крутящий момент. Этот обмен происходит по очень простому уравнению, которое можно записать так:
Этот обмен происходит по очень простому уравнению, которое можно записать так:
Момент входной * Скорость входная = Момент выходной * Скорость выходная
Скорость входную можно найти, просто просматривая табличку приводного электродвигателя. Момент входной легко определить по этой скорости и механической мощности из той же таблички. Затем просто подставим выходную скорость или требуемый крутящий момент в правую часть уравнения.
Например, предположим, что ваш асинхронный двигатель при моменте на выходном валу 0,5 Н∙м имеет скорость 50 об/с, но вы хотите только 5 об/с. Тогда ваше уравнение будет выглядеть так:
0,5 Н∙м * 50 об/с = Момент выходной* 5 об/с.
Ваш выходной крутящий момент будет 5 Н∙м.
Теперь предположим, что с тем же мотором вам нужно 5 Н∙м, но при этом требуется минимальная скорость 10 об/с. Как бы узнать, способен ли на это ваш мотор вместе с зубчатой передачей (т. е., по сути, мотор-редуктор)? Обратимся снова к нашему уравнению
0,5 Н∙м * 50 об/с = 5 Н∙м * Скорость выходная,
Скорость выходная = 5 об/с.
Итак, вы определили, используя простое уравнение, что при показателе Момент выходной =5 Н∙м обеспечить скорость выходную в 10 об/с ваша зубчатая передача не способна. Вы только что сохранили себе кучу денег, так как не потратили их на механизм, который никогда не заработал бы.
Передаточное число зубчатой передачи
Мы записали уравнения, но как механически поменять местами крутящий момент и скорость? Для этого нужны две шестерни (иногда больше) различных диаметров, чтобы иметь конкретное передаточное число. В любой паре шестерен большее зубчатое колесо будет двигаться более медленно, чем меньшее, но оно будет передавать на выходной вал больший крутящий момент. Таким образом, чем больше величина разницы (или передаточное число) между двумя колесами, тем больше разница их скоростей и передаваемых крутящих моментов.
Передаточное число показывает, во сколько раз зубчатая передача изменяет скорость и вращающий момент. Для него, опять же, имеется очень простое уравнение.
Предположим, что передаточное число равно 3/1. Это будет означать, что вы увеличиваете ваш крутящий момент втрое, а скорость втрое снижаете.
Момент входной = 1,5 Н∙м, Скорость входная = 100 об/с,
Передаточное число = 2/3
Момент выходной = Момент входной * 2/3 = 1 Н∙м,
Скорость выходная = Скорость входная * 3/2 = 150 об/с.
Итак, на выходе передачи момент в полтора раза вырос, а скорость точно так же снизилась.
Применение
Высокие свойства зубчатых передач нашли отражение в широком спектре применений. Во многих промышленных механизмах используются редукторы, призванные понизить число оборотов вращения вала двигателя, для передачи на технологическое оборудование. Помимо изменения скорости, такое устройство также увеличивает механический момент. В итоге маломощный двигатель с большой скоростью вращения, способен приводить в движение медленный и тяжелый механизм.
С целью уменьшения габаритов редуктора его часто выполняют многоступенчатым. Большое количество зубчатых колес входят в последовательное зацепление между собой, обеспечивая высокое передаточное число. Классическим примером подобного устройства являются обычные механические часы. Благодаря множеству специально подобранных передач, скорости движения секундной, минутной и часовой стрелок отличаются друг от друга ровно в 60 раз.
Большое количество зубчатых колес входят в последовательное зацепление между собой, обеспечивая высокое передаточное число. Классическим примером подобного устройства являются обычные механические часы. Благодаря множеству специально подобранных передач, скорости движения секундной, минутной и часовой стрелок отличаются друг от друга ровно в 60 раз.
Меняя один комплект на другой, можно получить разные скорости выходного вала. Этот принцип действия лег в основу коробок переключения передач, широко используемых в автомобилестроении, станкостроении и других отраслях.
Обычное зубчатое колесо допускает применение и для повышения скорости выходного вала относительно входного. В общем случае для этого достаточно развернуть редуктор или поменять местами точки подключения двигателя и конечного механизма. Называется подобное устройство мультипликатор. Из особенностей его применения необходимо учитывать запас по мощности двигателя, сопоставимый с передаточным числом механизма.
Зубчатые колеса используются также для изменения направления движения. Две цилиндрические шестерни с одинаковым числом зубьев реализуют функцию смены направления вращения вала. Передачи конической или корончатой конструкции используются в случае необходимости смены положения оси в пространстве. Ведущая и ведомая шестерни в таких механизмах развернуты друг относительно друга на какой-либо угол, значение которого может достигать 90 градусов. При этом передаточное отношение часто равно единице, что обеспечивает одинаковые скорости валов.
Две цилиндрические шестерни с одинаковым числом зубьев реализуют функцию смены направления вращения вала. Передачи конической или корончатой конструкции используются в случае необходимости смены положения оси в пространстве. Ведущая и ведомая шестерни в таких механизмах развернуты друг относительно друга на какой-либо угол, значение которого может достигать 90 градусов. При этом передаточное отношение часто равно единице, что обеспечивает одинаковые скорости валов.
Наряду с простыми вариантами передач, содержащих зубчатые колеса, разработаны несколько специальных моделей. С целью снижения материалоемкости, в механизмах с ограниченным углом поворота, используют только часть зубчатого колеса. Такой сектор, обладая всеми основными свойствами зубчатого зацепления, отличается более низкой массой и стоимостью.
Еще один вариант, называемый планетарной передачей, также характеризуется малым весом и габаритами. При этом устройство обеспечивает высокое значение передаточного числа и пониженный уровень шума в процессе работы.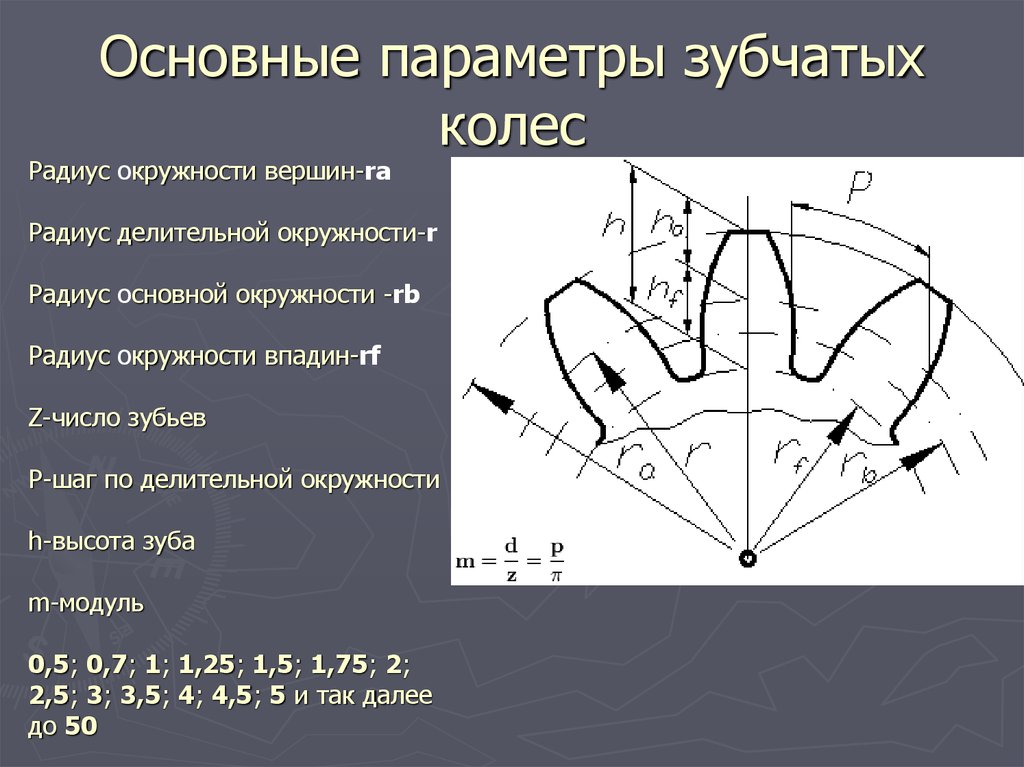 Конструктивно такая передача состоит из нескольких шестерен, имеющих разную степень свободы. За счет этого механизм может не только передавать вращение, но и складывать или выделять угловые скорости разных валов, находящихся на одной оси. Сегодня разработано большое число вариантов планетарных передач, отличающихся типом и взаимным расположением зубчатых колес. Планетарные передачи широко применяются в автомобильной и авиационной технике, тяжелом металлорежущем оборудовании. Среди недостатков, сдерживающих распространение передач данного типа, следует отметить низкий КПД и высокие конструктивные требования к точности изготовления отдельных деталей.
Конструктивно такая передача состоит из нескольких шестерен, имеющих разную степень свободы. За счет этого механизм может не только передавать вращение, но и складывать или выделять угловые скорости разных валов, находящихся на одной оси. Сегодня разработано большое число вариантов планетарных передач, отличающихся типом и взаимным расположением зубчатых колес. Планетарные передачи широко применяются в автомобильной и авиационной технике, тяжелом металлорежущем оборудовании. Среди недостатков, сдерживающих распространение передач данного типа, следует отметить низкий КПД и высокие конструктивные требования к точности изготовления отдельных деталей.
Достижение определенного передаточного числа
Если вы хотите достичь простой его величины, скажем 2 к 1, вы должны использовать две шестерни, одна из которых вдвое больше другой. Это не что иное, как отношение их диаметров. Если диаметр зубчатого колеса в 3 раза больше, чем у сцепленного с ним другого, то вы получите передаточное число 3/1 (или 1/3).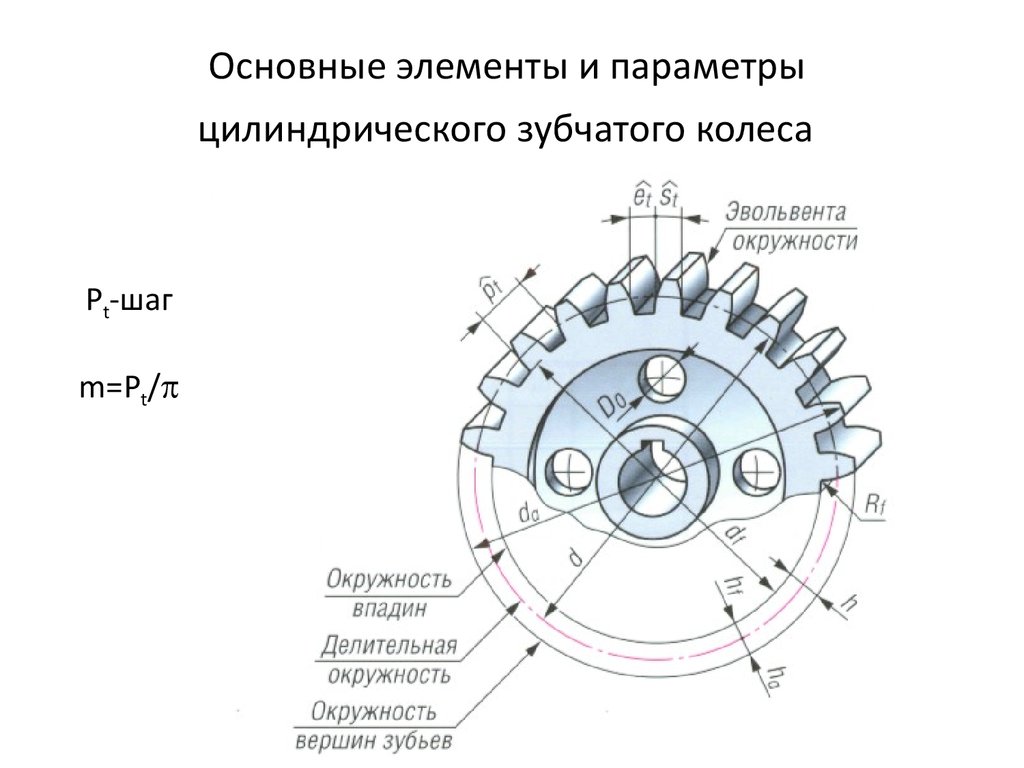
Для гораздо более точного способа вычислить передаточное число подсчитайте отношение зубьев на шестернях. Если одна из них имеет 28 зубьев и другая – 13, вы получите передаточное число 28 / 13 = 2,15 или 13 / 28 = 0,46. Подсчет зубьев всегда будет давать вам наиболее точную величину.
Эффективность передач
К сожалению, в зубчатой передаче вы имеете определенные энергетические потери. Это обусловлено очевидными причинами, такими как трение, рассогласование углов давления, смазкой, зазорами (расстоянием между сцепленными зубьями двух шестерен), а также угловыми моментами и т. д. Различные типы передач, разные виды зубчатых колес, различные материалы и износ шестерен, – все это будет влиять на КПД передачи. Возможные их комбинации дадут слишком большой список, поэтому точную величину КПД передачи, которые вы используете, вы сможете найти в документации на нее.
Предположим, что вы используете два цилиндрических зубчатых колеса. Обычное КПД такой передачи примерно
90%.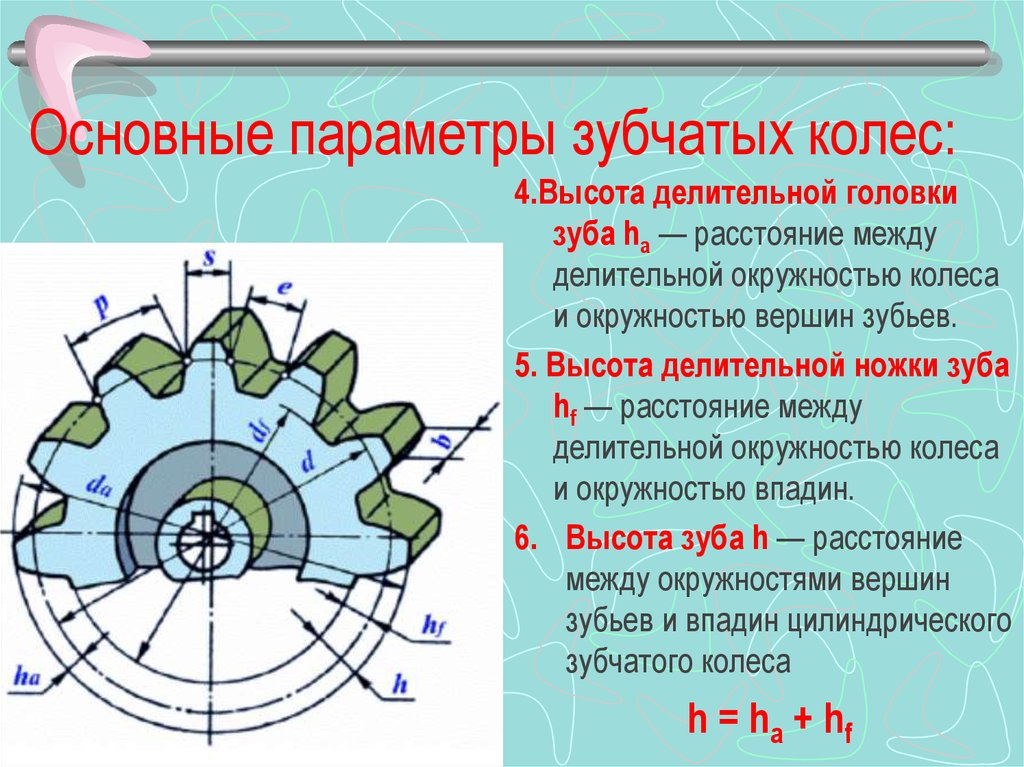 Умножьте это число на вашу скорость выходную и момент выходной, чтобы получить истинные выходные величины передачи.
Умножьте это число на вашу скорость выходную и момент выходной, чтобы получить истинные выходные величины передачи.
Если (из предыдущего примера):
Передаточное число = 2/3
Момент выходной = Момент входной * 2/3 = 1 Н∙м,
Скорость выходная = Скорость входная * 3/2 = 150 об/с,
Истинный Момент выходной = 1 Н∙м * 0,9= 0,9 Н∙м,
Истинная Скорость выходная = 150 об/с * 0,9 = 135 об/с.
Что представляет собой шестерня
Шестерня – это небольшое колесико с зубьями, которое крепится к специальной вращающейся оси. Поверхность у шестеренки в данном случае может быть как конической, так и цилиндрической.
Шестеренчатые передачи также имеют свою классификацию:
- Прямозубые. Наиболее распространенный вид шестеренок, у которых зубья зачастую располагаются в радиальных плоскостях.
- Скошенные. По-другому этот тип называется еще косозубым, а его использование в ходу у бензо- и электрических инструментов.
 По отношению к вращающейся оси они находятся под определенным углом.
По отношению к вращающейся оси они находятся под определенным углом. - Червячные. Их еще называют спиральными шестернями, которые используются преимущественно для рулевого управления автомобилем.
- Винтовые. Они имеют зачастую форму цилиндра, а также расположены по всей линии винта. Располагаются такие шестеренки на валах, которые расположены перпендикулярно к вращающейся оси.
Направление вращения шестерен
Разрабатывая любую зубчатую передачу, нужно понимать, как она изменяет направление вращения выходного вала. Две сцепленные шестерни всегда будут вращаться в противоположных направлениях. Это означает, что если одна вращается по часовой стрелке, то другая всегда будет вращаться против нее. Это вполне очевидно. Но что делать, если у вас есть передача, скажем, из шести сцепленных шестерен? Правило здесь следующее: входной и выходной валы у передач с нечетным числом шестерен всегда вращаются в одном направлении, а при четном числе шестерен – в противоположном.
Конструкция и параметры зубчатого колеса
Оно содержит венец с зубьями, диск и ступицу. Имеется три наиболее важных его параметра: модуль, диаметр делительной окружности и количество зубьев. Какую же делительную окружность имеет зубчатое колесо? Чертеж цилиндрического колеса с типовыми эвольвентными зубьями показан ниже.
Читать также: Для чего нужны кусачки
Например, зубчатое колесо с 22 зубьями и диаметром 44 мм имеет модуль m = 2 мм. Сцепленные шестерни должны обе иметь один модуль. Значения их стандартизованы, и как раз на делительной окружности модуль данного колеса принимает свое стандартное значение.
Высота головки зуба одного колеса меньше высоты ножки зуба второго, зацепляющегося с ним, благодаря чему образуется радиальный зазор c.
Для обеспечения бокового зазора δ между двумя сцепленными зубьями сумма их толщин принимается меньше их окружного шага p. Радиальный и боковой зазоры предусматриваются для создания необходимых условий смазки, нормальной работы передачи при неизбежных неточностях изготовления и сборки, тепловом увеличении размеров передачи и т. п.
п.
Основные параметры
Для обеспечения подвижности и работоспособности, конструкция отдельных деталей механической передачи должна быть согласована по размерам и геометрии. Для этого при описании подобных устройств принято использовать систему специальных параметров. В их число входят геометрические, массогабаритные и прочностные величины, закрепленные стандартами. Применение стандартных параметров позволяет сравнительно просто производить расчет унифицированных зубчатых передач и обеспечивает гарантированное сопряжение всех изделий между собой. Естественно, что для разных видов, параметры будут несколько отличаться. Далее рассматриваются термины, связанные с конструкцией эвольвентного цилиндрического колеса. Эти параметры, в своем большинстве, описывают основные характеристики и других вариантов колес.
В основе сечения зуба большинства шестерен лежит эвольвентный профиль, который получается на основе одноименной кривой. Его применение легко стандартизируется, характеризуется высокой технологичностью изготовления и низкими требованиями к качеству сборки механизма. Основными параметры эвольвентного зубчатого колеса считаются модуль зацепления и количество зубьев зубчатого колеса. При одном и том же наружном диаметре деталей значения этих величин могут существенно отличаться в разных вариантах конструкции.
Основными параметры эвольвентного зубчатого колеса считаются модуль зацепления и количество зубьев зубчатого колеса. При одном и том же наружном диаметре деталей значения этих величин могут существенно отличаться в разных вариантах конструкции.
Число зубьев определяет коэффициент передачи и геометрические размеры зубьев. На ведущем колесе редуктора оно выполняется меньшим, чем на ведомом. В итоге один нормальный оборот ведущей шестерни приводит к повороту ведомого колеса только на определенный угол. Отношение числа зубьев двух колес дает значение передаточного коэффициента. Размеры зубьев определяются как отношение их количества к длине окружности колеса. С целью упрощения расчетов и гарантированного обеспечения зацепления между разными колесами, предусмотрен дополнительный параметр, называемый модулем зацепления. Любые шестерни с одинаковым модулем обеспечивают взаимодействие между собой и могут использоваться для построения механизмов, без дополнительной обработки.
Сумма ширины зуба и впадины совместно дают шаг зубчатого колеса. Учитывая неравномерность профиля по радиусу и зависимость длины дуги от диаметра, в каждом колесе можно определить бесконечное число значений этого параметра. С целью стандартизации принято рассматривать шаг по делительной окружности, называемый так же окружным шагом. Отношение этого шага к числу пи дает модуль зацепления. В некоторых случаях для описания шестерен используют угловой шаг, измеряемый в градусах. Стандартами предусмотрены и несколько других угловых величин. Например, для упрощения настройки оборудования при изготовлении колес рассматривают угловую ширину зуба и угловую ширину впадины. Определяются они также на основе делительной окружности.
Учитывая неравномерность профиля по радиусу и зависимость длины дуги от диаметра, в каждом колесе можно определить бесконечное число значений этого параметра. С целью стандартизации принято рассматривать шаг по делительной окружности, называемый так же окружным шагом. Отношение этого шага к числу пи дает модуль зацепления. В некоторых случаях для описания шестерен используют угловой шаг, измеряемый в градусах. Стандартами предусмотрены и несколько других угловых величин. Например, для упрощения настройки оборудования при изготовлении колес рассматривают угловую ширину зуба и угловую ширину впадины. Определяются они также на основе делительной окружности.
Расчет зубчатого колеса
Он всегда ведется в составе расчета конкретной зубчатой передачи. Исходными данными для него обычно являются мощность (или крутящий момент), угловые скорости (или скорость одного вала и передаточное число), условия работы (характер нагрузки) и срок службы передачи.
Дальнейший порядок относится к закрытой цилиндрической прямозубой передаче.
1. Определение передаточного числа u.
2. Выбор материалов колес в зависимости от условий работы, назначение термообработки и значения твердости рабочих поверхностей зубьев.
3. Расчет зубьев передачи на изгиб.
4. Расчет зубьев передачи на контактную прочность (прочности контактирующих поверхностей зубьев).
5. Определение межосевого расстояния aW из условия контактной прочности и округление его значения до стандартного.
6. Задание модуля из соотношения m = (0,01 – 0,02) х aW и округление его значения до ближайшего стандартного. При этом в силовых передачах желательно иметь m ≥1,5 – 2 мм.
7. Определение суммарного числа зубьев передачи, числа зубьев шестерни и колеса.
8. Выбор коэффициентов формы зубьев для шестерни и колеса.
9. Проверка прочности зубьев по напряжениям изгиба.
10. Проведение геометрического расчета передачи.
11. Определение окружной скорости колеса и назначение соответствующей точности зацепления.
Расчет зубчатого колеса в составе открытой зубчатой передачи несколько отличается от приведенного, но в основном последовательность его такая же.
Важные замечания.
Смещение исходного контура при нарезке зубьев применяют для восстановления изношенных поверхностей зубьев колеса, уменьшения глубины врезания на валах-шестернях, для увеличения нагрузочной способности зубчатой передачи, для выполнения передачи с заданным межосевым расстоянием не равным делительному расстоянию, для устранения подрезания ножек зубьев шестерни и головок зубьев колеса с внутренними зубьями.
Смещение производящего контура на практике применяют обычно при изготовлении прямозубых колес и очень редко косозубых.
Это обусловлено тем, что по изгибной прочности косой зуб прочнее прямого, а необходимое межосевое расстояние можно обеспечить соответствующим углом наклона зубьев. Если высотную коррекцию изредка применяют для косозубых передач, то угловую практически никогда.
Косозубая передача работает более плавно и бесшумно, чем прямозубая. Как уже было сказано, косые зубья имеют более высокую прочность на изгиб и заданное межосевое расстояние можно обеспечить углом наклона зубьев и не прибегать к смещению производящего контура. Однако в передачах с косыми зубьями появляются дополнительные осевые нагрузки на подшипники валов, а диаметры колес имеют больший размер, чем прямозубые при том же числе зубьев и модуле. Косозубые колеса менее технологичны в изготовлении, особенно колеса с внутренними зубьями.
Однако в передачах с косыми зубьями появляются дополнительные осевые нагрузки на подшипники валов, а диаметры колес имеют больший размер, чем прямозубые при том же числе зубьев и модуле. Косозубые колеса менее технологичны в изготовлении, особенно колеса с внутренними зубьями.
Подписывайтесь
на анонсы статей в окнах, расположенных в конце каждой статьи или вверху каждой страницы.
Ссылка на скачивание файла: modul-zubchatogo-kolesa (xls 41,0KB).
Как обозначается точность изготовления зубчатых колес
При изготовлении любые их виды имеют ряд погрешностей, среди которых выделяют четыре основные:
- кинематическую погрешность, связанную в основном с радиальным биением зубчатых венцов;
- погрешность плавности работы, вызываемую отклонениями шага и профиля зубьев;
- погрешность контакта зубьев в передаче, которая характеризует полноту прилегания их поверхностей в зацеплении;
- боковой зазор между неработающими поверхностями зубьев.

Для контроля первых трех погрешностей стандартами установлены специальные показатели – степени точности от 1 до 12, причем точность изготовления увеличивается с уменьшением показателя. Для контроля четвертой погрешности изготовления имеются два показателя:
- вид сопряжения зубчатых колес – обозначается литерами A, B, C, D, E, H;
- допуск на боковой зазор – обозначается литерами x, y, z, a, b, c, d, e, h.
Для обоих показателей бокового зазора обозначения даны в порядке убывания его величины и допуска на него.
Условно точность зубчатых колес обозначается двумя способами. Если степень точности по первым трем погрешностям одинакова, то ставится один общий для них численный показатель степени точности, за которыми стоят литеры обозначения вида сопряжения и допуска на боковой зазор. Например:
8-Ас ГОСТ 1643 – 81.
Если точности по первым трем погрешностям разные, то в обозначении ставятся три численных показателя последовательно. Например:
5-4-3-Са ГОСТ 1643 – 81.
Типы зубчатых передач
Любое зубчатое колесо, независимо от его типа, делается и работает по одним и тем же вышеприведенным принципам. Однако различные их типы позволяют выполнить разные задачи. Некоторые виды передач обладают или высоким КПД, или высоким передаточным отношением, или же работают с непараллельными осями вращения шестерен, к примеру. Ниже приведены основные общие типы. Это не полный список. Также возможно и сочетание нижеприведенных типов.
Примечание: Приведены только типичные КПД передач. Из-за многих других возможных факторов приводимые КПД должны использоваться только в качестве справочных величин. Часто производители приводят ожидаемые КПД в паспортах для своих передач. Помните, что износ и смазка будут также существенно влиять на эффективность передач.
Подготовка чертежей
Процесс изготовления начинается с непосредственной подготовки чертежа. В этом случае производство существенно упрощается, существенно повышается точность получаемого изделия. При разработке чертежа указывается следующая информация:
При разработке чертежа указывается следующая информация:
- Диаметр посадочного отверстия. Для шестерен изготавливаются соответствующие валы, которые имеют определенный посадочный диаметр. Этот показатель стандартизирован, выбирается в зависимости от размеров изделия и величины предаваемого усилия.
- Размеры шпонки. Шпоночное отверстие может быть самым различным, размеры выбираются в зависимости от того, какие будут оказываться нагрузки. Стоит учитывать тот момент, что размеры шпонок стандартизированы.
- Модуль. Этот параметр считается наиболее важным, так как ошибочный модуль может снизить эксплуатационные характеристики механизма.
- Наружный и внутренний диаметр, определяющие размер зуба. Стоит учитывать, что этот элемент изделия характеризуется достаточно большим количеством особенностей.
- Угол расположения зуба относительно оси вращения. Выделяют шестерни с прямым и косым расположением зуба.
Изготовление шестерен любых размеров возможно только при применении специальных станков, которые предназначены для решения поставленной задачи.
Технологические задачи при производстве рассматриваемого изделия могут существенно отличаться. Важными моментами можно назвать следующее:
- Точность размеров. Наиболее точными размерами обладает отверстие, которое выступает в качестве посадочного для вала. В большинстве случаев его изготавливают по 7-му квалитету в случае, если к изделию не предъявляются больше требования.
- Точность формы. В большинстве случаев при изготовлении шестерен особые требования к точности формы не предъявляются. Однако, посадочное отверстие должно быть расположено в центральной части изделия, так как даже несущественно смещение может привести к отсутствию возможности использования изделия.
- Точность взаимного расположения. Больше всего требований предъявляется к тому, каким образом зубья и другие конструктивные элементы расположены относительно друг друга. При нарушении геометрической формы есть вероятность появления эффекта биения и других проблем при эксплуатации изделия.
- Твердость рабочей поверхности.
 Основные требования связаны с твердостью рабочей поверхности. Шестерни постоянно находятся в контакте, сила трения может стать причиной быстрого износа поверхности. Для получения требуемого показателя твердости проводится термическая обработка. Рекомендуемый показатель составляет HRC 45…60 при глубине цементации 1-2 мм. Как показывают проведенные исследования, твердость незакаленной поверхности составляет HB 180-270.
Основные требования связаны с твердостью рабочей поверхности. Шестерни постоянно находятся в контакте, сила трения может стать причиной быстрого износа поверхности. Для получения требуемого показателя твердости проводится термическая обработка. Рекомендуемый показатель составляет HRC 45…60 при глубине цементации 1-2 мм. Как показывают проведенные исследования, твердость незакаленной поверхности составляет HB 180-270. - Выбор подходящего материала также имеет значение. В зависимости от области применения изделия они могут изготавливаться из углеродистых, легированных сталей и пластмассы, в некоторых случаях чугуна. Легированные в сравнении с углеродистыми характеризуются большей прокаливаемостью, а также меньшей склонностью к деформации. Применяемые материал должен характеризоваться однородной структурой, за счет чего существенно повышается прочность после проведения термической обработки. При изготовлении высокоточных изделий проводится чередование механической и термической обработки.

Все основные параметры определяются на момент создания технологической карты. Самостоятельно создать карту достаточно сложно, так как для этого нужно обладать соответствующими навыками и знаниями.
Цилиндрические прямозубые колеса (КПД
Цилиндрическое зубчатое колесо имеет зубья, расположенные на цилиндрической поверхности. Передачи с ними являются наиболее часто используемыми типами благодаря своей простоте и максимальной эффективности среди всех других. Передаточное число для одной пары u ≤ 12,5. Не рекомендуется для очень высоких нагрузок, так как прямые зубья зубчатого колеса довольно легко ломаются.
Классификация
По направлению витка передачи в большинстве своем бывают правыми. Иногда встречается левое направление нити.
Червячные зацепления классифицируются по форме наружной поверхности червяка:
- цилиндрические;
- глобоидные.
Вогнутая поверхность ведущей детали увеличивает количество зубьев, находящихся одновременно в зацеплении. В результате возрастает КПД и мощность передачи. Недостаток глобоидных червяков в сложности изготовления. Витки должны быть одинаковой высоты при вогнутой наружной поверхности.
В результате возрастает КПД и мощность передачи. Недостаток глобоидных червяков в сложности изготовления. Витки должны быть одинаковой высоты при вогнутой наружной поверхности.
По форме нити резьбы различают червяки:
- архимедов;
- конволютный;
- нелинейный.
Архимедов червяк отличается прямой в сечении эвольвентой. У конволютного конфигурация выпуклая, близкая к форме обычной шестерни. Нелинейные профили имеют выпуклую и вогнутую поверхность.
Зубчатое колесо имеет зуб наклонный обратной конфигурации, по форме совпадающий с впадиной между нитями.
Расположение червяка относительно колеса может быть:
- верхнее;
- боковое;
- нижнее.
Верхнее оптимально подходит для скоростных передач. Боковое наиболее компактное. При картерном способе смазки – масло находится в поддоне и нижняя деталь, вращаясь, смазывает остальные, удобнее нижнее расположение червяка.
Червячные колеса относятся к косозубым. Оси деталей располагаются обычно под углом 90°. В сильно нагруженных механизмах угол может быть 45°.
В сильно нагруженных механизмах угол может быть 45°.
Зубчатые колеса по профилю зуба делят:
- роликовые;
- вогнутые;
- прямые.
По типу они могут быть:
- с непрерывным вращением – полные;
- зубчатый сектор.
Сектор может быть разной величины, от половины круга, до рабочей длины короче червяка.
Цилиндрические косозубые колеса (КПД
Они работают так же, как цилиндрические прямозубые, для передачи момента между параллельными валами, но у такой передачи более плавно происходит зацепление. Вследствие этого они создают меньше шума при работе и имеют меньшие габариты. У них большая нагрузочная способность. К сожалению, из-за сложной формы зубьев они, как правило, более дорогие.
Червячные передачи (КПД
Это передача с винтом-червяком на одном валу и червячным колесом на втором, перпендикулярном первому, валу. Они имеют очень высокое передаточное число. В расчетах принимают во внимание то, что у червяка (однозаходного) имеется только один зуб (виток).
Они имеют очень высокое передаточное число. В расчетах принимают во внимание то, что у червяка (однозаходного) имеется только один зуб (виток).
Для выполнения расчетов, чертежей и эскизов зубчатых колёс и других деталей зубчатых передач надо знать основные элементы и параметры зубчатых зацеплений и условности, принятые для изображения зубчатого венца.
Рис. 17. Шестерни с элементами фиксации на валу
Основным элементом зубчатого колеса является зуб.
Начальная поверхность делит зуб по его высоте на две неравные части – головку и ножку. Часть зуба, расположенная над делительной поверхностью, называется головкой зуба, а расположенная ниже делительной поверхности – ножкой зуба. Зубья с ободом составляют венец зубчатого колеса, который через диск или спицы соединён со ступицей, имеющей отверстие для вала, зачастую с элементами фиксации колеса на валу, например, при помощи шпоночного (рис. 17,
а
) или шлицевого (рис. 17,
б)
соединений.
Читать также: Показания ареометра для аккумулятора
Технологический процесс
Процесс изготовления шестерни на крупных производственных линиях максимально автоматизирован. Классический техпроцесс характеризуется следующими особенностями:
- Для начала определяются основные параметры изделия, к примеру, число зубьев, модуль и степень точности геометрических размеров.
- Следующий этап заключается в проведении заготовительной процедуры. Чаще всего проводится штамповка при использовании горизонтально-ковочной машины.
- Для повышения эксплуатационных характеристик выполняется нормализация. Подобная термическая обработка позволяет снизить напряжения внутри материала.
- Токарно-винторезная процедура позволяет получить заготовку требующихся размеров. Для этого выполняется точение поверхности и расточка фасок.
- После механической обработки прямозубых шестерен выполняется повторно нормализация.
- Заготовка подвергается зубофрезерной обработке.
 Для этого применяется полуавтомат 5306К или другое подобное оборудование.
Для этого применяется полуавтомат 5306К или другое подобное оборудование. - Следующий шаг заключается в слесарной обработке. Технологический процесс определяет появление заусенец и других дефектов, которые устраняются при применении полуавтомата 5525. На линиях с низкой производительностью зачистка проводится ручным методом.
- После получения зубьев выполняется термическая обработка, для чего часто применяется установка ТВЧ. Закалка позволяет существенно повысить твердость поверхности и ее износостойкость.
- Шлифование поверхности. Для получения поверхности требуемого качества выполняется шлифовка. Есть довольно больше количество различного оборудования, которое подходит для шлифования самых различных поверхностей.
- Большое распространение получили насадные шестерни. Они устанавливаются на валу, могут быть больших и малых размеров. Фиксация насадного варианта исполнения проводится за счет шпонки. Получить шпоночный паз можно при применении долбежного станка.
- Зубошлифование также проводится при применении специальных станков.

https://youtube.com/watch?v=KbjmqvPM-1c
В заключение отметим, что процедура зубофрезервания достаточно сложна, предусматривает применение специального оборудования.
Основные параметры редукторов с цилиндрическими зубчатыми колесами
ГОСТ 2185-66 устанавливает межосевые расстояния aW, номинальные передаточные числа и, коэффициенты ширины зубчатых колес ψba и дается рекомендуемые сочетания межосевых расстояний и общие номинальные передаточные числа для зубчатых цилиндрических передач, которые используются в двух- и трехступенчатых насосных редукторах общего назначения, что дает возможность для серийного изготовления редукторов.
Межосевые расстояния
Межосевые расстояния редукторов aw приведены в табл. 49. Величину межосевого расстояния определяют расчетом на усталостную контактную прочность поверхностей зубьев или выбирают конструктивно в зависимости от габаритных размеров приводимой машины. В табл. 50 и 51 приведены рекомендуемые стандартом межосевые расстояния для двух- и трехступенчатых редукторов и их распределение по отдельным ступеням.
50 и 51 приведены рекомендуемые стандартом межосевые расстояния для двух- и трехступенчатых редукторов и их распределение по отдельным ступеням.
Таблица 49
Межосевые расстояния редукторов, мм
Примечание. Предпочтительный ряд первый.
Таблица 50
Межосевые расстояния двухступенчатых трехосных редукторов, мм
Таблица 51
Межосевые расстояния трехступенчатых редукторов, мм
Таблица 52
Примечания.
1. Первый ряд следует предпочитать второму.
2. Для редукторов, которые должны быть кинематически согласованы между собой, допускается выбирать передаточные числа из ряда R40 (ГОСТ 8032-84).
3. Фактические значения передаточных чисел uф не должны отличаться от номинальных более чем на 2,5% при и ≤ 4,5 и на 4% при и > 4,5.
Таблица 53
Общие передаточные числа иобщ. двухступенчатых редукторов
двухступенчатых редукторов
Примечания:
1. Для всех редукторов первый ряд следует предпочитать второму.
2. Фактические значения передаточных чисел uф не должны отличаться от номинальных более чем на 4%.
Таблица 54
Общие передаточные числа иобщ. трехступенчатых редукторов
Примечания:
1. Для всех редукторов первый ряд следует предпочитать второму.
2. Фактические значения передаточных чисел иф не должны отличаться от номинальных более чем на 4%.
Передаточные числа
Номинальные передаточные числа и должны соответствовать указанным в табл. 52.
Рекомендуемые общие передаточные числа иобщ для двух- и трехступенчатых несоосных редукторов общего назначения приведены в табл. 53 и 54.
Распределение общего передаточного числа между отдельными ступенями передач в двух- и трехступенчатых редукторах (табл. 55 и 56) осуществляется при условии одинакового использования контактной прочности зубьев при одинаковой твердости их поверхностей, одинаковых коэффициентов ширины зубьев колес всех ступеней и распределения межосевых расстояний между отдельными ступенями, как это дано в табл. 50 и 5). В двухступенчатых редукторах с соосным расположением валов в одной горизонтальной плоскости при заданном распределении передаточных чисел между ступенями, с одинаковыми межосевыми расстояниями для выполнения условия равнопрочности приходится применять зубчатые колеса с разными коэффициентами ширины.
55 и 56) осуществляется при условии одинакового использования контактной прочности зубьев при одинаковой твердости их поверхностей, одинаковых коэффициентов ширины зубьев колес всех ступеней и распределения межосевых расстояний между отдельными ступенями, как это дано в табл. 50 и 5). В двухступенчатых редукторах с соосным расположением валов в одной горизонтальной плоскости при заданном распределении передаточных чисел между ступенями, с одинаковыми межосевыми расстояниями для выполнения условия равнопрочности приходится применять зубчатые колеса с разными коэффициентами ширины.
Таблица 55
Распределение общих передаточных чисел в двухступенчатых трехосных редукторах по отдельным ступеням зубчатых зацеплений
Таблица 56
Распределение общих передаточных чисел в трехступенчатых редукторах по отдельным ступеням зубчатых зацеплений
Таблица 57
Распределение общих передаточных чисел в двухступенчатых двухосных (соосных) редукторах с горизонтальным расположением валов в одной плоскости по отдельным ступеням зубчатых зацеплений
Если первая ступень имеет коэффициент ширины ψbа = 0,4, то вторая ступень должна иметь коэффициент ψbа не менее 0,6 при одних и тех же материалах шестерен и колес и твердости поверхностей зубьев.
Передаточные числа отдельных ступеней этих редукторов (табл. 53) устанавливаются при условии близкой контактной равнопрочности и одинакового погружения в масляную ванну зубчатых колес быстроходной и тихоходной ступеней при смазывании окунанием.
Ширина зубчатых колес
Ширина зубчатых колес b зависит от коэффициента ширины ψbа: b = ψbааw. Значения коэффициента ширины зубчатых колес ψbа (ГОСТ 2185-66) приведены в табл. 58.
Значения ширины зубчатых колес округляют до ближайшего числа из ряда R20 по ГОСТ 8032-84. Ширина канавки для выхода режущего инструмента в шевронных зубчатых колесах включается в величину ширины b. При различной ширине сопряженных зубчатых колес берется значение коэффициента ψbа зубчатого колеса с меньшей шириной.
При выборе коэффициента ширины ψbа необходимо принимать во внимание материал зубчатых колес и вид термообработки, точность изготовления, окружную скорость, величину модуля и осевого шага, характер нагрузки, схему редуктора и ряд других факторов. Рекомендуется выбирать узкие колеса, так как в этом случае получается более высокая точность изготовления и значительно снижается неравномерность распределения нагрузки по ширине, вызываемая деформацией валов и неточностями изготовления и монтажа редуктора. По этой же причине не рекомендуется отношение ширины шестерни к диаметру делительной окружности принимать больше 2,5.
Рекомендуется выбирать узкие колеса, так как в этом случае получается более высокая точность изготовления и значительно снижается неравномерность распределения нагрузки по ширине, вызываемая деформацией валов и неточностями изготовления и монтажа редуктора. По этой же причине не рекомендуется отношение ширины шестерни к диаметру делительной окружности принимать больше 2,5.
При твердости поверхностей зубьев НВ ≤ 350 рекомендуется задавать твердость зубьев шестерни на 30…50 единиц больше твердости зубьев колеса. В тех случаях, когда твердость зубьев шестерни значительно больше твердости зубьев колеса, ширина шестерни должна быть на 5… 10 мм больше, чем ширина колеса. В противном случае при относительном смещении шестерни и колеса в процессе эксплуатации на зубьях колеса образуется нежелательный уступ.
При твердости поверхностей зубьев обоих колес НВ ≥ 350 ширину колес можно принимать одинаковой. Для колес с цементированными, закаленными с поверхности зубьями коэффициент ширины ψbа рекомендуется принимать не более 0,4. ..0,5. При увеличении длины зубьев погрешности, возникающие при обработке, возрастают, что приводит к большим затруднениям при получении необходимого пятна контакта.
..0,5. При увеличении длины зубьев погрешности, возникающие при обработке, возрастают, что приводит к большим затруднениям при получении необходимого пятна контакта.
При поверхностной закалке происходит коробление зубьев; при этом с увеличением ширины колес ошибки в направлении зубьев возрастают. В случае применения широких колес лучше переходить на шевронное зацепление, так как длина зуба одной спирали составляет около половины общей ширины зубчатого колеса и ошибки в направлении зубьев значительно уменьшаются.
В прямозубых и косозубых передачах коэффициент ширины ψbа должен быть не более 0,4…0,6. При больших значениях коэффициента ψbа необходимо применять шевронное зацепление.
Быстроходные передачи изготовляются с шевронным зацеплением при коэффициенте ширины ψbа = 0,4… 1,0. При консольном расположении шестерен и колес рекомендуется выбирать коэффициент ширины ψbа не свыше 0,4. При дальнейшем увеличении ширины колеса (при консольном его расположении) сильно возрастает концентрация нагрузки по длине зубьев и эффект от использования материала колес резко снижается.
Таблица 58
Коэффициент ширины зубчатых колес
Модули
Значения модулей для цилиндрических зубчатых колес редукторов (ГОСТ 9563-60) приведены в табл. 59. Величину модуля определяют исходя из прочности зубьев по изгибу. По возможности выбирают наименьшие значения модулей, так как зубчатые колеса с малыми модулями нарезаются на зуборезных станках с большей точностью и с лучшей чистотой поверхности, имеют меньшую массу и меньшие потери на трение в зацеплении. При поверхностной закалке меньше искажается форма их зубьев и получается хорошая и более быстрая приработка зацепления.
Если зубчатое колесо должно работать при предельных контактных напряжениях, то значение модуля, полученного при расчете на изгиб, рекомендуется увеличивать на 10…15%, так как при выкрашивании поверхностей зубьев происходит ослабление их поперечного сечения и может произойти излом зуба.
Таблица 59
Значения модулей т, мм
Примечание. При назначении величин модулей первый ряд предпочтительнее.
При назначении величин модулей первый ряд предпочтительнее.
Углы наклона линии зубьев
Углы наклона зубьев в косозубых передачах должны быть 8…100. В косозубых передачах при угле наклона зуба свыше 10° необходимо устанавливать или радиально-упорные подшипники с увеличенным углом контакта, или в опоре с радиальным подшипником дополнительно устанавливать упорный подшипник, что удорожает конструкцию и требует более надежного и сложного торцового крепления подшипников на валах и в корпусах.
Уменьшение утла наклона зубьев, особенно в узких колесах с коэффициентом ширины ψbа 0,2…0Д нежелательно, так как величина осевого шага может быть больше ширины колеса. Вследствие этого осевой коэффициент перекрытия будет меньше единицы и передача будет работать менее плавно, с большими динамическими нагрузками, что ведет к быстрому износу и появлению дефектов на поверхностях зубьев.
Для установленных ГОСТом межосевых расстоянии в табл. 60 приведены суммарные числа зубьев z∑ и углы наклона зубьев β на делительном цилиндре при определенных интервалах передаточных чисел и модулей в нормальном сечении. Эти значения рекомендуются при коэффициенте ширины ψbа ≥ 0,4 при некорригированном и корригированном зацеплении с коэффициентом сдвига х1=-х2 соответственно для шестерни и колеса, но могут быть использованы и при ψbа < 0,4, но с проверкой, указанной в примечании к табл. 60.
60 приведены суммарные числа зубьев z∑ и углы наклона зубьев β на делительном цилиндре при определенных интервалах передаточных чисел и модулей в нормальном сечении. Эти значения рекомендуются при коэффициенте ширины ψbа ≥ 0,4 при некорригированном и корригированном зацеплении с коэффициентом сдвига х1=-х2 соответственно для шестерни и колеса, но могут быть использованы и при ψbа < 0,4, но с проверкой, указанной в примечании к табл. 60.
Подбор чисел зубьев шестерни и колеса в зависимости от принятого суммарного числа зубьев z∑ и передаточного числа и можно выполнить по табл. 62.
Таблица 60
Параметры передач с косозубыми колесами при ψbа ≥ 0,4 (зацепление некорригированное или корригированное с коэффициентом сдвига х1=-х2 )
Для шевронных колес угол наклона зубьев β равен 25…350. Рекомендуемые параметры передач с шевронными колесами при некорригированном или корригированном зацеплении с коэффициентом сдвига х1=-х2 соответственно для шестерни и колеса при коэффициенте ширины ψbа > 0,125 приведены в табл. 61, где для стандартных межосевых расстояний приведены суммарные числа зубьев z∑ сопряженных шестерни z1 и колеса z2 и углы наклона зубьев β по принятому модулю зацепления т в интервале передаточных чисел. Подбор чисел зубьев шестерни z1 и числа зубьев колеса z2 в зависимости от принятого суммарного числа зубьев z∑ и передаточного числа и передачи выполняется по табл. 62, где в числителе поставлено число зубьев колеса z2, а в знаменателе – суммарное число зубьев zz сопряженных шестерни и колеса. Для каждого значения передаточного числа и в верхней строке приведены наименьшие значения z2/z∑, а в нижней – наибольшие, соответствующие допустимым значениям рассматриваемого передаточного числа. В интервале наименьших и наибольших значений чисел зубьев z2 /z∑ может быть любое целое число из указанного интервала.
61, где для стандартных межосевых расстояний приведены суммарные числа зубьев z∑ сопряженных шестерни z1 и колеса z2 и углы наклона зубьев β по принятому модулю зацепления т в интервале передаточных чисел. Подбор чисел зубьев шестерни z1 и числа зубьев колеса z2 в зависимости от принятого суммарного числа зубьев z∑ и передаточного числа и передачи выполняется по табл. 62, где в числителе поставлено число зубьев колеса z2, а в знаменателе – суммарное число зубьев zz сопряженных шестерни и колеса. Для каждого значения передаточного числа и в верхней строке приведены наименьшие значения z2/z∑, а в нижней – наибольшие, соответствующие допустимым значениям рассматриваемого передаточного числа. В интервале наименьших и наибольших значений чисел зубьев z2 /z∑ может быть любое целое число из указанного интервала.
Продолжение табл. 60
Продолжение табл. 60
60
Примечание. Отдельные сочетания величин αW, Z∑, m ; β могут быть использованы и при ψ ba< 0,4, но с проверкой соблюдения условия
или
Таблица 61
Параметры передач с шевронными колесами при ψba ≥ 0,125 (зацепление некорригированное или корригированное с коэффициентом сдвига x1 = -х2)
Продолжение табл. 61
Продолжение табл. 61
Необходимо обратить внимание на то, что при подборе чисел зубьев шестерни или колеса в пределах 100 зубьев почти на всех зуборезных станках можно нарезать колеса с любым числом зубьев. При числе зубьев шестерни или колеса свыше 100 необходимо проверять возможности их нарезки на зуборезных станках. Например, при z1 = 50 и и = 2,5 по табл. 62 возможно применение всех значений суммарных чисел зубьев от 172 до 178 включительно, которым соответствуют значения чисел зубьев колес z2 от 122 до 128 включительно. Число зубьев колеса z2 = 127, как первоначальное число, или не применять или проверить возможность нарезки по паспорту зуборезного станка.
Число зубьев колеса z2 = 127, как первоначальное число, или не применять или проверить возможность нарезки по паспорту зуборезного станка.
Применение чисел зубьев меньше 17 допустимо после проверки на отсутствие подрезания зубьев. Допускаемые отклонения передаточных чисел в табл. 62 находятся в пределах, как это указано в примечании 3 к табл. 52.
Смотрите также
- Основные параметры редукторов с цилиндрическими зубчатыми колесами
- Конструкции, выбор и расчет цилиндрических редукторов
- Цилиндрические редукторы общего назначения
- Редукторы цилиндрические одноступенчатые горизонтальные типа ЦУ
- Редукторы цилиндрические двухступенчатые горизонтальные типа Н2У
- Редукторы цилиндрические двухступенчатые горизонтальные типа Ц2У-Н
- Редукторы цилиндрические трехступенчатые горизонтальные типа ЦЗУ
- Редукторы цилиндрические двухступенчатые соосные типа Ц2С
- Мотор-редукторы цилиндрические одноступенчатые типа МЦ
- Мотор-редукторы цилиндрические двухступенчатые соосные типа МЦ2С
- Цилиндрические редукторы привода машин среднего и тяжелого машиностроения
- Одноступенчатые редукторы
- Редукторы цилиндрические одноступенчатые типа РЦО*
- Редукторы цилиндрические одноступенчатые узкого и широкого типа
- Редукторы цилиндрические одноступенчатые типа Ц
- Редукторы цилиндрические одноступенчатые широкого типа усиленной конструкции
- Редукторы цилиндрические одноступенчатые с двумя горизонтальными разъемами
- Редукторы цилиндрические одноступенчатые с двумя ведущими валами
- Двухступенчатые редукторы
- Редукторы цилиндрические двухступенчатые типа РИД
- Редукторы цилиндрические двухступенчатые с масляной ванной
- Редукторы цилиндрические двухступенчатые типа Ц2Ш
- Редукторы цилиндрические двухступенчатые с усиленным корпусом
- Редукторы цилиндрические двухступенчатые соосные
- Редукторы цилиндрические двухступенчатые двухпоточные
- Редукторы цилиндрические двухступенчатые двухпоточные с приводом от двух электродвигателей
- Трехступенчатые редукторы
- Редукторы цилиндрические трехступенчатые типа РЦТ
- Редукторы цилиндрические трехступенчатые с масляной ванной
- Редукторы цилиндрические трехступенчатые с симметричным расположением колес
- Редукторы цилиндрические трехступенчатые вертикальные типа ЦСН
- Четырехступенчатые редукторы
- Редукторы узкого типа
- Редукторы усиленной конструкции
виды, типы, классификация, области применения
- Что такое зубчатые колеса
- Виды зубчатых колес
- Конструкция зубчатого колеса
- Основные параметры
- Диаметры окружностей
- Модули зубчатых колес
- Расчет параметров
- Применение
- Зубчатое колесо и шестерня — отличия
- Особенности зубчатых колес и шестерней
Зубчатые передачи весьма широко и продуктивно применяются в конструкциях современных машин, механизмов и устройств. Транспортные средства, энергетические установки, грузоподъемные устройства, авиационные установки, сельскохозяйственные машины, точные приборы — во всех них найдутся те или иные варианты зубчатого колеса. В технике зубчатая передача используется с целью распространения вращательного движения между осями валов, которые могут быть расположены параллельно, скрещиваться или пересекаться. Также, при помощи подобной передачи легко преобразовать вращательное движение, например, в поступательное, или реализовать эффективное преобразование крутящего момента и оборотов валов. Благодаря последнему свойству их используют в редукторах или мультипликаторах различных типов, а также коробках передач.
Транспортные средства, энергетические установки, грузоподъемные устройства, авиационные установки, сельскохозяйственные машины, точные приборы — во всех них найдутся те или иные варианты зубчатого колеса. В технике зубчатая передача используется с целью распространения вращательного движения между осями валов, которые могут быть расположены параллельно, скрещиваться или пересекаться. Также, при помощи подобной передачи легко преобразовать вращательное движение, например, в поступательное, или реализовать эффективное преобразование крутящего момента и оборотов валов. Благодаря последнему свойству их используют в редукторах или мультипликаторах различных типов, а также коробках передач.
Основными преимуществами подобного способа передачи мощностей являются высокий КПД; компактный конструктив; плавная работа; точность; долговечность; надежность; возможность осуществления передачи силы с использованием любого угла, передаточного числа (до нескольких тысяч) и большого диапазона скоростей (до 150 м/с). Эти качества и обусловили распространение использования зубчатых передач в технике. К негативным моментам можно отнести технологическую сложность производства; требовательность к точности обработки, материалам и обрабатывающему оборудованию. Выбор материала для зубчатого колеса один из наиболее важных критериев надежности и долговечности в дальнейшей его работе. Жесткость конструкции, обеспечивающая передаче высокую эффективность, к сожалению, не позволяет ей держать высокие значения динамических нагрузок, часто являющихся причиной разрушения механизма. В дополнение, этим передачам характерна повышенная шумность, снижения которой можно достичь повышением качества и точности при производстве изделий.
Эти качества и обусловили распространение использования зубчатых передач в технике. К негативным моментам можно отнести технологическую сложность производства; требовательность к точности обработки, материалам и обрабатывающему оборудованию. Выбор материала для зубчатого колеса один из наиболее важных критериев надежности и долговечности в дальнейшей его работе. Жесткость конструкции, обеспечивающая передаче высокую эффективность, к сожалению, не позволяет ей держать высокие значения динамических нагрузок, часто являющихся причиной разрушения механизма. В дополнение, этим передачам характерна повышенная шумность, снижения которой можно достичь повышением качества и точности при производстве изделий.
Что такое зубчатые колеса
В общем случае, шестерня, или зубчатое колесо — главная деталь одноименной передачи, имеет вид диска с расположенными на цилиндрической или конической поверхности зубьями. При помощи этих зубьев в процессе вращения происходит зацепление колес между собой, что позволяет реализовать перенос вращательного момента от одного вала, на котором расположено колесо, к другому. Зуб зубчатого колеса при вращении толкает зуб другого, сопряженного с ним, колеса, которое вследствие этого тоже начинает совершать вращательное движение.
Зуб зубчатого колеса при вращении толкает зуб другого, сопряженного с ним, колеса, которое вследствие этого тоже начинает совершать вращательное движение.
Сопряженная зубчатая передача должна всегда состоять из двух типов элементов: ведущих и ведомых. При этом ведущим, по определению, называют колесо передающее (сообщающее) вращение, ведомым — то зубчатое колесо, которое имеет большой диаметр с большим количеством зубьев и приводит во вращение. В большинстве случаев используется пара зубчатых колес, одно из которых с большим числом зубьев, а другое с меньшим. Иногда элемент, несущий меньше зубьев, считается шестерней, тогда колесом считают тот, у которого зубьев больше.
Технологии производства шестерней
Метод обкатки. Производство шестерней таким способом возможно с применением гребёнки – инструмента в форме зубчатой рейки с заточенной, режущей кромкой. Гребенка совершает поступательные или возвратно – поступательные движения относительно вращающейся вокруг своей оси заготовки.
Метод обкатки также возможен при помощи долбяка, имеющего форму режущего зубчатого колеса. Так как толщина металла не позволяет производить такой процесс одноэтапно, долбяк совершает возвратно – поступательные движения относительно заготовки несколько раз. Способ применим при производстве шестерней с внутренним зацеплением.
Возможна обкатка с применением червячной фрезы в качестве режущего инструмента, путём образования червячного зацепления с заготовкой шестерни. Нарезание зубцов шестерни производится при вращении червячной фрезы и заготовки под определённым углом относительно друг друга.
Основным преимуществом метода обкатки является возможность делать шестерни с различной формой зубцов одним и тем же инструментом, меняя его положение относительно заготовки на станке. Такая технология более точная, чем копирование.
Метод копирования (деления). Такое производство шестерней заключается в нарезании впадин зубчатого колеса режущей дисковой или пальцевой фрезой, поочерёдно поворачивающейся на один угловой шаг. Разновидностью приёма является штамповка и протягивание.
Разновидностью приёма является штамповка и протягивание.
Горячее и холодное накатывание. Метод основан на термическом послойном нагреве заготовки и её деформации, для вырезания зубьев, с последующей обкаткой для придания форме точности.
Изготовление конических шестерен. Это обкатка заготовки в станочном зацеплении с воображаемым производящим колесом. В процессе движения инструмент срезает припуск, образуя боковые поверхности зубчатого колеса.
Производство вал – шестерни. Такой сборный механизм состоит из самого вала и зубчатого колеса, размер зубцов которого равен размерам впадин вала. Делается в сборе.
Виды зубчатых колес
Все зубчатые колеса, виды которых также многочисленны, как и варианты их применения, делятся на основные типы по расположению осей валов и геометрии формы зубьев. Выделяют цилиндрические, конические, червячные, винтовые передачи. На практике, исходя из формы профиля зубьев, выделяют эвольвентные и круговые колеса, а по расположению — прямозубые и косозубые типы зубчатых колес.
Для параллельного случая расположения осей валов применяют цилиндрические передачи:
- прямозубые;
- с круговыми зубьями;
- шевронные;
- косозубые.
Конические передачи подходят для пересекающихся осей:
- с криволинейными зубьями;
- косозубые;
- с нулевым углом наклоном;
- прямозубые.
Когда оси перекрещиваются, тогда используют передачи:
- спироидные;
- гипоидные;
- винтовые;
- червячные.
Наибольшую распространенность среди машин и механизмов обрели цилиндрические зубчатые колеса. Им свойственна простота изготовления, надежность, малые габариты. Конические, червячные и винтовые виды зубчатых колес используют лишь тогда, когда компоновка машины предъявляет особые условия. Цилиндрические зубчатые передачи делятся на два существенных вида: внешнего и внутреннего зацепления. В первом варианте реализации колесо и шестерня, у которой внешнее зацепление, крутятся в направлениях, которые противоположны друг другу. Во втором — колесо внутреннего зацепления и шестерня внешнего зацепления совершают вращательное движение со направленно. Существует также реечная передача — в ней рейка с зубьями сопрягается с имеющей внешнее зацепление шестерней.
Во втором — колесо внутреннего зацепления и шестерня внешнего зацепления совершают вращательное движение со направленно. Существует также реечная передача — в ней рейка с зубьями сопрягается с имеющей внешнее зацепление шестерней.
Косозубые цилиндрические колеса имеют расположенные под углом к оси зубья. Сопряженные колеса имеют одинаковый наклон зубьев, но различные его направления. У одного наклон будет правым, у другого же — левым. Наличие наклона дает возможность передавать большие, по сравнению с прямозубыми, нагрузки, способствует плавному зацеплению зубьев и снижению шума.
Шевронные колеса представляют собой пару соединенных колес с косыми зубьями, имеющими равный угол наклона, но расположенными противоположно: одно с правым, второе с левым наклоном. Это позволяет уравновесить осевые силы, тем самым снизив нагрузку на подшипник. Колеса могут иметь в середине канавку. Колеса без канавки более прочны, но сложны в изготовлении.
Винтовые цилиндрические передачи, в свою очередь, применяют для вращения валов, когда угол их перекрещивания лежит в пределах от 0 до 90 градусов. Они похожи на косозубые колеса, однако винтовая передача имеет контакт точечный, а не линейный, как косозубая. Направление наклона зубьев у всех таких сопряженных колес одинаковое. Точечный контакт зубов вызывает повышение их износа, как следствие их используют только на небольших нагрузках.
Они похожи на косозубые колеса, однако винтовая передача имеет контакт точечный, а не линейный, как косозубая. Направление наклона зубьев у всех таких сопряженных колес одинаковое. Точечный контакт зубов вызывает повышение их износа, как следствие их используют только на небольших нагрузках.
Реечные передачи составляются из зубчатых колес и реек, которые также имеют зубья. Вращаясь, цилиндрическое колесо, перемещает сопряженную рейку по перпендикулярной оси колеса прямой. Таким способом движение из вращательного превращается в поступательное. Подобная передача бывает как с косыми зубьями, так и с прямыми.
Прямозубые конические колеса обладают зубьями, пересекающими оси этих колес. Коническое расположение позволяет вращать пересекающиеся или скрещивающиеся оси. Зубья также могут быть косыми, т.е. касательными к окружности. Угол наклона зубьев у таких колес составляет не больше тридцати градусов. Снабжение конических колес зубьями с нулевым углом наклона обеспечивает первым невысокие осевые и радиальные нагрузки, дает возможность применения подшипников скольжения. Эти качества делают передачи с использованием таких колес компактными, а изготовление не затратным.
Эти качества делают передачи с использованием таких колес компактными, а изготовление не затратным.
Использование криволинейных зубьев для применения в конических зубчатых колесах резко снижает шумность передач и повышает прочность. Конические передачи подобного рода всегда имеют в зацеплении как минимум два зуба, что дает им возможность выдерживать нагрузку, которая выше на 30% относительно идентичных прямозубых и колес, имеющих нулевой наклон.
Гипоидные зубчатые колеса подобны коническим, но ось ведущей шестерни у них смещена выше или ниже относительно оси колеса, которое она ведет. У таких передач шестерни имеют наклон зубьев больший, чем у колес. Нормальный шаг при этом у шестерни и зубчатого колеса будет одинаковый, а торцовый — у шестерни больше. Гипоидной передаче не присуще чистое качение или скольжение, все ее точки подвержены скольжению. Это придает ей плавность и повышенную бесшумность. Кроме того, притирка происходит быстрее и качественней. Минус — присутствие скольжения вызывает повышенный износ поверхности зубов, что требует применения для таких передач специализированных масел.
Червячные передачи цилиндрические имеют червяк, имеющий геометрию цилиндра, на котором нарезаются витки, идущие вдоль направления винтовой линии. Червячное колесо должно иметь вогнутые зубья. Линейный контакт таких зубьев обеспечивает передачу больших нагрузок. Скольжение у червячных значительно выше, чем у прочих зубчатых передач. В глобоидной передаче червяк обладает вогнутой формой. Эта особенность позволяет участвовать в процессе зацепления большему числу зубьев, что повышает величину передаваемых такой передачей нагрузок.
Спироидные передачи занимают промежуточное место между червячными и гипоидными вариантами. В отличие от червячной, у гипоидной передачи червяк имеет форму конуса и зацепляется с колесом, на котором зубья располагаются на торцевой стороне.
Форма зуба
Зацепления различаются по профилю и типу зубьев. По форме зуба различают эвольвентные, круговые и циклоидальные зацепления. Наиболее часто используемыми являются эвольвентные зацепления. Они имеют технологическое превосходство. Нарезка зубьев может производиться простым реечным инструментом. Эти зацепления характеризуются постоянным передаточным отношением, не зависящим от смещения межцентрового расстояния. Но при больших мощностях проявляются недостатки, связанные с небольшим пятном контакта в двух выпуклых поверхностях зубьев. Это может приводить к поверхностным разрушениям и выкрашиванию материала поверхностей.
Они имеют технологическое превосходство. Нарезка зубьев может производиться простым реечным инструментом. Эти зацепления характеризуются постоянным передаточным отношением, не зависящим от смещения межцентрового расстояния. Но при больших мощностях проявляются недостатки, связанные с небольшим пятном контакта в двух выпуклых поверхностях зубьев. Это может приводить к поверхностным разрушениям и выкрашиванию материала поверхностей.
В круговых зацеплениях выпуклые зубья шестерни сцепляются с вогнутыми колесами и пятно контакта значительно увеличивается. Недостатком этих передач является то, что появляется трение в колёсных парах. Виды зубчатых колёс:
- Прямозубые. Это наиболее часто используемый вид колёсных пар. Контактная линия у них параллельна оси вала. Прямозубые колёса сравнительно дешевы, но максимальный передаваемый момент у них меньше, чем у косозубых и шевронных колёс.
- Косозубые. Рекомендуется применять при больших частотах вращения, они обеспечивают более плавный ход и уменьшение шума.
 Недостатком является повышенная нагрузка на подшипники из-за возникновения осевых усилий.
Недостатком является повышенная нагрузка на подшипники из-за возникновения осевых усилий. - Шевронные. Обладают преимуществами косозубых колёсных пар и не нагружают подшипники осевыми силами, так как силы направлены в разные стороны.
- Криволинейные. Применяются при больших передаточных отношениях. Менее шумные и лучше работают на изгиб.
Прямозубые колёсные пары имеют наибольшее распространение. Их легко проектировать, изготавливать и эксплуатировать.
Конструкция зубчатого колеса
Металлические зубчатые колеса, чертеж которых иногда довольно сложен, имеют разнообразные варианты конструкций, однако в них можно выделить три основных компоненты: венец с зубьями, ступицу и сам колесный диск. Венец зубчатого колеса является основным компонентом и на него приходится основная нагрузка. Зубья имеют различную геометрию. Наружная часть у зуба — это вершина, прилегающие к ней боковые части — головка зуба. Внутренняя часть зуба называется его ножкой. Пространство между двумя ближними ножками образует впадину колеса. Чтобы крепить шестерню или колесо на валу, в центре диска располагается ступица, имеющая сквозное отверстие, форма которого напрямую зависит от сечения вала: она может иметь форму цилиндра, квадрата или любого другого многоугольника. В случае цилиндрических валов, ступица часто имеет т.н. шпоночный паз. В целях экономии материалов и веса колеса, его диск имеет толщину, меньшую по сравнению с толщиной обода и ступицы. Часто в диске для этих целей еще выполняют различные отверстия.
Пространство между двумя ближними ножками образует впадину колеса. Чтобы крепить шестерню или колесо на валу, в центре диска располагается ступица, имеющая сквозное отверстие, форма которого напрямую зависит от сечения вала: она может иметь форму цилиндра, квадрата или любого другого многоугольника. В случае цилиндрических валов, ступица часто имеет т.н. шпоночный паз. В целях экономии материалов и веса колеса, его диск имеет толщину, меньшую по сравнению с толщиной обода и ступицы. Часто в диске для этих целей еще выполняют различные отверстия.
Основные параметры
Чтобы обеспечивать возможность конструирования работоспособных зубчатых передач, размеры колес и шестерен, а также их прочностные и массогабаритные характеристики описываются специальными параметрами, величины которых хорошо стандартизированы ГОСТ. Так, эвольвентный профиль, положенный в основу сечения зуба подавляющего большинства колес, характеризуется модулем зацепления и имеющимся количеством зубьев на колесе или шестерне. Довольно часто, эвольвентные зубчатые колеса, имея один и тот же диаметр, могут иметь существенно различающие значения данных величин. Окружной модуль, служащий основной характеристикой для зубьев, по стандарту может иметь значения в диапазоне от 0,05 до 100 мм. Главными параметрами геометрии у различных зубчатых колес являются следующие диаметры: начальный, основной и делительный. Шагом зубчатого колеса называется общее расстояние ширины зуба и впадины. Так же важным параметром является радиус колеса. Радиуса зубчатых колес делятся: радиус окружности вершин, радиус делительной окружности, радиус основной окружности, радиус окружности впадин.
Довольно часто, эвольвентные зубчатые колеса, имея один и тот же диаметр, могут иметь существенно различающие значения данных величин. Окружной модуль, служащий основной характеристикой для зубьев, по стандарту может иметь значения в диапазоне от 0,05 до 100 мм. Главными параметрами геометрии у различных зубчатых колес являются следующие диаметры: начальный, основной и делительный. Шагом зубчатого колеса называется общее расстояние ширины зуба и впадины. Так же важным параметром является радиус колеса. Радиуса зубчатых колес делятся: радиус окружности вершин, радиус делительной окружности, радиус основной окружности, радиус окружности впадин.
Диаметры окружностей
Зубчатое колесо описывается несколькими окружностями, являющимися важными характеристиками их геометрии. Так, диаметр вершин дает максимальные размеры зубчатого колеса. Ему противоположен диаметр окружности впадин. Высчитав разность между этими двумя величинами и разделив ее пополам, получим полную длину зуба. Важным параметром считается диаметр делительной окружности, имеющий формулу d=pz/3,14, по нему можно определить окружной шаг p расположенных на колесе зубьев, иначе называемый шагом зацепления, имеющий геометрический смысл части длины этой окружности, приходящейся на каждый зуб. В общем случае, диаметр делительной окружности отделяет высоту головок и высоту ножек зуба. Он также задает кривую, являющуюся необходимой базой для построения самой эвольвенты, и используется для построения требуемого в конкретной задаче профиля зубьев колес и шестерен.
Важным параметром считается диаметр делительной окружности, имеющий формулу d=pz/3,14, по нему можно определить окружной шаг p расположенных на колесе зубьев, иначе называемый шагом зацепления, имеющий геометрический смысл части длины этой окружности, приходящейся на каждый зуб. В общем случае, диаметр делительной окружности отделяет высоту головок и высоту ножек зуба. Он также задает кривую, являющуюся необходимой базой для построения самой эвольвенты, и используется для построения требуемого в конкретной задаче профиля зубьев колес и шестерен.
Модули зубчатых колес
Чтобы упростить расчеты элементов, использующихся для зацепления, для зубчатых колес была введена стандартизованная ГОСТ величина, названная модулем. Модуль зубчатого колеса является частью от диаметра имеющейся делительной окружности зубчатого колеса, которая приходится на зуб: m=d/z. Таким образом, количество зубьев колеса, его собственный делительный диаметр и его модуль — во взаимовлиянии. Модуль можно расписать как отношение шага зацепления колеса и числа Пи: m=d/3,14. Когда передаваемая зубчатыми колесами нагрузка невелика, то лучше использовать малые модули. Малый модуль дает более длительный срок эксплуатации и упрощается обработка зубчатых колес. В данном случае на делительном диаметре разместится больше зубьев, а значит и зацепление будет происходить с большим их числом, что уменьшит нагрузку на отдельные зубья шестерен. У прямозубых цилиндрических колес бывает всего только один модуль, у косозубых — два: нормальный и окружной. В расчетах используют первый.
Когда передаваемая зубчатыми колесами нагрузка невелика, то лучше использовать малые модули. Малый модуль дает более длительный срок эксплуатации и упрощается обработка зубчатых колес. В данном случае на делительном диаметре разместится больше зубьев, а значит и зацепление будет происходить с большим их числом, что уменьшит нагрузку на отдельные зубья шестерен. У прямозубых цилиндрических колес бывает всего только один модуль, у косозубых — два: нормальный и окружной. В расчетах используют первый.
Расчет параметров
Для всех зубчатых колес инженерный расчет их параметров является задачей комплексной, в ходе решения которой принимается во внимание конструкция всей передачи. Вначале нужно определиться с числом зубьев и необходимым в задаче модулем зацепления. Для выбора последнего необходимы параметры прочности и предполагаемого срока службы колес; материала, из которого оно будет изготовлено. На основе этих данных рассчитывается минимально возможная в данной задаче величина модуля зацепления, которое затем приводится к стандартизованным значениям, находящимся из соответствующих таблиц. Передаточное отношение высчитывается с применением формулы u=z2z1, где z2 — это количество колесных зубьев, а z1 — количество зубьев, находящихся на шестерне. Оно позволяет понять, сколько всего нужно зубьев на колесах, подлежащих сопряжению. Зная модули и полученное число зубьев для всех колес и шестерней, можно произвести дальнейшие расчеты размеров требуемых деталей, используя стандартный метод для их расчетов.
Передаточное отношение высчитывается с применением формулы u=z2z1, где z2 — это количество колесных зубьев, а z1 — количество зубьев, находящихся на шестерне. Оно позволяет понять, сколько всего нужно зубьев на колесах, подлежащих сопряжению. Зная модули и полученное число зубьев для всех колес и шестерней, можно произвести дальнейшие расчеты размеров требуемых деталей, используя стандартный метод для их расчетов.
Обслуживание и расчёт
Техобслуживание заключается в осмотре механизма, проверке целостности зубьев и отсутствия сколов. Проверка правильности зацепления производится при помощи краски, наносимой на зубья. Изучается величина пятна контакта и его расположение по высоте зуба. Регулировка производится установкой прокладок в подшипниковых узлах.
Сначала надо определиться с кинематическими и силовыми характеристиками, необходимыми для работы механизма. Выбирается вид передачи, допустимые нагрузки и габариты, затем подбираются материалы и термообработка. Расчёт включает в себя выбор модуля зацепления, после этого подбираются величины смещений, число зубьев шестерни и колеса, межосевое расстояние, ширина венцов. Все значения можно выбирать по таблицам или использовать специальные компьютерные программы.
Все значения можно выбирать по таблицам или использовать специальные компьютерные программы.
Главными условиями, необходимыми для длительной работы зубчатых передач, являются износостойкость контактных поверхностей зубьев и их прочность на изгиб.
Достижению хороших характеристик и уделяется основное внимание при проектировании и изготовлении зубчатых механизмов.
Применение
Каждый из видов передач имеет свои преимущества и отрицательные качества. Нарезание прямозубых колес — довольно простой технологический процесс, поэтому они широко применяются в промышленности. Косозубые, как и прямозубые цилиндрические колеса, используются в тракторах, станках, коробках передач автотранспорта. Цилиндрические колеса с использованием внутреннего зацепления, благодаря компактности и прочности, нашли себя в самолетах, трансмиссиях автомобилей, редукторах, в шлицевых соединениях и сложных планетарных передачах, которые славятся своим особенно малым весом и габаритными размерами. При этом они предоставляют высокие передаточные числа и значительно сниженные уровни шумов при своей работе. Шевронные колеса, будучи трудоемкими в производстве, используются в больших редукторах и их ремонте, где требуется плавная и бесшумная передача значительных нагрузок. Конические колеса с нулевым наклоном и их прямозубые аналоги, имея высокую компактность и невысокую себестоимость изготовления, эксплуатируются в дифференциалах автомашин и станков. Криволинейные зубья обеспечивают коническим колесам особую прочность и малошумность, поэтому их можно найти в ответственных и скоростных передачах. Их используют практически везде: от самолетов до тракторов. Гипоидные зубчатые пары можно делать с большим передаточными числами (до 100:1), они часто используются в металлорежущем оборудовании.
При этом они предоставляют высокие передаточные числа и значительно сниженные уровни шумов при своей работе. Шевронные колеса, будучи трудоемкими в производстве, используются в больших редукторах и их ремонте, где требуется плавная и бесшумная передача значительных нагрузок. Конические колеса с нулевым наклоном и их прямозубые аналоги, имея высокую компактность и невысокую себестоимость изготовления, эксплуатируются в дифференциалах автомашин и станков. Криволинейные зубья обеспечивают коническим колесам особую прочность и малошумность, поэтому их можно найти в ответственных и скоростных передачах. Их используют практически везде: от самолетов до тракторов. Гипоидные зубчатые пары можно делать с большим передаточными числами (до 100:1), они часто используются в металлорежущем оборудовании.
Материалы для изготовления
Основной материал для изготовления колёсных пар — это сталь. Шестерня должна иметь более высокие прочностные характеристики, поэтому колёса часто изготавливают из разных материалов и подвергают разной термической или химико-термической обработке. Шестерни, изготовленные из легированной стали, подвергают поверхностному упрочнению методом азотирования, цементации или цианирования. Для углеродистых сталей используется поверхностная закалка.
Шестерни, изготовленные из легированной стали, подвергают поверхностному упрочнению методом азотирования, цементации или цианирования. Для углеродистых сталей используется поверхностная закалка.
Зубья должны обладать высокой поверхностной прочностью, а также более мягкой и вязкой сердцевиной. Это предохранит их от излома и износа поверхности. Колёсные пары тихоходных машин могут быть изготовлены из чугуна. В различных производствах применяются также бронза, латунь и различные пластики.
Зубчатое колесо и шестерня — отличия
Главными деталями в зубчатой передаче – зубчатое колесо и шестерня. Они применяются во многих промышленных узлах, машинах. Многие полагают, что зубчатое колесо и шестерня это одна и та же деталь и у них нет различий между собой. Специалисты, которые тесно связаны с промышленностью и машиностроением так не считают и уверяю, что это разные детали хоть и выполняют по сути одну и ту же функцию передачу вращательного движения. Давайте разберем основные моменты по данному вопросу.
Подытожим
Расчетные чертежи и схемы для шестеренок различных конфигураций преимущественно совпадают для косых и прямозубчатых версий. Основные различия возникают при расчетах на прочность. В графических отображениях применяются характеристики, ориентированные на типовые габаритные размеры шестеренок. Среди представленного ассортимента на рынке вполне реально подобрать зубчатое колесо с необходимыми характеристиками и прочностными показателями.
Источники
- https://mehmanxona.ru/tehnologii/vidy-shesterenok.html
- https://novoe-info.ru/chto-takoe-modul-shesterni/
- https://MechPrivod.com/market/zubchataya_shesterenka/shesterenka_zubchataya_cilindricheskaya/
- https://novoe-info.ru/kak-nayti-modul-zubchatogo-kolesa/
- https://doctordent.su/pulpit/kak-opredelit-modul-zuba-shesterni-po-diametru.html
- https://FB.ru/article/429020/modul-shesterni-vidyi-opredelenie-standartnyie-pokazateli
Особенности зубчатых колес и шестерней
Внешне зубчатое колесо и шестерня имеют схожесть в виде диска с расположенными на нем зубцами. Их расположение может быть как на конической, так и цилиндрической поверхности. Основной задачей данных деталей является передача крутящего момента. Для того чтобы получить и передать крутящий момент, нужна ответная шестерня, то есть пара. Мы разобрали выше, что существует ведомая деталь и ведущая. С ведущей начинается движение и дальнейшая передача крутящего момента на ведомую деталь. В этом ключевом моменте и есть отличие зубчатого колеса от шестерни, ведущая деталь является шестерней, а ведомая зубчатым колесом. Получается, что вся разница между ними в том какую роль в механизме выполняет деталь.
Их расположение может быть как на конической, так и цилиндрической поверхности. Основной задачей данных деталей является передача крутящего момента. Для того чтобы получить и передать крутящий момент, нужна ответная шестерня, то есть пара. Мы разобрали выше, что существует ведомая деталь и ведущая. С ведущей начинается движение и дальнейшая передача крутящего момента на ведомую деталь. В этом ключевом моменте и есть отличие зубчатого колеса от шестерни, ведущая деталь является шестерней, а ведомая зубчатым колесом. Получается, что вся разница между ними в том какую роль в механизме выполняет деталь.
Отметим что при работе двух зубчатых колес, колесо, которое имеет большее количество зубьев, называют шестерней. В ГОСТ 16530-83 есть пояснение, что зубчатое колесо и шестерня являются словами синонимами, шестерня является главным и ведущим зубчатым колесом. Существуют специалисты работающие в определенных областях промышленности и машиностроения, которые четко разделяют разницу между зубчатым колесом и шестерней. Они убеждены, что изготовление зубчатых колес это одно, а производство шестерней это другое, так как между ними есть различия.
Они убеждены, что изготовление зубчатых колес это одно, а производство шестерней это другое, так как между ними есть различия.
Как рассчитать передаточное число
Шестерня и колесо имеют разное количество зубов с одинаковым модулем и пропорциональный размер диаметров. Передаточное число показывает, сколько оборотов совершит ведущая деталь, чтобы провернуть ведомую на полный круг. Зубчатые передачи имеют жесткое соединение. Передающееся количество оборотов в них не меняется. Это негативно сказывается на работе узла в условиях перегрузок и запыленности. Зубец не может проскользнуть, как ремень по шкиву и ломается.
Расчет без учета сопротивления
В расчете передаточного числа шестерен используют количество зубьев на каждой детали или их радиусы.
u12 = ± Z2/Z1 и u21 = ± Z1/Z2,
Где u12 – передаточное число шестерни и колеса;
Z2 и Z1 – соответственно количество зубьев ведомого колеса и ведущей шестерни.
Знак «+» ставится, если направление вращения не меняется. Это относится к планетарным редукторам и зубчатым передачам с нарезкой зубцов по внутреннему диаметру колеса. При наличии паразиток – промежуточных деталей, располагающихся между ведущей шестерней и зубчатым венцом, направление вращения изменяется, как и при наружном соединении. В этих случаях в формуле ставится «–».
Это относится к планетарным редукторам и зубчатым передачам с нарезкой зубцов по внутреннему диаметру колеса. При наличии паразиток – промежуточных деталей, располагающихся между ведущей шестерней и зубчатым венцом, направление вращения изменяется, как и при наружном соединении. В этих случаях в формуле ставится «–».
При наружном соединении двух деталей посредством расположенной между ними паразитки, передаточное число вычисляется как соотношение количества зубьев колеса и шестерни со знаком «+». Паразитка в расчетах не участвует, только меняет направление, и соответственно знак перед формулой.
Обычно положительным считается направление движения по часовой стрелке. Знак играет большую роль при расчетах многоступенчатых редукторов. Определяется передаточное число каждой передачи отдельно по порядку расположения их в кинематической цепи. Знак сразу показывает направление вращения выходного вала и рабочего узла, без дополнительного составления схем.
Вычисление передаточного числа редуктора с несколькими зацеплениями – многоступенчатого, определяется как произведение передаточных чисел и вычисляется по формуле:
u16 = u12×u23×u45×u56 = z2/z1×z3/z2×z5/z4×z6/z5 = z3/z1×z6/z4
Способ расчета передаточного числа позволяет спроектировать редуктор с заранее заданными выходными значениями количества оборотов и теоретически найти передаточное отношение.
Зубчатое зацепление жесткое. Детали не могут проскальзывать относительно друг друга, как в ременной передаче и менять соотношение количества вращений. Поэтому на выходе обороты не изменяются, не зависят от перегруза. Верным получается расчет скорости угловой и количества оборотов.
КПД зубчатой передачи
Для реального расчета передаточного отношения, следует учитывать дополнительные факторы. Формула действительна для угловой скорости, что касается момента силы и мощности, то они в реальном редукторе значительно меньше. Их величину уменьшает сопротивление передаточных моментов:
- трение соприкасаемых поверхностей;
- изгиб и скручивание деталей под воздействием силы и сопротивление деформации;
- потери на шпонках и шлицах;
- трение в подшипниках.
Для каждого вида соединения, подшипника и узла имеются свои корректирующие коэффициенты. Они включаются в формулу. Конструктора не делают расчеты по изгибу каждой шпонки и подшипника. В справочнике имеются все необходимые коэффициенты. При необходимости их можно рассчитать. Формулы простотой не отличаются. В них используются элементы высшей математики. В основе расчетов способность и свойства хромоникелевых сталей, их пластичность, сопротивление на растяжение, изгиб, излом и другие параметры, включая размеры детали.
В справочнике имеются все необходимые коэффициенты. При необходимости их можно рассчитать. Формулы простотой не отличаются. В них используются элементы высшей математики. В основе расчетов способность и свойства хромоникелевых сталей, их пластичность, сопротивление на растяжение, изгиб, излом и другие параметры, включая размеры детали.
Что касается подшипников, то в техническом справочнике, по которому их выбирают, указаны все данные для расчета их рабочего состояния.
При расчете мощности, основным из показателей зубчатых зацепления является пятно контакта, оно указывается в процентах и его размер имеет большое значение. Идеальную форму и касание по всей эвольвенте могут иметь только нарисованные зубья. На практике они изготавливаются с погрешностью в несколько сотых долей мм. Во время работы узла под нагрузкой на эвольвенте появляются пятна в местах воздействия деталей друг на друга. Чем больше площадь на поверхности зуба они занимают, тем лучше передается усилие при вращении.
Все коэффициенты объединяются вместе, и в результате получается значение КПД редуктора. Коэффициент полезного действия выражается в процентах. Он определяется соотношением мощности на входном и выходном валах. Чем больше зацеплений, соединений и подшипников, тем меньше КПД.
Рост в течение клеточного цикла
Обзор
. 2003; 226:165-258.
doi: 10.1016/s0074-7696(03)01004-0.
Дж. М. Митчисон 1
принадлежность
- 1 Институт клеточной, животной и популяционной биологии Эдинбургского университета, Эдинбург EH9 3JT, Великобритания.
- PMID: 12921238
- DOI:
10.
 1016/s0074-7696(03)01004-0
1016/s0074-7696(03)01004-0
Обзор
Дж. М. Митчисон. Int Rev Cytol. 2003.
. 2003; 226:165-258.
дои: 10.1016/s0074-7696(03)01004-0.
Автор
Дж. М. Митчисон 1
принадлежность
- 1 Институт клеточной, животной и популяционной биологии Эдинбургского университета, Эдинбург EH9 3JT, Великобритания.
- PMID: 12921238
- DOI: 10.1016/s0074-7696(03)01004-0
Абстрактный
Во время клеточного цикла основные объемные параметры, такие как объем, сухая масса, общий белок и общая РНК, удваиваются, и такой рост является фундаментальным свойством клеточного цикла. Паттерны роста объема и общего белка или РНК образуют «оболочку», которая содержит и может ограничивать зубчатые колеса. Основные параметры роста клеточного цикла были установлены в более ранних работах, когда люди перешли от этой области к редукционистским подходам молекулярной биологии, но о закономерностях метаболизма известно очень мало. Большинство объемных свойств клеток постоянно увеличиваются в течение клеточного цикла, хотя точная картина этого увеличения может варьироваться. С самых первых дней были две популярные модели, основанные на экспоненциальном увеличении и линейном увеличении. В первом случае нет резкого изменения скорости увеличения в течение цикла, а наблюдается плавное увеличение в два раза. Во втором случае скорость увеличения остается постоянной на протяжении большей части цикла, но резко удваивается в точке изменения скорости (RCP). Считается, что экспоненциальное увеличение вызвано устойчивым ростом числа рибосом, а линейная картина вызвана удвоением структурных генов в течение S-периода, дающим RCP – эффект «дозы генов».
Паттерны роста объема и общего белка или РНК образуют «оболочку», которая содержит и может ограничивать зубчатые колеса. Основные параметры роста клеточного цикла были установлены в более ранних работах, когда люди перешли от этой области к редукционистским подходам молекулярной биологии, но о закономерностях метаболизма известно очень мало. Большинство объемных свойств клеток постоянно увеличиваются в течение клеточного цикла, хотя точная картина этого увеличения может варьироваться. С самых первых дней были две популярные модели, основанные на экспоненциальном увеличении и линейном увеличении. В первом случае нет резкого изменения скорости увеличения в течение цикла, а наблюдается плавное увеличение в два раза. Во втором случае скорость увеличения остается постоянной на протяжении большей части цикла, но резко удваивается в точке изменения скорости (RCP). Считается, что экспоненциальное увеличение вызвано устойчивым ростом числа рибосом, а линейная картина вызвана удвоением структурных генов в течение S-периода, дающим RCP – эффект «дозы генов». На почкующихся дрожжах есть эксперименты, соответствующие обеим моделям, но в целом слегка благоприятствующие «дозировке генов». У делящихся дрожжей нет убедительных доказательств экспоненциального роста. Все объемные свойства, за исключением потребления O2, по-видимому, следуют линейным закономерностям с RCP в течение короткого периода S. Кроме того, в клетках дикого типа имеется второстепенный RCP в G2, где скорость увеличивается на 70%. В клетках млекопитающих есть хорошие, но не исчерпывающие доказательства экспоненциального увеличения. Для Escherichia coli характерно экспоненциальное увеличение. Есть два важных момента: во-первых, некоторые белки не проявляют пиков периодического синтеза. Если они демонстрируют модели экспоненциального увеличения, то и они, и общая картина белка не будут регулироваться клеточным циклом. Однако, если общий белковый паттерн не является экспоненциальным, то большинство отдельных белков будут так регулироваться. Если эта закономерность большинства является линейной, то ее можно обнаружить по измерению скорости общего белка.
На почкующихся дрожжах есть эксперименты, соответствующие обеим моделям, но в целом слегка благоприятствующие «дозировке генов». У делящихся дрожжей нет убедительных доказательств экспоненциального роста. Все объемные свойства, за исключением потребления O2, по-видимому, следуют линейным закономерностям с RCP в течение короткого периода S. Кроме того, в клетках дикого типа имеется второстепенный RCP в G2, где скорость увеличивается на 70%. В клетках млекопитающих есть хорошие, но не исчерпывающие доказательства экспоненциального увеличения. Для Escherichia coli характерно экспоненциальное увеличение. Есть два важных момента: во-первых, некоторые белки не проявляют пиков периодического синтеза. Если они демонстрируют модели экспоненциального увеличения, то и они, и общая картина белка не будут регулироваться клеточным циклом. Однако, если общий белковый паттерн не является экспоненциальным, то большинство отдельных белков будут так регулироваться. Если эта закономерность большинства является линейной, то ее можно обнаружить по измерению скорости общего белка. Однако это было бы намного сложнее на уровне отдельных белков, где методы в настоящее время недостаточно чувствительны, чтобы обнаружить изменение скорости в два раза. На простом уровне это только экспоненциальное увеличение, которое не регулируется клеточным циклом в синхронной культуре. Существование «контроля размера» хорошо известно, и этот контроль изучался в течение длительного времени, но он оказался удивительно устойчивым к молекулярному анализу. Достижение критического размера запускает периодические события цикла, такие как S-период и митоз. Этот контроль действует как гомеостатический эффектор, который поддерживает постоянный «средний» размер клетки при делении в последовательных циклах в растущей культуре. Это жизненно важное звено, координирующее рост клеток с периодическими событиями цикла. Контроль размера присутствует во всех системах и, по-видимому, действует в начале S или митоза, когда клетка достигает критического размера, но молекулярный механизм, с помощью которого измеряется размер, остается неясным и сложным.
Однако это было бы намного сложнее на уровне отдельных белков, где методы в настоящее время недостаточно чувствительны, чтобы обнаружить изменение скорости в два раза. На простом уровне это только экспоненциальное увеличение, которое не регулируется клеточным циклом в синхронной культуре. Существование «контроля размера» хорошо известно, и этот контроль изучался в течение длительного времени, но он оказался удивительно устойчивым к молекулярному анализу. Достижение критического размера запускает периодические события цикла, такие как S-период и митоз. Этот контроль действует как гомеостатический эффектор, который поддерживает постоянный «средний» размер клетки при делении в последовательных циклах в растущей культуре. Это жизненно важное звено, координирующее рост клеток с периодическими событиями цикла. Контроль размера присутствует во всех системах и, по-видимому, действует в начале S или митоза, когда клетка достигает критического размера, но молекулярный механизм, с помощью которого измеряется размер, остается неясным и сложным. Простая версия может состоять в том, чтобы клетка обнаруживала критическую концентрацию генного продукта.
Простая версия может состоять в том, чтобы клетка обнаруживала критическую концентрацию генного продукта.
Похожие статьи
Еще раз о контроле размера делящихся дрожжей.
Швейцер А., Новак Б., Митчисон Дж.М. Швейцер А. и др. Дж. Клеточные науки. 1996, декабрь; 109 (часть 12): 2947–57. doi: 10.1242/jcs.109.12.2947. Дж. Клеточные науки. 1996. PMID:
Паттерны роста длины клеток у делящихся дрожжей обнаруживают новый механизм контроля размера, действующий в поздней фазе G2.
Хорват А., Рач-Монус А., Бухвальд П., Швейцер А. Хорват А. и др. Биол Клетка. 2016 сен; 108 (9): 259-77. doi: 10.1111/boc.201500066. Эпаб 2016 4 мая. Биол Клетка. 2016. PMID: 27063594
Макромолекулярная скученность: химия и физика встречаются с биологией (Аскона, Швейцария, 10–14 июня 2012 г. ).
).
Foffi G, Pastore A, Piazza F, Temussi PA. Фоффи Г. и др. физ.-биол. 2013 авг; 10 (4): 040301. дои: 10.1088/1478-3975/10/4/040301. Epub 2013 2 августа. физ.-биол. 2013. PMID: 23912807
Сильно увеличенные клетки делящихся дрожжей лишены какого-либо контроля размера и имеют тенденцию к линейному, а не билинейному росту.
Надь З., Медьес-Хорват А., Вёрёш Э., Швейцер А. Надь З. и др. Дрожжи. 2021 март; 38(3):206-221. doi: 10.1002/yea.3535. Epub 2020 26 ноября. Дрожжи. 2021. PMID: 33244789
Скорость роста биомассы в течение клеточного цикла прокариот.
Кох А.Л.
Кох АЛ.
Crit Rev Microbiol. 1993;19(1):17-42. дои: 10.3109/104084193021.
Crit Rev Microbiol. 1993. PMID: 8481211
Обзор.
PMID: 8481211
Обзор.
Посмотреть все похожие статьи
Цитируется
Количественный и пространственный анализ регуляторов клеточного цикла во время цикла делящихся дрожжей.
Карран С., Дей Г., Рис П., медсестра П. Курран С. и др. Proc Natl Acad Sci U S A. 2022 Sep 6;119(36):e2206172119. doi: 10.1073/pnas.2206172119. Epub 2022 29 августа. Proc Natl Acad Sci U S A. 2022. PMID: 36037351 Бесплатная статья ЧВК.
Массовые измерения с высоким разрешением одиночных почкующихся дрожжей выявляют сегменты линейного роста.
Куни А.П., Тануй Сапра К., Мартинес-Мартин Д., Флешнер Г., Адамс Д.Д., Мартин С., Гербер С., Рудольф Ф., Мюллер Д.Дж. Куни А.П. и др.
 Нац коммун. 2022 22 июня; 13 (1): 3483. doi: 10.1038/s41467-022-30781-y.
Нац коммун. 2022.
PMID: 35732645
Бесплатная статья ЧВК.
Нац коммун. 2022 22 июня; 13 (1): 3483. doi: 10.1038/s41467-022-30781-y.
Нац коммун. 2022.
PMID: 35732645
Бесплатная статья ЧВК.Обновленный взгляд на центросому как регулятор клеточного цикла.
Линь М., Се С.С., Чан К.Ю. Лин М. и др. Сотовый отдел 2022 14 февраля; 17 (1): 1. doi: 10.1186/s13008-022-00077-0. Сотовый отдел 2022. PMID: 35164835 Бесплатная статья ЧВК. Обзор.
Характеристика неэкспоненциального роста и бимодального распределения размеров клеток у делящихся дрожжей: аналитический подход.
Джиа С., Сингх А., Грима Р. Цзя С и др. PLoS Comput Biol. 18 января 2022 г .; 18 (1): e1009793. doi: 10.1371/journal.pcbi.1009793. Электронная коллекция 2022 янв. PLoS Comput Biol.
 2022.
PMID: 35041656
Бесплатная статья ЧВК.
2022.
PMID: 35041656
Бесплатная статья ЧВК.Изменения внутриклеточной плотности во время клеточного цикла возникают из-за регуляции роста кончика у делящихся дрожжей.
Odermatt PD, Miettinen TP, Lemière J, Kang JH, Bostan E, Manalis SR, Huang KC, Chang F. Odermatt PD, et al. Элиф. 2021 8 июня; 10: e64901. doi: 10.7554/eLife.64901. Элиф. 2021. PMID: 34100714 Бесплатная статья ЧВК.
Просмотреть все статьи “Цитируется по”
Типы публикаций
термины MeSH
Терминология зубчатых колес и формулы расчета зубьев: краткое руководство
Это упрощенная версия терминологии зубчатых колес и формул расчета зубьев
Этот пост предназначен для того, чтобы упростить терминологию зубчатых колес и формулы расчета зубьев для начинающих, а также для тех, кто давно изучил передачи, но хочет быстро освоить их снова.
Шестерни имеют множество параметров, для полного понимания которых потребуется немного математических и геометрических знаний. Тем не менее, вам не нужно слишком углубляться в базовые знания о зубчатых колесах, после того, как вы прочитаете этот пост, вы сможете делать предварительные проекты зубчатых колес или иметь эффективное общение с конструкторами зубчатых колес .
Давайте начнем с базовой формы шестерни, прямозубые шестерни:
1. Число зубьев (z)
Это довольно просто, это количество зубьев шестерни.
2. Контрольная окружность и контрольный диаметр (d)
Диаметр вершины (da) и диаметр корня (df) соответствуют верхней и нижней части зубьев.
Эталонный диаметр используется при проектировании и расчете зубчатых колес. Он напрямую связан с другими важными параметрами зубчатого колеса, такими как модуль (m), межосевое расстояние (c) и угол давления (α).
Диаметр вершины (da) и диаметр корня (df) соответствуют верхней и нижней части зубов.
Эталонный диаметр используется при проектировании и расчете зубчатых колес. Он напрямую связан с другими важными параметрами зубчатого колеса, такими как модуль (m), межосевое расстояние (c) и угол давления (α).
Поворот 2-х шестерен можно считать включенным поворотом 2-х опорных окружностей без проскальзывания. Передаточное число i=d2/d1. d1 и d2 относятся к эталонным диаметрам двух сопряженных шестерен (шестерня 1 — ведущая, шестерня 2 — ведомая).
Опорная окружность находится где-то между верхушкой и низом зубьев, обычно там, где толщина зуба равна шагу, но это не всегда так (о смещении профиля мы поговорим позже в этом посте).
3. Модуль (м)
Модуль, вероятно, является наиболее важным параметром зубчатого колеса, и он фигурирует почти везде в формулах расчета зубьев. На самом деле, это не так сложно понять, как вы можете себе представить. Сначала давайте разберемся, что такое шаг. Шаг — это длина дуги между соответствующими точками на соседних зубах, обычно на эталонной окружности.
Затем у нас есть эталонный диаметр d=длина окружности/π=шаг*z/π , чтобы упростить вычисления, мы определяем шаг/π как модуль, и теперь у нас есть уравнение d= m*z , это значительно упрощает вычисления, верно? Модули стандартизированы под следующими номерами (единица измерения : мм ):
Первая серия (рекомендуется): 0,1, 0,12, 0,15, 0,2, 0,25, 0,3, 0,4, 0,5, 0,6, 0,8, 1, 1,25, 1,5 , 2, 2,5, 3, 4, 5, 6, 8, 10, 12, 16, 20, 25, 32, 40, 50
Вторая серия (менее использованная): 0,35, 0,7, 0,9, 1,75, 2,25, 2,75, 3,25, 3,5, 3,75, 4,5, 5,5, 6,5, 7, 9, 11, 14, 18, 22, 28, 30, 36 , 45
Однако для литых пластмассовых шестерен нет необходимости использовать эти стандартные номера модулей, поскольку зубья не нарезаются стандартными зуборезами.
Теперь у нас есть передаточное число i=d2/d1=z2/z1 (шестерня 1 — ведущая, а шестерня 2 — ведомая).
Модуль также относится к высоте зуба, для стандартных шестерен высота зуба равна 2,25*м:
дополнение га=1*м , нижняя часть hf=1,25*м , высота зуба h=2,25*м .
4. Расстояние между центрами (a)
2 зубчатых зацепления всегда имеют один и тот же модуль, в противном случае они не совпадают. Теперь можно прийти к выводу, что a=(d1+d2)/z=m(z1+z2)/2 , но может немного отличаться при некоторых корректировках геометрии шестерни (смещении профиля зуба).
5. Угол давления (α)
Проще говоря, как следует из названия, это угол между направлением контактной силы в точке контакта зуба и направлением движения этой точки на профиле зуба.
В геометрии это угол между линией, нормальной к эвольвентному профилю зуба, и линией, нормальной к его радиальной линии.
Если вы хотите полностью понять угол давления, вам нужно углубиться, чтобы понять эвольвентную линию профиля зуба. Это просто более простой способ объяснения.
Различные точки на профиле зуба имеют разные углы зацепления, но когда мы говорим об угле зацепления зубчатого колеса, это обычно относится к углу опорной окружности. Большинство зубчатых колес используют угол давления 20°, некоторые — 14,5° или 25°. 2 сопрягаемые шестерни должны иметь одинаковый модуль и угол зацепления.
Большинство зубчатых колес используют угол давления 20°, некоторые — 14,5° или 25°. 2 сопрягаемые шестерни должны иметь одинаковый модуль и угол зацепления.
6. Минимальное количество зубьев (
z min ) без подрезки в шестернеВы не можете иметь любое количество зубьев шестерни, как хотите. Если зубьев слишком мало, нижняя часть зубьев будет ниже предельной точки, вследствие чего при изготовлении зубьев зуборезами будет срезана лишняя часть корня зуба.
Если зубья не обработаны зуборезами, а профили зубьев сохранились, то в трансмиссии заклинит 2 шестерни.
Формула для расчета минимального количества зубьев без подрезки:
z мин =2га*/sin 2 α
мин =17. Так, минимальное число зубьев для стандартных шестерен равно 17.
7. Коэффициент смещения профиля (x)
Обычно для профиля зуба надстройка зуба ha=1*m, а нижняя часть hf=1,25*m, однако профиль зубьев можно немного сдвинуть вверх или вниз:
Теперь у нас есть коэффициент сдвига профиля (x). При перемещении профиля вверх значение x положительное (x>0), а при перемещении профиля вниз значение x отрицательное (x<0).
При перемещении профиля вверх значение x положительное (x>0), а при перемещении профиля вниз значение x отрицательное (x<0).
С перемещением профиля зубьев теперь имеем:
- дополнение ha=(1+x)*m
- dedendum hf=(1,25-x)*m
Высота зуба h=ha+hf=2,25 * м, это все равно, что стандартные зубы.
Основными причинами смещения профиля являются:
1) При смещении профиля мы можем избежать подрезки зубьев с меньшим количеством зубьев. Формула выглядит следующим образом:
x мин =(17-z)/17
Например, если вы хотите, чтобы число зубьев было 14, тогда X=(17-14)/17=0,176
2)Точная настройка межосевого расстояния
a=[(m+x1)z1+(m+x2)z2]/2 , поэтому межосевое расстояние не обязательно должно быть (z1+z2)*m
3) Сделайте шестерню сильнее . Обычно шестерня выходит из строя раньше, чем шестерня, за счет положительного сдвига профиля нижняя часть шестерни становится шире (в то время как кончик становится уже), что делает ее прочнее.
In summary:
| # | Item | Symbol | Formula | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | teeth number | z | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | module | m | m=pitch/π | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | gear ratio | i | i=d2/d1=z2/z1 1: driving gear, and 2: driven gear | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | addendum coefficient | da* | da*=1+x x=0 for standard gears | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | dedendum coefficient | df* | df*=1.25-x | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | profile shift coefficient | x | Для стандартных зубчатых колес, x=0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | угол давления | α | α=20° для большинства зубчатых колес Другими менее используемыми являются 125° и 124,5°. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | опорный диаметр | d | d=mz | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | диаметр наконечника | da | da=d+2Ha* x m, da=(z+2ha*) m ) x m | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | диаметр хвостовика | df | df=d-2Hf* x m, df=(z-2hf*) x m 11 | дополнение | га | га=м x га* Для стандартных передач, га=м | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12 | Dedendum | HF | HF = M x HF* для стандартных передач, HF = 1,25M | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13 | Высота зуба | H | H = M. hf*HA*HA*HA*HA*HA*HA*HA*HA*HA*HA*HA*HA*HA*HA*HA*HA*HA*HA*HA*HA*HA*HA*HA*HA*HA / HF*hf*FUTH*HA*hf *f*hf*Fust. *=2,25 для большинства шестерен hf*HA*HA*HA*HA*HA*HA*HA*HA*HA*HA*HA*HA*HA*HA*HA*HA*HA*HA*HA*HA*HA*HA*HA*HA*HA / HF*hf*FUTH*HA*hf *f*hf*Fust. *=2,25 для большинства шестерен | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 14 | межосевое расстояние | a | a=m x (z1+z2) для стандартных шестерен a=[(m+x1)z1+(m+x2)z2]/2 для профильных шестерен | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15 | Минимальное количество зубьев без подрезки | Zmin | Zmin=2ha*/sin2α Zmin=17 при ha*=1, α=20° | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16 | Минимальное смещение профиля без подрезки | Xmin | Xmin=(17-z)03/17-z)03 19 апреля 2019 г. В… boyanmfg 19 января 2020 г. Вы должны с самого начала выбрать правильного производителя пресс-формы Для любого проекта по литью пластмасс под давлением изготовление пресс-формы является самой дорогой и трудоемкой его частью. Это… Изучение основ двигателей постоянного тока и малогабаритных двигателей постоянного токаЧто такое двигатель постоянного тока? Двигатель постоянного тока (DC) представляет собой вращающееся электрическое устройство, которое преобразует постоянный ток электрической энергии в механическую энергию. Подробнее Что такое мотор-редуктор постоянного тока? Мотор-редуктор представляет собой единую комбинацию двигателя и редуктора. Добавление редуктора к двигателю снижает скорость при увеличении выходного крутящего момента. Наиболее важными параметрами мотор-редукторов являются скорость (об/мин), крутящий момент (фунт-дюйм) и КПД (%).
База данных Motor Solution Процесс выбора двигателяНужна помощь в выборе двигателя, подходящего для вашего приложения? Ознакомьтесь с нашим руководством по выбору двигателя или посетите базу данных двигателей ISL. Процесс выбора двигателя на этапе концептуального проектирования может быть сложным, но наши инженеры готовы помочь. Мы обеспечиваем консьерж-подход ко всем нашим проектам двигателей постоянного тока и мотор-редукторов. Наша команда инженеров работает с вами, чтобы предоставить оптимальное решение для компонентов.
Contact Engineering Кривые рабочих характеристик редукторного двигателяХарактеристики двигателей и редукторов объединены в один график с отображением трех конкретных параметров. Этими тремя параметрами являются скорость, крутящий момент и КПД. Эти рабочие характеристики необходимы при выборе мотор-редуктора для вашего применения. Скорость/Обороты (Н) – ( единица измерения: об/мин) обозначено как прямая линия, показывающая зависимость между крутящим моментом мотор-редуктора и скоростью.
Как читать кривые производительности Например, давайте рассмотрим кривую производительности ниже (рис.
Кривые производительности редукторного двигателя являются полезным инструментом при выборе двигателя для вашего приложения. Чтобы получить максимальную отдачу от кривых производительности, важно полностью понять требования приложений. Вы можете использовать свои требования к нагрузке и скорости, чтобы определить требуемый крутящий момент. Большинство производителей двигателей постоянного тока и мотор-редукторов предоставляют рабочие характеристики по запросу. Все, что вам нужно знать о шестернях. Типы и детали Типы и деталиШестерни являются фундаментальной частью любого механизма из-за их способности передавать движение, силу и крутящий момент между различными компонентами. Существует огромное количество различных типов шестерен, в зависимости от того, какую задачу они выполняют: изменение скорости или силы вращения, изменение оси вращения, передача мощности между двигателем и другими движущимися элементами… Сегодня в Bitfab мы научим все, что вам нужно знать о шестернях. Что такое шестерня?Шестерня определяется как колесо с зубцами на кромке, обычно цилиндрическое, которое используется для передачи движения от элемента, производящего энергию, такого как двигатель, к месту, где мы хотим приложить усилие, с преобразованиями во вращении ось или скорость. Из каких частей состоит шестерня? Шестерня может быть очень сложной, но самые распространенные из них состоят из трех отдельных частей: зубчатого венца, передающего движение, подшипника, к которому присоединяется вал (двигателя или другой части механизма), и перегородка между ними, которая иногда выступает в виде герба. Перегородка или плечи шестерниЭто часть шестерни, которая соединяет венец и подшипник для передачи движения. Вариантов этой детали множество, так как в зависимости от технических требований можно сделать очень прочную, но тяжелую сплошную перегородку или менее прочные, но более легкие тонкие радиальные кронштейны. Элемент веса может иметь решающее значение, чтобы не добавлять лишнюю массу, так как, увеличивая вес движущегося элемента, мы увеличиваем инерцию в нашей системе. В связи с необходимостью поиска шестерни с соответствующей перегородкой существует множество промежуточных вариантов, с тонкими, толстыми, сплошными, перфорированными перегородками… Подшипник шестерни движение прилагается. Этот вал может быть от двигателя или от другой части механизма.Венчик шестерни Венец или обод шестерни — это место, где расположены зубья, и это часть шестерни, которая в значительной степени определяет поведение шестерни. Как форма, так и свойства формы и размера зубьев заставляют шестерню вести себя так или иначе. Поскольку свойства самого зубчатого колеса тесно связаны с тем, сколько у него зубьев и как они расположены, давайте сначала рассмотрим части зуба в зубчатом колесе. Части зубаКак видите, зуб состоит из следующих частей:
Геометрия короны: окружности, которые ее определяютКроме того, геометрия короны определяется серией окружностей, которые придают зубчатому колесу форму:
De esta manera nos quedaría el diente dividido en dos partes, el pie y la cabeza
Возвращаясь к коронке и по отношению к зубам, основные параметры коронки:
Типы зубчатых колесВ зависимости от того, что мы хотим сделать в нашем механизме, нам нужно будет выбрать тот или иной тип зубчатого колеса, поскольку каждое из них предназначено для определенной функции. Цилиндрические шестерни. прямое цилиндрическое зубчатое колесоНаиболее распространенный тип зубчатого колеса, используемый, когда необходимо уменьшить или увеличить усилие или скорость в условиях, когда скорость не очень высока. Винтовая цилиндрическая шестерняЧуть более усовершенствованная версия предыдущей. Более тихий и способный работать на более высоких скоростях. Они также двузубые. Также доступны с двойными спиральными зубьями в противоположных направлениях, которые поддерживают еще более высокие скорости и производительность. Коническая шестерня с прямыми зубьями Используются для изменения направления вращения в механизме, обычно перпендикулярного, когда не требуются высокие скорости. Коническая шестерня со спиральными зубьямиКак и предыдущие, они используются для изменения направления вращения, но в этом случае поддерживаемая скорость выше. Внутреннее зубчатое колесоОни работают так же, как традиционные внешние зубчатые колеса, но более компактны, чем внешнее зубчатое колесо с теми же характеристиками. Планетарные шестерниВ этом типе передач используется центральная шестерня, вокруг которой вращаются шестерни меньшего размера, отсюда и название, поскольку они напоминают нам о солнечной системе с солнцем в центре и планетами, вращающимися вокруг него. Червячная передачаЭти шестерни широко используются, поскольку они обеспечивают очень постоянную выходную скорость и работают без вибрации или шума. Кроме того, эти механизмы обычно достаточно компактны. Зубчатая рейка и шестерня Эти шестерни позволяют преобразовывать вращательное движение в линейное и наоборот, поэтому они чрезвычайно полезны. 2,972 Как работает трехскоростной концентратор
ОСНОВНОЕ ФУНКЦИОНАЛЬНОЕ ТРЕБОВАНИЕ: Предоставить велосипедисту возможность выбора трех различных передаточных чисел в трансмиссии велосипеда .КОНСТРУКТИВНЫЙ ПАРАМЕТР: 3 ступица скорости (это один из возможных конструктивных параметров) ГЕОМЕТРИЯ/КОНСТРУКЦИЯ И ЧАСТИ:
ОБЪЯСНЕНИЕ КАК ЭТО РАБОТАЕТ/ПРИМЕНЯЕТСЯ:
В трехскоростных втулках используется система планетарной передачи для достижения передаточного отношения между
звездочка и колесо.
Гонщик выбирает скорость с помощью переключателя передач. Переключатель тянет за трос который соединен с тросовым рычагом. Это приводит к вращению тросового рычага.
Тросовый рычаг давит на штифт, проходящий через ось. Этот пин соединен с планетарной передачи и заставляет ее двигаться из стороны в сторону при нажатии на рычаг. При смещении планетарной передачи из стороны в сторону зубчатого венца
и водила планетарной передачи зацепляются или расцепляются с колесом и цепью.
ДОМИНИРУЮЩАЯ ФИЗИКА: Передаточное число между водилом планетарной передачи и зубчатым венцом можно рассчитать на основе количество зубьев солнечной и планетарной шестерен:
ОГРАНИЧИВАЮЩИЕ ПАРАМЕТРЫ:
ДИАГРАММЫ/ГРАФЫ/ТАБЛИЦЫ: Нет Представлено ГДЕ МОЖНО НАЙТИ ТРИ СКОРОСТНЫЕ СТУПИЦЫ: Трехскоростные втулки в основном используются на велосипедах, выпущенных до 1970-х годов Современные ступицы с внутренним зацеплением основаны на этой конструкции, но используют несколько
системы планетарных передач, соединенные вместе для достижения большего количества скоростей.
ССЫЛКИ/ДОПОЛНИТЕЛЬНАЯ ИНФОРМАЦИЯ: Ступицы с внутренним зацеплением – http://www. Планетарные передачи – http://www.cs.cmu.edu/People/rapidproto/mechanisms/chpt7.html#HDR123 Как работает 14-скоростная втулка – http://www.rohloff.de/english/products/speedhub/speedwork.html Двигатели | Двигатель БэббиджаДвигателиЧарльз Бэббидж (1791-1871), пионер компьютерных технологий, разработал два класса двигателей: разностные машины и аналитические машины. Разностные машины названы так из-за математического принципа, на котором они основаны, а именно метода конечных разностей. Прелесть метода в том, что он использует только арифметическое сложение и устраняет необходимость в умножении и делении, которые сложнее реализовать механически. Разностные машины – это строго калькуляторы. Они перемалывают числа единственным известным им способом — многократным сложением по методу конечных разностей. Их нельзя использовать для общих арифметических вычислений. Аналитическая машина — это гораздо больше, чем калькулятор, и она знаменует собой переход от механизированной арифметики вычислений к полноценным вычислениям общего назначения. Обнаружение двоичных и десятичных чисел и ошибокВычислительные машины Бэббиджа представляют собой десятичные цифровые машины. Они десятичные, поскольку используют знакомые десять цифр от «0» до «9», и цифровые в том смысле, что только целые числа признаются действительными. Числовые значения представлены шестеренками, и каждой цифре числа соответствует свое колесо. Если колесо останавливается в положении, промежуточном между целыми числовыми значениями, значение считается неопределенным, и двигатель заклинивает, чтобы указать, что целостность расчета была нарушена. Заглушение – это форма обнаружения ошибок. Бэббидж рассматривал возможность использования систем счисления, отличных от десятичной, включая двоичную систему счисления, а также системы счисления 3, 4, 5, 12, 16 и 100. Он остановился на десятичной системе из соображений инженерной эффективности — чтобы уменьшить количество движущихся частей — а также для их повседневное знакомство. Разностная машина № 1Бэббидж начал свою деятельность в 1821 году с Разностной машины № 1, предназначенной для вычисления и табулирования полиномиальных функций. Проект описывает машину для расчета ряда значений и автоматической печати результатов в таблице. Неотъемлемой частью концепции дизайна является печатающее устройство, механически связанное с вычислительной секцией и являющееся неотъемлемой частью ее. Разностная машина № 1 — это первый законченный проект автоматической вычислительной машины. Время от времени Бэббидж менял мощность Машины. На чертеже 1830 года показана машина, выполняющая вычисления с шестнадцатью цифрами и шестью порядками разности. Для двигателя потребовалось около 25 000 деталей, поровну распределенных между вычислительной секцией и принтером. Если бы он был построен, то весил бы примерно четыре тонны и имел бы высоту около восьми футов. Работы по строительству двигателя были остановлены в 1832 году из-за спора с инженером Джозефом Клементом. Аналитическая машинаКогда строительный проект застопорился и освободился от гаек и болтов детального конструирования, Бэббидж задумал в 1834 году более амбициозную машину, позже названную Аналитической машиной, программируемую вычислительную машину общего назначения. Аналитическая машина обладает многими важными функциями, присущими современному цифровому компьютеру. Его можно было запрограммировать с помощью перфокарт – идея, заимствованная у жаккардового станка, используемого для ткачества сложных узоров на текстиле. В движке было «Хранилище», где могли храниться числа и промежуточные результаты, и отдельная «Мельница», где выполнялась арифметическая обработка. Он имел внутренний репертуар из четырех арифметических функций и мог выполнять прямое умножение и деление. Он также мог выполнять функции, для которых у нас есть современные названия: условное ветвление, зацикливание (итерация), микропрограммирование, параллельная обработка, итерация, фиксация, опрос и формирование импульса, среди прочего, хотя Бэббидж нигде не использовал эти термины. Логическая структура аналитической машины была по существу такой же, как та, которая доминировала в разработке компьютеров в эпоху электроники — отделение памяти («Хранилище») от центрального процессора («Мельница»), последовательная работа с использованием «цикл выборки-выполнения», а также средства для ввода и вывода данных и инструкций. Назвать Бэббиджа «первым компьютерным пионером» не случайно. Новая разностная машина Когда к 1840 году новаторская работа над аналитической машиной была практически завершена, Бэббидж начал рассматривать новую разностную машину. Между 1847 и 1849 гг.он завершил проектирование разностной машины № 2, улучшенной версии оригинала. Этот движок вычисляет числа длиной в тридцать одну цифру и может табулировать любой многочлен до седьмого порядка. Разностная машина № 2 и аналитическая машина имеют одинаковую конструкцию принтера — устройства вывода с замечательными характеристиками. Он не только производит распечатку на бумажном носителе в качестве контрольной копии, но также автоматически стереотипирует результаты, то есть отпечатывает результаты на мягком материале, например, на гипсе, который можно использовать в качестве формы, из которой сделанный. Устройство печатает результаты автоматически и допускает программируемое форматирование, т. е. позволяет оператору предварительно задать расположение результатов на странице. Изменяемые пользователем функции включают переменную высоту строки, переменное количество столбцов, переменные поля столбцов, автоматический перенос строк или перенос столбцов, а также оставление пустых строк через каждые несколько строк для удобства чтения. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


 Меньшие значения коэффициентов
относятся к колесам, выполненным из
стали, большие – из чугуна.
Меньшие значения коэффициентов
относятся к колесам, выполненным из
стали, большие – из чугуна. Общее название таких устройств — рейка-шестерня.
Общее название таких устройств — рейка-шестерня.
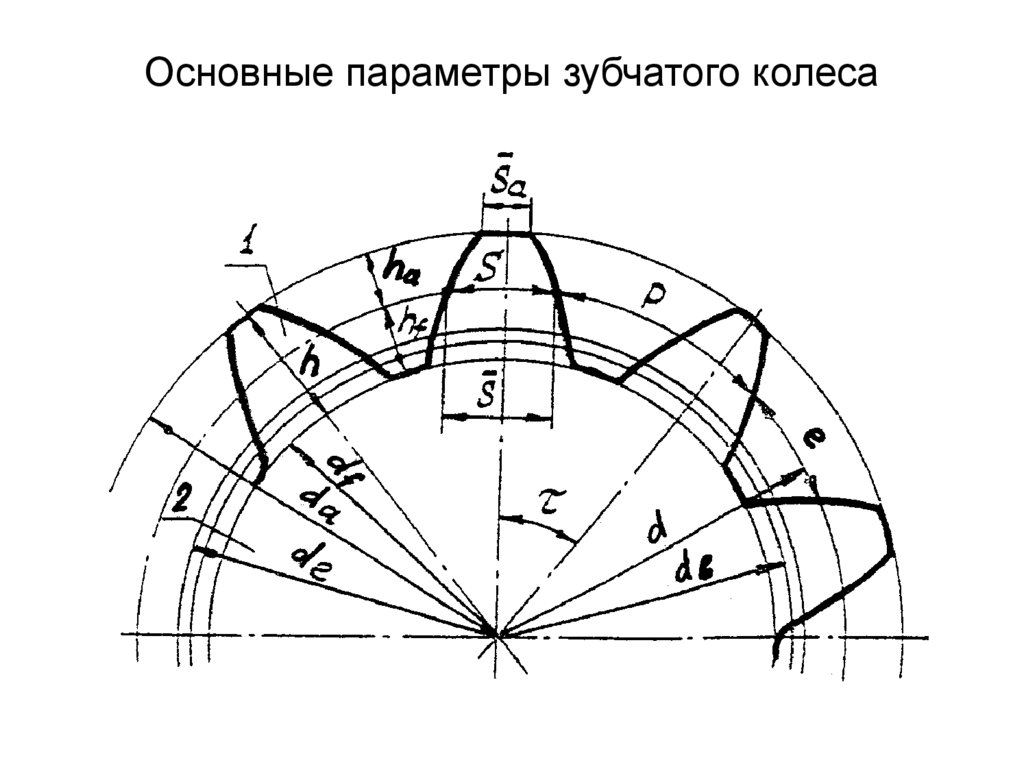 По отношению к вращающейся оси они находятся под определенным углом.
По отношению к вращающейся оси они находятся под определенным углом.