Коническая передача: Конические зубчатые передачи. Классификация, термины, определения
alexxlab | 12.02.1992 | 0 | Разное
Что такое конические передачи и как они работают?: Статьи
Что такое коническая шестерня и как она работает?
Эти зубчатые колеса представляют собой коническую передачу, которая преобразует механической энергию между двигателем и нагрузкой. Конические шестерни обычно используются в редукторах, используемых во многих промышленных процессах, таких как производственные линии и машиностроение. Также конические редукторы широко применяются в таких секторах, как горнодобывающая промышленность, авиастроение, фармацевтическая промышленность и текстильная промышленность. Потребности, для которых производятся редукторы, определяют конструкцию зубчатых колес (конические зубчатые колеса, цилиндрические зубчатые колеса, косозубые зубчатые колеса), а также их материалы (сталь, бронза, чугун).
Конические шестерни получили широкое распространение, потому что у них есть большие преимущества:
- Они занимают гораздо меньше места
- Высокая пропускная способность для передачи мощности
- Оптимальная производительность
- Простое обслуживание
- Исключает любую возможность проскальзывания
В этой статье мы сосредоточимся на том, что такое коническая зубчатая передача и как она работает. Это поможет разобраться в ее функциях и узнать, как выбрать наиболее подходящий редуктор для нашего проекта.
Это поможет разобраться в ее функциях и узнать, как выбрать наиболее подходящий редуктор для нашего проекта.
Характеристики конической передачи
Коническая зубчатая передача представляет собой две звездочки конической формы, которые служат для передачи мощности между пересекающимися осями, в пределах одного пространства. Конические шестерни можно очень похожи на гипоидные, которые также способны передавать мощность между двумя пересекающимися валами.
Форма зубов конической шестерни может быть прямой или спиральной, известной как коническая спираль. Различные типы шестерен можно классифицировать по характеристикам ширины зубьев, а также по ширине торца или центральному круговому шагу.
На следующем графике представлена номенклатура шестерен и их частей:
Виды конических передач
В зависимости от формы зубьев, существуют разные типы конических зубчатых колес, о которых мы узнаем ниже:
Коническая зубчатая передача
Благодаря сочетанию правой и левой спирали этот тип шестерни используется для передачи движения между валами, пересекающимися в одной плоскости. Поэтому они снижают скорость движения между перпендикулярными осями. Они обычно используются в трансмиссиях заднего моста для автомобилей и выделяются тем, что практически не издают звука. Основное отличие от прямозубых шестерен заключается в том, что края зубьев не параллельны оси вращения, а расположены под углом.
Поэтому они снижают скорость движения между перпендикулярными осями. Они обычно используются в трансмиссиях заднего моста для автомобилей и выделяются тем, что практически не издают звука. Основное отличие от прямозубых шестерен заключается в том, что края зубьев не параллельны оси вращения, а расположены под углом.
Коническая передача гипоидного типа
Эти придачи применяются реже и относятся типу косозубой конической шестерни, хотя разница в том, что эти устройства состоят из понижающей шестерни с несколькими зубьями и колеса с большим количеством зубцов. Конические гипоидные передачи используются в тех случаях, когда оси перпендикулярны, но располагаются в разных плоскостях.
Помимо промышленного оборудования, эти шестерни широко применяют в автомобильной промышленности. В частности, конические гипоидные передачи используют в автомобилях с задним приводом, чтобы установить соединение между приводным валом и колесами. В них используется тип масла для высокого давления.
Коническая прямозубая шестерня
Его прямые зубья расположены на поверхности зубчатого колеса. Эти шестерни применяются для передачи вращения между осями, пересекающимися в одной плоскости, как правило под углом 90 градусов. Хотя конические прямозубые шестерни используются только для снижения скорости между осями, расположенными под 90 градусов, их также можно встретить в редукторах с расположением осей 45, 60 или 70 градусов. В отличие от косозубых конических зубчатых колес, они имеют небольшую контактную поверхность.
Спирально-коническая шестерня
Особенность этих конических шестерен в том, что они работают разных плоскостях. Они выделяются своим сцеплением, так как зубья шестерни шире, чем у коронки. Благодаря этому они могут передавать очень высокие крутящие моменты без износа, поскольку зубья шестерни соединены с различными зубьями коронки.
Для чего используются конические шестерни?
Каждый тип конической передачи обычно используется для выполнения определенных операций:
Конические и цилиндрические шестерни
Эти шестерни не используются с другими типами зубчатых колес, отчасти из-за шума, который они вызывают при работе. Цилиндрические зубчатые колеса по-прежнему широко используются в часах, стоматологических и ручных дрелях или торговых автоматах. Также они все еще используются в определенных секторах, таких как грузоподъемная техника и т. д. Конические и цилиндрические шестерни обычно используются в оборудовании для консервирования и упаковки пищевых продуктов, садовом и газонном оборудовании, в токарных станках, в оборудовании для упаковки овощей, а также регулирующих клапанах.
Цилиндрические зубчатые колеса по-прежнему широко используются в часах, стоматологических и ручных дрелях или торговых автоматах. Также они все еще используются в определенных секторах, таких как грузоподъемная техника и т. д. Конические и цилиндрические шестерни обычно используются в оборудовании для консервирования и упаковки пищевых продуктов, садовом и газонном оборудовании, в токарных станках, в оборудовании для упаковки овощей, а также регулирующих клапанах.
Спиральные конические шестерни
Эти шестерни имеют измененную конструкцию зубьев. Конические шестерни используются в редукторах, когда важно изменить направление вращения валов.
В спирально-конических зубчатых колесах зубья изогнуты, чтобы обеспечить большее зацепление и больший контакт между зубьями, чем в прямолинейных конических зубчатых колесах. Это снижает вибрацию и шум, которые часто вызываются движением прямозубых конических зубчатых колес на высоких скоростях.
Спиральные конические шестерни обеспечивают высокий уровень контроля контакта с зубьями, а их конструкция допускает определенные отклонения при установке, не создавая чрезмерных нагрузок на оба конца зубьев. Поскольку их можно использовать на высоких скоростях, они часто используются в мотоциклетных и велосипедных передачах.
Поскольку их можно использовать на высоких скоростях, они часто используются в мотоциклетных и велосипедных передачах.
Гипоидные конические шестерни
Гипоидные конические шестерни используются во многих случаях, когда скорость превышает 1000 оборотов в минуту. Несмотря на это, они также эффективны для низкоскоростных устройств, требующих исключительной плавности движения или бесшумной работы.
В многоступенчатых редукторах гипоидные передачи часто используются для выходного каскада, где требуются более низкие скорости и более высокие крутящие моменты.
Чаще всего гипоидные редукторы используются в автомобильной промышленности, где они устанавливаются на задних мостах, особенно в больших грузовиках.
Углы спиралевидные расположены на шестерне, со смещением «ниже центра». Это способствует тому, что трансмиссионный вал может быть размещен в более низком пространстве, что, в свою очередь, снижает центр тяжести транспортного средства и не оказывает сильного влияния на автомобиль.
Реальные применения конических зубчатых колес
Конические зубчатые колеса используются в самых разных сферах применения, начиная от тех, что используются в горнодобывающей промышленности (колесные экскаваторы, приводы штабелеров и коллекторов, дноуглубительные работы, приводы мельниц, ленточные конвейеры и т. д.) до аэрокосмической отрасли.
Конические зубчатые колеса также используются в конусных дробилках и смесителях для песка, вилочных погрузчиках, градирнях, приводах лодок, высокоскоростной офсетной печати, упаковочных машинах для фармацевтических препаратов, производстве полиэтиленовых пакетов, автомобильных и железнодорожных трансмиссиях.
В области робототехники угловые конические зубчатые передачи используются для ограниченного пространства, в то время как в сталелитейном секторе они используются в прокатных станах.
В пищевой промышленности, конические шестерни играют решающую роль и применяются в оборудовании для упаковки и переработки пищевых продуктов, а также в оборудовании для производства консервных банок.
В каких редукторах применяются конические передачи
Мотор-редукторы серии KA
K37 K47, K57, K67, K77, K87, K97, K107, K127, K157, K167, K187
Лекция 7. Конические зубчатые передачи
Лекция 7 КОНИЧЕСКИЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ
П л а н л е к ц и и
1. Общие сведения.
2. Особенности геометрии зубьев и колес.
3. Усилия в зацеплении.
4. Условие работоспособности по контактной и изгибной прочности.
1. Общие сведения
Конические зубчатые передачи предназначены для передачи механической энергии между валами с пересекающимися осями под углом (рис. 7.1).
Наибольшее распространение имеют ортогональные ( = 90º) передачи. Конические передачи могут быть прямозубые (рис 7.2) и с круговыми зубьями.
Рис. 7.1
Рис. 7.2
1
Разновидностью конических передач являются гипоидные передачи, у которых оси вращения колес не пересекаются, а перекрещиваются.
Достоинства конических передач – возможность передачи механической энергии между валами с пересекающимися валами.
Недостатки конических передач:
меньшая нагрузочная способность. По опытным данным, она меньше нагрузочной способности передач цилиндрическими колесами до 20 %. Пересечение валов затрудняет расположение опор. Одно из конических колес (как правило, шестерню) располагают консольно, при этом увеличивается неравномерность распределения нагрузки по длине зуба, что приводит к снижению нагрузочной способности;
необходимость регулирования зацепления в передаче; большая сложность изготовления;
большие нагрузки на опоры из-за значительных осевых нагрузок.
2. Особенности геометрии зубьев и колес
Линии пересечения боковых поверхностей зубьев с делительной конической поверхностью называют линией зубьев.
Взависимости от формы линии зуба различают конические передачи
спрямыми зубьями (рис. 7.3, а), у которых линии зубьев проходят через вершину делительного конуса, с тангенциальными (рис. 7.3, б) и с круговыми зубьями (рис. 7.3, в).
Конические колеса с круговыми зубьями характеризуют наклоном зуба
всреднем сечении по ширине зубчатого венца. Угол наклона m – острый угол между касательной в данной точке к линии зуба и образующей делительного конуса.
Угол наклона m – острый угол между касательной в данной точке к линии зуба и образующей делительного конуса.
Передачи с прямыми зубьями имеют начальный линейный контакт
взацеплении, передачи с круговыми зубьями – точечный.
Рис. 7.3
2
Угол наклона для передач с прямым зубом составляет m = 0º, для передач с круговым зубом принимают m = 35º. Наличие наклона зуба повышает плавность работы, контактную прочность и прочность на изгиб, но увеличивает нагрузки на опоры и валы.
Конические колеса с круговыми зубьями обладают большой несущей способностью, работают с меньшим шумом по сравнению с прямозубыми.
Для повышения износостойкости и сопротивления зубьев заеданию смещение исходного контура выравнивают удельные скольжения в граничных точках зацепления. Шестерню и колесо выполняют с одинаковыми значениями смещений, но с разными знаками: шестерню – с положительным смещением, а колесо – с отрицательным.
Основные геометрические параметры зацепления конического коле-
са приведены на рис. 7.4. Это углы делительного конуса 1 и 2; внешнее конусное расстояние Re – длина отрезка образующей делительного конуса от его вершины до внешнего торца; Rm – среднее конусное расстояние; b – ширина венца зубчатого колеса, ограниченного двумя дополнительными конусами – внешним и внутренним.
7.4. Это углы делительного конуса 1 и 2; внешнее конусное расстояние Re – длина отрезка образующей делительного конуса от его вершины до внешнего торца; Rm – среднее конусное расстояние; b – ширина венца зубчатого колеса, ограниченного двумя дополнительными конусами – внешним и внутренним.
Пересечение делительных конусов с дополнительными конусами определяют диаметры делительных окружностей конического зубчатого колеса. Различают внешний de и средний dm делительные диаметры.
КОЛЕСО | de2 |
| |
| dm2 |
| δ2 | dm1 | de1 |
Re |
| δ1 |
|
|
|
| |
Rm |
|
|
|
b
ШЕСТЕРНЯ
Рис.
3
Передаточное число (мгновенное передаточное отношение) конической передачи вычисляют по формуле
i | de2 |
| dm2 | tg δ | 2 |
| 1 |
| Z2 | , |
|
|
|
| |||||||
| de1 |
| dm1 |
|
| tgδ1 |
| Z1 | ||
|
|
|
|
|
| |||||
где de1, de2, dm1, dm2 и 1, 2 – соответственно внешние, средние делительные диаметры и углы делительных конусов шестерни и колеса; Z1 и Z2 – число зубьев шестерни и колеса.
Для конической прямозубой передачи рекомендуют значение i до 3,15; при колесах с круговыми зубьями – до 6,3.
Осевая форма зуба. Зубья конических колес в зависимости от изменения размеров их нормальных сечений по длине выполняют трех осевых форм (рис. 7.5):
осевая форма I – нормально понижающиеся зубья (рис. 7.5, а). Вершины делительного конуса и конуса впадин совпадают, высота ножки зуба пропорциональна конусному расстоянию. Применяют для прямых зубьев,
а также ограниченно для круговых при m 2 мм и Z12 Z22 = 20–50;
осевая форма II – нормально сужающиеся зубья (рис. 7.5, б). Вершина конуса впадин расположена так, что ширина дна впадины колеса постоянна, а толщина зуба по делительному конусу пропорциональна конусному расстоянию. Эта форма обеспечивает оптимальную прочность на изгиб во всех сечениях, позволяет одним инструментом обрабатывать сразу обе поверхности зубьев колеса, что повышает производительность при нарезании зубчатых колес. Является основной для колес с круговыми зубьями.
осевая форма III – равновысокие зубья (рис. 7.5, в). Образующие конусов делительного, впадин и вершин параллельны. Высота зубьев постоянна по всей длине. Применяют для неортогональных передач с межосевым углом
40º и круговыми зубьями при Z12 Z22 60.
Рис. 7.5
4
Основные геометрические соотношения. В конических зубчатых колесах с осевыми формами I и II высота зуба, а следовательно, и модуль зацепления увеличиваются от внутреннего к внешнему дополнительному конусу (рис. 7.5, а, б). Для удобства измерения размеры конических колес принято определять по внешнему торцу зуба.
Максимальный модуль зубьев – внешний окружной модуль mte получают на внешнем торце колеса.
Ниже приведены основные геометрические соотношения для конических зубчатых передач (рис. 7.4).
Внешние делительные диаметры шестерни и колеса:
de1 = mteZ1, de2 = mteZ2.
Внешнее конусное расстояние
Re (0,5de1)2 (0,5de2 )2 0,5de1 1 i2 .
Ширина зубчатого венца: b = KbeRe. Для большинства конических передач коэффициент ширины зубчатого венца Kbe = 0,285. Тогда
b = 0,285 0,5de1 1 i2 = 0,143de1 1 i2 .
Среднее конусное расстояние
Rm = Re – 0,5d = Re – 0,5 0,285Re = 0,857Re.
Из условия подобия (рис. 7.4) следует
de1 dm1 . Re Rm
Тогда средний делительный диаметр шестерни
dm1 de1 Rm 0,857de1.
Re
Модуль окружной в среднем сечении mtm = 0,857mte.
Модуль нормальный в среднем сечении для кругового зуба ( m = 35º)
mn = mtm cos m ≈ 0,702mte.
Углы делительных конусов
tg 1 = | Z1 |
| 1 | , | 2 = 90º – 1. | |
Z2 |
| i | ||||
|
|
|
|
| ||
5
Для конических зубчатых колес с прямыми зубьями в качестве расчетного принимают внешний окружной модуль mte, для конических зубчатых колес с круговыми зубьями средний нормальный модуль mn в середине зубчатого венца.
Одной и той же зуборезной головкой можно нарезать конические колеса с модулями, изменяющимися в некотором непрерывном диапазоне. Поэтому допускается использовать нестандартные значения модуля.
Эквивалентное колесо. Для прямозубой передачи профили зубьев конического колеса на среднем дополнительном конусе близки к профилям зубьев цилиндрического прямозубого колеса с делительным эквивалентным диаметром dv.
Дополнив развертку среднего дополнительного конуса на плоскость до полной окружности, получим эквивалентное цилиндрическое колесо с числом зубьев Zv и делительным диаметром
dv = mnZv.
Рассмотрим связь между делительными эквивалентным диаметром dv и средним dm:
|
| dv = |
| dm |
| mnZ | . | |||
|
| cosδ |
| |||||||
|
|
|
|
| cosδ | |||||
Из равенства mnZv | = |
| mnZ |
| следует | зависимость для определения | ||||
|
|
| ||||||||
|
|
| cos δ |
|
|
|
|
| ||
эквивалентного числа зубьев |
|
|
|
|
|
|
|
|
| |
|
|
|
|
| Zv = |
| Z | , | ||
|
|
|
|
|
| |||||
|
|
|
|
| cos δ | |||||
т. е. фактическое коническое прямозубое колесо с числом зубьев Z в прочностных расчетах можно заменить цилиндрическим с эквивалентным числом
е. фактическое коническое прямозубое колесо с числом зубьев Z в прочностных расчетах можно заменить цилиндрическим с эквивалентным числом
зубьев Zv.
Для передачи с круговыми зубьями профили зубьев конического колеса в нормальном сечении близки к профилям зубьев эквивалентного цилиндрического прямозубого колеса. Эквивалентное число зубьев Zvn получают двойным приведением – конического колеса к цилиндрическому и кругового зуба к прямому зубу:
Z
Zvn = cos δ cos3βm .
6
3.Усилия в зацеплении
Вконической передаче местом приложения силы Fn (рис. 7.6), действующей перпендикулярно поверхности зуба, считают сечение на середине ширины зубчатого венца.
Силу Fn раскладывают на составляющие: Ft, Fr и Fa. Окружная сила Ft1 на шестерне
Ft1 = 2T1 103 , dm1
где T1 – вращающий момент, Н м; dm1 – средний делительный диаметр, мм.
В прямозубой передаче для определения составляющих запишем промежуточное выражение (αw = 20º угол зацепления)
R = Fttg αw.
Радиальная сила на шестерне
Fr1 = Rcos 1 = Fttg αw cos 1.
Осевая сила на шестерне
| Fa1 = Rsin 1 = Fttg αw sin 1. | ||
|
|
| ω2 |
|
| Т2 |
|
|
| Ft2 |
|
|
| Fr2 | Fa2 |
|
|
| |
|
| 1 |
|
| Fr1 |
| Ft1 |
|
| αw | |
Т1 |
| 1 | |
|
| Fa1 | |
ω1 |
|
| |
|
|
| |
Fn
Рис. 7.6
7.6
7
Силы на колесе (рис. 7.6):
Fr2 = Fa1, Fa2 = Fr1.
Впередаче с круговым зубом во избежание заклинивания зубьев при значительных зазорах в подшипниках необходимо обеспечить направление
осевой силы Fa1 на ведущей шестерне к основанию делительного конуса. Для этого направление вращения ведущей шестерни (если смотреть со стороны вершины делительного конуса) и направление наклона зубьев должны совпадать. Шестерня вращается против часовой стрелки, т. е. влево, и зуб шестерни левый.
Впередаче с круговым зубом при соблюдении этого условия: радиальная сила на шестерне
Fr1 = | Ft (tg αw cosδ1 sinβm sin δ1) | ; |
| ||
| cosβm | |
oсевая сила на шестерне
Fa1 = | Ft (tg αw sin δ1 sinβm cosδ1) | . |
| ||
| cosβm | |
Такие же знаки в формулах будут при вращении по часовой стрелкe ведущей шестерни с правым зубом.
Силы на колесе:
Fr2 = Fa1, Fa2 = Fr1.
4.Условие работоспособности по контактной
иизгибной прочности
Прочностной расчет конической передачи основан на допущении, что несущая способность зубьев конического колеса такая же, как у эквивалентного цилиндрического с той же длиной b зуба и профилем, соответствующим среднему дополнительному конусу (среднему сечению зуба). Прочность зубьев определяется зависимостями
H [ ]H, | F [ ]F, |
где H – контактное напряжение; F – напряжение изгиба; [ ]H и [ ]F – соответствующие допускаемые напряжения.
Для проверочного расчета вывод формулы в параметрах эквивалентной цилиндрической прямозубой передачи по среднему дополнительному конусу (см. рис. 7.4) имеет вид
рис. 7.4) имеет вид
8
H = ZмZHZ |
| KH Ft (iv 1) | 1 |
| , | (7.1) | |||
bdv1 |
| iv |
| H | |||||
|
|
|
|
|
|
| |||
где iv – передаточное число эквивалентной | цилиндрической | передачи; | |||||||
Н – коэффициент, учитывающий влияние на несущую способность передачи вида конических колес.
Передаточное число эквивалентной цилиндрической передачи
i | dv2 |
| dm2 |
| cos δ1 |
| i cos δ1 | . |
|
|
|
| |||||
v | dv1 |
| cos δ2 |
| dm1 |
| cos δ2 | |
|
|
|
| |||||
Учитывая, что cos 1 = sin 2, a tg 2 = i, получим
iv i sin δ2 i2. cos δ2
Диаметр эквивалентной цилиндрической шестерни
Заменяя функцию косинуса функцией тангенса:
cos δ1 |
| 1 | ||
|
| |||
|
| |||
1 tg2δ | ||||
|
| |||
|
| 1 | ||
и имея в виду, что tg δ1 1i , а dm1 0,857de1 , запишем
dv1 dm1 . cos δ1
cos δ1
dv1 dm1cosδ1 dm1 1 tg2δ1 dm1 (i2 1) / i2 0,857de1 i2 1/ i.
|
|
|
|
|
|
| 2T 103 |
|
|
|
|
| ||
|
|
|
| Ft1 | , b 0,143de1 | 1 i | 2 |
| ||||||
Подставив в формулу (7.1) значения iv, dv1, |
| 1 |
| , | ||||||||||
0,857de1 |
| |||||||||||||
с учетом условия прочности σH σH и рекомендуемых числовых значений Zм, | ||||||||||||||
ZH и Z , получим формулу для проверочного расчета стальных конических | ||||||||||||||
зубчатых передач |
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
| |||||
σH 6,7 104 | KH T1 |
|
| σ |
| . |
| (7.2) | ||||||
|
|
|
| |||||||||||
|
| d 3 i | H |
|
|
|
| H |
|
|
|
|
|
|
|
| e1 |
|
|
|
|
|
|
|
|
|
|
| |
Для прямозубых конических передач H 0,85. Для передач с круговыми зубьями значения H зависят от твердости зубчатых колес пары и передаточного числа ( H 1).
9
Коэффициент нагрузки для конических передач
KH KαKHβKHv.
Значения коэффициента Kα назначают так же, как и для цилиндрических зубчатых передач.
Коэффициент KH учитывает неравномерность распределения нагрузки по длине контактных линий.
В конических передачах шестерню располагают консольно, при этом вследствие меньшей жесткости консольного вала и деформаций опор повышена неравномерность распределения нагрузки по длине контактных линий в зацеплении. По этой причине конические колеса по сравнению с цилиндрическими работают с бóльшим шумом. С целью повышения жесткости опор валы устанавливают на конических роликовых подшипниках.
Для конических колес с прямыми зубьями
KHβ KH0 β ;
с круговыми зубьями, при условии KHβ 1, 2,
K Hβ K H0 β ,
где KH0 β коэффициент, выбираемый по таблицам или графикам для цилиндрических зубчатых передач в зависимости от значения коэффициента
относительной ширины ψbd b , твердости зубчатых колес и расположе- de1
ния передачи относительно опор. Для конических передач
ψbd 0,166i2 1.
Значение коэффициента KHv внутренней динамической нагрузки для передач с круговыми зубьями принимают таким же, как и для цилиндрических косозубых передач. Для конических прямозубых передач KHv назначают так же, как для цилиндрических прямозубых, но с условным понижением степени точности на единицу (например, для фактической степени точности 7 значение KHv принимают по степени точности 8).
Решив зависимость (7.2) относительно de, получим формулу проектировочного расчета для внешнего делительного диаметра шестерни стальных конических зубчатых передач
de1 1650 |
| KH T1 | ||
3 |
|
| . | |
i σ 2 | H | |||
|
| H |
|
|
10
Соседние файлы в папке Конспекты лекций
- #
17.
 03.2015981.3 Кб210Лекция 25. Основные принципы и правила конструирования.pdf
03.2015981.3 Кб210Лекция 25. Основные принципы и правила конструирования.pdf - #
17.03.2015256.4 Кб229Лекция 3. Основные требования к деталям.pdf
- #
17.03.2015397.57 Кб250Лекция 4. Механические передачи.pdf
- #
17.03.2015905.05 Кб660Лекция 5. Зубчатые передачи.pdf
- #
17.03.2015421.9 Кб292Лекция 6. Расчеты зубчатых передач.pdf
- #
17.03.2015526.36 Кб452Лекция 7. Конические зубчатые передачи.pdf
- #
17.03.2015567.73 Кб348Лекция 8. Червячные передачи.pdf
- #
17.03.20151.23 Mб397Лекция 9. Ременные передачи.pdf
В чем разница между червячной, конической, косозубой и прямозубой передачей?
Зубчатая передача — это наиболее важная часть многих механизмов и двигателей. Их наличие помогает увеличить выходной крутящий момент за счет обеспечения необходимого передаточного числа и позволяет регулировать направление движения выходного вала, например, приводного вала автомобиля. Ниже перечислены основные типы передач (шестерен) и рассмотрены их отличия друг от друга.
Их наличие помогает увеличить выходной крутящий момент за счет обеспечения необходимого передаточного числа и позволяет регулировать направление движения выходного вала, например, приводного вала автомобиля. Ниже перечислены основные типы передач (шестерен) и рассмотрены их отличия друг от друга.
- Прямозубая передача
Косозубые передачи позволяют добиться плавной работы благодаря постоянному контакту расположенных под углом зубьев.
Зубчатые колеса прямозубых передач монтируются последовательно на параллельных валах и позволяют достичь больших значений передаточного отношения.
Наиболее распространены прямозубые передачи, которые используются для обеспечения больших передаточных отношений. Зубья колес в таких передачах расположены под прямым углом, а сами зубчатые колеса установлены на параллельных валах. Прямозубые передачи используются в стиральных машинах, шуруповертах, заводных будильниках и прочих устройствах. Эти передачи довольно шумны вследствие механического столкновения зубчатых колес в момент вхождения в зацепление. Каждое зацепление вызывает громкий шум и вибрацию, именно поэтому прямозубые передачи не используются в сложной технике, такой как автомобили. Обычно передаточное число таких механизмов варьируется от 1:1 до 6:1.
Эти передачи довольно шумны вследствие механического столкновения зубчатых колес в момент вхождения в зацепление. Каждое зацепление вызывает громкий шум и вибрацию, именно поэтому прямозубые передачи не используются в сложной технике, такой как автомобили. Обычно передаточное число таких механизмов варьируется от 1:1 до 6:1.
- Косозубая передача
На вышеприведенном рисунке изображены два различных типа конических передач: прямозубая и спиральнозубая.
Косозубые передачи работают более плавно и тихо в сравнении с прямозубыми благодаря особому типу контакта зубьев. Зубья в данном случае расположены под углом к поверхности шестерни. Когда два зуба шестерен входят в зацепление, контакт между ними устанавливается постепенно, начиная с одного конца зуба. Контакт поддерживается на протяжении всего цикла зацепления. Зубья обычно расположены под углом от 15 до 30 градусов. Осевая нагрузка напрямую зависит от величины угла наклона зубьев. Косозубые передачи наиболее часто применяются в коробках передач. Они генерируют достаточно большую нагрузку, для восприятия которой используются упорные подшипники. Также косозубые передачи могут использоваться для передачи крутящего момента в случае, если зубчатые колеса устанавливаются под углом 90 градусов на перпендикулярных валах. Передаточное число обычно варьируется от 3:2 до 10:1.
Они генерируют достаточно большую нагрузку, для восприятия которой используются упорные подшипники. Также косозубые передачи могут использоваться для передачи крутящего момента в случае, если зубчатые колеса устанавливаются под углом 90 градусов на перпендикулярных валах. Передаточное число обычно варьируется от 3:2 до 10:1.
- Конические передачи
Конические передачи обычно используются для передачи вращения вала в другом направлении. Зубья конической передачи могут быть прямой, спиральной или гипоидной формы. Шестерни с прямыми зубьями имеют те же характеристики, что и шестерни прямой передачи, и также подвержены высоким нагрузкам в момент зацепления. Прямозубые конические передачи, как и прямозубые цилиндрические передачи, имеют передаточные числа от 3:2 до 5:1.
В данном двигателе используется редуктор, состоящий из гипоидных и спиральнозубых конических зубчатых колес.
На вышеприведенном рисунке показан вид двигателя в разрезе, иллюстрирующий работу спиральнозубой конической передачи.
Спиральнозубые шестерни функционально не отличаются от косозубых шестерен. Они обеспечивают низкие уровни шумов и вибраций в сравнении с прямозубыми шестернями. Спиральнозубые шестерни, имеющие зубья с правым наклоном, используются для вращения по часовой стрелке относительно оси. Шестерни с левым наклоном используются для вращения против часовой стрелки относительно оси. Передаточное число таких передач варьируется от 3:2 до 4:1.
В гипоидной передаче, изображенной выше, большое зубчатое колесо называется ведомым, а меньшее — ведущим.
Гипоидная передача является разновидностью спиральной передачи, в которой зубчатые колеса имеет не коническую, а гиперболоидную форму. В гипоидной передаче ведущее зубчатое колесо располагается эксцентрично относительно ведомого. Это позволяет использовать ведущую шестерню большего диаметра и обеспечивает большую площадь пятна контакта.
Ведущее и ведомое колеса всегда вращаются в противоположные стороны, а спиральный угол зубьев ведущего колеса обычно больше угла зубьев ведомого.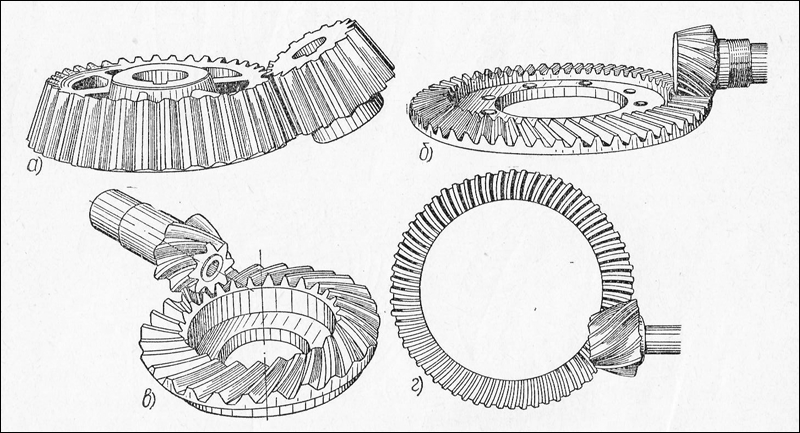 Благодаря большему передаточного числу, которое варьируется от 10:1 до 200:1, гипоидная передача широко используется в силовых трансмиссиях.
Благодаря большему передаточного числу, которое варьируется от 10:1 до 200:1, гипоидная передача широко используется в силовых трансмиссиях.
- Червячная передача
На рисунке изображена червячная передача в разрезе, что позволяет понять не только ее устройство, но и принцип работы. Особенности конструкции червячной передачи исключают ее вращение в обратном направлении.
Червячная передача используется в редукторах с большим передаточным числом, которое варьируется от 5:1 до 300:1. Пара конструктивно выполнена таким образом, чтобы червяк был в состоянии крутить шестерню, но шестерня не могла приводить в движение червяк. Угол подъема витка червяка является пологим, в результате чего шестерня удерживается на месте благодаря трению, возникающему при зацеплении. Червячные передачи используются в таком оборудовании как конвейеры, где блокировка обратного движения выполняет функцию тормоза или аварийного останова.
конические шестерни | KHK Производитель зубчатых колес
- ТОП >
- Конические шестерни
Что такое конические шестерни?
Стандартное определение конического зубчатого колеса — это коническое зубчатое колесо, передающее мощность между двумя пересекающимися осями.
Глядя на конические зубчатые колеса по различиям в углах винтовой линии, их можно в целом разделить на прямозубые конические зубчатые колеса, которые не имеют углов винтовой линии, и спирально-конические зубчатые колеса (включая нулевые конические зубчатые колеса), которые имеют углы винтовой линии. Однако из-за того, что производство прямозубых зубчатых колес становится редкостью, а также из-за того, что зубья прямозубых зубчатых колес не могут быть отполированы, что делает спирально-конические зубчатые колеса, которые можно полировать, лучшими с точки зрения снижения шума, спирально-конические зубчатые колеса, вероятно, станут чаще встречается в будущем.
Конические зубчатые колеса обычно можно классифицировать по их методам изготовления, а именно по методу Глисона и методу Клингельнберга, каждый из которых имеет различную форму зубьев, и в настоящее время в большинстве зубчатых колес используется метод Глисона. Кстати, все шестерни, производимые KHK, используют метод Глисона.
Кроме того, зубчатые колеса различаются по шагу зубьев (модулей и т. д.), полировке или нет, а также используемым материалам. Например, в случае материалов, S45C из машинной конструкционной углеродистой стали, SCM415 из машинной конструкционной легированной стали и MC9.01 из инженерного пластика и т. д. часто используются, а дюракон и т. д. используются для формованных из пластика деталей.
Пожалуйста, укажите здесь номер детали для цены и чертежа шестерни
ВНИМАНИЕ: Использование чертежей САПР
Профиль зуба, показанный на чертеже САПР, отличается от фактического профиля зубчатого колеса.
Также обратите внимание, что детали любой фаски, скругления или канавки с прорезями на чертеже САПР могут отличаться от истинных значений или формы на фактическом изделии.
Техническая информация о конических зубчатых колесах
С помощью этих технических данных вы можете просмотреть исчерпывающую информацию о зубчатых колесах KHK, такую как их характеристики, а также советы и предупреждения при их выборе и использовании.
MHP
Гипоидные передачи с высоким рационом
Модуль: 1-1,5
Отношение скорости: 15-60
Материал: SCM415
Установка: карбурбализация
Зуб закаленные, закаленные и отшлифованные шестерни, способные к быстрому замедлению.
Нажмите здесь, чтобы выбрать шестерни для сочинения
MBSG
Спиральные спиральные шестерни с конией
Модуль: 2 – 4
Соотношение скорости: 2
Материал: SCM415
. Утверждение: Карбуризация
Зуб Шестерни, которые были закалены и отшлифованы, обладают превосходной точностью, прочностью и стойкостью к истиранию. Возможны вторичные операции, кроме зубов.
Нажмите здесь, чтобы выбрать конические шестерни
SBSG
Шлифованные спирально-конические зубчатые колеса
Модуль: 2–4
Передаточное число: 1,5–3
Материал: S45C
Закалка: индукционная закалка зубьев шестерни
Покрытие зубьев: шлифованные зубья
Сорт: JIS 2
Закаленные и отшлифованные шестерни с хорошим балансом точности, износостойкости и стоимости.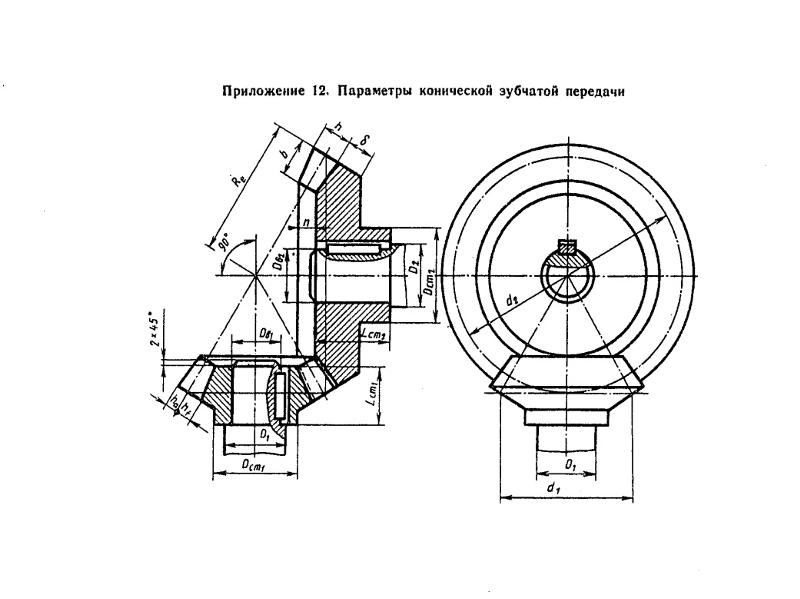 Возможны вторичные операции, кроме зубов.
Возможны вторичные операции, кроме зубов.
Нажмите здесь, чтобы выбрать конические шестерни
MBSA / MBSB
Конические спиральные шестерни с чистовым отверстием
Модуль: 2 – 6
Передаточное число: 1,5 – 3
Материал: SCM415
Закалка: Полное науглероживание
Покрытие зуба: Обрезной (нешлифованный) износостойкость. Можно использовать в готовом виде.
Нажмите здесь, чтобы выбрать конические шестерни
SBS
Спиральные конические шестерни
Модуль: 1 – 5
Передаточное число: 1,5 – 4
Материал: S45C
Закалка: Индукционная закалка зубьев шестерни
Покрытие зуба : Обработанное (нешлифованное)
Сорт : JIS 4
Закаленные шестерни с превосходной износостойкостью. Возможны вторичные операции, кроме зубов.
Нажмите здесь, чтобы выбрать конические шестерни
SB / SBY
Стальные конические шестерни
Модуль: 1 – 8
Передаточное число: 1,5 – 4
Материал: S45C
Закалка: нет
Марка: JIS 3
Многие модельные ряды доступны по низкой цене. Зубья могут быть дополнительно закалены.
Зубья могут быть дополнительно закалены.
Нажмите здесь, чтобы выбрать конические шестерни
SB
Стальные конические шестерни и валы-шестерни
Модуль: 1,5–3
Передаточное число: 5
Материал: S45C
Закалка: нет Класс: JIS 3
У нас есть много клиентов, которые используют его в качестве товара с прямым коническим зубчатым колесом.
Щелкните здесь, чтобы выбрать конические шестерни
SUB
Конические шестерни из нержавеющей стали
Модуль: 1,5–3
Передаточное число: 1,5–3
Материал : SUS303
Закалка : Нет
Покрытие зуба : Обработанный (нешлифованный)
Сорт : JIS 3
Шестерни из нержавеющей стали с защитой от ржавчины.
Нажмите здесь, чтобы выбрать конические шестерни
PB
Пластиковые конические шестерни
Модуль: 1 – 3
Передаточное отношение: 1,5 – 3
Материал: MC901
Закалка: нет : Эквивалент JIS 4
Нейлоновые шестерни можно использовать без смазки.
Нажмите здесь, чтобы выбрать конические шестерни
DB
Литые конические шестерни
Модуль: 0,5 – 1
Передаточное число: 2
Материал: Duracon (R) (M90-44) Недорогие шестерни, изготовленные методом литья под давлением. Подходит для легких нагрузок.
Нажмите здесь, чтобы выбрать конические шестерни
BB
Втулки из спеченного металла
Nissei KSP
Конические шестерни со шлифованной спиралью
Модуль: 1,5–6
Передаточное отношение : 1 – 2
Материал : SCM415
Закалка : Науглероживание
Обработка зубьев : Шлифованные зубья
Сорт : JIS 0
Зубчатые колеса, которые были закалены и отшлифованы, имеют нулевой класс точности, прочности, стойкости к истиранию и бесшумности. Вторичные операции могут быть даны кроме зубов.
Нажмите здесь, чтобы выбрать конические шестерни
Спиральные и прямые конические шестерни для конструкторов машин
Эта статья воспроизводится с разрешения.
Масао Кубота, Хагурума Нюмон, Токио: Ohmsha, Ltd., 1963.
Зубчатые колеса, используемые при пересечении двух валов, основаны на двух конусах, находящихся в контакте качения с вершинами, сходящимися в точке пересечения двух осей и имеющими зубья на одинаковом расстоянии от вершин. Это так называемые конические шестерни. Вышеупомянутые конусы называются делительными конусами, а их половинные углы вершины называются углами делительного конуса.
Рисунок 8.1 Углы наклона конических зубчатых колес
На рисунке 8.1 предположим, что угол наклона вала равен Σ , соответствующее количество зубьев z i ( i = 1, 2 ), угловая скорость ω i и угол делительного конуса (или просто угол наклона) ɣ 0i , то рассмотрим скорость вращения точки на common contact line of the cones at distance K from the apex :
ω 1 K sin ɣ 01 = ω 2 K sin ɣ 02
ɣ 01 + ɣ 02 = Σ, angular speed ratio ω 1 /ω 2 = z 2 / z 1
Therefore,
tan ɣ 01 = sin Σ / [( z 2 / z 1 ) + cos Σ ] , tan ɣ 02 = sin Σ / [( z 1 / z 2 ) + cos Σ ]
Normally, Σ = 90° so that :
tan ɣ 01 = z 1 / z 2 , tan ɣ 02 = z 2 / z 1 and ɣ 01 + ɣ 02 = 90°
In particular, when ɣ 01 + ɣ 02 = 45° , коническая шестерня называется угловой шестерней. Кроме того, когда Σ ≠ 90°, как показано на рисунке 8.2, называется угловой передачей.
Кроме того, когда Σ ≠ 90°, как показано на рисунке 8.2, называется угловой передачей.
Рисунок 8.2 Угловая шестерня
Когда большая шестерня имеет угол наклона 90°, она называется коронной шестерней. Он эквивалентен зубчатой рейке в прямозубом зубчатом колесе и становится основой для формы зубьев и нарезки зубьев.
Конические зубчатые колеса делятся на конические зубчатые колеса прямого и спирально-конического зубчатого колеса в зависимости от линий их зубьев на делительном конусе. Конические зубчатые колеса и торцевые зубчатые колеса также можно рассматривать как принадлежащие к группе спирально-конических зубчатых колес. Однако, поскольку они не основаны на делительном конусе и основаны на специальном методе нарезания зубьев, они обсуждаются отдельно от спирально-конических зубчатых колес.
Эффективность конических зубчатых колес
Поскольку большинство конических зубчатых колес представляют собой шестерни с пересекающимися валами, их зацепление почти всегда представляет собой контакт качения, поэтому их общий КПД высок, обычно 98-99%.
Прямые конические шестерни
Конические шестерни представляют собой конические шестерни, которые передают движение между двумя пересекающимися валами. Прямые конические шестерни – самые простые из этих конических шестерен, их зубья прямые и направлены к вершине конуса. Их легче изготовить, чем спирально-конические шестерни, и они не создают тяги внутрь (в отрицательном направлении), что упрощает конструкцию подшипника. С другой стороны, у них есть недостаток, заключающийся в том, что они не могут стачивать зубы после термической обработки.
Прямые конические зубчатые колеса делятся на две группы: профильные со смещением типа Глисона и непрофильные со смещением, называемые стандартным типом или типом Клингельнберга. В целом, в настоящее время наиболее широко используется система Глисона. Кроме того, использование компанией Gleason метода коронки зубьев, называемого шестернями Coniflex, позволяет производить шестерни, которые допускают незначительные ошибки при сборке или смещение из-за нагрузки, и повышает безопасность за счет устранения концентрации напряжений на краях зубьев.
Прямые конические зубчатые колеса обычно используются при относительно низких скоростях (окружная скорость менее 2 м/с). Их часто не используют, когда необходимо передать большие усилия. Как правило, они используются в станочном оборудовании, печатных машинах и дифференциалах.
Спиральные конические шестерни
Конические шестерни представляют собой конические шестерни, которые передают движение между двумя пересекающимися валами. Спирально-конические зубчатые колеса – это один из типов, в которых зубья изогнуты по спирали. В отличие от прямых конических шестерен, эти зубья контактируют друг с другом постепенно и плавно от одного конца к другому. Зацепление зубьев осуществляется, как и в прямозубых конических передачах, контактами качения на поверхности делительного конуса.
Что касается конструкции и нарезания зубьев, то, как и в прямозубых конических зубчатых колесах, тип Глисона наиболее широко используется в спирально-конических зубчатых колесах. Тем не менее, в Германии тип Клингельнберга с одинаковой глубиной зуба на носке и пятке все еще широко используется.
Преимущество спирально-конических зубчатых колес состоит в том, что они могут шлифовать зубья после термической обработки, что позволяет производить высокоточные зубчатые колеса. Кроме того, поскольку коэффициент контакта зубьев выше, чем у прямых конических шестерен, шум и вибрация снижаются, и они лучше подходят для высокоскоростных приложений. Например, шум и вибрация заметно снижаются при высокой рабочей скорости (более 10 м/с). Они также прочнее и долговечнее, чем прямые конические шестерни, что позволяет работать при более высоких нагрузках. С другой стороны, сложнее изготовить
спирально-конических зубчатых колес и требует внимания в отношении изменения направления тяги в зависимости от угла поворота и закручивания. Это некоторые из недостатков.
При использовании правая спираль сопрягается с левой спиралью. Что касается их применения, они часто используются в автомобильных редукторах и станках.
Форма зубьев конических шестерен
Эта статья воспроизводится с разрешения.
Масао Кубота, Хагурума Нюмон, Токио: Ohmsha, Ltd., 1963.
Спирально-конические шестерни представляют собой шестерни, зубья которых расположены на делительном конусе по изогнутым линиям, что обеспечивает бесшумную работу даже на высоких скоростях. В частности, когда окружная скорость превышает 5 м/с, трудно добиться бесшумной работы, и использование спирально-конических зубчатых колес считается желательным.
(a) Прямая / (b) Дуга окружности / (c) Эвольвента
Рисунок 8.13 Типы спирально-конических зубчатых колес (линии зубьев коронной шестерни)
Линия формы зуба определяется на основе стандартной формы зуба коронной шестерни ( пересечение поверхности коронки зуба и поверхности шага). Если это рассматривать как логарифмическую закрученную линию, угол наклона формы зуба будет постоянным независимо от радиуса, что является наиболее желательным с точки зрения зацепления зубьев. Однако для нарезки зуба это не удобно и в действительности используются несколько кривых, более подходящих для нарезки. Как показано на рис. 8.13, это наклонные прямые (форма Райнекера) [их иногда называют косозубыми коническими зубчатыми колесами], дуги окружности (форма Глисона) и эвольвенты (форма Клингельнберга). Кроме них, существуют трохоидные (форма Эрликона, форма Фиата) и спираль Архимеда и др.
Как показано на рис. 8.13, это наклонные прямые (форма Райнекера) [их иногда называют косозубыми коническими зубчатыми колесами], дуги окружности (форма Глисона) и эвольвенты (форма Клингельнберга). Кроме них, существуют трохоидные (форма Эрликона, форма Фиата) и спираль Архимеда и др.
В частности, как показано на рисунке 8.14, когда форма зуба представляет собой дугу окружности, а в средней точке формы зуба угол наклона равен 0, это называется передачей Зерола. В то время как нагрузка на зуб Zerol такая же, как и на прямой зуб, зацепление более плавное. Все зубчатые колеса с дугой окружности, кроме зубчатых колес Zerol, иногда называют косозубыми коническими зубчатыми колесами.
Рисунок 8.14 Коническая шестерня Zerol
В точке на линии зуба, где она пересекает образующую делительного конуса под углом β, если начерчено перпендикулярное поперечное сечение, то эквивалентное число зубьев цилиндрической шестерни z vi is
z vi = z i / cos ϓ 0i cos 3 β
and the normal to tooth surface pressure angle α n относится к углу давления на сферическую поверхность α s как
tan α s = tan α n / cos β
конец зубьев, если зубья изгибаются по часовой стрелке, это правая спираль, а если зубцы изгибаются против часовой стрелки, это левая спираль. Для сопрягаемых конических зубчатых колес, если одно зубчатое колесо является правоспиральным, то противоположное зубчатое колесо является левоспиральным.
Для сопрягаемых конических зубчатых колес, если одно зубчатое колесо является правоспиральным, то противоположное зубчатое колесо является левоспиральным.
Коническая шестерня
Эта статья воспроизводится с разрешения.
Masao Kubota, Haguruma Nyumon, Tokyo: Ohmsha, Ltd., 1963.
Комбинация винтовых реек, которые перемещаются прямолинейно с помощью зубчатых колес, или конических зубчатых колес, направляемых через винтовую рейку, называется коническим зубчатым колесом . Каждая шестерня считается похожей на косозубую шестерню на рис. 8.27, изменения модификации дополнения которой ориентированы в осевом направлении. Он образует точечный контакт там, где пересекаются контактные линии промежуточной рейки и каждой шестерни. Конические зубчатые колеса иногда используются вместо конических зубчатых колес, когда нагрузка невелика, потому что их можно нарезать с помощью модифицированных червячных станков или зуборезных станков, или путем прикрепления вспомогательного оборудования. В случае параллельных осей она становится конической сдвинутой шестерней (см. стр.93) и делает точечный контакт.
В случае параллельных осей она становится конической сдвинутой шестерней (см. стр.93) и делает точечный контакт.
Рис. 8.27 Коническая шестерня
1) Обрезка кромки зуба делительным цилиндром
Сборка и контакт зубьев конической шестерни
Важные моменты для сборки конической шестерни
Важные моменты для сборки конической шестерни:
- 4 Люфт
Люфт необходим, чтобы компенсировать производственную ошибку и сохранить толщину масляной пленки на поверхности зубчатого колеса.
- Зубчатый контакт
- На контакт зубьев конической шестерни влияют погрешность угла вала, погрешность оси вала и погрешность монтажного расстояния.
- Регулировка люфта также изменяет контакт зубьев, поскольку изменяется монтажное расстояние.
Допуск коробки передач для конической передачи
| 1 | Допуск угла вала | +2′ – 0 |
|---|---|---|
| 2 | Несоосность вала | ±0,025 |
| 3 | Монтажное расстояние | ±0,025 |
| 4 | Биение опорной поверхности крепления | 0,025 или менее |
| 5 | Установить биение цилиндрической поверхности | 0,025 или менее |
Показанные выше допуски являются общепринятыми ожидаемыми значениями и могут рассматриваться как ориентировочные.
Технические условия для зубчатых контактов
- Пик
- Низ
- Внутренний конец
- Внешний конец
- Направление следа зуба
- Глубина зуба
Контакт зубьев конической шестерни 1
Предотвращение сильного краевого контакта вдоль направления следа зуба в пределах 10 % длины следа зуба от обоих краев следа зуба
- Внутренний конец
- Внешний конец
- Прочный краевой контакт NG
- Прочный краевой контакт NG
Контакт с зубьями конической шестерни 2
Предотвращение сильного контакта по глубине зуба вблизи вершины или основания зуба шестерни
- Внутренний конец
- Внешний конец
- Сильный пиковый контакт NG
- Прочный нижний контакт NG
Контакт зуба конической шестерни 3
Контакт зуба должен включать центр рабочей глубины
- Внутренний конец
- Внешний конец
- Лучше расположить ближе к внутреннему концу
Ошибка сборки и контакт зубьев шестерни
- Ошибка сборки шестерни появляется на контакте зубьев
- Предпочтителен контакт зубьев вблизи внутреннего конца, как показано справа
- Влияние ошибки сборки на контакт зубьев показано ниже
- Внутренний конец
- Внешний конец
Зубчатый контакт с ошибкой монтажного расстояния
Слишком короткое монтажное расстояние
Слишком большое монтажное расстояние
При регулировке люфта с монтажным расстоянием контакт зубьев ухудшается, если перемещать только одну шестерню
Контакт зуба с ошибкой смещения (перекос вала)
При наличии ошибки оси вала (ошибка смещения или перекос вала) контакт зуба становится диагональным
Контакт зуба с ошибкой угла вала
Слишком большой угол наклона вала
Слишком маленький угол вала
Контакт зубьев при приложении нагрузки
Поскольку каждая шестерня имеет угол давления, при приложении нагрузки действует сила, исходящая от другой шестерни. Затем эта сила упруго деформирует вал, коробку передач, подшипник и, в конечном счете, ухудшает контакт зубьев при приложении нагрузки.
Затем эта сила упруго деформирует вал, коробку передач, подшипник и, в конечном счете, ухудшает контакт зубьев при приложении нагрузки.
Изменение контакта зубьев в зависимости от нагрузки 1
Без нагрузки
1. Обеспечьте контакт зубьев ближе к внутренней стороне, когда нет нагрузки
С нагрузкой
2. При приложении нагрузки контакт зубьев смещается к внешнему концу из-за изгиба вала. Зубной контакт становится большим, так как поверхность зуба упруго деформируется.
Изменение контакта зубьев в зависимости от нагрузки 2
Без нагрузки
Под нагрузкой
При приложении нагрузки ошибка угла вала и ошибка смещения возникают одновременно из-за изгиба вала
Контакт зубьев конической шестерни и жесткости вала
- Если шестерня плавно перемещается вручную при разгрузке, но при работе создает шум и вибрацию, контакт зубьев может быть нарушен из-за недостаточной жесткости внутренней части редуктора
- При сборке можно отрегулировать только ошибку расстояния сборки.
 Однако ошибка смещения и ошибка угла вала зависят от погрешности изготовления и жесткости редуктора, поэтому необходимо повысить жесткость на этапе проектирования
Однако ошибка смещения и ошибка угла вала зависят от погрешности изготовления и жесткости редуктора, поэтому необходимо повысить жесткость на этапе проектирования - Одна шестерня становится односторонней опорой, и контакт зубьев может ухудшиться при приложении нагрузки
Конструкция для повышения жесткости вала
Если жесткость вала низкая, контакт зубьев может ухудшиться при приложении нагрузки, даже если контакт зубьев хороший в собранном виде
1. Толстый вал / опора с обеих сторон / короткая выступающая часть подшипника
Как проверить контакт зубов
- Нанесите тонкий слой сурика или что-то подобное на поверхность зуба
- Поверните шестерню и проверьте расположение красного стержня, перенесенного на другую шестерню
Как проверить люфт
- Блокировка одной передачи
- Поместите циферблатный индикатор на поверхность зуба другой шестерни
- Переместите последнюю шестерню и прочтите значение на циферблатном индикаторе
Контакт зубьев шестерни
- Стандарт контакта зубьев, установленный Японской ассоциацией производителей зубчатых колес (JGMA): JGMA1002-01(2003)
- Этот стандарт описывает соотношение, распределение, точность, методы измерения и методы регистрации с использованием JIS B 1704:19.
 77 (контакт зубьев шестерни) и ISO/TR10064-4:1998 в качестве ссылки .
77 (контакт зубьев шестерни) и ISO/TR10064-4:1998 в качестве ссылки .
Ссылки по теме :
Типы зубчатых колес – Подробное описание типов зубчатых колес
Угловые зубчатые колеса – Подробное описание угловых зубчатых колес
Конические зубчатые колеса Zerol – Подробное описание конических зубчатых колес Zerol
Гипоидные зубчатые колеса – Подробное описание гипоидных зубчатых колес
Эквивалентные таблицы каждого стандарта, относящиеся к сырью и классам точности зубчатых колес
锥齿轮 – 中文页
Прецизионные конические и угловые зубчатые колеса производства SDP/SI
Продукция Зубчатые колеса Прецизионные конические и угловые зубчатые колеса
SDP/Si — известный производитель высокоточных стандартных и нестандартных конических и угловых зубчатых колес для широкого спектра применений.
Дюйм
Конические / угловые шестерни
Штыревой – Шаг 72
АГМА 10
1/8 ОТВЕРСТИЕ
Наборы Precision Matched Sets
Материал:
303 нержавеющая сталь
Алюминиевый сплав 2024-T4 или T351, анодированный перед резкой
Продается в комплекте
Серия: S1343Z-72
Конические шестерни
Тип зажима – Шаг 72
АГМА 10
1/8 ОТВЕРСТИЕ
Наборы Precision Matched Sets
Материал:
Нержавеющая сталь 303
Анодирование алюминиевого сплава 2024-T4 или T351 перед резкой
Продается в комплекте
Серия: S1353Z-72
Конические / угловые шестерни
Штыревой – Шаг 64
АГМА 10
3/16 ОТВЕРСТИЕ
Наборы Precision Matched Sets
Материал:
Нержавеющая сталь 303
Алюминиевый сплав 2024-T4 или T351, анодированный перед резкой
Продается в комплекте
Дюйм
Конические / угловые шестерни
Тип зажима – Шаг 64
АГМА 10
3/16 ОТВЕРСТИЕ
Наборы Precision Matched Sets
Материал:
Нержавеющая сталь 303
Алюминиевый сплав 2024-T4 или T351, анодированный перед резкой
Продается в комплекте
Серия: S1354Z-64
Конические / угловые шестерни
Штыревой – Шаг 48
АГМА 10
1/4 ОТВЕРСТИЯ
Наборы Precision Matched Sets
Материал:
Нержавеющая сталь 303
Алюминиевый сплав 2024-T4 или T351, анодированный перед резкой
Продается в комплекте
Серия: S1346Z-48
Конические / угловые шестерни
Тип зажима – Шаг 48
АГМА 10
1/4 ОТВЕРСТИЯ
Наборы Precision Matched Sets
Материал:
Нержавеющая сталь 303
Алюминиевый сплав 2024-T4 или T351, анодированный перед резкой
Продается в комплекте
Серия: S1356Z-48
Угловые шестерни
Шаг 48, 32, 24 и 20
Материал:
Латунь и сталь
Латунь
Серия: A 1B 4-Y
Сталь
Серия: А 1С 4-У
Формованные угловые шестерни
Шаг 48, 32, 24 и 16
Материал:
Нейлон и ацеталь
Нейлон
Серия: A 1M 4-Y
Ацеталь
№: A 1M 4-Y48015
Литые конические шестерни
Шаг 48, 32 и 24
Материал:
Нейлон и ацеталь
Нейлон
Серия: A 1M 3-Y
Ацеталь
Серия: A 1M 3-Y
Конические шестерни
Шаг 48, 32 и 24
Материал:
Латунь и сталь
Латунь
Серия: A 1B 3-Y
Сталь
Серия: А 1С 3-Й
Спиральные угловые шестерни
Модуль:
2, 2,5, 3, 3,5, 4 и 5
ИСО Класс 6
Уголок 35°
Материал:
Сталь AISI 1045, поверхности зубьев индукционная закалка до HRC 48. ..53
..53
Количество зубьев – 20
Серия: S13S1YM
Кол-во зубьев – 25
Серия: S13S1YM
Кол-во зубьев – 30
Серия: S13S1YM
Прямые и спиральные угловые шестерни
Модуль: 0,5, 0,8 и 1
ISO Класс 8
Прямой зуб продается как есть
Зубья Sprial 35° продаются только комплектами
Материал:
Латунь или сталь
Латунь — продается поштучно
Серия: А 1В 4М
Сталь — продается поштучно
Серия: А 1С 4М
Спираль, сталь
Продается как набор
Серия: А 1С44М
Спиральные угловые шестерни
Модуль:
1,25, 1,5, 2 и 2,25
ISO Класс 8
Продается только комплектами со шпоночным пазом или без него
Материал: Сталь
Модуль: 1,25
Без шпоночного паза
№: А 1С 4MYK12020S
Модуль: 1,5
Серия: А 1С 4М
Модуль: 2
Серия: А 1С 4М
Модуль: 2,5
№: А 1C44MY22020S
Прямые угловые шестерни
Модуль:
1,5, 2, 2,25, 2,75 и 3
ISO Класс 8
Продается поштучно
Со шпоночным пазом или без него
Материал: Сталь
Модуль: 1,5
Серия: А 1С 4М&
А 1С44М
Модуль: 2
Серия: А 1С 4М &
А 1С44М
Модуль: 2,5
Серия: А 1С 4М &
А 1С44М
Модуль: 2,75
№: А 1С 4MYK27020A
Модуль: 3
Серия: А 1С 4М &
А 1С44М
Прямые угловые шестерни
Модуль:
0,6, 1 и 1,5
Класс ISO 8
Материал:
Алюминий, латунь, сталь,
или нержавеющая сталь
алюминий 2024 T4
Серия: А 1А 4М
Латунь ASTM B-16
Серия: А 1В 4М
Сталь SAE 4140
Серия: А 1С 4М
Нержавеющая сталь AISI 416
Серия: А 1X 4M
Прямые угловые шестерни
Модуль:
0,5, 0,8, 1, 1,5, 2, 2,5, 3 и 3,5
Материал:
Ацеталь
16 зубьев
Серия: А 1 м 4 м
20 зубьев
Серия: А 1 м 4 м
30 зубьев
№: A 1M 4MYZ10A
Прямые угловые шестерни
Модуль:
1, 1,5, 2, 2,5, 3 и 3,5
Материал: Литой цинк
16 зубьев
Серия: А 1Д 4М
Земля
Спиральные конические шестерни
Модуль: 2, 2,5, 3 и 4
Класс ISO 6
Материал:
Сталь AISI 1045, поверхности зубьев индукционная закалка до HRC 48. ..53
..53
Соотношение 2:3
Серия: S13S2YM
Соотношение 1:2
Серия: S13S3YM
Соотношение 1:3
Серия: S13S4YM
Земля
Спиральные конические шестерни
Модуль: 0,5, 0,8 и 1
Класс ИСО 8
Материал:
Латунь или сталь
Соотношение 1:2 – Латунь
Серия: А 1В 3М
Соотношение 1:2 – Сталь
Серия: S13S3YM
Соотношение 1:3 – Сталь
Серия: S13S4YM
Прямой
Конические шестерни
Модуль: 1,5, 2, 2,5 и 3
Класс ISO 8
Материал:
Без шпоночного паза, сталь
Со шпоночным пазом, сталь AISI 1045, индукционная закалка поверхностей зубьев до HRC 48. …53
…53
Отделка:
Черный оксид, за исключением шлифованных отверстий и поверхностей зубьев.
Соотношение 1:2
Без шпоночного паза
Серия: А 1С 3М
Соотношение 1:3
Без шпоночного паза
Серия: А 1С 3М
Соотношение 1:2
Со шпоночным пазом
Серия: А 1С33М
Соотношение 1:3
Со шпоночным пазом
Серия: А 1С33М
Неметаллический
Литые конические шестерни
Модуль: 0,5, 0,8, 1, 1,5, 2, 2,5 и 3
Материал:
Ацеталь
Соотношение 1:1,5
Серия: A 1M 3MYZ15
Соотношение 1:2
Серия: A 1M 3M
Соотношение 1:3
Серия: A 1M33M
Соотношение 1:4
Серия: A 1M 3MYZ
Соотношение 1:5
Серия: A 1M 3MYZ10
Коническая шестерня из стального модуля 2 16 зубьев i=1,5:1 фрезерованные Артикул: 36104800
Перейти к содержимому
Maedler North America
0,00 $ Корзина
Поиск товаров
- Описание
- Дополнительная информация
| Артикул | 36104800 |
| Трансмиссия [i] | 1,5:1 (16/24) |
| Модуль | 2,0 |
| Кол-во зубьев | 16 |
| да [мм] | 35,5 |
| d [мм] | 32 |
| НД [мм] | 20 |
| NL [мм] | 8 |
| L1 [мм] | 21 |
| Длина [мм] | 22,6 |
| S [мм] | 13,1 |
| b [мм] | 12 |
| B H7 [мм] | 10 |
| E [мм] | 36 |
| Допустимый MD [Нм] | 0,57 |
| Вес [г] | 60 |
| Соответствующее встречное колесо [Артикул №] | 36104900 |
СТРАНИЦА ПРОДУКТА В КАТАЛОГЕ
ФАЙЛЫ САПР (нажмите для загрузки)
ДОПОЛНИТЕЛЬНАЯ ИНФОРМАЦИЯ
ДОПОЛНИТЕЛЬНАЯ ИНФОРМАЦИЯ
Предоставленные 3D-модели, изображения и технические чертежи выполнены с разумной тщательностью. Тем не менее ответственность за точность и правильность этих данных исключена.
Тем не менее ответственность за точность и правильность этих данных исключена.
Материал: до модуля 2: 11SMnPb30. Из модуля 2. 5: C45. Качество зубьев 8 по DIN 3967 (из модуля 2). С корончатыми, фрезерованными зубьями. Не закаленный – не притертый. Угол вала = 90º. Конические шестерни работают только в паре с указанным передаточным числом и с одним и тем же модулем.
Примечание для заказа: Эти шестерни продаются поштучно, а не парами. Для пары конических шестерен необходимо заказать две подходящие шестерни одного модуля с разным числом зубьев и одинаковым передаточным числом.
26,42 $
Доступность: 10 шт. в наличии (заказы доставляются в течение 1-2 недель)
Коническая шестерня стальная модуль 2 16 зубьев i=1,5:1 фрезерованная Артикул: 36104800 количество
Вам также может понравиться…
Конические шестерниКонические шестерни, сталь, система прямых зубьев, передаточное отношение 1:1 – 4:1Конические шестерни, сталь, система прямых зубьев, передаточное число 1,5:1Конические шестерни, червячные колеса, червяки
Коническая шестерня стальная модуль 2 24 зуба i=1,5:1 фрезерованные Артикул: 36104900
32,26 $ В корзину
Артикул 36104800_2505 Категории Конические зубчатые колеса, Конические зубчатые колеса, Сталь, Система прямых зубьев, передаточное число 1:1 – 4:1, Конические зубчатые колеса, Сталь, Система прямых зубьев, передаточное число 1,5:1, Конические зубчатые колеса, Червячные колеса, Червяки Теги Допустимый MD [Нм] 0,57, Соответствующее контрколесо [Артикул №] 36104900, Дюйм / Метрическая Метрическая, Модуль 2,0, Кол-во зубьев 26, Трансмиссия [i] 1,5: 1 (16/24), Вес [г ]60
Maedler North America — ваш идеальный партнер во всем, что связано с технологиями трансмиссии.




 03.2015981.3 Кб210Лекция 25. Основные принципы и правила конструирования.pdf
03.2015981.3 Кб210Лекция 25. Основные принципы и правила конструирования.pdf Однако ошибка смещения и ошибка угла вала зависят от погрешности изготовления и жесткости редуктора, поэтому необходимо повысить жесткость на этапе проектирования
Однако ошибка смещения и ошибка угла вала зависят от погрешности изготовления и жесткости редуктора, поэтому необходимо повысить жесткость на этапе проектирования 77 (контакт зубьев шестерни) и ISO/TR10064-4:1998 в качестве ссылки
77 (контакт зубьев шестерни) и ISO/TR10064-4:1998 в качестве ссылки