Коническая передача прямозубая: Конические зубчатые передачи. Классификация, термины, определения
alexxlab | 25.05.2023 | 0 | Разное
3.2.4. Конические прямозубые передачи
Цель – изучение области применения, способов изготовления и особенностей
эксплуатации зубчатых передач с коническими колесами. Студент должен иметь представление об особенностях геометрического, силового и прочностного расчетов этого типа передач, уметь правильно проектировать конические колеса.
Коническими называют
передачи с зубчатыми колесами, оси
которых расположены под некоторым
углом. Наибольшее распространение
получили передачи с углом 90° между
осями колес . Конические зубчатые
колеса выполняют с прямыми, косыми и
круговыми зубьями (рис. 3.4).
Экспериментальные исследования
показывают, что нагрузочная способность
конической прямозубой передачи
составляет лишь около 0,85 цилиндрической
аналогичных размеров. Прямозубые
конические колеса следует применять
при окружных скоростях колес до 2…3 м/с.
При серийном производстве конических
колес неточности изготовления и
остаточные деформации после термообработки
устраняют обычно притиркой на стендах,
заменяя этим трудоемкое шлифование.
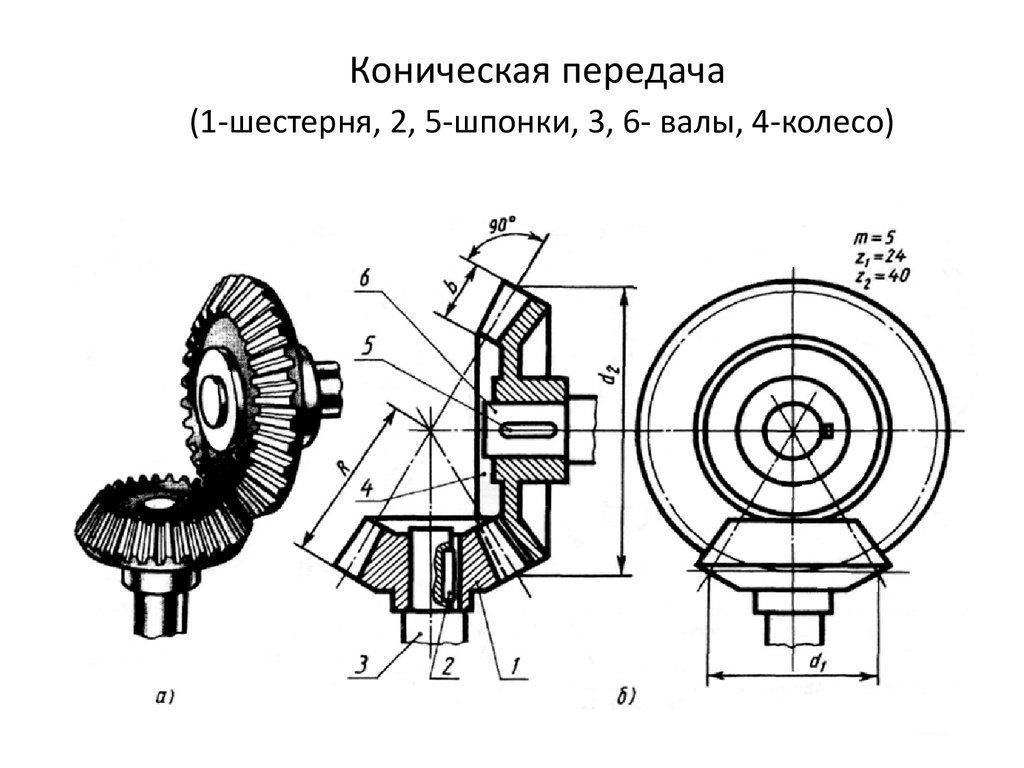
Основными геометрическими параметрами конической передачи являются : углы при вершине конусов 1, 2, делительные диаметры колеса на внешнем dl и среднем dm сечении, внешнее Rе и среднее Rm конусные расстояния, ширина зубчатого венца “b” (рис. 3.21).
Поскольку измерять размеры по внешнему контуру колеса удобнее, то их обычно указывают на чертежах. Размеры колеса в среднем сечении используют при силовых расчетах. В качестве стандартного расчетного модуля в конических колесах принимают внешний окружной делительный модуль me.
Из рис. 3.21 следуют следующие соотношения для геометрических параметров конической передачи. Внешнее конусное расстояние равно
Re = 0,5 me z,
где z – суммарное число зубьев шестерни и колеса. .
Рис. 3.21. Геометрические параметры
Ширина венца b 0,3 Re.
Среднее конусное расстояние Rm = Re – 0,5b.
Внешний окружной делительный модуль ml связан с окружным модулем в среднем сечении соотношением me = mm
Углы при вершинах делительных конусов 2 = 90 – 1.
Диаметры внешней делительной окружности – de, внешние диаметры вершин da и впадин df конических колес определяются из соотношений
de = me z, da = de + 2 me cos
df = de – 2,4 m
Средний делительный диаметр равен dm = de – b sin .
Передаточное число находится из соотношения
При условии 1 + 2 = 90
имеем u
= tg
2 = ctg
1.
Из этих соотношений при заданном значении
“u”
находят углы 1 и 2.
В зацеплении конической прямозубой передачи действуют следующие силы: окружная Ft, радиальная Fr и осевая Fa. Согласно рис. 3.22 выражения для этих сил запишутся в виде
Рис. 3.22 Усилия в коническом зацеплении
Направления сил на шестерне и колесе противоположны и согласно рис. 3.22 радиальная сила на шестерне равна осевой силе на колесе , а осевая сила на шестерне равна радиальной силе на колесе.
Расчет на прочность зубьев конических колес проводят по тем же формулам, что и для зубьев цилиндрических колес, но с учетом коэффициент снижения нагрузочной способности конической передачи = 0,85.
Напряжения изгиба определяют в среднем сечении конических колес из следующего соотношения :
Из приведенного соотношения при проведении проектировочных расчетов можно определить модуль в среднем сечении
,
где YF – коэффициент формы зуба определяют по
графику рис.
3.20 в зависимости от
эквивалентного числа зубьев
Коэффициенты KF и KFv принимают так же, как и для цилиндрических
зубчатых колес; – коэффициент ширины зубчатого колеса
по среднему модулю (
В приведенных формулах T1 – в Нм,
F и [F] – в МПа, mm – в мм.
Значение допускаемых напряжений [F] определяется по рекомендациям, приведенным в расчете цилиндрических передач.
Контактные напряжения в зубьях конических колес находят из соотношения
При проведении проектировочных расчетов величина среднего делительного диаметра шестерни может быть найдена из выражения для H
где = 0,3…0,6 – коэффициент ширины зубчатого колеса.
Размерность входящих в формулу величин
Т1 – в Нм,
[н ] – в МПа, dm1 – в мм.
Значения коэффициентов zн, zм и Kн принимают такими же, как для зубьев цилиндрических колес.
Из выражения для н можно определить внешний делительный диаметр колеса de2 (рис. 3.21) по формуле
где .
Для зубьев с низкой и средней твердостью рабочих поверхностей основным критерием работоспособности является контактная прочность, исходя из требований которой, определяют размеры зубчатого колеса, а затем выполняют проверочный расчет зубьев на изгиб. Для закаленных зубьев основным критерием работоспособности является прочность на изгиб. В данном случае сначала определяют модуль расчетом зубьев на изгиб, а затем выполняют проверочный расчет на контактную прочность.
В машиностроении
иногда находят применение конические
колеса с тангенциальными (косыми) и
круговыми зубьями. С конструкцией и
расчетом таких колес можно ознакомиться
в специальной литературе.
Контрольные вопросы
1. В каких случаях применяют конические редукторы в машиностроении ?
2. Назовите способы изготовления конических зубчатых колес.
3.Как производится смазка зубчатого зацепления и подшипников в опорах вала?
4. Какие посадки используют при установке зубчатых колес и на валах ?
5. Как определить передаточное отношение коничес-кой передачи ?
6. За счет каких регулировок получают качественное коническое зацепление и обеспечивают требуемый зазор в подшипниках быстроходной ступени ?
7. Какой параметр называется модулем зацепления и в каком сечении конического колеса он имеет стандарт-ное значение ?
8. Какие усилия возникают в конических зубчатых зацеплениях ?
9. Какие напряжения возникают в зубьях конических колес от действующих усилий в зацеплении ?
10. Какие подшипники устанавливают в опорах конических передач ?
Червячная, коническая, косозубая и прямозубая передачи
Передача с зубцами – это одна их главных составляющих большинства механизмов, используемых сегодня человеком.
Она позволяет увеличить выходной крутящий момент, регулировать движение выходного вала. Каждая из них имеет свои отличия и сферу применения.
Прямозубый тип передачи
Зубчатые шестерни представленных передач устанавливаются последовательно. Они обеспечивают более высокие значения передаточного отношения. Самыми часто применяемыми считаются пары, используемые для создания высоких передаточных соотношений.
В таких колесах зубцы располагаются под прямым углом. Подобные шестерни устанавливаются в бытовую технику, инструмент будильники и так далее. Они достаточно шумные, вызывают сильные вибрации. Их не используют в сложной, точной технике. Соотношение зубцов между колесом и шестерней изменяется от 1:1 до 6:1.
Передача косозубая
Если сравнивать с предыдущим вариантом, косозубые передачи работают тихо, имеют плавный ход. Это обеспечивает особый тип зубцов, а точнее их контакт. Они располагаются под наклоном к поверхности колеса.
Когда отдельные зубцы сцепляются друг с другом, контакт происходит постепенно. Угол наклона зубьев не превышает 15 – 30 градусов. От этого показателя зависит максимально допустимая осевая нагрузка.
Такие пары чаще всего используют в автомобильных коробках передач. Соотношение между зубцами изменяется от 3:2 до 10:1.
Конические типы передачи
Подобные типы чаще всего применяются для прокручивания коленвала в обратном направлении. Зубцы у такого колеса могут различаться по форме:
• прямой;
• спирального вида;
• гипоидной.
Изделия с прямыми зубами имеют подобные характеристики, как у прямозубой передачи. Они могут выдерживают повышенную нагрузку и имеют передаточное соотношение 3:2 – 5:1.
Модели со спиральными зубами не отличаются по функциям от шестерен с косыми зубами. Они практически не шумят и не вибрируют. Направление движения зависит от того, в какую сторону наклонены зубцы.
При наклоне вправо, движение происходит по часовой стрелке. Если наклон влево — против часовой стрелки. Передаточное соотношение – от 3 : 2 до 4 : 1.
У гипоидной передачи большее колесо ведомое, а меньшее — ведущее. Это один из подтипов спиральной передачи, где у зубцов гиперболоидная конструкция. Колеса по отношению друг к другу поворачиваются в разные стороны. Передаточное число довольно большое, от 10:1 до 200:1. Это позволяет использовать такие шестерни в силовой трансмиссии и машиностроении.
Червячная передача
Такая пара имеет особую конструкцию, которая не позволяет ей вращаться в обратном направлении. Она имеет особый принцип работы и применяется в редукторах, так как имеет очень высокое передаточное число (от 5:1 до 300:1).
Пара сделана так, чтобы червяк мог проворачивать шестерню, но не наоборот. Виток имеет пологий угол подъема, это удерживает колесо на месте во время сцепления. Зачастую они устанавливаются на конвейерных лентах.
Блокировка обратного движения в данном случае играет роль своеобразного тормоза и аварийной остановки.
СМОТРИТЕ ТАКЖЕ: Производство лазерных станков • Лазерные станки с ЧПУ • Как выбрать лазерный станок
передач | Шпора | спиральный | Скос | червь | Дистрибьютор промышленных запчастей | MN
Компании ISC и дочерние компании Adams-ISC являются дистрибьюторами деталей механической силовой передачи, включая открытые зубчатые передачи. Для получения дополнительной информации о предлагаемых нами брендах и/или ценах свяжитесь с нами по телефону 763-559-0033, по электронной почте [email protected] или заполните нашу контактную онлайн-форму.
Шестерни сгруппированы по пяти конструктивным категориям; шпоровые, винтовые, конические, гипоидные и червячные. Они также классифицируются по ориентации монтажа: параллельно или под углом. Ориентация вала, эффективность и скорость определяют тип конструкции для использования в любом конкретном приложении.
Типы открытых зубчатых колес
Прямозубые
Цилиндрические зубчатые колеса или прямозубые зубчатые колеса являются самым простым и наиболее широко используемым типом зубчатых колес из-за низкой стоимости, отсутствия торцевой тяги и низких эксплуатационных расходов. Край каждого зуба прямой и параллельный оси вращения. Форма зуба основана на эвольвентной форме зуба, которая обеспечивает качение, а не скользящий контакт между зубьями. Они зацепляются правильно, только если установлены на параллельные валы. Правильная смазка важна для предотвращения чрезмерного износа. Цилиндрические зубчатые колеса создают реактивные нагрузки только радиально по отношению к валу и не создают осевых осевых нагрузок.
Они используются в устройствах с низкой и средней скоростью, таких как приводы мельниц, подъемное оборудование, стиральные машины и отвертки. На высоких скоростях они шумят и быстро изнашиваются. Шестерни поставляются со ступицей или без нее, а шестерни доступны со сплошным, перепончатым или спицевым корпусом.
Нормальный диапазон соотношения составляет от 1:1 до 6:1.
Косозубая
Косозубая шестерня со скрещенными осями может использоваться, когда конструкция требует, чтобы валы передавали мощность под разными углами. Их лучше всего использовать для легких и умеренных нагрузок, и они требуют правильного типа смазки. Косозубые шестерни с углом наклона спирали 45 градусов широко используются и могут быть расположены как на параллельных, так и на перпендикулярных валах.
Червяк
Используются под прямым углом на непересекающихся валах и состоят из цилиндрического червяка, входящего в зацепление с более крупной шестерней, часто называемой колесом. Червяк имеет резьбу винтового типа и требует нескольких оборотов, чтобы сделать колесо за один оборот; таким образом, широкий диапазон передаточных чисел может быть получен в ограниченном пространстве. Они подходят для применений с ударными нагрузками. Винтовой механизм обеспечивает бесшумную работу, но червячные передачи имеют меньший КПД, чем другие типы передач.
Существует три типа конфигураций:
- Наименее распространенный цилиндрический червяк, находящийся в зацеплении с винтовой шестерней.
- Однооболочечный имеет зубчатое колесо с изогнутыми зубьями, которое частично наматывается на червяк.
- Двойной охват также имеет изогнутые зубья, но червяк вогнутой формы, который частично обвивает шестерню. Этот тип имеет самую высокую грузоподъемность и ударопрочность.
Типы червячных передач (L-R) Цилиндрические, одноконтурные, двухконтурные
Конические
Передают мощность между валами, оси которых пересекаются под углом. Эти шестерни имеют зубья, нарезанные на угловой или конической поверхности, и обычно имеют угол давления 20 градусов. Они создают осевую нагрузку на оба вала. Существует четыре основных типа конфигураций:
- Прямой: Наиболее распространен. Имеет конусообразную поверхность с прямыми зубьями, сужающимися к вершине. Когда валы расположены под прямым углом и вращаются с одинаковой скоростью, две сопряженные шестерни одинаковы и называются угловыми шестернями .
- Спираль: зубья изогнуты под углом для плавного контакта. Способны выдерживать более высокие крутящие нагрузки и скорости по сравнению с прямыми коническими зубчатыми колесами.
- Zerol: похожи на спиральные скосы, но их зубья изогнуты по длине. Как правило, они имеют угол спирали, равный нулю градусов.
- Косой зуб: похож на спиральный скос, за исключением того, что зубья не изогнуты; они обрезаны прямо и под углом к осевой линии вала.
Гипоидный
Напоминают спиральные конические шестерни и работают на валах с непересекающимися осевыми линиями. Таким образом, оба вала могут опираться на подшипники с обоих концов. Чтобы компенсировать смещение вала, поверхности шага представляют собой гиперболоиды вращения. Они подходят для передачи более тяжелых нагрузок и работают плавнее и тише, чем спиральные шестерни. Однако высокие контактные давления и скорости скольжения требуют использования специальных смазочных материалов.
Торцевая поверхность
Также называемая коронной шестерней, ось каждого зуба лежит в плоскости, перпендикулярной оси вала.
Сопряженная шестерня представляет собой прямозубую или косозубую шестерню. Шестерня и передняя шестерня обычно ориентированы под углом 90 градусов друг к другу. Они имеют меньшую грузоподъемность, чем конические зубчатые колеса , и не часто используются в промышленности.
Тяговые приводы
Тяговые приводы подобны шестерням и передают мощность через сопряженные ролики (конусы, цилиндры, диски, кольца или сферы). Доступны сухие и смазываемые типы. Они используются вместо ремней, шестерен или цепных приводов в условиях ограниченного пространства. Преимущества включают бесшумную работу, высокую скорость снижения, низкую вибрацию и высокую эффективность.
Ведущие бренды Мы предлагаем
Содержание на этой странице были созданы с использованием выдержки из Справочника по передаче (5 TH Edition) , который написан и продается Ассоциация дистрибьюторов (PTDA).
Закажите копию здесь
Сравнение коэффициентов полезного действия зубчатых колес – прямозубых, косозубых, конических, червячных, гипоидных, циклоидных
Сравнение коэффициентов полезного действия различных типов зубчатых колес при различных передаточных числах поможет нам сделать правильный выбор редуктора для наших применений.
Обратите внимание, что эти значения эффективности являются общими рекомендациями, а более точные значения см. в каталоге производителя.
Сравнение эффективности передачи. Таблица
| № | 10095 | . | 94-98% | |
| 2 | Прямой скос | 3:2 до 5:1 | 93-97% | |
| 3 | Spiral Bevel | 3:2 to 4:1 | 95-99% | |
| 4 | Worm | 5:1 to 75:1 | 50- 90% | |
| 5 | Гипоид | 10: 1–200: 1 | 80-95% | |
| 6 | Слайл | 3: 2 до 10: 1 | .0096 | 94-98% |
| 7 | Циклоид | 10: 1–100: 1 | 75% до 85% |
1.
Spep Gear. , и эти шестерни могут достичь гораздо более высокой эффективности по сравнению с другими типами передач. Его КПД варьируется от 94% до 98% при более низких передаточных числах.2. Эффективность прямого конического зубчатого колеса
Прямое коническое зубчатое колесо похоже на цилиндрическое зубчатое колесо с перпендикулярным расположением вала. Подобно цилиндрическим зубчатым передачам, эти шестерни также могут работать только с более низкими передаточными числами с более высоким КПД (9от 3% до 97%).
3. Эффективность спирально-конической шестерни
Из-за формы зуба и контакта спиральная коническая шестерня имеет меньший уровень шума и вибраций по сравнению с прямозубой конической шестерней и, следовательно, имеет более высокий КПД (от 95% до 99%).
4. Эффективность червячной передачи
Эффективность червячной передачи значительно меняется при изменении угла опережения, коэффициента трения и передаточного числа.
Расчет эффективности червячной передачи
Используйте следующее уравнение эффективности передачи для расчета КПД червячных передач.