Конические передачи: Конические зубчатые передачи. Классификация, термины, определения
alexxlab | 10.01.2023 | 0 | Разное
КОНИЧЕСКИЕ ПЕРЕДАЧИ С МНОГОПАРНЫМ КОНТАКТОМ
Автор:
Мельников Владимир Зиновьевич
Конические передачи (с прямыми и криволинейными зубьями) относятся к числу безальтернативных зубчатых передач и широко используются в трансмиссиях привода различных технологических и транспортных агрегатов. Обеспечение эффективности их применения, в частности, за счет повышения несущей способности и ресурса представляет собой сложную научно-техническую задачу.
Традиционные способы решения — путем повышения сопротивляемости передач действующим нагрузкам и точности их изготовления являются существенно затратными и не всегда результативными. Альтернативный путь решения — это снижение контактных давлений на зубья за счет одновременного взаимодействия нескольких пар зубьев, т. е. на основе многопарного зацепления. Обеспечение многопарного контакта в передаче возможно при условии, если активная линия зацепления будет больше двух шагов зацепления и коэффициент перекрытия εα, численно будет больше двух, т.
εα > 2. (1)
Реализация условия (1) производится путем модификации исходных данных на основе компьютерного моделирования геометрии передачи. Как показывает анализ выражений, определяющих геометрию конических передач [1], [2], величина коэффициента εα зависит в основном от значений параметров исходного контура, чисел зубьев и коэффициентов смещений, т. е.
εα = F(zc, xc, α, hα*, β ) > 2, (2)
где zc, xc — суммарные значения чисел зубьев и коэффициентов смещений зубчатых пар; α, hα*, β — угол профиля и коэффициент высоты головки исходного контура и угол наклона зубьев.
Геометрия многопарной передачи определяется путем высотно-профильной модификации исходного контура в пределах: α ≤ 20°; hα* >1, а также возможных смещений производящего контура. В n- парной передаче, где n- целая часть коэффициента перекрытия εα, величина парности зацепления n определяется как функция от значения εα, т. е.
n = INT (εα), (3)
где INT — оператор функции наибольшего целого числа, не превосходящего заданное числовое значение.
В общем случае активная линия зацепления состоит их двух участков — зон n- парного и (n + 1) — парного зацепления. При этом целая часть коэффициента εα, т. е. INT(εα) = n, а дробная часть характеризует область (n+1)-парного зацепления. Предварительный расчет передач по условию (1) производится на основе анализа потенциально возможных значений коэффициента перекрытия εα0:
εα0 = (4 . hα*)/(п . sin2α). (4)
Значения коэффициентов для отдельных исходных контуров приведены в таблице 1. Как следует из таблицы 1 условие (1) для передач со стандартным исходным контуром теоретически не осуществимо. Для реализации условия (1) необходима модификация как исходного, так и соответственно производящего контура. В общем случае для изготовления — парных передач требуется зуборезный инструмент, соответствующий выбранному исходному контуру.
В частности, за счет уменьшения радиального зазора в передаче до 0.05÷0,1 модуля m в допустимых пределах можно увеличивать высоту профиля зубьев и обеспечивать условие (1).
В таблице 2, например, приведены значения коэффициентов εα для двухпарных конических прямозубых передач с высотной модификацией профиля и исходными данными, исключающими подрез, интерференцию и заострение зубьев. Расчет передач производится при значениях m = 1, так как величина коэффициента εα в общем случае от модуля не зависит.
Как видно из таблицы 2 при высотной модификации исходного контура и использовании стандартного инструмента полная высота зубьев может быть увеличена, например до 2,45m, что приводит к образованию двухпарного контакта. Для конических передач с криволинейной формой зуба, в частности круговой, реализация двухпарного зацепления стандартным инструментом возможна только при малых углах наклона зубьев в пределах до 7°.
е. за счет высотно-профильной или только высотной модификации зубьев, когда hα* > 1,25m. В этих случаях для изготовления передач применяется специальный инструмент.Синтез n-парных конических передач возможен при любых произвольных значениях n, что указывает на широкие возможности параметрической оптимизации передач по различным критериям качества. В таблицах 3 и
Как следует из таблиц (3)-(6) при приблизительно равных значениях чисел зубьев колес и соответствующих им параметров исходного контура значения коэффициентов εα для передач с прямыми и круговыми зубьями отличаются весьма незначительно. При этом по аналогии с цилиндрическими передачами [7] нагрузка на зубья при многопарном зацеплении уменьшается в зависимости от величины парности контакта.
В первом приближении без учета жесткости и погрешностей изготовления прочностная выносливость многопарных передач по сравнению с аналогичными однопарными передачами увеличивается в среднем в n раз по изгибу и в √n раз по контакту. Это позволяет при близких значениях коэффициентов εα заменять передачи с круговым зубом на прямозубые, которые существенно менее трудоемки при изготовлении.
В дополнение к этому при использовании прямозубых передач также существенно упрощается и конструкция подшипниковых опор.
В виду того, что в этом случае осевая нагрузка на подшипники отсутствует, становится возможным вместо радиально-упорных подшипников устанавливать радиальные, которые и дешевле, и не требуют предварительного натяга. Такая замена существенно снижает общую трудоемкость изготовления и монтажа конических передач.Мельников Владимир Зиновьевич, к. т.н.
Московский государственный машиностроительный университет (МАМИ)
E-mail: [email protected]
Литература
1. ГОСТ 19624-74. Передачи зубчатые конические с прямыми зубьями. Расчет геометрии. М.: Изд-во стандартов, 1974. 26 с.
2. ГОСТ 19326-73. Передачи зубчатые конические с круговыми зубьями. Расчет геометрии. М.: Изд-во стандартов, 1974. 75 с.
3. Таратынов О. В., Мельников В. З., Болотина Е.
М. Коническая прямозубая передача с трехпарным зацеплением. Патент РФ на полезную модель № 131110. Бюл.№ 22 от 10.08.2013.4. Мельников В. З. Коническая передача с круговыми зубьями с трехпарным зацеплением. Патент РФ на полезную модель № 134265. Бюл. № 31 от 10.11.2013.
5. Мельников В. З., Таратынов О. В. Коническая прямозубая передача с четырехпарным зацеплением. Патент РФ на изобретение № 142182. Бюл. № 17 от 20.06.2014.
6. Мельников В. З. Коническая передача с круговыми зубьями с четырехпарным зацеплением. Патент РФ на полезную модель № 139974. Бюл. № 12 от 27.04.2014.
7. Мельников В. З. Синтез зубчатых передач с произвольным n-парным зацеплением. Вестник машиностроения. 2010. № 4, с. 29–31.
Проектирование конических зубчатых передач | 5ти томное издание «Методы Проектирования», автор Игнатьев Н.П.
Описание
Проектирование конических зубчатых передач
(Демоверсия)
ДЕМОВЕРСИЯ является сокращенным вариантом статьи (книги) позволяющим получить общее представление о содержащимся в ней материале, прежде всего, в части наличия примеров конструктивного исполнения рассматриваемых технических решений
1.
Общая характеристика и область применения конических передач
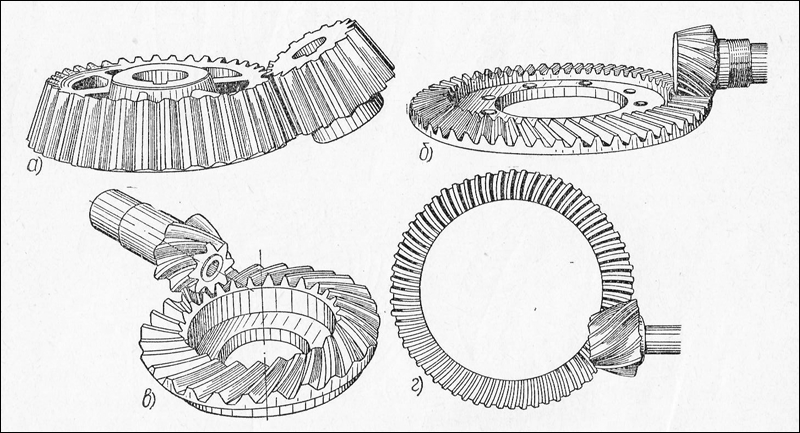
Коническая зубчатая передача предназначается для передачи вращения между пересекающимися валами, которые в большинстве машин и оборудования расположены в пространстве перпендикулярно друг другу (см. Рис 1а, б). При этом, в силу меньшей нагрузочной способности по сравнению с цилиндрическими зубчатыми передачами и большей чувствительности к погрешностям сборки конические передачи не рекомендуется применять в силовом приводе исполнительного механизма машины. Наиболее часто конические передачи находят применение в оборудование, в котором кинематическая схема предусматривает наличие вспомогательных механизмов перемещающихся в параллельном или перпендикулярном направлении к оси исполнительного механизма, например в холодно – высадочных и гвоздильных автоматах, во фрезерных и зубообрабатывающих станках. Помимо конической передачи с прямыми зубьями (см. Рис 1а) существуют конические передачи с круговым зубом (см.
Конические зубчатые передачи с круговым зубом, а также гипоидные и спироидные передачи по сравнению с коническими передачами с прямым зубом обладают рядом преимуществ:
– более высокая несущая способность,
– более высокая плавность зацепления и как следствие пониженный уровень шума,
– меньшая чувствительность к погрешностям сборки.
Поэтому, несмотря на определенную сложность проектирования и изготовления, эти типы конических зубчатых передач все больше находят применение в различных областях машиностроения. В частности, гипоидные передачи получили широкое распространение в автомобилестроении (применяются в редукторах задних мостов легковых и грузовых автомобилей), в вертолетостроении для изменения направления передаваемого вращения, а спироидные передачи применяются в различном технологическом оборудовании. Коническая зубчатая передача предназначается для передачи вращения между пересекающимися валами, которые в большинстве машин и оборудования расположены в пространстве перпендикулярно друг другу.
Конические передачи в машиностроении применяются в виде:
- конического, или коническо – цилиндрического редуктора (см. Рис 2 ),
- специального редуктора встроенного в привод (см. Рис. 3, 4)
- передачи, встроенная в привод машины, или оборудования (см. Рис 5, 6, 7),
- дифференциальных механизмов
На Рис 4 показана конструкция распределительного редуктора тепловоза. Его назначение передача получаемой от дизеля мощности, нескольким агрегатам локомотива, для этого он содержит коническую и две цилиндрические передачи, конструкция которых обеспечивает расположение выходных валов, позволяющее соединить их с приводимыми агрегатами (они расположены соосно входным валам приводимых агрегатов). Мощность подводится к верхнему валу 1 редуктора (см. разрез А – А), которая двумя потоками через цилиндрические зубчатые передачи 2 – 3 и 5 – 6 передается нижнему валу 4 (см.
разрез А – А) и промежуточному валу 7 (см. разрез Б – Б), при этом на последнем закреплена коническая шестерня 8 зацепляющаяся с конической шестерней 9 установленной на выходном валу 10. Нижний вал 4, промежуточный вал 7 и выходной вал 10 передают мощность соответствующим агрегатам локомотива.
Примером встроенной конической передачи служит привод вспомогательных механизмов (механизма реза, механизма переноса, механизма выталкивания из матриц, механизма подачи) многопозиционного холодно – высадочного автомата, который осуществляется от соответствующих кулачков, расположенных на двух взаимно перпендикулярно расположенных валах, соединенных коническими передачами с круговым зубом (см. Рис.5)
Этот привод содержит промежуточный вал 4, получающий привод от коленчатого вала 1 через пару цилиндрических зубчатых колес 2, 3, при этом последнее установлена на промежуточном валу 5. Через пару конических зубчатых колес 6, 7 вращение передается трехопорному продольному (распределительному) валу 8, на котором расположен кулачки механизма реза и механизма переноса, а через пару конических зубчатых колес 9, 10, передающих вращение кулачковому валу 11, на котором установлены кулачки механизма выталкивания из матриц и эксцентрик привода валковой подачи и кулачок механизма переталкивания заготовки.
Все валы конических зубчатых передач установлены на подшипниках качения, которые посредствам букс расположенных в соответствующих расточках станины 12 автомата. Такая кинематическая связь вспомогательных механизмов автомата работающего в тяжелом динамичном режиме требует беззазорной установки конических зубчатых колес на валах, для чего используются клиновые шпоночные соединения, и точной расточки отверстий под установку валов в станине на подшипниках качения.
Конический дифференциальный механизм обеспечивает суммирование движения, что позволяет изменять скорость и направления движения выходного вала (валов), что широко используется в ведущих мостах транспортных средств и коробках зубообрабатывающих станков
На Рис 7 показана конструктивная схема конического дифференциала главной передачи автомобиля. Он состоит из гипоидного колеса 1, жестко связанного с корпусом дифференциала 2, сателлитов 3, шарнирно установленных в корпусе 2 на оси и полуосевых шестерен 4. При прямолинейном движении автомобиля по ровной дороге оба колеса зад-него моста проходят одинаковые пути, встречая одинаковое сопротивление движению и вращаются с одинаковой скоростью.
При этом корпус дифференциала 2, сателлиты 3 и полуосевые шестерни 4 вращаются как одно целое (см. Рис 7а). В этом случае сателлиты 3 не вращаются вокруг своих осей, заклинивают полуосевые шестерни 4 и на оба колеса передается одинаковый крутящий момент. При повороте автомобиля внутреннее по отношению к центру колесо, вращается медленнее и вместе с ним замедляет свое вращение соответствующая полуосевая шестерня 4. При этом сателлиты 3 начинают вращаться во-круг своей оси в корпусе 2 и ускоряют вращение полуосевой шестерни 4 наружного колеса (см. Рис 7б). В результате колеса автомобиля начинают вращаться с разными скоростями, что необходимо при движении на повороте.
На Рис 8 показана конструкция редуктора заднего моста автомобиля, который выполнен на основе конического дифференциала. Он содержит расположенный в корпусе 2 на подшипниках 2 и 3 ведущий вал – шестрню 4 с установленной на нем полумуфтой 5, при этом его конический зубчатый венец 6 зацепляется с ведомым коническим зубчатым колесом, состоящим из венца 7, и установленной на подшипниках 10 в корпусе 1, сборной ступицей 8, две части которой соединены болтами 9.
В ступице 8, являющейся водилом Н конического дифференциала, установлена крестовина 11 с сателлитами 12, а в горизонтальной расточке ступицы 8 установлены центральные шестерни 13(а) и 13(b), шлицевые отверстия которых соединены с ответными концами полуосей 14, соединенных со ступицами ведущих колес автомобиля.
При движении автомобиля вращение сообщается ведущему валу – шестерне 4 редуктора заднего моста, который вращаясь в подшипниках 2 и 3 передает его коническому зубчатому колесу 3, ступица которого являющаяся водилом Н сообщает вращение центральным зубчатым колесам a и b конического дифференциала, посредствам конических шестерен – сателлитов 12. При этом центральные зубчатые колеса а и b посредствам полуосей 14 вращают ведущие колеса автомобиля. В таком дифференциальном редукторе угловые скорости вращения водила Н и центральных зубчатых колес связаны следующей зависимостью: wH = 0,5(wa+ wb) Если автомобиль движется по прямолинейному участку дороги то скорости обоих его колес одинаковы, поэтому выполняется равенство wa = wb = w В этом случае все звенья вращаются как одно целое.
При различных скоростях вращения колес, например при повороте автомобиля, выполняется неравенство: wa не равно wb, тогда центральные колеса а и b начинают вращаться относительно водила с разной скоростью. При остановке одного из колес автомобиля , например при развороте на месте, (скорость колеса b равна нулю) скорость второго колеса а будет в два раза больше скорости водила Н т. е. wa = 2wH Если оба колеса на касаются грунта, например задний мост автомобиля поддомкрачен то колеса будут вращаться в противоположные стороны, при этом w_a = -wb.
Помимо автомобилей конические дифференциалы применяются в станках, прежде всего зубообрабатыващих и различных приборах в частности в сканирующих устройствах. На Рис 9 показана конструкция дифференциала зубофрезерного станка 5К324. Он содержит, кинематически связанный с гитарой деления, вал 1 с коническим колесом 4, установленный на шарикоподшипниках в корпусе 7, который имеет возможность врашаться от червячной передачи 2, 3 и несет на себе вал – водило 5 с сателлитом 10, а также вал 9 выполненный за одно целое с коническим колесом 6 и соединенный посредствам конического колеса 8 с продолжением цепи обката станка.
В данном случае дифференциал используется для суммирования двух движений вала 1, получающего привод от гитары деления и червячной передачи, что необходимо при некоторых вариантах нарезания зубчатых колес.
2 Геометрические параметры конической передачи
2.1 Конические зубчатые передачи с прямыми зубьями
Расчет геометрических параметров конических передач с прямыми зубьями выполняется в соответствии с ГОСТ 19624-74. Исходный контур конического зубчатого зацепления определен ГОСТ13754-81 (для конических передач с прямым зубом при среднем окружном модуле m выше 1 мм ГОСТ предусматривает следующие параметры исходного контура: угол зацепления α = 20 град, коэффициент головки зуба h_ = 1, коэффициент радиального зазора c = 0,2.
Основными геометрическими параметрами конической зубчатой передачи с прямым зубом согласно ГОСТ 19624 – 74 (см.
Рис. 10) являются следующие:
Минимальное число зубьев конической шестерни выбираются, согласно рекомендаций ГОСТ 13754-68, приведенных в таб.1
Таблица 1
Для выполнения чертежа конического зубчатого колеса необходимо рассчитать его конструктивные размеры В, С, М (см. Рис 11).
В данном разделе статьи приводится информация по коническим передачам с круговым зубом, а также гипоидным и спироидным коническим передачам
3 Рекомендации по проектированию основных
элементов конической передачи
Работоспособность конической передачи обеспечивается величиной бокового зазора и пятна контакта в зацеплении, а для подшипников величиной осевого зазора и перекоса колец. Эти параметры обязательно указывается в технических требованиях сборочного чертежа и обеспечивается при сборке передачи (см.
раздел 6.2). Кроме того на работу конической передачи оказывает существенное влияние конструктивное исполнение его основных элементов, подшипниковых опор и валов в сборе с зубчатыми колесами, на которое оказывает влияние нагруженность передачи ее габариты и передаточное отношение колес.
Ведущая коническая шестерня в передаче чаще всего выполняется в виде вала – шестерни (см. Рис 5, 8), реже в виде отдельной детали (см. Рис 2а, б, г), а зубчатые колеса ввиду их значительно большего диаметра по сравнению с валом, на котором они устанав-ливаются, как правило, изготавливаются в виде отдельной детали (см. Рис 2а, б, г, Рис 8).
При конструировании подшипниковых опор валов конических зубчатых колес необходимо учитывать величину радиальных и осевых нагрузок имеющих место при работе передачи, а также расположение входного и выходного вала редуктора. На Рис 15 показаны варианты конструктивного исполнения ведущего вала конического редуктора в сборе с опорными подшипниками.
В данном разделе полной версии статьи даются рекомендации по применению конструкции ведущих валов конической передачи, варианты которой показаны на Рис 15, а также рекомендации по выбору материала и термообработки конических зубчатых колес
4 Допуски на геометрические параметры конических зубчатых колес
Допуски на геометрические параметры конических зубчатых колес назначаются в соответствии с ГОСТ 1758-81, который устанавливает 12 степеней точности.
В зависимости от степени точности передачи нормируются показатели кинематической точности, плавности работы и нормы контакта зубьев в передаче. Степень точности передачи выбирается в зависимости от ее назначения (силовая или кинематическая). Для предварительного выбора степени точности можно пользоваться рекомендациями приведенными в таб.4
Боковой зазор в конической зубчатой передаче jn обеспечивается за счет уменьшения толщины зуба колеса и шестерни путем дополнительного смещения исходного контура или другими словами зуборезного инструмента при нарезании зубьев. Боковой зазор в передаче jn необходим для компенсации температурных изменений в передаче при ее работе jn1, для обеспечения нормальных условий смазывания – jn2 для компенсации погрешности изготовления и сборки деталей входящих в передачу – jn3. Таким образом, минимальная величина бокового зазора в зубчатой передаче равна:
Величина бокового зазора , необходимого для компенсации температурных изменений в зубчатой передаче при ее работе определяют по следующей формуле:
Величина бокового зазора jn2, обеспечивающая нормальные условия смазывания, зависит от способа смазывания и окружной скорости передачи.
Ориентировочно, эта вели-чина составляет в микронах от 10m для тихоходных передач до 30m для быстроходных передач (V =15 м/сек). Величина бокового зазора jn3 необходимая для компенсации погрешности изготовления и сборки деталей входящих в передачу (зубчатые колеса, валы, подшипники, корпус) и упрощенно может быть рассчитана по следующей формуле:
В точных конических передачах, для которых необходимо установить минимальный боковой зазор, его величина рассчитывается по следующей формуле:
После выполнения расчета минимальной величины бокового зазора в передачи по ГОСТ 1758-81 выбирается наиболее близкий вид сопряжения.
Для конических передач отсчетных механизмов нормируется величина мертвого хода, при этом минимальная величина бокового зазора jmin определяется по следующей формуле:
После выполнения расчета минимальной величины бокового зазора в передаче по ГОСТ 1758-81 выбирается наиболее близкий вид сопряжения.
Таким образом, точность изготовления зубчатого колеса задается степенью точности, а требования к боковом зазору – видом сопряжения. Независимо от степени точности зубчатой передачи, ГОСТ 1758-81 устанавливает шесть видов сопряжения зубчатых колес A, B, C, D, E, H (см. Рис.16). Например, обозначение 7 – С ГОСТ 1758-81 соответствует зубчатому колесу 7(й) степени точности и виду сопряжения С. Требования по величине и допуску бокового зазора в зубчатой передаче указываются в таблице, которой сопровождается чертеж зубчатого колеса, требования по оформлению которой определены ГОСТ 2.405-75.
Для контроля величины утонения зубьев конического зубчатого колеса, которое обеспечивается при его нарезании, используется толщина зуба по постоянной хорде Sce, замер которой производится на определенной высоте зуба hce.
Для обеспечения нормальной работы конических зубчатых колес их рабочие и базовые поверхности должны быть выполнены с определенной шераховатостью.
Требования к шераховатости поверхностей конических зубчатых колес с m ≥ 1, установленные ГОСТ 2789-73 и ГОСТ 2.309-73, приведены в таб. 5.
Для конических зубчатых колес 6 – 9 степени точности в качестве показателей кинематической точности рекомендуется использовать: допуск на биение зубчатого венца Fr, в качестве показателя плавности работы – предельное отклонение шага fpt, в качестве показателя контакта зубьев – предельное отклонение межосевого расстояния fa. Все эти показатели, являющиеся параметрами для контроля зубчатого колеса и вместе с его основными показателями и справочными данными в соответствии с требованием ГОСТ 2.405-75, при оформлении чертежа колеса заносятся в таблицу (см. Рис 17)
Помимо перечисленных требований, которые в основном относятся к точности зубчатого венца колеса, необходимо назначить следующие требования по точности к его базовым размерам и поверхностям:
посадку базового отверстия D зубчатого колеса,
– допуск Δ на внешний диаметр вершин зубьев D1
– допуск Δ на расстояние L от базового торца до вершины делительного конуса,
– допуск Δ на смещение l от внешнего диаметра вершин зубьев до базового торца колеса,
– допуск Δ на угол α при вершине внешнего конуса колеса,
– допуск Δ на угол β дополнительного конуса,
– допуск Δ на длину ступицы B1,
– биение конусной поверхности заготовки колеса относительно отверстии D,
– биение торца ступицы колеса относительно базового отверстия D,
Посадка базового отверстия колеса D назначается по H6 – H8 в зависимости от степени точности передачи и условий ее работы, аналогично посадке цилиндрического зубчатого колеса.
Допуск Δ на внешний диаметр вершин зубьев колеса D1 назначается по h20 – h21. Допуск Δ на расстояние L от базового торца до вершины делительного конуса устанавливается по h21. Допуска Δ на расстояние l от внешнего диаметра вершин зубьев до базового торца, согласно рекомендациями работы [2], назначается по таб. 6 в зависимости от степени точности передачи и внешнего окружного модуля.
Допуск Δ на угол α при вершине внешнего конуса колеса, согласно рекомендациями работы [2], назначается в зависимости от степени точности передачи по табл. 7
Таблица 7
При назначении допуска Δ на угол β дополнительного конуса, используются данные таб. 7, которые увеличиваются на ± 15 град.
Допуск на длину ступицы B1 устанавливается по h21 и уточняется при расчете размерной цепи Г, показанной (см. Рис 32). Биение конусной поверхности заготовки колеса рассчитывается по следующей формуле:
Где Fr, радиальное биение зубчатого венца колеса, назначаемое согласно ГОСТ 1785 – 81, в зависимости от степени точности передачи. Биение торца ступицы колеса, рассчитывается согласно рекомендаций работы [1] по следующей формуле:
Погрешности формы базового отверстия колеса D назначается, согласно рекомендаций при веденных в таб.8 заимствованной из работы [6]
Таблица 8
В данном разделе полной версии статьи даются рекомендации по оформлению чертежей основных деталей конический передачи: вала – шестерни, конического зубчатого колеса, стакана , корпуса конического редуктора, а также конического зубчатого колеса с круговым зубом с указанием требований по точности обеспечивающих работоспособность передачи (см.
таб)
5. Прочностной расчет зубчатых колес конической передачи
Прочностной расчет конических зубчатых колес ведется по ГОСТ 21354-86 по среднему сечению, находящемуся на середине длины зуба. При этом конические колеса заменяют цилиндрическими, их диаметр начальной окружности и модуль равны диаметру начальной окружности и модулю в среднем сечении зуба конических колес, а профиль зуба соответствует профилю приведенных колес, полученных разверткой дополнительного конуса на плоскость. Расчет ведется по шестерне.
Для определения работоспособности проектируемой зубчатой передачи выполняется ее расчет на сопротивление усталости (контактную выносливость) активных поверхностей зубьев, на сопротивление усталости зубьев при изгибе (выносливость при изгибе),
Расчет передачи на сопротивление усталости (на контактную выносливость) ак-тивных поверхностей выполняется по следующей формуле:
Расчет зубьев передачи на сопротивление усталости при изгибе (на выносливость при изгибе) выполняется по следующей формуле:
6 Основы технологии изготовления основных деталей
и сборки конических передач
6.
1 Технология изготовления конических зубчатых колес
Технология изготовления конических зубчатых колес, также как и цилиндрических зависит от размеров, материала и термообработки (твердости) и геометрической формы колеса, от его степени точности, вида заготовки и масштабов производства. Для выполнения при изготовлении требований по точности параметров заложенных в чертеже конического зубчатого колеса необходимо в заготовке иметь надежные технологические базы, которые должны быть заложены в чертеже с учетом необходимых требований по их форме и взаимному расположению. Оптимальным вариантом выбора технологических баз для нарезания зубьев конического колеса является их совмещение с поверхностями на которые эта деталь устанавливается при сборке редуктора. Нарезание зубьев прямозубых и косозубых конических зубчатых колес с твердостью поверхности HB до 350 осуществляется зубостроганием по методу обката, зубостроганием по методу копирования, а также зубофрезерованием с использованием дисковых и пальцевых модульных фрез.
Конические зубчатые колеса с круговым зубом, а также гипоидные и спироидные нарезаются зуборезными головками. Зубчатые колеса с твердостью поверхности РRC боглее 35 и высокой степени точности после предварительной нарезки зубьев подвергаются зубошлифовке.
6.2 Сборка конических зубчатых передач
Общая сборка конического редуктора выполняется в следующей последовательности (см. таб). В полной версии статьи приводится описание сборочных переходов.
Для обеспечения при сборке передачи правильного сопряжения конических зубчатых колес (предельного осевого смещения зубчатого венца колеса и шестерни fAM) вал – шестерню и вал зубчатого колеса перемещают в осевом направлении. Величина осевого перемещения зависит от величины требуемого осевого зазора в передаче и определяется по следующей формуле: X = jn/(2sinа• cosф ) ;
Где:
– X, величина осевого смещения вала при регулировке
осевого зазора,
– jn, боковой зазор в передаче установленный в технических требованиях сборочного чертежа передачи,
– а, угол зацепления,
– ф, угол начального конуса перемещаемого в осевом направлении колеса или шестерни.
В полной версии статьи приводится описание операции контроля бокового зазора в конической передачи, рекомендации по обеспечению требуемого пятна контакта и размерные цепи определяющие собираемость конической передачи (см. таб)
7 Применение конических передач в приводах
различных механизмов
Конические передачи, в отличии от цилиндрических, обычно, используются для передачи вращения между приводными валами, которые расположены под углом к друг другу (см. Рис. 5, на котором показан привод вспомогательных механизмов холодно – высадочного автомата), причем угол взаимного расположения кинематически соединяемых валов может быть отличным от 90 град (см. Рис. 2в, на котором показан промежуточный редуктор вертолета), при этом, их передаточное отношение, обычно бывает, не более 3 – 4 (см. Рис. 8), а в отдельных случаях может достигать 7. Однако в ряде случаев применение специальных конструкций конических передач, в том числе совмещенных с другими видами передачи и механизмов, позволяет решать сложные задачи на проектирование, создавая комбинированные механизмы и агрегаты с совершенно новыми свойства- ми.
Рассмотрим такие конструкции.
На Рис 33 показана конструкция конических передач встроенных в колесный узел управляемого ведущего моста трактора. Он содержит жестко соединенный с рукавом 3 ведущего моста корпус 1 верхнего редуктора и корпус 2 нижнего редуктора, установленный на опорах 4 и 5 с возможностью поворота в расточке корпуса 1. В полости рукава 3 на подшипниках 8 установлены полуось 7 выполненный за одно целое с конической шестерней 6, а на подшипниках 11 установлен вертикальный вал 10, выполненный за одно целое с конической шестерней 9, которая находится в зацеплении шестерней 6. Шлицевый хвостовик 12 вала 10 соединен с конической шестерней 13, установленной в расточке корпуса 2 на подшипниках 14, которая зацепляется с коническим зубчатым колесом 15, закрепленным посредствам шлицевого соединения на цапфе16 диска 17, на котором устанавливается колесо трактора. Зубчатое колесо 15 закрыто крышкой 18 закрепленной на корпусе 2. Верхняя подшипниковая опора 4 состоит из подшипника 19, наружное кольцо которого установлено в стакане 20, расположенном в расточке корпуса 1, при этом, во внутреннем кольце подшипника 19 находится ось 21, установленная через регулировочные прокладки 23 в отверстии кронштейна 24 и закрепленная в нем с помощью болтов 22, а кронштейн 24 установлен на корпусе 2 посредствам призонных болтов 26.
Нижняя подшипниковая опора 5 выполнена на основе подшипника 25 наружное кольцо которого установлено в расточке корпуса 2, а в его внутреннее кольцо запрессована нижняя цапфа корпуса 1.
Работает колесный узел следующим образом. При движении трактора через полуось 7 крутящий момент передается ведущей шестерне 6 верхнего редуктора, которая зацепляясь с ведомой шестерней 9, передает его вертикальному валу 10, который будучи соединен посредствам шлицевого соединения с шестерней 13 нижнего редуктора сообщает крутящий момент ведомому коническому зубчатому колесу 15, приводящему через шлицевое соединение на цапфе 16 диска 17 колесо трактора. При необходимости свершения трактором поворота корпус 2 нижнего редуктора получая движение от отдельного привода (на Рис 33 этот привод не показан) поворачивается о подшипниковых опорах 4 и 5, продолжая в это время передавать вращение колесу трактора через встроенные конические передачи рассмотренные ранее.
В данном разделе полной версии статьи содержится 15 примеров
конструктивного исполнения конических зубчатых
передач и редукторов (см.
таб.)
ЛИТЕРАТУРА
1. Анухин В.И. Допуски и посадки. Питер 2008г.
2. Георгиев А. Н. Передачи спироидные с цилиндрическим червяком М.. Машиностроение 1977г
3. Дмитриев В. А. Детали машин Судостроение Ленинград 1970г
4. Дунаев П. Ф., Леликов О. П. Расчет допусков размеров. М.: Машиностроение 2001г
5. Игнатьев Н. П. Основы проектирования. Учебное пособие Азов 2011г.
6. Игнатьев Н. П. Обеспечение точности при проектировании приводов и механизмов. Справочно – методическое пособие. Азов 2012г.
7. Игнатьев Н. П. Проектирование сборочной оснастки и оборудования. Справочно – методическое пособие. Азов 2014г
8. Метрологический контроль конструкторской документации. Методические
рекомендации НИИМАШ. Москва 1976г.
9. Писмак К. М. Гипоидные передачи М.: Машиностроение 1964г
В полной версии статьи, включающей 48 страниц и 47 чертежей
Для приобретения полной версии статьи добавьте её в корзину.
Поставщик метрических конических шестерен
Метрические конические шестерни
KHK USA – Поставщик метрических конических шестерен премиум-класса
Посмотреть каталог метрических конических шестеренЧто такое коническая шестерня?
Коническое зубчатое колесо, имеющее конус в качестве делительной поверхности с зубьями, прорезанными вдоль его поверхности, называется коническим зубчатым колесом. Два вала, пересекающиеся друг с другом в одной точке, называются пересекающимися валами. Конические зубчатые колеса относятся к этому типу зубчатых колес с пересекающимися валами, которые используются для передачи вращательного движения между ними. Угол пересечения может быть любым, но обычно это прямой угол. Общий КПД конических зубчатых колес составляет около 9от 8 до 99%.
Типы конических зубчатых колес
Прямые конические зубчатые колеса
Когда зуб находится вдоль образующей конуса (перпендикулярная линия, соединяющая вершину с окружностью основания), такое зубчатое колесо называется прямым коническим зубчатым колесом.
Прямые конические шестерни относительно легко изготовить, и они имеют простую форму.
Спиральные конические шестерни
Это коническая шестерня с изогнутой формой зуба. По сравнению с прямыми коническими зубчатыми колесами они имеют большую контактную поверхность, что обеспечивает более плавное и менее шумное вращение. Они подходят для высокоскоростных операций с большой нагрузкой, но производственный процесс более сложен. Кроме того, искривление формы зуба создает осевую нагрузку , которая требует внимания. Спиральные конические зубчатые колеса классифицируются по методу нарезания зубьев и форме зубьев на форму Клингельнберга (Германия) и форму Глисона (США), но форма Глисона в настоящее время является основной.
Угловые зубчатые колеса
Пара зубчатых колес с одинаковым количеством зубьев, передающих движение между двумя прямоугольными валами, называются угловыми зубчатыми колесами. Они часто используются для изменения направления вращения, не влияя на скорость.
Угловые шестерни также бывают с прямыми и спиральными зубьями. Существуют также специальные угловые зубчатые колеса с углами вала, отличными от 90 градусов.
Гипоидные шестерни
Гипоидные шестерни иногда используются в автомобильных задних приводах и имеют коническую форму. Их можно рассматривать как разновидность спирально-конических зубчатых колес. Однако, поскольку вал-шестерня смещен от большого вала-шестерни, они классифицируются как шестерни с непересекающимися валами.
Зубчатые колеса Zerol
Конические зубчатые колеса Zerol представляют собой спирально-конические зубчатые колеса с почти нулевым углом наклона спирали и могут рассматриваться как прямые конические зубчатые колеса с изогнутыми зубьями. Они имеют характеристики как прямых, так и спиральных конических зубчатых колес. Осевая нагрузка, возникающая в зубчатых колесах Zerol, такая же, как и в прямозубых конических зубчатых колесах, поэтому прямозубые конические зубчатые колеса можно заменить на зубчатые колеса Zerol без изменения конструкции подшипника.
Конические шестерни категории
Стандартные конические зубчатые колеса KHK доступны в двух типах, со спиральными и прямыми зубьями, с передаточными числами от 1,5 до 5, и предлагаются с большим разнообразием модулей, количества зубьев, материалов и стилей.
Гипоидные шестерни с высоким передаточным числом (MPH)
Высокое передаточное отношение, высокая эффективность, высокая жесткость и компактность в сборе.
Купить Гипоидные шестерни с высоким передаточным числом (MPH)
Шлифованные спирально-конические зубчатые колеса (MBSG)
Высокопрочные, износостойкие и компактные для использования при высоких скоростях и крутящем моменте.
Купить Шлифованные конические зубчатые колеса (MBSG)
Шлифованные спирально-конические зубчатые колеса (SBSG)
Недорогое шлифованное зубчатое колесо, но поддающееся механической обработке, за исключением зубьев шестерни.
Купить Шлифованные конические зубчатые колеса (SBSG)
Спирально-конические зубчатые колеса с обработанным отверстием (MBSA – MBSB)
Готовы к использованию без выполнения дополнительных операций. Прочный и устойчивый к истиранию.
Купить Спирально-конические зубчатые колеса с обработанным отверстием (MBSA – MBSB)
Спирально-конические шестерни (SBS)
Большие номера зубьев и модулей предлагаются в этих доступных спиральных конических зубчатых колесах.
Купить Спирально-конические шестерни (SBS)
Конические зубчатые колеса Ground Zerol (SBZG)
Спиральные конические зубчатые колеса с углом наклона винтовой линии менее 10°. Воспринимает силы с одинаковых направлений. Прямые конические зубчатые…
Купить Конические зубчатые колеса Ground Zerol (SBZG)
Стальные конические шестерни (SB)
Популярная серия прямых конических шестерен для многих применений.
Купить Стальные конические шестерни (SB)
Конические шестерни и валы-шестерни (SBY)
Популярная серия прямых конических шестерен для многих применений.
Купить Конические шестерни и валы-шестерни (SBY)
Конические шестерни из нержавеющей стали (SUB)
Подходит для пищевого оборудования благодаря коррозионно-стойкому качеству SUS303.
Купить Конические шестерни из нержавеющей стали (SUB)
Пластиковые конические шестерни (PB)
Изделия из нейлона MC легкие и могут использоваться без смазки.
Купить Пластиковые конические шестерни (PB)
Литые конические зубчатые колеса (DB)
Литые, серийно выпускаемые, подходящие для офисных машин.
Купить Литые конические шестерни (DB)
Конические зубчатые колеса Nissei KSP (тип F)
Превосходные характеристики в отношении высокой скорости, низкого уровня шума и низкой вибрации.
Купить Спирально-конические шестерни Nissei KSP Ground (тип F)
Конические зубчатые колеса Nissei KSP (тип U)
Превосходные характеристики в отношении высокой скорости, низкого уровня шума и вибрации.
Купить Конические шестерни Nissei KSP Ground Spiral (тип U)
КОНИЧЕСКИЕ ЗУБЧАТЫЕ ШЕСТЕРНИ – ЗАПАС КГ
Конические зубчатые колеса чаще всего используются для передачи мощности под прямым углом 90°. Оси двух валов конических шестерен пересекаются, а поверхности зубчатых подшипников самих шестерен имеют коническую форму. Конические шестерни чаще всего устанавливаются на валах, разнесенных на 90 градусов. Конические зубчатые колеса обычно делятся на 2 типа: прямозубые конические зубчатые колеса и спирально-конические зубчатые колеса.
Прямые конические шестерни
В прямозубых конических шестернях зубья прямые и параллельны образующим делительного конуса.
По сравнению со спиральными угловыми зубчатыми колесами прямозубые конические зубчатые колеса могут быть меньшего размера. Мы стандартизировали прямозубые конические шестерни с модулем 0,5 из различных материалов.
Спиральные конические шестерни
Спиральные конические шестерни имеют зубья, образованные вдоль спиральных линий. Они чем-то аналогичны косозубым шестерням цилиндрического типа в том, что зубья расположены под углом; однако у спиральных шестерен зубья также изогнуты. Спиральные конические шестерни имеют преимущество в прочности, вибрации и уровне шума по сравнению с прямозубыми коническими шестернями. Недостатком спирально-конических зубчатых колес является то, что они создают осевую осевую нагрузку. Поэтому для их сборки требуется правильное расположение подшипников и прочная опора. Наши стандартные спиральные конические шестерни имеют передаточные числа 1:5, 1, 2:1 и 3:1.
Проектирование конических зубчатых колес – 3D-модели САПР и 2D-чертежи
Теперь вы можете проверить размеры наших стандартных конических зубчатых колес в нашем каталоге в формате PDF или в нашем средстве выбора зубчатых колес, предоставленном Part Community.
Бесплатные данные САПР доступны на веб-сайте. Нажмите на логотип ниже, чтобы получить доступ к селектору Mitre Gear.
Предложение по стандартным коническим зубчатым колесам
Пожалуйста, запросите расценки на наши конические зубчатые колеса через нашу страницу «Запрос предложения».
Модификация конического зубчатого колеса
Мы можем настроить наши стандартные конические зубчатые колеса в соответствии с вашими конкретными приложениями. Пожалуйста, проконсультируйтесь с нами. Предлагаем услуги по модификации редуктора. Пожалуйста, ознакомьтесь с подробностями и примерами модификаций на нашей странице «Модификация снаряжения».
Меры предосторожности при использовании
Пожалуйста, ознакомьтесь со следующими мерами предосторожности перед использованием наших конических зубчатых колес.
(PDF: «Меры предосторожности при использовании угловых и конических зубчатых колес» из нашего каталога)
| 304 КОНИЧЕСКИЕ ШЕСТЕРНИ ИЗ НЕРЖАВЕЮЩЕЙ СТАЛИ | ЛАТУННЫЕ КОНИЧЕСКИЕ ШЕСТЕРНИ | КОНИЧЕСКИЕ СТАЛЬНЫЕ ШЕСТЕРНИ |
| Материал (ISO) : SUS304 Модуль : 0,8 – 2,0 Соотношение : 2 : 1 JIS B 1704 класс 4 | Материал: C3604 Модуль: 0,5 – 2,0 Соотношение: 2:1 JIS B 1704 класс 4 | Материал (ISO) : C45 Модуль: 0,5 – 5,0 Соотношение: 2:1 JIS B 1704 класс 3 |
| Нержавеющая сталь SUS304 обладает лучшей коррозионной стойкостью, чем нержавеющая сталь 303. |
